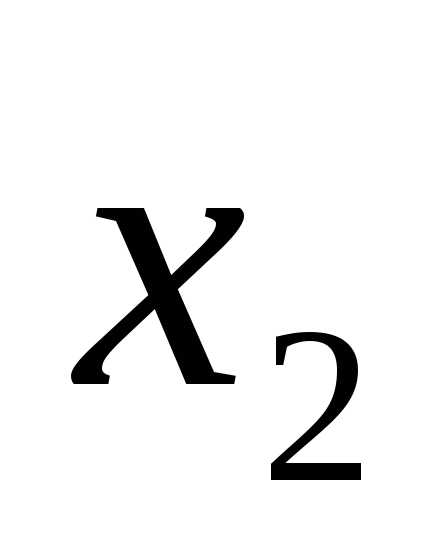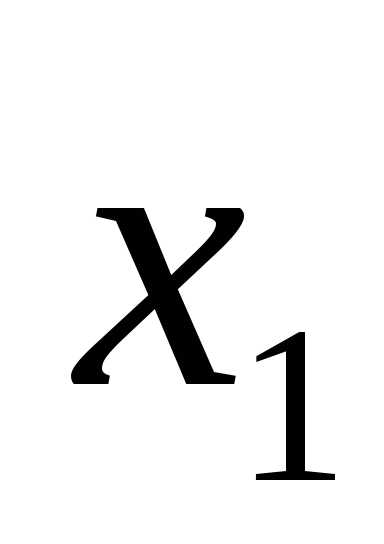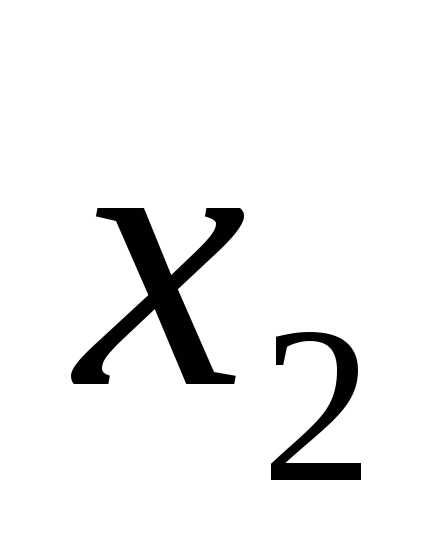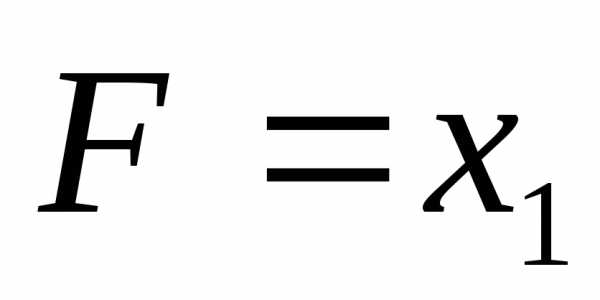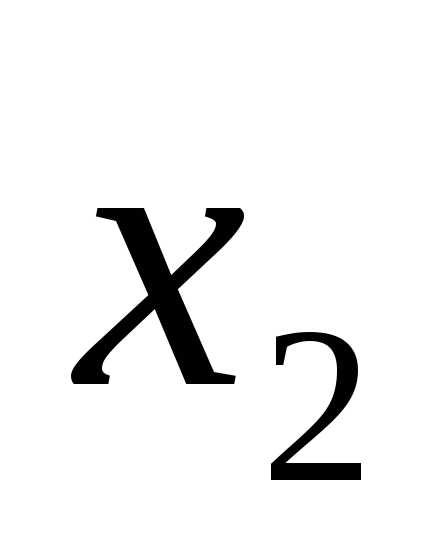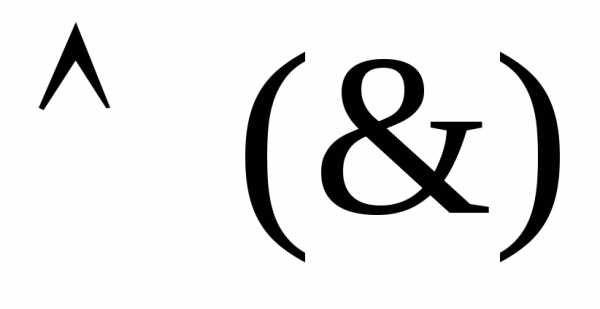Презентация на тему «Логические функции. Способы вычисления значений логических функций»
Ваша оценка презентации
Оцените презентацию по шкале от 1 до 5 баллов
Рецензии
Добавить свою рецензию
Аннотация к презентации
Посмотреть и скачать бесплатно презентацию по теме «Логические функции. Способы вычисления значений логических функций». pptCloud.ru — каталог презентаций для детей, школьников (уроков) и студентов.
Формат
pptx (powerpoint)
Количество слайдов
9
Слова
Конспект
Отсутствует
Содержание
- Слайд 1
Логические функции. Способы вычисления значений логических функций
- Слайд 3
2. Александра заполняла таблицу истинности для выражения F. Она успела заполнить лишь небольшой фрагмент таблицы:
- Слайд 8
Домашнее задание
Посмотреть все слайды
pptcloud.ru
Логические основы компьютера
Дидактический материал:1. Вычислить значение логической функции:
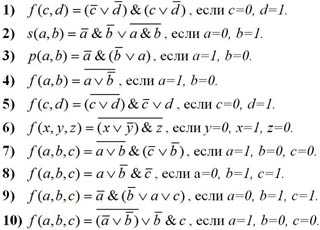
2. При заданных значениях переменных a=0, b=1, c=0. Определите истинные функции и расшифруй слово.
3. Определить истинные функции при заданных значениях переменных a=1, b=1, c=0, расшифруйте слово.
4. Задано значение функции от трех переменных. Найдите значение одной из переменных, если заданы значения двух других.
5. Построить таблицу истинности для логической функции.
6. Построить таблицу истинности для логической функции.
7. Упростить логическую функцию, используя законы булевой алгебры.
8. Упростить логическую функцию, используя законы булевой алгебры и составить таблицу истинности полученной функции.
9. По схеме составить логическую функцию и упростить полученное выражение. Построить таблицу истинности полученной функции.
10. Упростить логическую функцию, используя законы булевой алгебры, составить таблицу истинности и нарисовать схему.
11. По заданной функции составить таблицу истинности и нарисовать схему.
12. Для заданных логических функций необходимо проверить являются ли они эквивалентными.
13. Какой логический элемент необходимо добавить в схему, чтобы получить заданное значение функции при заданном значении переменных.
14. Определите функции, которые будут истинны, если истинны все три переменные. Расположи числа, соответствующие этим функциям, в порядке возрастания и прочитай фразу Козьмы Пруткова.
videouroki.net
Основные логические функции
Лабораторная работа №3Решение логических задач школьного курса повышенной сложности
Алгебра логики – раздел математической логики, изучающий высказывания, рассматриваемые со стороны их логических значений (истинности или ложности), и логические операции над ними. Алгебра логики возникла в середине 19 века в трудах Дж. Буля и развивалась затем в работах Ч. Пирса, П. С. Порецкого, Б. Рассела, Д. Гильберта и др. Создание алгебры логики представляло собой попытку решать традиционные логические задачи алгебраическими методами. С появлением теории множеств (70-е гг. 19 в.) и дальнейшим развитием математической логики (последняя четверть 19 в. — 1-я половина 20 в.), предмет алгебры логики значительно изменился. Основным предметом алгебры логики стали высказывания. Под высказыванием понимается каждое предложение, относительно которого имеет смысл утверждать, истинно оно или ложно. Примеры высказываний: «кит — животное», «все углы — прямые» и т.п. Первое из этих высказываний является, очевидно, истинным, а второе — ложным. Употребляемые в обычной речи логические связки «и», «или», «если…, то…», «эквивалентно», частица «не» и т. д. позволяют из уже заданных высказываний строить новые, более «сложные» высказывания. Истинность или ложность получаемых таким образом высказываний зависит от истинности и ложности исходных высказываний и соответствующей трактовки связок как операций над высказываниями.
В отличие от обычной алгебры, изучающей математические функции, алгебра логики изучает логические функции. Известно, что функция — это закон соответствия между переменными. Следовательно, логическая функция— это закон соответствия между логическими переменными.Логическая переменная— это такая переменная, которая может принимать одно из двух возможных значений: 0 («ложь») и 1 («истина»).
Логическим выражением называется выражение, о котором можно сказать истинно оно или ложно.
Примеры:
«5>8» — логическое выражение, т.к. о нем можно сказать, что оно ложно.
«Эту девочку зовут Юля» — логическое выражение.
«Подайте книгу» — это не логическое выражение, т.к. о нем нельзя сказать, истинно оно или ложно
Логическая функция может также принимать два значения.
Таким образом, логические переменные и функции определены на множестве двух значений — {0,1}.
ЭВМ строятся из компонентов с двумя устойчивыми состояниями. Одно состояние обозначается нулем, другое — единицей. На такие компоненты воздействуют двоичные сигналы. Под воздействием сигналов компоненты изменяют свои состояния, т. е. состояние компонентов или значения их выходных сигналов зависят от значений воздействующих сигналов. Очевидно, что функционирование компонентов ЭВМ следует описывать логическими функциями. По этой причине алгебра логики находит непосредственное и широкое применение при разработке и использовании средств электронной вычислительной техники.
Логические функции характеризуются (задаются) так называемыми таблицами истинности, или соответствия. Таблица истинности— это таблица, устанавливающая соответствие между возможными наборами значений логических переменных и значениями функций.
Функция отрицания
Отрицание – это логическая функция от одной переменной, которая принимает единичное значение при нулевом значении переменной и наоборот. Запись этой функции:
F=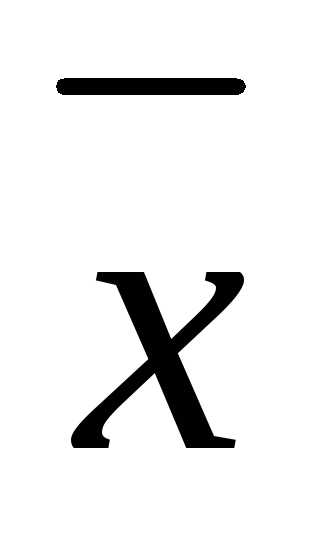 .
.
Конъюнкция может быть обозначена следующими символами:
¬,¯, не, not.
Черта над переменной xявляется признаком отрицания (инверсии). Таблица истинности этой функции представлена на рис. 1а. Функция логического отрицания описывает функционирование логического элемента НЕ (рис. 1б).
Условно-графическое обозначение элемента НЕ приведено на рис. 1в. Единичный сигнал на выходе элемента НЕ появляется при нулевом сигнале на входе (x=0,F=1) и, наоборот, нулевой сигнал на выходе появляется при единичном сигнале на входе (x=1,F=0). Графически отрицание можно представить с помощью кругов Эйлера (рис. 2).
а) б) в)
Рис. 1. Элемент НЕ
Рис. 2. Графическое представление отрицания на множестве
Функция логического умножения (конъюнкция)
Логическое умножение – это логическая функция, по крайней мере, от двух переменных, которая принимает единичное значение при единичных значениях всех переменных. Эта функция называется также конъюнкцией. Элементарная конъюнкция зависит от двух переменных. Она принимает единичное значение только тогда, когда и первая переменная и вторая переменная равны единице. Возможны различные варианты записи конъюнкции:
F=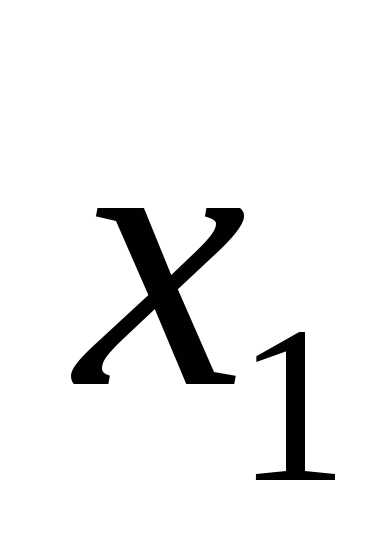
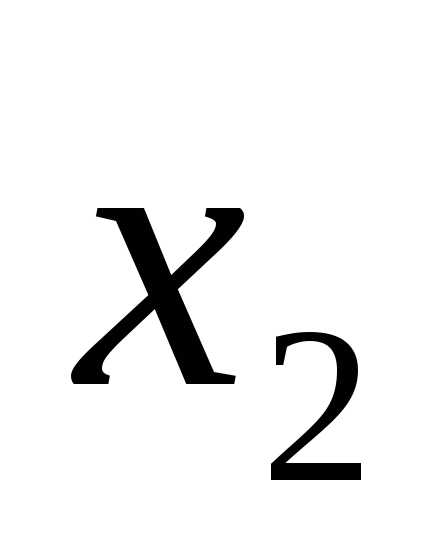 ;F=
;F=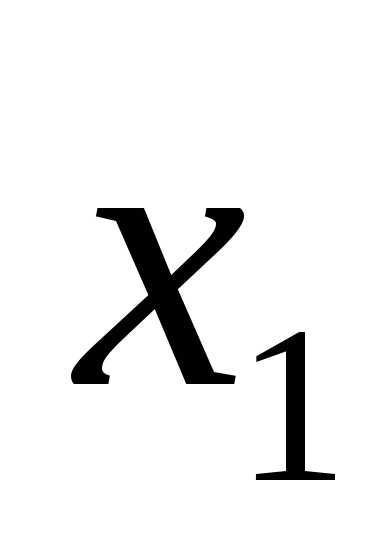 •
•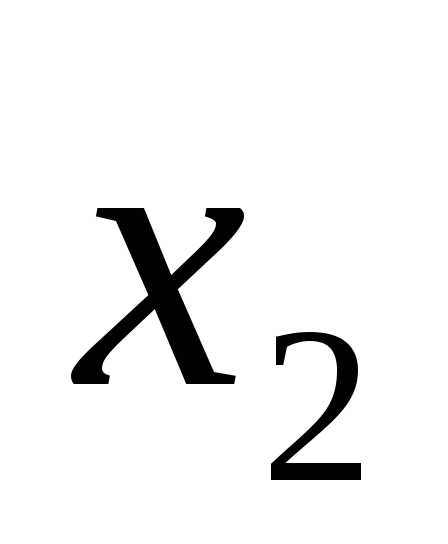 ;F=
;F=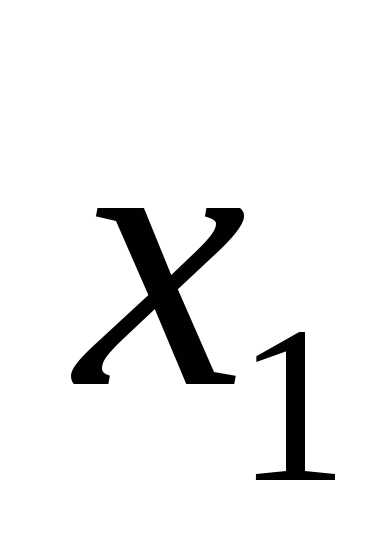
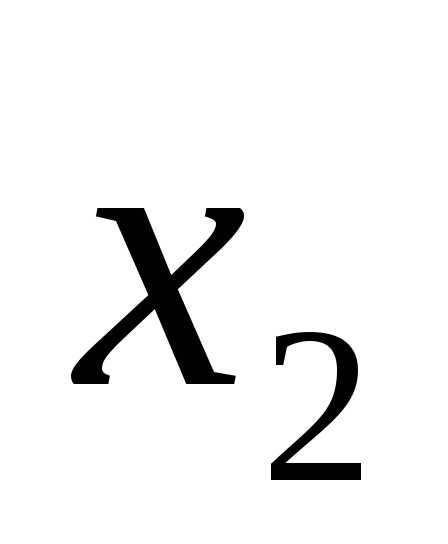 ;F=
;F=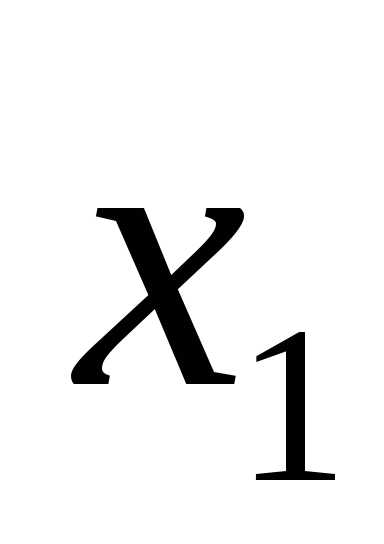 &
&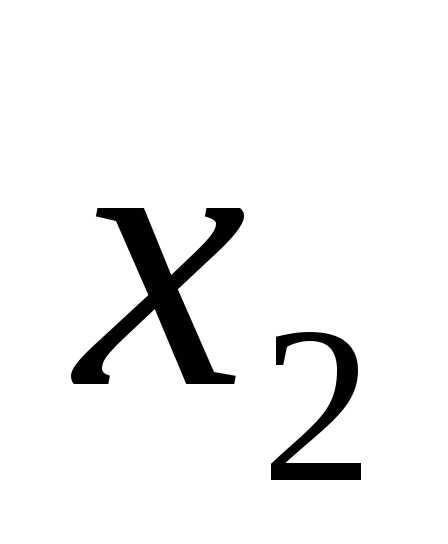 .
.
Конъюнкция может быть обозначена следующими символами:
, &, •, ∩, and, и.
Конъюнкция характеризуется таблицей истинности, представленной на рис. 3а. Из рассмотрения таблицы следует, что эта функция принимает единичное значение на наборе 4. Логическое умножение описывает работу элемента И (рис. 3б). Графически конъюнкцию можно представить с помощью кругов Эйлера (рис. 4).
а) б) в)
|
| F |
0 | 0 | 0 |
0 | 1 | |
1 | 0 | 0 |
1 | 1 | 1 |
Рис. 3. Элемент И
Рис. 4. Графическое представление конъюнкции на множествах
Конъюнкция на числовых множествах (операция пересечения): {a,b,c} {b,c,d,e}={b,c}.
Единичный сигнал появляется на выходе этого элемента только при наличии единичного сигнала и на входе 1, и на входе 2.
В общем случае элемент И может иметь n входов (рис. 3в). При этом он реализует конъюнкцию от n переменных, т.е.:
F=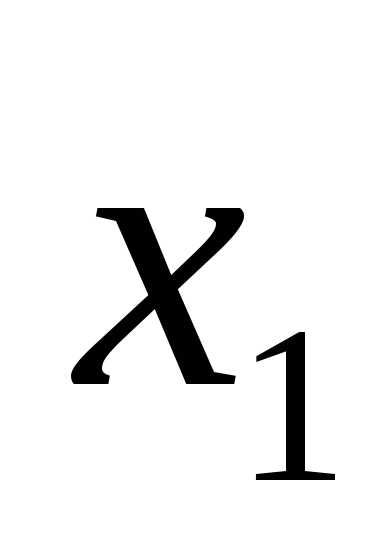 •
•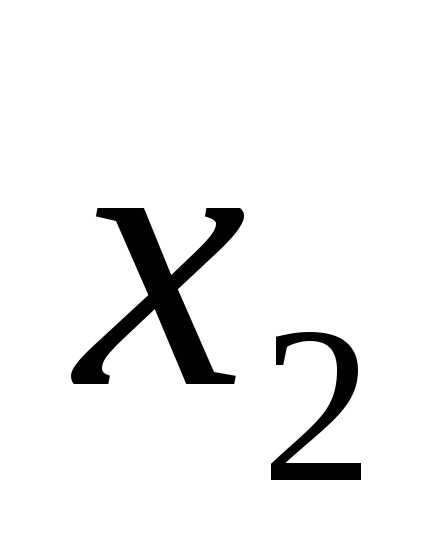 •
•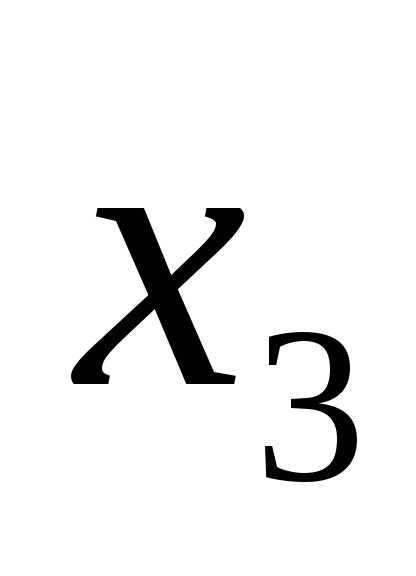 •…•
•…•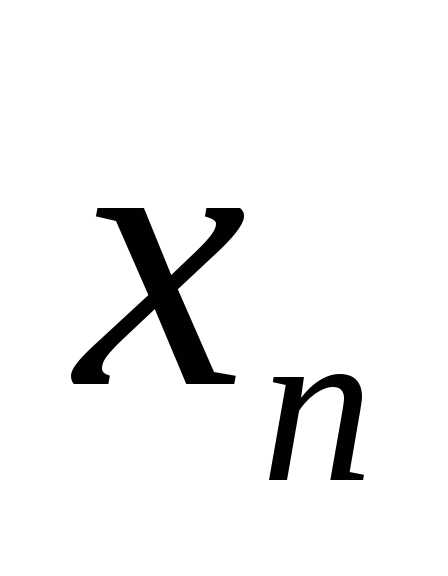 .
.
Функция логического сложения (дизъюнкция)
Логическое сложение – это логическая
функция, по крайней мере, от двух
переменных, которая принимает нулевое
значение при нулевых значениях всех
переменных. Эта функция называется
также дизъюнкцией. Таблица истинности
элементарной дизъюнкции представлена
на рис. 3а. Элементарная дизъюнкция
принимает единичное значение на наборах
1, 2, 3 и нулевое значение – только на
наборе 0. Функция записывается в одном
из двух видов: F=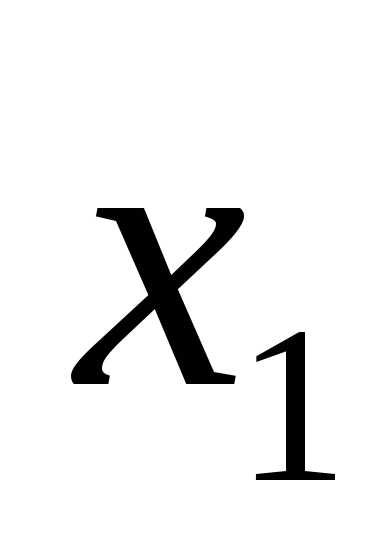
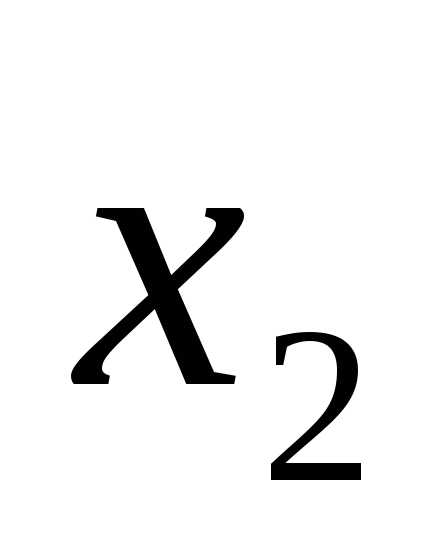 илиF=
илиF=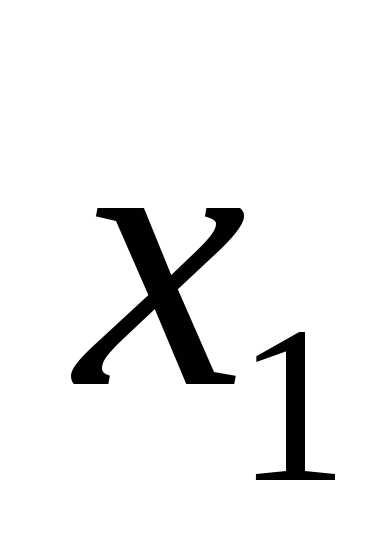 +
+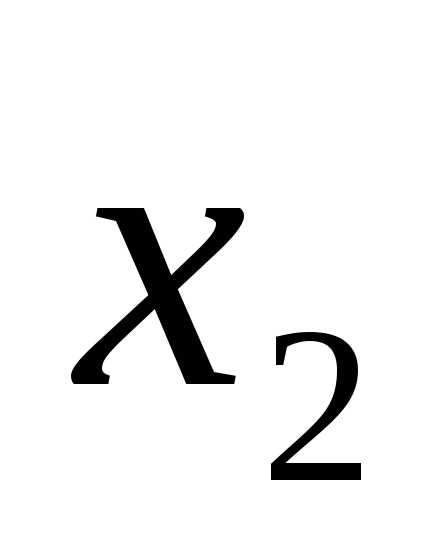 .
.
Знак «плюс» не является алгебраическим,
т.к. при 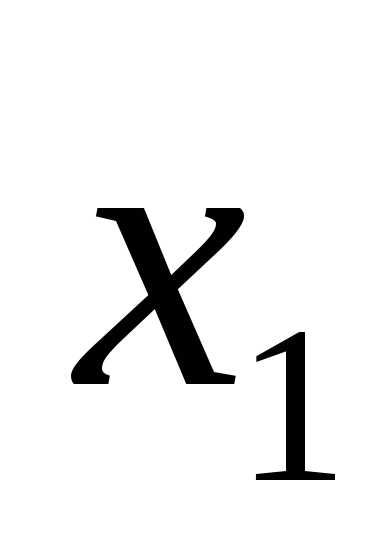 =1,
=1, 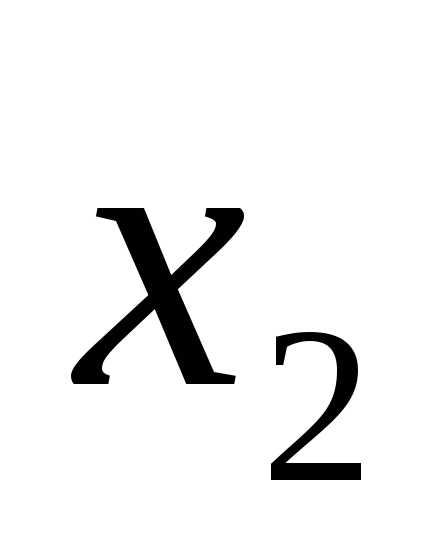 =1
дизъюнкцияF=
=1
дизъюнкцияF=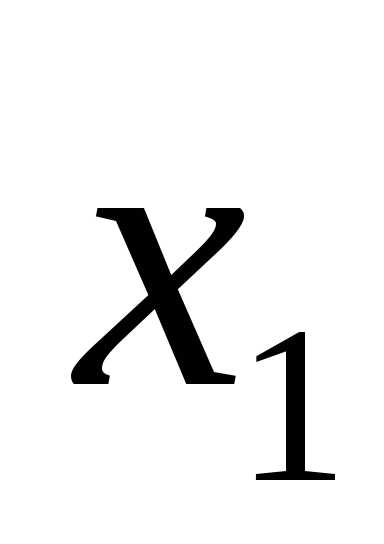 +
+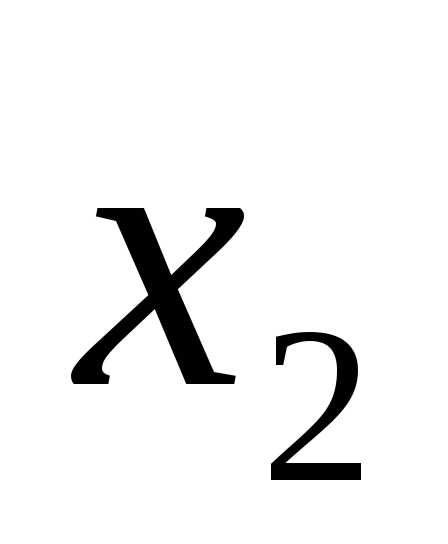 =1
=1
Дизъюнкция может быть обозначена следующими символами:
,
+, ,
or, или.
,
or, или.
Дизъюнкция описывает функционирование элемента ИЛИ (рис. 5б). Единичный сигнал на выходе этого элемента возникает тогда, когда или на входе 1, или на входе 2, или на двух входах единичные сигналы. И только в том случае, когда на оба входа поступают нулевые сигналы, на выходе элементов появляется нулевой сигнал.
В общем случае элемент ИЛИ может иметь n входов (рис. 5в). При этом он реализует дизъюнкцию от n переменных.
а) б) в)
|
| F |
0 | 0 | 0 |
0 | 1 | 1 |
1 | 0 | 1 |
1 | 1 | 1 |
Рис. 5. Элемент ИЛИ
Рис. 6. Графическое представление дизъюнкции на множествах
Дизъюнкция на числовых множествах (операция объединения): {a,b,c}{b,c,d,e}={a,b,c,d,e}.
Равнозначность (эквиваленция)
Равнозначность – это логическая функция от двух переменных, которая принимает единичное значение при одинаковых значениях переменных. Одинаковые по значению переменные называются равнозначными, поэтому функция носит название «равнозначность».
Запись функции:
F=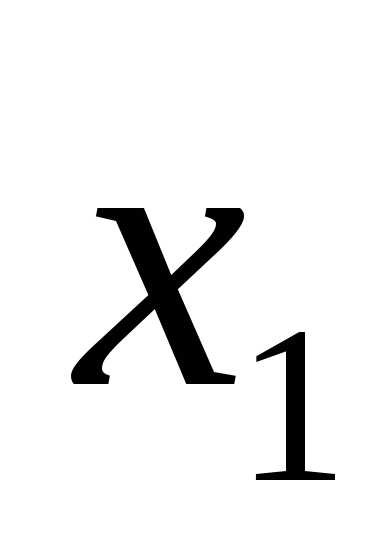
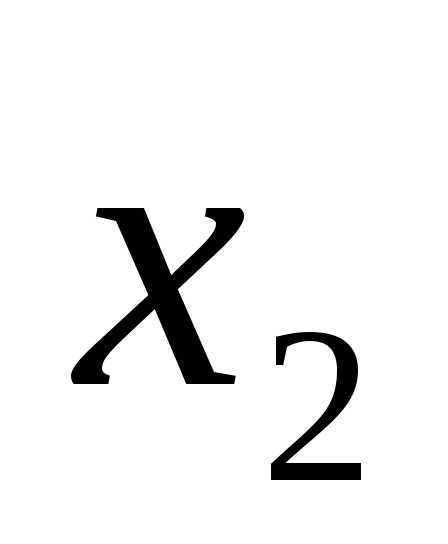 +
+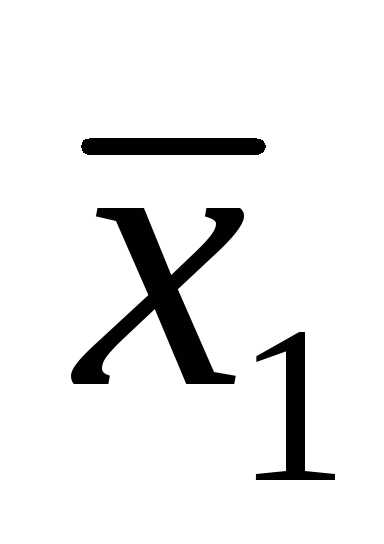
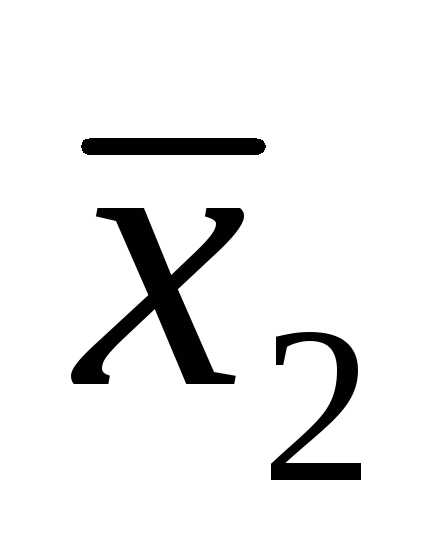 .
.
Таблица истинности функции равнозначности представлена на рис. 7а. Эта функция реализуется элементом равнозначности (сравнения), который показан на рис. 7б.
Эквиваленция может быть обозначена следующими символами:
~,
, ,
, .
.
Элемент используется для сравнения двоичных сигналов.
|
| F |
0 | 0 | 1 |
0 | 1 | 0 |
1 | 0 | 0 |
1 | 1 | 1 |
а) б)
Рис. 7. Элемент равнозначности
Логическое следование (импликация)
Обозначение логического следования:
F=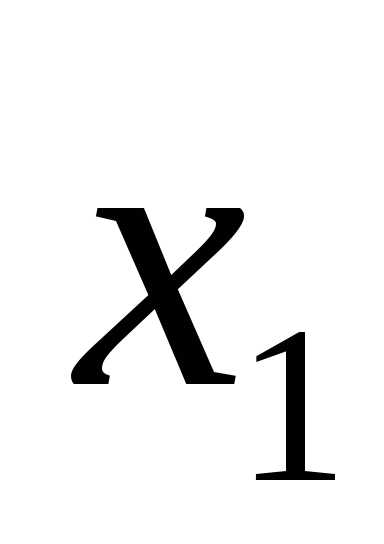 →
→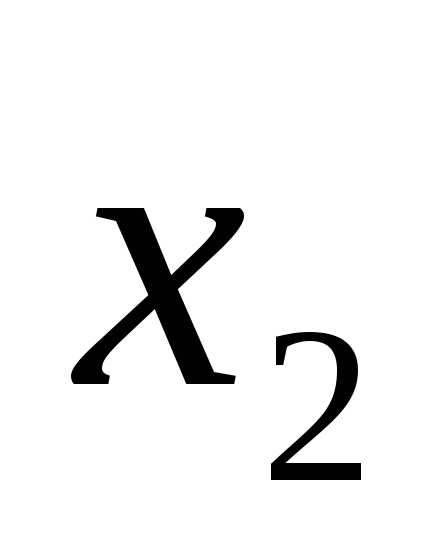 .
.
Высказывание F= →
→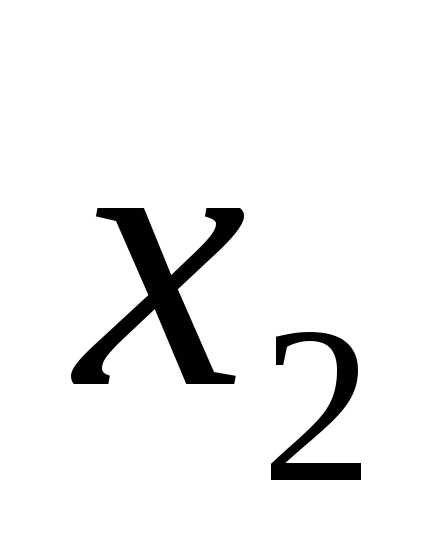 будем
считать истинным во всех случаях, кроме
случая, когда
будем
считать истинным во всех случаях, кроме
случая, когда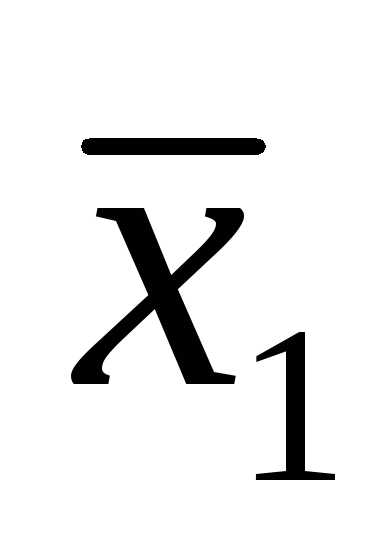 истинно, а
истинно, а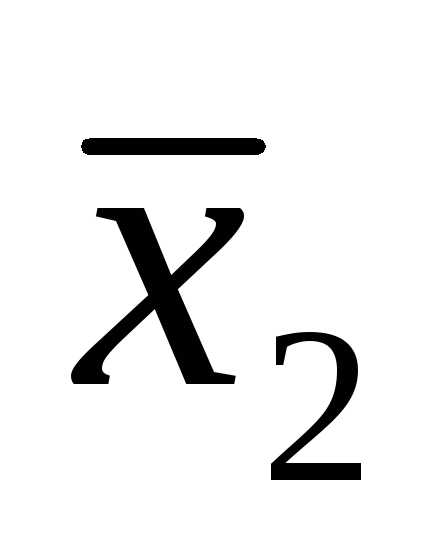 ложно. Таблица истинности представлена
на рис. 8.
ложно. Таблица истинности представлена
на рис. 8.
|
| F= |
0 | 0 | 1 |
0 | 1 | 0 |
1 | 0 | 0 |
1 | 1 | 1 |
Рис. 8. Элемент импликации
Импликация может быть обозначена следующими символами:→, ,.
Элемент (штрих) Шеффера
Обозначение:
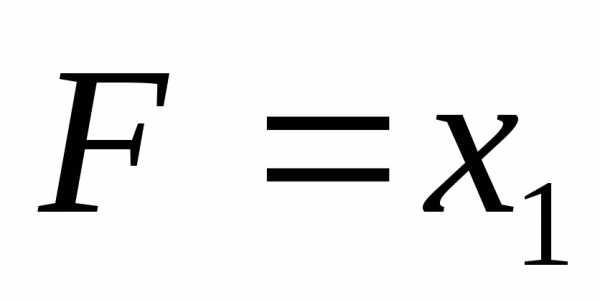
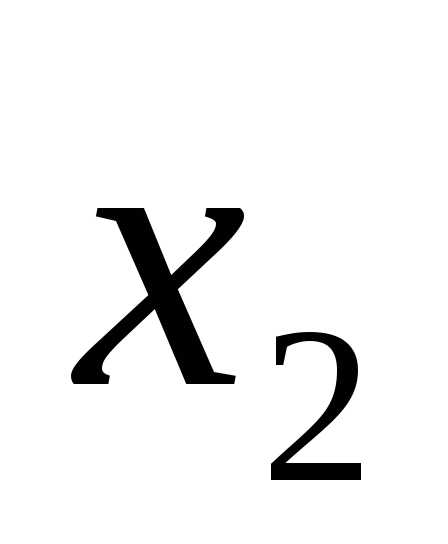 ;.
;.
Другое название этой функции: «И-НЕ».
Высказывание 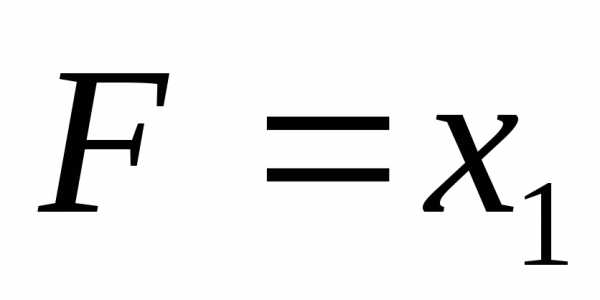
 будем считать ложным, когда
будем считать ложным, когда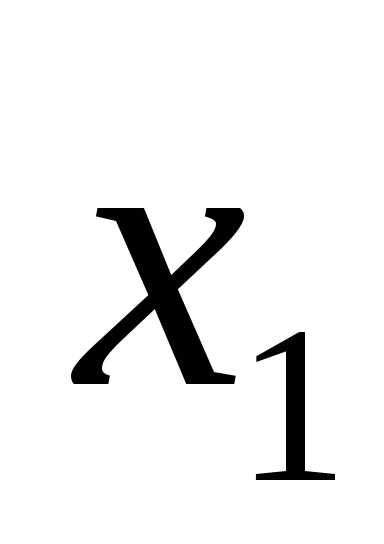 и
и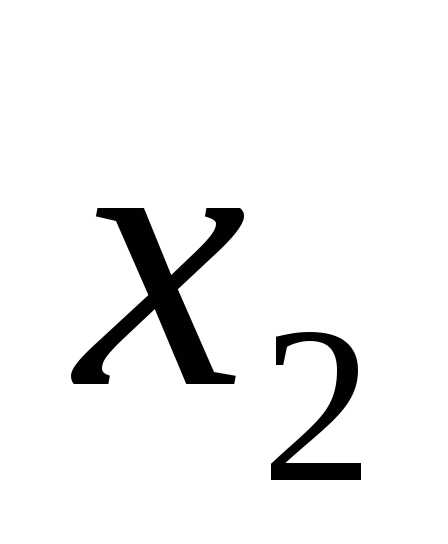 равны единице. Таблица истинности
представлена на рис. 9.
равны единице. Таблица истинности
представлена на рис. 9.
|
|
|
0 | 0 | 1 |
0 | 1 | 1 |
1 | 0 | 1 |
1 | 1 | 0 |
Рис. 9. Элемент (штрих) Шеффера
Элемент Вебба (стрелка Пирса)
Обозначение:
;.
Высказывание
будем считать истинным только тогда,
когда оба операнда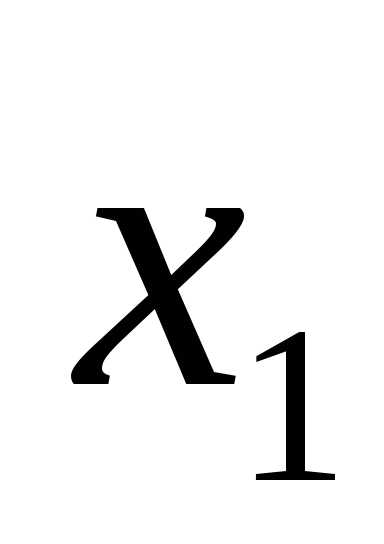 и
и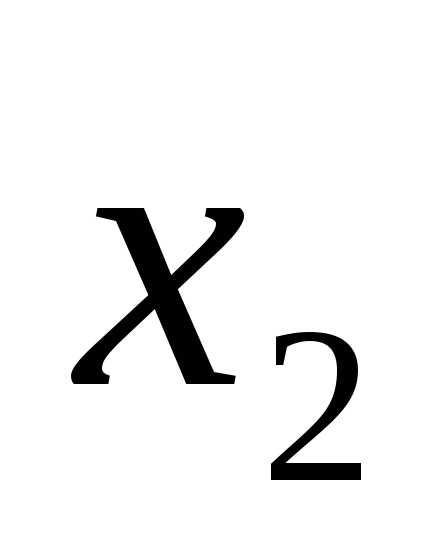 равны нулю. Таблица истинности представлена
на рис.10.
равны нулю. Таблица истинности представлена
на рис.10.
Другое название этой функции: «ИЛИ-НЕ».
Рис. 10. Элемент Вебба (стрелка Пирса)
Сложение по модулю 2.
Обозначение:
;;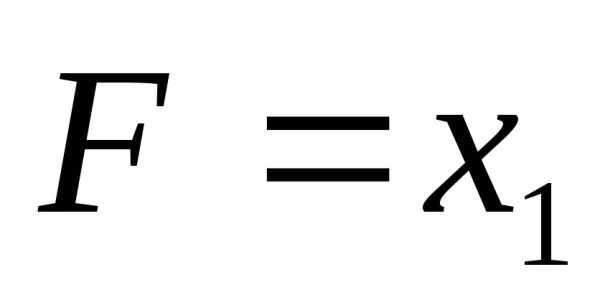 XOR
XOR 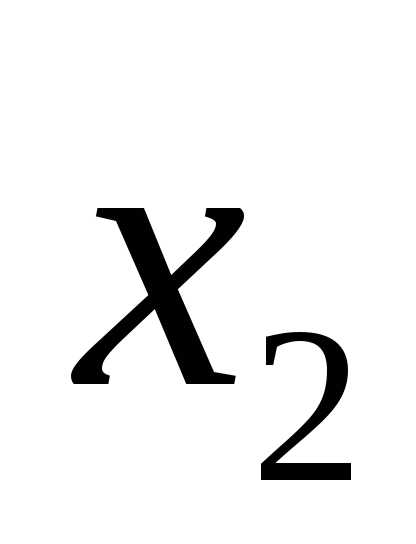 .
.
Высказывание
будем считать истинным, если первый
операнд не равен второму операнду
не равен второму операнду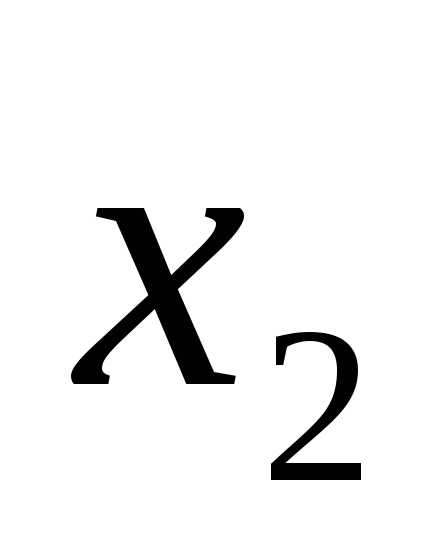 .
Таблица истинности представлена на
рис. 11.
.
Таблица истинности представлена на
рис. 11.
Другие названия этой функции: «исключающее ИЛИ», «логическое ЛИБО», «неравносильность», «неэквивалентность», «логическое сложение», «булево сложение».
Рис. 11. Сложение по модулю 2
Коимпликация
Обозначение:
; .
.
Высказывание
будем считать истинным, если первый
операнд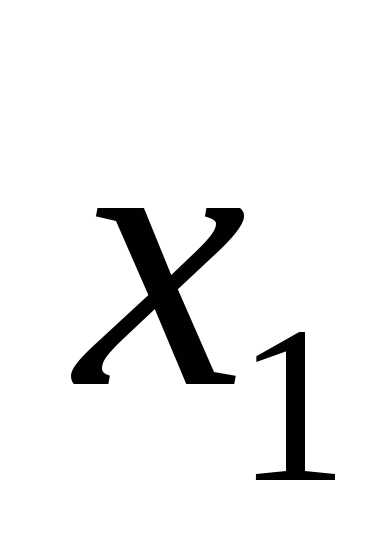 равен 1, а второй операнд
равен 1, а второй операнд 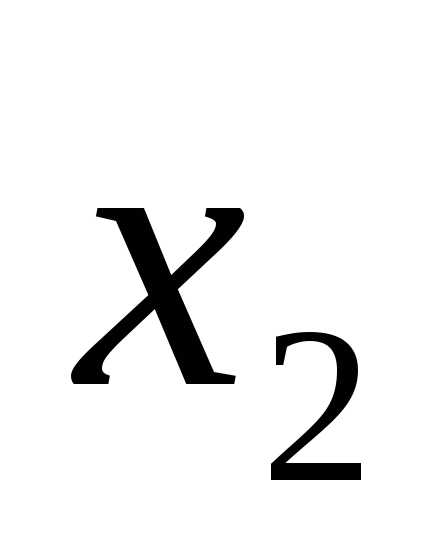 равен 0. Таблица истинности представлена
на рис. 12.
равен 0. Таблица истинности представлена
на рис. 12.
Рис. 12 Таблица истинности функции коимпликация
Приоритет операций в логическом выражении, не содержащем скобок:
Отрицание.
Конъюнкция, *, /, div,mod.
Дизъюнкция, +, -.
Операция отношения.
Для усиления операции используются скобки.
studfiles.net
Логические функции
Логические функции
Логическая переменная – это простое высказывание, содержащее только одну мысль. Ее символическое обозначение – латинская буква (A, B, X, Y, …). Значением логической переменной могут быть только константы ИСТИНА и ЛОЖЬ (1 и 0).
Логическая функция (составное высказывание) содержит несколько простых высказываний, соединенных между собой с помощью логических операций.
Логические операции – логическое действие.
Если логическую функцию выразить в виде формулы, в которую войдут логические переменные и знаки логических операций, то получится логическое выражение, значение которого можно вычислить. Значением логического выражения могут быть только ЛОЖЬ или ИСТИНА. При составлении логического выражения необходимо учитывать порядок выполнения логических операций, а именно: действия в скобках; инверсия; конъюнкция; дизъюнкция. В привычных символах — (…), НЕ(), И(), ИЛИ().
Решение логических выражений принято записывать в виде таблиц истинности – таблиц, в которых по действиям показано, какие значения принимает логическое выражение при всех возможных наборах его переменных.
Для составления таблицы необходимо определить:
количество строк в таблице (вычисляется как 2n, где n – количество переменных) + заголовок,
количество столбцов = количество переменных + количество логических операций,
последовательность выполнения логических операций.
Построить таблицу, указывая названия столбцов и возможные наборы значений исходных логических переменных.
Заполнить таблицу истинности по столбцам.
Пример 1
Построим таблицу истинности для выражения (A B) ( A B).
Количество строк = 22 (2-е переменные А и В) + 1(заголовок столбцов) = 5.
Количество столбцов = 2-е переменные (A, B) + 5 логических операций (, , , , ) = 7.
Расставим порядок выполнения операций: 1 5 2 4 3
(A B) ( A B)
Построим таблицу:
A | B | A B | A | B | A B | (A B) (A B) |
0 | 0 | 0 | 1 | 1 | 1 | 0 |
0 | 1 | 1 | 1 | 0 | 1 | 1 |
1 | 0 | 1 | 0 | 1 | 1 | 1 |
1 | 1 | 1 | 0 | 0 | 0 | 0 |
Пример 2
Построим таблицу истинности для логического выражения X Y Z.
Количество строк = 23 + 1 = 9.
Количество столбцов = 3-и логические переменные + 3-и логические операции = 6.
Порядок действий: 3 2 1
X Y Z.
Нарисуем и заполним таблицу.
X | Y | Z | Z | Y Z | X Y Z |
0 | 0 | 0 | 1 | 0 | 0 |
0 | 0 | 1 | 0 | 0 | 0 |
0 | 1 | 0 | 1 | 1 | 1 |
1 | 0 | 0 | 1 | 0 | 1 |
1 | 0 | 1 | 0 | 0 | 1 |
1 | 1 | 0 | 1 | 1 | 1 |
1 | 1 | 1 | 0 | 0 | 1 |
Логические формулы и функции в MS Excel
Пример 3. Введем в ячейку А1 формулу =7>5. Она вернет значение ИСТИНА. Скопируем содержимое A1 в А2 и исправим в А2 формулу: = 3>5. Эта формула вернет значение ЛОЖЬ. Правые части обеих формул представляют собой высказывания, т.е. утверждения, относительно которых можно заключить, верны они или нет. Арифметические формулы высказываниями не являются: они предписывают, как по исходным данным вычислить значение, и вопрос об их истинности или ложности не имеет смысла.
Операции сравнения
> | >= | < | <= | = | <> |
больше | больше или равно | меньше | меньше или равно | равно | не равно |
Обратите
внимание, что символ отношения «больше
или равно» изображается двумя знаками:
>
и =.
Причина в том, что на клавиатуре нет
знака 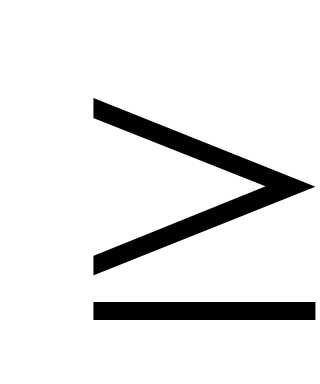 .
.
Имеются логические операции, которые позволяют строить сложные логические выражения. Эти операции реализованы в MS Excel как функции. Вот перечень логических операций и соответствующих им функций MS Excel, расположенных в порядке убывания приоритета.
Название | Обозначение | Функция MS Excel | Арифметический оператор |
Скобки | (…) | (…) | (…) |
Отрицание |
| НЕ | — унарный минус |
Конъюнкция |
| И | * — умножение |
Дизъюнкция |
| ИЛИ | + — сложение |
Здесь можно провести аналогию с арифметическими операторами: отрицанию соответствует унарный минус, конъюнкции — умножение, дизъюнкции — сложение. На самом деле в MS Excel приоритет логических операций не имеет значения, так как они реализованы в виде функций.
У логических функций аргументы могут принимать только два значения: ИСТИНА и ЛОЖЬ. Поэтому логические функции можно задать таблицей истинности, где перечислены все возможные значения аргументов и соответствующие им значения функций.
Таблица для функции НЕ имеет вид.
х | НЕ(x) |
ЛОЖЬ | ИСТИНА |
ИСТИНА | ЛОЖЬ |
Таблица для функций И и ИЛИ имеет вид.
x | y | И(x,y) | ИЛИ(x,y) |
ЛОЖЬ | ЛОЖЬ | ЛОЖЬ | ЛОЖЬ |
ЛОЖЬ | ИСТИНА | ЛОЖЬ | ИСТИНА |
ИСТИНА | ЛОЖЬ | ЛОЖЬ | ИСТИНА |
ИСТИНА | ИСТИНА | ИСТИНА | ИСТИНА |
Функция НЕ может иметь только один аргумент, а функции И и ИЛИ могут иметь два и более аргументов.
Пример 4. В ячейке А6 (с именем z) записано число. Выяснить, принадлежит ли оно отрезку [2, 5].
Решение. Присвоим ячейке А6 имя z. Введем в А6 число 3. Сначала сконструируем логическое выражение, решающее задачу. Для того чтобы z принадлежал отрезку [2, 5], нужно, чтобы одновременно были истинны два условия: x >= 2 и z <= 5.
((z >= 2) и (z <= 5)) В ячейке В6 разместим формулу =И(z>=2;z<=5). В В6 получим значение ИСТИНА.
Пример 5. В ячейке А6 (с именем z) записано число. Выяснить, при надлежит ли оно одному из лучей на числовой оси: (-, 2) или (5, ).
Для того чтобы z принадлежал хотя бы одному из лучей, нужно, чтобы был истинным хотя бы одно из условий: (z < 2) или (z > 5). В ячейке D6 разместим формулу =ИЛИ(z<2;z>5). А6 содержит число 3 поэтому формула возвращает ЛОЖЬ.
На приведенных примерах можно убедиться, что в логических выражениях число 1 ведет себя как ИСТИНА, а число 0 как ЛОЖЬ.
5
studfiles.net
Таблицы истинности, с формулами и примерами
Они могут принимать значения «истина» или «ложь» (1 или 0). Для функции, содержащей две переменные, наборов значений переменных всего четыре:
Значения логических функций определяются с помощью таблица истинности.
Таблицы истинности для основных двоичных логических функций
1. Конъюнкция (логическое умножение) – сложное логическое выражение, которое является истинным только в том случае, когда истинны оба входящих в него простых выражения.
Обозначение:
2. Дизъюнкция (логическое сложение) – это сложное логическое выражение, которое истинно, если хотя бы одно из простых логических выражений истинно и ложно, если оба простых логических выражения ложны.
Обозначение:
3. Импликация (логическое следствие) – это сложное логическое выражение, которое является ложным тогда и только тогда, когда условие истинно, а следствие ложно.
Обозначение:
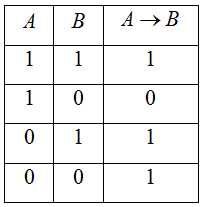
4. Эквиваленция – это сложное логическое высказывание, которое является истинным только при одинаковых значениях истинности простых выражений, входящих в него.
Обозначение:
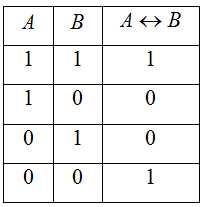
5. Логическое отрицание (инверсия) делает истинное высказывание ложным и, наоборот, ложное – истинным.
Обозначение:
6. Штрих Шеффера – операция, отрицающая конъюнкцию, т.е. значение ложно тогда и только тогда, когда оба простых выражения истинны.
Обозначение:
7. Стрелка Пирса – операция, отрицающая конъюнкцию, т.е. значение истинно тогда и только тогда, когда оба простых выражения ложны.
Обозначение:
Порядок выполнения логических операций
При построении таблицы истинности необходимо учитывать порядок выполнения логических операций:
- Инверсия
- Конъюнкция
- Дизъюнкция
- Импликация
- Эквиваленция
- Штрих Шеффера
- Стрелка Пирса
Для последних двух операций приоритет не определен.
Замечание. Если необходимо изменить указанный порядок выполнения логических операций используются скобки.
Примеры решения задач
ru.solverbook.com
Логические выражения и логическая таблица истинности. Правила построения
Логические выражения и таблица истинности
Примеры задач с решениями по этой теме Пройти тестирование по теме Контрольная по теме
Таблица истинности – таблица, показывающая, какие значения принимает составное высказывание при всех сочетаниях (наборах) значений входящих в него простых высказываний.
Логическое выражение – составные высказывания в виде формулы.
Равносильные логические выражения – логические выражения, у которых последние столбцы таблиц истинности совпадают. Для обозначения равносильности используется знак «=».
Алгоритм построения таблицы истинности:
1. подсчитать количество переменных n в логическом выражении;
2. определить число строк в таблице по формуле m=2n, где n – количество переменных;
3. подсчитать количество логических операций в формуле;
4. установить последовательность выполнения логических операций с учетом скобок и приоритетов;
5. определить количество столбцов: число переменных + число операций;
6. выписать наборы входных переменных;
7. провести заполнение таблицы истинности по столбцам, выполняя логические операции в соответствии с установленной в пункте 4 последовательностью.
Заполнение таблицы:
1. разделить колонку значений первой переменной пополам и заполнить верхнюю часть «0», а нижнюю «1»;
2. разделить колонку значений второй переменной на четыре части и заполнить каждую четверть чередующимися группами «0» и «1», начиная с группы «0»;
3. продолжать деление колонок значений последующих переменных на 8, 16 и т.д. частей и заполнение их группами «0» или «1» до тех пор, пока группы «0» и «1» не будут состоять из одного символа.
Пример 1. Для формулы A/\ (B \/ ¬B /\¬C) постройте таблицу истинности.
Количество логических переменных 3, следовательно, количество строк – 23 = 8.
Количество логических операций в формуле 5, количество логических переменных 3, следовательно количество столбцов – 3 + 5 = 8.
Пример 2. Определите истинность логического выражения F(А, В) = (А\/ В)/\(¬А\/¬В) .
1. В выражении две переменные А и В (n=2).
2. mстрок=2n, m=22=4 строки.
3. В формуле 5 логических операций.
4. Расставляем порядок действий
1) А\/ В; 2) ¬А; 3) ¬В; 4) ¬А\/¬В; 5) (А\/ В)/\(¬А\/¬В).
5. Кстолбцов=n+5=2+5=7 столбцов.
А | В | А\/ В | ¬А | ¬В | ¬А\/¬В | F |
0 | 0 | 0 | 1 | 1 | 1 | 0 |
0 | 1 | 1 | 1 | 0 | 1 | 1 |
1 | 0 | 1 | 0 | 1 | 1 | 1 |
1 | 1 | 1 | 0 | 0 | 0 | 0 |
Вывод: логическое выражение принимает значение истина при наборах F(0,1)=1 и F(1,0)=1.
Пример 3. Построёте таблицу истинности для логического выражения
F = (A\/ B) /\ ¬С
- В данной функции три логические переменные – А, В, С
- количество строк таблицы = 23 =8
- В формуле 3 логические операции.
- Расставляем порядок действий
1) А\/ В; 2) ¬С; 3) (AVB) /\ ¬С .
- количество столбцов таблицы = 3 + 3 = 6
А | В | С | A\/B | ¬С | (A\/B) /\ ¬С |
0 | 0 | 0 | 0 | 1 | 0 |
0 | 0 | 1 | 0 | 0 | 0 |
0 | 1 | 0 | 1 | 1 | 1 |
0 | 1 | 1 | 1 | 0 | 0 |
1 | 0 | 0 | 1 | 1 | 1 |
1 | 0 | 1 | 1 | 0 | 0 |
1 | 1 | 0 | 1 | 1 | 1 |
1 | 1 | 1 | 1 | 0 | 0 |
Пример 4. Определите истинность формулы: F = ((С \/В) => В) /\ (А /\ В) => В.
Построим таблицу истинности этой формулы.
Ответ: формула является тождественно истинной.
Пример 5. Символом F обозначено одно из указанных ниже логических выражений от трех аргументов: X, Y, Z.
Дан фрагмент таблицы истинности выражения F:
X | Y | Z | F |
0 | 0 | 0 | 1 |
0 | 0 | 1 | 0 |
0 | 1 | 0 | 1 |
Какое выражение соответствует F?
1) ¬X/\¬Y/\Z 2) ¬X\/¬Y\/Z 3) X\/Y\/¬Z 4) X\/Y\/Z
Решение (вариант 1, через таблицы истинности):
Чтобы решить данную задачу можно построить часть таблицы истинности для каждой из четырех функций, заданных в ответе для заданных наборов входных переменных, и сравнить полученные таблицы с исходной:
X | Y | Z | F | ¬X | ¬Y | ¬Z | ¬X/\¬Y/\Z | ¬X\/¬Y\/Z | X\/Y\/¬Z | X\/Y\/Z |
0 | 0 | 0 | 1 | 1 | 1 | 1 | 0 | 1 | 1 | 0 |
0 | 0 | 1 | 0 | 1 | 1 | 0 | 1 | 1 | 0 | 1 |
0 | 1 | 0 | 1 | 1 | 0 | 1 | 0 | 1 | 1 | 1 |
Очевидно, что значения заданной функции F совпадают со значениями выражения X\/Y\/¬Z. Следовательно, правильный ответ – 3.
Ответ: 3
Решение (Вариант 2):
Чтобы не строить таблицу истинности для каждого выражения, можно просто перепроверить предложенные ответы по заданной таблице истинности. Т.е. в каждую из четырех предложенных функций последовательно подставлять значения переменных X, Y и Z, из заданной таблицы истинности и вычислять значения логического выражения. Если значения вычисляемого выражения совпадут со значением F во всех трех строчках заданной таблицы, то это и есть искомое выражение.
Рассмотрим данный конкретный пример:
1) первое заданное выражение ¬X/\¬Y/\Z = 0 при X=0, Y=0, Z=0, что не соответствует первой строке таблицы;
2) второе заданное выражение ¬X\/¬Y\/Z = 1 при X=0, Y=0, Z=1, что не соответствует второй строке таблицы;
3) третье выражение X\/Y\/¬Z соответствует F при всех предложенных комбинациях X,Y и Z;
4) четвертое выражение X\/Y\/Z = 1 при X=0, Y=0, Z=1, что не соответствует второй строке таблицы.
Ответ: 3
mir-logiki.ru
Логические функции в Excel — НА ПРИМЕРАХ
В данной статье мы разберем сущность логических функций Excel: И, ИЛИ, ИСКЛИЛИ и НЕ. И разберем примеры решения логических функций, демонстрирующие их применение в MS Excel.
Вы узнаете, как расширить использование логических операторов и создать логические проверки для выполнения более сложных вычислений и более эффективного анализа данных. Логические функции, такие как И, ИЛИ, ИСКЛИЛИ и НЕ, помогут вам в этом.
Логические функции Excel – обзор
Microsoft Excel предоставляет четыре логические функции для работы с логическими значениями: И, ИЛИ, ИСКЛИЛИ и НЕ. Если вы хотите выполнить более одного сравнения в своей формуле или проверить несколько условий вместо одного, используете эти логические функции. Как и логические операторы, логические функции Excel возвращают значения ИСТИНА или ЛОЖЬ.
В следующей таблице приведено краткое описание того, что делает каждая логическая функция.
Логическая функция | Описание | Пример формулы | Описание формулы |
И | Возвращает значение ИСТИНА, если все аргументы имеют значение ИСТИНА | =И(A2>=10; B2<5) | Формула возвращает значение ИСТИНА, если значение в ячейке A2 больше или равно 10, а значение в B2 меньше 5, ЛОЖЬ — в противном случае. |
ИЛИ | Возвращает значение ИСТИНА, если хотя бы один аргумент имеет значение ИСТИНА | =ИЛИ(A2>=10; B2<5) | Формула возвращает ИСТИНА, если A2 больше или равно 10 или B2 меньше 5 или оба условия выполнены. Если ни одно из условий не выполнено формула возвращает ЛОЖЬ. |
ИСКЛИЛИ | Возвращает логическое исключающее ИЛИ всех аргументов | =ИСКЛИЛИ(A2>=10; B2<5) | Формула возвращает ИСТИНА, если A2 больше или равно 10 или B2 меньше 5. Если ни одно из условий не выполняется или оба условия не выполнены, формула возвращает ЛОЖЬ. |
НЕ | Меняет логическое значение своего аргумента на противоположное | =НЕ(A2>=10) | Формула возвращает ЛОЖЬ, если значение в ячейке A1 больше или равно 10; ИСТИНА в противном случае. |
В дополнение к четырем логическим функциям, описанным выше, Microsoft Excel предоставляет 3 условные функции: ЕСЛИ, ЕСЛИОШИБКА и ЕСНД.
Логическая функция И в Excel
Функция И наиболее популярна из логических функций. Она пригодится, когда вам нужно проверить несколько условий и убедиться, что все они выполнены. Технически, логическая функция И проверяет условия, которые вы указываете, и возвращает ИСТИНА, если в результате вычисления всех аргументов получается значение ИСТИНА, ЛОЖЬ в противном случае.
Синтаксис логической функции И выглядит следующим образом:
=И(логическое_значение1; [логическое_значение2] …)
Теперь давайте рассмотрим некоторые примеры формул, демонстрирующие, как использовать логическую функцию И в формулах Excel.
Формула | Описание |
=И(A2=»Яблоки»; B2>C2) | Логическая функция возвращает ИСТИНА, если A2 содержит «Яблоки», а B2 больше C2, ЛОЖЬ в противном случае. |
=И(B2>50; B2=C2) | Логическая функция возвращает ИСТИНА, если B2 больше 50, а B2 равно C2, ЛОЖЬ в противном случае. |
=И(A2=»Яблоки»; B2>=120; B2>C2) | Логическая функция возвращает ИСТИНА, если A2 содержит «Яблоки», B2 больше или равно 120, а B2 больше C2, ЛОЖЬ в противном случае. |
Логические функции в Excel – Использование логической функции И
Логическая функция ИЛИ в Excel
Как логическая функция И, функция Excel ИЛИ является базовой логической функцией, которая используется для сравнения двух значений или операторов. Разница в том, что логическая функция ИЛИ возвращает ИСТИНА, если хотя бы один, если аргументы оцениваются как ИСТИНА, и возвращает ЛОЖЬ, если все аргументы ЛОЖЬ. Логическая функция ИЛИ доступна во всех версиях MS Excel.
Синтаксис логической функции Excel ИЛИ очень похож на функцию И:
=ИЛИ(логическое_значение1; [логическое_значение2];…)
Теперь, давайте запишем несколько формул, чтобы вы поняли, как работает логическая функция ИЛИ в Excel.
Формула | Описание |
=ИЛИ(A2=»Яблоки»; A2=»Бананы») | Логическая функция возвращает ИСТИНУ, если A2 содержит «Яблоки» или «Бананы», в противном случае ЛОЖЬ. |
=ИЛИ(B2>=135; C2>=55) | Логическая функция возвращает ИСТИНУ, если B2 больше или равен 135 или C2 больше или равно 55, ЛОЖЬ в противном случае. |
=ИЛИ(B2=»»; C2=»») | Логическая функция возвращает ИСТИНУ, если ячейки B2 и/или C2 пустые, ЛОЖЬ в противном случае. |
Логические функции в Excel – Использование логической функции ИЛИ
Как и логическая функция Excel И, ИЛИ широко используется для расширения полезности других функций Excel, которые выполняют логические проверки, например, функция ЕСЛИ.
Логическая функция ИСКЛИЛИ в Excel
В Excel 2013 Microsoft представила функцию ИСКЛИЛИ, которая является логической функцией исключающего ИЛИ. Для тех, кто не знаком с понятием «Исключающего ИЛИ», сначала может быть немного сложно понять суть логической функции, но, надеюсь, приведенное ниже объяснение иллюстрируемое примерами формул поможет прояснить суть.
Синтаксис логической функции ИСКЛИЛИ идентичен синтаксису ИЛИ:
=ИСКЛИЛИ(логическое_значение1; [логическое_значение2];…)
В простейшей версии формулы ИСКЛИЛИ, содержащей только 2 логических оператора, логическая функция Excel ИСКЛИЛИ вернет ИСТИНУ, если любой из аргументов имеет значение ИСТИНА. Если оба аргумента ИСТИНА, либо оба ЛОЖЬ, ИСКЛИЛИ возвращает ЛОЖЬ. Рассмотрим примеры формул:
Формула | Результат | Описание |
=ИСКЛИЛИ(1>0; 2<1) | ИСТИНА | Логическая функция возвращает ИСТИНА, потому что первый аргумент ИСТИНА, а второй аргумент ЛОЖЬ. |
=ИСКЛИЛИ(1<0; 2<1) | ЛОЖЬ | Логическая функция возвращает ЛОЖЬ, потому что оба аргумента ЛОЖЬ. |
=ИСКЛИЛИ(1>0; 2>1) | ЛОЖЬ | Логическая функция возвращает ЛОЖЬ, потому что оба аргумента ИСТИНА. |
Когда добавляется больше логических операторов, функция ИСКЛИЛИ в Excel работает следующим образом:
- ИСТИНА, если нечетное число аргументов оценивается как ИСТИНА;
- ЛОЖЬ, если общее число ИСТИННЫХ утверждений четно, или если все операторы ЛОЖЬ.
Представленное ниже изображение наглядно это иллюстрирует:
Логические функции в Excel – Использование логической функции ИСКЛИЛИ
Логическая функция НЕ в Excel
Функция НЕ является одной из простейших логических функций Excel с точки зрения синтаксиса:
=НЕ(логическое_значение)
Логическая функция НЕ в Excel используется, чтобы изменить значение своего аргумента. Другими словами, если логическое значение ЛОЖЬ, функция НЕ возвращает ИСТИНА и наоборот. Например, обе приведенные ниже формулы возвращают ЛОЖЬ:
Логические функции в Excel – Использование логической функции НЕ
По сути, именно так используются логические функции в Excel. Конечно, эти примеры в общих чертах описали возможности логических функций И, ИЛИ, ИСКЛИЛИ и НЕ, но зная основы, вы теперь можете расширить свои знания, решая реальные задачи и создавая сложные формулы в ваших рабочих листах.
naprimerax.org

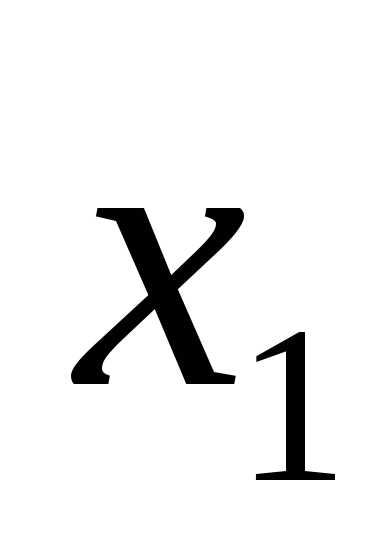
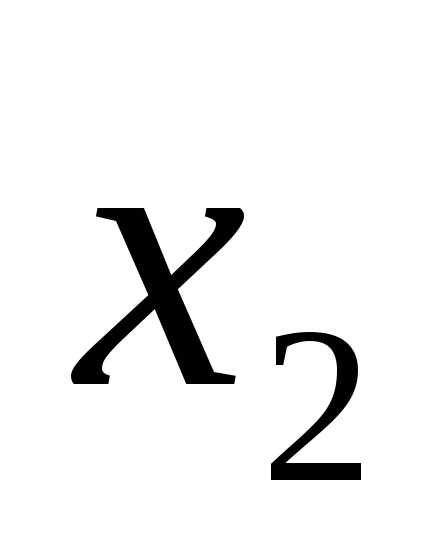
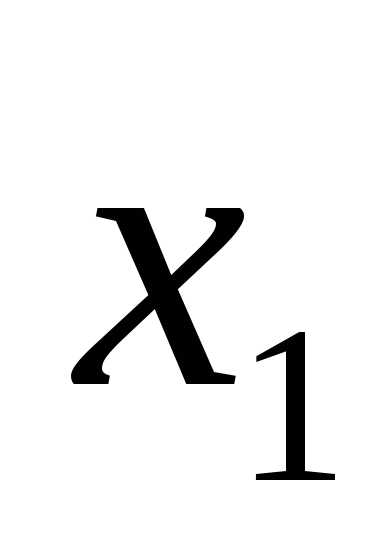
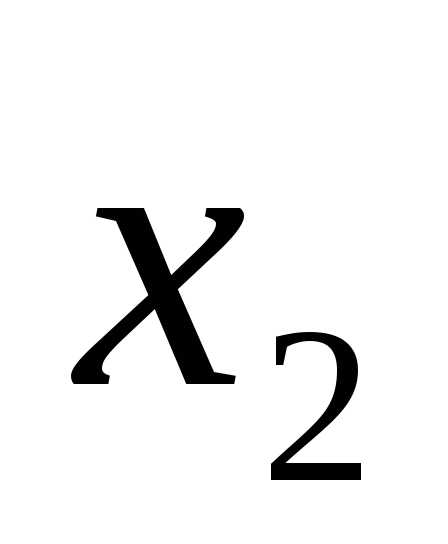
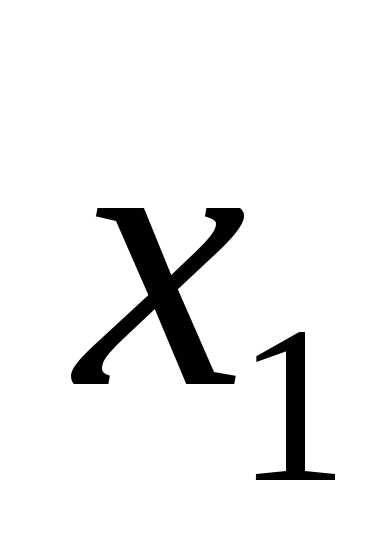
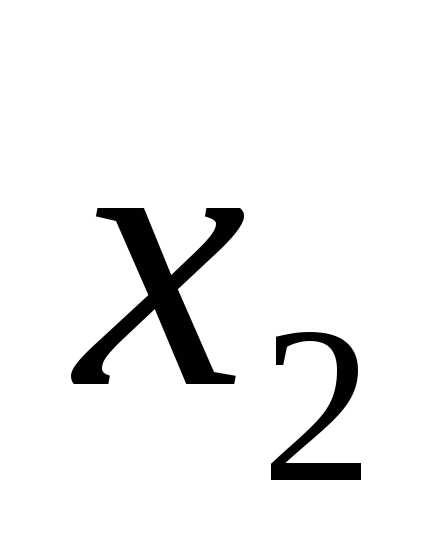
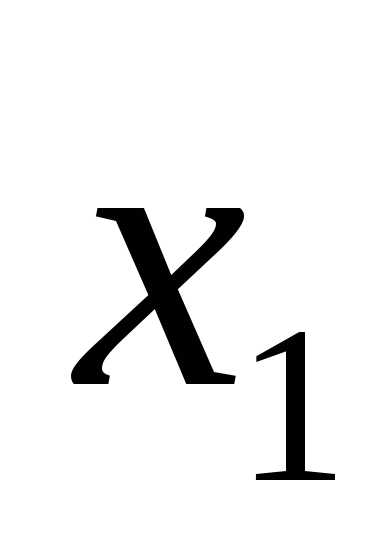
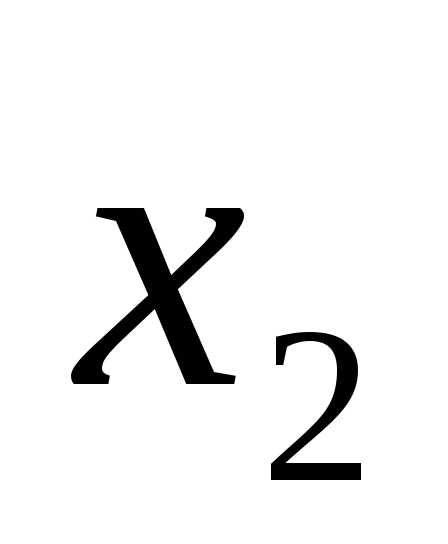
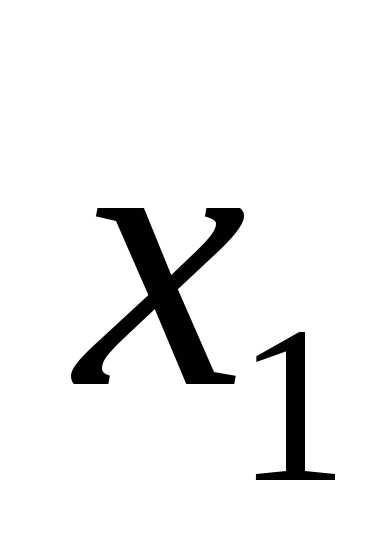 →
→