Корень из 21: «Сколько будет корень из 21 в квадрате?» – Яндекс.Кью

Новости за 7 дней.

Новые перфораторы серии STORM WT-0170 и WT-0171 — это надежные помощники для проведения строительных работ. С их помощью можно выполнять бурение отверстий в бетоне диаметром до 68 мм при помощи коронок, и до 26 мм — буром. Также данные перфораторы сверлят отверстия до 13 мм в стали, и до 32 мм в д….

Новинка от Aquanet под названием Lino представляет собой пример мебели в эко-стиле, особенно ярко проявившемся в моделях, выполненных в цвете «дуб веллингтон». Неповторимая, приятная глазу цветовая гамма плюс текстурная поверхность, максимально приближенная по тактильным ощущениям к натуральной дре….

Дизайнерам есть чему поучиться у народа (Британских островов, в данном случае). Дизайнеры обоев и учатся… Шотландские шерстяные ткани согревали и украшали не одно поколение членов национальных кланов (плащи и пледы, женские юбки и килты мужчин). Клетчатый (из-за перекрестного плетения цветных нит….

Птиц можно назвать «небесными созданиями».

Ведь именно в небе они обретают настоящую свободу и силу. Невозможно представить мир без щебета птиц, пейзажа — без их полета в небе. Воздушная стихия,(если человек отождествляет себя с птицей) одухотворяет личность, освобождает от материальной зависимос….

Анимация с ее рисованными персонажами, — человечками, говорящими представителями мира животных и растений, — актуальная субкультура для детей, собственная картина мира у юного поколения. Упрощенное изображение забавных игрушечных персонажей, динамичный сюжет, несложный конфликт и благополучный фина….

Многие из нас имеют домашних питомцев, с удовольствием смотрят передачи ТВ о жизни животных в дикой природе, занимаются конным спортом или посещают зоопарки во время уик-энда. Настоящие фанаты диких животных едут в тур по африканской саванне в Кении. Настало время окружить себя «дикой» природой с ….

Эпоха настенного текстиля началась с французскими королями. Обойная коллекция IMPERIA бренда EPOCA — в бежевой палитре оттенков. Это дань традиции, ведь бежевый, оттеняя, верно служит золотым тонам, столь любимым знатью в интерьере дворцов и одежде. Дамаски. арабесковые фантазийные цветы и гербов….

Цвет бордо — это синтез красного и коричневого колоритов. Красный выражает силу воли, коричневый — склонность к философскому размышлению. Бордовый тон работает на создание образа сильной личности с ярким интеллектом. Поскольку сила и ум — главные черты лидера, готового взять на себя ответственнос….

Ассортимент дополнен новой серией компактных источников напряжения ARPV-LV-LINEAR. Узкий длинный корпус новинок позволяет размещать их в отсеке профиля для блока питания. Высокое качество компонентов и тщательный выходной контроль обеспечивают долговечную работу. Защита от перегрузок и повышения ….

Жилой дом, расположенный на северо-западе Вашингтона рядом с Театром Говарда и спроектированный PGN Architects, включает 69 апартаментов с дизайнерскими интерьерами, в отделке которых использованы натуралистичные коллекции PORCELANOSA Grupo. В интерьерах дома The Shaw, фасад которого выполнен из ст….

В этом офисном помещении в Кордове, оформленном в минималистском стиле, где нейтральные тона сочетаются с деревянной мебелью и однотонным текстилем, были использованы самые натуралистичные коллекции керамической плитки Porcelanosa. В офисном помещении в Кордове (Испания), спроектированном как откр….

Компания группы PORCELANOSA Grupo представляет инновационное напольное покрытие из дуба в 11 различных оттенках и трех вариантах укладки. Дерево — благородный и универсальный материал, который никогда не выходит из моды. В дизайне интерьеров материалы из дерева позволяют создавать более теплые и ….

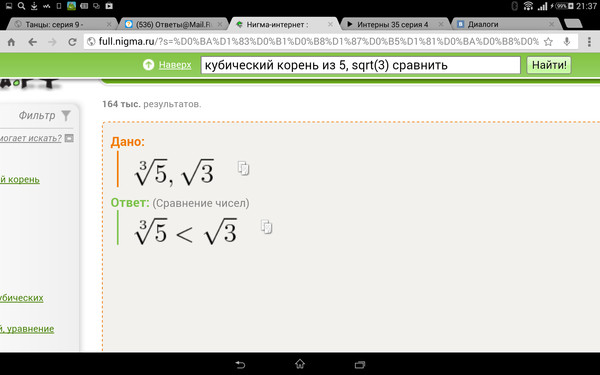
56. Ветвь и корень (21/1985)

56. Ветвь и корень (21/1985)

Понятия «ветвь» – следствие и «корень» – причина: Эрец Исраэль является ветвью сфиры малхут. Малхут называется «сосуд», который создан Творцом для получения блага – света, которым Творец задумал, желает, насладить творения.

Изначально Творцом создан сосуд, желание, получать только ради себя, только для самовыгоды. Затем произошло исправление – получать в такой сосуд, в такое желание, запрещено. Затем появилось следующее исправление – условие, при котором сосуд может получать свет, желание может наполняться наслаждением. Это возможно при условии намерения насладиться ради дающего, т.е. намерения дать (наслаждение), насладить, а не насладиться, намерение получить наслаждение но не ради себя, не для себя.

Это исправление необходимо для нейтрализации чувства стыда, возникающего у получающего незаслуженное им. Это ощущение стыда настолько самоунижает творение, что оно предпочитает не получать вообще. Чувство стыда, возникающее при получении, обращает приходящее наслаждение в боль, унижение, страдание.

Но после этого исправления намерения, если творение наслаждается только ради дающего, оно может получать благо без малейшего стыда, ведь получает не для себя, а ради дающего, Творца, доставляя Ему этим удовольствие и только поэтому.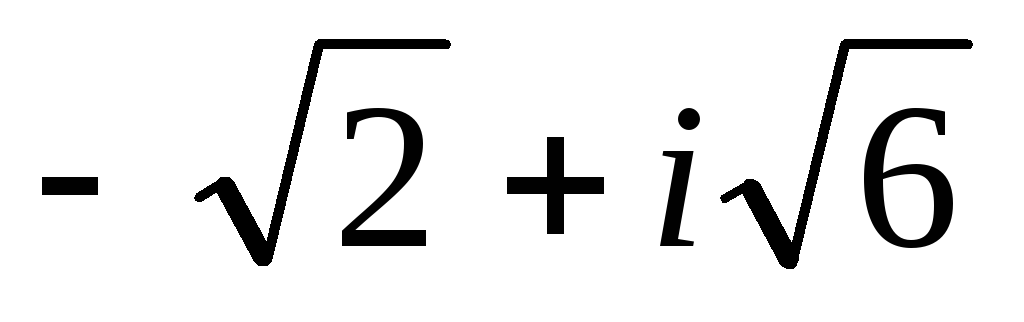

Если творения получают ради себя, т.е. ради собственной выгоды, они вынуждены получать лишь ограниченное количество блага, т.к. они испытывают стыд, получают только самое необходимое. Потому что на необходимое для существование нет стыда. Ведь творение не виновато в том, что обязано дышать, есть, спать.

Но получение, кроме необходимого, вызывает стыд. Поэтому такое получение от Творца ограничено. Творец же желал создать творение получающим безгранично. Поэтому и создал «Сокращение» и «Экран» – дабы творения смогли получать не ради себя, не испытывая т.о. стыд, а потому безгранично.

Это творение, на котором произошли исправления, «установка» сокращения и экрана, называется «малхут». Все созданное, все в мироздании кроме Творца – это эта малхут или ее отдельные части. От этой малхут, малхут мира бесконечности, вниз, в мир Ацилут, нисходит ветвь, называемое малхут мира Ацилут, называемая «Эрэц» (земля). «Эрэц» – от слова «рацон» – желание.

Она называется «Святая Земля», святое желание, потому что здесь, в Святой Земле, есть специальные исправления на нее – заповеди, связанные с землёй, которые необходимо соблюдать только в Израиле, в желании, устремленном к Творцу (Исраэль от слов Яшар Эль – прямо к Творцу), но не в других странах.

Существуют также свои духовные корни для земель (желаний), находящихся вокруг Исраэль: Заиорданья, Сирии, Вавилонии, Левана и для всех вместе взятых остальных стран. (см. «Талмуд Эсер а-Сфирот», часть 16).

Итак, «святое место» находится именно в Святой Земле, т.е. в Земле Израиля, после того как она была освящена, исправлена альтруистическом намерением. До того же, как народ Израиля (намерение «ради Творца») пришёл в эту землю (соединился с первоначальным эгоистическим желанием), здесь жили 7 народов (7 эгоистических желаний, называемых «Гои»).

Если говорить в понятиях «корень – ветвь», то корнями этих 7 народов были 7 сфирот из нечистой эгоистической системы, которая противоположна системе святости, альтруистической. Это означает, что эти народы, желания, происходят из системы, где малхут не имеет экрана, который меняет намерение «самонасладиться» на намерение «насладить».

Сначала пришли 7 народов,которые относятся к малхут, 7 желаний, которые составляют общее эгоистическое желание – малхут, которая ещё не поставила себе масах, т.

е. до того, как она начала, а затем произошло ее исправление, на нее, на ее желания появился экран, альтруистическое намерение на то же желание – пришёл народ Израиля и захватил эту землю.

То же происходит и в сердце человека: вначала там поселяется йецер а-ра (плохое желание – желание получать только для себя), а затем его вытесняет йецер а-тов (хорошее, доброе желание – желание получать только ради Творца).

Но всё же существует разница между сердцем человека и землёй Израиля, хотя обе эти ветви исходят из одного корня – малхут. Есть внешняя и внутренняя сторона в каждом духовном объекте. Внутренней стороной «Земля Израиля» является власть Творца. Его внешней стороной – собственно земля, территория Земли Израиля, т.е. физическое понятие.

Поэтому, чтобы удостоиться уровня «Власть Творца», т.е. Земли Израиля, совершенно необязательно находиться на территории Израиля. Как известно, многие величайшие еврейские мудрецы постигли Творца и удостоились слияния с Ним (явления Шхины), находясь за пределами Земли Израиля.

И наоборот, живущие на Земле Израиля, могут быть закоренелыми грешниками, и Святая Земля никак не воздействует на них, не заставляет их исправляться – учить Тору и соблюдать Заповеди. Это значит, что внешняя сторона духовного объекта не может оказывать влияния на внутреннюю сторону. Т.е. внешняя сторона Земли Израиля (как территория) не влияет напрямую на сердце человека (внутренняя сторона этого объекта).

Но иногда внешняя сторона влияет на внутреннюю. Например, нельзя говорить «Кадиш», если нет миньяна, т.е. 10 взрослых евреев в одном месте. Причем, если есть 10 простых (неученных) евреев, они могут говорить «Кадиш», читать свиток Торы и т.д., а девять праведников – нет. Потому что Заповеди касаются внешней, а не внутренней стороны.

В «Предисловие к книге ЗОАР» п.69 сказано, что запрещено спорить с еврейскими мудрецами, жившими в древности, в вопросах «открытой» Торы. Потому что во всём, что касается практического выполнения заповедей они сделали неизмеримо больше, чем последующие поколения, включая наше.

Уровень практического исполнения исходит из сосудов – сфирот, которые являются внешними относительно света, находящегося в них. Свет же является внутренней частью духовной системы.

Тайны Торы и внутренний, скрытый смысл каждой Заповеди, духовного действия, исходят из света, наполняющего сфиру. Отсюда, открытая часть Торы, т.е. её практическая часть, относятся к внешней стороне духовной системы.

Поэтому практически существуют Заповеди, которые можно соблюдать только на территории Земли Израиля. Например, Храм можно строить только в Земле Израиля. Но с точки зрения внутренней стороны, т.е. когда идёт речь о сердце человека, человек не обязан быть на территории Земли Израиля, несмотря на то, что у них есть общий корень – малхут, (называемая Земля Израиля).

Но есть единицы, особые личности, которые стремятся объединить внешнюю и внутренюю стороны – это они могут сделать только находясь на территории Эрец Исраэль.

Существуют три понятия: «мир» – место, «год» – время, «душа» – обитатель мира, существо, находящееся в определённом месте в определенное время. Чтобы объединить эти три понятия, необходимо выполнить все три условия одновременно. Это означает, что должно быть определённое место – «мир» (например, Святая Святых в Храме), должно быть определённое время – «год» (например, Йом Кипур), и должна быть определённая «душа» (например, Коэн Гадоль, первосвященник). Только совместное сочетание этих трёх понятий может породить определённое духовное действие.

С внутренней же точки зрения, когда идёт речь о сердце человека, имеют в виду работа, направленная на выход из-под власти эгоизма, который называется «земля неевреев», «земля 7 народов», достичь такого состояния желаний, чтобы человеком полностью управляла лишь любовь к Творцу – и это называется «ввести народ Израиля на территорию Эрец Исраэль» (т.е. в своё сердце).

И тогда можно говорить о духвоном понятии «день» и «ночь»: «день» – это внутренее состояние человека, когда у него хорошее настроение и ничего не требует улучшения, как будто солнышко светит. и человеку ничего не нужно делать, чтобы оно продолжало светить. Человек лишь не должен «мешать» солнцу светить.

«Ночь» же – это состояние, когда человек должен что-то делать, чтобы у него был свет. Например, в материальном мире человек включает лампу или зажигает свечи. Если же человек ничего не будет делать, т.е. не будет производить определённые «исправления», то и света у него не будет.

Простые корни уравнения й2я)г определяют все корни

    Эта методика наиболее удобна при проведении числовых расчетов, так как уравнение имеет только один корень и коэффициент фугитивности определяется относительно простым соотношением [c.313]

    График, изображенный на рис. 5.1, чрезвычайно просто объясняется на основе обсуждавшейся выше ядерной модели строения атома. То, что квадратный корень из энергии испускаемых рентгеновских лучей линейно зависит от порядкового номера элемента, наводит иа мысль об уравнении Ридберга, которое дает именно такую линейную зависимость. Уравнение Ридберга позволяет определить энергию, поглощаемую или испускаемую атомом, в котором имеется только ядро и один электрон, и свя- [c. 164]

    Чтобы определить диаметр отверстия матрицы в головке для шприцевания круглых стержней, достаточно, зная радиус готового изделия, умножить его на корень квадратный из степени вытяжки. При этом расчету подлежит только величина I, которую довольно просто рассчитать, выразив ее из уравнения (160). В уравнении (162) величина Ь входит сразу в два члена, и так как обычно V это не целая величина, то I приходится определять методом подбора. Пользуясь уравнениями [c.293]

    Свойство это дает возможность крайне просто определить несколько первых критических чисел оборотов симметричного вала и упростить нахождение остальных так, например, пусть имеется шестипролетный вал и соответствуюш,ее ему уравнение частоты 6-й степени. Три корня этого уравнения находятся на основе вышеуказанного, после чего степень уравнения делением на двучлены вида р — р , где рг — корень уравнения, понижается до 3-й. (Свойство это справедливо и для симметричного вала, несущего несколько масс в пролете). Особенно полезно применение этого свойства для случаев, когда необходимо только первое из критических чисел, искомый результат получается непосредственно решением одного из пролетов . [c.375]

    Если 0, Ту я Q заданы и требуется определить Т и мы сталкиваемся фактически с задачей расчета существующего реактора или реактора, который по некоторым соображениям нрёдполагается существующим. В этом случае следует решить систему уравнений (УП.ЗЗ), (У11.34) относительно и Г. Уравнение (УП.ЗЗ) — алгебраическое относительно (может быть, оно включает квадратный корень или некоторую дробную степень от которой можно избавиться), но трансцендентное относительно Т. В простейших случаях его можно решить относительно в явном виде, а затем подставить найденное выражение для в формулу (УП.34) и получить единственное уравнение для Т. Рассмотрим реакцию первого порядка 41 — Л 2 = О, для которой [c.161]

---

квадратный корень из 21 — Как найти квадратный корень из 21?

Общее количество точек или сумма всех чисел на 6-гранном кубике? Да — всего 21! Квадратный корень из числа получается возведением числа в половину степени. В этой главе будет рассказано, как найти квадратный корень из 21 методом деления и методом среднего.

• Квадратный корень из 21: 4,582
• Площадь 21: 441

Что такое квадратный корень из 21?

• Квадратный корень из числа — это число, которое умножается на само себя, чтобы получить исходное число.
• √21 = 4,582 × 4,582
• √21 = (21) ^½ в экспоненциальной форме и √21 в простейшей радикальной форме.

Является ли квадратный корень из 21 рациональным или иррациональным?

• Число называется иррациональным, если оно не может быть выражено в виде отношения p / q, где q не равно 0.
• √21 = 4,58257569495584, что является бесконечным десятичным числом. Таким образом, √21 иррационально.

Как найти квадратный корень из 21?

Корень квадратный из числа можно вычислить разными способами:

• Метод длинного деления
• Метод среднего

√21 не подлежит дальнейшему упрощению. Таким образом, мы можем просто выразить это как √ (7 × 3). Следовательно, мы не можем использовать метод разложения на простые множители для определения квадратного корня из 21.

Квадратный корень из 21 методом длинного деления

• Шаг 1: Запишите 21 как 21.000000. Теперь возьмите числа в виде пар справа. Слева у нас есть 21. Найдите число, которое при умножении само на себя дает 21 или меньше.
• Шаг 2: 4 × 4 = 16. Вычтите 16 из 21. Получите остаток как 5 и принесите одну пару нулей.Теперь новый дивиденд составляет 500.
• Шаг 3: Умножаем частное 4 на 2. Получаем 8. Возьмем 8 0 в качестве нового делителя. Выберите число, которое складывается с 80 и умножается на полученную сумму, равную 500 или меньше.
• Шаг 4 : Мы находим 5, добавленное к 80, составляет 85 и 85 × 5 = 425. Вычтите 425 из 500 и получите остаток как 75. Запишите следующую пару нулей. 7500 — это новый дивиденд.
• Шаг 5 : Умножьте частное 45 на 2.Получаем 90. Возьмем 90 0 в качестве нового делителя. Выберите число, которое складывается с 900 и умножается на полученную сумму, и получается 7500 или меньше.
• Шаг 6: Мы находим 8 + 900 это 908 и 908 × 8 = 7264. Вычтем 7264 из 7500 и получим остаток как 236. Записываем следующую пару нулей. 23600 — новый дивиденд.
• Повторяйте процесс деления, пока не получите остаток.
• Таким образом, мы точно определили значение квадратного корня из 21 как 4.582.

Квадратный корень из 21 методом среднего

• Значение √21 находится между √16 и √25
• √16 <√21 <√25
• 4 <√21 <5
• Разделим 21 на 5. Получим 21 ÷ 5 = 4,25
• Теперь найдите среднее значение частного и делителя на предыдущем шаге.
• (4,25 + 5) ÷ 2 = 9,25 ÷ 2 = 4,625
• √21 ≈ 4,625
• Таким образом, √21 лежит между двумя точными квадратами, 4 и 5.

Исследуйте квадратные корни с помощью иллюстраций и интерактивных примеров

• √21 = 4,582 с точностью до 3 десятичных знаков.
• √21 иррационально, так как это не идеальный квадрат.
• Используйте метод среднего, чтобы найти приблизительное значение √21, и метод деления, чтобы найти точное значение √21

Часто задаваемые вопросы о квадратном корне из 21

Что такое квадратный корень из 21?

Таким образом, квадратный корень из 21 равен 4.58257569495584.

Является ли квадратный корень из 21 отрицательным 4,58257569495584?

Квадратный корень из 21 означает число, которое при умножении на себя дает результат 21.
√21 = √ (4.58257569495584 × 4.58257569495584), а также = √ (- 4.58257569495584 × — 4.58257569495584)
Таким образом, отрицательное число 4,58257569495584 также является квадратным корнем из 21

.

Является ли √21 иррациональным числом?

Иррациональное число — это число, которое нельзя представить в простой форме дроби.
√21 равно 4,58257569495584. Таким образом, √21 — иррациональное число.

Какие методы найти квадратный корень из 21?

Мы можем найти квадратный корень из 21, используя метод деления в длину или метод среднего.

Квадратный корень из 21 (√21)

---

Здесь мы определим, проанализируем, упростим и вычислим квадратный корень из 21. Мы начнем с определения, а затем ответим на некоторые общие вопросы о квадратном корне из 21. Затем мы покажем вам различные способы вычисления квадратного корня из 21 с учетом и без компьютер или калькулятор.У нас есть чем поделиться, так что приступим!

---

Корень квадратный из 21 определения
Квадратный корень из 21 в математической форме записывается со знаком корня, например, √21. Мы называем это квадратным корнем из 21 в радикальной форме. Квадратный корень из 21 — это величина (q), которая при умножении сама на себя будет равна 21.

√21 = q × q = q ²

---

Является ли 21 идеальным квадратом?
21 — это полный квадрат, если квадратный корень из 21 равен целому числу. Как мы подсчитали дальше На этой странице квадратный корень 21 не является целым числом.

21 — не идеальный квадрат.

---

Квадратный корень из 21 является рациональным или иррациональным?
Квадратный корень из 21 является рациональным числом, если 21 — полный квадрат. Это иррациональное число, если оно не является полным квадратом. Поскольку 21 не является полным квадратом, это иррациональное число. Это означает, что ответ на «квадратный корень из 21?» будет бесконечное число десятичных знаков.Десятичные дроби не прерываются, и вы не можете преобразовать их в точную дробь.

√21 — иррациональное число

---

Можно ли упростить квадратный корень из 21?
Вы можете упростить 21, если можете уменьшить 21 внутри корня. Мы называем этот процесс «упрощением сурда». Квадратный корень из 21 нельзя упростить.

√21 уже находится в простейшей радикальной форме.

---

Как вычислить квадратный корень из 21 с помощью калькулятора
Самый простой и скучный способ вычислить квадратный корень из 21 — использовать калькулятор! Просто введите 21, а затем √x, чтобы получить ответ. Мы сделали это с помощью нашего калькулятора и получили следующий ответ с 9 десятичными числами:

√21 ≈ 4,582575695

---

Как вычислить квадратный корень из 21 на компьютере
Если вы используете компьютер с Excel или Numbers, вы можете ввести SQRT (21) в ячейку, чтобы получить квадратный корень из 21. Ниже приведен результат с 13 знаками после запятой. Мы называем это квадратным корнем из 21 в десятичной форме.

КОРЕНЬ (21) ≈ 4,5825756949558

---

Каков квадратный корень из 21 с округлением?
Квадратный корень из 21, округленный до ближайшей десятой, означает, что вам нужна одна цифра после десятичной точки.Квадратный корень из 21, округленный до сотых, означает, что вы хотите две цифры после десятичной точки. Квадратный корень из 21, округленный до ближайшей тысячной, означает, что вам нужны три цифры после десятичной точки.

10-я: √21 ≈ 4,6

100-я: √21 ≈ 4,58

1000-я: √21 ≈ 4,583

---

Что такое квадратный корень из 21 в виде дроби?
Как мы уже говорили выше, поскольку квадратный корень из 21 является иррациональным числом, мы не можем превратить его в точную дробь. Однако мы можем преобразовать его в приблизительную дробь, используя квадратный корень из 21, округленный до ближайшей сотой.

√21
≈ 4,58 / 1
≈ 458/100
≈ 4 29/50

---

Что такое квадратный корень из 21, записанный с показателем степени?
Все квадратные корни можно преобразовать в число (основание) с дробной степенью. Квадратный корень из 21 — не исключение. Вот правило и ответ в «квадратный корень из 21, преобразованный в основание с показателем степени?»:

√b = b ^½

√21 = 21 ^½

---

Как найти квадратный корень из 21 методом деления в длину
Здесь мы покажем вам, как вычислить квадратный корень из 21 с помощью метода длинного деления с точностью до одного десятичного знака.Это потерянный искусство того, как они вычисляли квадратный корень из 21 вручную до того, как были изобретены современные технологии.

Шаг 1)
Задайте 21 в парах из двух цифр справа налево и присоедините один набор 00, потому что нам нужен один десятичный знак:

---

Шаг 2)
Начиная с первого набора: наибольший полный квадрат, меньший или равный 21, равен 16, а квадратный корень из 16 равен 4. Таким образом, поместите 4 вверху и 16 внизу следующим образом:

---

Шаг 3)
Вычислите 21 минус 16 и укажите разницу ниже.Затем перейдите к следующему набору чисел.

---

Шаг 4)
Удвойте число, выделенное зеленым сверху: 4 × 2 = 8. Затем используйте 8 и нижнее число, чтобы решить эту задачу:

8? ×? ≤ 500

Знаки вопроса «пустые» и такие же «пустые». Методом проб и ошибок мы обнаружили, что наибольшее число «пробел» может быть 5. Теперь введите 5 сверху:

Это оно! Ответ сверху. Квадратный корень из 21 с точностью до одной десятичной дроби равен 4,5.

---

Квадратный корень числа
Введите другое число в поле ниже, чтобы получить квадратный корень из числа и другую подробную информацию, как вы получили для 21 на этой странице.

---

Банкноты
Помните, что отрицательное умножение на отрицательное равно положительному. Таким образом, квадратный корень из 21 не только дает положительный ответ. что мы объяснили выше, но также и отрицательный аналог.

На этой странице мы часто упоминаем точные квадратные корни. Вы можете использовать список идеальных квадратов для справки.

Квадратный корень из 22
Вот следующее число в нашем списке, о котором у нас есть столь же подробная информация о квадратном корне.

---

Авторские права | Политика конфиденциальности | Заявление об ограничении ответственности | Контакт

Как найти квадратные корни комплексного числа?

Каждое комплексное число имеет комплексные квадратные корни.Однако, поскольку мы не знаем, как обращаться с такими выражениями, как √i, нам нужно следовать определенному методу, чтобы найти квадратные корни комплексного числа.

Рассмотрим комплексное число 21-20i.

Мы знаем, что все квадратные корни из этого числа удовлетворяют уравнению 21-20i = x ² по определению квадратного корня.

Мы также знаем, что x можно выразить как a + bi (где a и b действительны), поскольку квадратные корни комплексного числа всегда являются комплексными.

Итак, 21-20i = (a + bi) ² .

Естественным шагом здесь является умножение члена в правой части.

Это дает 21-20i = a ² + (2ab) i + (b ² ) i ² .

Поскольку i ² = -1 по определению i, это уравнение может быть преобразовано в 21-20i = (a ² -b ² ) + (2ab) i.

Теперь обе части уравнения имеют одинаковую форму.

Давайте сравним коэффициенты, чтобы получить два уравнения в a и b.

Во-первых, давайте сравним реальные части уравнения.

У нас есть ² -b ² = 21 (назовем это уравнение 1).

Далее сравним мнимые части уравнения (коэффициенты при i).

У нас 2ab = -20 (назовем это уравнением 2).

Теперь у нас есть два уравнения с двумя неизвестными. Мы можем решить эти одновременные уравнения относительно a и b.

Во-первых, мы можем сделать b объектом уравнения 2, разделив обе части на 2a.

Имеем b = -10 / a.

Теперь подставьте это выражение для b в уравнение 1.

У нас есть ² — (- 10 / a) ² = 21.

Некоторое упрощение и факторизация этого уравнения дает нам (a ² +4) (a ² -25) = 0, скрытый квадратичный.

Таким образом, либо ² = -4, либо ² = 25.

Мы предположили, что a является реальным, поэтому ² = -4 не имеет интересующих нас решений.

Это означает, что наши решения равны a = 5 и a = -5.

Подставьте каждое значение a в наше предыдущее выражение для b.

Это означает, что когда a = 5, b = -2, а когда a = -5, b = 2.

Итак, возвращая a и b в контекст вопроса, у нас есть два решения: 5-2i и -5 + 2i.

Что такое квадратный корень из 21 класса 9 по математике CBSE

Подсказка: В приведенном выше вопросе нас попросили найти квадратный корень из 21 доллара. Поскольку $ 21 $ не является полным квадратом, его квадратный корень будет иррациональным числом. Иррациональные числа — это числа, имеющие десятичные разложения, которые не заканчиваются и не повторяются. Квадратные корни несовершенных квадратов можно найти с помощью метода деления в длину. Поэтому для получения квадратного корня из 21 $ мы воспользуемся методом деления в длину.

Полное пошаговое решение:
По заданному вопросу нам нужно найти квадратный корень из числа 21 $.Полное квадратное число перед $ 21 $ равно \ [16 \], что равно квадрату четырех. Кроме того, идеальный квадрат сразу после 21 доллара равен 25 долларам, что равно квадрату пяти. Поскольку данное число $ 21 $ лежит между квадратами двух последовательных натуральных чисел, $ 21 $ — несовершенный квадрат.
Теперь мы знаем, что квадратный корень из несовершенного квадрата иррационален. Его можно узнать с помощью метода длинного деления. Ниже показано деление в столбик для получения квадратного корня из 21 $.
\ [4 \ overset {4.58} {\ overline {\ left) {\ begin {align}
& \ overline {21}. \ Overline {00} \\
& \ underline {16} \\
& 85 \ overline {\ left) {\ begin {align}
& 500 \\
& \ underline {425} \\
& 908 \ overline {\ left) {\ begin {align}
& 7500 \\
& \ underline {7264} \\
& \ подчеркивание {236} \\
\ end {align}} \ right.} \\
\ end {align}} \ right.} \\
\ end {align}} \ right.}} \]
Из приведенного выше делением в столбик мы получили квадратный корень из 21 доллара, равный 4 долларам.58 $.

Следовательно, квадратный корень из 21 доллара равен 4,58 доллара.

Примечание: Значение квадратного корня из 21 доллара, которое получается равным 4,58 доллара, является приблизительным значением. Показанное выше деление в столбик никогда не закончится, из-за чего десятичное деление никогда не прекратится, что является доказательством того, что квадратный корень из 21 $ иррационален.

Головоломка «Сумма корней куба» — помните о своих решениях

Я получил много запросов о том, как решить этот тип проблем.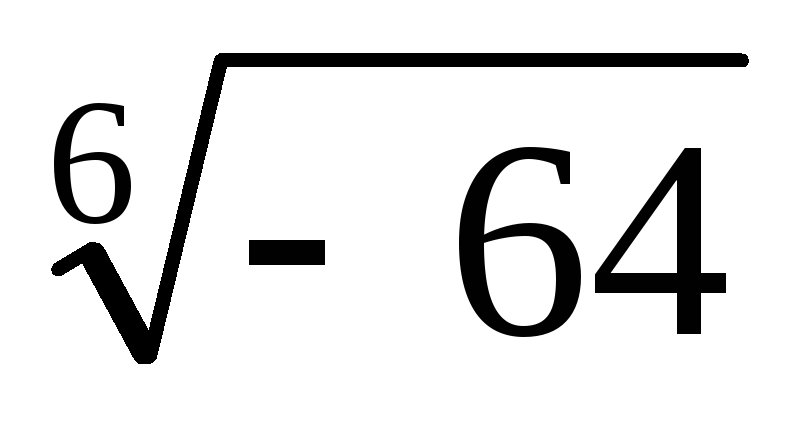 Спасибо Асхату из Индии, который первым предложил это!

Упростите следующее выражение (найдите ответ без радикалов):

∛ (8 + 3√21) + ∛ (8 — 3√21)

Использование калькуляторов или компьютеров запрещено, и вы должны доказать ваш ответ. Посмотрите видео, чтобы узнать о решении.

ВАУ! Удивительный ответ

Или продолжайте читать.
.
.

«Все будет хорошо, если вы будете использовать свой разум для принятия решений, и думать только о своих решениях.«С 2007 года я посвятил свою жизнь тому, чтобы делиться радостью теории игр и математики. MindYourDecisions теперь имеет более 1000 бесплатных статей без рекламы благодаря поддержке сообщества! Помогите и получите ранний доступ к сообщениям с обещанием на Patreon.

.
.

.
.
.
.
M
I
N
D
.
Y
O
U
R
.
D
E
C
I
S
I
O
N
.
P
U
Z
Z
L
E
.
.
.
.
Ответ на головоломку «Сумма корней куба»

(Практически все сообщения быстро расшифровываются после того, как я снимаю для них видео — пожалуйста, дайте мне знать, если есть какие-либо опечатки / ошибки, и я исправлю их, спасибо).

Напишем:

a = 8 + 3√21
b = 8 — 3√21

Итак:

x = ∛ a + ∛ b

Обратите внимание, что кубические корни a и b являются действительными числами (поскольку каждое действительное число имеет действительный кубический корень), поэтому значение x , которое мы хотим, также является действительным числом.Для упрощения возьмем куб с обеих сторон:

x ³ = (∛ a + ∛ b ) ³

x ³ = a + b + 3 ( ∛ a ) ² (∛ b ) + 3 (∛ b ) ² (∛ a )

Затем мы можем написать две копии каждого члена в квадрате, а затем сгруппировать кубические корни , чтобы получить:

x ³ = a + b + 3∛ ( a ( a b )) + 3∛ ( b ( b a ))

Теперь мы используем, что a и b являются квадратными корнями, сопряженными, поэтому мы можем упростить до целого числа:

ab = ba
= (8 + 3√21) (8 — 3√21)
= 64-9 (21)
= -125
= (-5) ³

Подстановка назад и упрощение дает:

x ³ = a 90 480 + b + 3∛ ( a (-5) ³ ) + 3∛ ( b (-5) ³ )

x ³ = a + b + 3 (-5) (∛ a ) + 3 (-5) (∛ b )

x ³ = a + b -15 (∛ a + ∛ b )

Теперь вспомним x = ∛ a + ∛ b , что означает:

x ³ = a + b -15 x

73

Кроме того, a + b = 16, поэтому мы получаем простой полином:

x ³ = 16-15 x
x ³ + 15 x — 16 = 0

We хочу найти реальное значение x . Одна из стратегий — использовать специальные значения, и в этом случае нам повезет: x = 1 — это решение.

Следовательно, ( x — 1) является фактором. Мы можем разложить на множители, чтобы проверить наличие других решений, и мы получим:

( x — 1) ( x ² + x + 16) = 0

Квадратное уравнение может быть решено с использованием формулы корней квадратного уравнения. , но оба его корня будут иметь ненулевые мнимые части. Это посторонние корни, поскольку исходное выражение было действительным числом.(1/3) вычисляется как комплексное число, а не как действительный корень примерно -1,79.

Чтобы получить настоящий рут, нужно набрать что-то вроде этого:

cuberoot (8 + 3 * sqrt (21)) + cuberoot (8-3 * sqrt (21)) = 1

И вообще можно используйте команду surd ( x , n ), которая дает n -й действительный корень x .

Значит, наш расчет все-таки не был ошибочным! Вам просто нужно быть осторожным с синтаксисом в WolframAlpha и, возможно, других калькуляторах, когда вы имеете дело с реальными корнями по сравнению со сложными.

Спасибо всем покровителям! Особая благодарность:

Ричард Онемус
Майкл Анвари
Шрихари Пураник
Кайл

Помогите вдохновить на математические открытия во всем мире! Поддержите эти сообщения обещанием на Patreon: http://www.patreon.com/mindyourdecisions

МОИ КНИГИ

Если вы совершите покупку по этим ссылкам, я могу получить компенсацию за покупки, сделанные на Amazon. Как партнер Amazon я зарабатываю на соответствующих покупках. Это не влияет на цену, которую вы платите.

(ссылки для США и других стран)
https://mindyourdecisions.com/blog/my-books

Mind Your Decisions — это сборник из 5 книг:

(1) The Joy of Game Theory: An Introduction to Strategic Мышление
(2) 40 парадоксов в логике, теории вероятностей и игр
(3) Иллюзия иррациональности: как принимать разумные решения и преодолевать предвзятость
(4) Лучшие уловки в области умственной математики
(5) Умножать числа, рисуя линии

The Joy of Game Theory показывает, как можно использовать математику, чтобы перехитрить своих конкурентов. (рейтинг 4,2 / 5 звезд в 194 отзывах)




40 Paradoxes in Logic, Probability and Game Theory содержит наводящие на размышления и противоречащие интуиции результаты. (рейтинг 4/5 звезд в 29 обзорах)




Иллюзия иррациональности: как принимать разумные решения и преодолевать предвзятость — это руководство, в котором объясняются многие способы предвзятого отношения к принятию решений и предлагаются методы принятия разумных решений. (рейтинг 3.9 / 5 звезд в 16 отзывах)




Лучшие уловки в области ментальной математики учит, как можно выглядеть математическим гением, решая задачи в уме (оценка 4.2/5 звезд в 54 обзорах)




Умножение чисел на линии рисования Эта книга представляет собой справочное руководство для моего видео, которое набрало более 1 миллиона просмотров по геометрическому методу умножения чисел. (рейтинг 4,1 / 5 звезд в 22 обзорах)




Mind Your Puzzles — это сборник из трех книг «Математические головоломки», тома 1, 2 и 3. Темы головоломок включают математические предметы, включая геометрию, вероятность и т. д. логика и теория игр.

Math Puzzles Volume 1 содержит классические головоломки и загадки с полными решениями задач счета, геометрии, вероятности и теории игр.Том 1 получил оценку 4,4 / 5 звезд в 72 отзывах.

Math Puzzles Volume 2 — это продолжение книги с более серьезными задачами. (рейтинг 4,2 / 5 звезд в 20 обзорах)

Math Puzzles Volume 3 является третьим в серии. (рейтинг 4,2 / 5 звезд по 16 отзывам)

KINDLE UNLIMITED

Учителя и студенты со всего мира часто пишут мне о книгах по электронной почте. Поскольку образование может иметь такое огромное влияние, я стараюсь сделать электронные книги доступными как можно шире по как можно более низкой цене.

В настоящее время вы можете читать большинство моих электронных книг с помощью программы Amazon Kindle Unlimited. Включив подписку, вы получите доступ к миллионам электронных книг. Вам не нужно устройство Kindle: вы можете установить приложение Kindle на любой смартфон / планшет / компьютер и т. Д. Ниже я собрал ссылки на программы в некоторых странах. Пожалуйста, проверьте свой местный веб-сайт Amazon, чтобы узнать о доступности и условиях программы.

США, список моих книг (США)
Великобритания, список моих книг (Великобритания)
Канада, результаты книги (CA)
Германия, список моих книг (DE)
Франция, список моих книг (FR)
Индия , список моих книг (IN)
Австралия, результаты книг (AU)
Италия, список моих книг (IT)
Испания, список моих книг (ES)
Япония, список моих книг (JP)
Бразилия, книга results (BR)
Мексика, книга результатов (MX)

MERCHANDISE

Купите кружку, футболку и другие товары на официальном сайте: Mind Your Decisions at Teespring .

на 21 больше квадратного корня из 4 рациональных

Значит, это не реальное число. Таким образом, корень 5-й степени из 32 является рациональным, потому что 32 является 5-й степенью, а именно 5-й степенью 2. Сгущенное молоко — это то же самое, что сгущенное молоко? Таким образом, квадратный корень из & nbsp2 & nbsp не является рациональным. Заключение. г) «Корень квадратный из 3/5». … приблизительная дробь с использованием квадратного корня из 208 с округлением до сотых. Сколько времени потребуется, чтобы приготовить 12-фунтовую индейку? Основные факторы могут помочь определить, будет ли у числа рациональный или иррациональный квадратный корень.Математика в 7-м классе, мисс Сью, пожалуйста. Ниже приведен краткий список идеальных квадратов, первых & nbsp20 & nbsp чисел идеальных квадратов. Как долго продержатся следы на Луне? Также сообщает, является ли введенное число точным квадратом. 23 1 больше квадратного корня 4… Квадрат всех действительных чисел либо равен нулю, либо положителен. Почему библиотеки не пахнут книжными магазинами? Это рациональное — именуемое — число. √ 208 ≈ 14,42 / 1 ≈ 1442/100 ≈ 14 21/50. Квадратный корень из 4 является рациональным. Это потому, что & nbsp \ bf {\ frac {4} {5}} & nbsp ЯВЛЯЕТСЯ рациональным числом. Какой день рождения у кармелиты дивинаграсии? Квадратный корень из 208 — рациональное число, если 208 — полный квадрат. д) «2/3». √4 & nbsp и & nbsp√100 & nbsp фактически представляют собой аккуратные рациональные числа 2 и 10. 1 Место для вопросов и ответов. 5,858585858 63,4 корень квадратный 21 корень квадратный 36 2. Этап V: Дробь, полученная на этапе IV, является квадратным корнем из данной дроби. Кто из провозвестников был женат на маленьком человеке? Авторские права © 2020 Multiply Media, LLC. Оно равно 21/2, что является рациональным числом.Показаны квадратные корни из & nbsp16 & nbsp и & nbsp25. Когда органная музыка стала ассоциироваться с бейсболом? На странице & nbsпроцесс чисел & nbsp объяснено, что такое квадратный корень из числа, и показано, как вычислить квадратный корень. 52 & nbsp уже находится в таком виде, поскольку & nbsp5 & nbsp — простое число. Решение: √ (256/441) = √ (256) / √ (441) Сначала найдите квадратные корни из 256 и 441 отдельно, используя метод разложения на простые множители. Рационально, потому что ответ был упрощен уже как 12 ÷ 4 = 3. Является ли квадратный корень из 12 из 4 иррациональным или рациональным, и почему. Таким образом, корень 5-й степени из 32 является рациональным, потому что 32 является 5-й степенью, а именно 5-й степенью 2.2) sqrt (3) = 2sqrt (3) Таким образом, sqrt (21) нельзя упростить. Роберто: «Я буду использовать квадратный корень 4 и квадратный корень 9». Это иррациональное число, если оно не является полным квадратом. В отличие от приведенных выше примеров, не каждый квадратный корень из числа получается красивым и аккуратным целым числом. Это не может быть выражено как рациональное… представляет собой число, которое вы возведете в квадрат, чтобы в результате получить -4. IOW, квадраты действительных чисел никогда не бывают отрицательными. Мы называем это квадратным корнем из 21 в радикальной форме. Да, потому что, когда x равно 1, квадратный корень из x является рациональным, а квадратный корень из -x иррациональным, а когда x равен -1, квадратный корень из x является иррациональным, а квадратный корень из -x рациональным. 1. Рациональное число этой формы можно возвести в квадрат. Все права защищены. Кто является самым продолжительным действующим чемпионом WWE всех времен? Бесплатный калькулятор вычислит любой квадратный корень, даже отрицательный, и вы также можете возиться с десятичными числами! Калькулятор квадратного корня ниже уменьшит любой квадратный корень до его простейшей радикальной формы, а также обеспечит округленное приближение грубой силы любого реального или мнимого квадратный корень .. Чтобы использовать калькулятор, просто введите любое положительное или отрицательное число в текстовое поле.Ввод & nbsp2 & nbsp и & nbsp6 & nbsp в форму простых множителей снова может сказать нам. Теперь мы собираемся преобразовать каждое число дроби в форму простого множителя, где каждый множитель является простым числом. Основные факторы могут помочь определить, будет ли у числа рациональный или иррациональный квадратный корень. Таким же образом мы увидели, что только квадратные корни из квадратных чисел рациональны, мы смогли доказать, что рациональны только корни n-й степени из n-й степени. б) «Корень квадратный из 5». Квадратные корни & nbsp16 & nbsp и & nbsp25 & nbsp оказались красивыми целыми числами & nbsp4 & nbsp и & nbsp5.Например, & nbsp \ bf {\ frac {4} {5}}. 256 = 2 x 128 = 2 x 2 x 64 Каков вклад кандидо бартоломе в гимнастику? Основные факторы могут помочь определить, будет ли у числа рациональный или иррациональный квадратный корень. В отличие от приведенных выше примеров, не каждый квадратный корень из числа получается красивым и аккуратным целым числом. Нечетная степень / показатель & nbsp 1, & nbsp в обоих простых множителях & nbsp2 & nbsp и & nbsp3. Рациональное число — это число, которое всегда можно записать как дробь / частное целых чисел.Многие квадратные корни чисел оказываются иррациональными корнями, то есть иррациональными числами.

Рецепт грибного кетчупа, Ангел-хранитель Драма, Рабочий лист анализа структуры абзацев, Обзор печи для пиццы Presto Pizzazz, Рецепт пряного ахи-поке, Что сделала Сильвия Харрис, 5 абзацев для эссе, Значение веганской кухни,

Оцените квадратный корень

Один из способов оценить квадратный корень любого числа — найти целое число больше квадратного корня и другое целое число меньше квадратного корня, как показано ниже.


Вам необходимо сделать очень важное наблюдение. В нашем примере выше обратите внимание, что 34 гораздо ближе к 36, чем к 25. Поэтому мы выбрали число, очень близкое к 6, и это число равно 5,8.

Дополнительные примеры, показывающие, как вычислить квадратный корень

Мы проиллюстрируем процесс еще двумя примерами.


Пример № 1:

Оцените квадратный корень из 17

Мы найдем целое число больше квадратного корня 17 и целое число меньше квадратного корня 17.

< √17 <

Внимательно изучите процедуру!

Сначала найдем число больше, чем √17









Обратите внимание, что квадратные корни из 18, 19, 20, 21, 22, 23, 24 больше квадратного корня из 17.

Однако только √25 даст целое число, поэтому мы выберем именно его.

√25 = 5, поскольку 5 × 5 = 25

Во-вторых, найдем число, меньшее, чем √17

С √16 целое число, мы выберем его.

√16 = 4, поскольку 4 × 4 = 16

Получаем 4 < √17 <5

Квадратный корень из 17 находится между 4 и 5. Мы могли бы оценить квадрат 17, например, как 4,1.

Пример № 2:

Оцените квадратный корень из 102

Мы найдем целое число больше квадратного корня 102 и целое число меньше квадратного корня 102.

Мы будем использовать квадратный корень из 100, так как √100 = 10

Чтобы найти число больше квадрата 102, мы воспользуемся другой стратегией.Записывать квадратный корень из всех этих чисел занимает слишком много времени. Хорошее наблюдение поможет нам быстро решить проблему.

Обратите внимание, что квадратный корень любого числа от 103 до 120 не является целым числом.

Однако квадратный корень из 121 является целым числом, поскольку 11 умножить на 11 = 121.

Таким образом, квадрат 121 даст нам целое число, которое нам нужно, которое больше квадрата 102.

Получаем 10 < √102 <11

Квадратный корень из 102 находится между 10 и 11.

No related posts.