Вычислите корень из – Калькулятор корней онлайн

Содержание

5 методов вычисления квадратного корня

При решении различных задач из курса математики и физики ученики и студенты часто сталкиваются с необходимостью извлечения корней второй, третьей или n-ой степени. Конечно, в век информационных технологий не составит труда решить такую задачу при помощи калькулятора. Однако возникают ситуации, когда воспользоваться электронным помощником невозможно.

К примеру, на многие экзамены запрещено приносить электронику. Кроме того, калькулятора может не оказаться под рукой. В таких случаях полезно знать хотя бы некоторые методы вычисления радикалов вручную.

Извлечение квадратного корня при помощи таблицы квадратов

Один из простейших способов вычисления корней заключается в использовании специальной таблицы. Что же она собой представляет и как ей правильно воспользоваться?

При помощи таблицы можно найти квадрат любого числа от 10 до 99. При этом в строках таблицы находятся значения десятков, в столбах — значения единиц. Ячейка на пересечении строки и столбца содержит в себе квадрат двузначного числа. Для того чтобы вычислить квадрат 63, нужно найти строку со значением 6 и столбец со значением 3. На пересечении обнаружим ячейку с числом 3969.

Поскольку извлечение корня — это операция, обратная возведению в квадрат, для выполнения этого действия необходимо поступить наоборот: вначале найти ячейку с числом, радикал которого нужно посчитать, затем по значениям столбика и строки определить ответ. В качестве примера рассмотрим вычисление квадратного корня 169.

Находим ячейку с этим числом в таблице, по горизонтали определяем десятки — 1, по вертикали находим единицы — 3. Ответ: √169 = 13.

Аналогично можно вычислять корни кубической и n-ой степени, используя соответствующие таблицы.

Преимуществом способа является его простота и отсутствие дополнительных вычислений. Недостатки же очевидны: метод можно использовать только для ограниченного диапазона чисел (число, для которого находится корень, должно быть в промежутке от 100 до 9801). Кроме того, он не подойдёт, если заданного числа нет в таблице.

Разложение на простые множители

Если таблица квадратов отсутствует под рукой или с её помощью оказалось невозможно найти корень, можно попробовать разложить число, находящееся под корнем, на простые множители. Простые множители — это такие, которые могут нацело (без остатка) делиться только на себя или на единицу. Примерами могут быть 2, 3, 5, 7, 11, 13 и т. д.

Рассмотрим вычисление корня на примере √576. Разложим его на простые множители. Получим следующий результат: √576 = √(2 ∙ 2 ∙ 2 ∙ 2 ∙ 2 ∙ 2 ∙ 3 ∙ 3) = √(2 ∙ 2 ∙ 2)² ∙ √3². При помощи основного свойства корней √a² = a избавимся от корней и квадратов, после чего подсчитаем ответ: 2 ∙ 2 ∙ 2 ∙ 3 = 24.

Что же делать, если у какого-либо из множителей нет своей пары? Для примера рассмотрим вычисление √54. После разложения на множители получаем результат в следующем виде: √54 = √(2 ∙ 3 ∙ 3 ∙ 3) = √3² ∙ √(2 ∙ 3) = 3√6. Неизвлекаемую часть можно оставить под корнем. Для большинства задач по геометрии и алгебре такой ответ будет засчитан в качестве окончательного. Но если есть необходимость вычислить приближённые значения, можно использовать методы, которые будут рассмотрены далее.

Метод Герона

Как поступить, когда необходимо хотя бы приблизительно знать, чему равен извлечённый корень (если невозможно получить целое значение)? Быстрый и довольно точный результат даёт применение метода Герона. Его суть заключается в использовании приближённой формулы:

√R = √a + (R — a) / 2√a,

где R — число, корень которого нужно вычислить, a — ближайшее число, значение корня которого известно.

Рассмотрим, как работает метод на практике, и оценим, насколько он точен. Рассчитаем, чему равен √111. Ближайшее к 111 число, корень которого известен — 121. Таким образом, R = 111, a = 121. Подставим значения в формулу:

√111 = √121 + (111 — 121) / 2 ∙ √121 = 11 — 10 / 22 ≈ 10,55.

Теперь проверим точность метода:

10,55² = 111,3025.

Погрешность метода составила приблизительно 0,3. Если точность метода нужно повысить, можно повторить описанные ранее действия:

√111 = √111,3025 + (111 — 111,3025) / 2 ∙ √111,3025 = 10,55 — 0,3025 / 21,1 ≈ 10,536.

Проверим точность расчёта:

10,536² = 111,0073.

После повторного применения формулы погрешность стала совсем незначительной.

Вычисление корня делением в столбик

Этот способ нахождения значения квадратного корня является чуть более сложным, чем предыдущие. Однако он является наиболее точным среди остальных методов вычисления без калькулятора

Допустим, что необходимо найти квадратный корень с точностью до 4 знаков после запятой. Разберём алгоритм вычислений на примере произвольного числа 1308,1912.

Разделим лист бумаги на 2 части вертикальной чертой, а затем проведём от неё ещё одну черту справа, немного ниже верхнего края. Запишем число в левой части, разделив его на группы по 2 цифры, двигаясь в правую и левую сторону от запятой. Самая первая цифра слева может быть без пары. Если же знака не хватает в правой части числа, то следует дописать 0. В нашем случае получится 13 08,19 12.
Подберём самое большое число, квадрат которого будет меньше или равен первой группе цифр. В нашем случае это 3. Запишем его справа сверху; 3 — первая цифра результата. Справа снизу укажем 3×3 = 9; это понадобится для последующих расчётов. Из 13 в столбик вычтем 9, получим остаток 4.
Припишем следующую пару чисел к остатку 4; получим 408.
Число, находящееся сверху справа, умножим на 2 и запишем справа снизу, добавив к нему _ x _ =. Получим 6_ x _ =.
Вместо прочерков нужно подставить одно и то же число, меньшее или равное 408. Получим 66×6 = 396. Напишем 6 справа сверху, т. к. это вторая цифра результата. Отнимем 396 от 408, получим 12.
Повторим шаги 3—6. Поскольку снесённые вниз цифры находятся в дробной части числа, необходимо поставить десятичную запятую справа сверху после 6. Запишем удвоенный результат с прочерками: 72_ x _ =. Подходящей цифрой будет 1: 721×1 = 721. Запишем её в ответ. Выполним вычитание 1219 — 721 = 498.
Выполним приведённую в предыдущем пункте последовательность действий ещё три раза, чтобы получить необходимое количество знаков после запятой. Если не хватает знаков для дальнейших вычислений, у текущего слева числа нужно дописать два нуля.

В результате мы получим ответ: √1308,1912 ≈ 36,1689. Если проверить действие при помощи калькулятора, можно убедиться, что все знаки были определены верно.

Поразрядное вычисление значения квадратного корня

Метод обладает высокой точностью. Кроме того, он достаточно понятен и для него не требуется запоминать формулы или сложный алгоритм действий, поскольку суть способа заключается в подборе верного результата.

Извлечём корень из числа 781. Рассмотрим подробно последовательность действий.

Выясним, какой разряд значения квадратного корня будет являться старшим. Для этого возведём в квадрат 0, 10, 100, 1000 и т. д. и выясним, между какими из них находится подкоренное число. Мы получим, что 10² < 781 < 100², т. е. старшим разрядом будут десятки.
Подберём значение десятков. Для этого будем по очереди возводить в степень 10, 20, …, 90, пока не получим число, превышающее 781. Для нашего случая получим 10² = 100, 20² = 400, 30² = 900. Значение результата n будет находиться в пределах 20 < n <30.

Аналогично предыдущему шагу подбирается значение разряда единиц. Поочерёдно возведём в квадрат 21,22, …, 29: 21² = 441, 22² = 484, 23² = 529, 24² = 576, 25² = 625, 26² = 676, 27² = 729, 28² = 784. Получаем, что 27 < n < 28.
Каждый последующий разряд (десятые, сотые и т. д. ) вычисляется так же, как было показано выше. Расчёты проводятся до тех пор, пока не будет достигнута необходимая точность.

Видео

Из видео вы узнаете, как извлекать квадратные корни без использования калькулятора.

liveposts.ru

Вычисление квадратного корня из любого числа без калькулятора

Во время сдачи ЕГЭ по математике использование калькулятора, как известно, запрещено. Поэтому любой репетитор по математике всегда заставляет своих учеников считать все устно или на бумаге. Но время от времени встречаются задачи, при решении которых требуется извлекать квадратные корни из достаточно больших чисел, и на ЕГЭ по математике такие задачи тоже есть. С проблемой нахождения алгоритма вычисления квадратного корня из вещественного числа читатель может столкнуться (помимо ЕГЭ по математике) на различного рода математических конкурсах и олимпиадах. Итак, как найти квадратный корень без использования калькулятора?

Как репетитор по физике и математике, занимающийся подготовкой к ЕГЭ и ГИА, предлагаю вашему вниманию один действенный алгоритм, не претендующий на максимальную эффективность, но работающий безотказно с любыми вещественными числами. Приведенный метод может со временем стать столь же известным, как, к примеру, метод умножения двух чисел «столбиком», ведь он во многом на него похож.

Вот наглядная схема алгоритма вычисления квадратного корня из любого числа без использования калькулятора (кликабельно):

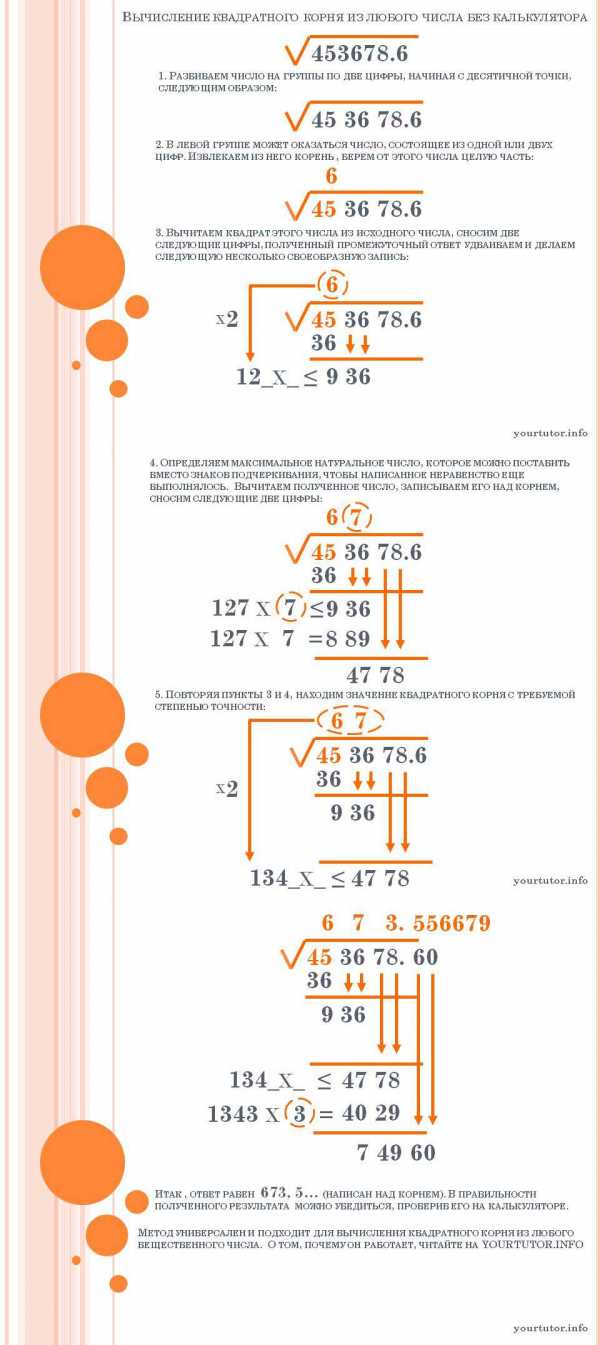
Алгоритм вычисления квадратного корня из любого вещественного числа без использования калькулятора

Однако, вопрос о том, почему данный алгоритм работает, остается пока открытым. Для того, чтобы разобраться в этом, возьмем, для примера, число, цифрами которого являются и То есть само число имеет вид Пусть корнем будет число , состоящее из цифр и То есть Выполним «столбиком» умножение

Последовательно:

То есть:

Проанализировав это разложение, понимаем, что разделяя число на пары и числу в первой паре мы ставим в соответствие число, содержащееся в Иначе говоря, квадратный корень из числа округленный до нижнего целого числа, есть

Теперь, зная значение для нахождения необходимо вычислить значение выражения или, что то же самое, значение выражения Поразмыслив над этим, понимаем, что в этом, собственно, и состоит суть действия, совершаемого при подборе числа, которое необходимо подставить на четвертом шаге алгоритма вместо знаков подчеркивания. Таким образом мы находим Зная и знаем

Такой подход может быть обобщен на случай любого количества разрядов в исходном числе. Если корень не является рациональным, вычисления могут продолжаться сколь угодно долго (с любой необходимой степенью точности). Вот такой простой алгоритм. Запомните его, возможно, он пригодится вам при сдаче ЕГЭ по математике.

Репетитор по математике
Сергей Валерьевич

yourtutor.info

❶ Как вычислить корень 🚩 как вычислить корень из 9 🚩 Математика

14 июня 2011

Автор КакПросто!

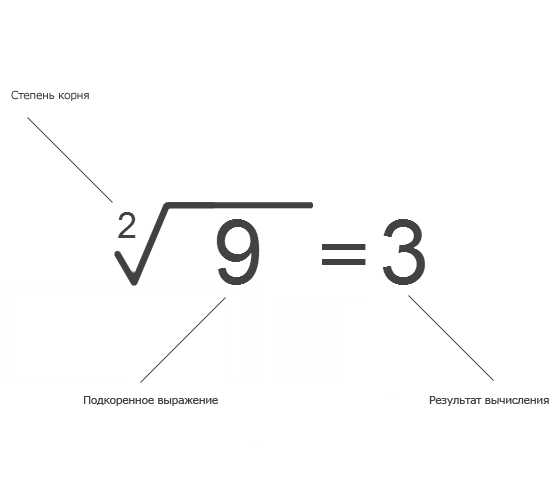
В математике существует такое понятие, как «корень». У него есть подкоренное выражение и степень, которая обозначается слева от знака корня. Корень второй степени называется квадратным, а третьей – кубическим. Функция извлечения корня из числа является обратной функции возведения числа в степень.

Статьи по теме:

Вам понадобится

Установленная система семейства Windows;
факультативно – подключение к интернет и установленный браузер.

Инструкция

Для примера, вычислим квадратный корень – корень второй степени – из числа 9.
Запустите в Windows приложение Калькулятор. В пункте меню «Вид» убедитесь, что текущим является «Обычный». Введите число 9 и нажмите кнопку «sqrt». Результатом будет число 3. Если теперь это число умножить само на себя, т.е. возвести во 2 степень, то обратно получим число 9
3? = 3 * 3 = 9 Далее, рассмотрим пример извлечения из числа 8 кубического корня – корня третьей степени. В Калькуляторе переключитесь через меню в пункте «Вид» на «Инженерный». Фиолетовыми символами обозначены различные функции инженерного калькулятора. Найдите кнопку с функцией, которая расположена точно посередине этого поля. Это функция «X^Y», т.е. произвольное число X возвести в степень Y.Если X возвести в степень, показатель которой обратный другому числу, например, 1/Y, это будет равносильно извлечению из числа X корня степени Y. В нашем примере это 8 в степени (1/3)

Вычислим значение обратного числа для показателя возводимой степени. Введите 3, найдите и нажмите в правом нижнем углу поля функций кнопку «1/X». Результатом будет длинное периодическое число 0,33333… Возьмите его в память, нажав рядом справа на кнопку «M+». Теперь введите 8, нажмите «X^Y» и извлеките значение для Y из памяти, нажав «MR». Нажмите кнопку «=» или Enter на клавиатуре. Результатом будет число 2. Если теперь это число умножить само на себя трижды, т.е. возвести в 3 степень, то обратно получим число 8
2? = 2 * 2 * 2= 8Для извлечения из числа квадратного и кубического корня достаточно возвести число в степень 0,5 и 0,25 соответственно.

Видео по теме

Обратите внимание

Степень квадратного (второй степени) корня при написании опускается, т.е. слева от знака корня число 2 отсутствует, но при вычислении это надо учитывать и указывать его.

Источники:

Квадратный корень из 1000 ответ