ВЫВОД ФОРМУЛЫ ЧИСЛА СОЧЕТАНИЙ С ПОВТОРЕНИЯМИ. ПРИМЕНЕНИЕ ФОРМУЛЫ — КиберПедия
Объект исследования: формула комбинаторики для числа сочетаний с повторениями.
Результаты, полученные лично автором: рассмотрен способ построения форумы числа сочетаний с повторениями. Решены задачи, использующие данную формулу.
Сочетания с повторениями – это сочетание n объектов по k в предположении, что каждый объект может участвовать в сочетании несколько раз. Таким образом, сочетание с повторениями из n элементов по k элементов (при этом допускается, что m>n) может содержать любой элемент сколько угодно раз от 1 до k включительно или не содержать его совсем, т. е. каждое сочетание с повторениями из n элементов по k элементов может состоять не только из k различных элементов, но и k каких угодно и как угодно повторяющихся элементов.
Существует специальная формула для вычисления числа сочетаний с повторениями. Выведем эту формулу, используя пример. Пусть в кондитерском магазине продаются пирожные 4 видов: корзиночки, наполеоны, песочные и эклеры. Если куплено 3 корзиночки (к), 1 наполеон (н), 2 песочных (п) и 1 эклер (э), то получим такую запись:111|1|11|1.
В этой записи палочки отделяют одну группу пирожных от другой. Если же куплено 2 корзиночки и 5 песочных, то получим запись 11||11111|. Ясно, что разным покупкам соответствуют при этом разные комбинации из 7 единиц и 3 палочек. Обратно, каждой комбинации единиц и палочек соответствует какая-то покупка. Например, комбинации |111|1111| соответствует покупка 3 наполеонов и 4 песочных (крайние группы отсутствуют).
В результате мы получим столько единиц, сколько предметов входит в комбинацию, т. е. k, а число палочек будет на 1 меньше, чем число типов предметов, т. е. n–1. Таким образом, мы получим перестановки с повторениями из k единиц и n–1 палочек. Различным комбинациям при этом соответствуют различные перестановки с повторениями, а каждой перестановке с повторениями соответствует своя комбинация.
Итак, число сочетаний с повторениями из элементов n типов по k равно числу P(k, n–1) перестановок с повторениями из n–1 палочек и k единиц, то есть , поэтому
Рассмотрим задачу. Сколько можно построить различных прямоугольных параллелепипедов, длина каждого ребра которых является целым числом от 1 до 10? Ответ:
Материал поступил в редколлегию 24.04.2017
УДК 519.253
Е.В. Киселёва
Научный руководитель: доцент кафедры «Высшая математика»,
к.т.н. А.Г. Белоусов
Анализ качества результатов социологических
Опросов
Объект исследования: результаты социологических опросов.
Результаты, полученные лично автором: проанализированы данные реальных социологических исследований, на основе которых предложена методика выявления недостоверности результатов опросов, опирающаяся на методы теории вероятности и математической статистики.
Результаты социологических опросов, как правило, представляют собой не только информацию, но и средство влияния на принятие решений, также они могут влиять на общественное мнение. Поскольку проведение масштабных опросов требует значительных затрат, а в случае использования результатов опросов в ненаучных целях требуются данные, подтверждающие определённый тезис, в некоторых случаях публикуются фальшивые результаты опросов: действительные результаты – иные, либо опрос на самом деле не проводится.
Сфальсифицированные результаты опросов можно условно разделить на три уровня: 1) фальсификация выявляется с помощью комбинирования арифметики и методов теории вероятностей и математической статистики, 2) выявление фальсификации требует существенного опыта в сфере теории вероятностей и математической статистики, 3) соблюдение требований предыдущего уровня, а также сбор дополнительных эмпирических данных. При этом анализ, как правило, не предоставляет строгого доказательства, что результаты опроса недостоверные, но он может позволить выявить данные, являющиеся недостоверными с высокой вероятностью.
К признакам потенциально сфальсифицированных результатов опросов, по нашему мнению, относятся: общее кратное процентов голосов, круглые величины в процентах, погрешности при суммировании процентов. Рассмотрим более детально случаи «странных» результатов с использованием центральной предельной теоремы (ЦПТ) – для вопросов с выбором нескольких вариантов.
В анкетных листах нередко встречаются вопросы, где можно выбрать несколько вариантов ответа, всего не более k, при этом вариант вида «затрудняюсь ответить» не предусматривается. Любой респондент может выбрать число вариантов от 1 до k. Допустим, выбор варианта респондентом – случайная величина. Таким образом, количество процентов, набираемых всеми вариантами по всей выборке, – случайная величина, являющаяся суммой большого числа n одинаково распределённых независимых случайных величин (никакой респондент не знает, какие варианты выбирают другие респонденты), где n – размер выборки. Согласно ЦПТ распределение суммарного процента должно быть близко к нормальному. Следовательно, если суммарный процент оказался близок к 100 или 100k, это может быть вызвано наличием сфабрикованных данных, поскольку такое случайное событие маловероятно. Если в опросе есть ряд вопросов с k>1, и хотя бы 3-4 вопроса дают суммарный процент ответов, близкий к одной из границ, следует тщательно изучить данные опроса на предмет подтасовок или непреднамеренных ошибок.
Так, в нескольких найденных источниках приводятся случаи при k=3, когда суммарный процент составлял более 260, что требует дополнительных исследований на предмет причин таких показателей. Особенно важна проверка близости к верхней границе (300% для k=3). Естественно, постоянная близость суммы процентов к одному и тому же значению, включая «идеальное» 50(k+1), также должна являться аргументом для расследования.
Ещё одним примером возможного низкого качества результатов опроса может являться следующая ситуация. Так, в публикациях, касающихся опросов проводимых среди студентов вузов, насчитывающих 5-10 тыс. чел., часто фигурирует размер выборки порядка 100-200. Допустим, в некотором вузе есть 5 тыс. студентов, и по данным было опрошено 200 студентов, то есть 0,04=4% от контингента. Вероятность неучастия в опросе составит 0,96 для взятого наугад студента, для каждого последующего она медленно убывает, если все предыдущие ответили отрицательно. Если есть разнообразие по курсам и специальностям среди студентов (гарантированная случайность выборки), то для 50 человек вероятность отсутствия среди них участника опроса составит менее 13%. Уже для 60 студентов она составит менее 9%. При увеличении числа потенциальных «неучастников» с высокой долей вероятности можно утверждать, что: имел место несуществующий опрос, или репрезентативность выборки оказалась крайне низкая (например, посещено 2-3 поточных лекции, где и было отобрано 200 респондентов).
Преимущества математических методов анализа заключаются в том, что большинство из них достаточно быстры в применении и не требуют детальных данных об опросе. Кроме того, большинство из них могут быть использованы «здесь и сейчас», на основе компьютерных технологий и интернет-ресурсов.
Положительные результаты применения математических методов свидетельствуют о высокой вероятности некачественных данных, однако не гарантируют, что не имеет место случайности, или что результаты вызваны не преднамеренной подтасовкой, а ошибками при обеспечении репрезентативности данных и подсчётах результатов организаторами опроса. Вследствие этого целесообразно использовать математические методы как дополнение к нематематическим способам выявления подтасовок.
Материал поступил в редколлегию 27.04.2017
УДК 519.2
Е.В. Минаков
Научный руководитель: ассистент кафедры «Высшая математика»,
А.О. Алейникова
cyberpedia.su
Основная формула комбинаторики
Основная формула комбинаторики
Пусть имеется k групп элементов, причем i-я группа состоит из ni элементов. Выберем по одному элементу из каждой группы. Тогда общее число N способов, которыми можно произвести такой выбор, определяется соотношением N=n1*n2*n3*…*nk.
Пример 2. Сколько трехзначных четных чисел можно составить из цифр 0, 1, 2, 3, 4, 5, 6, если цифры могут повторяться?
Решение: n1=6 (т.к. в качестве первой цифры можно взять любую цифру из 1, 2, 3, 4, 5, 6), n
Итак, N=n1*n2*n3=6*7*4=168.
В том случае, когда все группы состоят из одинакового числа элементов, т.е. n1=n2=…nk=n можно считать, что каждый выбор производится из одной и той же группы, причем элемент после выбора снова возвращается в группу. Тогда число всех способов выбора равно nk.Такой способ выбора носит названиевыборки с возвращением.
Пример 3. Сколько всех четырехзначных чисел можно составить из цифр 1, 5, 6, 7, 8?
Решение. Для каждого разряда четырехзначного числа имеется пять возможностей, значит N=5*5*5*5=54=625.
Рассмотрим множество, состоящие из n элементов. Это множество будем называть генеральной совокупностью.
Определение 1. Размещением из n элементов по mназывается любой упорядоченный набор из m различных элементов, выбранных из генеральной совокупности в n элементов.
Пример 4.Различными размещениями из трех элементов {1, 2, 3} по два будут наборы (1, 2), (2, 1), (1, 3), (3, 1), (2, 3),(3, 2). Размещения могут отличаться друг от друга как элементами, так и их порядком.
Число размещений обозначается Anm и вычисляется по формуле:
Замечание: n!=1*2*3*…*n (читается: «эн факториал»), кроме того полагают, что 0!=1.
Пример 5. Сколько существует двузначных чисел, в которых цифра десятков и цифра единиц различные и нечетные?
Решение: т.к. нечетных цифр пять, а именно 1, 3, 5, 7, 9, то эта задача сводится к выбору и размещению на две разные позиции двух из пяти различных цифр, т.е. указанных чисел будет:
Определение 2. Сочетанием из n элементов по m называется любой неупорядоченный набор из m различных элементов, выбранных из генеральной совокупности в n элементов.
Определение 3. Перестановкой из n элементов называется любой упорядоченный набор этих элементов.
Пример 7a. Всевозможными перестановками множества, состоящего из трех элементов {1, 2, 3} являются: (1, 2, 3), (1, 3, 2), (2, 3, 1), (2, 1, 3), (3, 2, 1), (3, 1, 2).
2. горох
Классическое и геометрическое определение вероятностей.
Условная вероятность
ПримерИгральная кость подбрасывается один раз. Известно, что выпало более трёх очков. Какова вероятность того, что выпало чётное число очков?
Зная, что выпало более трёх очков, мы можем сузить множество всех возможных элементарных исходов до трёх одинаково вероятных исходов: , из которых событию благоприятствуют ровно два: . Поэтому .
Посмотрим на вопрос с точки зрения первоначального эксперимента. Пространство элементарных исходов при одном подбрасывании кубика состоит из шести точек: . Слова «известно, что выпало более трёх очков» означают, что в эксперименте произошло событие . Слова «какова при этом вероятность того, что выпало чётное число очков?» означают, что нас интересует, в какой доле случаев при осуществлении происходит и . Вероятность события , вычисленную в предположении, что о результате эксперимента уже что-то известно (событие произошло), мы будем обозначать через .
Мы хотим найти, какую часть составляют исходы, благоприятствующие внутри (т.е. одновременно и ), среди исходов, благоприятствующих .
Мы пришли к выражению, которое можно считать определением условной вероятности.
Решение.
Пусть А – попадание первого стрелка, ;
В – попадание второго стрелка, .
Тогда — промах первого, ;
— промах второго, .
Найдем нужные вероятности.
а) АВ – двойное попадание,
б) – двойной промах, .
в) А+В – хотя бы одно попадание,
.
г) – одно попадание,
7. Формула полной вероятности.
Пусть событие А может произойти только совместно с одним из событий Н1, Н2,…, Нп, образующих полную группу несовместных событий. Тогда события Н1, Н2,…, Нп называются гипотезами.
Теорема. Вероятность события А, наступающего совместно с гипотезами Н1, Н2,…, Нп, равна:
где P(Hi) – вероятность i той гипотезы, а P(A/Hi) – вероятность события А при условии реализации этой гипотезы. Формула носит название формулы полной вероятности.
Доказательство.
Можно считать событие А суммой попарно несовместных событий АН1, АН2,…, АНп. Тогда из теорем сложения и умножения следует, что
что и требовалось доказать.
8. Формула Байеса.
Пусть — полная группа событий, и — некоторое событие, вероятность которого положительна. Тогда условная вероятность того, что имело место событие , если в результате эксперимента наблюдалось событие , может быть вычислена по формуле:
Доказательство.По определению условной вероятности,
9. Сводка основных правил теории вероятности.
10. Схема с повторением независимых испытаний (схема Бернулли). Формула Бернулли.
Испытания независимы, если вероятность элементарных исходов не зависят от предыдущих испытаний.
– число независимых испытаний – может произойти с вероятностью С какой вероятностью событие произойдет раз
, где – вероятность успеха – вероятность неуспеха – число сочетаний способов
Доказательство:
Теорема: Если Вероятность p наступления события Α в каждом испытании постоянна, то вероятность того, что событие A наступит k раз в n независимых испытаниях, равна: , где .
[править]Доказательство
Так как в результате независимых испытаний, проведенных в одинаковых условиях, событие наступает с вероятностью , следовательно противоположное ему событие с вероятностью .
Обозначим — наступление события в испытании с номером . Так как условия проведения опытов одинаковые, то эти вероятности равны. Пусть в результате опытов событие наступает раз, тогда остальные раз это событие не наступает. Событие может появиться раз в испытаниях в различных комбинациях, число которых равноколичеству сочетаний из элементов по . Это количество сочетаний находится по формуле:
.
При этом вероятность каждой комбинации равна произведению вероятностей:
.
Применяя теорему сложения вероятностей несовместных событий, получим окончательную Формулу Бернулли:
, где .
11. Теорема Пуассона. Функция Лапласа. Интегральная формула Муавра-Лапласа.
Теорема Пуассона.Пусть есть Пусть также дана последовательность такая, что
Тогда
Функция Лапласа
Правило трех сигм
В теории вероятностей квадратичное отклонение σx случайной величины x (от ее математического ожидания) определяется как квадратный корень из дисперсии Dx и называют также стандартным отклонением величины x. Для любой случайной величины x с математическим ожиданием mx и квадратичным отклонением σx вероятность отклонения x от mx, больших по абсолютной величине k·σx, k > 0, не превосходит 1/k2 (неравенство Чебышева). В случае нормального распределения указанная вероятность при k = 3 равна 0.0027. В практических задачах, приводящих к нормальному распределению, чаще всего пренебрегают возможностью отклонения от среднего, большего 3·σx.
18. Закон распределения Пуассона. Функция надежности. Интенсивность отказов. Показательный закон.
Распределение Пуассона — это частный случай биномиального распределения (при n >> 0 и приp –> 0 (редкие события)).
Из математики известна формула, позволяющая примерно подсчитать значение любого члена биномиального распределения:
где a = n · p — параметр Пуассона (математическое ожидание), а дисперсия равна математическому ожиданию.
Пусть элемент (то есть некоторое устройство) начинает работать в момент времени t0 = 0 и должен проработать в течение периода времени t. Обозначим за Т непрерывную случайную величину — время безотказной работы элемента, тогда функция F(t) = p(T > t) определяет вероятность отказа за время t. Следовательно, вероятность безотказной работы за это же время равна
R(t) = p(T > t) = 1 — F(t).
Эта функция называется функцией надежности.
19. Центральная предельная теорема.
Центральная Предельная Теорема 1 Пусть — последовательность независимых одинаково распределенных с.в. с конечной дисперсией. Обозначим и . Тогда
где — функция распределения стандартного нормального закона.
20. Закон Больших чисел.
Теорема Чебышева
Теорема. Если Х1, Х2, …, Хn— попарно независимые случайные величины, причем дисперсии их равномерно ограничены (не превышаю постоянного числа С), то, как бы мало не было положительное числоe, вероятность неравенства
будет сколь угодно близка к единице, если число случайных величин достаточно велико.
Т.е. можно записать:
Часто бывает, что случайные величины имеют одно и то же математическое ожидание. В этом случае теорема Чебышева несколько упрощается:
Дробь, входящая в записанное выше выражение есть не что иное как среднее арифметическое возможных значений случайной величины.
Теорема утверждает, что хотя каждое отдельное значение случайной величины может достаточно сильно отличаться от своего математического ожидания, но среднее арифметическое этих значений будет неограниченно приближаться к среднему арифметическому математических ожиданий.
Отклоняясь от математического ожидания как в положительную так и в отрицательную сторону, от своего математического ожидания, в среднем арифметическом отклонения взаимно сокращаются.
Таким образом, величина среднего арифметического значений случайной величины уже теряет характер случайности.
23. Следствие из теоремы Чебышева.
Если дисперсии независимых случайных величин ограничены одной и той же постоянной С, то, как бы мало не было данное положительное число Е, вероятность того, что отклонение средней арифметической этих случайных величин от средней арифметической их математических ожиданий а1, а2, …, аn не превзойдет по абсолютной величине Е, как угодно близка к единице, если число случайных величин достаточно велико.
Следствие.
Если независимые случайные величины имеют одинаковые, равные a, математические ожидания, дисперсии их ограничены одной и той же постоянной С, а число случайных величин достаточно велико, то, сколько мало ни было данное положительное число Е, как угодно близка к единице вероятность того, что отклонение средней арифметической этих случайных величин от а не превзойдет по абсолютной величине Е.
При доказательстве теоремы Чебышева и следствия из нее с помощью неравенства Чебышева получаем такие оценки:
, (63)
24. Закон больших чисел в форме Бернулли.
(ЗБЧ Бернулли).Пусть событие может произойти в любом из независимых испытаний с одной и той же вероятностью , и пусть — число осуществлений события в испытаниях. Тогда . При этом для любого
Доказательство.Заметим, что есть сумма независимых, одинаково распределённых случайных величин, имеющих распределение Бернулли с параметром (индикаторовтого, что в соответствующем испытании произошло ): , где
и ,
Осталось воспользоваться ЗБЧ в форме Чебышёва и неравенством .
25. Случайные векторы. Совместный закон распределения двух случайных величин.
Горох!)))
Основная формула комбинаторики
Пусть имеется k групп элементов, причем i-я группа состоит из ni элементов. Выберем по одному элементу из каждой группы. Тогда общее число N способов, которыми можно произвести такой выбор, определяется соотношением N=n1*n2*n3*…*nk.
Пример 2. Сколько трехзначных четных чисел можно составить из цифр 0, 1, 2, 3, 4, 5, 6, если цифры могут повторяться?
Решение: n1=6 (т.к. в качестве первой цифры можно взять любую цифру из 1, 2, 3, 4, 5, 6), n2=7 (т.к. в качестве второй цифры можно взять любую цифру из 0, 1, 2, 3, 4, 5, 6), n3=4 (т.к. в качестве третьей цифры можно взять любую цифру из 0, 2, 4, 6).
Итак, N=n1*n2*n3=6*7*4=168.
В том случае, когда все группы состоят из одинакового числа элементов, т.е. n1=n2=…nk=n можно считать, что каждый выбор производится из одной и той же группы, причем элемент после выбора снова возвращается в группу. Тогда число всех способов выбора равно nk.Такой способ выбора носит названиевыборки с возвращением.
Пример 3. Сколько всех четырехзначных чисел можно составить из цифр 1, 5, 6, 7, 8?
Решение. Для каждого разряда четырехзначного числа имеется пять возможностей, значит N=5*5*5*5=54=625.
Рассмотрим множество, состоящие из n элементов. Это множество будем называть генеральной совокупностью.
Определение 1. Размещением из n элементов по mназывается любой упорядоченный набор из m различных элементов, выбранных из генеральной совокупности в n элементов.
Пример 4.Различными размещениями из трех элементов {1, 2, 3} по два будут наборы (1, 2), (2, 1), (1, 3), (3, 1), (2, 3),(3, 2). Размещения могут отличаться друг от друга как элементами, так и их порядком.
Число размещений обозначается Anm и вычисляется по формуле:
Замечание: n!=1*2*3*…*n (читается: «эн факториал»), кроме того полагают, что 0!=1.
Пример 5. Сколько существует двузначных чисел, в которых цифра десятков и цифра единиц различные и нечетные?
Решение: т.к. нечетных цифр пять, а именно 1, 3, 5, 7, 9, то эта задача сводится к выбору и размещению на две разные позиции двух из пяти различных цифр, т.е. указанных чисел будет:
Определение 2. Сочетанием из n элементов по m называется любой неупорядоченный набор из m различных элементов, выбранных из генеральной совокупности в n элементов.
Определение 3. Перестановкой из n элементов называется любой упорядоченный набор этих элементов.
Пример 7a. Всевозможными перестановками множества, состоящего из трех элементов {1, 2, 3} являются: (1, 2, 3), (1, 3, 2), (2, 3, 1), (2, 1, 3), (3, 2, 1), (3, 1, 2).
2. горох
infopedia.su
Комбинаторные формулы
Пусть имеется множество, состоящее из n элементов. Обозначим его
. Перестановкой из n элементов называется заданный порядок во множестве .Примеры перестановок:
1)распределение n различных должностей среди n человек;
2)расположение n различных предметов в одном ряду.
Сколько различных перестановок можно образовать во множестве
? Число перестановок обозначается Pn (читается “Р из n”).Чтобы вывести формулу числа перестановок, представим себе n ячеек, пронумерованных числами
1,2,…n. Все перестановки будем образовывать, располагая элементы Un в этих ячейках. В первую ячейку можно занести любой из n элементов (иначе: первую ячейку можно заполнить n различными способами). Заполнив первую ячейку, можно найти n–1 вариантов заполнения второй ячейки. Таким образом, существует n(n–1) вариантов заполнения двух первых ячеек. При заполнении первых двух ячеек можно найти n–2 варианта заполнения третьей ячейки, откуда получается, что три ячейки можно заполнить n(n-1)(n-2) способами. Продолжая этот процесс, получим, что число способов заполнения n ячеек равно . ОтсюдаPn = n(n – 1)(n – 2)…×3×2×1
Число n(n – 1)(n – 2)…×3×2×1, то есть произведение всех натуральных чисел от 1 до n, называется «n-факториал» и обозначается n! Отсюда Pn =n!
По определению считается: 1!=1; 0!=1.
Пример. Сколько существует вариантов замещения 5-ти различных вакантных должностей 5-ю кандидатами?
.Размещениями из n элементов по k элементов будем называть упорядоченные подмножества, состоящие из k элементов множества
(множества, состоящего из n элементов). Число размещений из n элементов по k элементов обозначается (читается «А из n по k»).Одно размещение из n элементов по k элементов может отличаться от другого как набором элементов, так и порядком их расположения.
Примеры задач, приводящих к необходимости подсчета числа размещений
1) Сколькими способами можно выбрать из 15 человек 5 кандидатов и назначить их на 5 различных должностей?
2) Сколькими способами можно из 20 книг отобрать 12 и расставить их в ряд на полке?
В задачах о размещениях полагается k<n. В случае, если k=n, то легко получить
Для подсчета
используем тот же метод, что использовался для подсчета Pn , только здесь возьмем лишь k ячеек. Первую ячейку можно заполнить n способами, вторую, при заполненной первой, можно заполнить n–1 способами. Таким образом, существует п(п–1) вариантов заполнения первых двух ячеек. Можно продолжать этот процесс до заполнения последней k–й ячейки. Эту ячейку при заполненных первых k–1 ячейках можно заполнитьn–(k–1) (или n–k+1) способами. Таким образом, все k ячеек заполняются числом способов, равным
Отсюда получаем:
Пример. Сколько существует различных вариантов выбора 4-х кандидатур из 9-ти специалистов для поездки в 4 различных страны?
Сочетаниями из n элементов по k элементов называются подмножества, состоящие из k элементов множества
(множества, состоящего из n элементов).Одно сочетание от другого отличается только составом выбранных элементов (но не порядком их расположения, как у размещений).
Число сочетаний из n элементов по k элементов обозначается
(читается «C из n по k»).Примеры задач, приводящих к подсчету числа сочетаний:
1) Сколько существует вариантов выбора 6-ти человек из 15 кандидатов для назначения на работу в одинаковых должностях?
2) Сколькими способами можно из 20 книг отобрать 12 книг?
Выведем формулу для подсчета числа сочетаний. Пусть имеется множество
и нужно образовать упорядоченное подмножество множества , содержащее k элементов (то есть образовать размещение). Делаем это так:1) выделим какие-либо k элементов из n элементов множества
Это, согласно сказанному выше, можно сделать способами;2) упорядочим выделенные k элементов, что можно сделать
способами. Всего можно получить вариантов (упорядоченных подмножеств), откуда следует: , то есть (1)Пример: 6 человек из 15 можно выбрать числом способов, равным
Несложно понять, что осуществить выбор подмножества из т элементов множества, насчитывающего п элементов, можно, выбрав п–т элементов, которые не войдут в интересующее нас подмножество. Отсюда следует свойство числа сочетаний
Эту формулу можно доказать, используя формулу (1).
Задачи на подсчет числа подмножеств конечного множества называются комбинаторными. Рассмотрим некоторые комбинаторные задачи.
1.Из семи заводов организация должна выбрать три для размещения трех различных заказов. Сколькими способами можно разместить заказы?
Так как из условия ясно, что каждый завод может либо получить один заказ, либо не получить ни одного, и что выбрав три завода, можно по-разному разместить среди них заказы, здесь нужно считать число размещений
2.Если из текста задачи 1 убрать условие различия трех заказов, сохранив все остальные условия, получим другую задачу. Теперь способ размещения заказов определяется только выбором тройки заводов, так как все эти заводы получат одинаковые заказы, и число вариантов определяется как число сочетаний.3.Имеются 7 заводов. Сколькими способами организация может разместить на них три различных производственных заказа? (Заказ нельзя дробить, то есть распределять его на нескольких заводах).
В отличие от условия первой задачи, здесь организация может отдать все три заказа первому заводу или, например, отдать два заказа второму заводу, а один — седьмому.
Задача решается так. Первый заказ может быть помещен семью различными способами (на первом заводе, на втором и т.д.). Поместив первый заказ, имеем семь вариантов помещения второго (иначе, каждый способ помещения первого заказа может сопровождаться семью способами помещения второго). Таким образом, существует 7×7=49 способов размещения первых двух заказов. Разместив их каким-либо образом, можем найти 7 вариантов помещения третьего (иначе, каждый способ размещения первых двух заказов может сопровождаться семью различными способами помещения третьего заказа). Следовательно, существуют 49×7=73 способов размещения трех заказов. (Если бы заказов было n, то получилось бы 7n способов размещения).
4.Как решать задачу 3, если в ее тексте вместо слов «различных производственных заказа» поставить «одинаковых производственных заказа»? Это трудная задача. Ниже приводится аналогичная задача– Задача V с решением.
5.Добавим к условию задачи 1 одну фразу: организация также должна распределить три различных заказа на изготовление деревянных перекрытий среди 4-х лесопилок. Сколькими способами могут быть распределены все заказы?
Каждый из
способов распределения заказов на заводах может сопровождаться способами размещения заказов на лесопилках. Общее число возможных способов размещения всех заказов будет равно6. Риэлтерская фирма предлагает на продажу 5 больших квартир и 4 малогабаритных квартиры. Банк намеревается купить 4квартиры, причём среди них не должно быть более двух малогабаритных. Сколько вариантов выбора имеет банк?
Банк может купить 4 большие квартиры. У него есть возможность выбрать 4 из 5-ти предлагаемых квартир, и число вариантов здесь равно
. Если банк решит купить три большие квартиры и одну малогабаритную, то число вариантов выбора у него будет равно . Если будет принято решение купить две малогабаритных квартиры и две больших квартиры, то число вариантов будет равным . Таким образом, у банка есть 105 вариантов выбора.mirznanii.com
Элементы комбинаторики
Лекция №17-18
Элементы комбинаторики
1. Кортежи и декартово произведение множеств
Определение.
Пусть даны множества
.Кортежем длины n составленным из элементов этих множеств
называется конечная последовательность
,
где для всехk ()
имеем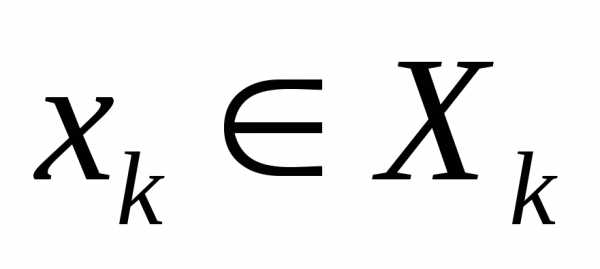 .
Элемент
.
Элемент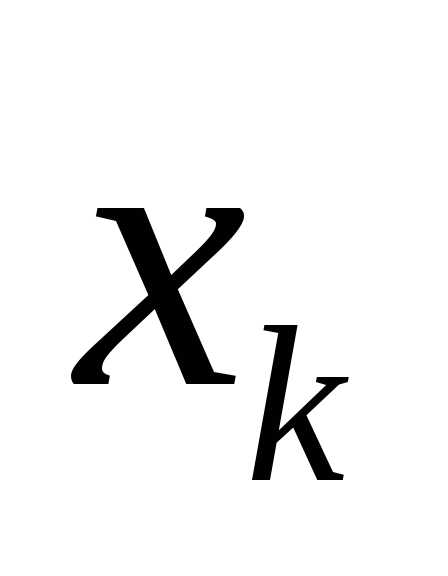 называетсяk-ой
координатой (или k-ой
координатой) кортежа
называетсяk-ой
координатой (или k-ой
координатой) кортежа  .
.
Пример 1.
Из множеств A = {a,b,c} и B = {1,2} можно составить 6 картежей длины 2: (a,1), (a,2), (b,1), (b,2), (c,1), (c,2).
Определение.
Два кортежа равны в том и только в том случае, когда они имеют одинаковую длину, причем их координаты стоящие на местах с одинаковыми номерами равны.
Определение.
Пусть
– некоторое множества. Ихдекартовым
произведением называют множество состоящее из всех
кортежей вида
,
где ,.
Декартово произведение этих множеств
обозначается так.
,.
Декартово произведение этих множеств
обозначается так.
Пример.
Пусть даны два множества = {1,2,3} и B = {x,y}. Тогда
,
.
Этот пример
показывает, что, вообще говоря, декартовы
произведения 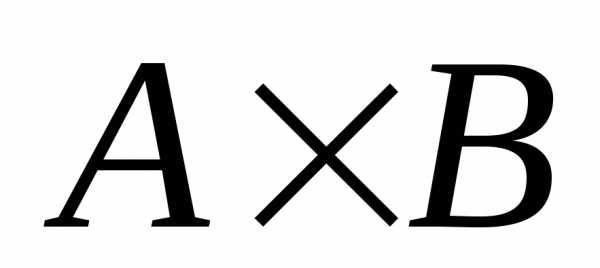 и
и 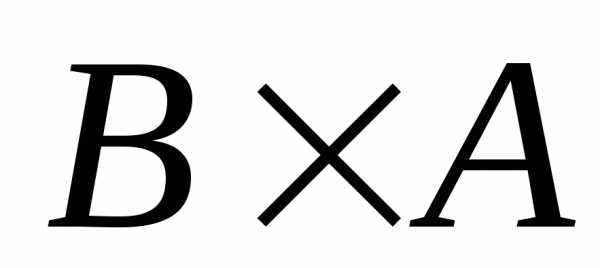 различны, хотя они содержат одинаковое
число элементов. Различны и множества
, и
– первое состоит из троек (a,b,c),
второе – из пар вида ((a,b),c),
а третье – из пар вида (a,(b,c)),
где во всех трех случаях
различны, хотя они содержат одинаковое
число элементов. Различны и множества
, и
– первое состоит из троек (a,b,c),
второе – из пар вида ((a,b),c),
а третье – из пар вида (a,(b,c)),
где во всех трех случаях  ,
,  ,
, 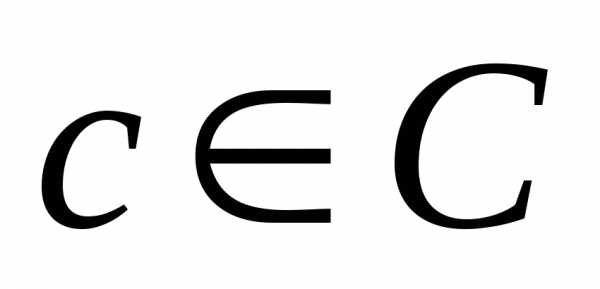 .
.
Если хотя бы одно из множеств пусто, то считают их декартово произведение пустым .
2. Основные законы комбинаторики. Правило суммы.
Пример 2.
Если на блюде лежат 7 яблока и 4 груши, то выбрать один плод можно 7+4=11 способами. В общем виде: если элемент a можно выбрать m способами, а элемент b n способами, причем любой выбор элемента a будет отличен от выбора элемента b, то выбор a или b можно сделать m+n способами. На языке теории множеств это правило формулируется следующим образом.
Теорема I.
Если пересечение конечных множеств A и B пусто , то число элементов в их объединении равно сумме чисел элементов множествA и B:
. (1)
Следствие.
Если конечные
множества
попарно не пересекаются, то есть еслипри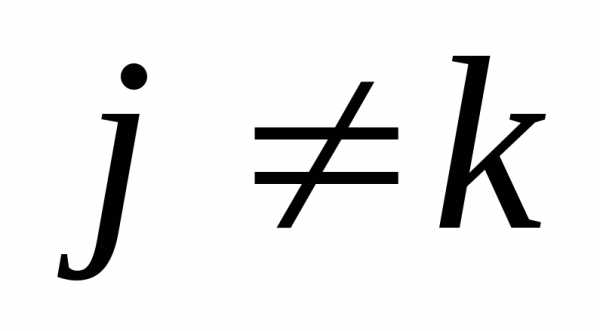 ,
то справедливо равенство
,
то справедливо равенство
. (2)
Рассмотрим случай, когда множества могут иметь не пустые пересечения.
Теорема II.
Для любых конечных множеств A и B верно равенство
. (3)
Формула (3) является частным случаем более общей формулы
, (4)
которую называют формулой включений и исключений. При m = 3 имеем число элементов
. (5)
Пример 2.
В группе обучается 42 студента. Из них 16 участвуют в секции по легкой атлетике, 24 – в футбольной секции, 15 – в шахматной секции, 11 – в секции по легкой атлетике и в футбольной, 8 легкоатлетической и шахматной, 12 – в футбольной и шахматной, а 6 во всех трех секциях. Остальные студенты увлекаются только туризмом. Сколько туристов является туристами.
Решение.
Пусть V – множество всех студентов, А – число студентов в секции по легкой атлетике, В – футбольной, С – шахматной, D – туристической. По условию имеем причем.
n(V)=42, n(A)=16, n(B)=24, n(C)
= 15, n( )
= 11, n(
)
= 11, n( )
= 8,
)
= 8,
n(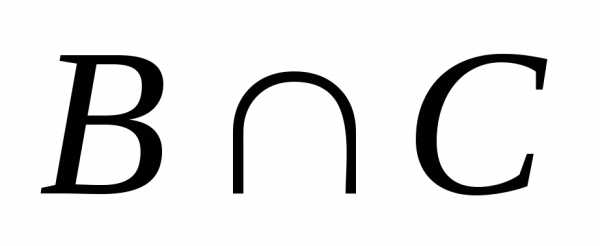 )
= 12, n()
= 6.
)
= 12, n()
= 6.
По формуле (5) получаем .
Поэтому .
Ответ: туризмом занимается 12 студентов.
3. Правило произведения
Теорема 1.
Если множества A и B конечны, то число пар в их декартовом произведении равно произведению чисел элементов этих множеств.
. (6)
Доказательство.
Множество 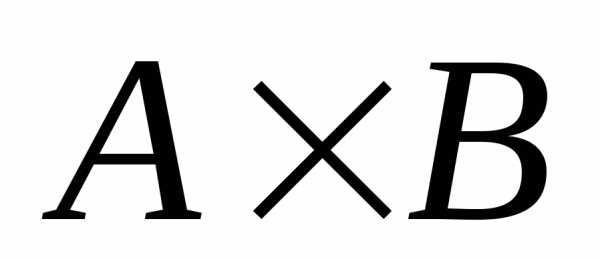 состоит из пар вида (a,b),
где
состоит из пар вида (a,b),
где  ,
, 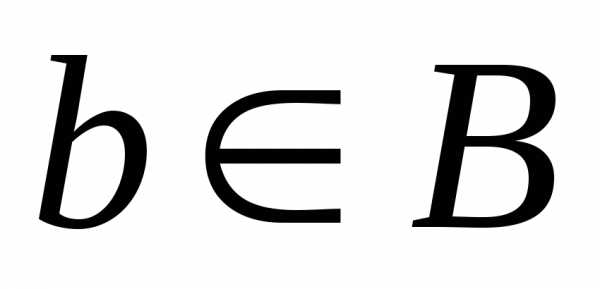 .
Если
и ,
то эти пары можно записать в виде
следующей таблицы:
.
Если
и ,
то эти пары можно записать в виде
следующей таблицы:
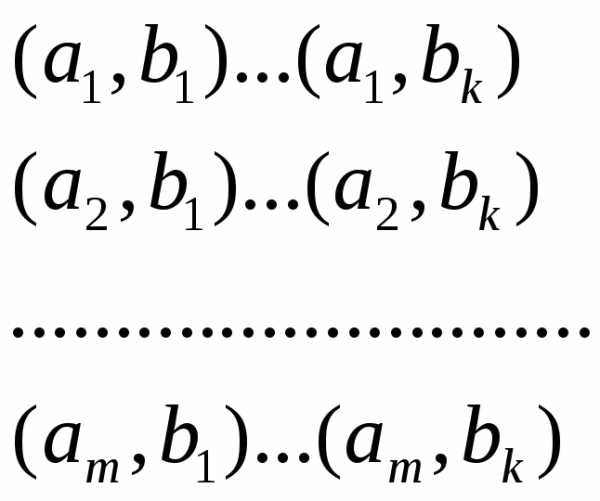
Число этих пар
равно 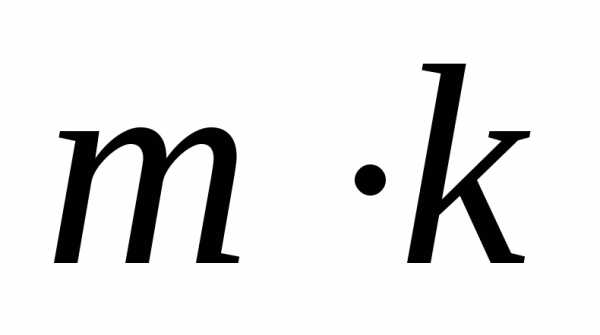 ,
то есть.
С помощью метода математической индукции
формула обобщается на любое число
множеств.
,
то есть.
С помощью метода математической индукции
формула обобщается на любое число
множеств.
Теорема 2.
Если множества конечны, то справедливо равенство
. (7)
Пример.
Сколько номеров, состоящих из двух букв, за которыми идут 5 цифр можно составить используя 32 буквы и 10 цифр?
Решение.
Обозначим множество
из 32 букв через A,
а множество из 10 цифр через B.
Каждый номер требуемого вида является
кортежем из декартова произведения
,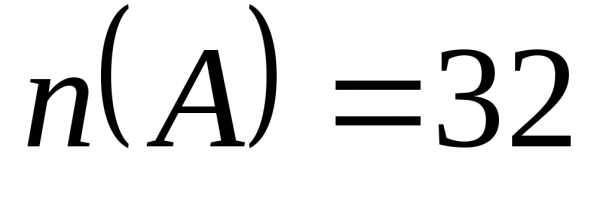 ,
,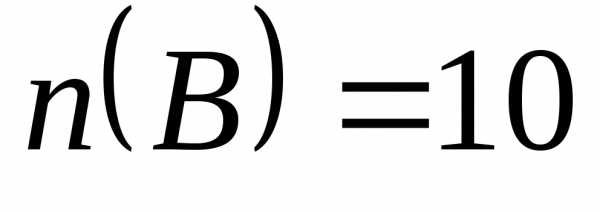 .
.
По формуле (7) .
Обобщение теоремы 2.
Если первую
координату кортежа длины k можно выбрать 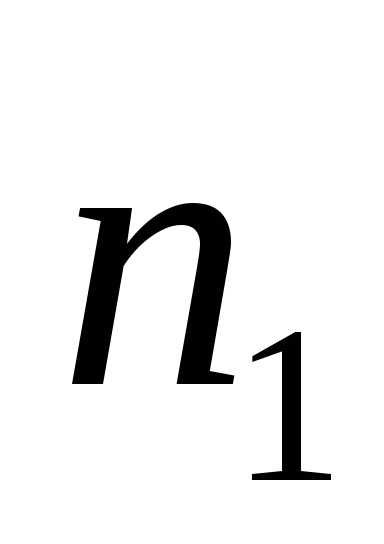 способами, при любом выборе первой
координаты вторая выбирается
способами, при любом выборе первой
координаты вторая выбирается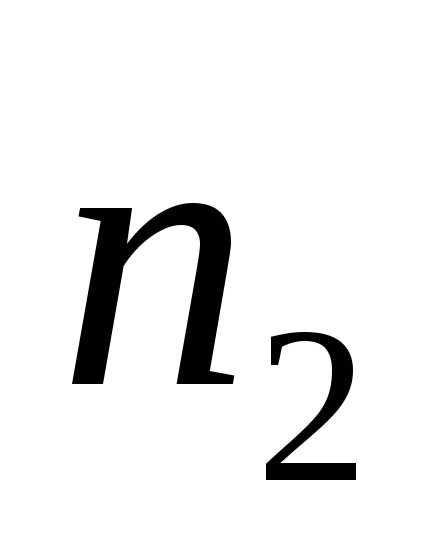 способами, при любом выборе первых двух
координат третья выбирается
способами, при любом выборе первых двух
координат третья выбирается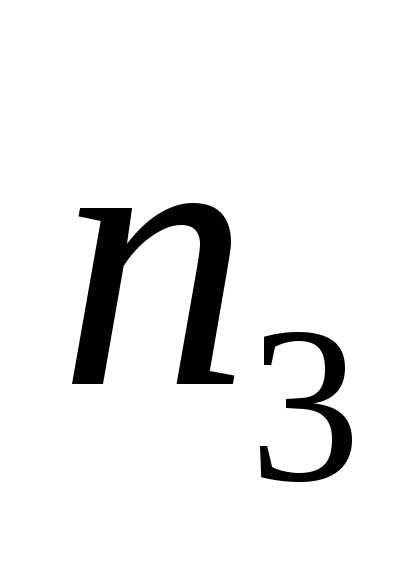 способами и так далее доk-ой
координаты включительно, то общее число
полученных таким образом картежей равно
способами и так далее доk-ой
координаты включительно, то общее число
полученных таким образом картежей равно 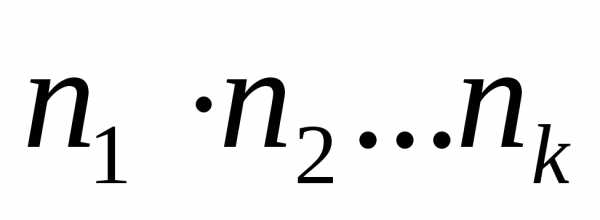
Основные формулы комбинаторики.
1. Размещения с повторениями.
Определение.
Кортежами длины k составленные из элементов m – элементного множества X называют размещениями
с повторениями из m элементов по k.
Число этих кортежей обозначают 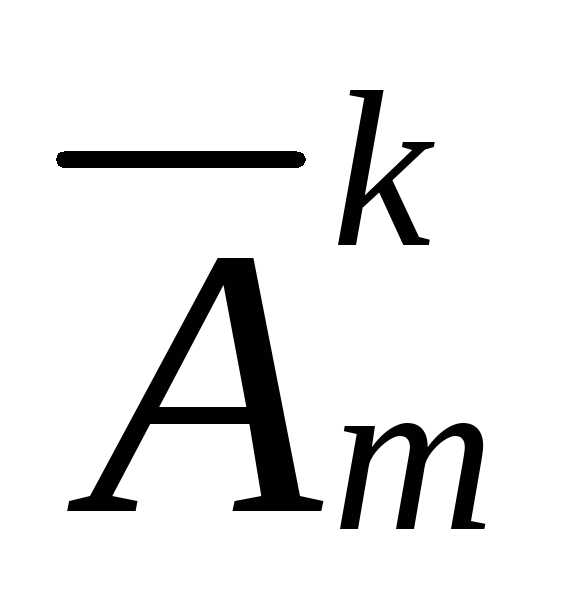 (букваA
от французского слова arrangement
– размещение. Черта сверху указывает
на возможность повторения элементов).
(букваA
от французского слова arrangement
– размещение. Черта сверху указывает
на возможность повторения элементов).
 .
(8)
.
(8)
Пример.
Сколько пятизначных номеров можно составить из 9 цифр 1,2,3,4,5,6,7,8,9?
Решение.
Такие номера являются кортежами длины 5, составленными из элементов множества X = {1,2,3,4,5,6,7,8,9}. По формуле (8) их число равно .
2. Размещения без повторений.
Определение
Упорядоченное
множество длины k составленное из элементов m – элементарного множества X называют размещениями
без повторений из m элементов множества X по k и обозначают 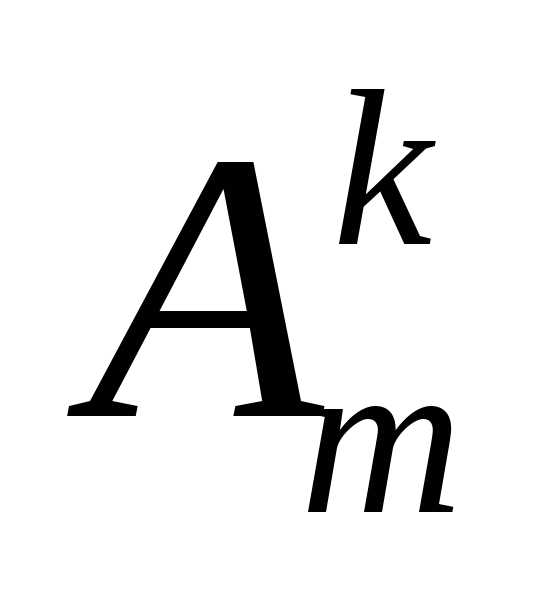 .
Число размещений без повторений изm
элементов по k находится по формуле
.
Число размещений без повторений изm
элементов по k находится по формуле
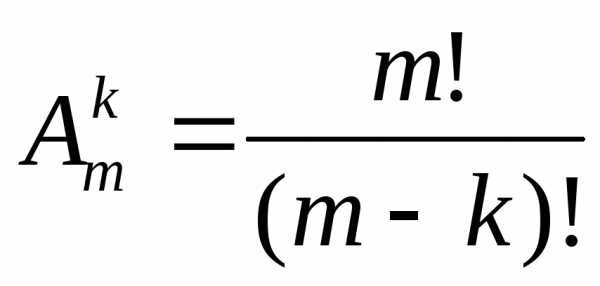 . (9)
. (9)
Пример.
Сколькими способами можно выбрать из группы, состоящей из 40 студентов старосту, профорга, физорга.
Решение.
Любой такой выбор является размещением без повторений из 40 элементов по 3.
.
3. Перестановки без повторений.
Определение.
Перестановками
без повторений из m
элементов называют размещения
без повторений из этих элементов по m.
Число перестановок из m
элементов обозначают 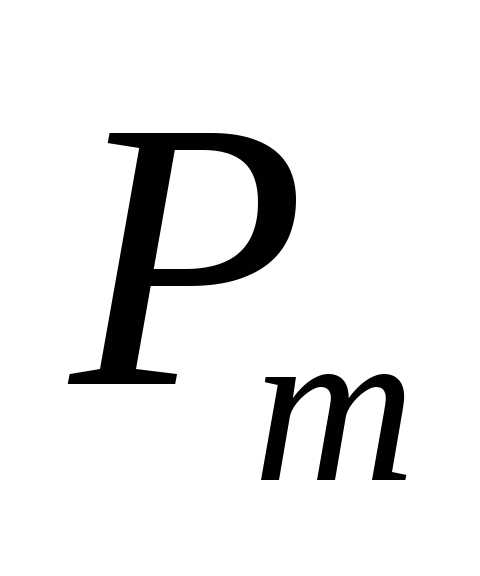 от французского словаpermutation
– перестановка и находятся по формуле
от французского словаpermutation
– перестановка и находятся по формуле
. (10)
4. Сочетания без повторений
Определение.
Будем строить из
элементов множества X не кортежи, а подмножества. k – элементные подмножества m – элементного множества X называют сочетаниями
без повторений из элементов этого множества по k.
Их число обозначают 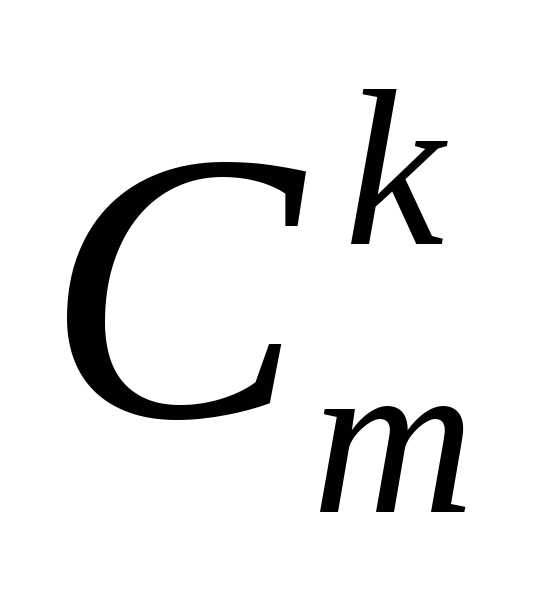 .
От французского словаcombination
– комбинация.
.
От французского словаcombination
– комбинация.
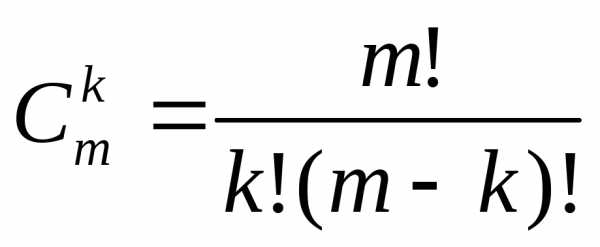 . (11)
. (11)
Пример.
Сколькими способами можно составить команду по бегу из четырех человек для соревнования по бегу если имеется 7 бегунов?
Решение.
Элементы комбинаторики
5. Перестановки с повторениями
Перестановкой с повторениямисоставаиз буквназывают любой кортеж длины,
в который буква входит
входит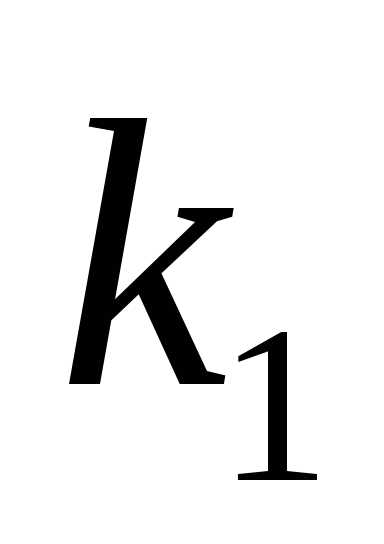 раз, …, а буква
раз, …, а буква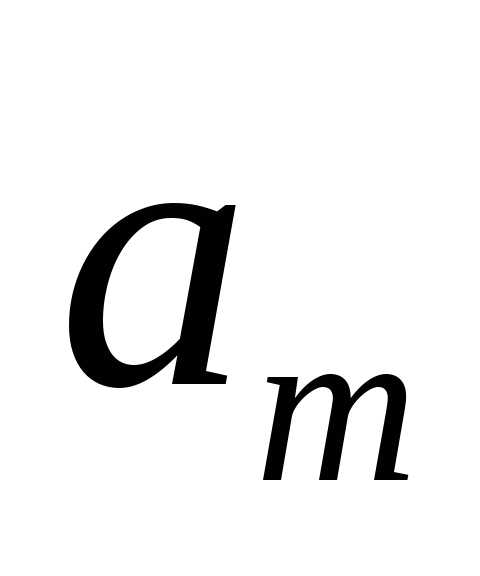 входит
входит раз. Число таких перестановок обозначают.
раз. Число таких перестановок обозначают.
. (1)
Пример.
Кортеж (a,b,a,a,c,b,b,b,c) является перестановкой с повторениями из трех буква, четырех буквbи двух буквс. Его состав выражается кортежем (3,4,2). Мы считаем из буквa,b,cбукваa– первая,b– вторая,c – третья.
6. Сочетания с повторениями
Пусть имеются предметы mвидов и из них составляют набор, состоящий
изk– элементов. Два
таких набора считаются одинаковыми в
том и только в том случае, когда они
имеют одинаковый состав. Такие наборы
назовем сочетаниями с повторениями изmэлементов поk.
Число сочетаний с повторениями изmэлементов поkобозначим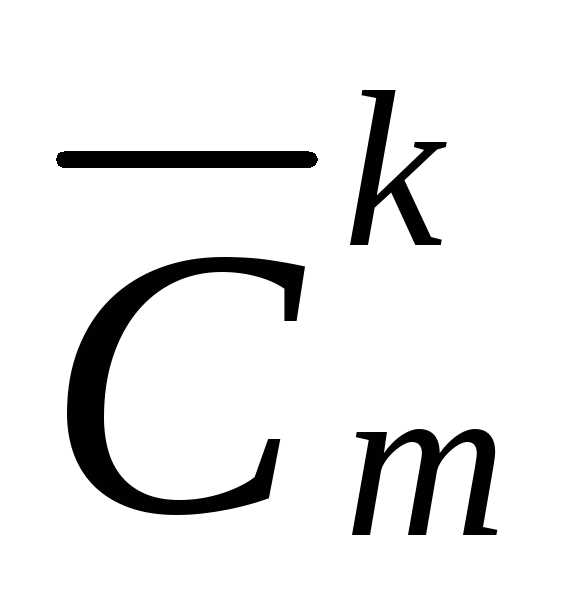 ,
,
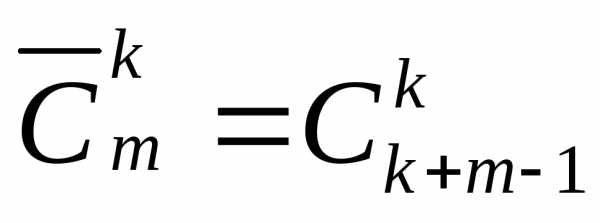 . (2)
. (2)
Пример.
Сколько наборов из семи пирожных можно составить, если в продаже имеются четыре сорта пирожных?
Решение.
Сочетания и биномиальные коэффициенты
Рассмотрим формулы
1) .
2) .
3) .
4) Можно показать, что .
Коэффициенты при каждом члене можно найти при помощи «треугольника Паскаля»
Если n – большое число, то ясно, что по
треугольнику Паскаля вычислять
коэффициенты правой части долго. Поэтому
желательно знать общую формулу вычисления 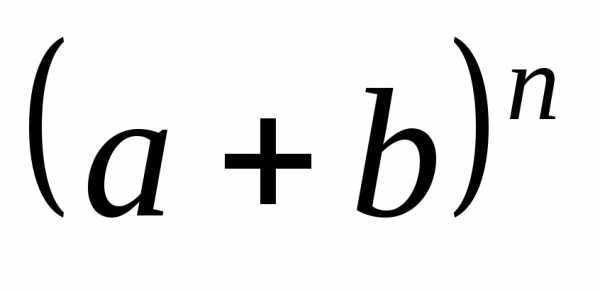 .
Эта формула носит название формулы
бинома Ньютона и имеет вид
.
Эта формула носит название формулы
бинома Ньютона и имеет вид
, (3)
где 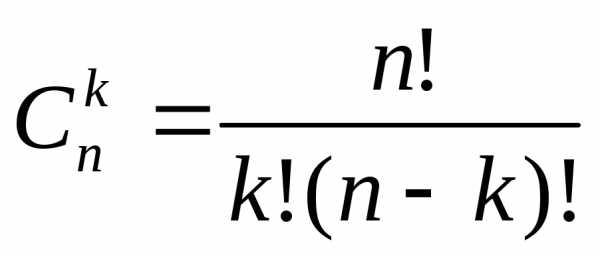 .
.
Применим формулу
бинома Ньютона для 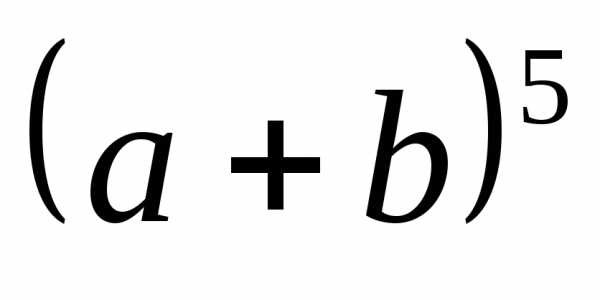 .
.
Пример.
В почтовом отделении продают открытки 10 сортов. Сколькими способами можно купить в нем: а) 12 открыток? б) 8 открыток? в) 8 различных открыток?
Решение.
а)
б)
в)
Домашнее задание.
1. У филателиста есть 8 различных марок на космическую тему и 10 различных марок на спортивную тему. Сколькими способами он сможет наклеить 3 марки одного вида и 3 марки второго вида в альбом на 6 пронумерованных мест?
2. В лаборатории работают 8 физиков и 10 химиков. Надо создать рабочие группы по трем темам. В первую группу должны войти 4 физика, во вторую 5 химиков, а третья должна состоять из 3 человека которые могут быть как физиками, так и химиками. Сколькими способами можно создать такие группы.
3. Доказать, что (правило Паскаля).
7
studfiles.net
