X y обратная функция – Обратная функция — урок. Алгебра, 10 класс.

Обратные функции (определение и свойства)

Определение и свойства

Определение обратной функции
Пусть функция имеет область определения X и множество значений Y. И пусть она обладает свойством:
для всех .
Тогда для любого элемента из множества Y можно поставить в соответствие только один элемент множества X, для которого . Такое соответствие определяет функцию, которая называется обратной функцией к . Обратная функция обозначается так:
.

Из определения следует, что
;
  для всех  ;
  для всех  .

Лемма о взаимной монотонности прямой и обратной функций
Если функция строго возрастает (убывает), то существует обратная функция , которая также строго возрастает (убывает).
Доказательство ⇓

Свойство о симметрии графиков прямой и обратной функций
Графики прямой и обратной функций симметричны относительно прямой .
Доказательство ⇓

Теорема о существовании и непрерывности обратной функции на отрезке
Пусть функция непрерывна и строго возрастает (убывает) на отрезке . Тогда на отрезке определена и непрерывна обратная функция , которая строго возрастает (убывает).
Доказательство ⇓

Для возрастающей функции . Для убывающей – .

Теорема о существовании и непрерывности обратной функции на интервале
Пусть функция непрерывна и строго возрастает (убывает) на открытом конечном или бесконечном интервале . Тогда на интервале определена и непрерывна обратная функция , которая строго возрастает (убывает).
Доказательство ⇓

Для возрастающей функции .
Для убывающей: .

Аналогичным образом можно сформулировать теорему о существовании и непрерывности обратной функции на полуинтервале.

Если функция непрерывна и строго возрастает (убывает) на полуинтервале или , то на полуинтервале или определена обратная функция , которая строго возрастает (убывает). Здесь .

Если строго возрастает, то интервалам и соответствуют интервалы и . Если строго убывает, то интервалам и соответствуют интервалы и .
Эта теорема доказывается тем же способом, что и теорема о существовании и непрерывности обратной функции на интервале.

Примеры обратных функций

Арксинус

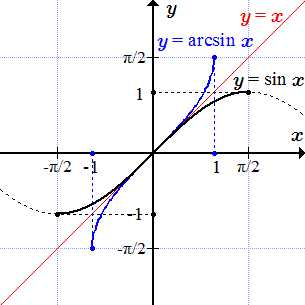
Графики y = sin x и обратной функции y = arcsin x.

Рассмотрим тригонометрическую функцию синус: . Она определена и непрерывна для всех значений аргумента , но не является монотонной. Однако, если сузить область определения, то можно выделить монотонные участки. Так, на отрезке , функция определена, непрерывна, строго возрастает и принимает значения от –1 до +1. Поэтому имеет на нем обратную функцию, которую называют арксинусом. Арксинус имеет область определения и множество значений .

Логарифм

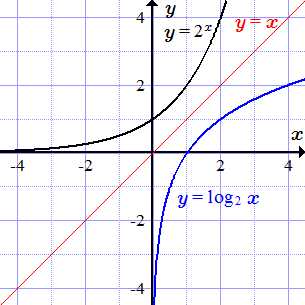
Графики y = 2^x и обратной функции y = log₂ x.

Показательная функция определена, непрерывна и строго возрастает при всех значений аргумента . Множеством ее значений является открытый интервал . Обратной функцией является логарифм по основанию два. Он имеет область определения и множество значений .

Квадратный корень

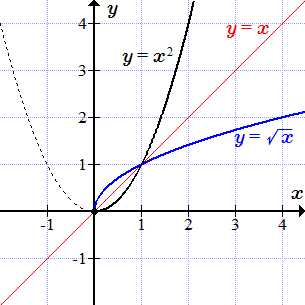
Графики y = x² и обратной функции .

Степенная функция определена и непрерывна для всех . Множеством ее значений является полуинтервал . Но она не является монотонной при всех значений аргумента. Однако, на полуинтервале она непрерывна и строго монотонно возрастает. Поэтому если, в качестве области определения, взять множество , то существует обратная функция, которая называется квадратным корнем. Обратная функция имеет область определения и множество значений .

Пример. Доказательство существования и единственности корня степени n

Докажите, что уравнение , где n – натуральное, – действительное неотрицательное число, имеет единственное решение на множестве действительных чисел, . Это решение называется корнем степени n из числа a. То есть нужно показать, что любое неотрицательное число имеет единственный корень степени n.

Решение

Рассмотрим функцию от переменной x:
(П1)   .

Докажем, что она непрерывна.
Используя определение непрерывности, покажем, что
.
Применяем формулу бинома Ньютона:
(П2)  
.
Применим арифметические свойства пределов функции. Поскольку , то отлично от нуля только первое слагаемое:
.
Непрерывность доказана.

Докажем, что функция (П1) строго возрастает при .
Возьмем произвольные числа , связанные неравенствами:
, , .
Нам нужно показать, что . Введем переменные . Тогда . Поскольку , то из (П2) видно, что . Или
.
Строгое возрастание доказано.

Найдем множество значений функции при .
В точке , .
Найдем предел .
Для этого применим неравенство Бернулли. При имеем:
.
Поскольку , то и .
Применяя свойство неравенств бесконечно больших функций находим, что .
Таким образом, , .

Согласно теореме об обратной функции, на интервале определена и непрерывна обратная функция . То есть для любого существует единственное , удовлетворяющее уравнению . Поскольку у нас , то это означает, что для любого , уравнение имеет единственное решение, которое называют корнем степени n из числа x:
.

Доказательства свойств и теорем

Доказательство леммы о взаимной монотонности прямой и обратной функций

Формулировка ⇑

Пусть функция имеет область определения X и множество значений Y. Докажем, что она имеет обратную функцию. Исходя из определения ⇑, нам нужно доказать, что
для всех .

Допустим противное. Пусть существуют числа , так что . Пусть при этом . Иначе, поменяем обозначения, чтобы было . Тогда, в силу строгой монотонности  f, должно выполняться одно из неравенств:
если  f  строго возрастает;
если  f  строго убывает.
То есть . Возникло противоречие. Следовательно, имеет обратную функцию .

Пусть функция строго возрастает. Докажем, что и обратная функция также строго возрастает. Введем обозначения:
. То есть нам нужно доказать, что если , то .

Допустим противное. Пусть , но .

Если , то . Этот случай отпадает.

Пусть . Тогда, в силу строгого возрастания функции , , или . Возникло противоречие. Поэтому возможен только случай .

Для строго возрастающей функции лемма доказана. Аналогичным образом можно доказать эту лемму и для строго убывающей функции.

Доказательство свойства о симметрии графиков прямой и обратной функций

Формулировка ⇑

Пусть – произвольная точка графика прямой функции :
(2.1)   .
Покажем, что точка , симметричная точке A относительно прямой , принадлежит графику обратной функции :
.
Из определения обратной функции следует, что
(2.2)   .
Таким образом, нам нужно показать (2.2).

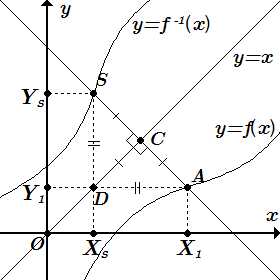
График обратной функции y = f  ^–1(x) симметричен графику прямой функции y = f(x) относительно прямой y = x.

Из точек A и S опустим перпендикуляры на оси координат. Тогда
,   .

Через точку A проводим прямую, перпендикулярную прямой . Пусть прямые пересекаются в точке C. На прямой строим точку S так, чтобы . Тогда точка S будет симметрична точке A относительно прямой .

Рассмотрим треугольники и . Они имеют две равные по длине стороны: и , и равные углы между ними: . Поэтому они конгруэнтны. Тогда
.

Рассмотрим треугольник . Поскольку , то
.
Тоже самое относится к треугольнику :
.
Тогда
.

Теперь находим и :
;
.

Итак, уравнение (2.2):
(2.2)  
выполняется, поскольку , и выполняется (2.1):
(2.1)   .

Так как мы выбрали точку A произвольно, то это относится ко всем точкам графика :
все точки графика функции , симметрично отраженные относительно прямой , принадлежат графику обратной функции .
Далее мы можем поменять и местами. В результате получим, что
все точки графика функции , симметрично отраженные относительно прямой , принадлежат графику функции .
Отсюда следует, что графики функций и симметричны относительно прямой .

Свойство доказано.

Доказательство теоремы о существовании и непрерывности обратной функции на отрезке

Формулировка ⇑

Пусть обозначает область определения функции – отрезок .

1. Покажем, что множеством значений функции является отрезок :
,
где .

Действительно, поскольку функция непрерывна на отрезке , то по теореме Вейерштрасса она достигает на нем минимума и максимума . Тогда по теореме Больцано – Коши функция принимает все значения из отрезка . То есть для любого существует , для которого . Поскольку и есть минимум и максимум, то функция принимает на отрезке только значения из множества .

2. Поскольку функция строго монотонна, то согласно вышеприведенной лемме ⇑, существует обратная функция , которая также строго монотонна (возрастает, если возрастает ; и убывает, если убывает ). Областью определения обратной функции является множество , а множеством значений – множество .

3. Теперь докажем, что обратная функция непрерывна.

3.1. Пусть есть произвольная внутренняя точка отрезка : . Докажем, что обратная функция непрерывна в этой точке.

Пусть ей соответствует точка . Поскольку обратная функция строго монотонна, то есть внутренняя точка отрезка :
.
Согласно определению непрерывности нам нужно доказать, что для любого имеется такая функция , при которой
(3.1)   для всех .

Заметим, что мы можем взять сколь угодно малым. Действительно, если мы нашли такую функцию , при которой неравенства (3.1) выполняются при достаточно малых значениях , то они будут автоматически выполняться и при любых больших значениях , если положить при .

Возьмем настолько малым, чтобы точки и принадлежали отрезку :
.
Введем и упорядочим обозначения:



.

Преобразуем первое неравенство (3.1):
(3.1)   для всех .
;
;
;
(3.2)   .
Поскольку строго монотонна, то отсюда следует, что
(3.3.1)   , если возрастает;
(3.3.2)   , если убывает.
Поскольку обратная функция также строго монотонна, то из неравенств (3.3) следуют неравенства (3.2).

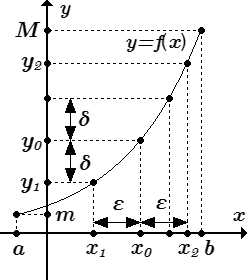
Для любого ε > 0 существует δ, так что |f  ^-1(y) – f  ^-1(y₀)| < ε для всех |y – y₀| < δ.

Неравенства (3.3) определяют открытый интервал, концы которого удалены от точки на расстояния и . Пусть есть наименьшее из этих расстояний:
.
В силу строгой монотонности , , . Поэтому и . Тогда интервал будет лежать в интервале, определяемом неравенствами (3.3). И для всех значений , принадлежащих ему будут выполняться неравенства (3.2).

Итак, мы нашли, что для достаточно малого , существует , так что
при .
Теперь изменим обозначения.
Для достаточно малого , существует такое , так что
при .
Это означает, что обратная функция непрерывна во внутренних точках .

3.2. Теперь рассмотрим концы области определения. Здесь все рассуждения остаются теми же самыми. Только нужно рассматривать односторонние окрестности этих точек. Вместо точки будет или , а вместо точки – или .

Так, для возрастающей функции , . Обратная функция непрерывна в точке , поскольку для любого достаточно малого имеется , так что
при .
Обратная функция непрерывна в точке , поскольку для любого достаточно малого имеется , так что
при .

Для убывающей функции , .
Обратная функция непрерывна в точке , поскольку для любого достаточно малого имеется , так что
при .
Обратная функция непрерывна в точке , поскольку для любого достаточно малого имеется , так что
при .

Теорема доказана.

Доказательство теоремы о существовании и непрерывности обратной функции на интервале

Формулировка ⇑

Пусть обозначает область определения функции – открытый интервал . Пусть – множество ее значений. Согласно приведенной выше лемме ⇑, существует обратная функция , которая имеет область определения , множество значений и является строго монотонной (возрастает если возрастает и убывает если убывает ). Нам осталось доказать, что
1) множеством является открытый интервал , и что
2) обратная функция непрерывна на нем.
Здесь .

1. Покажем, что множеством значений функции является открытый интервал :
.

Как и всякое непустое множество, элементы которого имеют операцию сравнения, множество значений функции имеет нижнюю и верхнюю грани:
.
Здесь и могут быть конечными числами или символами и .

1.1. Покажем, что точки и не принадлежат множеству значений функции. То есть множество значений не может быть отрезком .

Если или является бесконечно удаленной точкой: или , то такая точка не является элементом множества. Поэтому она не может принадлежать множеству значений.

Пусть (или ) является конечным числом. Допустим противное. Пусть точка (или ) принадлежит множеству значений функции . То есть существует такое , для которого (или ). Возьмем точки и , удовлетворяющие неравенствам:
.
Поскольку функция строго монотонна, то
, если f возрастает;
, если f убывает.
То есть мы нашли точку, значение функции в которой меньше (больше ). Но это противоречит определению нижней (верхней) грани, согласно которому
для всех .
Поэтому точки и не могут принадлежать множеству значений функции .

1.2. Теперь покажем, что множество значений является интервалом , а не объединением интервалов и точек. То есть для любой точки существует , для которого .

Согласно определениям нижней и верхней граней, в любой окрестности точек и содержится хотя бы один элемент множества . Пусть – произвольное число, принадлежащее интервалу : . Тогда для окрестности существует , для которого
.
Для окрестности существует , для которого
.

Поскольку и , то . Тогда
(4.1.1)   если возрастает;
(4.1.2)   если убывает.
Неравенства (4.1) легко доказать от противного. Но можно воспользоваться леммой ⇑, согласно которой на множестве существует обратная функция , которая строго возрастает, если возрастает и строго убывает, если убывает . Тогда сразу получаем неравенства (4.1).

Итак, мы имеем отрезок , где если возрастает;
если убывает.
На концах отрезка функция принимает значения и . Поскольку , то по теореме Больцано – Коши, существует точка , для которой .

Поскольку , то тем самым мы показали, что для любого существует , для которого . Это означает, что множеством значений функции является открытый интервал .

2. Теперь покажем, что обратная функция непрерывна в произвольной точке интервала :  . Для этого применим предыдущую теорему ⇑ к отрезку . Поскольку , то обратная функция непрерывна на отрезке , в том числе и в точке .

Теорема доказана.

Использованная литература:
О.И. Бесов. Лекции по математическому анализу. Часть 1. Москва, 2004.
С.М. Никольский. Курс математического анализа. Том 1. Москва, 1983.

Автор: Олег Одинцов.     Опубликовано: 27-10-2018   Изменено: 23-11-2018

1cov-edu.ru

Обратная функция — ПриМат

Определение

Пусть функция $y=f(x)$ с областью определения $ D(f)$ и множеством значений $R(f)$. Обратная к $f$ — функция $f^{-1}$ определяется как функция с областью определения $D(f^{-1})=R(f)$  и множеством значений $R(f^{-1})=D(f)$ , такая что $f^{-1}(y)=x$ тогда и только тогда, когда $f(x)=y$. Таким образом,  $f^{-1}$ возвращает $y$ обратно в $x$.

График

Переход от функции $y=f(x)$, $x\in X$, к обратной функции $x=f^{-1}(y)$, $y\in Y$ (если она существует), сводится к изменению ролей множеств $X$ и $Y$. Следовательно, графики функций $y=f(x)$ и $x=f^{-1}(y)$ на плоскости $XOY$ совпадают. Но обычно и для обратной функции аргумент обозначают через $x$, т.е. записывают ее в виде $y=f^{-1}(x)$. График функции $y=f^{-1}(x)$ получается из графика функции $y=f(x)$ с помощью преобразования плоскости $XOY$, переводящей каждую точку $(x,y)$ в точку $(y,x)$, то есть симметрией относительно прямой $y=x$.

Спойлер

1. Найти функцию, обратную функции $y=3x+5$.
   Решение: Функция $y=3x+5$ определена и возрастает на всей числовой оси. Следовательно, обратная функция существует и возрастает. Разрешая уравнение относительно $x$ получим $x=\frac{y-5}{3}$.
2. Показать, что функция $y=\frac{k}{x}$, на множестве $X = \{x \mid x > 0\}$, где $(k\neq 0)$ обратна сама себе.
   Решение: Функция $y=\frac{k}{x}$ определена и строго монотонна $x > 0$ . Следовательно, обратная функция существует. Область значений функции — в зависимости от $k$: если $k > 0$, то $y >0$; если $k < 0$, то $y <0$. Разрешая уравнение относительно $x$, получим $x = \frac{k}{y}$. Итак $f^{-1}(y)=\frac{k}{y}$, $f^{-1}(x) = \frac{k}{x} = f(x)$.

[свернуть]

Источники

• Лысенко З.М. Конспект лекций по курсу математического анализа. (Тема «Свойства функций непрерывных на отрезке»).

Литература

Лимит времени: 0

Информация

Тест по теме «Обратная функция»

Вы уже проходили тест ранее. Вы не можете запустить его снова.

Тест загружается…

Вы должны войти или зарегистрироваться для того, чтобы начать тест.

Вы должны закончить следующие тесты, чтобы начать этот:

1. С ответом
2. С отметкой о просмотре

Поделиться ссылкой:

Похожее

ib.mazurok.com

Обратная функция — Википедия

Материал из Википедии — свободной энциклопедии

Обра́тная фу́нкция — функция, обращающая зависимость, выражаемую данной функцией. Например, если функция от x даёт y, то обратная ей функция от y даёт x. Обратная функция функции f{\displaystyle f} обычно обозначается f−1{\displaystyle f^{-1}}, иногда также используется обозначение finv{\displaystyle f^{\mathrm {inv} }}.

Определение

Функция g:Y→X{\displaystyle g:Y\to X} является обратной к функции f:X→Y{\displaystyle f:X\to Y}, если выполнены следующие тождества:

• f(g(y))=y{\displaystyle f(g(y))=y} для всех y∈Y;{\displaystyle y\in Y;}
• g(f(x))=x{\displaystyle g(f(x))=x} для всех x∈X.{\displaystyle x\in X.}

Видео по теме

Существование

Чтобы найти обратную функцию, нужно решить уравнение y=f(x){\displaystyle y=f(x)} относительно x{\displaystyle x}. Если оно имеет более чем один корень, то функции, обратной к f{\displaystyle f} не существует. Таким образом, функция f(x){\displaystyle f(x)} обратима на интервале (a;b){\displaystyle (a;b)} тогда и только тогда, когда на этом интервале она взаимно-однозначна.

Для непрерывной функции F(y){\displaystyle F(y)} выразить y{\displaystyle y} из уравнения x−F(y)=0{\displaystyle x-F(y)=0} возможно в том и только том случае, когда функция F(y){\displaystyle F(y)} строго монотонна (см. теорема о неявной функции). Тем не менее, непрерывную функцию всегда можно обратить на промежутках её строгой монотонности. Например, x{\displaystyle {\sqrt {x}}} является обратной функцией к x2{\displaystyle x^{2}} на [0,+∞){\displaystyle [0,+\infty )}, хотя на промежутке (−∞,0]{\displaystyle (-\infty ,0]} обратная функция другая: −x{\displaystyle -{\sqrt {x}}}.

Примеры

• Если F:R→R+,F(x)=ax{\displaystyle F:\mathbb {R} \to \mathbb {R} _{+},\;F(x)=a^{x}}, где a>0,{\displaystyle a>0,} то F−1(x)=loga⁡x.{\displaystyle F^{-1}(x)=\log _{a}x.}
• Если F(x)=ax+b,x∈R{\displaystyle F(x)=ax+b,\;x\in \mathbb {R} }, где a,b∈R{\displaystyle a,b\in \mathbb {R} } фиксированные постоянные и a≠0{\displaystyle a\neq 0}, то F−1(x)=x−ba.{\displaystyle F^{-1}(x)={\frac {x-b}{a}}.}
• Если F(x)=xn,x≥0,n∈Z{\displaystyle F(x)=x^{n},x\geq 0,n\in \mathbb {Z} }, то F−1(x)=xn.{\displaystyle F^{-1}(x)={\sqrt[{n}]{x}}.}

Свойства

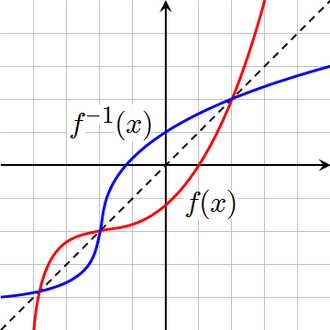Графики функции и обратной ей

• Областью определения F−1{\displaystyle F^{-1}} является множество Y{\displaystyle Y}, а областью значений — множество X{\displaystyle X}.
• По построению имеем:

y=F(x)⇔x=F−1(y){\displaystyle y=F(x)\Leftrightarrow x=F^{-1}(y)}

или

F(F−1(y))=y,∀y∈Y{\displaystyle F\left(F^{-1}(y)\right)=y,\;\forall y\in Y},

F−1(F(x))=x,∀x∈X{\displaystyle F^{-1}(F(x))=x,\;\forall x\in X},

или короче

F∘F−1=idY{\displaystyle F\circ F^{-1}=\mathrm {id} _{Y}},

F−1∘F=idX{\displaystyle F^{-1}\circ F=\mathrm {id} _{X}},

где ∘{\displaystyle \circ } означает композицию функций, а idX,idY{\displaystyle \mathrm {id} _{X},\mathrm {id} _{Y}} — тождественные отображения на X{\displaystyle X} и Y{\displaystyle Y} соответственно.

• Такое отображение G:Y→X{\displaystyle G\colon \,Y\to X}, что F∘G=idY{\displaystyle F\circ G=\mathrm {id} _{Y}} («обратное справа»), называется сечением отображения F{\displaystyle F}.

• Функция F{\displaystyle F} является обратной к F−1{\displaystyle F^{-1}}:

(F−1)−1=F{\displaystyle \left(F^{-1}\right)^{-1}=F}.

Разложение в степенной ряд

Обратная функция аналитической функции может быть представлена в виде степенного ряда:

F−1(y)=∑k=0∞Ak(x0)(y−f(x0))kk!,{\displaystyle F^{-1}(y)=\sum _{k=0}^{\infty }A_{k}(x_{0}){\frac {(y-f(x_{0}))^{k}}{k!}},}

где коэффициенты Ak{\displaystyle A_{k}} задаются рекурсивной формулой:

An(x)={x,n=0An−1′(x)F′(x),n>0{\displaystyle A_{n}(x)={\begin{cases}x,n=0\\{\frac {A_{n-1}'(x)}{F'(x)}},n>0\end{cases}}}

См. также

wiki2.red

Обратная функция — Википедия. Что такое Обратная функция

Материал из Википедии — свободной энциклопедии

Обра́тная фу́нкция — функция, обращающая зависимость, выражаемую данной функцией. Например, если функция от x даёт y, то обратная ей функция от y даёт x. Обратная функция функции f{\displaystyle f} обычно обозначается f−1{\displaystyle f^{-1}}, иногда также используется обозначение finv{\displaystyle f^{\mathrm {inv} }}.

Определение

Функция g:Y→X{\displaystyle g:Y\to X} является обратной к функции f:X→Y{\displaystyle f:X\to Y}, если выполнены следующие тождества:

• f(g(y))=y{\displaystyle f(g(y))=y} для всех y∈Y;{\displaystyle y\in Y;}
• g(f(x))=x{\displaystyle g(f(x))=x} для всех x∈X.{\displaystyle x\in X.}

Существование

Чтобы найти обратную функцию, нужно решить уравнение y=f(x){\displaystyle y=f(x)} относительно x{\displaystyle x}. Если оно имеет более чем один корень, то функции, обратной к f{\displaystyle f} не существует. Таким образом, функция f(x){\displaystyle f(x)} обратима на интервале (a;b){\displaystyle (a;b)} тогда и только тогда, когда на этом интервале она взаимно-однозначна.

Для непрерывной функции F(y){\displaystyle F(y)} выразить y{\displaystyle y} из уравнения x−F(y)=0{\displaystyle x-F(y)=0} возможно в том и только том случае, когда функция F(y){\displaystyle F(y)} строго монотонна (см. теорема о неявной функции). Тем не менее, непрерывную функцию всегда можно обратить на промежутках её строгой монотонности. Например, x{\displaystyle {\sqrt {x}}} является обратной функцией к x2{\displaystyle x^{2}} на [0,+∞){\displaystyle [0,+\infty )}, хотя на промежутке (−∞,0]{\displaystyle (-\infty ,0]} обратная функция другая: −x{\displaystyle -{\sqrt {x}}}.

Примеры

• Если F:R→R+,F(x)=ax{\displaystyle F:\mathbb {R} \to \mathbb {R} _{+},\;F(x)=a^{x}}, где a>0,{\displaystyle a>0,} то F−1(x)=loga⁡x.{\displaystyle F^{-1}(x)=\log _{a}x.}
• Если F(x)=ax+b,x∈R{\displaystyle F(x)=ax+b,\;x\in \mathbb {R} }, где a,b∈R{\displaystyle a,b\in \mathbb {R} } фиксированные постоянные и a≠0{\displaystyle a\neq 0}, то F−1(x)=x−ba.{\displaystyle F^{-1}(x)={\frac {x-b}{a}}.}
• Если F(x)=xn,x≥0,n∈Z{\displaystyle F(x)=x^{n},x\geq 0,n\in \mathbb {Z} }, то F−1(x)=xn.{\displaystyle F^{-1}(x)={\sqrt[{n}]{x}}.}

Свойства

Графики функции и обратной ей

• Областью определения F−1{\displaystyle F^{-1}} является множество Y{\displaystyle Y}, а областью значений — множество X{\displaystyle X}.
• По построению имеем:

y=F(x)⇔x=F−1(y){\displaystyle y=F(x)\Leftrightarrow x=F^{-1}(y)}

или

F(F−1(y))=y,∀y∈Y{\displaystyle F\left(F^{-1}(y)\right)=y,\;\forall y\in Y},

F−1(F(x))=x,∀x∈X{\displaystyle F^{-1}(F(x))=x,\;\forall x\in X},

или короче

F∘F−1=idY{\displaystyle F\circ F^{-1}=\mathrm {id} _{Y}},

F−1∘F=idX{\displaystyle F^{-1}\circ F=\mathrm {id} _{X}},

где ∘{\displaystyle \circ } означает композицию функций, а idX,idY{\displaystyle \mathrm {id} _{X},\mathrm {id} _{Y}} — тождественные отображения на X{\displaystyle X} и Y{\displaystyle Y} соответственно.

• Такое отображение G:Y→X{\displaystyle G\colon \,Y\to X}, что F∘G=idY{\displaystyle F\circ G=\mathrm {id} _{Y}} («обратное справа»), называется сечением отображения F{\displaystyle F}.

• Функция F{\displaystyle F} является обратной к F−1{\displaystyle F^{-1}}:

(F−1)−1=F{\displaystyle \left(F^{-1}\right)^{-1}=F}.

Разложение в степенной ряд

Обратная функция аналитической функции может быть представлена в виде степенного ряда:

F−1(y)=∑k=0∞Ak(x0)(y−f(x0))kk!,{\displaystyle F^{-1}(y)=\sum _{k=0}^{\infty }A_{k}(x_{0}){\frac {(y-f(x_{0}))^{k}}{k!}},}

где коэффициенты Ak{\displaystyle A_{k}} задаются рекурсивной формулой:

An(x)={x,n=0An−1′(x)F′(x),n>0{\displaystyle A_{n}(x)={\begin{cases}x,n=0\\{\frac {A_{n-1}'(x)}{F'(x)}},n>0\end{cases}}}

См. также

wiki.sc

Обратная функция Википедия

Обра́тная фу́нкция — функция, обращающая зависимость, выражаемую данной функцией. Например, если функция от x даёт y, то обратная ей функция от y даёт x. Обратная функция функции f{\displaystyle f} обычно обозначается f−1{\displaystyle f^{-1}}, иногда также используется обозначение finv{\displaystyle f^{\mathrm {inv} }}.

Определение

Функция g:Y→X{\displaystyle g:Y\to X} является обратной к функции f:X→Y{\displaystyle f:X\to Y}, если выполнены следующие тождества:

• f(g(y))=y{\displaystyle f(g(y))=y} для всех y∈Y;{\displaystyle y\in Y;}
• g(f(x))=x{\displaystyle g(f(x))=x} для всех x∈X.{\displaystyle x\in X.}

Существование

Чтобы найти обратную функцию, нужно решить уравнение y=f(x){\displaystyle y=f(x)} относительно x{\displaystyle x}. Если оно имеет более чем один корень, то функции, обратной к f{\displaystyle f} не существует. Таким образом, функция f(x){\displaystyle f(x)} обратима на интервале (a;b){\displaystyle (a;b)} тогда и только тогда, когда на этом интервале она взаимно-однозначна.

Для непрерывной функции F(y){\displaystyle F(y)} выразить y{\displaystyle y} из уравнения x−F(y)=0{\displaystyle x-F(y)=0} возможно в том и только том случае, когда функция F(y){\displaystyle F(y)} строго монотонна (см. теорема о неявной функции). Тем не менее, непрерывную функцию всегда можно обратить на промежутках её строгой монотонности. Например, x{\displaystyle {\sqrt {x}}} является обратной функцией к x2{\displaystyle x^{2}} на [0,+∞){\displaystyle [0,+\infty )}, хотя на промежутке (−∞,0]{\displaystyle (-\infty ,0]} обратная функция другая: −x{\displaystyle -{\sqrt {x}}}.

Для существования обратной функции не являются необходимыми ни непрерывность, ни монотонность исходной функции. Пример: функция y=x+D(x),{\displaystyle y=x+D(x),} где D(x){\displaystyle D(x)} — функция Дирихле, разрывна и не монотонна, однако обратная для неё существует^[1]: x=y−D(y).{\displaystyle x=y-D(y).}

Примеры

• Если F:R→R+,F(x)=ax{\displaystyle F:\mathbb {R} \to \mathbb {R} _{+},\;F(x)=a^{x}}, где a>0,a≠1,{\displaystyle a>0,a\neq 1,} то F−1(x)=loga⁡x.{\displaystyle F^{-1}(x)=\log _{a}x.}
• Если F(x)=ax+b,x∈R{\displaystyle F(x)=ax+b,\;x\in \mathbb {R} }, где a,b∈R{\displaystyle a,b\in \mathbb {R} } фиксированные постоянные и a≠0{\displaystyle a\neq 0}, то F−1(x)=x−ba.{\displaystyle F^{-1}(x)={\frac {x-b}{a}}.}
• Если F(x)=xn,x≥0,n∈Z{\displaystyle F(x)=x^{n},x\geq 0,n\in \mathbb {Z} }, то F−1(x)=xn.{\displaystyle F^{-1}(x)={\sqrt[{n}]{x}}.}

Свойства

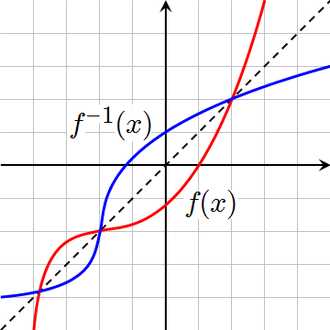Графики функции и обратной ей

• Областью определения F−1{\displaystyle F^{-1}} является множество Y{\displaystyle Y}, а областью значений — множество X{\displaystyle X}.
• По построению имеем:

y=F(x)⇔x=F−1(y){\displaystyle y=F(x)\Leftrightarrow x=F^{-1}(y)}

или

F(F−1(y))=y,∀y∈Y{\displaystyle F\left(F^{-1}(y)\right)=y,\;\forall y\in Y},

F−1(F(x))=x,∀x∈X{\displaystyle F^{-1}(F(x))=x,\;\forall x\in X},

или короче

F∘F−1=idY{\displaystyle F\circ F^{-1}=\mathrm {id} _{Y}},

F−1∘F=idX{\displaystyle F^{-1}\circ F=\mathrm {id} _{X}},

где ∘{\displaystyle \circ } означает композицию функций, а idX,idY{\displaystyle \mathrm {id} _{X},\mathrm {id} _{Y}} — тождественные отображения на X{\displaystyle X} и Y{\displaystyle Y} соответственно.

• Такое отображение G:Y→X{\displaystyle G\colon \,Y\to X}, что F∘G=idY{\displaystyle F\circ G=\mathrm {id} _{Y}} («обратное справа»), называется сечением отображения F{\displaystyle F}.

• Функция F{\displaystyle F} является обратной к F−1{\displaystyle F^{-1}}:

(F−1)−1=F{\displaystyle \left(F^{-1}\right)^{-1}=F}.

Разложение в степенной ряд

Обратная функция аналитической функции может быть представлена в виде степенного ряда:

F−1(y)=∑k=0∞Ak(x0)(y−f(x0))kk!,{\displaystyle F^{-1}(y)=\sum _{k=0}^{\infty }A_{k}(x_{0}){\frac {(y-f(x_{0}))^{k}}{k!}},}

где коэффициенты Ak{\displaystyle A_{k}} задаются рекурсивной формулой:

An(x)={x,n=0An−1′(x)F′(x),n>0{\displaystyle A_{n}(x)={\begin{cases}x,n=0\\{\frac {A_{n-1}'(x)}{F'(x)}},n>0\end{cases}}}

См. также

Примечания

1. ↑ Шибинский В. М. Примеры и контрпримеры в курсе математического анализа. Учебное пособие. — М.: Высшая школа, 2007. — С. 29—30. — 543 с. — ISBN 978-5-06-005774-4.

wikiredia.ru

ОБРАТНАЯ ФУНКЦИЯ — это… Что такое ОБРАТНАЯ ФУНКЦИЯ?



ОБРАТНАЯ ФУНКЦИЯ

ОБРАТНАЯ функция — функция, обращающая зависимость, выражаемую данной функцией. Так, если y = f (x) — данная функция, то переменная х, рассматриваемая как функция переменной у: х = ?(y), является обратной по отношению к данной функции у = f (x). Напр., х= есть обратная функция по отношению к y = x3.

Большой Энциклопедический словарь. 2000.

• ОБРАТНАЯ ТЕОРЕМА
• ОБРАТНО ПРОПОРЦИОНАЛЬНЫЕ ВЕЛИЧИНЫ

Смотреть что такое «ОБРАТНАЯ ФУНКЦИЯ» в других словарях:

• ОБРАТНАЯ ФУНКЦИЯ — (inverse function) Функция, обратная какой либо другой функции. Если у=f(x), то обратная функция может быть записана так: х=f 1(у). Обратная функция от обратной функции является первоначальной функцией. Хотя для многих функций, например линейной …   Экономический словарь

• обратная функция — — [[http://www.rfcmd.ru/glossword/1.8/index.php?a=index d=23]] Тематики защита информации EN function s inverse …   Справочник технического переводчика

• Обратная функция — Не следует путать с Обратная величина. Обратная функция  функция, обращающая зависимость, выражаемую данной функцией. Содержание 1 Определение 2 Существование 3 Примеры …   Википедия

• обратная функция — функция, обращающая зависимость, выражаемую данной функцией. Так, если у = f(x)  данная функция, то переменная х, рассматриваемая как функция переменной у : х = φ(у), является обратной по отношению к данной функции у = f(х). Например, у = х3. * * …   Энциклопедический словарь

• обратная функция — atvirkštinė funkcija statusas T sritis fizika atitikmenys: angl. inverse function vok. inverse Funktion, f rus. обратная функция, f pranc. fonction inverse, f …   Fizikos terminų žodynas

• Обратная функция —         Функция, обращающая зависимость, выражаемую данной функцией. Так, если у = f (x) данная функция, то переменная х, рассматриваемая как функция переменной у, х = φ (y), является обратной по отношению к данной функции у = f (x). Например, О …   Большая советская энциклопедия

• ОБРАТНАЯ ФУНКЦИЯ — функция, определенная на множестве значений заданной функции и ставящая в соответствие каждому его элементу множество всех тех элементов из области определения рассматриваемой функции, к рые в него отображаются, т. е. его полный прообраз. Если… …   Математическая энциклопедия

• ОБРАТНАЯ ФУНКЦИЯ — функция, обращающая зависимость, выражаемую данной функцией. Так, если y = f(x) данная функция, то переменная х, рассматриваемая как функция переменной у:х = ф(у), является обратной по отношению к данной функции y = f(x). Напр., х = 3корень из y… …   Естествознание. Энциклопедический словарь

• ОБРАТНАЯ ФУНКЦИЯ — ф ция, обращающая зависимость, выражаемую данной ф цией. Если дана ф ция у = f(x), то О. ф. будет х = Ф(у). Напр., для у = kx + b(k не равно 0) О. ф. будет х = (у b)/k, a для у = ех будет х = 1nу. Графики обратных тригонометрических функций: 1… …   Большой энциклопедический политехнический словарь

• Функция Аккермана — Функция Аккермана  простой пример вычислимой функции, которая не является примитивно рекурсивной. Она принимает два неотрицательных целых числа в качестве параметров и возвращает натуральное число, обозначается . Эта функция растёт очень… …   Википедия

Книги

• Тригонометрия, С.П. Глазенап, Автор предлагаемого учебника по тригонометрии русский ученый профессор Сергей Павлович Глазенап [Глазенап С. П.], астроном, инициатор создания и руководитель строительства Петербургской… Серия: — Издатель: ЁЁ Медиа, Подробнее  Купить за 1439 руб
• Обратные функции. Теория и задачи, В. А. Тарасов, Описаны теория и методы решения задач разной сложности по теме`Обратная функция`. Чтобы облегчить восприятие и усвоение этой сложной темы, в первой части работы в общем виде изучен аргумент… Издатель: Илекса, Производитель: Илекса, Подробнее  Купить за 131 грн (только Украина)
• Обратные функции Теория и задачи, Тарасов В., Научитесь решать прямые и обратные задачи и выясните, что для каждой монотонной функции существует обратная функция. А также узнаете, как связаны между собой графики прямой и обратной функций… Подробнее  Купить за 118 руб

Другие книги по запросу «ОБРАТНАЯ ФУНКЦИЯ» >>

dic.academic.ru

Обратная функция Вики

Обра́тная фу́нкция — функция, обращающая зависимость, выражаемую данной функцией. Например, если функция от x даёт y, то обратная ей функция от y даёт x. Обратная функция функции f{\displaystyle f} обычно обозначается f−1{\displaystyle f^{-1}}, иногда также используется обозначение finv{\displaystyle f^{\mathrm {inv} }}.

Определение[ | код]

Функция g:Y→X{\displaystyle g:Y\to X} является обратной к функции f:X→Y{\displaystyle f:X\to Y}, если выполнены следующие тождества:

• f(g(y))=y{\displaystyle f(g(y))=y} для всех y∈Y;{\displaystyle y\in Y;}
• g(f(x))=x{\displaystyle g(f(x))=x} для всех x∈X.{\displaystyle x\in X.}

Существование[ | код]

Чтобы найти обратную функцию, нужно решить уравнение y=f(x){\displaystyle y=f(x)} относительно x{\displaystyle x}. Если оно имеет более чем один корень, то функции, обратной к f{\displaystyle f} не существует. Таким образом, функция f(x){\displaystyle f(x)} обратима на интервале (a;b){\displaystyle (a;b)} тогда и только тогда, когда на этом интервале она взаимно-однозначна.

Для непрерывной функции F(y){\displaystyle F(y)} выразить y{\displaystyle y} из уравнения x−F(y)=0{\displaystyle x-F(y)=0} возможно в том и только том случае, когда функция F(y){\displaystyle F(y)} строго монотонна (см. теорема о неявной функции). Тем не менее, непрерывную функцию всегда можно обратить на промежутках её строгой монотонности. Например, x{\displaystyle {\sqrt {x}}} является обратной функцией к x2{\displaystyle x^{2}} на [0,+∞){\displaystyle [0,+\infty )}, хотя на промежутке (−∞,0]{\displaystyle (-\infty ,0]} обратная функция другая: −x{\displaystyle -{\sqrt {x}}}.

Для существования обратной функции не являются необходимыми ни непрерывность, ни монотонность исходной функции. Пример: функция y=x+D(x),{\displaystyle y=x+D(x),} где D(x){\displaystyle D(x)} — функция Дирихле, разрывна и не монотонна, однако обратная для неё существует^[1]: x=y−D(y).{\displaystyle x=y-D(y).}

Примеры[ | код]

• Если F:R→R+,F(x)=ax{\displaystyle F:\mathbb {R} \to \mathbb {R} _{+},\;F(x)=a^{x}}, где a>0,a≠1,{\displaystyle a>0,a\neq 1,} то F−1(x)=loga⁡x.{\displaystyle F^{-1}(x)=\log _{a}x.}
• Если F(x)=ax+b,x∈R{\displaystyle F(x)=ax+b,\;x\in \mathbb {R} }, где a,b∈R{\displaystyle a,b\in \mathbb {R} } фиксированные постоянные и a≠0{\displaystyle a\neq 0}, то F−1(x)=x−ba.{\displaystyle F^{-1}(x)={\frac {x-b}{a}}.}
• Если F(x)=xn,x≥0,n∈Z{\displaystyle F(x)=x^{n},x\geq 0,n\in \mathbb {Z} }, то F−1(x)=xn.{\displaystyle F^{-1}(x)={\sqrt[{n}]{x}}.}

Свойства[ | код]

Графики функции и обратной ей

• Областью определения F−1{\displaystyle F^{-1}} является множество Y{\displaystyle Y}, а областью значений — множество X{\displaystyle X}.
• По построению имеем:

y=F(x)⇔x=F−1(y){\displaystyle y=F(x)\Leftrightarrow x=F^{-1}(y)}

или

F(F−1(y))=y,∀y∈Y{\displaystyle F\left(F^{-1}(y)\right)=y,\;\forall y\in Y},

F−1(F(x))=x,∀x∈X{\displaystyle F^{-1}(F(x))=x,\;\forall x\in X},

или короче

F∘F−1=idY{\displaystyle F\circ F^{-1}=\mathrm {id} _{Y}},

F−1∘F=idX{\displaystyle F^{-1}\circ F=\mathrm {id} _{X}},

где ∘{\displaystyle \circ } означает композицию функций, а idX,idY{\displaystyle \mathrm {id} _{X},\mathrm {id} _{Y}} — тождественные отображения на X{\displaystyle X} и Y{\displaystyle Y} соответственно.

• Такое отображение G:Y→X{\displaystyle G\colon \,Y\to X}, что F∘G=idY{\displaystyle F\circ G=\mathrm {id} _{Y}} («обратное справа»), называется сечением отображения F{\displaystyle F}.

• Функция F{\displaystyle F} является обратной к F−1{\displaystyle F^{-1}}:

(F−1)−1=F{\displaystyle \left(F^{-1}\right)^{-1}=F}.

Разложение в степенной ряд[ | код]

Обратная функция аналитической функции может быть представлена в виде степенного ряда:

F−1(y)=∑k=0∞Ak(x0)(y−f(x0))kk!,{\displaystyle F^{-1}(y)=\sum _{k=0}^{\infty }A_{k}(x_{0}){\frac {(y-f(x_{0}))^{k}}{k!}},}

где коэффициенты Ak{\displaystyle A_{k}} задаются рекурсивной формулой:

An(x)={x,n=0An−1′(x)F′(x),n>0{\displaystyle A_{n}(x)={\begin{cases}x,n=0\\{\frac {A_{n-1}'(x)}{F'(x)}},n>0\end{cases}}}

См. также[ | код]

Примечания[ | код]

1. ↑ Шибинский В. М. Примеры и контрпримеры в курсе математического анализа. Учебное пособие. — М.: Высшая школа, 2007. — С. 29—30. — 543 с. — ISBN 978-5-06-005774-4.

ru.wikibedia.ru

No related posts.