Постройте график функции y = x^2 – 1
Задание.
Постройте график функции y = x^2 — 1.
Ответ
Выполним необходимый анализ функции для ее построения.
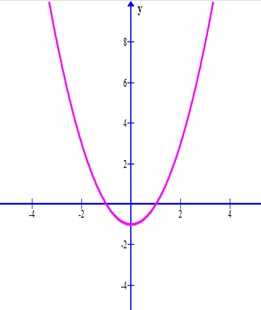
Определим вид функции. Поскольку она содержит квадрат аргумента х, то такая функция является квадратной, а ее графиком будет парабола. Парабола определена на всей числовой прямой. Поскольку перед квадратом х стоит знак «плюс» (условно), то ветви параболы будут направлены вверх.
Чтобы построить график параболы, необходимо вычислить координаты ее вершины, а также определить несколько ключевых точек, через которые она будет проходить.
Определим координаты вершины параболы:
Итак, получили, что вершина параболы находится в точке с координатами (0; —1).
Определим несколько точек, через которые парабола будет проходить. Для этого возьмем четыре значения х и вычислим для них значение функции у.
Первое значение х = 1: —точка с координатами (1; 0).
Второе значение х = 2: —точка с координатами (2; 3).
Третье значение х = —1: —точка с координатами (—1; 0).
Отметим полученные точки на координатной плоскости и проведем через них плавную кривую. Получили график функции y = x^2 — 1.
ru.solverbook.com
Постройте график функции y = 2x – 1
Задание.
Построить график функции y = 2x — 1.
Решение.
Рассмотрим саму функцию, поданную в виде , где k равно 2, а b равно —1. Такие функции называют линейными.
О линейных функциях известно, что их аргументы, а также значения самих функций ничем не ограничены, так как графиком этих функций является бесконечная прямая. Очень удобным является то, что для построения графика линейной функции вполне достаточно найти 2 точки, которые будут принадлежать этой функции, и соединить их прямой. График функции будет построен.
Наша задача сводится к тому, что нужно определить эти две точки.
Точки можно находить двумя способами:
первый — определить, в каких точках функция пересекается с осями координат;
второй — определить две любые точки прямой, подставив любые значения аргумента х.
Попробуем воспользоваться первым способом.
Если функция будет пересекать ось Ох, то для нее переменная у будет равна нулю. Подставим данное значение в уравнение функции и решим его:
Итак, первая точка функции имеет координаты .
Когда же функция пересекает ось Оу, то наоборот, переменная х равна нулю. Подставим ее значение ф уравнение функции и найдем вторую координату:
Вторая точка с координатами (0; —1).
Осталось нанести точки на плоскость и соединить прямой.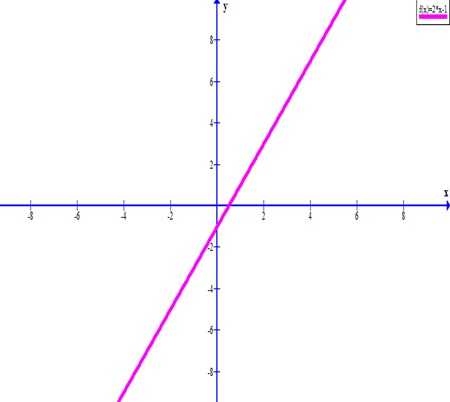
ru.solverbook.com
Постройте график функции y = 2^x +1
Задание.
Постройте график функции y = 2^х + 1.
Решение.
Построение графика любой функции необходимо начинать с анализа уравнения этой функции.
В уравнении функции видим в качестве одного из слагаемых число в неизвестной степени. Подобные функции называют показательными, к тому же они могут существовать при любом значении в показателе степени.
Обычно показательные функции не являются ни четными, ни нечетными, но, чтобы в этом убедиться, проверим четность данной функции. Для этого подставим в уравнение функции значение —х вместо х и проанализируем полученный результат:
Полученная функция ни четная, а также и не нечетная.
Далее найдем точки, через которые будет проходить функция, и которые помогут построить ее график. Так как говорилось выше, что в показателе степени может быть любое число, то будем брать не только положительные, но и отрицательные числа:
Найденных точек достаточное количество для получения адекватного графика заданной функции.
Найдем точку пересечения с осью Оу:
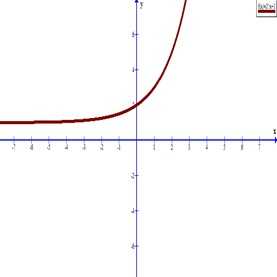
— точка(0; 2).
Точка пересечения с осью Ох находится немного сложнее:
— уравнение решения не имеет, так как положительное число в любой степени будет положительным.
Следовательно, график функции с осью Ох пересекаться не будет.
Нанесем точки на график и соединим линией.
ru.solverbook.com
