5. Криволинейные системы координат в трехмерном пространстве
Цилиндрическая система координат
Цилиндрические координаты точки Р(ρ,φ,z) – это полярные координаты ρ, φ проекции этой точки на плоскость Оху и апликата данной точки z (рис.10).
Рис.10 Рис.11
Формулы перехода от цилиндрических координат к декартовым можно задать следующим образом:
x = ρ cosφ, y = ρ sinφ, z = z. (24)
Сферическая система координат
Зададим формулы перехода от сферических координат к декартовым:
x = ρ sinθ cosφ, y = ρ sinθ sinφ, z = ρ cosθ. (25)
6. Якобиан и его геометрический смысл
Рассмотрим общий случай замены переменных в двойном интеграле. Пусть в плоскости О ху дана область D, ограниченная линией L. Предположим, что х и у являются однозначными и непрерывно дифференцируемыми функциями новых переменных u и v:
x = φ(u, v), y = ψ(u, v). (26)
Рассмотрим прямоугольную систему координат Оuv, точка Р΄(u, v) которой соответствует точке Р(х, у) из области D. Все такие точки образуют в плоскости Оuv область D΄, ограниченную линией L΄. Можно сказать, что формулы (26) устанавливают взаимно однозначное соответствие между точками областей D и D΄. При этом линиям u = const и v = const в плоскости Оuv будут соответствовать некоторые
линии в плоскости Оху.
Рис. 12 .
Рассмотрим в плоскости Оuv прямоугольную площадку ΔS΄, ограниченную прямыми u = const, u+Δu = const, v = const и v+Δv = const. Ей будет соответствовать криволинейная площадка ΔS в плоскости Оху (рис.12). Площади рассматриваемых площадок тоже будем обозначать ΔS΄ и ΔS. При этом ΔS΄ = Δu Δv. Найдем площадь ΔS. Обозначим вершины этого криволинейного четырехугольника Р1, Р2, Р3, Р4, где
P1(x1, y1), x1 = φ(u, v), y1 = ψ(u, v);
P2(x2, y2), x2 = φ(u+Δu, v), y2 = ψ(u+Δu, v);
P3(x3, y3), x3 = φ(u+Δu, v+Δv), y3 = ψ(u+Δu, v+Δv);
P4(x4, y4), x4 = φ(u, v+Δv), y4 = ψ(u, v+Δv).
Заменим малые приращения Δu и Δv соответствующими дифференциалами. Тогда
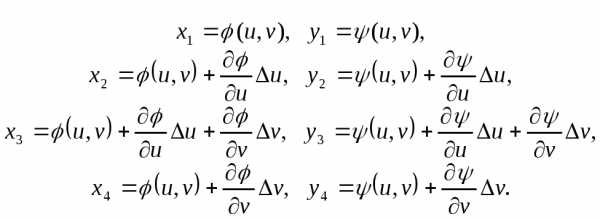
При этом четырехугольник Р1 Р2 Р3 Р4 можно считать параллелограммом и определить его площадь по формуле из аналитической геометрии:
(27)
Определение 6. Определитель 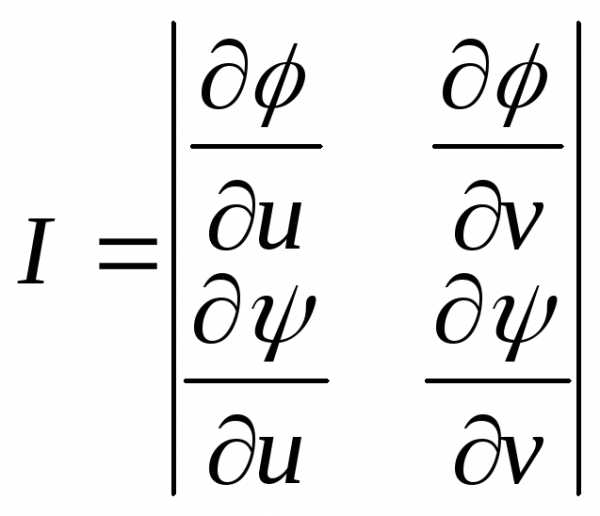 называетсяфункциональным
определителем или якобианом функций φ(х, у) и ψ(х, у).
называетсяфункциональным
определителем или якобианом функций φ(х, у) и ψ(х, у).
Другая форма записи
якобиана: 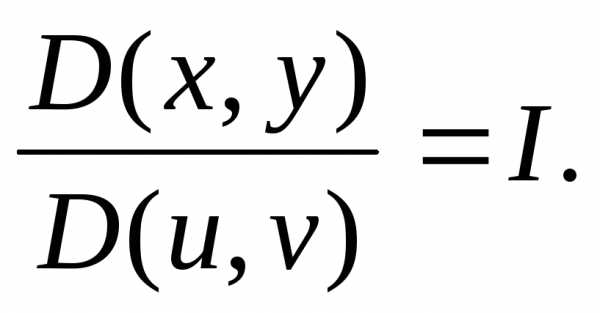
Переходя к пределу при в равенстве (27), получим геометрический смысл якобиана:
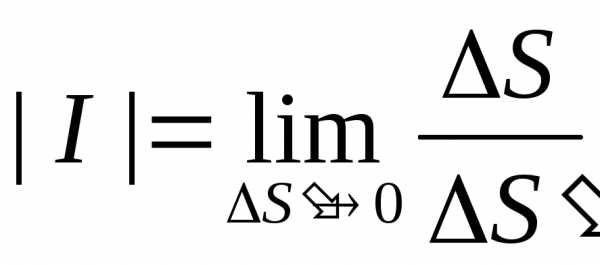 ,
(28)
,
(28)
то есть модуль якобиана есть предел отношения площадей бесконечно малых площадок ΔS и ΔS΄.
Замечание. Аналогичным образом можно определить понятие якобиана и его геометрический смысл для п-мерного пространства: если x1 = φ1(u1, u2,…,un), x2 = φ2(u1, u2,…,un),…, xn = φ(u1, u2,…, un), то
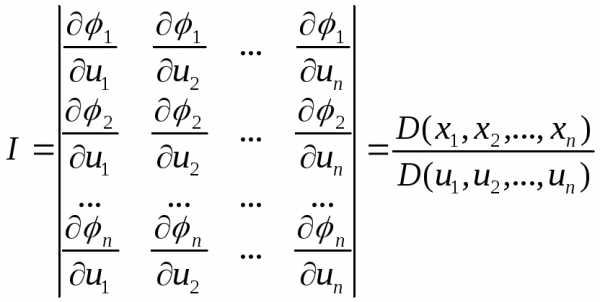 (29)
(29)
При этом модуль якобиана дает предел отношения «объемов» малых областей пространств х1, х2,…, хп и u1, u2,…, un .
7. Замена переменных в кратных интегралах
Исследуем общий случай замены переменных на примере двойного интеграла.
Пусть в области D задана непрерывная функция z = f(x,y), каждому значению которой соответствует то же самое значение функции z = F(u, v) в области D΄, где
F(u, v) = f(φ(u, v), ψ(u, v)). (30)
Рассмотрим интегральную сумму
где интегральная сумма справа берется по области D΄
(здесь ). Переходя к пределу при , получимформулу преобразования координат в двойном интеграле:
(31)
Аналогичным образом можно вывести подобную формулу для тройного интеграла:
(32)
где x = φ(u, v, w),
y = ψ(u, v, w), z = χ(u, v, w), 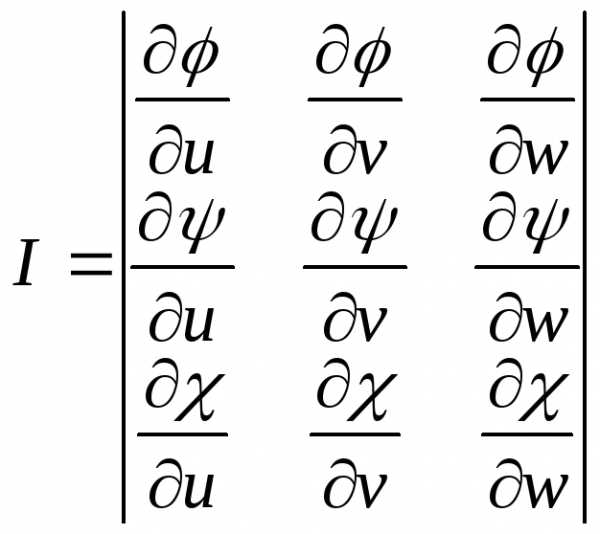 ,
(33)
,
(33)
а область V пространства Оxyz отображается в область V΄ пространства Ouvw.
Переход к цилиндрическим и сферическим координатам
в тройном интеграле
Найдем, используя формулы (25), (26) и (33), якобианы перехода от декартовых координат к цилиндрическим и сферическим:
для цилиндрических координат
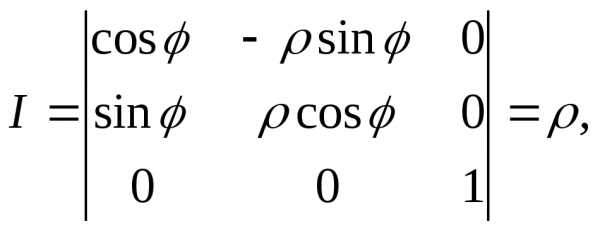 (34)
(34)
для сферических координат
(35)
Тогда формулы перехода к цилиндрическим или сферическим координатам в тройном интеграле будут выглядеть так:
, (36)
где смысл обозначений понятен из предыдущего текста.
Пример 5.
Вычислим интеграл от функции по области, ограниченной поверхностями x² + y² = 1, y = 0, y = x, z = 0, z = 1.
Пример 6.
Пусть подынтегральная функция u = 1, а область интегрирования – шар радиуса R с центром в начале координат. Тогда
.
studfiles.net
Переход к сферическим координатам в тройном интеграле. Примеры решения задач
Переход к сферическим координатам в тройном интеграле
Задача
Вычислить тройной интеграл , перейдя к сферической системе координат, где V-часть области, ограниченной поверхностями , , , , лежащая выше плоскости . Решение
Область интегрирования – это часть шара , лежащая выше плоскости в первом октанте.
Если область интегрирования ограничена сферической поверхностью, то переход к сферическим координатам, как правило, значительно облегчает вычисление интеграла.
В сферической системе координат, центр которой совпадает с началом декартовой системы координат, каждой точке с декартовыми координатами соответствуют сферические координаты , где r – длина вектора , – угол между вектором и положительным направлением оси , – угол между вектором и положительным направлением оси .
Переменные могут принимать следующие значения: , , .
Формулы перехода от декартовой системы координат к
сферической системе координат имеют вид
Якобиан перехода .
Следовательно,
.
Уравнениям границ области в декартовых координатах будут соответствовать уравнения в сферических координатах: ,
или , ; .
Задачи 2. Найти объем тела, заданного неравенствамиСферическая система координат:
www.matem96.ru
2. Сферические координаты в Rn. Их ортогональность
Сферические
координаты в 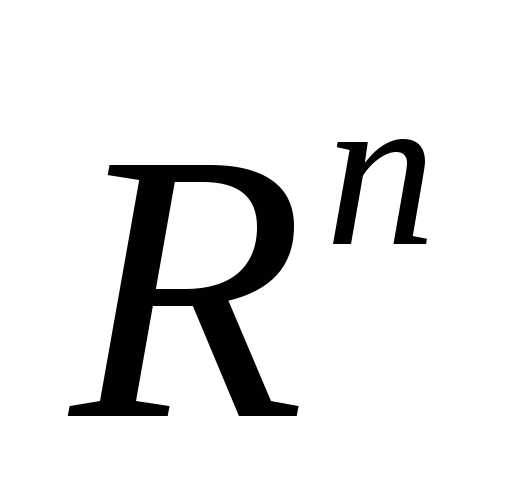 задаются отображением
задаются отображением
,
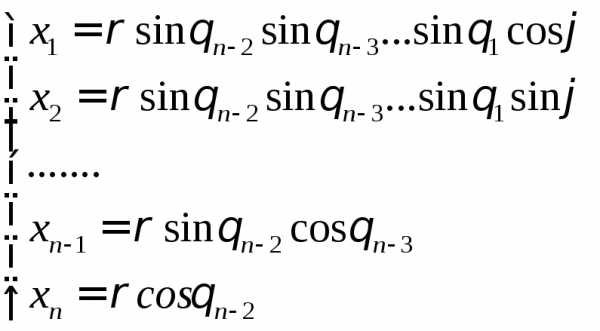 .
.
Найдем касательные векторы и коэффициенты Ламе
………….
Убеждаемся в ортогональности сферических координат и вычисляем Якобиан:
,
.
3.
Вычисление объема  n-мерного
шара
n-мерного
шара
Имеем
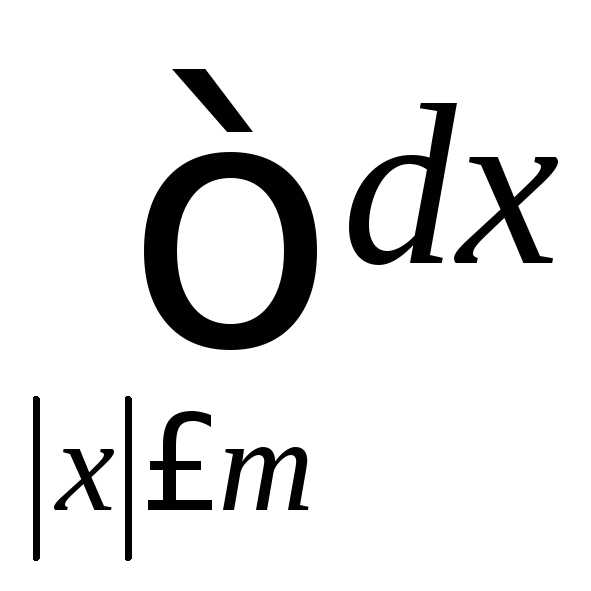 —
объем шара радиуса
—
объем шара радиуса 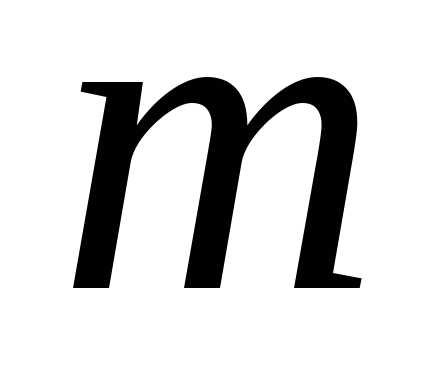 .
Переход к повторному интегралу дает
.
Переход к повторному интегралу дает
.
Пусть
.
Получим рекуррентную формулу для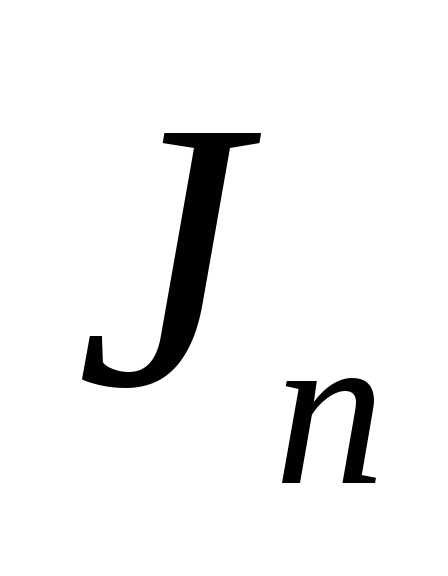 :
:
Разбирая различные случаи, получим
если 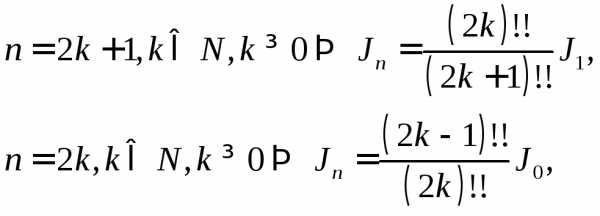
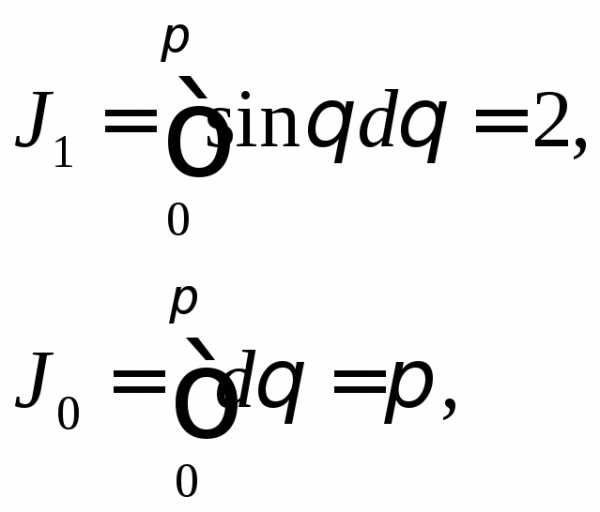
Имеем
,
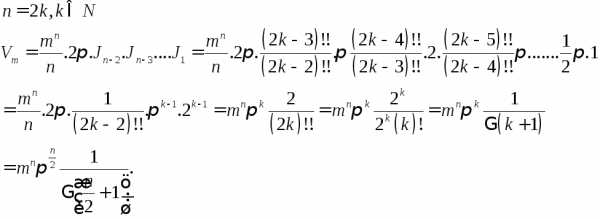
ЛЕКЦИЯ 12
Оператор Лапласа в ортогональных координатах. Оператор Лапласа в полярных координатах в R2, цилиндрических и сферических
координатах в R3
1. Оператор Лапласа в ортогональных координатах
Дифференциальный
оператор Лапласа второго порядка  задается равенством
задается равенством
Тогда
— уравнение Лапласа.
Если 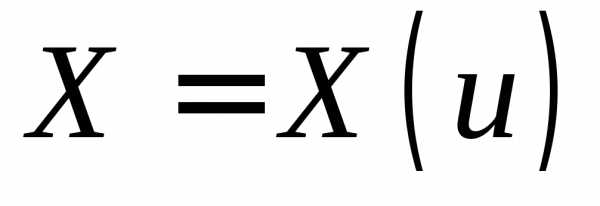 — ортогональные координаты, то оператор
Лапласа в новых координат примет
следующий вид :
— ортогональные координаты, то оператор
Лапласа в новых координат примет
следующий вид :
2. Оператор Лапласа в полярных координатах в R2, цилиндрических и сферических координатах в R3
Оператор
Лапласа в полярных координатах в 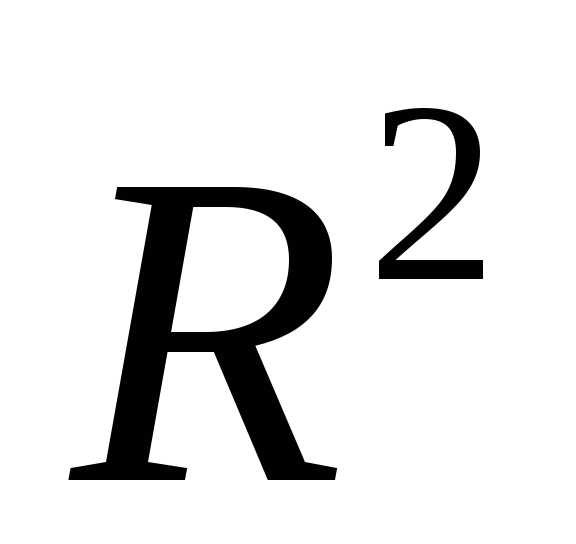 :
:
.
Оператор Лапласа в цилиндрических координатах:

Оператор Лапласа в сферических координатах:
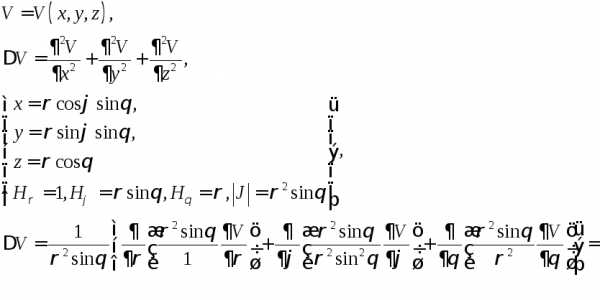
ЛЕКЦИЯ 13
Кратные
несобственные интегралы 1-го и 2-го рода.
Абсолютная сходимость. Признак сравнения.
Сходимость кратных интегралов 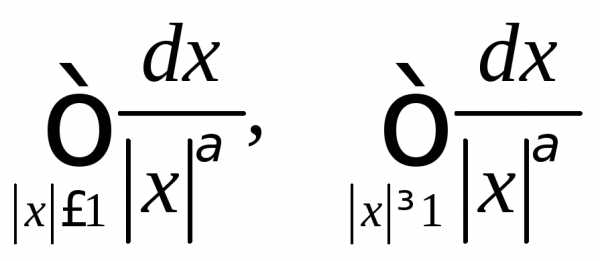
1. Кратные несобственные интегралы 1-го. Абсолютная сходимость.
Признак сравнения
Пусть 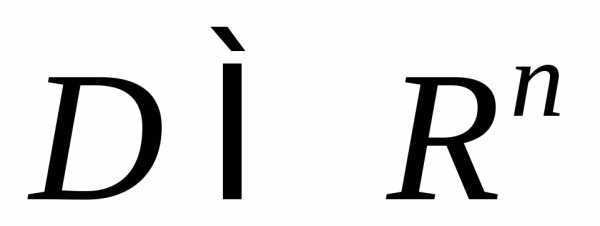 —
неограниченная область,
—
неограниченная область,
,
,для любого .
.
Последовательность
множеств 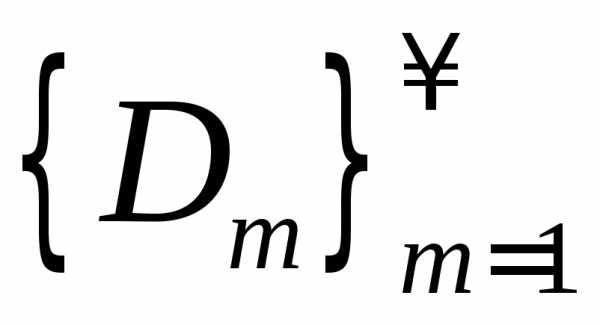 из
из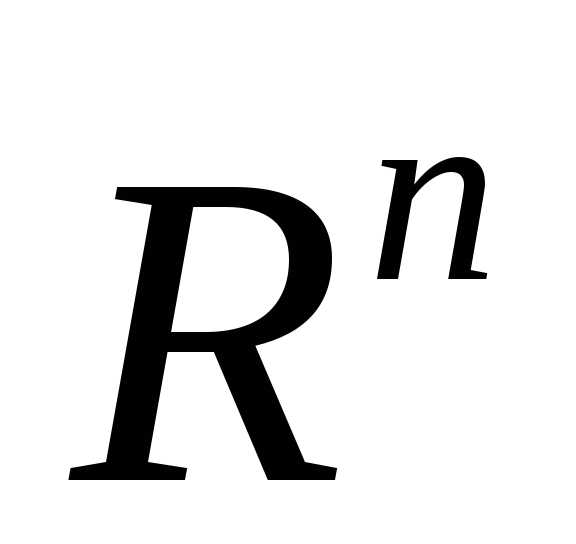 называется
называется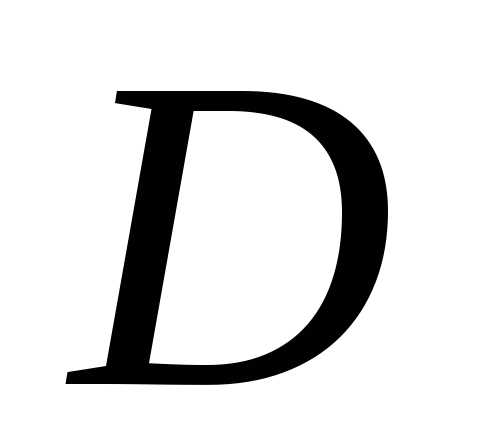 -допустимой,
если
-допустимой,
если
1. ограничены, измеримы по Жордану,
2. ,,
3.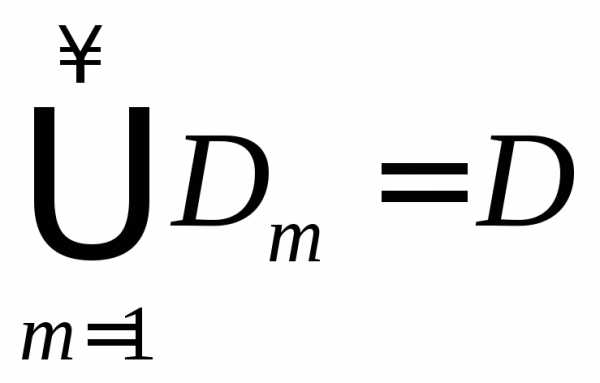 .
.
Пример
: 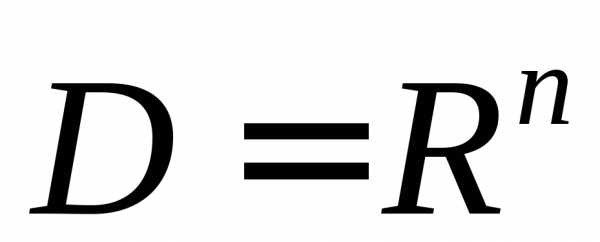 ,
,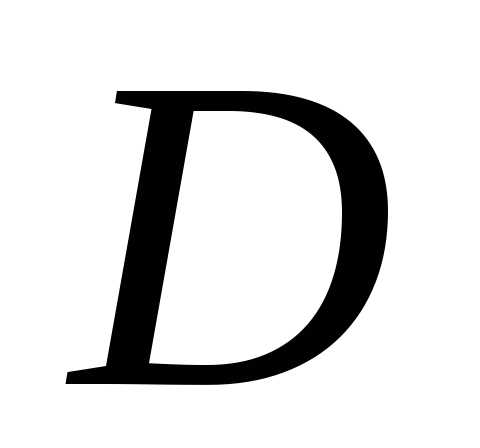 -допустимой
последовательностью будет, например,
последовательность шаров.
-допустимой
последовательностью будет, например,
последовательность шаров.
Число  называется несобственным интегралом
первого рода от функции
называется несобственным интегралом
первого рода от функции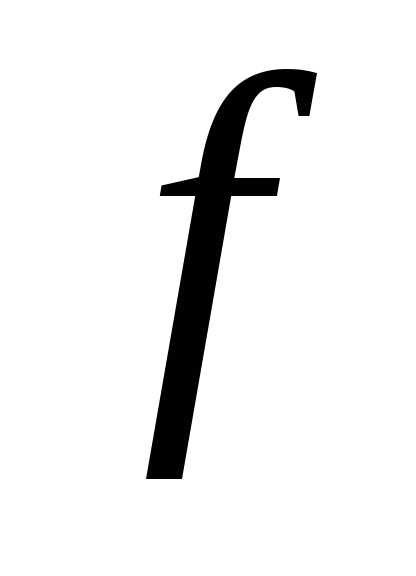 по неограниченной области, если для
любой последовательности
по неограниченной области, если для
любой последовательности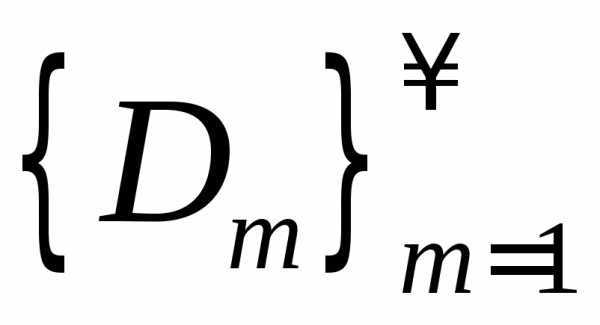 ,
,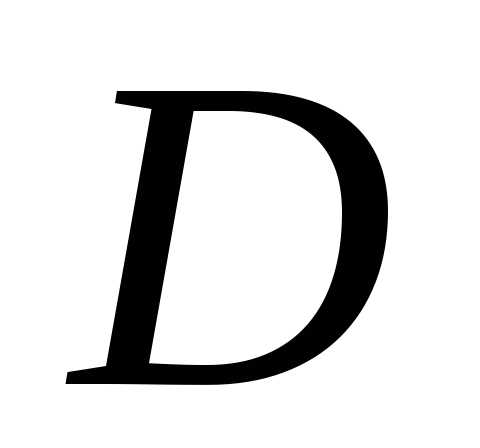 -допустимых
множеств, существует
-допустимых
множеств, существует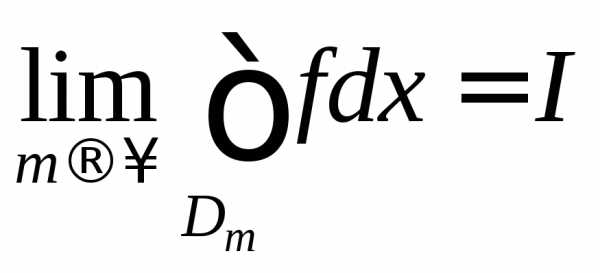 .
.
В
случае сходимости значение несобственного
интеграла полагается равным 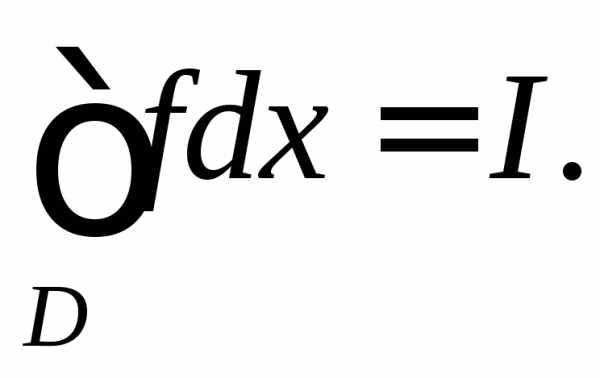
Если
сходится интеграл 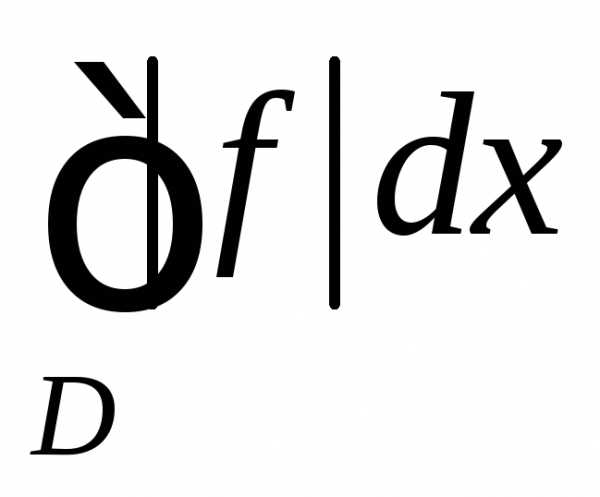 ,то говорят,
что интеграл
,то говорят,
что интеграл 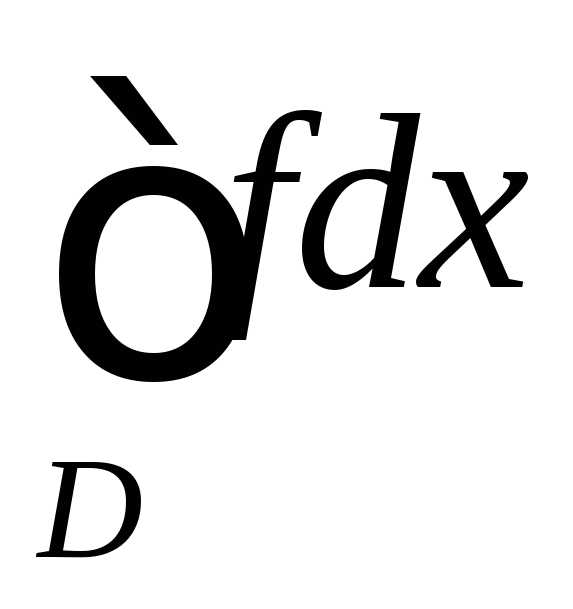 сходится абсолютно.
сходится абсолютно.
Теорема. Несобственный
интеграл 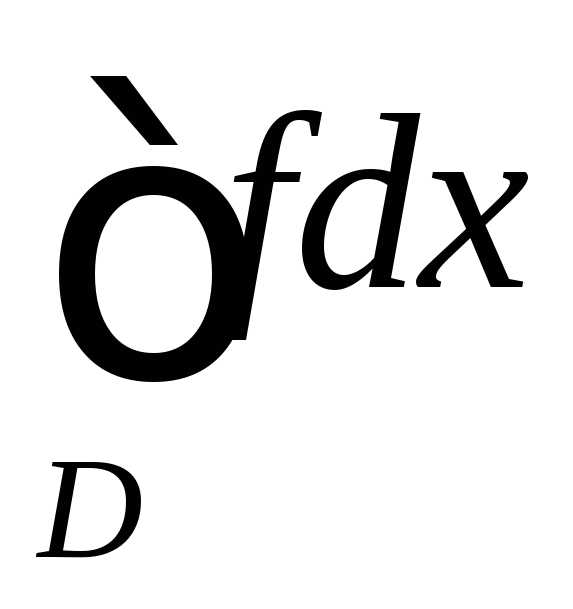 сходится
сходится
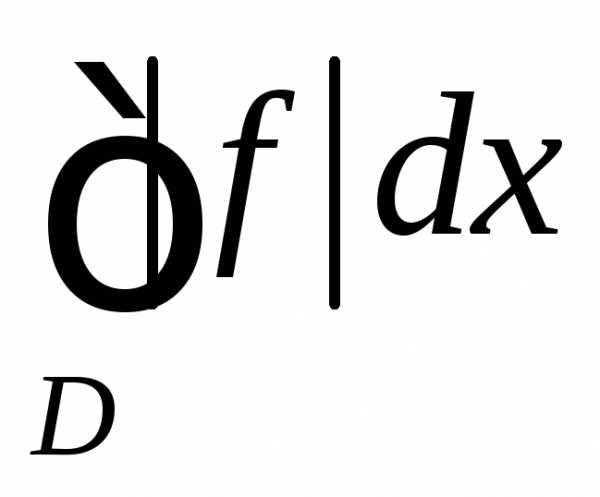 — сходится.
— сходится.
Интеграл 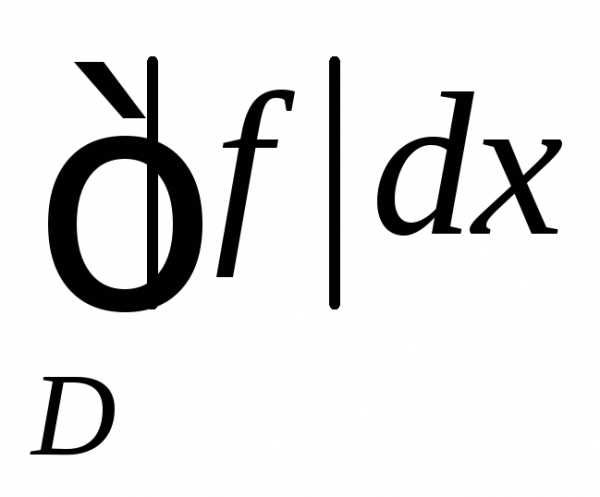 сходится
сходится  последовательность
последовательность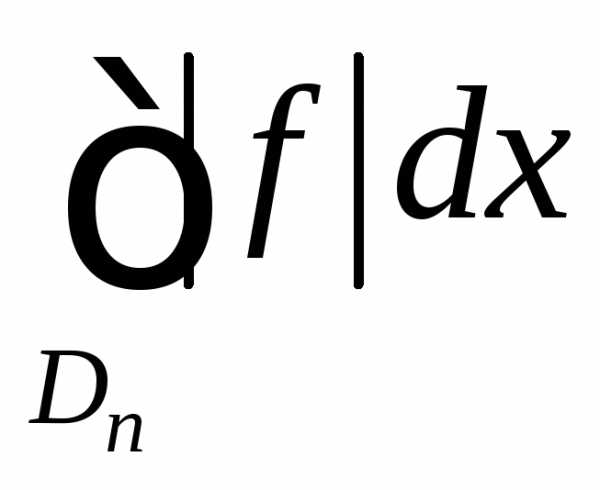 ограниченная хотя бы для одной
последовательности
ограниченная хотя бы для одной
последовательности -допустимых
множеств.
-допустимых
множеств.
Эта теорема указывает на большую разницу между одномерным и многомерным случаями.
Признак сравнения можно записать в следующей форме.
Теорема. Пусть функции 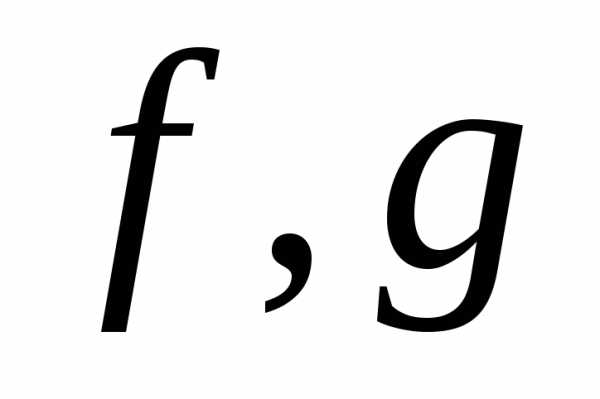 интегрируемы
на любом измеримом по Жордану компакте,
содержащемся в множестве
интегрируемы
на любом измеримом по Жордану компакте,
содержащемся в множестве 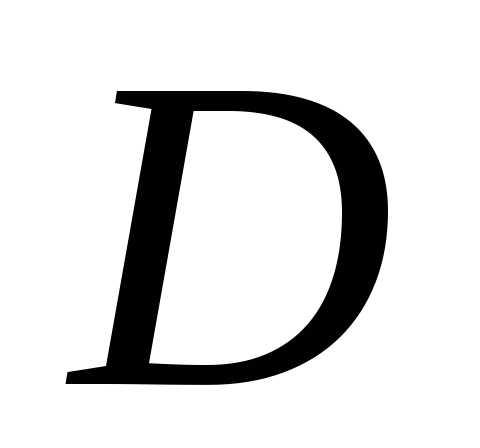 и.
Тогда
и.
Тогда
если несобственный интеграл
 сходится, то несобственный интеграл
тоже
сходится, то несобственный интеграл
тоже сходится;
сходится;если несобственный интеграл
 расходится, то несобственный интеграл
расходится, то несобственный интеграл тоже расходится.
тоже расходится.
2. Сходимость кратных интегралов
Рассмотрим несобственный интеграл
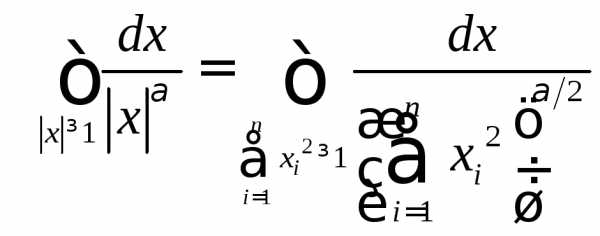 .
.
При 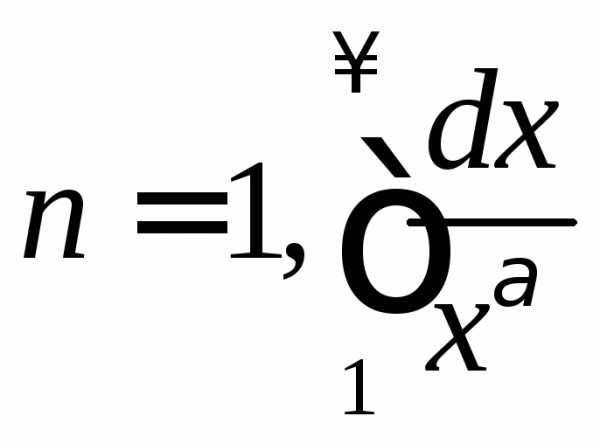 —
сходится при
—
сходится при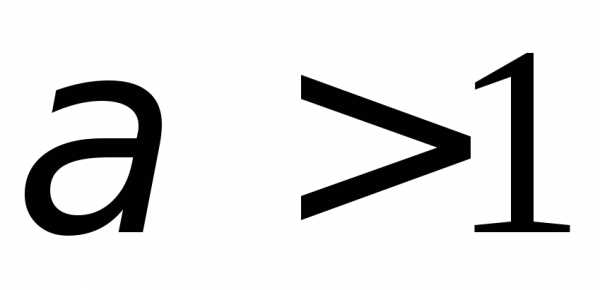 и расходится при
и расходится при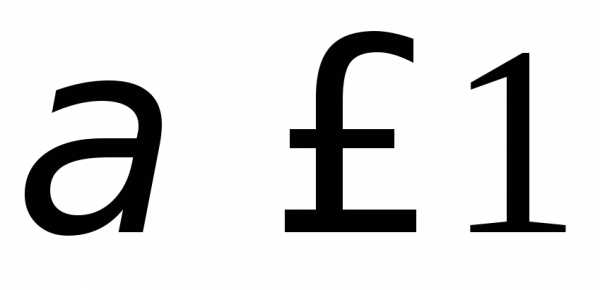 .
.
При ,
.
В полярной системе координат ,
.
При
каких  интеграл ограничен по
интеграл ограничен по

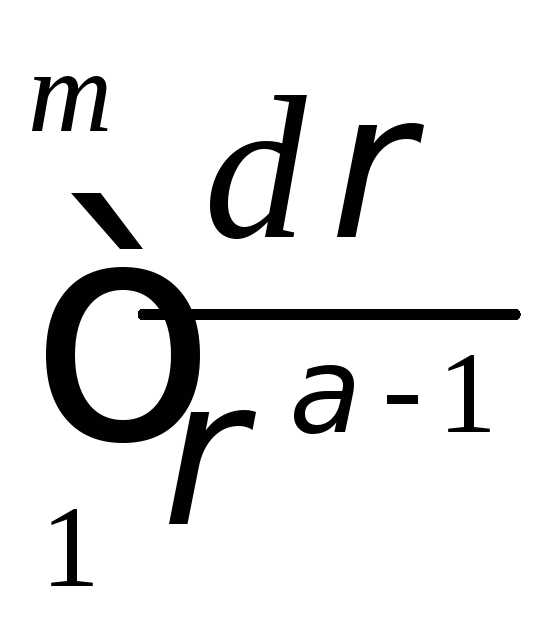 сходится.
сходится.
Для
исследования сходимости интеграла 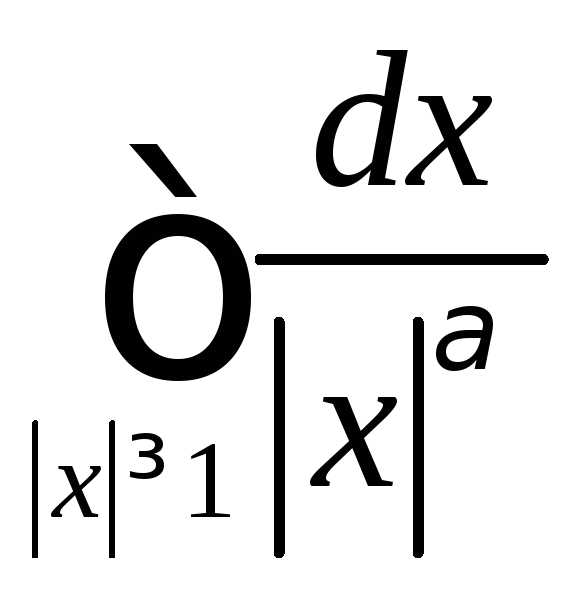 будем использовать сферическую систему
координат
будем использовать сферическую систему
координат
,
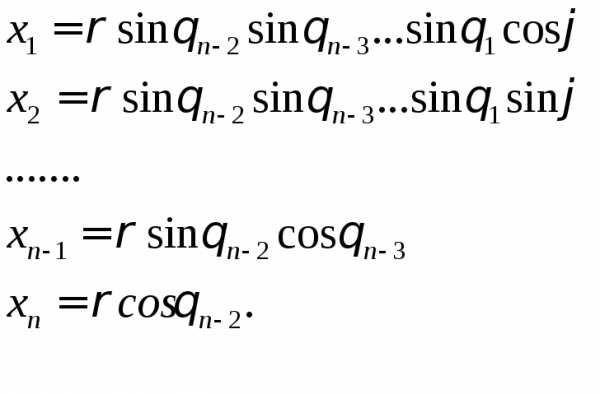
В ней
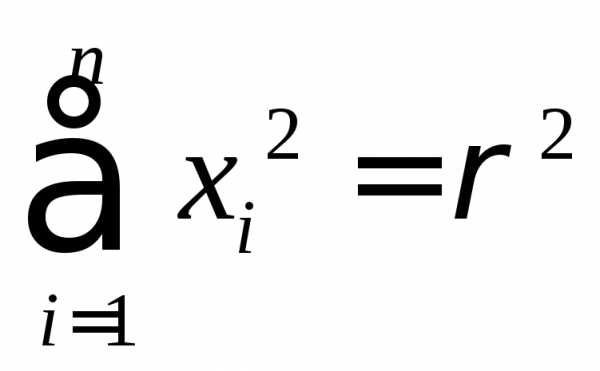 ,
,
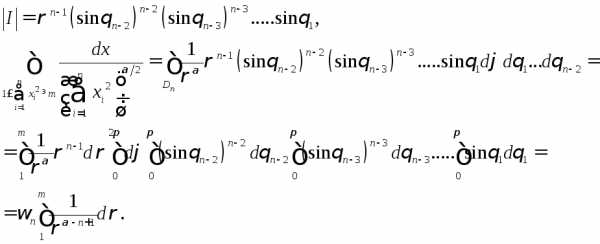
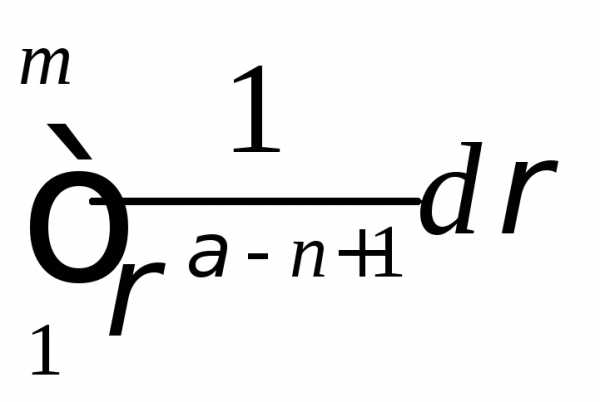 —
ограничен
—
ограничен  сходится.
сходится.
Здесь 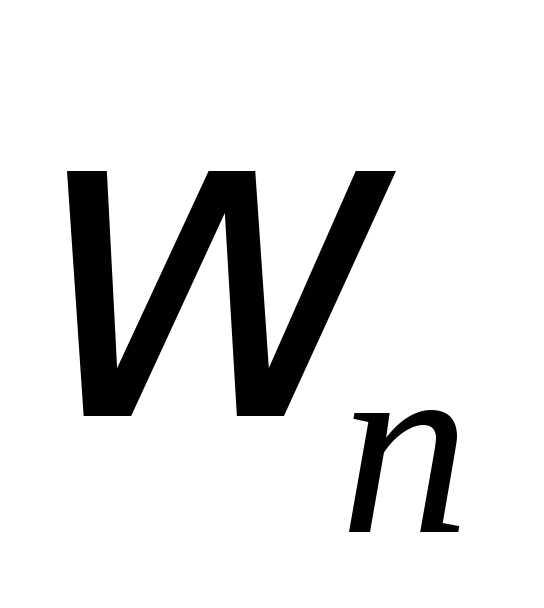 есть
площадь поверхности сферы единичного
радиуса.
есть
площадь поверхности сферы единичного
радиуса.
При 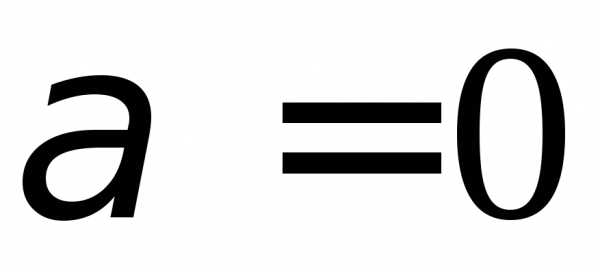 ,
,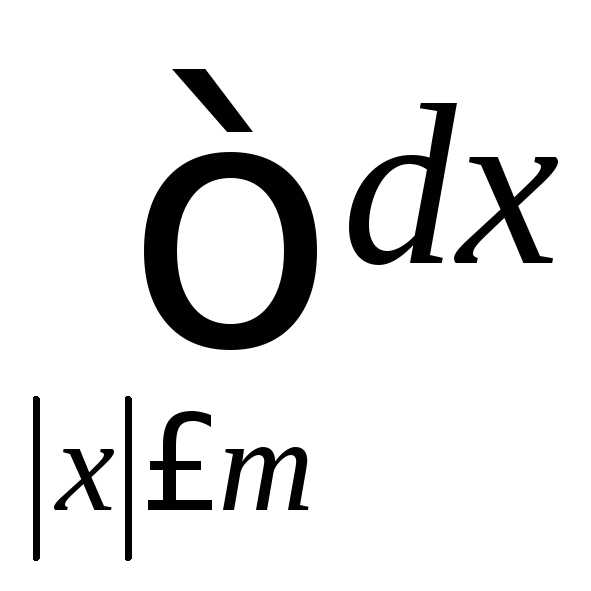 —
объем шара радиуса
—
объем шара радиуса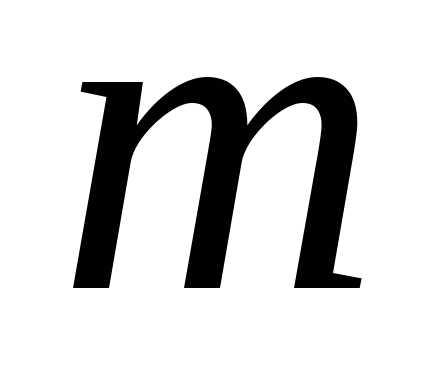 ,
,
Имеем .
3. Кратные несобственные интегралы 2-го рода. Абсолютная сходимость.
Признак сравнения
Пусть 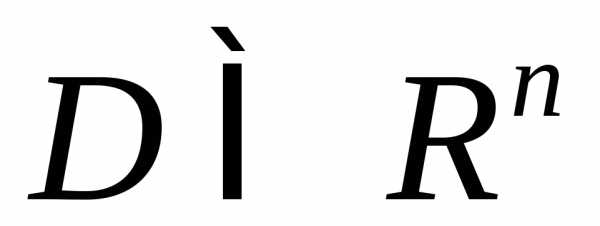 —
измеримая по Жордану область,
—
измеримая по Жордану область,
, ,.
Последовательность
множеств 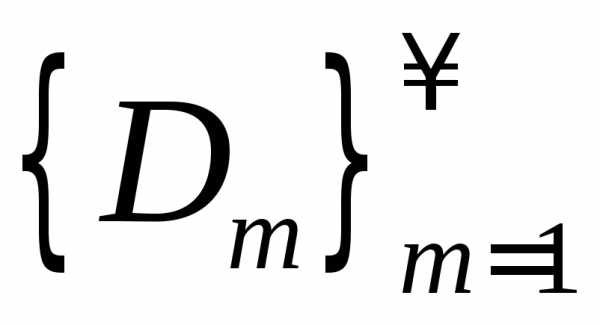 из
из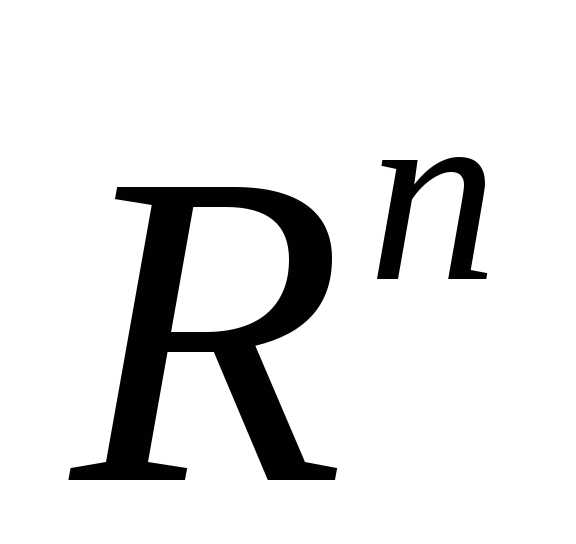 называется
называется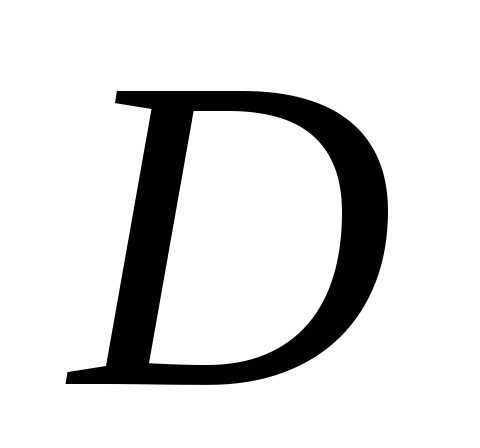 -допустимой
, если
-допустимой
, если
1. ограничены, измеримы по Жордану,
2. ,,
3.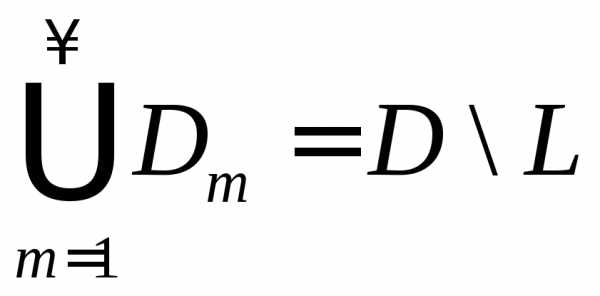 .
.
Пример
:
,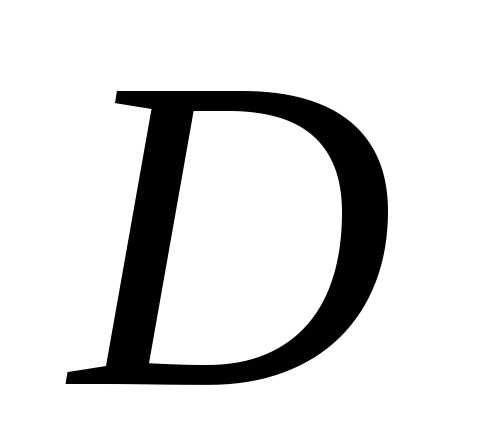 -допустимой
последовательностью будет , например,
последовательность множеств.
-допустимой
последовательностью будет , например,
последовательность множеств.
Число 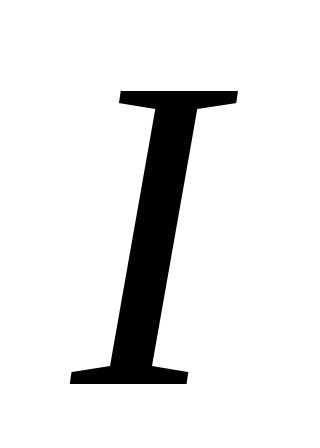 называется несобственным интегралом
второго рода от функции
называется несобственным интегралом
второго рода от функции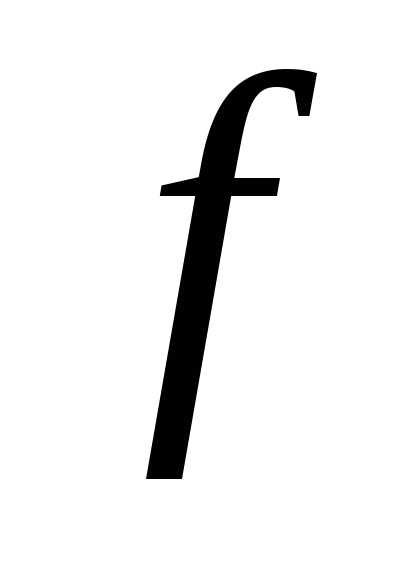 по ограниченной области
по ограниченной области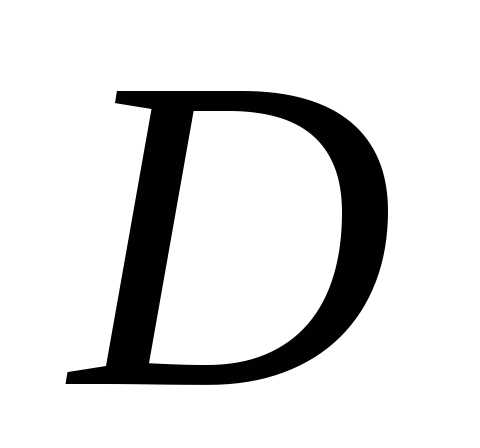 ,
если для любой последовательности
,
если для любой последовательности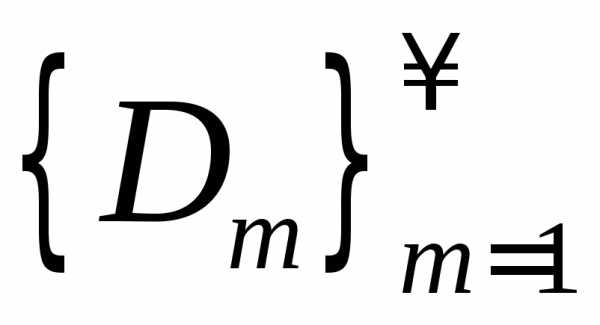 ,
,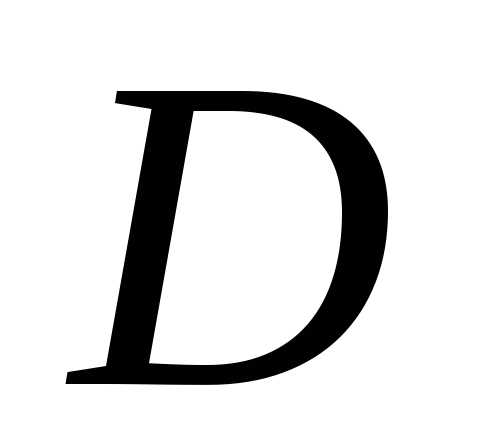 -допустимых
множеств существует
-допустимых
множеств существует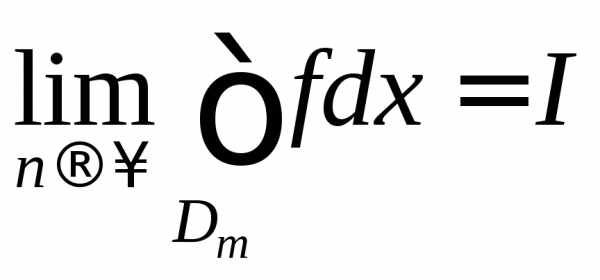 .
.
Если
сходится интеграл 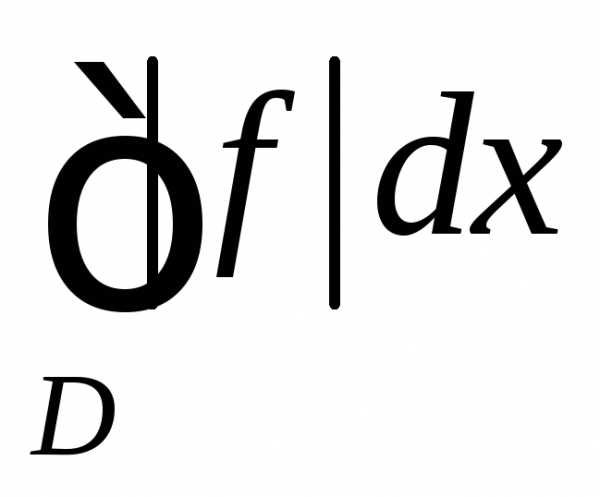 ,то говорят,
что интеграл
,то говорят,
что интеграл 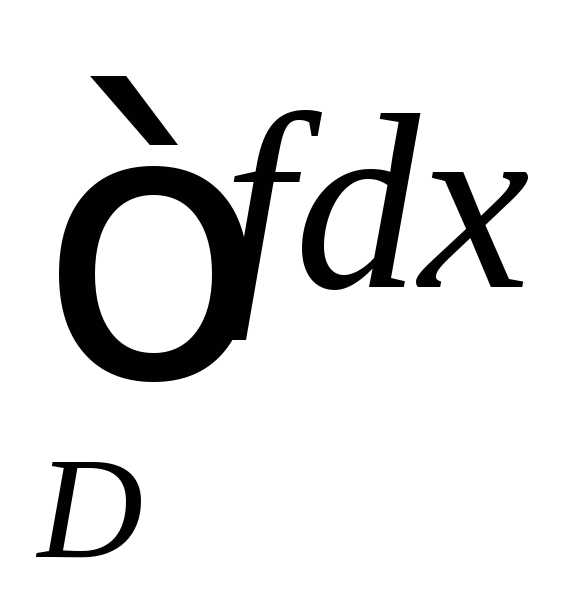 сходится абсолютно.
сходится абсолютно.
Теорема. Несобственный
интеграл 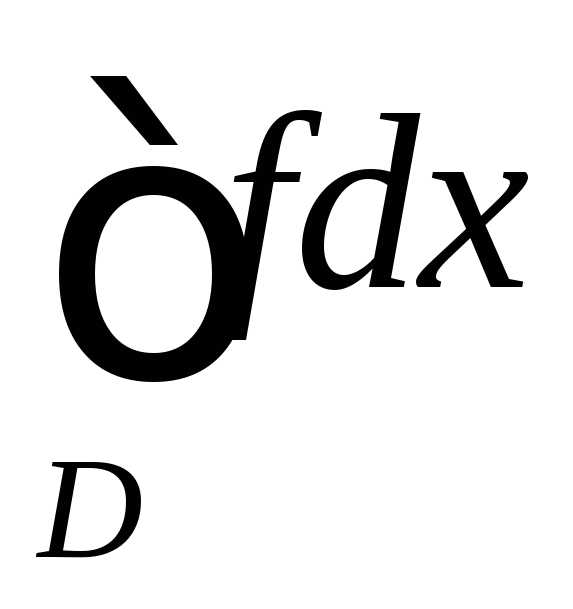 сходится
сходится
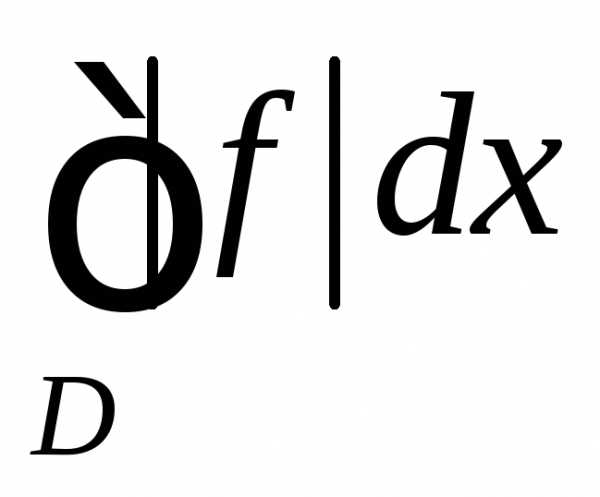 — сходится.
Интеграл
— сходится.
Интеграл 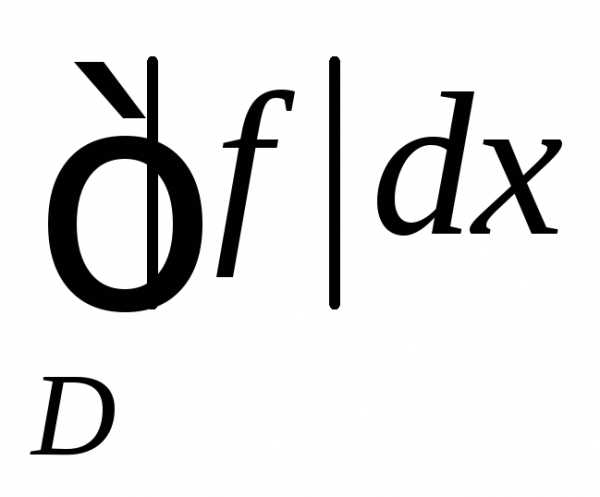 сходится
сходится  последовательность
последовательность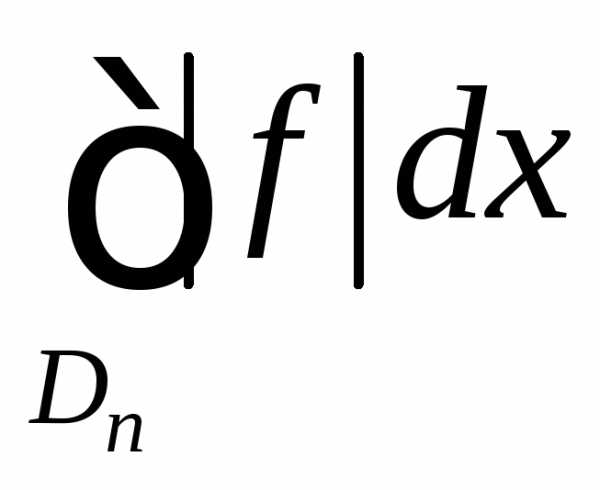 ограниченная хотя бы для одной
последовательности
ограниченная хотя бы для одной
последовательности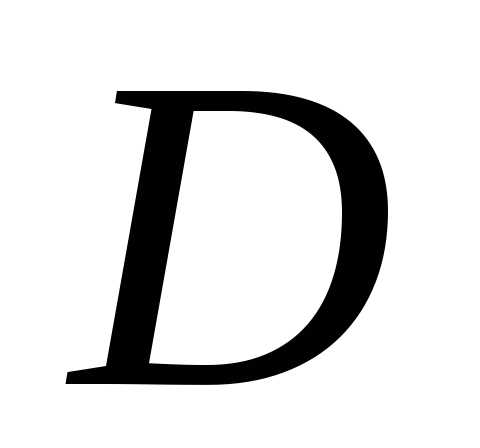 -допустимых
множеств.
-допустимых
множеств.
Признак сравнения можно записать в следующей форме.
Теорема. Пусть функции 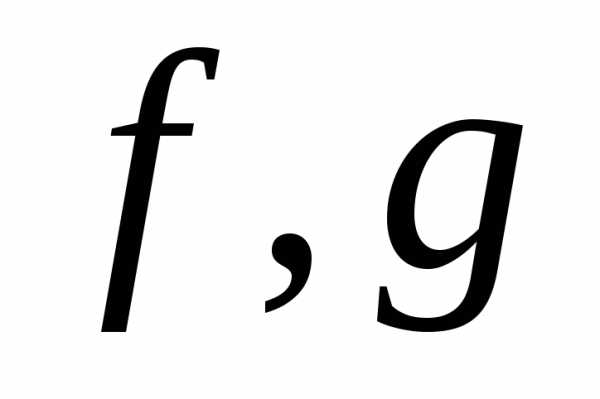 интегрируемы
на любом измеримом по Жордану компакте,
содержащемся в множестве
интегрируемы
на любом измеримом по Жордану компакте,
содержащемся в множестве 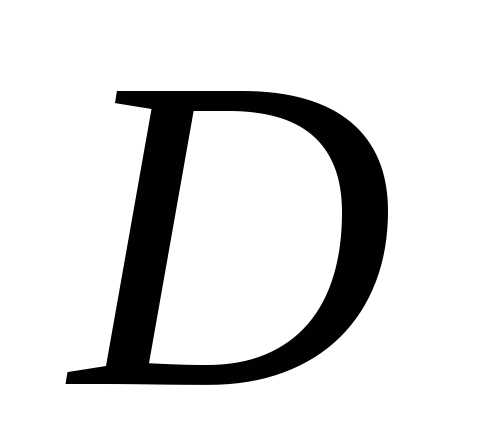 и.
Тогда имеем
и.
Тогда имеем
если несобственный интеграл
 сходится, то несобственный интеграл
сходится, то несобственный интеграл тоже сходится;
тоже сходится;если несобственный интеграл
 расходится, то несобственный интеграл
расходится, то несобственный интеграл тоже расходится.
тоже расходится.
studfiles.net
П.2.3. Вычисление тройного интеграла в сферических координатах.
Точка в трехмерном пространстве описывается тремя координатами (x,y,z) которые являются проекциями точки на оси Oх, Oу и Oz. Используем другой подход. Введем r — расстояние от начала координат до точки, j— угол поворота в плоскости Oxy, y — угол, который отсчитывают от плоскости Oxy. Сферические координаты (r,j,y) связаны с декартовыми координатами соотношениями , где 0£j<2p, -p/2£y£p/2, 0£r<+¥. Якобиан перехода к сферическим координатам равен (проверить самостоятельно). Тогда справедлива формула замены в тройном интеграле:
(20)
Сферические координаты удобно применять в случае, когда область интегрирования есть шар или его часть, так как уравнение его границы — сферы x2+y2+z2=R2, где R— радиус сферы, в сферических координатах имеет вид r=R. Удобно также переходить и в случае, если подынтегральная функция содержит выражения вида x2+y2+z2=r².Если область G ограничена эллипсоидом x2/a2+y2/b2+z2/с2=1, то используют обобщенные сферические координаты , где якобиан . В этих координатах уравнение эллипсоида имеет простой вид r=1.
Пример 1: Вычислить , где G – шар .
Решение: Границей области G является сфера x2+y2+z2=1, уравнение которой в сферических координатах имеет вид r=1. Так как r – расстояние до начала координат, то для любой точки шара выполняется неравенство . Угол φ вводится в плоскости Oxy так же, как и в полярных координатах. Проекция шара на плоскость Oxy — круг, а для круга . Угол отклонения ψ от плоскости Oxy принимает наибольшее значение для точек, лежащих на оси Оz при z>0 и наименьшее значение на оси Oz при z<0. Поэтому для шара всегда . Таким образом, при переходе к сферическим координатам шар G преобразуется в область Ω, которая является прямоугольным параллелепипедом: , , .
Пример 2: Вычислить , где G – часть шара , лежащая в первом октанте (x>0, y>0, z>0).
 |
Рис.40
Решение: Область G приведена на рис. 40. Как уже говорилось, для всех точек шара справедливо . Проекцией области G на плоскость Оху является часть круга, лежащего в первой четверти, поэтому . Угол ψ принимает в данной области наименьшее значение ψ=0 для точек координатной плоскости z=0 , а наибольшее значение для точек на оси Оz при z>0. Расставляем пределы интегрирования:
 Пример 3: Вычислить тройной интеграл , если область G ограничена сферой .
Пример 3: Вычислить тройной интеграл , если область G ограничена сферой .
Рис.41
Решение: Преобразуем уравнение сферы к каноническому виду, выделив полный квадрат по z: . Сфера с центром в точке (0,0,1/2) радиуса 1/2, касается начала координат и расположена выше координатной плоскости z=0 (рис. 41). Ее уравнение в сферических координатах имеет вид r=sinψ, так что для всех внутренних точек выполняется неравенство . Так как проекцией области G на плоскость Оху является круг, то .Угол отклонения ψ для данной области изменяется в пределах . Расставляем пределы интегрирования:
Пример 4: Перейти к сферическим координатам и вычислить , где G— объем, ограниченный поверхностями x2+y2=z2, x2+y2+z2=a2, z=0, x=0, y=0
Решение: Область G— это часть шара, лежащего в первом октанте и вырезанного конусом (рис.42).Как уже говорилось, для шара в первом октанте , , а угол ψ наименьшее значение принимает на поверхности конуса. Найдем его из уравнения конуса, преобразовав к сферическим координатам: r²(cos²φ+sin²φ)cos²ψ=r²sin²ψ или tgψ=1,откуда получаем .
Перейдем к сферическим координатам:
 | |||
 | |||
Рис.42 Рис.43
Пример 5: В интеграле перейти к сферическим координатам и расставить пределы интегрирования, если G – общая часть двух шаров и .
Решение: Область G приведена на рис.43. Из рисунка видно, что нижней границей области является сфера со смещенным центром, ее уравнение r=2Rsinψ, а верхней – сфера с центром в начале координат, уравнение которой r=R. Поэтому область G необходимо разбить на две области конической поверхностью, проходящей через линию пересечения двух сфер. Найдем ее уравнение: 2Rsinψ=R или sinψ=1/2 , откуда получаем . В первой области при координата r изменяется от 0 до 2Rsinψ, а во второй области при r изменяется от 0 до R. В обоих случаях , так как проекциями этих областей на плоскость Оху является круг. В итоге получаем
Замечание: При решении некоторых задач, например, связанных с радиолокацией, удобнее отсчитывать угол y не от плоскости Oху, а от оси Oz. Приведем данные координаты:
, где 0£j<2p, 0£y£p, 0£r<+¥, .
infopedia.su
Сферическая система координат — Википедия
Точка имеет три декартовых и три сферических координатыСферическую систему координат удобно определять, соотносясь с декартовой прямоугольной системой координат (см. рисунок):
Сферическими координатами называют систему координат для отображения геометрических свойств фигуры в трёх измерениях посредством задания трёх координат , где — кратчайшее расстояние до начала координат, а и — зенитный и азимутальный углы соответственно.
Понятия зенит и азимут широко используются в астрономии. Вообще зенит — это направление вертикального подъёма над произвольно выбранной точкой (точкой наблюдения), принадлежащей так называемой фундаментальной плоскости. В качестве фундаментальной плоскости в астрономии может быть выбрана плоскость, в которой лежит экватор, или плоскость, в которой лежит горизонт, или плоскость эклиптики и т. д., что порождает разные системы небесных координат. Азимут — угол между произвольно выбранным лучом фундаментальной плоскости с началом в точке наблюдения и другим лучом этой плоскости, имеющим общее начало с первым.
Применительно к нашему рисунку сферической системы координат, фундаментальная плоскость — это плоскость xy. Зенит — некая удалённая точка, лежащая на оси Z и видимая из начала координат. Азимут отсчитывается от оси X до проекции радиус-вектора r на плоскость xy. Это объясняет названия углов, как и то, что сферическая система координат может служить обобщением (пусть хотя бы и приближённым) множества видов систем небесных координат.
Три координаты определены как:
Угол называется зенитным, или полярным, или нормальным, а также он может быть назван английским словом colatitude, а угол — азимутальным. Углы и не имеют значения при , а не имеет значения при (то есть при или ).
Такое соглашение установлено в стандарте (ISO 31-11</span>ruen). Кроме того может использоваться соглашение, когда вместо зенитного угла , используется угол между радиус-вектором точки r и плоскостью xy, равный — . Он называется широтой и может быть обозначен той же буквой . Широта может изменяться в пределах . При этом соглашении углы и не имеют значения при , так же как и в первом случае, а не имеет значения при (то есть при или ).
Переход к другим системам координат[править]
Декартова система координат[править]
Если заданы сферические координаты точки, то переход к декартовым осуществляется по формулам:
Обратно, от декартовых к сферическим:
(здесь, конечно, требуется определенное естественное уточнение для значений вне первого октанта; то же для всех формул с арктангенсом здесь и ниже; впрочем, замена на соответствующую формулу с арккосинусом снимает этот вопрос в отношении координаты ).
Якобиан преобразования от декартовых к сферическим будет равен:
Таким образом, элемент объёма при переходе от декартовых к сферическим координатам будет выглядеть следующим образом:
Цилиндрическая система координат[править]
Если заданы сферические координаты точки, то переход к цилиндрическим осуществляется по формулам:
Обратно от цилиндрических к сферическим:
Якобиан преобразования от сферических к цилиндрическим:
Дифференциальные характеристики[править]
Вектор , проведённый из точки в точку , равен
где
ортогональные единичные векторы сферических координат в направлении увеличения , соответственно, а — единичные векторы декартовых координат. Сферические координаты являются ортогональными, поэтому метрический тензор имеет в них диагональный вид:
- Квадрат дифференциала длины дуги:
Остальные равны нулю.
wp.wiki-wiki.ru
23. Переход к сферическим координатам
Формулы , , преобразуют сферические координаты точки M в декартовы координаты этой точки и переводят область (или ) изменения сферических координат на все пространство Oxyz.
Геометрически: R — радиус-ветор OM точки M; j — угол между осью Ox и проекцией радиус-вектора R на плоскость Oxy; y — угол между осью Oz и радиус-вектором R, отсчитываемый по ходу стрелки часов (рис.14.18).
Обратное преобразование имеет вид
, ,
,
Фиксируя в последних формулах , получим тройку координатных поверхностей: сферу, полуплоскость, полуконус, соответственно (рис.14.18).Якобиан преобразования
.
При переходе в тройном интеграле к сферическим координатам справедлива формула:
, (3.7)
Где W — область изменения сферических координат точек области V из Oxyz.
Пример 12. Вычислить тройной интеграл , где .
Ñ Область V ограничена полусферой и полуконусом (рис.14.18). Для удобства вычисления тройного интеграла перейдем к сферическим координатам по формулам: , при этом . Неравенства, описывающие V , преобразуются: а)
Б) .
Так как нет ограничений на , то . В итоге, область интегрирования в сферических координатах есть (этот же результат можно было усмотреть из чертежа). Тогда по формуле (3.7) =½повторный интеграл «расщепился» в произведение определенных интегралов ½=
=. #
Пример 13. Вычислить тройной интеграл , где V ограничена полусферой , цилиндром И плоскостью .
Ñ Тело V и проекция его на плоскость Oxy — круг радиуса R изображены на рис.14.19 и 14.20. Для вычисления I перейдем к цилиндрическим координатам по формулам . Поверхности, ограничивающие V преобразуются: а) , б) , в) Z=A . Так как нет ограничений на координату , то (или .Область интегрирования в цилиндрических координатах есть .
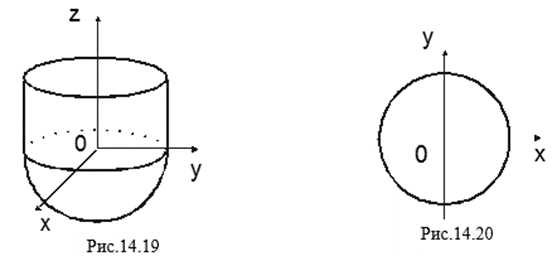
Тогда по формуле (3.6) = = == = ==. #
Задачи для самостоятельного решения
Перейти в тройном интеграле к цилиндрическим координатам или сферическим координатам и расставить пределы интегрирования:
52. V – область, находящаяся в первом октанте и ограниченная поверхностями , .
53. V – область, ограниченная поверхностями .
54. .
55. .
Перейдя к цилиндрическим или сферическим координатам, вычислить интегралы:
56. . 57. .
58. . 59. .
60. , где .
61. , где .
62. , где область V ограничена поверхностью .
| < Предыдущая | Следующая > |
|---|
matica.org.ua
Сферическая система координат — Википедия
Точка имеет три декартовых и три сферических координатыСферическую систему координат удобно определять, соотносясь с декартовой прямоугольной системой координат (см. рисунок):
Сферическими координатами называют систему координат для отображения геометрических свойств фигуры в трёх измерениях посредством задания трёх координат , где — кратчайшее расстояние до начала координат, а и — зенитный и азимутальный углы соответственно.
Понятия зенит и азимут широко используются в астрономии. Вообще зенит — это направление вертикального подъёма над произвольно выбранной точкой (точкой наблюдения), принадлежащей так называемой фундаментальной плоскости. В качестве фундаментальной плоскости в астрономии может быть выбрана плоскость, в которой лежит экватор, или плоскость, в которой лежит горизонт, или плоскость эклиптики и т. д., что порождает разные системы небесных координат. Азимут — угол между произвольно выбранным лучом фундаментальной плоскости с началом в точке наблюдения и другим лучом этой плоскости, имеющим общее начало с первым.
Применительно к нашему рисунку сферической системы координат, фундаментальная плоскость — это плоскость xy. Зенит — некая удалённая точка, лежащая на оси Z и видимая из начала координат. Азимут отсчитывается от оси X до проекции радиус-вектора r на плоскость xy. Это объясняет названия углов, как и то, что сферическая система координат может служить обобщением (пусть хотя бы и приближённым) множества видов систем небесных координат.
Три координаты определены как:
Угол называется зенитным, или полярным, или нормальным, а также он может быть назван английским словом colatitude, а угол — азимутальным. Углы и не имеют значения при , а не имеет значения при (то есть при или ).
Такое соглашение установлено в стандарте (ISO 31-11</span>ruen). Кроме того может использоваться соглашение, когда вместо зенитного угла , используется угол между радиус-вектором точки r и плоскостью xy, равный — . Он называется широтой и может быть обозначен той же буквой . Широта может изменяться в пределах . При этом соглашении углы и не имеют значения при , так же как и в первом случае, а не имеет значения при (то есть при или ).
Переход к другим системам координат[править]
Декартова система координат[править]
Если заданы сферические координаты точки, то переход к декартовым осуществляется по формулам:
Обратно, от декартовых к сферическим:
(здесь, конечно, требуется определенное естественное уточнение для значений вне первого октанта; то же для всех формул с арктангенсом здесь и ниже; впрочем, замена на соответствующую формулу с арккосинусом снимает этот вопрос в отношении координаты ).
Якобиан преобразования от декартовых к сферическим будет равен:
Таким образом, элемент объёма при переходе от декартовых к сферическим координатам будет выглядеть следующим образом:
Цилиндрическая система координат[править]
Если заданы сферические координаты точки, то переход к цилиндрическим осуществляется по формулам:
Обратно от цилиндрических к сферическим:
Якобиан преобразования от сферических к цилиндрическим:
Дифференциальные характеристики[править]
Вектор , проведённый из точки в точку , равен
где
ортогональные единичные векторы сферических координат в направлении увеличения , соответственно, а — единичные векторы декартовых координат. Сферические координаты являются ортогональными, поэтому метрический тензор имеет в них диагональный вид:
- Квадрат дифференциала длины дуги:
Остальные равны нулю.
www.wiki-wiki.ru

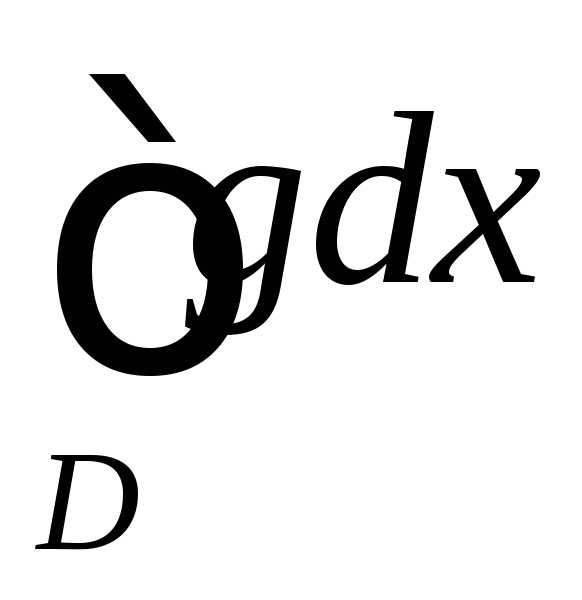 сходится, то несобственный интеграл
тоже
сходится, то несобственный интеграл
тоже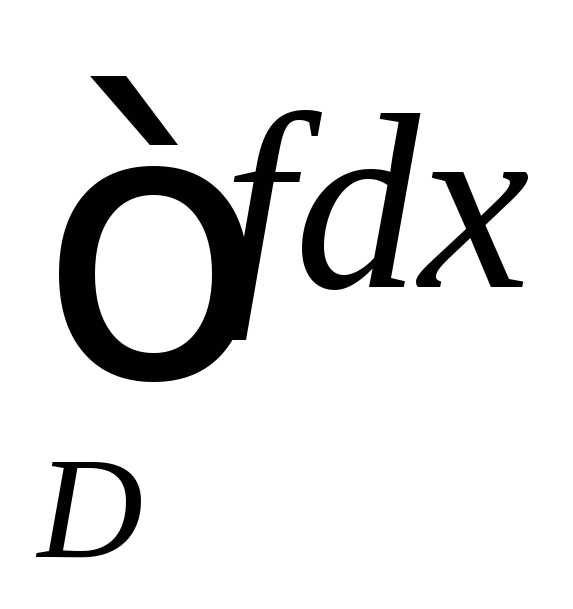 сходится;
сходится;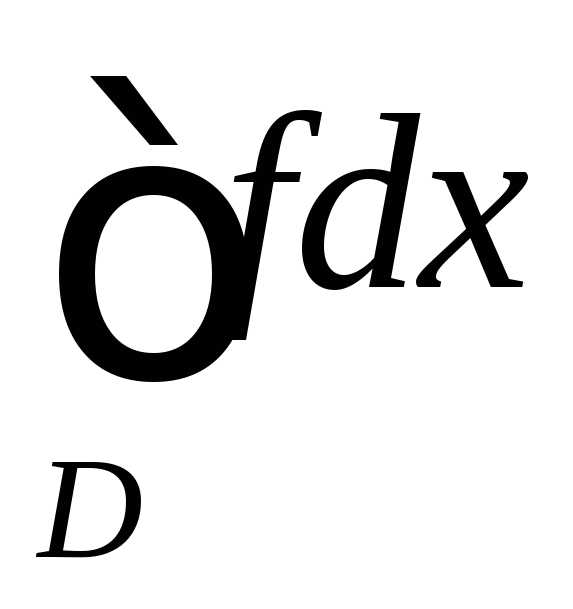 расходится, то несобственный интеграл
расходится, то несобственный интеграл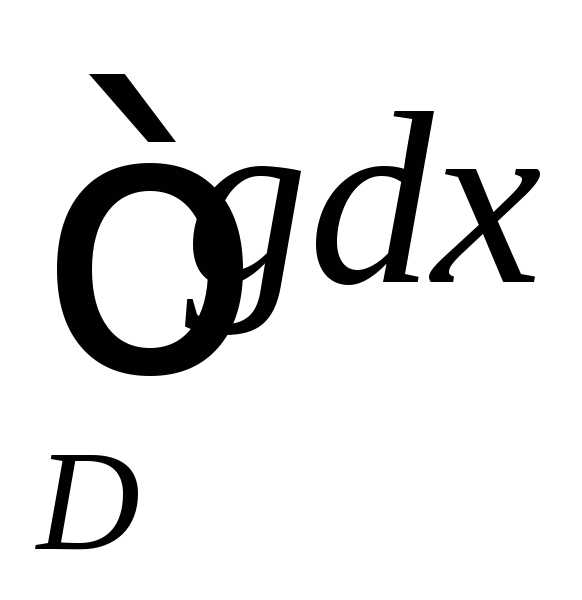 тоже расходится.
тоже расходится.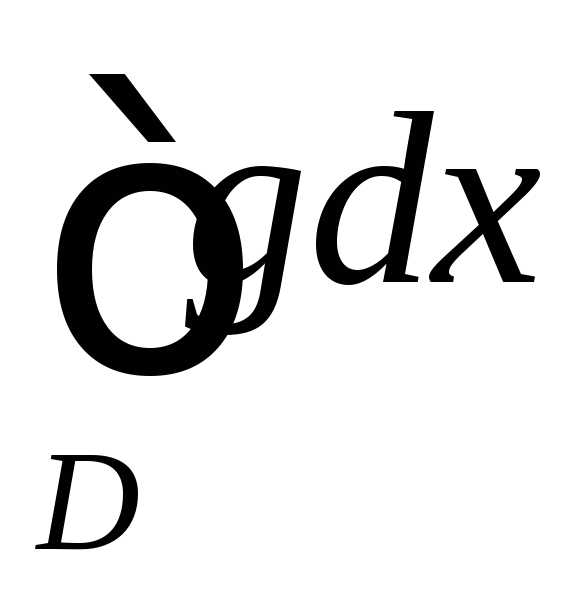 сходится, то несобственный интеграл
сходится, то несобственный интеграл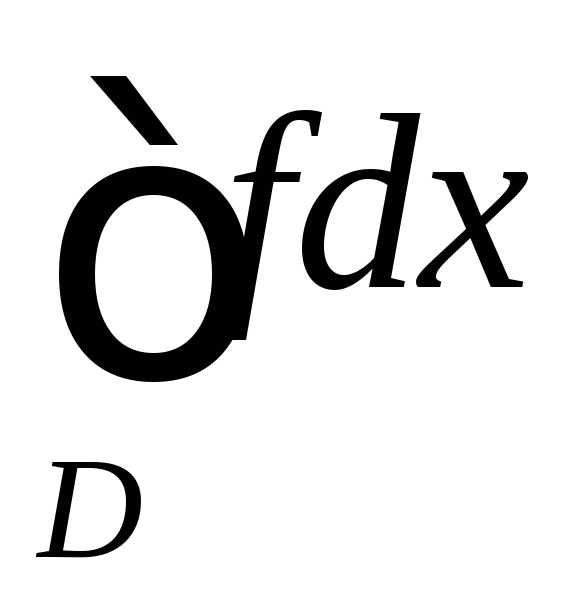 тоже сходится;
тоже сходится;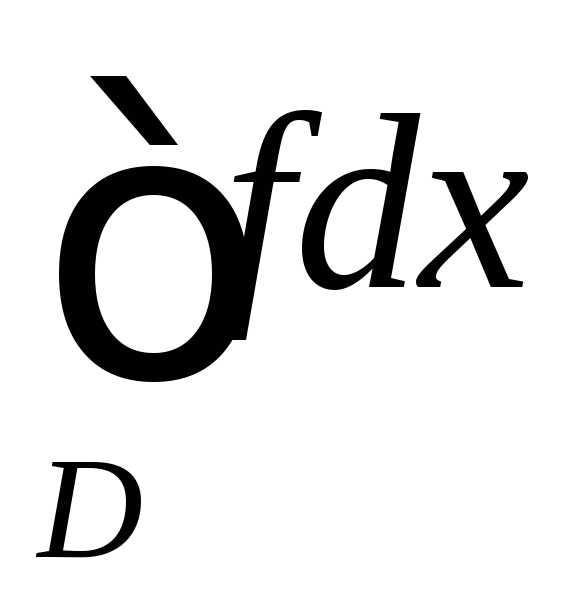 расходится, то несобственный интеграл
расходится, то несобственный интеграл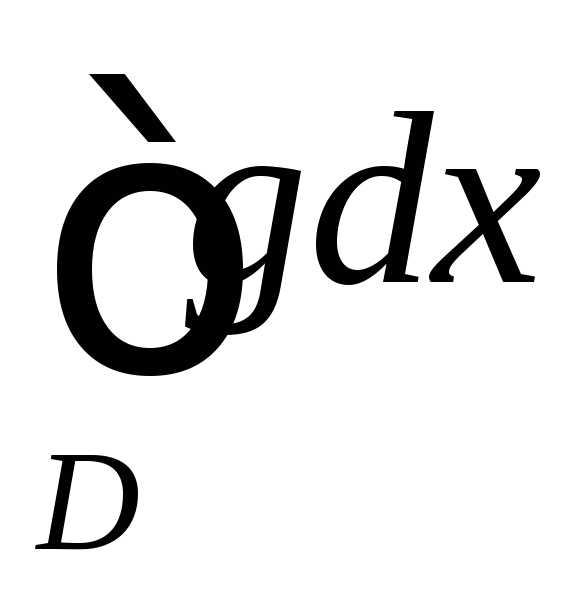 тоже расходится.
тоже расходится.