Задача о брахистохроне | Математика, которая мне нравится
Задача о брахистохроне была поставлена Иоганном Бернулли в Acta Eruditorum в июне 1696 года. Он представил проблему следующим образом:
“Я, Иоганн Бернулли, обращаюсь к самым блестящим математикам в мире. Ничто не является более привлекательным для умных людей, чем честная, сложная задача, решение которой, возможно, дарует славу и останется вечным памятником. Следуя примеру Паскаля, Ферма и т.д., я надеюсь получить благодарность всего научного сообщества, указывая лучшим математикам нашего времени проблему, на которой они смогут проверить свои методы и силу своего интеллекта. Если кто-то представит мне решение предлагаемой задачи, я публично объявлю его достойным похвалы’’.
Задача была следующей:
Даны две точки и , лежащие в вертикальной плоскости. Какова траектория точки, движущейся только под действием силы тяжести, которая начинает двигаться из и достигает за кратчайшее время?
Возможно, мы слишком углубляемся в ссылки Иоганна Бернулли на Паскаля и Ферма, но интересно отметить, что самая известная задача Паскаля была связана с циклоидой, о которой на данный момент Иоганн Бернулли знал, что она является решением задачи о брахистохроне, и что его метод решения этой задачи использовал идеи Ферма.
Иоганн Бернулли не был первым, кто рассматривал задачу о брахистохроне. Галилей в 1638 году изучал эту проблему в своей знаменитой работе “Беседы о двух новых науках’’. Его вариант задачи был сначала таким: найти прямую линию, соединяющую точку с точкой на вертикальной прямой, которую можно достичь за наименьшее время. Он правильно рассчитал, что такая прямая из точки будет составлять угол в к вертикали при достижении необходимой вертикальной прямой в точке .
Он вычислил время, необходимое для точки, чтобы перейти от к по прямой линии, затем он показал, что точка достигнет быстрее, если она будет двигаться по двум отрезкам и , где — точка на окружности.
Лучшая прямая Галилея
Хотя Галилей был совершенно прав в этом, но он сделал ошибку, когда он далее утверждал, что путь наискорейшего спуска от до будет дугой окружности — неверное заключение.
Результат Галилея
Вернемся к Иоганну Бернулли. Он изложил задачу в Acta Eruditorum и хотя и знал сам, как ее решать, бросил вызов другим. Лейбниц убедил Иоганна Бернулли дать больше времени для решения задачи, чем шесть месяцев, которые тот изначально предполагал отвести на это, чтобы зарубежные математики также имели возможность принять участие в ее решении. Было получено пять решений: Ньютона, Якоба Бернулли, Лейбница и Лопиталя плюс решение самого Иоганна Бернулли.
Теперь Иоганн Бернулли и Лейбниц намеренно искушали Ньютона этой задачей. Учитывая спор о дифференциальном исчислении, неудивительно, что Иоганн Бернулли включил в свой вызов такие слова:
“…еще меньше тех, кто способен решить наши замечательные задачи, да, меньше даже среди истинных математиков, гордящихся тем, что [они] … удивительно расширили границы (
По словам Кондуитта, биографа Ньютона, он решил задачу в вечер после возвращения домой из Королевского монетного двора. Ньютон
“… в разгар спешной большой перечеканки он не приходил домой из Тауэра до четырех часов (дня), очень устал, но не лег спать, пока не решил задачу, что произошло в четыре часа утра’’.
Ньютон послал свое решение Чарльзу Монтегю, графу Галифаксу, который был министром финансов и основателем Английского банка. Монтегю был главным покровителем и другом Ньютона в течение всей его жизни и, кроме того, гражданским мужем племянницы Ньютона. Он был президентом Королевского общества в с 1695 по 1698 г., так что было естественно, что Ньютон отправить ему решение задачи о брахистохроне. Однако, как писал он впоследствии, этот эпизод не понравился Ньютону:
“Я не люблю, когда иностранцы пристают и дразнят меня вещами, относящимися к математике…’’
Королевское общество опубликовано решение Ньютона анонимно в Трудах Королевского общества в январе 1697 г. Его решение было объяснено Монтегю следующим образом:
“Задача. Требуется найти кривую , по которой вес, под действием своей тяжести наиболее быстро спустится из точки в точку .
Решение. Пусть из данной точки проведена неограниченная прямая линия параллельно горизонтали. Пусть на ней будет описана произвольная циклоида , пересекающая прямую (предполагается, что нарисованную и представленную при необходимости) в точке , и вторая циклоида , основание и высота которой относятся к основанию и высоте первой как к соответственно. Последняя циклоида будет проходить через точку , и она будет той кривой, по которой вес силой своей тяжести спустится наиболее быстро из точки в точку ’’.
Диаграмма Ньютона
Майский выпуск 1697 г. Acta Eruditorum содержал решение Лейбница задачи о брахистохроне на стр. 205, решение Иоганна Бернулли — на страницах 206-211, решение Якова Бернулли — на страницах 211-214, и латинский перевод решения Ньютона на стр. 223. Решение Лопиталя не было опубликовано до 1988 года, когда, почти 300 лет спустя, Жан Пейффер опубликовал его в Приложении 1 в P. Costabel and J. Peiffer (eds.), Bernoulli, Johann I Der Briefwechsel von Johann I Bernoulli. Band 2: Der Briefwechsel mit Pierre Varignon: Erster Teil: 1692-1702, Die Gesammelten Werke der Mathematiker und Physiker der Familie Bernoulli (Basel, 1988). Иоганн Бернулли представил тех, кто решал задачу, сказав:
“… мой старший брат является четвертым из тех, кого три великие страны — Германия, Англия и Франция, по одному из каждой, дали для объединения со мной в таких красивых поисках, в поисках одной истины’’.
В своем решение Иоганн Бернулли делит плоскость на полосы, и он предполагает, что частица движется по прямой в каждой полосе. Таким образом, путь ее кусочно-линейный. Задача состоит в определении угла, под которым направлен отрезок в каждой полосе, и для этого он обращается к принципу Ферма, а именно к тому, что свет всегда проходит расстояние за кратчайшее время. Если — скорость в одной полосе, направленная под углом к вертикали, и скорость в следующей полосе, направленная под углом к вертикали, то по обычному закону синуса
Циклоида как предел полос
В пределе, когда полосы становятся бесконечно узкими, отрезки становятся кривой, у которой в каждой точке угол отрезка с вертикалью становится углом касательной к кривой, который она составляет с вертикалью. Если — скорость в точке и — угол, который составляет касательная с вертикалью, то кривая удовлетворяет уравнению
Галилей показал, что скорость удовлетворяет условию
(где — ускорение силы тяжести). Подстановка дает уравнение кривой
или
Воспользуемся тем, что и , чтобы получить
для константы .
Циклоида удовлетворяет этому уравнению. Чтобы убедиться в этом, отметим, что
так что
Гюйгенс в 1659 году показал (к этому его привела задача Паскаля о циклоиде), что циклоида является решением задачи о таутохроне, а именно задачи о нахождении кривой, для которой время, затраченное частицей, скользящей вниз по ней под действием однородной силы тяжести, в самой нижней точке не зависит от выбора начальной точки.
Иоганн Бернулли закончил свое решение задачи о брахистохроне такими словами:
“Прежде чем я закончу, я должен еще раз выразить восхищение, которое я чувствую по поводу неожиданного тождества таутохроны Гюйгенса и моей брахистохроны. Я считаю особенно замечательным то, что это совпадение может иметь место только при выполнении гипотезы Галилея, так что мы даже получаем из этого доказательство его правоты. Природа всегда стремится действовать самым простым способом, и поэтому здесь позволяет одной кривой выполнять две различные функции, в то время как при любом другом предположении нам понадобились бы две кривые…’’
Несмотря на добрые слова, которыми Иоганн Бернулли описал решение задачи о брахистохроне своего брата Якоба Бернулли (см. выше), между братьями разгорелся серьезный спор после публикации Acta Eruditorum в мае 1697 г. Именно Якоб Бернулли теперь спорил со своим братом. Возвращаясь к первоначальному вопросу Галилея о времени достижения вертикальной линии, а не точки, он спрашивал:
“Для данных начальной точки и вертикальной прямой, из всех циклоид с одной и той же начальной точкой с одним и тем же горизонтальным основанием которая позволит точке, подвергающейся действию только однородной силы тяжести тяжести, достичь вертикальной прямой наиболее быстро?’’
Иоганн Бернулли решил эту задачу, показав, что циклоида, которая позволит точке наиболее быстро достичь данной вертикали, — та, которая пересекает эту вертикаль под прямым углом. Существует огромное количество информации, согласно Вариньону (см. P. Costabel and J. Peiffer (eds.), Bernoulli, Johann I Der Briefwechsel von Johann I Bernoulli. Band 2: Der Briefwechsel mit Pierre Varignon: Erster Teil: 1692–1702, Die Gesammelten Werke der Mathematiker und Physiker der Familie Bernoulli (Basel, 1988)), Якоб Бернулли поставил перед Иоганном Бернулли изопериметрические задачи, и между двумя братьями возник ожесточенный спор об этих задачах, в котором также участвовал и Вариньон. Это был неприятный инцидент, но он имел большое значение для математики, так как задачи, о которых спорили, непосредственно привели к основанию вариационного исчисления. Ссоры между братьями Бернулли подробно рассмотрены в R. Thiele, Das Zerwürfnis Johann Bernoullis mit seinem Bruder Jakob, Natur, Mathematik und Geschichte, Acta Hist. Leopold. No. 27 (1997), 257–276, где наряду с математическими деталями автор рассматривает и психологические аспекты. Он убедительно доказывает, что плохие отношения между ними должны были начаться дома из-за строгого и недоброго отца.
Методы, которые братья разработали для решения задач и которые они оспаривали друг у друга, были обобщены Эйлером в Methodus inveniendi lineas curvas maximi minimive proprietate gaudentes sive solutio problematis isoperimetrici latissimo sensu accepti, опубликованных в 1744 году. В этой работе, русская версия названия которой “Метод нахождения плоских кривых, показывающий некоторые свойства максимумов и минимумов”, Эйлер обобщает задачи, исследованные братьями Бернулли, но сохраняет геометрический подход, разработанный Иоганном Бернулли для их решения. Он обнаружил то, что сейчас известно как уравнения Эйлера-Лагранжа для поиска стационарных точек и экстремумов функционалов.
Идея состоит в нахождении функции, на которой достигается максимум или минимум определенной величины, удовлетворяющей некоторым ограничениям. Например, Иоганн Бернулли перед Эйлером поставил определенные геодезические задачи, которые, как и задача о брахистохроне, были такого типа. Здесь задача состояла в нахождении кривых наименьшей длины, лежащих на данной поверхности. Эйлер, однако, отметил, что геометрический подход к таким задачам не был идеальным, и он давал только необходимые условия, которым должно удовлетворять решение. Вопрос о существовании решения не был решен Эйлером.
Лагранж в 1760 году опубликовал эссе о новом методе нахождения максимумов и минимумов неопределенных интегральных формул. Он дал аналитический метод, применимый к задачам вариационного исчисления. Во введении к своей работе Лагранж приводит историческое развитие идей, которые мы описали выше, но кажется целесообразным закончить эту статью, приведя слова Лагранжа, которые отражают в действительности все достижения:
“Первая задача этого типа [вариационного исчисления], которую решили математики — это задача о брахистохроне, или кривой наискорейшего спуска, предложенная Иоганном Бернулли в конце прошлого века. Ее решение было найдено рассмотрением частных случаев, и только спустя некоторое время, исследуя изопериметрические кривые, великий математик, о котором мы говорим, и его знаменитый брат Якоб Бернулли дали некоторые общие правила для решения ряда других задач того же типа. Поскольку, однако, правила не были достаточно общими, знаменитый Эйлер взял на себя задачу сведения всех этих исследований в общий метод, который он привел в своем “Рассуждении о новом методе определения максимумов и минимумов неопределенных интегральных формул’’ — оригинальной работе, в которой освещена глубокая наука исчисления. Тем не менее, несмотря на то что метод гениальный и мощный, надо признать, что он не так прост, как можно было бы надеяться в работе по чистому анализу…’’
Затем Лагранж переходит к описанию введенного им символа дифференциала . Он пишет:
“…метод, который требует только прямого использования принципов дифференциального и интегрального исчисления, но я должен настоятельно подчеркнуть, что поскольку мой метод требует, чтобы величину можно было изменять двумя различными способами, для различения этих двух вариантов я ввел новый символ в мои расчеты. Таким образом, выражает разность , отличную от , но которая, однако, будет удовлетворять тем же правилам, такую, что там, где имеем для любого уравнения , можно в равной степени записать , и так же в других случаях’’.
J.J. O’Connor, E.F. Robertson, The brachistochrone problem. Перевод статьи http://www-history.mcs.st-and.ac.uk/HistTopics/Brachistochrone.html
hijos.ru
Оптимизация. Обзор методов
Оптимизация — важный раздел современной прикладной математики, объединяющий широкий спектр разнообразный методов, позволяющих решать важные практические задачи.
Например, задачу о распределении инвестиций по разным проектам и предприятиям, нахождение оптимальных сроков замены и ремонта оборудования, если известны годовой доход и остаточная стоимость в зависимости от времени эксплуатации.
Именно такие задачи возникают в нефтедобывающей отрасли, когда необходимо обоснованно принимать решение о сроках ремонта или замены насосного оборудования. Это оборудование может выходить из строя в случайные моменты времени, что приводит к существенному ущербу и неоправданным потерям.
Очевидно, задачи оптимизации тесно связаны с теорией вероятностей, статистикой и анализом данных в самом широком смысле, так как требуется оценить состояние системы по реальным данным и далее применить принципы оптимального управления.
Имеется несколько важных принципов, которые нужно знать и с пользой применять на практике, например, принцип оптимальности Беллмана или принцип оптимальности Понтрягина и др.
Вы можете не знать детали методов, но должны понимать существо дела и основной стрим оптимизационных моделей, детали выяснятся позднее, их можно найти в справочниках и специализированных изданиях.
Мы начнем с увлекательной задачи о линии наискорейшего спуска или задачи о брахистохроне, в действительности это целый класс очень интересных задач.
Начнем с практического вопроса.
Представьте, вы возводите жилое здание и у вас возникает вопрос, как кратчайшим образом доставлять предметы с верхних этажей на нижние, используя только силу тяжести.
Естественно рассмотреть наклонный пандус, который позволяет за оптимальное время скатывать предметы с верхних этажей на нижние.
Задача о брахистохроне (линии наибыстрейшего ската).
Термин брахистохрон имеет греческое происхождение и состоит из двух слов хронос – время, брахисто – самый короткий (βραχιστoζ – короткий, χρoνoζ – время).
Формальная постановка задачи такая.
В вертикальной плоскости даны точки A и B. Определить путь, по которому под действием собственной тяжести, тело, начав двигаться из точки A, достигнет точку B за кратчайшее время.
Дадим набросок решения, стараясь выделить главный аналитический принцип.
Рассматривается идеальный случай, предмет скатывается только под действием силы тяжести.
Прежде всего мы можем предположить, что нам достаточно провести прямую линию, соединяющую точки А и В.
Отрезок прямой будет кратчайшим расстоянием между А и В, однако не факт, что время, затраченное на движение по этому отрезку будет наименьшим.
Из физических соображений ясно, что вначале тело должно максимально ускориться, чтобы затем это ускорение работало на всем пути. Двигаясь по прямой, тело имеет постоянное ускорение.
Это заставляет предположить, что есть траектории, которые позволяют спускать груза за время меньшее, чем при движении по прямой.
Продолжим рассуждения.
Введем декартову систему координат с центром в точке А, пусть точка В располагается, для определенности, в 4-м квадранте, ее координаты x1 > 0, y1 < 0.
Конечно, возможно симметричное расположение точки В относительно оси y, но мы рассмотрим именно этот случай.
Если точка В лежит просто на оси y, то решение очевидно, это отрезок прямой (0, y1).
Проведем какую-то линию, соединяющую точки А и В, обозначим ее y = y(x).
Всякой линии y = y(x), соединяющей точки А и В, сопоставим время спуска T по этой линии.
Ясно, что время Т зависит от самой линии, где-то тело сильнее ускоряется, где-то слабее, мы рассматриваем движение только под действием силы тяжести.
Заметим, что в начальный момент времени t = 0, y(0) = 0 (тело находится в точке А), в момент окончания спуска тело попадает в точку В, следовательно, y(T) = y1.
Итак, формально нам нужно перебрать все линии, соединяющие А и В, и найти оптимальную линию, для которой время Т минимально.
Это и будет линия наискорейшего спуска.
Вопрос: как это сделать?
Воспользуемся символистикой математического анализа.
Формально скорость скатывания тела по дуге определяется выражением
Отсюда:
Время спуска Т по всей линии вычисляется как сумма
=
Интеграл берется по кривой .
Линия задана в явном виде как функция от , поэтому можно считать, что интегрирование ведется от 0 до .
Дифференциал дуги можно вычислить (проделайте это упражнение или обратитесь к стандартной книге по математическому анализу)
Итак, время спуска по кривой задается выражением:
(1)
В этом выражении присутствует скорость тела , ее нужно найти.
Попадая в точку по оси х, тело проходит по оси y расстояние , закон сохранения энергии дает равенство:
В начальный момент времени скорость и высота равны 0, следовательно, поэтому:
(2)
Подставляя формулу (2) в формулу (1), имеем окончательное выражение для времени движения по нашей линии :
(3)
Итак, формально нужно найти минимум функционала (3) на кривых удовлетворяющих условию:
Следующие калькуляции потребуют некоторого напряжения, хотя идея простая.
Нам удобно ввести обозначение для подынтегральной функции в (3).
Обозначим:
Принцип Эйлера утверждает, что экстремальное значение функционала
является решением уравнения:
= с (4)
это частная производная по ,
Следовательно, формально имеем:
(5)
Подставим (5) в (4) и проведем алгебраические преобразования.
После возведения в квадрат имеем выражение через :
(6)
Данное дифференциальное уравнение можно решить, формально имеем:
(7)
Проинтегрируем левую и правую часть (7), получим:
(8)
Для сокращения калькуляций обозначим новая константа, сделаем стандартную замену переменных:
После элементарных вычислений (проделайте их!) получим следующие уравнения линии :
(9)
(10)
Константу нужно подобрать так, чтобы кривая проходила через конечную точку В с координатами .
Как пользоваться этими уравнениями?
Достаточно просто, это время, представьте, вы выбрали константу например, положив далее берем последовательные значения = 0, 0.1 и тд.
На рисунке ниже показана одна такая кривая:
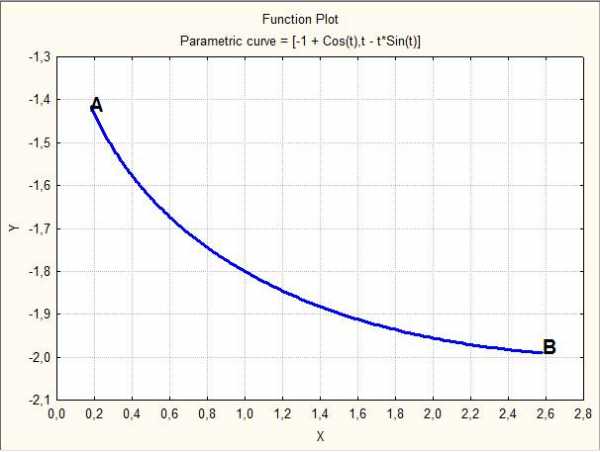
Рис. 1
С помощью уравнений (9), (10) мы можем определить положение тела, двигающегося под действием силы тяжести по линии наискорейшего спуска, в любой момент времени.
Уравнения (9), (10) позволяют определить пару констант t1, c1 и тем самым определить отрезок кривой кратчайшего спуска между точками А и В.
Эта замечательная кривая называется циклоидой!
Эта кривая относится к классу трансцендентных кривых, уравнение которых не может быть записано в виде многочленов от x, y, однако параметрические уравнений (9), (10) позволяют исследовать эту кривую и вывести ее замечательные свойства.
Для приближенного решения уравнений (9), (10), — а так и поступают на практике! — воспользуйтесь численными методами решения уравнений, описанными на нашем портале.
Итак, если вам необходимо сконструировать пандус для скорейшего спуска грузов с верхних этажей на нижние, то его образующими будут циклоиды!
Заметьте, важен принцип рассуждения, вначале мы поняли, что решение может быть отличным от прямой линии, затем формализовали задачи и использовали математическую символику, позволяющую записать решение в виде уравнений (9), (10).
Конечно, это задача имеет много вариаций, можно рассматривать движение частицы в поле действия определенных сил, движение луча в неоднородной среде и тд.
Обсуждение задачи.
Мы свели задачу о линии кратчайшего времени спуска к нахождению экстремума некоторого функционала
Термина функционал не нужно бояться, это то же самое что функция, только немного сложнее, его значение зависит от самой линии и ее производной
Возникает вопрос, как находить экстремумы функционалов, например, минимальные или максимальные значения.
Мы знаем, как находить максимальные или минимальные значения функций. Необходимым условием таких экстремумов является обращение в нуль производной.
Естественная идея состоит в том, чтобы обобщить методы нахождения экстремумов функций на функционалы.
Это естественное обобщение достигается с помощью принципа Эйлера.
В нашем рассуждении использовался знаменитый принцип Эйлера, см. (4), утверждающий, что экстремальное значение функционала
является решением уравнения:
= с
Имеется множество численных методов поиска экстремума функций, очевидно, эти методы можно распространить и на поиск экстремумов функционалов.
Приведем несколько задач на брахистохрону:
Найдите длину брахистохроны между точками А и В, сравните ее с длиной прямой АВ. Объясните качественно, за счет чего достигается эффект меньшего времени спуска по циклоиде.
Объясните, почему выпуклая вверх циклоида, симметричная относительно прямой АВ, не является брахистохроной.
Ограничим возможные кривые только ломаными линиями, рассмотрим различные ломанные линии, соединяющие точки А и В. Как нужно расположить N точек А, , N > 1 чтобы ломаная линия была линией наикратчайшего спуска. Какой принцип оптимальности здесь можно применить? Заметьте, что в точках излома отсутствуют производные.
Дальнейшие задачи для самостоятельных размышлений:
Найти плоскую кривую, соединяющую две заданные точки плоскости и лежащую выше оси x , которая при вращении вокруг этой оси образует поверхность наименьшей (наибольшей) площади.
Найти форму тяжелой однородной нерастяжимой нити, подвешенной за концы (изгиб нити возникает за счет силы тяжести).
В заключении заметим, что знаменитая задача Дидоны, описанная нами в разделе геометрия, также может быть решена аналитическими методами, попробуйте найти это решение.
Для этого, прежде всего, введите декартову систему координат и запишите функционал, экстремум которого нужно найти.
Далее примените принцип Эйлера для нахождения экстремума и проведите математические выкладки.
Изобразим графически задачу наискорейшего спуска, чтобы наглядно убедиться в том, что материальная точка быстрее спустится именно по брахистохроне, а не по прямой. Для этого напишем небольшой макрос в Microsoft Excel во встроенной среде разработки Visual basic for Application (VBA).
Для начала сделаем некоторую предварительную подготовку: построим графики брахистохроны и прямой в Microsoft Excel. Согласно теории, уравнение брахистохроны в декартовых координатах имеет вид:
Введем в первый столбец рабочего листа цифры от 0 до 2 с шагом 0.1.
Рис. 2
Во второй столбец введем следующую формулу и растянем ее на 22 строки:
Рис. 3
В итоге получим следующие данные:
Рис. 4
Теперь займемся построением прямой, с которой будем сравнивать брахистохрону. Мы знаем, что данная прямая должна проходить через точки (0;0) и (2; 3.14). Воспользуемся уравнением прямой по двум точкам:
Решаем уравнение:
Получаем уравнение прямой: y = 1.57x
Теперь вбиваем в третий столбец следующую формулу, и растягиваем ее на 22 строки:
Рис. 5
Получаем в итоге:
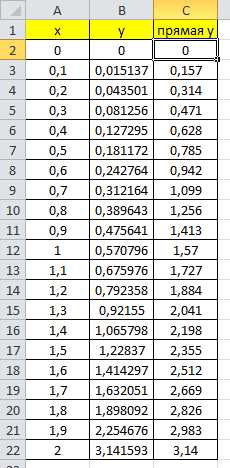
Рис. 6
Построим точечный график по имеющимся столбцам. Для этого выделим прямоугольную область A1:С22, затем выберем пункт меню Вставить -> Диаграмма -> Точечная.
Рис. 7
В результате у нас должен получиться следующий график:

Рис. 8
Теперь займемся созданием шариков, которые будут скатываться по нашим кривым. Начальное положение шариков уже известно, это точка (2; 3.14). Чтобы шарики красиво, реалистично скатывались, сделаем координату по Oy немного побольше, чтобы шарики не были «нанизаны» на кривые, а находились на их поверхности.
Сделаем следующую табличку для координат шариков на брахистохроне (шарик БР) и на прямой (шарик ПР).
Рис. 9
Кликнем правой кнопкой мыши на графике, выберем пункт «Выбрать данные».
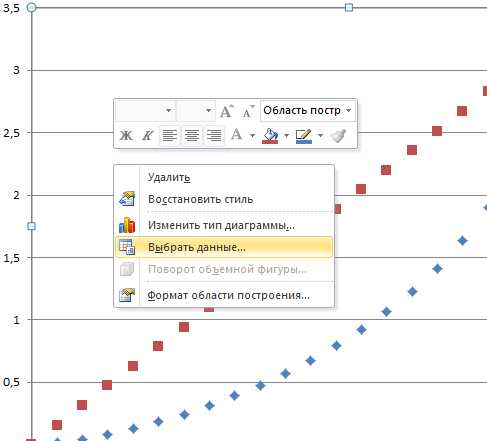
Рис. 10
Затем нажмем «Добавить ряд», в названии укажем «Шарик БР», в поле «Значения Х» укажем ячейку F2, в поле «Значения Y» укажем ячейку G2.
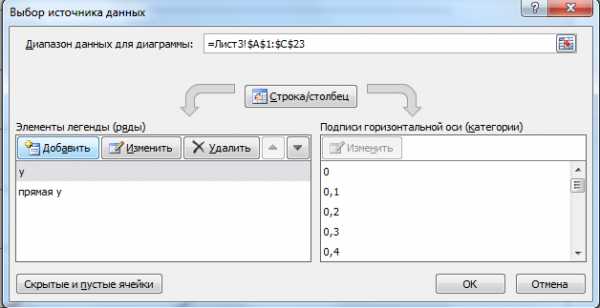
Рис. 11
Рис. 12
Аналогичным образом добавим шарик на прямой (ячейки будут соответственно h3 и I2).
Чтобы кривые были более красивыми и цельными, изменим тип диаграмм. Кликнем правой кнопкой мыши на кривой брахистохроны и прямой, выберем пункт «Изменить тип диаграммы для ряда…»:

Рис. 13
И в том же меню Диаграмма -> Точечная, выберем третий по счету вид (Точечная с гладкими кривыми):
Рис. 14
Получим такой график:

Рис. 15
На следующем этапе сделаем наши шарики более круглыми и объемными. Нажмем на один из них правой кнопкой мыши, выберем «Формат ряда данных».
Рис. 16
В следующем меню сделаем настройки:

Рис. 17

Рис. 18
Аналогичным образом сделаем синий объемный шарик на брахистохроне. Получим такой вид:
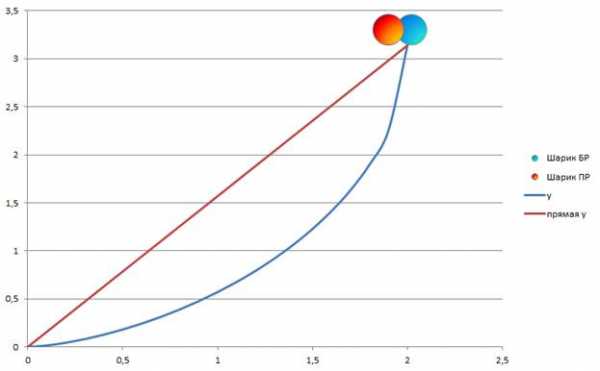
Рис. 19
Теперь напишем макрос на VBA, который будет управлять нашими шариками. Нажмем Alt+F11, и перейдем в среду разработки VBA. В приложении приведен подробный листинг макроса с комментариями.
А вот и результат нашей работы:
Рис. 20
Sub Лист3_Кнопка1_Щелчок()
Dim BrahY(22), BrahX(22) As Double
Dim i As Double
Cells(2, 6) = 2 ‘начальное положение шариков
Cells(2, 7) = 3.3
Cells(2, 8) = 2
Cells(2, 9) = 3.3
BrahX(1) = 1.9 ‘координаты Х брахистохроны
BrahX(2) = 1.8
BrahX(3) = 1.7
BrahX(4) = 1.6
BrahX(5) = 1.5
BrahX(6) = 1.4
BrahX(7) = 1.3
BrahX(8) = 1.2
BrahX(9) = 1.1
BrahX(10) = 1
BrahX(11) = 0.8
BrahX(12) = 0.7
BrahX(13) = 0.6
BrahX(14) = 0.5
BrahX(15) = 0.3
BrahX(16) = 0.18
BrahX(17) = 0.12
BrahX(18) = 0.08
BrahX(19) = 0.04
BrahX(20) = 0.015
BrahX(21) = 0
BrahX(22) = 0
BrahY(1) = 3.141592654 ‘ координаты Y брахистохроны
BrahY(2) = 2.254675947
BrahY(3) = 1.898091545
BrahY(4) = 1.632050981
BrahY(5) = 1.414297436
BrahY(6) = 1.28369699
BrahY(7) = 1.05798034
BrahY(8) = 0.921549779
BrahY(9) = 0.79235835
BrahY(10) = 0.675976311
BrahY(11) = 0.570796327
BrahY(12) = 0.475641469
BrahY(13) = 0.389642509
BrahY(14) = 0.312164471
BrahY(15) = 0.242764342
BrahY(16) = 0.181172147
BrahY(17) = 0.127295218
BrahY(18) = 0.081255987
BrahY(19) = 0.043501109
BrahY(20) = 0.015136917
BrahY(21) = 0
BrahY(22) = 0
Application.Wait (Now + TimeValue(«0:00:1»))
For i = 0 To 2.2 Step 0.1 ‘ в цикле меняем координаты шариков
Cells(2, 6) = BrahX(i * 10 + 1)
Cells(2, 7) = BrahY(i * 10 + 1)
Cells(2, 8) = 2.2 — i
Cells(2, 9) = 1.57 * (2.2 — i) + 0.22 ‘немножко поднимаем шарик над прямой
Application.Wait (1000)
Next i
Application.Wait (Now + TimeValue(«0:00:2»))
Cells(2, 6) = 2
Cells(2, 7) = 3.3
Cells(2, 8) = 2
Cells(2, 9) = 3.3
End Sub
В начало
Содержание портала
statistica.ru
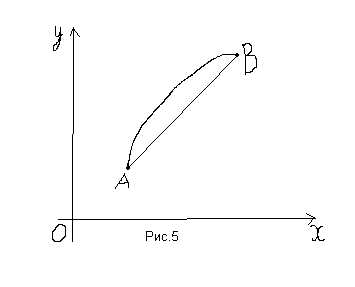
44. Задача о брахистохроне.
Предположим, что точки илежат в плоскостис осью, направленной вниз (рис.5). Положимии пусть– уравнение дуги, соединяющей точкиитак, что,,,. Скорость движения вдоль кривой пусть равна. Тогда время спуска равно
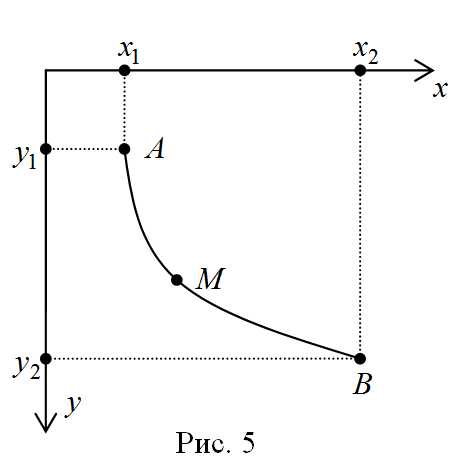
.
Чтобы найти скорость vкак функцию координатыx, воспользуемся законом сохранения энергии:
,
где — начальная скорость движения частицы. Тогда
,
и задача свелась к выбору функции , для которой интеграл
достигает наименьшего значения из всех возможных.
Так как функция зависит только оти, то уравнение Эйлера допускает первый интеграл:
.
Разрешая это уравнение относительно , находим
,
где мы положили . Таким образом, мы получили дифференциальное уравнение первого порядка в разделяющихся переменных. Решая его, имеем:
.
Для вычисления интеграла удобно воспользоваться заменой
. Тогда
.
Мы пришли к решению в параметрической форме
Это и есть кривая наибыстрейшего спуска, известная под названием циклоиды. Можно показать, что выбор постоянных ипозволяет провести циклоиду через произвольные две заданные точки. Напомним, что величинане является произвольной постоянной.
57. Задача Майера.
Интегральный функционал.
F – дифференцируемая функция своих аргументов.
При отсутствии ограничений на x и u задача называется задачей Лагранжа и является классической задачей вариационного исчисления. В качестве примера можно рассмотреть агрегат, который должен дать максимальное количество продукции. При этом функция F (x, u, t) имеет смысл мгновенной производительности, а интеграл – полную выработку продукции.
Задача Майера.
Минимизируется функционал
J(x, u)=[x(T), T].
Например, задача о достижении наибольшей дальности ракетой.
Формально задача Майера является более общей, чем задача Лагранжа. Любая задача Лагранжа может рассматриваться как частный случай задачи Майера.
Действительно, достаточно ввести новую скалярную переменную
xn+1=F(x, u, t),
–новый фазовый вектор
и вектор
тогда система будет описываться уравнением:
а минимизации подлежит функционал
24 66. Системы, оптимальные по быстродействию.
Задача определения оптимального по быстродействию программного управления состоит в нахождении управлений , при которых объект
(1.1)
переводится из состояния
(1.2)
в состояние
(1.3)
(x(0),x(1)иt0— заданы, аt1— неизвестно), при этом функционал
(1.4)
принимает наименьшее значение.
Опираясь на теорему принципа максимума Л. С. Понтрягина, выведем необходимые условия оптимальности по быстродействию.
Из (1.4) следует, что , и поэтому
Вводя функцию
(1.5)
Запишем (1.1) и сопряженную систему в виде
(1.6)
(1.7)
При фиксированных xиψH1 становится функциейu. Обозначим
Очевидно, что
Таким образом, необходимое условие для оптимальности по быстродействию принимает вид
(1.8)
3 68. Допустимое управление.
Мы будем рассматривать поведение объекта, состояние которого в каждый момент времени характеризуется n переменными х1, х2, …, хn (например, координатами и скоростями). Векторное пространство X векторной переменной х={х1, х2,…, хn} является фазовым пространством рассматриваемого объекта. Поведение (движение) объекта заключается (с математической точки зрения) в том, что переменные х1, х2, …, хn меняются с течением времени. Предполагается, что движением объекта можно управлять, т. е. что объект снабжен некоторыми «рулями», от положения которых зависит движение объекта. Положения «рулей» характеризуются точкой u некоторой области управления U, которая может быть любым топологическим хаусдорфовым пространством. В приложениях важен случай, когда U является замкнутой областью некоторого r – мерного евклидова пространства Е; в этом случае задание точки u=(u1, u2,…, ur)U равносильно заданию системы числовых параметров u1, u2, …, ur.
Каждую функцию u=u(t), определенную на некотором отрезке t0tt1 времени t и принимающую значения в пространстве U, мы будем называть управлением. В дальнейшем предполагается, что выбран некоторый класс D управлений; управления, принадлежащие этому классу, будут называться допустимыми. От класса D допустимых управлений требуется только, чтобы он удовлетворял следующим трем условиям.
1) Все управления u=u(t), принадлежащие классу D (т.е. допустимые), должны быть измеримыми и ограниченными. Управление u=u(t), t0tt1, называется измеримым, если для любого открытого множества OU множество тех значений t, для которых u(t)O, измеримо на отрезке t0tt1. Управление ограниченно, если множество всех точек u(t), t0tt1, имеет в пространстве U компактное замыкание. (Если, в частности, U есть замкнутое подмножество векторного пространства переменной u=(u1, u2,…, ur), то измеримость и ограниченность имеют обычный смысл.)
2) Если u(t), t0tt1, – допустимое управление и если и v – произвольная точка пространства U, a t’, t» – такие числа, что t0 t’t»t1, то управление u1(t), t0tt1, определяемое формулой
также является допустимым.
3) Если отрезок t0tt1 можно разбить точками деления на конечное число частичных отрезков, на каждом из которых управление u(t) допустимо, то это управление допустимо и на всем отрезке t0tt1. Допустимое управление, рассматриваемое на частичном отрезке, также является допустимым. Управление, получающееся из допустимого управления u(t), t0tt1, сдвигом времени (т. е. управление u1(t)=u(t—), t0+<t<t1 + ), также является допустимым.
В качестве класса допустимых управлений можно взять, например, класс всех измеримых ограниченных управлений. Другим примером может служить множество всех кусочно–непрерывных управлений (т.е. таких управлений u=u(t), каждое из которых непрерывно для всех рассматриваемых t, за исключением лишь конечного числа моментов времени, где функция u(t) может терпеть разрывы первого рода). Этот класс допустимых управлений, по – видимому, наиболее интересен для технических применений развиваемой здесь теории; такие управления соответствуют предположению о «безынерционности» рулей. Можно также рассматривать класс всех кусочно – постоянных управлений, класс кусочно – линейных управлений и т. п. В дальнейшем класс D допустимых управлений предполагается фиксированным.
studfiles.net
Задача о брахистохроне — 5 Февраля 2014 — Примеры решений задач
Задача о брахистохроне — линии наискорейшего ската, первая задача, положившая начало развитию вариационного исчисления.
Среди всех линий, соединяющих точки и , требуется найти ту, по которой материальная точка, двигаясь под влиянием силы тяжести из без начальной скорости, достигнет пункта в кратчайшее время.
Для решения этой задачи мы должны будем рассмотреть всевозможные линии, соединяющие и . Если взять какую-либо одну определенную линию , то ей будет отвечать какое-то определенное значение времени ската по ней материальной точки. Время будет зависеть от выбора , и из всех линий, соединяющих и , нужно выбрать ту, которой отвечает наименьшее значение .
Постановка задачи о брахистохроне.
Проведем через точки и вертикальную плоскость. Линия наискорейшего ската должна, очевидно, лежать в ней, и для ее разыскания мы можем ограничиться только линиями, лежащими в этой плоскости. Примем точку за начало координат, ось направим горизонтально, ось — вертикально вниз (рис. 1). Координаты точки будут ; координаты же точки назовем . Возьмем любую линию, которая может быть задана уравнением
$$
где — непрерывно дифференцируемая функция. Так как линия проходит через и , функция на концах отрезка должна удовлетворять условиям
$$
Если взять на линии произвольную точку , то скорость движения материальной точки в этом месте линии будет связана с координатой точки известным из физики соотношением
$, или $
Время, необходимое для того, чтобы материальная точка прошла элемент дуги линии, имеет значение
$$
и поэтому полное время ската точки вдоль линии от до , равно
$$
Разыскание брахистохроны равносильно решению следующей минимальной задачи: среди всевозможных функций (1), удовлетворяющих условиям (2), нужно найти ту, которой соответствует наименьшее значение интеграла (3).
Подробное решение задачи о брахистохроне с помощью вариационного исчисления.
www.reshim.su
Вариационное исчисление
Функционалы– это переменные величины, значения которых определяются выбором одной или нескольких функций.
Например, функционалом является длина
дуги  ,
которая соединяет две точки (рис.1).
Величина
,
которая соединяет две точки (рис.1).
Величина может быть вычислена, если задано
уравнение кривой
может быть вычислена, если задано
уравнение кривой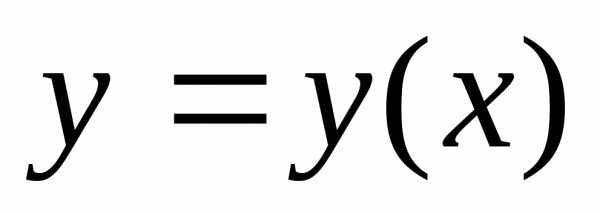 ,
тогда длина кривой вычисляется как
интеграл:
,
тогда длина кривой вычисляется как
интеграл:

Площадь Sтакже является
некоторым функционалом, так как она
определяется выбором функции двух
переменных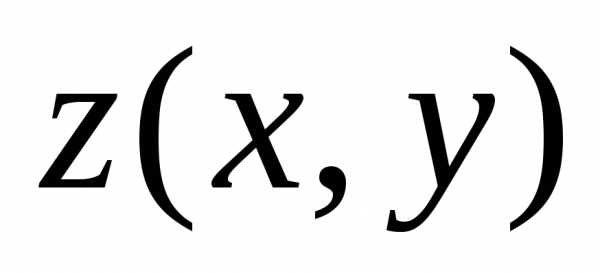 ,
и вычисляется по формуле:
,
и вычисляется по формуле:
Здесь D– проекция поверхности на плоскостьOxy.
Вариационное исчисление изучает методы, позволяющие находить максимум и минимум функционалов. Задачи, направленные на нахождение минимума и максимума функционалов называются вариационными.
Задача о брахистохроне
Это задача о быстрейшем спуске из заданной точки А в заданную точку B. Эту задачу предложил Бернулли. И было показано, что наискорейший спуск определяется не по прямой, а по некоторой кривой.
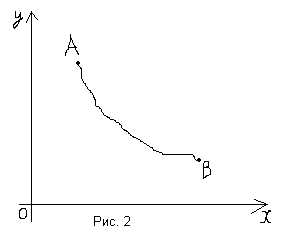
Задача о геодезических линиях
Требуется определить линию наименьшей длины, соединяющую две заданные точки на некоторой поверхности (рис.3).
Это типичная задача на условный экстремум. Она формулируется следующим образом:
Требуется найти минимум функционала
Изопериметрическая задача
Здесь требуется найти замкнутую кривую
длины 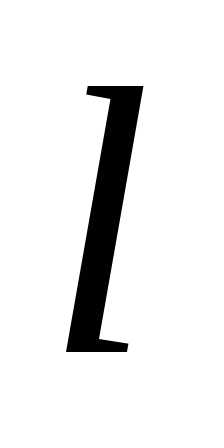 ,
которая ограничивает максимальную
площадьS. И такой линией
является окружность.
,
которая ограничивает максимальную
площадьS. И такой линией
является окружность.
Здесь требуется определить экстремум функционала .
Существуют и другие наиболее распространенные виды функционалов:
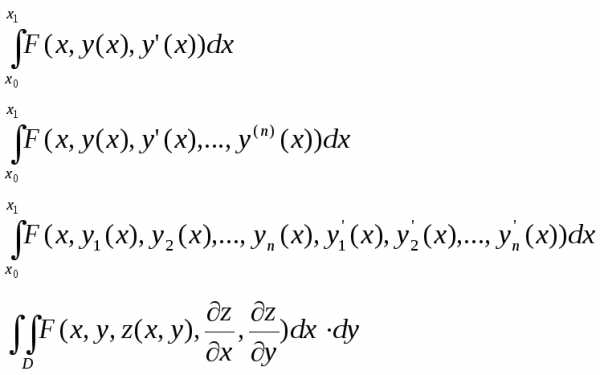
Вариация функционала и ее свойства
Методы решения вариационных задач и поиска экстремума функционала идейно весьма схожи с методами поиска экстремума функции.
Переменная величина zназывается функцией переменногоx, если каждой переменной области измененияxсоответствует числуy.
Приращением или вариацией
 аргумента
аргумента функционала
функционала называется разность функций.
При этом все это рассматривается в
некотором классе функций.
называется разность функций.
При этом все это рассматривается в
некотором классе функций.Функционал
 называется непрерывным, если малому
изменениюсоответствует
малое изменение функционала
называется непрерывным, если малому
изменениюсоответствует
малое изменение функционала .
.
Возникает вопрос: какие из двух функций 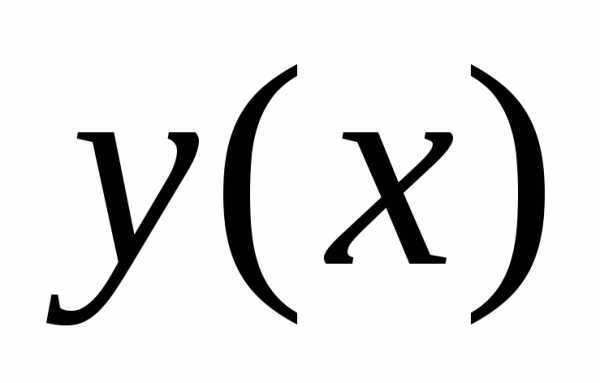 и
и считаются мало отличающимися?
считаются мало отличающимися?
Например, можно считать, что эти две функции близки в том случае, если их разность мала для любогоxтам, где эти функции определены.
Функционал вида:
Из за наличия  лишь в исключительных случаях будет
непрерывным. Поэтому кривые будут
близки, если выполняются условия:и.
То есть будут близки по своим значениям
и производным.
лишь в исключительных случаях будет
непрерывным. Поэтому кривые будут
близки, если выполняются условия:и.
То есть будут близки по своим значениям
и производным.
Если для двух функций
 и
и разность,
то это близостьнулевогопорядка.
разность,
то это близостьнулевогопорядка.Если наряду с этим, мала разность их производных , то это близостьпервогопорядка.
Когда есть разность kпроизводных, то это близостьk-гопорядка.
На рисунке 4 кривые близки в смысле первого порядка.
На рисунке 5 кривые близки в смысле нулевого порядка.
Функция 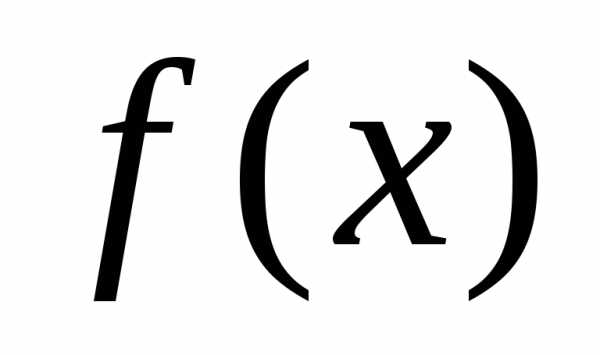 непрерывная
в точке
непрерывная
в точке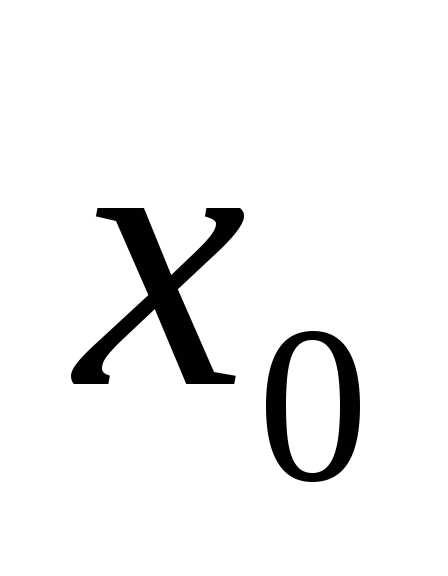 ,
если для любого
,
если для любого можно подобрать такое
можно подобрать такое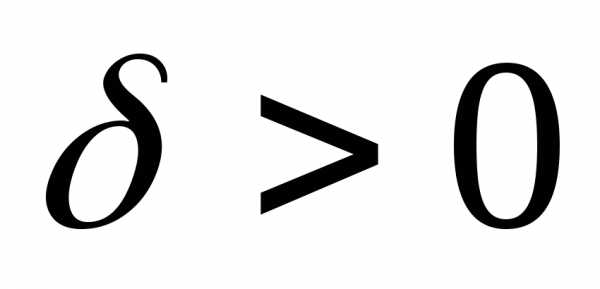 и такое, что модуль разности,
когда
и такое, что модуль разности,
когда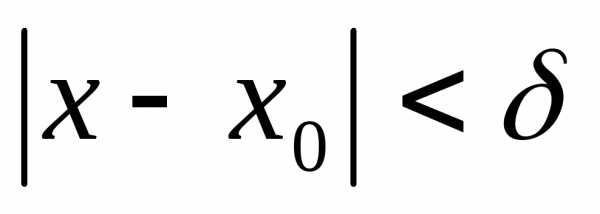 .
.
3а. Функционал  непрерывен при
непрерывен при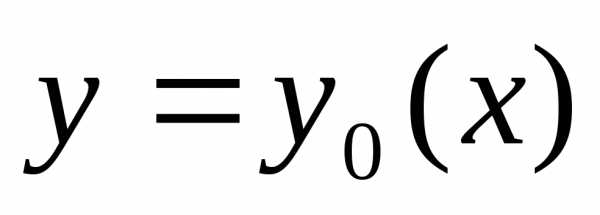 в
смысле близостиk-го
порядка, если для любого
в
смысле близостиk-го
порядка, если для любого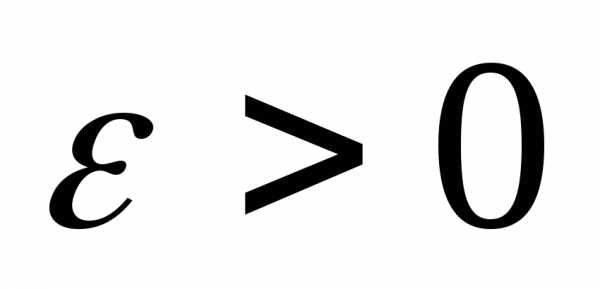 можно подобрать
можно подобрать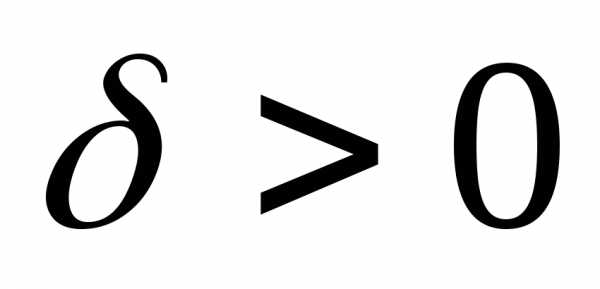 такое, что:
такое, что:
При:

При этом считается, что функционал
рассматривается на определенном классе,
то есть 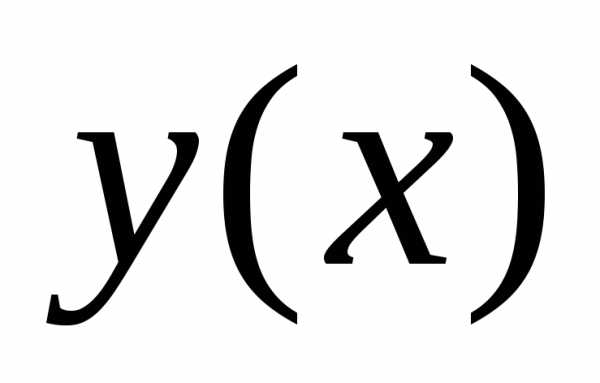 должен принадлежать определенному
классу функций.
должен принадлежать определенному
классу функций.
Можно ввести в рассмотрение расстояние
между двумя функциями 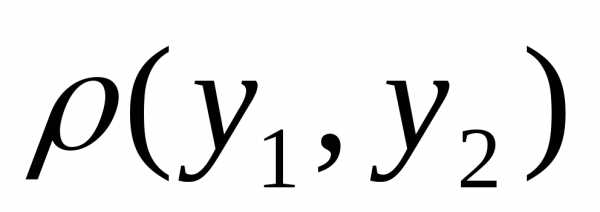 ,
при этом.
Тогда близкими можно считать кривые,
для которых расстояние между двумя
функциями мало. В качестве этого
расстояния можно взять величину:
,
при этом.
Тогда близкими можно считать кривые,
для которых расстояние между двумя
функциями мало. В качестве этого
расстояния можно взять величину:
Тогда это будет близость нулевого порядка. Если теперь в качестве расстояния взять величину:
и теперь предположить, что функции  необходимое
количество раз дифференцируемо, то это
близостьk-го порядка.
необходимое
количество раз дифференцируемо, то это
близостьk-го порядка.
Линейным функционалом называют функционал
 удовлетворяющий следующим условиям:
удовлетворяющий следующим условиям:
Где c– произвольная постоянная.
Пример линейного факториала:
Если приращение функционала можно представить в виде:
Где
— линейный по отношению к функционал;
функционал;
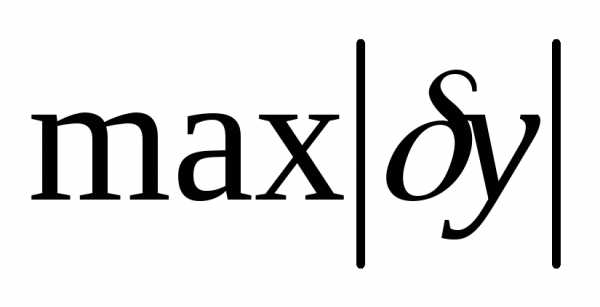 — максимальное значение
— максимальное значение прии
прии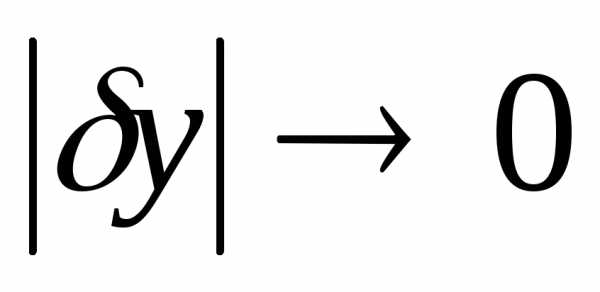 ,
то линейная по отношению к
,
то линейная по отношению к часть
приращение функционала, то есть,
называется вариацией функционала и
обозначается —
часть
приращение функционала, то есть,
называется вариацией функционала и
обозначается — .
.
Вариация функционала – это главная
линейная по отношению к  часть
приращение функционала. При исследовании
функционалов вариация играет такую же
роль, какую играет дифференциал при
исследовании функции. Можно дать и
другое, почти эквивалентное определение
дифференциала функции и вариации
функционала.
часть
приращение функционала. При исследовании
функционалов вариация играет такую же
роль, какую играет дифференциал при
исследовании функции. Можно дать и
другое, почти эквивалентное определение
дифференциала функции и вариации
функционала.
Рассмотрим значение функции
при
фиксированных значениях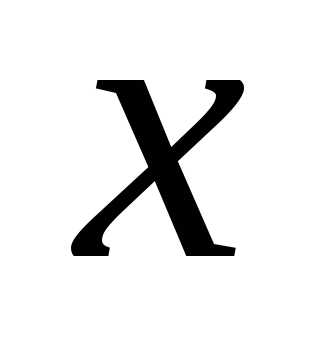 и
и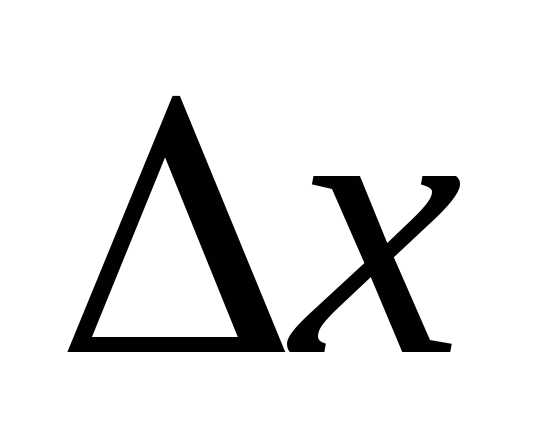 .
И пусть только меняется значение
.
И пусть только меняется значение .
Получим приращение значений функции
при изменении
.
Получим приращение значений функции
при изменении .
При
.
При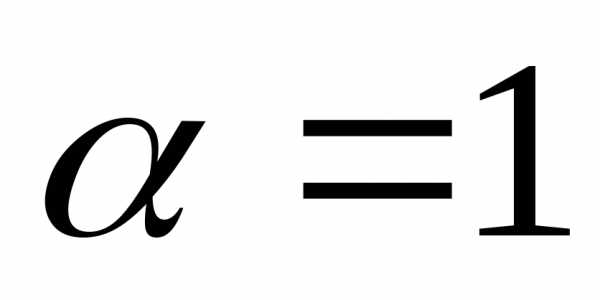 мы
получим.
мы
получим.
Если  ,
то.
,
то.
Производная от функции
по при
при равно дифференциалу функции
равно дифференциалу функции в
точке
в
точке .
.
Правило дифференцирования сложной функции:
Это же справедливо и для функции
нескольких переменных
.
Вводится дополнительная переменная и ее можно представить следующим образом:
и ее можно представить следующим образом:
Возьмем производную по  :
:
Рассмотрим функционал  и запишем его следующим образом:.
А теперь вариацию функционала рассмотрим
как производную последнего функционала
по
и запишем его следующим образом:.
А теперь вариацию функционала рассмотрим
как производную последнего функционала
по при
при .
Если функционал имеет вариацию в смысле
главной линейной части приращения, то
его приращение будет иметь вид:
.
Если функционал имеет вариацию в смысле
главной линейной части приращения, то
его приращение будет иметь вид:
Производная функционала по  при
при :
:
Так как в силу линейности и справедливости равенства:
Следует:
при
Если существует вариация в смысле главной линейной части приращения функционала, то существует и вариация в смысле производной по параметру при начальном значении параметра. И оба эти определения эквиваленты.
Второе определение вариации несколько шире первого, так как существуют примеры функционалов, из приращения которых нельзя выделить главные линейные части. Но вариации в смысле второго определения существуют.
Вариация функционала
 равна.
равна.
Функционал 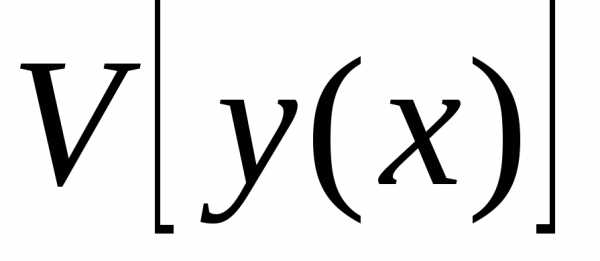 достигает на кривой
достигает на кривой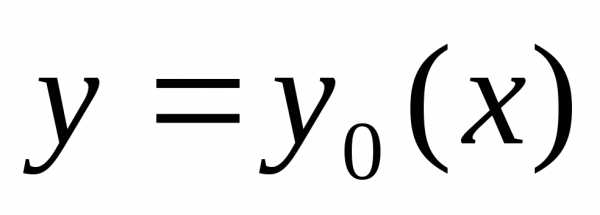 максимума,
если значения функционала
максимума,
если значения функционала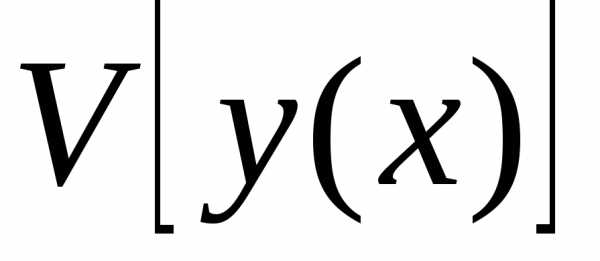 на любой близкой к
на любой близкой к не
больше, чем
не
больше, чем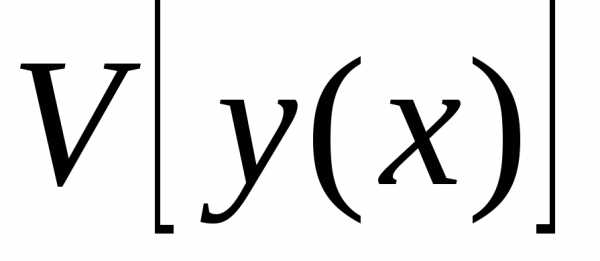 .
.
То есть:
Если 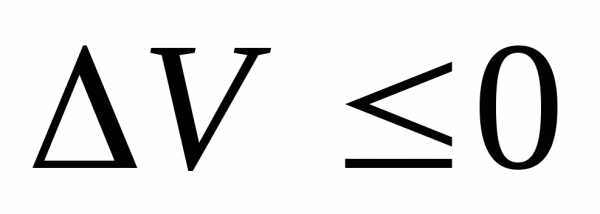 и
и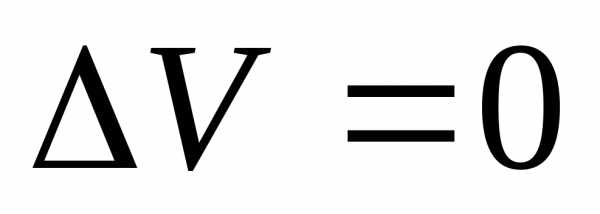 только,
когда,
то говорят, что на кривой
только,
когда,
то говорят, что на кривой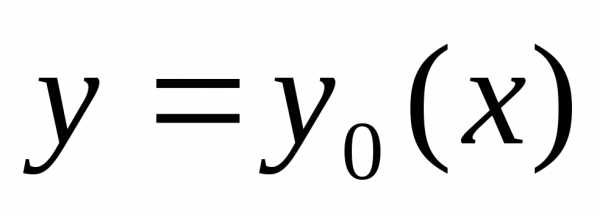 достигается строгий максимум. В этом
случае
достигается строгий максимум. В этом
случае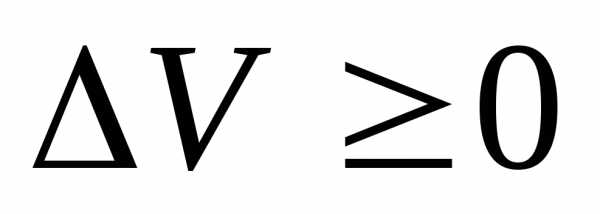 .
Таким образом для всех кривых, близких
к
.
Таким образом для всех кривых, близких
к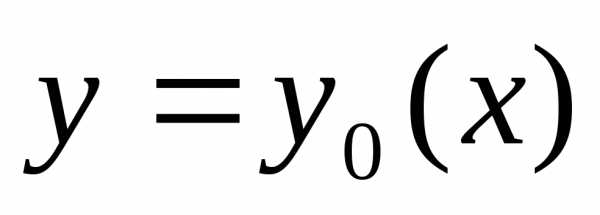 ,
справедлива следующая теорема:
,
справедлива следующая теорема:
Если функционал 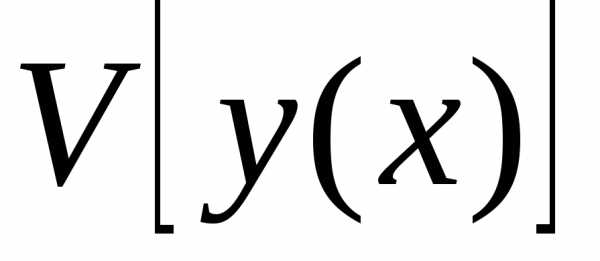 ,
имеющий вариацию, достигает максимума
или минимума при
,
имеющий вариацию, достигает максимума
или минимума при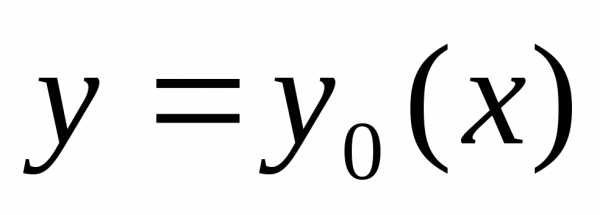 ,
где
,
где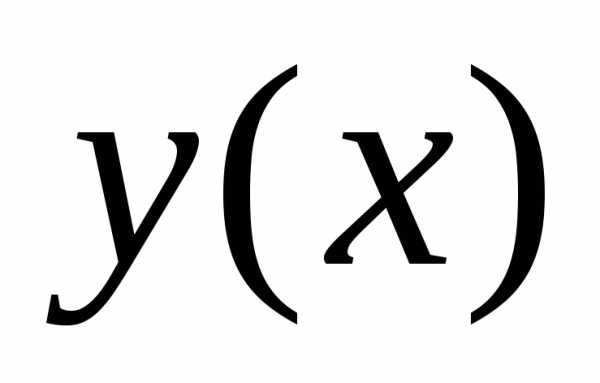 —
внутренняя точка области определения
функционала, то при
—
внутренняя точка области определения
функционала, то при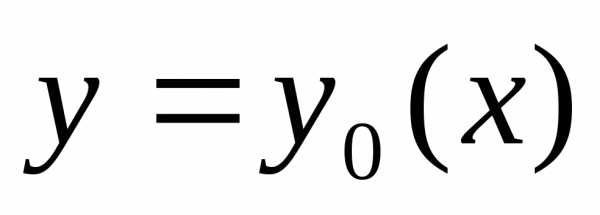
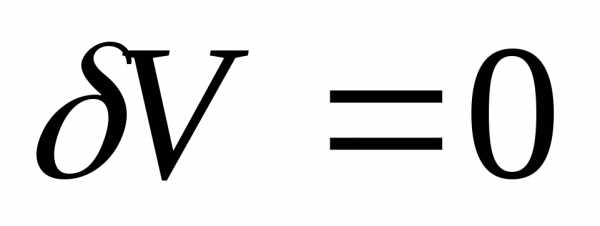 .
.
Доказательство
При фиксированном значении  и
и функционалявляется
функцией параметра
функционалявляется
функцией параметра ,
которая при
,
которая при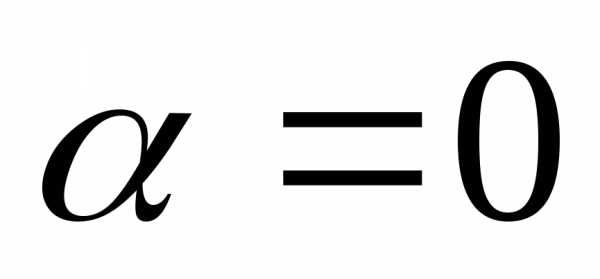 по предположению достигает максимума
или минимума.
по предположению достигает максимума
или минимума.
Следовательно
А это значит, что вариация 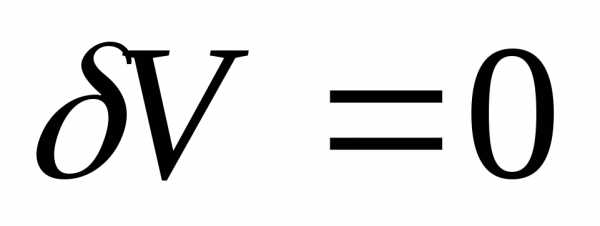 .
.
Говоря о максимуме или минимуме, мы имели ввиду наибольшее значение функционала только по отношению к значению функционала на близких кривых. Но как было указано раньше, близость кривых может быть понятна различно. Поэтому в определении максимума или минимума нужно указывать, какого порядка близость имеется ввиду.
Если функционал  достигает на кривой
достигает на кривой максимума или минимума по отношению ко
всем кривым, для которых модуль разностимал, то есть по отношению к кривым
максимума или минимума по отношению ко
всем кривым, для которых модуль разностимал, то есть по отношению к кривым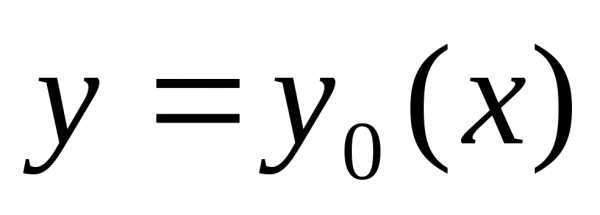 в смысле близости нулевого порядка, то
максимум или минимум называется сильным.
в смысле близости нулевого порядка, то
максимум или минимум называется сильным.
Если теперь функционал достигает максимума или минимума лишь в смысле близости первого порядка, то есть по отношению к кривым, близким по направлению к касательным, то максимум или минимум называется слабым.
Если на кривой 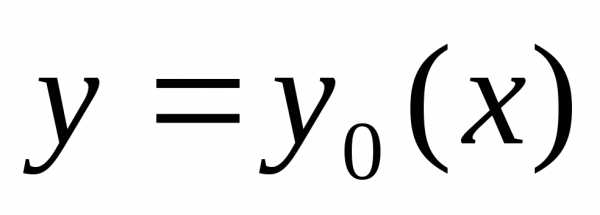 достигается сильный экстремум, то и
подавно достигается слабый экстремум.
Если кривые
достигается сильный экстремум, то и
подавно достигается слабый экстремум.
Если кривые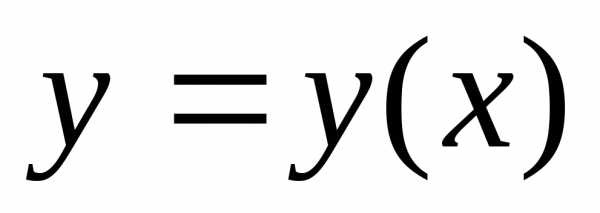 близки
к кривой
близки
к кривой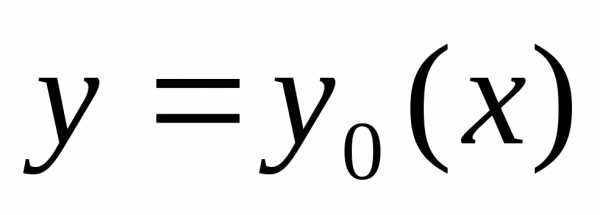 в смысле одного и того же порядка. Однако,
возможно, что на кривой
в смысле одного и того же порядка. Однако,
возможно, что на кривой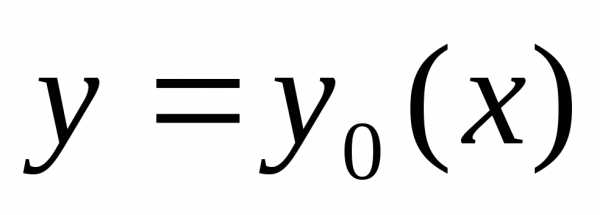 достигается слабый максимум или минимум,
и в то же время не достигается сильный
максимум или минимум. То есть среди
кривых
достигается слабый максимум или минимум,
и в то же время не достигается сильный
максимум или минимум. То есть среди
кривых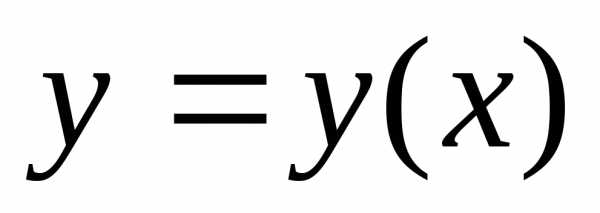 ,
близких к кривым
,
близких к кривым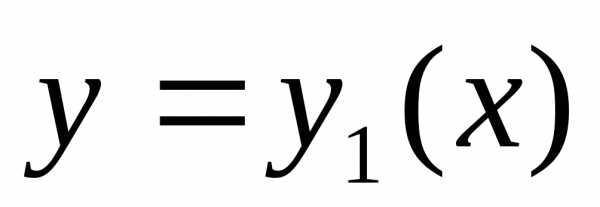 ,
близких как по координатам, так и по
направлениям касательных, может не быть
таких, для которых выполняется неравенство:.
,
близких как по координатам, так и по
направлениям касательных, может не быть
таких, для которых выполняется неравенство:.
А среди кривых  ,
близких по ординате, но уже не близких
по направлениям касательных. Здесь
могут найтись кривые, для которых может
выполнено такое же неравенство.
,
близких по ординате, но уже не близких
по направлениям касательных. Здесь
могут найтись кривые, для которых может
выполнено такое же неравенство.
studfiles.net
Задача о брахистохроне или как льва узнают по когтям
Поиск ЛекцийОсновы вариационного исчисления — I
Методические указания
и варианты заданий
для самостоятельной работы студентов
III курса специальностей КМ и ДПМ
Пермь 2006
УДК 517 (075.8)
Основы вариационного исчисления, ч.I: методические указания и варианты заданий для самостоятельной работы студентов III курса / Сост. доц. В.В. Малыгина; Пермь: Изд-во Перм. гос. техн. ун-та, 2006. 32 с.
Методическое пособие предназначено для студентов III курса специальностей КМ и ДПМ, изучающих дисциплину «Основы вариационного исчисления». Кратко изложены необходимые теоретические сведения из курса вариационного исчисления, которые сопровождаются разбором типовых примеров. Даны варианты заданий для самостоятельной работы.
Рецензент – канд. техн. наук, доцент кафедры ВММ И.Н. Бояршинова.
©Пермский государственный технический университет, 2006
Введение
Как известно из курса дифференциального исчисления, вопрос отыскания экстремумов гладкой функции сводится к исследованию нулей ее производной; более того, введению самого понятия производнойкак раз и способствовали попытки решения задач на отыскание наибольшего и наименьшего значения функции.
Аппарат дифференцирования оказался простым, универсальным и эффективным методом, с помощью которого удается решать практически любые задачи на экстремум, если интересующая нас величина может быть задана как функция, то есть представляет собой отображение числового множества в числовое множество. А если область определения или множество значений – не числа? Получается, что тогда у нас нет ни функции, ни ее производной, ни, стало быть, метода решения задач на экстремум? Но ведь для объектов, не являющихся функциями, задачи на экстремум ничуть не утрачивают своей актуальности, и необходимо как-то научиться их решать.
Метод решения задач на экстремум для отображений более общей природы, чем функции, и составляет суть классического вариационного исчисления, основы которого были заложены в XVIII в. в работах двух выдающихся математиков того времени – Леонарда Эйлера и Жозефа Луи Лагранжа.
Рассмотрим – вслед за Эйлером и Лагранжем – задачу о нахождении наибольшего и наименьшего значения функционалов – отображений, областью определения которых являются произвольные пространства, а множеством значений – числа (вещественные или комплексные). Легко привести примеры функционалов. Возьмем в качестве области определения плоскость или трехмерное пространство – получим функционал, который мы называли раньше функцией двух или трех переменных. Пусть область определения – множество непрерывных на отрезке функций. Поставим в соответствие каждой функции число – значение определенного интеграла от функции по данному отрезку – и мы снова получим функционал, на этот раз интегрального вида.
Для функционалов удалось построить столь же простой и красивый метод решения задач на отыскание экстремумов, как и для функций. Это оказалось возможным как раз потому, что для функционалов нашелся аналог дифференциала. Им оказалось введенное в работах Лагранжа понятие вариации функционала, которое явилось основой нового раздела математики (и дало ему название).
Оказалось, что замена дифференцирования варьированием сохраняет практически без изменений теоремы классического анализа, на которых базируется решение задач на экстремум: в точке экстремума первая вариация необходимо равна нулю, а характер критической точки (максимум, минимум, отсутствие экстремума) определяется свойствами второй вариации.
Основываясь на этих результатах, можно, выстраивая подходящие функционалы, получать решения многих задач, связанных с нахождением экстремумов.
Из истории вариационного исчисления
Задача о брахистохроне или как льва узнают по когтям
Возьмем две точки (А и В) и соединим их всевозможными кривыми, идущими сверху вниз (см. рисунок). Если материальная точка начнет падать из А по одной из кривых под действием силы тяжести, то через некоторое время она попадет в точку В. Это время можно рассматривать как функцию, заданную на множестве всех кривых, идущих из точки А в точку В. Возникает задача об отыскании кривой, двигаясь по которой падающая точка быстрее всего попадет в точку В. Такую кривую назвали брахистохроной (от греческих слов «брахистос» – кратчайший и «хронос» – время).
История задачи о брахистохроне начинается с 1696 года. Ее формулировка и первое решение принадлежат Иоганну Бернулли. Им же задача была предложена Лейбницу, который посоветовал Бернулли опубликовать «столь прекрасную и до сих пор неслыханную задачу» для состязания между геометрами, предоставив годичный срок для решения. По истечении срока оказалось, что только трое математиков сумели найти решение задачи о брахистохроне: Лопиталь, Якоб Бернулли и … некий таинственный автор, опубликовавший решение без подписи в одном английском журнале. Но Иоганн Бернулли сразу угадал анонима: лишь один человек в Англии мог решить задачу с таким блеском – сэр Исаак Ньютон. Как писал сам Бернулли, он узнал Ньютона, как льва узнают по когтям.
Интересно, что термин «брахистохрона» оказался нужен только для постановки задачи. После ее решения выяснилось, что брахистохрона – это давно известная математикам и механикам циклоида.
Рекомендуемые страницы:
Поиск по сайту
poisk-ru.ru
Задачи о времени спуска по заданным аналитически кривым. Задача о брахистохроне. Все мои размышления основаны на теории вариационного исчисления
Творческая работа
ученика вечерней общеобразовательной школы №3г. Ставрополя
Кириченко Даниила
Руководитель: учитель математики Завгородний И.С.
Задачи о времени спуска по заданным аналитически кривым. Задача о брахистохроне.
Все мои размышления основаны на теории вариационного исчисления.
Справочник по математике – Бронштейн и Семендяев стр.493
Справочник по математике – Корн стр.348
I Что я точно знаю, так это, что вся теория дана для движения без трения.
Если ввести трение то возникает большая проблема. Часть этой проблемы изложена в моей работе.
II Время падения тел зависит от формы кривой, по которой тело скользит без трения
III Если разность уровней одинакова, то скорость тел в конце пути одинакова и не зависит от формыкривой
IV Что я не знаю, но хотел бы знать, как зависит ускорение, скорость спускаемого тела от координаты или от времени.
Время падения тела по кривой (трения нет) можно найти так
,закон сохранения энергии
t– время, y=y(x) – уравнение кривой, v– скорость, g – ускорение свободного падения.
Рассмотрим падение тела с двух позиций:
Iпозиция – теория на основе элементарной физики
II позиция – на основе вариационного исчисления.
Задача: Найти время спуска по наклонной линии с углом .
I позиция

II позиция
Уравнениепрямой
В проекции на ось x-ов
Есть смысл взять помодулю, тогда
Как видно, оба случая дают один и тот же результат. Так и хочется сказать, что физика и математика не конфликтуют.
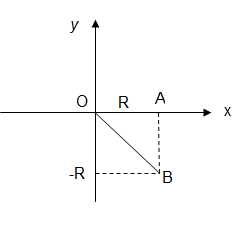
Теперь используем обе позиции для нахождения t(времени спуска) при движении тела по части окружности радиуса R.
R
y
позицияКак видно, здесь время изменяется, и решить задачу элементарным путем не удастся. Я бы сказал так «Физика дает отбой»
позиция.
Уравнение окружности
;
;
;
Замена:
Еще замена:
]
Заметим, что ;
Итеграл из разряда “неберущихся”.
Мой учитель посоветовал мне пользоваться Г.Б. Двайт “Таблицы интегралов и другие математические формулы” страница 141.
Я во всем разобрался и сумел вычислить интеграл двумя способами, чтобы убедиться, что результат правильный.
Используем гамма функцию Г(n)
Интеграл имеет конечную величину при
;
;; ;
;
Итак подсчитаем наш интеграл двумя способами
способ
. У нас p=
способ
.
Итак находим время t
;
Э
 то
время спуска по
окружности
то
время спуска по
окружности
Время спуска по прямой
Удивительно, но по расчету время спуска по прямой больше времени спуска по окружности
Напомним, что все расчеты произведены без учета силы трения.
Интересно, какой бы результат был бы получен с учетом силы трения, но это тема другой творческой работы.
gigabaza.ru

 аргумента
аргумента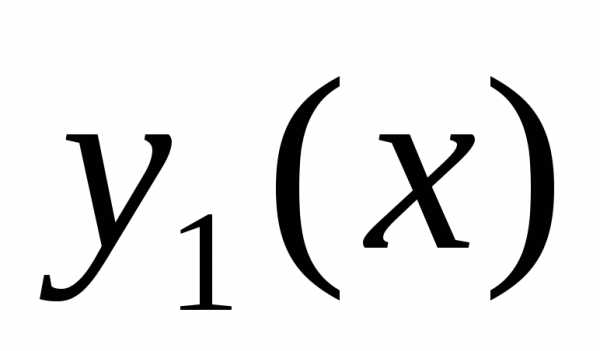 функционала
функционала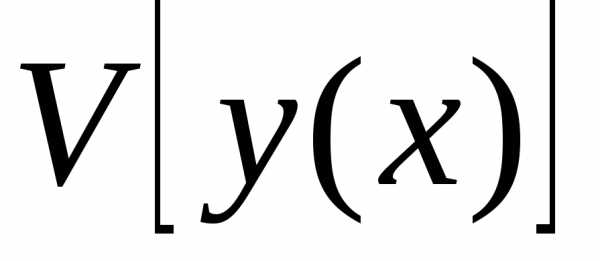 называется разность функций.
При этом все это рассматривается в
некотором классе функций.
называется разность функций.
При этом все это рассматривается в
некотором классе функций.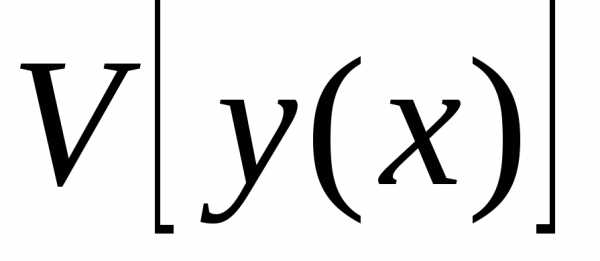 называется непрерывным, если малому
изменениюсоответствует
малое изменение функционала
называется непрерывным, если малому
изменениюсоответствует
малое изменение функционала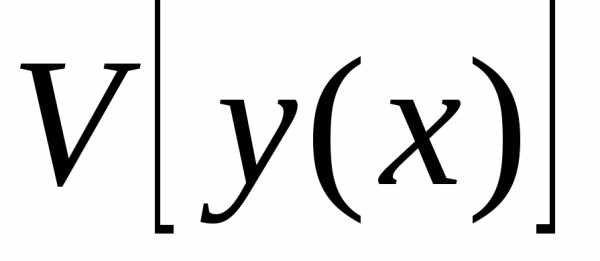 .
.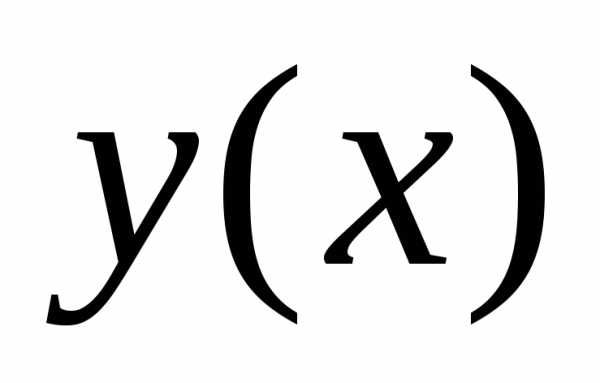 и
и разность,
то это близостьнулевогопорядка.
разность,
то это близостьнулевогопорядка.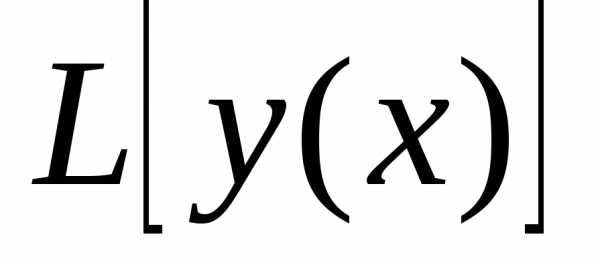 удовлетворяющий следующим условиям:
удовлетворяющий следующим условиям: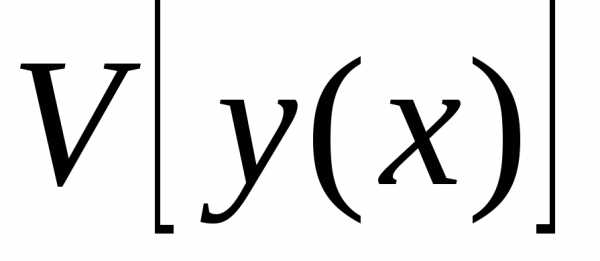 равна.
равна.