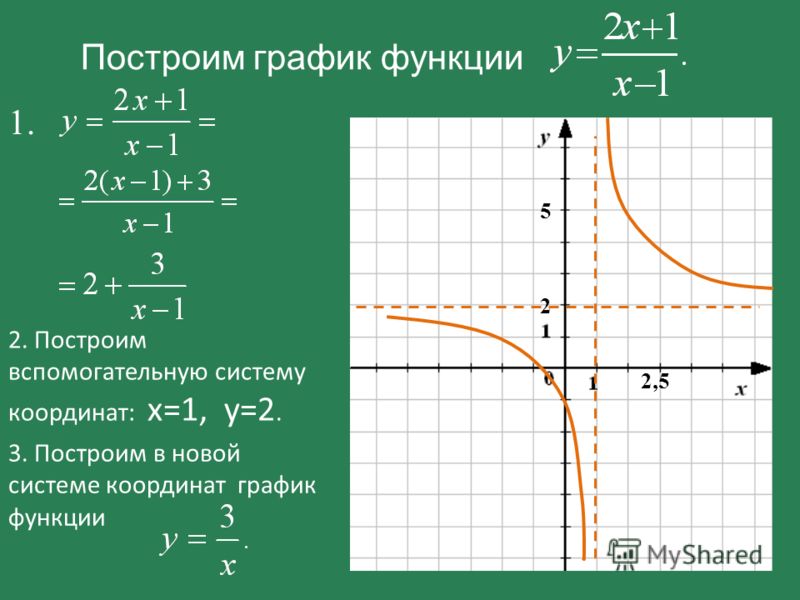
Построить обратную функцию онлайн: Калькулятор Обратных Функций

{-1}(f(x)) = x\), для всех \(x\) в соответствующем наборе.

Теперь вычисление обратной функции в целом не обязательно является простым алгебраическим упражнением, поскольку оно обычно включает в себя Решение для х начиная с исходной функции \(y = f(x) \), что может быть алгебраически сложно или невозможно.

Но, когда вы имеете дело с линейная функция формы \(y = ax + b\), то становится немного проще Решите для х и, наконец, найти обратное.

Содержание

Как найти обратную линейную функцию?

Во-первых, вы начинаете с допустимой линейной функции формы \(y = ax + b\). Ваша первая задача состоит в том, чтобы Решите для х :

\[ax = y-b\] \[\Rightarrow x = \frac{y-b}{a}\]

Теперь вы сделаете острое наблюдение: «Что произойдет, если \(a = 0\)», и вы будете правы в этом. {-1}(x) = \frac{x-b}{a}\]

Как пользоваться этим калькулятором

Чтобы найти обратную линейную функцию с шагами, просто поместите допустимую линейную функцию формы \(y = ax + b\).

Если вы укажете правильную линейную функцию, калькулятор покажет вам все шаги, необходимые для получения обратной функции, а также вы получите график исходной функции и его обратное, если обратное существует.

Обратите внимание, что этот калькулятор работает только для линейных функций. Вычисление обратной функции, которая не является линейной, может быть более сложным, и это не всегда возможно.

Пример

Найдите обратную функцию следующей линейной функции \(y = 3x — 2\).

Отвечать:

Чтобы найти функцию, обратную заданной линейной функции, необходимо выполнить следующие шаги.

Шаг 1 — Решение для x : Первым шагом в поиске обратного уравнения линейного уравнения является решение \(x\):

Нам было предложено следующее уравнение:

\[\displaystyle y=3x-2\]

Помещая \(x\) в левую часть и \(y\) и константу в правую часть, мы получаем

\[\displaystyle 3x = y + 2\]

Теперь, находя \(x\), получаем следующее

\[\displaystyle x=\frac{1}{3}y+\frac{2}{3}\]

и упрощая все термины, которые нуждаются в упрощении, окончательно получаем следующее

\[\displaystyle x=\frac{1}{3}y+\frac{2}{3}\]

Следовательно, на основе представленного уравнения мы заключаем, что результатом решения для \(x\) из данного уравнения является \(\displaystyle x=\frac{1}{3}y+\frac{2}{3}\).

{-1}(x)=\frac{1}{3}x+\frac{2}{3}\).

Обратная функция 10 класс онлайн-подготовка на Ростелеком Лицей

Функция из X в Y, прямая и обратная задачи, пример обратной задачи. Примеры для разъяснения

Пусть задана функция , множество и множество . Функция из в : Каждому элементу из первого множества соответствует единственный элемент второго множества . С этой функцией связано две основные задачи:

1 задача – прямая. Вычислить значение функции по заданному значению аргумента.

задано, необходимо вычислить .

2 задача – обратная. Найти те значения аргумента, при которых функция принимает заданное значение . Задаем , далее необходимо решить уравнение , которое может иметь одно решение, второе решение и т. д. …

Пример обратной задачи: требуется найти время для достижения ракетой заданной высоты, самолетом скорости звука, автомобилем заданной скорости 100 км/ч. Нас будет интересовать такая обратная задача, которая имеет единственное решение.

Пример №1

Пусть – множество слов. Слово – конечная последовательность букв, смысл здесь не важен. – множество слов из тех же букв, но записанных в обратном порядке.

Например: .

Итак, задана функция, два множества и соответствие между ними. Обратная задача для этой функции имеет единственное решение. Слову «ток» из множества соответствует единственное слово «кот» из множества .

Пример №2

Пусть задано множество , состоящее из двух элементов и множество , состоящее также из двух элементов . Для этих множество возможно четыре функции :

а) 1→3 б)1→4

2→4 2→3

Нас интересует количество решений в обратной задаче. Рассмотрим первую функцию. Мы видим, что 3 соответствует только один элемент и 4 соответствует только один элемент, аналогично и во второй функции. Таким образом, обратная задача для этих двух функций имеет единственное решение. Запишем еще две функции:

в)1→3 г)1→4

2→3 2→4

Каждому элементу из первого множества соответствует единственный элемент из второго множества. Обратная задача имеет здесь не единственное решение. 3 соответствует пара элементов 1 и 2, также 4 соответствует пара элементов 1 и 2.

Итак, мы рассмотрели второй пример и выяснили, что обратная задача может иметь единственное решение или нет. Здесь довольно простой случай, так как возможен перебор. Давайте рассмотрим случаи, когда перебор невозможен.

Пример №3

Числовая функция . Область определения функции – множество всеx положительных чисел: . Мы знаем график этой функции. Нарисуем его схематически (рис. 1).

Рис. 1. График функции

Нас интересует обратная задача, то есть сколько решений имеет она при заданном . Перебор здесь невозможен, однако можно просто решить уравнение , если задан, то . При любом , единственный.

Пример №4

. Область определения . Нарисуем схематичный график этой функции (рис. 2).

Рис. 2. График функции , область определения .

Вот ветвь параболы – график данной функции. Нас интересует обратная задача. Сколько решений она имеет. Здесь также можно решить уравнение.

. При любом допустимом , – единственное число.

Пример №5

, область определения – все действительные числа, . График этой функции нам известен – парабола (рис. 3).

Рис. 3. График функции , область определения – все действительные числа

Итак, нам необходимо узнать, сколько решений имеет обратная задача. Если , то легко видеть, что 16 достигается и при -4, и при +4. Таким образом, уравнение имеет не единственное решение.

Следует отметить, что единственное решение обратная задача имеет для монотонных функций. В примере 3 функция монотонно убывает, каждый достигается при одном значении . В примере 4 функция монотонно возрастает, то есть каждый y достигается только при одном значении x.

Повторение: монотонная функция

Числовую функцию называют возрастающей или убывающей на множестве ∈ , если для любых чисел , таких, что , имеем , то есть большему значению аргумента соответствует большее значение функции. Чем больше аргумент, тем больше функция, эта функция монотонно возрастает.

Если большему значению аргумента соответствует меньшее значение функции, то есть , то такую функцию называют убывающей.

Теорема 1

Пусть – монотонная функция. Тогда уравнение имеет единственное решение для любого из множества значений функции.

Предположим, что функция монотонно возрастает на отрезке принимает значение из отрезка (рис. 4). Необходимо доказать, что любое значение эта монотонная функция принимает при единственном значении аргумента .

Рис. 4. График функции

Доказательство

Докажем методом от противного. Предположим, что существует такое значение из множества значений функции, что уравнение имеет не единственное решение. Например, два решения . Если это так, тогда значение в точке ==, но функции монотонны, значит, или . Получаем противоречие. Значит, наше предположение было неверно. При любом значении обратная задача для монотонной функции имеет единственное решение.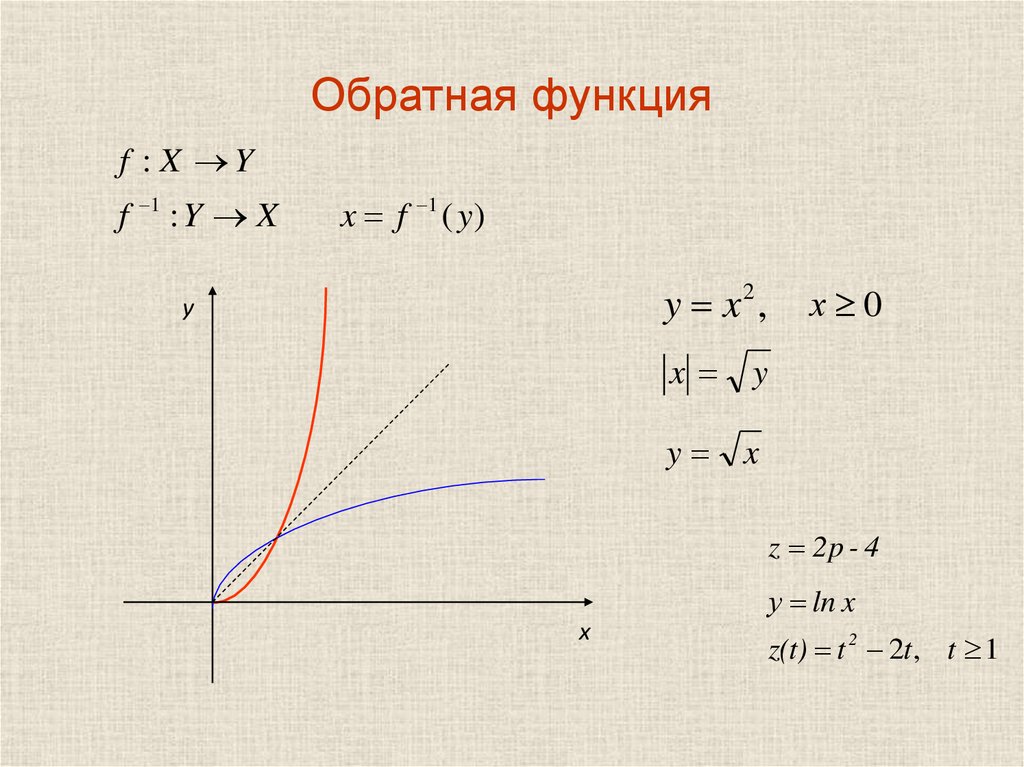 Теорема доказана.

Комментарии: монотонность гарантирует, что бесчисленное множество таких уравнений имеет единственное решение.

(Почему их бесчисленное множество? Потому что в множестве значений бесчисленное множество .)

Определение обратной функции

Пусть – монотонная функция. Доказано, что уравнение , имеет единственное решение при любом . Это означает, что закон, который сопоставляет каждому числу единственное решение уравнения , также является функцией с областью определения и множеством значений . Эта функция называется обратной к функции и обозначается . Функция , обратная функция, устанавливает взаимно однозначное соответствие между множествами и . – множество значений исходной функции. – область определения исходной функции. В силу определения обратной функции, ее график – множество точек . Напомним, что графиком прямой функции является множество точек вида .

Естественно, что графики прямой и обратной функции каким-то образом взаимосвязаны между собой.

Теорема 2

Графики прямой и обратной функций симметричны относительно прямой . График прямой функции . График обратной функции .

Доказать: и симметричны относительно .

Доказательство.

Рис. 5. Графики прямой функции и обратной функций

Имеем прямоугольные треугольники и треугольник (рис. 5). Они равны по двум катетам, значит, гипотенузы равны. Следовательно, треугольник равнобедренный. Из равенства углов 1 и 2 следует равенство углов 3 и 4, значит, в этом треугольнике прямая – биссектриса, то есть ось симметрии этого треугольника, является и медианой, и высотой. Значит, точки и симметричны относительно прямой , значит, графики прямой и обратной функции симметричны относительно данной прямой.

Следствие из теоремы 2

Из теоремы вытекает одинаковый характер монотонности прямой функции и обратной функции . То есть обе функции одновременно либо монотонно возрастают, либо монотонно убывают.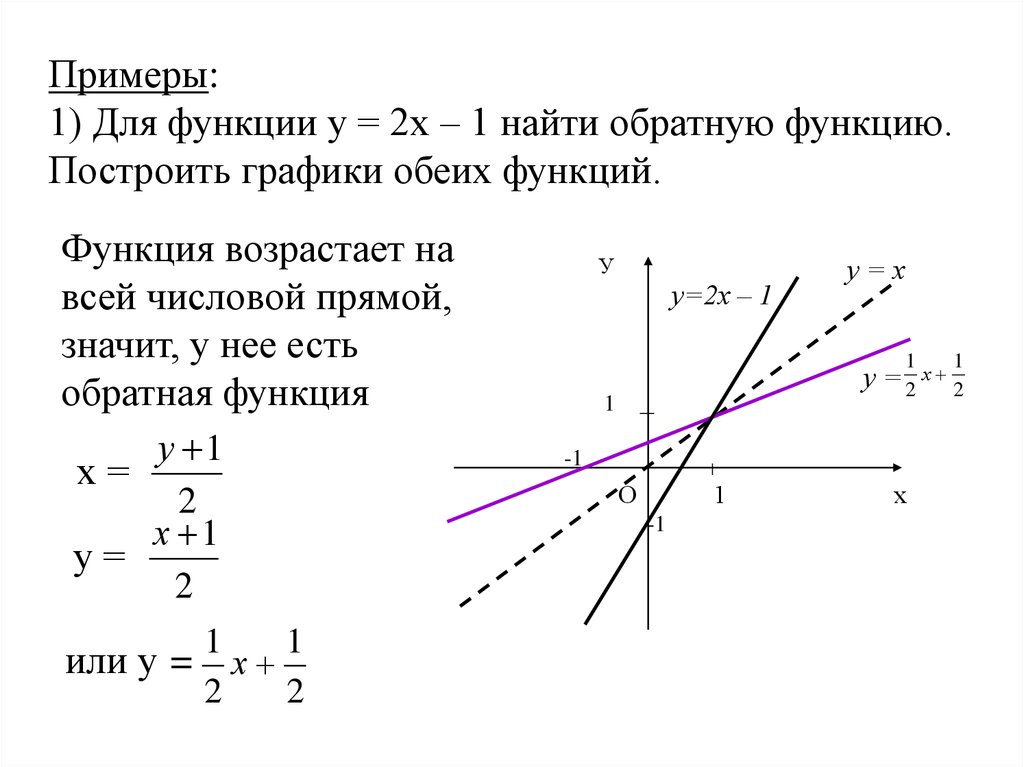

Методика построения обратной функции и построение ее графика

Поговорим о методике построения обратной функции и о методике построения графика обратной функции. Нам дано: функция монотонна. Требуется найти обратную функцию и построить ее график.

Рис. 6. Графики возрастающих функций и графики убывающих функций

Рисуем прямую , далее график прямой функции мы знаем, что график обратной функции симметричен ему относительно .

Рис. 7. Построение графика обратной функции

Таким образом, принцип построения понятен. Мы можем получить график обратной функции, отразив график прямой функции относительно прямой . Чтобы получить саму обратную функцию, необходимо решить уравнение .

Другими словами, выражаем через и получаем , это в осях , меняем местами и для удобства восприятия: в осях . Аргумент по оси , функция по оси .

Приведем пример.

Задана прямая функция. Мы знаем, что эта функция монотонна, значит, существует обратная функция.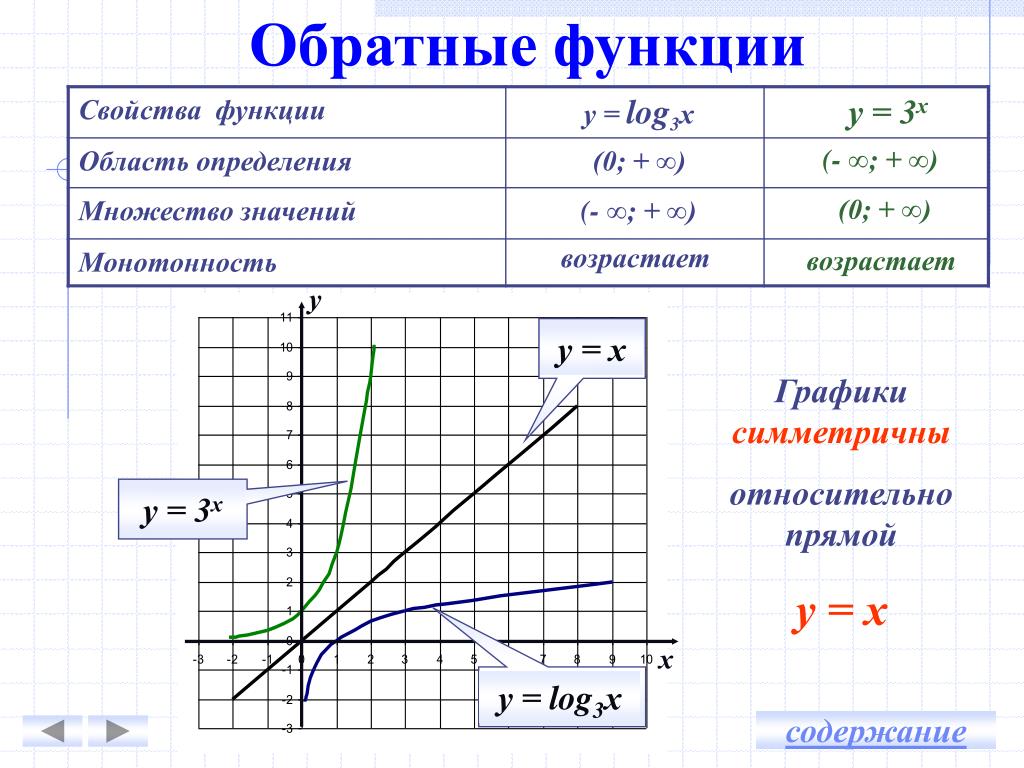 Имеем функцию , после переобозначения получаем удобную для нас функцию .

Построим графики (рис. 8).

Рис. 8. Построение графиков прямой и обратной функций

Ось симметрии , график прямой функции – парабола , проходит через точки (0;0) и через точку (1;1). График обратной функции проходит через те же точки, эти точки лежат на оси симметрии.

Вывод

Мы рассмотрели общую методику построения графиков обратной функции и привели конкретный пример. Таким образом, мы узнали, что такое обратная функция, узнали, что монотонная функция имеет обратную себе.

Список литературы

Алгебра и начала анализа, 10 класс (в двух частях). Учебник для общеобразовательных учреждений (профильный уровень) под ред. А. Г. Мордковича. – М.: Мнемозина, 2009.

Алгебра и начала анализа, 10 класс (в двух частях). Задачник для общеобразовательных учреждений (профильный уровень) под ред. А. Г. Мордковича. – М.: Мнемозина, 2007.
Виленкин Н.Я., Ивашев-Мусатов О.С., Шварцбурд С.И. Алгебра и математический анализ для 10 класса (учебное пособие для учащихся школ и классов с углубленным изучением математики). – М.: Просвещение, 1996.
Галицкий М.Л., Мошкович М.М., Шварцбурд С.И. Углубленное изучение алгебры и математического анализа. – М.: Просвещение, 1997.
Сборник задач по математике для поступающих во ВТУЗы (под ред. М.И. Сканави). – М.: Высшая школа, 1992.
Мерзляк А.Г., Полонский В.Б., Якир М.С. Алгебраический тренажер. – К.: А.С.К., 1997.
Саакян С.М., Гольдман А.М., Денисов Д.В. Задачи по алгебре и началам анализа (пособие для учащихся 10 –11 классов общеобразов. учреждений). – М.: Просвещение, 2003.

Карп А.П. Сборник задач по алгебре и началам анализа : учеб. пособие для 10 –11 кл. с углубл. изуч. математики. – М.: Просвещение, 2006.

Домашнее задание

Постройте график функции .
Ответьте на вопрос: какова область определения данной функции.
Укажите промежутки монотонности данной функции.

Дополнительные рекомендованные ссылки на ресурсы сети Интернет

Интернет-портал 5klass.net (Источник).
Интернет-портал Mathematics-repetition.com (Источник).
Интернет-портал Mathematics-tests.com (Источник).

Стратегии, ресурсы и советы EdTech

Дата: 30 апреля 2020 г. Автор: karengreenhaus 0 комментариев

Я преподаю курс алгебраических рассуждений, посвященный основам понимания обратных чисел (целых, обратных) и обратных операций. Это один из моих любимых курсов для преподавания, потому что он действительно подчеркивает важность предварительных знаний о свойствах сложения и умножения, точного математического словаря и того, как часто наши «хитрости», помогающие учащимся, действительно мешают их истинному пониманию. Одним из них является нахождение обратных функций.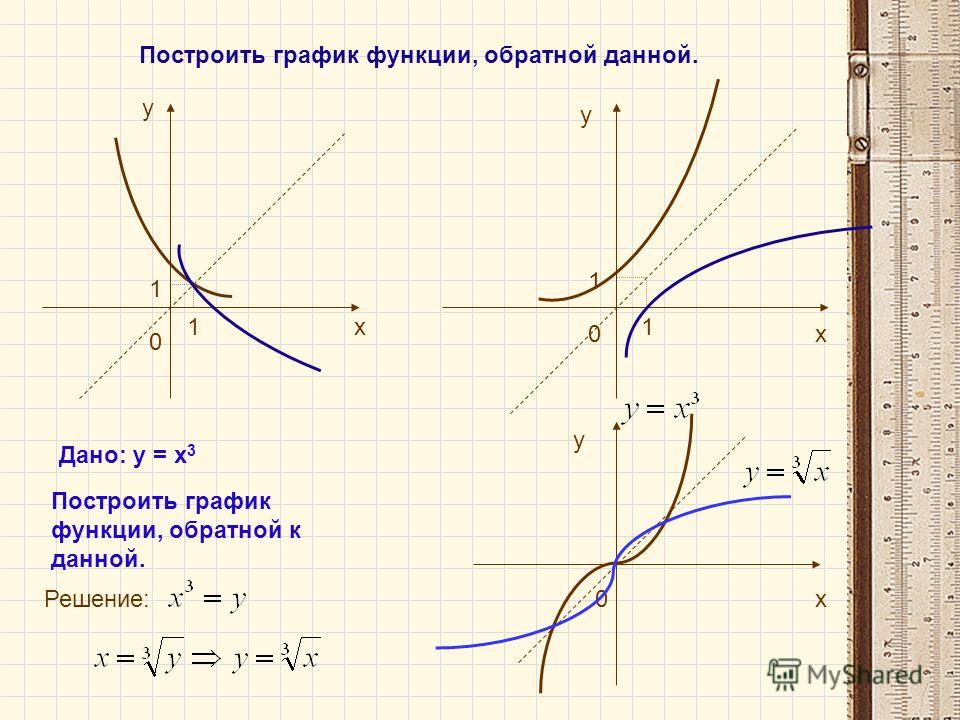 Мы склонны учить трюку «поменять местами x и y в исходной функции, а затем найти y». Никаких рассуждений, никакого реального понимания того, что такое обратная функция. Если вместо этого мы посмотрели на исходную функцию, определили операции, которые происходили с независимой переменной, определили обратные операции/числа (т.е. мультипликативную обратную, НЕ деление; аддитивную обратную, НЕ вычитание), а затем применили их к независимой переменной в «обратный» порядок, мы могли бы построить обратный из обратных операций/чисел.

Пример:

Еще одна вещь, которую мы забываем или делаем недостаточно часто, — это визуализация обратных функций, чтобы учащиеся видели симметрию обратных функций как отражение функции тождества. А затем свяжите их с примерами из реального мира, чтобы учащиеся поняли, что точки в исходной функции представляют в контексте, а затем ТАКЖЕ что точки/обратные точки в обратной функции представляют в контексте.

Вот пример визуальной симметрии (отражения) обратных функций сверху по сравнению с функцией тождества, y=x (обратите внимание — мы ограничили исходную функцию значениями x больше или равными нулю, чтобы выделить симметрия):

Сегодняшние общие уроки сосредоточены на работе с функциями в контексте реальной ситуации, а также на поиске инверсий этих функций и анализе их в контексте ситуации. Что мне особенно нравится в обоих действиях, так это то, что они используют обратные операции для нахождения обратных функций. Например, одна из них — радикальная функция — квадратный корень, и для нахождения обратной мы делаем обратную операцию возведения в квадрат. А для экспоненциальной функции мы используем обратный логарифм. Это невероятно!

В своем видеообзоре я использую графический калькулятор CG50 – в обзоре кратко рассказывается о каждом действии, а затем демонстрируется, как построить график функции, ее обратной функции и функции тождества, чтобы визуально увидеть, как обратные функции связаны с их исходной функцией (отражения над функцией идентификации).

Вот ссылки на два занятия, а также видеообзор:

Цунами — развитие продвинутого алгебраического мышления
Дозировки ацетаминофена – развитие продвинутого алгебраического мышления
- Обзор видео — графические функции CG50, инверсии и функция идентификации

Обязательно посетите Casio Cares: https://www.casioeducation.com/remote-learning

Вот быстрые ссылки:

Casio Education
Скачать портативные эмуляторы Casio
Активности для бесплатной загрузки
Краткие справочные руководства (инструкции)
Служба поддержки YouTube (мой)
Поддержка YouTube (Casio)

Нравится:

Нравится Загрузка…

Нахождение обратной функции — Криста Кинг Математика

Как определить обратные функции

В этом уроке мы рассмотрим определение обратной функции и как найти обратную функцию.

Если вы помните из прошлого урока, функция обратима (имеет обратную), если она взаимно однозначна. Теперь давайте немного подробнее рассмотрим, как найти инверсию и что делает инверсия. 93}???

Обратите внимание, как изменились координаты ???x??? и ???y???-значения поменялись местами. Теперь давайте посмотрим, как вычислить инверсию алгебраически.

Вычисление и построение графиков обратных функций

Пройти курс

Хотите узнать больше об Алгебре 2? У меня есть пошаговый курс для этого. 🙂

Учить больше

Нахождение обратной функции