Задачи на размещение сочетание и перестановку с решением – основные формулы. Перестановки, размещения, сочетания. Задачи с решением по комбинаторике

«Задачи на подсчет числа размещений, перестановок, сочетаний»

Урок ________

Тема программы: Комбинаторика

Тема: «Задачи на подсчет числа размещений, перестановок, сочетаний».

Цели:

— повторить формулы для нахождения числа различных видов комбинаций: размещений, перестановок, сочетаний без повторов; изучить формулы для нахождения числа различных видов комбинаций: размещений, перестановок, сочетаний с повторами, научиться распознавать задачи на нахождение размещений, перестановок, сочетаний; решить простейшие комбинаторные задачи с помощью этих формул;

— развивать познавательный интерес студентов, логическое мышление, умение применять знания в изменённой ситуации, делать выводы и обобщения; развивать  умения сравнивать, систематизировать, обобщать;

— формировать научное мировоззрение у обучающихся,  культуру математической речи,  информационную и  коммуникативную культуру студентов; воспитание дружелюбного отношения друг другу, умение работать в коллективе.

Оборудование:

Ход урока

I. Организационный момент

Преподаватель проверяет готовность к уроку.

Я рада приветствовать всех Вас на сегодняшнем уроке.

II. Мотивация. Сообщение темы, целей урока

1. Вопросы:

1. Определения: перестановки, размещения, сочетания.

2. Важен ли порядок? В каких соединениях? (размещение)

2. Решение задач:

№1. Экзамен состоит из 5 задач, которые можно решать в любом порядке. Сколькими способами можно расставить задачи. (способов)

№2. В магазине продается 8 различных наборов марок, посвященных спортивной тематике. Сколькими способами можно выбрать из них 3 набора. (способа)

№3. Сколько четырехзначных чисел, в которых нет одинаковых цифр, можно составить из цифр 0, 2, 4, 6, 8. (всего чисел А, а чисел начинающихся с нуля —, тогда А—=96)

Тема сегодняшнего урока «Задачи на подсчет числа размещений, перестановок, сочетаний.». Давайте вместе попробуем сформулировать цели урока:

— научиться распознавать задачи на нахождение размещений, перестановок, сочетаний;

— решать простейшие комбинаторные задачи с помощью этих формул.

III. Изучение новой темы

1. Перестановка

Рассмотрим слово «КВАНТ», состоящее из 5 различных букв. Если менять порядок букв, получим 5!=120 перестановок

Если проделать то же самое со словом «АТАКА», то перестановок будет меньше, потому что, меняя местами 1,3 и 5-ю буквы, будем получать то же самое слово. Т.к. три буквы А можно менять местами 3!=6 способами, то перестановок будет в слове «АТАКА» в 6 раз меньше, т.е.

Вывод: Перестановками в такой выборке, где есть один элемент, называются перестановками с повторениями. Обозначается : Р_{(n1, n2,….., nk)}

Р(n1, n2,….., nk)₌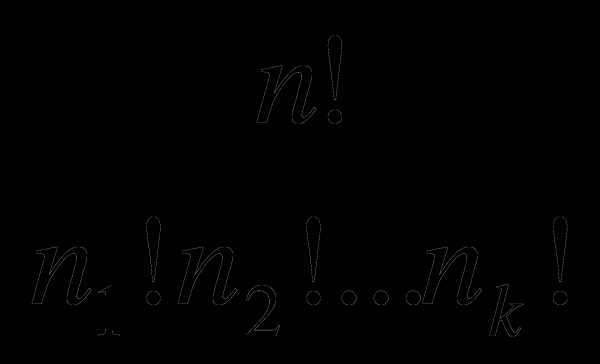

, где n- количество повторений элементов

Задача: Сколько различных перестановок можно сделать из букв слова «МАТЕМАТИКА»

Решение:

Всего – 10 букв

«М» — 2 повтора

«А» — 3 повтора

«Т» — 2 повтора

«Е» — 1 повтор

«И» — 1 повтор

«К»- 1 повтор

перестановки

Ответ: 151200 перестановки

2. Сочетания.

Рассмотрим следующую задачу.

В почтовом отделении продаются открытки 10 сортов. Сколькими способами можно купить 8 различных открыток?

Решение. Данная задача на отыскание числа сочетаний без повторений, т.к. требуется купить 8 различных открыток

Ответ: 45 способов

Проделаем то же самое, но только определим «Сколькими способами можно купить в нем 8 открыток?

Решение.

Данная задача на отыскание числа сочетаний с повторениями из n = 10 элементов по k =8. Следовательно, она решается по формуле

 

Ответ : 24310 способов

Вывод: Иными словами, выборки которые отличаются количеством элементов хотя бы одного типа, называются сочетаниями с повторениями, а их общее число будем обозначать .

Задача: В кондитерской имеется 3 вида пирожных. Сколькими способами можно купить 9 пирожных?

Решение. В задаче требуется найти число всевозможных групп по 9 элементов, которые можно составить из данных трех различных элементов, причем указанные элементы в каждой группе могут повторяться, а сами группы отличаются друг от друга хотя бы одним элементом. Это задача на отыскание числа сочетаний с повторениями из трех элементов по девять. Следовательно,

3. Размещения.

Рассмотрим задачу:

В лифт восьмиэтажного дома вошли 5 пассажиров. Сколькими различными способами могут выйти пассажиры на каждом этаже, начиная со второго?

способов

А теперь ту же задачу, но вопрос сформулируем иначе.

В лифт восьмиэтажного дома вошли 5 пассажиров. Сколькими способами могут выйти пассажиры на каждом этаже, начиная со второго?

Задача такого вида называется «размещения с повторением», обозначается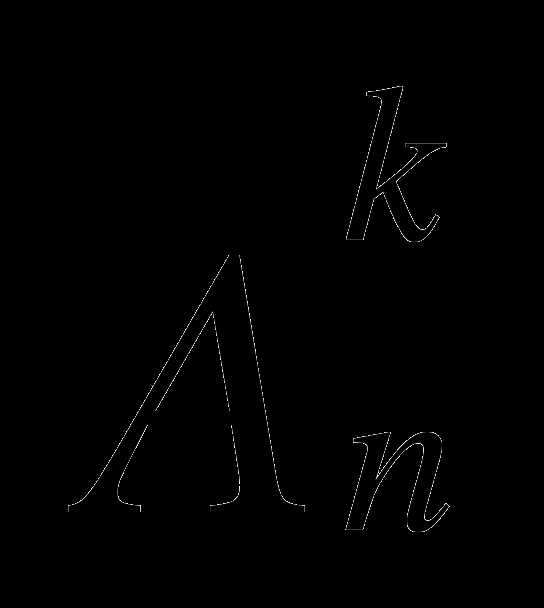

  и вычисляется по принципу умножения.

Вычисляется по следующей формуле:

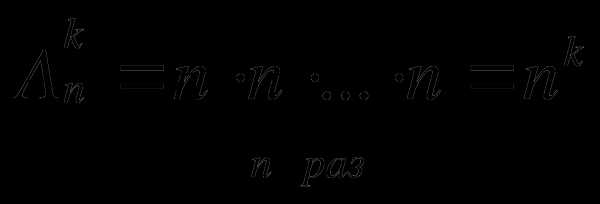
Решение. Задача сводится к распределению 5 пассажиров по 7 этажам (т. е. набор упорядоченный), причем возможны повторения (т. е. несколько пассажиров могут выйти на одном этаже). Таким образом, задача сводится к нахождению числа размещений с повторениями:

Задача: Сколькими способами девочка Яна может разложить 12 кукол по трём ящикам, если каждый ящик может вместить все куклы?

Ответ: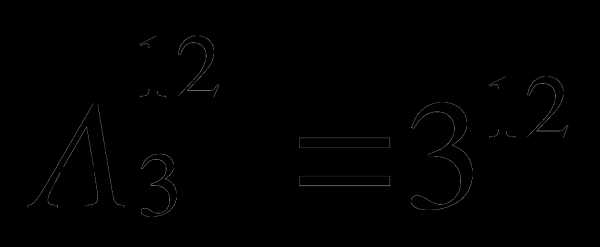 

IV. Закрепление.

Задача №1. Буквы азбуки Морзе состоят из символов – точка и тире. Сколько букв получим, если потребуем, чтобы каждая буква состояла не более чем из пяти указанных символов?

Решение. Число всех букв, каждая из которых записывается одним символом, равно 

Число всех букв, каждая из которых записывается двумя символами, равно .

Число всех букв, каждая из которых записывается тремя символами, равно .

Число всех букв, каждая из которых записывается четырьмя символами, равно .

Число всех букв, каждая из которых записывается пятью символами, равно .

Число всех указанных букв будет равно 62.

Задача №2. Сколько всего чисел (не больше 100000) можно составить из цифр 1, 2, 3, 4 и 5 в каждом из которых цифры расположены в неубывающем порядке?

Решение. Это задача о числе сочетаний из пяти цифр по одному, по два, по три, по четыре и по пяти с повторениями в каждом случае. Поскольку , , , , , то существует чисел, удовлетворяющих условию задачи.

V. Подведение итогов занятия. Рефлексия.

(Обобщаются новые знания, делаются выводы о достигнутых целях урока. Поощряются активные студенты, выставляются обоснованные преподавателем оценки.)

1) Подведем итоги нашего занятия.

Проверь себя:

1. Соединения виды перечислить?

2. На какие они делятся ? ( повторения и без)

3. Важен ли порядок? В каких соединениях? (размещение)

4) Формулы нахождения: перестановок, размещения, соединения с повторениями и без.

2) Обсуждение и выставление оценок за урок.

3) Рефлексия:

Достиг ли ты своих целей? ______________

Оцени степень усвоения: _______________

Продолжи одно из предложений:

“Мне понятно…

“Я запомнил…

“Мне на уроке…

“Я думаю…

VI. Домашнее задание

Решите задачи:

1. Сколькими способами можно разместить 8 пассажиров по трем вагонам?

Ответ: .

2. Сколькими способами Буратино, кот Базилио и лиса Алиса могут поделить между собой 5 одинаковых золотых монет?

Ответ: .

3. Сколько различных браслетов можно сделать из 5 одинаковых изумрудов, 6 одинаковых рубинов и 7 одинаковых сапфиров ( всего в браслет входит 18 камней)? ( =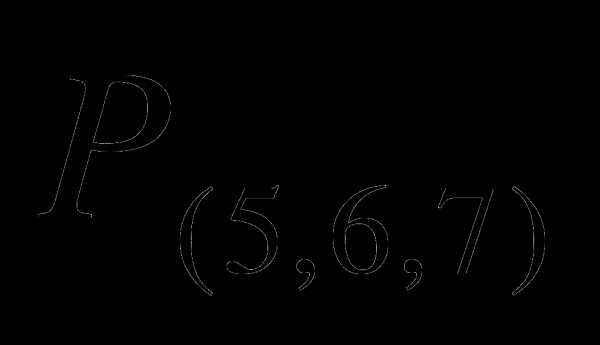

)

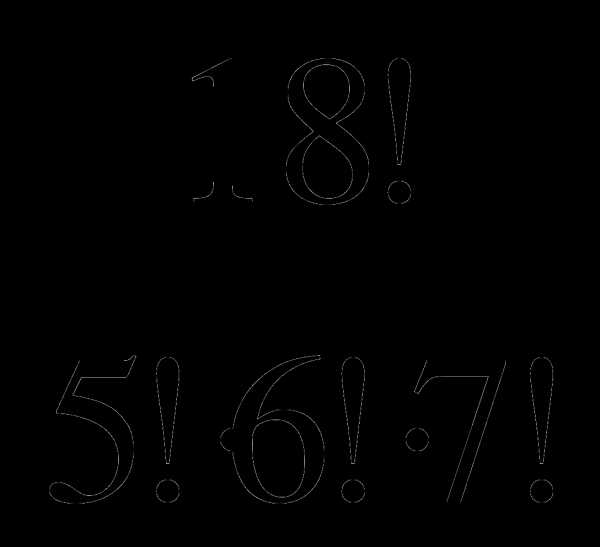
infourok.ru

«Основные понятия комбинаторики при решении задач. Перестановки, размещения и сочетания»

Министерство образования и науки Республики Бурятия

ГОСУДАРСТВЕННОЕ БЮДЖЕТНОЕ ПРОФЕССИОНАЛЬНОЕ ОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ

«БУРЯТСКИЙ РЕСПУБЛИКАНСКИЙ ТЕХНИКУМ СТРОИТЕЛЬНЫХ И ПРОМЫШЛЕННЫХ ТЕХНОЛОГИЙ»

Методическая разработка открытого занятия

по УД МАТЕМЕТИКА

«Основные понятия комбинаторики при решении задач. Перестановки, размещения и сочетания»

г.Кяхта, 2018г

Рассмотрено на заседании ЦК Общеобразовательных дисциплин

«___»__________________2018г

Протокол №_______

Председатель ЦК: ______ / Цыдыпова Т.С./

Согласовано

методист «БРТСиПТ»: _____________________ С.Ц. Дылгырова

«Утверждаю»

Зам директора по УМР

__________/Бурантарова Е.А./ «____»____________2018г

Разработала: Цыдыпова Т.С., преподаватель математики.

СОДЕРЖАНИЕ

2. Технологическая карта учебного занятия ……………………………

6

3. План учебного занятия ………………………………………………..

8

4. Ход занятия …………………………………………………………….

8

5. Список литературы ……………………………………………………

16

Аннотация методической разработки

Представителям самых различных специальностей приходится решать задачи, в которых рассматриваются те или иные комбинации, составленные из букв, цифр и иных объектов. Область математики, в которой изучаются вопросы о том, сколько различных комбинаций можно составить из заданных объектов, называется комбинаторикой.

Основа хорошего понимания комбинаторики умение считать, думать, рассуждать, находить удачные решения задач. Все эти навыки и способности можно выработать, если быть настойчивым, трудолюбивым и внимательным на уроках, самостоятельно и с интересом заниматься.

Открытое занятие по теме «Основные понятия комбинаторики при решении задач. Перестановки, размещения и сочетания». Задачи на подсчет числа размещений, перестановок, сочетаний. Решение задач на перебор вариантов знакомит обучающихся с новым разделом математики: «Комбинаторика», основными понятиями и задачами, использованием в практических целях и в жизни человека.

Задачи с использованием элементов комбинаторики входят в состав экзамена по математике. Поэтому у обучающихся должны формироваться первоначальные представления о комбинаторных задачах.

На занятии будут использованы такие виды деятельности, как практические, самостоятельные работы, решение задач. Данный урок поможет обучающимся по-другому посмотреть на окружающий мир. После данного занятия они смогут объективно оценивать некоторые вещи, опираясь на математические подсчеты.

Они учатся решать комбинаторные задачи на «перестановки», «сочетания», «размещения» по формулам, что развивает логическое мышление.

Данная тема является вторым занятием в разделе «Комбинаторика» рабочей программы.

Предварительно была подготовлена презентация по теме. Решение задач на повторение метода перебора вариантов, дерева возможных вариантов, правила произведения, которые наглядно демонстрирует основные шаги объяснения предыдущего материала. Так же были подготовлены листы с таблицами «Верите ли вы, что…», где ребята должны ответить на вопросы в начале занятия и вернуться к ним в конце занятия. Карточки с самостоятельной работой.

Современное общество живёт в ситуации постоянных изменений ценностей и идеалов, при высокой степени неопределённости условий принятия решений и неоднозначности многих жизненных выборов. В связи с этим большое значение приобретает целенаправленная работа техникума по формированию у подрастающего поколения целостного взгляда на мир и место человека в этом мире.

Открытое занятие по теме «Основные понятия комбинаторики при решении задач. Перестановки, размещения и сочетания» было проведено в рамках недели общеобразовательных дисциплин в группе КАМ1.

Проведённый мною открытое занятие осуществляет в первую очередь задачу системности использованию полученных знаний в жизни человека. На уроке применила мультимедийный проектор, компьютер, материалы презентации, дидактический материал для индивидуальной и групповой работы на занятии.

Данная методическая разработка может быть использована учителями общеобразовательных школ, преподавателями СПО. При воплощении можно опираться на основную идею или фрагменты данной методической разработки, вносить изменения и дополнения, учитывая свой опыт.

Данная методическая разработка опубликована на сайте: https://infourok.ru/user/cidipova-tatyana-sergeevna.

Технологическая карта учебного занятия

Цель: повторить основные понятия комбинаторики с помощью решения задач. Ввести формулы перестановки, размещения и сочетания.

Задачи:

Образовательная:

— создать условия для осознанного понимания решения простейших задач на применение элементов комбинаторики;

— изучить формулы размещения, перестановки и сочетания;

— сформировать у студентов первичные умения и навыки решения задач.

— продолжить формирование у студентов представления о комбинаторике и ее применении в жизни человека.

Развивающая:

— развивать познавательный интерес студентов, логическое мышление, умение применять знания в изменённой ситуации, делать выводы и обобщения;

— развивать умения сравнивать, систематизировать, обобщать.

Воспитательные:

— воспитывать чувство ответственности за качество и результат выполняемой работы;

— формировать культуру математической речи;

— воспитание дружелюбного отношения друг другу, умение работать коллективе.

Тип учебного занятия: комбинированный.

Форма учебного занятия: урок.

Используемые технологии: элементы проблемного обучения.

Используемые методы обучения: активные и интерактивные методы обучения. Проблемно-поисковый, метод беседы, методы организации и осуществления учебно-познавательной деятельности, методы контроля за эффективностью учебно-познавательной деятельности. 

— словесный: устный опрос; эвристическая беседа

— наглядный: показ иллюстраций, карточка с самостоятельной работой.

— практический: решение задач.

Формы организации познавательной деятельности: фронтальная; индивидуальная форма организации познавательной деятельности.

Развитие общих компетенций:

• ОК 4. Осуществлять поиск и использовать информацию, необходимую для эффективного выполнения профессиональных задач, профессионального и личностного развития.

• ОК 6. Работать в коллективе и команде, взаимодействовать с руководством, коллегами, социальными партнерами.

• ОК 7. Брать на себя ответственность за работу членов команды (подчиненных), результат выполнения заданий.

Учебно-методическое обеспечение урока:

• дидактические средства и методические средства: тексты самостоятельной работы;

• технические средства: проектор, экран, ноутбук с презентацией, листы с опорным конспектом, задачами, учебная доска.

Учебно-материальное оснащение:

1. Башмаков М.И. Математика: учебник для 10 класса: среднее (полное) общее образование (базовый уровень). – 5-е изд. – М.: Издательский центр «Академия», 2014.

2. Башмаков М.И. Математика: 10 класс. Сборник задач: среднее (полное) общее образование. – 3-е изд. – М.: Издательский центр «Академия», 2017г.

Планируемые образовательные результаты:

личностные

-умение ясно, точно, грамотно излагать свои мысли в устной и письменной речи, понимать смысл поставленной задачи,

-умение контролировать процесс и результат учебной математической деятельности;

-способность к эмоциональному восприятию математических объектов, задач, решений, рассуждений

метапредметные

-умение самостоятельно ставить цели, выбирать и создавать алгоритмы для решения учебных математических проблем;

-умение применять теоретические знания в реальных жизненных ситуациях

предметные

— овладение навыками устных и письменных вычислений;

— умение точно и грамотно выражать свои мысли в устной и письменной речи с применением математической терминологии;

— вычислять значения выражений, выбирая удобный порядок действий

План учебного занятия:

1. Организационный момент.

2. Мотивация учебной деятельности (постановка цели и задач занятия).

3. Актуализация знаний

1. Фронтальный опрос.

2. Решение задач на повторение.

4. Изучение нового материала

1. Введение понятия перестановка, формулы перестановки, решение задач.

2. Введение понятия размещение, формулы размещения, решение задач.

3. Введение понятия сочетание, формула сочетания, решение задач.

5. Закрепление (решение задач).

6. Подведение итогов (домашнее задание, рефлексия).

7. Самостоятельная работа.

Ход занятия

1. Организационный момент. Здравствуйте, ребята! Сегодня на занятии у нас гости, мы их всех прекрасно знаем, поприветствуем наших гостей. Садитесь. Отметка студентов отсутствующих на занятии.

2. Мотивация учебной деятельности (слайд 1).

Вперед поедешь – голову сложишь,

направо поедешь – коня потеряешь, налево поедешь – меча лишишься.

— Какая проблема возникла перед богатырем? (Проблема выбора дальнейшего пути движения (слайд 2)).

— Как богатырь выходит из данной ситуации? (А дальше говорится о том, как он выходит из данного положения, в которое попал в результате выбора).

— А вы когда-нибудь находились перед выбором? И как часто это происходит в вашей жизни?

Выбирать разные пути или варианты приходится каждому человеку. Эти пути и варианты складываются в самые разнообразные комбинации.

— Какой раздел математики занят поисками ответов на эти вопросы? (комбинаторика).

(Слайд 3) «Учимся не для техникума, а для жизни»

Сенека Люций Анней

Эти слова, я хочу взять эпиграфом к нашему занятию. Так как постоянно вы задаете вопросы: «А зачем она нам нужна?», «Может ли она чем-то помочь в реальной жизни?»…

Перед вами листочек с таблицей «Верите ли вы, что…»

«Верите ли вы, что…»

Да

Нет

Не знаю

в нач

в кон

в нач

в кон

в нач

в кон

С этой наукой вы сталкиваетесь каждый день?

Комбинаторика поможет стать востребованным в реальной жизни?

Достаточно купить три билета для «крупного» выигрыша в лото?

И в игре, и в жизни можно предугадать действия соперника?

Комбинаторика применима во всех сферах жизнедеятельности человека?

— Раз мы говорим о комбинаторике, сегодня мы повторим основные понятия, правила комбинаторики, и их применение при решении задач. Введем понятия перестановки, размещения и сочетания. Тема будет написана на доске.

3. Актуализация знаний.

1. Фронтальный опрос:

— Дайте определение комбинаторики. (На каждой парте лежат листочки с опорными конспектами, ребята внимательно читают определения, один зачитывает громко всей группе, каждый повторяет еще раз и проговаривают между собой). (Комбинаторика – это раздел математики, изучающий вопрос о том, сколько комбинаций определенного типа можно составить из данных элементов).

— Дайте определение факториала числа. (Факториал числа – это произведение натуральных чисел от 1 до самого числа (включая данное число) или n –факториалом называется произведение первых подряд идущих n натуральных чисел).

— Как обозначается факториал? (Обозначается факториал восклицательным знаком-!).

— Чему равен факториал 0 и 1? (Факториал 0 и 1 равен единице).

— Сформулировать правило произведения и суммы.

Правило суммы.  Если два действия А и В взаимно исключают друг друга, причем действие А можно выполнить m способами, а В – n способами, то выполнить одно любое из этих действий (либо А, либо В) можно

n + m способами.

Правило произведения.  Пусть требуется выполнить последовательно k действий. Если первое действие можно выполнить n₁ способами, второе действие n₂ способами, третье – n₃ способами и так до k-го действия, которое можно выполнить n_k  способами, то все k действий вместе могут быть выполнены:

2. Решение задач

1) Вычислите факториалы следующих чисел.

3! =6 5! = 120 6! = 720 7! = 5040 0!=1

2) Вычислите значения выражений.

а) 5!+6! = 120+720=840

б) .

3) Упростить выражение: а) ; б) .

4) Решить задачу: а) Из пункта A в B ведут три дороги, из B в C пять дорог, из С в D четыре дороги. Сколько вариантов проезда у водителя из пункта А в В? (Слайд 4)

Решение: .

б) Значение цветов флага России: (Слайд 5-11)

белый цвет — символизирует мир, чистоту, непорочность, совершенство;

синий цвет –символизирует веру, верность и постоянство;

красный цвет — символизирует энергию, силу, кровь, пролитую за Отечество.

Задача: Сколько можно получить различных флагов, состоящих из 3-х горизонтальных цветных полос: красной, белой и синей? (первый ряд методом перебора, второй ряд – методом дерева возможных вариантов, третий ряд – по правилу произведения).

— Как называются задачи такого типа? (Задачи такого типа называются комбинаторными задачами).

— Вы сейчас предложили несколько способов решения выше указанной задачи. Но есть еще способ решения данной задачи – это решение с использованием основных понятий комбинаторики (перестановки, размещения, сочетания). Давайте более подробно остановимся на каждом понятии.

IV. Изучение нового материала. Перестановки, размещения, сочетания. (слайд 12)

1. Перестановки. Перестановками из n элементов называются такие соединения из всех n элементов, которые отличаются друг от друга порядком расположения элементов. (слайд 13)

Число перестановок из n элементов обозначается символом Pn и вычисляется по формуле: Pn = n!

Вернемся к нашей задаче.

Задача 1. Сколько можно получить различных флагов, состоящих из 3-х горизонтальных цветных полос: красной, белой и синей? (слайд 14)

Pn = n! = 3! = 1*2*3=6 (способов)

Ответ: 6 способов.

Задача 2. (Слайд 15-17)

Проказница-Мартышка,

Осёл,

Козёл

Да косолапый Мишка

Затеяли сыграть Квартет.

Достали нот, баса, альта, две скрипки

И сели на лужок под липки —

Пленять своим искусством свет.

Сколькими способами герои могли пересесть?

Решение: Pn = n! = 4! = 1*2*3*4=24 (способа).

2. Размещения. Размещениями из n элементов по k в каждом называются такие соединения, которые отличаются друг от друга либо самими элементами (хотя бы одним), либо порядком их расположения. Количество размещений обозначается и вычисляется по формуле

. (Слайд 18)

Задача 3. Сколько различных двузначных чисел можно составить из множества цифр , причем так, чтобы цифры числа были различны? 
Решение: Искомое число чисел. (слайд 19)

3. Сочетания. Сочетаниями из n элементов по k в каждом называются такие соединения, которые отличаются друг от друга хотя бы одним элементом. Количество сочетаний обозначается  и вычисляется по формуле. (Слайд 20)

Задача 4. В ящике находится 15 деталей. Сколькими способами можно взять 4 детали? (Слайд 21)

Решение:

.

V. Закрепление знаний

1) Решение простейших комбинаторных задач

(Студенты работают у доски, решают простейшие комбинаторные задачи).

А) Сколькими способами можно рассадить 5 человек за столом?

Б) В студенческой группе 23 человека. Сколькими способами можно выбрать старосту и его заместителя?

 способами. 

В) Сколькими способами из колоды в 36 карт можно выбрать 3 карты?

2) Найти ошибки в решениях задач: Сейчас каждый из вас выступит в роли учителя. Студент решил задачу. Проверьте, верно, ли решена задача:

А) Сколькими способами из восьми человек можно избрать комиссию, состоящую из пяти членов?

С =

Ответ: 56. (верно)

Б) Сколько четырехбуквенных слов можно образовать из букв слова сапфир?

P₄=4! = 1*2*3*4 =24 (неверно)

(А).

VI. Подведение итогов (домашнее задание, рефлексия).

1) Решить задачу (дифференцированные задачи)

Задача на «3»

1. Сколько различных четырехзначных чисел можно составить из цифр 2, 3, 5, 7.

Задачи на «4»

2. Восемь студентов обменялись рукопожатиями. Сколько было рукопожатий?

3. Сколькими способами можно составить трехцветный полосатый флаг из пяти различных по цвету отрезков материи?

Задача на «5»

4. Сколько словарей надо издать, чтобы можно было выполнять переводы с любого из шести языков на любой из них?

2) Рабочая тетрадь: Стр. 52-55, С/р 4.1 «Элементы комбинаторики».

Рефлексия: В качестве домашнего задания было найти ответы на вопросы: области применения комбинаторики.

учебные заведения (составление расписаний)

сфера общественного питания (составление меню)

лингвистика (рассмотрение вариантов комбинаций букв)

спортивные соревнования (расчёт количества игр между участниками)

агротехника (размещение посевов на нескольких полях)

география (раскраска карт)

биология (расшифровка кода ДНК)

криптография (разработка методов шифрования)

Я предлагаю вернуться к нашей таблице «Верите ли вы, что…» и еще раз ответить на данные вопросы.

Перед вами листочек с таблицей «Верите ли вы, что…»

«Верите ли вы, что…»

Да

Нет

Не знаю

в нач

в кон

в нач

в кон

в нач

в кон

С этой наукой вы сталкиваетесь каждый день?

Комбинаторика поможет стать востребованным в реальной жизни?

Достаточно купить три билета для «крупного» выигрыша в лото?

И в игре, и в жизни можно предугадать действия соперника?

Комбинаторика применима во всех сферах жизнедеятельности человека?

— Так может ли комбинаторика помочь в реальной жизни? В чем?

VII. Самостоятельная работа.

Вариант 1.

1. Сколькими способами можно составить расписание одного учебного дня из 5 различных уроков?

1) 30 2) 100 3) 120 4) 5

2. На 1 курсе 12 учащихся, имеющих по математике оценки «4-5». Сколькими способами можно сформировать команду из 4 человек для участия в математической олимпиаде?

1) 128 2) 495 3) 36 4) 48

3. Сколько существует различных двузначных чисел, в записи которых можно использовать цифры 1, 2, 3, 4, 5, 6, если цифры в числе должны быть различными?

1) 10 2) 60 3) 20 4) 30

№ задания 1 2 3

№ ответа 3 2 4

Вариант 2.

1. Сколько различных пятизначных чисел можно составить из цифр 1, 2, 3, 4, 5?

1) 100 2) 30 3) 5 4) 120

2. Имеются помидоры, огурцы, лук. Сколько различных салатов можно приготовить, если в каждый салат должно входить 2 различных вида овощей?

1) 3 2) 6 3) 2 4) 1

3. Сколькими способами из 8 учебных предметов можно составить расписание учебного дня из 4 различных уроков.

1) 10000 2) 1680 3) 32 4) 1600

№ задания 1 2 3

№ ответа 4 1 2

Вариант 3.

1. Сколькими способами можно расставить 4 различные книги на книжной полке?

1) 24 2) 4 3) 16 4) 20

2. Сколько диагоналей имеет выпуклый семиугольник?

1) 30 2) 21 3) 14 4) 7

3. В футбольной команде 11 человек. Необходимо выбрать капитана и его заместителя. Сколькими способами это можно сделать?

1) 22 2) 11 3) 150 4) 110

№ задания 1 2 3

№ ответа 1 2 4

Вариант 4

1. Сколькими способами могут встать в очередь в билетную кассу 5 человек?

1) 5 2) 120 3) 25 4) 100

2. Сколькими способами из 15 учеников класса можно выбрать трёх для участия в праздничном концерте?

1) 455 2) 45 3) 475 4) 18

3. В теннисном турнире участвуют 10 спортсменов. Сколькими способами теннисисты могут завоевать золото, серебро и бронзу?

1) 600 2) 100 3) 300 4)720

№ задания 1 2 3

№ ответа 2 1 4

Вариант 5

1. Сколькими способами могут быть расставлены 5 участниц финального забега на 5-ти беговых дорожках?

1. 10 2) 20 3) 120 4) 50

2. Сколькими способами из 7 человек можно выбрать комиссию, состоящую из 3 человек?

1. 35 2) 30 3) 70 4) 45

3. На соревнованиях по лёгкой атлетике наш техникум представляла команда из 10 спортсменов. Сколькими способами тренер может определить, кто из них побежит в эстафете на первом, втором, третьем и четвёртом этапах?

1. 120 2) 1560 3) 4800 4) 5040

№ задания 1 2 3

№ ответа 3 1 4

Спасибо за урок! До свидания.

Список литературы

1. Башмаков М.И. Математика. Задачник: учебное пособие для студентов учреждений сред. проф. Образования/М.И. Башмаков. — 5-е изд., стер. -М.: Издательский центр «Академия», 2014.

2. Башмаков М.И. Математика: алгебра и начала математического анализа, геометрия: учебное пособие для студентов учреждений сред. проф. Образования/М.И. Башмаков -М.: Издательский центр «Академия», 2016.

3. Мордкович А.Г. Математика: алгебра и начала математического анализа, геометрия. 10-11 классы. В 2ч./А.Г. Мордкович, П.В. Семенов. — М.: Мнемозина, 2015г.

4. Богомолов Н.В. Практические занятия по высшей математике. – М.: Высшая школа, 1999.

5. Валуцэ И.И. и др. Математика для техникумов на базе средней школы: учеб. пособ. – М.: Наука, 1990.

6. Гмурман В.Е. Теория вероятностей и математическая статистика. Москва «Высшая школа» 1998.

7. Дадаян А.А. Математика: учеб. – М.: ФОРУМ: ИНФРА-М, 2005

8. Данко П.Е. Высшая математика в упражнениях и задачах: В 2т. учеб. пособ. – М.: Высш. шк., 1998

9. Зайцев И.Л. Элементы высшей математики для техникумов. – М., 1972

10. Математика для техникумов. Алгебра и начала анализа: В 2-х частях. учеб. /Каченовский М.И. и др. под ред. Г.Н. Яковлева. – М.: Наука, 1987

infourok.ru

Задачи по теме «Комбинаторика»

Задачи для решения на закрепление нового материала

Задача № 1. Сколькими способами могут быть расставлены 5 участниц финального

забега на 5-ти беговых дорожках?

Решение: Р₅ = 5!= 1 ∙2 ∙3 ∙4 ∙5 = 120 способов.

Задача №2. Сколько трехзначных чисел можно составить из цифр 1,2,3, если каждая

цифра входит в изображение числа только один раз?

Решение: Число всех перестановок из трех элементов равно Р₃=3!, где 3!=1 * 2 * 3=6

Значит, существует шесть трехзначных чисел, составленных из цифр 1,2,3.

Задача № 3. Сколькими способами четверо юношей могут пригласить четырех из шести

девушек на танец?

Решение: два юноши не могут одновременно пригласить одну и ту же девушку. И

варианты, при которых одни и те же девушки танцуют с разными юношами,

считаются разными, поэтому:

Задача № 4. Сколько различных трехзначных чисел можно составить из цифр 1, 2, 3, 4, 5,

6, 7, 8, 9 при условии, что в записи числа каждая цифра используется только

один раз?

Решение: В условии задачи предложено подсчитать число всевозможных комбинаций из

трех цифр, взятых из предположенных девяти цифр, причём порядок

расположения цифр в комбинации имеет значение (например, числа 132)

и 231 различные). Иначе говоря, нужно найти число размещений из девяти

элементов по три.

По формуле числа размещений находим:

Ответ: 504 трехзначных чисел.

Задача №5 Сколькими способами из 7 человек можно выбрать комиссию, состоящую из 3

человек?

Решение: Чтобы рассмотреть все возможные комиссии, нужно рассмотреть все

возможные 3 – элементные подмножества множества, состоящего из 7

человек. Искомое число способов равно

Задача № 6. В соревновании участвуют 12 команд. Сколько существует вариантов

распределения призовых (1, 2, 3) мест?

Решение: А₁₂³ = 12 ∙11 ∙10 = 1320 вариантов распределения призовых мест. Ответ: 1320 вариантов.

Задача № 7. На соревнованиях по лёгкой атлетике нашу школу представляла команда из

10 спортсменов. Сколькими способами тренер может определить, кто из них

побежит в эстафете 4100 м на первом, втором, третьем и четвёртом этапах?

Решение: Выбор из 10 по 4 с учётом порядка: 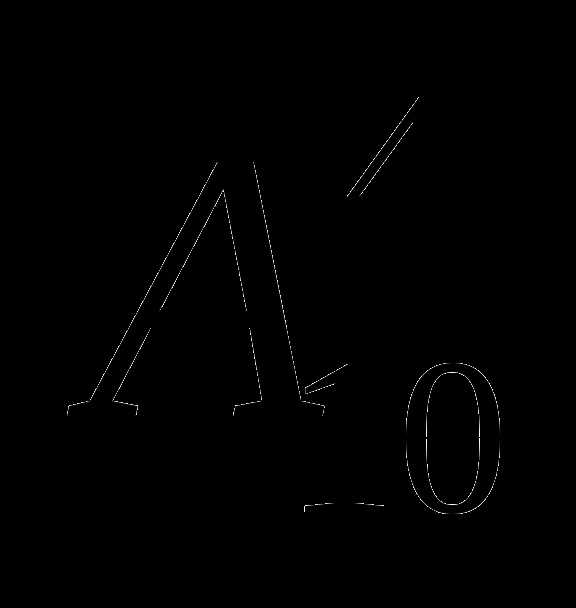способов.

Ответ: 5040 способов.

Задача № 8. Сколькими способами можно выложить в ряд красный, черный, синий и

зеленый шарики?

Решение: На первое место можно поставить любой из четырех шариков (4 способа), на

второе – любой из трех оставшихся (3 способа), на третье место – любой из

оставшихся двух (2 способа), на четвертое место – оставшийся последний шар.

Всего 4 · 3 · 2 · 1 = 24 способа.

Р₄ = 4! = 1 · 2 · 3 · 4 = 24. Ответ: 24 способа.

Задача № 9. Учащимся дали список из 10 книг, которые рекомендуется прочитать во

время каникул. Сколькими способами ученик может выбрать из них 6 книг?

Решение: Выбор 6 из 10 без учёта порядка: способов.

Ответ: 210 способов.

Задача № 10. В 9 классе учатся 7 учащихся, в 10 — 9 учащихся, а в 11 — 8 учащихся. Для

работы на пришкольном участке надо выделить двух учащихся из 9 класса,

трех – из 10, и одного – из 11 . Сколько существует способов выбора

учащихся для работы на пришкольном участке?

Решение: Выбор из трёх совокупностей без учёта порядка, каждый вариант выбора из

первой совокупности (С₇²) может сочетаться с каждым вариантом выбора из

второй (С₉³) ) и с каждым вариантом выбора третьей (С₈¹) по правилу

умножения получаем:

Ответ: 14 112 способов.

Задача № 11. Девятиклассники Женя, Сережа, Коля, Наташа и Оля побежали на

перемене к теннисному столу, за которым уже шла игра. Сколькими

способами подбежавшие к столу пятеро девятиклассников могут занять

очередь для игры в настольный теннис?

Решение: Первым в очередь мог встать любой девятиклассник, вторым – любой из

оставшихся троих, третьим – любой из оставшихся двоих и четвёртым –

девятиклассник, подбежавший предпоследним, а пятым – последний. По

правилу умножения у пяти учащихся существует 5· 4321=120 способов

занять очередь.

infourok.ru

Задачи на размещения без повторений

Задача в общем виде: Дано конечное множество. Необходимо найти число способов упорядочивания каждого к-элементного подмножества.

1. Борис Николаевич решил подарить жене, дочери и брату по новому автомобилю. В автосалоне есть 12 марок, удовлетворяющих всем требованиям. Сколькими способами он может сделать подарки?

2. В Небыляндию ведут 7 дорог. Сколькими способами можно туда сходить и вернуться, не проходя дважды по одной дороге?

3. Сколькими способами можно составить трехцветный полосатый флаг, если имеются ткани пяти различных цветов? Решите эту задачу при условии, что одна полоса должна быть красной.

4. В цехе работают 8 токарей. Сколькими способами можно поручить трем из них изготовление различных видов деталей (по одному виду на каждого)?

5. Сколькими способами можно опустить 5 писем в 11 почтовых ящиков, если в каждый из них опускают не более одного письма?

6. Сколько трехзначных чисел можно составить из цифр 0, 1, 2, 3, 4, 5 (без повторений)?

7. Сколько четных трехзначных чисел можно составить из цифр 1, 2, 3, 4, 5, 6, 7 (без повторений)?

8. У мамы 2 яблока, 3 груши и 4 апельсина. Каждый день в течение пяти дней подряд она выдает по 1 фрукту. Сколькими способами это может быть сделано?

9. Учащиеся седьмых классов решили высадить около школы три аллеи. На ярмарке были саженцы березы, липы, дуба, клена, рябины, ели, акации, тополя и каштана. Сколькими способами ребята могут закупить саженцы, если они решили в одну аллею высаживать только одинаковые деревья? На сколько увеличится количество способов, если на другой день, когда пришли ребята, на ярмарке появились ещё и саженцы осины?

10. Сколько трехзначных чисел можно составить из цифр числа 564731, если каждую использовать не более одного раза?

Задачи на размещения с повторениями

Задача в общем виде: Дано конечное множество М. Необходимо найти число способов упорядочивания к-элементных «подмножеств», каждое из которых может содержать одинаковые элементы.

1. Монету бросают трижды. Сколько разных последовательностей орлов и решек можно при этом получить?

2. Каждую клетку квадратной таблицы 4 × 4 можно покрасить в черный или белый цвет. Сколько существует различных раскрасок этой таблицы?

3. Сколько существует 6-значных чисел, в записи которых есть хотя бы одна четная цифра?

4. Пусть на диск сейфа нанесено 12 букв, а секретное слово состоит из 5 букв. Сколько неудачных попыток может быть сделано человеком, не знающим секретного слова?

5. Сколькими способами можно надеть 5 различных колец на пальцы одной руки, исключая большой палец?

6. Сколько существует пятизначных номеров, не содержащих цифр 0 и 8?

7. Имеется набор 16 карточек. На четырех из них написана буква «А», на четырех – буква «Б», на четырех – буква «В», и на четырех – буква «Г». Сколько различных комбинаций можно получить, выбирая из набора 4 карточки и располагая их в некотором порядке?

8. На железнодорожной станции 5 светофоров. Сколько может быть дано различных сигналов, если каждый светофор имеет 3 состояния: красный, желтый, зеленый?

9. Сколько четных четырехзначных чисел можно составить из цифр числа 123153?

10. Сколько существует способов расстановки 20 разных книг по 5 полкам?

studfiles.net

12. РАЗМЕЩЕНИЯ С ПОВТОРЕНИЯМИ | Решение задач по математике и другим пр

Пусть выбор k элементов из некоторого множества, состоящего из n элементов, производится с возвращением и с упорядочением их в последовательную цепочку. Различными исходами такого выбора будут всевозможные наборы (вообще говоря, с повторениями) отличающиеся либо составом элементов, либо порядком их следования. Получаемые в результате комбинации называются размещениями с повторениями из n элементов по k элементов.

Поясним это на следующем примере. Пусть имеется три элемента: a, b и c. Тогда из этих трёх элементов можно составить девять размещений с повторениями по два элемента: ab, ac, ba, bc, ca, cb, aa, bb, cc.

Таким образом, размещение с повторениями из n элементов по k элементов (при этом допускается, что m>n) может содержать любой элемент сколько угодно раз от 1 до k включительно или не содержать его совсем, т. е. каждое размещение с повторениями из n элементов по k элементов может состоять не только из различных элементов, но и k каких угодно и как угодно повторяющихся элементов.

Число размещений с повторениями можно найти из принципа умножения. Первый элемент размещения можно выбрать n способами. Второй элемент также можно выбрать n способами (ведь элементы могут повторяться) и т. д. По принципу умножения находим

. (10.1)

Пример 10.1. В лифт восьмиэтажного дома вошли 5 пассажиров. Сколькими способами могут выйти пассажиры на каждом этаже, начиная со второго?

Решение. Задача сводится к распределению 5 пассажиров по 7 этажам (т. е. набор упорядоченный), причем возможны повторения (т. е. несколько пассажиров могут выйти на одном этаже). Таким образом, задача сводится к нахождению числа размещений с повторениями:

Пример 10.2. Сколькими способами можно 5 шариков разбросать по 8 лункам, если каждая лунка может вместить все 5 шариков?

Решение. Данная задача есть задача на отыскание числа размещений с повторениями

.

Пример 10.3. Буквы азбуки Морзе состоят из символов – точка и тире. Сколько букв получим, если потребуем, чтобы каждая буква состояла не более чем из пяти указанных символов?

Решение. Число всех букв, каждая из которых записывается одним символом, равно .

Число всех букв, каждая из которых записывается двумя символами, равно .

Число всех букв, каждая из которых записывается тремя символами, равно .

Число всех букв, каждая из которых записывается четырьмя символами, равно .

Число всех букв, каждая из которых записывается пятью символами, равно .

Число всех указанных букв будет равно 62.

Упражнения

10.1. Сколькими способами девочка Яна может разложить 12 кукол по трём ящикам, если каждый ящик может вместить все куклы?

Ответ: .

10.2. Сколькими способами Пончик может рассовать 6 конфет по 9 карманам, если каждый карман может вместить все конфеты?

Ответ: .

10.3. Сколькими способами можно разместить 8 пассажиров по трем вагонам?

Ответ: .

10.4. Сколькими различных восьмизначных чисел можно написать, пользуясь только тремя цифрами 3, 5, 7 при условии, что цифра 5 в каждом числе встречается ровно два раза?

Ответ: .

10.5. Из цифр 1, 2, 3, 4, 5 составлены всевозможные пятизначные числа (повторение цифр разрешается). Сколько среди них чисел, у которых: 1) a=1; 2) a¹2; 3) a=3, b=2; 4) a=3, b=4, c=5?

Ответ: .

10.6. Сколько чисел, меньших миллиона, можно написать с помощью цифр: а) 8 и 9; б) 7, 8, 9; в) 0, 8, 9 (с цифры 0 число начинаться не может)?

Ответ: а) Так как с помощью двух цифр 8 и 9 можно написать 2k k-значных числа, то общее количество искомых чисел равно . б) Для трёх цифр аналогично получаем . в) Учтём, что для первой цифры есть только две возможности выбора. Тогда получим чисел.

10.7. Имеется три курицы, четыре утки и два гуся. Сколькими способами можно выбрать из них несколько птиц так, чтобы среди выбранных оказались и куры, и утки, и гуси?

Ответ: Каждая курица может либо войти, либо не войти в число выбранных. Поэтому имеем 23 способов выбора кур. Так как по условию хотя бы одна курица должна быть выбрана (т. е. не может быть случая, когда ни одной курицы не будет выбрано), то число выбора кур будет на единицу меньше: способов выбора кур. Точно так же есть способов выбора уток и способов выбора гусей. Всего способов.

< Предыдущая		Следующая >

matica.org.ua

Задачи на сочетание размещение и перестановки с решением

Ответы и объяснения. Алинабяка ? kolobok19702009; ученый. Пусть х — 1 катет, тогда х+3 — 2 катет,зная, что площадь равна 77 составим уравнение 0,5х*(х+3)=77 0,5х^2+1.5x-77=0 решаем квадратное уравнение и получим х=-14 х=11 1 катет =11 2 катет 11+3=14. Комментарии; Отметить нарушение. 4.0.

Задачи по комбинаторике. Примеры решений

На данном уроке мы коснёмся элементов Комбинаторики, которые потребуются для дальнейшего изучения Теории вероятностей. Следует отметить, что комбинаторика является самостоятельным разделом высшей математики (а не частью тервера) и по данной дисциплине написаны увесистые учебники, содержание которых, порой, ничуть не легче абстрактной алгебры. Однако нам будет достаточно небольшой доли теоретических знаний, и в данной статье я постараюсь в доступной форме разобрать основы темы с типовыми комбинаторными задачами. А многие из вас мне помогут 😉

Чем будем заниматься? В узком смысле комбинаторика – это подсчёт различных комбинаций, которые можно составить из некоторого множества дискретных объектов. Под объектами понимаются какие-либо обособленные предметы или живые существа – люди, звери, грибы, растения, насекомые и т. д. При этом комбинаторику совершенно не волнует, что множество состоит из тарелки манной каши, паяльника и болотной лягушки. Принципиально важно, что эти объекты поддаются перечислению – их три (дискретность) и существенно то, что среди них нет одинаковых.

С множеством разобрались, теперь о комбинациях. Самыми распространёнными видами комбинаций являются перестановки объектов, их выборка из множества (сочетание) и распределение (размещение). Давайте прямо сейчас посмотрим, как это происходит:

Перестановки, сочетания и размещения без повторений

Не пугайтесь малопонятных терминов, тем более, некоторые из них действительно не очень удачны. Начнём с хвоста заголовка – что значит «Без повторений»? Это значит, что в данном параграфе будут рассматриваться множества, которые состоят из Различных объектов. Например, … нет, кашу с паяльником и лягушкой предлагать не буду, лучше что-нибудь повкуснее =) Представьте, что перед вами на столе материализовалось яблоко, груша и банан (при наличии таковых ситуацию можно смоделировать и реально). Выкладываем фрукты слева направо в следующем порядке:

Яблоко / груша / банан

Вопрос первый: сколькими способами их можно переставить?

Одна комбинация уже записана выше и с остальными проблем не возникает:

Яблоко / банан / груша

Груша / яблоко / банан

Груша / банан / яблоко

Банан / яблоко / груша

Банан / груша / яблоко

Хорошо, здесь не составило особого труда перечислить все возможные случаи, но как быть, если предметов больше? Уже с четырьмя различными фруктами количество комбинаций значительно возрастёт!

Пожалуйста, откройте справочный материал Основные формулы комбинаторики (методичку удобно распечатать) и в пункте №2 найдите формулу количества перестановок.

Никаких мучений – 3 объекта можно переставить способами.

Вопрос второй: сколькими способами можно выбрать а) один фрукт, б) два фрукта, в) три фрукта, г) хотя бы один фрукт?

Зачем выбирать? Так нагуляли же аппетит в предыдущем пункте – для того, чтобы съесть! =)

А) Один фрукт можно выбрать, очевидно, тремя способами – взять либо яблоко, либо грушу, либо банан. Формальный подсчёт проводится по Формуле количества сочетаний:

Запись в данном случае следует понимать так: «сколькими способами можно выбрать 1 фрукт из трёх?»

Б) Перечислим все возможные сочетания двух фруктов:

Количество комбинаций легко проверить по той же формуле:

Запись понимается аналогично: «сколькими способами можно выбрать 2 фрукта из трёх?».

В) И, наконец, три фрукта можно выбрать единственным способом:

Кстати, формула количества сочетаний сохраняет смысл и для пустой выборки:

способом можно выбрать ни одного фрукта – собственно, ничего не взять и всё.

Г) Сколькими способами можно взять Хотя бы один фрукт? Условие «хотя бы один» подразумевает, что нас устраивает 1 фрукт (любой) или 2 любых фрукта или все 3 фрукта:

способами можно выбрать хотя бы один фрукт.

Читатели, внимательно изучившие вводный урок по Теории вероятностей, уже кое о чём догадались. Но о смысле знака «плюс» позже.

Для ответа на следующий вопрос мне требуется два добровольца… …Ну что же, раз никто не хочет, тогда буду вызывать к доске =)

Вопрос третий: сколькими способами можно раздать по одному фрукту Даше и Наташе?

Для того чтобы раздать два фрукта, сначала нужно их выбрать. Согласно пункту «бэ» предыдущего вопроса, сделать это можно способами, перепишу их заново:

Но комбинаций сейчас будет в два раза больше. Рассмотрим

poiskvstavropole.ru

Задачи на подсчет числа размещений, перестановок, сочетаний.

Занятие

Тема: Задачи на подсчет числа размещений, перестановок, сочетаний.

Количество часов: 2 часа

Цель: повторить формулы для нахождения числа различных видов комбинаций: размещений, перестановок, сочетаний; научиться распознавать задачи на нахождение размещений, перестановок, сочетаний; решить простейшие комбинаторные задачи с помощью этих формул.

План:

1. Задача.

2. Выводы из решения задачи.

3. Решение задач с использованием данных формул.

Вопрос 1. Задача.

Задача.

“У вас есть 9 разных книг из серии “Занимательная математика”. Сколькими способами можно:

1) расставить их на полке;

2) подарить три из них победителям школьной олимпиады, занявшим первые три призовых места;

3) выбрать три из них для подарка своему племяннику”

Для ответа на первый вопрос задачи вспомним:

Вопросы преподавателя

Ответы обучающихся

1. Как называются различные комбинации выстраивания нескольких предметов друг за другом?

– Перестановками

2. Что называется перестановками из n элементов?

– Перестановками из n элементов называются комбинации из n элементов, отличающиеся друг от друга только порядком следования элементов

3. Чем отличаются друг от друга две различные перестановки?

– Порядком следования элементов

4. По какой формуле можно вычислить число всевозможных перестановок из n элементов?

–

5. Рассчитаем число всевозможных перестановок из 9 книг на полке

Для ответа на второй вопрос задачи вспомним:

Вопросы преподавателя

Ответы обучающихся

1. Как можно выбрать три книги из девяти для трех победителей?

– Произвольно, наборы из трех книг могут отличаться либо книгами, либо порядком их дарения

2. Как можно назвать наборы из 9 книг по 3 в каждом?

– Размещениями из 9 книг по 3

3. Что называется размещениями из n элементов по k элементов?

– Размещениями из n элементов по k элементов – называются комбинации из n элементов по k каждой, отличающиеся друг от друга либо составом, либо порядком расположения элементов

4. Чем отличаются друг от друга две различные комбинации-размещения?

– Порядком следования элементов

– Составом элементов

5. По какой формуле можно вычислить число всевозможных размещений из n элементов по k элементов?

–

6. Рассчитаем число всевозможных размещений из 9 книг по 3 для победителей

Для ответа на третий вопрос задачи подумаем:

Вопросы преподавателя

Ответы обучающихся

1. Важно ли для племянника в каком порядке располагаются книги в его подарочном наборе?

– Нет

2. Как можно назвать комбинации из 9 книг по 3 в каждой?

-Сочетаниями из 9 книг по 3

3. Что называется сочетаниями из n элементов по k элементов?

– Сочетаниями из n элементов по k элементов – называются комбинации из n элементов по k каждой, отличающиеся друг от друга составом

4. Чем отличаются друг от друга две различные комбинации-сочетания?

– Составом элементов

5. По какой формуле можно вычислить число всевозможных сочетаний из n элементов по k элементов?

–

6. Рассчитаем число всевозможных сочетаний из 9 книг на полке 3 для победителей

Вопрос 2. Выводы из решения задачи.

Вопросы преподавателя

Ответы обучающихся

1. В науке и практике часто встречаются задачи, решая которые приходится составлять различные комбинации из конечного числа элементов и подсчитывать число комбинаций. Такие задачи называются комбинаторными. Для нахождения комбинаций – размещений, перестановок и сочетаний и их числа существуют специальные способы. Назовите признаки, по которым можно отличить друг от друга эти комбинации?

– Порядок следования элементов

– Состав элементов

2. Зафиксируем наличие перечисленных признаков в обобщающую таблицу:

Признаки

Порядок следования элементов

+

–

+

Состав элементов

–

+

+

Среди перечисленных ниже задач выделить те, в которых требуется найти

а)размещения;
б)перестановки;
в) сочетания.

Номера выбранных задач и способ нахождения числа комбинаций записать в таблицу:

Вопросы

Формула

 

 

 

№ задач

 

 

 

Задачи:

1. Сколько разных двузначных чисел можно составить из цифр 1, 2, 3, 4, 5, 6, 7, 8, если цифры в записи числа используются только один раз?

2. Сколько существует четырёхзначных чисел, в записи которых участвуют лишь цифры 1, 2, 3, 4, 5, причём цифры в записи числа не повторяются?

3. Сколькими способами можно составить четырёхцветный флаг из горизонтальных полос одинаковой ширины, имея четыре различных цвета?

4. Сколькими способами можно выбрать шесть делегатов на конференцию из 150 человек?

5. В полуфинале по шахматам участвуют 20 шахматистов, а в финал попадут только трое. Сколькими способами может образоваться финальная тройка?

6. Сколькими способами можно разместить на полке 5 книг?

7. Сколькими способами можно обозначить вершины треугольника, используя буквы A, B, C, D, E ?

8. На тренировке 12 баскетболистов. Сколько разных пятёрок может составить тренер?

9. Сколько разных шестерок может составить тренер из 10 волейболистов?

10. Сколькими способами можно расставить на шахматной доске 8 ладей так, чтобы они не “били” друг друга?

11. Сколькими способами можно премировать одинаковыми призами троих человек из семи участников?

12. Сколькими способами можно составить флаг из четырёх горизонтальных полос различных цветов, если имеется материал различных цветов?

13. В отряде 12 человек. Надо выбрать старосту и двух заместителей. Сколькими способами это можно сделать?

14. Сколькими способами можно разместить шесть человек за столом, на котором поставлено шесть приборов?

15. Сколько аккордов, содержащих три звука, можно взять на 12 клавишах одной октавы?

16. Курьер должен разнести пакеты в семь различных учреждений. Сколько маршрутов он может выбрать?

17. Сколько шестизначных чисел (без повторения цифр) можно составить из цифр: а) 1, 2, 5, 6, 7, 8? б) 0, 2, 5, 6, 7, 8?

18. Сколькими способами может разместиться семья из трех человек в четырехместном купе, если других пассажиров в купе нет?

Вопрос 3. Решить предложенные выше задачи, используя соответствующие формулы.

Вопросы для самопроверки:

1. Назовите формулу для вычисления числа перестановок.

2. Назовите формулу для вычисления числа размещений.

3. Назовите формулу для вычисления числа сочетаний.

Список литературы и ссылки на Интернет-ресурсы, содержащие информацию по теме:

1. Никольский С.М., Потапов М.К., Решетников Н.Н., Шевкин А.В. Алгебра и начала математического анализа. 10 класс: учеб. для общеобразоват. организаций: базовый и углубл. уровни – М.: Просвещение, 2014. – 431 с.: ил.

2. Пратусевич М.Я., Столбов К.М., Головин А.Н. Алгебра и начала математического анализа. 10 класс: учеб. для общеобразоват. организаций: углубл. уровень – М.: Просвещение, 2014. – 415 с.: ил.

3. Yaklass.ru (Источник).

4. Bymath.net (Источник).

infourok.ru