Задачи на составление уравнения 7 класс – Конспект урока алгебры в 7 классе «Уравнения. Решение задач на составление уравнений»

Содержание

Конспект урока алгебры в 7 классе «Уравнения. Решение задач на составление уравнений»

Тема: Уравнения. Решение задач на составление уравнений

1) Организационный этап.

Приветствие, проверка присутствующих.

Давайте улыбнёмся друг другу и с хорошим настроением начнём наш урок.

2) Постановка цели и задач урока. Мотивация учебной деятельности учащихся.

Математику не зря называют «царицей наук», ей больше, чем какой-либо другой науке, свойственны красота, изящность и точность. Одно из замечательных качеств математики — любознательность. Постараемся доказать это на уроке. Скажите, какую тему мы изучали на прошлом уроке? (Уравнения. Решения задач с помощью уравнений). Посмотрите на экран, решали ли мы такие уравнения? (Ответы учащихся: да, решали). А такие? А хотели бы проявить любознательность и решить похожее уравнение? Как вы думаете, какая цель нашего урока? (Предполагаемые цели ученика: научиться решать уравнения более сложные, чем те, способы решения которых ему известны.)

Мы изучили очень важную главу в курсе алгебры «УРАВНЕНИЯ». Вы знаете и умеете решать уравнения, приводимые к линейным, составлять различные уравнения по условию задачи. Знания не только надо иметь, но и надо уметь их показать, что вы и сделаете на сегодняшнем уроке, а я вам в этом помогу.

Итак, цель нашего урока: Повторение и закрепление полученных знаний по теме «Уравнения. Решение задач на составление уравнений», применение полученных знаний к решению уравнений и задач различного уровня сложности.

Откройте тетради, запишите число, тему. Сегодня на уроке мы продолжим работу по теме «Уравнения. Решение задач на составление уравнений».

3) Проверка домашнего задания, воспроизведение и коррекция опорных знаний учащихся. Актуализация знаний.

Начнём урок с проверки домашнего задания, потому что, чтобы узнать что-то новое, необходимо повторить уже изученный материал. У кого возникли трудности при решении домашнего задания? Все справились? Нет таких. А мне интересно, как вы справились с №157.

№157. Старинная задача. Послан человек из Москвы в Вологду и велено ему проходить во всякий день по 40 вёрст. На следующий день вслед ему был послан другой человек и велено ему проходит по 45 вёрст в день. Через сколько дней второй догонит первого?

Решение. Пусть второй человек догонит первого через х дней, тогда за эти дни он пройдет 45х верст. Первый человек, так как он шел на день дольше, пройдет 40(х + 1) верст. Зная, что они пройдут одинаковое расстояние, составим и решим уравнение:

х = 8.

Значит, второй человек догонит первого через 8 дней.

+ если ваши решения совпадают с решениями на доске

— если есть ошибки и вы не понимаете, почему не так

№150, №151, №153, №163.

4) Первичное закрепление в знакомой ситуации (типовые) в изменённой ситуации (конструктивные)

1. Корнем уравнения называется…

2. Решить уравнение — …

3. Равносильные уравнения — …

4. Линейное уравнение с одной переменной — …

Задание 1. Запишите в виде выражения:

г) произведение суммы чисел a и b и числа с.

Задание 2. Установить соответствие между уравнением и его решением.

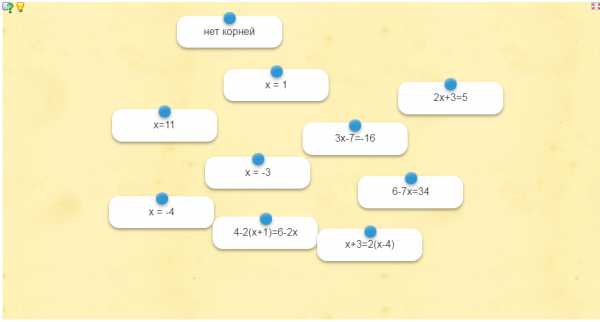
Ребята, у нас началась творческая работа. Был объявлен конкурс на составление уравнения. По итогам конкурса я предоставлю слово Мелешко Дарье, так как, на мой взгляд, её уравнение более сложное из всех представленных. Все остальные уравнения я также оценила, и мы будем рассматривать их на следующих уроках в качестве повторения темы.

(На слайде представлено уравнение, которое я составила самостоятельно. Так как в 5 классе мы решали уравнения с натуральными числами, дробями, в 6м – с использованием свойств сложения и вычитания, а также уравнения с пропорцией, у меня возникла идея, что получится, если соединить все те уравнения, которые мы решали в прошлых классах. И вот что у меня получилось:

Я предлагаю приступить к решению, в качестве подсказки на слайде выделено место для фиксирования промежуточного результата.)

Задание 3. Решить уравнение:

Ответ:

(57х — 6)/3 = 39 (х + 2)

Уравнение для Даши:

Ответ: 733/2000

Прежде чем приступить к решению задачи, давайте повторим этапы решения.

Задание 4. Расставить этапы решения задачи с помощью уравнения по порядку.

Задание 5. Задача. Из двух городов, расстояние между которыми равно 270 км, выехали одновременно навстречу друг другу автомобиль и автобус. Через 2 ч после начала движения расстояние между ними составляло 30 км. Найдите скорость автомобиля и автобуса, если скорость автомобиля на 10 км/ч больше скорости автобуса.

Решение с помощью презентации, уравнение решают самостоятельно.

(2х + 10) · 2 = 270 – 30,

(2х + 10) · 2 = 240,

2х + 10 = 120,

2х = 110,

х = 55.

Значит, скорость автобуса 55 км/ч, а скорость автомобиля – 65 км/ч.

Ответ: 55 км/ч, 65 км/ч.

Физкультминутка

Цель: снять утомление, обеспечить активный отдых и повысить умственную работоспособность учащихся.

Упражнения:

1) «Черепаха»: наклоны головы вперед -назад.

2) «Маятник»: наклоны головы вправо-влево.

3) «Собачка»: вращение головы вокруг воображаемой оси, проходящей через нос и затылок.

4) «Сова»: поворот головы вправо-влево.

5) «Весы»: левое плечо вверх, правое вниз. Поменять положение рук.

6) «Тянемся — потянемся»: руки вверх, вытягиваем позвоночник.

А теперь займемся решением задач

5) Творческое применение и добывание знаний в новой ситуации (проблемные задания)

Задача, составленная Соловьевой Юлией.

(Изучив все предложенные задачи в учебнике, я составила следующую задачу:

В магазин фруктов привезли ящики с бананами, апельсинами, грушами и персиками. Ящиков с грушами было на 20 штук меньше, чем ящиков с апельсинами и в 4 раза меньше, чем ящиков с персиками. Ящиков с бананами привезли в 3 раза больше, чем ящиков с апельсинами и грушами вместе. Найти, сколько всего ящиков привезли, если ящиков с бананами и грушами было на 50 штук больше, чем ящиков с персиками и апельсинами.

В качестве подсказки, я представляю схему условия, которую необходимо дополнить.)

Задача 6. В магазин фруктов привезли ящики с бананами, апельсинами, грушами и персиками. Ящиков с грушами было на 20 штук меньше, чем ящиков с апельсинами и в 4 раза меньше, чем ящиков с персиками. Ящиков с бананами привезли в 3 раза больше, чем ящиков с апельсинами и грушами вместе. Найти, сколько всего ящиков привезли, если ящиков с бананами и грушами было на 50 штук больше, чем ящиков с персиками и апельсинами.

Ответ: 140 ящиков

Уравнение (3(2х + 20) + х) – 50 = 4х + х + 20

Х = 5.

Груши – 5 шт., апельсины – 25 шт., персики – 20 шт., бананы – 90 шт.

Задача для Юли: Петя, Саша и Маша решали задачу. Петя решил её быстрее всех. Саша решил задачу только через 10 минут после того, как её решил Петя, а Маша решила задачу через 20 минут после того, как её решил Саша. Сколько минут решала задачу Маша, если эту задачу ребята решили ща 49 минут?

Уравнение: х + х + 10 + х + 10 + 20 = 49.

Ответ: Петя за 3 минуты, Саша за 13 минут, Маша за 33 минуты.

Самостоятельная работа

Ответы зафиксировать с помощью системы Mimio Vote.

1. Укажите уравнение, корнем которого является число 3.

А) (х — 3)(х + 3) = 2

Б) (х + 3)² = 0

В) (х + 2)(х — 1) = 10

Г) |х| = -3

2. Какое из следующих уравнений имеет корни?

А) х + 2 = х + 3

Б) |x + 2| = -2

В) х² = 0

Г) х² = -4

3. Составьте по условию задачи уравнение, обозначив буквой х количество конфет, которые съела Алена.

Три подружки съели 23 конфеты. При этом Тамара съела в 3 раза больше конфет, чем Алена, но на 2 конфеты меньше, чем Наташа. Сколько конфет съела Алена?

А) 3х + 2 =23

Б) 7х + 2 = 23

В) 3х – 2 = 23

Г) 7х – 2 = 23

4. Укажите уравнение, которое не является линейным уравнением с одной переменной.

А) х(х — 5) = 0

Б) 2х + 3 (х — 4) = 5

В) 0,3 (х — 4) = 0,5 (х + 1)

В) x – 1 = 2 (x — 4)

5. Решите уравнение 0,3х – 0,45 = 0.

А) -15

Б) 15

В) 1,5

Г) -1,5

6. Укажите, при каком значении а уравнение ax – 5 = 0 имеет один корень.

А) а ≠ 0

Б) а = 0

В) а = 5

Г) нет таких значений а

7. Укажите, при каком условии уравнение a·x = 0 имеет бесконечно много корней.

А) а ≠ 0

Б) а = 0

В) а = 5

Г) нет условий

8. Выясните, какие из следующих уравнений равносильны:

1) х² = 25; 2) х – 5 = 0; 3) (х — 5)(х + 5) = 0.

А) 2 и 3

Б) 1 и 2

В) 1, 2 и 3

Г) 1 и 3

9. Решите уравнение Укажите два целых числа, между которыми находится его корень.

А) 0; 1

Б) 3; 4

В) -4; -3

Г) -1; 0

10. Составьте уравнение к задаче, обозначив буквой х собственную скорость теплохода.

Расстояние от одной пристани на реке до другой теплоход проходит за 6 часов, а обратно за 5 часов. Найдите собственную скорость теплохода, если скорость течения реки равна 2 км/ч.

А) 6х = 5(х + 2)

Б) 6(х + 2) = 5(х — 2)

В) 6(х — 2) = 5х

Г) 6(х — 2) = 5(х + 2)

6) Информация о домашнем задании, инструктаж по его выполнению

I уровень — №246, №248, №252.

II уровень — №1188, №1189.

7) Рефлексия (подведение итогов занятия)

Наше занятие подходит к концу. Пожалуйста, поделитесь с нами своими мыслями о сегодняшнем занятии (хотите одним предложением).

Вам для этого помогут слова:

1. Было интересно …

2. Было трудно …

3. Я выполнял задания …

4. Я понял, что …

5. Теперь я могу …

6. Я научился …

7. У меня получилось …

9. Я смог …

10. Меня удивило …

11. Мне захотелось …

12. Я попробую…

Резервные задания:

1. Верно ли решено уравнение

2. Правильно или неправильно составлено уравнение по условию задачи?

Обозначение неизвестного

Уравнение

Верно/

неверно

Расстояние от А до В автомобиль проехал за 2 часа, а грузовик за 2,5 часа. Чему равно расстояние от А до В, если известно, что скорость автомобиля была на 20 км/ч больше скорости грузовика?

х (км/ч) – скорость грузовика

2,5х = 2(х + 20)

Сумма трёх чисел равна 92. Второе число меньше первого в 2 раза, больше третьего на 12. Найдите эти числа.

х – второе число

2х + х + (х + 12) = 92

—

3. Старинная задача

Уже около 4000 лет назад вавилоняне и египтяне решали разные задачи землемерия, строительства и военного дела с помощью уравнений. Уравнение первой и второй степеней умели решать в древности также китайские и индийские ученые.

Задача Бхаскара (крупнейший индийский математик и астроном XII века).

Некто сказал другу: «Дай мне 100 рупий, и я буду вдвое богаче тебя». Друг ответил: «Дай ты мне только 10, и я стану в 6 раз богаче тебя». Сколько было у каждого?

Решение:

170; 40. Вводя вспомогательное неизвестное, Бхаскара принимает, что первый имеет 2х – 100, тогда по условию задачи второй имеет х+100. Второе условие приводит к уравнению.

6(2х-100-10)=х+100+10, откуда х=70.

infourok.ru

Урок математики в 7 классе по теме Решение задач с помощью составления уравнений

Ход урока

I. Работа начинается с ввода или так называемого “запуска” раздела.

Обобщение и систематизация знаний по теме “ Задачи, решаемые с помощью уравнения”.

Примеры задач:

1. За 9 ч по течению реки теплоход проходит тот же путь, что за 11 ч против течения. Найдите собственную скорость теплохода, если скорость течения реки 2 км/ч.

Пусть собственная скорость теплохода – Х км/ч. Заполним таблицу значений трёх величин.

3. В первую бригаду привезли раствора цемента на 50 кг меньше, чем во вторую. Каждый час работы первая бригада расходовала 150 кг раствора, а вторая – 200кг. Через 3 ч работы в первой бригаде осталось раствора в 1,5 раза больше, чем во второй. Сколько раствора привезли в каждую бригаду?

Пусть в первую бригаду привезли Х кг раствора, тогда во вторую – Х + 50 кг. Заполним таблицу значений величин для двух бригад:

5. Книгу в 296 страниц ученик прочитал за три дня. Во второй день он прочитал на 20% больше, чем в первый, а в третий – на 24 страницы больше, чем во второй. Сколько страниц прочитал ученик в первый день?

Пусть в первый день ученик прочитал Х страниц, тогда во второй день ученик прочитал Х + 0,2Х = 1,2Х страниц, а в третий день прочитал 1,2Х + 24. Составим уравнение:
Х + 1,2Х +1,2Х + 24 = 296. Решив это уравнение, получим Х = 80, то есть ученик прочитал в первый день 80 страниц.

6. На солнышке грелось несколько кошек. У них лап на 10 больше, чем ушей. Сколько кошек грелось на солнышке?
Пусть грелось Х кошек, тогда у этих кошек 2Х ушей и 4Х лап. Составим уравнение:
4Х – 2Х = 10. Решив это уравнение, получим Х = 5,то есть 5 кошек грелось на солнышке.

II. Самостоятельная работа учащихся.

Каждый ученик получает индивидуальную карточку с задачами. Правильность решения проверяет преподаватель, при необходимости он оказывает помощь в решении. После проверки ученику выставляется в оценочный лист плюс или оценка.

Примеры карточек для первой группы:

Карточка № 1.

1. (Старинная задача.) Послан человек из Москвы в Вологду и велено ему проходить во всякий день по 40 вёрст. На следующий день вслед ему был послан другой человек и велено ему проходить по 45 вёрст в день. Через сколько дней второй догонит первого?

2. Чтобы сделать вовремя заказ, артель стеклодувов должна была изготовлять в день по 40 изделий. Однако она изготовляла ежедневно на 20 изделий больше и выполнила заказ на 3 дня раньше срока. Каков был срок выполнения заказа?

Ответ: № 1 – 8 дней, № 2 – 9 дней.

Карточка № 2.

1. Кооператив наметил изготовить партию мужских сорочек за 8 дней. Выпуская в день на 10 сорочек больше, чем предполагалось, он выполнил план за один день до срока. Сколько сорочек в день должен был выпускать кооператив?

2. На ферме 1000 кроликов и кур, у них 3150 ног. Сколько кроликов и сколько кур на ферме?

Ответ: № 1 – 70 сорочек, № 2 – 575 кроликов и 425 кур..

Карточка № 3.

1. Из пункта А вышла грузовая машина со скоростью 60км/ч. Через 2 ч вслед за ней из пункта А вышла легковая машина со скоростью 90 км/ч. На каком расстоянии от пункта А легковая машина догонит грузовую?

2. Чтобы выполнить задание в срок, токарь должен изготавливать по 24 детали в день. Однако он ежедневно перевыполнял норму на 15 деталей и уже за 6дней до срока изготовил 21 деталь сверх плана. Сколько деталей изготовил токарь?

Ответ: № 1 – 360 км, № 2 – 408 деталей.

Карточка № 4.

1. От турбазы до привала туристы шли со скоростью 4,5км/ч, а возвращались на турбазу со скоростью 4км/ч, затратив на обратный путь на 15 мин больше. На каком расстоянии от турбазы был сделан привал?

2. На одном складе было 185 т угля, а на другом – 237 т. Первый склад стал отпускать ежедневно по 15 т угля, а второй – по 18 т. Через сколько дней на втором складе угля будет в полтора раза больше, чем на первом?

Ответ: № 1 – 9 км, № 2 – 9 дней.

Примеры карточек для второй группы:

Карточка № 5.

1. Из пункта А выехал велосипедист. Одновременно вслед за ним из пункта В , отстоящего от пункта А на расстоянии 60 км/ч, выехал мотоциклист. Велосипедист ехал со скоростью 12 км/ч, а мотоциклист – со скоростью 30 км/ч. На каком расстоянии от пункта А мотоциклист догонит велосипедиста?

2. Три бригады изготовили 65 деталей. Первая бригада изготовила на 10 деталей меньше, чем вторая, а третья – 30% того числа деталей, которые изготовили первая и вторая детали вместе. Сколько деталей изготовила каждая бригада?

Ответ: № 1 – 40 км, № 2 – 20, 30, 15 деталей.

Карточка № 6.

1. Расстояние между пристанями М и N равно 162 км. От пристани М отошёл теплоход со скоростью 45 км/ч. Через 45 мин от пристани N навстречу ему отошёл другой теплоход, скорость которого 36 км/ч. Через сколько часов после отправления первого теплохода они встретятся?

2. Бригада рабочих должна была изготовить определённое количество деталей за 20 дней. Однако она ежедневно изготавливала на 70 деталей больше, чем планировалось первоначально. Поэтому уже за 7 дней до срока ей осталось изготовить 140 деталей. Сколько деталей должна была изготовить бригада?

Ответ: № 1 – 2 ч, № 2 – 3000 деталей.

Карточка № 7.

1. От пристани А отошел теплоход со скоростью 40 км/ч. Через 1 ч вслед за ним отошёл другой теплоход со скоростью 60 км/ч. Через сколько часов после своего отправления и на каком расстоянии от А второй теплоход догонит первый?

2. В хозяйстве имеются куры и овцы. Сколько тех и других, если у них вместе 19 голов и 46 ног?

Ответ: № 1 – 2 ,5 ч; 150 км, № 2 – 4 овцы и15 кур.

Карточка № 8.

1. Сумму в 74 р. заплатили девятнадцатью монетами по 2 р. и 5 р. Сколько было монет по 2 р.?

2. За 4 ч катер проходит по течению расстояние, в 2,4 раза большее, чем за 2 ч против течения. Какова скорость катера в стоячей воде, если скорость течения 1,5 км/ч?

Ответ: № 1 – 7 монет, № 2 – 16,5 км/ч.

Примеры карточек для третьей группы:

Карточка № 9.

1. Со станции М и N, расстояние между которыми 380 км, одновременно навстречу друг другу вышли два поезда. Скорость поезда, отправившегося со станции N, была больше скорости другого поезда на 5 км/ч. Через 2 ч после отправления поездам оставалось пройти до встречи 30 км. Найдите скорость поездов.

2. В одном резервуаре 380 м³ воды, а в другом 1500 м³. В первый резервуар каждый час поступает 80 м³ воды, а из второго каждый час выкачивают 60 м³. Через сколько часов воды в резервуаре станет поровну?

Ответ: № 1 – 85 и 90км/ч, № 2 – 56 ч.

Карточка № 10.

1. Сумму в 74 р. заплатили девятнадцатью монетами по 2 р. и 5 р. Сколько было монет по 2 р.?

2. Скашивая ежедневно по 60 га вместо 50 га, бригада сумела скосить луг на один день быстрее, чем планировалось. Какова площадь луга?

Ответ: № 1 – 7 монет, № 2 – 300 га.

Карточка № 11.

1. (Старинная задача.) Летели галки, сели на палки: по две сядут – одна палка лишняя, по одной сядут – одна галка лишняя. Сколько было галок и сколько палок?

2. Турист рассчитал, что если он будет идти к железнодорожной станции со скоростью 4км/ч, то опоздает к поезду на полчаса, а если он будет идти со скоростью 5км/ч, то придёт на станцию за 6 мин до отправления поезда. Какое расстояние должен пройти турист?

Ответ: № 1 – 4 галки и 3 палки, № 2 – 12 км.

Карточка № 12.

1. (Задача С.А. Рачинского.) Я дал одному ученику 3 ореха, а всем остальным по 5 . Если бы я всем дал по 4 ореха, у меня осталось бы 15. Сколько было орехов?

2. К числу приписали справа нуль. Число увеличилось на 405. Найдите первое число.

Ответ: № 1 – 83 ореха, № 2 – 45.

Раздел считается введённым в работу, если каждая карточка с заданиями выполнена хотя бы одним учеником.

infourok.ru

Конспект урока алгебры в 7 классе по теме «Решение текстовых задач на движение с помощью составления уравнений с одной переменной». Учебник «Алгебра-7» под редакцией Теляковского С.А.

Конспект урока алгебры в 7 классе

по теме «Решение текстовых задач на движение с помощью составления уравнений с одной переменной».

Учебник «Алгебра-7» под редакцией Теляковского С.А.

Тема: Решение текстовых задач на движение с помощью составления уравнений с одной переменной.

Цели урока:

Образовательные: формирование знаний, умений и навыков учащихся решать текстовые задачи с помощью уравнений.

Развивающие: развивать умения работать в группе, формировать учебно–познавательные навыки по работе с дополнительным материалом, развивать логическое мышление, внимание;
Воспитательные: воспитывать интерес к математике, старательность, активность, мобильность, взаимопомощь, ответственность перед товарищами.

Ход урока.

1.Организационный этап.

Учитель приветствует учеников.

Проверка домашнего задания.

Сильные ученики отвечают на вопросы, которые возникли у более слабых учащихся в процессе выполнения домашнего задания.

Актуализация опорных знаний.

Написание «Теоретического текста».

Учитель раздает каждому учащемуся текст для проверки уровня усвоения обязательного теоретического материала. В тексте пропущены слова, которые ученики должны вставить. Проверка организована в форме «взаимопроверки» с демонстрацией правильных ответов на экране.

На предыдущем уроке мы изучали решение задач с помощью линейных уравнений .Много текстовых задач отображают некоторую жизненную ситуацию и используют нематематические понятия, такие задачи называют реальной математикой. Чтобы составить математическую модель задачи, надо сначала выбрать основную переменную , а потом составить соответствующее уравнение.Ответ необходимо проверить по содержанию задачи, а не уравнения. После того, как мы составили уравнение к задаче и чтобы его решить, уравнение необходимо привести к линейному.Для этого надо помнить такое правило-ориентир:

Избавляемся от знаменателей.;
Раскрываем скобки;
Переносим члены с переменными в левую часть уравнения, а другие-в правую, меняя знаки на противоположные;
Приводим подобные слагаемые;

Я считаю, что умение решать текстовые задачи необходимо для того, чтобы….

4.Мотивация учебной деятельности.

Я хочу, чтобы каждый из вас объяснил, почему считает необходимым научиться решать текстовые задачи………

Ребята! Сегодня на уроке мы должны будем с вами познакомиться с алгоритмом решения задач на движение, обращая особое внимание на табличную запись условия. Работая над новой темой, мы проследим вместе с вами, как ранее изученный материал связан с новым, как постепенно происходит расширение и углубление знаний. Одним словом, мы будем объединять отдельные факты в целостный пласт.Я буду вам помогать в процессе систематизации ваших знаний. Мы приступаем к работе.

5.Решение задач с помощью опорных схем.

Коллективное решение задачи на историческую тематику.

История сохранила нам мало фактов биографии древнего математика Диофанта. Все, что про него было известно, взято из надписи на его гробнице, составленной в виде математической задачи.

Путник! Тут прах похоронен Диофанта. И числа расскажут, о диво, как долго жизнь его длилась

Шестая часть ее прошла счастливым детством

х/6

Двенадцатая часть жизни еще прошла-

покрылась пушком его борода

х/12

Седьмую в бездетном браке провел Диофант

х/7

Прошло пятилетие: он был счастлив рождением прекрасного первенца-сына

Коему судьба только половину жизни прекрасной и светлой дала по сравнению с отцом

х/2

И в горе глубоком старик земной жизни конец принял, прожив только года 4 после того, как без сына остался.

Скажи, сколько лет жизни достигнув, принял смерть Диофант?

х=х/6+х/12/+ х/7+5+х/2+4

Решив уравнение, получаем, что х=84, имеем такие эпизоды биографии Диофанта: женился в 21 год, стал отцом в 38 лет, потерял сына в 80 лет.

Диофант Александрийский — древнегреческий математик.

До нас дошло стихотворение-задача, из которого видно, что Диофант прожил 84 года. Вот его содержание: «детство Диофанта продолжалось одну шестую часть его жизни, спустя ещё одну двенадцатую у него начала расти борода, он женился спустя ещё одну седьмую, через пять лет у него родился сын, сын прожил половину жизни отца, и отец умер через четыре года после смерти горько оплакиваемого им сына».

Своё основное произведение «Арифметика» Диофант посвятил Дионисию — вероятно, епископу Александрии. До нас дошло шесть первых книг «Арифметики» из тринадцати. Диофант ввёл буквенные обозначения для неизвестного, его квадрата, знака равенства и знака отрицательного числа.

Занимался неопределёнными уравнениями. Ввёл в алгебру буквенную символику.

Большую часть своей жизни Диофант Александрийский посвятил изучению алгебраических уравнений в целых числах. В дошедших до нас книгах «Арифметика» содержатся задачи и решения, в которых Диофант поясняет, как выбрать неизвестное, чтобы решить уравнение вида ax=b или ax=b. Способы решения полных квадратных уравнений изложены в книгах, которые не сохранились.

6.Формирование умений решать задачи на движение с помощью составления линейных уравнений с одной переменной.

Очень важно при решении любой задачи хорошо разобраться с условием и правильно его записать. Способ записи условия с помощью таблицы очень наглядный.

С задачами на движение вы встречались в начальной школе и в 5 классе. Вы знаете, что в этих задачах присутствуют три величины. Назовите мне их. Как находится расстояние? Время? Скорость?

Вы знакомы с формулами нахождения этих величин

Повторение формул: V = S : t

S = V • t

T=s:v

Интерактивная игра «Аквариум». Учитель объединяет учеников в группы по 5-6 человек и предлагает им ознакомиться с заданием. Эта группа читает задание вслух. Остальные учащиеся слушают, не вмешиваясь в процесс обсуждения. Но после дискуссии каждая группа поддерживает или выдвигает свои идеи. Наиболее удачное решение записывается на доске.

1.Катер прошел расстояние между пристанями по течению реки за 4 часа, а против течения- за 6 часов. Найдите собственную скорость катера, если течение реки 1,5 км/ч.

Образец записи.

Пусть собственная скорость катера х км/ч. Когда катер двигался по течению реки, его скорость была (х+1,5) км/ч и за 4 часа он проплыл расстояние 4(х-1,5) км. Если катер двигался против течения река, то его скорость была (х-1,5) км/ч, и за 6 часов он проплыл расстояние 6(х-1,5) км. По условию задачи катер проплыл по течению и против течения одинаковое расстояние, поэтому

4(х+1,5)=6(х-1,5)

Решим уравнение.

4(х+1,5)=6(х-1,5),

4х+6-6х-9,

4х-6х=-9-6,

-2х=-15,

Х=7,5.

Получаем, что собственная скорость катера 7,5 км/ч.

Ответ: 7,5 км/ч.

2. По шоссе идут две машины с одной и той же скоростью. Если первая увеличит скорость на 10 км/ч, а вторая уменьшит скорость на 10 км/ч, то первая за 2ч пройдёт столько же, сколько вторая за 3ч. С какой скоростью идут автомашины?

Х км/ч — скорость автомашины

Скорость

Время

Расстояние

первая

машина

(x + 10)

км/ч

50 + 10 = 60

2 ч

(x + 10)2 = (x – 10)3

вторая

машина

(x – 10)

км/ч

50 – 10 = 40

3 ч

60 * 2 = 40 * 3

120 = 120 (верно)

(Наименование в таблице можно не писать.)

Решение: (x + 10)2 = (x – 10)3

Раскроем скобки и приведём уравнение к виду ax = b:

2х + 20 = 3х — 30

2х — 3х = — 30 — 20

— х = — 50

х = — 50 : ( — 1 )

х = 50

Ответ: 50 км/ч.

3.Какова скорость теплохода, если по течению реки он проплывает за 2ч

то же расстояние, что за 4ч против течения? Скорость течения реки

3 км/ч.

Скорость

Время

Расстояние

по течению

реки

(x + 3)

км/ч

9 + 3 =12

2ч

(x + 3)2 = (x — 3)4

против

течения реки

(x – 3)

км/ч

9 – 3 = 6

4ч

12 * 2 = 6 * 4

24 = 24 (верно)

(Наименование в таблице можно не писать.)

Решение: (x + 3)2 = (x – 3)4

Раскроем скобки и приведём уравнение к виду ax = b:

2x + 6 = 4x — 12

2x — 4x = — 12 — 6

— 2x = — 18

x = -18 : (- 2)

x = 9

Ответ: 9 км/ч.

7. Итог урока. Рефлексия.

Учитель задает вопросы, которые касаются не только изученного материала, но и те, которые подводят их к рефлексии:

-что на уроке было главным?

— что было интересно?

— чему вы научились?

— чем пополнили свои знания?

8. Домашнее задание.

infourok.ru

Задание по алгебре для 7 класса по теме «Задачи на составление уравнений»

Вариант 1.

1. При переезде, семья Зингельшухеров упаковывала книги в коробки. Всего книг было 120. В самую маленькую коробку вошло в 2 раза меньше книг, чем в коробку среднюю. Когда заполнились эти коробки, выяснилось, что в третью коробку вошло ровно столько же книг, сколько и в две первые. Какое количество книг было упаковано в каждую коробку?

2. Из Реутова в Великий Устюг выехал автобус с детьми на новогоднюю елку, а через четыре часа ему навстречу, со скоростью на 20 км/ч большей чем автобус, выехал грузовик с подарками тем детям, которые не попали на елку. Транспорт встретился ровно на половине пути между городами через 10 часов после отправления автобуса. С какой скоростью двигался автобус с детьми?

3. В бригаде всего 20 мастеров: столяров и плотников. Когда в бригаду пришли еще 4 столяра, то плотников стало ровно в два раза больше, чем плотников. Сколько столяров и плотников было в бригаде до прихода новых работников?

Вариант 2.

1. Старый пират Флинт сумел собрать коллекцию из 180 разных золотых монет, которые решил хранить в трех альбомах. Когда заполнился первый альбом, выяснилось, что в него входит столько же, сколько и в два оставшихся. При этом в самый маленький альбом входит в восемь раз меньше монет, чем во второй по величине. Сколько монет входит в каждый из альбомов?

2. Нападающий сборной Канады подхватил шайбу у своих ворот и начал атаку на ворота сборной России. Через две секунды этот маневр заметил наш защитник и, со скоростью на 4 м/с больше чем у североамериканца, помчался навстречу. Встреча, силовой прием россиянина и отобранная у канадца шайба – все это произошло в центре площадки, когда игроки проехали одинаковое расстояние. Причем встреча для канадца произошла через 10 секунд после того, как он начал движение. С какими скоростями мчались навстречу друг другу хоккеисты?

3. Вова и Дима сыграли в морской бой 19 партий. Если бы они сыграли еще одну и ее выиграл Дима, то все равно, Вова бы имел в три раза больше выигрышей, чем Дима. Сколько партий выиграл Вова, а сколько Дима?

xn--j1ahfl.xn--p1ai

Конспект урока «Решение задач с помощью уравнениЙ» (7 класс)

Решение задач с помощью уравнений А 7

Цели урока: 1) обеспечить понимание уравнения в качестве математической модели некоторой жизненной ситуации, описанной в текстовой задаче; выделить этапы решения задач алгебраическим методом; формировать умение составлять уравнение по условию задачи и решать его;

2) развивать внимание, познавательную активность, логическое мышление;

3) воспитывать аккуратность при записи чисел, трудолюбие.

Тип урока: урок изучения нового материала

Оборудование: учебник

Ход урока

I. Организационный момент

II. Проверка домашнего задания

Проверить выполнение домашнего задания и ответить на вопросы, возникшие у учащихся при его выполнении.

III. Актуализация опорных знаний

IV. Усвоение новых знаний

Задачи № 1 (по учебнику)

Можно воспользоваться таблицей:

Сперва в таблице стрелками обозначаем и подписываем все зависимости, затем видим, что неизвестны все четыре клеточки, значит, обозначить переменной удобно главный вопрос задачи, например, количество яблок в корзине первоначально. Затем, по стрелкам, заполняем все клеточки. Последняя стрелка даст уравнение: 5(х – 10) = 2х + 10.

Задача № 2 (по учебнику) самостоятельно

VI. Формирование умений и навыков

№ 143.

Решение:

Пусть в одной кассе было х билетов, тогда во второй – (х + 36) билетов. Зная, что всего было продано 392 билета, составим уравнение:

х + (х + 36) = 392;

х + х + 36 = 392;

2х = 356;

х = 178.

Следовательно, в первой кассе было продано 178 билетов.

Так как х + 36 = 178 + 36 = 214, то во второй кассе было продано 214 билетов.

Ответ: 178 и 214 билетов.

№ 146.

Решение:

Анализ условия:

Пусть х м – длина одного тоннеля, тогда (х + 17) м – длина другого. Так как наземная часть составляет 703 м, а вся трасса – 6940 м, то длина тоннелей в сумме составляет (6940 – 703) м. Зная, что длина тоннелей равна х + (х + 17) м, составим уравнение:

х + (х + 17) = 6940 – 703;

х + х + 17 = 6237;

х + х = 6237 – 17;

2х = 6220;

х = 3110.

Значит, длина одного тоннеля равна 3110 м. Так как х + 17 = = 3110 + 17 = 3127, то длина другого тоннеля равна 3127 м.

Ответ: 3110 м и 3127 м.

№ 148.

Анализ условия:

Пусть х деталей изготовил второй рабочий, тогда первый изготовил (х + 0,15х) деталей. Зная, что вместе они изготовили 86 деталей, составим уравнение:

х + (х + 0,15х) = 86;

х + х + 0,15х = 86;

2,15х = 86;

х = 86 : 2,15;

х = 40.

Значит, второй рабочий изготовил 40 деталей. Так как х + 0,15х = 40 +
+ 0,15 · 40 = 40 + 6 = 46, то первый рабочий изготовил 46 деталей.

Ответ: 46 деталей и 40 деталей.

VII. Подведение итогов урока

Ребята, а что мы сегодня делали на уроке?…

Что называется уравнением с одной переменной?…

Что называется корнем уравнения?…

Сколько корней может иметь уравнение?….

Какие уравнения называются равносильными?…..

VIII. Домашнее задание п 8, № 144, 149

infourok.ru

Урок алгебры в 7 классе «Решение задач на составление уравнений»

План-конспект урока

1. Ф.И.О. Чуприна Ольга Николаевна

2. Место работы МБОУ СОШ № 18 посёлка Паркового Тихорецкого района

3. Должность учитель математики

4. Предмет алгебра

5. Класс 7

6.Тема урока Решение задач на составление уравнений

7. Базовый учебник Алгебра. 7 класс: Г.В.Дорофеев, С.Б.Суворова, Е.А.Бунимович и др. – М.: Просвещение, 2017

8. Цель урока: Развить умения решать текстовые задачи алгебраическим способом: составлять уравнение по условию задачи, решать составленное уравнение.. проводить рассуждения, основанные на интерпретации условия поставленной задачи, для поиска целых корней некоторых несложных нелинейных уравнений

9. Планируемые результаты

личностные: вoспитание трудолюбия, коммуникабельности, интереса к умственной деятельности;

предметные: владеть базовым понятийным аппаратом по теме «Решение уравнений»

уметь применять свойства уравнений;

уметь решать уравнения;

уметь решать текстовые задачи способом составления уравнений.

Метапредметные: формировать умение создавать обобщение, развивать речь, внимание, мышление, память; решать задачи на составление линейного уравнения, по условию задачи

умение логически рассуждать; умение работать умение распознавать верные и неверные утверждения и решения; умение действовать в соответствии с предложенным алгоритмом; применение приёмов самоконтроля при решении учебных задач; умение видеть математическую задачу в несложных практических ситуациях.

Тип урока: изучение новой темы

Деятельность учителя

Деятельность ученика

УУД

1. Организационный момент

Постановка цели и задач урока.

Тема урока определяется учащимися при помощи диалога с учителем:

Подписать число, тему

Регулятивные— постанoвка учебной цели

2. Устная работа

Повторение изученного ранее материала: алгоритм решения линейных уравнений

Карточка 1 на каждой парте. Дети работают в парах. Первые справившиеся с заданием пары показывают свое решение с помощью документ-камеры, отвечают на вопросы одноклассников и учителя

Регулятивные — определяют цель учебной деятельности, осуществляют поиск средств её достижения.

Познавательные -подведение под понятие, анализ объектов.

Коммуникативные-взаимоконтроль,

3. Объяснение нового материала.

Алгоритм решения задач с помощью уравнений:

I – х (ед.изм.) – это обычно то, что требуется узнать в задаче

II – через х выражается все остальное

III – составляется уравнение с помощью предложений в которых есть фразы «больше, меньше, во…, на…» Например: если х больше у на 10, то уравнение будет таким

х= у + 10

Цель учащихся научиться применять алгоритм решения задач с помощью уравнений для составления уравнения к любой задачи.

Познавательные-

выбор эффективных

способов решения задач, анализ

объектов для выделения свойств и признаков объектов, построение логической цепи рассуждения.

Регулятивные –

выявление объективной учебной информации

Коммуникативные—

использовать речевые средства для дискуссии и аргументации.

4. Разбор решения задачи 1 п.7.6 из учебника.

Решить задачи № №758(а), 759(а), 760(а), 762(а), 763(а).

Задачи №760 и 763 решают в парах

Карточка № 2 для каждой пары своя задача

Дети проводят работу по составлению и решению уравнений по условию задач на движение.

Карточку 2 решают дети в группах по 4 ученика. Затем защищают свое решение. Чтобы затратить меньше времени, дети свое решение показывают через документ- камеру

Познавательные-

выбор эффективных способов решения задачи,

рефлексия способов и условий действий.

Регулятивные-

контроль усвоения учебной информации

Коммуникативные-взаимоконтроль, работа в парах

5. Заключительный этап

Решаем старинную задачу: В 1881г. была найдена зарытой в земле близ Бахшали (северо-западная Индия) рукопись неизвестного автора, которая, как полагают, относится к VI-VIII вв. В этом памятнике, написанном на березовой коре и известным под названием ”Бахшалийской рукописи”, содержится такая задача:

“Из четырех жертвователей второй дал вдвое больше первого, третий – втрое больше второго, четвертый – вчетверо больше третьего, а все вместе дали 132. Сколько дал первый?”

Решение:

Пусть первый дал х то следующие дали 2х, 6х, 24х, все же вместе дали 132.

х+2х+6х+24х=132

33х=132

х=4

Следовательно, первый дал 4, второй 8, третий 24, четвертый 96.

Познавательные-

выбор эффективных способов решения задачи,

рефлексия способов и условий действий.

Регулятивные-

самодиагностика и коррекция собственных учебных действий.

Коммуникативные-взаимоконтроль,

6. Подведение итогов урока. рефлексия

Ответы учащихся. В соответствии с целью урока

Познавательные—

рефлексия способов и условий действия.

Регулятивные-

оценивание результатов выполненной деятельности.

Коммуникативные-

использовать речевые средства для дискуссии и аргументации своей позиции.

7. Домашнее задание. №№№ №758(б), 759(б), 760(б), 762(б), 763(б).

Карточка 1. Решить уравнения:

1) 3х + 2 =11.

2) 5(х – 3) + 2 = 3 (х – 4) + 2х ‒ 1.

3) 2 (х + 3) = 5 – 6х.

4) – 6 (5 – 3х) = 8х – 7.

5) 5(x — 2) = 45

Карточка 2. Решить задачу:

I. За 9 ч по течению реки теплоход проходит тот же путь, что за 11 ч против течения. Найдите собственную скорость теплохода, если скорость течения реки 2 км/ч.

II. На солнышке грелось несколько кошек. У них лап на 10 больше, чем ушей. Сколько кошек грелось на солнышке?

III. (Старинная задача.) Послан человек из Москвы в Вологду и велено ему проходить во всякий день по 40 вёрст. На следующий день вслед ему был послан другой человек и велено ему проходить по 45 вёрст в день. Через сколько дней второй догонит первого?

IV. От турбазы до привала туристы шли со скоростью 4,5км/ч, а возвращались на турбазу со скоростью 4км/ч, затратив на обратный путь на 15 мин больше. На каком расстоянии от турбазы был сделан привал?

V. (Задача С.А. Рачинского.) Я дал одному ученику 3 ореха, а всем остальным по 5 . Если бы я всем дал по 4 ореха, у меня осталось бы 15. Сколько было орехов?

Решения:

№758(а)

х – (км/ч) – скорость туриста

(х + 10) –(км/ч) – скорость велосипедиста

0,5х(км) – прошел турист до встречи

0,5(х + 10)(км) – проехал велосипедист до встречи

0,5х + 0,5(х + 10) = 9

х = 4

4 км/ч – скорость туриста

Ответ: 4 км/ч

№759(а)

х – (км/ч) скорость пассажирского поезда

(х – 30) –(км/ч) – скорость электропоезда

2х –(км) — проехал до разъезда п.п.

2(х – 30) –(км) — проехал до разъезда эл.п.

2х + 2(х – 30) = 300

х = 90

2х = 180(км) – расстояние от А до разъезда

2(х – 30) = 120(км) — расстояние от В до разъезда

Ответ: 180 км от А, 120км от В

№ 760(а)

х – (км/ч) скорость 1 поезда

(х + 20) –(км/ч) – скорость 2 поезда

3х –(км) — проехал 1 поезд.

3(х + 20) –(км) — проехал до разъезда эл.п.

Всего проехали 480 км

3х + 3(х + 20) = 480

х = 70(км/ч) скорость 1 поезда

70 + 20 = 90(км/ч) – скорость 2 поезда

Ответ: 70 км/ч, 90км/ч.

№ 762(а)

х км/ч – скорость течения реки

(30 + х) (км/ч) – скорость катера по течению реки

(30 — х) (км/ч) – скорость катера против течения реки

3,5(30 + х) (км) – прошел катер по течению реки

4(30 — х) (км) – прошел катер против течения реки

3,5(30 + х) = 4(30 — х)

х = 2(км/ч) – скорость течения реки

3,5 * (30 + 2) = 112 (км) прошел катер по течению реки

Ответ: 2км/ч, 112км

№763(а)

х(ч) – плыла лодка по течению реки

(8 – х) (ч) – плыла лодка против течения реки

8 + 2 = 10(км/ч) –скорость лодки по течению реки

8 – 2 = 6(км/ч) – скорость лодки против течения реки

10х(км) – проплыла лодка по течению реки

6(8 – х) (км) — проплыла лодка против течения реки

10х = 6(8 – х)

х = 3(ч) – плыла лодка по течению реки

10 * 3 * 2 = 60(км) – проплыла лодка всего

Ответ: 3 часа, 60км.

Решение задач карточки 2

х(км/ч) – собственная ск. теплохода

(х + 2)(км/ч) – скорость тепл-да по течению реки

(х – 2)(км/ч) – скорость тепл-да против течения реки

9(х + 2)(км) – прошел тепл-д по течению реки

11(х – 2)(км) – прошел тепл-д против течения реки

9(х + 2) = 11(х – 2)

х = 20(км/ч) – собственная скорость теплохода

Ответ: 20 км/ч.

II.

х(кошек) – грелось на солнышке

2х-было ушей

4х – было лап

4х = 2х + 10

х = 5(кошек) грелось на солнышке

Ответ: 5 кошек

III.

х (дней) – первый шел до встречи

(х -1) (дней) – второй шел до встречи

40х (верст) – прошел первый

45(х – 1) (верст) – прошел второй

40х = 45(х -1)

х = 9

через 9 дней после выхода первого второй его догонит

Ответ: через 9 дней

IV.

х(ч) – туристы шли до привала

(х + 15/60)(ч) = (х + 0,25) (ч) – туристы шли обратно

4,5х(км – туристы прошли до привала

4(х + 0,25)(км) – туристы прошли до турбазы

4,5х = 4(х + 0,25)

х = 2(км) от турбазы был сделан привал

Ответ: 2 км.

х (учеников) всего

(х – 1) учеников получили по 5 орехов

3 + 5(х – 1)(орехов) – было всего

4х(орехов) — получили бы все ученики

3 + 5(х – 1) = 4х + 15

х = 17

4 * 17 + 15 = 83(ореха)

Ответ: 83 ореха.

multiurok.ru

Урок алгебры «Решение задач на составление уравнений» для 7 класса

План-конспект урока

1. Ф.И.О. Чуприна Ольга Николаевна

2. Место работы МБОУ СОШ № 18 посёлка Паркового Тихорецкого района

3. Должность учитель математики

4. Предмет алгебра

5. Класс 7

6.Тема урока Решение задач на составление уравнений

7. Базовый учебник Алгебра. 7 класс: Г.В.Дорофеев, С.Б.Суворова, Е.А.Бунимович и др. – М.: Просвещение, 2017

9. Планируемые результаты

личностные: вoспитание трудолюбия, коммуникабельности, интереса к умственной деятельности;

предметные: владеть базовым понятийным аппаратом по теме «Решение уравнений»

уметь применять свойства уравнений;

уметь решать уравнения;

уметь решать текстовые задачи способом составления уравнений.

Тип урока: изучение новой темы

1. Организационный момент

Постановка цели и задач урока.

Тема урока определяется учащимися при помощи диалога с учителем:

Подписать число, тему

Регулятивные— постанoвка учебной цели

2. Устная работа

Повторение изученного ранее материала: алгоритм решения линейных уравнений

Регулятивные — определяют цель учебной деятельности, осуществляют поиск средств её достижения.

Познавательные -подведение под понятие, анализ объектов.

Коммуникативные-взаимоконтроль,

3. Объяснение нового материала.

Алгоритм решения задач с помощью уравнений:

I – х (ед.изм.) – это обычно то, что требуется узнать в задаче

II – через х выражается все остальное

х= у + 10

Познавательные-

выбор эффективных

способов решения задач, анализ

объектов для выделения свойств и признаков объектов, построение логической цепи рассуждения.

Регулятивные –

выявление объективной учебной информации

Коммуникативные—

использовать речевые средства для дискуссии и аргументации.

4. Разбор решения задачи 1 п.7.6 из учебника.

Решить задачи № №758(а), 759(а), 760(а), 762(а), 763(а).

Задачи №760 и 763 решают в парах

Карточка № 2 для каждой пары своя задача

Дети проводят работу по составлению и решению уравнений по условию задач на движение.

Познавательные-

выбор эффективных способов решения задачи,

рефлексия способов и условий действий.

Регулятивные-

контроль усвоения учебной информации

Коммуникативные-взаимоконтроль, работа в парах

5. Заключительный этап

Решение:

Пусть первый дал х то следующие дали 2х, 6х, 24х, все же вместе дали 132.

х+2х+6х+24х=132

33х=132

х=4

Следовательно, первый дал 4, второй 8, третий 24, четвертый 96.

Познавательные-

выбор эффективных способов решения задачи,

рефлексия способов и условий действий.

Регулятивные-

самодиагностика и коррекция собственных учебных действий.

Коммуникативные-взаимоконтроль,

6. Подведение итогов урока. рефлексия

Ответы учащихся. В соответствии с целью урока

Познавательные—

рефлексия способов и условий действия.

Регулятивные-

оценивание результатов выполненной деятельности.

Коммуникативные-

использовать речевые средства для дискуссии и аргументации своей позиции.

7. Домашнее задание. №№№ №758(б), 759(б), 760(б), 762(б), 763(б).

Карточка 1. Решить уравнения:

1) 3х + 2 =11.

2) 5(х – 3) + 2 = 3 (х – 4) + 2х ‒ 1.

3) 2 (х + 3) = 5 – 6х.

4) – 6 (5 – 3х) = 8х – 7.

5) 5(x — 2) = 45

Карточка 2. Решить задачу:

II. На солнышке грелось несколько кошек. У них лап на 10 больше, чем ушей. Сколько кошек грелось на солнышке?

Решения:

№758(а)

х – (км/ч) – скорость туриста

(х + 10) –(км/ч) – скорость велосипедиста

0,5х(км) – прошел турист до встречи

0,5(х + 10)(км) – проехал велосипедист до встречи

0,5х + 0,5(х + 10) = 9

х = 4

4 км/ч – скорость туриста

Ответ: 4 км/ч

№759(а)

х – (км/ч) скорость пассажирского поезда

(х – 30) –(км/ч) – скорость электропоезда

2х –(км) — проехал до разъезда п.п.

2(х – 30) –(км) — проехал до разъезда эл.п.

2х + 2(х – 30) = 300

х = 90

2х = 180(км) – расстояние от А до разъезда

2(х – 30) = 120(км) — расстояние от В до разъезда

Ответ: 180 км от А, 120км от В

№ 760(а)

х – (км/ч) скорость 1 поезда

(х + 20) –(км/ч) – скорость 2 поезда

3х –(км) — проехал 1 поезд.

3(х + 20) –(км) — проехал до разъезда эл.п.

Всего проехали 480 км

3х + 3(х + 20) = 480

х = 70(км/ч) скорость 1 поезда

70 + 20 = 90(км/ч) – скорость 2 поезда

Ответ: 70 км/ч, 90км/ч.

№ 762(а)

х км/ч – скорость течения реки

(30 + х) (км/ч) – скорость катера по течению реки

(30 — х) (км/ч) – скорость катера против течения реки

3,5(30 + х) (км) – прошел катер по течению реки

4(30 — х) (км) – прошел катер против течения реки

3,5(30 + х) = 4(30 — х)

х = 2(км/ч) – скорость течения реки

3,5 * (30 + 2) = 112 (км) прошел катер по течению реки

Ответ: 2км/ч, 112км

№763(а)

х(ч) – плыла лодка по течению реки

(8 – х) (ч) – плыла лодка против течения реки

8 + 2 = 10(км/ч) –скорость лодки по течению реки

8 – 2 = 6(км/ч) – скорость лодки против течения реки

10х(км) – проплыла лодка по течению реки

6(8 – х) (км) — проплыла лодка против течения реки

10х = 6(8 – х)

х = 3(ч) – плыла лодка по течению реки

10 * 3 * 2 = 60(км) – проплыла лодка всего

Ответ: 3 часа, 60км.

Решение задач карточки 2

х(км/ч) – собственная ск. теплохода

(х + 2)(км/ч) – скорость тепл-да по течению реки

(х – 2)(км/ч) – скорость тепл-да против течения реки

9(х + 2)(км) – прошел тепл-д по течению реки

11(х – 2)(км) – прошел тепл-д против течения реки

9(х + 2) = 11(х – 2)

х = 20(км/ч) – собственная скорость теплохода

Ответ: 20 км/ч.

II.

х(кошек) – грелось на солнышке

2х-было ушей

4х – было лап

4х = 2х + 10

х = 5(кошек) грелось на солнышке

Ответ: 5 кошек

III.

х (дней) – первый шел до встречи

(х -1) (дней) – второй шел до встречи

40х (верст) – прошел первый

45(х – 1) (верст) – прошел второй

40х = 45(х -1)

х = 9

через 9 дней после выхода первого второй его догонит

Ответ: через 9 дней

IV.

х(ч) – туристы шли до привала

(х + 15/60)(ч) = (х + 0,25) (ч) – туристы шли обратно

4,5х(км – туристы прошли до привала

4(х + 0,25)(км) – туристы прошли до турбазы

4,5х = 4(х + 0,25)

х = 2(км) от турбазы был сделан привал

Ответ: 2 км.

х (учеников) всего

(х – 1) учеников получили по 5 орехов

3 + 5(х – 1)(орехов) – было всего

4х(орехов) — получили бы все ученики

3 + 5(х – 1) = 4х + 15

х = 17

4 * 17 + 15 = 83(ореха)

Ответ: 83 ореха.

infourok.ru

Конспект урока алгебры в 7 классе «Уравнения. Решение задач на составление уравнений»

Урок математики в 7 классе по теме Решение задач с помощью составления уравнений

Задание по алгебре для 7 класса по теме «Задачи на составление уравнений»

Конспект урока «Решение задач с помощью уравнениЙ» (7 класс)

Урок алгебры в 7 классе «Решение задач на составление уравнений»

Урок алгебры «Решение задач на составление уравнений» для 7 класса

Добавить комментарий Отменить ответ