Формула разности арифметической прогрессии — энциклопедический справочник и словарь для студента от А до Я
ОПРЕДЕЛЕНИЕ Арифметическая прогрессия представляет собой последовательность чисел, каждая из которых, начиная со второй, отличается от предыдущей тем же числом d, которое называется разностью прогрессии. Другими словами, разница в арифметической прогрессии — это разница между следующим и предыдущим членами прогрессии. Если \(\
A=\left\{a_{1}, a_{2}, \dots, a_{n}, \dots\right\}
\) является арифметической прогрессией, а \(\
a_{n}
\) является ее n-м членом, то разность \(\
d=a_{n+1}-a_{n}
\) Если разность арифметической прогрессии является положительным числом, то прогрессия будет возрастать, если отрицательно — уменьшаться. В случае, когда известны первые члены \(\
a_{1}
\) и n-й \(\
a_{n}
\) прогрессии, разность d может быть найдена следующим образом: \(\
d=\frac{a_{n}-a_{1}}{n-1}
\) Примеры решения проблем ПРИМЕР 1 найти разницу арифметической прогрессии, в которой \(\
a_{1}=10, a_{5}=22
\) Поскольку известны первые и пятые члены арифметической прогрессии, различия соответственно равны \(\
d=\frac{a_{n}-a_{1}}{n-1}=\frac{a_{5}-a_{1}}{5-1}=\frac{22-10}{4}=3
\) ПРИМЕР 2 В арифметической прогрессии десятый член равен -30, а двадцатый — (-40). Найдите разницу в прогрессии. Согласно условию задачи \(\
a_{10}=-30, a_{20}=-40
\) Мы находим их выражения через первый член прогрессии и разности: \(\
\left\{\begin{array}{l}{a_{1}+9 d=-30} \\ {a_{1}+19 d=-40}\end{array}\right.
\) Мы решим полученную систему, для чего сначала вычитаем первое уравнение из второго уравнения. В результате мы получим: \(\
10 \mathrm{d}=-10
\) Где мы получаем \(\
d=-1
\)
sciterm.ru
Как найти разность арифметической прогрессии: формулы и примеры решений
Многие слышали об арифметической прогрессии, но не все хорошо представляют, что это такое. В данной статье дадим соответствующее определение, а также рассмотрим вопрос, как найти разность прогрессии арифметической, и приведем ряд примеров.
Математическое определение
Итак, если речь идет о прогрессии арифметической или алгебраической (эти понятия определяют одно и то же), то это означает, что имеется некоторый числовой ряд, удовлетворяющий следующему закону: каждые два соседних числа в ряду отличаются на одно и то же значение. Математически это записывается так:
an + 1-an = d
Здесь n означает номер элемента an в последовательности, а число d — это разность прогрессии (ее название следует из представленной формулы).
О чем говорит знание разности d? О том, как «далеко» друг от друга отстоят соседние числа. Однако знание d является необходимым, но не достаточным условием для определения (восстановления) всей прогрессии. Необходимо знать еще одно число, которым может быть совершенно любой элемент рассматриваемого ряда, например, a4, a10, но, как правило, используют первое число, то есть a1.

Формулы для определения элементов прогрессии
В общем, информации выше уже достаточно, чтобы переходить к решению конкретных задач. Тем не менее до того, как будет дана прогрессия арифметическая, и найти разность ее будет необходимо, приведем пару полезных формул, облегчив тем самым последующий процесс решения задач.
Несложно показать, что любой элемент последовательности с номером n может быть найден следующим образом:
an = a1 + (n — 1) * d
Действительно, проверить эту формулу может каждый простым перебором: если подставить n = 1, то получится первый элемент, если подставить n = 2, тогда выражение выдает сумму первого числа и разности, и так далее.
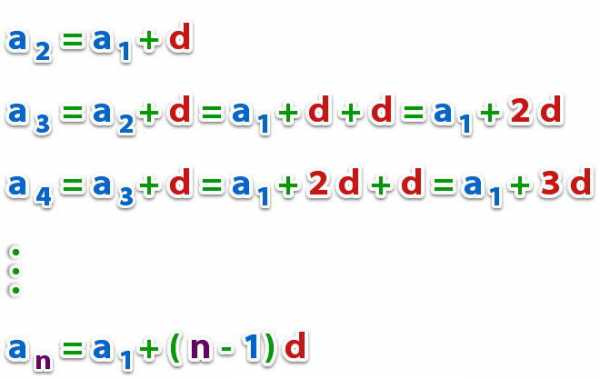
Условия многих задач составляются таким образом, что по известной паре чисел, номера которых в последовательности также даны, необходимо восстановить весь числовой ряд (найти разность и первый элемент). Сейчас мы решим эту задачу в общем виде.
Итак, пусть даны два элемента с номерами n и m. Пользуясь полученной выше формулой, можно составить систему из двух уравнений:
an = a1 + (n — 1) * d;
am = a1 + (m — 1) * d
Для нахождения неизвестных величин воспользуемся известным простым приемом решения такой системы: вычтем попарно левую и правую части, равенство при этом останется справедливым. Имеем:
an = a1 + (n — 1) * d;
an — am = (n — 1) * d — (m — 1) * d = d * (n — m)
Таким образом, мы исключили одну неизвестную (a1). Теперь можно записать окончательное выражение для определения d:
d = (an — am) / (n — m), где n > m
Мы получили очень простую формулу: чтобы вычислить разность d в соответствии с условиями задачи, необходимо лишь взять отношение разностей самих элементов и их порядковых номеров. Следует обратить на один важный момент внимание: разности берутся между «старшим» и «младшим» членами, то есть n > m («старший» — имеется в виду стоящий дальше от начала последовательности, его абсолютное значение может быть как больше, так и меньше более «младшего» элемента).
Выражение для разности d прогрессии следует подставить в любое из уравнений в начале решения задачи, чтобы получить значение первого члена.
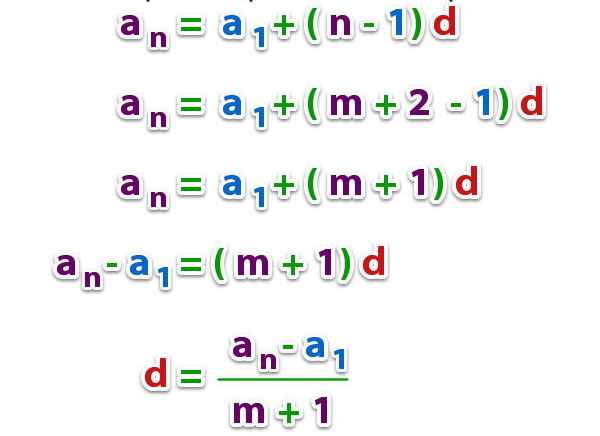
Далее в статье приведем примеры решения задач на вычисления d и на восстановление числового ряда алгебраической прогрессии. Здесь же хотелось бы отметить один важный момент.
В наш век развития компьютерных технологий многие школьники стараются найти решения для своих заданий в Интернете, поэтому часто возникают вопросы такого типа: найти разность арифметической прогрессии онлайн. По подобному запросу поисковик выдаст ряд web-страниц, перейдя на которые, нужно будет ввести известные из условия данные (это могут быть как два члена прогрессии, так и сумма некоторого их числа) и моментально получить ответ. Тем не менее такой подход к решению задачи является непродуктивным в плане развития школьника и понимания сути поставленной перед ним задачи.
Рекомендуется по указанным причинам самостоятельно решать подобные задачи. Кроме того, они не являются сложными.
Решение без использования формул

Решим первую задачу, при этом не будем использовать никакие из приведенных формул. Пусть даны элементы ряда: а6 = 3, а9 = 18. Найти разность прогрессии арифметической.
Известные элементы стоят близко друг к другу в ряду. Сколько раз нужно добавить разность d к наименьшему, чтобы получить наибольшее из них? Три раза (первый раз добавив d, мы получим 7-й элемент, второй раз — восьмой, наконец, третий раз — девятый). Какое число нужно добавить к трем три раза, чтобы получить 18? Это число пять. Действительно:
3 + 5 + 5 + 5 = 18
Таким образом, неизвестная разность d = 5.
Конечно же, решение можно было выполнить с применением соответствующей формулы, но этого не было сделано намеренно. Подробное объяснение решения задачи должно стать понятным и ярким примером, что такое арифметическая прогрессия.
Задача, подобная предыдущей
Теперь решим похожую задачу, но изменим входные данные. Итак, следует найти разность прогрессии арифметической, если а3 = 2, а9 = 19.
Конечно, можно прибегнуть снова к методу решения «в лоб». Но поскольку даны элементы ряда, которые стоят относительно далеко друг от друга, такой метод станет не совсем удобным. А вот использование полученной формулы быстро приведет нас к ответу:
d = (а9 — а3) / (9 — 3) = (19 — 2) / (6) = 17 / 6 ≈ 2,83
Здесь мы округлили конечное число. Насколько это округление привело к ошибке, можно судить, проверив полученный результат:
a9 = a3 + 2,83 + 2,83 + 2,83 + 2,83 + 2,83 + 2,83 = 18,98
Этот результат отличается всего на 0,1 % от значения, данного в условии. Поэтому использованное округление до сотых можно считать успешным выбором.
Задачи на применение формулы для an члена

Рассмотрим классический пример задачи на определение неизвестной d: найти разность прогрессии арифметической, если а1 = 12, а5 = 40.
Когда даны два числа неизвестной алгебраической последовательности, причем одним из них является элемент a1, тогда не нужно долго думать, а следует сразу же применить формулу для an члена. В данном случае имеем:
a5 = a1 + d * (5 — 1) => d = (a5 — a1) / 4 = (40 — 12) / 4 = 7
Мы получили точное число при делении, поэтому нет смысла проверять точность рассчитанного результата, как это было сделано в предыдущем пункте.
Решим еще одну аналогичную задачу: следует найти разность арифметической прогрессии, если а1 = 16, а8 = 37.
Используем аналогичный предыдущему подход и получаем:
a8 = a1 + d * (8 — 1) => d = (a8 — a1) / 7 = (37 — 16) / 7 = 3
Что еще следует знать о прогрессии арифметической
Помимо задач на нахождение неизвестной разности или отдельных элементов, часто необходимо решать проблемы суммы первых членов последовательности. Рассмотрение этих задач выходит за рамки темы статьи, тем не менее для полноты информации приведем общую формулу для суммы n чисел ряда:
∑ni = 1(ai) = n * (a1 + an) / 2
fb.ru
разность прогрессии — это… Что такое разность прогрессии?
- разность прогрессии
- мат. arithmetical ratio
Большой англо-русский и русско-английский словарь. 2001.
- разность потенциалов
- разность разделенная
Смотреть что такое «разность прогрессии» в других словарях:
РАЗНОСТЬ — (1) потенциалов (напряжение (см. (2))) количественная характеристика электрического поля неподвижных электрических зарядов () между двумя его точками, равная работе электрического поля по перемещению единичного положительного заряда из одной… … Большая политехническая энциклопедия
Арифметические прогрессии из простых чисел — Несколько простых чисел могут быть членами арифметической прогресии. Все последовательности простых чисел, являющихся строго последовательными элементами некоторой арифметической прогрессии, конечны, однако существуют сколь угодно длинные такие… … Википедия
Теорема Дирихле о простых числах в арифметической прогрессии — У этого термина существуют и другие значения, см. Теорема Дирихле. Теорема Дирихле о простых числах в арифметической прогрессии гласит: Каждая арифметическая прогрессия, первый член и разность которой натуральные взаимно простые числа,… … Википедия
Арифметическая прогрессия — У этого термина существуют и другие значения, см. Прогрессия. Арифметическая прогрессия числовая последовательность вида , то есть последовательность чисел (членов прогрессии), каждое из которых, начиная со второго, получается из… … Википедия
Чисел теория — наука о целых числах. Понятие целого числа (См. Число), а также арифметических операций над числами известно с древних времён и является одной из первых математических абстракций. Особое место среди целых чисел, т. е. чисел…, 3 … Большая советская энциклопедия
ИНТЕРПОЛЯЦИЯ — (interpolatio), пополнение эмпйрич. ряда значений какой либо величины недостающими промежуточными значениями ее. Интерполирование может быть произведено тремя способами: математич., графич. и логическим. В основе их лежит общая им гипотеза о том … Большая медицинская энциклопедия
Норфолк Иоанн — английский математик. Жил в первой половине XV в., т. е. в эпоху сравнительного упадка занятий математикой в Англии. В настоящее время известны читанные им в 1445 г. лекции о прогрессиях. Приписывая сохранение сведений об этих последних в Европе… … Энциклопедический словарь Ф.А. Брокгауза и И.А. Ефрона
Норфольк Иоанн — английский математик. Жил в первой половине XV в., т. е. в эпоху сравнительного упадка занятий математикой в Англии. В настоящее время известны читанные им в 1445 г. лекции о прогрессиях. Приписывая сохранение сведений об этих последних в Европе… … Энциклопедический словарь Ф.А. Брокгауза и И.А. Ефрона
ПРОГРЕССИЯ — последовательность чисел, получаемых по некоторому правилу. Термин ныне во многом устарел и встречается только в сочетаниях арифметическая прогрессия и геометрическая прогрессия . Арифметическая прогрессия это последовательность чисел, в которой… … Энциклопедия Кольера
РАСПРЕДЕЛЕНИЕ ПРОСТЫХ ЧИСЕЛ — раздел теории чисел, в к ром изучаются закономерности распределения простых чисел (п. ч.) среди натуральных чисел. Центральной является проблема наилучшего асимптотич. выражения при функции p(х), обозначающей число п. ч., не превосходящих х, а… … Математическая энциклопедия
Арифметика — Ганс Себальд Бехам. Арифметика. XVI век Арифметика (др. греч. ἀ … Википедия
dic.academic.ru
разность арифметической прогрессии — это… Что такое разность арифметической прогрессии?
- разность арифметической прогрессии
- common difference
Большой англо-русский и русско-английский словарь. 2001.
- разность n-го порядка
- разность векторов
Смотреть что такое «разность арифметической прогрессии» в других словарях:
Теорема Дирихле о простых числах в арифметической прогрессии — У этого термина существуют и другие значения, см. Теорема Дирихле. Теорема Дирихле о простых числах в арифметической прогрессии гласит: Каждая арифметическая прогрессия, первый член и разность которой натуральные взаимно простые числа,… … Википедия
РАЗНОСТЬ — (1) потенциалов (напряжение (см. (2))) количественная характеристика электрического поля неподвижных электрических зарядов () между двумя его точками, равная работе электрического поля по перемещению единичного положительного заряда из одной… … Большая политехническая энциклопедия
Арифметические прогрессии из простых чисел — Несколько простых чисел могут быть членами арифметической прогресии. Все последовательности простых чисел, являющихся строго последовательными элементами некоторой арифметической прогрессии, конечны, однако существуют сколь угодно длинные такие… … Википедия
Арифметическая прогрессия — У этого термина существуют и другие значения, см. Прогрессия. Арифметическая прогрессия числовая последовательность вида , то есть последовательность чисел (членов прогрессии), каждое из которых, начиная со второго, получается из… … Википедия
ПРОГРЕССИЯ — последовательность чисел, получаемых по некоторому правилу. Термин ныне во многом устарел и встречается только в сочетаниях арифметическая прогрессия и геометрическая прогрессия . Арифметическая прогрессия это последовательность чисел, в которой… … Энциклопедия Кольера
ЛОГАРИФМ — число, применение которого позволяет упростить многие сложные операции арифметики. Использование в вычислениях вместо чисел их логарифмов позволяет заменить умножение более простой операцией сложения, деление вычитанием, возведение в степень… … Энциклопедия Кольера
РАСПРЕДЕЛЕНИЕ ПРОСТЫХ ЧИСЕЛ — раздел теории чисел, в к ром изучаются закономерности распределения простых чисел (п. ч.) среди натуральных чисел. Центральной является проблема наилучшего асимптотич. выражения при функции p(х), обозначающей число п. ч., не превосходящих х, а… … Математическая энциклопедия
Чисел теория — наука о целых числах. Понятие целого числа (См. Число), а также арифметических операций над числами известно с древних времён и является одной из первых математических абстракций. Особое место среди целых чисел, т. е. чисел…, 3 … Большая советская энциклопедия
Арифметика — Ганс Себальд Бехам. Арифметика. XVI век Арифметика (др. греч. ἀ … Википедия
Карацуба — Карацуба, Анатолий Алексеевич Карацуба Анатолий Алексеевич Дата рождения: 31 января 1937(1937 01 31) … Википедия
Карацуба, Анатолий Алексеевич — Карацуба Анатолий Алексеевич Дата рождения: 31 января 1937 … Википедия
dic.academic.ru
разность прогрессии — это… Что такое разность прогрессии?
- разность прогрессии
Mathematics: arithmetical ratio
Универсальный русско-английский словарь. Академик.ру. 2011.
- разность при нормальными приращениями времени
- разность прямых восхождений
Смотреть что такое «разность прогрессии» в других словарях:
РАЗНОСТЬ — (1) потенциалов (напряжение (см. (2))) количественная характеристика электрического поля неподвижных электрических зарядов () между двумя его точками, равная работе электрического поля по перемещению единичного положительного заряда из одной… … Большая политехническая энциклопедия
Арифметические прогрессии из простых чисел — Несколько простых чисел могут быть членами арифметической прогресии. Все последовательности простых чисел, являющихся строго последовательными элементами некоторой арифметической прогрессии, конечны, однако существуют сколь угодно длинные такие… … Википедия
Теорема Дирихле о простых числах в арифметической прогрессии
Арифметическая прогрессия — У этого термина существуют и другие значения, см. Прогрессия. Арифметическая прогрессия числовая последовательность вида , то есть последовательность чисел (членов прогрессии), каждое из которых, начиная со второго, получается из… … Википедия
Чисел теория — наука о целых числах. Понятие целого числа (См. Число), а также арифметических операций над числами известно с древних времён и является одной из первых математических абстракций. Особое место среди целых чисел, т. е. чисел…, 3 … Большая советская энциклопедия
ИНТЕРПОЛЯЦИЯ — (interpolatio), пополнение эмпйрич. ряда значений какой либо величины недостающими промежуточными значениями ее. Интерполирование может быть произведено тремя способами: математич., графич. и логическим. В основе их лежит общая им гипотеза о том … Большая медицинская энциклопедия
Норфолк Иоанн — английский математик. Жил в первой половине XV в., т. е. в эпоху сравнительного упадка занятий математикой в Англии. В настоящее время известны читанные им в 1445 г. лекции о прогрессиях. Приписывая сохранение сведений об этих последних в Европе… … Энциклопедический словарь Ф.А. Брокгауза и И.А. Ефрона
Норфольк Иоанн — английский математик. Жил в первой половине XV в., т. е. в эпоху сравнительного упадка занятий математикой в Англии. В настоящее время известны читанные им в 1445 г. лекции о прогрессиях. Приписывая сохранение сведений об этих последних в Европе… … Энциклопедический словарь Ф.А. Брокгауза и И.А. Ефрона
ПРОГРЕССИЯ — последовательность чисел, получаемых по некоторому правилу. Термин ныне во многом устарел и встречается только в сочетаниях арифметическая прогрессия и геометрическая прогрессия . Арифметическая прогрессия это последовательность чисел, в которой… … Энциклопедия Кольера
РАСПРЕДЕЛЕНИЕ ПРОСТЫХ ЧИСЕЛ — раздел теории чисел, в к ром изучаются закономерности распределения простых чисел (п. ч.) среди натуральных чисел. Центральной является проблема наилучшего асимптотич. выражения при функции p(х), обозначающей число п. ч., не превосходящих х, а… … Математическая энциклопедия
Арифметика — Ганс Себальд Бехам. Арифметика. XVI век Арифметика (др. греч. ἀ … Википедия
universal_ru_en.academic.ru
разность арифметической прогрессии — это… Что такое разность арифметической прогрессии?
- разность арифметической прогрессии
common difference
Русско-английский математический словарь. 2013.
- разность
- разный
Смотреть что такое «разность арифметической прогрессии» в других словарях:
Теорема Дирихле о простых числах в арифметической прогрессии — У этого термина существуют и другие значения, см. Теорема Дирихле. Теорема Дирихле о простых числах в арифметической прогрессии гласит: Каждая арифметическая прогрессия, первый член и разность которой натуральные взаимно простые числа,… … Википедия
РАЗНОСТЬ — (1) потенциалов (напряжение (см. (2))) количественная характеристика электрического поля неподвижных электрических зарядов () между двумя его точками, равная работе электрического поля по перемещению единичного положительного заряда из одной… … Большая политехническая энциклопедия
Арифметические прогрессии из простых чисел — Несколько простых чисел могут быть членами арифметической прогресии. Все последовательности простых чисел, являющихся строго последовательными элементами некоторой арифметической прогрессии, конечны, однако существуют сколь угодно длинные такие… … Википедия
Арифметическая прогрессия — У этого термина существуют и другие значения, см. Прогрессия. Арифметическая прогрессия числовая последовательность вида , то есть последовательность чисел (членов прогрессии), каждое из которых, начиная со второго, получается из… … Википедия
ПРОГРЕССИЯ — последовательность чисел, получаемых по некоторому правилу. Термин ныне во многом устарел и встречается только в сочетаниях арифметическая прогрессия и геометрическая прогрессия . Арифметическая прогрессия это последовательность чисел, в которой… … Энциклопедия Кольера
ЛОГАРИФМ — число, применение которого позволяет упростить многие сложные операции арифметики. Использование в вычислениях вместо чисел их логарифмов позволяет заменить умножение более простой операцией сложения, деление вычитанием, возведение в степень… … Энциклопедия Кольера
РАСПРЕДЕЛЕНИЕ ПРОСТЫХ ЧИСЕЛ — раздел теории чисел, в к ром изучаются закономерности распределения простых чисел (п. ч.) среди натуральных чисел. Центральной является проблема наилучшего асимптотич. выражения при функции p(х), обозначающей число п. ч., не превосходящих х, а… … Математическая энциклопедия
Чисел теория — наука о целых числах. Понятие целого числа (См. Число), а также арифметических операций над числами известно с древних времён и является одной из первых математических абстракций. Особое место среди целых чисел, т. е. чисел…, 3 … Большая советская энциклопедия
Арифметика — Ганс Себальд Бехам. Арифметика. XVI век Арифметика (др. греч. ἀ … Википедия
Карацуба — Карацуба, Анатолий Алексеевич Карацуба Анатолий Алексеевич Дата рождения: 31 января 1937(1937 01 31) … Википедия
Карацуба, Анатолий Алексеевич — Карацуба Анатолий Алексеевич Дата рождения: 31 января 1937 … Википедия
mathematical_ru_en.academic.ru
Что такое разность в арифметической прогрессии
Данная методическая разработка предназначена для изучения темы по геометрии в курсе изучения 7 класса Теоремы об углах,образованных двумя параллельными прямыми секущей .Не секрет,что многие дети испытывают затруднения при изучении данной темы.Основная причина-не.
Арифметическая прогрессия
Числовую последовательность, каждый член которой, начиная со второго, равен сумме предыдущего члена и одного и того же числа d, называют Арифметической прогрессией.
Число D называют Разностью арифметической прогрессии
Если разность между последующим и предыдущим членами последовательности есть одно и то же число, то это Арифметическая прогрессия. Разумеется, при этом предполагается, что обнаруженная закономерность справедлива не только для явно выписанных членов последовательности, но и для всей последовательности в целом.
Арифметическая прогрессия считается Конечной, если рассматриваются только ее первые несколько членов.
Арифметическая прогрессия является:
Возрастающей последовательностью, если D > 0, например, 1, 3, 5, 7, 9,11.
Таким образом, каждый член арифметической прогрессии, начиная со второго, равен среднему арифметическому двух соседних с ним членов. Этим объясняется название «арифметическая» прогрессия.
Арифметическая прогрессия может быть задана следующими способами:
В) формулой вида, An = k·n + b , где k и b – числа, n – номер? N
Сумма n членов арифметической прогрессии:
Основные определения и данные для арифметической прогрессии сведенные в одну таблицу:
При хранении бревен строевого леса их укладывают так, как показано на рисунке. Сколько бревен находится в одной кладке, если в ее основании положено 12 бревен?
Кладку бревен рассмотрим в виде арифметической прогрессии, где а1= 1, а2= 2, аn= 12
Ответ: 78 бревен.
Найти сумму двенадцати первых членов арифметической прогрессии, если: а1 = -5, d = 0,5
Что такое разность в арифметической прогрессии
Арифметическая прогрессия
Числовую последовательность, каждый член которой, начиная со второго, равен сумме предыдущего члена и одного и того же числа d, называют Арифметической прогрессией.
Число D называют Разностью арифметической прогрессии
Если разность между последующим и предыдущим членами последовательности есть одно и то же число, то это Арифметическая прогрессия. Разумеется, при этом предполагается, что обнаруженная закономерность справедлива не только для явно выписанных членов последовательности, но и для всей последовательности в целом.
Арифметическая прогрессия считается Конечной, если рассматриваются только ее первые несколько членов.
Арифметическая прогрессия является:
Возрастающей последовательностью, если D > 0, например, 1, 3, 5, 7, 9,11.
Таким образом, каждый член арифметической прогрессии, начиная со второго, равен среднему арифметическому двух соседних с ним членов. Этим объясняется название «арифметическая» прогрессия.
Арифметическая прогрессия может быть задана следующими способами:
В) формулой вида, An = k·n + b , где k и b – числа, n – номер? N
Сумма n членов арифметической прогрессии:
Основные определения и данные для арифметической прогрессии сведенные в одну таблицу:
При хранении бревен строевого леса их укладывают так, как показано на рисунке. Сколько бревен находится в одной кладке, если в ее основании положено 12 бревен?
Кладку бревен рассмотрим в виде арифметической прогрессии, где а1= 1, а2= 2, аn= 12
Ответ: 78 бревен.
Найти сумму двенадцати первых членов арифметической прогрессии, если: а1 = -5, d = 0,5
Что такое разность в арифметической прогрессии
Арифметическая прогрессия.
К этой теме имеются дополнительные
Для тех, кто сильно «не очень. «
И для тех, кто «очень даже. » )
Арифметическая прогрессия — это ряд чисел, в котором каждое число больше (или меньше) предыдущего на одну и ту же величину.
Эта тема частенько представляется сложной и непонятной. Индексы у буковок, n-й член прогрессии, разность прогрессии — всё это как-то смущает, да. Разберёмся со смыслом арифметической прогрессии и всё сразу наладится.)
Понятие арифметической прогрессии.
Арифметическая прогрессия — понятие очень простое и чёткое. Сомневаетесь? Зря.) Смотрите сами.
Я напишу незаконченный ряд чисел:
Сможете продлить этот ряд? Какие числа пойдут дальше, за пятёркой? Каждый. э-э-э. короче, каждый сообразит, что дальше пойдут числа 6, 7, 8, 9 и т. д.
Усложним задачу. Даю незаконченный ряд чисел:
Сможете уловить закономерность, продлить ряд, и назвать седьмое число ряда?
Если сообразили, что это число 20 — я вас поздравляю! Вы не только почувствовали ключевые моменты арифметической прогрессии, но и успешно употребили их в дело! Если не сообразили — читаем дальше.
А теперь переведём ключевые моменты из ощущений в математику.)
Первый ключевой момент.
Арифметическая прогрессия имеет дело с рядами чисел. Это и смущает поначалу. Мы привыкли уравнения решать, графики строить и всё такое. А тут продлить ряд, найти число ряда.
Ничего страшного. Просто прогрессии — это первое знакомство с новым разделом математики. Раздел называется «Ряды» и работает именно с рядами чисел и выражений. Привыкайте.)
Второй ключевой момент.
В арифметической прогрессии любое число отличается от предыдущего На одну и ту же величину.
В первом примере эта разница — единичка. Какое число ни возьми, оно больше предыдущего на единичку. Во втором — тройка. Любое число больше предыдущего
poiskvstavropole.ru
