4.3. Продуктивные модели Леонтьева
Матрица A, все элементы которой
неотрицательны, называетсяпродуктивной,
если для любого вектора с неотрицательными компонентами
существует решение уравнения вектор
с неотрицательными компонентами
существует решение уравнения вектор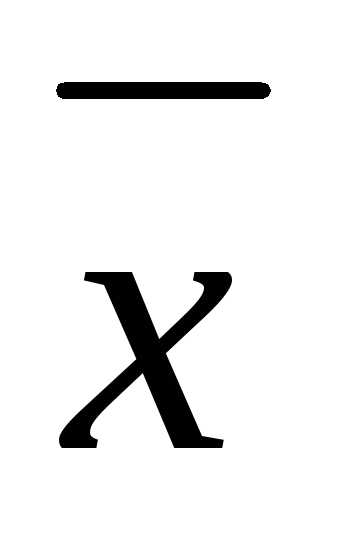 ,
все элементы которого неотрицательны.
В таком случае и модель Леонтьева
называется продуктивной.
,
все элементы которого неотрицательны.
В таком случае и модель Леонтьева
называется продуктивной.
Для уравнения типа (57) разработана соответствующая математическая теория исследования решения и его особенностей. Укажем некоторые ее основные моменты. Приведем без доказательства важную теорему, позволяющую устанавливать продуктивность матрицы.
Теорема.Если для матрицыAс
неотрицательными элементами и некоторого
вектора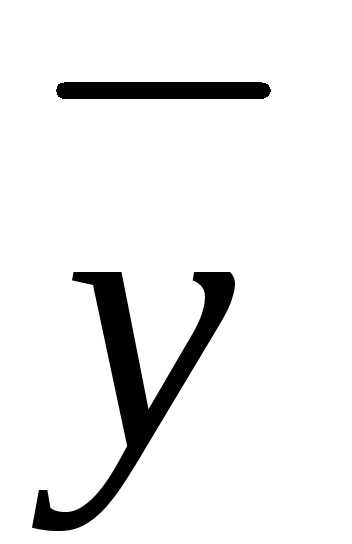
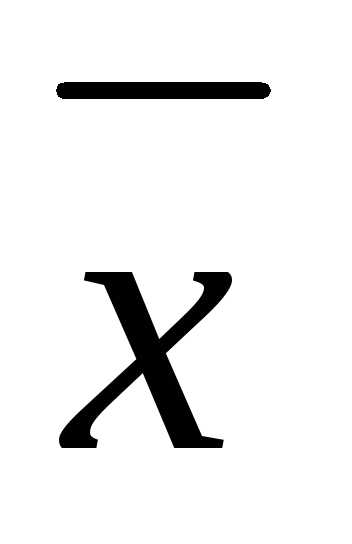 с
неотрицательными компонентами, то
матрицаAпродуктивна.
с
неотрицательными компонентами, то
матрицаAпродуктивна.Иными
словами, достаточно установить наличие
положительного решения системы (57) хотя
бы для одного положительного вектора  ,
чтобы матрицаAбыла
продуктивной. Перепишем систему (57) с
использованием единичной матрицыEв виде
,
чтобы матрицаAбыла
продуктивной. Перепишем систему (57) с
использованием единичной матрицыEв виде
. (58)
Если
существует обратная матрица 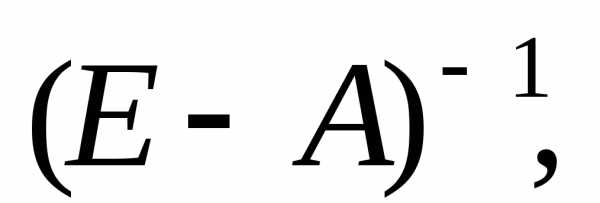 то
существует и единственное решение
уравнения (58):
то
существует и единственное решение
уравнения (58):
(59)
Матрица 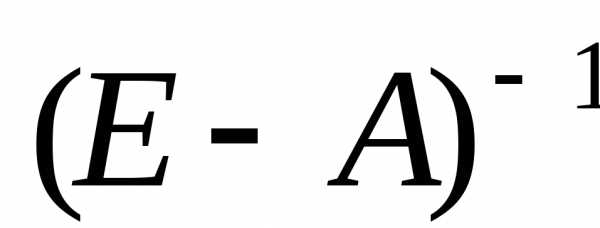 называется матрицейполных затрат.
называется матрицейполных затрат.
Первый
критерий продуктивности. МатрицаAпродуктивна тогда и только тогда, когда
матрица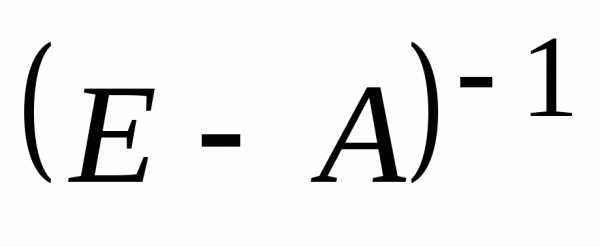 существует и ее элементы неотрицательны.
существует и ее элементы неотрицательны.
Второй критерий продуктивности. МатрицаAс неотрицательными элементами продуктивна, если сумма элементов по любому ее столбцу (строке) не превосходит единицы:
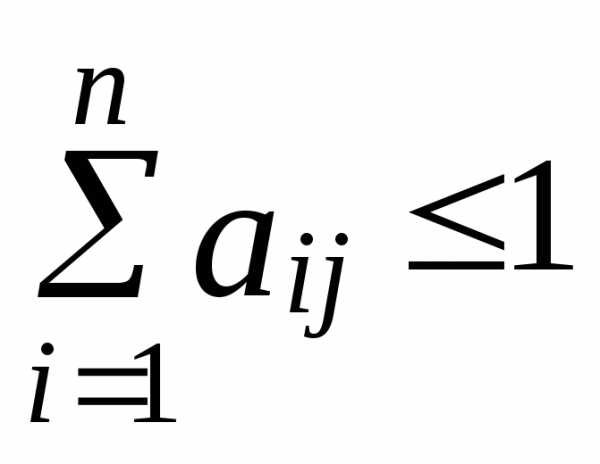 ,
,
причем хотя бы для одного столбца (строки) эта сумма строго меньше единицы.
Рассмотрим применение модели Леонтьева на примерах.
Пример 14.
В таблице 2 приведены данные по балансу за некоторый период между пятью отраслями промышленности.
Найти векторы конечного потребления и валового выпуска, а также матрицу коэффициентов прямых затрат и определить, является ли она продуктивной в соответствии с приведенными выше критериями.
Таблица 2
Данные по балансу
№ | Отрасль | Потребление xij | Конечный продукт yi | Валовой выпуск xi | ||||
1 | 2 | 3 | 4 | 5 | ||||
1 | Станкостроение | 15 | 12 | 24 | 23 | 16 | 10 | 100 |
2 | Энергетика | 10 | 3 | 35 | 15 | 7 | 30 | 100 |
3 | Машиностроение | 10 | 5 | 10 | 10 | 10 | 5 | 50 |
4 | Автомобильная промышленность | 10 | 5 | 10 | 5 | 5 | 15 | 50 |
5 | Добыча и переработка углеводородов | 7 | 15 | 15 | 10 | 3 | 50 | 100 |
Данные
в таблице 2 приведены в соответствии с
соотношениями (52): 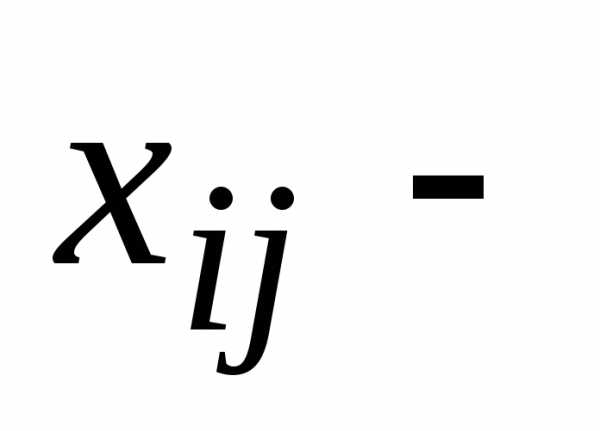 первые
пять столбцов,- шестой столбец,
первые
пять столбцов,- шестой столбец,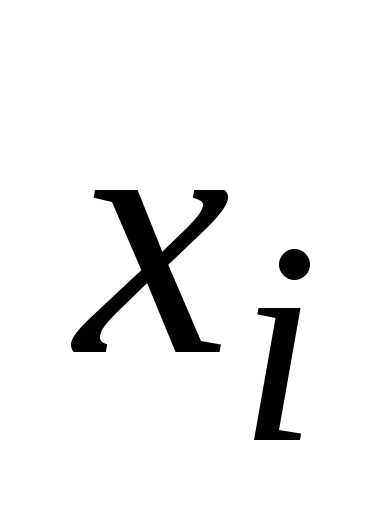 —
последний столбец (i,j=1,
2, 3, 4, 5).
—
последний столбец (i,j=1,
2, 3, 4, 5).
Согласно используемым обозначениям,
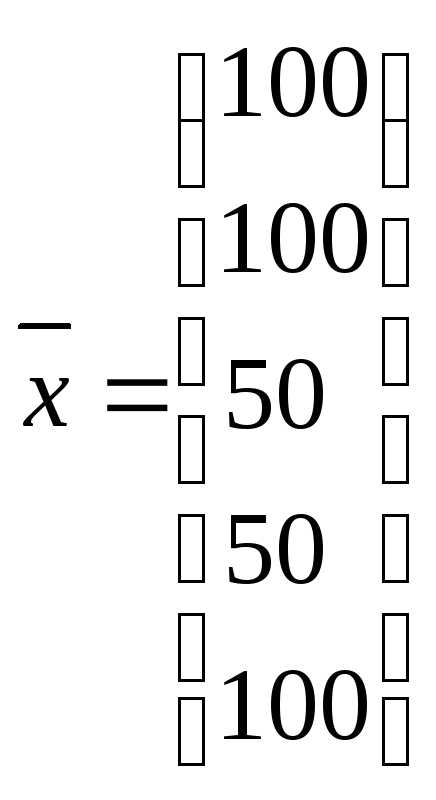 ,
, 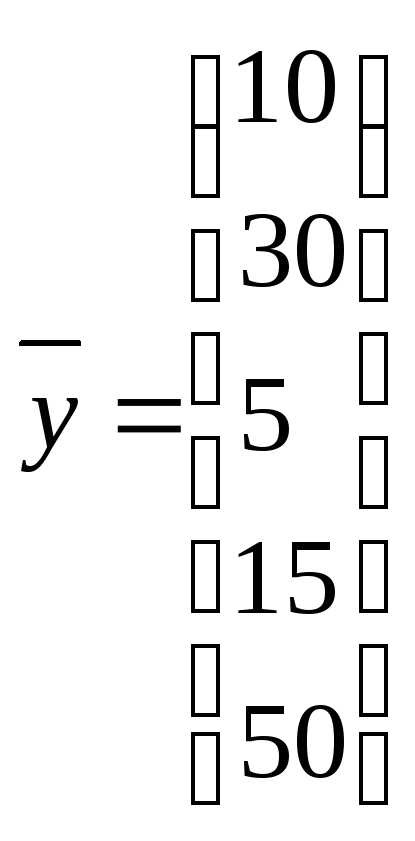 ,
,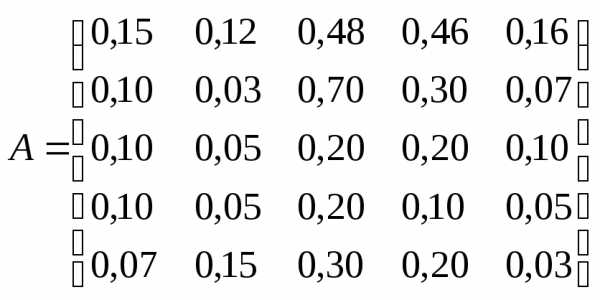 .
.
Все элементы матрицы A положительны, однако нетрудно видеть, что их сумма в третьем и четвертом столбцах больше единицы. Следовательно, условия второго критерия продуктивности не соблюдены, и матрица A не является продуктивной.
Экономическая причина этой непродуктивности заключается в том, что внутреннее потребление отраслей 3 и 4 слишком велико в соотношении с их валовым выпуском.
Пример 15.
Таблица 3 содержит данные баланса трех отраслей промышленности за некоторый период. Требуется найти объем валового выпуска продукции, если конечное потребление по отраслям увеличить соответственно до 60, 70 и 30.
Таблица 3
Данные по балансу
№ п/п | Отрасль | Потребление | Конечный продукт | Валовой выпуск | ||
1 | 2 | 3 | ||||
1 | Добыча и переработка углеводородов | 5 | 35 | 20 | 40 | 100 |
2 | Энергетика | 10 | 10 | 20 | 60 | 100 |
3 | Машиностроение | 20 | 10 | 10 | 10 | 50 |
Решение.
Выпишем
векторы валового выпуска 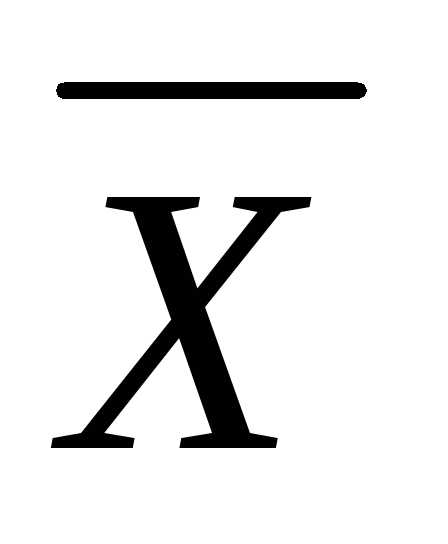 и
конечного потребления
и
конечного потребления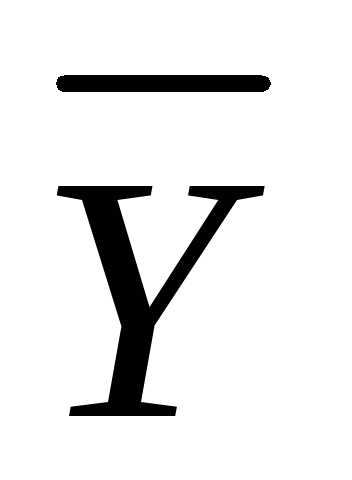 :
:
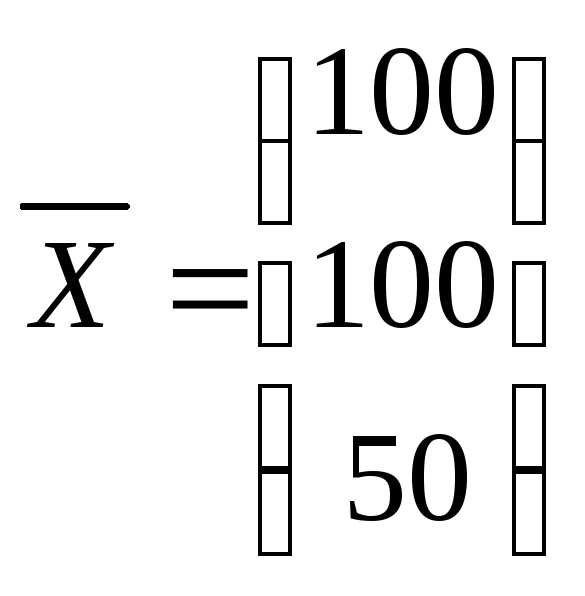 ,
, 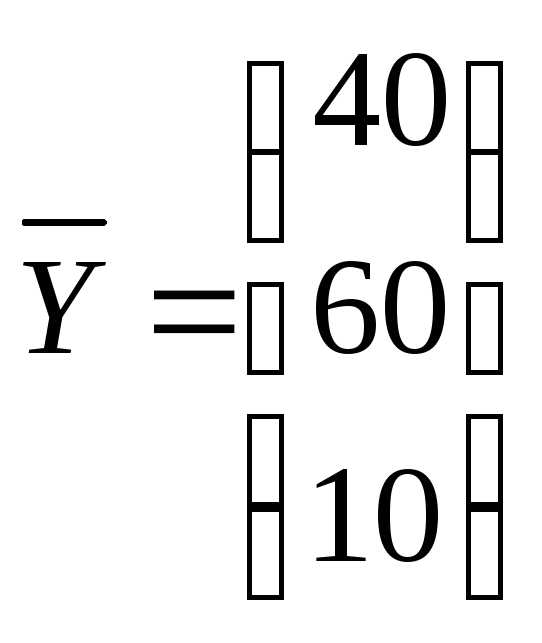 ,
,
Согласно
формулам
вычислим :
:
;
;
.
В результате получаем матрицу коэффициентов прямых затрат:

Требования:  неотрицателен;
неотрицателен;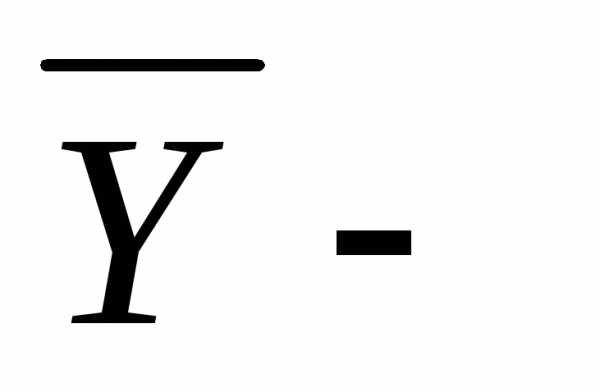 неотрицателен;A– из неотрицательных
элементов – выполнены.
неотрицателен;A– из неотрицательных
элементов – выполнены.
Если
существует 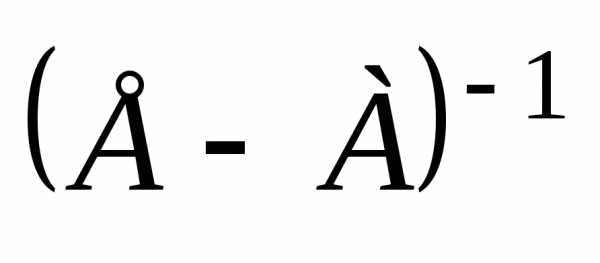 ,
то существует и единственное решение
уравнения
,
то существует и единственное решение
уравнения
Матрица 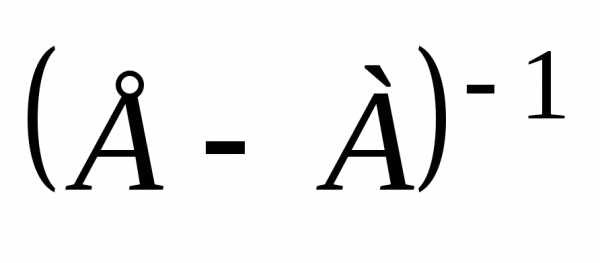 есть матрица полных затрат.
есть матрица полных затрат.
1) Матрица Aпродуктивна тогда
и только тогда, когда матрица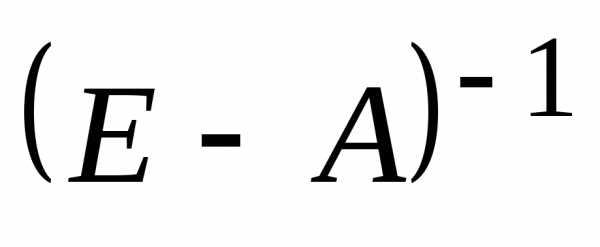 существует и ее элементы неотрицательны.
существует и ее элементы неотрицательны.
2) Матрица Aс неотрицательными
элементами продуктивна, если сумма
элементов по любому ее столбцу (строке)
не превосходит единицы: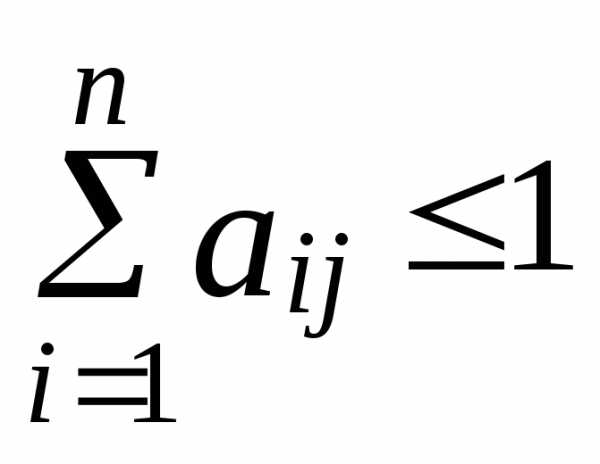
Вывод.Все условия выполнены. МатрицаAудовлетворяет критериям продуктивности.
Новый вектор конечного продукта должен иметь вид:
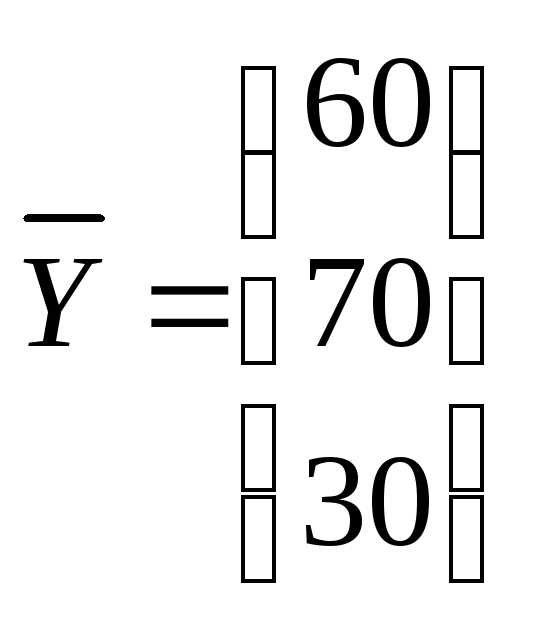 .
.
Компоненты 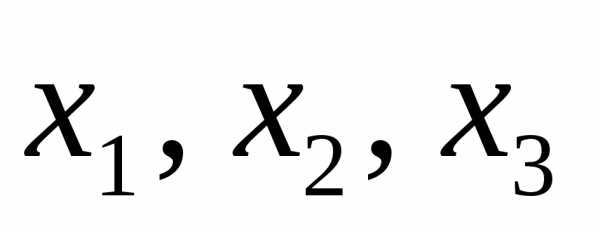 неизвестного
неизвестного находятся из системы уравнений, которая,
согласно (59), имеет вид:
находятся из системы уравнений, которая,
согласно (59), имеет вид:
или
 ;
;  ;
; .
.
.
Выводы.Чтобы обеспечить заданное увеличение
компонент вектора конечного продукта
с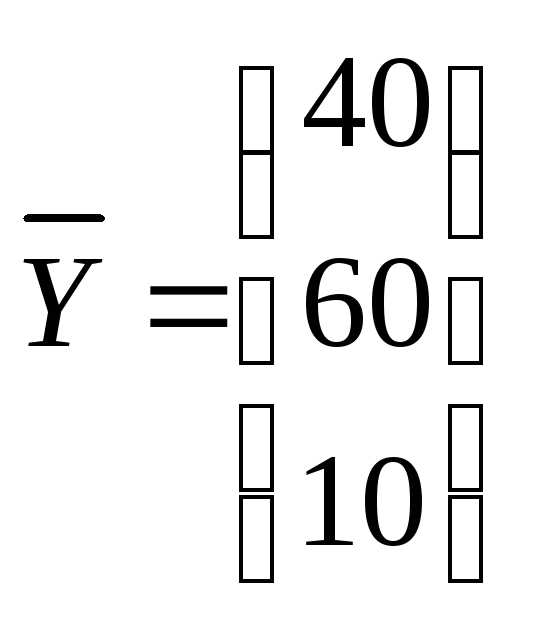 до
до ,
необходимо увеличить соответствующие
валовые выпуски: добычу и переработку
углеводородов со 100 до 152,14, то есть на
52,14%, уровень энергетики со 100 до 135,8, то
есть на 35,8%, выпуск машиностроения с 50
до 92,51, то есть на 85,02%.
,
необходимо увеличить соответствующие
валовые выпуски: добычу и переработку
углеводородов со 100 до 152,14, то есть на
52,14%, уровень энергетики со 100 до 135,8, то
есть на 35,8%, выпуск машиностроения с 50
до 92,51, то есть на 85,02%.
studfiles.net
Тема 3. Системы линейных уравнений. Модель Леонтьева.
…Система
уравнений вида: 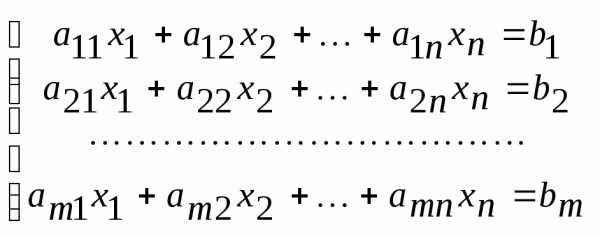 называетсясистемой
называетсясистемой  линейных уравнений с
линейных уравнений с неизвестными.
Числа
неизвестными.
Числа  называются коэффициентами системы,
называются коэффициентами системы,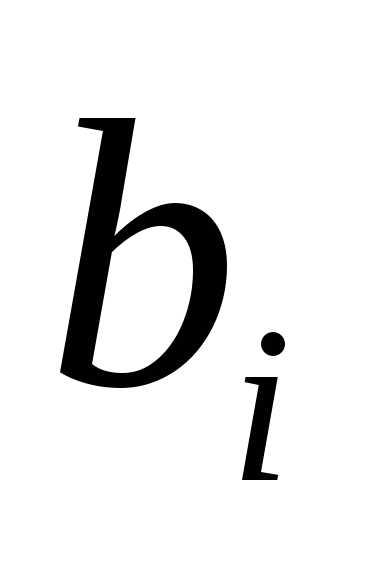 — свободными членами системы,
— свободными членами системы, — неизвестными системы.
— неизвестными системы.
В
матричной форме система имеет вид:
,
где ,
, ,
, .Здесь
.Здесь -матрица
системы,
-матрица
системы,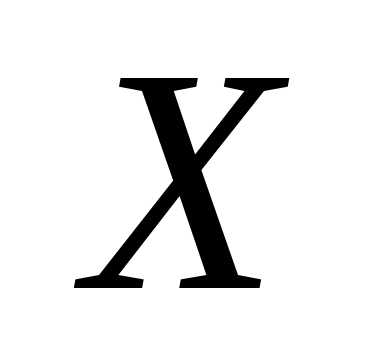 -матрица-столбец
неизвестных,
-матрица-столбец
неизвестных, -матрица-столбец
свободных членов.
-матрица-столбец
свободных членов.
Если 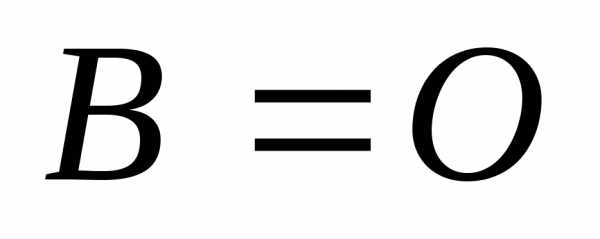 ,
то система называетсяоднородной, в противном
случае неоднородной.
,
то система называетсяоднородной, в противном
случае неоднородной.
Система,
матрица  которой является треугольной с
диагональными элементами
которой является треугольной с
диагональными элементами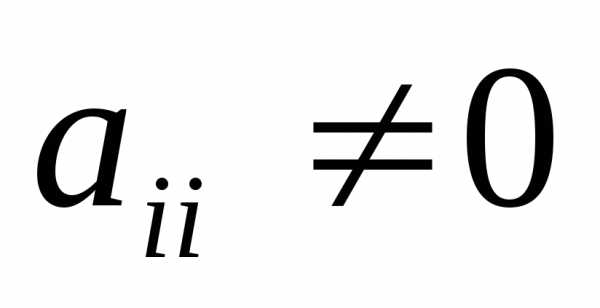 ,
называетсятреугольной. Система,
матрица
,
называетсятреугольной. Система,
матрица  которой является трапециевидной,
называетсятрапециевидной.
которой является трапециевидной,
называетсятрапециевидной.
Решением системы называется всякий упорядоченный набор чисел , обращающий каждое уравнение системы в равенство. Совокупность всех решений называетсямножеством решений системы.
Система называется совместной, если она имеет, по крайней мере, одно решение; определённой, если она имеет только одно решение; неопределённой, если она имеет бесконечно много решений; несовместной, если она не имеет решений.
Однородная система уравнений всегда совместна, так как всегда имеет, по крайней мере, нулевое решение . Треугольная система является определённой, трапециевидная система – неопределённой.
Две системы называются эквивалентными, если множества их решений совпадают.
Элементарными преобразованиями систем уравнений называются:
1) перестановка уравнений;
2) перестановка местами слагаемых 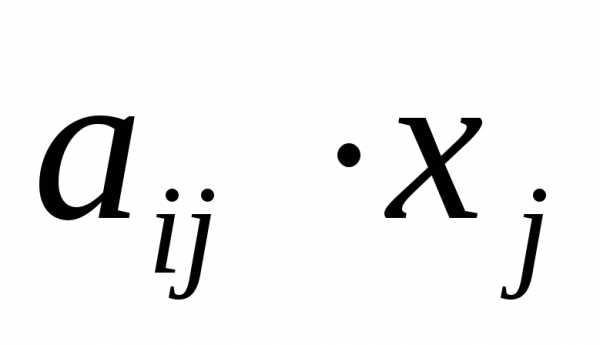 в каждом из уравнений системы;
в каждом из уравнений системы;
3) умножение уравнения на число, отличное от нуля;
4) прибавление к уравнению другого, умноженного на любое число;
5) вычёркивание уравнения вида: .
Основными точными методами решения систем линейных уравнений являются методы: Крамера, обратной матрицы и Гаусса.
Если
число уравнений в системе 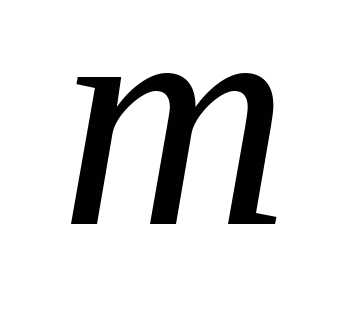 совпадает с числом неизвестных
совпадает с числом неизвестных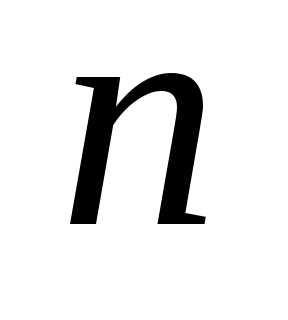 и определитель матрицы системы,
то система имеет единственное решение,
которое можно найти:
и определитель матрицы системы,
то система имеет единственное решение,
которое можно найти:
а) методом
Крамера по формулам: 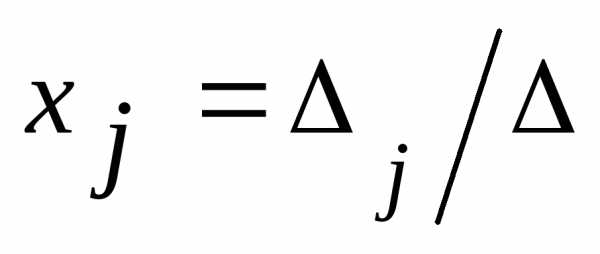 ,
,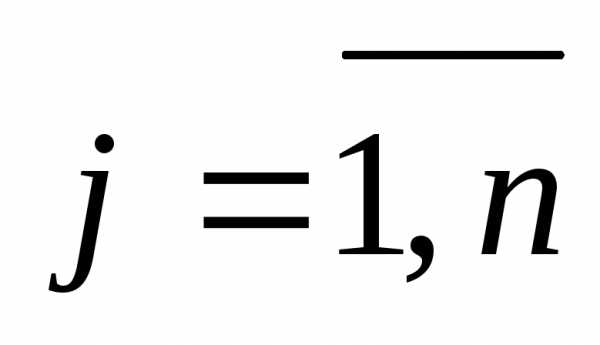 ,где
,где  —
определитель, получаемый из определителя
матрицы системы
—
определитель, получаемый из определителя
матрицы системы заменой
заменой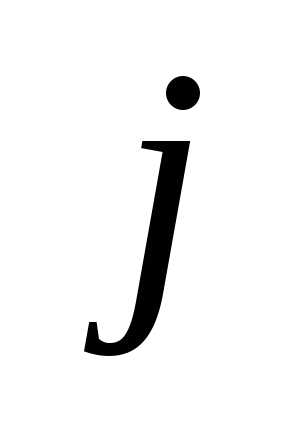 -ого
столбца на столбец свободных членов;
-ого
столбца на столбец свободных членов;
б) методом обратной матрицы по формуле .
Методом Гаусса находят решение произвольной системы линейных уравнений. Метод состоит в приведении системы уравнений, с помощью элементарных преобразований, к системе специального вида, эквивалентной исходной, решение которой очевидно. Преобразования по методу Гаусса выполняют в два этапа. Первый этап называют прямым ходом, второй — обратным.
В
результате прямого
хода выясняют:
совместна или нет система и если совместна
то, сколько имеет решений — одно или
бесконечно много, а также, в случае
бесконечного множества решений, указывают
базисные и свободные неизвестные для
записи общего решения системы.
Преобразования прямого хода выполняют,
как правило, над расширенной матрицей
системы
,
которую получают, приписывая справа к
матрице системы столбец свободных членов
столбец свободных членов .
В результате элементарных преобразований
строк и перестановкой столбцов, матрица
системы
.
В результате элементарных преобразований
строк и перестановкой столбцов, матрица
системы должна быть приведена к матрице
должна быть приведена к матрице треугольного или трапециевидного вида
с элементами
треугольного или трапециевидного вида
с элементами .
При этом, система уравнений, матрица
которой
.
При этом, система уравнений, матрица
которой ,
является треугольной с диагональными
элементами
,
является треугольной с диагональными
элементами  ,
будет иметь единственное решение;
система уравнений, матрица которой
,
будет иметь единственное решение;
система уравнений, матрица которой ,
является трапециевидной с элементами
,
является трапециевидной с элементами ,
будет иметь бесконечно много решений.
Если, при выполнении преобразований
расширенной матрицы
,
будет иметь бесконечно много решений.
Если, при выполнении преобразований
расширенной матрицы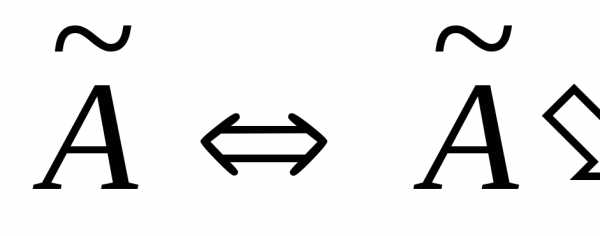 ,
в преобразованной матрице
,
в преобразованной матрице появится строка,
где
появится строка,
где ,
то это говорит о несовместности исходной
системы уравнений. Базисные неизвестные
указывают, выписывая базисный минор
преобразованной матрицы системы
,
то это говорит о несовместности исходной
системы уравнений. Базисные неизвестные
указывают, выписывая базисный минор
преобразованной матрицы системы .
Базисными являются неизвестные
преобразованной системы, столбцы
коэффициентов
.
Базисными являются неизвестные
преобразованной системы, столбцы
коэффициентов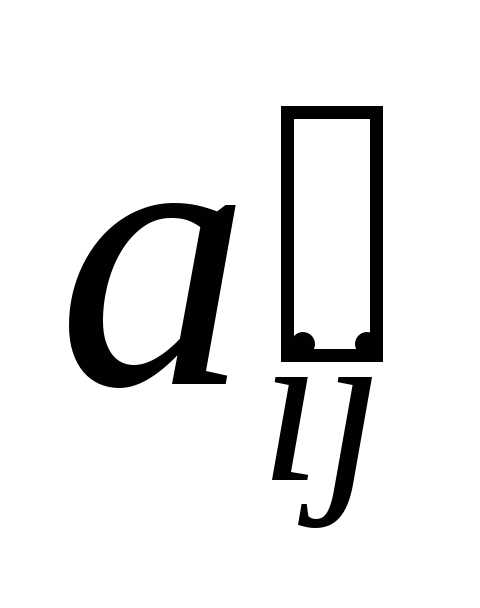 при которых образуют базисный минор
(определитель максимального порядка,
отличный от нуля). Свободными являются
неизвестные, не являющиеся базисными.
при которых образуют базисный минор
(определитель максимального порядка,
отличный от нуля). Свободными являются
неизвестные, не являющиеся базисными.
В
результате обратного хода находят решение системы, записывая его
в виде общего решения, если их бесконечно
много. Преобразования обратного хода
часто выполняют, над уравнениями системы,
соответствующей последней расширенной
матрице  прямого хода. В случае единственного
решения, его получают, находя последовательно
значения всех неизвестных из уравнений
системы, начиная с последнего. В случае,
когда решений бесконечно много, их
записывают в виде общего решения. Для
этого свободным неизвестным придают
разные произвольные постоянные значения:
прямого хода. В случае единственного
решения, его получают, находя последовательно
значения всех неизвестных из уравнений
системы, начиная с последнего. В случае,
когда решений бесконечно много, их
записывают в виде общего решения. Для
этого свободным неизвестным придают
разные произвольные постоянные значения: ,
, ,…,
,…, ,
и последовательно из уравнений системы,
начиная с последнего, находят значения
всех базисных неизвестных. Полученное
решение называют общим. Придавая
произвольным постоянным, конкретные
значения, находят частные решения
системы уравнений.
,
и последовательно из уравнений системы,
начиная с последнего, находят значения
всех базисных неизвестных. Полученное
решение называют общим. Придавая
произвольным постоянным, конкретные
значения, находят частные решения
системы уравнений.
Уравнениями межотраслевого
баланса, описывающими
процесс производства и потребления
продукции 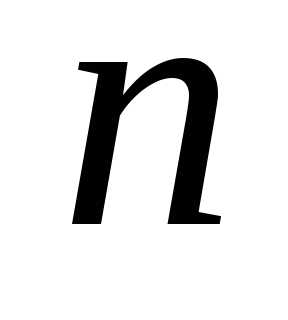 -отраслевой
экономикой, называют уравнения
-отраслевой
экономикой, называют уравнения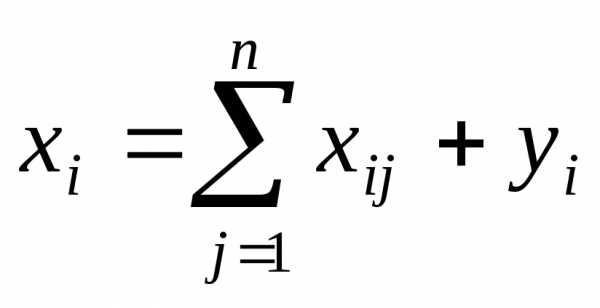 ()
, где
()
, где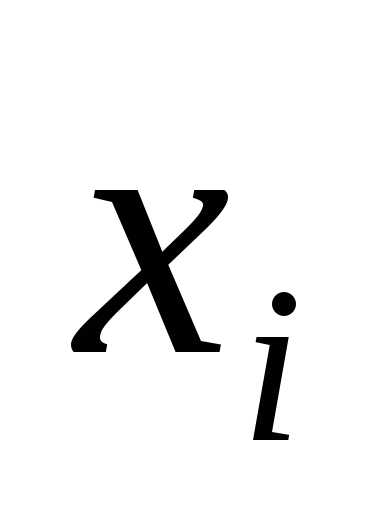 —
объём выпуска валовой продукции
—
объём выпуска валовой продукции -ой
отраслью,
-ой
отраслью, —
объём продукции
—
объём продукции -ой
отрасли, потребляемый
-ой
отрасли, потребляемый -ой
отраслью для производства своей
продукции,
-ой
отраслью для производства своей
продукции, — объём выпуска конечной продукции
— объём выпуска конечной продукции -ой
отраслью, предназначенной для реализации
в непроизводственной сфере.
-ой
отраслью, предназначенной для реализации
в непроизводственной сфере.
Если
предположить, что
(гипотеза линейности), где — постоянные числа, характеризующие
технологию производства (показывают
затраты продукции
— постоянные числа, характеризующие
технологию производства (показывают
затраты продукции -ой
отрасли на производство 1 единицы
продукции
-ой
отрасли на производство 1 единицы
продукции -ой
отрасли) и называемыекоэффициентами
прямых затрат, то
уравнения межотраслевого баланса
запишутся в виде:
().
Их называют уравнениями линейного
межотраслевого баланса илилинейной
моделью Леонтьева многоотраслевой
экономики и записывают, как правило, в матричном
виде:
,
где
-ой
отрасли) и называемыекоэффициентами
прямых затрат, то
уравнения межотраслевого баланса
запишутся в виде:
().
Их называют уравнениями линейного
межотраслевого баланса илилинейной
моделью Леонтьева многоотраслевой
экономики и записывают, как правило, в матричном
виде:
,
где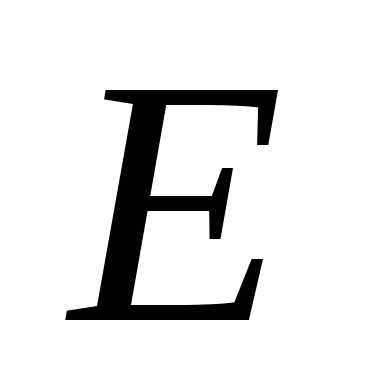 —
единичная матрица;
—
единичная матрица;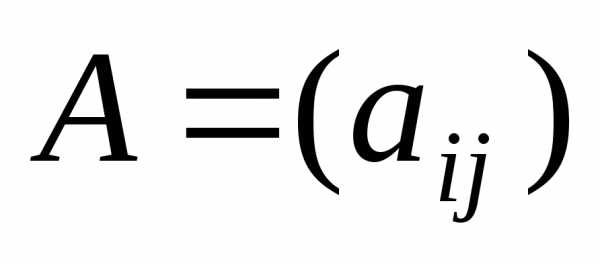 —
матрица коэффициентов прямых затрат;и- векторы (матрицы-столбцы) валового и
конечного продукта, соответственно.
—
матрица коэффициентов прямых затрат;и- векторы (матрицы-столбцы) валового и
конечного продукта, соответственно.
Основная
задача линейного межотраслевого баланса
состоит в отыскании вектора 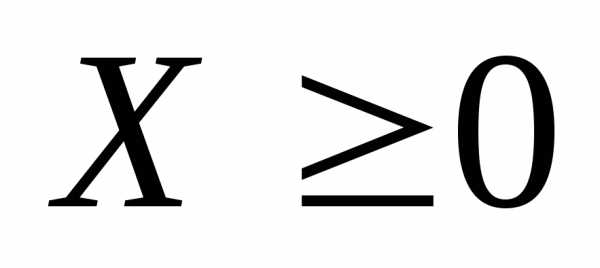 ,
который при известной матрице прямых
затрат
,
который при известной матрице прямых
затрат обеспечивает заданный вектор конечного
продукта
обеспечивает заданный вектор конечного
продукта .
Вектор
.
Вектор находится по формуле,
где
находится по формуле,
где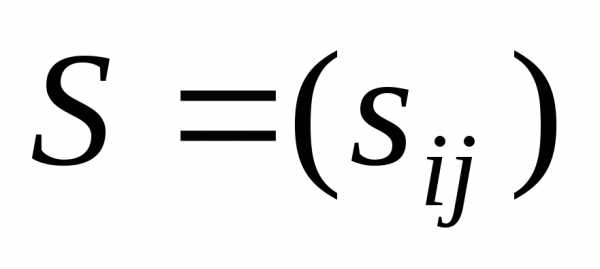 —
матрицакоэффициентов
полных затрат,
элемент
—
матрицакоэффициентов
полных затрат,
элемент  которой показывает величину валового
выпуска продукции
которой показывает величину валового
выпуска продукции -ой
отрасли, необходимой для обеспечения
выпуска 1 единицы конечного продукта
-ой
отрасли, необходимой для обеспечения
выпуска 1 единицы конечного продукта -ой
отрасли. Решение такой задачи существует
только для продуктивных матриц
-ой
отрасли. Решение такой задачи существует
только для продуктивных матриц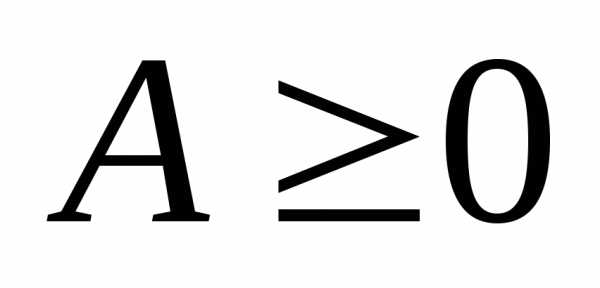 .
.
Матрица 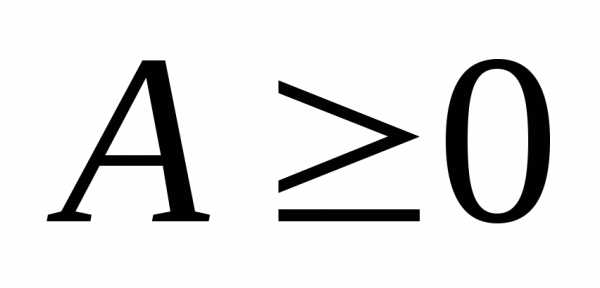 называетсяпродуктивной,
если для любого вектора
называетсяпродуктивной,
если для любого вектора  существует решение
существует решение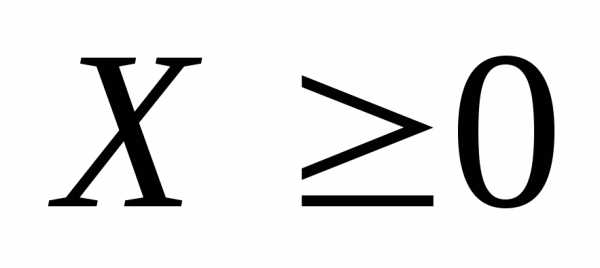 уравнения Леонтьева:.
уравнения Леонтьева:.
Матрица 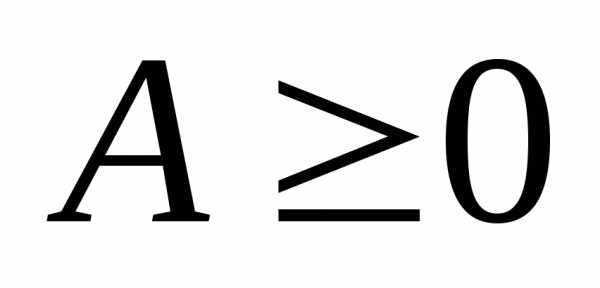 будет продуктивной, если сумма элементов
по каждому её столбцу (строке) не
превосходит единицы:
будет продуктивной, если сумма элементов
по каждому её столбцу (строке) не
превосходит единицы: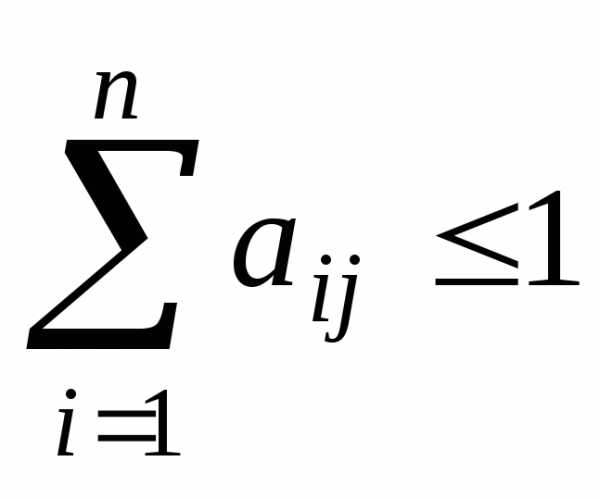
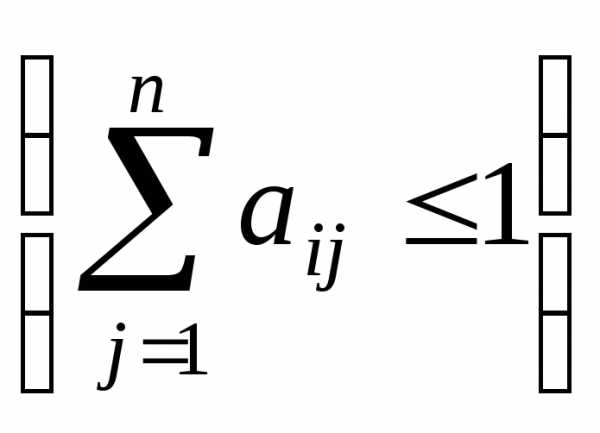 ,
причём хотя бы для одного столбца
(строки) эта сумма строго меньше единицы.
,
причём хотя бы для одного столбца
(строки) эта сумма строго меньше единицы.
Чистой
продукцией отрасли
называется разность между валовой
продукцией этой отрасли и затратами
продукции всех отраслей на производство
данной отрасли. Объёмы 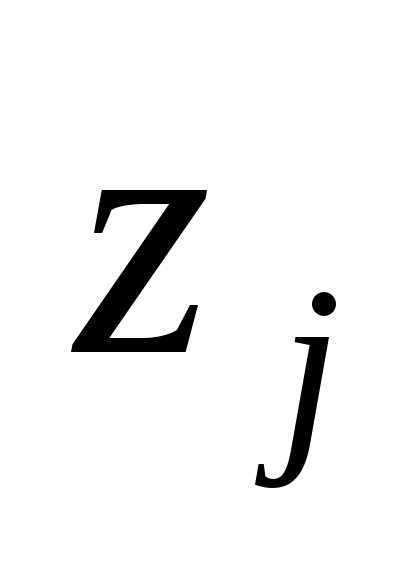 выпуска чистой продукции
выпуска чистой продукции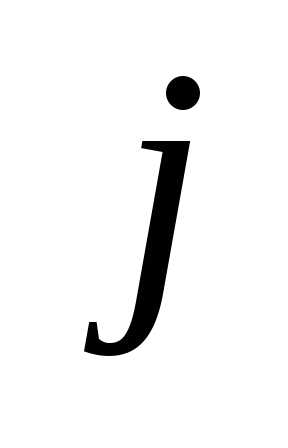 -ой
отрасли вычисляют по формулам:
-ой
отрасли вычисляют по формулам: ().
().
studfiles.net
Матрица А, все элементы которой неотрицательны, называется продуктивной, если для любого вектора с неотрицательными компонентами существует решение уравнения (16.6) — вектор , все элементы которого неотрицательны. В таком случае и модель Леонтьева называется продуктивной.
Для уравнения типа (16.6) разработана соответствующая математическая теория исследования решения и его особенностей. Укажем некоторые ее основные моменты. Приведем без доказательства важную теорему, позволяющую устанавливать продуктивность матрицы.
ТЕОРЕМА 16.1. Если для матрицы А с неотрицательными элементами и некоторого вектора с неотрицательными компонентами уравнение (16.6) имеет решение с неотрицательными компонентами, то матрица А продуктивна.
Иными словами, достаточно установить наличие положительного решения системы (16.6) хотя бы для одного положительного вектора , чтобы матрица А была продуктивной. Перепишем систему (16.6) с использованием единичной матрицы Е в виде
Если существует обратная матрица (E — А)-1 , то существует и единственное решение уравнения (16.7):
Матрица (Е — А)-1 называется Матрицей полных затрат.
Существует несколько критериев продуктивности матрицы А. Приведем два из них.
Первый критерий продуктивности. Матрица А продуктивна тогда и только тогда, когда матрица (Е — А)-1 существует и ее элементы неотрицательны.
Второй критерий продуктивности. Матрица А с неотрицательными элементами продуктивна, если сумма элементов по любому ее столбцу (строке) не превосходит единицы:
Причем хотя бы для одного столбца (строки) эта сумма строго меньше единицы.
Рассмотрим применение модели Леонтьева на несложных примерах.
Пример 1. В табл. 16.4 приведены данные по балансу за некоторый период времени между пятью отраслями промышленности. Найти векторы конечного потребления и валового выпуска, а также матрицу коэффициентов прямых затрат и определить, является ли она продуктивной в соответствии с приведенными выше критериями.

Решение. В данной таблице приведены составляющие баланса в соответствии с соотношениями (16.2): Xij — первые пять столбцов, Уi — шестой столбец, Xi — последний столбец (I,J = 1, 2, 3, 4, 5). Согласно формулам (16.3) и (16.4), имеем
Все элементы матрицы А положительны, однако нетрудно видеть, что их сумма в третьем и четвертом столбцах больше единицы. Следовательно, условия второго критерия продуктивности не соблюдены и матрица А не является продуктивной. Экономическая причина этой непродуктивности заключается в том, что внутреннее потребление отраслей 3 и 4 слишком велико в соотношении с их валовыми выпусками.
Пример 2. Табл. 16.5 содержит данные баланса трех отраслей промышленности за некоторый период времени. Требуется найти объем валового выпуска каждого вида продукции, если конечное потребление по отраслям увеличить соответственно до 60, 70 и 30 условных денежных единиц.
Решение. Выпишем векторы валового выпуска и конечного потребления и матрицу коэффициентов прямых затрат. Согласно формулам (16.3) и (16.4), имеем
Матрица А удовлетворяет обоим критериям продуктивности. В случае заданного увеличения конечного потребления новый вектор конечного продукта будет иметь вид
Требуется найти новый вектор валового выпуска *, удовлетворяющий соотношениям баланса в предположении, что матрица А не изменяется. В таком случае компоненты X1, X2, х3 неизвестного вектора * находятся из системы уравнений, которая согласно (16.4) имеет в данном случае вид
В матричной форме эта система выглядит следующим образом:
Или
Где матрица (Е — А) имеет вид
Решение системы линейных уравнений (16.11) при заданном векторе правой части (16.9) (например, методом Гаусса) дает новый вектор * как решение системы уравнений баланса (16.10):
Таким образом, для того чтобы обеспечить заданное увеличение компонент вектора конечного продукта, необходимо увеличить соответствующие валовые выпуски: добычу и переработку углеводородов на 52,2%, уровень энергетики — на 35,8% и выпуск продукции машиностроения — на 85% по сравнению с исходными величинами, указанными в табл. 16.5.
| < Предыдущая | Следующая > |
|---|
matica.org.ua
Модель межотраслевого баланса Леонтьева
Введение
Модель межотраслевого баланса Леонтьева
Рассмотрим n отраслей промышленности, каждая из которых производит свою продукцию. Обозначим
— валовой выпуск продукции отрасли i , продукция каждой отрасли потребляется в данной отрасли и во всех других отраслях экономики (в противном случае соответствующее значение переменной равно нулю), часть продукции потребляется вне сферы материального производства и называется конечным продуктом. Обозначим — величина продукта, произведенного в отрасли i , потребляемого в отрасли j , — величина конечного продукта отрасли i . Тогда производство и потребление продукции каждой отрасли может быть записано в видеили для всех отраслей экономики региона в виде системы уравнений
(1.5.1)Построенная система линейных уравнений носит название системы балансовых уравнений , т.к. определяет объемы произведенной и потребляемой продукции по отраслям.
Величина
называется коэффициентом прямых затрат и определяет долю продукции отрасли i , которая потребляется в отрасли j . Тогда и систему межотраслевого баланса можно представить в виде системы линейных уравнений (1.5.2)Обозначим матрицы
и рассмотрим матричное уравнение (1.5.3), соответствующее системе (1.5.2)
, (1.5.3)в котором матрица (вектор) Х называется вектором валового выпуска по отраслям, матрица А называется матрицей прямых затрат или технологической матрицей, матрица (вектор) Y называется вектором конечного продукта. Матричное уравнение (1.5.3) носит название модели межотраслевого баланса Леонтьева и позволяет решать задачи трех видов:
1) по известным величинам валового выпуска продукции отраслей Х и технологической матрице А можно вычислить величину конечного продукта Y :
из моде ли
где Е – единичная матрица. Следовательно,
(1.5.4)2) по заданным величинам конечного продукта Y и технологической матрице А можно определить необходимый выпуск продукции Х:
из модели
Следовательно,
(1.5.5)3) по известным величинам валового выпуска некоторых отраслей
, заданным значениям конечного продукта других отраслей и матрице прямых затрат А можно определить конечный продукт первых отраслей и валовой выпуск вторых, используя модель Леонтьева в виде системы уравнений (1.5.2).Матрица
называется матрицей полных затрат , так как каждый ее элемент — величина валового выпуска отрасли , необходимого для обеспечения выпуска единицы конечного продукта отрасли .Матрица
называется продуктивной , то есть существует решение в модели Леонтьева, если найдется такой вектор (матрица) , что .Критерий продуктивности. Для того, чтобы матрица прямых затрат была продуктивной необходимо и достаточно, чтобы выполнялось одно из условий:
1) существует обратная матрица
, все элементы которой неотрицательны,2) матричный ряд
сходится, причем его сумма равна ,3) наибольшее по модулю собственное значение
матрицы , то есть решение характеристического уравнения , было строго меньше единицы,4) все главные миноры матрицы положительны.
Цели и задачи курсовой работы
Практическое применение матричных моделей в экономическом анализе и управлении является основной целью данной работы.
Основными задачами курсовой работы являются:
· расширение теоретических знаний по математике и ее применению в экономических исследованиях,
· приобретение практических навыков использования моделей матричного исчисления для решения экономических задач и задач управления,
· проведение анализа исходной и получаемой статистической информации по экономике регионов,
· оценка выбора управленческих решений для моделирования экономической ситуации.
Задание по курсовой работе
1. Среди городов Московской области или регионов России студенту необходимо выбрать административный объект, экономику которого он будет (условно) моделировать. Название города или региона участвует в названии темы курсовой работы, например, «Применение модели межотраслевого баланса Леонтьева для управления экономикой Курской области».
2. Для выбранного региона определить три основных отрасли экономики, участвующие в модели №1 – А1, А2, А3 (например, А1 – самолетостроение, А2 – пищевая промышленность и т.д.) и пять основных отраслей, участвующих в модели №2.
Задача № 1
3. Заполнить выбранными характеристиками (название региона, А1, А2, А3,
, , ) таблицу 1:Таблица 1. Имеются исходные данные об исполнении баланса за 2005 год в городе N (в условных денежных единицах) (Задача №1) :
4. Составить балансовые уравнения модели и определить потоки средств производства по отраслям. Оценить имеющийся вклад отраслей в суммарный конечный продукт региона.
5. Найти технологическую матрицу коэффициентов прямых затрат А.
6. Исследовать матрицу А на продуктивность и найти матрицу коэффициентов полных затрат В. Сделать вывод о существовании решения в матричной модели Леонтьева.
7. Найти величины конечного продукта отдельно по всем отраслям и в целом по региону, если в его структуре предполагаются следующие изменения:
Вариант 1 : конечный прод
mirznanii.com
Лабораторная работа № 8 модель леонтьева
Цель работы: исследование эффективности производства экономической системы по имеющейся количественной информации об объёме необходимых производственных затрат.
Продуктивные матрицы
Рассмотрим экономическую систему, сфера производства которой состоит из n отраслей, выпускающих n видов продукта, причём каждая отрасль выпускает только один вид.
Предположим, что для производства k–ой отраслью единицы k–го продукта требуется aik ≥ 0 единиц i –го продукта, производимого i –й отраслью. Соответствующая таблица затрат имеет вид:
1-й продукт | …… | k–й продукт | …… | n–й продукт | |
1- я отрасль | a11 | … | a1k | … | a1n |
…… | … | … | … | … | … |
i – я отрасль | ai1 | … | aik | … | ain |
…… | … | … | … | … | … |
n — я отрасль | an1 | … | ank | … | ann |
или проще:

Полученная неотрицательная матрица А называется матрицей материальных затрат или технологической матрицей.
Замечание. Матрица А даёт информацию о сложившейся структуре межотраслевых связей, о существующей технологии производства и используется в текущем и долгосрочном планировании.
Будем считать дополнительно, что сложившаяся технология неизменна (стационарна) и что производство линейно. Последнее означает, что если для выпуска единицы k–го продукта требуется aik единиц i–го продукта, то для выпуска хk единиц k–го продукта необходимо aik хk единиц i–го продукта.
Предположим, что за некоторый фиксированный отрезок времени (неделя, месяц, год) выпущено х1 единиц 1-го продукта, х2 единиц 2-го продукта, …, хn единиц n-го продукта.
Таким образом, задан столбец х, называемый столбцом выпуска или режимом работы отраслей:
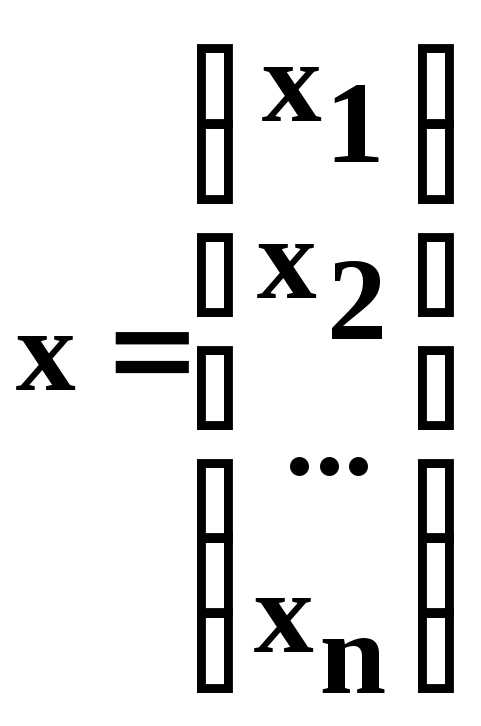 .
.
При заданном столбце выпуска х совокупные затраты i–го продукта в рассматриваемой производственной сфере равны
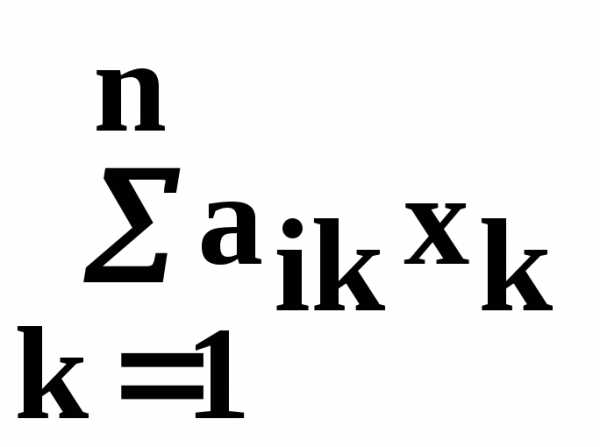 , i =
1, …,n.
, i =
1, …,n.
Из этих величин составляется столбец совокупных материальных затрат в сфере производства:
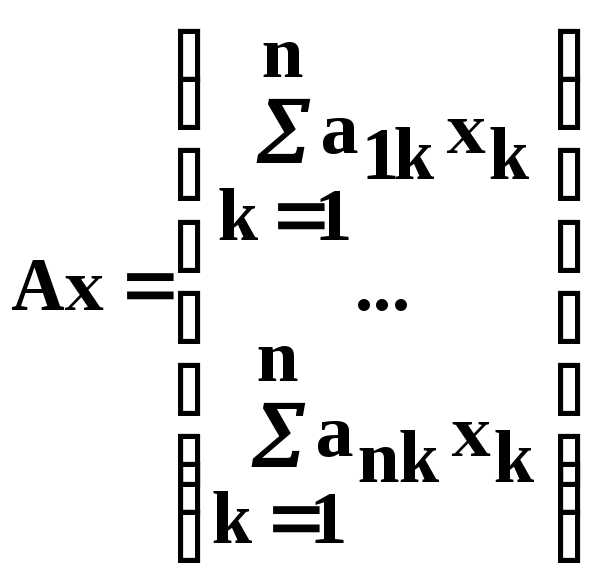 .
.
Матрица материальных затрат А ≥ 0 называется продуктивной, если найдётся такой столбец выпуска х > 0, для которого выполняется неравенство
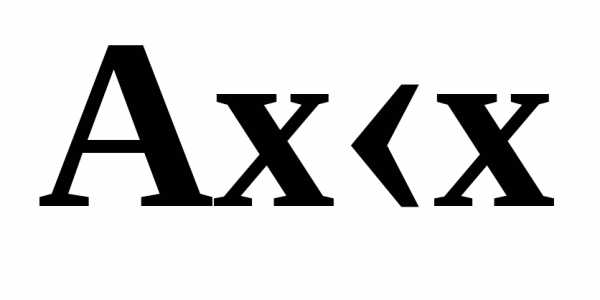 .
.
Это неравенство означает, что существует хотя бы один режим работы отраслей приведённой экономической системы, при котором каждого продукта выпускается больше, чем затрачивается на его производство. Таким образом, сфера производства создаёт положительный столбец прибавочного (конечного) продукта:
.
Возникает естественный вопрос: как следует поступить, чтобы сравнительно несложным путём и как можно раньше выяснить, является ли предъявленная матрица материальных затрат исследуемой сферы производства продуктивной или, напротив, производство убыточно и совокупные материальные затраты превышают объём выпуска?
Справедлив следующий общий факт.
ТЕОРЕМА. Для любой неотрицательной квадратной матрицы А ≥ 0 формулируемые ниже условия равносильны.
Матрица А продуктивна.
Для любого столбца с > 0 существует, и притом ровно один, столбец выпуска х > 0 такой, что
.
Столбца выпуска х > 0, совокупные затраты на создание которого удовлетворяют условию
,
не существует.
Наиболее собственное значение матрицы А удовлетворяет неравенству
.
Выше сказанное
означает, что при выполнении хотя бы
одного из условий (1-4), выполняются и все
остальные. В частности, выполнение
неравенства  позволяет утверждать, что матрица
продуктивна.
позволяет утверждать, что матрица
продуктивна.
В приводимых ниже примерах ограничимся рассмотрением случая, когда n=2, т.е. сфера производства экономической системы состоит из двух отраслей.
Пример 1. Для ответа на вопрос, является ли матрица
продуктивной, найдём её собственные значения.
Имеем:
,
откуда .
Найдём корни уравнения:
,
Окончательно: .
Ответ: матрица А продуктивна.
Из той же теоремы вытекает, что если матрица материальных затрат А продуктивна, то любой столбец прибавочного продукта может быть произведён при соответствующем режиме работы отраслей.
Итак, пусть матрица 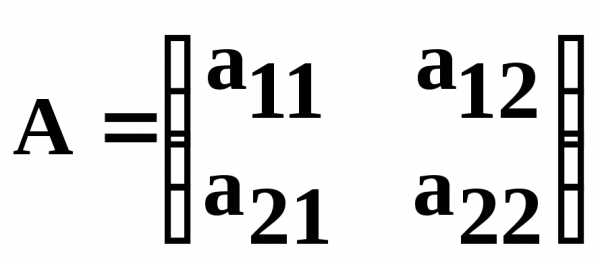 продуктивна и
продуктивна и 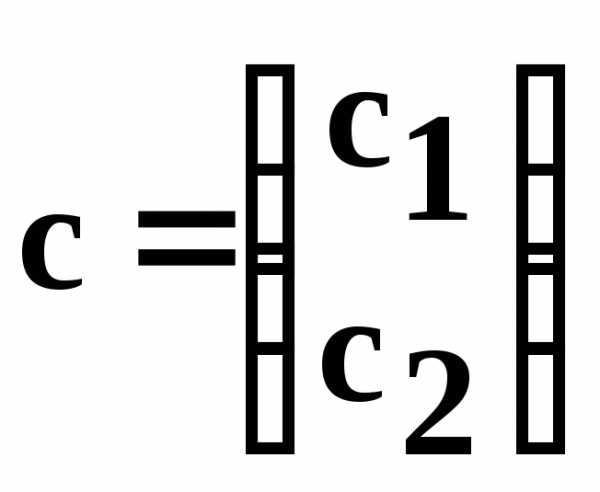 —
столбец конечного продукта. Покажем,
как найти режим работы отраслей,
обеспечивающий этот продукт.
—
столбец конечного продукта. Покажем,
как найти режим работы отраслей,
обеспечивающий этот продукт.
Запишем матричное равенство более подробно:
,
после перемножения:
и вычитания:
окончательно получим
(1 – а11) х1 – а12 х2 = с2,
— а21 х1 + (1 – а22)х2 = с2.
Для продуктивной матрицы построенная система имеет решение при любых с1 и с2.
Рассмотрим конкретный пример.
Пример 2. Пусть
 ,
, 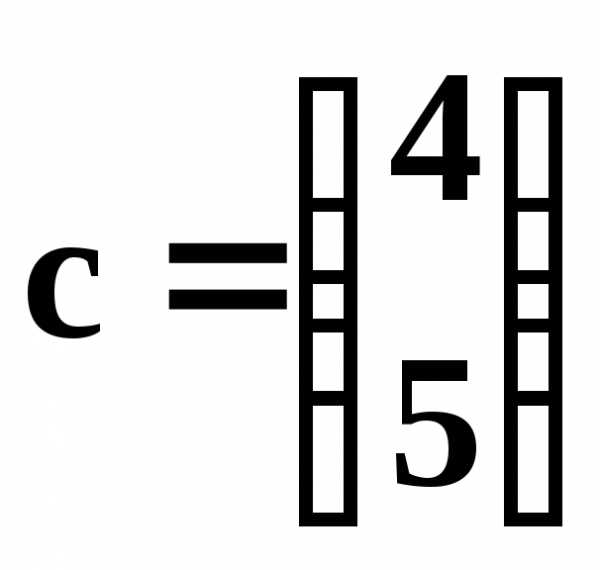 .
.
После преобразований получим:
2/3 х1 – 1/2 х2 = 4,
— 1/12 х1 + ¾ х2 = 5.
Решение системы уравнений найдём методом исключения неизвестной, умножая первое уравнение на 3/2 и складывая со вторым, получим
(1 — 1/12) х1 = 11, 11/12 х1 = 11, х1 =12.
Подобным образом, умножая первое уравнение на 1/8 и складывая со вторым, получим х2 = 8.
Таким образом, для
того чтобы обеспечить прибавочный
продукт  ,
необходимо, чтобы столбец выпуска был
равен
,
необходимо, чтобы столбец выпуска был
равен 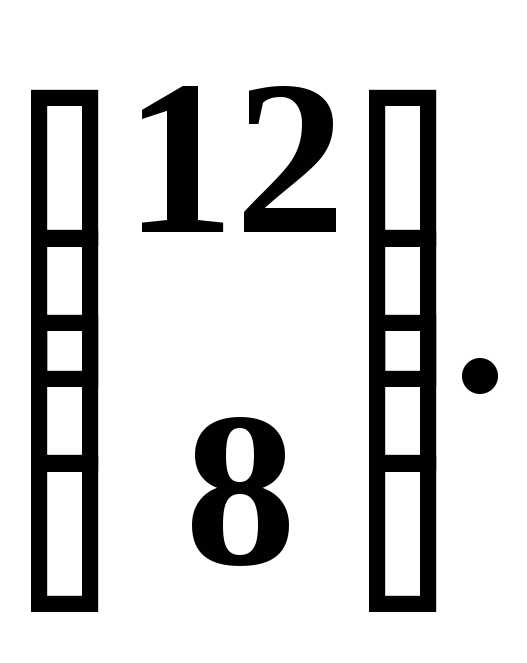
studfiles.net
2.2. Балансовые модели
Статическая модель Леонтьева
Понятие об СНС
СНС (система национальных счетов)- это система взаимосвязанных показателей и классификаций, используемых для описания и анализа наиболее общих результатов и аспектов экономического процесса на макроуровне.
СНС сформулирована в категориях и терминах рыночной экономики, ее концепции и определения предполагают, что описываемая с ее помощью экономика функционирует на основе действия рыночных механизмов и институтов.
Современную СНС можно представить как систему взаимосвязанных блоков информации, каждый из которых описывает тот или иной аспект экономического процесса, а взятые вместе, они обеспечивают описание общей картины экономического процесса.
В центре системы находится блок данных о наиболее важных макроэкономических показателях: валовом внутреннем продукте (ВВП), национальном доходе и их наиболее важных компонентах.
Одним из важных разделов современной СНС является межотраслевой баланс
Понятие о межотраслевом балансе
Балансовая модель производства записывается в виде системы уравнений, каждое из которых выражает требование равенства (баланса) между количеством продукции, произведенной отдельным экономическим объектом и совокупной потребностью в этом продукте.
Под экономическим объектом обычно понимают так называемую чистую отрасль, производящую определенный вид продукта или группу однородных видов продукции
Под экономической системой понимается совокупность взаимосвязанных, взаимозависимых чистых отраслей.
МОБ могут строиться не только для экономики страны в целом, но и для отдельных экономических районов, предприятий с несколькими технологическими процессами.
МОБ представляет собой таблицу, характеризующую связи между отраслями (экономическими объектами) экономической системы (другими словами, таблица характеризует межотраслевые потоки товаров и услуг в течение фиксированного периода времени – года).
Экономическая система состоит из n взаимосвязанных отраслей (продуктов).
Валовой продукт i-отрасли
обозначим через 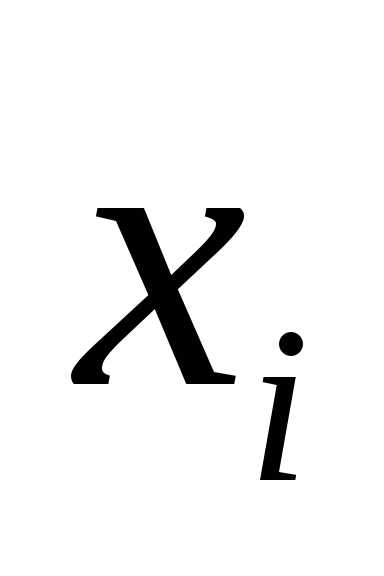 ,
,
конечный продукт
каждой отрасли – через  .
.
Отрасли взаимосвязаны, т.е. каждая из них использует продукцию других отраслей в качестве сырья, полуфабрикатов и т.д.
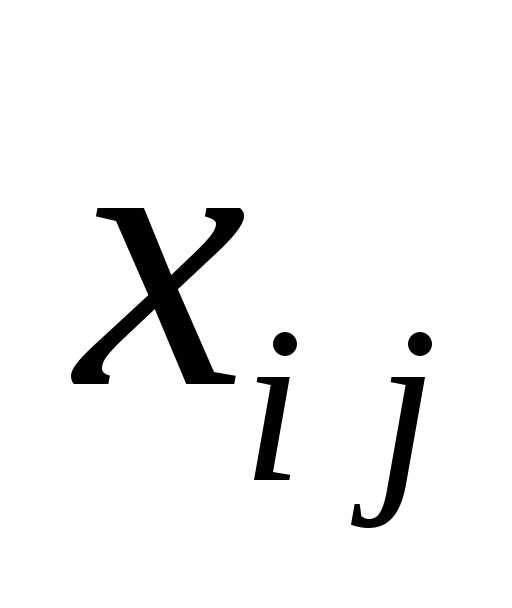 — затраты продукции i-отрасли,
связанные с производством продукта j-отрасли
в объеме
— затраты продукции i-отрасли,
связанные с производством продукта j-отрасли
в объеме  .
.
Вся информация о системе сводится в таблицу – МОБ.
МОБ состоит из трех квадрантов.
Первый квадрант
Отрасли | Конечный продукт | Валовой продукт | ||||||
1 | … | k | … | n | Производ. потребление | |||
1 | x11 | … | x1k | … | x1n |
| y1 | x1 |
: | … | … | … | … | … | … | … | … |
k | xk1 | … | xkk | … | xkn |
| yk | xk |
: | … | … | … | … | … | … | … | … |
n | xn1 | … | xn k | … | xn n |
| yn | xn |
Производст. затраты |
| … |
| … |
|
|
|
|
Валовая добавленная стоимость | V1 | … | Vk | … | Vn |
| ||
Валовой продукт | x1 | … | xk | … | xn |
| ||
1 –
электроэнергетика, k – угольная
промышленность. Тогда 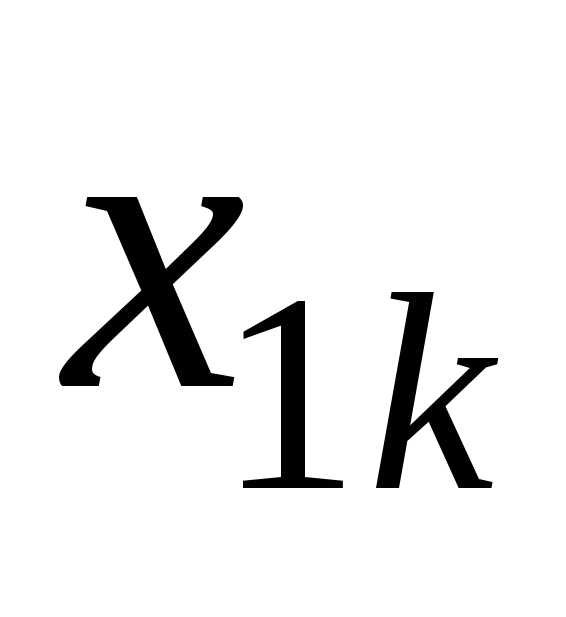 — годовые затраты электроэнергии на
добычу угля;
— годовые затраты электроэнергии на
добычу угля; 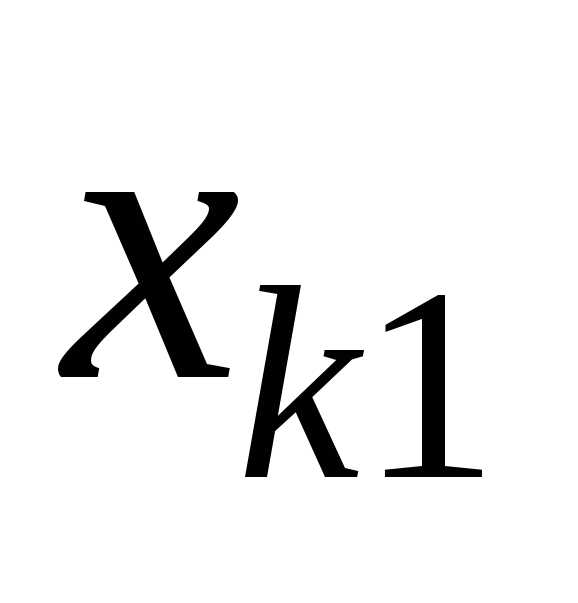 —
затраты угля на производство электроэнергии.
Через
—
затраты угля на производство электроэнергии.
Через 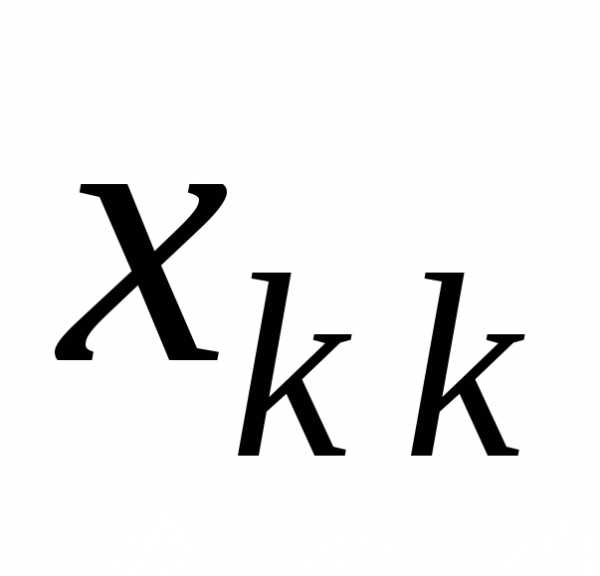 обозначена стоимость продукта,
расходуемого внутри отрасли на собственные
нужды.
обозначена стоимость продукта,
расходуемого внутри отрасли на собственные
нужды.
Отрасль как на элемент столбца: — объемы поставок продукта i-отрасли другим отраслям, входящим в экономическую систему, в том числе и самой себе.
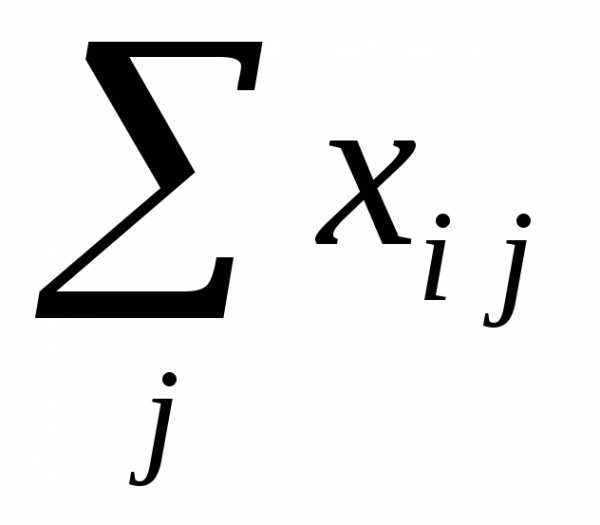 — суммарное
производственное потребление продукта i—
отрасли
— суммарное
производственное потребление продукта i—
отрасли  в i-строку
(n+1)-столбца
МОБ.
в i-строку
(n+1)-столбца
МОБ.
Отрасль как на элемент строки: в столбце с номером k расположены объемы текущих производственных затрат входящих в систему отраслей на производство продукта k-отрасли.
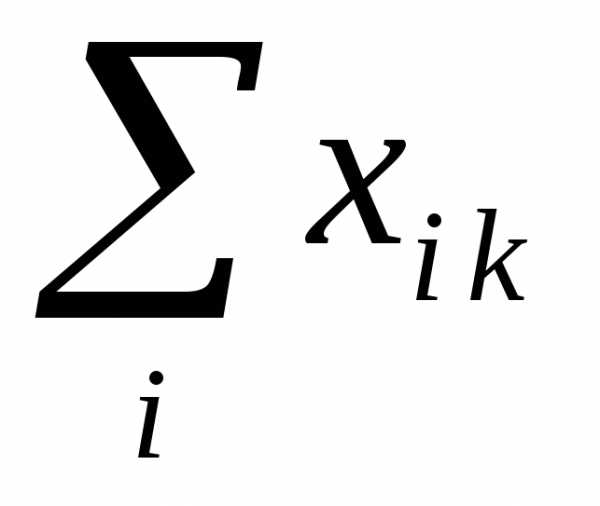 — текущие
производственные затраты k-отрасли
за год
— текущие
производственные затраты k-отрасли
за год
 в
в  -столбец
-столбец  -строки
-строки
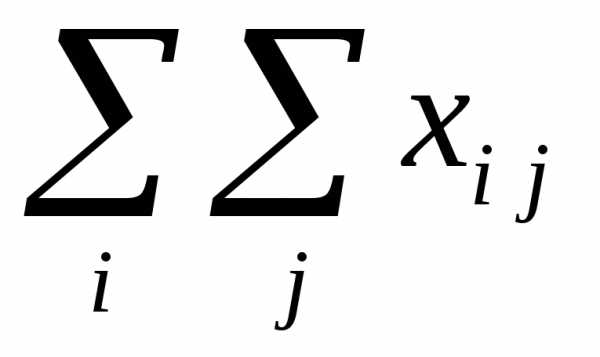
 — промежуточный
продукт экономической системы
— промежуточный
продукт экономической системы
Таблица — первый квадрант МОБ
Второй квадрант МОБ : конечный и валовой продукты отраслей
Конечный продукт — продукт, идущий на личное и общественное потребление (не используемый в производственных нуждах). Сюда включаются накопления и возмещение выбытия основных фондов, прирост запасов, расходы на содержание госаппарата и оборону, затраты, связанные с обслуживанием населения (здравоохранение, просвещение и т.д.), личное потребление населения, сальдо экспорта и импорта
Ко 2-му квадранту
относятся также суммарный конечный
продукт 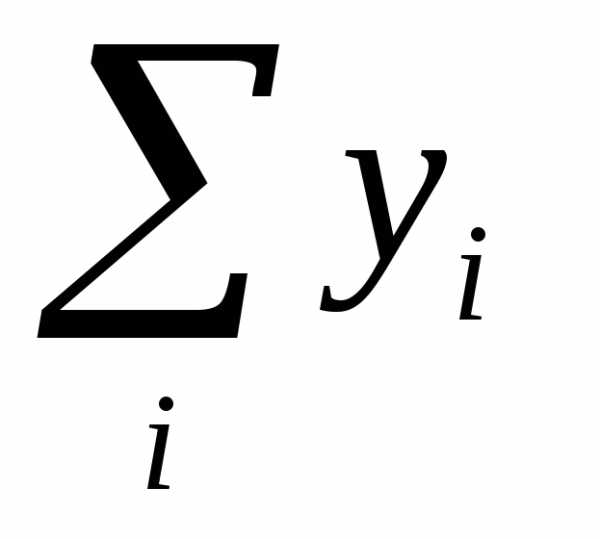 и суммарный валовой продукт
и суммарный валовой продукт  .
.
Валовой (суммарный) выпуск i-отрасли равен
(1)
Квадранты I и II МОБ отражают баланс между производством и потреблением
Третий квадрант: объем валового продукта по отраслям;
валовая добавленная стоимость (условно чистый продукт) отраслей .
В состав валовой добавленной стоимости входят амортизационные отчисления (потребление основного капитала), идущие на возмещение изношенных основных фондов, зарплата, прибыль, косвенные налоги, минус субсидии, и т.д.
(2)
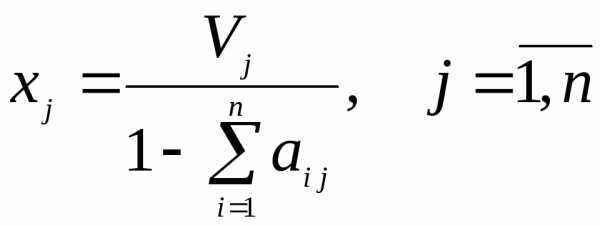

Из (1) следует
(3)
Из (2) получаем
(4)
Центральным показателем СНС является валовой внутренний продукт (ВВП). Он характеризует стоимость конечных товаров и услуг в ценах покупателя, произведенных резидентами данной страны за определенный промежуток времени.
Ключевые слова – конечные товары и услуги. Это означает, что состав ВВП входят товары, которые использованы на конечное потребление, накопление и экспорт, и не включаются промежуточные товары и услуги, израсходованные в процессе производства в виде сырья, материалов, топлива, энергии и т.д.
Другое важное слово – валовой. Это означает, что при исчислении ВВП из стоимости не вычитается потребление основного капитала.
Балансовая модель «Затраты – выпуск»
(Модель Леонтьева)
коэффициенты
прямых затрат  -отрасли
(или технологические коэффициенты
-отрасли
(или технологические коэффициенты  -отрасли)
-отрасли)
Совокупность величин
 ,
показывающих, какие затраты всех
отраслей необходимы для выпуска единицы
продукции
,
показывающих, какие затраты всех
отраслей необходимы для выпуска единицы
продукции  —
отрасли, называется технологией
производства продукта
—
отрасли, называется технологией
производства продукта  —
й отрасли
—
й отрасли
Сделаем два предположения:
будем считать сложившуюся технологию производства неизменной в течение некоторого промежутка времени:
технология производства линейная; это означает, что для производства валового продукта в количестве
 необходимы затраты всех отраслей в
объемах
,
т.е.
имеют место соотношения.
необходимы затраты всех отраслей в
объемах
,
т.е.
имеют место соотношения.
Коэффициенты прямых затрат:
1. Статистический
метод.
Коэффициенты 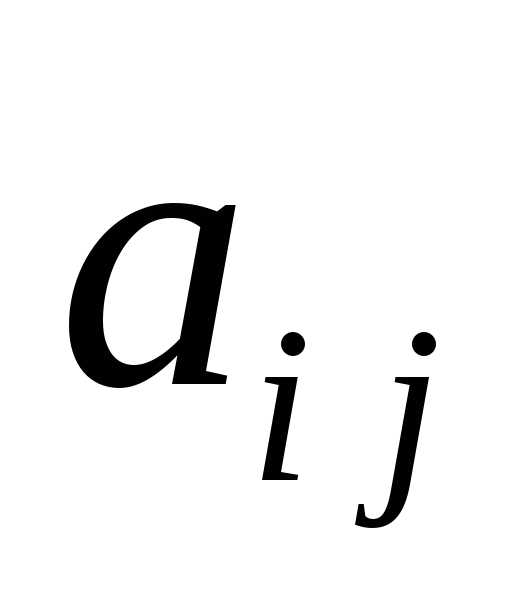 находятся на основе анализа отчетных
балансов за предыдущие годы.
находятся на основе анализа отчетных
балансов за предыдущие годы.
2. Нормативный метод. Строится модель отрасли МОБ. В этой модели отрасль рассматривается в виде совокупности отдельных производств, для каждого из которых уже разработаны нормативы затрат. Если заранее знать, какую продукцию будут выпускать предприятия отрасли, то по нормам затрат рассчитываются среднеотраслевые коэффициенты прямых затрат.
,  (7)
(7)
Второе свойство
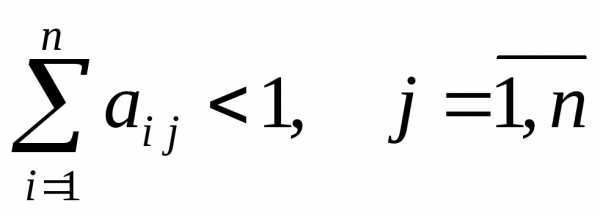 ,
,  (8)
(8)
затраты всех отраслей на 1 рубль произведенной продукции оказываются меньше 1 рубля. Такое производство является рентабельным.
(9)
баланс распределения продукции
(9а)
— вектор валового выпуска;
— вектор конечного продукта
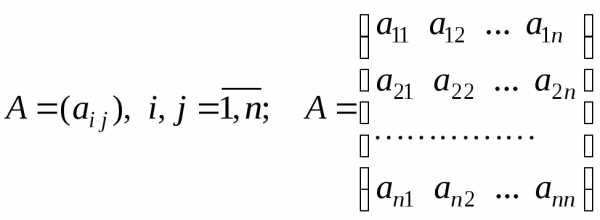
— матрица прямых затрат (матрица технологических коэффициентов)
(10)
модель «Затраты – выпуск» или статическая модель Леонтьев.
Основные свойства неотрицательных матриц
1) Неотрицательная квадратная матрица называется неразложимой, если одновременной перестановкой строк и столбцов ее нельзя привести к виду
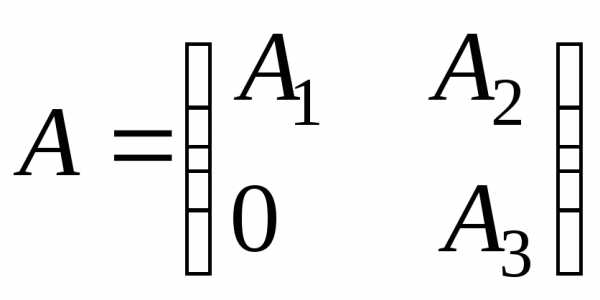 ,
,
где
подматрицы,  .
.
В противном случае матрица – разложима
2)
— неотрицательная
квадратная матрица. Среди ее собственных
чисел (характеристических корней)
существует собственное число 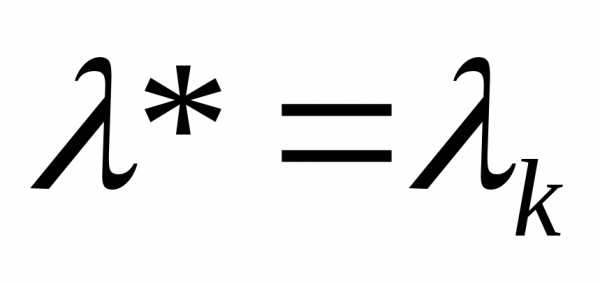 и соответствующий ему собственный
вектор
и соответствующий ему собственный
вектор  такие, что
такие, что
— корень 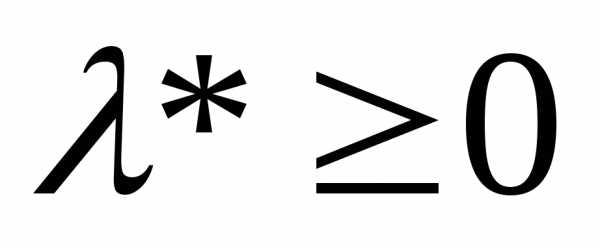 — действительный и неотрицательный, не
меньший модуля любого другого собственного
числа,
— действительный и неотрицательный, не
меньший модуля любого другого собственного
числа,
;
— собственный
вектор  ;
;
— если неотрицательная матрица А неразложима, то она имеет положительное собственное число , такое, что модули всех остальных собственных чисел этой матрицы не превосходят его
.
Характеристическому
корню  отвечает единственный (с точностью до
скалярной величины) собственный вектор
отвечает единственный (с точностью до
скалярной величины) собственный вектор  .
.
Число 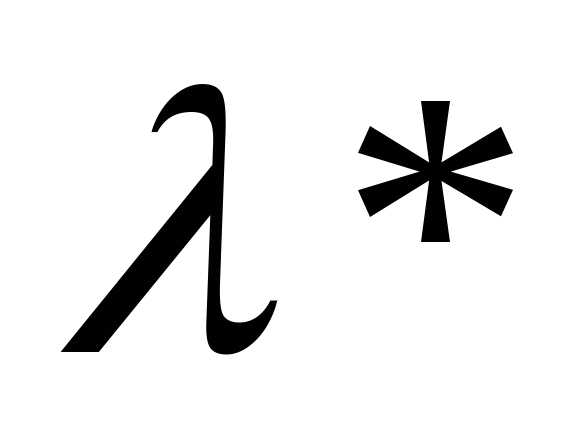 и вектор
и вектор  называются главными
собственным числом и собственным
вектором матрицы А или корнем и вектором Фробениуса.
называются главными
собственным числом и собственным
вектором матрицы А или корнем и вектором Фробениуса.
Планирование в модели Леонтьева
(11)
Постановка
задачи. Основная
задача,
возникающая в краткосрочном планировании
производства: при заданном конечном
продукте  требуется определить необходимый выпуск
валового продукта
требуется определить необходимый выпуск
валового продукта
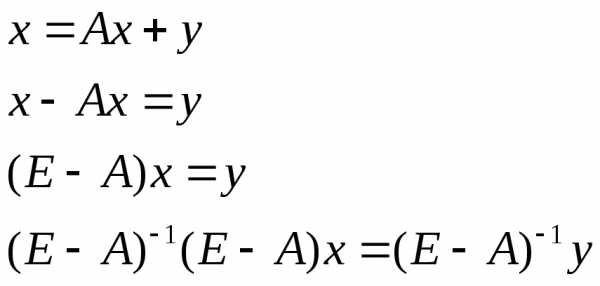
, (12)
т.е. ответить на вопрос, любой ли конечный спрос может быть удовлетворен при существующей технологии производства.
Затем валовой продукт распределить.
Когда решение
системы существует для 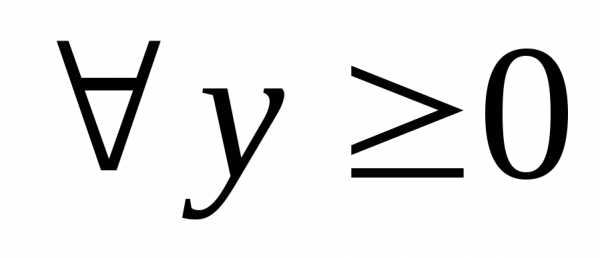 ,
говорят, что модель Леонтьева (и матрица А) продуктивна.
,
говорят, что модель Леонтьева (и матрица А) продуктивна.
Условия продуктивности модели Леонтьева.
Конкретно продуктивность модели Леонтьева определяется величиной главного собственного числа матрицы А.
Теорема.
Модель Леонтьева (11) продуктивна тогда
и только тогда, когда  .
.
Если 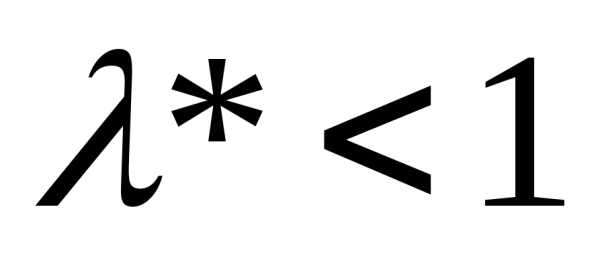 ,
то существует продуктивное решение
,
то существует продуктивное решение 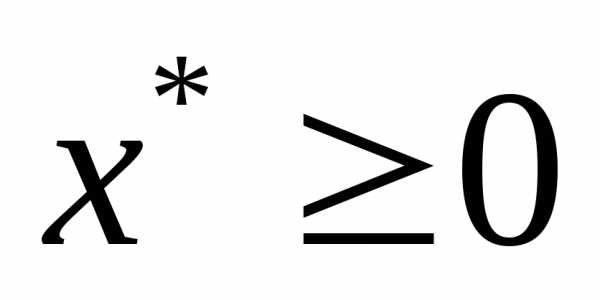 модели Леонтьева, которое удовлетворяет
условию
модели Леонтьева, которое удовлетворяет
условию
 (13)
(13) 
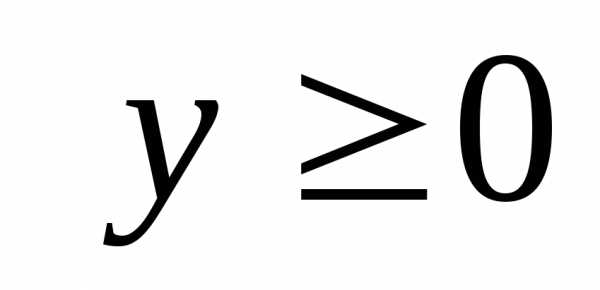
При 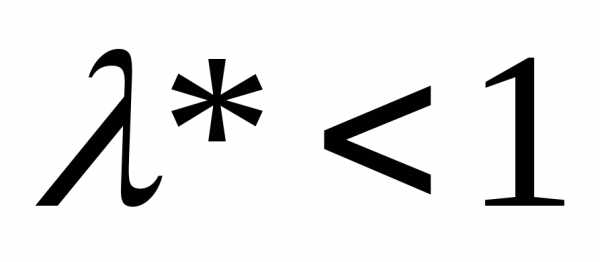 может быть осуществлено расширенное
воспроизводство валового продукта.
может быть осуществлено расширенное
воспроизводство валового продукта.
При 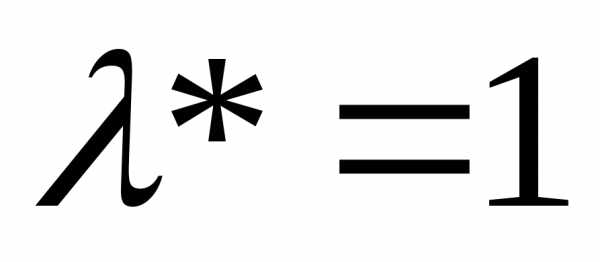
 — простое воспроизводство.
— простое воспроизводство.
При 

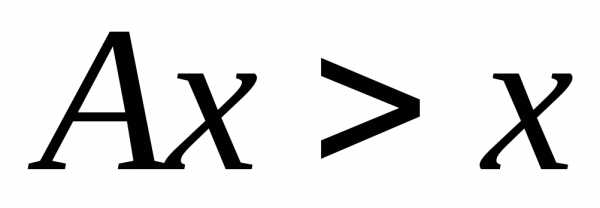 — экономика терпит убытки,
— экономика терпит убытки,
являясь нерентабельной
1. Оценка матрицы
технологических коэффициентов 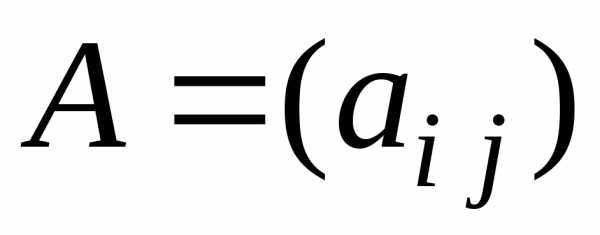
2.
3.
Матрица полных затрат
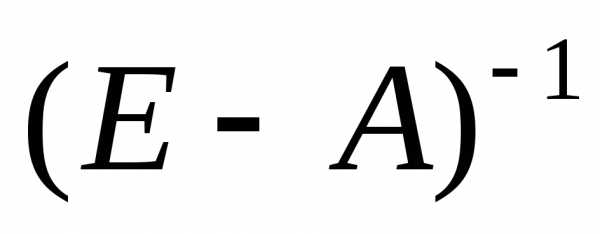
studfiles.net
Модель Леонтьева межотраслевого баланса — Мегаобучалка
Постановка задачи. Пусть имеется n отраслей промышленности, каждая из которых производит продукцию, которая идет как для внутреннего потребления данной отраслью и другими отраслями, так и для конечного личного или общественного потребления. Обозначим хi – общий (валовый) объем продукции i-отрасли, хij – объем продукции i-отрасли, потребляемой j-отраслью, yi – объем конечного продукта i-отрасли. Имеем соотношение баланса:
Введем коэффициенты прямых затрат . Если считать, что эти коэффициенты постоянны в течение некоторого периода времени, то xij = aij xj , и соотношение баланса примет вид:
или в матричном виде Х = А٠Х + У.
Задача состоит в нахождении такого вектора Х, который при известной матрице прямых затрат А обеспечивает конечный продукт У.
Решая полученное матричное уравнение, находим Х = (Е–А)–1 У.
Матрица (Е – А)–1 называется матрицей полных затрат.
Чтобы матричное уравнение было разрешимо, необходимо, чтобы матрица А была продуктивной. Есть несколько критериев продуктивности матрицы. Например, если максимум сумм элементов столбцов не более 1 и хоть одна сумма строго меньше 1, то матрица продуктивна.
Пример 1.9. Решение задачи поиска межотраслевого баланса[3, c. 99 – 104].
Имеется две отрасли производства, в таблице 1.9 указаны объёмы производства и потребления.
Таблица 1.9
| Производство | Потребление | Конечный продукт | Валовый продукт | |
| Энергетика | Машиностроение | |||
| Энергетика | ||||
| Машиностроение |
Необходимо вычислить объем валового выпуска продукции каждой отрасли, если конечный продукт 1-й отрасли должен увеличиться в 2 раза, 2-й на 20 %.
Из таблицы 1.9 имеем:
х1 = 500, х2 = 400, у1 = 240, у2 = 85, х11 = 100, х21 = 275, х12 =160, х22 = 40.
Построим матрицу прямых затрат:
а11 = = = 0,2; а12 = = = 0,4;
а21 = = = 0,55; а22 = = = 0,1.
А = , Е –А = – = .
Проверим матрицу А на продуктивность:
0,2 + 0,55 = 0,75 < 1, 0,4 + 0,1 = 0,5 < 1, т. е. матрица А продуктивна.
Найдем обратную к ней. Вычислим определитель:
0,8٠0,9 –0,55٠ 0,4 = 0,5.
Тогда,
Вычислим по данным условия задачи новый вектор конечного продукта
У = (У1, У2):
У1 = 240٠2 = 480, У2 = 85 ٠(1+ 0,2) = 102. Имеем Унов =
Тогда Х = = .
1.15. В таблице 1.10 приведены данные об исполнении баланса за отчетный период в усл. ден. ед.
Таблица 1.10
| Отрасль | Потребление | Конечный продукт | Валовый продукт | ||
| Сфера обслуживания | Лёгкая промышленность | ||||
| Произ-водство | Сфера обслуживания | ||||
| Лёгкая пром-ть |
Вычислить необходимый объем валового выпуска каждой отрасли, если конечное потребление сферы обслуживания увеличится вдвое, а лёгкой промышленности сохранится на прежнем уровне.
1.16. Продуктивна ли матрица А:
1) 2) .
1.17. Экономика разделена на три отрасли. В таблице 1.11 заданы коэффициенты прямых затрат и конечная продукция отраслей.
Таблица 1.11
| Отрасль | Потребление | Конечный продукт | |||
| Сфера обслуживания | Лёгкая промышленность | Сельское хозяйство | |||
| Произ-водство | Сфера обслуживания | 0,3 | 0,25 | 0,2 | |
| Лёгкая промышленность | 0,15 | 0,12 | 0,03 | ||
| Сельское хозяйство | 0,1 | 0,05 | 0,08 |
Найти объем валовой продукции каждой отрасли, межотраслевые поставки, чистую продукцию отраслей.
1.18. Дана матрица полных затрат
Найти приращение валового выпуска ∆Х, обеспечивающее приращение конечной продукции ∆У = (10, 30, 20).
1.19. Отрасль состоит из 4-х предприятий; вектор выпуска продукции и матрица внутреннего потребления имеют вид:
Х = А = 
Пользуясь моделью Леонтьева, найти вектор объемов конечного продукта, предназначенного для реализации вне отрасли.
1.20. Данные баланса трех отраслей промышленности за некоторый промежуток времени даны в таблице 1.12. Требуется найти объем валового выпуска каждого вида продукции, если конечное потребление увеличить соответственно:
1) до 60, 70 и 30 единиц;
2) на 30, 10 и 50 %.
Решить задачу методом обратной матрицы.
Таблица 1.12
| № п/п | Отрасль | Потребление отрасли | Конечный продукт | Валовый выпуск | ||
| Добыча и переработка углеводородов | ||||||
| Энергетика | ||||||
| Машиностроение |
Контрольные задания
Вариант 1.
1. Решить матричное уравнение:
.
2. Решить систему методом Крамера:
3. При каких значениях параметра к система не имеет решений, имеет бесконечно много:
4. Решить методом Гаусса:
Вариант 2.
1. Продуктивна ли матрица:
2. Решить систему матричным методом:
3. Решить методом Гаусса:
4. Решить задачу.
В первенстве России по футболу Спартак и Динамо вместе набрали на 11 очков больше, чем удвоенное число очков ЦСКА, утроенное число очков Динамо на 2 очка меньше, чем сумма удвоенного числа очков Спартака и ЦСКА. Известно, что число очков, набранных каждой командой, лежит в диапазоне от 15 до 25. Найти количество набранных каждой командой очков.
Вариант 3.
1. При каком значении m матрица не имеет обратной:
2. Решить систему матричным методом:
3. Решить методом Гаусса:

4. При каких значениях параметров а, в, с система имеет решение
x = 2, y = 1, z = 3:
Векторная алгебра
В этом параграфе рассматривается привычное понятие вектора, алгебраическая и геометрическая интерпретация операций над векторами, вводится обобщающее понятие векторного пространства как множества объектов разной природы, для которых заданы алгебраические операции сложения и умножения на число, удовлетворяющее определенным свойствам [3, c. 130].
megaobuchalka.ru

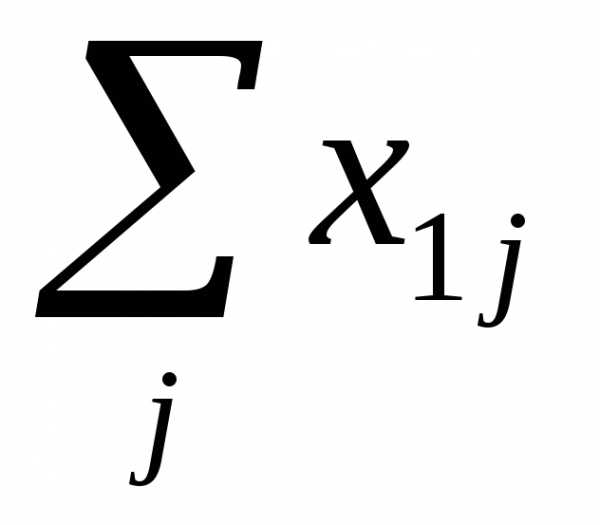

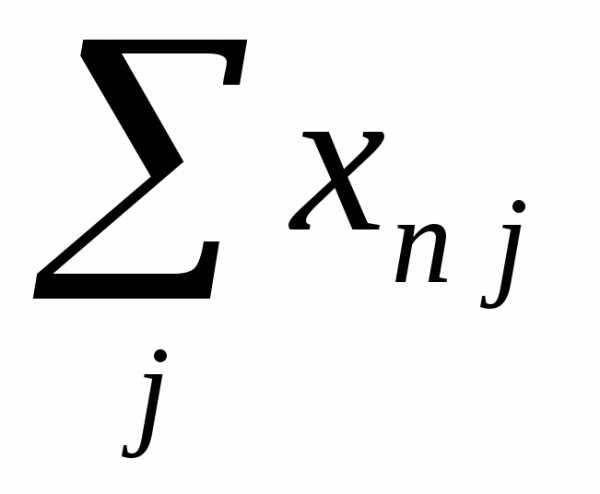
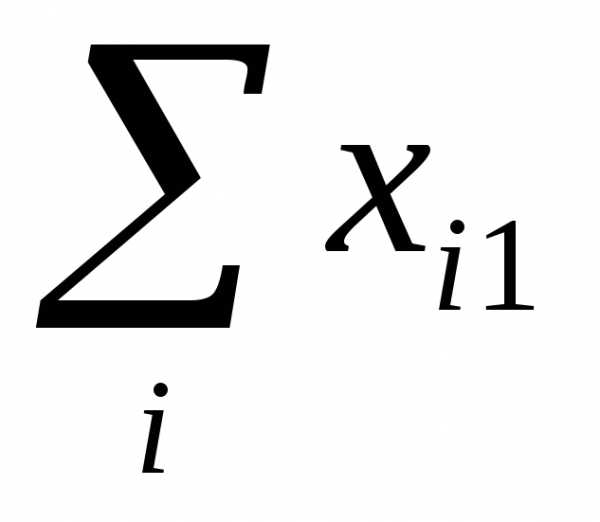
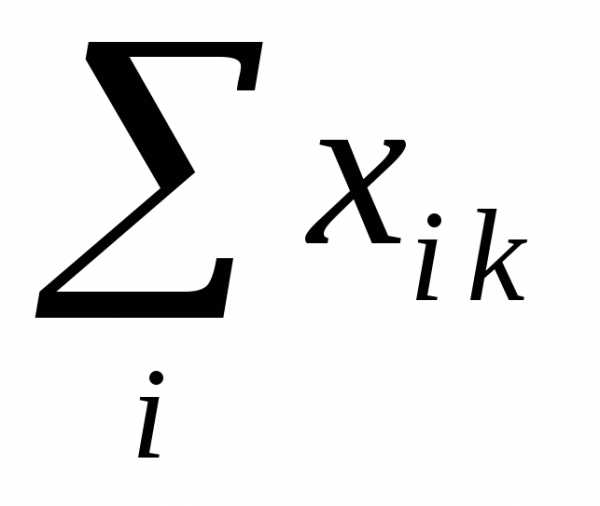

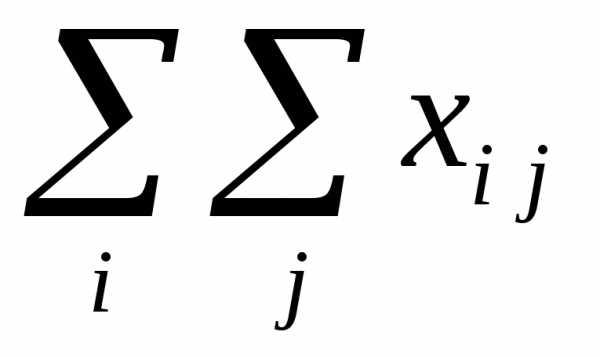
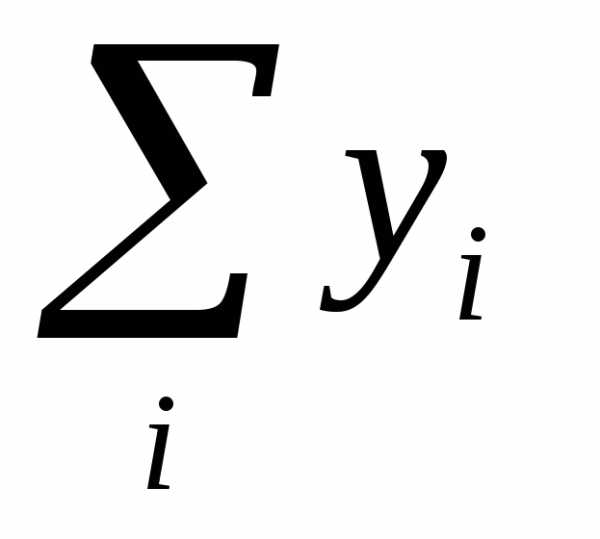
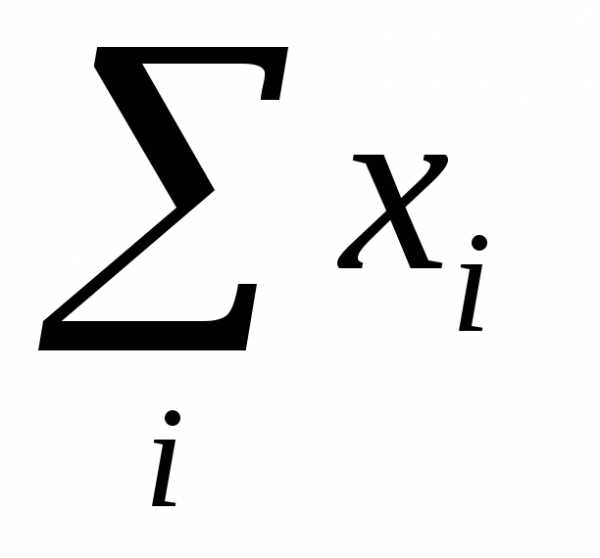
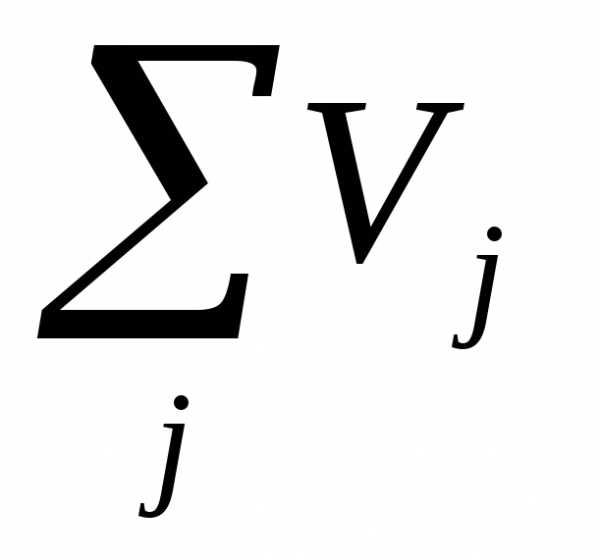
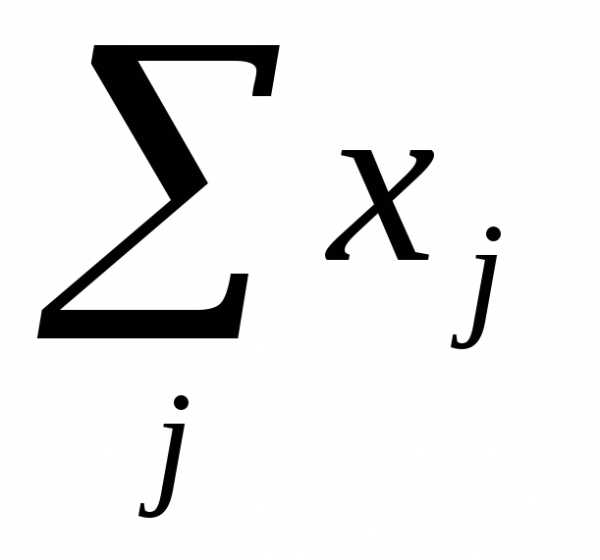
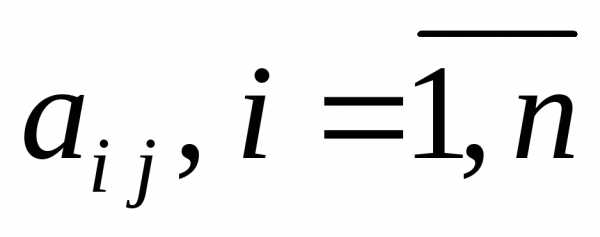 ,
показывающих, какие затраты всех
отраслей необходимы для выпуска единицы
продукции
,
показывающих, какие затраты всех
отраслей необходимы для выпуска единицы
продукции  —
отрасли, называется технологией
производства продукта
—
отрасли, называется технологией
производства продукта  —
й отрасли
—
й отрасли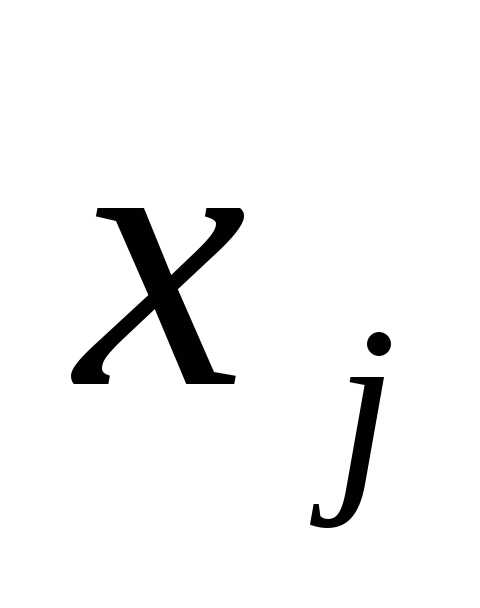 необходимы затраты всех отраслей в
объемах
,
т.е.
имеют место соотношения.
необходимы затраты всех отраслей в
объемах
,
т.е.
имеют место соотношения.