Задачи на вычисление дробей – Задачи на дроби

Содержание

Применение дробей

Этот урок будет интересным и познавательным. Мы научимся применять дроби для различных жизненных случаев.

Нахождение дроби от числа

Мы уже говорили, что дробь это часть от чего-либо. Эта часть может быть чем угодно. Например, от пиццы это половина пиццы:

Но применение дробей не заканчивается на одной пицце. Например, можно узнать сколько составляет от десяти сантиметров:

Как вы уже догадались от десяти сантиметров составляют пять сантиметров. Ведь это простейшая дробь, которая означает половину от чего-то. У нас было десять сантиметров. Мы разделили эти десять сантиметров пополам и получили пять сантиметров.

Попробуем узнать, сколько составляет от одного часа. Вспоминаем, что час это 60 минут. Нам нужно найти (половину) от 60 минут. Нетрудно догадаться, что половина от 60 минут это 30 минут. Значит от одного часа составляет 30 минут или полчаса.

Попробуем найти от одного центнера. Центнер это 100 кг. Требуется найти (половину) от 100 кг. Нетрудно догадаться, что половина от 100 кг это 50 кг. Значит от одного центнера составляют 50 кг.

Поскольку мы занимаемся математикой, значит в большинстве случаев будем иметь дело с числами. Например, найдём от числа 12.

Итак, нужно найти половину от числа 12. Нетрудно догадаться, что половиной от числа 12 является число 6. Значит числа 12 составляет число 6.

Чтобы легче было находить дробь от числа, можно пользоваться следующим правилом:

Чтобы найти дробь от числа, нужно это число разделить на знаменатель дроби, и полученный результат умножить на числитель дроби.

Попробуем проследить весь процесс работы этого правила. Для примера возьмём десять сантиметров:

Пусть требуется найти от этих десяти сантиметров. Читаем первую часть правила:

Чтобы найти дробь от числа, нужно это число разделить на знаменатель дроби

Итак, делим десять сантиметров на знаменатель дроби . Знаменатель этой дроби равен числу 2. Поэтому делим десять сантиметров на 2

10 см : 2 = 5 см

Читаем вторую часть правила:

и полученный результат умножить на числитель дроби

Итак, умножаем пять сантиметров на числитель дроби . Числитель дроби в данном случае единица. Поэтому умножаем пять сантиметров на единицу:

5 см × 1 = 5 см

Мы нашли от десяти сантиметров. Видим, что от десяти сантиметров составляют пять сантиметров:

Почему же после деления числа на знаменатель дроби приходиться умножать полученный результат на числитель дроби? Дело в том, что знаменатель дроби показывает на сколько частей что-либо разделено, а числитель показывает сколько частей было взято.

В нашем примере десять сантиметров были разделены на две части (пополам), и из этих частей была взята одна часть. Умножая одну часть на числитель дроби, мы тем самым указываем сколько частей мы берём от чего-то. То есть умножив пять сантиметров на числитель дроби , мы тем самым указали, что берем одну часть из двух.

Пример 2. Найти от 10 см.

Применим правило нахождения дроби от числа:

Сначала делим 10 сантиметров на знаменатель дроби

10 см : 5 = 2 см

Получили два сантиметра. Этот результат нужно умножить на числитель дроби

2 см × 2 = 4 см

Мы нашли от десяти сантиметров. Видим, что от десяти сантиметров составляют четыре сантиметра.

Весь процесс решения можно увидеть на следующем рисунке:

Сначала десять сантиметров были разделены на пять равных частей. Затем было взято две части из этих пяти частей:

Пример 3. Найти от числа 56.

Чтобы найти от числа 56, нужно это число разделить на знаменатель дроби , и полученный результат умножить на числитель дроби .

Итак, сначала делим число 56 на знаменатель дроби

56 : 8 = 7

Теперь умножаем полученное результат на числитель дроби

7 × 3 = 21

Получили ответ 21. Значит от числа 56 составляет 21.

Пример 4. Найти от одного часа.

Один час это 60 минут. Задание можно понимать, как нахождение от 60 минут.

Сначала разделим 60 минут на знаменатель дроби

60 мин : 4 = 15 мин

Теперь умножим полученные 15 минут на числитель дроби

15 мин × 2 = 30 мин

Получили в ответе 30 минут. Значит от одного часа составляют тридцать минут или полчаса.

Пример 5. Найти от одного метра.

Один метр это сто сантиметров. Сначала разделим 100 см на знаменатель дроби

100 см : 5 = 20 см

Теперь умножим полученные 20 см на числитель дроби

20 см × 4 = 80 см

Получили ответ 80 см. Значит от одного метра составляют 80 см.

Нахождение целого числа по дроби

Зная часть числа и сколько это составляет от целого числа, можно найти изначальное целое число. Это обратная задача к той, которую мы рассматривали в предыдущей теме. Там мы искали дробь от числа, деля это число на знаменатель дроби, и полученный результат умножая на числитель дроби.

А сейчас наоборот, зная дробь и сколько это составляет от числа, найти изначальное целое число.

Например, если длины линейки составляют шесть сантиметров и нам говорят найти длину всей линейки, то мы должны понимать, что от нас требуют найти изначальное целое число (длину всей линейки) по дроби . Давайте решим эту задачу.

Требуется найти длину всей линейки по дроби . Известно, что длины всей линейки составляют 6 см.

Мы уже знаем каким образом получились эти 6 см. Имелась какая-то длина, её разделили на пять частей, поскольку знаменатель дроби это число 5. Затем было взято две части от пяти частей, поскольку числитель дроби это число 2.

Чтобы узнать длину всей линейки, сначала нужно узнать длину одной части. Как это узнать? Попробуем догадаться, внимательно изучив следующий рисунок:

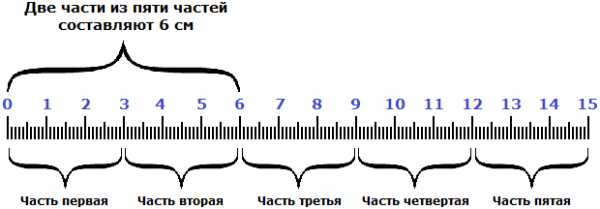
Если две части длины линейки составляют 6 см, то нетрудно догадаться, что одна часть составляет 3 см. А чтобы получить эти 3 см, надо 6 разделить на 2

6 см : 2 = 3 см

Итак, мы нашли длину одной части. Одна часть из пяти или длины линейки составляет 3 см. Если частей всего пять, то для нахождения длины линейки, нужно взять три сантиметра пять раз. Другими словами, умножить 3 см на число 5

3 см × 5 = 15

Мы нашли длину линейки. Она составляет 15 сантиметров. Это можно увидеть на следующем рисунке.

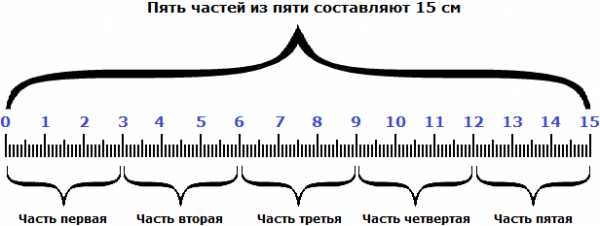
Видно, что пять частей из пяти или составляют пятнадцать сантиметров.

Чтобы легче было находить число по его дроби, можно пользоваться следующим правилом:

Чтобы найти число по его дроби, нужно известное число разделить на числитель дроби, и полученный результат умножить на знаменатель дроби.

Пример 2. Число 20 это от всего числа. Найдите это число.

Знаменатель дроби показывает, что число, которое мы должны найти, разделено на пять частей. Если этого числа составляет число 20, то для нахождения всего числа, сначала нужно найти (одну часть из пяти) от всего числа. Для этого 20 надо разделить на числитель дроби

20 : 4 = 5

Мы нашли от всего числа. Эта часть равна 5. Чтобы найти всё число, нужно полученный результат 5 умножить на знаменатель дроби

5 × 5 = 25

Мы нашли от всего числа. Другими словами, нашли всё число, которое от нас требовали найти. Это число 25.

Пример 3. Десять минут это времени приготовления каши. Найдите общее время приготовления каши.

Знаменатель дроби показывает, что общее время приготовления каши разделено на три части. Если времени приготовления каши составляет десять минут, то для нахождения общего времени приготовления, нужно сначала найти времени приготовления. Для этого 10 нужно разделить на числитель дроби

10 мин : 2 = 5 мин

Мы нашли времени приготовления каши. времени приготовления каши составляют пять минут. Для нахождения общего времени приготовления, нужно 5 минут умножить на знаменатель дроби

5 мин × 3 = 15 мин

Мы нашли времени приготовления каши, то есть нашли общее время приготовления. Оно составляет 15 минут.

Пример 4. массы мешка цемента составляет 30 кг. Найти общую массу мешка.

Знаменатель дроби показывает, что общая масса мешка разделена на четыре части. Если массы мешка составляет 30 кг то для того, чтобы найти общую массу мешка нужно сначала найти массы мешка. Для этого 30 надо разделить на числитель дроби .

30кг : 2 = 15кг

Мы нашли массы мешка. массы мешка составляет 15 кг. Теперь, чтобы найти общую массу мешка, надо 15кг умножить на знаменатель дроби

15кг × 4 = 60кг

Мы нашли массы мешка. Другими словами, нашли общую массу мешка. Общая масса мешка цемента составляет 60 кг.

Деление меньшего числа на большее

В жизни часто возникают ситуации, когда требуется разделить меньшее число на большее. Например, представим ситуацию. Имеется трое друзей:

И требуется поровну разделить между ними два яблока. Как это сделать? Друзей трое, а яблок всего два. Мы попали в ситуацию в которой требуется разделить меньшее число на большее (два яблока на троих).

Для таких случаев предусмотрено следующее правило:

При делении меньшего числа на большее получается дробь, в числителе которой делимое, а в знаменателе – делитель.

Давайте применим это правило. Оно говорит, что при делении меньшего числа на большее получается дробь, в числителе которой делимое, а в знаменателе делитель. Делимое у нас это два яблока. Записываем в числителе число 2:

А делитель у нас это трое друзей (вспоминаем, что делитель показывает на сколько частей надо разделить делимое). Записываем тройку в знаменателе нашей дроби:

Забавно, но дробь это ответ к нашей задаче. Каждому другу достанется яблока. Почему так произошло?

Чтобы разделить два яблока на троих, надо разрезать ножом каждое яблоко на три части и раскидать поровну эти куски между тремя друзьями:

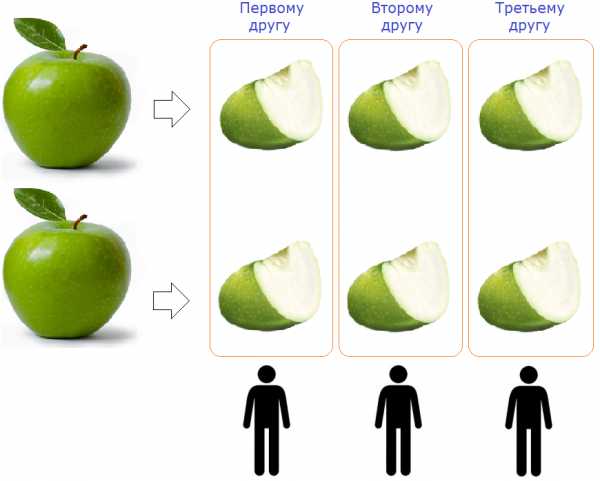
Как видно на рисунке, каждое яблоко было разделено на три части и раскидано поровну на троих друзей. Каждому другу досталось яблока (два кусочка из трёх).

Какую часть одно число составляет от другого

Иногда возникает необходимость узнать какую часть первое число составляет от второго. Для таких случаев предусмотрено следующее правило:

Чтобы узнать какую часть первое число составляет от второго, надо первое число разделить на второе.

Например, яблоко разделили на пять одинаковых долек. Какую часть яблока составляют две дольки?

Чтобы ответить на этот вопрос, надо первое число разделить на второе. Первое число это 2, второе — 5. Получается дробь .

Значит две дольки из пяти долек составляют две пятых. Это можно увидеть на следующем рисунке:

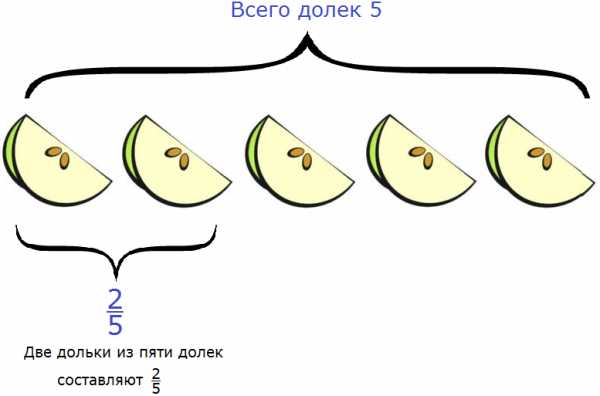
Итак, две дольки яблока из пяти составляют две пятых.

Возникает вопрос, а как узнать какое число первое, а какое второе? Для этого нужно посмотреть на вопрос, который поставлен в задаче. То число, которое указано в вопросе задачи, оно и будет первым числом. Например, в предыдущей задаче вопрос был поставлен так:

«Какую часть яблока составляют две такие дольки?»

Если внимательно присмотреться к вопросу, то можно обнаружить, что в нём указано число 2. Оно и стало первым числом.

Иногда в вопросе мелькает сразу два числа. Например: какую часть составляет число 2 от числа 10?

В этом случае первым числом будет то, которое в вопросе расположено раньше. В данном случае первое число это 2, а второе 10. Делим 2 на 10, получаем дробь . Значит число 2 от числа 10 составляет (две десятых).

Дробь означает, что число 10 разделено на десять частей, и от этих десяти частей взято две части.

Также, эту дробь можно сократить на 2. После сокращения дроби на 2 получаем дробь .

Дробь тоже может послужить ответом к задаче. Она будет означать, что число 10 разделено на пять частей, и от этих пяти частей взята одна часть.

Таким образом, число 2 составляет (одну пятую) от числа 10.

Пример 3. Какую часть составляет число 5 от числа 15?

Делим первое число на второе. Первое число 5, а второе 15. Делим 5 на 15, получаем дробь . Эту дробь можно сократить на 5

Получили аккуратную дробь . Значит ответ будет выглядеть следующим образом:

Число 5 составляет (одну третью) от числа 15.

Это можно даже проверить. Для этого нужно найти от числа 15. Если мы всё сделали правильно, то должны получить число 5.

Итак, найдём от числа 15. Как находить дробь от числа мы уже знаем

15 : 3 = 5

5 × 1 = 5

Получили ответ 5. Значит задача была решена правильно.

Пример 4. Какую часть 3 см составляют от 12 см?

Делим первое число на второе. Первое число это 3, а второе 12. Получаем дробь . Эту дробь можно сократить на 3

Получили ответ . Значит 3 см составляют (одну четвёртую) от 12 см.

Проверим правильно ли мы решили эту задачу. Для этого найдём от 12 см. Если мы всё сделали правильно, то должны получить 3 см.

Делим 12 на знаменатель дроби

12 см : 4 = 3 см

Умножаем полученные 3 см на числитель дроби

3 см × 1 = 3 см

Получили ответ 3 см. Значит задача была решена правильно.

Задания для самостоятельного решения

Задание 1. Найдите от числа 30. Задание 2. Найдите от числа 30. Задание 3. Найдите от числа 30. Задание 4. Найдите от числа 48. Задание 5. Найдите от числа 48. Задание 6. Найдите от 120 см.

120 см : 3 = 40 см
40 см × 2 = 80 см

Задание 7. Найдите от 150 см.

150 см : 3 = 50 см
50 см × 2 = 100 см

Задание 8. Найдите целое число по дроби, если известно, что этого числа составляет число 16. Задание 9. Найдите целое число по дроби, если известно, что этого числа составляет число 32. Задание 10. Найдите целое число по дроби, если известно, что этого числа составляет число 150.

150 : 5 = 30
30 × 8 = 240

Задание 11. Найдите длину пути от дома до школы, если известно, что этого пути составляют 4 км.

4 км : 2 = 2 км
2 км × 3 = 6 км

Задание 12. Найдите длину рулетки, если известно, что этой рулетки составляют 100 см.

100 см : 5 = 20 см
20 см × 8 = 160 см

Понравился урок?
Вступай в нашу новую группу Вконтакте и начни получать уведомления о новых уроках

Навигация по записям

spacemath.xyz

Решение задач на дроби

Селянина Людмила Петровна,
Учитель математики МОУ СОШ №2 , г Нерюнгри, РС(Якутия)

Урок математики в 6 классе по теме: «Решение задач на нахождение дроби от числа и числа по его дроби»
Цели:

Формирование умений и навыков в решении задач по данной теме;
Развитие умений анализировать условие задачи и относить ее к тому или иному типу;
Развитие логического мышления;
Формирование умений применять приемы сравнения, обобщения, выделение главного.
Развитие критического мышления, самостоятельность и ответственность, формирование коммуникативных и социальных компетенции.

ХОД УРОКА

Организационный момент. Мотивация

В этом году мы изучаем обыкновенные дроби и уже научились складывать, вычитать, умножать их и применять умножение при решении задач на нахождение дроби от числа, числа по его дроби.

Великий русский писатель Лев Николаевич Толстой говорил:
«Человек подобен дроби: в знаменателе – то, что он о себе думает, в числителе – то, что он есть на самом деле. Чем больше знаменатель, тем меньше дробь».
Как вы понимаете эти слова?

Подготовка учащихся к самостоятельной деятельности.

1. На доске записаны дроби:

, , , , , .

2.Вопросы:

Назовите правильные дроби. Как определяли?
Назовите неправильные дроби. Как определяли?
Выделите целую часть у неправильных дробей.
Найдите произведение 1 и 3 дробей. Каким правилом пользовались?
Разделите третью дробь на пятую. Какое правило применяли?
Назовите равные дроби.
Как найти дробь от числа?
Как найти число по его дроби?

3.Сообщение темы урока: «Решение задач на нахождение дроби от числа и числа по его дроби»

4.Проблемное задание

Задачи на нахождение дроби от числа и числа по его дроби — одна из самых трудных, нужных и важных тем не только в математике, но и других науках. Умения решать такие задачи широко используется в повседневной жизни. Эти задачи сейчас включены в задания ГИА и ЕГЭ. Поэтому передо мной, как перед учителем математики, стоит проблема научить учеников различать и решать задачи по данной теме. Давайте сегодня на уроке найдем способ решения этой проблемы.

Для решения проблемы подготовлен кейс, в котором предложены необходимые материалы: информация о дробях, старинные задачи на дроби, правила нахождения дроби от числа и числа по его дроби, различные задачи. Вы должны ознакомиться с предложенной информацией и, опираясь на нее, отобрать задачи на нахождение дроби от числа, числа по его дроби, обосновать свой выбор. Найти какой – то признак, характерное свойство, по которому вы определили тип задачи. Это может быть алгоритм, формула, схема, ключевое слово.

5.Самостоятельная деятельность учащихся

Работа с кейсом в группе:

1. Изучите материал кейса
2. Проведите исследование задач (определите тип задачи на дроби)
3. Оформите решение задач в индивидуальных бланках.
4. Обсудите результаты исследования. Выдвинете идеи, предложения по решению данной проблемы.
5. Данные оформите в виде чего – либо на форматках.

6 . Анализ и рефлексия совместной деятельности.

Основная задача этого этапа: выделить образовательные и учебные результаты работы с кейсом.

1. Обсуждение результатов исследования работы в группах.
2. Выработка рекомендаций по результатам работы.
3. Выводы записать на доске и в бланке.

7.Подведение итогов:

Вывод: Для определения типа задачи с дробями, можно использовать:

1. Формула

а — величина принятая за 1(целое)

b – часть целой величины

— дробь целого или части

1. Схема

1. Ключевые слова:

«От», «что составляет», «это составляет» «которого равны»

1. Алгоритм.

Приложение 1

Ученик(ца):___________________________________________________

ТЕМА урока: _________________________________________________________

_________________________________________________________

Нахождение дроби от числа

Нахождение числа по его дроби

Вывод: Для определения типа задачи с дробями, можно использовать:

Приложение 2

Задачи для исследования

1.Для ремонта школы купили 15 кг гвоздей, но всего использовали всех гвоздей. Сколько гвоздей израсходовали?

2. Во время ремонта использовали купленной краски, что составило 18 кг краски. Сколько краски было куплено?

3. Путешественник прошел за 2 дня 20 км. В первый день он прошел всего расстояния. Сколько километров прошел путешественник в первый день?

4.Пшеницей засеяно 2400 га, это составляет всего поля. Найдите площадь поля.

Работа с кейсом в группе:

Изучите материал кейса
Проведите исследование задач (определите тип задачи на дроби)
Оформите решение задач в индивидуальных бланках.
Обсудите результаты исследования. Выдвинете идеи, предложения по решению данной проблемы.
Данные оформите в виде чего – либо на форматках.

Кейс:

Из истории дробей

Первой дробью, с которой познакомились люди, была половина. Следующей дробью была треть. И у египтян, и у вавилонян были специальные обозначения для дробей 1/3 и 2/3 , не совпадавшие с обозначениями для других дробей.

Египтяне все дроби старались записать как суммы долей, то есть дробей вида 1/n. Например, вместо 8/15 они писали 1/3 + 1/5. Единственным исключением была дробь 2/3.

В папирусе Ахмеса (древнеегипетское учебное руководство по арифметике и геометрии периода Среднего царства, переписанное около 1650 до н. э. писцом по имени Ахмес на свиток папируса длиной 5,25 м. и шириной 33 см.)

есть задача: «Разделить 7 хлебов между 8 людьми». Если резать каждый хлеб на 8 частей, придется провести 49 разрезов.

А по-египетски эта задача решалась так. Дробь 7/8 записывали в виде долей: 1/2 + 1/4 + 1/8. Значит, каждому человеку надо дать полхлеба, четверть хлеба и восьмушку хлеба; поэтому четыре хлеба разрезаем пополам, два хлеба — на 4 части и один хлеб — на 8 долей, после чего каждому даем его часть.

Старинные задачи на дроби

Эти задачи пришли к нам из глубины веков, от наших предков. Разные народы нашей планеты придумывали их, оттачивали условия и логику заданий. Они остроумны и занимательны, в них собраны замечательные находки многих поколений.

Задача из «Арифметики» Леонтия Филипповича Магницкого. Учебник арифметики, по которому учился Михаил Васильевич Ломоносов. Эта задача трехвековой давности.

Один человек выпьет бочонок за 14 дней, а с женой выпьет тот же бочонок за 10 дней. За сколько дней жена его отдельно выпьет этот бочонок?

Решение.

Весь бочонок принят за — 1.

1)1:14=бочонка пьёт один человек в день.

1:10=бочонка пьёт муж и жена в день.

2) пьёт жена в день.

3)1:дней понадобится жене чтобы выпить бочонок.

Ответ: 35 дней понадобится жене чтобы выпить бочонок.

Старинная задача

Четыре плотника хотят построить дом. Первый плотник может построить дом за год, второй — за 2 года, третий — за 3 года, четвертый — за 4 года. За сколько лет они построят дом при совместной работе?

Решение.

Вся работа принята за – а.

1) 1:1=1за 1 год 1-ый плотник сделает всю работу.

1:2=(работы) делает 2-ой плотник за 1 год.

1:3=(работы) делает 3-ий плотник за 1 год.

1:4=(работы) делает 4-ый плотник за 1 год.

2)1+(домов) сделают плотники за 1 год, работая совместно.

3)1:(года) понадобится плотникам, чтобы сделать 1 дом.

Ответ: за года или 175 дней часа сделают плотники 1 дом работая совместно.

Нахождение дроби от числа:

Чтобы найти дробь от числа, нужно умножить число на эту дробь.

Задача 1. В лесу 800 деревьев. Сосны составляют всех деревьев. Сколько сосен в лесу?

Нахождение числа по его дроби:

Чтобы найти число по данному значению его дроби, надо это значение разделить на дробь

Задача 2. В лесу 200 сосен, что составляет всех деревьев. Сколько деревьев в лесу?

В повседневной жизни мы тоже часто сталкиваемся с такими понятиями, как половина, треть, четверть. С самого детства мы слышим такие выражения: «весит четверть килограмма», «одна вторая листа» или «три четверти часа». Во всех этих случаях мы говорим о дробях: одна четверть, две четверти, три четверти, одна вторая и треть — все это дроби. Люди разных профессий используют дроби в процессе работы, даже не задумываясь об этом. Например, врач, назначая количество лекарства больному, повар, отмеряя необходимые ингредиенты, продавец, водопроводчик, слесарь и даже музыкант. Да и мы пользуемся дробями с самого детства, не подозревая об этом («Мама, дай мне половинку яблока», «Давай разделим шоколадку поровну», «Я еще четверть часика поиграю в компьютер»).

И раз древние египтяне, вавилоняне, римляне и др. могли использовать дроби и проводить вычисления с использованием дробей, то и современный человек, даже имея современную вычислительную технику, обязан уметь пользоваться дробями. Дроби применяются при решении различных типов задач.

infourok.ru

«Решение задач на нахождение дроби от числа и числа по его дроби»

учитель математики Александровской средней школы Рязанского района

ГОРБАН СВЕТЛАНА НИКОЛАЕВНА.

Прежде чем решать задачу – прочитай условие

Жак Адамар

Цели:

формирование умений и навыков в решении задач по данной теме;
развитие умения анализировать условие задачи и относить её к тому или иному типу;
— умение видеть математическую задачу в контексте проблемной ситуации в других дисциплинах, в окружающей жизни;
отработка умений и навыков самостоятельной работы, работы в парах;
развитие логического мышления;
формирование умений применять приёмы сравнения, обобщения, выделения главного;
воспитание познавательного интереса.

Тип урока: применение знаний.

ХОД УРОКА

I. Организационный момент

Проверка настроения: приём “Смайлики” (у каждого ученика на столе 3 карточки, нужно показать ту, которая соответствует настроению перед уроком).

II. Мотивация и сообщение темы и цели урока

Учитель: Девизом нашего урока будут слова Жака Адамара « Прежде чем решать задачу – прочитай условие».

Историческая справка (сообщил ученик). Жак Саломон Адамар – французский математик, родился в декабре 1865 года в Версале. В детстве увлекался языками. Победил на конкурсе знатоков греческого и латинского языков. Среднее образование получил в лицее Людовика Великого. Высшее образование в Париже. Был избран членом Французской Академии наук. Его интересы не ограничивались только одной наукой математикой. Он был блистательным учёным во многих областях. Жаку Адамару в 1892 году была присвоена степень доктора философии. Он занимался теорией чисел, дифференциальными уравнениями, теорией аналитических функций.

Учитель: Начнём мы сегодня наш урок с отгадывания ребусов.

На интерактивной доске появляются ребусы (через документ-камеру).

Ученики: Дробь и задача.

Учитель: Правильно, молодцы. Дроби применяются при решении различных типов задач. Давайте вспомним, а какие типы задач мы уже решали? Я прочитаю вам стихотворения, а вы догадайтесь какие типы задач, с использованием дроби, мы сегодня будем решать.

Дробь от числа хотим найти,
Не надо никого тревожить.
Нам надо данное число
На эту дробь умножить. (Cтихотворение крепится на доске.)

Ученики: Задачи на нахождение дроби от числа.

Учитель: Верно.

Если вы должны найти
Число по его дроби,
То на дробь вы поделите
Значенье данной дроби. ( Cтихотворение крепится на доске.)

Ученики: Задачи на нахождение числа по его дроби.

Учитель: Правильно, ребята. Мы будем решать задачи на нахождение дроби от числа и числа по его дроби. Также научимся анализировать условие различных задач и относить их к тому или иному типу, повторим правила. Запишите число и тему урока в тетрадь «Решение задач на нахождение дроби от числа и числа по его дроби».

III. Актуализация и коррекция опорных знаний

Учитель: Но, чтобы решать данные задачи, вы должны уметь выполнять различные действия с дробями (устно).

На доске записаны дроби :

, , , , , .

Вопросы:

Назовите правильные дроби. Как определяли?
Назовите неправильные дроби. Как определяли?
Выделите целую часть у неправильных дробей.
Найдите произведение 1 и 3 дробей. Каким правилом пользовались?
Разделите третью дробь на пятую. Какое правило применяли?
Назовите равные дроби.
Переведите 20%, 13%, 5%, 10%, 0, 4% в десятичные дроби.

Найдите: 0,5 от 200; 3/ 5 от 30; 50% от 60; 4% от 500.

Найдите число, если: 0,5 его равны 50; 3/5 его равны 15; 20% его равны 4.

IV. Работа по теме урока.

1. Незнайке предложили решить задачу. Жители Солнечного города присутствуют на представлении в цирке. Фокусник хочет всех угостить мороженым. Он попросил Незнайку сосчитать, сколько всего жителей, если на представлении присутствуют 15 малышек, и это составляет 3/5 всех зрителей.

Вот как посчитал Незнайка: 15*3/5=9 (чел.)

— Что же получилось после представления, как вы думайте? (Мороженого всем не хватило.)

— В чем ошибка Незнайки? (Вместо того чтобы искать число по данному значению дроби, Незнайка нашёл дробь от числа.)

— Исправьте Незнайку и выясните сколько же всего жителей Солнечного города было на представлении? Решение запишите в тетрадь.

15:3/5=15*5/3=25. (Ответ: 25 жителей.) (проверить устно).

На доске задача: решите самостоятельно в тетради.

2. Незнайке фокусник подарил 65 воздушных шаров и попросил раздать жителям Солнечного города, но по дороге Незнайка наткнулся на куст шиповника, 3/5 шаров лопнуло. Сколько шаров осталось у Незнайки?

1)65*3/5=39(ш.)-лопнуло. 2)65-39=26(ш.) – осталось. (Ответ: 26 шаров.)

(проверить через документ — камеру).

V. Физкультминутка «Елочка»

VI. Закрепление изученного материала.

На доске задача:

3. В хоре 80 учащихся, из них – мальчики. Сколько мальчиков в хоре?

Заполнение таблицы:

Вопросы к задаче:

Что есть всё число в задаче? (Всего учащихся)
Известно ли оно? (80)
О какой дроби от числа говорится в задаче? ()
Известно ли значение этой дроби? (Нет, его надо найти)
О каком типе задач идёт речь? (Нахождение дроби от числа)

Другая задача:

4. В хоре 20 мальчиков, что составляет всех учащихся в хоре. Сколько всего учащихся в хоре?

Вопросы к задаче:

Что есть всё число в задаче? (Всего учащихся)
Известно ли оно? (нет)
А каким оно будет целым или частью? (целым)
О каком типе задач идёт речь? (Нахождение числа по его дроби)

Решение задач (работа в парах).

Учитель: Ну а теперь настало время применять наши знания к решению задач. Перед вами лежит конверт с различными задачами. Распределите их на две группы: задачи на нахождение дроби от числа и задачи на нахождение числа от дроби. На работу вам отводится 5 минут (Проверка через документ камеру).

Задачи:

За неделю лиса утащила 15 кур, что составило 3/5 всех кур в курятнике. Сколько всего кур было?
В хоре 80 учащихся, 25% из них – мальчики. Сколько мальчиков в хоре?
Алиса упала в сказочный колодец и за одну минуту пролетела 90 км. Какова глубина колодца, если за 1 минуту Алиса пролетела 3/4 всего расстояния?
Девочка собрала 15 грибов, 2/5 этих грибов белые. Сколько белых грибов собрала девочка?
Матушка перед балом задала Золушке много работы. Чтобы выполнить 3/5 этой работы, Золушке понадобилось 6 часов. За какое время Золушка выполнит всю работу?
Мама купила 6 килограммов конфет. Витя сразу съел 2/3 этих конфет, и ему стало плохо. После какого количества съеденных конфет у Вити разболелся живот?
Трактористы вспахали поле за три дня. В первый день они вспахали 25% поля, во второй день 60% поля, а в третий день – остальные 36га. Найдите площадь поля.
Белочка за зиму съела 3/4 запаса орехов. Сколько орехов заготовила белочка на зиму, если съела 240 орехов?

Учитель: Вернёмся к эпиграфу “Прежде чем решать задачу – прочитай условие”, а я добавляю: и определи, к какому типу она относится, затем решай.

Учитель: А теперь попробуйте самостоятельно выполнить тест (2 варианта) (проверка с помощью интерактивной доски).

Вариант 1

А. 21 Б. 15 В. Г. 7

А. 24см Б. 13,5см В. 36 см Г. 4,5см

А. 100 Б. 200 В. 20 Г. 72

А. 25км Б. 81км В. 45км Г. 90км

А. кг Б. 9кг В. 10кг Г. 6кг

Вариант 2

А. 10 Б. 6 В. 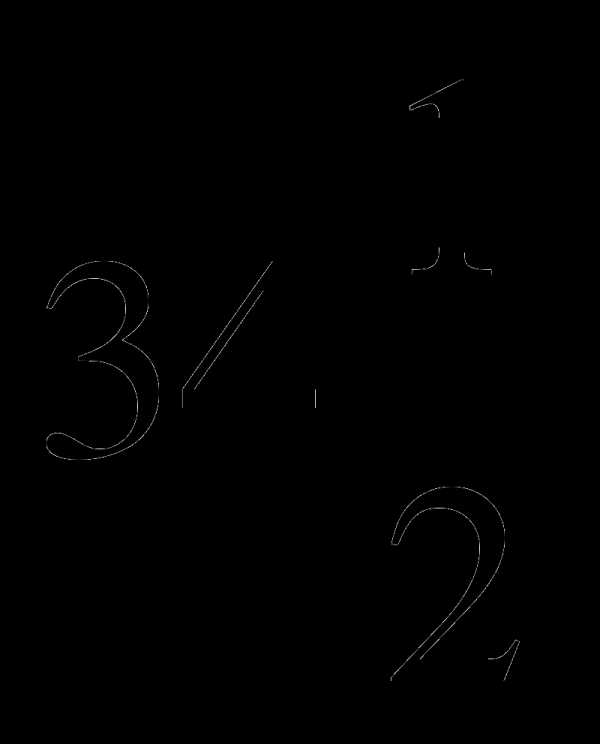Г. 7,5

А. 6кг Б. 4кг В. 2кг Г. 3кг

А. 3 Б. В. Г. 24

Матушка перед балом задала Золушке много работы. Чтобы выполнить 3/5 этой работы, Золушке понадобилось 6 часов. За какое время Золушка выполнит всю работу?

А. 3,6 Б. В. Г. 10

А. кг Б. 6кг В. кг Г. кг

Проверка теста, выставление оценок (слайд)

( критерии – слайд)

VII. Подведение итогов

Выставление оценок.
Какие типы задач сегодня на уроке мы решали?
Чем отличаются и что общего в условиях этих задач?

VIII. Задание на дом

Домашнее задание творческое: каждому ученику нужно составить по одной задаче каждого типа.

IХ. Этап рефлексии

Учитель: У каждого из вас на столе смайлики (зелёный, жёлтый, красный). Уходя из класса, прикрепите на доску один из них. Урок окончен. До свидания.

Смайлик зелёного цвета обозначает: “Я удовлетворён уроком, урок был полезен для меня, я много, с пользой и хорошо работал на уроке, и получил заслуженную оценку, я понимал всё, о чём говорилось и что делалось на уроке”.
Смайлик жёлтого цвета обозначает: “Урок был интересен, я принимал в нём активное участие, урок был в определённой степени полезен для меня, я отвечал с места, я сумел выполнить ряд заданий, мне было на уроке достаточно комфортно”.
Смайлик красного цвета обозначает: “Пользы от урока я получил мало, я не очень понимал, о чём идёт речь, мне это не очень нужно, домашнее задание я не понял, к ответу на уроке я был не готов”.

infourok.ru

Задачи на нахождение дроби от числа

5.3А

Школа:

Дата:

ФИО учителя:.

класс: 5

Участвовали:

Не участвовали:

Тема урока

Задачи на нахождение дроби от числа

Цели обучения, которые достигаются на данном уроке (ссылка на учебную программу)

5.1.2.13 преобразовывать неправильную дробь в смешанное число и смешанное число в неправильную дробь;

5.1.2.14 применять основное свойство дроби при сокращении обыкновенных дробей;

5.1.2.21 выполнять умножение обыкновенных дробей, смешанных чисел;

5.1.2.24 находить часть числа и число по его части

Цели урока

Сформировать навык нахождение дроби от числа; уметь умножать обыкновенные дроби ; умножать натуральное число на дробь, дробь на дробь, и смешанного числа на дробь;

Критерии оценивания

Учащиеся определяют, задачи на нахождение дроби от числа Учащиеся знают, алгоритм решения текстовых задач.

Учащиеся применяют, полученные знания для решения текстовых задач.

Языковые цели

Термины: дробь, целое, часть, часть от числа, обыкновенная дробь, десятичная дробь; числитель; знаменатель.

Лексика: типы задач: нахождение части числа; нахождение число по его части;

Привитие ценностей

Создать условия для разностороннего развития способностей и самореализации учащихся, а также для формирования у них общечеловеческие и социальные ценности (честность, забота об окружающих, уважение жизни; демократия, патриотизм, терпимость, ответственность).

Межпредметные связи

Экономика, физика, биология.

Навыки использования ИКТ

Интерактивная доска, интерактивные методы, активные методы .

Предварительные знания

Умножение обыкновенных дробей и смешанных чисел; взаимно обратные числа.

Ход урока

Запланированные этапы урока

Виды упражнений, запланированных на урок:

Ресурсы

Начало урока

Середина урока

Эпиграф к уроку:

«Недостаточно лишь понять задачу, необходимо желание решить её. Где есть желание, найдётся путь!»

Д.Пойа

I.Организационный момент.

Метод «Самолётик пожеланий» — создание позитивного настроя класса на урок и творческой атмосферы.

Учащиеся делятся на 3 группы и распределяют роли в группах.

Разминка «Распутай клубок»

+ =

ответы.

543 — =

365 + 178 =

* 2 =

: 3 =

II.Актуализация знаний, проверка усвоения материала:

Устный счет

Фронтальная работа с классом.

Игра «Молчанка»

Учитель задает вопрос, ученики, молча на пальцах, показывают номер правильного ответа

Вопросы:

1.Какая дробь выражает четверть?

2. Указать дробь, равную дроби 3

3. Найти дробь, равную 4

4. Какая дробь выражает «Половину»?

5. Указать дробь больше 1, но меньше 2

6. Чему равна сумма дроби и ?

III. Работа в группах.

Метод «Мозговой штурм»

Группе дается задание:

Пример. Рассмотрим задачу.

В книге 160 страниц. Юра прочитал 4/5 книги. Сколько страниц прочитал Юра?

Прежде всего найдём в задаче целое. Это — вся книга и в ней всего 160 страниц.

Посмотрим на дробь (часть) от целого: 4/5. Знаменатель равен 5, значит, целое разделили на 5 частей и мы можем найти сколько страниц составляет 1/5 часть.

160 : 5 = 32 (стр.) — составляет 1/5 часть страниц.
Числитель дроби равен 4, значит взято 4 части.
32 · 4 = 128 (стр.) — составляют 4/5 книги.

Оба действия можно записать кратко, в соответствии с правилом нахождения части от целого.

Чтобы найти дробь (часть) от числа, нужно это число умножить на данную дробь

Физкультминутка!

Игра «Молчанка»

Верное высказывание — сидим руки вверх; ложное — встаём.

Верно ли, что при умножении дробей множители нужно приводить к общему знаменателю?

Верно ли, произведение частного и делителя равно делимому?

Верно ли, что делитель может быть равен нулю?

Верно ли, чтобы найти число по его дроби нужно разделить на эту дробь число ей соответствующее?

Верно ли, что при сложении дробей слагаемые нужно приводить к общему знаменателю?

Верно ли, чтобы найти дробь от числа, надо число разделить на эту дробь?

Верно ли, что число состоящее из целой части и дробной части называют смешанным

числом?

Слайд, листы самооценивания

Слайд, оценивание в устной форме

Решение задач. Работа в группах

Метод «Джигсо» Задание:

Выполнить решение задач по следующей схеме:

Рассчитаться в группе от 1 до 3 (каждому члену группы присваивается номер от 1до 3)
Решают задачу своего номера.
Собираются в сменные группы по номеру задачи и обсуждают решения.
Возвращаются в исходные группы и проверяют решения по образцу.

Задачи для группы

Дифференциация

Задача№1. В книге 140 страниц. Володя прочитал этой книги. Сколько страниц прочитал Володя?

Реши задачи:
Задача№2. Площадь одной комнаты 21 м², а площадь второй комнаты составляет площади первой комнаты. Найдите площадь двух комнат.

Реши задачи:
Задача№3

Периметр треугольника 37 см . одна его сторона составляет от периметра, другая — . найти все стороны треугольника.

Ответ : 112

Ответ: 30 м2

Ответ:

15см,10см,

Дескрипторы

составляют краткую запись условия

Содержание соответствует заявленной теме.

Свободное, без чтения, изложение материала.

выполняют вычисления

знает формулы площади прямоугольника;

знает формулу периметра треугольника

находят ответ задачи

Отчётливость произношения, отбор необходимых речевых средств

составляют постер

Оригинальность выступления

Регламент

Слайд, постер, смайлики

Слайд

, ,

Конец урока

Итог урока: Рефлексия

«Четыре Я»

Учитель предлагает разместить на круге в соответствующем секторе, стикеры с фразами, которые участники продолжают самостоятельно:

Я узнал…
Я научился…
Я проявил себя …
Я смогу применить …

Чем ближе к центру размещаются стикеры с надписями, тем сильнее эффект!

Задание на дом:— придумывает задачу;

Придумайте и оформите с решением свою задачу.

Обратите внимание на то, чтобы ваши работы были интересны по содержанию, содержали верную математическую информацию по теме, были красиво оформлены.

Критерии

— выполняет вычисления; Дескриптор: — знает формулы площади и периметра прямоугольника, квадрата, и.т.д.;

— находит ответ задачи;

— красочно оформляет задачу.

Дифференциация – каким способом вы хотите больше оказывать поддержку? Какие задания вы даете ученикам более способным по сравнению с другими?

Оценивание – как Вы планируете проверять уровень усвоения материала учащимися?

Охрана здоровья и соблюдение техники безопасности

Учащимся будут предложены для обсуждения задачи разного уровня сложности. Дифференциация заключается в ожидании от более способных учащихся более аргументированных и более креативных ответов. Разработала в конце урока.

На всех этапах урока применяла формативное оценивание: оценивание устное, стикерами, по критериям, смайликами.

Охрана здоровья, соблюдение техники безопасности, физминутка

Рефлексия по уроку

Была ли реальной и доступной цель урока или учебные цели?

Все ли учащиеся достигли цели обучения? Если ученики еще не достигли цели, как вы думаете, почему? Правильно проводилась дифференциация на уроке?

Эффективно ли использовали вы время во время этапов урока? Были ли отклонения от плана урока, и почему?

Используйте данный раздел урока для рефлексии. Ответьте на вопросы, которые имеют важное значение в этом столбце.

Итоговая оценка

Какие две вещи прошли действительно хорошо (принимайте в расчет, как преподавание, так и учение)?

Какие две вещи могли бы улучшить Ваш урок (принимайте в расчет, как преподавание, так и учение)?

Что нового я узнал из этого урока о своем классе или об отдельных учениках, что я мог бы использовать при планировании следующего урока?

infourok.ru

Задачи на дроби — математика, презентации

Бухарина Галина Владимировна

МАОУ СОШ№5. г.Челябинск

Если вы хотите научиться плавать, то смело входите в воду, а если хотите научиться решать задачи — решайте их

Д. Пойа.

Считай несчастным тот день или тот час, в который ты не усвоил ничего нового и ничего не прибавил к своему образованию»

Я.-А. Коменский

установите связь между этими понятиями

ДРОБЬ ЗАДАЧИ

ЦЕЛОЕ ЧАСТИ

Предлагаю каждому ученику

поставить личную цель для себя:

Я решу все задачи сам(а)
Я решу все задачи,

если мне помогут,

но буду стараться сам(а)

Я пока еще не готов(а) все решить сам(а),

буду учиться.

Общая цель к концу урока:

могу применять дроби

при решении задач.

Какие знания

будут необходимы нам на уроке?

Дробь на дробь просто умножить:

Надо числители и знаменатели

Взять и перемножить!

Не сложно дроби и разделить:

Стоит лишь вам заменить

Вторую дробь, ей обратной,

Деление на умножение,

Задание станет приятным,

Без осложнения.

Дробь от числа хотим найти —

Не надо никого тревожить.

Нам надо данное число

Всего на эту дробь умножить.

Если вы должны найти

Число по его дроби,

То на дробь вы поделите

Значенье данной дроби.

Счет и вычисления –

основа порядка в голове.

И. Песталоцци.

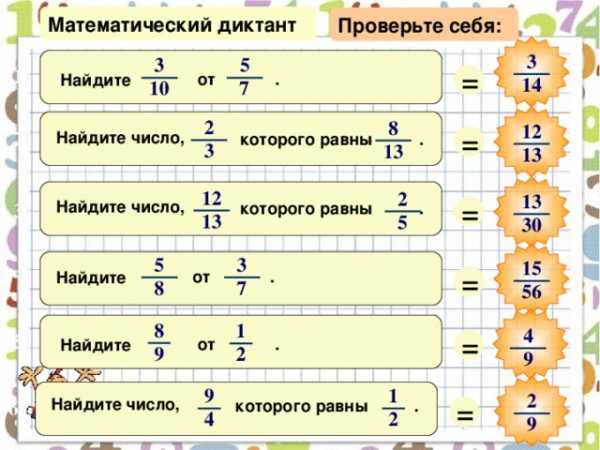
Математический диктант

Проверьте себя:

от .

Найдите

1 2

Найдите число,

которого равны .

1 3

Найдите число,

которого равны .

1 3

3 0

от .

Найдите

от .

Найдите

Найдите число,

которого равны .

Шел отряд солдат:

десять рядов по семь солдат в ряд.

8/10 их было усатых.

Сколько там было усатых солдат?

Сколько там было безусых солдат?

4 /10 их было носатых.

Сколько там было носатых солдат?

Сколько там было курносых солдат?

Рисуй глазами треугольник

Рисуй глазами треугольник.

Теперь его переверни

Вершиной вниз.

И вновь глазами

ты по периметру веди.

Рисуй восьмерку вертикально.

Ты головою не крути,

А лишь глазами осторожно

Ты вдоль по линиям води.

И на бочок ее клади.

Теперь следи горизонтально,

И в центре ты остановись.

Зажмурься крепко, не ленись.

Глаза открываем мы, наконец.

Зарядка окончилась.

Ты – молодец!

Аист пролетает без посадки 400 км, что составляет

расстояния, которое пролетает летучая мышь, и

лишь от пути, который может преодолеть

египетская цапля. Перелетная саранча пролетает без

посадки расстояние в большее, чем аист. Во

сколько раз путь перелета саранчи больше, чем у

летучей мыши?

Г.В. Дорофеев, Л.Г. Петерсон, 5 класс (часть 2). № 350 (2).

Масса муравья составляет 1 /10 массы груза, который

он может перетащить за 1 раз. Какова масса муравья,

если за 1 раз он может перетащить груза?

Математика 5 класс (часть 2). Г.В. Дорофеев, Л.Г. Петерсон. № 489.

Муравей щелкает челюстями

со скоростью 230 км/ч

Муравей за работой

III

VII

VIII

Длина минутной стрелки Кремлевских курантов – 328 см.

Высота цифр на циферблате составляет

от длины минутной

стрелки.

Вычисли высоту цифр на циферблате Кремлевских курантов.

XII

Математика 5 класс (часть 2). Г.В. Дорофеев, Л.Г. Петерсон. № 543 (1).

Предельный возраст белки 6 лет,

что составляет предельного возраста зайца.

Сколько лет может прожить заяц?

Г.В. Дорофеев, Л.Г. Петерсон, 5 класс (часть 2). № 496.

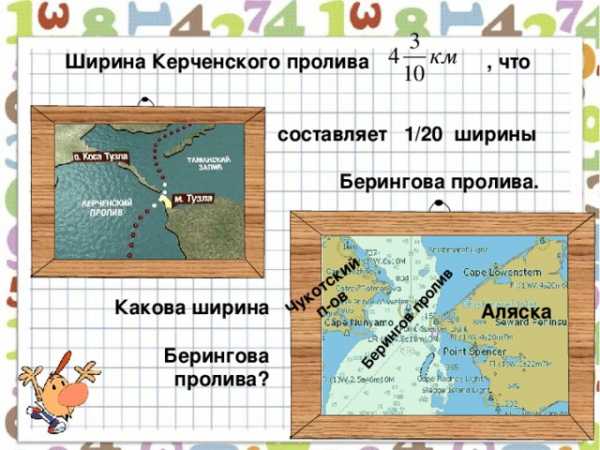
Берингов пролив

Чукотский

п-ов

Ширина Керченского пролива , что

составляет 1/ 20 ширины

Берингова пролива.

Какова ширина

Берингова пролива?

Аляска

Г.В. Дорофеев, Л.Г. Петерсон, 5 класс (часть 2). № 497.

При размоле пшеницы получается муки всего

количества, манной крупы , а остальную часть

составляют отруби. Сколько муки и манной крупы

получили, если масса отрубей составила 36 кг?

Схема (3)

Г.В. Дорофеев, Л.Г. Петерсон, 5 класс (часть 2). № 559. Сделайте клик по кнопке «Схема» ( 3 раза)

36кг

Мука

Высший сорт

3м

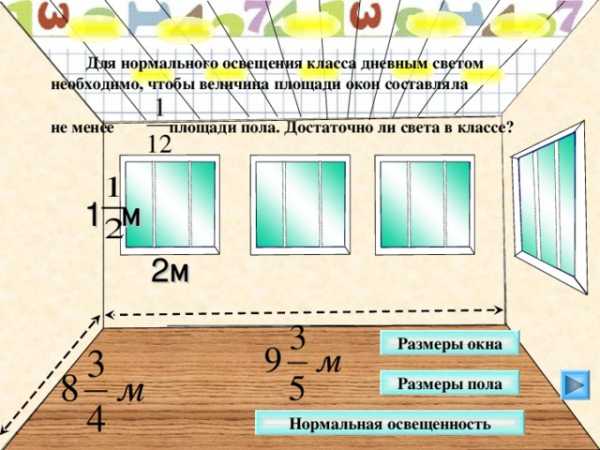
Для нормального освещения класса дневным светом

необходимо, чтобы величина площади окон составляла

не менее площади пола. Достаточно ли света в классе?

1 м

2м

Математика 5 класс (часть 2). Г.В. Дорофеев, Л.Г. Петерсон. № 513.

Размеры окна

Размеры пола

Нормальная освещенность

нахождение дроби от числа нахождение числа по его дроби

от

Что составляет

Подведение итогов урока

Оцените свою работу на уроке. Что получалось? Над чем надо ещё работать? Что надо повторить?

Домашнее задание

СПАСИБО

ЗА УРОК

kopilkaurokov.ru

Решение задач на нахождение дроби от числа и числа по его дроби. 6-й класс

Разделы: Математика

Тип урока: комплексное применение знаний.

Цели:

систематизация знаний по темам: «Действия с дробями», «Нахождение дроби от числа», «Нахождение числа по его дроби»;
отработка практических навыков выполнения действий с дробями;
расширение кругозора учащихся;
развитие познавательной активности, внимания, памяти, интереса к предмету математики;
воспитание здорового образа жизни, бережного отношения к животным.

ХОД УРОКА

1. Организационный момент

Стихотворение читает ребенок:

Нам радостно, нам весело!
Смеемся мы с утра.
Но вот пришло мгновенье,
Серьезным быть пора.
Влево, вправо повернулись,
Друг другу улыбнулись
И в работу окунулись .

Мотивация урока.

– Здравствуйте! Я рада видеть вас всех на уроке математики.
– Какое настроение вы принесли на урок, я узнаю по индикаторам настроения
(Ученики показывают картинку, соответствующую их настроению в начале урока)
– Начать работу по теме урока мне хотелось бы с высказывания древнегреческого философа Саади «Ученик, который учится без желания – это птица без крыльев» . И мне хотелось бы, чтобы было у вас желание учиться, узнавать новое, неопознанное не только на сегодняшнем уроке, а всегда и только в этом случае своими «крыльями» будете взлетать все выше и выше.

2. Актуализация знаний учащихся

– Тема нашего урока: Решение задач на нахождение дроби от числа и числа по его дроби.
– Как вы думаете, чем мы сегодня будем заниматься на уроке? (ответы учащихся)
– Правильно, сегодня на уроке мы повторим и закрепим навыки решения задач по данной теме.
– А результатом работы послужит выполнение теста в конце урока.
– Открываем тетради и записываем тему урока
Тогда – в путь! И пусть девизом урока будут слова:

Думать – коллективно!
Решать – оперативно!
Отвечать – доказательно!
Бороться – старательно!
И открытия нас ждут обязательно!

– Наш урок пройдет в форме электронного журнала «Дроби вокруг нас». Любой журнал имеет страницы, так и мы рассмотрим следующие страницы

Содержание

1. Историческая страница
2. Страница устной работы
3. Страница «Вмире животных»
4. Страница «Путешествия»
5. Страница «Здоровье»

– Итак, открываем первую страницу журнала это – «Историческая». Вы уже многое знаете из истории возникновения дробей, а сегодня мы продолжим знакомство с возникновением дробей и ученик приготовил разные виды записи дробей

Выступление ученика и плакат ученика

Первой дробь была дробь 1/2?. Посмотрите, как изображали дроби в Древнем Египте.

Первым дробную черту ввел итальянский ученый Фибоначчи.

1) – Спасибо. Молодцы. А сейчас мы посмотрим кто внимательно слушал и сможет ответить на мой вопрос: Кто первым изобрел черту дроби?
– Правильно, Фибоначчи, молодцы.
2) – А сейчас возьмите фломастеры и листочки на парте и запишите дробь как Древние Египтяне – 1 вариант, как Древние Китайцы – 2 вариант.

– Покажите теперь друг друг, у кого получилось?
– Оказывается приемы записи дробей в древности нам известны и мы даже можем их использовать, но конечно, же традиционная запись нам удобнее и привычнее для выполнения различных заданий, поэтому мы продолжаем работу с дробями в их привычноим виде.
Переходим к следующей странице Страница устной работы

3. Устная работа

На доске записаны дроби (Презентация, слайд 8)

Вопросы:

– Назовите правильные дроби. Как определяли?
– Назовите неправильные дроби. Как определяли?
– Выделите целую часть у неправильных дробей.
– Найдите произведение 1 и 3 дробей. Каким правилом пользовались?
– Разделите третью дробь на пятую. Какое правило применяли?
– Назовите равные дроби.

– Как найти число по заданной дроби?

Найти число, если:

1/6 его составляют 360
5/6 его составляют 60
0,5 его составляют 100

– Как найти дробь от числа?

Найти:

1/2 от 60
8/9 от 18.

– На этой странице мы повторили правила нахождения дроби от числа и числа по его дроби. Я вижу, что вы хорошо справились с заданиями, знаете правила.
– Посмотрите мы повторили 2 правила. Сколько типов задач по данной теме существует? (Два)
– Скажите, а когда задачу становиться легко решить? (Когда известен тип задачи)
– Правильно, значит самое главное уметь определять тип задачи.
– Поэтому сейчас я вам предлагаю 2 типа задач, они очень похожи и мы будем определять тип каждой задачи.

4. Комплексное применение знаний

– Итак, я приготовила для вас на парте таблицы – посмотрите.
Задание таково: по условиям двух задач заполнить таблицу, т.е. определить все число, дробь от числа и соответственно определить тип задачи, и решить её. Время работы 4 минуты

Тип задачи	Всё число	Дробь от числа	Значение дроби от числа	Решение задачи
1. Нахождение дроби от числа			?
2. Нахождение числа по его дроби	?

Вопросы к задаче1:

– Что есть всё число в задаче? (Всего учащихся)
– Известно ли оно? (50)
– О какой дроби от числа говорится в задаче? (2/5)
– Известно ли значение этой дроби? (Нет, его надо найти)
– О каком типе задач идёт речь? (Нахождение дроби от числа)

Решаем задачу 2
Проверяем решение

Сделаем проверку таблицы:

Тип задачи	Всё число	Дробь от числа	Значение дроби от числа	Решение задачи
1. Нахождение дроби от числа	50		?	50 · = 20
2. Нахождение числа по его дроби	?		20	20 : = 50

– Мы рассмотрели два типа задач, ответьте на мой вопрос: чтобы не допускать ошибок при решении как нам нужно читать условие? (внимательно)

5. Тренировочные упражнения

Следующая страница «В мире животных»

Мама-слониха имеет массу 600 кг.
Найдите массу слонёнка, если известно, что она составляет 1/5 часть от массы большого слона.

Два ученика решают на оборотах доски, а остальные в тетради, затем проверяем решение – 2 оценки.

При проверке проговорить тип задачи.

Решение: 600*1/5 =120 кг

Задача про тигренка.

Маленькому тигренку на обед положено 3 кг мяса, а он съел только ? от куска мяса. Сколько килограммов мяса съел тигренок? (Все ученики решают в тетради. Затем проверка решения.)

Решение: 3 * 3/4 = 21/4 кг мяса

– Каким правилом мы пользовались, решая эти задачи? (Нахождением дроби от числа)
– Ребята, а вы видели маленького тигренка и маленького слоненка? Где? А как вы думаете в неволе животным живется хорошо?
– А вот то место, где и тигренку и слоненку было бы комфортно…

6. Физминутка

Уголок природы (музыкальное сопровождение)

– Ребята! Что вы видите на слайде? Да, это любимое место отдыха каждого из нас – замечательный уголок природы. Воздух здесь чистый и свежий. Выполним дыхательную зарядку.

Дышим носом глубоко
Дышим носом глубоко –
Поднимаемся легко.
Я дышу,
Дышу свободно,
Глубоко и тихо –
Как угодно.
Выполню задание,
Задержу дыхание.
Раз, два, три, четыре –
Снова дышим:
Глубже, шире…

– Мы отдохнули, побывали в теплом, уютном месте, а теперь продолжим работу. Перелистывая страницы журнала, мы переходим к Странице «Путешествия». На этой странице нам представлена задача на вычисление длины пути между Москвой и Санкт-Петербургом, а это современный скоростной поезд Сапсан.

Поезд проехал 600 км, что составило 2/3 пути. Сколько километров составляет весь путь?

Два ученика решают на оборотах доски, а остальные в тетради, затем проверяем решение – 2 оценки.

Решаем: 600 : 2/3 = 900 км

– Как вы думаете, должен чувствовать себя человек, отправляющийся в путешествие?
– Правильно, он должен быть здоровым!

Ну а следующая страница в журнале – страница «Здоровья»

Задача: Минимальный объем молочных продуктов, необходимый 12-летнему школьнику, составляет 3/20 от всей выпиваемой за день жидкости, что составляет 300 грамм. Какой объем жидкости в среднем употребляет 12-летний школьник?

Решение самостоятельно, затем проверка

Решение: 300 : = 2000г

ВОСПИТАНИЕ ЗОЖ

– Скажите ребята, а зачем 12-летнему учащемуся потреблять молочные продукты?
– А вы употребляете молочные продукты? Какие?
– А какие продукты еще полезны ученикам?
– Ребята, скажите а последние две задачи мы решали, используя какое правило?
– Большую часть журнала мы рассмотрели, и следующим заданием является выполнение теста по вариантам (раздаются задания).

7. Самостоятельная работа по вариантам (Приложение)

Затем проверка правильности решения

1 вариант

1 – в, 2 – а, 3 – б, 4 – 24%

2 вариант

1 – а, 2 – а, 3 – а, 4 – 42%

8. Рефлексия

– Ребята, вам понравилось на уроке, а какое настроение у вас сейчас? Покажите мне индикаторы вашего настроения на уроке.
Уходя из класса, прикрепите на доску одну из них.

9. Подведение итогов
– Выставление оценок 4 учащихся за решение задач на доске, отметить самых активных учеников, а остальные получат оценки за тест.
– Ребята, а какие цели мы ставили сегодня на уроке?
– Удалось ли нам их достигнуть?
– Какие типы задач сегодня на уроке мы решали?
– Сформулируйте правила нахождение дроби от числа и числа по его дроби.
– Чем отличаются и что общего в условиях этих задач?
– А какие вам понравились больше всего? были интересны? Познавательны?

9. Домашнее задание

– Ребята, а домашнее задание я вам сегодня приготовила необычное. Посмотрите это картина с Незнайкой, которую вам необходимо разукрасить, но предварительно решив задания и выбрав правильный цвет.

Урок заканчиваю словами великого русского писателя Л.Н. Толстого:

«Человек есть дробь. Числитель – это достоинство человека, знаменатель – это оценка человеком самого себя. Увеличить своего числителя – свои достоинства, не во власти человека, но всякий может уменьшить своего знаменателя – свое мнение о самом себе, и этим уменьшением приблизиться к совершенству».

ЕСЛИ ОСТАНЕТСЯ ВРЕМЯ

1) Инструктаж по домашнему заданию

– Посмотрите задание, что вам опять придется делать? А давайте посмотрим, все ли запомнили какие типы задач как решаются я прочитаю стихотворение, а вы догадайтесь к какому типу задач оно относится.

Дробь от числа хотим найти,
Не надо никого тревожить.
Нам надо данное число
На эту дробь умножить.

(Нахождение дроби от числа)

Если вы должны найти
Число по его дроби,
То на дробь вы поделите
Значенье данной дроби.

(Нахождение числа по его дроби)

2) Кроссворд

7.06.2015

xn--i1abbnckbmcl9fb.xn--p1ai

как решать задачи с дробями

Как решать задачи с дробями. Чтобы решить задачу с дробями, нужно научиться делать с ними арифметические действия. Они могут быть десятичные, но чаще всего используются натуральные дроби с числителем и знаменателем. Только после этого можно переходить на решения математических задач с дробными величинами. Инструкция 1 Дробью называют запись деления одного числа на другое. Зачастую это сделать нацело нельзя, поэтому и оставляют это действие «неоконченным» . Число, которое является делимым (оно стоит над или перед знаком дроби) , называются числителем, а второе число (под знаком дроби или после него) – знаменателем. Если числитель больше знаменателя, дробь называется неправильной, и из нее можно выделить целую часть. Если числитель меньше знаменателя, то такая дробь называется правильной, и ее целая часть равна 0. 2 Задачи с дробями делятся на несколько видов. Определите, к какому из них относится задача. Простейший вариант – нахождение доли числа, выраженной дробью. Для решения этой задачи достаточно умножить это число на дробь. Например, на склад завезли 8 т картошки. В первую неделю было продано 3/4 от ее общего количества. Сколько картошки осталось? Чтобы решить эту задачу, число 8 умножьте на 3/4. Получится 8∙3/4=6 т. 3 Если нужно найти число по его части, умножьте известную часть числа на дробь, обратную той, которая показывает какова доля данной части в числе. Например, 8 человек из класса составляют 1/3 от общего количества учеников. Сколько детей учится в классе? Поскольку 8 человек это часть, которая представляет 1/3 от всего количества, то найдите обратную дробь, которая равна 3/1 или просто 3. Затем для получения количества учеников в классе 8∙3=24 ученика. 4 Когда нужно найти какую часть числа составляет одно число от другого, поделите число, которое представляет часть на то, которое является целым. К примеру, если расстояние между городами 300 км, а автомобиль проехал 200 км, какую часть этот составит от всего пути? Поделите часть пути 200 на полный путь 300, после сокращения дроби получите результат. 200/300=2/3. 5 Чтобы найти часть неизвестную долю от числа, когда есть известная, возьмите целое число за условную единицу, и отнимите от нее известную долю. Например, если уже прошло 4/7 части урока, сколько еще осталось? Возьмите весь урок как условную единицу и отнимите от нее 4/7. Получите 1-4/7=7/7-4/7=3/7.

Все очень просто, главное понять, как действовать со смешанными дробями, а сама задача ничем не отличается от обычной) Вообщем действия с дробями: СЛОЖЕНИЕ При сложении (вычитании) дробей с одинаковыми знаменателямиполучается дробь с тем же знаменателем, а её числитель равен сумме (разности) числителей рассматриваемых дробей. ВЫЧИТАНИЕ При сложении (вычитании) дробей с разными знаменателямипредварительно нужно привести их к общему знаменателю. Для упрощения вычислений желательно приводить дроби к наименьшему общему знаменателю, хотя это не является обязательным. УМНОЖЕНИЕ) При умножении дробей получается дробь, числитель которой равен произведению числителей, а знаменатель – произведению знаменателей. Числитель умножаешь на числитель, знаменатель-соответственно) ДЕЛЕНИЕ! Сама часто путаюсь тут) Для того, чтобы разделить первую дробь на вторую, нужно первую дробь умножить на перевернутую вторую. А со смешанными числами многое не изменяется) При делении или умножении сначала нужно преобразовать смеш. число в неправильную дробь Чтобы преобразовать смеш. число в неправильную дробь надо: 1. Знаменатель умножить на целую часть 2. К этому прибавить числитель 3. Сумма этого- это ЧИСЛИТЕЛЬ 4. Знаменатель остается прежним) При сложении или вычитании совсем необязательно это делать) Но можно) И еще, меня всегда ругали за то, что забывала сократить дробь! Чтобы сократить дробь, надо и числитель, и знаменатель разделить на их нод (общий делитель) Если это возможно) НАДЕЮСЬ НА ТО, ЧТО ПОМОГЛА=)

просто. этого не знает только придурак

Спасибо ребят

touch.otvet.mail.ru

Применение дробей

Нахождение дроби от числа

Нахождение целого числа по дроби

Деление меньшего числа на большее

Какую часть одно число составляет от другого

Задания для самостоятельного решения

Навигация по записям

Решение задач на дроби

«Решение задач на нахождение дроби от числа и числа по его дроби»

Задачи на нахождение дроби от числа

Задачи на дроби — математика, презентации

Решение задач на нахождение дроби от числа и числа по его дроби. 6-й класс

как решать задачи с дробями

Добавить комментарий Отменить ответ