Mathway | Популярные задачи
| 1 | Найти объем | сфера (5) | |
| 2 | Найти площадь | окружность (5) | |
| 3 | Найти площадь поверхности | сфера (5) | |
| 4 | Найти площадь | окружность (7) | |
| 5 | Найти площадь | окружность (2) | |
| 6 | Найти площадь | окружность (4) | |
| 7 | Найти площадь | окружность (6) | |
| 8 | Найти объем | сфера (4) | |
| 9 | Найти площадь | окружность (3) | |
| 10 | Вычислить | (5/4(424333-10220^2))^(1/2) | |
| 11 | Разложить на простые множители | 741 | |
| 12 | Найти объем | сфера (3) | |
| 13 | Вычислить | 3 квадратный корень из 8*3 квадратный корень из 10 | |
| 14 | Найти площадь | окружность (10) | |
| 15 | Найти площадь | окружность (8) | |
| 16 | Найти площадь поверхности | сфера (6) | |
| 17 | Разложить на простые множители | 1162 | |
| 18 | Найти площадь | окружность (1) | |
| 19 | Найти длину окружности | окружность (5) | |
| 20 | Найти объем | сфера (2) | |
| 21 | Найти объем | сфера (6) | |
| 22 | Найти площадь поверхности | сфера (4) | |
| 23 | Найти объем | сфера (7) | |
| 24 | Вычислить | квадратный корень из -121 | |
| 25 | Разложить на простые множители | 513 | |
| 26 | Вычислить | квадратный корень из 3/16* квадратный корень из 3/9 | |
| 27 | Найти объем | прямоугольный параллелепипед (2)(2)(2) | |
| 28 | Найти длину окружности | окружность (6) | |
| 29 | Найти длину окружности | окружность (3) | |
| 30 | Найти площадь поверхности | сфера (2) | |
| 31 | Вычислить | 2 1/2÷22000000 | |
| 32 | Найти объем | прямоугольный параллелепипед (5)(5)(5) | |
| 33 | Найти объем | прямоугольный параллелепипед (10)(10)(10) | |
| 34 | Найти длину окружности | окружность (4) | |
| 35 | Перевести в процентное соотношение | 1. 2-4*-1+2 2-4*-1+2 | |
| 45 | Разложить на простые множители | 228 | |
| 46 | Вычислить | 0+0 | |
| 47 | Найти площадь | окружность (9) | |
| 48 | Найти длину окружности | окружность (8) | |
| 49 | Найти длину окружности | окружность (7) | |
| 50 | Найти объем | сфера (10) | |
| 51 | Найти площадь поверхности | сфера (10) | |
| 52 | Найти площадь поверхности | сфера (7) | |
| 53 | Определить, простое число или составное | 5 | |
| 54 | Перевести в процентное соотношение | 3/9 | |
| 55 | Найти возможные множители | 8 | |
| 56 | Вычислить | (-2)^3*(-2)^9 | |
| 57 | Вычислить | 35÷0. 2 2 | |
| 60 | Преобразовать в упрощенную дробь | 2 1/4 | |
| 61 | Найти площадь поверхности | сфера (12) | |
| 62 | Найти объем | сфера (1) | |
| 63 | Найти длину окружности | окружность (2) | |
| 64 | Найти объем | прямоугольный параллелепипед (12)(12)(12) | |
| 65 | Сложение | 2+2= | |
| 66 | Найти площадь поверхности | прямоугольный параллелепипед (3)(3)(3) | |
| 67 | Вычислить | корень пятой степени из 6* корень шестой степени из 7 | |
| 68 | Вычислить | 7/40+17/50 | |
| 69 | Разложить на простые множители | 1617 | |
| 70 | Вычислить | 27-( квадратный корень из 89)/32 | |
| 71 | Вычислить | 9÷4 | |
| 72 | Вычислить | 2+ квадратный корень из 21 | |
| 73 | Вычислить | -2^2-9^2 | |
| 74 | Вычислить | 1-(1-15/16) | |
| 75 | Преобразовать в упрощенную дробь | 8 | |
| 76 | Оценка | 656-521 | |
| 77 | Вычислить | 3 1/2 | |
| 78 | Вычислить | -5^-2 | |
| 79 | Вычислить | 4-(6)/-5 | |
| 80 | Вычислить | 3-3*6+2 | |
| 81 | Найти площадь поверхности | прямоугольный параллелепипед (5)(5)(5) | |
| 82 | Найти площадь поверхности | сфера (8) | |
| 83 | Найти площадь | окружность (14) | |
| 84 | Преобразовать в десятичную форму | 11/5 | |
| 85 | Вычислить | 3 квадратный корень из 12*3 квадратный корень из 6 | |
| 86 | Вычислить | (11/-7)^4 | |
| 87 | Вычислить | (4/3)^-2 | |
| 88 | Вычислить | 1/2*3*9 | |
| 89 | Вычислить | 12/4-17/-4 | |
| 90 | Вычислить | 2/11+17/19 | |
| 91 | Вычислить | 3/5+3/10 | |
| 92 | Вычислить | 4/5*3/8 | |
| 93 | Вычислить | 6/(2(2+1)) | |
| 94 | Упростить | квадратный корень из 144 | |
| 95 | Преобразовать в упрощенную дробь | 725% | |
| 96 | Преобразовать в упрощенную дробь | 6 1/4 | |
| 97 | Вычислить | 7/10-2/5 | |
| 98 | Вычислить | 6÷3 | |
| 99 | Вычислить | 5+4 | |
| 100 | Вычислить | квадратный корень из 12- квадратный корень из 192 |
Как решить 78 разделить на 2? – Обзоры Вики
Используя калькулятор, если вы введете 78, разделенные на 2, вы получите 39. Вы также можете выразить 78/2 в виде смешанной дроби: 39 0/2.
Вы также можете выразить 78/2 в виде смешанной дроби: 39 0/2.
Отсюда, как решить 25 разделить на 2? Поместите эту цифру в частное над знаком деления. Умножьте самую новую цифру частного (2) на делитель 2 . Вычтите 4 из 5 . Результат деления 25÷2 25÷2 равен 12 с остатком 1 .
Как решить 39, разделенное на 2? Используя калькулятор, если вы наберете 39, разделенные на 2, вы получите 19.5. Вы также можете выразить 39/2 в виде смешанной дроби: 19 1/2.
Кроме того, как вы работаете 68 разделить на 2? Используя калькулятор, если вы наберете 68, разделенное на 2, вы получите 34.
Как разделить 216? Делители числа — это точные делители числа, в результате чего остаток равен 0. Делители 216 — это числа, которые точно делят 216. Давайте разделим 216 на несколько чисел, например 2, 3 и 4. Вы заметите, что числа 2, 3 и 4 являются точными делителями числа 216.
Как решить 75 разделить на 2?
Используя калькулятор, если вы введете 75, разделенные на 2, вы получите 37. 5.
5.
Как решить 22 разделить на 2? Поместите эту цифру в частное над знаком деления. Умножьте самую новую цифру частного (1) на делитель 2 . Вычтите 2 из 2 . Результат деления 22÷2 22÷2 равен 11 .
Как вы рассчитываете, что 56 разделить на 2?
Используя калькулятор, если вы введете 56, разделенные на 2, вы получите 28.
Также как решить 41 разделить на 2? Результат деления 41÷2 на 41÷2 равен 20 с остатком 1 .
Каким будет остаток от 37, разделенный на 2?
Результат деления 37 ÷ 2 37 ÷ 2 равен 18 с остатком 1 .
Как решить 88, разделенное на 2? Используя калькулятор, если вы наберете 88, разделенные на 2, вы получите 44.
Как решить 66 разделить на 2?
Используя калькулятор, если вы введете 66, разделенные на 2, вы получите 33. Вы также можете выразить 66/2 в виде смешанной дроби: 33 0/2.
Как сделать 100 разделенных на 2?
Используя калькулятор, если вы введете 100, разделенные на 2, вы получите 50. Вы также можете выразить 100/2 в виде смешанной дроби: 50 0/2.
Как получить 36 разделить на 6? Используя калькулятор, если вы наберете 36, разделенное на 6, вы получите 6. Вы также можете выразить 36/6 как смешанную дробь: 6 0/6. Если вы посмотрите на смешанную дробь 6 0/6, вы увидите, что числитель такой же, как остаток (0), знаменатель — это наш исходный делитель (6), а целое число — это наш окончательный ответ (6) .
Как решить 108, разделенное на 12? 108 делить на 12 равно 9.
Как вы рассчитываете, что 64 разделить на 4?
Мы пишем 644 в формате длинного деления. Следовательно, 64 ÷ 4 =16 с остатком 0 .
Как решить 90, разделенные на 2? 90 разделить на 2 — это 45.
Как вы рассчитываете, что 76 разделить на 2?
Используя калькулятор, если вы введете 76, разделенные на 2, вы получите 38.
Чему равно 37.5 в виде дроби? Таблица перевода процентов в дроби
| Процент | Доля |
|---|---|
| 37.5% | 3/8 |
| 40% | 2/5 |
| 42.86% | 3/7 |
| 44.44% | 4/9 |
Можно ли 8 разделить на 2?
Используя калькулятор, если вы введете 8, разделенные на 2, вы получите 4.
Как написать 14 разделить на 2? Используя калькулятор, если вы наберете 14, разделенное на 2, вы получите 7. Вы также можете выразить 14/2 в виде смешанной дроби: 7 0/2.
Как решить 39 разделить на 3?
39 разделить на 3 равно 13. 39 ÷ 3 = 13.
Сколько 78 разделить на 6 с использованием длинного деления?
Запутались в длинном делении? К концу этой статьи вы сможете разделить 78 на 6, используя деление в длинную сторону, и сможете применить ту же технику к любой другой задаче на деление в длинную сторону! Давайте взглянем.
Хотите быстро научиться или показать учащимся, как решить деление 78 на 6 с помощью деления в большую сторону? Включи это очень быстрое и веселое видео прямо сейчас!
Итак, первое, что нам нужно сделать, это уточнить термины, чтобы вы знали, что представляет собой каждая часть деления:
- Первое число, 78, называется делимым.
- Второе число 6 называется делителем.
Здесь мы разберем каждый шаг процесса длинного деления на 78, разделенного на 6, и объясним каждый из них, чтобы вы точно поняли, что происходит.
78 разделить на 6 пошаговое руководство
Шаг 1
Первый шаг — поставить задачу деления с делителем слева и делимым справа, как показано ниже:
Шаг 2
Мы можем вычислить, что делитель (6) входит в первую цифру делимого (7), 1 раз(а). Теперь, когда мы это знаем, мы можем поставить 1 вверху:
Шаг 3
Если мы умножим делитель на результат предыдущего шага (6 x 1 = 6), то теперь мы можем добавить этот ответ под делимым:
Шаг 4
Далее из второй цифры делимого (7 — 6 = 1) вычтем результат предыдущего шага и запишем этот ответ ниже:
9007 2Шаг 5
Переместите вторую цифру делимого (8) вниз следующим образом:
| 1 | |||||
| 6 | 7 | 8 | |||
| — | 6 | ||||
| 1 |
Шаг 6
Делитель (6) входит в нижнее число (18) 3 раза, поэтому мы можем поставить 3 сверху:
| 1 | |||||
| 6 | 7 | 8 | |||
| — | 6 | ||||
| 1 | 8 |
| 1 | 3 | ||||
| 6 | 7 900 1 | 8 |
Шаг 7
Если мы умножим делитель на результат предыдущего шага (6 x 3 = 18), то теперь мы можем добавить этот ответ под делимым:
9003 8 6| 9003 6 | 1 | 3 | ||
| 6 | 7 | 8 | ||
| — | ||||
| 1 | 8 | |||
| 1 | 8 |
Шаг 8
Далее вычтем результат предыдущего шага из третьей цифры делимого (18 — 18 = 0) и запишем этот ответ ниже:
9 0072Итак, сколько будет 78 разделить на 6?
Если вы дочитали до этого урока, молодец! Больше не осталось цифр, чтобы двигаться вниз от делимого, а это значит, что мы решили задачу деления в длинную сторону.
Ваш ответ — это верхнее число, а любой остаток будет нижним числом. Итак, для 78, разделенных на 6, окончательное решение:
13
Остаток 0
Процитируйте, дайте ссылку или ссылку на эту страницу
Если вы нашли этот контент полезным в своем исследовании, пожалуйста, сделайте нам большую услугу и используйте инструмент ниже, чтобы убедиться, что вы правильно ссылаетесь на нас, где бы вы ни использовали это. Мы очень ценим вашу поддержку!
«Сколько 78 разделить на 6 с использованием длинного деления?». VisualFractions.com . По состоянию на 24 мая 2023 г. http://visualfractions.com/calculator/long-division/what-is-78-divided-by-6-using-long-division/.
«Сколько 78 разделить на 6 с использованием длинного деления?». VisualFractions.
 com , http://visualfractions.com/calculator/long-division/what-is-78-divided-by-6-using-long-division/. По состоянию на 24 мая 2023 г.
com , http://visualfractions.com/calculator/long-division/what-is-78-divided-by-6-using-long-division/. По состоянию на 24 мая 2023 г.Сколько 78 разделить на 6 с использованием длинного деления?. VisualFractions.com. Получено с http://visualfractions.com/calculator/long-division/what-is-78-divided-by-6-using-long-division/.
Дополнительные вычисления для вас
Теперь вы изучили метод деления 78 на 6, вот несколько других способов, которыми вы можете выполнить расчет:
- С помощью калькулятора, если вы набрали 78 разделить на 6 , вы получите 13.
- Вы также можете представить 78/6 в виде смешанной дроби: 13 0/6
- Если вы посмотрите на смешанную дробь 13 0/6, вы увидите, что числитель совпадает с остатком (0), знаменатель — это наш первоначальный делитель (6), а целое число — это наш окончательный ответ (13 ).
Калькулятор деления на длинное деление
Введите еще одну задачу на деление на длинное деление
Следующая задача на деление на длинное деление
Хотите еще больше деления на длинное деление, но не хотите вводить два числа в калькулятор выше? Не беспокойся. Вот следующая задача, которую вам нужно решить:
Вот следующая задача, которую вам нужно решить:
Сколько будет 78, разделенное на 7 в длинное деление?
Случайные задачи на длинное деление
Если вы добрались до этого конца страницы, значит, вы ДЕЙСТВИТЕЛЬНО любите задачи на длинное деление, а? Ниже приведена куча случайно сгенерированных вычислений для вашего долгого деления удовольствия:
Чему равно 459, разделенное на 896 с использованием длинного деления?
Чему равно 713, разделенное на 948 с использованием длинного деления?
Чему равно 152, разделенное на 553 с использованием длинного деления?
Чему равно 468, разделенное на 939 в длинное деление?
Чему равно 995, разделенное на 996 в длинное деление?
Сколько 289 разделить на 570 с помощью деления в большую сторону?
Чему равно 270, разделенное на 806 с помощью деления в большую сторону?
Чему равно 885, разделенное на 911 с использованием длинного деления?
Что такое 908 разделить на 984 с использованием длинного деления?
Сколько будет 269, разделенное на 635 с использованием длинного деления?
Чему равно 568, разделенное на 586 в длинное деление?
Чему равно 365, разделенное на 573 в длинное деление?
Чему равно 549, разделенное на 907 в длинное деление?
Чему равно 24, разделенное на 444 в длинное деление?
Чему равно 432, разделенное на 915 с использованием длинного деления?
Чему равно 762, разделенное на 988 с использованием длинного деления?
Сколько будет 589 разделить на 910 с использованием длинного деления?
Чему равно 541, разделенное на 725 с использованием длинного деления?
Чему равно 866, разделенное на 921 с использованием длинного деления?
Чему равно 791, разделенное на 907 с использованием длинного деления?
Чему равно 855, разделенное на 871 с использованием длинного деления?
Чему равно 328, разделенное на 882 с использованием длинного деления?
Чему равно 348, разделенное на 956 с помощью деления в большую сторону?
Чему равно 48, разделенное на 932 в длинное деление?
Чему равно 618, разделенное на 779 в длинное деление?
Чему равно 940, разделенное на 971 с использованием длинного деления?
Чему равно 985, разделенное на 990 в длинное деление?
Чему равно 703, разделенное на 810 с использованием длинного деления?
Сколько будет 324, разделенное на 527 с использованием длинного деления?
Чему равно 121, разделенное на 243 в длинное деление?
Чему равно 393, разделенное на 587 в длинном делении?
Чему равно 820, разделенное на 963 с использованием длинного деления?
Чему равно 80, разделенное на 650 с использованием длинного деления?
Что такое 998 разделить на 999 в длинное деление?
Чему равно 516, разделенное на 829 с использованием длинного деления?
Чему равно 72, разделенное на 332 с использованием длинного деления?
Сколько 106 разделить на 115 в длинное деление?
Чему равно 517, разделенное на 644 в длинное деление?
Чему равно 445, разделенное на 475 в длинное деление?
Чему равно 852, разделенное на 957 с использованием длинного деления?
Чему равно 549, разделенное на 787 в длинное деление?
Чему равно 239, разделенное на 576 в длинное деление?
Чему равно 403, разделенное на 722 с использованием длинного деления?
Чему равно 593, разделенное на 963 в длинное деление?
Чему равно 662, разделенное на 709 с использованием длинного деления?
Чему равно 399, разделенное на 652 в длинное деление?
Сколько 191 разделить на 214 в длинное деление?
Сколько 196 разделить на 940 в длинное деление?
Чему равно 569, разделенное на 1000 с использованием длинного деления?
Чему равно 790, разделенное на 810 с использованием длинного деления?
Что такое 392 разделить на 641 с использованием длинного деления?
Чему равно 430, разделенное на 616 с использованием длинного деления?
Чему равно 412, разделенное на 929 с использованием длинного деления?
Чему равно 747, разделенное на 956 с использованием длинного деления?
Чему равно 415, разделенное на 646 с использованием длинного деления?
Чему равно 847, разделенное на 873 в длинное деление?
Чему равно 682, разделенное на 814 с использованием длинного деления?
Чему равно 58, разделенное на 766 в длинном делении?
Чему равно 220, разделенное на 431 в длинном делении?
Чему равно 227, разделенное на 555 с использованием длинного деления?
Чему равно 987, разделенное на 995 в длинное деление?
Чему равно 637, разделенное на 674 в длинное деление?
Сколько 386 разделить на 614 с помощью деления в большую сторону?
Чему равно 48, разделенное на 247 в длинное деление?
Чему равно 143, разделенное на 299 в длинное деление?
Чему равно 615, разделенное на 942 в длинное деление?
Чему равно 65, разделенное на 70 в прямом делении?
Что такое 929 разделить на 989 с использованием длинного деления?
Чему равно 332, разделенное на 480 в длинное деление?
Чему равно 650, разделенное на 898 с использованием длинного деления?
Сколько будет 33 разделить на 172 с помощью деления в длинное число?
Чему равно 962, разделенное на 986 в длинное деление?
Чему равно 403, разделенное на 463 в длинное деление?
Сколько 513 разделить на 823 в длинное деление?
Чему равно 631, разделенное на 949 с использованием длинного деления?
Сколько будет 920 разделить на 968 с использованием длинного деления?
Чему равно 965, разделенное на 979 с использованием длинного деления?
Чему равно 612, разделенное на 947 с использованием длинного деления?
Чему равно 637, разделенное на 890 в длинное деление?
Чему равно 71, разделенное на 670 в длинное деление?
Чему равно 471, разделенное на 895 в длинное деление?
Чему равно 619, разделенное на 696 в длинное деление?
Чему равно 505, разделенное на 686 с использованием длинного деления?
Чему равно 654, разделенное на 959 с использованием длинного деления?
Чему равно 550, разделенное на 756 с использованием длинного деления?
Чему равно 53, разделенное на 187 в длинном делении?
Чему равно 773, разделенное на 912 в длинное деление?
Чему равно 677, разделенное на 921 в длинное деление?
Чему равно 215, разделенное на 464 в длинное деление?
Чему равно 31, разделенное на 717 с использованием длинного деления?
Чему равно 615, разделенное на 646 с использованием длинного деления?
Чему равно 867, разделенное на 934 в длинное деление?
Чему равно 286, разделенное на 553 в длинном делении?
Чему равно 448, разделенное на 878 в длинное деление?
Чему равно 25, разделенное на 291 с использованием длинного деления?
Чему равно 603, разделенное на 920 с использованием длинного деления?
Чему равно 750, разделенное на 982 с использованием длинного деления?
Чему равно 974, разделенное на 991 в длинное деление?
Чему равно 330, разделенное на 514 с использованием длинного деления?
Сколько 117 разделить на 742 в длинное деление?
Сколько 220 разделить на 434 с помощью деления в длинное число?
Сколько будет 78 разделить на 6?
Деление — одна из основ арифметики. Для общего ознакомления с подразделением ознакомьтесь с этой статьей.
Для самостоятельного расчета деления, возможно, стоит также ознакомиться с нашим разделом о длинном делении.
Для общего ознакомления с подразделением ознакомьтесь с этой статьей.
Для самостоятельного расчета деления, возможно, стоит также ознакомиться с нашим разделом о длинном делении.
Научиться самостоятельно решать эти проблемы поможет вам в школе и в жизни. Мы рекомендуем отрабатывать задачи на деление вручную и проверять решение с помощью калькулятора.
Забавный факт : невозможно любое число разделить на 0. Любое число, деленное на 0, не определено.
Как рассчитать это самостоятельно?
Есть несколько способов самостоятельно рассчитать задачи на деление. Первый способ, самый простой, это
пользоваться калькулятором.
Еще один способ, которому часто учат в школах, — это деление на полные числа. Длинное деление – это метод
разделить два числа. Это легко учиться и весело практиковать!
Ознакомьтесь с нашей длинной статьей о делении, чтобы узнать, как это сделать. сам.
сам.
Отдел реальных приложений
Концепция деления может быть применена ко многим ситуациям реальной жизни. Решая такую задачу, как «78 разделить на 6», мы можем подумать о том, как это можно применить к повседневным сценариям. Вот некоторые Примеры:
- Делитесь ресурсами: Если у вас есть 78 конфет и вы хотите разделить их поровну между 6 друзей, каждый получит по 13 конфет.
- Расходы на разделение: Если группа из 6 друзей собирается поужинать и общий счет составляет 78 долларов, каждый друг должен внести по 13 долларов, чтобы покрыть расходы.
- Распределение рабочей нагрузки: Если вам нужно выполнить 78 задач и вы хотите их распределить
равномерно в течение 6 дней, вам нужно будет выполнять 13 задач в день, чтобы выполнить свою
цель.

Понимание деления и умение выполнять вычисления, такие как «78 разделить на 6», может помочь вы принимаете обоснованные решения в различных аспектах жизни.
Стратегии и советы отдела
При решении задач на деление, таких как «78 разделить на 6», важно иметь некоторые стратегии. и советы в виду. Вот несколько советов, которые помогут вам в вычислениях деления:
- Оценка: Прежде чем углубляться в вычисления, сделайте быструю оценку, чтобы получить приблизительное представление о результат. Это может помочь вам проверить, является ли ваш окончательный ответ разумным.
- Деление в степени 10: Если вы делите число, являющееся степенью 10 (например, 10, 100,
1000), вы можете быстро найти ответ, переместив десятичную точку в делимом (число
делим) влево на столько разрядов, сколько нулей в делителе.

Если разные основания но одинаковые степени: Свойства степеней, действия со степенями
Как перемножить одно видео несколько раз ?
NoFake A.
1) Если надо умножить два числа с одинаковыми основаниями, но разными показателями степеней, то общее основание возводится в сумму степеней.
Пример:
3⁴*3³=3⁴⁺³=3⁷
2) Если основания разные, а показатели одинаковые, то нужно возводить в степень произведение оснований.
5²*2²=(5*2)²=10²=100
3) Если разные и основания, и показатели степеней, то сущесвует два варианта:
а) Выделить одинаковое основание, т.е. разложить один из множителей.
б) Привести к общему показателю:
Екатерина Шмелева5Всего 1 ответ.Чему равно 6÷2(1+2)?
Александр Кульков2В пособии для математических факультетов педагогических институтов по курсу методики преподавания математики, по которому учили наших преподавателей алгебры в педагогических ВУЗах Советского Союза сказано:
По нижеприведённой ссылке Вы можете скачать:
Методика преподавания алгебры, Курс лекций, Шустеф М. Ф., 1967 г.
Ф., 1967 г.
https://russianclassicalschool.ru/biblioteka/matematika.html
Приложенный мной текст на 43-й странице пособия.Так что, для тех, кто хорошо учился в советской школе 6:2(1+2) = 1
Александр Черанёв52Всего 10 ответов.Если наложить на трейлер свою озвучку, меня забанят на YouTube?
Dyhanie1Если накладываешь на свое видео чужую музыку, за это в YouTube не банят. За это могут или рекламу свою на ваш ролик добавить или то место звуковой дорожки где эта музыка есть, отключить, и то, если такое требование выставляет правообладатель этой музыки. Бывает что такой ролик блокируют только для некоторых других стран. Самое серьезное, что могут сделать за такое “преступление”, так это заблокировать только сам ролик, но не аккаунт пользователя.
Я пишу это для случая с музыкой, так как такой вариант точно знаю. Какие будут санкции за использование чужой картинки в своем ролике я точно не скажу. Могу лишь предполагать, что в случае если вы будете использовать в своем ролике чужой видео ряд, наказание более строго чем за музыку не будет.

Кроме того, частично в своих видео я использую фрагменты видео других авторов и правообладателей. За это меня на YouTube вообще никогда никак не наказывали.
Исходя из всего вышеизложенного, думаю, если на трейлер наложить свой звук, никто Вас за это не забанит.
Bloom1Всего 2 ответа.Как перемножить одно видео несколько раз ?
Добрый день.Скажите подалуйста с одним вопросом. Есть видео 30-ти секунд, надо его много раз скопировать и соединить, чтобы видео на 5-6 часов было длиной…. другими словами 30 секундное видео 1500 раз соединить. Какие есть программы или онлайн сервисы? Или может быть есть другой способ сделать ?chchkkxjhc chcjjkck4
Можно.
Всего 1 ответ.
Любой файловый менеджер справится (не стандартный)Владимир –3Нужна формула в таблице!!! Если число меньше 1000 умножать на 1,3, если больше 1000 то на 1,1 Можно так сделать?
Guest1Через ЕСЛИ.
Гость2Всего 1 ответ.
Например, исходное в А1, а нужно результат в С1, тогда там, в С1, пишешь:
=если (а1<1000;a1*1. 3;a1*1.1)
3;a1*1.1)
{здесь не совсем так как ты написала, не < и >, а < и >=}
Если разделители десятичных разрядов не точки, а запятые, замени.Вам также может понравиться
Степенные, показательные и логарифмические уравнения и неравенства. Профильный уровень 10 класс онлайн-подготовка на
Степенные уравнения
Вернемся в начальную школу. Вспомните, как мы начинали учиться писать. Сначала писали прописи, учились работать с базовыми элементами: как писать буквы, как правильно их соединять в слоги и слова. А уже потом перешли к написанию предложений и длинных текстов. Такой путь можно проследить в любом деле, которое осваивает человек.
Плотник не сразу сделает деревянную мебель, сначала он должен научиться обрабатывать древесину. Программист сначала учит простейшие команды, синтаксис языка и только потом он сможет разрабатывать сайты и писать сложные программы.
Этот же путь, от базовых вещей к сложным задачам, можно проследить и в курсе алгебры.
 Сначала мы изучали основы: сложение с умножением, извлечение корня, преобразование тригонометрических выражений. А затем учились применять изученные базовые принципы и свойства для решения математических моделей реальных задач.
Сначала мы изучали основы: сложение с умножением, извлечение корня, преобразование тригонометрических выражений. А затем учились применять изученные базовые принципы и свойства для решения математических моделей реальных задач.Глобально можно выделить две такие задачи. Первая – это исследование функций. Любой процесс можно с некоторой точностью описать функцией одной или нескольких переменных. Построив график функции, описав ее свойства, мы сможем исследовать и охарактеризовать этот процесс: быстро ли он проходит, от чего зависит и прочее.
Вторая глобальная задача – решение уравнений, неравенств и их систем. Вспомните: при решении различных практических задач мы чаще всего получаем математическую модель в виде уравнения, неравенства или их систем, которые нужно научиться решать.
Мы изучили свойства степеней и логарифмов, научились работать с графиками соответствующих функций. Теперь перейдем ко второй задаче: решению степенных, показательных и логарифмических уравнений, неравенств и их систем.

Начнем со степенных уравнений. Для их решения нам понадобится следующее утверждение: если , то для всех действительных . Исключение – четные значения . Для них, если , то или .
Это легко увидеть, построив графики левой и правой частей равенства. Для всех показателей степени , каждому значению функции соответствует ровно один аргумент (см. рис. 1).
Рис. 1. Для всех показателей степени , каждому значению функции соответствует ровно один аргумент
Таким образом, если значения функции равны, то равны и аргументы. Исключение – четные значения . По графику видим, что каждому значению функции соответствует два противоположных значения аргумента (см. рис. 2). И если значения функций равны, то их аргументы или равны, или противоположны.
Рис. 2. При четных каждому значению функции соответствует два противоположных значения аргумента
Идея решения степенных уравнений: представить левую и правую части как степени с одинаковым показателем. И затем использовать указанное ранее свойство.

Задание 1. Решить уравнение:
Решение.
Слева третья степень, представим правую часть как третью степень выражения:
Получаем:
Показатели равны, это нечетные числа. Поэтому можем сказать, что равны и основания:
Получили линейное уравнение:
Ответ: .
Как видите, используя указанное свойство мы свели решение нашего уравнения к тому, которое мы уже умеет решать. В дальнейшем мы будем подробно останавливаться лишь на первой части решения – сведению уравнения к линейному, квадратному или любому другому, алгоритм решения которых вы уже знаете.
Задание 2. Решить уравнение:
Решение.
Сразу отметим, что степень с отрицательным целым показателем определена только для ненулевого основания:
Т. е. ОДЗ: . Слева – минус четвертая степень, сделаем справа такую же степень:
Тогда:
Степень четная, значит основания или равны, или противоположны:
Получили линейные уравнения, которые вы можете решить самостоятельно.
 Получаем ответ:
Получаем ответ:Оба решения входят в ОДЗ.
Ответ: .
Задание 3. Решить уравнение:
Решение.
Слева – седьмая степень, нужно представить число справа в виде седьмой степени. Подобрать целое число, которое при возведении в степень даст , не получится. Поэтому используем свойство степени:
Тогда:
Получим:
Степени равны и нечетные, поэтому:
Ответ: .
Сформулируем общий алгоритм решения степенных уравнений:
1. указать ОДЗ уравнения, для отрицательных степеней – основание не равно , для нецелых степеней – основание больше либо равно нулю;
2. представить уравнение в виде , при необходимости использовать свойства степени;
3. записать следствие:
или для четных значений ;
для всех остальных степеней;
4. решить полученное уравнение и сверить ответы с ОДЗ.
Простейшие показательные уравнения и неравенства
Мы рассмотрели степенные уравнения – уравнения, у которых неизвестная стояла в основании степени.
 Теперь рассмотрим уравнения, в которых неизвестная стоит в показателе степени – показательные уравнения. Идея их решения очень похожа на ту, что мы использовали при решении степенных уравнений. Нужно свести уравнение к виду:
Теперь рассмотрим уравнения, в которых неизвестная стоит в показателе степени – показательные уравнения. Идея их решения очень похожа на ту, что мы использовали при решении степенных уравнений. Нужно свести уравнение к виду:Т. е. так, чтобы слева и справа были степени с одинаковым основанием.
Из того, что следует, что . Это следует из монотонности графика показательной функции: каждому значению функции соответствует ровно одно значение аргумента (см. рис. 3). Если значения функций равны, то равны и их аргументы.
Рис. 3. Графики функций при и
Задание 4. Решить уравнение:
Решение.
Слева – основание , сделаем справа такое же:
Тогда:
Из этого следует, что:
Получили линейное уравнение:
Ответ: .
Задание 5. Решить уравнение:
Решение.
Здесь видим в основании и . Это все целые степени тройки, поэтому удобно левую и правую части привести к основанию .
 Применяя свойства степени, получаем:
Применяя свойства степени, получаем:Получаем уравнение:
Основание равны, значит, равны и степени:
Решая это линейное уравнение, получаем ответ:
Ответ: .
Идея решения показательных неравенств очень похожа. Нужно привести неравенство к виду ; между частями может быть любой другой знак, все выводы будут аналогичными. Затем возможны два варианта.
Первый вариант – основание . Тогда соответствующая показательная функция будет возрастающей (см. рис. 4). Значит, большему значению функции соответствует больший аргумент. И из будет следовать, что . Знак неравенства не поменялся.
Рис. 4. График функции при
Второй вариант – основание . Тогда соответствующая функция будет убывающей (см. рис. 5). Большему значению функции соответствует меньший аргумент. Значит, из следует, что . Знак неравенства изменился на противоположный.
Рис. 5. График функции при
В обоих случая получаем неравенство, обычно линейное или квадратное, которое решаем стандартными методами.
 Если вы не помните методы решения неравенств, можете их повторить, посмотрев уроки Линейные неравенства. Системы и совокупности неравенств; Решение квадратных неравенств. Метод интервалов.
Если вы не помните методы решения неравенств, можете их повторить, посмотрев уроки Линейные неравенства. Системы и совокупности неравенств; Решение квадратных неравенств. Метод интервалов.Задание 6. Решить неравенство:
Решение.
Приводим левую и правую часть к одинаковым основаниям. Слева – основание . Справа из можно сделать степень с любым основанием: . Нужно – делаем :
Получаем:
Основания одинаковы и больше . Значит, для показателей степени знак неравенства не поменяется:
Решая неравенство, получаем:
Ответ: .
Задание 7. Решить неравенство:
Решение.
Неравенство выглядит громоздко, но оно не сложнее предыдущего. Действуем по алгоритму. Смотрим на основания степеней – это взаимообратные дроби. Чтобы сделать основания одинаковыми, запишем:
Тогда:
Получаем неравенство:
Основание уже одинаковые. Они больше или меньше ? , значит, будет меньше .
 Поэтому записываем неравенство для показателей степени и меняем знак:
Поэтому записываем неравенство для показателей степени и меняем знак:Получили квадратное неравенство. Решая его, получаем ответ:
Ответ:.
Теперь рассмотрим несколько задач, где не так очевидно, как можно привести обе части к одинаковому основанию.
Задание 8. Решить неравенство:
Решение.
Чтобы представить число в виде степени с основанием , воспользуемся основным логарифмическим тождеством. Вспомним: для любых положительных и . Тогда:
Получаем неравенство:
Основания равны и больше . Значит:
Получаем ответ:
Ответ: .
Задание 9. Решить уравнение:
Решение.
Здесь в левой части стоит разность степенных выражений. Прежде чем решать по алгоритму, упростим левую часть, разложив ее на множители:
Получим уравнение:
Разделив обе части уравнения на , получим:
, т. е.:
Ответ: .

С решением еще одного показательного уравнения вы можете ознакомиться ниже.
Пример решения показательного уравненияЗадание. Решить уравнение:
Решение.
Здесь мы видим разные основания: и , которые сложно будет свести к одному. Можно попробовать это сделать с помощью основного логарифмического тождества, но это долгий путь. Если не получается привести к одинаковым основаниям, то можно попробовать привести к одинаковым показателям степени – в этом случае тоже можно воспользоваться свойствами степени для упрощения выражений. Поступим следующим образом.
Для начала отметим, что , следовательно:
Теперь можем разделить обе части уравнения на и применить свойство степеней, поскольку степени и теперь одинаковые:
Теперь представим в виде степени с основанием :
В итоге:
Ответ: .
Простейшие логарифмические уравнения и неравенства
Рассмотрим теперь решение логарифмических уравнений.
 Общая идея решения нам уже знакома – привести левую и правую части к логарифмам с одинаковым основанием:
Общая идея решения нам уже знакома – привести левую и правую части к логарифмам с одинаковым основанием:Как и показательная, логарифмическая функция также имеет лишь один аргумент для каждого значения функции (см. рис. 6).
Рис. 6. Графики функций при и
Из равенства логарифмов будет следовать равенство подлогарифмических выражений:
Итак, наша задача: привести левую и правую части уравнения к логарифмам с одинаковым основанием, используя различные свойства логарифмов. Все так же, как и в показательных уравнениях. Единственное, что нужно учесть ОДЗ: подлогарифмическое выражение всегда больше 0 (ОДЗ: ).
Задание 10. Решить уравнение:
Решение.
Для начала выпишем ОДЗ: . Переходим к решению. Основания логарифмов равны, можем приравнять выражения под логарифмами:
Корни данного квадратного уравнения:
Выполним проверку:
:
Неравенства верны.
:
Неравенства верны.

Оба корня входят в ОДЗ.
Ответ: .
Задание 11. Решить уравнение:
Решение.
ОДЗ:
Чтобы привести левую часть к логарифму с основанием , воспользуемся одним из свойств логарифма: для любого значения .
Таким образом:
Получаем уравнение:
Основания логарифмов равны, значит:
Решая уравнение, получаем . Корень входит в ОДЗ:
Ответ: .
Это же уравнение можно было решить и с помощью определения логарифма. Подробнее об этом – ниже.
Еще один способ решения уравненияПосмотрим на уравнение . По определению, логарифм – это степень, в которую нужно возвести основание логарифма, чтобы получить то, что под логарифмом. Т. е., нужно возвести в степень, чтобы получить :
Мы получили такое же уравнение, корнем которого также будет . Это вполне естественно – решая разными способами, мы получили такой же ответ. Возможно, кому-то этот способ покажется более простым.
 Что ж, можете его использовать. Но обратите внимание, что он не такой универсальный. Он подойдет только в случае, если в одной из частей уравнения стоит число.
Что ж, можете его использовать. Но обратите внимание, что он не такой универсальный. Он подойдет только в случае, если в одной из частей уравнения стоит число.Задание 12. Решить уравнение:
Решение.
Записываем ОДЗ:
Теперь нужно привести обе части уравнения к одинаковому основанию. По слагаемым понятно, что это будет основание . По свойству логарифмов:
Получаем уравнение:
Основание логарифмов равны, значит, можем записать:
Получили квадратное уравнение. Попробуйте решить его самостоятельно. Его корни:
Проверяем ОДЗ:
:
Неравенства верны.
:
Первое и второе неравенства неверны.
Получаем ответ:
Ответ: .
С решением еще одного логарифмического уравнения вы можете ознакомиться в ответвлении.
Пример решения логарифмического уравненияЗадание.
 Решить уравнение:
Решить уравнение:Решение.
Сразу записываем ОДЗ:
Вспомним, что:
Чтобы удобнее было приводить к одинаковому основанию, так и запишем:
Слева и справа основания разные. Что делать? Вспомним свойство логарифма для положительных и :
Поскольку , то:
Теперь внесем коэффициент перед логарифмом, используя свойство:
Получили уравнение:
Основания равны, значит:
По свойству степени:
Получили квадратное уравнение:
Его корни: , .
Проверяем:
:
Неравенства неверны.
:
Неравенства верны.
Получаем ответ:
Ответ: .
Наконец, рассмотрим простейшие логарифмические неравенства. Идея та же: привести к одинаковому основанию. Далее, как и в показательных неравенствах, смотрим на основание.
Если , то записываем неравенство уже без логарифмов и знак не меняем:
Если , то знак меняем на противоположный:
Также на забываем учесть ОДЗ: .

Задание 13. Решить неравенство:
Решение.
ОДЗ:
Левую часть неравенства нужно представить, как логарифм с основанием . По свойству логарифмов:
Тогда:
Основания логарифмов одинаковые и больше 1. Можем записать неравенство для подлогарифмических выражений, не меняя знак:
С учетом ОДЗ получаем систему неравенств:
Получаем ответ:
Ответ: .
Метод замены в показательных и логарифмических уравнениях и неравенствах
Мы разобрали простейшие показательные и логарифмические уравнения и неравенства. В них мы всегда могли свести левую и правую части к одинаковым основаниям. Сейчас мы разберем несколько задач, которые можно свести к этим самым простейшим уравнениям и неравенствам.
Метод, который нам понадобится, мы уже использовали при решении рациональных и тригонометрических уравнений – это метод замены. Нужно увидеть одинаковые блоки выражений в условии и заменить их новой переменной (Практика.
 Решение квадратных и дробно-рациональных уравнений. Практика. Тригонометрические уравнения и неравенства. Базовый уровень).
Решение квадратных и дробно-рациональных уравнений. Практика. Тригонометрические уравнения и неравенства. Базовый уровень).Задание 14. Решить уравнение:
Решение.
Укажем ОДЗ:
Обратите внимание, что в первом слагаемом логарифм в квадрате. Поэтому использовать свойства логарифмов с одинаковым основанием не получится. Но у нас есть повторяющийся элемент: . Введем замену:
Тогда:
Получаем уравнение:
Получили квадратное уравнение. Его корни:
Не забываем выполнить обратную замену:
Теперь у нас два простейших уравнения. Итак, в первом уравнении:
Во втором:
Значение можно вычислить:
Оба корня входят в ОДЗ.
Ответ: .
В некоторых уравнениях замена не сразу очевидна. Сначала нужно преобразовать уравнение, чтобы ее увидеть.
Задание 15. Решить уравнение:
Решение.
Тут у нас два слагаемых с неизвестными.
 Давайте сначала приведем их к одинаковому основанию:
Давайте сначала приведем их к одинаковому основанию:Значит:
Чтобы увидеть замену, воспользуемся свойствами степени:
Теперь видно, какую замену нужно сделать:
Тогда:
Получаем квадратное уравнение:
Решая его, получаем:
Делаем обратную замену:
В первом уравнении:
Второе уравнение не имеет решений, поскольку показательные выражение могут быть только положительными.
Ответ: .
Еще раз обратим внимание, как мы преобразовали выражение :
Такой прием достаточно распространен в показательных уравнениях, поэтому можете запомнить его.
С помощью замены можно решать и неравенства.
Задание 16. Решить неравенство:
Решение.
Чтобы увидеть замену, преобразуем , используя свойства степеней:
Теперь видно замену:
Тогда:
Получаем неравенство:
Получили дробно-рациональное неравенство.
 Вы уже знаете, как решать такие неравенства. Попробуйте решить его самостоятельно, свериться можно ниже.
Вы уже знаете, как решать такие неравенства. Попробуйте решить его самостоятельно, свериться можно ниже.
Решение дробно-рационального неравенстваЗадание. Решить неравенство:
Решение.
Решим неравенство методом интервалов. Для этого перенесем все слагаемые в одну сторону:
И решим соответствующее уравнение:
ОДЗ:
Умножаем обе части равенства на :
По теореме Виета корни уравнения:
Расставляем особые точки ОДЗ и корни на оси (см. рис. 1).
Рис. 1. Иллюстрация к заданию
Методом пробной точки определяем знаки на интервалах (см. рис. 2):
:
Знак .
:
Знак .
:
Знак .
:
Знак .
Рис. 2. Иллюстрация к заданию
Выбираем интервалы со знаком :
Ответ: .
Решив неравенство, получаем:
Делаем обратную замену:
Решим каждом по отдельности:
выполняется автоматически (вспомните почему).
 Тогда первое неравенство превращается в . Решаем его:
Тогда первое неравенство превращается в . Решаем его:Второе неравенство:
Получаем:
Ответ: .
Показательные уравнения повышенной сложности
Давайте рассмотрим более сложные примеры показательных уравнений.
Задание 17. Решить уравнение:
Решение.
Мы видим похожие выражение, но основания их – обратные дроби. Значит, можем записать:
Тогда можем применить прием, о котором мы говорили ранее:
Можем сделать замену:
Тогда:
Получаем уравнение:
ОДЗ:
Умножаем обе части на :
Решая это уравнение, получаем единственный корень . Делаем обратную замену:
Хоть у нас в показателе и стоит синус, принцип неизменный: приводим обе части уравнения к одному основанию:
Основания равны, следовательно . Как видите, вся сложность состоит лишь в том, что в итоге мы получили не линейное или квадратное уравнение, а тригонометрическое.
 Но и их мы уже умеем решать:
Но и их мы уже умеем решать:Ответ: .
Есть еще один тип показательных уравнений, которые решаются заменой. Это однородные уравнения. С подобным типом мы уже сталкивались ранее, например, в тригонометрии. Показательные однородные уравнения похожи на них: у них также должна быть одинаковая степень у всех слагаемых, а в правой части – стоять ноль.
Задание 18. Решить уравнение:
Решение.
Для начала, как и во всех показательных уравнениях, попробуем привести степени к одинаковым основаниям, разложив имеющиеся основания на простые множители:
Получаем:
Видим, что это однородное уравнение: у слагаемых степени одинаковы: , справа в уравнении стоит . Идея решения похожа у всех однородных уравнений: делим на . Это выражение не равно нулю, имеем право делить. Получим:
Или, применив свойства степеней:
Теперь уже можем сделать замену:
Тогда:
Получаем квадратное уравнение:
Его корни:
Делаем обратную замену:
Первое уравнение не имеет решений, второй уравнение имеет корень .

Ответ: .
Логарифмические уравнения и неравенства повышенной сложности
Последнее, на что мы обратим наше внимание на сегодняшнем уроке, это более сложные логарифмические уравнения и неравенства.
Задание 19. Решить уравнение:
Решение.
Вся сложность заключается лишь в том, что неизвестная стоит в основании логарифма, с этим мы еще не сталкивались. Но ничего страшного, действуем по обычному алгоритму.
Первое – указываем ОДЗ. Основание логарифма больше нуля и не равно . Т. е. ОДЗ:
. Приводим левую и правую части к одинаковому основанию. По свойству логарифма:
Получаем:
Основания равны, значит:
Получили квадратное уравнение, корни которого и . Второй корень не входит в ОДЗ. Получаем ответ: .
Ответ: .
В неравенстве также может встретиться переменная в основании логарифма. Алгоритм решения при этом никак не изменится, но будет одно отличие – мы не будем знать, основание больше или меньше 1.
 А это, напомним, влияет на смену знака неравенства. Поэтому нужно будет рассмотреть два случая: когда основание больше и когда меньше 1. С примером решения подобного неравенства вы можете ознакомиться в ответвлении.
А это, напомним, влияет на смену знака неравенства. Поэтому нужно будет рассмотреть два случая: когда основание больше и когда меньше 1. С примером решения подобного неравенства вы можете ознакомиться в ответвлении.
Неравенство с неизвестной в основании логарифмаЗадание. Решить неравенство:
Решение.
Для начал выпишем ОДЗ. Под логарифмом – положительная величина:
В основании логарифма – положительная величина не равная единице:
Переходим к решению. Представим левую часть неравенства в виде логарифма с основанием :
Получим:
Основание одинаковы. Но мы не знаем, больше они или меньше. Рассматриваем 2 случая:
1. при знак неравенства не изменится:
Решая неравенство, получим:
Но в рассматриваемом случае , следовательно, останутся только значения (см. рис. 1).
Рис. 1. Иллюстрация к заданию
2. при знак неравенства изменится противоположный:
Решая неравенство, получим:
Это соответствует нашему случаю, значит, все решения подойдут (см.
 рис. 2).
рис. 2).Рис. 2. Иллюстрация к заданию
В итоге получаем (см. рис. 3):
Рис. 3. Иллюстрация к заданию
Осталось учесть ОДЗ: . Изобразим эти условие на оси и найдем пересечение ОДЗ с областью полученных решений (см. рис. 4).
Рис. 4. Иллюстрация к заданию
Получаем ответ: .
В конце урока разберем еще одно логарифмическое неравенство. Алгоритм его решения абсолютно такой же, как и в более простом примере, разобранном ранее: указываем ОДЗ, приводим к одному основанию и решаем полученную систему неравенств. Сложность данного примера будет заключаться лишь в количестве полученных неравенств в системе. Поэтому мы посмотрим, как их количество можно уменьшить и упростить решение.
Задание 20. Решить неравенство:
Решение.
ОДЗ:
Приведем обе части к одному основанию. По свойству логарифмов:
Получаем неравенство:
Основание логарифмов равны и меньше .
 Записываем неравенство для подлогарифмических выражений и меняем знак неравенства:
Записываем неравенство для подлогарифмических выражений и меняем знак неравенства:С учетом ОДЗ получаем систему неравенств:
Осталось решить эту систему. Можно решать каждое по отдельности. А можно и облегчить себе задачу: , , значит, их произведение также положительное. А из первого неравенства мы знаем, что больше либо равно этому произведению. Значит, оно тоже точно положительно. Получается, второе неравенство автоматически выполняется, если верны 1, 3 и 4 неравенства. Значит, можем его не рассматривать. Остается система из трех неравенств:
Их уже придется решать. Попробуйте сделать это самостоятельно, проверить себя можно ниже.
Решение системы неравенствЗадание. Решить систему неравенств:
Решение.
Решим первое неравенство:
Раскроем скобки и перенесем все слагаемые в левую сторону
Разделим на :
Решим полученное неравенство методом интервалов:
По теореме Виета:
Расставим точки на оси (см.
 рис. 1).
рис. 1).Рис. 1. Иллюстрация к заданию
Это квадратичный многочлен с положительным коэффициентом при , значит, знаки на интервалах будут (см. рис. 2).
Рис. 2. Иллюстрация к заданию
Выберем нужные интервалы (см. рис. 3).
Рис. 3. Иллюстрация к заданию
На этой же оси отметим решения двух остальных неравенств (см. рис. 4):
, значит:
, значит:
Рис. 4. Иллюстрация к заданию
Видим, что пересечений у всех трех решений нет. Значит, система не имеет решений.
Ответ: .
Список рекомендованной литературы.
- Алимов Ш. А., Колягин Ю. М., Ткачева М. В. Математика. Алгебра и начала математического анализа, геометрия. 10-11класс. Учебник. – АО «Издательство “Просвещение”».
- Мордкович А. Г., Семенов П. В. Математика. Алгебра и начала математического анализа, геометрия. 10-11класс. Учебник. – ООО «ИОЦ МНЕМОЗИНА», 2019.
- Никольский С.
 М., Потапов М. К., Решетников Н.Н. Алгебра и начала математического анализа, геометрия. 10 класс. Учебник. – АО «Издательство “Просвещение”»
М., Потапов М. К., Решетников Н.Н. Алгебра и начала математического анализа, геометрия. 10 класс. Учебник. – АО «Издательство “Просвещение”»
Рекомендованные ссылки на ресурсы интернет.
- Интернет-портал «yaklass.ru»
- Интернет-портал «yaklass.ru»
- Интернет-портал «math.md»
Рекомендованное домашнее задание.
- Решить уравнения: а) ; б)
- Решить уравнения: а) ; б)
- Решить неравенства: а) ; б)
Арифметика. Почему нельзя складывать члены с разными показателями?
Задавать вопрос
спросил
Изменено 7 лет, 3 месяца назад
Просмотрено 24к раз
$\begingroup$ 99$. Когда вы используете несколько терминов, показатели складываются вместе.
Когда вы используете несколько терминов, показатели складываются вместе.Почему нельзя добавлять термины с разными показателями?
Кто-то сказал, что это из-за свойств алгебры:
Коммутативное свойство: $a + b = b + a$ и $ab = ba$.
Ассоциативность: $a + (b + c) = b + (c + a)$ и $a \cdot (b \cdot c) = b \cdot (a \cdot c)$.
Распределительное свойство: $x(a+b) = xa + xb$.
Так как же эти свойства предполагают, что вы не можете складывать члены, когда степени разные, но вы можете умножать члены с разными показателями степени? 93 &\equiv& (x \times x) + (x \times x \times x) \\ &\equiv& \ldots\ldots? \конец{массив}
$\endgroup$ $\begingroup$Во-первых, то, что вы называете коммуникативным, на самом деле называется коммутативным, и тот факт, что $ab=ba$, не имеет к этому никакого отношения. В некоммутативных кольцах не вдруг становится возможным складывать одночлены разных степеней.
Когда дело доходит до сложения (или умножения) многочленов, это просто вопрос определения.
 Сложение просто определяется как оно есть, и если у вас есть несколько одночленов разной степени, вы не можете их сложить. Если я совершенно не осознаю этого, там нет ничего глубокого. Суть в том, чтобы рассматривать полиномы как формальные объекты, а не как соответствующие им карты, если только для этого нет веской причины. 92=?$$
Сложение просто определяется как оно есть, и если у вас есть несколько одночленов разной степени, вы не можете их сложить. Если я совершенно не осознаю этого, там нет ничего глубокого. Суть в том, чтобы рассматривать полиномы как формальные объекты, а не как соответствующие им карты, если только для этого нет веской причины. 92=?$$Если вы вынесете за скобки как можно больше $x$, единственный случай, когда у вас останутся только числа в скобках (которые вы, конечно, можете добавить), это когда показатели степени одинаковы. Вы можете упростить $3+6$ до $9$, но вы не можете упростить $3+6x$ ни во что, так что в данном случае это ни к чему не приведет.
$\endgroup$Усовершенствованная научная нотация: изменение оснований, сложение и вычитание — математические модули Ohlone Biotechnology
- Различные экспоненциальные основания
- Сложение и вычитание
- Решения
Иногда нам нужно взять число в экспоненциальном представлении и изменить его, чтобы оно имело другую экспоненциальную основу.
 Переписывание числа в экспоненциальной записи с использованием другой экспоненциальной базы технически «нарушает» правило записи в экспоненциальной записи: наш коэффициент a должен быть больше или равен 1, но меньше 10. Почему и должны быть между этими номерами? Потому что это просто обычный способ написать это.
Переписывание числа в экспоненциальной записи с использованием другой экспоненциальной базы технически «нарушает» правило записи в экспоненциальной записи: наш коэффициент a должен быть больше или равен 1, но меньше 10. Почему и должны быть между этими номерами? Потому что это просто обычный способ написать это.Итак, зачем нам вообще переписывать базы, если мы не придем к стандартной форме научных обозначений?
Во-первых, мы можем использовать это изменение основания для добавления или вычитания чисел в экспоненциальном представлении, как мы рассмотрим во втором разделе этого руководства. Во-вторых, использование другой экспоненциальной базы может упростить визуализацию числа для тех, кто не знаком с научными обозначениями, такими как запись 100 x 10 10 вместо 1,00 x 10 12 .
Давайте начнем с изучения изменения основания с 10 8 на 10 5 . Как бы выглядело число 4,5 x 10 5 , если бы мы захотели записать его экспоненциальную базу как 10 8 вместо 10 5 ?
Если вы читали Модуль 1 (Научная нотация), вы, наверное, догадались, что мы будем использовать еще одно свойство показателей степени.
 Ты прав. Мы будем использовать специальное свойство экспонент, модифицированное под наши нужды:
Ты прав. Мы будем использовать специальное свойство экспонент, модифицированное под наши нужды:10 m-n = x
, где m – заданный (исходный) показатель степени
, а n – новый показатель степени 90 003Итак, что такое x в этом свойстве? В данном случае x – это количество знаков, на которое мы переместим десятичную дробь, чтобы получить новое число. Если x отрицательное, переместите десятичную дробь влево. Если x положительно, сдвиньте десятичную дробь вправо.
Пример 1 – Отрицательный «x»
Давайте еще раз посмотрим на запись 4,5 x 10 5 с экспоненциальной основой 10 8 :
4,5 x 10 5 ⇒ x 10 8- Используйте указанное выше свойство, чтобы найти x : 10 m-n = х; поэтому 10 5-8 = -3
- Переместить десятичную дробь x раз: (0,0045 x 10 8 )
- Чек: 4,5 x 10 5 = 450 000 ✔; 0,0045 x 10 8 = 450 000 ✔
Поскольку мы проверили наш ответ на шаге 3, вы можете видеть, что оба ответа эквивалентны.

Совет : Быстро перепроверьте свой ответ с помощью калькулятора. Введите 0,0045 x 10 8 и нажмите клавишу ввода. В зависимости от того, в каком режиме находится ваш калькулятор, он выдаст вам 4,5 x 10 5 или 450 000.
Пример 2. Положительный «x»
Давайте попробуем аналогичный пример, где x является положительным, а не отрицательным: запишите 6,32 x 10 6 с экспоненциальной основой 10 4 .
6,32 x 10 6 ⇒ x 10 4
- Используйте указанное выше свойство, чтобы найти x :10 m-n = x ; 10 6-4 = +2
- Переместить десятичную дробь x раз: (632 x 10 4 )
- Чек: 6,32 x 10 6 = 6 320 000 ✔ ; 632 x 10 4 = 6 320 000 ✔
Всегда проверяйте свои ответы! Проверка поможет вам обнаружить любые ошибки, которые вы, возможно, допустили.

Ниже приведены несколько чисел, которые мы хотим переписать с другим экспоненциальным основанием. Попробуйте решить задачи самостоятельно.
Проверка на понимание #1: экспоненциальное представление в экспоненциальном представлении
Перепишите следующие числа с их новой экспоненциальной основой (решения для проверки на понимание приведены в конце этого руководства).
Напишите 3,98 x 10 8 с экспоненциальным основанием 10 4 .
Запись 4.9x 10 3 с экспоненциальным основанием 10 9 .
Запишите 1,45 x 10 -5 с экспоненциальным основанием 10 -8 .
Запишите 7,4 x 10 -2 с экспоненциальным основанием 10 2 .
Сложение и вычитание чисел в экспоненциальном представлении, к сожалению, не так просто, как умножение и деление чисел, поскольку мы не можем складывать или вычитать коэффициенты, как при умножении/делении.

Давайте посмотрим, что произойдет, если мы попытаемся сложить коэффициенты и части экспоненты:
Мы можем вычислить, что 2500 + 450 = 2950, но если мы рассмотрим те же самые числа, записанные в экспоненциальном представлении, и попытаемся сложить, используя те же методы, что и при умножении и делении, мы получим
2500 = 2,5 x 10 3
450 = 4,5 x 10 2
Добавьте десятичные части и части экспоненты:
2,5 x 10 3
903 09 +4,5 x 10 2
≠ 7,0 x 10 5Что неправильно добавлять таким образом? Есть три проблемы:
- Коэффициенты не представляют одинаковые разрядные значения (хотя 2,5 + 4,5 = 7, мы видим, что это не дает нам ничего близкого к правильному ответу 2950).
- Мы не можем сложить части экспоненты вместе, и
- Нет свойств показателей степени для сложения или вычитания чисел в экспоненциальном представлении
Нет свойств показателей степени? Совсем? Ничего?
До этого момента мы снова и снова использовали свойства экспонент для решения задач научной записи, включая умножение и деление.
 В этом используется вся та работа, которую вы проделали, изменяя экспоненциальные основания.
В этом используется вся та работа, которую вы проделали, изменяя экспоненциальные основания.Давайте еще раз посмотрим на сложение чисел в начале этого раздела, изменив основание экспоненциального выражения из введения:
2,5 x 10 3
+4,5 x 10 2
=- Измените одно из чисел так, чтобы оба имели одинаковую экспоненциальную основу: 4,5 x 10 2 становится 0,45 x 10 3
- Задача перезаписи с измененным экспоненциальным основанием: (2,5 x 10 3 ) + (0,45 x 10 3 )
- Добавить коэффициенты
2,5 x 10 3
+0,45 x 10 3
2,95 x 10 3Важно отметить, что вы НЕ добавляете основания — например, 10 3 + 10 3 ≠ 10 6 .
Потренируйтесь складывать и вычитать числа в экспоненциальном представлении.

Формула котангенса: определение, формула, таблица, график, свойства
Тангенс и котангенс суммы и разности аргументов, примеры
- Тангенс и котангенс суммы
- Тангенс и котангенс разности
- Примеры
п.1. Тангенс и котангенс суммы
Для вывода формул тангенса и котангенса суммы используем формулы синуса и косинуса суммы, полученные в §13 данного справочника.
\begin{gather*} tg(\alpha+\beta)=\frac{sin(\alpha+\beta)}{cos(\alpha+\beta)}=\frac{sin\alpha cos\beta+cos\alpha sin\beta}{cos\alpha cos\beta-sin\alpha sin\beta}=\frac{\frac{sin\alpha cos\beta+cos\alpha sin\beta}{cos\alpha cos\beta}}{\frac{cos\alpha cos\beta-sin\alpha sin\beta}{cos\alpha cos\beta}}=\\ =\frac{tg\alpha+tg\beta}{1-tg\alpha\cdot tg\beta}\\ \\ ctg(\alpha+\beta)=\frac{cos(\alpha+\beta)}{sin(\alpha+\beta)}=\frac{cos\alpha cos\beta-sin\alpha sin\beta}{sin\alpha cos\beta+cos\alpha sin\beta}= \frac{\frac{cos\alpha cos\beta-sin\alpha sin\beta}{sin\alpha sin\beta}}{\frac{sin\alpha cos\beta+cos\alpha sin\beta}{sin\alpha sin\beta}}=\\ =\frac{ctg\alpha\cdot ctg\beta-1}{ctg\alpha+ ctg\beta} \end{gather*}п.
 2. Тангенс и котангенс разности
2. Тангенс и котангенс разностиДля вывода формулы тангенса и котангенса разности используем формулы синуса и косинуса разности, полученные в §13 данного справочника. \begin{gather*} tg(\alpha-\beta)=\frac{sin(\alpha-\beta)}{cos(\alpha-\beta)}=\frac{sin\alpha cos\beta-cos\alpha sin\beta}{cos\alpha cos\beta+sin\alpha sin\beta}=\frac{\frac{sin\alpha cos\beta-cos\alpha sin\beta}{cos\alpha cos\beta}}{\frac{cos\alpha cos\beta+sin\alpha sin\beta}{cos\alpha cos\beta}}=\\ =\frac{tg\alpha-tg\beta}{1+tg\alpha\cdot tg\beta}\\ \\ ctg(\alpha-\beta)=\frac{cos(\alpha-\beta)}{sin(\alpha-\beta)}=\frac{cos\alpha cos\beta+sin\alpha sin\beta}{sin\alpha cos\beta-cos\alpha sin\beta}= \frac{\frac{cos\alpha cos\beta+sin\alpha sin\beta}{sin\alpha sin\beta}}{\frac{sin\alpha cos\beta-cos\alpha sin\beta}{sin\alpha sin\beta}}=\\ =\frac{ctg\alpha\cdot ctg\beta+1}{ctg\beta-ctg\alpha}=-\frac{ctg\alpha\cdot ctg\beta+1}{ctg\alpha-ctg\beta} \end{gather*}
\begin{gather*} tg(\alpha+\beta) =\frac{tg\alpha+tg\beta}{1-tg\alpha\cdot tg\beta},\ \ \ ctg(\alpha+\beta) =\frac{ctg\alpha\cdot ctg\beta-1}{ctg\alpha+ ctg\beta}\\ \\ tg(\alpha-\beta) =\frac{tg\alpha-tg\beta}{1+tg\alpha\cdot tg\beta},\ \ \ ctg(\alpha-\beta)=-\frac{ctg\alpha\cdot ctg\beta+1}{ctg\alpha-ctg\beta} \end{gather*}
п.
 2\alpha\)
2\alpha\)
г*) \(tg\alpha tg\beta+tg\beta tg\gamma+tg\gamma tg\alpha\), если \(\alpha+\beta+\gamma=\frac\pi2\)
По условию \(\gamma=\frac\pi2-(\alpha+\beta)\). Подставляем: \begin{gather*} tg\alpha tg\beta+tg\beta tg\left(\frac\pi2-(\alpha+\beta)\right)+tg\left(\frac\pi2-(\alpha+\beta)\right)tg\alpha=\\ =tg\alpha tg\beta+ctg(\alpha+\beta)\cdot (tg\alpha+tg\beta)=tg\alpha tg\beta+\frac{tg\alpha+tg\beta}{tg(\alpha+\beta)}=\\ =tg\alpha tg\beta+\frac{(tg\alpha+tg\beta)(1-tg\alpha tg\beta)}{tg\alpha+tg\beta}=tg\alpha tg\beta+1-tg\alpha tg\beta=1 \end{gather*} Ответ: 1Пример 3.Докажите, что \(\alpha+\beta=\frac\pi4\), если \(tg\alpha=\frac25,\ tg\beta=\frac37,\ \ 0\lt\alpha\lt\frac\pi2,\ \ 0\lt\beta\lt\frac\pi2\)
Найдем тангенс суммы: \begin{gather*} tg(\alpha+\beta)=\frac{tg\alpha+tg\beta}{1-tg\alpha\cdot tg\beta}=\frac{\frac25+\frac37}{1-\frac25\cdot\frac37}=\frac{\frac{14+15}{35}}{\frac{35-6}{35}}=\frac{29}{29}=1\\ \alpha+\beta=\frac\pi4+\pi k \end{gather*} По условию: \begin{gather*} \begin{cases} 0\lt\alpha\lt\frac\pi2\\ 0\lt\beta\lt\frac\pi2 \end{cases} \Rightarrow 0\lt\alpha+\beta\lt\pi\\ 0\lt\frac\pi4+\pi k\lt \pi\Rightarrow k = 0 \end{gather*} Значит: \(\alpha+\beta=\frac\pi4\)
Что и требовалось доказать.
Рейтинг пользователей
за неделю- за неделю
- один месяц
- три месяца
-
Если число находится за пределами ограничения, coTH возвращает #NUM! (значение ошибки).
-
Если значение «число» не является числом, coTH возвращает #VALUE! (значение ошибки).
-
Используется следующая формула:
Помогай другим
Отвечай на вопросы и получай ценные призы каждую неделю
См. подробности
COTH (функция COTH) — Служба поддержки Майкрософт
Excel для Microsoft 365 Excel для Microsoft 365 для Mac Excel для Интернета Excel 2021 Excel 2021 для Mac Excel 2019 Excel 2019 для Mac Excel 2016 Excel 2016 для Mac Excel 2013 Excel для Mac 2011 Еще…Меньше
В этой статье описаны синтаксис формулы и использование функции COTH в Microsoft Excel.
Описание
Возвращает гиперболический котангенс гиперболического угла.
Синтаксис
COTH(число)
Аргументы функции COTH описаны ниже.
 27.
27.Пример
Скопируйте образец данных из следующей таблицы и вставьте их в ячейку A1 нового листа Excel. Чтобы отобразить результаты формул, выделите их и нажмите клавишу F2, а затем — клавишу ВВОД. При необходимости измените ширину столбцов, чтобы видеть все данные.
| 1 | 3 | ||||
| 6 | 7 | 8 | |||
| 900 38 — | 6 | ||||
| 1 | 8 | ||||
| — | 1 | 8 | |||
| 0 |
|
Формула |
Описание |
Результат |
|
=COTH(2) |
Возвращает гиперболический котангенс числа 2 (1,037). |
1,037 |
К началу страницы
определений и примеров котангенса — Club Z! Обучение
Определения и примеры формул котангенса
Введение
Котангенс — это тригонометрическая функция, обратная функции тангенса. Он обозначается символом «кроватка» и определяется как отношение косинуса к синусу угла. В этом сообщении блога мы рассмотрим формулу котангенса и несколько примеров того, как ее можно использовать. Мы также углубимся в его историю и то, как он используется в современном мире. Так что, если вы хотите узнать больше об этой увлекательной теме, читайте дальше!
Что такое котангенс?
В математике котангенс является обратной функцией тангенса. Котангенс угла равен длине прилежащей стороны, деленной на длину противолежащей стороны. Другими словами, это мера того, насколько острым является угол.
Другими словами, это мера того, насколько острым является угол.
Функцию котангенса можно использовать для решения задач по тригонометрии и геометрии. Например, его можно использовать для нахождения длин сторон треугольника, когда известны два угла и одна сторона. Его также можно использовать для нахождения углов в треугольнике, когда известны две стороны и один угол.
Функция котангенса также важна в исчислении. Он используется в интегралах и производных с участием тригонометрических функций. Например, его можно использовать для нахождения площади под кривой, заданной тригонометрической функцией.
Формула котангенса
Котангенс угла – это отношение длины прилежащей стороны к длине противолежащей стороны. Другими словами, это функция, обратная касательной. Котангенс можно записать в виде дроби с горизонтальной чертой, например:
cot(?) = смежный / противоположный
Или это можно записать в виде отношения следующим образом:
cot(?) = 1 / tan(?)
Котангенс является важной тригонометрической функцией, которая имеет множество применений по математике и физике. Он используется в исчислении для вычисления производных и интегралов, и он появляется во многих формулах в физике.
Он используется в исчислении для вычисления производных и интегралов, и он появляется во многих формулах в физике.
Свойства котангенса
Котангенс – это отношение стороны, примыкающей к углу прямоугольного треугольника, к стороне, противолежащей этому углу. Это также величина, обратная касательной.
Котангенс угла обозначается символом: ?
Чтобы найти котангенс угла, разделите длину прилежащей стороны на длину противолежащей стороны:
cot(?) = прилежащая ÷ противолежащая = a/b
Функция котангенса не определена, когда ? = 0° или ? = 180°, потому что в этих случаях смежная и противоположная стороны равны. Следовательно, мы не можем делить на ноль.
Закон котангенса
В математике котангенс является обратной функцией тангенса. Котангенс угла – это отношение длины прилежащей стороны к длине противолежащей стороны. Другими словами, это наклон линии, касательной к кривой в данной точке. Его можно рассматривать как меру того, насколько «крутой» является кривая в данной точке.
Функция котангенса имеет ряд полезных свойств, которые можно вывести из ее определения как функции, обратной функции тангенса. К ним относятся:
– функция котангенса является нечетной, что означает, что она меняет знак, когда x изменяется на -x. Это означает, что он симметричен относительно начала координат (0,0).
— диапазоном функции котангенса являются все действительные числа, кроме тех, которые находятся между двумя вертикальными асимптотами (где функция тангенса не определена).
— Областью определения функции котангенса являются все действительные числа, кроме тех, где есть вертикальные асимптоты (где функция тангенса не определена). 9-1.
Период котангенса — это расстояние между двумя последовательными максимумами или минимумами на его графике. Как и в случае с синусоидальным или косинусоидальным графиком, период котангенсного графика будет в два раза больше длины одного полного цикла. Формула для расчета периода котангенса:
P = 2 * pi / |b|
где P — период, а b — коэффициент при x в уравнении y = cot(x). Например, если y = cot(x), то период будет равен 2 * пи / 1 или просто 2 * пи.
Например, если y = cot(x), то период будет равен 2 * пи / 1 или просто 2 * пи.
Котангенс единичной окружности
Котангенс является обратной функцией тангенса. Он определяется как отношение длины прилежащей стороны к длине противолежащей стороны в прямоугольном треугольнике. Котангенс можно использовать для нахождения углов в треугольниках, когда известны две стороны. Его также можно использовать для поиска недостающих сторон в треугольнике, когда известны два угла и одна сторона. Котангенс также определен на единичной окружности. Единичная окружность — это окружность с радиусом 1. Котангенс единичной окружности определяется как координата x точки, в которой линия, проведенная из начала координат, пересекает единичную окружность.
Область, диапазон и график котангенса
Область: все действительные числа
Диапазон: все действительные числа, кроме 0
График котангенса: График котангенса представляет собой волну, которая начинается в бесконечности, приближается к 0, затем отрицательная бесконечность. Он имеет вертикальные асимптоты при x=0 и x=(-n)*pi, где n — любое целое число.
Он имеет вертикальные асимптоты при x=0 и x=(-n)*pi, где n — любое целое число.
Производная и интеграл котангенса
Производная котангенса является обратной величиной тангенса:
$$\frac{d}{dx}\cot x = \frac{1}{\tan x}$$
Интеграл котангенса есть натуральный логарифм тангенса:
$$\int \cot x \, dx = \ln |\tan x| + C$$
Заключение
Мы надеемся, что эта статья помогла прояснить любую путаницу, связанную с формулой котангенса и ее различными приложениями. Как видите, формула котангенса — мощный инструмент, который можно использовать для решения самых разных задач. Немного потренировавшись, вы сможете использовать его как профессионал!
Участки
Альтернативные формы
Альтернативная форма в предположении, что x действительно
Корни
9000 2Свойства как действительная функция
Разложение в ряд при x = 0
Производная
Неопределенный интеграл
Тождества
Альтернативные представления
Представления рядов
Плюсы и минусы формулы котангенса
Сегодня мы рассмотрим формулу котангенса и то, как ее можно использовать в математике. Котангенс угла определяется как отношение косинуса угла к синусу этого угла. Эту формулу часто записывают как cot x = cos x sin x.
Котангенс угла определяется как отношение косинуса угла к синусу этого угла. Эту формулу часто записывают как cot x = cos x sin x.
Коэффициент котангенса равен длине прилежащей стороны угла, деленной на длину противоположной стороны, поэтому его также можно записать как cb x = c b или cot x = cbx. Это соотношение также может быть выражено через тангенс, который будет выглядеть либо как cot θ = 1/tan θ, либо как cot θ = tan (π/2 – θ).
В прямоугольном треугольнике котангенс угла равен длине прилежащей стороны, деленной на противолежащую сторону. Затем эту формулу можно использовать для определения других сторон и углов в прямоугольном треугольнике, если известны одна сторона и один угол.
По этой формуле также можно определить тангенс угла; она равна отношению его противоположной стороны к прилежащей стороне. Знание этой информации позволяет вам вычислять углы, для которых иначе вы бы не знали, как решить.
В заключение давайте повторим, что мы узнали:
• Формула котангенса записывается как cot x = cos x sin x или cbx =c b
• В прямоугольном треугольнике она равна длина его смежной стороны, деленная на его противоположную сторону
• Его также можно выразить через тангенс: либо 1/тангенс θ, либо тангенс (π/2 -θ)
• Формула тангенса равна отношению его противоположной стороны над соседней стороной
• Зная эту информацию, вы можете вычислить углы, которые иначе не смогли бы решить для
Надеюсь, этот блог прояснил любую путаницу с формулой котангенса и ее отношением к треугольникам!
Формула раскладушки
Формула котангенса используется для вычисления котангенса заданного угла. Котангенс угла равен косинусу угла, деленному на синус угла. Математически это можно выразить как cot x = cos x / sin x. Чтобы найти котангенс угла, нужно сначала вычислить косинус и синус этого угла, а затем разделить одно на другое. Например, если у нас есть угол θ с косинусом и синусом, равными 0,5 и 0,866 соответственно, то его котангенс будет рассчитан как 0,5/0,866 = 0,57735.
Котангенс угла равен косинусу угла, деленному на синус угла. Математически это можно выразить как cot x = cos x / sin x. Чтобы найти котангенс угла, нужно сначала вычислить косинус и синус этого угла, а затем разделить одно на другое. Например, если у нас есть угол θ с косинусом и синусом, равными 0,5 и 0,866 соответственно, то его котангенс будет рассчитан как 0,5/0,866 = 0,57735.
Источник: commons.wikimedia.org
Что такое котангенс угла θ?
Котангенс θ — это тригонометрическое отношение, измеряющее угол в прямоугольном треугольнике. Он равен длине прилежащей стороны, деленной на длину стороны, противоположной углу. Это отношение может быть выражено как кроватка (θ) = смежный / противоположный. Важно отметить, что котангенс θ применим только к прямоугольным треугольникам, так как он зависит от двух сторон с углом 90 градусов между ними.
Формула котангенса угла
Формула cot θ выражается двумя способами. Во-первых, это cot θ = 1/tan θ. Это означает, что котангенс угла равен обратной величине тангенса этого угла. Второе выражение для cot θ – это tan(90° – θ). Это означает, что котангенс угла равен тангенсу дополнительного угла (180° – θ). В обоих случаях cot θ можно рассчитать, взяв обратное (или обратное) значение тангенса θ.
Это означает, что котангенс угла равен обратной величине тангенса этого угла. Второе выражение для cot θ – это tan(90° – θ). Это означает, что котангенс угла равен тангенсу дополнительного угла (180° – θ). В обоих случаях cot θ можно рассчитать, взяв обратное (или обратное) значение тангенса θ.
Нахождение котангенса треугольника
Чтобы найти котангенс треугольника, вам сначала нужно знать длины сторон, прилегающих к рассматриваемому углу и противоположных ему. Чтобы вычислить отношение котангенса, разделите длину прилежащей стороны на длину противолежащей стороны. Например, если у вас есть треугольник с углом θ и двумя сторонами с длинами a и b, то отношение котангенса будет записано как cot θ = a/b. Это даст вам соотношение между этими двумя сторонами для этого конкретного угла.
Значение слова «кроватка» в калькуляторах
Котангенс, или котангенс, представляет собой тригонометрическую функцию, которая используется для вычисления отношения длин сторон треугольника. Детскую кроватку можно использовать для вычисления углов и сторон треугольника. Кроме того, кроватку можно использовать в более сложных вычислениях, таких как вектора и комплексные числа. Чтобы использовать кроватку в калькуляторе, ее часто выражают как COT(x), где x представляет собой угол, выраженный в радианах. Чтобы преобразовать градусы в радианы, вы можете использовать функцию РАДИАНЫ. Выход COT(x) будет котангенсом x.
Детскую кроватку можно использовать для вычисления углов и сторон треугольника. Кроме того, кроватку можно использовать в более сложных вычислениях, таких как вектора и комплексные числа. Чтобы использовать кроватку в калькуляторе, ее часто выражают как COT(x), где x представляет собой угол, выраженный в радианах. Чтобы преобразовать градусы в радианы, вы можете использовать функцию РАДИАНЫ. Выход COT(x) будет котангенсом x.
Сравнение функций Cot и Cos
Котангенс (cot) и косинус (cos) — две основные тригонометрические функции, используемые в математике. Cot является обратной функцией тангенса, что означает, что для каждого угла котангенс этого угла равен обратной величине его тангенса. Косинус, с другой стороны, является обратной функцией синуса, что означает, что для каждого угла косинус этого угла равен обратной величине его синуса. Котангенс и косинус связаны тем, что оба они используют углы для вычисления отношения между двумя сторонами прямоугольного треугольника.
Значение θ в тригонометрии
В тригонометрии θ — это угол в треугольнике. Он широко известен как угол «тета» и обычно используется для вычисления сторон прямоугольного треугольника. В частности, это один из острых углов треугольника, и его синус, косинус и тангенс можно рассчитать, используя отношения противолежащего катета к гипотенузе и прилежащего катета к гипотенузе для синуса и косинуса соответственно, а также отношение противолежащего катета. к соседней стороне для касательной.
Что означает θ в математике?
В математике θ (греческая буква «тета») обычно используется для обозначения угла. Углы обычно измеряются в градусах, а θ обычно используется как символ для неизвестной меры угла. Он также иногда используется в качестве переменной для указания произвольного угла при решении уравнений или выполнении вычислений с использованием углов.
Значение котангенса в градусах
Значение cot (отношение косинуса и синуса угла) для любого заданного градуса равно отношению косинуса этого угла к синусу этого угла. Таким образом, для любой заданной степени, если мы обозначим ее как ‘x’, то cot(x) = cos(x)/sin(x). Однако в тех случаях, когда синус заданного угла равен 0, тогда значение cot неопределенно или равно бесконечности (∞), так как потребовалось бы взять отношение, где знаменатель равен 0. Это происходит при 0°, 180° и 360°.
Таким образом, для любой заданной степени, если мы обозначим ее как ‘x’, то cot(x) = cos(x)/sin(x). Однако в тех случаях, когда синус заданного угла равен 0, тогда значение cot неопределенно или равно бесконечности (∞), так как потребовалось бы взять отношение, где знаменатель равен 0. Это происходит при 0°, 180° и 360°.
Источник: intomath.org
Является ли котангенс обратным тангенсу?
Да, cot (котангенс) является обратной величиной tan (тангенса). Котангенс — это отношение прилежащего катета к гипотенузе прямоугольного треугольника, а тангенс — это отношение противолежащего катета к прилежащему. Поскольку эти два отношения являются обратными друг другу, отсюда следует, что cot является обратным отношением tan.
Обратная функция котангенса
Обратная функция котангенса, также известная как арккот или арккотангенс, представляет собой математическую функцию, которая берет котангенс числа и возвращает его угол в радианах. Область определения и диапазон функции арккота равны -∞ < x < ∞ и 0 < y < π соответственно.

 com , http://visualfractions.com/calculator/long-division/what-is-78-divided-by-6-using-long-division/. По состоянию на 24 мая 2023 г.
com , http://visualfractions.com/calculator/long-division/what-is-78-divided-by-6-using-long-division/. По состоянию на 24 мая 2023 г.
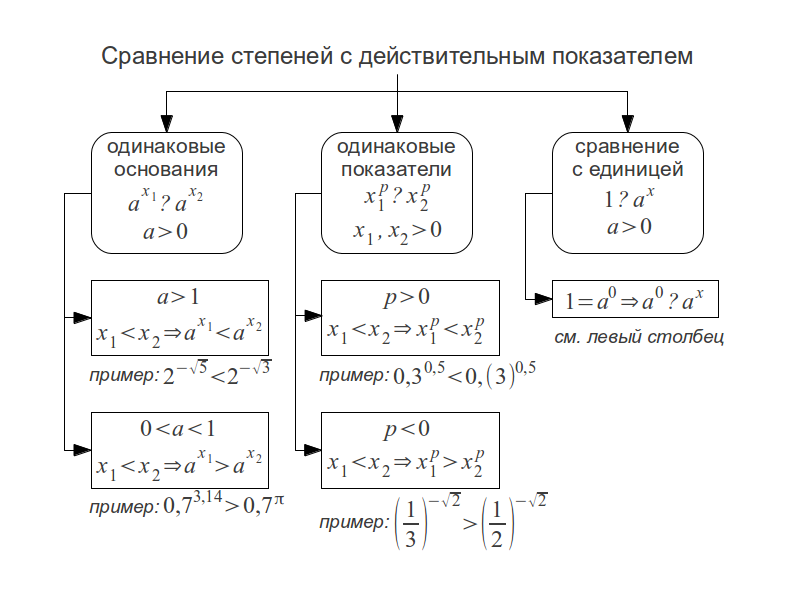
 3;a1*1.1)
3;a1*1.1) Сначала мы изучали основы: сложение с умножением, извлечение корня, преобразование тригонометрических выражений. А затем учились применять изученные базовые принципы и свойства для решения математических моделей реальных задач.
Сначала мы изучали основы: сложение с умножением, извлечение корня, преобразование тригонометрических выражений. А затем учились применять изученные базовые принципы и свойства для решения математических моделей реальных задач.

 Получаем ответ:
Получаем ответ: Теперь рассмотрим уравнения, в которых неизвестная стоит в показателе степени – показательные уравнения. Идея их решения очень похожа на ту, что мы использовали при решении степенных уравнений. Нужно свести уравнение к виду:
Теперь рассмотрим уравнения, в которых неизвестная стоит в показателе степени – показательные уравнения. Идея их решения очень похожа на ту, что мы использовали при решении степенных уравнений. Нужно свести уравнение к виду: Применяя свойства степени, получаем:
Применяя свойства степени, получаем: Если вы не помните методы решения неравенств, можете их повторить, посмотрев уроки Линейные неравенства. Системы и совокупности неравенств; Решение квадратных неравенств. Метод интервалов.
Если вы не помните методы решения неравенств, можете их повторить, посмотрев уроки Линейные неравенства. Системы и совокупности неравенств; Решение квадратных неравенств. Метод интервалов. Поэтому записываем неравенство для показателей степени и меняем знак:
Поэтому записываем неравенство для показателей степени и меняем знак:
 Общая идея решения нам уже знакома – привести левую и правую части к логарифмам с одинаковым основанием:
Общая идея решения нам уже знакома – привести левую и правую части к логарифмам с одинаковым основанием:
 Что ж, можете его использовать. Но обратите внимание, что он не такой универсальный. Он подойдет только в случае, если в одной из частей уравнения стоит число.
Что ж, можете его использовать. Но обратите внимание, что он не такой универсальный. Он подойдет только в случае, если в одной из частей уравнения стоит число. Решить уравнение:
Решить уравнение:
 Решение квадратных и дробно-рациональных уравнений. Практика. Тригонометрические уравнения и неравенства. Базовый уровень).
Решение квадратных и дробно-рациональных уравнений. Практика. Тригонометрические уравнения и неравенства. Базовый уровень). Давайте сначала приведем их к одинаковому основанию:
Давайте сначала приведем их к одинаковому основанию: Вы уже знаете, как решать такие неравенства. Попробуйте решить его самостоятельно, свериться можно ниже.
Вы уже знаете, как решать такие неравенства. Попробуйте решить его самостоятельно, свериться можно ниже. Тогда первое неравенство превращается в . Решаем его:
Тогда первое неравенство превращается в . Решаем его: Но и их мы уже умеем решать:
Но и их мы уже умеем решать:
 А это, напомним, влияет на смену знака неравенства. Поэтому нужно будет рассмотреть два случая: когда основание больше и когда меньше 1. С примером решения подобного неравенства вы можете ознакомиться в ответвлении.
А это, напомним, влияет на смену знака неравенства. Поэтому нужно будет рассмотреть два случая: когда основание больше и когда меньше 1. С примером решения подобного неравенства вы можете ознакомиться в ответвлении.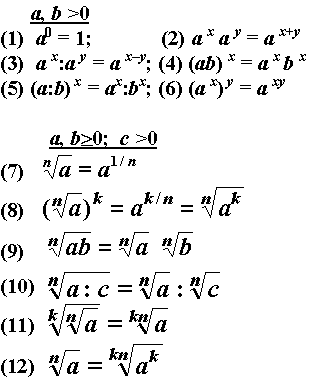 рис. 2).
рис. 2). Записываем неравенство для подлогарифмических выражений и меняем знак неравенства:
Записываем неравенство для подлогарифмических выражений и меняем знак неравенства: рис. 1).
рис. 1). М., Потапов М. К., Решетников Н.Н. Алгебра и начала математического анализа, геометрия. 10 класс. Учебник. – АО «Издательство “Просвещение”»
М., Потапов М. К., Решетников Н.Н. Алгебра и начала математического анализа, геометрия. 10 класс. Учебник. – АО «Издательство “Просвещение”» Когда вы используете несколько терминов, показатели складываются вместе.
Когда вы используете несколько терминов, показатели складываются вместе. Сложение просто определяется как оно есть, и если у вас есть несколько одночленов разной степени, вы не можете их сложить. Если я совершенно не осознаю этого, там нет ничего глубокого. Суть в том, чтобы рассматривать полиномы как формальные объекты, а не как соответствующие им карты, если только для этого нет веской причины. 92=?$$
Сложение просто определяется как оно есть, и если у вас есть несколько одночленов разной степени, вы не можете их сложить. Если я совершенно не осознаю этого, там нет ничего глубокого. Суть в том, чтобы рассматривать полиномы как формальные объекты, а не как соответствующие им карты, если только для этого нет веской причины. 92=?$$ Переписывание числа в экспоненциальной записи с использованием другой экспоненциальной базы технически «нарушает» правило записи в экспоненциальной записи: наш коэффициент a должен быть больше или равен 1, но меньше 10. Почему и должны быть между этими номерами? Потому что это просто обычный способ написать это.
Переписывание числа в экспоненциальной записи с использованием другой экспоненциальной базы технически «нарушает» правило записи в экспоненциальной записи: наш коэффициент a должен быть больше или равен 1, но меньше 10. Почему и должны быть между этими номерами? Потому что это просто обычный способ написать это. Ты прав. Мы будем использовать специальное свойство экспонент, модифицированное под наши нужды:
Ты прав. Мы будем использовать специальное свойство экспонент, модифицированное под наши нужды:


 В этом используется вся та работа, которую вы проделали, изменяя экспоненциальные основания.
В этом используется вся та работа, которую вы проделали, изменяя экспоненциальные основания.
 2\alpha\)
2\alpha\)
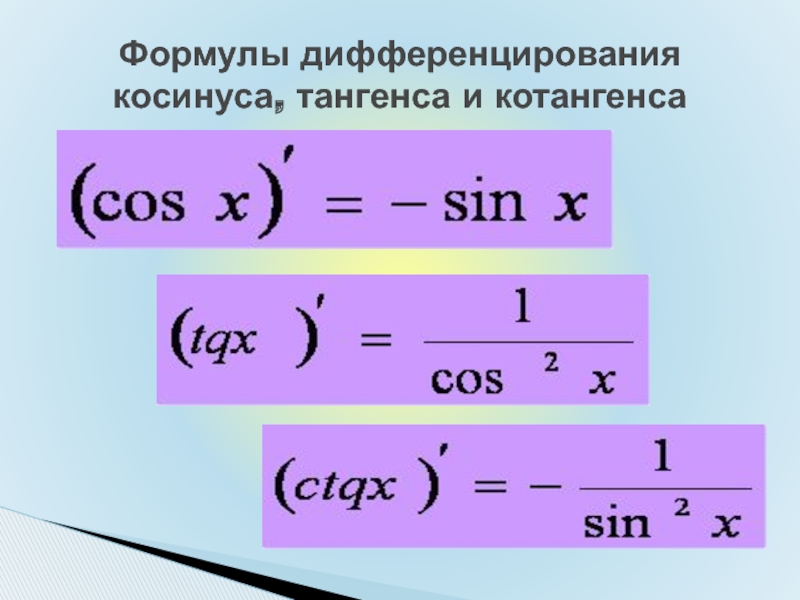 27.
27.
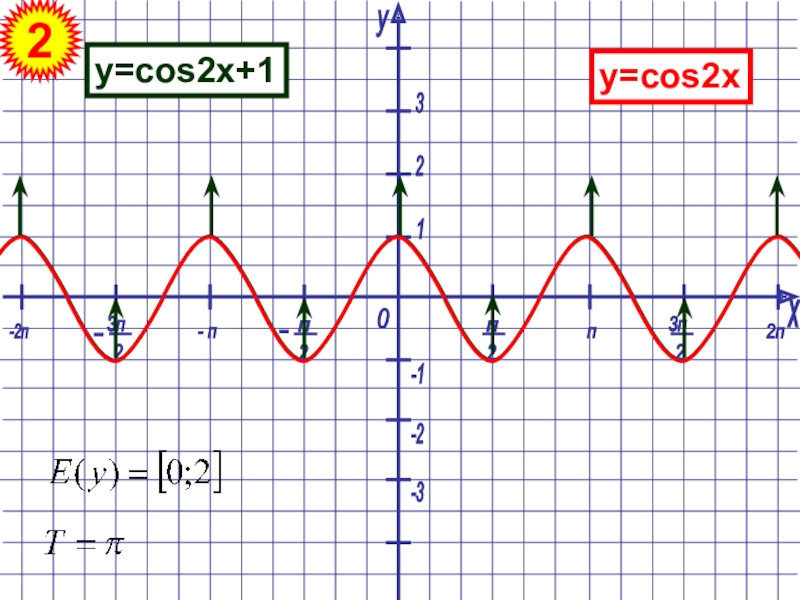 Решение квадратных неравенств
Решение квадратных неравенств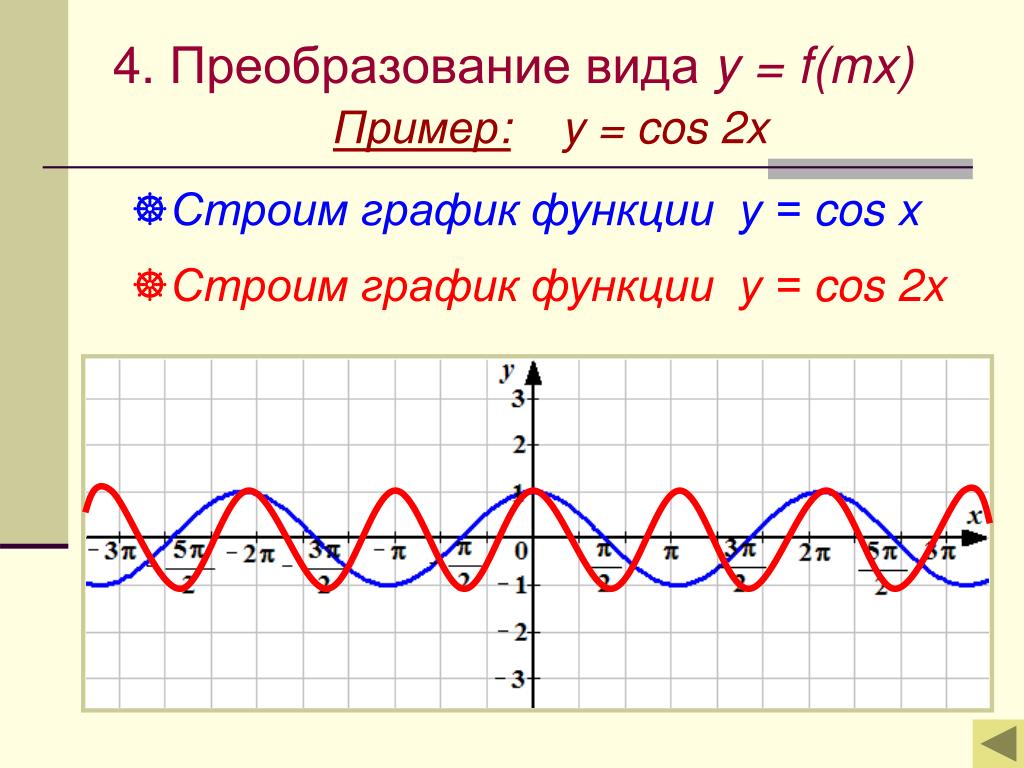 Кто упадёт первым?
Кто упадёт первым? .. ⋅ a
n разів
для a ∈ R, n ∈ N, n 2
a0
= 1, де а ≠ 0 a2
= а
a–n
=
1
—
аn для а ≠ 0, n ∈ N
a
m
—
n
= am
n
, а > 0, m ∈ Z, n ∈ N, n 2
ax
⋅ ay
= ax + y аx
—
аy = ax – y
(ax
)y
= ax ⋅ y
(ab)x
= ax
⋅ bx
(a
–
b)
x
=
аx
—
bx
a > 0, а ≠ 1, b > 0, c > 0, k ≠ 0
alogab
= b logаа = 1 logа1 = 0
logа(b ⋅ c) = logаb + logаc
logа
b
–
c = logаb – logаc
logаbn
= n ⋅ logаb
logаk b = 1
–
k
⋅ logаb
an = a1 + d(n – 1) Sn =
a1 + аn
—
2
⋅ n
Pn = 1 ⋅ 2 ⋅ 3 ⋅ … ⋅ n = n! C
k
n =
n!
—
k! ⋅ (n – k)!
Ak
n =
n!
—
(n – k)!
P(A) =
k
–
n
bn = b1 ⋅ qn – 1
Sn =
b1(qn
– 1)
—
q – 1
, (q ≠ 1)
a =
a, якщо а 0,
–a, якщо а < 0
.. ⋅ a
n разів
для a ∈ R, n ∈ N, n 2
a0
= 1, де а ≠ 0 a2
= а
a–n
=
1
—
аn для а ≠ 0, n ∈ N
a
m
—
n
= am
n
, а > 0, m ∈ Z, n ∈ N, n 2
ax
⋅ ay
= ax + y аx
—
аy = ax – y
(ax
)y
= ax ⋅ y
(ab)x
= ax
⋅ bx
(a
–
b)
x
=
аx
—
bx
a > 0, а ≠ 1, b > 0, c > 0, k ≠ 0
alogab
= b logаа = 1 logа1 = 0
logа(b ⋅ c) = logаb + logаc
logа
b
–
c = logаb – logаc
logаbn
= n ⋅ logаb
logаk b = 1
–
k
⋅ logаb
an = a1 + d(n – 1) Sn =
a1 + аn
—
2
⋅ n
Pn = 1 ⋅ 2 ⋅ 3 ⋅ … ⋅ n = n! C
k
n =
n!
—
k! ⋅ (n – k)!
Ak
n =
n!
—
(n – k)!
P(A) =
k
–
n
bn = b1 ⋅ qn – 1
Sn =
b1(qn
– 1)
—
q – 1
, (q ≠ 1)
a =
a, якщо а 0,
–a, якщо а < 0
 Cos2x выражается через различные тригонометрические функции, и каждая из его формул используется для упрощения сложных тригонометрических выражений и решения задач интегрирования. Это тригонометрическая функция двойного угла, которая помогает узнать значение cos при удвоении угла x.
Cos2x выражается через различные тригонометрические функции, и каждая из его формул используется для упрощения сложных тригонометрических выражений и решения задач интегрирования. Это тригонометрическая функция двойного угла, которая помогает узнать значение cos при удвоении угла x.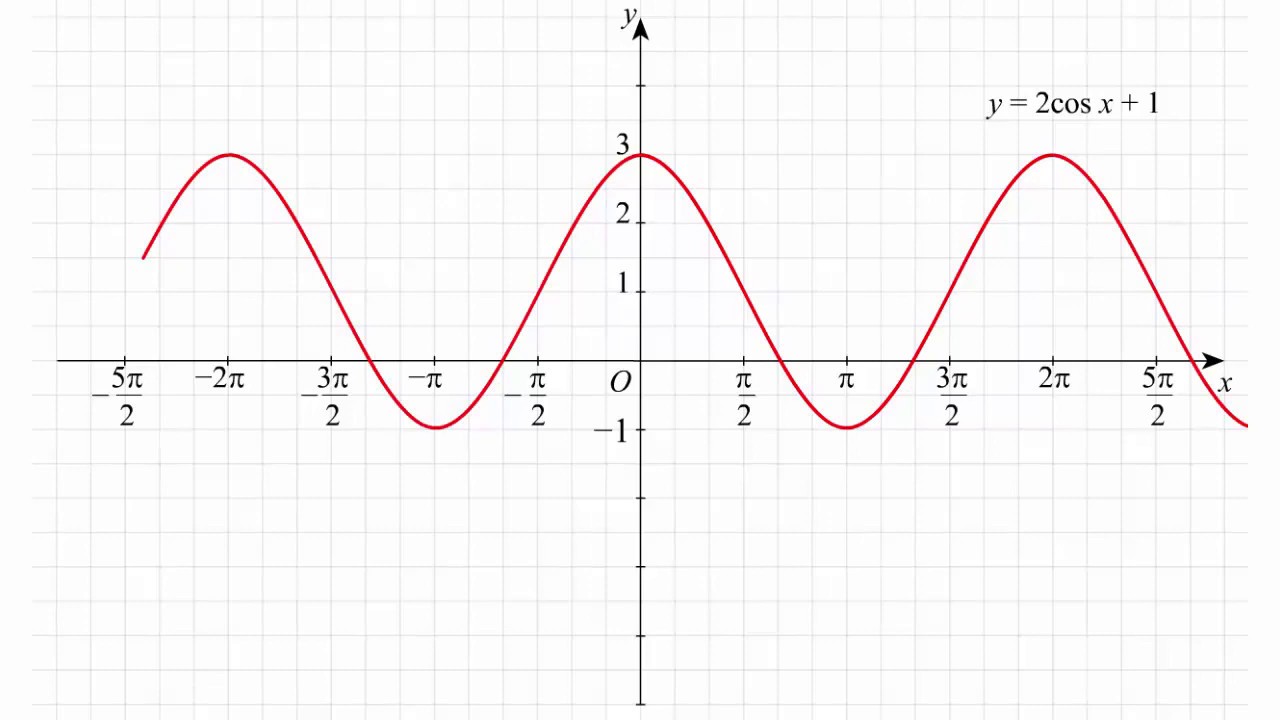 Используя формулу сложения углов для функции косинуса, мы можем заменить a = x и b = x в формуле для cos (a + b).
Используя формулу сложения углов для функции косинуса, мы можем заменить a = x и b = x в формуле для cos (a + b).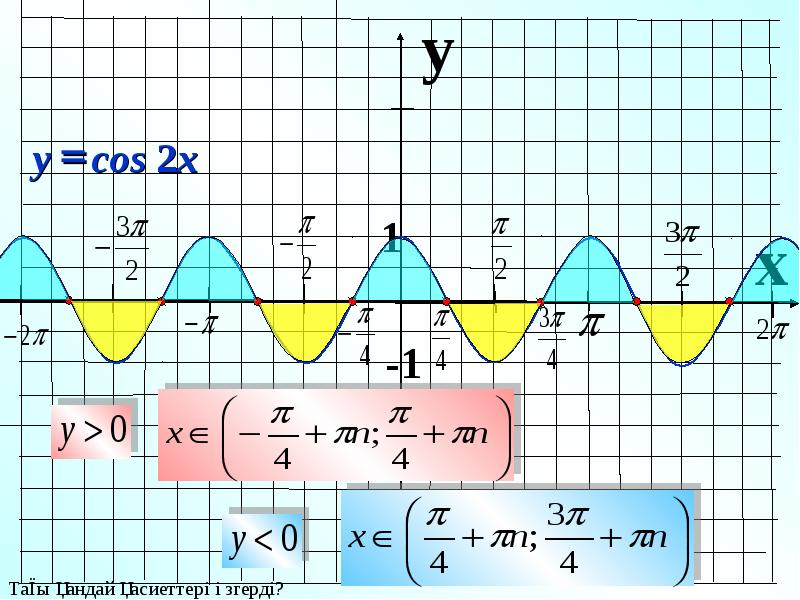
 Рассмотрим пример, демонстрирующий применение формулы cos2x.
Рассмотрим пример, демонстрирующий применение формулы cos2x.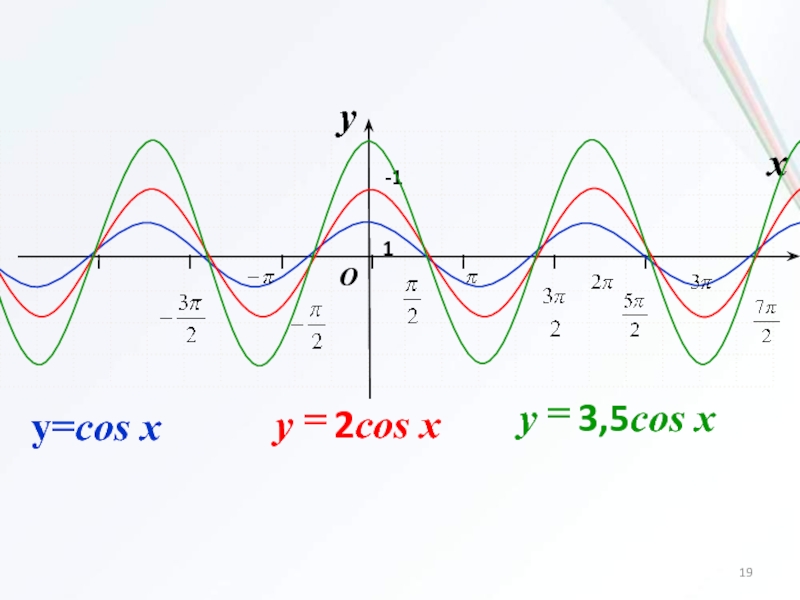
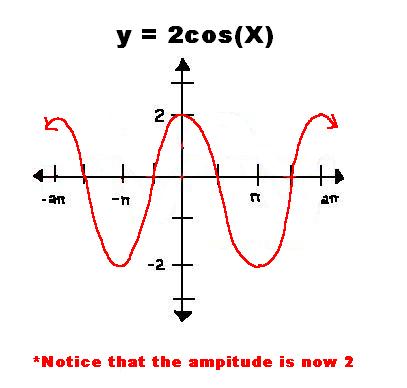 Это важное тригонометрическое тождество, которое можно использовать для решения различных задач тригонометрии и интегрирования. Значение cos 2x повторяется через каждые π радиан, cos 2x = cos (2x + π). Он имеет значительно более узкий график, чем cos x. Это тригонометрическая функция, которая возвращает значение функции cos двойного угла.
Это важное тригонометрическое тождество, которое можно использовать для решения различных задач тригонометрии и интегрирования. Значение cos 2x повторяется через каждые π радиан, cos 2x = cos (2x + π). Он имеет значительно более узкий график, чем cos x. Это тригонометрическая функция, которая возвращает значение функции cos двойного угла.

 Если sec x = 17/8, найдите значение cos 2x по формуле.
Если sec x = 17/8, найдите значение cos 2x по формуле. 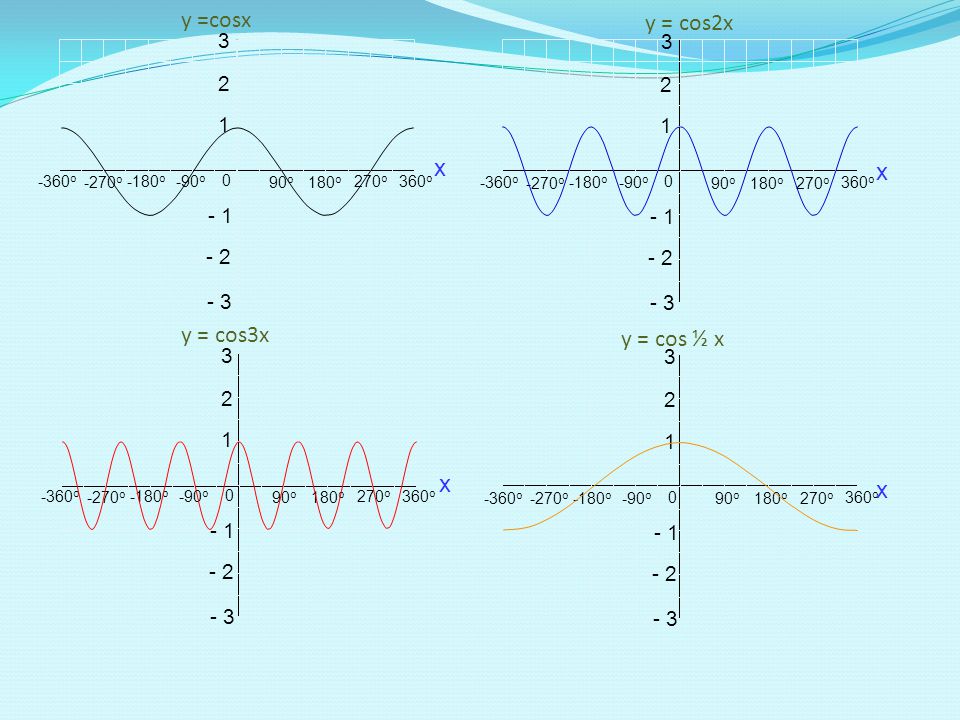
 Пересмотр ответов не допускается.
Пересмотр ответов не допускается. Квалификационный аттестат переоформляется на новом бланке на основании письменного заявления.
Квалификационный аттестат переоформляется на новом бланке на основании письменного заявления.
 Сведения об этом хранятся на протяжении 3 лет. В течение этого периода повторно сдать квалификационный экзамен нельзя. Постановление о дисквалификации можно оспорить в суде.
Сведения об этом хранятся на протяжении 3 лет. В течение этого периода повторно сдать квалификационный экзамен нельзя. Постановление о дисквалификации можно оспорить в суде. Долетят ли дроны до Челябинска?
Долетят ли дроны до Челябинска? После смерти отца москвичка судится с государством за свою жилплощадь
После смерти отца москвичка судится с государством за свою жилплощадь Кто из южноуральцев попал в топ-20 богатейших наследников России
Кто из южноуральцев попал в топ-20 богатейших наследников России Внедрен новый налог для самозанятых — налог на профессиональный доход. Появятся новые формы 2-НДФЛ и 3-НДФЛ.
Внедрен новый налог для самозанятых — налог на профессиональный доход. Появятся новые формы 2-НДФЛ и 3-НДФЛ. Поддержка в «1С.Практика автоматизации с пользой для бизнеса»;
Поддержка в «1С.Практика автоматизации с пользой для бизнеса»; Челябинск».
Челябинск». Конкурирующие предприятия
Конкурирующие предприятия 
 США U
США U  Чистая приведенная стоимость инвестиционного проекта представляет собой
Чистая приведенная стоимость инвестиционного проекта представляет собой com › тема › everfi-module-3-answers
com › тема › everfi-module-3-answers Лоренцо Аранда … Nishtha 2.0 Модуль 2 ответы || ICT …
Лоренцо Аранда … Nishtha 2.0 Модуль 2 ответы || ICT … 
 Педагогический (научно-педагогический) состав
Педагогический (научно-педагогический) состав {2}}\).
{2}}\). {i \theta}\): 9{i\theta}=\cos\theta+i\sin\theta\).
{i \theta}\): 9{i\theta}=\cos\theta+i\sin\theta\). Его также можно представить в виде диаграммы ниже.
Его также можно представить в виде диаграммы ниже.



 Так как e i∅ = cos∅ + isin∅ мы знаем это уже в тригонометрии.
Так как e i∅ = cos∅ + isin∅ мы знаем это уже в тригонометрии.

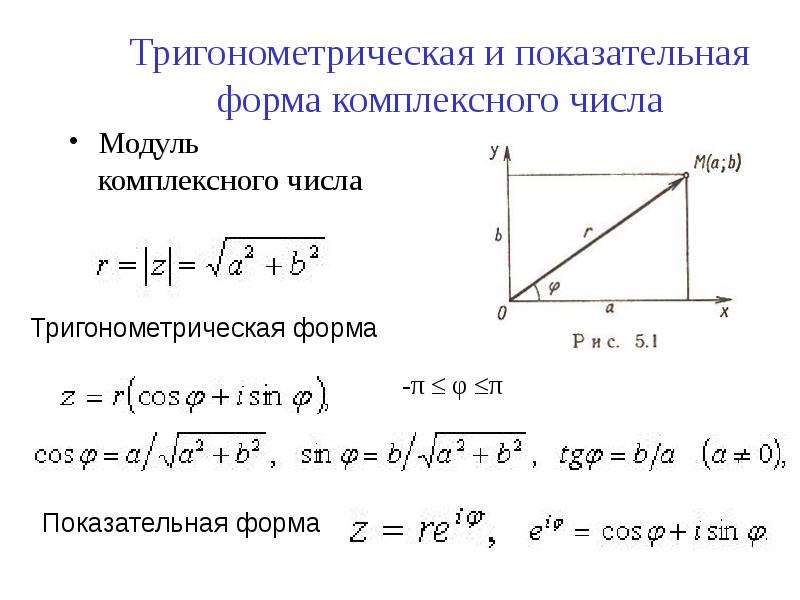


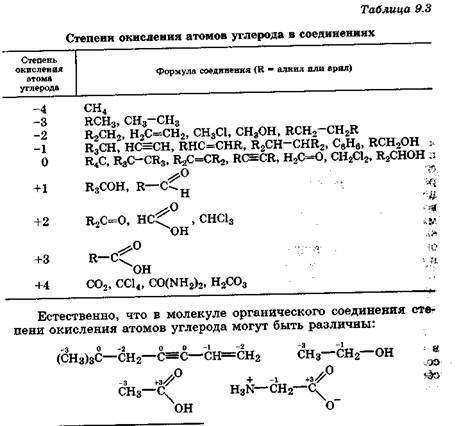 youtube.com/watch?v=GSpjM5XSxwE
youtube.com/watch?v=GSpjM5XSxwE
 – Гродно : ГГАУ, 2016. – 26 с.
– Гродно : ГГАУ, 2016. – 26 с. Использование таких пособий, в которых рассмотрены важнейшие теоретические вопросы в доступной и сжатой форме, позволит студентам быстрее и эффективнее изучить материал.
Использование таких пособий, в которых рассмотрены важнейшие теоретические вопросы в доступной и сжатой форме, позволит студентам быстрее и эффективнее изучить материал. Лекция по курсу «Общая химия» для студентов инженерно-технологического факультета / З.В. Апанович. – Гродно : ГГАУ, 2016. – 31 с.
Лекция по курсу «Общая химия» для студентов инженерно-технологического факультета / З.В. Апанович. – Гродно : ГГАУ, 2016. – 31 с. Использование такого пособия, в котором рассмотрены важнейшие вопросы в доступной и сжатой форме, позволит студентам быстрее и эффективнее изучить материал.
Использование такого пособия, в котором рассмотрены важнейшие вопросы в доступной и сжатой форме, позволит студентам быстрее и эффективнее изучить материал. 12.2016 12:03
12.2016 12:03

 Целью данного пособия является оказание помощи в изучении теоретического материала, а также выработка навыков экспериментальной работы.
Целью данного пособия является оказание помощи в изучении теоретического материала, а также выработка навыков экспериментальной работы. ст.
ст. A. и Grassian, V.H. : Угольная кислота: важное промежуточное соединение в химии поверхности карбоната кальция, J. Am. хим. Soc., 126, 8068–8069, https://doi.org/10.1021/ja04, 2004.
A. и Grassian, V.H. : Угольная кислота: важное промежуточное соединение в химии поверхности карбоната кальция, J. Am. хим. Soc., 126, 8068–8069, https://doi.org/10.1021/ja04, 2004.
 2006. Т. 75. С. 105–153.
2006. Т. 75. С. 105–153. Б. : Эксперименты по активации CCN адипиновой кислотой: влияние фазы частиц и покрытий из адипиновой кислоты на растворимые и нерастворимые частицы, Atmos. хим. Phys., 8, 3735–3748, https://doi.org/10.5194/acp-8-3735-2008, 2008.
Б. : Эксперименты по активации CCN адипиновой кислотой: влияние фазы частиц и покрытий из адипиновой кислоты на растворимые и нерастворимые частицы, Atmos. хим. Phys., 8, 3735–3748, https://doi.org/10.5194/acp-8-3735-2008, 2008. Am. хим. Соц., 30, 1711–1714, 1908.
Am. хим. Соц., 30, 1711–1714, 1908.
 , and Friedrich, J. : TEM-Untersuchungen der Mikrostrukturen von Verbrennungsaerosolen, Berichte des Forschungszentrums Jülich; JUEL-2700, ISSN 0366-0885, 1992.
, and Friedrich, J. : TEM-Untersuchungen der Mikrostrukturen von Verbrennungsaerosolen, Berichte des Forschungszentrums Jülich; JUEL-2700, ISSN 0366-0885, 1992. Aerosol Sci., обзор, 2010 г.
Aerosol Sci., обзор, 2010 г.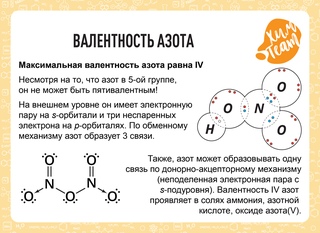 хим. Phys., 7, 1961–1971, https://doi.org/10.5194/acp-7-1961-2007, 2007.
хим. Phys., 7, 1961–1971, https://doi.org/10.5194/acp-7-1961-2007, 2007. Окружающая среда, 39, 359–369, 2005.
Окружающая среда, 39, 359–369, 2005. К., и Пратер, К. А. : Влияние метода генерации частиц на кажущуюся гигроскопичность нерастворимых минеральных частиц, Aerosol Sci. Технологии, 44, 830–846, 2010.
К., и Пратер, К. А. : Влияние метода генерации частиц на кажущуюся гигроскопичность нерастворимых минеральных частиц, Aerosol Sci. Технологии, 44, 830–846, 2010.


 По истечении этого времени они автоматически удаляются.
По истечении этого времени они автоматически удаляются. Наш конвертер файлов проанализирует содержимое исходного HTML файла до мельчайших деталей и воссоздаст содержимое в целевом DOC формате.
Наш конвертер файлов проанализирует содержимое исходного HTML файла до мельчайших деталей и воссоздаст содержимое в целевом DOC формате.

 Наша бесплатная служба преобразования проанализирует содержимое исходного HTML-файла до мельчайших деталей и воссоздаст содержимое в целевом формате Word.
Наша бесплатная служба преобразования проанализирует содержимое исходного HTML-файла до мельчайших деталей и воссоздаст содержимое в целевом формате Word.
 Вы можете скачать результат сразу или отправить ссылку на скачивание ворда на почту позже.
Вы можете скачать результат сразу или отправить ссылку на скачивание ворда на почту позже. Он отлично подходит для преобразования любых документов, таких как Microsoft Word, Excel, PowerPoint, PDF, Google Docs, Sheets и многих других. Вы также можете использовать этот инструмент для создания веб-контента с нуля или просто для очистки грязной разметки.
Он отлично подходит для преобразования любых документов, таких как Microsoft Word, Excel, PowerPoint, PDF, Google Docs, Sheets и многих других. Вы также можете использовать этот инструмент для создания веб-контента с нуля или просто для очистки грязной разметки.  Создавайте контент прямо в окне браузера, не устанавливая никаких расширений или плагинов для управления подсветкой синтаксиса и другими функциями редактирования текста.
Создавайте контент прямо в окне браузера, не устанавливая никаких расширений или плагинов для управления подсветкой синтаксиса и другими функциями редактирования текста.
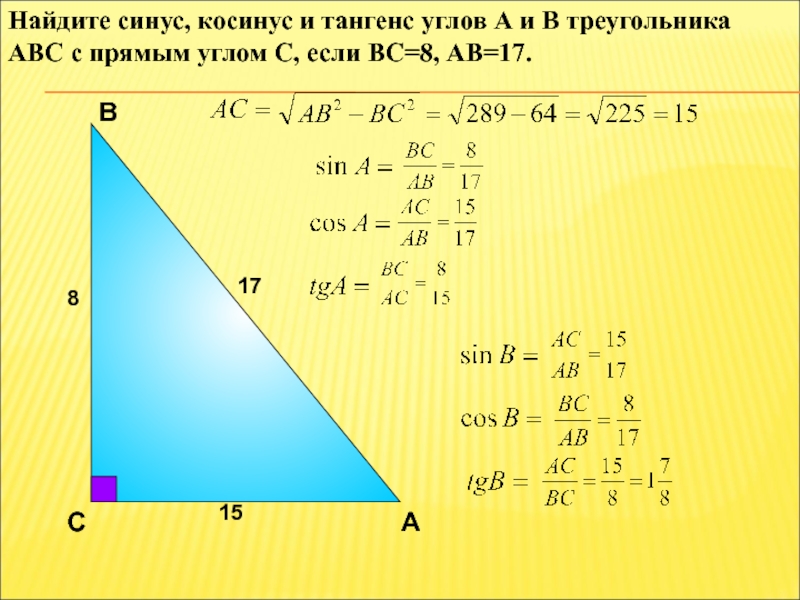 Особенно рекомендовано для турбодизельных двигателей с прямым впрыском. Разработано в соответствии с требованиями концерна VW.
Свойства продукта:
— Исключительная топливная экономичность за счет оптимальных антифрикционных свойств;
— Высокоэффективный пакет присадок и маловязкая синтетическая основа обеспечивают уверенный холодный пуск в любых условиях, благодаря чему значительно снижается пусковой износ двигателя;
— За счет превосходных моюще-диспергирующих свойств и высочайшей термоокислительной стабильности эффективно борется со всеми видами отложений и поддерживает в чистоте детали двигателя на протяжении всего интервала между заменами;
— Эстеровые компоненты масла обеспечивают отличные противоизносные свойства за счёт исключительной прочности масляной плёнки, что в сочетании с превосходной прокачиваемостью значительно увеличивает срок службы двигателя даже в режимах движения «Start-stop»;
— Совместимо со всеми системами нейтрализации отработавших газов, DPF, TWC, EGR и SCR за счет применения технологии Mid SAPS;
— Современный пакет присадок в сочетании с синтетической основой сохраняет мощностные параметры двигателя на протяжении всего интервала между заменами.
Особенно рекомендовано для турбодизельных двигателей с прямым впрыском. Разработано в соответствии с требованиями концерна VW.
Свойства продукта:
— Исключительная топливная экономичность за счет оптимальных антифрикционных свойств;
— Высокоэффективный пакет присадок и маловязкая синтетическая основа обеспечивают уверенный холодный пуск в любых условиях, благодаря чему значительно снижается пусковой износ двигателя;
— За счет превосходных моюще-диспергирующих свойств и высочайшей термоокислительной стабильности эффективно борется со всеми видами отложений и поддерживает в чистоте детали двигателя на протяжении всего интервала между заменами;
— Эстеровые компоненты масла обеспечивают отличные противоизносные свойства за счёт исключительной прочности масляной плёнки, что в сочетании с превосходной прокачиваемостью значительно увеличивает срок службы двигателя даже в режимах движения «Start-stop»;
— Совместимо со всеми системами нейтрализации отработавших газов, DPF, TWC, EGR и SCR за счет применения технологии Mid SAPS;
— Современный пакет присадок в сочетании с синтетической основой сохраняет мощностные параметры двигателя на протяжении всего интервала между заменами. Предназначено для дизельных и бензиновых двигателей легковых автомобилей, легких внедорожников, микроавтобусов и легких грузовиков, где требуется уровень эксплуатационных свойств API SN/CH-4 и ACEA C2/C3 данного класса вязкости.
Масло не предназначено для использования в тяжелых грузовиках и иной подобной технике!
Допуски: API SN/SM/CFИзготовитель:MANNOL В наличии на складе 10 974 ₽Артикул: 3038Трансмисионное масл MANNOL 8208 O.E.M. for Toyota Lexus ATF T-IV 20лF Type T-IV
ПродуктыТрансмиссионные масла и жидкостиСерия O.E.M.MANNOL O.E.M. ATF Type T-IV
MANNOL O.E.M. ATF Type T-IV 8208
Специальное трансмиссионное синтетическое масло (ATF) для автоматических коробок передач (АКПП) автомобилей TOYOTA/LEXUS c коробками TOYOTA и AISIN AW нового поколения. Обеспечивает бесперебойную работу АКПП, гарантирует минимальный износ, продолжительный срок службы трансмиссий и экономию топлива. Разработано на основании требований компании AISIN WARNER.
Свойства продукта:
— Синтетическая основа высочайшего качества со стабильно высоким индексом вязкости в комбинации с многофункциональным пакетом присадок сохраняет все свои свойства в широком диапазоне температур: обеспечивает хорошие смазочные свойства при низких (-45°C) температурах зимой и обеспечивает стабильную масляную плёнку при экстремальных нагрузках и температурах летом;
— Высокотехнологичная комбинация присадок обеспечивает хорошие антифрикционные свойства для зубчатых зацеплений и необходимые фрикционные свойства для фрикционных элементов, что обеспечивает существенную экономию топлива, плавное без рывков переключение передач и увеличение срока службы всех элементов трансмиссии.
Предназначено для дизельных и бензиновых двигателей легковых автомобилей, легких внедорожников, микроавтобусов и легких грузовиков, где требуется уровень эксплуатационных свойств API SN/CH-4 и ACEA C2/C3 данного класса вязкости.
Масло не предназначено для использования в тяжелых грузовиках и иной подобной технике!
Допуски: API SN/SM/CFИзготовитель:MANNOL В наличии на складе 10 974 ₽Артикул: 3038Трансмисионное масл MANNOL 8208 O.E.M. for Toyota Lexus ATF T-IV 20лF Type T-IV
ПродуктыТрансмиссионные масла и жидкостиСерия O.E.M.MANNOL O.E.M. ATF Type T-IV
MANNOL O.E.M. ATF Type T-IV 8208
Специальное трансмиссионное синтетическое масло (ATF) для автоматических коробок передач (АКПП) автомобилей TOYOTA/LEXUS c коробками TOYOTA и AISIN AW нового поколения. Обеспечивает бесперебойную работу АКПП, гарантирует минимальный износ, продолжительный срок службы трансмиссий и экономию топлива. Разработано на основании требований компании AISIN WARNER.
Свойства продукта:
— Синтетическая основа высочайшего качества со стабильно высоким индексом вязкости в комбинации с многофункциональным пакетом присадок сохраняет все свои свойства в широком диапазоне температур: обеспечивает хорошие смазочные свойства при низких (-45°C) температурах зимой и обеспечивает стабильную масляную плёнку при экстремальных нагрузках и температурах летом;
— Высокотехнологичная комбинация присадок обеспечивает хорошие антифрикционные свойства для зубчатых зацеплений и необходимые фрикционные свойства для фрикционных элементов, что обеспечивает существенную экономию топлива, плавное без рывков переключение передач и увеличение срока службы всех элементов трансмиссии.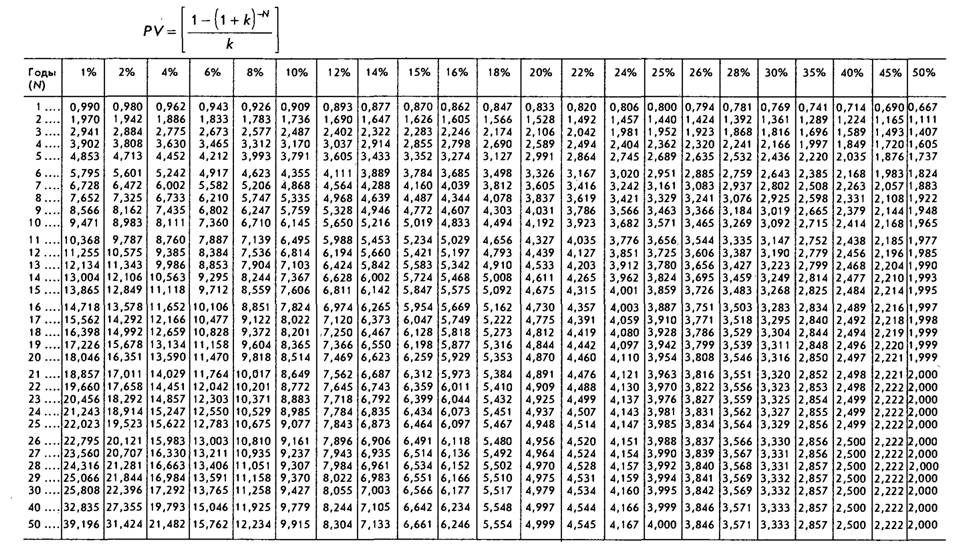 Обеспечивает слаженную и плавную работу сцеплений;
— Обладает повышенной термоокислительной и химической стабильностью и стойкостью к высокотемпературной термической деградации на протяжении всего срока эксплуатации. Это позволяет снизить образование шлама, лака, нагара и других углеродистых отложений, увеличить интервал замены масла и обеспечить долговечность деталей трансмиссии, что снижает затраты на обслуживание техники;
— Защищает от коррозии металлические детали из черных и цветных сплавов как в процессе работы, так и в нерабочем состоянии;
— Эффективно противостоит аэрации и пенообразованию;
— Обеспечивает совместимость со всеми материалами уплотнений, предотвращает их разбухание, затвердевание и усадку, что позволяет снизить затраты на запчасти и предотвращает утечки;
— Снижает шум.
Рекомендуется для АКПП Toyota и Aisin AW где требуется соответствие требованиям TOYOTA TYPE-IV. Может заменять жидкости T, T-II T-III.Изготовитель:MANNOL В наличии на складе 9 263 ₽Артикул: 1934Масло компрессорное MANNOL Compressor Oil ISO 100 20лДопуски: DIN 51 506 VBL, VCL & VDL
ISO 100
ISO L DAA, DAB, DAG & DAHИзготовитель:MANNOL В наличии на складе 9 188 ₽Артикул: 1382Трансмисионное масло MANNOL 8103 Extra Getriebeoel 75W-90 20лДопуски: SAE 75W-90 API GL 4/GL 5 LS MAN 342 Type M1/M2/M3 MACK GO-J/GO-J PlusSCANIA STO 1:0
Универсальное энергосберегающее всесезонное синтетическое трансмиссионное масло последнего поколения для всех типов механических коробок передач.
Обеспечивает слаженную и плавную работу сцеплений;
— Обладает повышенной термоокислительной и химической стабильностью и стойкостью к высокотемпературной термической деградации на протяжении всего срока эксплуатации. Это позволяет снизить образование шлама, лака, нагара и других углеродистых отложений, увеличить интервал замены масла и обеспечить долговечность деталей трансмиссии, что снижает затраты на обслуживание техники;
— Защищает от коррозии металлические детали из черных и цветных сплавов как в процессе работы, так и в нерабочем состоянии;
— Эффективно противостоит аэрации и пенообразованию;
— Обеспечивает совместимость со всеми материалами уплотнений, предотвращает их разбухание, затвердевание и усадку, что позволяет снизить затраты на запчасти и предотвращает утечки;
— Снижает шум.
Рекомендуется для АКПП Toyota и Aisin AW где требуется соответствие требованиям TOYOTA TYPE-IV. Может заменять жидкости T, T-II T-III.Изготовитель:MANNOL В наличии на складе 9 263 ₽Артикул: 1934Масло компрессорное MANNOL Compressor Oil ISO 100 20лДопуски: DIN 51 506 VBL, VCL & VDL
ISO 100
ISO L DAA, DAB, DAG & DAHИзготовитель:MANNOL В наличии на складе 9 188 ₽Артикул: 1382Трансмисионное масло MANNOL 8103 Extra Getriebeoel 75W-90 20лДопуски: SAE 75W-90 API GL 4/GL 5 LS MAN 342 Type M1/M2/M3 MACK GO-J/GO-J PlusSCANIA STO 1:0
Универсальное энергосберегающее всесезонное синтетическое трансмиссионное масло последнего поколения для всех типов механических коробок передач. Рекомендуется для использования во всех типах синхронизированных механических коробок передач (включая тяжелые), в дифференциалах (включая LS с избыточным трением), в рулевом оборудовании и других деталях трансмиссии, где встречаются чрезмерное давление и ударная нагрузка и в которых использование Стандарты GL-4 и / или GL-5 предписаны.Изготовитель:MANNOL В наличии на складе 11 388 ₽Артикул: 3074Трансмисионное масло MANNOL 8219 O.E.M. ATF SP-IV 20лACURA DW-1, тип ATF 3.0, тип ATF 3.1
BENTLEY PY112995PA
BMW 83 22 0 142 516, 83 22 0 397 114, 83 22 2 152 426,
CHRYSLER 05127382AA, 68043742AA, 68157995AA
DODGE 05127382AA, 68043742AA, 68157995AA
FORD XT-10-QLVC, XT-6-QSP, XT-6-DSP
HONDA DW-1, тип ATF 3.0, тип ATF 3.1
HYUNDAI NWS-9638 T-5, SP-IV, SPH-IV, SP-IV-RR
INFINITI Matic S, Matic W
JAGUAR Fluid 8432
JEEP 05127382AA, 68043742AA, 68157995AA
KIA NWS-9638 T-5, SP-IV, SPH-IV, SP-IV-RR
LAND ROVER TYK500050, LR0022460
LEXUS Scion FZ, тип WS, JWS 3324
LINCOLN XT-10-QLVC, XT-6-QSP, XT-6-DSP
MASERATI 231603
MAZDA FZ, FW 6A EL, FW 6AX EL
MB 236,12, 236,14, 236,15, 236,41
MERCURY XT-10-QLVC, XT-6-QSP, XT-6-DSP
MINI 83 22 0 142 516, 83 22 0 397 114, 83 22 2 152 426,
MITSUBISHI ATF-J3, Dia Queen ATF-PA
NISSAN Matic S / W
OPEL GM SATURN GMC AW1 / VI, GM SATURN GMC 88863400, GM SA
ПОРШЕ 000 043 304 00
SAAB 93 165 147 AW-1
TOYOTA Scion FZ, тип WS, JWS 3324
ZF Lifeguardfluid 6/8Изготовитель:MANNOL В наличии на складе 11 612 ₽0Избранное
Рекомендуется для использования во всех типах синхронизированных механических коробок передач (включая тяжелые), в дифференциалах (включая LS с избыточным трением), в рулевом оборудовании и других деталях трансмиссии, где встречаются чрезмерное давление и ударная нагрузка и в которых использование Стандарты GL-4 и / или GL-5 предписаны.Изготовитель:MANNOL В наличии на складе 11 388 ₽Артикул: 3074Трансмисионное масло MANNOL 8219 O.E.M. ATF SP-IV 20лACURA DW-1, тип ATF 3.0, тип ATF 3.1
BENTLEY PY112995PA
BMW 83 22 0 142 516, 83 22 0 397 114, 83 22 2 152 426,
CHRYSLER 05127382AA, 68043742AA, 68157995AA
DODGE 05127382AA, 68043742AA, 68157995AA
FORD XT-10-QLVC, XT-6-QSP, XT-6-DSP
HONDA DW-1, тип ATF 3.0, тип ATF 3.1
HYUNDAI NWS-9638 T-5, SP-IV, SPH-IV, SP-IV-RR
INFINITI Matic S, Matic W
JAGUAR Fluid 8432
JEEP 05127382AA, 68043742AA, 68157995AA
KIA NWS-9638 T-5, SP-IV, SPH-IV, SP-IV-RR
LAND ROVER TYK500050, LR0022460
LEXUS Scion FZ, тип WS, JWS 3324
LINCOLN XT-10-QLVC, XT-6-QSP, XT-6-DSP
MASERATI 231603
MAZDA FZ, FW 6A EL, FW 6AX EL
MB 236,12, 236,14, 236,15, 236,41
MERCURY XT-10-QLVC, XT-6-QSP, XT-6-DSP
MINI 83 22 0 142 516, 83 22 0 397 114, 83 22 2 152 426,
MITSUBISHI ATF-J3, Dia Queen ATF-PA
NISSAN Matic S / W
OPEL GM SATURN GMC AW1 / VI, GM SATURN GMC 88863400, GM SA
ПОРШЕ 000 043 304 00
SAAB 93 165 147 AW-1
TOYOTA Scion FZ, тип WS, JWS 3324
ZF Lifeguardfluid 6/8Изготовитель:MANNOL В наличии на складе 11 612 ₽0Избранное При использовании данного сайта вы даете свое согласие на использование cookie-файлов.
При использовании данного сайта вы даете свое согласие на использование cookie-файлов.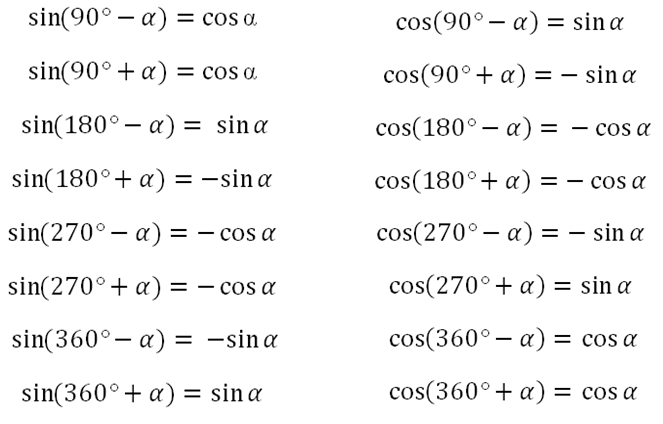 )/3
)/3 Рабочая тетрадь для чайников с онлайн-практикой Explore Book Купить на Amazon.
Рабочая тетрадь для чайников с онлайн-практикой Explore Book Купить на Amazon. 0, 5.0), в формат величина/угол.
0, 5.0), в формат величина/угол.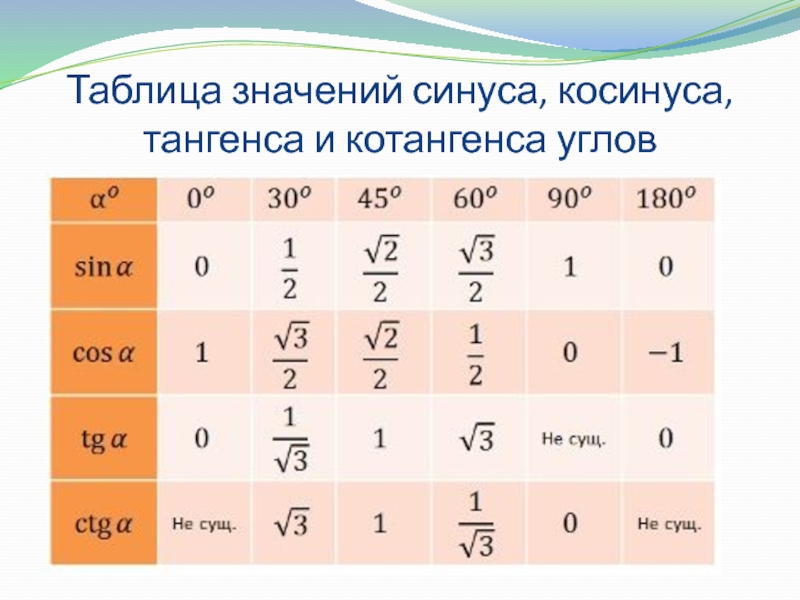
 1. Смотритель выпросил отпуск (1) и (2)не сказав никому ни слова о своём намерени.. пешком(3) отправ..лся за своей дочерью. 2. Подр..стая (4)ребёнок сам читает стихи о зелёном дубе (5) выр..сш..м у лукоморья. 9. Укажите предложение, в котором допущена грамматическая ошибка. 1) Это рассказ о человеке, возвратившемся после войны в родной город. 2) Приготовленные мамой оладьи были необыкновенно вкусны. 3) Изображая любой предмет, художник передает его собственное мироощущение. 4) Пользуясь автомобильными справочниками, требуется много времени на ремонт машины. 10. В каком ряду все предлоги пишутся слитно? 1) (на)подобие пирамиды, (из)под сугроба, (от)лени 2) (во)преки желанию, (в)следствие урагана, (на)встречу мечте 3) (ко)мне, (под)ле скамейки, (из)под стола 4) (в)течение занятия, (в)продолжение триместра (не)смотря на угрозы 11. Укажите правильный вариант объяснения написания выделенного слова (выделенных слов) в предложении «Мы чувствовали, что отцу не хочется разговаривать. Инна (то)же молчала».
1. Смотритель выпросил отпуск (1) и (2)не сказав никому ни слова о своём намерени.. пешком(3) отправ..лся за своей дочерью. 2. Подр..стая (4)ребёнок сам читает стихи о зелёном дубе (5) выр..сш..м у лукоморья. 9. Укажите предложение, в котором допущена грамматическая ошибка. 1) Это рассказ о человеке, возвратившемся после войны в родной город. 2) Приготовленные мамой оладьи были необыкновенно вкусны. 3) Изображая любой предмет, художник передает его собственное мироощущение. 4) Пользуясь автомобильными справочниками, требуется много времени на ремонт машины. 10. В каком ряду все предлоги пишутся слитно? 1) (на)подобие пирамиды, (из)под сугроба, (от)лени 2) (во)преки желанию, (в)следствие урагана, (на)встречу мечте 3) (ко)мне, (под)ле скамейки, (из)под стола 4) (в)течение занятия, (в)продолжение триместра (не)смотря на угрозы 11. Укажите правильный вариант объяснения написания выделенного слова (выделенных слов) в предложении «Мы чувствовали, что отцу не хочется разговаривать. Инна (то)же молчала». 1) тоже — всегда пишется слитно; 2) то же — всегда пишется раздельно; 3) тоже — здесь сочинительный союз, поэтому пишется слитно; 4) то же — здесь местоимение то с частицей же, поэтому пишется раздельн 12. Укажите предложение, в котором частица пишется через дефис. 1) Всё те(же) мы, но время уже не то. 2) На безлюдной барже не слишком(то) уютно. 3) Всё вроде(бы) отлично и здорово.
1) тоже — всегда пишется слитно; 2) то же — всегда пишется раздельно; 3) тоже — здесь сочинительный союз, поэтому пишется слитно; 4) то же — здесь местоимение то с частицей же, поэтому пишется раздельн 12. Укажите предложение, в котором частица пишется через дефис. 1) Всё те(же) мы, но время уже не то. 2) На безлюдной барже не слишком(то) уютно. 3) Всё вроде(бы) отлично и здорово. Прохожий случайно задел её и тележка сдвинулась с места. Получается, что прохожий применил силу к тележке и вызвал её движение;
Прохожий случайно задел её и тележка сдвинулась с места. Получается, что прохожий применил силу к тележке и вызвал её движение;

 Он читал 12 страниц в час. Чтению в первый день он посвятил 4 часа, поэтому для нахождения количества прочитанных страниц в первый день, нужно 12 умножить на 4
Он читал 12 страниц в час. Чтению в первый день он посвятил 4 часа, поэтому для нахождения количества прочитанных страниц в первый день, нужно 12 умножить на 4 Определить какой из насосов выкачал больше вёдер.
Определить какой из насосов выкачал больше вёдер. Выполненная работа равна производительности умноженной на время работы:
Выполненная работа равна производительности умноженной на время работы: Производительность была равна двум, поскольку по определению производительность есть работа, выполненная за единицу времени – в нашем случае два этажа за неделю.
Производительность была равна двум, поскольку по определению производительность есть работа, выполненная за единицу времени – в нашем случае два этажа за неделю. Принтер работал с производительностью 70 страниц в час и напечатал 350 страниц. Определить время работы принтера.
Принтер работал с производительностью 70 страниц в час и напечатал 350 страниц. Определить время работы принтера.


 Первый мастер может покрасить забор за 20 минут, а второй мастер – за 30 минут. За сколько минут, работая вместе, они могут покрасить забор?
Первый мастер может покрасить забор за 20 минут, а второй мастер – за 30 минут. За сколько минут, работая вместе, они могут покрасить забор? Для этого сложим дроби, выражающие производительность первого и второго мастеров:
Для этого сложим дроби, выражающие производительность первого и второго мастеров: Чтобы определить время за которое он завершил оставшуюся часть работы, воспользуемся формулой нахождения времени.
Чтобы определить время за которое он завершил оставшуюся часть работы, воспользуемся формулой нахождения времени. × 0,4 = 24 мин.
× 0,4 = 24 мин. Обозначим её через единицу:
Обозначим её через единицу: Вода, которая вытекает равна части сосуда, поскольку в условии сказано, что полный сосуд опорожняется за 20 минут.
Вода, которая вытекает равна части сосуда, поскольку в условии сказано, что полный сосуд опорожняется за 20 минут. Обозначим эту работу через единицу:
Обозначим эту работу через единицу: На работу требовалось затратить 10 ч. Проработано было 8 ч. Значит осталось еще 2 часа. На 2 часа приходятся оставшиеся 50 метров траншеи. Если разделить 50 метров на 2, то можно определить сколько метров экскаватор прокладывает за один час:
На работу требовалось затратить 10 ч. Проработано было 8 ч. Значит осталось еще 2 часа. На 2 часа приходятся оставшиеся 50 метров траншеи. Если разделить 50 метров на 2, то можно определить сколько метров экскаватор прокладывает за один час: Совместная производительность обоих кранов равна сумме дробей и
Совместная производительность обоих кранов равна сумме дробей и ..
.. Сколько времени ему понадобится, чтобы напечатать 87 страниц?
Сколько времени ему понадобится, чтобы напечатать 87 страниц? »
» Однако, если контент должен включать в себя подробные исследования, ссылки, цитаты или графику, например, для статьи в блоге или школьного эссе, продолжительность может увеличиться до 1,7 часа.
Однако, если контент должен включать в себя подробные исследования, ссылки, цитаты или графику, например, для статьи в блоге или школьного эссе, продолжительность может увеличиться до 1,7 часа.  Если вы хотите узнать, сколько времени займет написание эссе или книги, ознакомьтесь с таблицей ниже:
Если вы хотите узнать, сколько времени займет написание эссе или книги, ознакомьтесь с таблицей ниже: 0 minutes
0 minutes Если вы хотите узнать, сколько времени займет написание эссе или книги, ознакомьтесь с таблицей ниже:
Если вы хотите узнать, сколько времени займет написание эссе или книги, ознакомьтесь с таблицей ниже: