Таблица знаков в геометрии и их значения: пересечение, подобие
Sign in
Password recovery
Восстановите свой пароль
Ваш адрес электронной почты
MicroExcel.ru Математика Знаки и символы в геометрии
Ниже представлена таблица с основными математическими символами и знаками, которые используются в геометрии с 7 класса и старше.
| Знак | Название | Значение/описание | Пример |
| ∠ | угол | фигура, состоящая из двух лучей и вершины | ∠ABC = 30° |
| ru/wp-content/uploads/2020/01/ostr-ugol.png" class="stbSkipLazy aligncenter size-full" width="40" height="40" data-full="https://microexcel.ru/wp-content/uploads/2020/01/ostr-ugol.png" />» data-order=»<img src="https://microexcel.ru/wp-content/uploads/2020/01/ostr-ugol.png" class="stbSkipLazy aligncenter size-full" width="40" height="40" data-full="https://microexcel.ru/wp-content/uploads/2020/01/ostr-ugol.png" />»> | острый угол | угол от 0 до 90 градусов | ∠AOB = 60° |
| ru/wp-content/uploads/2020/01/pryamoy-ugol.png" class="stbSkipLazy aligncenter size-full" width="40" height="40" data-full="https://microexcel.ru/wp-content/uploads/2020/01/pryamoy-ugol.png" />» data-order=»<img src="https://microexcel.ru/wp-content/uploads/2020/01/pryamoy-ugol.png" class="stbSkipLazy aligncenter size-full" width="40" height="40" data-full="https://microexcel.ru/wp-content/uploads/2020/01/pryamoy-ugol.png" />»> | прямой угол | угол, равный 90 граусам | ∠AOB = 90° |
| ru/wp-content/uploads/2020/01/tupoy-ugol.png" class="stbSkipLazy aligncenter size-full" width="40" height="40" data-full="https://microexcel.ru/wp-content/uploads/2020/01/tupoy-ugol.png" />» data-order=»<img src="https://microexcel.ru/wp-content/uploads/2020/01/tupoy-ugol.png" class="stbSkipLazy aligncenter size-full" width="40" height="40" data-full="https://microexcel.ru/wp-content/uploads/2020/01/tupoy-ugol.png" />»> | тупой угол | угол от 90 до 180 градусов | ∠AOB = 120° |
| ru/wp-content/uploads/2020/01/razvernuty-ugol-1.png" class="stbSkipLazy aligncenter size-full" width="80" height="240" data-full="https://microexcel.ru/wp-content/uploads/2020/01/razvernuty-ugol-1.png" />» data-order=»<img src="https://microexcel.ru/wp-content/uploads/2020/01/razvernuty-ugol-1.png" class="stbSkipLazy aligncenter size-full" width="80" height="240" data-full="https://microexcel.ru/wp-content/uploads/2020/01/razvernuty-ugol-1.png" />»> | развернутый угол | угол, равный 180 градусам | ∠AOB = 180° |
| ° (или deg) | градус | единица измерения угла, равна 1/360 окружности | 45° |
| ′ | минута | единица измерения угла, 1° = 60′ | α = 70°59′ |
| ″ | секунда | единица измерения угла, 1′ = 60″ | α = 70°59′59″ |
| ru/wp-content/uploads/2020/01/line-exc.png" class="stbSkipLazy aligncenter size-full" width="30" height="30" data-full="https://microexcel.ru/wp-content/uploads/2020/01/line-exc.png" />» data-order=»<img src="https://microexcel.ru/wp-content/uploads/2020/01/line-exc.png" class="stbSkipLazy aligncenter size-full" width="30" height="30" data-full="https://microexcel.ru/wp-content/uploads/2020/01/line-exc.png" />»> | линия | бесконечная прямая без начала и конца | |
| ru/wp-content/uploads/2020/01/line-segment-exc.png" class="stbSkipLazy aligncenter size-full" width="30" height="30" data-full="https://microexcel.ru/wp-content/uploads/2020/01/line-segment-exc.png" />» data-order=»<img src="https://microexcel.ru/wp-content/uploads/2020/01/line-segment-exc.png" class="stbSkipLazy aligncenter size-full" width="30" height="30" data-full="https://microexcel.ru/wp-content/uploads/2020/01/line-segment-exc.png" />»> | отрезок | участок на прямой между точками A и B | |
| ru/wp-content/uploads/2020/01/ray-exc.png" class="stbSkipLazy aligncenter size-full" width="35" height="35" data-full="https://microexcel.ru/wp-content/uploads/2020/01/ray-exc.png" />» data-order=»<img src="https://microexcel.ru/wp-content/uploads/2020/01/ray-exc.png" class="stbSkipLazy aligncenter size-full" width="35" height="35" data-full="https://microexcel.ru/wp-content/uploads/2020/01/ray-exc.png" />»> | луч | бесконечная прямая, имеющая начало в точке A, но не имеющая конца | |
| ru/wp-content/uploads/2020/01/arc-exc.png" class="stbSkipLazy aligncenter size-full" width="30" height="30" data-full="https://microexcel.ru/wp-content/uploads/2020/01/arc-exc.png" />» data-order=»<img src="https://microexcel.ru/wp-content/uploads/2020/01/arc-exc.png" class="stbSkipLazy aligncenter size-full" width="30" height="30" data-full="https://microexcel.ru/wp-content/uploads/2020/01/arc-exc.png" />»> | дуга | дуга, образованная между точками A и B | |
| ⊥ | перпендикулярность | линии (прямые), расположенные под углом 90° по отношению друг к другу | AC ⊥ BC |
| || | параллельность | непересекающиеся прямые (линии) | AB || CD |
| ∩ | пересечение | множество одинаковых элементов, принадлежащих как множеству A, так и B | A ∩ B |
| ∈ / ∉ | принадлежность/ непринадлежность | элемент является/не является элементом заданного множества | a ∈ S |
| ≅ | конгуэнтность | эквивалентность геометрических форм и размеров | ∆ABC ≅ ∆XYZ |
| ~ | подобие | та же форма, но разные размеры | ∆ABC ~ ∆XYZ |
| Δ | треугольник | фигура треугольника | ΔABC ≅ ΔBCD |
| |x-y| | дистанция | дистанция между точками X и Y | | x-y | = 5 |
| π | константа «Пи» | отношение длины окружности к диаметру круга, π = C/d | 141592654…</nobr>» data-order=»<nobr>π = 3.141592654…</nobr>»>π = 3.141592654… |
| рад (rad) или c | радиан | единица измерения угла | 360° = 2π c |
microexcel.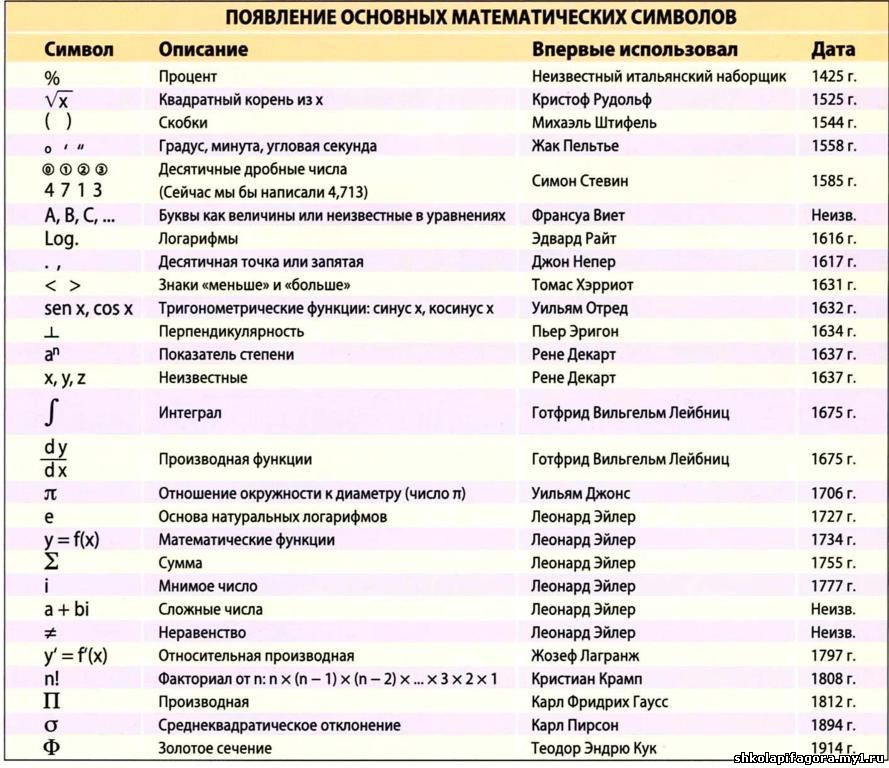 ru
ru
ЧАЩЕ ВСЕГО ЗАПРАШИВАЮТ
Таблица знаков зодиака
Нахождение площади трапеции: формула и примеры
Нахождение длины окружности: формула и задачи
Римские цифры: таблицы
Таблица синусов
Тригонометрическая функция: Тангенс угла (tg)
Нахождение площади ромба: формула и примеры
Нахождение объема цилиндра: формула и задачи
Тригонометрическая функция: Синус угла (sin)
Геометрическая фигура: треугольник
Нахождение объема шара: формула и задачи
Тригонометрическая функция: Косинус угла (cos)
Нахождение объема конуса: формула и задачи
Таблица сложения чисел
Нахождение площади квадрата: формула и примеры
Что такое тетраэдр: определение, виды, формулы площади и объема
Нахождение объема пирамиды: формула и задачи
Признаки подобия треугольников
Нахождение периметра прямоугольника: формула и задачи
Формула Герона для треугольника
Что такое средняя линия треугольника
Нахождение площади треугольника: формула и примеры
Нахождение площади поверхности конуса: формула и задачи
Что такое прямоугольник: определение, свойства, признаки, формулы
Разность кубов: формула и примеры
Степени натуральных чисел
Нахождение площади правильного шестиугольника: формула и примеры
Тригонометрические значения углов: sin, cos, tg, ctg
Нахождение периметра квадрата: формула и задачи
Теорема Фалеса: формулировка и пример решения задачи
Сумма кубов: формула и примеры
Нахождение объема куба: формула и задачи
Куб разности: формула и примеры
Нахождение площади шарового сегмента
Что такое окружность: определение, свойства, формулы
Что означает знак дуги в геометрии – как обозначается дуга в геометрии
Что такое геометрия дуга
Дуга (геометрия) — это… Что такое Дуга (геометрия)?
Дуга — связное подмножество окружности.
Свойства
*Длина дуги L радиуса R с центральным углом alpha, измеренным в радианах, вычисляется по формуле: L=Ralpha
Wikimedia Foundation. 2010.
- WASD Улица Воздвиженка
Смотреть что такое «Дуга (геометрия)» в других словарях:
Дуга — Дуга: В математике Дуга (геометрия) участок кривой между двумя её точками. Дуга окружности кривая линия, лежащая на окружности и ограниченная двумя точками. Дуга (теория графов) Другое Дуга (география) Дуга (анатомия) Дуга (физика) Дуга… … Википедия
Геометрия — (γήμετρώ земля, μετρώ мерю). Понятия о пространстве, положении и форме принадлежат к числу первоначальных, с которыми человек был знаком уже в глубокой древности. Первые шаги в Г. были сделаны египтянами и халдеями. В Греции Г. была введена… … Энциклопедический словарь Ф. А. Брокгауза и И. А. Ефрона
АФФИННАЯ ДИФФЕРЕНЦИАЛЬНАЯ ГЕОМЕТРИЯ — раздел геометрии, изучающий дифференциально геометрич. свойства кривых и поверхностей, сохраняющиеся при преобразованиях аффинной группы или ее подгрупп. Наиболее полно изучена дифференциальная геометрия эквиаффинного пространства. В эквиаффинной … Математическая энциклопедия
свойства кривых и поверхностей, сохраняющиеся при преобразованиях аффинной группы или ее подгрупп. Наиболее полно изучена дифференциальная геометрия эквиаффинного пространства. В эквиаффинной … Математическая энциклопедия
РИМАНОВА ГЕОМЕТРИЯ — теория риманова пространства. Р и м а н о в ы м п р о с т р а н с т в о м наз. n мерное связное дифференцируемое многообразие М п, на к ром задано дифференцируемое поле ковариантного, симметрического и положительно определенного тензора gранга 2 … Математическая энциклопедия
Сферическая геометрия — математическая дисциплина, изучающая геометрические образы, находящиеся на сфере, подобно тому как планиметрия изучает геометрические образы, находящиеся на плоскости. Всякая плоскость, пересекающая сферу, даёт в сечении… … Большая советская энциклопедия
Хорда (геометрия) — У этого термина существуют и другие значения, см. Хорда. 1 секущая, 2 хорда … Википедия
СФЕРИЧЕСКАЯ ГЕОМЕТРИЯ — математич. дисциплина, изучающая геометрич. образы, находящиеся на сфере, подобно тому как планиметрия изучает геометрич. образы, находящиеся на плоскости. Всякая плоскость, пересекающая сферу, дает в сечении нек рую окружность; если секущая… … Математическая энциклопедия
дисциплина, изучающая геометрич. образы, находящиеся на сфере, подобно тому как планиметрия изучает геометрич. образы, находящиеся на плоскости. Всякая плоскость, пересекающая сферу, дает в сечении нек рую окружность; если секущая… … Математическая энциклопедия
ГЕОДЕЗИЧЕСКАЯ ЛИНИЯ — геодезиче ская, геометрическое понятие, обобщающее понятие прямой (или отрезка прямой) евклидовой геометрии на случай пространств более общего вида. Определения Г. л. в различных пространствах зависят от того, какая из структур (метрика, линейный … Математическая энциклопедия
Декарт Рене — (Descartes) (латинизир. Картезий; Cartesius) (1596 1650), французский философ, математик, физик и физиолог. С 1629 в Нидерландах. Заложил основы аналитической геометрии, дал понятия переменной величины и функции, ввёл многие алгебраические… … Энциклопедический словарь
Жорданова кривая — Кривая или линия геометрическое понятие, определяемое в разных разделах геометрии различно. Содержание 1 Элементарная геометрия 2 Параметрические определения 3 Кривая Жордана … Википедия
Содержание 1 Элементарная геометрия 2 Параметрические определения 3 Кривая Жордана … Википедия
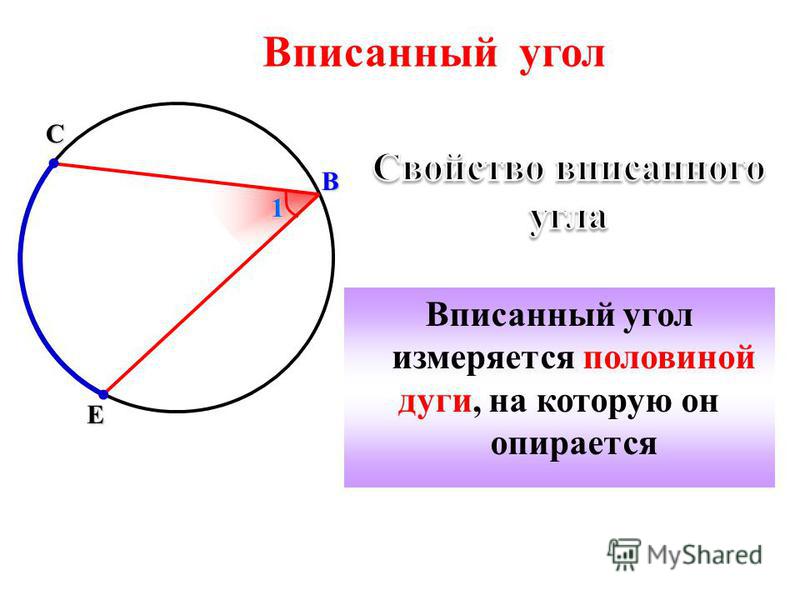
Дуга окружности. Полуокружность определение. Длина дуги окружности. Угол и дуга окружности
Дуга окружности
Что такое дуга окружности?
Дугу окружности принято обозначать тремя точками: две точки – это концы дуги и одна произвольная промежуточная точка. Пример дуги:
На картинке представлены две дуги: ACB и ADB.
Полуокружность определение
Полуокружностью называют дугу окружности, если отрезок, соединяющий её концы, в нашем случае AB, есть диаметр окружности.
На картинке ACB – полуокружность:
Градусная мера дуги окружности
Рассмотрим три случая.
Первый случай
Градусной мерой дуги ACB является градусная мера центрального угла AOB:
Второй случай
Градусной мерой дуги BED является градусная мера центрального угла BOD (на рисунке выше), в данном случае это 180 0 , т. е. развернутый угол.
Третий случай
Градусной мерой большей дуги окружности ACB рассчитывается по формуле: 360 градусов минус величина угла AOB. Пример: пусть угол AOB = 90 0 , тогда градусная мера дуги ACB равна 360 0 — 90 0 = 270 0 .
Пример: пусть угол AOB = 90 0 , тогда градусная мера дуги ACB равна 360 0 — 90 0 = 270 0 .
А чему равна сумма градусных мер дуг ADB и ACB?
Градусная мера дуги ADB равна 90 0 по условию.
Сумма градусных мер дуг ADB и ACB равна 90 0 + 270 0 = 360 0 .
Это и понятно, ведь эти две дуги охватывают всю окружность, а окружности соответсвуют 360 0 .
Каким условным знаком обозначается дуга окружности?
0 нравится комментировать 10 лет Ответы Mail. Ru Образование ВУЗы, Колледжи Все вопросы
Авто, Мото Автострахование Выбор автомобиля, мотоцикла Оформление авто-мото сделок ГИБДД, Обучение, Права Сервис, Обслуживание, Тюнинг ПДД, Вождение Прочие Авто-темы Автоспорт Бизнес, Финансы Макроэкономика Производственные предприятия Собственный бизнес Страхование Банки и Кредиты Недвижимость, Ипотека Бухгалтерия, Аудит, Налоги Остальные сферы бизнеса Долги, Коллекторы Знакомства, Любовь, Отношения Любовь Знакомства Отношения Расставания Дружба Прочие взаимоотношения Компьютеры, Связь Интернет Железо Программное обеспечение Прочее компьютерное Мобильные устройства Офисная техника Мобильная связь Образование Детские сады Школы ВУЗы, Колледжи Дополнительное образование Образование за рубежом Прочее образование Философия, Непознанное Мистика, Эзотерика Психология Религия, Вера Прочее непознанное Философия Путешествия, Туризм Самостоятельный отдых Документы Отдых в России Отдых за рубежом Прочее туристическое Семья, Дом, Дети Строительство и Ремонт Беременность, Роды Воспитание детей Мебель, Интерьер Домашняя бухгалтерия Домоводство Загородная жизнь Свадьба, Венчание, Брак Организация быта Прочие дела домашние Спорт Футбол Хоккей Экстрим Другие виды спорта Занятия спортом События, результаты Спортсмены Зимние виды спорта Стиль, Мода, Звезды Мода Светская жизнь и Шоубизнес Прочие тенденции стиля жизни Стиль, Имидж Темы для взрослых Другое О проектах Mail.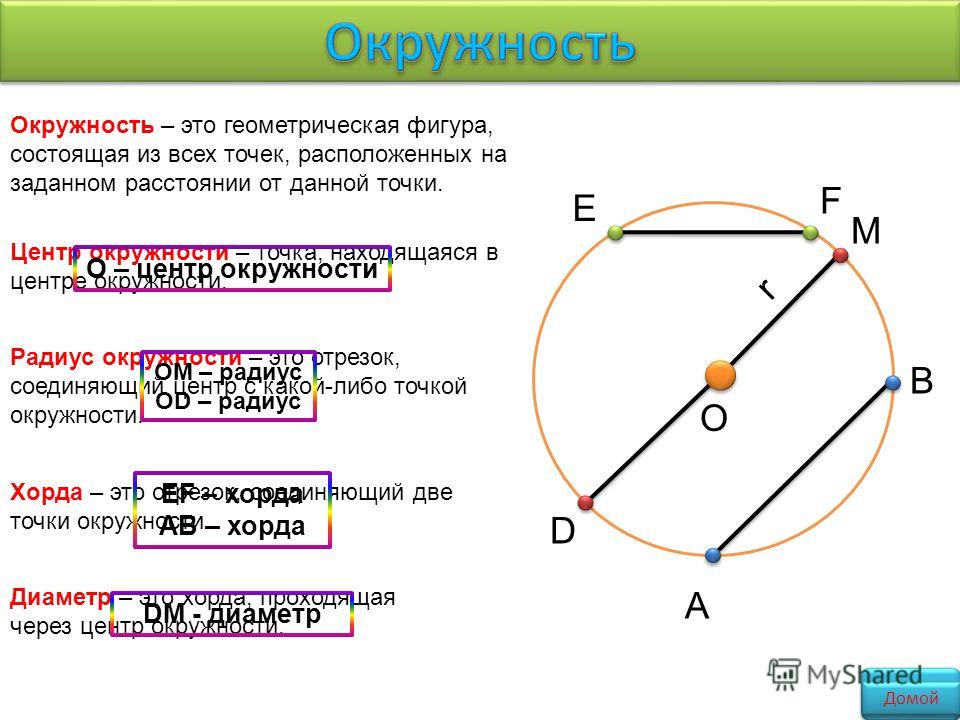 Ru Ответы Mail. ru Почта Mail. ru Прочие проекты Новости Mail. Ru Агент Mail. ru Мой Мир Mail. ru ICQ Облако Mail. ru Красота и Здоровье Коррекция веса Здоровый образ жизни Врачи, Клиники, Страхование Болезни, Лекарства Косметика, Парфюмерия Баня, Массаж, Фитнес Уход за волосами Маникюр, Педикюр Детское здоровье Салоны красоты и СПА Прочее о здоровье и красоте Животные, Растения Домашние животные Комнатные растения Сад-Огород Дикая природа Прочая живность Города и Страны Вокруг света Карты, Транспорт, GPS Климат, Погода, Часовые пояса Коды, Индексы, Адреса ПМЖ, Недвижимость Прочее о городах и странах Общество, Политика, СМИ Общество Политика Прочие социальные темы Средства массовой информации Еда, Кулинария Закуски и Салаты Первые блюда Вторые блюда Напитки Десерты, Сладости, Выпечка Консервирование Торжество, Праздник Готовим детям Готовим в … Покупка и выбор продуктов На скорую руку Прочее кулинарное Фотография, Видеосъемка Обработка и печать фото Обработка видеозаписей Выбор, покупка аппаратуры Уход за аппаратурой Техника, темы, жанры съемки Прочее фото-видео Товары и Услуги Идеи для подарков Техника для дома Прочие промтовары Сервис, уход и ремонт Прочие услуги Досуг, Развлечения Хобби Концерты, Выставки, Спектакли Охота и Рыбалка Клубы, Дискотеки Рестораны, Кафе, Бары Советы, Идеи Игры без компьютера Прочие развлечения Новый Год День Святого Валентина Восьмое марта Наука, Техника, Языки Гуманитарные науки Естественные науки Лингвистика Техника Работа, Карьера Написание резюме Подработка, временная работа Кадровые агентства Отдел кадров, HR Профессиональный рост Смена и поиск места работы Обстановка на работе Трудоустройство за рубежом Прочие карьерные вопросы Гороскопы, Магия, Гадания Гороскопы Гадания Сны Прочие предсказания Магия Юридическая консультация Административное право Гражданское право Конституционное право Семейное право Трудовое право Уголовное право Финансовое право Жилищное право Право социального обеспечения Военная служба Паспортный режим, регистрация Прочие юридические вопросы Юмор Золотой фонд Искусство и Культура Музыка Литература Кино, Театр Живопись, Графика Архитектура, Скульптура Прочие искусства Компьютерные и Видео игры Прочие Браузерные Клиентские Консольные Мобильные Программирование Другие языки и технологии Java JavaScript jQuery MySQL Perl PHP Python Веб-дизайн Верстка, CSS, HTML, SVG Системное администрирование Домашние задания Другие предметы Литература Математика Алгебра Геометрия Иностранные языки Химия Физика Биология История География Информатика Экономика Русский язык Обществознание Плесский колледж бизнеса и туризма Компания «Azimyt-K»
Ru Ответы Mail. ru Почта Mail. ru Прочие проекты Новости Mail. Ru Агент Mail. ru Мой Мир Mail. ru ICQ Облако Mail. ru Красота и Здоровье Коррекция веса Здоровый образ жизни Врачи, Клиники, Страхование Болезни, Лекарства Косметика, Парфюмерия Баня, Массаж, Фитнес Уход за волосами Маникюр, Педикюр Детское здоровье Салоны красоты и СПА Прочее о здоровье и красоте Животные, Растения Домашние животные Комнатные растения Сад-Огород Дикая природа Прочая живность Города и Страны Вокруг света Карты, Транспорт, GPS Климат, Погода, Часовые пояса Коды, Индексы, Адреса ПМЖ, Недвижимость Прочее о городах и странах Общество, Политика, СМИ Общество Политика Прочие социальные темы Средства массовой информации Еда, Кулинария Закуски и Салаты Первые блюда Вторые блюда Напитки Десерты, Сладости, Выпечка Консервирование Торжество, Праздник Готовим детям Готовим в … Покупка и выбор продуктов На скорую руку Прочее кулинарное Фотография, Видеосъемка Обработка и печать фото Обработка видеозаписей Выбор, покупка аппаратуры Уход за аппаратурой Техника, темы, жанры съемки Прочее фото-видео Товары и Услуги Идеи для подарков Техника для дома Прочие промтовары Сервис, уход и ремонт Прочие услуги Досуг, Развлечения Хобби Концерты, Выставки, Спектакли Охота и Рыбалка Клубы, Дискотеки Рестораны, Кафе, Бары Советы, Идеи Игры без компьютера Прочие развлечения Новый Год День Святого Валентина Восьмое марта Наука, Техника, Языки Гуманитарные науки Естественные науки Лингвистика Техника Работа, Карьера Написание резюме Подработка, временная работа Кадровые агентства Отдел кадров, HR Профессиональный рост Смена и поиск места работы Обстановка на работе Трудоустройство за рубежом Прочие карьерные вопросы Гороскопы, Магия, Гадания Гороскопы Гадания Сны Прочие предсказания Магия Юридическая консультация Административное право Гражданское право Конституционное право Семейное право Трудовое право Уголовное право Финансовое право Жилищное право Право социального обеспечения Военная служба Паспортный режим, регистрация Прочие юридические вопросы Юмор Золотой фонд Искусство и Культура Музыка Литература Кино, Театр Живопись, Графика Архитектура, Скульптура Прочие искусства Компьютерные и Видео игры Прочие Браузерные Клиентские Консольные Мобильные Программирование Другие языки и технологии Java JavaScript jQuery MySQL Perl PHP Python Веб-дизайн Верстка, CSS, HTML, SVG Системное администрирование Домашние задания Другие предметы Литература Математика Алгебра Геометрия Иностранные языки Химия Физика Биология История География Информатика Экономика Русский язык Обществознание Плесский колледж бизнеса и туризма Компания «Azimyt-K»
Mail.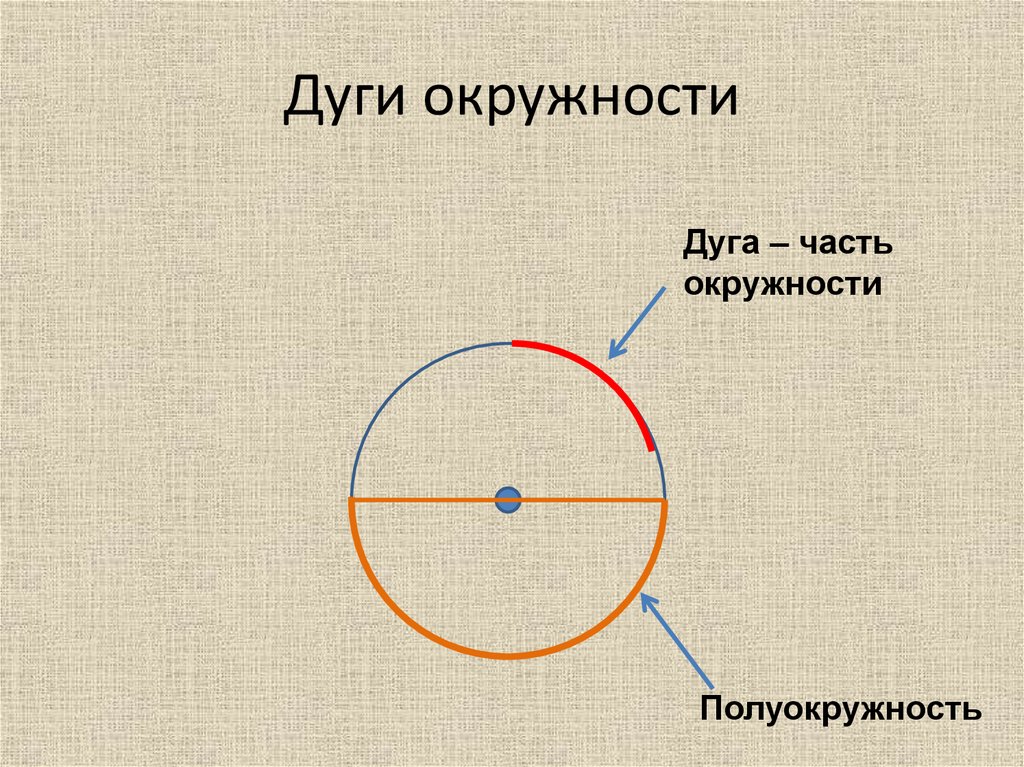 RuПочтаМой МирИгрыНовостиЗнакомстваПоискВсе проекты Вход в личный кабинет Помощь Обратная связь Полная версия Главная Все проекты
RuПочтаМой МирИгрыНовостиЗнакомстваПоискВсе проекты Вход в личный кабинет Помощь Обратная связь Полная версия Главная Все проекты
Дуга — связное подмножество окружности.
Свойства
*Длина дуги L радиуса R с центральным углом alpha, измеренным в радианах, вычисляется по формуле: L=Ralpha
Wikimedia Foundation. 2010.
- WASD Улица Воздвиженка
Смотреть что такое «Дуга (геометрия)» в других словарях:
Дуга — Дуга: В математике Дуга (геометрия) участок кривой между двумя её точками. Дуга окружности кривая линия, лежащая на окружности и ограниченная двумя точками. Дуга (теория графов) Другое Дуга (география) Дуга (анатомия) Дуга (физика) Дуга… … Википедия
Геометрия — (γήμετρώ земля, μετρώ мерю). Понятия о пространстве, положении и форме принадлежат к числу первоначальных, с которыми человек был знаком уже в глубокой древности. Первые шаги в Г. были сделаны египтянами и халдеями. В Греции Г. была введена… … Энциклопедический словарь Ф. А. Брокгауза и И. А. Ефрона
была введена… … Энциклопедический словарь Ф. А. Брокгауза и И. А. Ефрона
АФФИННАЯ ДИФФЕРЕНЦИАЛЬНАЯ ГЕОМЕТРИЯ — раздел геометрии, изучающий дифференциально геометрич. свойства кривых и поверхностей, сохраняющиеся при преобразованиях аффинной группы или ее подгрупп. Наиболее полно изучена дифференциальная геометрия эквиаффинного пространства. В эквиаффинной … Математическая энциклопедия
РИМАНОВА ГЕОМЕТРИЯ — теория риманова пространства. Р и м а н о в ы м п р о с т р а н с т в о м наз. n мерное связное дифференцируемое многообразие М п, на к ром задано дифференцируемое поле ковариантного, симметрического и положительно определенного тензора gранга 2 … Математическая энциклопедия
Сферическая геометрия — математическая дисциплина, изучающая геометрические образы, находящиеся на сфере, подобно тому как планиметрия изучает геометрические образы, находящиеся на плоскости. Всякая плоскость, пересекающая сферу, даёт в сечении… … Большая советская энциклопедия
Хорда (геометрия) — У этого термина существуют и другие значения, см. Хорда. 1 секущая, 2 хорда … Википедия
Хорда. 1 секущая, 2 хорда … Википедия
СФЕРИЧЕСКАЯ ГЕОМЕТРИЯ — математич. дисциплина, изучающая геометрич. образы, находящиеся на сфере, подобно тому как планиметрия изучает геометрич. образы, находящиеся на плоскости. Всякая плоскость, пересекающая сферу, дает в сечении нек рую окружность; если секущая… … Математическая энциклопедия
ГЕОДЕЗИЧЕСКАЯ ЛИНИЯ — геодезиче ская, геометрическое понятие, обобщающее понятие прямой (или отрезка прямой) евклидовой геометрии на случай пространств более общего вида. Определения Г. л. в различных пространствах зависят от того, какая из структур (метрика, линейный … Математическая энциклопедия
Декарт Рене — (Descartes) (латинизир. Картезий; Cartesius) (1596 1650), французский философ, математик, физик и физиолог. С 1629 в Нидерландах. Заложил основы аналитической геометрии, дал понятия переменной величины и функции, ввёл многие алгебраические… … Энциклопедический словарь
Жорданова кривая — Кривая или линия геометрическое понятие, определяемое в разных разделах геометрии различно.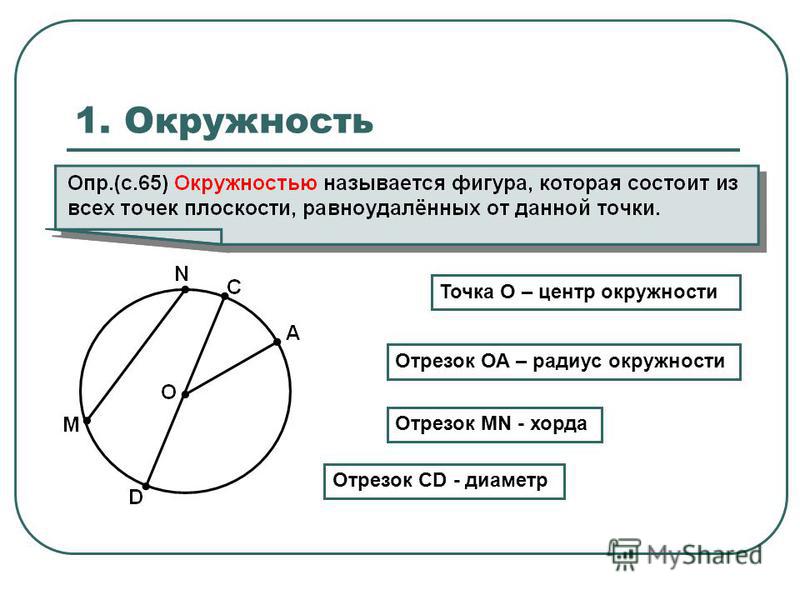
Полуокружностью называют дугу окружности, если отрезок, соединяющий её концы, в нашем случае AB, есть диаметр окружности.
Xn—-8sbanwvcjzh9e. xn--p1ai
14.02.2019 20:13:03
2019-02-14 20:13:03
Источники:
Https://xn—-8sbanwvcjzh9e. xn--p1ai/geometrii/chto-oznachaet-znak-dugi-v-geometrii-kak-oboznachaetsya-duga-v-geometrii. html
Окружность: радиус, хорда, диаметр и дуга | Геометрия » /> » /> .keyword { color: red; }
Что такое геометрия дуга
Окружность — это геометрическая фигура, образованная замкнутой кривой линией, все точки которой одинаково удалены от одной и той же точки.
Точка, от которой одинаково удалены все точки окружности, называется Центром окружности. Центр окружности обычно обозначают большой латинской буквой O:
Окружность делит плоскость на две области — Внутреннюю и внешнюю.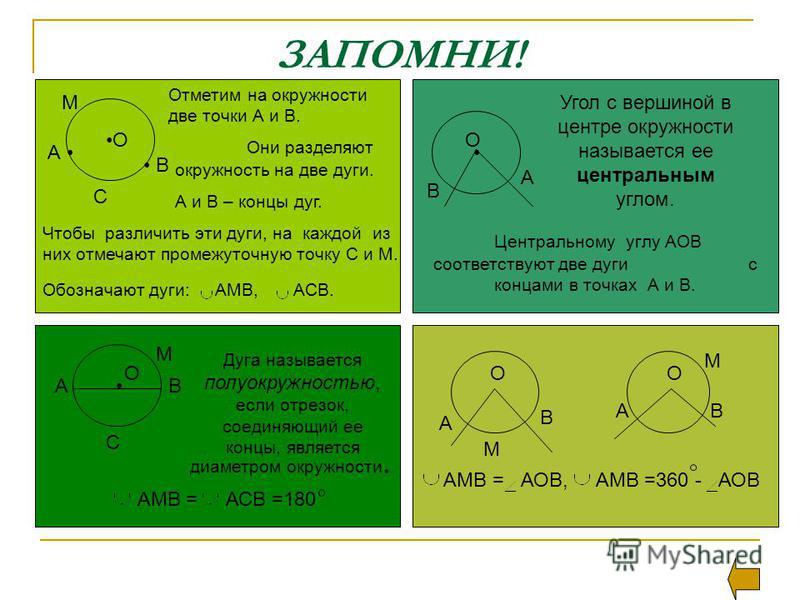 Геометрическая фигура, ограниченная окружностью, — это Круг:
Геометрическая фигура, ограниченная окружностью, — это Круг:
Построение окружности циркулем
Для построения окружности используют специальный прибор — Циркуль:
Установим циркулю произвольный раствор (расстояние между ножками циркуля) и, поставив его ножку с остриём в какую-нибудь точку плоскости (например, на листе бумаги), станем вращать циркуль вокруг этой точки. Другая его ножка, снабжённая карандашом или грифелем, прикасающимся к плоскости, начертит на плоскости замкнутую линию — окружность:
Радиус, хорда и диаметр
Радиус — это отрезок, соединяющий любую точку окружности с центром. Радиусом также называется расстояние от точки окружности до её центра:
Все радиусы окружности имеют одну и ту же длину, то есть они равны между собой. Радиус обозначается буквой R или R.
Хорда — это отрезок, соединяющий две точки окружности. Хорда, проходящая через центр, называется Диаметром окружности.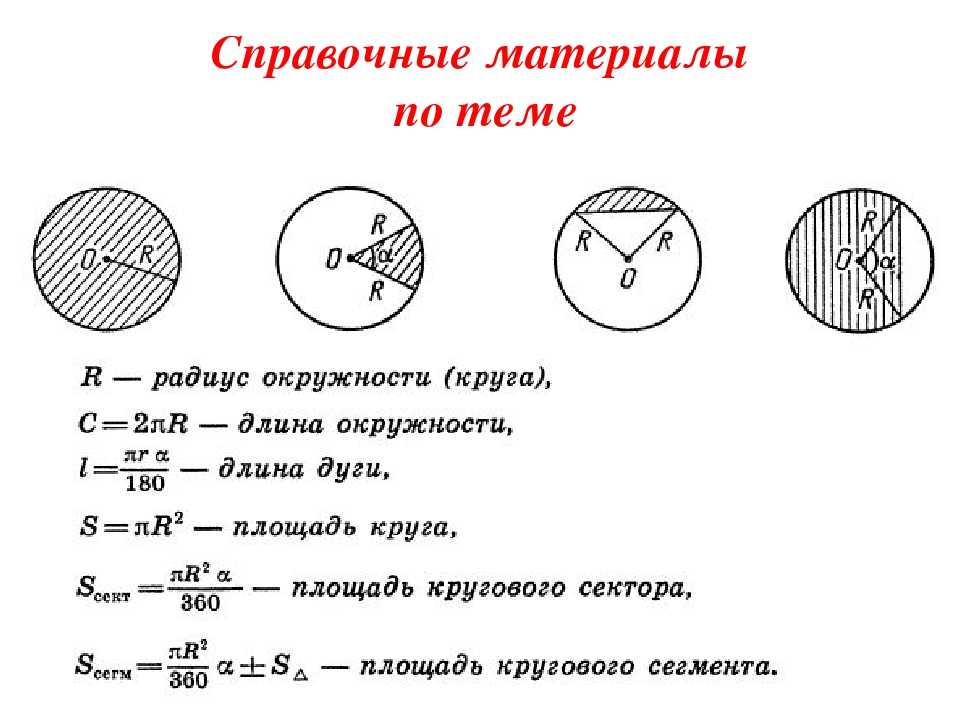
Диаметр обозначается буквой D. Диаметр окружности в два раза больше её радиуса:
D = 2R.
Дуга — это часть окружности, ограниченная двумя точками. Любые две точки делят окружность на две дуги:
Чтобы различать дуги, на которые две точки разделяют окружность, на каждую из дуг ставят дополнительную точку:
Для обозначения дуг используется символ :
Для обозначения дуг используется символ :
Построение окружности циркулем.
Izamorfix. ru
18.02.2018 3:38:55
2018-02-18 03:38:55
Источники:
Https://izamorfix. ru/matematika/planimetriya/okruzhnost. html
Дуга (геометрия) | это. Что такое Дуга (геометрия)? » /> » /> .keyword { color: red; }
Что такое геометрия дуга
Дуга — Дуга: В математике Дуга (геометрия) участок кривой между двумя её точками. Дуга окружности кривая линия, лежащая на окружности и ограниченная двумя точками.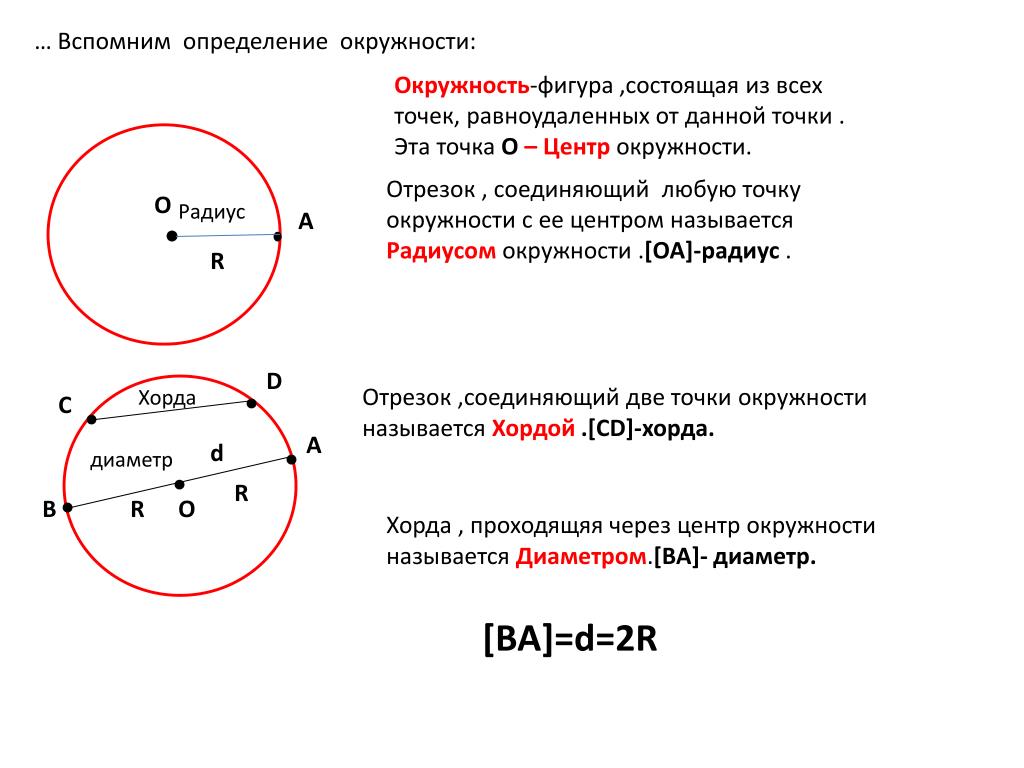 Дуга (теория графов) Другое Дуга (география) Дуга (анатомия) Дуга (физика) Дуга… … Википедия
Дуга (теория графов) Другое Дуга (география) Дуга (анатомия) Дуга (физика) Дуга… … Википедия
Геометрия — (γήμετρώ земля, μετρώ мерю). Понятия о пространстве, положении и форме принадлежат к числу первоначальных, с которыми человек был знаком уже в глубокой древности. Первые шаги в Г. были сделаны египтянами и халдеями. В Греции Г. была введена… … Энциклопедический словарь Ф. А. Брокгауза и И. А. Ефрона
АФФИННАЯ ДИФФЕРЕНЦИАЛЬНАЯ ГЕОМЕТРИЯ
РИМАНОВА ГЕОМЕТРИЯ — теория риманова пространства. Р и м а н о в ы м п р о с т р а н с т в о м наз. n мерное связное дифференцируемое многообразие М п, на к ром задано дифференцируемое поле ковариантного, симметрического и положительно определенного тензора gранга 2 … Математическая энциклопедия
Сферическая геометрия — математическая дисциплина, изучающая геометрические образы, находящиеся на сфере, подобно тому как планиметрия изучает геометрические образы, находящиеся на плоскости. Всякая плоскость, пересекающая сферу, даёт в сечении… … Большая советская энциклопедия
Всякая плоскость, пересекающая сферу, даёт в сечении… … Большая советская энциклопедия
Хорда (геометрия) — У этого термина существуют и другие значения, см. Хорда. 1 секущая, 2 хорда … Википедия
СФЕРИЧЕСКАЯ ГЕОМЕТРИЯ — математич. дисциплина, изучающая геометрич. образы, находящиеся на сфере, подобно тому как планиметрия изучает геометрич. образы, находящиеся на плоскости. Всякая плоскость, пересекающая сферу, дает в сечении нек рую окружность; если секущая… … Математическая энциклопедия
ГЕОДЕЗИЧЕСКАЯ ЛИНИЯ — геодезиче ская, геометрическое понятие, обобщающее понятие прямой (или отрезка прямой) евклидовой геометрии на случай пространств более общего вида. Определения Г. л. в различных пространствах зависят от того, какая из структур (метрика, линейный … Математическая энциклопедия
Декарт Рене — (Descartes) (латинизир. Картезий; Cartesius) (1596 1650), французский философ, математик, физик и физиолог.
Жорданова кривая — Кривая или линия геометрическое понятие, определяемое в разных разделах геометрии различно. Содержание 1 Элементарная геометрия 2 Параметрические определения 3 Кривая Жордана … Википедия
N мерное связное дифференцируемое многообразие М п, на к ром задано дифференцируемое поле ковариантного, симметрического и положительно определенного тензора gранга 2 Математическая энциклопедия.
Dic. academic. ru
26.11.2018 14:36:08
2018-11-26 14:36:08
Источники:
Https://dic. academic. ru/dic. nsf/ruwiki/178028
Вставка математических знаков
Word для Microsoft 365 Word 2021 Word 2019 Word 2016 Word 2013 Word 2010 Word 2007 Еще…Меньше
В Word можно вставлять математические символы в уравнения и текст.
На вкладке Вставка в группе Символы щелкните стрелку рядом с надписью Формула и выберите Вставить новую формулу.
В области Работа с формулами в группе Символы на вкладке Конструктор щелкните стрелку Еще.
Щелкните стрелку рядом с именем набора символов, а затем выберите набор символов, который вы хотите отобразить.
Щелкните нужный символ.
Доступные наборы символов
В группе Символы в Word доступны указанные ниже наборы математических символов. Щелкнув стрелку Еще, выберите меню в верхней части списка символов, чтобы просмотреть группы знаков.
|
Набор символов |
Подгруппа |
Определение |
|---|---|---|
|
Основные математические символы |
Нет |
Часто используемые математические символы, такие как > и < |
|
Греческие буквы |
Строчные буквы |
Строчные буквы греческого алфавита |
|
Прописные буквы |
Прописные буквы греческого алфавита |
|
|
Буквоподобные символы |
Нет |
Символы, которые напоминают буквы |
|
Операторы |
Обычные бинарные операторы |
Символы, обозначающие действия над двумя числами, например + и ÷ |
|
Обычные реляционные операторы |
Символы, обозначающие отношение между двумя выражениями, такие как = и ~ |
|
|
Основные N-арные операторы |
Операторы, осуществляющие действия над несколькими переменными |
|
|
Сложные бинарные операторы |
Дополнительные символы, обозначающие действия над двумя числами |
|
|
Сложные реляционные операторы |
Дополнительные символы, обозначающие отношение между двумя выражениями |
|
|
Стрелки |
Нет |
Символы, указывающие направление |
|
Отношения с отрицанием |
Нет |
Символы, обозначающие отрицание отношения |
|
Наборы знаков |
Наборы знаков |
Математический шрифт Script |
|
Готические |
Математический шрифт Fraktur |
|
|
В два прохода |
Математический шрифт с двойным зачеркиванием |
|
|
Геометрия |
Нет |
Часто используемые геометрические символы |
Дополнительные сведения
Вставка флажка или другого символа
Что означает знак подковы в геометрии?
В разделе собраны математические символы, которые невозможно корректно отобразить с помощью ввода на клавиатуре. Весь представленный набор можно разделить на несколько групп:
Весь представленный набор можно разделить на несколько групп:
- знаки операций – сложение, вычитание, деление, умножение, сумма;
- символы интегралов – двойные, тройные, интеграл по объему, поверхности, с правым и левым обходом;
- знаки сравнения – больше, меньше;
- примерно равно, не равно, эквивалентно, тождественно;
- геометрические символы – отображение угла, пропорции, диаметра, перпендикуляра, параллельности, пересечения;
- геометрические фигуры — треугольники, дуги, параллелограмм, ромб;
- знак извлечения из корня, степень числа;
- для теории множеств — пустое множество, принадлежит, подмножество, объединение, пересечение;
- логические — следовательно, и, или, отрицание, равносильно;
- иные символы – бесконечность, существует, принадлежит, оператор набла, троеточия для матриц, скобки потолков числа, для теории групп.
Как ввести в «Ворд»?
Для вставки символа заходим в верхние меню редактора и ищем колонку «Вставка», наводим на колонку курсором мыши без нажатия правой кнопки. Высвечивается несколько наименования разделов, необходимо нажать на «Символ» , где можно путем перелистывания за счет колеса мыши искать необходимый знак, либо в строке поиска выбрать категорию (статистические или математические) и найти знак. Прописной или заглавный символ высветится в рабочей области окна вставки , вам только стоит нажать правой кнопкой мыши «вставить» или «окей».
Высвечивается несколько наименования разделов, необходимо нажать на «Символ» , где можно путем перелистывания за счет колеса мыши искать необходимый знак, либо в строке поиска выбрать категорию (статистические или математические) и найти знак. Прописной или заглавный символ высветится в рабочей области окна вставки , вам только стоит нажать правой кнопкой мыши «вставить» или «окей».
Первый способ
Скажем сразу — для этого способа мы будем использовать символ тильда в виде одной волнистой черты, в то время как в знаке приблизительно черты две. Тем менее, тильду часто используют в качестве символа примерно, так что проблем быть не должно.
Используйте англоязычную раскладку. Если используется русскоязычная, переключите ее, нажав Shift+Ctrl:
Или Shift+Alt:
Или используйте языковую иконку, которая находится на панели задач:
Теперь найдите символ тильды (слева от цифры 1, часто на этой же клавише можно увидеть букву ё).
Однако если нажать на указанную клавишу, вы увидите совсем другой символ, поэтому предварительно нажмите на Shift и, удерживая его, нажмите на клавишу тильда, после чего отпустите Shift.
Что у вас должно получиться:
Конвертация кода в знак
Первый способ заключается в конвертации юникода символа в знак. В любом месте документа набираем 2248 и одновременно нажимаем «Alt» + «X».
- 2248 ➟ Alt + x = ≈
Вторая возможность связана с ASCII-кодом и преобразование идёт следующим чередом:
- зажимаем Alt>;
- вводим на правой цифровой клавиатуре 8776;
- отпускаем Alt и цифры превращаются в ≈.
Оба варианта работают в Word, Excel и других офисных программах.
Дела давние, дела древние. Возникновение приметы о подковах
Первыми назвали лошадиную подкову символом счастья древние египтяне. И объясняется это достаточно просто, без участия каких-либо сверхъестественных сил: найдя подкову с копыта лошади фараона, можно было сказочно разбогатеть. Изготовлялись эти подковы не из железа, а из золота. Золото – металл мягкий и недостаточно надёжный, поэтому лошади фараона частенько теряли свои подковы во время праздничных шествий и парадов.
Со временем древнеегипетская примета получила распространение и в других странах. Поверье, что лошадиная подкова дарует удачу, прижилось и сохранилось до наших дней, несмотря на борьбу христианской церкви с суевериями и бытовым мистицизмом. Путники искренне радовались, если на дороге им удавалось найти подкову, частенько брали её с собой в дорогу, а по возвращении прибивали около входа в дом.
Подкова над входом в славянских избах была не сувениром, а подарком коня удачи. Наши предки знали: «Кто подкову на дороге найдет и сторожем у своих дверей поставит, тот счастье и удачу в дом привадит». Подкова может быть найденной или подаренной, но обязательно уже использованной, не новой.
Исторически подкова не является очень уж древним предметом. Во-первых, она предназначена защитить копыта лошади от износа и повреждения в соприкоснавении с твёрдым грунтом ранних дорог. Перед появлением металлических подков в Европе использовались сплетённые «чулки» для лошадей из лыка, тростника, кожи, растительных волокон и т. д. Первые металлические аналоги современных подков (гиппосандалии) начали использоваться в Древнем Риме, а современный вид подкова приобрела, и их крепить металлическими гвоздями начали только в Средние века. У разных европейских народов есть собственное повествование о значении подковы, как символа удачи, благодати и счастья. Самая известная из них- это англосаксонская легенда о Св. Дунстане и Дьяволе. К будущему Кентерберийскому архиепископу Дунстану (909-988) явился сам дьявол и попросил подковать ему копыто. Дунстан, который был ещё и кузнецом, согласился на такую сделку. Однако подковал дьявола так крепко (по другому варианту легенды — приковал дьявола к стене), что тот, испытывая невероятную боль, попросил пощады. Взамен на свободу дьявол поклялся, что никогда не войдет в дверь, над которой висит подкова.
д. Первые металлические аналоги современных подков (гиппосандалии) начали использоваться в Древнем Риме, а современный вид подкова приобрела, и их крепить металлическими гвоздями начали только в Средние века. У разных европейских народов есть собственное повествование о значении подковы, как символа удачи, благодати и счастья. Самая известная из них- это англосаксонская легенда о Св. Дунстане и Дьяволе. К будущему Кентерберийскому архиепископу Дунстану (909-988) явился сам дьявол и попросил подковать ему копыто. Дунстан, который был ещё и кузнецом, согласился на такую сделку. Однако подковал дьявола так крепко (по другому варианту легенды — приковал дьявола к стене), что тот, испытывая невероятную боль, попросил пощады. Взамен на свободу дьявол поклялся, что никогда не войдет в дверь, над которой висит подкова.
Бытовало поверие, что дьявол всегда ходит кругами, но дойдя то конца подковы (разорванного круга), он вынужден повернуть обратно (некоторые в боком прибитой подкове узревали асоциации с латинской буквой «C»- первой буквой в имени Христа). Весьма вероятно, что эта христианская версия значения подковы как оберегающего предмета, была перенята христианами у древних языческих кельтов, которые верили, что над дверьми прибита подкова в силе отразить вторжение Faery и других потусторонних гостей. На Британских островах это поверие очень сильно и до сих пор. Например, чтобы отогнать дьявола, подкова была зарыта в портале Стейнинфилдской церкви в Суффолке, шотландские моряки верят, что прибита к мачте подкова защищает его от бурь, такую же к мачте своего корабля распорядился прибить и легендарный адмирал Нельсон. Подкова спасала от попадания молнии и налёта ведьм, потому её вешали не только над дверьми или на дверях, но и везде, где злая сила могла попасть в дом (окна, камин, печь и т.д.).
Весьма вероятно, что эта христианская версия значения подковы как оберегающего предмета, была перенята христианами у древних языческих кельтов, которые верили, что над дверьми прибита подкова в силе отразить вторжение Faery и других потусторонних гостей. На Британских островах это поверие очень сильно и до сих пор. Например, чтобы отогнать дьявола, подкова была зарыта в портале Стейнинфилдской церкви в Суффолке, шотландские моряки верят, что прибита к мачте подкова защищает его от бурь, такую же к мачте своего корабля распорядился прибить и легендарный адмирал Нельсон. Подкова спасала от попадания молнии и налёта ведьм, потому её вешали не только над дверьми или на дверях, но и везде, где злая сила могла попасть в дом (окна, камин, печь и т.д.).
Тут секрет кроется в поверьях о том, что железом, сталью, и собственно, металлом (шпагой, мечом, жезлом) можно контролировать и порабощать неземные силы. Теоретических подтверждений тому можно найти в сотнях книг по ритуальной магии, оккультизму, в древних мифах и преданиях. Практически же, например, в Германии, подкову, для предотвращения возрождения казнённых ведьм, помещали на крышке гроба.
Практически же, например, в Германии, подкову, для предотвращения возрождения казнённых ведьм, помещали на крышке гроба.
Тут-то именно в подкове и переплелось множество мистико-магических аспектов. Во-первых, она рождалась в кузне посредством огня, раскалённого металла и опытной человеческой силы. Под грохотом тяжёлого ударяющего молота и наковальни, под звонкою песнью творения, когда из чего-то аморфного получается что-то конкретное и новое. Не даром ковать значит — Творить, не даром у индоевропейских народов с Божественным кузнецом и кузней связаны мифы о сотворении (выковке) Мира и Небесных светил.
Во-вторых, на магические свойства металлических изделий в древности смотрели с большой долей уважения. И не только потому, что в Средние Века железо по цене весьма серьёзно приближалась к золоту и серебру, не только потому, что найти на дороге вещь металическую означало найти вещь дорогую и полезную (отсюда, видимо, и пошли народные поверия, что найти на дороге подкову, значит найти своё счастье), не только потому, что железо годится как для мира (соха), так и для войны (оружие). Интуитивная основа архетипичных глубин всплывает в простом народе не до конца осознанными повериями, за которыми кроется символизм первообразов, первосимволов, первосмыслов. И здесь по сути речь идёт не о подкове как о предмете для ковки лошадей, а о символическом образе «Подковы». Неком ограждённом пространстве, в котором обитает Нечто.
Интуитивная основа архетипичных глубин всплывает в простом народе не до конца осознанными повериями, за которыми кроется символизм первообразов, первосимволов, первосмыслов. И здесь по сути речь идёт не о подкове как о предмете для ковки лошадей, а о символическом образе «Подковы». Неком ограждённом пространстве, в котором обитает Нечто.
Итак, Подкова — некое архетипичное вместилище, сравнимое с женским символизмом Чаши, Чревом. Примечательно, что по всей Европе — от Италии до Скандинавии, и от Ирландии до России подкову вешают на дверях и экзотерический смысл сего везде одинаков. Отличается лишь само положение подвешенного символа. В Большинстве стран Европы (Германия, Литва, Россия, Балканы, Италия, Испания) подкову вешают рожками вниз, так как думается, что благодать будет сыпатся на голову хозяев дома; в Англии и в Ирландии, наоборот, рожками вверх — это символизирует что «счастье сохраняется в доме, а не убегает».
Есть основание предполагать, что возрастающую форму подковы (рожками вниз) можно связывать с древнеевропейскими лунными Богинями, льющими свой сокровенный серебренный свет познания на этот мир. Таким образом человек, его родичи и дом находится как бы под священной защитой богини, а точнее — её материнской женственности.
Таким образом человек, его родичи и дом находится как бы под священной защитой богини, а точнее — её материнской женственности.
Символисты связывают значение формы современной подковы с символизмом женских половых органов, а через них — рождением, становлением, накоплением, материнским утробом, лаской и охраной. В Ирландии (101 пример) и Великобритании (45 примеров) это на камне, зданиях или скалах вырезаны фигуры Sheela-na-Gigs, которые собою представляют образы обнажённых женщин с явно преувеличенной «женственостью» (грудь, половые органы). Эти образы сохранились даже на некоторых церквях! Из таких примеров самый известный находится на стене храма Kilpeck (Герефордшир, Англия) и датируется 1140 годом. Исследователи полагают, что такие материнские образы защищают от злых духов, смерти и всякого зла, т.е. здесь мы можем сделать вывод, что символика Sheela-na-Gigs в смысловом и даже в визуальном плане, вполне соответсвует символизму Подковы. Счастье, благополучие в доме, домашний очаг, охрана, оберег, общность рода/семьи.
Архетипичный символизм подковы (или, скорей всего, влияние арчетипичного символа через образ подковы) настоль глубоко вбит в подсознание, что поверх дверей её прибивают даже те, кто себя считает далёким от «всяких суеверий». И вовсе не важно, верит человек в защитные качества символа, или же это дело «моды», одни и те же протосимволы всплывают сами по себе и присутствуют в нашей жизни разными образами и визуальными поверхностными проявлениями: подковы, подковообразные фибулы, строго геральдические и простейшие «интуитивные» рисунки (дуги, кружки), элементы архитектурного декора, сны, визуализации, рунические и идеограмические знаки и т.д. Ведь и маленькие дети рисуют круги, кресты, свастики и треугольники не потому, что видят в них некую идеологическую или историческую подоплёку, а просто-напросто потому, что символы сии практически живут у них в крови.
В геральдике подкова присутствует по всей Европе, как на гербах городов, так и на гербах дворянских родов. Общепринятое геральдическое значения — удача; вторичные смыслы — рост, выносливость. Наличие кованых лошадей (о символике лошади во всех её аспектах можно написать сотни, тысячи страниц. Это была бы отдельная и гигантская по своим масштабам работа) показывало социальный статус владельца, богатство, стремление. Польский исследователь Папроцкий написал даже особое сочинение о подковах, как эмблемах в гербах, под заглавием «Strom czyli о herbach ze znakiem podkow». Большое об этом предмете рассуждение есть в конце Силезского гербовника (Stambuch szlezkie) того же автора (1609 г.). На различных гербах присутствуют как «одиночные подковы», так и подковы, как один из элементов герба: подкова и стрела, подкова в когтях сокола, подкова и кресты, подкова поверх восьмиконечной звезды и т.д.
Наличие кованых лошадей (о символике лошади во всех её аспектах можно написать сотни, тысячи страниц. Это была бы отдельная и гигантская по своим масштабам работа) показывало социальный статус владельца, богатство, стремление. Польский исследователь Папроцкий написал даже особое сочинение о подковах, как эмблемах в гербах, под заглавием «Strom czyli о herbach ze znakiem podkow». Большое об этом предмете рассуждение есть в конце Силезского гербовника (Stambuch szlezkie) того же автора (1609 г.). На различных гербах присутствуют как «одиночные подковы», так и подковы, как один из элементов герба: подкова и стрела, подкова в когтях сокола, подкова и кресты, подкова поверх восьмиконечной звезды и т.д.
Произведение П
С произведением в математике работает точно такое же правило, только мы не складываем все элементы, а перемножаем их друг на друга:
А если это перевести в цикл, то алгоритм получится почти такой же, что и в сложении:
Общая характеристика
Главная задача знаков — описание этапов осуществляемых действий. Математическое уравнение или выражение имеет одиночную пару квадратных, фигурных и других скобок, а также может использовать их некоторое количество.
Математическое уравнение или выражение имеет одиночную пару квадратных, фигурных и других скобок, а также может использовать их некоторое количество.
Читайте также: Народные приметы про веник, его магические свойства, заговоры на веник. Приметы на веник у двери, на новый, старый, банный, свадебный, на покупку, новоселье, в подарок
Значение и разновидности
Скобки — это парные знаки, используемые во всевозможных областях. Чтобы правильно выстроить фразу в русском языке, для понимания смысла текста в предложении они употребляются как знаки препинания. С начальных классов школы изучают основы этих знаков.
В расчетах первая из скобок считается открывающей, а вторая — замыкающей. Оба знака соответствуют друг другу, но также используются те, в которых открытие или закрытие не различается (косые /…/, прямые скобки |…|, двойные прямые ||…||. Раскрывать значение можно чаще всего в математике, физике, химии и остальных науках для указания важности выполнения операции в формулах. На компьютерной клавиатуре представлены все виды знаков препинания.
На компьютерной клавиатуре представлены все виды знаков препинания.
Разновидности:
- Круглые ().
- Квадратные [ ].
- Фигурные { }.
- Угловые ⟨ ⟩ (< > в ASCII-текстах).
Открытие круглых () произошло в 1556 году для подкоренного выражения. По правилу первым выполняется действие внутри знака, затем произведение или определение частного (деление), а в конце — суммирование и разница.
В Microsoft word, Excel включена электронная конфигурация этих знаков. Часто используемые виды скобок, следующие: (), [ ], { }(), [ ], { }. Также встречаются двойные, называемые обратными (]] и [ [) или << и >> в виде уголка. Их использование является двойственным — с открывающейся и замыкающей скобочкой.
Основные цели квадратной скобки в математике:
- Взятие целой части числового значения.
- Округление до близкого знака.
- Возведение в степень, взятие производной или подсчёт подинтегрального выражения.

- Приоритет операций. Примером может быть следующий способ: [(5+6)*2]3.
Другие варианты расчета:
- Векторное произведение — с = [a, b] = [a*b] = a*b.
- Закрытие сегмента [1;2] означает, что в множество включены цифры 1 и 2.
- Коммутатор [А, В = [А, В].
- Заменяют круглые скобки при записи матриц по правилам.
- Одна [ объединяет несколько уравнений или неравенств.
- Нотация Айверсона.
Квадратные скобки в математике обозначают, что действие выполняется последовательно. Эти знаки позволяют разграничить операции.
Треугольные актуальны в теории групп. Правило записи ⟨ a ⟩ n характеризует циклическую группу порядка n, сформированную элементом a.
Круглые (операторные) () используются в математике для описания первостепенности действий. Например, (1 +5)*3 означает, что нужно сначала сложить 1 и 5, а затем полученную величину перемножить на 3. Наряду с квадратными, используются для записи разных компонент векторов, матриц и коэффициентов.
На уроке математики преподаватель объясняет, как раскрыть скобки в уравнении для последующего решения. Фигурная одинарная { встречается при решении систем уравнений, обозначает пересечение данных, а [[ используется при их слиянии.
Одинарные или двойные выражения
Употребление [] происходит реже. Одно уравнение со скобками объединяет несколько значений или неравенств различных размеров. Для решения совокупности нужно выполнить любое условие. Конец, завершение действия замыкает закрывающий знак.
В персональных компьютерах, ноутбуках, нетбуках встроена кодировка Юникод, закрепленная не за левыми или правыми объединяющими знаками, а за открывающими и замыкающими, поэтому при воспроизведении печатного текста со скобочками в режиме «справа налево» каждый знак меняет внешнее направление на обратное.
Квадратные скобки в уравнении означают, что установлен порядок действий, задаются границы промежутков и необходимость выполнения действия над выражением. Двойные квадратные скобки необходимы для записи выражений наряду с круглыми для рационального порядка действий.
По правилам интервал [−a;+a] записывается в виде нестрогого неравенства −a≤x≤a, означающего, что x находится на промежутке от −a до a включительно.
Также используются в математике как круглые, так и прямые знаки, означающие, что на конце отрезка, рядом с которым имеется круглая скобка, равенство строгое, а на том, где скобка квадратная — нестрогое. Интервал (−5;5] иначе записывается неравенством $5.
В середине парного знака с отделяющей точкой или запятой указываются два числа — наименьшее, затем большее, ограничивающие интервал. Круглая скобочка, прилегающая к цифре, означает невключение числа в промежуток, а квадратная — добавление.
В некоторых учебных пособиях для вузов встречаются расшифровки числовых интервалов, в которых вместо круглой скобочки (применяется обратная квадратная скобка ], и наоборот. В обозначениях запись ]0, 1[ равносильна (0, 1).
Открытая квадратная скобка (символ [) значит, что совокупность представляет систему уравнений разных размеров, для которых справедливы все множества решений для каждого уравнения, входящего в общее задание. Например, [x+11=2yy2−12=0
Например, [x+11=2yy2−12=0
Прежде чем решать задачу или выполнять задание, нужно правильно определить принципы действий. В некоторых случаях скобочки могут быть не нужны, а иногда их обязательно нужно поставить.
Второй способ
Если вам нужны исключительно две волнистые черты, их тоже можно поставить, но способ чуть более долгий.
На клавиатуре своего устройства нажмите Win+R.
Появится окно «Выполнить». Добавьте команду charmap.exe, нажмите ОК.
Запущена таблица символов Windows.
Выбираете шрифт Arial, затем в списке находите символ приблизительно (примерно), нажимаете на него левой клавишей мыши, а затем по очереди — на кнопки «Выбрать» и «Копировать».
Теперь вставляете символ в определенное место вашего текста.
Готово.
Что означает знак подковы в геометрии?
В разделе собраны математические символы, которые невозможно корректно отобразить с помощью ввода на клавиатуре. Весь представленный набор можно разделить на несколько групп:
Весь представленный набор можно разделить на несколько групп:
- знаки операций – сложение, вычитание, деление, умножение, сумма;
- символы интегралов – двойные, тройные, интеграл по объему, поверхности, с правым и левым обходом;
- знаки сравнения – больше, меньше;
- примерно равно, не равно, эквивалентно, тождественно;
- геометрические символы – отображение угла, пропорции, диаметра, перпендикуляра, параллельности, пересечения;
- геометрические фигуры — треугольники, дуги, параллелограмм, ромб;
- знак извлечения из корня, степень числа;
- для теории множеств — пустое множество, принадлежит, подмножество, объединение, пересечение;
- логические — следовательно, и, или, отрицание, равносильно;
- иные символы – бесконечность, существует, принадлежит, оператор набла, троеточия для матриц, скобки потолков числа, для теории групп.
Общая характеристика
Главная задача знаков — описание этапов осуществляемых действий. Математическое уравнение или выражение имеет одиночную пару квадратных, фигурных и других скобок, а также может использовать их некоторое количество.
Математическое уравнение или выражение имеет одиночную пару квадратных, фигурных и других скобок, а также может использовать их некоторое количество.
Значение и разновидности
Скобки — это парные знаки, используемые во всевозможных областях. Чтобы правильно выстроить фразу в русском языке, для понимания смысла текста в предложении они употребляются как знаки препинания. С начальных классов школы изучают основы этих знаков.
В расчетах первая из скобок считается открывающей, а вторая — замыкающей. Оба знака соответствуют друг другу, но также используются те, в которых открытие или закрытие не различается (косые /…/, прямые скобки |…|, двойные прямые ||…||. Раскрывать значение можно чаще всего в математике, физике, химии и остальных науках для указания важности выполнения операции в формулах. На компьютерной клавиатуре представлены все виды знаков препинания.
Разновидности:
- Круглые ().
- Квадратные [ ].
- Фигурные { }.
- Угловые ⟨ ⟩ (< > в ASCII-текстах).

Открытие круглых () произошло в 1556 году для подкоренного выражения. По правилу первым выполняется действие внутри знака, затем произведение или определение частного (деление), а в конце — суммирование и разница.
В Microsoft word, Excel включена электронная конфигурация этих знаков. Часто используемые виды скобок, следующие: (), [ ], { }(), [ ], { }. Также встречаются двойные, называемые обратными (]] и [ [) или << и >> в виде уголка. Их использование является двойственным — с открывающейся и замыкающей скобочкой.
Основные цели квадратной скобки в математике:
- Взятие целой части числового значения.
- Округление до близкого знака.
- Возведение в степень, взятие производной или подсчёт подинтегрального выражения.
- Приоритет операций. Примером может быть следующий способ: [(5+6)*2]3.
Другие варианты расчета:
- Векторное произведение — с = [a, b] = [a*b] = a*b.

- Закрытие сегмента [1;2] означает, что в множество включены цифры 1 и 2.
- Коммутатор [А, В = [А, В].
- Заменяют круглые скобки при записи матриц по правилам.
- Одна [ объединяет несколько уравнений или неравенств.
- Нотация Айверсона.
Квадратные скобки в математике обозначают, что действие выполняется последовательно. Эти знаки позволяют разграничить операции.
Треугольные актуальны в теории групп. Правило записи ⟨ a ⟩ n характеризует циклическую группу порядка n, сформированную элементом a.
Круглые (операторные) () используются в математике для описания первостепенности действий. Например, (1 +5)*3 означает, что нужно сначала сложить 1 и 5, а затем полученную величину перемножить на 3. Наряду с квадратными, используются для записи разных компонент векторов, матриц и коэффициентов.
На уроке математики преподаватель объясняет, как раскрыть скобки в уравнении для последующего решения. Фигурная одинарная { встречается при решении систем уравнений, обозначает пересечение данных, а [[ используется при их слиянии.
Одинарные или двойные выражения
Употребление [] происходит реже. Одно уравнение со скобками объединяет несколько значений или неравенств различных размеров. Для решения совокупности нужно выполнить любое условие. Конец, завершение действия замыкает закрывающий знак.
В персональных компьютерах, ноутбуках, нетбуках встроена кодировка Юникод, закрепленная не за левыми или правыми объединяющими знаками, а за открывающими и замыкающими, поэтому при воспроизведении печатного текста со скобочками в режиме «справа налево» каждый знак меняет внешнее направление на обратное.
Квадратные скобки в уравнении означают, что установлен порядок действий, задаются границы промежутков и необходимость выполнения действия над выражением. Двойные квадратные скобки необходимы для записи выражений наряду с круглыми для рационального порядка действий.
По правилам интервал [−a;+a] записывается в виде нестрогого неравенства −a≤x≤a, означающего, что x находится на промежутке от −a до a включительно.
Также используются в математике как круглые, так и прямые знаки, означающие, что на конце отрезка, рядом с которым имеется круглая скобка, равенство строгое, а на том, где скобка квадратная — нестрогое. Интервал (−5;5] иначе записывается неравенством $5.
В середине парного знака с отделяющей точкой или запятой указываются два числа — наименьшее, затем большее, ограничивающие интервал. Круглая скобочка, прилегающая к цифре, означает невключение числа в промежуток, а квадратная — добавление.
В некоторых учебных пособиях для вузов встречаются расшифровки числовых интервалов, в которых вместо круглой скобочки (применяется обратная квадратная скобка ], и наоборот. В обозначениях запись ]0, 1[ равносильна (0, 1).
Открытая квадратная скобка (символ [) значит, что совокупность представляет систему уравнений разных размеров, для которых справедливы все множества решений для каждого уравнения, входящего в общее задание. Например, [x+11=2yy2−12=0
Прежде чем решать задачу или выполнять задание, нужно правильно определить принципы действий. В некоторых случаях скобочки могут быть не нужны, а иногда их обязательно нужно поставить.
В некоторых случаях скобочки могут быть не нужны, а иногда их обязательно нужно поставить.
Второй способ
Если вам нужны исключительно две волнистые черты, их тоже можно поставить, но способ чуть более долгий.
На клавиатуре своего устройства нажмите Win+R.
Появится окно «Выполнить». Добавьте команду charmap.exe, нажмите ОК.
Запущена таблица символов Windows.
Выбираете шрифт Arial, затем в списке находите символ приблизительно (примерно), нажимаете на него левой клавишей мыши, а затем по очереди — на кнопки «Выбрать» и «Копировать».
Теперь вставляете символ в определенное место вашего текста.
Готово.
Первый способ
Скажем сразу — для этого способа мы будем использовать символ тильда в виде одной волнистой черты, в то время как в знаке приблизительно черты две. Тем менее, тильду часто используют в качестве символа примерно, так что проблем быть не должно.
Используйте англоязычную раскладку. Если используется русскоязычная, переключите ее, нажав Shift+Ctrl:
Если используется русскоязычная, переключите ее, нажав Shift+Ctrl:
Или Shift+Alt:
Или используйте языковую иконку, которая находится на панели задач:
Теперь найдите символ тильды (слева от цифры 1, часто на этой же клавише можно увидеть букву ё).
Однако если нажать на указанную клавишу, вы увидите совсем другой символ, поэтому предварительно нажмите на Shift и, удерживая его, нажмите на клавишу тильда, после чего отпустите Shift.
Что у вас должно получиться:
Дела давние, дела древние. Возникновение приметы о подковах
Первыми назвали лошадиную подкову символом счастья древние египтяне. И объясняется это достаточно просто, без участия каких-либо сверхъестественных сил: найдя подкову с копыта лошади фараона, можно было сказочно разбогатеть. Изготовлялись эти подковы не из железа, а из золота. Золото – металл мягкий и недостаточно надёжный, поэтому лошади фараона частенько теряли свои подковы во время праздничных шествий и парадов.
Со временем древнеегипетская примета получила распространение и в других странах. Поверье, что лошадиная подкова дарует удачу, прижилось и сохранилось до наших дней, несмотря на борьбу христианской церкви с суевериями и бытовым мистицизмом. Путники искренне радовались, если на дороге им удавалось найти подкову, частенько брали её с собой в дорогу, а по возвращении прибивали около входа в дом.
Подкова над входом в славянских избах была не сувениром, а подарком коня удачи. Наши предки знали: «Кто подкову на дороге найдет и сторожем у своих дверей поставит, тот счастье и удачу в дом привадит». Подкова может быть найденной или подаренной, но обязательно уже использованной, не новой.
Исторически подкова не является очень уж древним предметом. Во-первых, она предназначена защитить копыта лошади от износа и повреждения в соприкоснавении с твёрдым грунтом ранних дорог. Перед появлением металлических подков в Европе использовались сплетённые «чулки» для лошадей из лыка, тростника, кожи, растительных волокон и т. д. Первые металлические аналоги современных подков (гиппосандалии) начали использоваться в Древнем Риме, а современный вид подкова приобрела, и их крепить металлическими гвоздями начали только в Средние века. У разных европейских народов есть собственное повествование о значении подковы, как символа удачи, благодати и счастья. Самая известная из них- это англосаксонская легенда о Св. Дунстане и Дьяволе. К будущему Кентерберийскому архиепископу Дунстану (909-988) явился сам дьявол и попросил подковать ему копыто. Дунстан, который был ещё и кузнецом, согласился на такую сделку. Однако подковал дьявола так крепко (по другому варианту легенды — приковал дьявола к стене), что тот, испытывая невероятную боль, попросил пощады. Взамен на свободу дьявол поклялся, что никогда не войдет в дверь, над которой висит подкова.
д. Первые металлические аналоги современных подков (гиппосандалии) начали использоваться в Древнем Риме, а современный вид подкова приобрела, и их крепить металлическими гвоздями начали только в Средние века. У разных европейских народов есть собственное повествование о значении подковы, как символа удачи, благодати и счастья. Самая известная из них- это англосаксонская легенда о Св. Дунстане и Дьяволе. К будущему Кентерберийскому архиепископу Дунстану (909-988) явился сам дьявол и попросил подковать ему копыто. Дунстан, который был ещё и кузнецом, согласился на такую сделку. Однако подковал дьявола так крепко (по другому варианту легенды — приковал дьявола к стене), что тот, испытывая невероятную боль, попросил пощады. Взамен на свободу дьявол поклялся, что никогда не войдет в дверь, над которой висит подкова.
Бытовало поверие, что дьявол всегда ходит кругами, но дойдя то конца подковы (разорванного круга), он вынужден повернуть обратно (некоторые в боком прибитой подкове узревали асоциации с латинской буквой «C»- первой буквой в имени Христа). Весьма вероятно, что эта христианская версия значения подковы как оберегающего предмета, была перенята христианами у древних языческих кельтов, которые верили, что над дверьми прибита подкова в силе отразить вторжение Faery и других потусторонних гостей. На Британских островах это поверие очень сильно и до сих пор. Например, чтобы отогнать дьявола, подкова была зарыта в портале Стейнинфилдской церкви в Суффолке, шотландские моряки верят, что прибита к мачте подкова защищает его от бурь, такую же к мачте своего корабля распорядился прибить и легендарный адмирал Нельсон. Подкова спасала от попадания молнии и налёта ведьм, потому её вешали не только над дверьми или на дверях, но и везде, где злая сила могла попасть в дом (окна, камин, печь и т.д.).
Весьма вероятно, что эта христианская версия значения подковы как оберегающего предмета, была перенята христианами у древних языческих кельтов, которые верили, что над дверьми прибита подкова в силе отразить вторжение Faery и других потусторонних гостей. На Британских островах это поверие очень сильно и до сих пор. Например, чтобы отогнать дьявола, подкова была зарыта в портале Стейнинфилдской церкви в Суффолке, шотландские моряки верят, что прибита к мачте подкова защищает его от бурь, такую же к мачте своего корабля распорядился прибить и легендарный адмирал Нельсон. Подкова спасала от попадания молнии и налёта ведьм, потому её вешали не только над дверьми или на дверях, но и везде, где злая сила могла попасть в дом (окна, камин, печь и т.д.).
Тут секрет кроется в поверьях о том, что железом, сталью, и собственно, металлом (шпагой, мечом, жезлом) можно контролировать и порабощать неземные силы. Теоретических подтверждений тому можно найти в сотнях книг по ритуальной магии, оккультизму, в древних мифах и преданиях. Практически же, например, в Германии, подкову, для предотвращения возрождения казнённых ведьм, помещали на крышке гроба.
Практически же, например, в Германии, подкову, для предотвращения возрождения казнённых ведьм, помещали на крышке гроба.
Тут-то именно в подкове и переплелось множество мистико-магических аспектов. Во-первых, она рождалась в кузне посредством огня, раскалённого металла и опытной человеческой силы. Под грохотом тяжёлого ударяющего молота и наковальни, под звонкою песнью творения, когда из чего-то аморфного получается что-то конкретное и новое. Не даром ковать значит — Творить, не даром у индоевропейских народов с Божественным кузнецом и кузней связаны мифы о сотворении (выковке) Мира и Небесных светил.
Во-вторых, на магические свойства металлических изделий в древности смотрели с большой долей уважения. И не только потому, что в Средние Века железо по цене весьма серьёзно приближалась к золоту и серебру, не только потому, что найти на дороге вещь металическую означало найти вещь дорогую и полезную (отсюда, видимо, и пошли народные поверия, что найти на дороге подкову, значит найти своё счастье), не только потому, что железо годится как для мира (соха), так и для войны (оружие). Интуитивная основа архетипичных глубин всплывает в простом народе не до конца осознанными повериями, за которыми кроется символизм первообразов, первосимволов, первосмыслов. И здесь по сути речь идёт не о подкове как о предмете для ковки лошадей, а о символическом образе «Подковы». Неком ограждённом пространстве, в котором обитает Нечто.
Интуитивная основа архетипичных глубин всплывает в простом народе не до конца осознанными повериями, за которыми кроется символизм первообразов, первосимволов, первосмыслов. И здесь по сути речь идёт не о подкове как о предмете для ковки лошадей, а о символическом образе «Подковы». Неком ограждённом пространстве, в котором обитает Нечто.
Итак, Подкова — некое архетипичное вместилище, сравнимое с женским символизмом Чаши, Чревом. Примечательно, что по всей Европе — от Италии до Скандинавии, и от Ирландии до России подкову вешают на дверях и экзотерический смысл сего везде одинаков. Отличается лишь само положение подвешенного символа. В Большинстве стран Европы (Германия, Литва, Россия, Балканы, Италия, Испания) подкову вешают рожками вниз, так как думается, что благодать будет сыпатся на голову хозяев дома; в Англии и в Ирландии, наоборот, рожками вверх — это символизирует что «счастье сохраняется в доме, а не убегает».
Есть основание предполагать, что возрастающую форму подковы (рожками вниз) можно связывать с древнеевропейскими лунными Богинями, льющими свой сокровенный серебренный свет познания на этот мир. Таким образом человек, его родичи и дом находится как бы под священной защитой богини, а точнее — её материнской женственности.
Таким образом человек, его родичи и дом находится как бы под священной защитой богини, а точнее — её материнской женственности.
Символисты связывают значение формы современной подковы с символизмом женских половых органов, а через них — рождением, становлением, накоплением, материнским утробом, лаской и охраной. В Ирландии (101 пример) и Великобритании (45 примеров) это на камне, зданиях или скалах вырезаны фигуры Sheela-na-Gigs, которые собою представляют образы обнажённых женщин с явно преувеличенной «женственостью» (грудь, половые органы). Эти образы сохранились даже на некоторых церквях! Из таких примеров самый известный находится на стене храма Kilpeck (Герефордшир, Англия) и датируется 1140 годом. Исследователи полагают, что такие материнские образы защищают от злых духов, смерти и всякого зла, т.е. здесь мы можем сделать вывод, что символика Sheela-na-Gigs в смысловом и даже в визуальном плане, вполне соответсвует символизму Подковы. Счастье, благополучие в доме, домашний очаг, охрана, оберег, общность рода/семьи.
Архетипичный символизм подковы (или, скорей всего, влияние арчетипичного символа через образ подковы) настоль глубоко вбит в подсознание, что поверх дверей её прибивают даже те, кто себя считает далёким от «всяких суеверий». И вовсе не важно, верит человек в защитные качества символа, или же это дело «моды», одни и те же протосимволы всплывают сами по себе и присутствуют в нашей жизни разными образами и визуальными поверхностными проявлениями: подковы, подковообразные фибулы, строго геральдические и простейшие «интуитивные» рисунки (дуги, кружки), элементы архитектурного декора, сны, визуализации, рунические и идеограмические знаки и т.д. Ведь и маленькие дети рисуют круги, кресты, свастики и треугольники не потому, что видят в них некую идеологическую или историческую подоплёку, а просто-напросто потому, что символы сии практически живут у них в крови.
В геральдике подкова присутствует по всей Европе, как на гербах городов, так и на гербах дворянских родов. Общепринятое геральдическое значения — удача; вторичные смыслы — рост, выносливость. Наличие кованых лошадей (о символике лошади во всех её аспектах можно написать сотни, тысячи страниц. Это была бы отдельная и гигантская по своим масштабам работа) показывало социальный статус владельца, богатство, стремление. Польский исследователь Папроцкий написал даже особое сочинение о подковах, как эмблемах в гербах, под заглавием «Strom czyli о herbach ze znakiem podkow». Большое об этом предмете рассуждение есть в конце Силезского гербовника (Stambuch szlezkie) того же автора (1609 г.). На различных гербах присутствуют как «одиночные подковы», так и подковы, как один из элементов герба: подкова и стрела, подкова в когтях сокола, подкова и кресты, подкова поверх восьмиконечной звезды и т.д.
Наличие кованых лошадей (о символике лошади во всех её аспектах можно написать сотни, тысячи страниц. Это была бы отдельная и гигантская по своим масштабам работа) показывало социальный статус владельца, богатство, стремление. Польский исследователь Папроцкий написал даже особое сочинение о подковах, как эмблемах в гербах, под заглавием «Strom czyli о herbach ze znakiem podkow». Большое об этом предмете рассуждение есть в конце Силезского гербовника (Stambuch szlezkie) того же автора (1609 г.). На различных гербах присутствуют как «одиночные подковы», так и подковы, как один из элементов герба: подкова и стрела, подкова в когтях сокола, подкова и кресты, подкова поверх восьмиконечной звезды и т.д.
Конвертация кода в знак
Первый способ заключается в конвертации юникода символа в знак. В любом месте документа набираем 2248 и одновременно нажимаем «Alt» + «X».
- 2248 ➟ Alt + x = ≈
Вторая возможность связана с ASCII-кодом и преобразование идёт следующим чередом:
- зажимаем Alt>;
- вводим на правой цифровой клавиатуре 8776;
- отпускаем Alt и цифры превращаются в ≈.

Оба варианта работают в Word, Excel и других офисных программах.
Произведение П
С произведением в математике работает точно такое же правило, только мы не складываем все элементы, а перемножаем их друг на друга:
А если это перевести в цикл, то алгоритм получится почти такой же, что и в сложении:
Как ввести в «Ворд»?
Для вставки символа заходим в верхние меню редактора и ищем колонку «Вставка», наводим на колонку курсором мыши без нажатия правой кнопки. Высвечивается несколько наименования разделов, необходимо нажать на «Символ» , где можно путем перелистывания за счет колеса мыши искать необходимый знак, либо в строке поиска выбрать категорию (статистические или математические) и найти знак. Прописной или заглавный символ высветится в рабочей области окна вставки , вам только стоит нажать правой кнопкой мыши «вставить» или «окей».
Знак совмещения в геометрии
Содержание
- Знаки плюс, минус, плюс минус, равно, не равно, примерно равно, умножения, деления, сумма
- Степени и корни
- Ещё знаки – существует, пустое множество, принадлежит, подмножество, бесконечность
- Сравнение – больше меньше или равно
- Интегралы
- Геометрические – диаметр, угол, градус, перпендикуляр, параллельность, диаметр, пропорциональности, подобия, пересечения, объединения
- Фигуры – треугольники, дуги, параллелограмм, ромб
- Логические – следовательно, и, или, отрицания, тождественный
Таблица обозначений абстрактной алгебры — В абстрактной алгебре повсеместно используются символы для упрощения и сокращения текста, а также стандартные обозначения для некоторых групп. Ниже приведён список наиболее часто встречающихся алгебраических обозначений, соответствующие команды в … Википедия
Ниже приведён список наиболее часто встречающихся алгебраических обозначений, соответствующие команды в … Википедия
История математических обозначений — Математические обозначения это символы, используемые для компактной записи математических уравнений и формул[1]. Помимо цифр и букв различных алфавитов (латинского, в том числе в готическом начертании, греческого и еврейского),… … Википедия
Список математических аббревиатур — Статья содержит список общеупотребительных аббревиатур математических функций, операторов и др. математических терминов. Содержание 1 Аббревиатуры 1.1 Латиница 1.2 Греческий алфавит … Википедия
Набор символов Юникод — Юникод, или Уникод (англ. Unicode) стандарт кодирования символов, позволяющий представить знаки практически всех письменных языков. Стандарт предложен в 1991 году некоммерческой организацией «Консорциум Юникода» (англ. Unicode Consortium,… … Википедия
Математические обозначения — Список используемых в математике специфических символов можно увидеть в статье Таблица математических символов Математические обозначения («язык математики») сложная графическая система обозначений, служащая для изложения абстрактных… … Википедия
Знак плюс-минус — У этого термина существуют и другие значения, см. Плюс минус (значения). ± ∓ Знак плюс минус (±) математический символ, который ставится перед некоторым выражением и означает, что значение этого выражения может быть как положительным, так и … Википедия
Плюс минус (значения). ± ∓ Знак плюс минус (±) математический символ, который ставится перед некоторым выражением и означает, что значение этого выражения может быть как положительным, так и … Википедия
Список обозначений в физике — Необходимо проверить качество перевода и привести статью в соответствие со стилистическими правилами Википедии. Вы можете помочь … Википедия
Знаки операций — или математические символы знаки, которые символизируют определённые математические действия со своими аргументами. К самым распространённым относятся: Плюс: + Минус: , − Знак умножения: ×, ∙ Знак деления: :, ∕, ÷ Знак возведения в… … Википедия
Знаки опеций — Знаки операций или математические символы знаки, которые символизируют определённые математические действия со своими аргументами. К самым распространённым относятся: Плюс: + Минус: , − Знак умножения: ×, ∙ Знак деления: :, ∕, ÷ Знак возведения… … Википедия
Знаки операторов — Знаки операций или математические символы знаки, которые символизируют определённые математические действия со своими аргументами. К самым распространённым относятся: Плюс: + Минус: , − Знак умножения: ×, ∙ Знак деления: :, ∕, ÷ Знак возведения… … Википедия
К самым распространённым относятся: Плюс: + Минус: , − Знак умножения: ×, ∙ Знак деления: :, ∕, ÷ Знак возведения… … Википедия
| Состояние | отпатрулирована |
В математике повсеместно используются символы для упрощения и сокращения текста. Ниже приведён список наиболее часто встречающихся математических обозначений, соответствующие команды в TeX, объяснения и примеры использования. Список и смысл обозначений соответствует международным стандартам ISO 31-11 и ISO 80000-2.
Кроме указанных символов, иногда используются их зеркальные отражения, например, A ⊂ B <displaystyle Asubset B> обозначает то же, что и B ⊃ A . <displaystyle Bsupset A.>
Знаки операций, или математические символы — знаки, которые символизируют определённые математические действия со своими аргументами.
Нажмите, чтобы скопировать и вставить символ
Знаки плюс, минус, плюс минус, равно, не равно, примерно равно, умножения, деления, сумма
Степени и корни
Ещё знаки – существует, пустое множество, принадлежит, подмножество, бесконечность
Сравнение – больше меньше или равно
Интегралы
Геометрические – диаметр, угол, градус, перпендикуляр, параллельность, диаметр, пропорциональности, подобия, пересечения, объединения
Фигуры – треугольники, дуги, параллелограмм, ромб
Логические – следовательно, и, или, отрицания, тождественный
В разделе собраны математические символы, которые невозможно корректно отобразить с помощью ввода на клавиатуре. Весь представленный набор можно разделить на несколько групп:
Весь представленный набор можно разделить на несколько групп:
- знаки операций – сложение, вычитание, деление, умножение, сумма, тождество;
- символы интегралов – двойные, тройные, интеграл по объему, поверхности, с правым и левым обходом;
- знаки сравнения – больше, меньше, равно;
- геометрические символы – отображение угла, пропорции, диаметра;
- геометрические фигуры;
- знак извлечения из корня, степень;
- иные символы – бесконечность, множество, квантор существования.
Использование данных иконок – единственный вариант корректного отображения ряда математических символов на сайте или в сообщении в любой операционной системе конечного пользователя. Достаточно лишь скопировать закодированный значок. Применение изображений для этих целей значительно усложняет процесс, требует подгонки при разработке и наполнении интернет-ресурса. Кроме того, медиа-контент занимает большой объем дискового пространства.
Математические символы подойдут для публикаций в социальных сетях, создания сообщений в чатах и форумах, разработки интернет-страниц.
Математика, как язык всех наук, не может обходиться без системы записи. Многочисленные понятия, и операторы обрели своё начертание по мере развития этой науки. Так как в стандартные алфавиты эти символы не входят, напечатать их с клавиатуры может оказаться проблематично. Отсюда можно скопировать и вставить.
Консорциуму Юникода не чужды проблемы учёных, поэтому в таблицу было включено множество различных знаков. Если тут нет того, что нужно, воспользуйтесь поиском по сайту или посмотрите в разделах математические символы , разнообразные математические символы-A , разнообразные математические символы-B , дополнительные математические операторы . Буквы для формул можно взять в наборе греческие буквы и блоке математические буквенно-цифровые символы .
Числа для степеней составляются из маленьких цифр. Там же собраны дроби.
Геометрия: Дуги
Я знаю, что только что бросил вам много новой терминологии, но я еще не закончил. Я соединил точки на окружности отрезками прямых линий. Также возможно соединить точки на окружности, используя извилистую часть окружности. Предположим, у вас есть две точки А и В на окружности, как показано на рис. 17.3. Точки между A и B образуют отрезок ¯AB, а точки между A и B, лежащие на окружности, составляют дугу AB. Поскольку дуга AB кривая (она состоит из части окружности), ей дается сокращение ˆAB.
Также возможно соединить точки на окружности, используя извилистую часть окружности. Предположим, у вас есть две точки А и В на окружности, как показано на рис. 17.3. Точки между A и B образуют отрезок ¯AB, а точки между A и B, лежащие на окружности, составляют дугу AB. Поскольку дуга AB кривая (она состоит из части окружности), ей дается сокращение ˆAB.
Рисунок 17.2 ¯AB и ˆAB на окружности.
Есть только одна проблема с этой идеей. На самом деле есть две дуги, которые включают точки на окружности между A и B, и вам нужно уметь их различать. Вы можете сделать это, указав точку между A и B на правильной части круга. Таким образом, верхняя дуга — это ˆADB, а нижняя дуга — это ˆAEB. Если A и B — концы диаметра, ˆADB и ˆAEB называются полуокружностями. Дуга окружности представляет собой полуокружность, часть полуокружности (называемую малой дугой) или большую, чем полуокружность, но меньшую, чем весь круг (называемую большой дугой).
Эврика!
Разница между ¯AB и ˆAB заключается в том, что ˆAB — это часть окружности, соединяющая A и B, а ¯AB — отрезок прямой, соединяющий A и B.
Касательная
Если две дуги являются частью две окружности с разными радиусами, то они не могут иметь одинаковую кривизну (или быть конгруэнтными). Единственный способ, которым две дуги могут быть конгруэнтны, — это если окружности, на которых они находятся, конгруэнтны, а их длины дуг конгруэнтны.
Поскольку вы можете измерять длины отрезков, естественно спросить об измерении дуг. Дуги имеют длину и изгиб. Чтобы измерить длину дуги, представьте, что вы выпрямляете дугу и измеряете ее длину линейкой. Две дуги слева на рис. 17.3 имеют одинаковую длину, но разную кривизну. Дуги справа имеют одинаковую кривизну, но разную длину. Таким образом, при измерении длины дуги необходимо учитывать две характеристики: фактическую длину и кривизну. По кругу (или по конгруэнтным кругам) конгруэнтные дуги — это дуги, которые совпадают как по длине, так и по кривизне.
По кругу (или по конгруэнтным кругам) конгруэнтные дуги — это дуги, которые совпадают как по длине, так и по кривизне.
Рисунок 17.3 Слева: две дуги одинаковой длины, но с разной кривой. Справа: две дуги с одинаковой кривой, но разной длины.
Кривизна дуги измеряется в градусах. Меру ˆAB будем обозначать mˆAB. Чтобы измерить дугу, мне нужно познакомить вас с центральным углом. Центральный угол окружности — это угол, вершина которого является центром окружности, а стороны — радиусами окружности. Причина, по которой центральные углы необходимы при измерении кривизны дуги ˆAB, видна на рис. 17.4. Малая дуга AB и центральный угол ACB связаны друг с другом. С каждой дугой связан центральный угол, а с каждым центральным углом связана дуга. Если вам дан центральный угол, его перехваченная дуга определяется двумя точками пересечения угла с окружностью и всеми точками дуги внутри угла.
Рисунок 17.4 Центральный угол и соответствующая ему малая дуга.
Соответствие между центральными углами и пересекаемыми дугами можно использовать для определения кривизны дуги (также известной как ее градусная мера). Чтобы закрепить эту идею, вам понадобится постулат.
- Постулат 17.1 : Постулат центрального угла. В окружности градусная мера центрального угла равна градусной мере дуги, на которую он опирается.
Этот постулат позволяет вам определить градусное измерение дуги путем определения измерения ее центрального угла. Поскольку вы уже подробно изучили углы, вы заложили основу для понимания градусного измерения дуги. Малая дуга имеет соответствующий центральный угол, градусная мера которого меньше 180º; у полукруга центральный угол прямой, поэтому его градусная мера равна 180º; и большая дуга имеет градусную меру больше 180º. Поскольку понятие градусного измерения дуги и измерения центрального угла объединены, допускается измерение центрального угла больше 180º. А если вы добавите постулат сложения углов (постулат 4. 2), вы увидите, что градусное измерение всего круга в два раза больше градусного измерения полукруга. Другими словами, градусное измерение окружности составляет 360º. На рис. 17.5 показаны некоторые центральные углы и образующие их дуги.
2), вы увидите, что градусное измерение всего круга в два раза больше градусного измерения полукруга. Другими словами, градусное измерение окружности составляет 360º. На рис. 17.5 показаны некоторые центральные углы и образующие их дуги.
Рисунок 17.5 Центральные углы и образующие их дуги.
Последний термин, который мне нужно определить для вас, — это сектор круга. Представьте, что вы заказали кусок пиццы. Два прямых края пиццы можно рассматривать как радиусы круга (при условии, что она была разрезана правильно), а часть пиццы с корочкой — это дуга круга. Весь кусок пиццы является сектором круга. Сектор окружности — это область, ограниченная двумя радиусами окружности и дугой, на которую она опирается.
Solid Facts
Дуга — это часть окружности, определяемая двумя точками и всеми точками между ними.
Конгруэнтные дуги — это дуги на окружностях с конгруэнтными радиусами, имеющими одинаковую градусную меру.
Малая дуга — это дуга, градусная мера которой находится в диапазоне от 0° до 180°.
Полуокружность — это дуга, градусная мера которой равна точно 180º.
Большая дуга — это дуга, градусная мера которой составляет от 180° до 360°.
Сектор окружности — это область, ограниченная двумя радиусами окружности и дугой, на которой она пересекается.
Вы уже видели постулат сложения сегментов и постулат сложения углов. Существует также Постулат Сложения Дуги, который говорит именно то, что вы ожидаете от него сказать.
- Постулат 17.2 : Постулат сложения дуги. Если B лежит между A и C на окружности, то mˆAB + mˆBC = mˆAC.
Вы будете использовать этот постулат, когда будете комбинировать дуги окружностей.
Выдержки из Полное руководство по геометрии для идиотов © 2004 г. Дениз Сечей, доктор философии. Все права защищены, включая право на полное или частичное воспроизведение в любой форме. Используется по договоренности с Alpha Books , членом Penguin Group (USA) Inc.
Используется по договоренности с Alpha Books , членом Penguin Group (USA) Inc.
Чтобы заказать эту книгу непосредственно у издателя, посетите веб-сайт Penguin USA или позвоните по телефону 1-800-253-6476. Вы также можете приобрести эту книгу на Amazon.com и в Barnes & Noble.
Меры дуги: значение, примеры и формула
Очень важно знать анатомию круга и особенно углы внутри него. В этой статье рассматриваются свойства меры дуги , формула меры дуги и способы ее нахождения в геометрическом контексте.
Дуга и ее мера
Есть два важных определения, о которых следует знать:
Дуга окружности
Дуга — это ребро окружности сектор , т. е. ребро, ограниченное двумя точки в круге.
Длина дуги — это размер дуги, т. е. расстояние между двумя ограничивающими точками на окружности.
Мера дуги
Если мы представим себе дугу как ребро между двумя точками A и B на окружности, то мера дуги будет величиной угла между А, центром окружности , и B.
По отношению к длине дуги мерой дуги является размер угла, из которого выходит длина дуги.
Вот эти определения показаны графически:
Нахождение меры дуги Исходное исследование StudySmarter
Радианы и градусы
Прежде чем мы введем формулу для измерения дуги, давайте вспомним градуса и радиана .
Чтобы преобразовать радианы в градусы : разделите и умножьте на 180.
Чтобы преобразовать градусы в радианы : разделите на 180 и умножьте на.
Вот некоторые из наиболее распространенных ракурсов, которые вы должны распознать.
| Degrees | 0 | 30 | 45 | 60 | 90 | 120 | 180 | 270 | 360 |
| Radians | 0 |
Формулы измерения дуги и длины дуги
Нахождение меры дуги с радиусом
:
Где
- r — радиус окружности
- — длина дуги в радианах
- S — длина дуги переставляя формулу: .

Найдите меру дуги, показанную в следующем круге, относительно ее радиуса, r .
Используя формулу:
Нам нужна мера дуги с точки зрения r , поэтому нам нужно изменить это уравнение
:Нахождение меры дуги с длиной окружности
Если нам не дан радиус, r , то есть второй метод нахождения меры дуги . Если мы знаем окружность окружности, а также длину дуги, то отношение между мерой дуги и (или в зависимости от того, хотите ли вы измерять дугу в градусах или радианах) равно отношению между длина дуги и длина окружности.
Где
Найдите длину дуги x следующего круга с длиной окружности 10 см.
Используя формулу :
Переставляя, получаем:
на 3 с.ф.
Измерения дуги — ключевые выводы
Часто задаваемые вопросы об измерениях дуги
Измерение дуги — это угол, из которого выходит дуга окружности.

Как найти меру дуги: зная радиус и длину дуги, мерой дуги является длина дуги, деленная на радиус. Учитывая окружность, отношение между мерой дуги и 360 градусами равно отношению между длиной дуги и окружностью.
Мерой дуги является длина дуги, деленная на радиус.
Мерой дуги является длина дуги, деленная на радиус.
В геометрии мерой дуги является длина дуги, деленная на радиус.
Тест Final Arc Measures
Вопрос
Что такое длина сегмента?
Показать ответ
Ответить
Длина отрезка — это расстояние между двумя точками на прямой.
Показать вопрос
Вопрос
Какова площадь сегмента круга?
Показать ответ
Ответ
Это площадь, ограниченная хордой и краем окружности.
Показать вопрос
Вопрос
Как называется отрезок, концы которого лежат на окружности?
Показать ответ
Ответить
Аккорд.

Показать вопрос
Вопрос
Как называется хорда, проходящая через центр окружности?
Показать ответ
Ответить
Диаметр.
Показать вопрос
Вопрос
Разбивает ли хорда, кроме диаметра, любую другую хорду на большую и малую дуги?
Показать ответ
Ответ
Показать вопрос
Вопрос
Верно ли следующее свойство?
Равные хорды окружности образуют равные углы в центре.
Показать ответ
Ответ
Показать вопрос
Вопрос
Делит ли биссектриса из центра окружности хорду пополам?
Показать ответ
Ответ
Показать вопрос
Вопрос
Аккорды, равноудаленные от центра окружности, равны по длине?
Показать ответ
Ответ
Показать вопрос
Вопрос
Верно ли следующее утверждение?
Теорема о пересекающихся хордах утверждает, что произведения пересечений на пересекающихся хордах равны.

Показать ответ
Ответ
Показать вопрос
Вопрос
Диаметр делит круг на:
Показать ответ
Ответить
Полукруги.
Показать вопрос
Вопрос
Будут ли соответствующие длины дуг равными, если хорды имеют одинаковую длину?
Показать ответ
Ответ
Показать вопрос
Вопрос
Две малые дуги конгруэнтны, если:
Показать ответ
Ответ
их соответствующие хорды конгруэнтны.
Показать вопрос
Вопрос
Если одна хорда является биссектрисой другой хорды, то:
Показать ответ
Ответить
первая хорда является диаметром.
Показать вопрос
Вопрос
Определить «дугу» окружности
Показать ответ
Ответ
Дуга или длина дуги — это край сектора круга.
Показать вопрос
Вопрос
Определить меру дуги.
Показать ответ
Ответ
По отношению к длине дуги мерой дуги является угол, из которого исходит длина дуги.

Показать вопрос
Вопрос
Что такое длина сегмента?
Показать ответ
Ответить
Длина отрезка — это расстояние между двумя точками на отрезке.
Показать вопрос
Вопрос
Длину отрезка можно определить, используя координаты двух точек.
Показать ответ
Ответ
Показать вопрос
Вопрос
Середина G между точками A, (2, 4) и B, (3, -3) равна…
Показать ответ
Ответ
(2.5, 0.5)
Показать вопрос
Вопрос
Какова длина сегмента окружности?
Показать ответ
Ответить
Отрезок окружности может быть либо диаметром окружности, когда прямая проходит через центр окружности, либо хордой, если прямая проходит в любом другом месте, кроме центра окружности. .
Показать вопрос
Вопрос
Длина отрезка между точками C и B будет называться…
Показать ответ
Ответ
отрезок CB
Показать вопрос
Вопрос
Найдите длину отрезка круга радиусом 7 см, который стягивается на 60° в центре.

Показать ответ
Ответ
Показать вопрос
Вопрос
Найдите длину отрезка круга радиусом 5 см, который стягивается на 210° в центре.
Показать ответ
Ответить
90,66 см
Показать вопрос
Вопрос
Найти середину между началом координат и точкой Z (8, 6)
Показать ответ
Ответ
(4, 3)
Вопрос
6 Что
5 являются двумя компонентами отрезка
Показать ответ
Ответ
Дуга и хорда
Показать вопрос
Вопрос
Длина отрезка не может быть рассчитана, если заданы конечная точка и середина.
Показать ответ
Ответить
Показать вопрос
Вопрос
Длина отрезка рассчитывается по теореме Пифагора.
Показать ответ
Ответ
Показать вопрос
Вопрос
Средняя точка между определенной точкой J (2, 5) и другой точкой W равна (-1, 3). Найдите координаты точки W.
Показать ответ
Ответ
(-4, 1)
Показать вопрос
Длина дуги — Темы по тригонометрии
Темы | Дом
5
Определение радианной меры
с = r θ
Угол в 1 радиан
Доказательство теоремы
ОБЫЧНО считать, что буква s обозначает длину дуги, которая называется длиной дуги.
 В геометрии мы говорим, что дуга «стягивает» угол θ; буквально «тянется под».
В геометрии мы говорим, что дуга «стягивает» угол θ; буквально «тянется под».Длина окружности равна длине дуги. А отношение длины окружности к диаметру лежит в основе радианного измерения. Это соотношение является определением π.
№ = С
Д. Так как D = 2 r , то
№ = С
2 рили
С
р= 2π . Это отношение — 2π — длины окружности к радиусу называется радианной мерой 1 оборота, который равен четырем прямым углам в центре. Окружность опирается на эти четыре прямых угла.
Радианная мера θ = с
рТаким образом, мера радиана основана на отношении — числе — которое фактически находится в круг.
 Радианная мера — это действительное число, которое указывает отношение кривой линии к прямой, дуги к радиусу. Для отношения s к r действительно определяет уникальный центральный угол θ.
Радианная мера — это действительное число, которое указывает отношение кривой линии к прямой, дуги к радиусу. Для отношения s к r действительно определяет уникальный центральный угол θ.Теорема. В любых окружностях одинаковое отношение длины дуги к радиусу определяет уникальный центральный угол, на который опираются дуги. Пропорционально,
тогда и только тогда, когда
θ1 = θ2.
Ниже мы докажем эту теорему.
Пример 1. ;Если s равно 4 см, а r равно 5 см, то число , т. е. , является мерой центрального угла в радианах.
В этом центральном углу дуга составляет четыре пятых радиуса.
Пример 2. Угол 0,75 радиана означает, что дуга составляет три четверти радиуса. с = 0,75 r
Пример 3.
 В окружности радиусом 10 см центральный угол θ пересекает дугу 8 см.
В окружности радиусом 10 см центральный угол θ пересекает дугу 8 см.а) В чем измеряется этот угол в радианах?
Ответить . По определению:
θ = с
р= 8
10= .8 б) При том же центральном угле θ какова длина дуги в окружности, радиус которой равен 5 см?
Ответить . Для заданного центрального угла отношение дуги к радиусу одинаково во всех окружностях. Пропорционально,
8 : 10 = ? : 5
5 — это половина 10. Недостающий член будет половиной 8. Эта дуга равна 4 см.
Пример 4.
а) При центральном угле 2,35 радиан какое отношение имеет дуга к радиусу?
Ответ . Это число равно отношению. Дуга в 2,35 раза больше радиуса.
b) На какой квадрант круга приходится 2,35 радиана?
Ответ.  Так как π = 3,14, то
Так как π = 3,14, то №
2– это половина от этого: 1,57. 3π
2= 3,14 + 1,57 = 4,71. Таким образом, угол в 2,35 радиана больше 1,57, но меньше 3,14. Он попадает во второй квадрант.
в) Если радиус равен 10 см, а центральный угол равен 2,35 радиана, то какой длины дуга? Ответить . Пусть определение θ,
θ = с
рстать формулой для нахождения s :
с = r θ Следовательно,
с = 10 × 2,35 = 23,5 см
Из-за простоты этой формулы радианы используются исключительно в теоретической математике.
Задача 1.

а) Под центральным углом №
5, примерно какое отношение имеет а) дуга к радиусу? Возьми №3.
Радиан №
5равно этому отношению. Принимая №3, , то дуга составляет примерно три пятых радиуса.
b) Если радиус равен 15 см, какой примерно длины дуга?
с = r θ15 · 3
5= 9 см Задача 2. В окружности радиусом 4 см найдите длину дуги, на которую опирается каждый из этих углов. Снова возьмите π3.
а) №
4с = r θ4 · 3
4= 3 см б) №
6с = r θ4 · 3
6= 4 · ½ = 2 см в) 3π
2с = r θ4 · 3 · 3
2= 4 · 9
2= 2 · 9 = 18 см г) 2π.
 (Здесь длина дуги – это вся окружность!)
(Здесь длина дуги – это вся окружность!)s = r θ = 4 · 2π4 · 6 = 24 см Задача 3. В какой квадрант окружности попадает каждый угол, измеренный в радианах? (См. рисунок выше.)
а) θ = 2 2 радиана больше №
2, но меньше π. (См. рисунок выше.) Следовательно, θ = 2 попадает во второй квадрант.
б) θ = 5 5 радиан больше 3π
2, но меньше 2π. (См. рисунок выше.) Следовательно, θ = 5 попадает в четвертый квадрант.
в) θ = 14 14 радиан больше, чем 2 оборота, , но чуть меньше 2¼: 6,28 + 6,28 = 12,56. (См. рисунок выше.) Следовательно, θ = 14 попадает в первый квадрант.

Угол в 1 радиан
Угол в 1 радиан определяется как центральный угол, стягивающая дуга которого равна радиусу.
Это часто цитируется как определение меры в радианах. Но существует ли такой угол на самом деле? Можно ли нарисовать одну кривую линию, равную прямой? Можно нарисовать угол в 2π радиан. Это четыре прямых угла, опирающихся на окружность. Мы также можем нарисовать углы в радианах , , , , и их кратные. Это те углы, которые на самом деле возникают.
Можно определить угол в 1 радиан. Но опять же: существует ли такой угол?
См. Первые принципы элементов Евклида, Комментарий к определениям; обратите внимание, в частности, что определение утверждает только то, как будет использоваться слово или имя. Он не утверждает, что то, что было определено, существует.
Доказательство теоремы
В любых кругах одно и то же отношение длины дуги к радиусу
определяет уникальный центральный угол, на который опираются дуги;
и наоборот, равные центральные углы определяют одинаковое отношение
отношения длины дуги к радиусу.
Пропорционально,
тогда и только тогда, когда
θ1 = θ2.
Для,
тогда и только тогда, когда
Теперь 2π r — это длина окружности каждого круга. И каждая окружность представляет собой «дугу», которая стягивает четыре прямых угла в центре.
Но в одном и том же круге дуги имеют такое же отношение друг к другу, как и центральные углы, на которые они опираются. (Теорема 16.) Следовательно,
и
Следовательно, согласно строке (1),
тогда и только тогда, когда
θ1 = θ2.
Таким образом, одно и то же отношение длины дуги к радиусу определяет уникальный центральный угол, на который опираются дуги. Что мы и хотели доказать.
Следующая тема: Определения тригонометрических функций
острого углаТемы | Дом
Пожалуйста, сделайте пожертвование, чтобы TheMathPage оставался онлайн.

Даже 1 доллар поможет.Copyright © 2022 Лоуренс Спектор
Вопросы или комментарии?
Электронная почта: [email protected]
Центральный угол в геометрии — определение, формулы, примеры
Центральный угол — это угол, образованный двумя сторонами и имеющий вершину в центре окружности. Два плеча образуют два радиуса окружности, пересекающие дугу окружности в разных точках. Центральный угол помогает разделить круг на сектора. Кусок пиццы – хороший пример центрального угла. Круговая диаграмма состоит из нескольких секторов и помогает представлять различные величины.
Транспортир — это простой пример сектора с центральным углом 180º. Центральный угол также можно определить как угол, образованный дугой окружности в центре окружности. Давайте узнаем больше о теореме о центральном угле и о том, как найти центральный угол, с помощью примеров и часто задаваемых вопросов.
1. 
Определение центрального угла 2. Теорема центрального угла 3. Как найти центральный угол? 4. Решенные примеры центральных углов 5. Практические вопросы по центральным углам 6. Часто задаваемые вопросы о центральных углах Определение центрального угла
Центральный угол – это угол, образуемый дугой окружности в центре окружности. Радиус-векторы образуют плечи центрального угла. Другими словами, это угол, вершина которого является центром окружности с двумя линиями радиуса в качестве сторон, которые пересекаются в двух разных точках окружности. Когда эти две точки соединяются, они образуют дугу. Центральный угол — это угол, образуемый этой дугой в центре окружности. 90}{2 \pi r}\)
Здесь «s» — длина дуги, а «r» — радиус окружности. Это формула нахождения центрального угла в градусах.
 Чтобы найти центральный угол в радианах, нужно длину дуги разделить на длину радиуса окружности.
Чтобы найти центральный угол в радианах, нужно длину дуги разделить на длину радиуса окружности.Теорема центрального угла
Теорема: Угол, образуемый дугой в центре окружности, в два раза больше угла, образуемого дугой в любой другой точке окружности.
ИЛИ
Теорема о центральном угле утверждает, что центральный угол окружности в два раза больше угла, образуемого дугой в другом сегменте окружности.
∠AOB = 2 × ∠ACBЦентральный угол = 2 × Угол в другом сегменте
Как найти центральный угол?
Центральный угол — это угол между любыми двумя радиусами окружности. Чтобы найти центральный угол, нам нужно найти длину дуги (расстояние между двумя точками пересечения двух радиусов с окружностью) и длину радиуса. Приведенные ниже шаги показывают, как рассчитать центральный угол в радианах.
Чтобы найти центральный угол, нужно выполнить три простых шага.
\(\text{Центральный угол} = \dfrac{\text{Длина дуги}}{Радиус}\)
Важные примечания
Центральный угол окружности измеряется в радианах и шестидесятеричных единицах измерения.

Единица измерения радиан – радианы, а единица измерения шестидесятеричной системы – градусы.
Радиан × (180/π) = Шестидесятеричное число
Темы, связанные с центральным углом
Ознакомьтесь с этими интересными статьями, чтобы узнать о центральном угле и связанных с ним темах.
- Калькулятор центрального угла
- Прямой угол
- Острый угол
- Прямая линия
- Биссектриса
Пример 1: Сэм измеряет угол в треугольнике с помощью транспортира как 60º. Преобразуйте угол в радианы.
Решение:
Данный угол 60° выражен в шестидесятеричной мере.
Радиан = π/180° × Шестидесятеричный
Радиан = π/180° × 60°Радиан = π/3
Следовательно, центральный угол равен π/3 радиан.
Пример 2. Ларри нарисовал круг и разрезал его на четыре равные части, используя два диаметра.
 Как вы можете помочь Ларри измерить центральный угол или вписанный угол каждой части круга?
Как вы можете помочь Ларри измерить центральный угол или вписанный угол каждой части круга? Решение:
Ларри разрезает круг на четыре равные части.
Полный угол в окружности = 360°
Угол каждого квадранта = 360°/4
Следовательно, центральный угол квадранта равен 90°.
Пример 3: Салли отмечает дугу длиной 8 дюймов и измеряет ее центральный угол как 120 градусов. Каков радиус дуги?
Решение:Радиус дуги = 8 дюймов
Центральный угол = 120°
Центральный угол = (длина дуги × 360°)/(2 π × радиус)
радиус = (длина дуги × 360°)/ (2 π × центральный угол)
радиус = (8 × 360°) / (2 π × 120°)
радиус = 12/π
Следовательно, радиус равен 12/π дюймов.
Пример 4. Джим использует компас, чтобы нарисовать дугу длиной 11 дюймов и радиусом 7 дюймов. Как Джиму без транспортира вычислить угол этой дуги?
Решение:
Длина дуги = 11 дюймов
Радиус дуги = 7 дюймов
Угол дуги = (длина дуги × 360°)/(2 π r)
Угол = (11 × 360°)/ (2 × 22/7 × 7)
Угол = 90°
Следовательно, угол дуги равен 90°.
Пример 5: Джордж хочет создать сад в форме сектора радиусом 42 фута и центральным углом 120 градусов. Вычислите площадь травы, которая требуется для покрытия сада.
Решение:
Учитывая, что форма сада представляет собой сектор.
Радиус = 42 фута
Центральный угол = 120°
Площадь травы, необходимая для покрытия сада, равна площади сектора.
Площадь сектора = θ/360° × π r 2
Площадь =(120°/360°) × π × 42 2
Площадь = 1/3 × 22/7 × 42 × 42
Площадь = 22 × 2 × 42
Площадь = 1848
Следовательно, площадь сектора составляет 1848 квадратных футов.
перейти к слайдуперейти к слайдуперейти к слайдуперейти к слайдуперейти к слайду
Развивайте логическое мышление и повышайте его уверенность!
Благодаря гибкому учебному плану Куэмат выходит за рамки традиционных методов обучения.
 Мы делаем математику увлекательной. Проверьте, как!
Мы делаем математику увлекательной. Проверьте, как!Забронировать бесплатный пробный урок
перейти к слайдуперейти к слайдуперейти к слайдуперейти к слайдуперейти к слайду
Часто задаваемые вопросы по центральному углу
Что такое центральный угол?
Согласно определению центрального угла в геометрии, это угол, образуемый дугой окружности в центре окружности. Два радиуса составляют стороны угла. Центральный угол помогает узнать пропорцию кривой по отношению к окружности.
Как измерить центральный угол окружности?
Центральный угол окружности измеряется либо в градусах, либо в радианах. Измеряется с помощью длины дуги и длины радиуса окружности. Формула для измерения центрального угла (в радианах) = (длина дуги)/(длина радиуса).
Сколько градусов составляет центральный угол окружности?
Градус центрального угла — это угол, образованный дугой в центре окружности.

Что такое теорема о центральном угле?
Теорема о центральном угле утверждает, что угол, образуемый дугой в центре окружности, в два раза больше угла, образуемого в любой точке окружности.
Что такое центральный угол кривой?
Центральный угол кривой — это угол, образуемый ею в центре кривой. Линии в конце кривой соединяются в центре, образуя центральный угол, и эти линии являются плечами угла или радиусами.
Как найти центральный угол дуги?
Чтобы найти центральный угол дуги, соедините концы дуги с центром окружности, используя радиус-векторы. Угол между двумя радиусами представляет собой центральный угол дуги. Кроме того, формула для нахождения центрального угла дуги представляет собой длину дуги, деленную на радиус дуги.
Какой центральный угол образует полуокружность?
Центральный угол, образованный полуокружностью, равен 180°. Полукруг представляет собой половину круга, и, следовательно, центральный угол полукруга составляет половину полного угла круга.

Что такое вписанный угол?
Угол, образуемый дугой в любой точке окружности, называется вписанным углом. Берется дуга окружности и берется любая точка на окружности, отличная от дуги. Концы дуги соединяем с точкой на окружности, с линией. Угол между этими прямыми и точкой на окружности является вписанным углом.
В чем разница между центральным углом и вписанным углом?
Центральный угол — это угол, образуемый дугой в центре окружности. Вписанный угол — это угол, опирающийся на дугу в любой точке окружности. Центральный угол в два раза больше вписанного угла дуги окружности.
В чем разница между рефлекторным и выпуклым углами?
Как рефлекторный, так и выпуклый угол могут быть центральными углами окружности. Угол рефлекса больше 180 градусов и меньше 360 градусов. Угол выпуклости меньше 180 градусов. Для заданной дуги окружности сумма угла ее выпуклости и угла отражения равна полному углу. Полный угол равен 360 градусам. Угол выпуклости + угол отражения = полный угол
Скачать БЕСПЛАТНЫЕ учебные материалы
Рабочие листы углов
Центральные углы и дуги
Существует несколько различных углов, связанных с окружностями.
 Возможно, первое, что приходит на ум, это центральный угол. Это способность центрального угла проходить по дуге в 360 градусов, которая определяет количество градусов, которое обычно считается заключенным в окружность.
Возможно, первое, что приходит на ум, это центральный угол. Это способность центрального угла проходить по дуге в 360 градусов, которая определяет количество градусов, которое обычно считается заключенным в окружность.Центральные углы — это углы, образованные любыми двумя радиусами окружности. Вершина является центром окружности. На рисунке 1 ∠ AOB является центральным углом.
Рисунок 1 Центральный угол окружности.
Дуги
дуга окружности является непрерывной частью окружности. Он состоит из двух конечных точек и всех точек на окружности между этими конечными точками. Символ используется для обозначения дуги. Этот символ пишется над конечными точками, образующими дугу. Существует три типа дуг:
- Полуокружность: дуга, концы которой являются конечными точками диаметра. Он назван с использованием трех точек. Первая и третья точки являются конечными точками диаметра, а средняя точка является любой точкой дуги между конечными точками.

- Малая дуга: дуга, которая меньше полукруга. Второстепенная дуга называется с использованием только двух конечных точек дуги.
- Большая дуга: дуга, которая больше, чем полукруг. Он назван по трем пунктам. Первая и третья — это конечные точки, а средняя точка — это любая точка на дуге между конечными точками.
На рисунке 2 AC – это диаметр. представляет собой полукруг.
Рисунок 2 Диаметр круга и полукруга.
На рисунке 3 это малая дуга окружности P .
Рисунок 3 Малая дуга окружности.
На рисунке 4 это большая дуга окружности Q .
Рисунок 4 Большая дуга окружности.
Дуги измеряются тремя различными способами. Они измеряются в градусах и в единицах длины следующим образом:
- Градусная мера полукруга: Это 180°.
 Его единичная длина равна половине длины окружности.
Его единичная длина равна половине длины окружности.
- Градусная мера малой дуги: Определяется так же, как мера соответствующего центрального угла. Единица его длины — это часть окружности. Его длина всегда меньше половины окружности.
- Градусная мера большой дуги: Это 360° минус градусная мера малой дуги, которая имеет те же конечные точки, что и большая дуга. Его единичная длина является частью окружности и всегда больше половины окружности.
В этих примерах m обозначает градусную меру дуги AB , l обозначает длину дуги AB и обозначает саму дугу.
Пример 1: На рисунке 5 окружность O с диаметром AB имеет OB = 6 дюймов. Найдите (a) m и (b) l .
Рисунок 5 Градусная мера и длина дуги полукруга.
представляет собой полукруг. м = 180°.

Поскольку это полукруг, его длина составляет половину окружности.
Постулат 18 (Постулат сложения дуги): Если B является точкой на , то m + m = m .
Пример 2: Используйте рисунок 6 , чтобы найти м ( м = 60°, м = 150°).
Рис. 6 Использование постулата сложения дуги .
Пример 3: Используйте фигуру круга P с диаметром QS, чтобы ответить на следующие вопросы.
а. Найти м
б. Найти м
в. Найти м
д. Найти м
Рисунок 7 Нахождение градусных мер дуг.
и . m (Градусная мера малой дуги равна мере ее соответствующего центрального угла.)
б. = 180° ( является полукругом.)
с . м = 130°
д.
 м = 310° ( является большой дугой.) Градусная мера большой дуги равна 360° минус градусная мера малой дуги, которая имеет те же конечные точки, что и большая дуга.
м = 310° ( является большой дугой.) Градусная мера большой дуги равна 360° минус градусная мера малой дуги, которая имеет те же конечные точки, что и большая дуга.Следующие теоремы об дугах и центральных углах легко доказываются.
Теорема 68: В окружности, если два центральных угла имеют одинаковую меру, то соответствующие им малые дуги имеют одинаковую меру.
Теорема 69: В окружности, если две малые дуги имеют одинаковую меру, то их соответствующие центральные углы имеют одинаковую меру.
Пример 4: На рисунке 8 показана окружность O с диаметрами AC и BD. Если м ∠1 = 40°, найдите каждое из следующего.
Рисунок 8 Окружность с двумя диаметрами и хордой (не диаметральной).
а. m = 40° (мера малой дуги равна мере ее соответствующего центрального угла.)
б. м = 40° (Поскольку вертикальные углы имеют равные меры, м ∠1 = м ∠2.
 Тогда мера малой дуги равна мере соответствующего ей центрального угла.)
Тогда мера малой дуги равна мере соответствующего ей центрального угла.)в. M = 140 ° (по постулату 18 , M + M = M — это полукруга, SO M + 40 ° = 180 °, или M = 140519).
д. m ∠ DOA = 140° (мера центрального угла равна мере соответствующей ему малой дуги.)
эл. m ∠3 = 20° (Поскольку радиусы окружности равны, OD = OA . Поскольку, если две стороны треугольника равны, то углы, противолежащие этим сторонам, равны, m ∠3 = м ∠4. Поскольку сумма углов любого треугольника равна 180°, м ∠3 + м ∠4 + м ∠ DOA ∠ 02 = 9 м 8 0 9 9 9 м 9 9 0°. м ∠3 и м ∠ DOA с 140°,
ф. m ∠4 = 20° (как обсуждалось выше, m ∠3 = m ∠4.)
Тригонометрические функции
Тригонометрические функции — это периодические волновые функции, которые используются в математике и физике.
 Функции можно сгруппировать в три взаимосвязанные группы: основные функции: синус, косинус и тангенс. Взаимные функции: косеканс, секанс и котангенс. И дуговые функции: арксинус, арккосинус и арктангенс.
Функции можно сгруппировать в три взаимосвязанные группы: основные функции: синус, косинус и тангенс. Взаимные функции: косеканс, секанс и котангенс. И дуговые функции: арксинус, арккосинус и арктангенс.Калькуляторы часто имеют возможность переключения между системами радиан и градус-угол, но некоторые языки программирования и калькуляторы предоставляют реализации функций только с использованием радианов. Это связано с тем, что радианы являются предпочтительной единицей измерения углов в математике [1] и с использованием радианов функции наследуют полезные свойства.
Определение круга
Тригонометрические функции обычно вводятся с использованием геометрии прямоугольного треугольника, как показано на этой странице. Позже определения расширяются с использованием геометрии круга, как показано ниже. Этот веб-сайт называет их «круговыми определениями» тригонометрических функций.
Каждая из функций принимает угол в радианах в качестве входных данных и возвращает отношение в качестве выходных данных.
 Геометрически определения соответствуют кругу с радиусом и точкой, образующей угол (тета). Функции можно визуализировать с помощью геометрии единичного круга. Это можно увидеть, подставив в приведенные выше определения круга.
Геометрически определения соответствуют кругу с радиусом и точкой, образующей угол (тета). Функции можно визуализировать с помощью геометрии единичного круга. Это можно увидеть, подставив в приведенные выше определения круга.Основные функции
Основные функции — это наиболее часто используемые тригонометрические функции.
Синус
При заданном угле в радианах функция синуса возвращает синус угла. Например, при заданном угле в радианах функция синуса возвращает значение .
Этот пример можно визуализировать, нарисовав окружность и точку, соответствующую введенному углу. Поскольку функция возвращает соотношение, размер круга не имеет значения. Это показано ниже
Все возможные выходы функции могут быть отображены на единичном круге. Геометрически, если в качестве входных данных задан угол, функция синуса возвращает вертикальную составляющую точки, соответствующую углу на единичной окружности. Это показано в интерактиве ниже.
 Нажмите и перетащите любую синюю контрольную точку.
Нажмите и перетащите любую синюю контрольную точку.Косинус
При заданном угле в радианах функция косинуса возвращает косинус угла. Например, при заданном угле функция косинуса возвращает значение .
Этот пример можно визуализировать, нарисовав окружность и точку, соответствующую введенному углу. Размер круга не имеет значения, так как функция возвращает отношение. Этот круг показан ниже.
Все возможные выходы функции могут быть отображены на единичном круге. Геометрически, при заданном угле функция косинуса возвращает горизонтальную составляющую точки, соответствующую углу на единичной окружности. Это показано в интерактиве ниже. Нажмите и перетащите любую синюю контрольную точку.
Касательная
При заданном угле в радианах функция тангенса возвращает тангенс угла. Геометрически результат функции можно изобразить линией, проведенной касательной к точке на единичной окружности, образованной из угла. Ниже показан график функции тангенса.

Ниже приведен интерактивный элемент, который визуализирует вывод функции касательной к единичной окружности. Нажмите и перетащите любую синюю контрольную точку.
Взаимные функции
Функции секанс, косеканс и котангенс являются обратными функциями косинуса, синуса и тангенса. Как и основные функции, эти функции принимают угол на окружности в качестве входных данных и возвращают тригонометрическое соотношение. Каждая функция может быть выражена как величина, обратная ее аналогу.
Примечание: Примечание. Косеканс и секанс не так распространены, как котангенс, и в основном включены по историческим причинам.
Косеканс
Функция косеканса возвращает значение, обратное синусоидальной функции. Функция также может быть записана в терминах синуса.
На приведенном ниже графике черным цветом показаны выходные данные функции косеканса, а зеленым — функции синуса.
Секанс
Функция секанса возвращает обратную величину функции косинуса.
 Функция также может быть записана в терминах косинуса.
Функция также может быть записана в терминах косинуса.На приведенном ниже графике черным цветом показаны выходные данные функции секанса, а зеленым — функции косинуса.
Котангенс
Функция котангенса возвращает обратную величину функции тангенса. Функция также может быть записана в терминах тангенса.
Функция визуализирована на графике ниже, на котором функция тангенса показана зеленым цветом, а котангенс — черным.
Выход котангенса может быть визуализирован на единичной окружности как другая линия, касательная к точке на единичной окружности, соответствующей углу.
Рисунок 1: Тангенс и котангенс единичной окружности.
Функции дуги
Функции дуги обратны косинусу, синусу и тангенсу. Учитывая отношение двух сторон прямоугольного треугольника, функции возвращают соответствующий угол. Префикс arc используется, поскольку выходной угол возвращается в радианах, что соответствует длине дуги окружности окружности.

Примечание: При вводе действительных чисел функции дуги иногда возвращают связанный угол, а не истинный угол в координатной плоскости. Есть две стратегии возврата всех углов. 1) использовать приведенную ниже функцию ATAN2, которая принимает два числа в качестве входных данных, или 2) расширить определения функции дуги, чтобы использовать комплексные числа.
ArcSine
Функция ArcSine является обратной функцией синуса. Учитывая числовое значение, функция ArcSine возвращает соответствующий угол. График функции приведен ниже.
Обратите внимание, что функция возвращает только углы в пределах первого и четвертого квадрантов системы координат. Таким образом, следующее выражение верно не для всех углов.
Арккосинус
Функция ArcCosine обратна функции косинуса. Учитывая значение, функция ArcCosine возвращает соответствующий угол. График функции приведен ниже.
Обратите внимание, что функция возвращает только углы в пределах первого и второго квадрантов системы координат.
 Таким образом, следующее выражение верно не для всех углов.
Таким образом, следующее выражение верно не для всех углов.См. atan2 ниже для функции, которая возвращает углы во всех квадрантах.
Арктангенс
Функция ArcTangent обратна касательной. При заданном значении функция ArcTangent возвращает соответствующий угол. График функции приведен ниже.
Обратите внимание, что функция возвращает только углы в пределах первого и четвертого квадрантов системы координат. Таким образом, следующее выражение верно не для всех углов.
Однако показанная ниже улучшенная версия работает.
Арктангенс 2
Функция «Арктангенс 2» является улучшенной версией функций дуги и возвращает углы во всех квадрантах системы координат. Учитывая координаты точки, функция возвращает угол, соответствующий точке.
Примечание: Будьте внимательны при вводе аргументов функции
ATAN2в калькуляторах и языках программирования, так как их порядок не соответствует.