Какая линия ограничивает фигуру круг. Рэмп «геометрическая фигура круг
Круг, его части, их размеры и соотношения — вещи, с которыми ювелир постоянно сталкивается. Кольца, браслеты, касты, трубки, шары, спирали — много всего круглого приходится делать. Как же всё это посчитать, особенно если тебе посчастливилось в школе прогулять уроки геометрии?..
Давайте сначала рассмотрим, какие у круга бывают части и как они называются.
- Окружность — линия, ограничивающая круг.
- Дуга — часть окружности.
- Радиус — отрезок, соединяющий центр круга с какой-либо точкой окружности.
- Хорда — отрезок, соединяющий две точки окружности.
- Сегмент — часть круга, ограниченная хордой и дугой.
- Сектор — часть круга, ограниченная двумя радиусами и дугой.
Интересующие нас величины и их обозначения:
Теперь посмотрим, какие задачи, связанные с частями круга, приходится решать.
- Найти длину развертки какой-либо части кольца (браслета).
Задан диаметр и хорда (вариант: диаметр и центральный угол), найти длину дуги. - Есть рисунок на плоскости, надо узнать его размер в проекции после сгибания в дугу. Заданы длина дуги и диаметр, найти длину хорды.
- Узнать высоту детали, полученной сгибанием плоской заготовки в дугу. Варианты исходных данных: длина дуги и диаметр, длина дуги и хорда; найти высоту сегмента.
Задан диаметр и хорда (вариант: диаметр и центральный угол), найти длину дуги.Жизнь подскажет и другие примеры, а эти я привел только для того, чтобы показать необходимость задания каких-нибудь двух параметров для нахождения всех остальных. Вот этим мы и займемся. А именно, возьмем пять параметров сегмента: D, L, X, φ и H. Затем, выбирая из них все возможные пары, будем считать их исходными данными и путем мозгового штурма находить все остальные.
Чтобы зря не грузить читателя, подробных решений я приводить не буду, а приведу лишь результаты в виде формул (те случаи, где нет формального решения, я оговорю по ходу дела).
И еще одно замечание: о единицах измерения.
И только центральный угол во всех случаях измеряется в градусах и ни в чём другом. Потому что, как показывает практика, люди, проектирующие что-нибудь круглое, не склонны измерять углы в радианах. Фраза «угол пи на четыре» многих ставит в тупик, тогда как «угол сорок пять градусов» — понятна всем, так как это всего на пять градусов выше нормы. Однако, во всех формулах будет присутствовать в качестве промежуточной величины еще один угол — α. По смыслу это половина центрального угла, измеренная в радианах, но в этот смысл можно спокойно не вникать.
1. Даны диаметр D и длина дуги L
; длина хорды ;
высота сегмента ; центральный угол .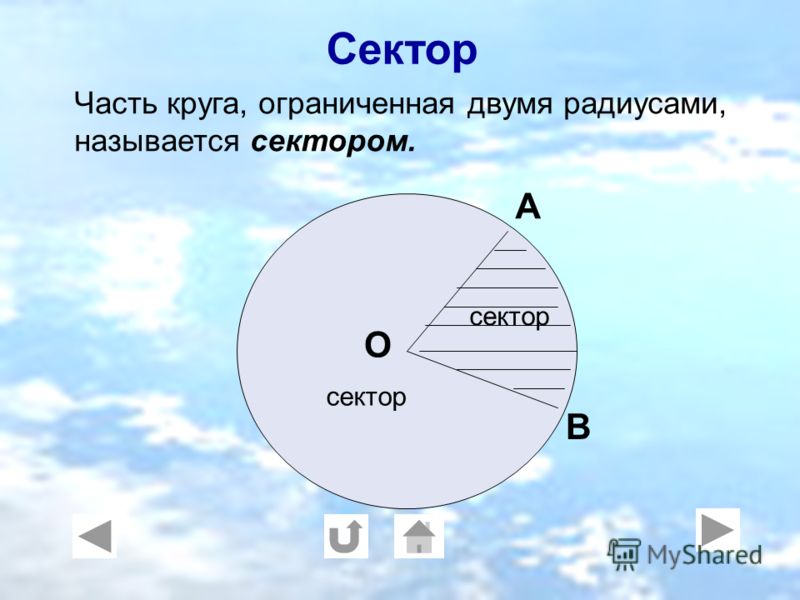
2. Даны диаметр D и длина хорды X
; длина дуги ;
высота сегмента ; центральный угол .
Поскольку хорда делит круг на два сегмента, у этой задачи не одно, а два решения. Чтобы получить второе, нужно в приведенных выше формулах заменить угол α на угол .
3. Даны диаметр D и центральный угол φ
; длина дуги ;
длина хорды ; высота сегмента .
4. Даны диаметр D и высота сегмента H
; длина дуги ;
длина хорды ; центральный угол .
6. Даны длина дуги L и центральный угол φ
; диаметр ;
длина хорды ; высота сегмента .
8. Даны длина хорды X и центральный угол φ
; длина дуги ;
диаметр ; высота сегмента .
9. Даны длина хорды X и высота сегмента H
; длина дуги ;
диаметр ; центральный угол .
10. Даны центральный угол φ и высота сегмента H
; диаметр ;
длина дуги ; длина хорды .
Внимательный читатель не мог не заметить, что я пропустил два варианта:
5. Даны длина дуги L и длина хорды X
7.
Даны длина дуги L и высота сегмента HЭто как раз те два неприятных случая, когда у задачи нет решения, которое можно было бы записать в виде формулы. А задача-то не такая уж редкая. Например, у вас есть плоская заготовка длины L, и вы хотите согнуть ее так, чтобы ее длина стала X (или высота стала H). Какого диаметра взять оправку (ригель)?
Задача эта сводится к решению уравнений:
; — в варианте 5
; — в варианте 7
и хоть они и не решаются аналитически, зато легко решаются программным способом. И я даже знаю, где взять такую программу: на этом самом сайте, под именем . Всё то, что я тут длинно рассказываю, она делает за микросекунды.
Для полноты картины добавим к результатам наших вычислений длину окружности и три значения площадей — круга, сектора и сегмента. (Площади нам очень помогут при вычислении массы всяких круглых и полукруглых деталей, но об этом — в отдельной статье.) Все эти величины вычисляются по одним и тем же формулам:
длина окружности ;
площадь сектора ;
площадь сегмента ;
И в заключение еще раз напомню о существовании абсолютно бесплатной программы, которая выполняет все перечисленные вычисления, освобождая вас от необходимости вспоминать, что такое арктангенс и где его искать.
Урок математики в 1 классе с ГУО на тему: «Геометрическая фигура: круг»
Цель: Познакомить с геометрической фигурой – кругом. Учить отличать круг от других геометрических фигур и правильно его называть. Закрепить названия цветов. Воспитывать уважительное отношение друг к другу.
I Организационный момент.
1. Кто ходит в гости по утрам,
Тот поступает мудро!
Тарам-парам, тарам-парам,
На то оно и утро!
Дети, какое сейчас время суток? (утро)
Следом за утром приходит … (день)
Часто из гостей возвращаются, когда наступает….(вечер) (С помощью картинок)
2. Посмотрите внимательно на картинки, что на них общее? Чем они все похожи? (на всех картинках нарисовано солнце)
II. Сообщение темы.
Солнце круглое. Сегодня на уроке мы познакомимся с геометрической фигурой – кругом. Поучимся отличать его от других фигур, будем находить предметы круглой формы.
III. Знакомство с фигурой.
1.К нам на урок пришёл гость – Винни-Пух.
Он прилетел на воздушных шарах. (Детям раздаются воздушные шары) Шар круглый. (Предложить обвести шар ладонью, пальцем.)
2. Посмотрите на Винни-Пуха, какие части тела у него круглые?
3. Вини-Пух очень любит покушать, и поэтому принёс с собой набор посуды (плоскостные изображения посуды круглой и квадратной формы). Но Вини-Пух любит есть только из посуды круглой формы. Помогите выбрать посуду круглой формы.
4. Пока Вини-Пух добирался до нас, у него разбилось несколько тарелок. Помогите, склейте их! (Дети собирают разрезную картинку)
Какой формы тарелка?
5. Посмотрите вокруг, найдите круглые предметы в нашем классе.
IV. Физ. минутка (хороводная игра)
Ровным кругом друг за другом
Мы идём за шагом шаг.
Дружно вместе все на месте
Делаем вот так!
(Водящий выбирается по очереди)
V. Закрепление изученного
1. У Вини-Пуха много друзей. Он принёс их портреты. (Изображения из геометрических фигур. Рассматриваем, обговариваем, кто это).
Скажите, что у них круглое?
2. Детям раздаются наборы геом.фигур. Найдите круг. (Тактильное обследование, прокатить круг по столу). Обговорить цвет и размер фигур.
Почему круг катится? (потому что нет углов)
Почему колёса круглые? (потому что нет углов, они могут катиться)
3. Выкладывание по образцу изображения из набора геом. фигур. (Друг Винни)
VI. Работа в тетради.
- Пальчиковая гимнастика.
- Объяснение задания.
- Работа в тетради.
VII. Итог: С какой фигурой познакомились? Чем занимались на уроке?
Сегодня мы будем делать цыплёнка. Каким цветом цыпленок? Правильно, жёлтый. Из всех кругов выбери только желтые круги. Потом отложи отдельно голубые круги и зеленые.
Сначала просто выкладываем цыплёнка на бумаге без клея, чтобы у малыша было понимание того, что мы делаем, это также поможет избежать ошибок при работе с клеем.
Большой жёлтый круг будет туловищем цыпленка. Куда мы его положим? (предлагаем ребенку самому выбрать место на листе бумаги).
Кружок поменьше будет головой. Где у нашего цыплёнка будет голова? (ребёнок пусть снова сам выберет место, в какую сторону будет смотреть цыплёнок: вверх на небо и солнце или вниз на травку, может он будет клевать зернышки. Помогайте малышу фантазировать, предлагайте варианты. Маленьким можно подсказать, посоветовать, но не настаивайте, пусть он сам сделает выбор)
Где маленький чёрный кружок? Это будет глаз. Маленький треугольник — клюв, два одинаковых треугольника — лапки. Разложи фигуры на свои места.
Чего не хватает нашему цыпленку? Правильно, крыльев! У нас есть ещё 2 жёлтых круга, один мы отложим — это будет солнце, а из второго сделаем крылья. Как ты думаешь, как из одного круга сделать два крыла? (с этим справятся дети от трёх лет. Пусть ребёнок подержит круг в руках, повертит, приложит к бумаге, возможно, у него появится ответ).
Мы разрежем круг напополам. Для этого давай найдем центр круга. Где центр (середина) у круга? (можно дать ребенку карандаш и предложить самому найти и отметить центр с тыльной (не цветной!) стороны листа.
Даже если точка не в центре, а где-то рядом, ничего страшного, похвалите кроху! Если ребёнок мал, сделайте все сами, объясняя каждое действие).
Через центр теперь проведем прямую линию, которая разделит круг напополам. По этой линии мы разрежем наш круг на две части. Получилось два крыла (обязательно разрезайте через точку (центр), указанную ребёнком, во-первых, ребёнок будет чувствовать, что его мнение важно для вас и вы прислушиваетесь к нему, а во-вторых — аппликация будет более художественной)
В ходе занятия для детей постарше можно объяснить, что такое полукруг (или вспомнить эту фигуру)
Посмотри, какие фигуры у нас получились. Это фигура называется полукруг. Пол круга — полукруг (повторяем несколько раз и предлагаем повторить название)
Где будут крылышки у нашего цыплёнка?
Цыплёнка выложили на бумаге, теперь можно приклеить его.
Цыплёнок готов.
Давай возьмём большие зелёные круги (или 1 круг) — это будет наша травка. Как ты думаешь, как из круга сделать травку? Правильно, снова разрезать напополам (повторяем шаги, как с крылышками: даём ребёнку отметить центр, разрезаем и приклеиваем снизу).
На небо приклеиваем солнышко.
Облака можно сделать разными способами:
1. Наклеить кружки внахлёст, формируя облако. Разный размер кружков сделает форму облака более натуральной.
2. Разрезать круги напополам и также наклеивать внахлёст.
У нас получилось по-другому: Поля захотела сложить круги напополам и приклеить только одну половину круга. Таким образом мы уже делали другие поделки и этот вариант ей понравился.
Когда бумага окончательно высохнет, можно дорисовать солнечные лучи и цветы на травке карандашом. Можно сделать это пластилином. Пусть малыш выбирает сам.
Форма круга является интересной с точки зрения оккультизма, магии и древних значений, придаваемых ей людьми. Все мельчайшие составляющие вокруг нас — атомы и молекулы — имеют круглую форму. Солнце круглое, Луна круглая, наша планета тоже круглая. Молекулы воды — основы всего живого — тоже имеют круглую форму.
Данная фигура в древних помыслах культур
Круг — это символ единства. Он присутствует в разных культурах во многих мельчайших деталях. Мы даже не придаем столько значения этой форме, как это делали наши предки.
Издавна круг — это знак бесконечной линии, который символизирует время и вечность. В дохристианскую эпоху он был древним знаком колеса солнца. Все точки в эквивалентны, линия круга не имеет ни начала, ни конца.
А центр круга был источником бесконечного вращения пространства и времени для масонов. Круг — конец всех фигур, недаром в нем была заключена тайна творения, по мнению масонов. Форма циферблата часов, имеющая тоже такую форму, обозначает собой непременное возвращение в точку отправления.
Эта фигура имеет глубокий магический и мистический состав, которым его наделили многие поколения людей из разных культур. Но что собой представляет круг как фигура в геометрии?
Что такое окружность
Часто понятие круга путают с понятием окружности.
Это немудрено, ведь они между собой очень тесно взаимосвязаны. Даже названия их схожи, что вызывает много путаницы в незрелых умах школьников. Чтобы разобраться, «кто есть кто», рассмотрим эти вопросы подробнее.
По определению, окружностью является такая кривая, которая замкнута, и каждая точка которой находится равноудалённо от точки, именуемой центром окружности.
Что необходимо знать и чем уметь пользоваться, чтобы построить окружность
Чтобы построить окружность, достаточно выбрать произвольную точку, которую можно обозначить как О (именно так в большинстве источников именуются центр окружности, не будем отходить от традиционных обозначений). Следующим этапом идет использование циркуля — инструмента для черчения, который состоит из двух частей с закрепленными на каждой из них либо иглой, либо пишущим элементом.
Эти две части соединены между собой шарниром, что позволяет выбирать произвольный радиус в определенных границах, связанных с длиной этих самых частей.
С помощью данного прибора в произвольную точку О устанавливается остриё циркуля, а карандашом уже очерчивается кривая, которая из итоге получается окружностью.
Какими величинами характеризуется окружность
Если соединить при помощи линейки центр окружности и любую произвольную точку на кривой, полученной в результате работы циркулем, мы получим Все такие отрезки, именуемые радиусами, будут равны. Если же соединить при помощи линейки прямой линией две точки на окружности и центр, мы получим ее диаметр.
Для окружности также характерно вычисление ее длины. Чтобы ее найти, необходимо знать либо диаметр, либо радиус окружности и воспользоваться формулой, представленной на рисунке ниже.
В этой формуле С — длина окружности, r — радиус окружности, d — диаметр, а число Пи — константа со значением 3,14.
Кстати, константа Пи была вычислена как раз из окружности.
Оказалось, что независимо от того, каков диаметр круга, соотношение длины окружности и диаметра одинаковое, равное примерно 3,14.
В чем же главное отличие круга от окружности
По сути, окружность — это линия. Она не является фигурой, она является кривой замкнутой линией, не имеющей ни конца, ни начала. А то пространство, что расположено внутри нее — это пустота. Простейшим примером окружности выступает обруч или, по-иному, хула-хуп, который дети используют на занятии физической культуры или же взрослые, для того чтобы создать себе стройную талию.
Теперь мы подошли к понятию того, что такое круг. Это в первую очередь фигура, то есть некое множество точек, ограниченных линией. В случае круга этой линией выступает окружность, рассмотренная выше. Выходит, что круг — это окружность, в середине которой не пустота, а множество точек пространства. Если натянуть на хула-хуп ткань, то мы уже не сможем его крутить, ведь он будет уже не окружностью — его пустота замещена тканью, куском пространства.
Перейдем непосредственно к понятию круга
Круг — геометрическая фигура, которая является частью плоскости, ограниченной окружностью.
Для него также характерны такие понятия, как радиус и диаметр, рассмотренные выше при определении окружности. И вычисляются они точно таким же образом. Радиус круга и радиус окружности являются идентичными по размеру. Соответственно, длина диаметра тоже аналогична в обоих случаях.
Так как круг является частью плоскости, то для него характерно наличие площади. Вычислить ее можно снова-таки при помощи радиуса и числа Пи. Формула выглядит следующими образом (см. рисунок ниже).
В данной формуле S — площадь, r — радиус круга. Число Пи — снова та же константа, равная 3,14.
Формула круга, для вычисления которой возможно также использовать диаметр, изменяется и принимает вид, представленный на следующем рисунке.
Одна четвертая появляется из того, что радиус — это 1/2 диаметра. Если радиус в квадрате, выходит, что соотношение преобразуется до вида:
r*r = 1/2*d*1/2*d;
Круг — это фигура, в которой можно выделить отдельные части, например сектор. Выглядит он как часть круга, которая ограничена отрезком дуги и его двумя радиусами, проведенными из центра.
Формула, которая позволяет вычислить площадь данного сектора, представлена на нижеследующем рисунке.
Использование фигуры в задачах с многоугольниками
Также круг — геометрическая фигура, которая часто используется в комплекте с другими фигурами. Например, такими как треугольник, трапеция, квадрат или ромб. Нередко встречаются задачи, где нужно найти площадь вписанного круга или, наоборот, описанного вокруг определенной фигуры.
Вписанный круг является таким, который соприкасается со всеми сторонами многоугольника. С каждой стороной любого многоугольника у окружности должна быть точка соприкосновения.
Для определенного вида многоугольника определение радиуса вписанной окружности вычисляется по отдельным правилам, которые доступно объясняются в курсе геометрии.
Можно привести для примера несколько из них. Формула круга, вписанного в многоугольники, может вычисляться следующим образом (ниже на фото приведено несколько примеров).
Несколько простых примеров из жизни, для того чтобы закрепить понимание разницы между кругом и окружностью
Перед нами Если он открыт, то железная каемка люка — это окружность. Если он закрыт, то крышка выступает в роли круга.
Окружностью также можно назвать любое кольцо — золотое, серебряное или бижутерию. Кольцо, которое держит на себе связку ключей, — тоже окружность.
А вот круглый магнит на холодильнике, тарелка или блинчики, испеченные бабушкой, -это круг.
Горлышко бутылки или банки при виде сверху — это окружность, а вот крышка, которая закроет это горлышко, при том же виде сверху является кругом.
Таких примеров можно привести множество, и для усвоения такого материала их нужно приводить, чтобы дети лучше улавливали связь теории с практикой.
Тема урока
Геометрические фигуры
Что такое геометрическая фигура
Геометрические фигуры – это совокупность множества точек, линий, поверхностей или тел, которые расположены на поверхности, плоскости или пространстве и формирует конечное количество линий.
Термин «фигура» в какой-то степени формально применяется к множеству точек, но как правило фигурой принято называть такие множества, которые расположенные на плоскости и ограничиваются конечным числом линий.
Точка и прямая — это основные геометрические фигуры, расположенные на плоскости.
К самым простым геометрическим фигурам на плоскости принадлежат — отрезок, луч и ломаная линия.
Что такое геометрия
Геометрия – это такая математическая наука, которая занимается изучением свойств геометрических фигур. Если дословно перевести на русский язык термин «геометрия», то он обозначает «землемерие», так как в стародавние времена основной задачей геометрии, как науки, стало измерение расстояний и площадей на поверхности земли.
Практическое применение геометрии бесценно во все времена и независимо от профессии. Без знаний геометрии не может обойтись ни рабочий, ни инженер, ни архитектор и даже художник.
В геометрии есть такой раздел, который занимается изучением различных фигур на плоскости и называется планиметрия.
Вам уже известно, что фигурой называют произвольное множество точек, находящиеся на плоскости.
К геометрическим фигурам принадлежат: точка, прямая, отрезок, луч, треугольник, квадрат, круг и другие фигуры, которые изучает планиметрия.
Точка
Из выше изученного материала вам уже известно, что точка относится к главным геометрическим фигурам. И хотя это самая малая геометрическая фигура, но она необходима для построения других фигур на плоскости, чертеже или изображении и является основой для всех остальных построений. Ведь построение более сложноватых геометрических фигур складывается из множества точек, характерных для данной фигуры.
В геометрии точки обозначают прописными буквами латинского алфавита, например, такими, как: А, В, С, D ….
А теперь подведем итог, и так, с математической точки зрения, точка является таким абстрактным объектом в пространстве, который не имеет объема, площади, длины и других характеристик, но остается одним из фундаментальных понятий в математике.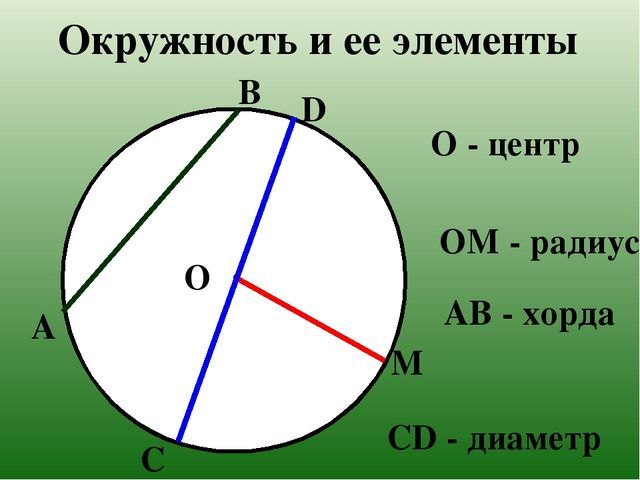
Точка – это такой нульмерный объект, которые не имеет определения. По определению Евклида, точкой называют то, что невозможно определить.
Прямая
Как и точка, прямая относится к фигурам на плоскости, которая не имеет определения, так как состоит из бесконечного множества точек, находящихся на одной линии, которая не имеет ни начала ни конца. Можно утверждать, что прямая линия бесконечна и не имеет предела.
Если же прямая начинается и заканчивается точкой, то она уже не является прямой и называется отрезком.
Но иногда прямая, с одной стороны имеет точку, а с другой нет. В таком случае прямая превращается в луч.
Если же взять прямую и на ее средине поставить точку, то она разобьет прямую на два противоположно направленных луча. Данные лучи являются дополнительными.
Если же перед вами несколько отрезков, соединенных между собой так, что конец первого отрезка становиться началом второго, а конец второго отрезка — началом третьего и т. д., и эти отрезки находятся не на одной прямой и при соединении имеют общую точку, то такая цепочка является ломаной линией.
Задание
Какая ломаная линия называется незамкнутой?
Как обозначается прямая?
Как называется ломаная линия, у которой четыре замкнутых звена?
Какое название имеет ломаная линия с тремя замкнутыми звеньями?
Когда конец последнего отрезка ломаной совпадает с началом 1-го отрезка, то такую ломаную линию называют замкнутой. Примером замкнутой ломаной является любой многоугольник.
Плоскость
Как точка и прямая, так и плоскость является первичным понятием, не имеет определения и у нее нельзя увидеть ни начала, ни конца. Поэтому, при рассмотрении плоскости, мы рассматриваем только ту ее часть, которая ограничивается замкнутой ломаной линией. Таким образом, плоскостью можно считать любую гладкую поверхность. Этой поверхностью может быть лист бумаги или стола.
Угол
Фигура, которая имеет два луча и вершину, называется углом. Место соединения лучей, является вершиной этого угла, а его сторонами считаются лучи, которые этот угол образуют.
Задание:
1. Как в тексте обозначают угол?
2. Какими единицами можно измерить угол?
3. Какие бывают углы?
Параллелограмм
Параллелограмм — это четырехугольник, противолежащие стороны которого попарно параллельны.
Прямоугольник, квадрат и ромб являются частными случаями параллелограмма.
Параллелограмм, имеющий прямые углы равные 90 градусам, является прямоугольником.
Квадрат — это тот же параллелограмм, у него и углы и стороны равны.
Что до определения ромба, то это такая геометрическая фигура, все стороны которого равны.
Кроме того, следует знать, что любой квадрат является ромбом, но не каждый ромб может быть квадратом.
Трапеция
При рассмотрении такой геометрической фигуры, как трапеция, можно сказать, что в частности она, как и четырехугольник имеет одну пару параллельных противолежащих сторон и является криволинейной.
Окружность и круг
Окружность — геометрическое место точек плоскости, равноудалённых от заданной точки, называемой центром, на заданное ненулевое расстояние, называемое её радиусом.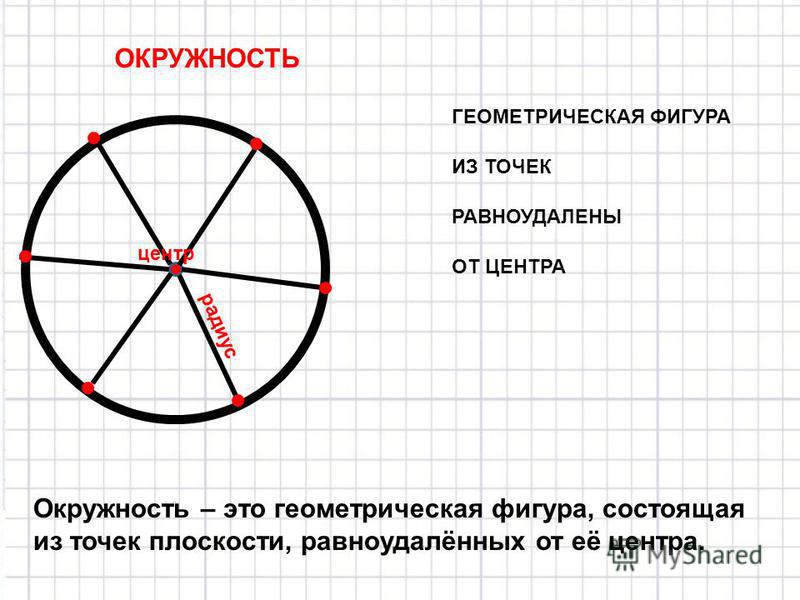
Треугольник
Также к простым геометрическим фигурам принадлежит и уже изучаемый вами треугольник. Это один из видов многоугольников, у которого часть плоскости ограничена тремя точками и тремя отрезками, которые соединяют эти точки попарно. Любой треугольник имеет три вершины и три стороны.
Задание: Какой треугольник называют вырожденным?
Многоугольник
К многоугольникам относятся геометрические фигуры разных форм, у которых замкнутая ломаная линия.
В многоугольнике все точки, которые соединяют отрезки, являются его вершинами. А отрезки, из которых состоит многоугольник, являются его сторонами.
А известно ли вам, что возникновение геометрии уходит в глубину веков и связано с развитием различных ремесел, культуры, искусства и наблюдением за окружающим миром. Да и название геометрических фигур является тому подтверждением, так как их термины, возникли не просто так, а благодаря своей схожести и подобию.
Ведь термин «трапеция» в переводе с древнегреческого языка от слова «трапезион» обозначает столик, трапеза и другие производные слова.
«Конус» произошел от греческого слова «конос», что в переводе звучит, как сосновая шишка.
«Линия» имеет латинские корни и происходит от слова «линум», в переводе это звучит, как льняная нить.
А знаете ли вы, что если взять геометрические фигуры с одинаковым периметром, то среди них обладателем самой большой площади оказался круг.
Окружность и круг в школьном учебнике и в окружающем мире
- Авторы
- Руководители
- Файлы работы
- Наградные документы
Чудинов В.Е. 1
1Муниципальное автономное общеобразовательное учреждение «Средняя общеобразовательная школа №24
Паршева В.В. 1
1Муниципальное автономное общеобразовательное учреждение «Средняя общеобразовательная школа №24
Автор работы награжден дипломом победителя II степени
Диплом школьникаСвидетельство руководителя
Текст работы размещён без изображений и формул.
Полная версия работы доступна во вкладке «Файлы работы» в формате PDF
ВВЕДЕНИЕ
Окружность и круг – это геометрические фигуры, которые с древних времен до настоящего времени нашли широкое применение в жизни людей. Формы круга, окружности мы встречаем повсюду: это и колесо машины, и велосипеда, и монеты, и диск Луны. На первый взгляд, кажется, что круг — очень обычная и простая фигура, но это далеко не так. На самом деле окружность и круг таят в себе множество загадок и тайн, имеют увлекательную историю их изучения. Математики стали активно заниматься изучением этих геометрических фигур очень давно.
Окружность и круг – это понятия, которые изучаются в школьном курсе математики с начальных классов, но тем не менее нас заинтересовали некоторые вопросы, связанные с этими понятиями. Мы обнаружили , что в учебниках разных авторов одно и то же понятие окружности определяются по разному, нам неизвестна история появления понятий окружность и круг, интересно было узнать как велико применение окружности и круга.
Гипотеза: выполнив работу, мы уточним понятие окружности, установим разные способы построения окружности, способы нахождения центра и измерения диаметра окружности.
Объект исследования: окружность.
Предмет исследования: обобщение сведений об окружности.
Задачи исследования:
1). Изучить историю возникновения понятия окружности и циркуля.
2). Проанализировать и обобщить информацию об окружности.
3).Проверить экспериментальным путем способы: построения окружности, нахождения центра и диаметра окружности.
4). Проанализировать информацию о применении окружности в окружающей жизни.
Методы исследования:
— анализ учебников по геометрии и справочной литературы;
— компьютерное моделирование в ИГС GEOGEBRA
ОСНОВНАЯ ЧАСТЬ
Окружность и круг в школьном учебнике и в окружающем мире
1.
1. Истории возникновения окружности.
Круг и окружность – одни из самых древнейших фигур в геометрии. Первобытным людям очень важна была форма предметов, которые их окружали. Свои названия круг и окружность получили только в Древней Греции, хотя были известны задолго до Античности. Философы древнего мира придавали окружности большое значение. Древние греки видели в ней венец совершенства. Античные ученые рассматривали прямые и окружности как единственный пример «совершенных» фигур, потому что в геометрии считались допустимыми только построения с помощью циркуля и линейки, а движение планет моделировалось как наложение вращений по окружностям. Теории окружностей посвящена III книга «Начал» Евклида. Изучением и применением окружностей занимался Архимед. Архимед в III веке до н.э. обосновал в свое небольшой работе «Измерение круг» следующее положение: отношение любой окружности к ее диаметру меньше 3 целых 1/7 и больше 3 целых 10/71. Он доказал, что площадь круга площади любого описанного около него правильного многоугольника, но больше площади вписанного; что при неограниченном удвоении числа сторон разность площадей этих многоугольников равна нулю; при неограниченном удвоении его сторон.
Для вычисления площади круга остается найти значение, к которому стремится значение площади правильного многоугольника. Пифагор считал круг воплощением нескончаемого Времени и Пространства, символом всего сущего, Вселенной. “Из всех фигур прекраснейшая – круг”, – считал Пифагор.
Окружность, наряду с прямой, является самой распространённой фигурой практически во всех областях человеческой деятельности. Еще с самых давних времен люди пользовались для перевозки тяжестей круглыми бревнами. История исследования и применения окружности уходит в глубокую древность; особенную важность придало этой теме изобретение колеса. Окружность уникальна тем, что каждая ее точка равноудалена от центра. Именно благодаря этому свойству стало возможным изобретение колеса, потому что все точки обода колеса должны быть на одинаковом расстоянии от оси. Достоверно известно, что тележное колесо существовало в Месопотамии еще в 3500-3000 гг. до н. э.
Вывод.
Изучив информацию из различных источников мы сделали вывод, что окружность и круг люди в своей жизни используют с незапамятных времен.
1.2. Истории возникновения циркуля.
Латинское слово «circulus» означает «окружность, круг». В русский язык слово «циркуль», вероятно, пришло через польский или немецкий языки – от слов «cyrkul» или «Zirkel».
Ци́ркуль (от лат. circulus — круг, окружность) — инструмент для черчения окружностей и дуг, также может быть использован для измерения расстояний, в частности, на картах. Может быть использован в геометрии, черчении, для других целей в жизни человека.
История циркуля началась еще несколько тысячелетий назад. Легенды и мифы Древней Греции повествуют нам о том, что этот прибор был изобретен Талосом – племянником Дедала. Талос изобрел устройство, позволяющее рисовать абсолютно идеальный круг, соединив два одинаковых по длине стержня.
В ходе раскопок древнего кургана во Франции археологами был найден циркуль, возраст которого составляет около двух тысяч лет. Чуть меньше возраст бронзовых циркулей, найденных во время археологических раскопок древнегреческого города Помпеи. Их возраст насчитывает около 1900 лет. В древней Руси для вычерчивания окружности тоже применялся циркуль. С его помощью наши предки создавали геометрические узоры. В древности на Руси циркуль называли «кружало». Стальные циркули (конец VIII века — середина XI в.) археологи нашли при раскопках в Новгороде и в Ленском районе Архангельской области в урочище около д. Тохта на берегу реки Яренга (1928г. А.С. Сидоров).
2.1.Сравнение понятий окружности в различных источниках.
В учебной литературе приведены следующие понятия окружности.
Анатасян Л.С. окружностью называет геометрическую фигуру, состоящую из всех точек плоскости, расположенных на заданном расстоянии от данной точки [1].
А.Г.Мерзляк окружностью считает геометрическое место точек, равноудаленных от заданной точки [7].
Глейзер Г.Д. окружностью называет геометрическую фигуру, состоящую из всех точек плоскости, находящихся на данном расстоянии от данной точки этой же плоскости [ 3].
Приведем пример: электрическая лампочка на столбе освещает круг, ограниченный окружностью, все точки которой удалены от лампочки на одно и то же расстояние. По первому определению центром окружности может быть лампочка и радиусом – отрезок, соединяющий лампочку и любую точку окружности. С другой стороны: центром может быть основание столба и радиусом – отрезок, соединяющий основание столба и любую точку окружности. Следовательно, окружность имеет два центра и два радиуса, чего не может быть.
Первое определение неточное. Видимо авторы предполагают, что ученик помнит, что все фигуры в планиметрии, которая изучается в 7 классе, принадлежат одной плоскости.
Мы провели несколько экспериментов.
1. На поверхности шара провели замкнутую линию. Все ее точки равноудалены от одной точки — центра сферы, но линия не является окружностью, т. к, точки линии и центр сферы не лежат в одной плоскости.
2 . Построили сферу, цилиндр, конус и сечения их плоскостями в ИГС GeoGebra .
Сечения сферы – это круги, они ограничены окружностями. Таким образом, на сфере можно изобразить окружность – это линия пересечения поверхности шара (сферы) с плоскостью, которая пересекает шар.
Е сли построить секущую плоскость цилиндра перпендикулярно его оси, то в сечении получаются равные круги, на боковой поверхности – равные окружности, центры которых находятся на оси цилиндра.
Е сли построить секущую плоскость конуса перпендикулярно его оси, то в сечении получаются круги, на боковой поверхности – окружности разных радиусов, центры которых находятся на оси конуса.
Итак, можно сделать вывод, что все точки окружности и ее центр должны находиться в одной плоскости, в противном случае эта линия не будет окружностью.
2 .2. Точки, отрезки, связанные с понятием окружность.
Отрезок, соединяющий центр окружности с любой ее точкой, называется радиусом окружности.
О трезок, соединяющий две точки окружности, называется ее хордой. Хорда, проходящая через центр окружности, называется диаметром. Диаметр окружности в два раза больше ее радиуса. Радиусы одной окружности равны между собой, следовательно, и диаметры одной окружности равны между собой. Две окружности равны, если равны их радиусы (диаметры).Центр окружности является серединой любого диаметра.
Взаимное расположение точек:
— Все точки окружности удалены от центра на одно и то же расстояние; например АС=r.
— Все точки, расположенные внутри окружности, удалены от центра меньше, чем на радиус; например, ОD<r.
— Все точки, расположенные вне окружности, удалены от центра больше, чем на радиус; например, ОH>r.
Возник проблемный вопрос: сколько точек надо выбрать, чтобы построить единственную окружность, проходящую через эту точку?
П остроив в ИГС GeoGebra окружности, мы пришли к следующим выводам:
-Через одну точку можно провести множество окружностей: центр и радиус выбираются произвольно.
— Через две точки можно провести множество окружностей, их центры лежат на серединном перпендикуляре к отрезку, соединяющего выбранные точки, радиус определяется точкой на серединном перпендикуляре и одной из выбранных точек.
— Окружность однозначно определяется тремя точками.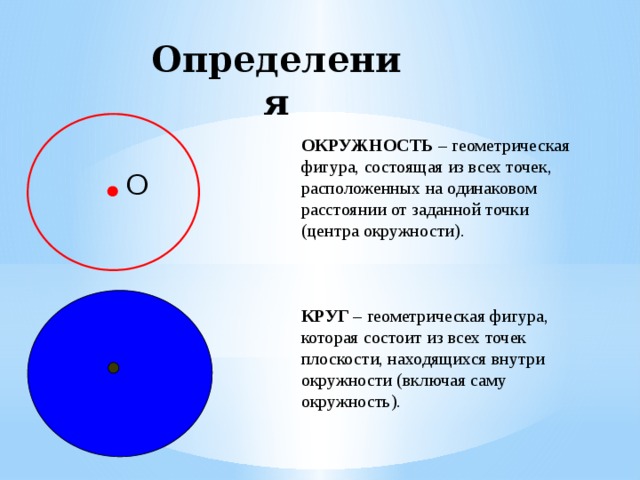
Также, при построении окружности в ИГС GeoGebra, мы подтвердили следующие свойства окружности:
— Когда точка движется по плоскости — расстояние между этой точкой и некоторой неподвижной точкой остается постоянным, она описывает окружность.
— Окружность не имеет конца. Мы можем двигать сколько угодно острие карандаша по окружности и все же конца окружности не найдем.
— Окружность может скользить сама по себе. Если начертим на бумаге вокруг монеты окружность, то края монеты и окружность на бумаге будут представлять собой одну и ту же окружность. Можем медленно вращать монету таким образом, чтобы края ее все время совпадали с окружностью, начерченной на бумаге. Другие кривые (эллипс, парабола, гипербола) не могут скользить вдоль самих себя.
Выводы. 1. Окружность определяется тремя точками плоскости.
2.
Окружность обладает очень важным, замечательным свойством: все точки окружности удалены от центра на одно и то же расстояние, поэтому при вращении вокруг центра окружность будет скользить по самой себе (т. е. копия окружности скользит по самой окружности).
2.3. Способы изображения окружности.
В древности, для того, чтобы очертить круг, брали колышек и веревку. К веревке прикрепляли уголек , кусочек мела, заостренную палочку и чертили окружность. Позже веревку заменили тонкой веточкой или дощечкой. Это позволило очертить окружности только заданного радиуса, Наконец, и эта проблема была решена – к одной дощечке прикрепили другую и скрепили их между собой. Таким образом, был изобретен циркуль.
Все мы использовали циркуль в школе на уроках геометрии и черчения для рисования окружностей и дуг. Как правило, циркуль изготавливают из металла. Он представляет собой две одинаковые по длине «ножки», на конце одной их них находится игла, а другой – грифель.
Есть также циркули с одной ножкой с иглой на конце, а в качестве второй выступает карандаш. Однако циркуль применяется не только для рисования окружностей, но и для измерения расстояний, например на картах. В таком случае используют циркуль с иглами на концах, без грифеля. В измерительном циркуле на концах обеих ножек находятся иглы.
Алгоритм построения окружности с помощью циркуля.
1) Отметили в тетради точку и назвали ее буквой О (это будет центр окружности).
2) Взяли циркуль и линейку, отмерили нужное расстояние (например, 4см) между «ножками» циркуля.
3) Поставили иголку циркуля в точку О, одной рукой придерживая лист, а другой чертили окружность «ножкой» циркуля, касаясь бумаги грифелем, провели замкнутую линию.
4) Все время контролировали сохранение нужного радиуса, удерживали циркуль за головку. Наклон делали в сторону движения.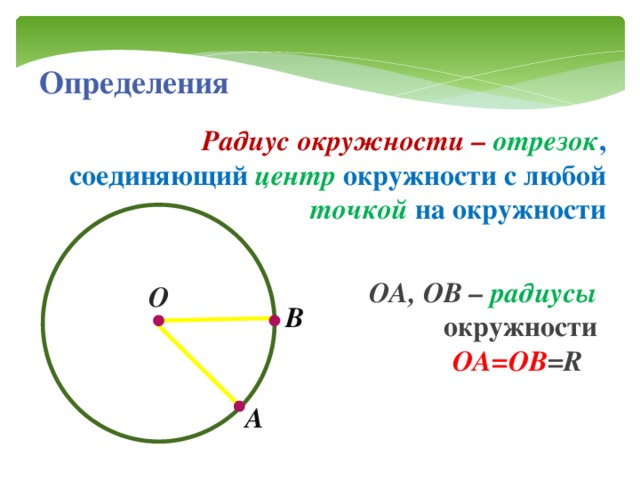
Правила работы с циркулем. Циркуль – это чертежный инструмент. На одном конце у него находится игла, на другом грифель или карандаш. С ним надо обращаться осторожно, чтобы не уколоться и не поломать грифель карандаша.
Изображая окружность, мы придерживались правил работы с циркулем: циркуль готов к работе, когда иголка циркуля и грифель находятся на одном уровне. Взять нужный размер и затянуть винт. При проведении окружности нужно циркуль держать за головку.
НЕЛЬЗЯ:
— при работе с циркулем оставлять циркуль в раскрытом виде;
— подносить циркуль иглой к лицу;
— передавать циркуль соседу «иглой вперед»;
— держать циркуль вверх концами;
Окончив, работу циркуль надо положить в футляр.
Чтобы построить окружность на местности (например, при разметке ф утбольного поля, площадки для игры в баскетбол, для разметки круглой клумбы, круглого бассейна) применяют веревку, на одном конце которой закреплен стержень, а на другом мел или острый предмет, которыми чертят окружность.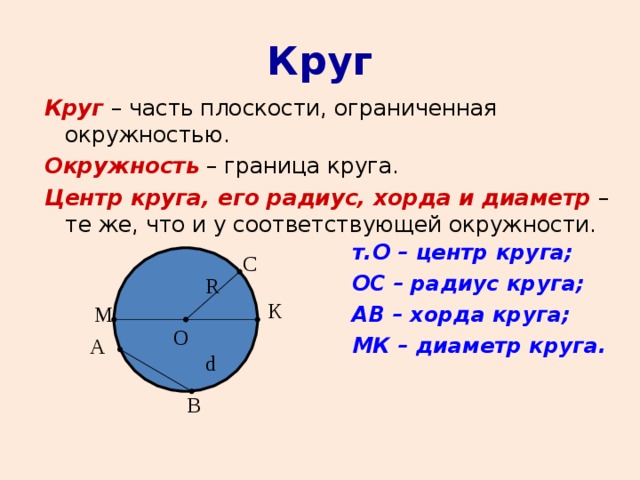
2.4. Способы нахождения центра окружности.
Начертив окружность с помощью циркуля, мы легко определим её центр по точке иглы в центе. Но бывают случаи, когда есть окружность, но не обозначен центр. Для того, чтобы найти центр окружности, мы провели несколько экспериментов.
Первый эксперимент: «Как найти центр круга (окружности), если круг вырезан из бумаги?»
Наша окружность была начерчена на листе бумаги. Мы обвели её по периметру, положив на лист бумаги, затем вырезали по начерченной линии круг. Затем согнули его вчетверо и нашли центр. Он находился точно на линии пересечения сгибов.
Второй эксперимент: «Как найти центр окружности с помощью прямоугольного треугольника». Мы действовали по следующему алгоритму.
1.Приложили прямоугольный треугольник вершиной к любой точке окружности во внутренней части окружности так, чтобы вершина прямого угла была на окружности, а катеты пересекали окружность в двух точках.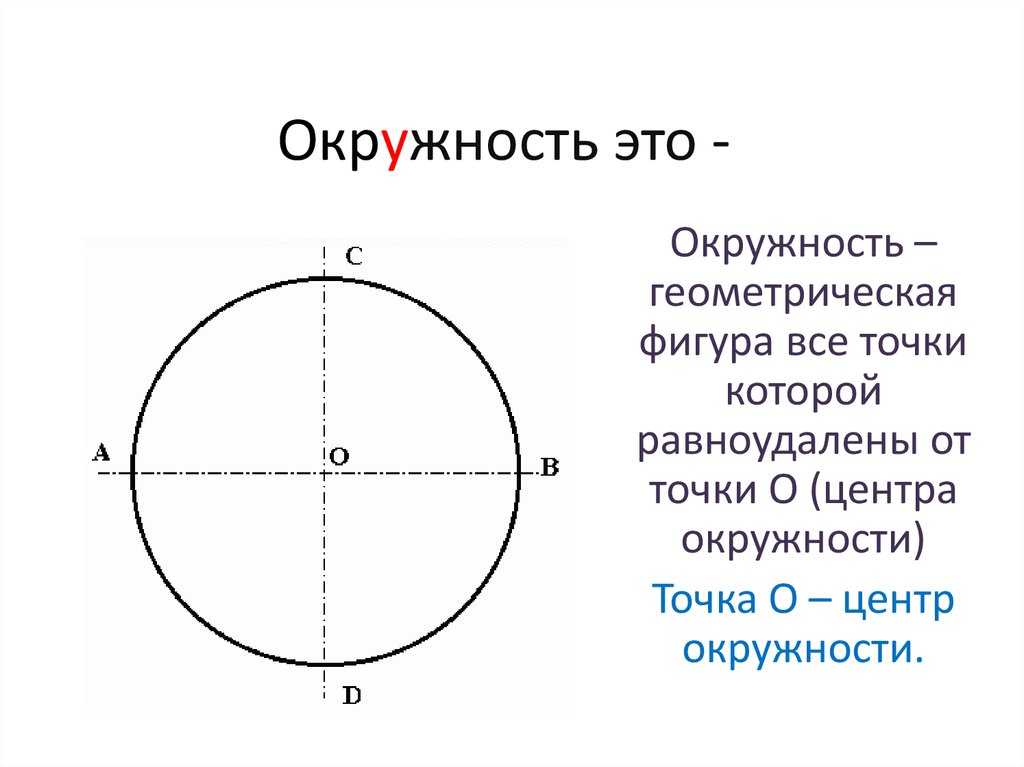
2. Провели прямую через эти две точки (линию по гипотенузе треугольника).
3. Изменили положение треугольника, вершина должна быть на окружности, а катеты пересекать окружность. Через точки пересечения катетов с окружностью провели прямую (треугольник повернули на некоторый угол и операции 1 и 2 повторили).
4.Получили точку пересечения полученных отрезков. Она и является центром окружности.
Таким образом, оказалось, что какой-бы прямой угол с помощью прямоугольного треугольника не вписать в окружность – гипотенуза полученного треугольника является диаметром окружности.
Т ретий эксперимент: «Нахождение центра окружности (круга) с помощью угольника – центроискателя».
2.5. Способы нахождения диаметра окружности.
Диа́метр — отрезок, соединяющий две точки на окружности и проходящий через центр окружности, а также длина этого отрезка.
Диаметр равен двум радиусам. Обобщённо диаметром фигуры называется максимальное расстояние между точками этой фигуры, или точная верхняя грань всевозможных расстояний, если максимальное не существует.
К ак же измерить диаметр круга? Мы провели эксперимент по измерению диаметра круга с помощью линейки и двух чертежных треугольников.
На производстве диаметр можно вычислить несколькими способами.
1 . С помощью специального инструмента – штангенциркулем. Штангенци́ркуль — это универсальный измерительный прибор, предназначенный для высокоточных измерений наружных и внутренних линейных размеров, а также глубин отверстий. Штангенциркуль — один из самых распространённых приборов измерения, благодаря простой конструкции, удобству в обращении и быстроте в работе.
2. С помощью мерной вилки (например измерить диаметр ствола)
3 .
С помощью центроискателя.
4. С помощью рулетки измерить длину окружности (обхват ствола) и вычислить по формуле: L=2πr; 2r=d; L=πd.d=L/π.
5. В тетради в клеточку окружность можно нарисовать по числовым заклинаниям (Приложение 1)
3. Применение окружности в разных сферах жизни.
Круг и окружность в жизни человека имеют очень важную роль, и в жизни без круглых предметов обойтись невозможно. Рассмотрим поподробнее применение свойств окружности.
1. Применение свойства окружности в технике и быту: колеса телег, вагонов, автомобилей делаются круглые, точки их окружности равноудалены от центра, поэтому, когда колеса катятся, высота оси не меняется и телега, вагон, повозка движутся плавно.
2. Применение кругов и окружностей в промышленности:
— В промышленности, для того чтобы сделать какую- либо деталь круглой формы, обрабатывают ее на станке.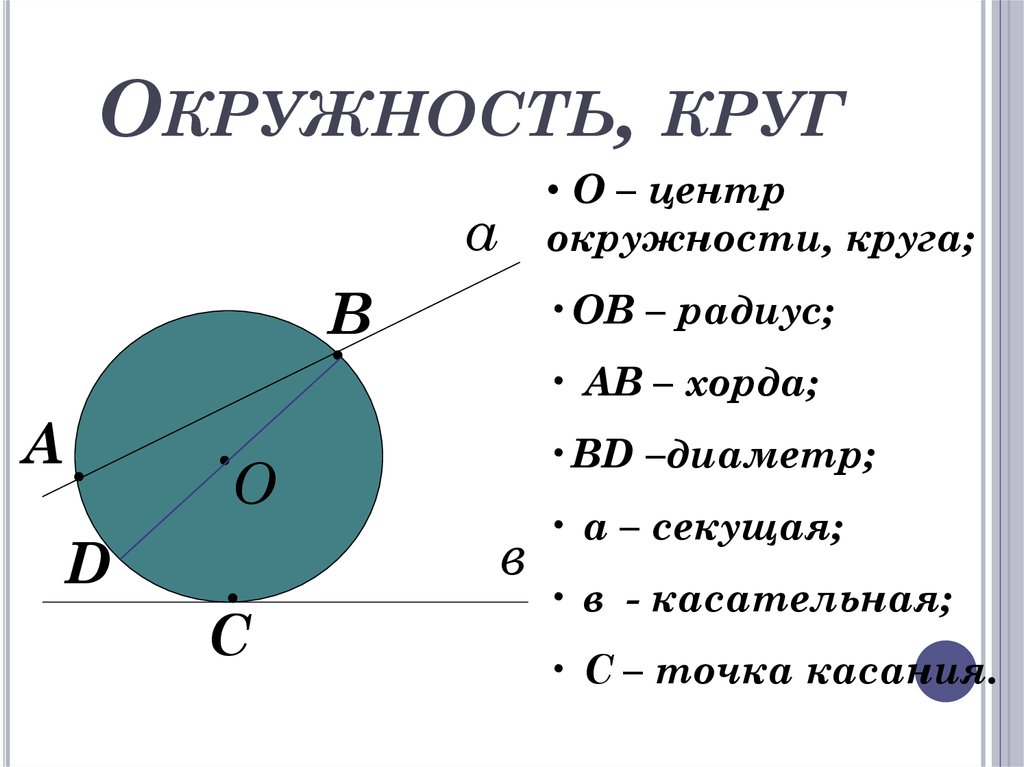
Обрабатываемая деталь укрепляется специальным механизмом, который вращается вместе с осью станка. Нож станка приближается по мере надобности к обрабатываемой детали при помощи другого механизма. Когда деталь вращается, нож срезает выступающие части. Все точки детали, через которые прошел нож, находятся от центра на расстоянии, равном расстоянию от центра до верхушки ножа. Части детали, находящиеся ближе к центру, остаются незатронутыми ножом. После некоторого числа оборотов, во время которых деталь продолжает обрабатываться, нож пройдет через всю наружную часть детали. Край детали становится окружностью, потому что все точки ее находятся на одинаковом расстоянии от центра, равном расстоянию от центра до верхушки ножа.
— Шкивы машин также круглые. Если бы шкивы не были совершенно круглыми, приводной ремень не был бы все время одинаково натянут и благодаря этому мог бы порваться.
— Точильный камень – пример применения круга для заточки ножей и топоров.
— Круглая пила употребляется для пилки дров, а также в столярных мастерских.
3. Применение окружности и круга в повседневной жизни: круг и окружность используется не только в средствах передвижения (в автомобилях, велосипедах, самокатах мотоциклах, в роликовых коньках), но и в различных станках, спортивных сооружениях, и в спортивных залах, и на детских площадках и в парке аттракционов. Форму круга имеют монеты, часы, дорожные знаки, диск луны, солнечный круг, праздничный пирог, пуговицы, клумба, спортивные кольца, арена цирка, стол, диск для компьютера.
Проанализировав варианты применения окружности, мы поняли, что знания о круге и окружности позволяют человеку решать многие практические задачи в повседневной жизни: разбить клумбу или фонтан, сделать круглую крышу, окно или крышку, сшить головной убор, связать салфетку, сделать елочную игрушку, сделать выкройку платья или юбки, нарисовать узор и т.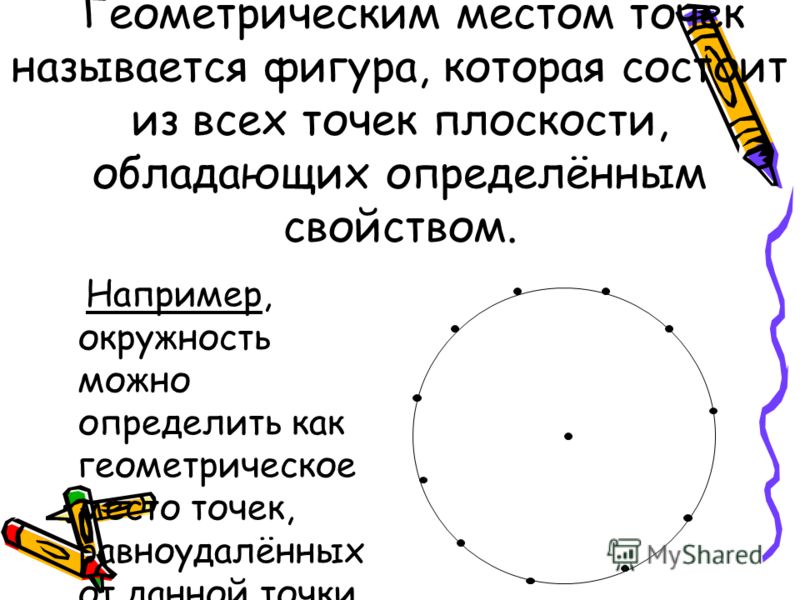
п.
ЗАКЛЮЧЕНИЕ
Цель и задачи исследования выполнены. Наша гипотеза подтвердилась: мы уточним понятие окружности, установим разные способы построения окружности, способы нахождения центра и измерения диаметра окружности.
Изучив материалы школьных учебников и, проделав собственные измерительные исследования с окружностью, мы пришли к следующим выводам:
— с незапамятных времен люди используют в своей жизни круг и окружность;
— все точки окружности и ее центр должны находиться в одной плоскости, в противном случае эта линия не будет окружностью;
— все точки окружности удалены от центра на одно и то же расстояние, поэтому при вращении вокруг центра окружность будет скользить по самой себе;
— чтобы построить окружность надо воспользоваться циркулем;
— центр окружности можно найти разными способами.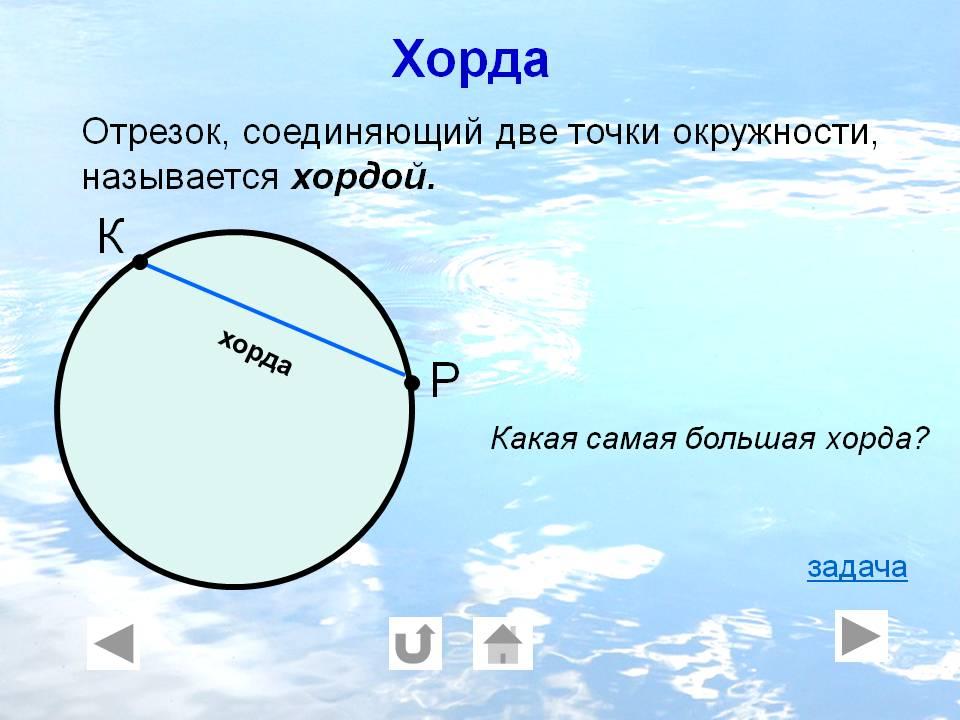
— мы поняли, что знания о круге и окружности позволяют человеку решать многие практические задачи в повседневной жизни.
Окружность – это единственная кривая, которая может “скользить сама по себе”, вращаясь вокруг центра. Это свойство окружности дает ответ на вопросы, почему для ее вычерчивания используют циркуль, и почему колеса делают круглыми, а не квадратными или треугольными. Круг в жизни человека имеет очень важную роль, и без использования круглых предметов обойтись невозможно.
ИСТОЧНИКИ ИНФОРМАЦИИ
1. Атанасян Л. С., Бутузов В.Ф., Кадомцев С.Б., Позняк Э.Г., Юдина И.И. Геометрия, 7-9: Учебник для общеобразовательных учреждений //М., «Просвещение», 2005- 384с.;
2. Барыбин К.С. Геометрия для 6-8 классов средней школы //М.,»Просвещение», 1966-318с.;
3. Глейзер Г.Д., Геометрия. Учебное пособие для 6-9 классов сменной школы.
Под редакцией Скопец З.А.//М., «Просвещение», 1978-120с.;
4. Депман И.Я., Виленкин Н.Я. За страницами учебника математики: Пособие для учащихся 5-6 классов средней школы //М.,»Просвещение», 1989-287с.;
5. Ершова А. П. Голобородько В.В. Крижановский А.Ф. Тетрадь-конспект по геометрии по учебнику Л.С. Атанасяна и др. для 7класса //М., «Илекса»,2003-96с.;
6. Карпушина Н.М., Развивающие задачи по геометрии, 7 класс //М., «Школьная пресса», 2004-76с.;
7. Мерзляк А.Г. Геометрия. 7 класс. Учебник для учащихся общеобразовательных организаций / А.Г. Мерзляк, В.Б. Полонский, М.С. Якир. – М.: Вентана-Граф, 2019. – 192с.
8. Энциклопедический словарь юного математика / Сост. А.П. Савин.- М.: Педагогика, 1989. – 352с.
ПРИЛОЖЕНИЕ 1 Как начертить окружность по точкам
Идёт урок геометрии.
Нужно начертить в тетради окружность, а циркуля с собой нет. Что делать? Есть простой и эффективный способ нарисовать такую окружность. Вам понадобится лишь тетрадь в клетку и следующее числовое заклинание: “три — один, один — один, один — три”.
Второе числовое заклинание : «Один – пять – один- — два – четыре – четыре — два – один — пять — один»
ПРИЛОЖЕНИЕ 2 Буклеты
Просмотров работы: 590
Диаметр — базовая геометрия
Все ресурсы по базовой геометрии
9 Диагностические тесты 164 практических теста Вопрос дня Карточки Learn by Concept
← Предыдущая 1 2 3 4 5 6 7 8 Следующая →
Справка по основам геометрии » Плоская геометрия » Круги » Диаметр
Укажите диаметр круга, длина окружности которого равна .
Возможные ответы:
Правильный ответ:
Объяснение:
Сообщить об ошибке
Периметр круга равен 36 π.
Каков диаметр круга?
Возможные ответы:
36
18
72
6
3
Правильный ответ:
36
Пояснение:
Периметр круга = 2 πr = πd
Следовательно, d = 36
Сообщить об ошибке
Две окружности имеют только одну общую точку. Обе окружности имеют радиусы . Если точка находится на первом круге, а точка на втором круге, какова максимально возможная длина линии?
Возможные ответы:
20
24
6
12
18
Правильный ответ:
24
Объяснение:
Первый шаг — нарисовать две окружности, соприкасающиеся в одной точке. Чтобы максимизировать длину , точка и точка должны быть на противоположных концах, как показано на диаграмме.
Если радиус круга , то диаметр будет . Следовательно, длина будет .
Сообщить об ошибке
Как называется сегмент, выделенный зеленым цветом?
Возможные ответы:
Диагональ
Радиус
Диаметр
Луч
Хорда
Правильный ответ:
Диаметр
Объяснение:
Диаметр — это максимальное расстояние между двумя точками по периметру окружности. Диаметр проходит через центр окружности.
Сообщить об ошибке
Площадь круга . Каков его диаметр?
Возможные ответы:
Правильный ответ:
Объяснение:
Сначала найдите радиус:
Обратите внимание, что , где радиус, а диаметр.
Следовательно, .
Сообщить об ошибке
Круг имеет площадь . Каков диаметр круга?
Возможные ответы:
Правильный ответ:
Объяснение:
Площадь круга определяется уравнением , где – площадь, а – радиус. Используйте заданную площадь в этом уравнении и решите, чтобы найти радиус круга.
Чтобы найти диаметр круга, умножьте его радиус на .
Сообщить об ошибке
Круг имеет радиус 7 дюймов. Каков диаметр круга?
Возможные ответы:
дюйма
дюйма
дюйма
дюйма
дюйма
Правильный ответ:
дюйма
Объяснение:
Диаметр круга можно записать как , где .
.
Следовательно, диаметр круга равен 14 дюймам.
Сообщить об ошибке
Две стороны прямоугольного треугольника имеют соответственно 3 и 4 длины. Чему равна площадь окружности, описанной около треугольника?
Возможные ответы:
Правильный ответ:
Объяснение:
Чтобы окружность содержала все 3 вершины, гипотенуза должна быть равна диаметру окружности. Гипотенуза и, следовательно, диаметр равны 5, так как это должен быть прямоугольный треугольник 3-4-5.
Уравнение площади круга: A = πr 2 .
Сообщить об ошибке
Если площадь круга , каков его диаметр?
Возможные ответы:
Правильный ответ:
Пояснение:
Прежде чем мы сможем найти диаметр этого круга, нам нужно найти его радиус.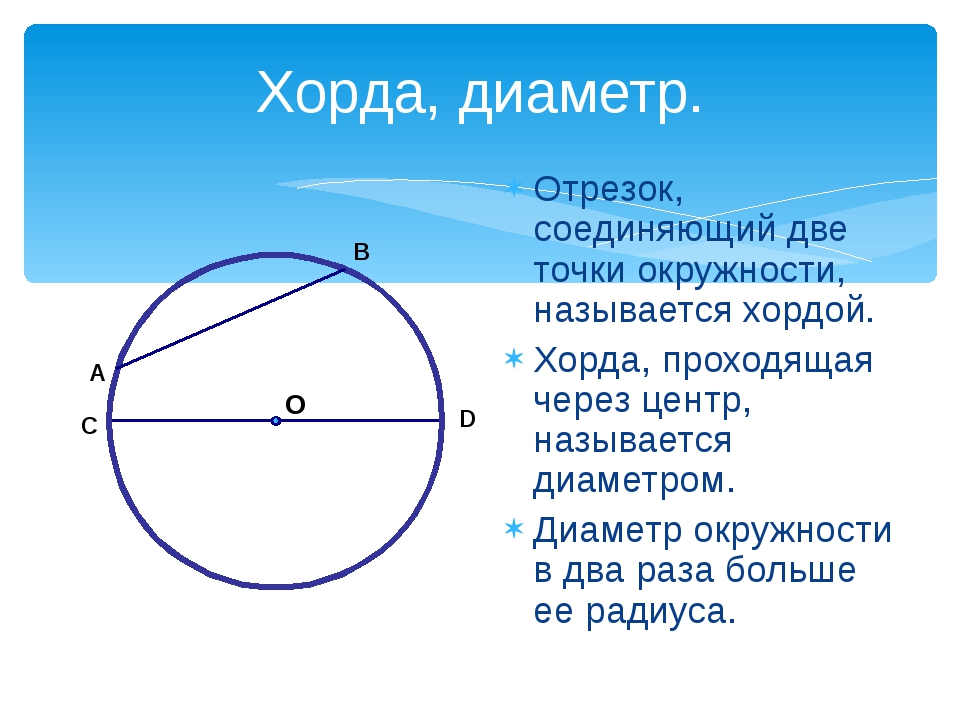
Нам нужно использовать формулу площади окружности:
Учитывая, что площадь равна , мы можем найти радиус
отмените пи и извлеките из него корень, чтобы найти ‘r’.
Теперь, когда радиус найден, мы можем найти диаметр, умножив его на 2.
Сообщить об ошибке
Найдите диаметр круга, площадь которого равна .
Возможные ответы:
Правильный ответ:
Пояснение:
Вспомните, как найти площадь круга:
Затем введите информацию, указанную в вопросе.
Отсюда видно, что мы можем найти радиус.
Теперь вспомним связь между радиусом и диаметром.
Подставьте значение радиуса, чтобы найти диаметр.
Сообщить об ошибке
← Назад 1 2 3 4 5 6 7 8 Далее →
Уведомление об авторских правах
Все ресурсы по базовой геометрии
9 Диагностические тесты 164 практических теста Вопрос дня Карточки Learn by Concept
Полное руководство по кругам
Свойства кругов
Все знают, что такое круг.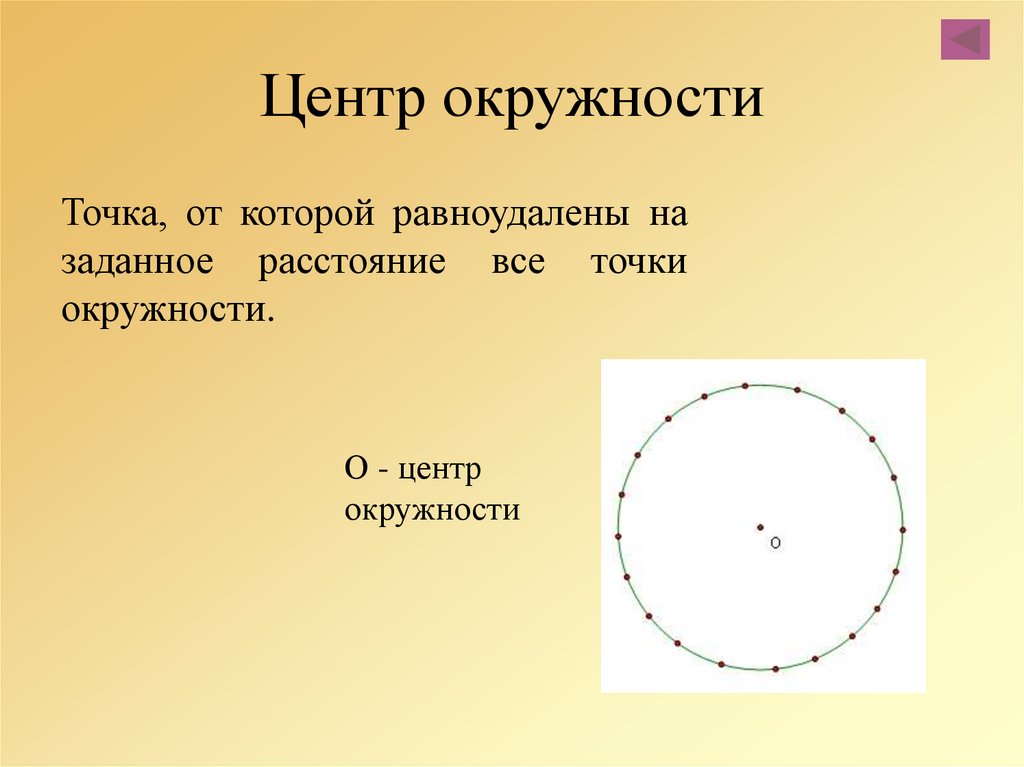
Мы видим их каждый день по всему миру. Чего мы можем не видеть, так это того, насколько важны круги и как различные свойства круга делают его полезным во многих отношениях. Чтобы понять, как эту уникальную форму можно использовать для решения проблем и понимания окружающего мира, важно понимать свойства круга.
Окружность определяется как фигура с одинаковым расстоянием до всех точек от ее центра. Углов нет, поэтому форма круглая. Чтобы отличить круги друг от друга, их можно назвать по точке в центре.
Круги бывают любого размера, и их можно дополнительно различать, определяя площадь и сечения.
Площадь круга
Радиус, диаметр и длина окружности определяют площадь круга. Окружность — это площадь внешней стороны круга, и ее можно найти, только сначала найдя диаметр и радиус круга. Радиус определяется путем измерения от центра центра к внешней стороне, а диаметр определяется путем измерения расстояния поперек середины или с помощью уравнения 9.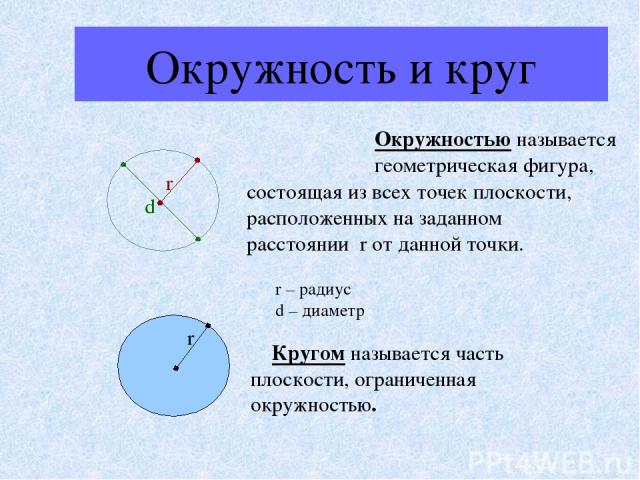
0007 R x 2 = D
Окружность найти немного сложнее. Во-первых, важно понимать число Пи. Для основных математических задач число Пи равно 3,14. Однако полное значение числа Пи еще предстоит определить, поскольку считается, что это бесконечное число. Чтобы найти длину окружности, уравнение 2 π x R = C
Должно быть ясно, что радиус окружности является наиболее важным измерением. Нахождение этого измерения позволяет определить любое другое геометрическое свойство окружности с помощью правильного уравнения. Это доказывается далее, когда мы пытаемся найти площадь круга. Площадь находится с помощью уравнения π x R 2 .
Сечения круга
Поскольку круги представляют собой группу точек, находящихся на равном расстоянии от центральной точки, можно определять углы и линии внутри круга. Эти линии называются трансверсалями. Чтобы было ясно, трансверсали определяются как линия, которая пересекает две или более линий и может существовать внутри круга или использоваться для нахождения круга.