Что такое параллелограмм: определение, свойства, признаки
Sign in
Password recovery
Восстановите свой пароль
Ваш адрес электронной почты
MicroExcel.ru Математика Геометрия Что такое параллелограмм: определение, свойства, признаки
В данной публикации мы рассмотрим определение, свойства и признаки (с рисунками) одной из основных геометрических фигур – параллелограмма.
- Определение параллелограмма
- Свойства параллелограмма
- Свойство 1
- Свойство 2
- Свойство 3
- Свойство 4
- Свойство 5
- Свойство 6
- Свойство 7
- Свойство 8
- Свойство 9
- Свойство 10: тождество параллелограмма
- Признаки параллелограмма
Определение параллелограмма
Параллелограмм – это четырехугольник, противоположные стороны которого попарно параллельны.
AB || CD, BC || AD
Обычно параллелограмм записывается путем перечисления четырех его вершин, например, ABCD. А пары параллельных сторон, чаще всего, обозначаются маленькими латинскими буквами, в нашем случае – a и b.
А пары параллельных сторон, чаще всего, обозначаются маленькими латинскими буквами, в нашем случае – a и b.
Частные случаи параллелограмма: квадрат, ромб и прямоугольник.
Свойства параллелограмма
Свойство 1
Противолежащие (или противоположные) стороны параллелограмма равны.
- AB = CD
- BC = AD
Свойство 2
Противолежащие углы параллелограмма равны.
- ∠ABC = ∠ADC
- ∠BAD = ∠BCD
Свойство 3
Сумма углов параллелограмма, прилежащих к одной стороне, равняется 180°.
Для рисунка выше: α + β = 180°.
Свойство 4
Любая из двух диагоналей параллелограмма делит его на два равных треугольника.
△ABC = △ADC
Свойство 5
Диагонали параллелограмма в точке пересечения делятся пополам.
- AE = EC
- BE = ED
Свойство 6
Точка пересечения диагоналей параллелограмма (также называется центром симметрии) одновременно является точкой пересечения его средних линий.
Средняя линия четырехугольника – это отрезок, который соединяет середины его противоположных сторон.
В данном случае средние лини – это отрезки FM и EN.
Свойство 7
Угол между двумя высотами в параллелограмме равен его острому углу.
- BL – высота, проведенная к стороне CD
- BK – высота, проеденная к стороне AD
- ∠KBL = ∠BAK
Свойство 8
Биссектрисы углов параллелограмма, прилежащих к одной стороне, взаимно перпендикулярны (т.е. расположены под углом 90° друг к другу).
- AP – биссектриса ∠BAD
- BR – биссектриса ∠ABC
- AP перпендикулярна BR
Свойство 9
Биссектрисы двух противолежащих углов параллелограмма параллельны.
Углы ABC и ADC противолежащие. Их биссектрисы параллельны, т.е. BR || DP.
Свойство 10: тождество параллелограмма
Сумма квадратов диагоналей параллелограмма равняется удвоенной сумме квадратов его смежных сторон.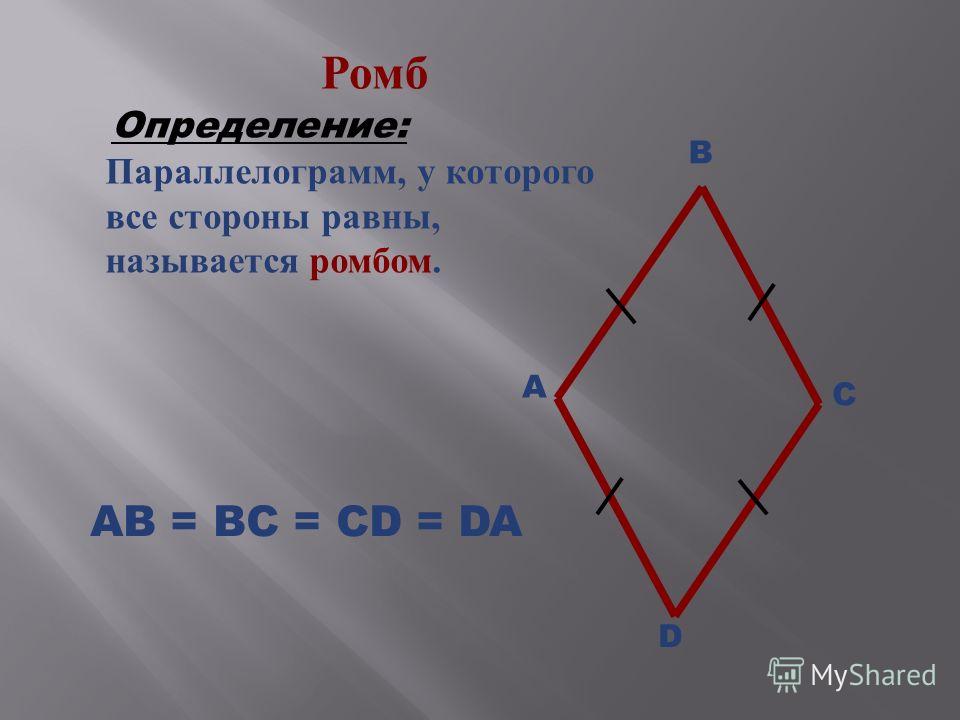
Признаки параллелограмма
Четырехугольник ABCD без самопересечений является параллелограммом, если для него справедливо одно из утверждений ниже:
- Две противоположные стороны одновременно равны и параллельны.
- Все противолежащие углы попарно равны.
- Все противоположные стороны попарно равны.
- Все противоположные стороны попарно параллельны.
- Обе диагонали в точке пересечения делятся пополам.
ЧАЩЕ ВСЕГО ЗАПРАШИВАЮТ
Таблица знаков зодиака
Нахождение площади трапеции: формула и примеры
Нахождение длины окружности: формула и задачи
Римские цифры: таблицы
Таблица синусов
Тригонометрическая функция: Тангенс угла (tg)
Нахождение площади ромба: формула и примеры
Нахождение объема цилиндра: формула и задачи
Тригонометрическая функция: Синус угла (sin)
Геометрическая фигура: треугольник
Нахождение объема шара: формула и задачи
Тригонометрическая функция: Косинус угла (cos)
Нахождение объема конуса: формула и задачи
Таблица сложения чисел
Нахождение площади квадрата: формула и примеры
Что такое тетраэдр: определение, виды, формулы площади и объема
Нахождение объема пирамиды: формула и задачи
Признаки подобия треугольников
Нахождение периметра прямоугольника: формула и задачи
Формула Герона для треугольника
Что такое средняя линия треугольника
Нахождение площади треугольника: формула и примеры
Нахождение площади поверхности конуса: формула и задачи
Что такое прямоугольник: определение, свойства, признаки, формулы
Разность кубов: формула и примеры
Степени натуральных чисел
Нахождение площади правильного шестиугольника: формула и примеры
Тригонометрические значения углов: sin, cos, tg, ctg
Нахождение периметра квадрата: формула и задачи
Теорема Фалеса: формулировка и пример решения задачи
Сумма кубов: формула и примеры
Нахождение объема куба: формула и задачи
Куб разности: формула и примеры
Нахождение площади шарового сегмента
Что такое окружность: определение, свойства, формулы
Задачи на параллелограмм 8 класс онлайн-подготовка на Ростелеком Лицей
Повторение определения, свойств и признака параллелограмма
Сегодня мы основное внимание уделим задачам на параллелограмм. Для этого нам необходимо владеть определением параллелограмма, его свойствами и признаками. Повторим эти факты, обобщим и структурируем их.
Для этого нам необходимо владеть определением параллелограмма, его свойствами и признаками. Повторим эти факты, обобщим и структурируем их.
Определение. Параллелограмм – четырехугольник, у которого каждые две противоположные стороны параллельны (см. Рис. 1).
Рис. 1. Параллелограмм
Основные свойства параллелограмма:
Теорема. Первый признак параллелограмма. Если в четырехугольнике две противоположные стороны равны и параллельны (см. Рис. 2), то этот четырехугольник – параллелограмм. параллелограмм.
Рис. 2. Первый признак параллелограмма
Рис. 3. Второй признак параллелограмма
Теорема. Второй признак параллелограмма. Если в четырехугольнике каждые две противоположные стороны равны (см. Рис. 3), то этот четырехугольник – параллелограмм. параллелограмм.
Теорема. Третий признак параллелограмма.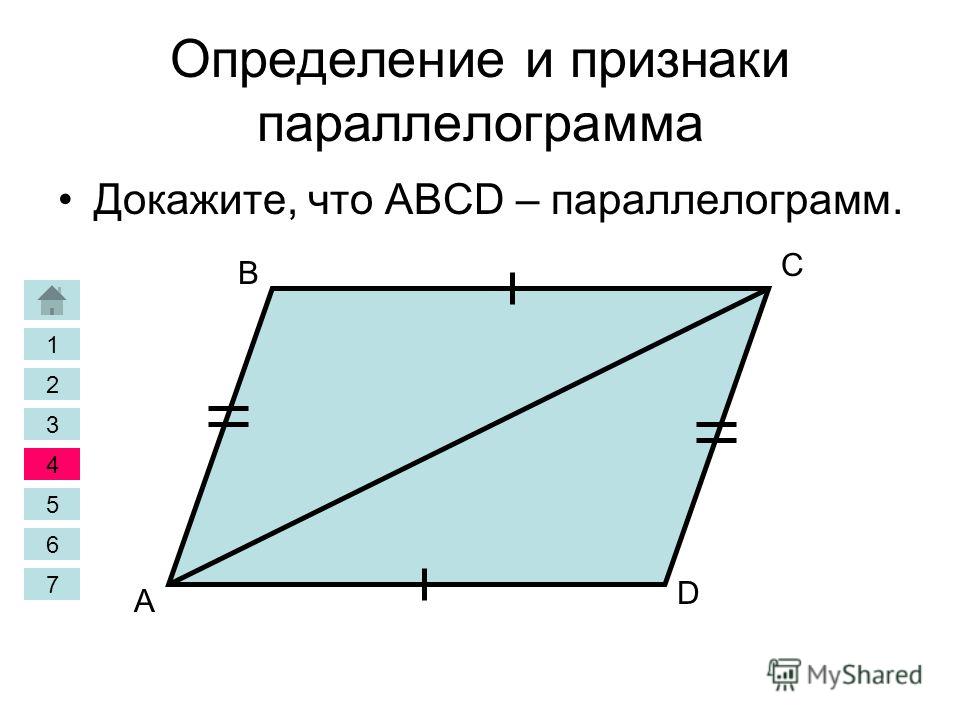 Если в четырехугольнике диагонали точкой пересечения делятся пополам (см. Рис. 4), то этот четырехугольник – параллелограмм. параллелограмм.
Если в четырехугольнике диагонали точкой пересечения делятся пополам (см. Рис. 4), то этот четырехугольник – параллелограмм. параллелограмм.
Рис. 4. Третий признак параллелограмма
Задачи на параллелограммы
Теперь рассмотрим решение задач с использованием определения, свойств и признаков параллелограмма.
Пример 1. В параллелограмме проведены биссектрисы и , которые пересекаются в точке . Найти .
Решение. Изобразим Рис. 5.
Рис. 5
Обозначим для удобства: . Следовательно, поскольку и биссектрисы.
По теореме о сумме внутренних углов треугольника .
Вспомним свойство параллелограмма о сумме углов, прилежащих к одной стороне: . Тогда:
.
Ответ. .
Пример 2. Прямая , проведенная через середину стороны параллельно стороне треугольника пересекает третью его сторону в середине. Доказать, что – это середина .
Доказательство. Изобразим Рис. 6 с дополнительными построениями: проведем .
Рис. 6
Рассмотрим четырехугольник :
параллелограмм по определению. Тогда по свойству равенства противоположных сторон , но по условию еще известно, что , следовательно, .
Рассмотрим треугольники и :
по второму признаку равенства треугольников (по стороне и прилежащим углам).
Из равенства указанных треугольников следует равенство их соответствующих сторон, т.е., например, что . Это означает, что точка является серединой стороны . Что и требовалось доказать.
Доказано.
3. Теорема Фалеса
Теорема Фалеса. Если параллельные прямые, которые пересекают стороны угла, отсекают на одной его стороне равные отрезки, то они отсекают равные отрезки и на другой его стороне.
Доказательство. Изобразим Рис. 7.
Рис. 7. Теорема Фалеса
Рассмотрим . В нем точка – середина стороны , а прямая . Из предыдущего примера следует, что точка делит сторону на две равные части, т.е. . Равенство двух отрезков, ближайших к вершине угла доказано. Аналогично доказывается попарное равенство всех остальных отрезков на второй стороне угла, если проводить прямые параллельные первой стороне угла через начало первого отрезка в любой рассматриваемой паре.
Аналогично доказывается попарное равенство всех остальных отрезков на второй стороне угла, если проводить прямые параллельные первой стороне угла через начало первого отрезка в любой рассматриваемой паре.
Доказано.
4. Пример задачи на применение теоремы Фалеса
Рассмотрим пример на доказанную теорему.
Пример 3. Дан отрезок , разделить его на три равные части.
Решение. Изобразим указанный отрезок на Рис. 8 и сделаем дополнительные построения: отложим три равных отрезка любой длины вдоль одной прямой, не совпадающей с указанным в условии отрезком.
Рис. 8. Применение теоремы Фалеса
Соединим прямой точки и , а затем проведем прямые, параллельные прямой , через точки и : . Полученные при пересечении отрезка точки и будут делить отрезок на три равных части по теореме Фалеса. Необходимое построение выполнено и задача решена.
Ответ: построено.
Методы, которые мы рассмотрели сегодня на примерах, демонстрирующих свойства и признаки параллелограмма, помогут нам в дальнейшем при работе с параллелограммами в более сложных случаях. А на следующем уроке мы познакомимся с таким видом четырехугольников, как трапеция, и обсудим ее свойства.
А на следующем уроке мы познакомимся с таким видом четырехугольников, как трапеция, и обсудим ее свойства.
Список литературы
- Александров А.Д. и др. Геометрия, 8 класс. – М.: Просвещение, 2006.
- Бутузов В.Ф., Кадомцев С.Б., Прасолов В.В. Геометрия, 8 класс. – М.: Просвещение, 2011.
- Мерзляк А.Г., Полонский В.Б., Якир С.М. Геометрия, 8 класс. – М.: ВЕНТАНА-ГРАФ, 2009.
Дополнительные рекомендованные ссылки на ресурсы сети Интернет
- Narod.ru (Источник).
- Фестиваль педагогических наук «Открытый урок» (Источник).
Домашнее задание
- № 50 (г, д, е, ж, з, и), 51 (б, в, г, ж), 52 (б, в, е, ж). Бутузов В.Ф., Кадомцев С.Б., Прасолов В.В. Геометрия, 8 класс. – М.: Просвещение, 2011.
- В параллелограмме см, см, биссектрисы углов и пересекают сторону в точках и . Найдите длину отрезка .
- Угол между высотами параллелограмма, проведенными из вершины тупого угла, равен .
 Найдите периметр параллелограмма, если его высоты равны 4 см и 6 см.
Найдите периметр параллелограмма, если его высоты равны 4 см и 6 см. - ∗ Через середину диагонали параллелограмма проведена прямая, которая пересекает стороны и в точках и соответственно. Докажите, что четырехугольник параллелограмм.
Как сформулировать и доказать утверждения о свойствах параллелограмма, теоремы о признаках данной фигуры
Параллелограммом называют четырёхугольник (фигура, что состоит из четырёх точек и отрезков, последовательно их соединяющих), у которого противоположные стороны попарно параллельны. Его свойства впервые детально изучали греческие математики Евклид и Пифагор. Конец эпохи Средневековья принёс людям полную теорию об этой фигуре.
…
Оглавление:
- История возникновения термина
- Доказательство признаков фигуры
- Теорема признаков паралелограмма
- Теорема о диагоналях
История возникновения термина
О некоторых видах четырёхугольников, квадратов, прямоугольников, равносторонних и прямоугольных трапеций знали ещё давно. Первые найденные работы принадлежат египетским и вавилонским математикам.
Первые найденные работы принадлежат египетским и вавилонским математикам.
Интересно знать: что такое выпуклый четырехугольник, его особенности и признаки.
Термин «параллелограмм» греческого происхождения, считают что его придумал Евклид (приблизительно 300 годов до нашей эры). Ещё известно, что эта фигура и её свойства были знакомы ученикам школы Пифагора, раньше их называли пифагорейцами.
В «Началах» Евклида приведена следующая теорема: в параллелограмме противоположные стороны равны, а диагонали разделяют его по половине. Но в данной книге не было написано о свойствах точки их сечения. Ещё этот учёный не упоминает о прямоугольнике и ромбе.
Это интересно: в геометрии луч — это что такое, основное понятие.
Полную теорию сделали только в конце Средневековья, а в книгах она появилась в семнадцатом столетии. Теоремы и свойства параллелограмма основывались на аксиомах Евклида.
«Диагональ» — это слово греческого происхождения, «диа» означало «через», а «гониос» — «угол».
Это можно понять как отрезок, что соединяет вершины углов.
Нужно сказать, что Евклид, как и большинство математиков того времени, для названия отрезка, который соединяет противоположные вершины четырёхугольника или прямоугольника, использовал другой термин — «диаметр». Это можно объяснить тем, что первые геометры свои мысли основывали на вписании круга в прямоугольник. В Средние века для названия приведённых отрезков использовали оба термина. Только в семнадцатом столетии «диагональ» стала общепринятой.
Это интересно: разность векторов, определение разности.
Доказательство признаков фигуры
На следующем рисунке изображён параллелограмм ABCD, где AB параллельно CD и AD параллельно BC:
Сумма любых двух соседних углов параллелограмма равна 180 градусам — это первая подсказка о том, как сформулировать и доказать утверждения о признаках параллелограмма.
На этом рисунке углы A и B фигуры ABCD есть внутренними односторонними углами для параллельных прямых AD и BC . Поэтому углы A + B равны 180 градусам. Аналогично это свойство можно привести для любой другой пары соседних (если вершины есть концами одной и той же стороны) углов.
Нужно знать! Что такое горизонталь и горизонтальное положение.
Теорема признаков паралелограмма
- Теорема признаков параллелограмма гласит, что это выпуклый четырёхугольник. Исходя из предыдущего правила, угол А намного меньше 180 градусов, как и B, C, D, поэтому его называют опухлым четырёхугольником. Диагонали этой фигуры могут пересекаться.
- У параллелограмма противоположные стороны и углы равны.
Диагональ АС разбивает фигуру на два треугольника ABC и ADC. АС — общая сторона двоих треугольников и САD эквивалентен АСВ также с САВ и АСD. Тогда ∆АВС = ∆СDA, по стороне и двумя прилегающими углами. Это значит, что АВ=СD, BC=AD и B=D, как соответствующие элементы в различных треугольниках. В результате угол BAC + CAD равен ВСА + DCA и BAD = BCD.
В результате угол BAC + CAD равен ВСА + DCA и BAD = BCD.
Теорема о диагоналях
- Периметр (сумма длин всех сторон четырёхугольника, которую обозначают буквой Р) параллелограмма эквивалентен 2 (АВ +ВС) или АВ + ВС + СD + DA.
- Теорема о диагоналях параллелограмма гласит, что точкой пересечения они делятся ровно пополовине.
По условию задачи O — это точка пересечения диагоналей AC и BD параллелограмма. AB эквивалентно BC, как противоположные, не имеющие своей общей вершины. CAD равен ACB также BDA и DBC, АD и BC секущими AC и B. D. Следуя дальше ∆АОD = ∆ COB, по стороне и двух прилегающих углах. Тогда, А = ОС, ВО = ОD, как соответствующие стороны разных треугольников.
Высотой называется перпендикуляр, проведённый из любой точки стороны фигуры к прямой, что имеет противоположную сторону.
На этом рисунке MN — это высота. Следуя за известным определением, из каждой вершины можно провести две высоты (BF и BT, которые приведены в соответствии к сторонам AD и CD).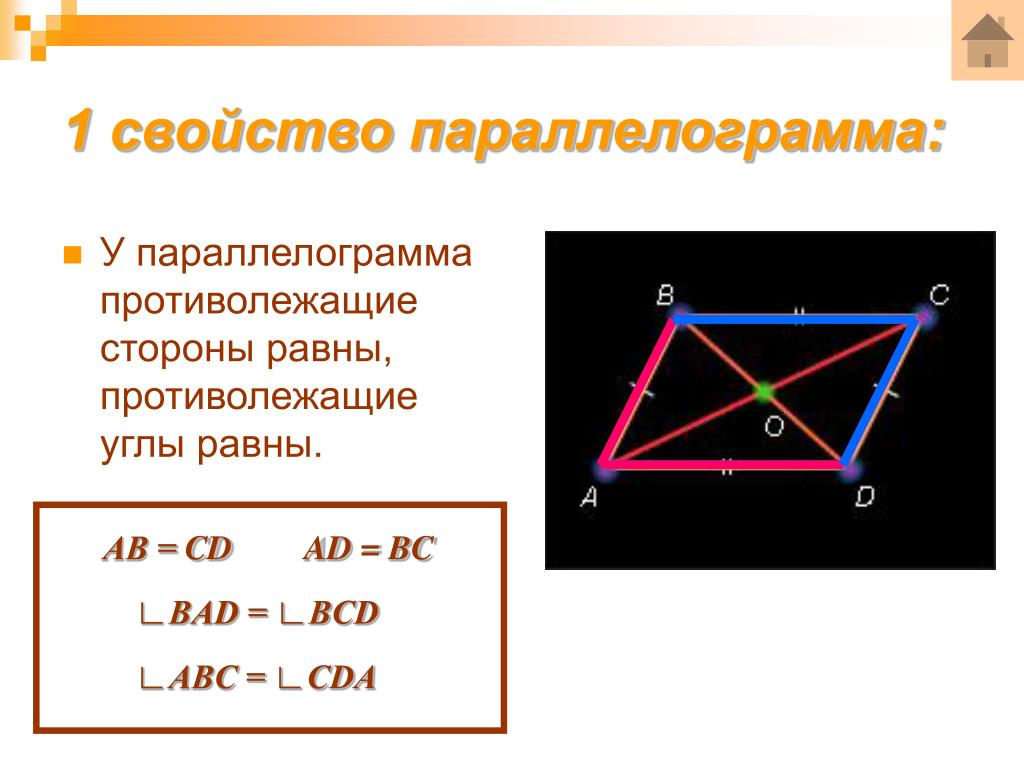
Свойства параллелограмма с доказательствами 8 класса :
- Две стороны равны и параллельны.
- Противоположные стороны попарно равны.
- Диагонали пересекаются и этой точкой делятся ровно пополам.
- Противоположные углы попарно равны.
Теперь нужно вернуться к первому рисунку, чтобы до конца понять все признаки параллелограмма и доказательства любых признаков.
В нём AD = BC и AD || BC. Провели диагональ AC и получили ∆CAD и ∆ACB. CAD эквивалентен ВСА, как внутренние разносторонние углы при пересечениях прямых AD и BC секущей AC, ещё она является их общей стороной. Условия задачи говорят: AD=BC. Значит, что, ∆CAD=∆ACB, ACD = CAB. Из-за того, что они были созданы в таких условиях AB || CD, по признаку параллельных прямых.
Что такое параллелограмм? [Определение, свойства, примеры доказательств]
Руководство по пониманию свойств параллелограмма, доказательств и примеров вычислений
Что такое параллелограмм?
Содержание
- Что такое параллелограмм?
- Свойства параллелограммов и теоремы
- При ДАННОМ параллелограмме Теоремы для сторон, углов и диагоналей
- При попытке ДОКАЗАТЬ параллелограмм Теоремы для сторон, углов и диагоналей
- Примеры доказательств параллелограмма
- Как доказать параллелограмм
Определение: Параллелограмм – это четырехугольник с четырьмя сторонами, противоположные стороны которого равны и параллельны.
Как выглядит параллелограмм? Конкретные типы параллелограммов включают прямоугольники и квадраты. Эти формы часто встречаются и используются в окружающем нас мире.
Давайте посмотрим, из чего состоит параллелограмм и как доказать это математически.
Свойства параллелограммов и теоремы
Когда ДАН параллелограмм Теоремы для сторон, углов и диагоналей
Как доказать, что четырехугольник является параллелограммом.
Если вам дано доказательство, включающее диаграмму и представленное как параллелограмм, можно использовать одно или несколько свойств:
- Если четырехугольник является параллелограммом, противоположных сторон параллельны. Когда противоположные стороны параллельны, мы знаем, что противоположные стороны имеют одинаковый наклон.
- Если четырехугольник является параллелограммом, то противоположных сторон равны. Это означает, что противоположные стороны равны по длине.
 Это означает, что расстояние между вершинами равно.
Это означает, что расстояние между вершинами равно. - Если четырехугольник является параллелограммом, то противоположных углов равны. Это можно использовать, чтобы найти меру недостающего угла.
- Если четырехугольник является параллелограммом, то последовательных углов являются дополнительными. Это означает, что углы в сумме составляют 180 градусов. Это можно использовать для нахождения недостающих углов
- Если четырехугольник является параллелограммом, то диагоналей делят друг друга пополам. Это свойство можно использовать совместно с теоремой о средней точке. Он также используется для нахождения длин диагоналей. Более сложное доказательство может использовать это свойство, чтобы найти или доказать треугольники, образованные диагоналями параллелограмма. Используя другие теоремы, можно доказать конгруэнтность треугольников.
При попытке ДОКАЗАТЬ параллелограмм Теоремы для сторон, углов и диагоналей
Диагонали параллелограмма равны?
Если вы пытаетесь доказать, что фигура является параллелограммом, можно использовать любую из следующих теорем.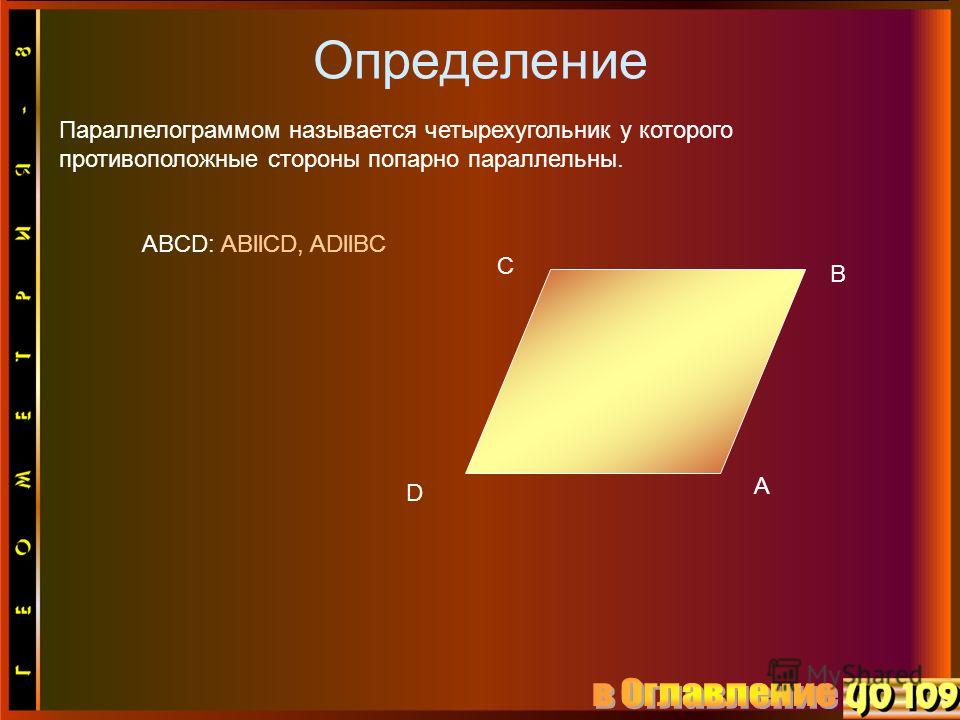
- Если обе пары противоположных сторон четырехугольника параллельны, то четырехугольник является параллелограммом.
- Если обе пары противолежащих сторон четырехугольника равны, то четырехугольник является параллелограммом.
- Если обе пары противоположных углов четырехугольника равны, четырехугольник является параллелограммом.
- Если последовательные
- Если диагоналей четырехугольника делят друг друга пополам, то четырехугольник является параллелограммом.
Пытаясь доказать, что фигура является параллелограммом, начните с изучения полученной информации. Некоторая информация может быть в данном разделе, например, параллельные линии или конгруэнтные меры. Информация может быть скрыта в других формах. Если треугольники вписаны в четырехугольник, вам, возможно, придется взглянуть на эти свойства, например, у равнобедренных треугольников есть пара конгруэнтных сторон. Часто свойства параллельных прямых, пересекаемых секущей, необходимы для нахождения параллельных сторон.
Часто свойства параллельных прямых, пересекаемых секущей, необходимы для нахождения параллельных сторон.
Общая идея всех типов доказательств состоит в том, чтобы посмотреть, какая информация вам предоставляется, что вам нужно доказать и какой информации не хватает, чтобы получить ее.
Примеры доказательств параллелограмма
Как доказать параллелограмм
Из этого примера доказательства мы знаем, что диаграмма является параллелограммом. Это дает нам все теоремы, упомянутые ранее. Поскольку нам нужно доказать, что два треугольника конгруэнтны, нам нужно посмотреть, что нам нужно для этого, конгруэнтные стороны и углы. Вот теоремы и то, как они помогают нам найти доказательство.
| Если четырехугольник является параллелограммом, то противоположных углов равны. | ||
Если четырехугольник является параллелограммом, то противоположные сторон равны. |
Теперь мы можем доказать конгруэнтность треугольников с помощью SAS. Обратите внимание, что есть и другие способы доказать, что углы равны, это один из примеров.
На этом примере доказательства нам нужно показать, что данный четырехугольник является параллелограммом. Для большинства доказательств не требуется доказывать, что это четырехугольник, поскольку он имеет четыре стороны.
Поскольку одно из данных показывает нам, что пара противоположных сторон параллельна, мы хотим начать с попытки доказать, что другая пара сторон параллельна. Вот теоремы и то, как они помогают нам найти доказательство.
| Если две прямые пересекаются секущей и внутренние углы равны, то прямые параллельны. *Это должно быть известно из предыдущих знаний | ||
Если обе пары противоположных сторон четырехугольника параллельны, то четырехугольник является параллелограммом. |
в кембриджском словаре английского языка
Амбар в форме параллелограмма будет сделан из дерева и покрыт зеркальной пленкой по цене 5000 долларов.
От Huffington Post
Впоследствии они изготовили конструкцию, в которой центр масс системы был расположен соответствующим образом за счет добавления параллелограммных соединений.
Из Кембриджского корпуса английского языка
Каждый параллелограмм 
Из Кембриджского корпуса английского языка
Существует параллелограмм механизм, ограничивающий вращение подвижной платформы.
Из Кембриджского корпуса английского языка
Каждая подцепь содержит один пространственный параллелограмм четырех стержней, соединенных сферическими суставами.
Из Кембриджского корпуса английского языка
Для этого исследования мы выбрали иллюзорный квадрат в сравнении с параллелограммом , прямой треугольник в сравнении с перевернутым треугольником и ромб в сравнении с параллелограммом.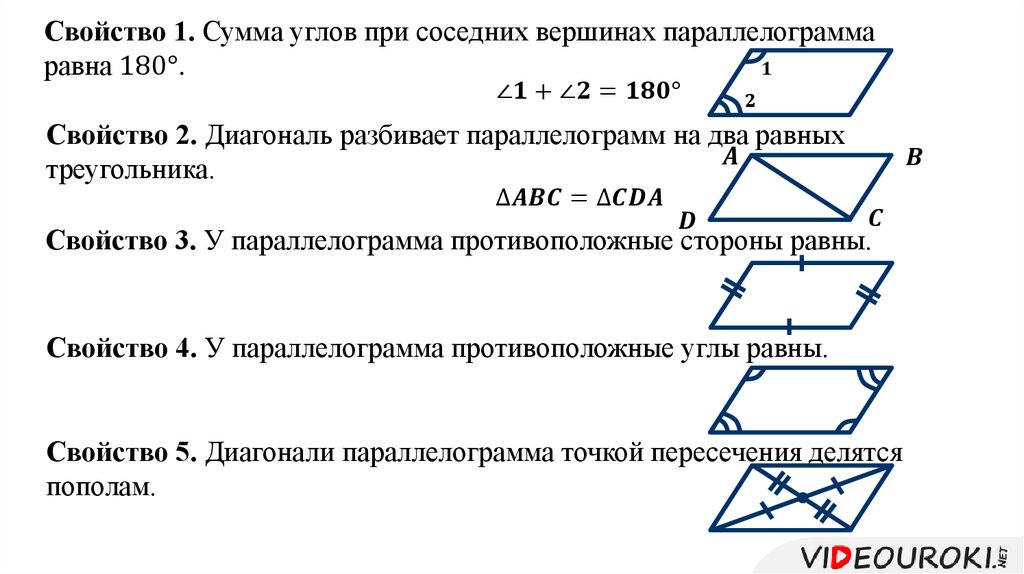
Из Кембриджского корпуса английского языка
Далее мы хотели бы поговорить о параллелограммах следующего вида.
Из Кембриджского корпуса английского языка
Его внутреннюю часть можно замостить с помощью трансляций основных параллелограммов.
Из Кембриджского корпуса английского языка
Даже в завершенном браке параллелограмм по-прежнему очевидны своенравные движения как вперед, так и назад; элементы продолжают появляться снова, требуя комбинации и выдачи.
Из Кембриджского корпуса английского языка
Также было решено встроить шарнирные параллелограммы, передающие движение внутрь корпуса пальца, чтобы иметь компактную конструкцию.
Из Кембриджского корпуса английского языка
Роль параллелограммов состоит в том, чтобы ограничивать ориентацию платформы параллельно рабочей поверхности.
Из Кембриджского корпуса английского языка
Соединительное звено ck несет призматический скользящий шарнир, который освобождает параллелограмм от поперечных силовых составляющих.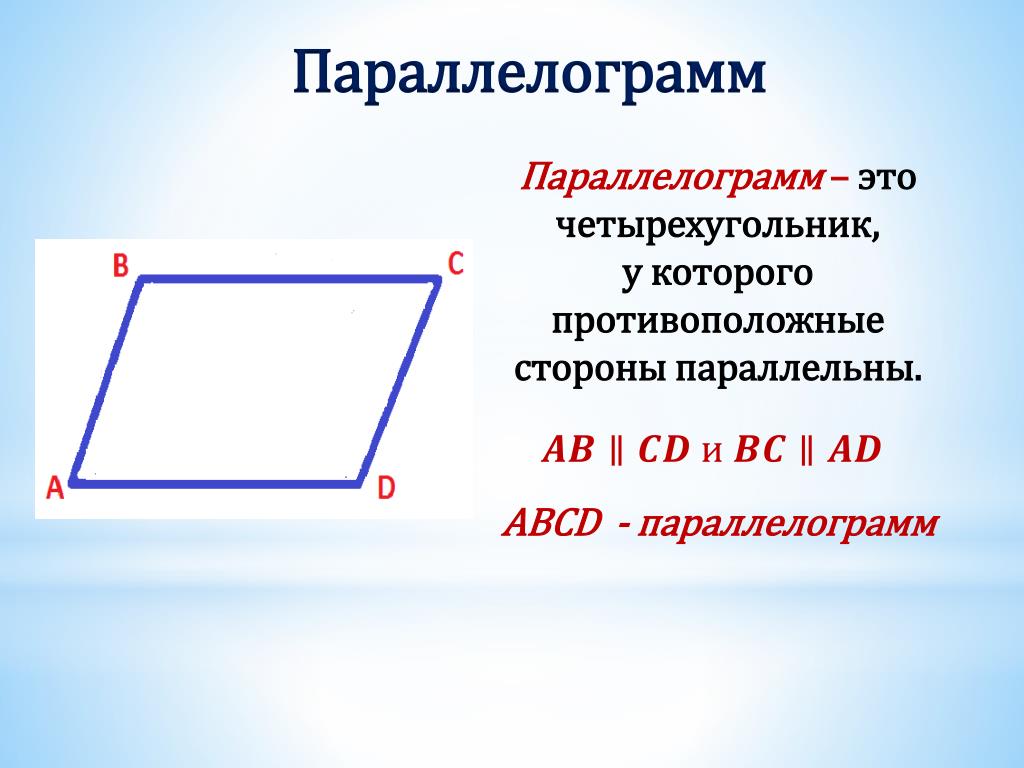
Из Кембриджского корпуса английского языка
Каждая из трех цепочек содержит по одному параллелограмму .
Из Кембриджского корпуса английского языка
Окончательное введение письменности, несомненно, оказало глубокое влияние на оба компонента языковых изменений 9.0175 параллелограмм сил.
Из Кембриджского корпуса английского языка
Кроме того, с помощью параллелограмма можно улучшить угол наклона или способность вращения.
Из Кембриджского корпуса английского языка
Эти примеры взяты из корпусов и источников в Интернете. Любые мнения в примерах не отражают мнение редакторов Кембриджского словаря, издательства Кембриджского университета или его лицензиаров.
Параллелограмм – определение, типы и свойства
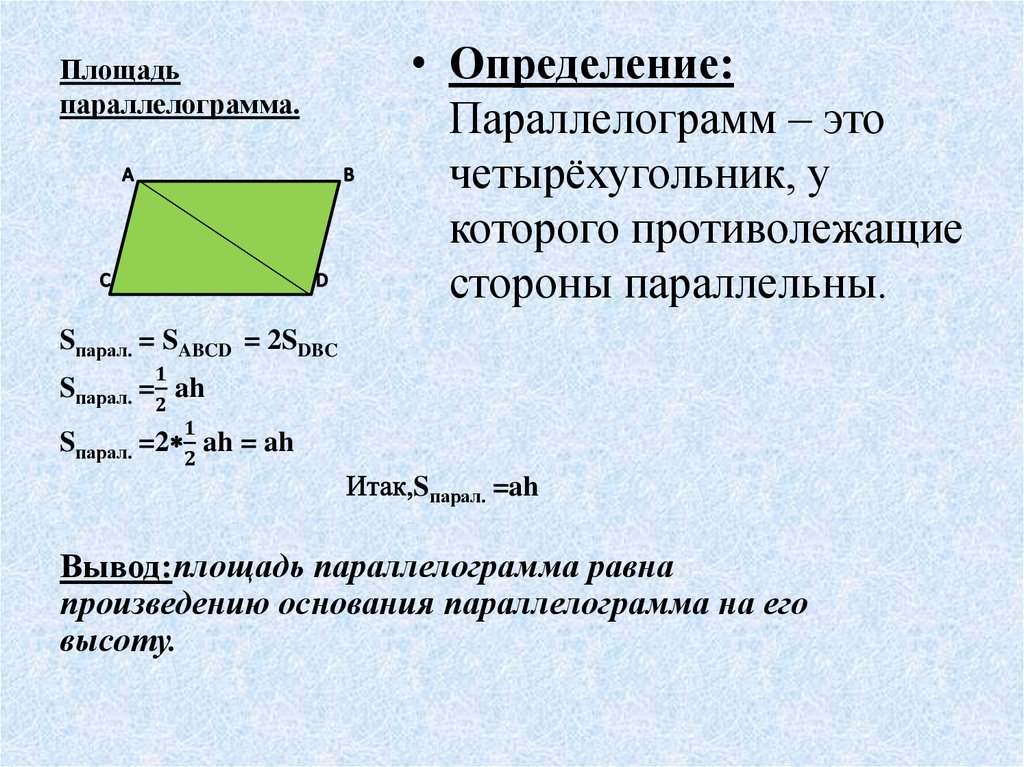
Параллелограмм – это четырехугольник, две стороны которого параллельны. Противоположные стороны и углы параллелограмма равны. Площадь параллелограмма зависит от его основания и высоты.
На приведенном выше рисунке вы можете видеть,
AB // CD, AD // BC
Кроме того, AB = CD и AD = BC
И, ∠A =∠C, ∠B =∠D
(изображение будет загружено в ближайшее время)
Свойства параллелограмма
Вот различные свойства параллелограмма
Противоположные стороны параллелограмма равны
Противоположные углы параллелограмма равны
2 3 3
Последовательные углы параллелограмма являются дополнительными
Диагонали параллелограмма всегда делят друг друга пополам
Каждая диагональ параллелограмма делит его пополам на два равных треугольника
Если какой-либо из углов параллелограмма прямой, то другие его углы также быть прямым углом.

Типы параллелограмма
Три различных типа параллелограмма:
Квадрат
Прямоугольник
Ромб
Трапеция
Трапеция представляет собой разновидность четырехугольника, две стороны которого параллельны. Параллельные стороны трапеции называются основаниями, а непараллельные стороны трапеции называются катетами. Трапецию также называют трапецией. Иногда параллелограмм также рассматривается как трапеция, две стороны которой параллельны.
На приведенном выше рисунке стороны AB и CD параллельны друг другу, тогда как стороны BC и AD не параллельны. h — это расстояние между двумя параллельными сторонами, которые представляют собой высоту трапеции.
(изображение скоро будет загружено)
Свойства трапеции —
Вот различные свойства трапеции
Одна пара противоположных сторон параллельна в трапеции другое
Стороны трапеции, которые не параллельны, не равны, за исключением равнобедренной трапеции
Сумма внутренних сторон трапеции равна 360 градусам, т.
 е. +∠D = 360°
е. +∠D = 360°Сумма двух смежных углов равна 180°. Отсюда следует, что два смежных угла являются дополнительными.
Катеты или непараллельные стороны равнобедренной трапеции конгруэнтны.
Типы трапеций —
Трапеции бывают трех различных типов, а именно:
Равнобедренная трапеция. Ноги или непараллельные стороны равнобедренной трапеции равны по длине.
Разносторонняя трапеция — Все стороны и углы разносторонней трапеции имеют разную величину.
Прямая трапеция. Прямая трапеция состоит как минимум из двух прямых углов.
Воздушный змей Определение —
Воздушный змей — это четырехугольник с двумя парами смежных и равных (равной длины) сторон.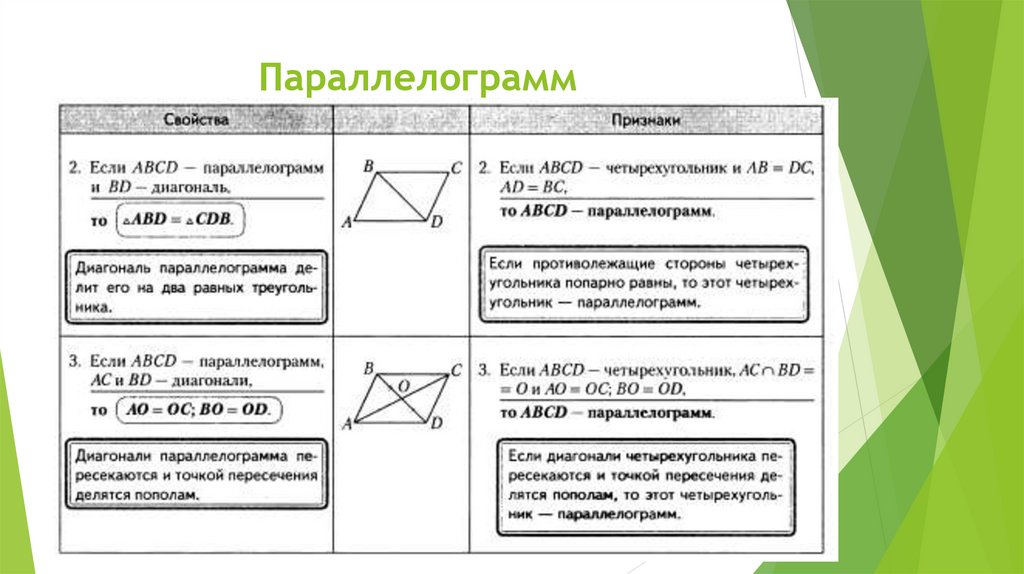 Это означает, что воздушный змей
Это означает, что воздушный змей
Многоугольник
Замкнутая форма
Плоская фигура
(изображение будет загружено в ближайшее время) 3 3
Вот некоторые важные свойства воздушного змея:
Воздушный змей симметричен с точки зрения углов.
Две диагонали воздушного змея пересекаются пополам под углом 90 градусов.
Главная диагональ воздушного змея делит другую диагональ пополам.
Меньшая диагональ воздушного змея делит его на два равнобедренных треугольника.
Углы воздушного змея равны, тогда как неравные стороны воздушного змея встречаются.

Воздушный змей можно рассматривать как пару конгруэнтных треугольников с общим основанием.
Решенные примеры —
Найдите периметр змея, чьи боковые стороны составляют 21 см и 15см
Решение:
Указано
A = 21CM
5757575. 9027. 902.
757575757575. 9027. a+b)]
Периметр воздушного змея 2(21+15)
Периметр воздушного змея = 72 см
Найдите площадь параллелограмма, основание которого равно 5 см, а высота 7 см.
Решение – Дано, основание = 5 см, высота = 7 см
Площадь = основание * высота
Площадь = 5 * 7
Площадь = 35 кв. см.
Найдите периметр трапеции, стороны которой равны 6 см, 7 см, 8 см и 9 см
Решение: Периметр трапеции = сумма всех ее сторон 30 см
Значит, периметр трапеции равен 30 см
Время викторины —
1. Какой из следующих четырехугольников является правильным четырехугольником?
Какой из следующих четырехугольников является правильным четырехугольником?
Rectangle
Square
Rhombus
None of these
2. In an isosceles parallelogram, we have
Pair of parallel sides equal
Пара непараллельных сторон равна
Пара непараллельных сторон перпендикулярна
Ничего из этого.
3. What do we call parallel sides of the trapezium
Edges of trapezium
Angles of trapezium
Legs of trapezium
Bases of trapezium
4.

 Найдите периметр параллелограмма, если его высоты равны 4 см и 6 см.
Найдите периметр параллелограмма, если его высоты равны 4 см и 6 см. Это можно понять как отрезок, что соединяет вершины углов.
Это можно понять как отрезок, что соединяет вершины углов.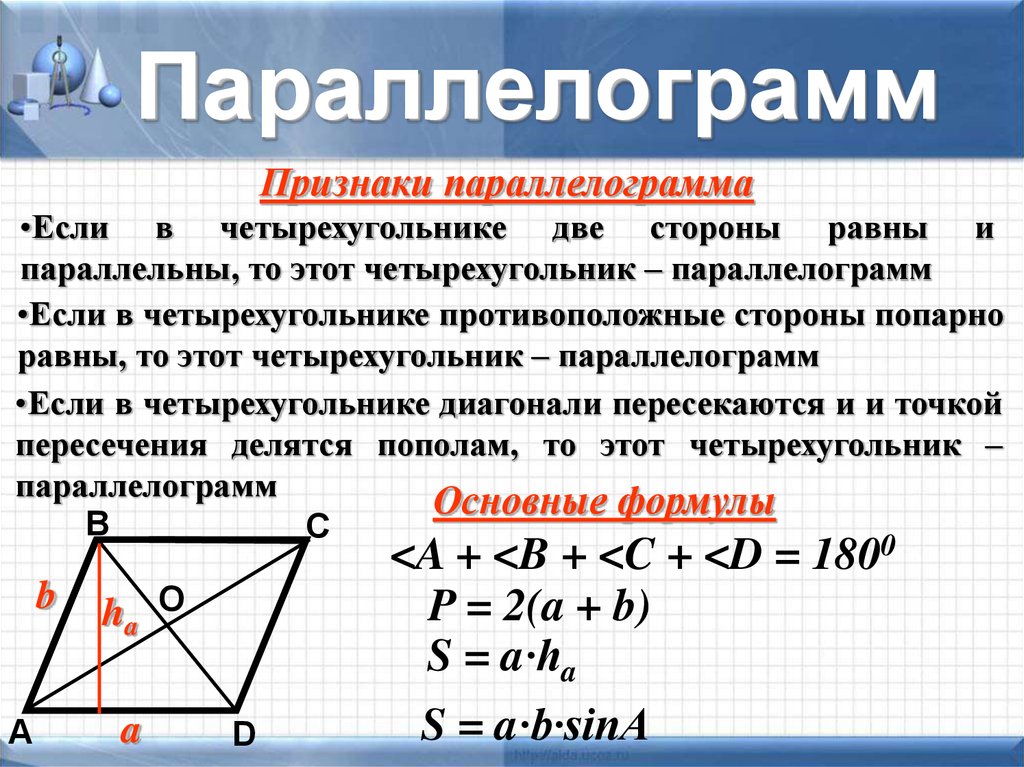 Это означает, что расстояние между вершинами равно.
Это означает, что расстояние между вершинами равно.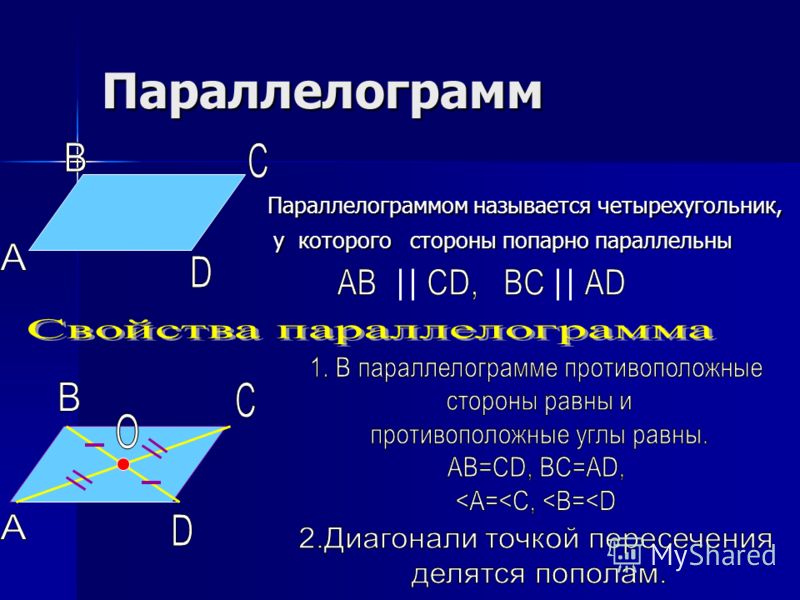
 е. +∠D = 360°
е. +∠D = 360°