Что такое радиус в геометрии: Радиус и диаметр окружности — определения, свойства, формулы

Геометрия Сфера и шар

Материалы к уроку

Конспект урока

Сфера и шар

В курсе планиметрии вы познакомились с понятием окружности и круга. Вспомним, что окружность — это множество точек плоскости, расположенных на заданном расстоянии от данной точки (центр окружности). Кругом называется часть плоскости, ограниченная окружностью.	Окружность- множество точек плоскости, расположенных на заданном расстоянии от данной точки.. Круг-часть плоскости внутри окружности.
Аналогично понятию окружности на плоскости вводится понятие сферы в пространстве. Поверхность, состоящая из всех точек пространства, расположенных на заданном расстоянии от данной точки, называется сферой.	Сфера- поверхность, состоящая из всех точек пространства , расположенных на заданном расстоянии от данной точки
Данная точка — центр сферы (на рисунке точка О). Данное расстояние — радиус сферы (на рисунке — отрезок ОС). Радиусом сферы также называют отрезок, соединяющий центр окружности с любой точкой сферы. Диаметром сферы называют отрезок, проходящий через центр и любые две точки сферы (на рисунке — отрезок DC). Аналогично диаметру окружности, диаметр сферы равен двум радиусам.	О- центр сферы. ОС- радиус сферы R. DC-диаметр сферы D. D=2R
Шаром называется тело, ограниченное сферой. Существует и другое определение шара  — шаром радиуса R с центром в точке О называется тело, которое содержит все точки пространства, расположенные от точки О на расстоянии, не превышающем R (включая О), и не содержит других точек. Очевидно, что центр, радиус, диаметр сферы являются центром, радиусом, диаметром шара.	Шар -тело, ограниченное сферой. Или: Шар радиуса R с центром в точке О -тело, содержащее все точки пространства, расположенные от точки О на расстоянии, не превышающем R (включая О), и не содержит других точек. Центр, радиус, диаметр сферы -центр, радиус, диаметр шара.
Сфера может быть получена вращением полуокружности вокруг её диаметра, а шар — вращением полукруга вокруг его диаметра.	Сфера получена вращением полуокружности АСВ вокруг её диаметра АВ.
Разберём несколько задач, применяя полученные знания.   Задача 1. Точки А и В лежат на сфере с центром О, О не лежит на отрезке АВ. Доказать, что если М — середина отрезка АВ, то ОМ┴АВ.   Доказательство: 1.АО=ОВ как радиусы, АМ=МВ — по условию, тогда треугольник АОВ – равнобедренный.     2.Отрезок ОМ — медиана треугольника АОВ. В равнобедренном треугольнике медиана, проведённая к основанию, является высотой, поэтому ОМ┴АВ.   Таким образом, мы доказали, что если М — середина отрезка АВ, то ОМ┴АВ. Что и требовалось доказать.	Дано: А и В∈ сфере, О∉АВ, АМ=МВ Доказать: ОМ┴АВ    Доказательство: 1. АО=ОВ= R     АМ=МВ (по условию) Δ АОВ-равнобедренный.   2.ОМ-медиана ΔАОВ ОМ-высота    ОМ┴АВ                                                            Ч.т.д.
Задача 2. Точки А и В лежат на сфере радиусом R. Найти расстояние от центра сферы до прямой АВ, если  АВ=m.       Решение: 1.Дополнительное построение: проведём плоскость через точки А, В и О (центр сферы). В сечении получим окружность радиуса r.   2.Треугольник АОВ — равнобедренный, так как АО и ОВ — радиусы.   Дополнительное построение: проведём высоту ОМ, которая является и медианой. ОМ — искомое расстояние от центра сферы до прямой АВ.   Найдём его. 3.Поскольку АВ=m, ОМ — медиана, то  МА=МВ=m/2 4. Найдём ОМ из прямоугольного треугольника АОМ по теореме Пифагора	Дано:  А и В ∈сфере, R-радиус, АВ=m Найти: расстояние от центра сферы до прямой АВ. Решение: 1.Д.п. проведём плоскость АВО   Сечение- окружность радиуса r.

 

Остались вопросы по теме? Наши репетиторы готовы помочь!

• Подготовим к ЕГЭ, ОГЭ и другим экзаменам

• Найдём слабые места по предмету и разберём ошибки

• Повысим успеваемость по школьным предметам

• Поможем подготовиться к поступлению в любой ВУЗ

Выбрать репетитораОставить заявку на подбор

ГДЗ по геометрии Атанасян 8 класс.

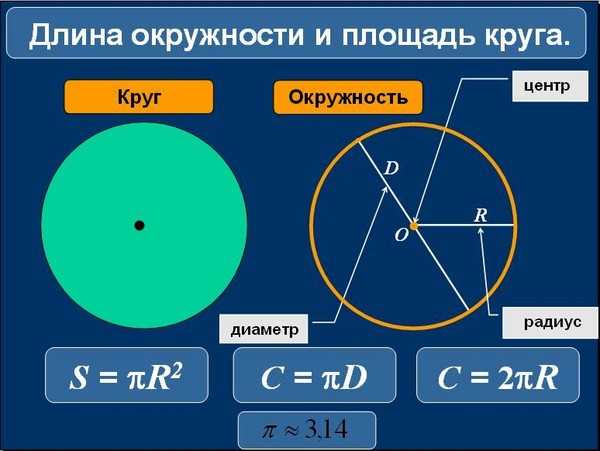Гл.VIII №725. Найдите радиус окружности… – Рамблер/класс ГДЗ по геометрии Атанасян 8 класс. Гл.VIII №725. Найдите радиус окружности… – Рамблер/класс

Интересные вопросы

Школа

Подскажите, как бороться с грубым отношением одноклассников к моему ребенку?

Новости

Поделитесь, сколько вы потратили на подготовку ребенка к учебному году?

Школа

Объясните, это правда, что родители теперь будут информироваться о снижении успеваемости в школе?

Школа

Когда в 2018 году намечено проведение основного периода ЕГЭ?

Новости

Будет ли как-то улучшаться система проверки и организации итоговых сочинений?

Вузы

Подскажите, почему закрыли прием в Московский институт телевидения и радиовещания «Останкино»?

Нужна помощь, не мешало бы разобраться.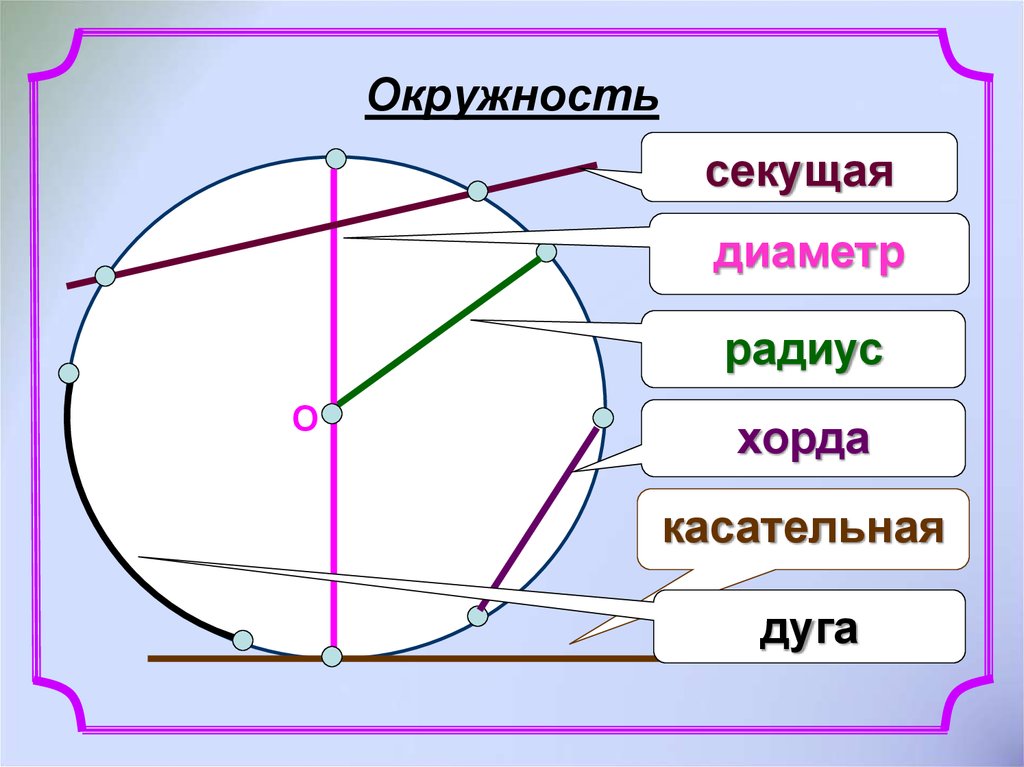 Задача Гл.VIII №725.
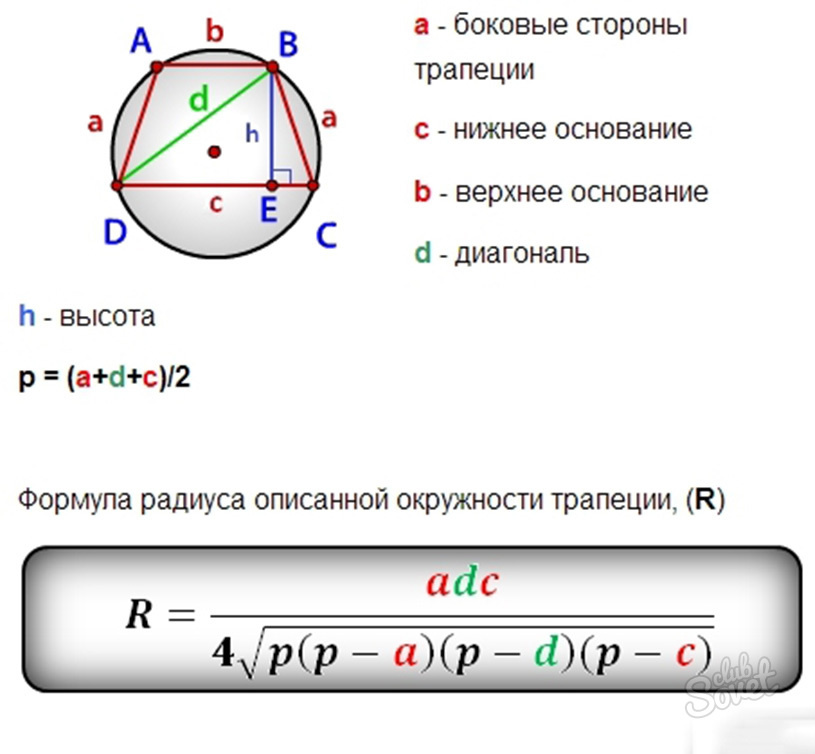
Найдите радиус окружности, вписанной в прямоугольную трапецию с основаниями а и b.
 

ответы

Я могу тебе помочь, ответ на задачу Гл.VIII №725 будет такой:

Пусть АВСD — трапеция с основаниям и АD и ВС

r — радиус вписанной в нее окружности.
Проведем высоту СН и, учитывая, что СН = 2r, DН =
= а —b и = (а — r) + (b — r) = а + b — 2r, применим

теорему Пифагора к треугольнику СDН: (а — b)2 + 4r2 =
= (а + b — 2r)2 →

Ответ: 

ваш ответ

Можно ввести 4000 cимволов

отправить

дежурный

Нажимая кнопку «отправить», вы принимаете условия  пользовательского соглашения

похожие темы

Экскурсии

Мякишев Г.Я.

Психология

Химия

похожие вопросы 5

Изобразите № 1240 ГДЗ Геометрия 9 класс Атанасян Л.С.

Изобразите тетраэдр DABC, отметьте точку К на ребре DC и точки М и N граней АВС и ACD. Постройте сечение тетраэдра плоскостью MNK. (Подробнее…)

ГДЗГеометрия9 классАтанасян Л.С.

ГДЗ по геометрии 8 класс Атанасян. Гл.VIII №649. Постройте хорду АВ так….

Если не затруднит, объясните задачу Гл.VIII №649.
 Начертите окружность с центром О и отметьте на ней точку А. Постройте хорду АВ  (Подробнее…)

ГДЗАтанасян Л.С.Геометрия8 класс

ГДЗ по геометрии 8 класс Атанасян. Гл.VIII №677. Докажите, что точка О является центром.

Объясните, как решить задачу Гл.VIII №677.
Биссектрисы внешних углов при вершинах В и С треугольника АВС пересекаются в точке О. (Подробнее…)

ГДЗ8 классАтанасян Л.С.Геометрия

Определите длину № 25 ГДЗ Математика 6 класс Никольский С.М.

План комнаты имеет вид прямоугольника со сторонами 40 мм
и 31 мм. Определите длину и ширину комнаты, если численный
масштаб (Подробнее…)

ГДЗМатематика6 классНикольский С. М.

Задание 8 Текст. Текст и его план. Русский язык.4 класс. Канакина В.П., Горецкий В.Г. ГДЗ

Приветствую, как ответить на вопросы к заданию?
Прочитайте.
Первая вахта (Подробнее…)

ГДЗРусский языкКанакина В.П.Горецкий В.Г.4 класс

Радиус

— ГИС Вики | Энциклопедия ГИС

Чтобы узнать о других значениях, см. Радиус (значения).

Иллюстрация круга

В классической геометрии радиусом круга или сферы называется любой отрезок прямой от центра до периметра. В более широком смысле, радиус круга или сферы представляет собой длину любого такого сегмента, которая составляет половину диаметра. ^[1]

В более общем смысле — в геометрии, науке, технике и многих других контекстах — радиус чего-либо (например, цилиндра, многоугольника, механической части, дыры или галактики) обычно относится к расстоянию от его центра или оси симметрии до точки на периферии: обычно точки, наиболее удаленной от центр или ось (

самая удаленная или максимальный радиус ) или, иногда, ближайшая точка ( короткая или минимальный радиус ). ^[2] Если объект не имеет явного центра, термин может относиться к радиусу описанной окружности , радиус его описанной окружности или описанной сферы. В любом случае радиус может быть больше половины диаметра (который обычно определяется как максимальное расстояние между любыми двумя точками фигуры).

inradius геометрической фигуры обычно является радиусом наибольшего круга или сферы, содержащейся в ней. Внутренний радиус кольца, трубы или другого полого предмета является радиусом его полости.

Радиус правильного многоугольника (или многогранника) — это расстояние от его центра до любой из его вершин; что также является его радиусом описанной окружности. ^[3] Внутренняя сторона правильного многоугольника также называется апофегмой.

В теории графов радиус графа является минимальным по всем вершинам u максимального расстояния от u до любой другой вершины графа. ^[4]

Название происходит от латинского radius , что означает «луч», но также и спицу колеса колесницы.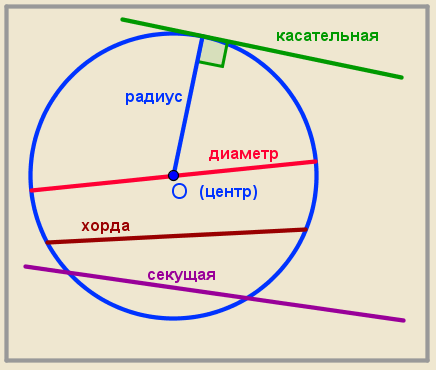 Множественное число в английском языке — радиусов (как на латыни), но можно использовать радиусов , хотя это редко. ^[5]

Содержание

• 1 Формулы для окружностей
  • 1.1 Радиус окружности
  • 1.2 Радиус от области
  • 1.3 Радиус по трем точкам
• 2 Формулы для правильных многоугольников
  • 2.1 Радиус сбоку
• 3 Формулы для гиперкубов
  • 3.1 Радиус сбоку
• 4 Каталожные номера

Формулы для окружностей

Радиус от окружности

Радиус окружности с периметром (окружностью) C составляет

Радиус от площади

Радиус круга с площадью A составляет

Радиус из трех точек

для вычисления радиуса круга, проходящего через три точки P ₁ , P ₂ , P _{3 , следующие. :}

где θ угол

Формулы для правильных многоугольников

Эти формулы предполагают правильный многоугольник с n сторон.

Радиус со стороны

Радиус можно вычислить со стороны s следующим образом: где

Каталожные номера

1. ↑ Определение радиуса на mathwords.com. Проверено 08 августа 2009 г.
2. ↑ Роберт Кларк Джеймс, Гленн Джеймс (1992), Математический словарь . 548 страниц, Springer ISBN 0412990415, 9780412990410
3. ↑ Барнетт Рич, Кристофер Томас (2008), Очерк геометрии Шаума , 4-е издание, 326 страниц. Макгроу-Хилл Профессионал. ISBN 0071544127 , 9780071544122 . Онлайн-версия по состоянию на 08 августа 2009 г.
4. ↑ Джонатан Л. Гросс, Джей Йеллен (2006), Теория графов и ее приложения . 2-е издание, 779 страниц; КПР Пресс. ISBN 158488505X , 9781584885054 . Онлайн-версия доступна 08 августа 2009 г.
5. ↑ Определение радиуса на Dictionary.reference.com. Проверено 08 августа 2009 г.

Круговые факты для детей — площадь, радиус, диаметр, окружность, дуга, касательная, хорда, сектор, сегмент

Круговые факты для детей — площадь, радиус, диаметр, окружность, дуга, касательная, хорда, сектор, сегмент

Логические головоломки денег . Круг фактов Ознакомьтесь с нашими круговыми фактами для детей и узнайте интересную информацию об этом двухмерном многоугольнике. Узнайте, что такое радиус, диаметр и длина окружности, как измерить площадь круга, что такое хорда круга, сектор и отрезок и многое другое. Читайте и наслаждайтесь фактами и мелочами из нашего круга, прежде чем взглянуть на всю другую интересную информацию, посвященную удивительному миру геометрии.

Круг — это круглая двухмерная фигура, похожая на букву «О». На строгом математическом языке круг относится к границе формы, а «диск» используется для обозначения всей формы, включая внутреннюю часть. Прямая линия от центра круга к краю называется радиусом. Прямая линия, которая проходит от одной стороны круга к другой через центр, называется диаметром. Расстояние по внешней стороне круга называется окружностью. Все точки на краю круга находятся на одинаковом расстоянии от центра. Значение числа Пи (π) с точностью до 2 знаков после запятой равно 3,14, оно пригодится при вычислении длины окружности и площади круга. Длину окружности можно найти по следующей формуле: Длина окружности = π d Площадь круга можно найти по следующей формуле: Площадь = π r² Дуга является частью окружности круга. Хорда — это прямая линия, соединяющая две точки на окружности, диаметр — это пример хорды (самой длинной из возможных). Сегмент — это область между хордой и дугой, к которой она примыкает. Касательная — это прямая линия, которая касается одной точки окружности. Сектор — это область между дугой и двумя радиусами. No related posts. Добавить комментарий Отменить ответ Ваш адрес email не будет опубликован. Обязательные поля помечены * Комментарий * Имя * Email * Сайт