Формулы по геометрии
Формулы по геометрии
Площадь плоских фигур
Площадь треугольника
через основание и высоту
через две стороны и угол
формула Герона
через радиус вписсанной окружности
через радиус описсанной окружности
площадь прямоугольного треугольника
площадь равнобедренного треугольника
площадь равностороннего треугольника
площадь параллелограмма
площадь ромба
площадь прямоугольника
площадь квадрата
площадь трапеции
площадь правильного 6-угольника
площадь круга
площадь эллипса
площадь сектора круга
площадь сегмента круга
площадь кольца
площадь сектора кольца
Площадь поверхности тел
площадь поверхности куба
площадь поверхности параллелепипеда
площадь поверхности правильной пирамиды
боковая поверхность правильной усеченной пирамиды
площадь поверхности конуса
площадь поверхности усеченного конуса
площадь поверхности цилиндра
площадь поверхности сферы
площадь поверхности шарового сегмента
площадь поверхности шарового сектора
площадь боковой поверхности шарового слоя
Периметр фигур
периметр треугольника
периметр прямоугольника
периметр квадрата
периметр параллелограмма
периметр ромба
периметр трапеции
периметр круга или длина окружности
Радиус описанной окружности
радиус описанной окружности треугольника
радиус описанной окружности квадрата
радиус описанной окружности прямоугольника
радиус описанной окружности равнобедренной трапеции
радиус описанной окружности правильного шестиугольника
радиус описанной окружности правильного многоугольника
Объем тел
объем куба
объем параллелепипеда
объем пирамиды
объем правильной пирамиды
объем тетраэдра
объем усеченной пирамиды
объем конуса
объем усеченного конуса
объем цилиндра
объем шара
объем шарового сегмента
объем шарового сектора
объем шарового слоя
|
1.
|
|||||||||||||||||||||||||||
| 1 2 3 4 5 6 7 8 | |||||||||||||||||||||||||||
Признаки параллельности прямых |
|||||||||||||||||||||||||||
Признаки равенства треугольников |
|||||||||||||||||||||||||||
Теорема Пифагора |
|||||||||||||||||||||||||||
Рассчитать стороны прямоугольного треугольникаКатет a Катет b Гипотенуза c =
|
|||||||||||||||||||||||||||
| Гипотенуза c Катет a Катет b = | |||||||||||||||||||||||||||
|
|||||||||||||||||||||||||||
Радиус вписанной и описанной окружностей правильных многоугольников |
|||||||||||||||||||||||||||
Рассчитать радиус вписанной и описанной окружностейСторона a Число углов n Радиус R = Радиус r = |
|||||||||||||||||||||||||||
Теорема синусов |
|||||||||||||||||||||||||||
Рассчитать сторону треугольникаСторона а sin (α= °) sin (β= °) Сторона b =Рассчитать угол треугольникаСторона а sin (α= °) Сторона b Угол β = °
|
|||||||||||||||||||||||||||
Теорема косинусов |
|||||||||||||||||||||||||||
Рассчитать сторону треугольникаСторона b Сторона с cos (α= °) Сторона a =Рассчитать угол треугольникаСторона а Сторона b Сторона c Угол α = ° |
|||||||||||||||||||||||||||
Радиус вписанной и описанной окружностей |
|||||||||||||||||||||||||||
|
Рассчитать радиус описанной и вписанной окружности Сторона а Сторона b Сторона c
Площадь S = Радиус R = Радиус r = |
|||||||||||||||||||||||||||
| 1 2 3 4 5 6 7 8 | |||||||||||||||||||||||||||
геометрических формул и уравнений | Примеры, Методы, Таблица
Примечание: эта страница содержит устаревшие ресурсы, которые больше не поддерживаются. Вы можете продолжать использовать эти материалы, но мы можем поддерживать только наши текущие рабочие листы, доступные как часть нашего членского предложения.
Вы можете продолжать использовать эти материалы, но мы можем поддерживать только наши текущие рабочие листы, доступные как часть нашего членского предложения.
Квадрат – это четырехугольник, у которого четыре равные стороны и четыре прямых угла.
Для квадрата, сторона которого состоит из s единиц:
Площадь квадрата = сторона x сторона = s 2 кв. единиц
Например, если у нас есть квадрат, одна сторона которого равна 6 см, его площадь будет рассчитана как:
Площадь = сторона x сторона = 6 x 6 = 36 см 2
Прямоугольник является разновидностью четырехугольника равные противоположным сторонам и четырем прямым углам.
Площадь прямоугольника с длиной ‘ l ‘ и шириной ‘b’ равна l x b
Например, рассмотрим прямоугольник длиной 8 см и шириной 7 см, как показано на рис. рисунок ниже.
Треугольник — это многоугольник, состоящий из трех ребер и трех вершин. Вершины соединяются вместе, образуя три стороны треугольника. Площадь, занимаемая этими тремя сторонами, называется площадью треугольника.
Площадь, занимаемая этими тремя сторонами, называется площадью треугольника.
Площадь треугольника определяется как: 1/2 x b x h
Где b = основание треугольника (или любая сторона треугольника)
И
H = высота треугольника от этого основания (или стороны )
На следующем рисунке показаны основание и высота треугольника:
Приведенная выше формула применима независимо от того, является ли треугольник разносторонним (у него разные стороны), равнобедренным треугольником (у которого две стороны равны) или равносторонним треугольником (у которого все стороны равны).
Давайте лучше разберемся на примере. Предположим, у нас есть треугольник, одна сторона которого равна 6 см, а высота основания равна 8 см, как показано на следующем рисунке:
Площадь этого треугольника равна
1/2 x b x h
Где b = 6 см, а h = 8 см
Следовательно, площадь = 1/2 x 6 x 8 = 24 см 2
Пространство, занимаемое кругом, называется его площадью.
Площадь круга с радиусом ‘r’ (расстояние от центра до точки на границе) определяется как πr 2 , где π = 22/7 или 3,14 (приблизительно)
Например, предположим, что у нас есть круг с радиусом 7 см, как показано на рисунке ниже.
Его площадь определяется как:
Площадь = πr 2 = (22/7) x 7 x 7 = 154 см 2
Предположим, что вместо радиуса нам дан диаметр круга, как мы вычисляем площадь?
Мы знаем, что в круге радиус равен половине диаметра. Математически
r = d/2, где d — диаметр, а r — радиус.
Итак, делим заданный диаметр наполовину и получаем радиус.
Пример
Предположим, нам нужно найти площадь круга диаметром 4,2 см.
Здесь диаметр (d) = 4,2 см
Из соотношения между радиусом и диаметром имеем r = d/2.
Отсюда r = 4,2/2 = 2,1 см
Теперь площадь этого круга = = πr 2 = (22/7) x 4,2 x 4,2 = 55,44 см 2
Длина, равняется границе круг называется его окружностью . Он определяется как 2πr, где r — радиус. Другими словами, окружность круга — это то же, что периметр для других геометрических фигур, таких как прямоугольник квадрата.
Он определяется как 2πr, где r — радиус. Другими словами, окружность круга — это то же, что периметр для других геометрических фигур, таких как прямоугольник квадрата.
Рассмотрим круг радиусом 7 см. Для того, чтобы найти его длину окружности, нам нужно воспользоваться формулой 2πr.
Следовательно, длина окружности этого круга = 2πr = 2 x (22/7) x 7 = 44 см.
Обратите внимание на единицы измерения периметра и площади. В то время как единицы площади всегда в квадратных единицах, в случае периметра они всегда в стандартных единицах длины, таких как м, см, дм, км и т. д.
Многогранник, содержащий две пары конгруэнтных параллельных оснований, называется прямоугольная призма. Он считается призмой из-за поперечного сечения по длине. Основание прямоугольной призмы представляет собой прямоугольник. Он имеет три измерения, как показано на рисунке ниже:
Объем прямоугольной призмы определяется как:
V = длина x ширина x высота
Где
l = длина основания призмы
w = ширина основания призмы
h = высота призмы
Например, у нас есть прямоугольная призма, длина основания которой равна 6 см; ширина основания 5 см, а высота 4 см. Тогда объем будет равен:
Тогда объем будет равен:
Объем (V) = l x w x h
Где
l = 6 см, w = 5 см и h = 4 см
Объем = 6 х 5 х 4 = 120 куб. см
Не единицы объема. Объем любой геометрической фигуры всегда выражается в кубических единицах.
Количество (в любой форме), которое может удержаться в цилиндре, называется его объемом. Другими словами, объем цилиндра – это занимаемое им пространство. Основание правильного круглого цилиндра представляет собой круг на обоих концах, которые проходят параллельно друг другу, как показано на рисунке ниже.
Объем прямого кругового цилиндра определяется как:
| Объем = площадь основания x высота цилиндра |
Поскольку основание представляет собой круг, его площадь определяется как πr 2
90 002 Следовательно, объем прямоугольного цилиндра становится πr 2 hПример
Предположим, мы хотим найти объем правильного круглого цилиндра, радиус которого в основании равен 5 см, а высота цилиндра равна 7 см.
На следующем рисунке показаны заданные размеры этого цилиндра.
Его объем определяется как πr 2 ч = (22/7) x 5 x 5 x 7 = 550 куб. см
Конус представляет собой пирамиду с круглым основанием. Его объем равен 1/3πr 2 ч, где «r» — радиус основания конуса, а «h» — его высота.
Предположим, мы хотим вычислить объем конуса с радиусом 6 см и высотой 14 см.
Его объем будет равен:
V = 1/3πr 2 h = (1/3) x (22/7) x 6 x 14 = 88 куб. см
Вышеприведенные формулы можно обобщить в таблице ниже.
Приведенные ниже формулы обычно требуются в геометрии для расчета длин, площадей и объемов. Вы можете использовать их, чтобы помочь детям с домашним заданием по математике.
Список формул| Площадь квадрата | = длина 2 (д x д) | |
| Площадь прямоугольника | = длина х высота | |
| Площадь треугольника | = 1/2 х длина х высота |
| Площадь круга | = ?r 2 (? = 3,14 примерно) | |
| Длина окружности | длина окружности = 2 r (? x диаметр) | |
| Объем прямоугольной призмы | = длина х высота х глубина | |
| Объем цилиндра | = площадь основания x высота = ? (г/2) 2 х в | |
| Объем конуса | = 1/3 x площадь основания x высота = 1/3 x ?(d/2) 2 x h |
Мы тратим много времени на изучение и сбор информации на этом сайте. Если вы сочтете это полезным в своем исследовании, используйте приведенный ниже инструмент, чтобы правильно указать ссылку Helping with Math в качестве источника. Мы ценим вашу поддержку!
Если вы сочтете это полезным в своем исследовании, используйте приведенный ниже инструмент, чтобы правильно указать ссылку Helping with Math в качестве источника. Мы ценим вашу поддержку!
Базовые формулы геометрии — GeeksforGeeks
В математике геометрия выступает как дисциплина изучения и предмет для анализа форм и структур вместе с их свойствами. Приведенная ниже статья иллюстрирует стандартные фиксированные или производные формулы геометрии для расчета различных параметров конкретной формы. Эти формулы используются для определения неизвестных сторон, углов или других его величин.
Формула базовой геометрии
Формула представляет собой математическое правило, которое формируется путем вывода взаимосвязи между двумя или более физическими величинами или математическими соотношениями. формулы обычно представляются в символической форме с помощью математических символов. Эти символические представления формул состоят из переменных, констант, операционных знаков и терминов.
Геометрические формулы являются стандартными производными формулами для расчета параметров фигур. Этими параметрами являются площадь, объем, периметр, окружность, общая площадь поверхности, площадь боковой поверхности и т. Д. Каждая форма, изучаемая в геометрии, имеет для них свою собственную формулу. Эти формулы перечислены ниже.
Квадрат
- Периметр Квадрата = 4а
- Площадь Квадрата = а 2
Где а — длина стороны квадрата
Прямоугольник
- Периметр прямоугольника = 2(l + b)
- Площадь прямоугольника = л × ш
Где ‘l’ длина и ‘b’ ширина
Треугольник
- Площадь треугольника = A = 1/2 × b × h
Где ‘b’ основание треугольника
и «h» высота треугольника
Трапеция
- Площадь трапеции = A = 1/2 × (b1 + b2) × h
Где b1 и b2 — основания T рапезоид
а, h высота трапеции
Окружность
- Площадь окружности = A = π × r2
- Длина окружности = A = 2πr
Где «r» — радиус круга
Куб
- Площадь поверхности куба = 6a 2
Где «a» — длина сторон куба
Цилиндр 900 03
- Площадь криволинейной поверхности цилиндра = 2πrh
- Общая площадь поверхности цилиндра = 2πr(r + h)
- Объем цилиндра = V = πr2h
Где «r» — радиус основания цилиндра
, а «h» — высота Цилиндр
Конус
- Площадь криволинейной поверхности конуса = πrl
- Общая площадь поверхности конуса = πr(r + l) = πr[r + √(h 2 + р 2 )]
- Объем конуса = V = 1/2× πr 2 h
Здесь ‘r’ — радиус основания конуса
, а h — высота конуса
9 0079 Сфера
- Площадь поверхности сферы = 4πr 2
- Объем сферы = 4/3 × πr 3
Где r – радиус сферы
Примеры задач
Задача 1. Если радиус круг 14 см. Найдите площадь данного круга.
Если радиус круг 14 см. Найдите площадь данного круга.
Решение:
Дано
Радиус окружности равен 14см.
Имеем,
Площадь круга (A)=πr 2
=>22/7 x 14 x 14
=>616см 2
Задача 2. Найдите площадь треугольника с основанием 12см и высотой 8см.
Решение:
Дано
Основание треугольника 12см.
Высота треугольника 8см.
Имеем,
Площадь треугольника(A)=1/2 x b x h
=>1/2 x 12 x 8
=>48см 2
Задача 3. Найдите периметр заданного прямоугольник длиной 10 см и шириной 4 см.
Решение:
Дано
Длина прямоугольника 10см.
Ширина прямоугольника 4см.
Имеем,
Периметр прямоугольника(P)= 2(l+b)
=>2(10+4)
=>2 x 14
=>28см
900 79 Задача 4. Найти периметр квадрата, длина которого 5 см.
Найти периметр квадрата, длина которого 5 см.
Решение:
Дано
Длина квадрата 5см.
Имеем,
Периметр квадрата(P)= 4l
=> 4 x 5
=>20см
Задача 5. Найдите объем сферы, имеющей радиус 9см.
Решение:
Дано
Радиус сферы равен 9см.
У нас есть
Объем сферы (V)=4/3 πr 3
=>4/3 x 22/7 x (9) 3
=>3054,85 см 900 09 3
Задача 6. Вычислить площадь трапеции с основаниями 8см и 10см и высотой 12см.
Решение:
Дано
Пусть основания трапеции равны b1 и b2 со значениями 8см и 10см соответственно.
Высота трапеции 12см.
У нас есть,
Площадь трапеции = A =1/2 × (b1 + b2) × h
=>1/2 x (8 +10) x 12
=>1/2 x 18 x 12
=> 216/2
=>108см 2
Задача 7.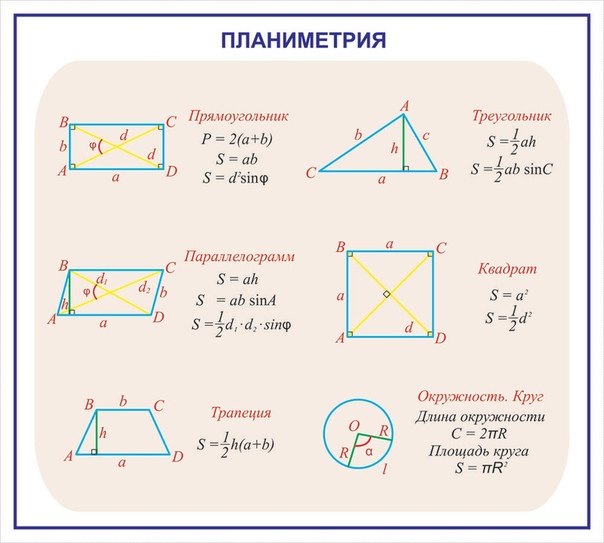

 Признаки параллельности прямых.
Признаки параллельности прямых. 