Глава 19. Гипербола
Глава 19. ГиперболаГиперболой называется геометрическое место точек, для которых разность расстояний до двух фиксированных точек плоскости, называеых фокусами, есть постоянная величина; указанная разность берется по абсолютному значению и обозначается через2а. Фокусы гиперболы обозначают буквами и , расстояние между ними — через 2с. По определению гиперболы , или .
Пусть дана гипербола. Если оси декатовой прямоугольной системы координат выбраны так, что фокусы данной гиперболы располагаются на оси абсцисс симметрично относительно начала координат, то в этой системе координат уравнение гиперболы имеет вид
(1)
где . Уравнение вида (1) называется каноническим уравнением гиперболы. При указанном выборе системы координат оси координат являются осями симметрии гиперболы, а начало координат — ее центром симметрии (рис.
). Оси симметрии гиперболы называются просто ее осями, центр симметрии — центром гиперболы. Гипербола пересекает одну из своих осей; точки пересечения называются вершинами гиперболы. На рис. Вершины гиперболы суть точки А’ и А.
Прямоугольник со сторонами 2а и 2b, расположенный симметрично относительно осей гиперболы и касающийся ее в вершинах, называется основным прямоугольником гиперболы.
Отрезки длиной 2a и 2b, соединяющие середины сторон основного прямоугольника гиперболы, также называют ее осями. Диагонали основного прямоугольника (неограниченно продолженного) являются асимптотами гиперболы, их уравнения суть
,
Уравнение
(2)
определяет гиперболу, симметричную
относительно координатных осей, с фокусами на
оси ординат; уравнение (2), как и уравнение (1),
называется каноническим уравнением гиперболы; в
этом случае постоянная разность расстояний от
произвольной точки гиперболы до фокусов равна 2b.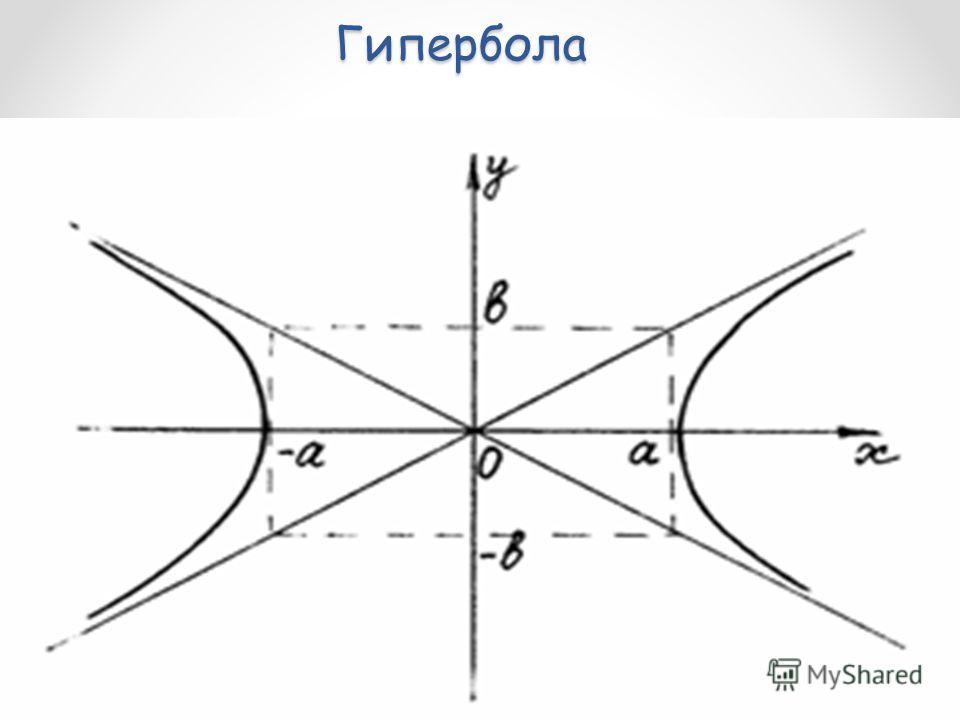
Две гиперболы, которые определяются уравнениями
,
в одной и той же системе координат, называются сопряженными.
Гипербола с равными полуосями (a=b) называется равносторонней; ее каноническое уравнение имеет вид
или
Число
где а — расстояние от центра гиперболы до ее вершины, называется эксцентриситетом гиперболы. Очевидно, для любой гиперболы . Если М(x; y) — произвольная точка гиперболы, то отрезки и (см. рис.) называются фокальными радиусами точки М. Фокальные радиусы точек правой ветви гиперболы вычисляются по формулам
, ,
фокальные радиусы точек левой ветви — по формулам
, .
Если гипербола задана уравнением (1), то прямые, определяемые уравнениями
, ,
называются ее директрисами (см. рис.).
Если гипербола задана уравнением (2), то
директрисы определяются уравнениями
рис.).
Если гипербола задана уравнением (2), то
директрисы определяются уравнениями
, .
Каждая директриса обладает следующим свойством: если r — расстояние от произвольной точки гиперболы до некоторого фокуса, d — расстояние от той же точки до односторонней с этим фокусом директрисы, то отношение r/d есть постоянная величина, равная эксцентрисистету гиперболы:
.
| Текст издания: | © Д.В.Клетеник «Сборник задач по аналитической геометрии». М., Наука, Физматлит, 1998. | |
| Решение задач: | © Кирилл Кравченко,
http://a-geometry.narod.ru/. Все права принадлежат мне, если не оговорено иное 😉 |
Сайт управляется системой uCoz
Гипербола (математика) | это.
 .. Что такое Гипербола (математика)?
.. Что такое Гипербола (математика)?У этого термина существуют и другие значения, см. Гипербола.
Гипербола и её фокусы
Сечения конусов плоскостью (с эксцентриситетом, большим единицы)
Гипе́рбола (др.-греч. ὑπερβολή, от ὑπερ — «верх» + βαλειν — «бросать») — геометрическое место точек M Евклидовой плоскости, для которых абсолютное значение разности расстояний от M до двух выделенных точек и (называемых фокусами) постоянно. Точнее,
- причем
Наряду с эллипсом и параболой, гипербола является коническим сечением и квадрикой. Гипербола может быть определена как коническое сечение с эксцентриситетом, большим единицы.
Содержание
|
История
Термин «гипербола» (греч. ὑπερβολή — избыток) был введён Аполлонием Пергским (ок. 262 год до н. э. — ок. 190 год до н. э.), поскольку задача о построении точки гиперболы сводится к задаче о приложении с избытком.
Определения
Гипербола может быть определена несколькими путями.
Коническое сечение
Три основных конических сечения
Гипербола может быть определена, как множество точек, образуемое в результате сечения кругового конуса плоскостью, отсекающей обе части конуса. Другими результатами сечения конуса плоскостью являются парабола, эллипс, а также такие вырожденные случаи, как пересекающиеся и совпадающие прямые и точка, возникающие, когда секущая плоскость проходит через вершину конуса. В частности, пересекающееся прямые можно считать вырожденной гиперболой, совпадающей со своими асимптотами.
Другими результатами сечения конуса плоскостью являются парабола, эллипс, а также такие вырожденные случаи, как пересекающиеся и совпадающие прямые и точка, возникающие, когда секущая плоскость проходит через вершину конуса. В частности, пересекающееся прямые можно считать вырожденной гиперболой, совпадающей со своими асимптотами.
Как геометрическое место точек
Через фокусы
Гипербола может быть определена, как Геометрическое место точек, абсолютная величина разности расстояний от которых до двух заданных точек, называемых фокусами, постоянна.
Для сравнения: кривая постоянной суммы расстояний между двумя точками — эллипс, постоянного отношения — окружность Аполлония, постоянного произведения — овал Кассини.
Через директрису и фокус
Геометрическое место точек, для которых отношение расстояния до фокуса и до заданной прямой, называемой директрисой, постоянно и больше единицы, называется гиперболой. Заданная постоянная называется эксцентриситетом гиперболы.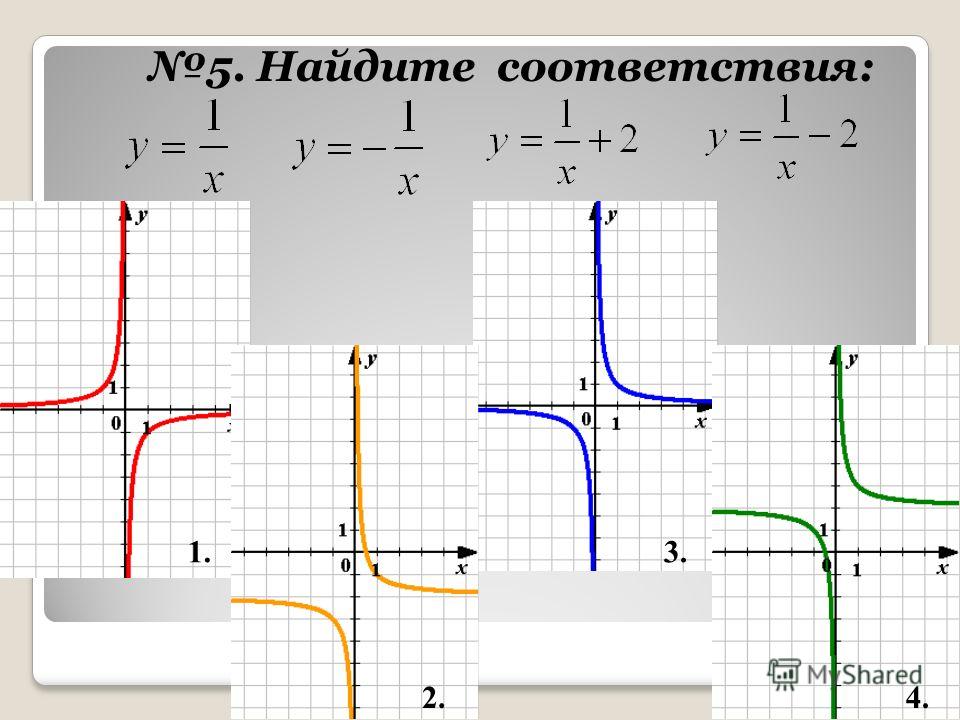
Связанные определения
Асимптоты гиперболы (красные кривые), показанные голубым пунктиром, пересекаются в центре гиперболы,
a — расстояние от центра C до каждой из вершин
b — длина перпендикуляра, опущенного из каждой из вершин на асимптоты
c — расстояние от центра C до любого из фокусов, F1 и F2,
θ — угол, образованный каждой из асимптот и осью, проведённой между вершинами
- Гипербола состоит из двух отдельных кривых, которые называют ветвями.

- Ближайшие друг к другу точки двух ветвей гиперболы называются вершинами.
- Кратчайшее расстояние между двумя ветвями гиперболы называется большой осью гиперболы.
- Середина большой оси называется центром гиперболы.
- Расстояние от центра гиперболы до одной из вершин называется большой полуосью гиперболы.
- Обычно обозначается a.
- Расстояние от центра гиперболы до одного из фокусов называется фокальным расстоянием.
- Обычно обозначается c.
- Оба фокуса гиперболы лежат на продолжении большой оси на одинаковом расстоянии от центра гиперболы. Прямая, содержащая большую ось гиперболы, называется действительной или поперечной осью гиперболы.
- Прямая, перпендикулярная действительной оси и проходящая через её центр называется мнимой или сопряженной осью гиперболы.
- Отрезок между фокусом гиперболы и гиперболой, перпендикулярный её действительной оси, называется

- Расстояние от фокуса до асимптоты гиперболы называется прицельным параметром.
- Обычно обозначается b.
- В задачах, связанных с движением тел по гиперболическим траекториям расстояние от фокуса до ближайшей вершины гиперболы называется перицентрическим расстоянием
- Обычно обозначается ..
Соотношения
Для характеристик гиперболы определённых выше подчиняются следующим соотношениям
- .
- .
- .
- .
- .
- .
- .
- .
Типы гипербол
Равнобочная гипербола
Гиперболу, у которой , называют равнобочной. Равнобочная гипербола в некоторой прямоугольной системе координат описывается уравнением
Гиперболы, связанные с треугольником
- гипербола Енжабека — кривая, изогонально сопряженная прямой Эйлера;
- гипербола Киперта — кривая, изогонально сопряженная прямой проходящей через точка Лемуана и центр описанной окружности данного треугольника.

См. также Треугольник#Эллипсы, параболы и гиперболы
Уравнения
Декартовы координаты
Гипербола задаётся уравнением второй степени в декартовых координатах (x, y) на плоскости:
- ,
где коэффициенты Axx, Axy, Ayy, Bx, By, и C удовлетворяют следующему соотношению
и
Канонический вид
Перемещением центра гиперболы в начало координат и вращением её относительно центра уравнение гиперболы можно привести к каноническому виду
- ,
где a и b — полуоси[источник?].
Полярные координаты
График гиперболы в полярных координатах
Если полюс находится в фокусе гиперболы, а вершина гиперболы лежит на продолжении полярной оси, то
Если полюс находится в фокусе гиперболы, а полярная ось параллельна одной из асимптот, то
Параметризация ветви гиперболы с помощью гиперболических функций
Уравнения в параметрической форме
Подобно тому, как эллипс может быть представлен уравнениями в параметрической форме, в которые входят тригонометрические функции, гипербола в прямоугольной системе координат, центр которой совпадает с её центром, а ось абсцисс проходит через фокусы, может быть представлена уравнениями в параметрической форме, в которые входят гиперболические функции[1].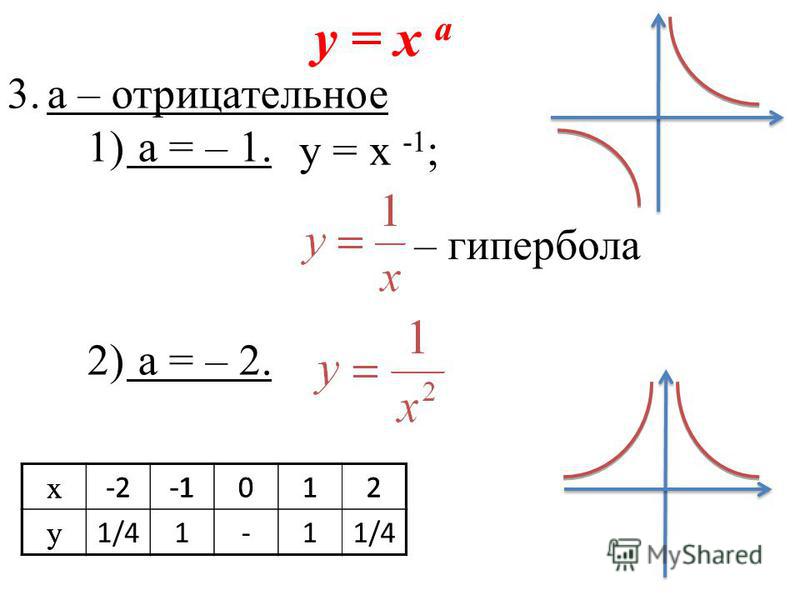
В первом уравнении знак «+» соответствует правой ветви гиперболы, а «-» — её левой ветви.
Свойства
- Оптическое свойство. Свет от источника, находящегося в одном из фокусов гиперболы, отражается второй ветвью гиперболы таким образом, что продолжения отраженных лучей пересекаются во втором фокусе.
- Иначе говоря, если и фокусы гиперболы, то касательная в любой точки гиперболы является биссектрисой угла .
- Для любой точки лежащей на гиперболе отношение расстояний от этой точки до фокуса к расстоянию от этой же точки до директрисы есть величина постоянная.
- Гипербола обладает зеркальной симметрией относительно действительной и мнимой осей, а также вращательной симметрией при повороте на угол 180° вокруг центра гиперболы.
- Каждая гипербола имеет сопряженную гиперболу, для которой действительная и мнимая оси меняются местами, но асимптоты остаются прежними. Это соответствует замене a и b друг на друга в формуле, описывающей гиперболу.
 Сопряженная гипербола не является результатом поворота начальной гиперболы на угол 90°; обе гиперболы различаются формой.
Сопряженная гипербола не является результатом поворота начальной гиперболы на угол 90°; обе гиперболы различаются формой.
Асимптоты
Две сопряженные гиперболы (голубая и зелёная) обладают совпадающими асимптотами (красные). Эти гиперболы единичные и равнобочные, так как a = b = 1
Для гиперболы, заданной в каноническом виде
уравнения двух асимптот имеют вид:
- .
Диаметры и хорды
Диаметры гиперболы
Диаметром гиперболы, как и всякого конического сечения, является прямая, проходящая через середины параллельных хорд. Каждому направлению параллельных хорд соответствует свой сопряженный диаметр. Все диаметры гиперболы проходят через её центр. Диаметр, соответствующий хордам, параллельным мнимой оси, есть действительная ось; диаметр соответствующий хордам, параллельным действительной оси, есть мнимая ось.
Угловой коэффициент параллельных хорд и угловой коэффициент соответствующего диаметра связан соотношением
Если диаметр a делит пополам хорды, параллельные диаметру b, то диаметр b делит пополам хорды, параллельные диаметру a.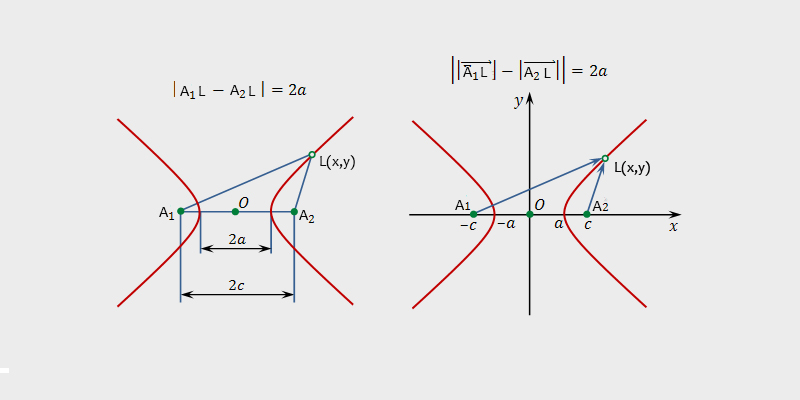 Такие диаметры называются взаимно сопряженными. Главными диаметрами называются взаимно сопряженные и взаимно перпендикулярные диаметры. У гиперболы есть только одна пара главных диаметров — действительная и мнимая оси.
Такие диаметры называются взаимно сопряженными. Главными диаметрами называются взаимно сопряженные и взаимно перпендикулярные диаметры. У гиперболы есть только одна пара главных диаметров — действительная и мнимая оси.
Определение центра гиперболы по её графику
Касательная и нормаль
Поскольку гипербола является гладкой кривой, в каждой её точке (x0, y0) можно провести касательную и нормаль. Уравнение касательной к гиперболе, заданной каноническим уравнением, имеет вид:
- ,
или, что то же самое,
- .
| Вывод уравнения касательной |
|---|
Уравнение касательной произвольной плоской линии имеет вид Каноническое уравнение гиперболы можно представить в виде пары функций
Тогда производная этих функций имеет вид
Подставив это уравнение в общее уравнение касательной, получим |
Уравнение нормали к гиперболе имеет вид:
- .

| Вывод уравнения нормали |
|---|
Уравнение нормали произвольной плоской линии имеет вид
Каноническое уравнение гиперболы можно представить в виде пары функций
Тогда производная этих функций имеет вид
Подставив это уравнение в общее уравнение нормали, получим
|
Кривизна и эволюта
Синим цветом показана гипербола. Зелёным цветом — эволюта правой ветви этой гиперболы (эволюта левой ветви вне рисунка. Красным цветом показан круг, соответствующий кривизне гиперболы в ей вершине)
Кривизна гиперболы в каждой её точке (x, y) определяется из выражения:
- .
Соответственно, радиус кривизны имеет вид:
- .
В частности, в точке (a, 0) радиус кривизны равен
- .
| Вывод формулы для радиуса кривизны |
|---|
Формула для радиуса кривизны плоской линии, заданной параметически, имеет вид:
Воспользуемся параметрическим представлением гиперболы: Тогда, первая производная x и y по t имеет вид
а вторая производная — Подставляя эти значения в формулу для кривизны получаем:
|
Координаты центров кривизны задаются парой уравнений:
Подставив в последнюю систему уравнений вместо x и y их значения из параметрического представления гиперболы, получим пару уравнений, задающих новую кривую, состоящую из центров кривизны гиперболы. Эта кривая называется эволютой гиперболы.
Эллиптическая система координат
Применения
- Семейство конфокальных (софокусных) гипербол вместе с семейством софокусных эллипсов образуют двумерную эллиптическую систему координат.
- Другие ортогональные двумерные координатные системы, построенные с помощью гипербол, могут быть получены с помощью других конформных преобразований.
 Например, преобразование w = z² отображает декартовы координаты в два семейства ортогональных гипербол.
Например, преобразование w = z² отображает декартовы координаты в два семейства ортогональных гипербол.
См. также
- Каустика
- Гиперболоид
- en:Smoothed octagon#Construction
Примечания
- ↑ Погорелов А. В. Геометрия. — М.: Наука, 1983. — С. 15—16. — 288 с.
Литература
- Бронштейн И. Гипербола // Квант. — 1975. — № 3.
- Математическая энциклопедия (в 5-и томах). М.: Советская энциклопедия, 1982.
- Маркушевич А. И. Замечательные кривые // Популярные лекции по математике. — Гостехиздат, 1952. — В. 4.
Гипербола
Знаете ли вы, что орбита космического корабля иногда может быть гиперболой?
Космический корабль может использовать гравитацию планеты, чтобы изменить свой путь и оттолкнуть его на высокой скорости от планеты и обратно в космос, используя технику, называемую «гравитационной рогаткой».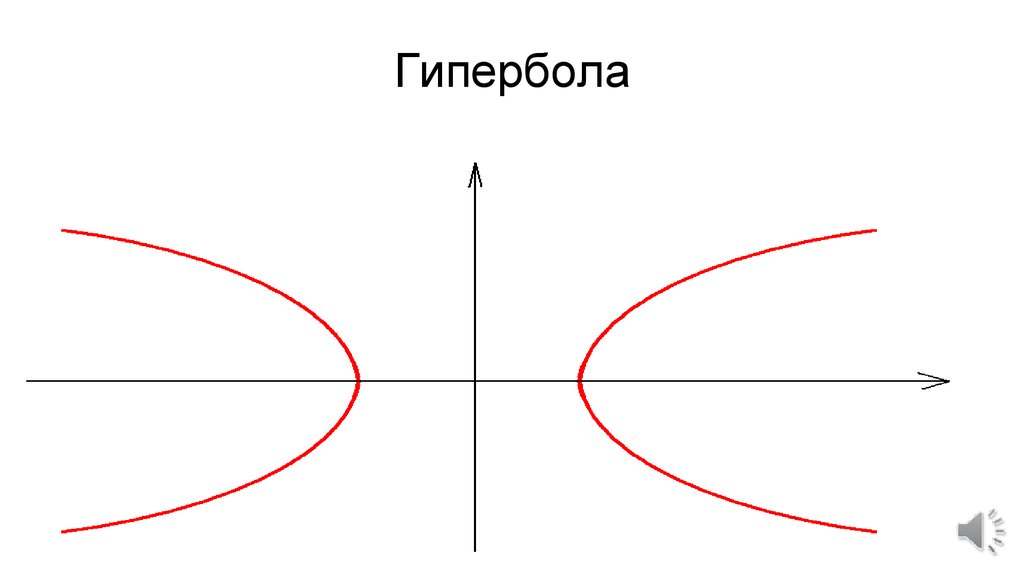
Если это произойдет, то траектория космического корабля будет гиперболой .
(Играйте с этим в Gravity Freeplay)
Определение
Гипербола — это две кривые, похожие на бесконечные луки.
Глядя только на одну из кривых:
любая точка P ближе к F , чем к G на некоторую постоянную величину
Другая кривая является зеркальным отражением и ближе к G, чем к F.
Другими словами, расстояние от P до F всегда меньше расстояния от P до G на некоторую постоянную величину. (А для другой кривой от P до G всегда меньше от P до F на эту постоянную величину.)
В виде формулы:
|PF − PG| = константа
- PF — расстояние от P до F
- PG — это расстояние от P до G
- || функция абсолютного значения (превращает любое отрицательное значение в положительное)
Каждый лук называется ветвью , а F и G называются фокусом .
Попробуйте сами:
Попробуйте переместить точку P : что вы заметили в длинах PF и PG ?
Также попробуйте поставить точку P на другой ветке.
Есть и другие интересные вещи:
На схеме видно:
- ось симметрии (проходящая через каждый фокус)
- две вершины (где каждая кривая делает свой самый крутой поворот)
- расстояние между вершинами (2а на диаграмме) постоянная разность между длинами PF и PG
- две асимптоты , которые не являются частью гиперболы, но показывают, куда пойдет кривая, если продолжать ее бесконечно в каждом из четырех направлений
И, строго говоря, есть еще другая ось симметрии , которая идет посередине и разделяет две ветви гиперболы.
Коническая секция Вы также можете получить гиперболу, разрезав двойной конус. Срез должен быть круче, чем у параболы, но Итак, гипербола является коническим сечением (сечением конуса). |
Уравнение
Поместив гиперболу на график x-y (с центром по осям x и y), уравнение кривой будет таким:
x 2 а 2 − у 2 б 2 = 1
Также:
Одна вершина находится в точке (a, 0), а другая — в точке (−a, 0)
.Асимптоты — это прямые:
- у = (б/а)х
- у = -(б/а)х
(Примечание: уравнение аналогично уравнению эллипса: x 2 /a 2 + y 2 /b 2 = 1 , за исключением «-» вместо » +»)
Эксцентриситет
Любая ветвь гиперболы также может быть определена как кривая, где расстояния любой точки от:
- фиксированная точка ( фокус ) и
- фиксированная прямая ( директриса ) всегда находятся в одном и том же соотношении.

Это отношение называется эксцентриситетом, и для гиперболы оно всегда больше 1.
Эксцентриситет (обычно обозначаемый буквой е) показывает, насколько «неизогнутая» (в отличие от окружности) гипербола является.
На этой диаграмме:
- P — точка на кривой,
- F это фокус и
- N — точка на директрисе, так что PN перпендикулярно директрисе.
Эксцентриситет представляет собой отношение PF/PN и рассчитывается по формуле:
e = √(a 2 +b 2 ) a
Используя «a» и «b» из диаграммы выше.
Широкая кишка прямой кишки
Широкая прямая кишка — это линия, проходящая через фокус и параллельная директрисе. Длина прямой кишки 2b 2 /a. |
1 шт.
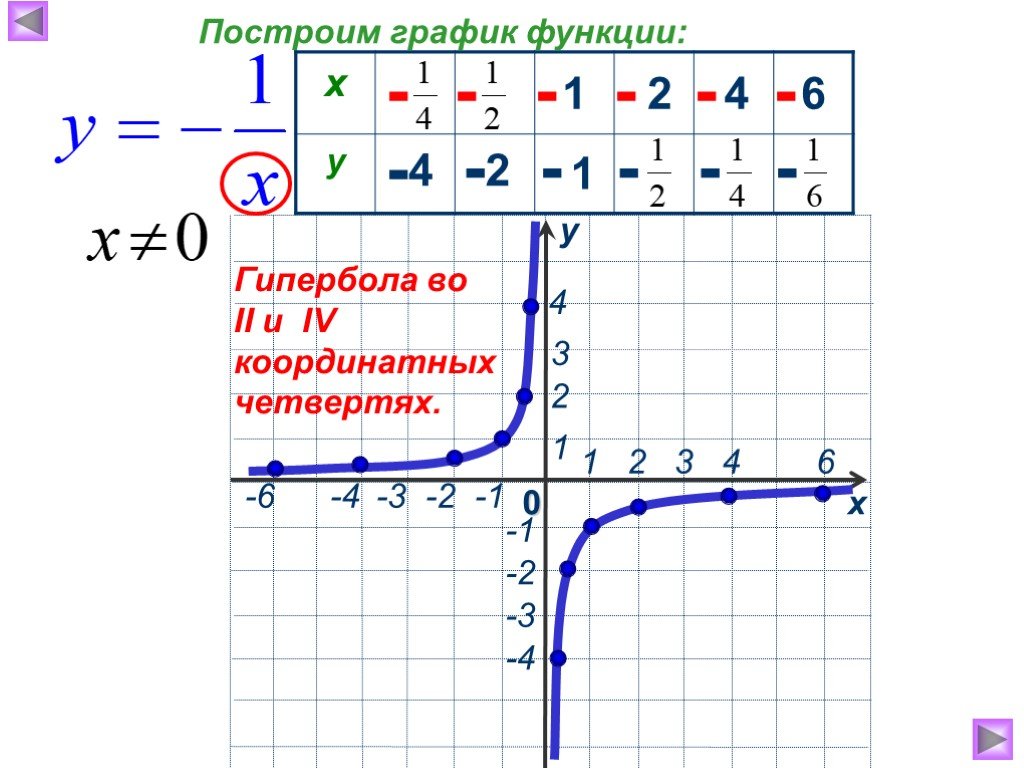
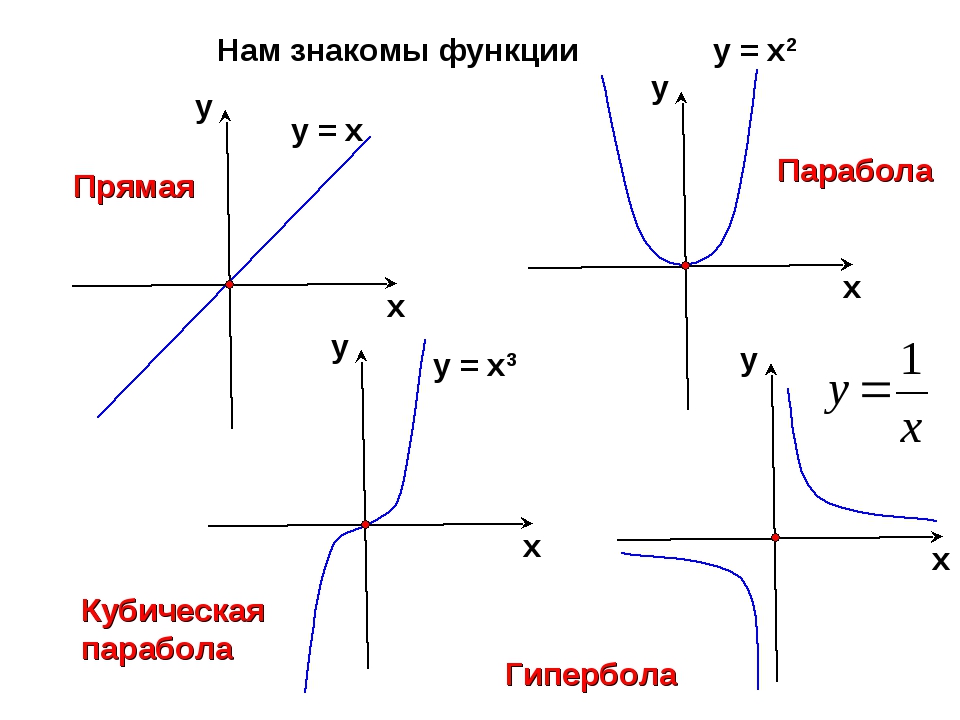
Обратная функция y = 1/x является гиперболой!
этимология — Риторика против математики: многоточие/эллипс, притча/парабола, гипербола/гипербола
спросил
Изменено 2 месяца назад
Просмотрено 13 тысяч раз
Имеют ли многоточие , притча и гипербола из риторики что-либо общее с геометрическими кривыми эллипс , парабола и 3 гипербола3 , используемые в математике 901?
Существуют три геометрические кривые , известные как конические сечения:
Эллипс: кривая на плоскости, окружающая две фокальные точки, такая, что прямая линия, проведенная из одной из фокальных точек в любую точку кривой, а затем обратно в другую фокальную точку, имеет одинаковую длину для каждой точки на изгиб.

Парабола: двумерная зеркально-симметричная кривая, имеющая приблизительно U-образную форму при ориентации, как показано на схеме.
Гипербола: состоит из двух частей, называемых соединенными компонентами или ответвлениями, которые являются зеркальным отображением друг друга и напоминают две бесконечные дуги.
Есть также три термина в лингвистике с аналогичными названиями (фактически во многих языках с одинаковыми названиями): в контексте остальных элементов.
- Джон умеет играть на гитаре, а Мэри на скрипке.
Притча: краткий дидактический рассказ в прозе или стихах, иллюстрирующий один или несколько поучительных уроков или принципов.
- Новая одежда императора
Гипербола: использование преувеличения в качестве риторического приема или фигуры речи.
- Этот чемодан весил тонну!
Есть ли у них что-то общее? Есть ли этимологическая или иная причина, связывающая каждую пару вместе? Многоточие чем-то напоминает эллипс и т. д.? Есть ли между ними аналогия?
д.? Есть ли между ними аналогия?
- Etymology
- Математика
- Аналогия
- RHETORIC
- ГРЕК
В древне -греке, где были изобретены 900.604. parabole» — это «сопоставление/обстановка бок о бок» — с использованием латинских морфов «сопоставление» или «смежность». В риторике это сравнение, которое ставит рядом два термина ; позже оно обозначает вымысел, который «положен рядом» и параллелен («лежит рядом») с реальностью. В геометрии это коническое сечение, образованное пересечением конуса с плоскостью с таким же наклоном к оси, как и одна из сторон конуса — плоскость параллельна этой стороне.
 В риторике это означает опущение одного или нескольких слов, необходимых для полноты смысла — таким образом, высказывание не достигает завершенности. В геометрии это коническое сечение, в котором наклон секущей плоскости меньше — меньше — наклона стороны конуса.
В риторике это означает опущение одного или нескольких слов, необходимых для полноты смысла — таким образом, высказывание не достигает завершенности. В геометрии это коническое сечение, в котором наклон секущей плоскости меньше — меньше — наклона стороны конуса.11
Эти английские термины косвенно происходят от соответствующих древнегреческих корней:
- ἔλλειψις (эллипсис) : несоответствие / упущение
- παρά- (пара-) : «рядом с» или «приложение»
- ὐπερ- (супер-) : «превышать»
Отношение риторических терминов к этим истокам должно быть очевидным. Вместо этого я сосредоточусь на конических сечениях.
Мы знаем, что Аполлоний Пергский (ок. 200 г. до н. э.) называл конические сечения родственниками их нынешних английских названий. Неясно, придумал ли он эти термины или они уже использовались в то время. Точная причина, по которой были выбраны эти слова, также является предметом обоснованных предположений; Джефф Миллер цитирует некоторые источники.
Точная причина, по которой были выбраны эти слова, также является предметом обоснованных предположений; Джефф Миллер цитирует некоторые источники.
Одним из простых объяснений является то, что термины для конических сечений относятся к углу между конусом и секущей плоскостью. Если секущая плоскость пара параллельна ровно одной образующей конуса, то коника не ограничена и называется бола пара . Если плоскость пересекается под меньшим углом, это эллипс; если он пересекается под большим углом, это гипербола.
Однако объяснение параболы может быть сложнее. Согласно онлайн-словарю этимологии,
парабола (н.)
1570-е годы, от современной латыни parabola, от греческого parabole «парабола, сравнение, аналогия; применение» (см. притча ), названная так Аполлонием Пергским около 210 г. до н.э. потому что он получается путем «приложения» данной площади к данной прямой линии. В пифагорейской геометрии оно имело иной смысл.


 1 Соотношения
1 Соотношения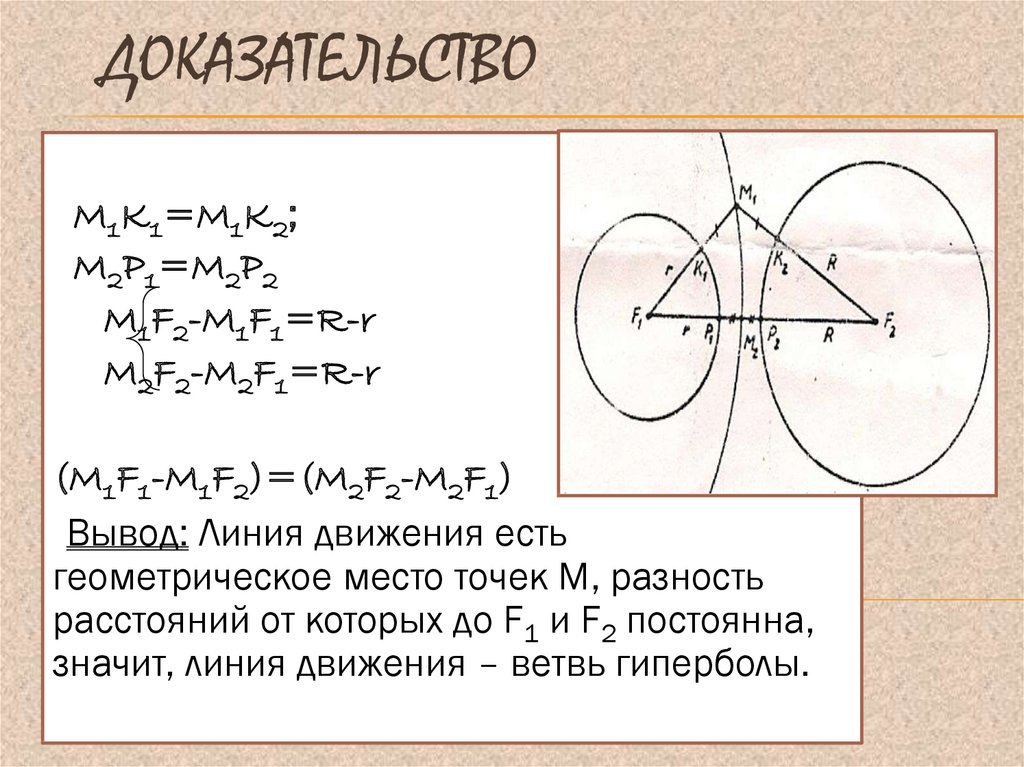

 Сопряженная гипербола не является результатом поворота начальной гиперболы на угол 90°; обе гиперболы различаются формой.
Сопряженная гипербола не является результатом поворота начальной гиперболы на угол 90°; обе гиперболы различаются формой.

 Например, преобразование w = z² отображает декартовы координаты в два семейства ортогональных гипербол.
Например, преобразование w = z² отображает декартовы координаты в два семейства ортогональных гипербол.