Композиция из букв т по геометрии: Конструирование из Т

Условия формирования у детей дошкольного возраста геометрических представлений в различных видах деятельности

%PDF-1.5 % 1 0 obj > /Metadata 4 0 R >> endobj 5 0 obj /Title >> endobj 2 0 obj > endobj 3 0 obj > endobj 4 0 obj > stream

Условия формирования у детей дошкольного возраста геометрических представлений в различных видах деятельности

Перова О. В.1.52017-11-30T00:50:01+05:002017-11-30T00:50:01+05:00 endstream endobj 6 0 obj > /ExtGState > /ProcSet [/PDF /Text /ImageB /ImageC /ImageI] /XObject > >> /MediaBox [0 0 595. 5 842.25] /Contents [123 0 R 124 0 R 125 0 R] /Group > /Tabs /S /StructParents 0 /Annots [126 0 R] >> endobj 7 0 obj > /ProcSet [/PDF /Text /ImageB /ImageC /ImageI] >> /MediaBox [0 0 595.5 842.25] /Contents 127 0 R /Group > /Tabs /S /StructParents 1 >> endobj 8 0 obj > /ExtGState > /ProcSet [/PDF /Text /ImageB /ImageC /ImageI] >> /MediaBox [0 0 595.5 842.25] /Contents 128 0 R /Group > /Tabs /S /StructParents 2 >> endobj 9 0 obj > /ExtGState > /ProcSet [/PDF /Text /ImageB /ImageC /ImageI] >> /MediaBox [0 0 595.5 842.25] /Contents 129 0 R /Group > /Tabs /S /StructParents 3 >> endobj 10 0 obj > /ExtGState > /ProcSet [/PDF /Text /ImageB /ImageC /ImageI] >> /MediaBox [0 0 595.5 842.25] /Contents 130 0 R /Group > /Tabs /S /StructParents 4 >> endobj 11 0 obj > /ExtGState > /ProcSet [/PDF /Text /ImageB /ImageC /ImageI] >> /MediaBox [0 0 595.5 842.25] /Contents 131 0 R /Group > /Tabs /S /StructParents 5 >> endobj 12 0 obj > /ExtGState > /ProcSet [/PDF /Text /ImageB /ImageC /ImageI] >> /MediaBox [0 0 595. 5 842.25] /Contents 134 0 R /Group > /Tabs /S /StructParents 6 >> endobj 13 0 obj > /ExtGState > /ProcSet [/PDF /Text /ImageB /ImageC /ImageI] >> /MediaBox [0 0 595.5 842.25] /Contents 135 0 R /Group > /Tabs /S /StructParents 7 >> endobj 14 0 obj > /ExtGState > /ProcSet [/PDF /Text /ImageB /ImageC /ImageI] >> /MediaBox [0 0 595.5 842.25] /Contents 137 0 R /Group > /Tabs /S /StructParents 8 >> endobj 15 0 obj > /ExtGState > /ProcSet [/PDF /Text /ImageB /ImageC /ImageI] >> /MediaBox [0 0 595.5 842.25] /Contents 138 0 R /Group > /Tabs /S /StructParents 9 >> endobj 16 0 obj > /ExtGState > /ProcSet [/PDF /Text /ImageB /ImageC /ImageI] >> /MediaBox [0 0 595.5 842.25] /Contents 139 0 R /Group > /Tabs /S /StructParents 10 >> endobj 17 0 obj > /ExtGState > /ProcSet [/PDF /Text /ImageB /ImageC /ImageI] >> /MediaBox [0 0 595.5 842.25] /Contents 140 0 R /Group > /Tabs /S /StructParents 11 >> endobj 18 0 obj > /ExtGState > /ProcSet [/PDF /Text /ImageB /ImageC /ImageI] >> /MediaBox [0 0 595. 5 842.25] /Contents 141 0 R /Group > /Tabs /S /StructParents 12 >> endobj 19 0 obj > /ProcSet [/PDF /Text /ImageB /ImageC /ImageI] >> /MediaBox [0 0 595.5 842.25] /Contents 142 0 R /Group > /Tabs /S /StructParents 13 >> endobj 20 0 obj > /ExtGState > /ProcSet [/PDF /Text /ImageB /ImageC /ImageI] >> /MediaBox [0 0 595.5 842.25] /Contents 143 0 R /Group > /Tabs /S /StructParents 14 >> endobj 21 0 obj > /ExtGState > /ProcSet [/PDF /Text /ImageB /ImageC /ImageI] >> /MediaBox [0 0 595.5 842.25] /Contents 144 0 R /Group > /Tabs /S /StructParents 15 >> endobj 22 0 obj > /ExtGState > /ProcSet [/PDF /Text /ImageB /ImageC /ImageI] >> /MediaBox [0 0 595.5 842.25] /Contents 145 0 R /Group > /Tabs /S /StructParents 16 >> endobj 23 0 obj > /ExtGState > /ProcSet [/PDF /Text /ImageB /ImageC /ImageI] >> /MediaBox [0 0 595.5 842.25] /Contents 146 0 R /Group > /Tabs /S /StructParents 17 >> endobj 24 0 obj > /ExtGState > /ProcSet [/PDF /Text /ImageB /ImageC /ImageI] >> /MediaBox [0 0 595. 5 842.25] /Contents 147 0 R /Group > /Tabs /S /StructParents 18 >> endobj 25 0 obj > /ExtGState > /ProcSet [/PDF /Text /ImageB /ImageC /ImageI] >> /MediaBox [0 0 595.5 842.25] /Contents 149 0 R /Group > /Tabs /S /StructParents 19 >> endobj 26 0 obj > /ExtGState > /ProcSet [/PDF /Text /ImageB /ImageC /ImageI] >> /MediaBox [0 0 595.5 842.25] /Contents 150 0 R /Group > /Tabs /S /StructParents 20 >> endobj 27 0 obj > /ExtGState > /ProcSet [/PDF /Text /ImageB /ImageC /ImageI] >> /MediaBox [0 0 595.5 842.25] /Contents 151 0 R /Group > /Tabs /S /StructParents 21 >> endobj 28 0 obj > /ExtGState > /ProcSet [/PDF /Text /ImageB /ImageC /ImageI] >> /MediaBox [0 0 595.5 842.25] /Contents 152 0 R /Group > /Tabs /S /StructParents 22 >> endobj 29 0 obj > /ExtGState > /ProcSet [/PDF /Text /ImageB /ImageC /ImageI] >> /MediaBox [0 0 595.5 842.25] /Contents 153 0 R /Group > /Tabs /S /StructParents 23 >> endobj 30 0 obj > /ExtGState > /ProcSet [/PDF /Text /ImageB /ImageC /ImageI] >> /MediaBox [0 0 595. 5 842.25] /Contents 154 0 R /Group > /Tabs /S /StructParents 24 >> endobj 31 0 obj > /ExtGState > /ProcSet [/PDF /Text /ImageB /ImageC /ImageI] >> /MediaBox [0 0 595.5 842.25] /Contents 155 0 R /Group > /Tabs /S /StructParents 25 >> endobj 32 0 obj > /ExtGState > /ProcSet [/PDF /Text /ImageB /ImageC /ImageI] >> /MediaBox [0 0 595.5 842.25] /Contents 156 0 R /Group > /Tabs /S /StructParents 26 >> endobj 33 0 obj > /ExtGState > /ProcSet [/PDF /Text /ImageB /ImageC /ImageI] >> /MediaBox [0 0 595.5 842.25] /Contents 157 0 R /Group > /Tabs /S /StructParents 27 >> endobj 34 0 obj > /ExtGState > /ProcSet [/PDF /Text /ImageB /ImageC /ImageI] >> /MediaBox [0 0 595.5 842.25] /Contents 158 0 R /Group > /Tabs /S /StructParents 28 >> endobj 35 0 obj > /ExtGState > /ProcSet [/PDF /Text /ImageB /ImageC /ImageI] >> /MediaBox [0 0 595.5 842.25] /Contents 159 0 R /Group > /Tabs /S /StructParents 29 >> endobj 36 0 obj > /ExtGState > /ProcSet [/PDF /Text /ImageB /ImageC /ImageI] >> /MediaBox [0 0 595. 5 842.25] /Contents 161 0 R /Group > /Tabs /S /StructParents 30 >> endobj 37 0 obj > /ExtGState > /ProcSet [/PDF /Text /ImageB /ImageC /ImageI] >> /MediaBox [0 0 595.5 842.25] /Contents 162 0 R /Group > /Tabs /S /StructParents 31 >> endobj 38 0 obj > /ExtGState > /ProcSet [/PDF /Text /ImageB /ImageC /ImageI] >> /MediaBox [0 0 595.5 842.25] /Contents 163 0 R /Group > /Tabs /S /StructParents 32 >> endobj 39 0 obj > /ExtGState > /ProcSet [/PDF /Text /ImageB /ImageC /ImageI] >> /MediaBox [0 0 595.5 842.25] /Contents 164 0 R /Group > /Tabs /S /StructParents 33 >> endobj 40 0 obj > /ExtGState > /ProcSet [/PDF /Text /ImageB /ImageC /ImageI] >> /MediaBox [0 0 595.5 842.25] /Contents 165 0 R /Group > /Tabs /S /StructParents 34 >> endobj 41 0 obj > /ExtGState > /ProcSet [/PDF /Text /ImageB /ImageC /ImageI] >> /MediaBox [0 0 595.5 842.25] /Contents 166 0 R /Group > /Tabs /S /StructParents 35 >> endobj 42 0 obj > /ExtGState > /ProcSet [/PDF /Text /ImageB /ImageC /ImageI] >> /MediaBox [0 0 595. 5 842.25] /Contents 168 0 R /Group > /Tabs /S /StructParents 36 >> endobj 43 0 obj > /ExtGState > /ProcSet [/PDF /Text /ImageB /ImageC /ImageI] >> /MediaBox [0 0 595.5 842.25] /Contents 169 0 R /Group > /Tabs /S /StructParents 37 >> endobj 44 0 obj > /ExtGState > /ProcSet [/PDF /Text /ImageB /ImageC /ImageI] >> /MediaBox [0 0 595.5 842.25] /Contents 170 0 R /Group > /Tabs /S /StructParents 38 >> endobj 45 0 obj > /ExtGState > /ProcSet [/PDF /Text /ImageB /ImageC /ImageI] >> /MediaBox [0 0 595.5 842.25] /Contents 171 0 R /Group > /Tabs /S /StructParents 39 >> endobj 46 0 obj > /ExtGState > /ProcSet [/PDF /Text /ImageB /ImageC /ImageI] >> /MediaBox [0 0 595.5 842.25] /Contents 173 0 R /Group > /Tabs /S /StructParents 40 >> endobj 47 0 obj > /ExtGState > /ProcSet [/PDF /Text /ImageB /ImageC /ImageI] >> /MediaBox [0 0 595.5 842.25] /Contents 175 0 R /Group > /Tabs /S /StructParents 41 >> endobj 48 0 obj > /ExtGState > /ProcSet [/PDF /Text /ImageB /ImageC /ImageI] >> /MediaBox [0 0 595. 5 842.25] /Contents 176 0 R /Group > /Tabs /S /StructParents 42 >> endobj 49 0 obj > /ExtGState > /ProcSet [/PDF /Text /ImageB /ImageC /ImageI] >> /MediaBox [0 0 595.5 842.25] /Contents 177 0 R /Group > /Tabs /S /StructParents 43 >> endobj 50 0 obj > /ExtGState > /ProcSet [/PDF /Text /ImageB /ImageC /ImageI] >> /MediaBox [0 0 595.5 842.25] /Contents 178 0 R /Group > /Tabs /S /StructParents 44 >> endobj 51 0 obj > /ExtGState > /ProcSet [/PDF /Text /ImageB /ImageC /ImageI] >> /MediaBox [0 0 595.5 842.25] /Contents 179 0 R /Group > /Tabs /S /StructParents 45 >> endobj 52 0 obj > /ExtGState > /XObject > /ProcSet [/PDF /Text /ImageB /ImageC /ImageI] >> /MediaBox [0 0 595.5 842.25] /Contents 181 0 R /Group > /Tabs /S /StructParents 46 >> endobj 53 0 obj > /ExtGState > /Pattern > /ProcSet [/PDF /Text /ImageB /ImageC /ImageI] >> /MediaBox [0 0 595.5 842.25] /Contents 184 0 R /Group > /Tabs /S /StructParents 47 >> endobj 54 0 obj > /ExtGState > /ProcSet [/PDF /Text /ImageB /ImageC /ImageI] >> /MediaBox [0 0 595. 5 842.25] /Contents 185 0 R /Group > /Tabs /S /StructParents 48 >> endobj 55 0 obj > /ExtGState > /ProcSet [/PDF /Text /ImageB /ImageC /ImageI] >> /MediaBox [0 0 595.5 842.25] /Contents 186 0 R /Group > /Tabs /S /StructParents 49 >> endobj 56 0 obj > /ExtGState > /ProcSet [/PDF /Text /ImageB /ImageC /ImageI] >> /MediaBox [0 0 595.5 842.25] /Contents 187 0 R /Group > /Tabs /S /StructParents 50 >> endobj 57 0 obj > /ExtGState > /ProcSet [/PDF /Text /ImageB /ImageC /ImageI] >> /MediaBox [0 0 595.5 842.25] /Contents 188 0 R /Group > /Tabs /S /StructParents 51 >> endobj 58 0 obj > /ExtGState > /ProcSet [/PDF /Text /ImageB /ImageC /ImageI] >> /MediaBox [0 0 595.5 842.25] /Contents 189 0 R /Group > /Tabs /S /StructParents 52 >> endobj 59 0 obj > /ExtGState > /ProcSet [/PDF /Text /ImageB /ImageC /ImageI] >> /MediaBox [0 0 595.5 842.25] /Contents 190 0 R /Group > /Tabs /S /StructParents 53 >> endobj 60 0 obj > /ExtGState > /ProcSet [/PDF /Text /ImageB /ImageC /ImageI] >> /MediaBox [0 0 595. 5 842.25] /Contents 191 0 R /Group > /Tabs /S /StructParents 54 >> endobj 61 0 obj > /ExtGState > /ProcSet [/PDF /Text /ImageB /ImageC /ImageI] >> /MediaBox [0 0 595.5 842.25] /Contents 192 0 R /Group > /Tabs /S /StructParents 55 >> endobj 62 0 obj > /ExtGState > /ProcSet [/PDF /Text /ImageB /ImageC /ImageI] >> /MediaBox [0 0 595.5 842.25] /Contents 193 0 R /Group > /Tabs /S /StructParents 56 >> endobj 63 0 obj > /ExtGState > /ProcSet [/PDF /Text /ImageB /ImageC /ImageI] >> /MediaBox [0 0 595.5 842.25] /Contents 194 0 R /Group > /Tabs /S /StructParents 57 >> endobj 64 0 obj > /ExtGState > /ProcSet [/PDF /Text /ImageB /ImageC /ImageI] >> /MediaBox [0 0 595.5 842.25] /Contents 195 0 R /Group > /Tabs /S /StructParents 58 >> endobj 65 0 obj > /ExtGState > /ProcSet [/PDF /Text /ImageB /ImageC /ImageI] >> /MediaBox [0 0 595.5 842.25] /Contents 196 0 R /Group > /Tabs /S /StructParents 59 >> endobj 66 0 obj > /ExtGState > /ProcSet [/PDF /Text /ImageB /ImageC /ImageI] >> /MediaBox [0 0 595. 5 842.25] /Contents 197 0 R /Group > /Tabs /S /StructParents 60 >> endobj 67 0 obj > /ExtGState > /ProcSet [/PDF /Text /ImageB /ImageC /ImageI] >> /MediaBox [0 0 595.5 842.25] /Contents 198 0 R /Group > /Tabs /S /StructParents 61 >> endobj 68 0 obj > /ExtGState > /ProcSet [/PDF /Text /ImageB /ImageC /ImageI] >> /MediaBox [0 0 595.5 842.25] /Contents 199 0 R /Group > /Tabs /S /StructParents 62 >> endobj 69 0 obj > /ExtGState > /ProcSet [/PDF /Text /ImageB /ImageC /ImageI] >> /MediaBox [0 0 595.5 842.25] /Contents 200 0 R /Group > /Tabs /S /StructParents 63 >> endobj 70 0 obj > /ExtGState > /ProcSet [/PDF /Text /ImageB /ImageC /ImageI] >> /MediaBox [0 0 595.5 842.25] /Contents 201 0 R /Group > /Tabs /S /StructParents 64 >> endobj 71 0 obj > /ExtGState > /ProcSet [/PDF /Text /ImageB /ImageC /ImageI] >> /MediaBox [0 0 595.5 842.25] /Contents 202 0 R /Group > /Tabs /S /StructParents 65 >> endobj 72 0 obj > /ExtGState > /ProcSet [/PDF /Text /ImageB /ImageC /ImageI] >> /MediaBox [0 0 595. 5 842.25] /Contents 203 0 R /Group > /Tabs /S /StructParents 66 >> endobj 73 0 obj > /ExtGState > /ProcSet [/PDF /Text /ImageB /ImageC /ImageI] >> /MediaBox [0 0 595.5 842.25] /Contents 204 0 R /Group > /Tabs /S /StructParents 67 >> endobj 74 0 obj > /ExtGState > /ProcSet [/PDF /Text /ImageB /ImageC /ImageI] >> /MediaBox [0 0 595.5 842.25] /Contents 205 0 R /Group > /Tabs /S /StructParents 68 >> endobj 75 0 obj > /ExtGState > /ProcSet [/PDF /Text /ImageB /ImageC /ImageI] >> /MediaBox [0 0 595.5 842.25] /Contents 206 0 R /Group > /Tabs /S /StructParents 69 >> endobj 76 0 obj > /ExtGState > /ProcSet [/PDF /Text /ImageB /ImageC /ImageI] >> /MediaBox [0 0 595.5 842.25] /Contents 207 0 R /Group > /Tabs /S /StructParents 70 >> endobj 77 0 obj > /ExtGState > /ProcSet [/PDF /Text /ImageB /ImageC /ImageI] >> /MediaBox [0 0 595.5 842.25] /Contents 208 0 R /Group > /Tabs /S /StructParents 71 >> endobj 78 0 obj > /ExtGState > /ProcSet [/PDF /Text /ImageB /ImageC /ImageI] >> /Annots [209 0 R 210 0 R 211 0 R 212 0 R 213 0 R 214 0 R] /MediaBox [0 0 595. 5 842.25] /Contents 215 0 R /Group > /Tabs /S /StructParents 72 >> endobj 79 0 obj > /ExtGState > /ProcSet [/PDF /Text /ImageB /ImageC /ImageI] >> /Annots [216 0 R 217 0 R 218 0 R] /MediaBox [0 0 595.5 842.25] /Contents 219 0 R /Group > /Tabs /S /StructParents 79 >> endobj 80 0 obj > /ExtGState > /ProcSet [/PDF /Text /ImageB /ImageC /ImageI] >> /Annots [220 0 R] /MediaBox [0 0 595.5 842.25] /Contents 221 0 R /Group > /Tabs /S /StructParents 83 >> endobj 81 0 obj > /ExtGState > /ProcSet [/PDF /Text /ImageB /ImageC /ImageI] >> /MediaBox [0 0 595.5 842.25] /Contents 222 0 R /Group > /Tabs /S /StructParents 85 >> endobj 82 0 obj > /ExtGState > /ProcSet [/PDF /Text /ImageB /ImageC /ImageI] >> /MediaBox [0 0 595.5 842.25] /Contents 223 0 R /Group > /Tabs /S /StructParents 86 >> endobj 83 0 obj > /ExtGState > /ProcSet [/PDF /Text /ImageB /ImageC /ImageI] >> /MediaBox [0 0 595.5 842.25] /Contents 224 0 R /Group > /Tabs /S /StructParents 87 >> endobj 84 0 obj > /ExtGState > /ProcSet [/PDF /Text /ImageB /ImageC /ImageI] >> /MediaBox [0 0 595. 5 842.25] /Contents 225 0 R /Group > /Tabs /S /StructParents 88 >> endobj 85 0 obj > /ExtGState > /ProcSet [/PDF /Text /ImageB /ImageC /ImageI] >> /MediaBox [0 0 595.5 842.25] /Contents 226 0 R /Group > /Tabs /S /StructParents 89 >> endobj 86 0 obj > /ExtGState > /ProcSet [/PDF /Text /ImageB /ImageC /ImageI] >> /MediaBox [0 0 595.5 842.25] /Contents 227 0 R /Group > /Tabs /S /StructParents 90 >> endobj 87 0 obj > /ExtGState > /ProcSet [/PDF /Text /ImageB /ImageC /ImageI] >> /MediaBox [0 0 595.5 842.25] /Contents 228 0 R /Group > /Tabs /S /StructParents 91 >> endobj 88 0 obj > /ExtGState > /ProcSet [/PDF /Text /ImageB /ImageC /ImageI] >> /MediaBox [0 0 595.5 842.25] /Contents 230 0 R /Group > /Tabs /S /StructParents 92 >> endobj 89 0 obj > /ExtGState > /ProcSet [/PDF /Text /ImageB /ImageC /ImageI] >> /MediaBox [0 0 595.5 842.25] /Contents 232 0 R /Group > /Tabs /S /StructParents 93 >> endobj 90 0 obj > /ExtGState > /ProcSet [/PDF /Text /ImageB /ImageC /ImageI] >> /MediaBox [0 0 595. 5 842.25] /Contents 233 0 R /Group > /Tabs /S /StructParents 94 >> endobj 91 0 obj > /ExtGState > /ProcSet [/PDF /Text /ImageB /ImageC /ImageI] >> /MediaBox [0 0 595.5 842.25] /Contents 234 0 R /Group > /Tabs /S /StructParents 95 >> endobj 92 0 obj > /ExtGState > /ProcSet [/PDF /Text /ImageB /ImageC /ImageI] >> /MediaBox [0 0 595.5 842.25] /Contents 235 0 R /Group > /Tabs /S /StructParents 96 >> endobj 93 0 obj > /ExtGState > /ProcSet [/PDF /Text /ImageB /ImageC /ImageI] >> /MediaBox [0 0 595.5 842.25] /Contents 236 0 R /Group > /Tabs /S /StructParents 97 >> endobj 94 0 obj > /ExtGState > /XObject > /ProcSet [/PDF /Text /ImageB /ImageC /ImageI] >> /MediaBox [0 0 595.5 842.25] /Contents 240 0 R /Group > /Tabs /S /StructParents 98 >> endobj 95 0 obj > /ExtGState > /XObject > /ProcSet [/PDF /Text /ImageB /ImageC /ImageI] >> /MediaBox [0 0 595.5 842.25] /Contents 242 0 R /Group > /Tabs /S /StructParents 99 >> endobj 96 0 obj > /ExtGState > /ProcSet [/PDF /Text /ImageB /ImageC /ImageI] >> /MediaBox [0 0 595. 5 842.25] /Contents 243 0 R /Group > /Tabs /S /StructParents 100 >> endobj 97 0 obj > /ExtGState > /ProcSet [/PDF /Text /ImageB /ImageC /ImageI] >> /MediaBox [0 0 595.5 842.25] /Contents 244 0 R /Group > /Tabs /S /StructParents 101 >> endobj 98 0 obj > /ExtGState > /ProcSet [/PDF /Text /ImageB /ImageC /ImageI] >> /MediaBox [0 0 595.5 842.25] /Contents 245 0 R /Group > /Tabs /S /StructParents 102 >> endobj 99 0 obj > /ExtGState > /ProcSet [/PDF /Text /ImageB /ImageC /ImageI] >> /MediaBox [0 0 595.5 842.25] /Contents 246 0 R /Group > /Tabs /S /StructParents 103 >> endobj 100 0 obj > /ExtGState > /ProcSet [/PDF /Text /ImageB /ImageC /ImageI] >> /MediaBox [0 0 595.5 842.25] /Contents 247 0 R /Group > /Tabs /S /StructParents 104 >> endobj 101 0 obj > /ExtGState > /ProcSet [/PDF /Text /ImageB /ImageC /ImageI] >> /MediaBox [0 0 595.5 842.25] /Contents 248 0 R /Group > /Tabs /S /StructParents 105 >> endobj 102 0 obj > /ExtGState > /ProcSet [/PDF /Text /ImageB /ImageC /ImageI] >> /MediaBox [0 0 595. 5 842.25] /Contents 249 0 R /Group > /Tabs /S /StructParents 106 >> endobj 103 0 obj > /ExtGState > /ProcSet [/PDF /Text /ImageB /ImageC /ImageI] >> /MediaBox [0 0 595.5 842.25] /Contents 250 0 R /Group > /Tabs /S /StructParents 107 >> endobj 104 0 obj > /ExtGState > /ProcSet [/PDF /Text /ImageB /ImageC /ImageI] >> /MediaBox [0 0 595.5 842.25] /Contents 251 0 R /Group > /Tabs /S /StructParents 108 >> endobj 105 0 obj > /ExtGState > /ProcSet [/PDF /Text /ImageB /ImageC /ImageI] >> /MediaBox [0 0 595.5 842.25] /Contents 252 0 R /Group > /Tabs /S /StructParents 109 >> endobj 106 0 obj > /ExtGState > /ProcSet [/PDF /Text /ImageB /ImageC /ImageI] >> /MediaBox [0 0 595.5 842.25] /Contents 253 0 R /Group > /Tabs /S /StructParents 110 >> endobj 107 0 obj > /ExtGState > /ProcSet [/PDF /Text /ImageB /ImageC /ImageI] >> /MediaBox [0 0 595.5 842.25] /Contents 254 0 R /Group > /Tabs /S /StructParents 111 >> endobj 108 0 obj > /ExtGState > /XObject > /ProcSet [/PDF /Text /ImageB /ImageC /ImageI] >> /MediaBox [0 0 595. Wb37c Aώ

Геометрия. Движение — презентация онлайн

Компьютерная презентация к уроку геометрии по теме «Движение», 9 класс.

Учитель: Юрко Олеся Александровна, Учитель математики МОУ СОШ №12 г.Балашова СОДЕРЖАНИЕ РАБОТЫ Введение.

Движение.

Виды движения.

Поворот.

Параллельный перенос.

Великие о симметрии.

Осевая симметрия.

Центральная симметрия.

Скользящая симметрия.

Зеркальная симметрия.

Симметрия в растениях.

Симметрия в животном мире.

Загадочные снежинки.

Симметрия в архитектуре.

Симметрия в литературе.

Заключение.

Литература.

Симметрия – это идея, с помощью которой человек веками пытался объяснить и создать порядок, красоту и совершенство.

Г.

Вейль ВВЕДЕНИЕ Принципы симметрии играют важную роль в физике и математике, химии и биологии, технике и архитектуре, живописи и скульптуре, поэзии и музыке.

Законы природы, управляющие неисчерпаемой в своём многообразии картиной явлений, в свою очередь, также подчиняются принципам симметрии.

Движение.

Виды движения.

Движение плоскости – это отображение плоскости на себя, сохраняющее расстояния.

Виды движения:1.

Симметрия: ─ осевая, ─ центральная, ─ скользящая.

─ зеркальная.2.

Параллельный перенос:3.

Поворот.

ПОВОРОТ Преобразование, при котором каждая точка А фигуры (тела) поворачивается на один и тот же уголα вокруг заданного центра О, называется вращением или поворотом плоскости.

ТочкаО называется центром вращения, а уголα — углом вращения.

ПОВОРОТ ПАРАЛЛЕЛЬНЫЙ ПЕРНОС Преобразование, при котором каждая точка фигуры (тела) перемещается в одном и том же направлении на одно и то же расстояние, называется параллельным переносом.

ПАРАЛЛЕЛЬНЫЙ ПЕРЕНОС ВЕЛИКИЕ О СИММЕТРИИ… Термин «симметрия» придумал скульптор Пифагор Регийский.

Древние греки полагали, что Вселенная симметрична просто потому, что она прекрасна.

Первую научную школу в истории человечества создал Пифагор Самосский.

«Симметрия – это некая «средняя мера», — считал Аристотель .

Римский врач Гален (2 в.

н.

э.) под симметрией понимал покой души и уравновешенность.

ВЕЛИКИЕ О СИММЕТРИИ… Леонардо да Винчи считал, что главную роль в картине играют пропорциональность и гармония, под которыми он понимал симметрию.

Альбрехт Дюрер (1471-1528 г.г.) утверждал, что каждый художник должен знать способы построения правильных симметричных фигур.

Термин «симметрия» (σνμμετρυα, греч.) — соразмерность, пропорциональность, одинаковость в расположении частей.

ОСЕВАЯ СИММЕТРИЯ Преобразование, при котором каждая точка А фигуры (или тела) преобразуется в симметричную ей относительно некоторой оси l точку А1, при этом отрезок АА1 l , называется осевой симметрией.

ЦЕНТРАЛЬНАЯ СИММЕТРИЯ Преобразование, переводящее каждую точку А фигуры (тела) в точку А1, симметричную ей относительно центра О, называется преобразованием центральной симметрии или просто центральной симметрией.

СКОЛЬЗЯЩАЯ СИММЕТРИЯ Скользящей симметрией называется такое преобразование, при котором последовательно выполняются осевая симметрия и параллельный перенос.

ЗЕРКАЛЬНАЯ СИММЕТРИЯ Если преобразование симметрии относительно плоскости переводит фигуру (тело) в себя, то фигура называется симметричной относительно плоскости, а данная плоскость – плоскостью симметрии этой фигуры.

ЗЕРКАЛЬНАЯ СИММЕТРИЯ СИММЕТРИЯ В РАСТЕНИЯХ Внимательное наблюдение показывает, что основу красоты многих форм, созданных природой, составляет симметрия.

Ярко выраженной симметрией обладают листья, ветви, цветы, плоды.

Зеркальная симметрия характерна для листьев, но встречается и у цветов.

Для цветов характерна поворотная симметрия.

СИММЕТРИЯ В РАСТЕНИЯХ СИММЕТРИЯ В ЖИВОТНОМ МИРЕ Симметрия встречается и в животном мире.

Однако в отличие от мира растений симметрия в животном мире наблюдается не так часто.

Рассмотрим, например, бабочку.

ЗАГАДОЧНЫЕ СНЕЖИНКИ Он сыплет с неба мелкой крупой, летает вокруг фонарей огромными пушистыми хлопьями, стоит столбом в лунном свете ледяными иглами.

Казалось бы, какая ерунда! Всего-то замёрзшая вода.

Но сколько вопросов возникает у человека, глядящего на снежинки.

ЗАГАДОЧНЫЕ СНЕЖИНКИ Снежинка – это группа кристалликов, образованная более чем из двухсот ледяных частичек.

Симметрия – это свойство кристаллов совмещаться друг с другом в различных положениях путём поворотов, параллельных переносов, отражений.

СИММЕТРИЯ В АРХИТЕКТУРЕ Нагляднее всего видна симметрия в архитектуре.

Особенно блистательно использовали симметрию в архитектурных сооружениях древние зодчие.

В сознании древнегреческих архитекторов симметрия стала олицетворением закономерности, целесообразности, красоты.

СИММЕТРИЯ В АРХИТЕКТУРЕ СИММЕТРИЯ В ЛИТЕРАТУРЕ В литературных произведениях существует симметрия образов, положений, мышления.

В греческой трагедии — виновный становится жертвой такого же преступления.

В «Евгении Онегине» А.

С.

Пушкина мы наблюдаем симметрию положений : «Онегин, отвергнувший когда-то любовь Татьяны, сам через несколько лет вынужден испытывать горечь отвергнутой любви».

СИММЕТРИЯ В ЛИТЕРАТУРЕ Буквы русского языка тоже можно рассмотреть с точки зрения симметрии.

Вертикальная ось симметрии : А;

Д;

Л;

М;

П;

Т;

Ф;

Ш.

Горизонтальная ось симметрии : В;

Е;

З;

К;

С;

Э;

Ю.

И вертикальные, и горизонтальные оси симметрии : Ж;

Н;

О;

Х.

Ни вертикальные, ни горизонтальные оси : Б;

Г;

И;

Й;

Р;

У;

Ц;

Ч;

Щ;

Я.

СИММЕТРИЯ В ЛИТЕРАТУРЕ В русском языке есть «симметричные слова – палиндромы, которые можно читать одинаково в двух направлениях: Шалаш, казак, радар, Алла, Анна, кок, поп.

Могут быть палиндромическими и предложения.

А роза упала на лапу Азора.

Я иду с мечём судия.

Г.Р.

Державин.

СИММЕТРИЯ В ОРНАМЕНТАХ Принцип симметрия используется в построении орнамента.

Орнамент (от лат.

Ornamentum – украшение) – узор, состоящий из повторяющихся, ритмически упорядоченных элементов.

ЗАКЛЮЧЕНИЕ Природа в различных своих творениях, казалось бы, очень далеких друг от друга, может использовать одни и те же принципы.

И человек в своих творениях: живописи, скульптуре, архитектуре… Основополагающими принципами красоты при этом являются пропорции и симметрия.

ЛИТЕРАТУРА Глейзер Г.Д.

Геометрия.

– 12-ое изд.- М., «Просвещение» ,1992.

Компанеец А.С.

Симметрия в микро- и макро мире.- М., Наука, 1978.

с.

276.

Наливкин Д.В.

Элементы симметрии органического мира.

– Изв.

Биол.

Науч – исслед.

ин-та при Пермском ун-те, т.

3, 1952, вып.

8, с.

291-297.

Опарин А.И.

Возникновение жизни на Земле.- М., 1987, 458 с.

Руденко В.

Н.

Геометрия 7-9 классы — М.: Просвещение, 1994.

Скопец З.А.

Геометрические миниатюры.- М., «Просвещение» , 1990.

Тарасов Л.

В.

Этот удивительный симметричный мир.

– М.: Просвещение, 1982.

Рисование фигур с помощью инструментов группы «Фигура» в Photoshop

Руководство пользователя Отмена

Поиск

Последнее обновление Jun 21, 2022 03:26:37 PM GMT

1. Руководство пользователя Photoshop
2. Введение в Photoshop
   1. Мечтайте об этом. Сделайте это.
   2. Новые возможности Photoshop
   3. Редактирование первой фотографии
   4. Создание документов
   5. Photoshop | Часто задаваемые вопросы
   6. Системные требования Photoshop
   7. Перенос наборов настроек, операций и настроек
   8. Знакомство с Photoshop
3. Photoshop и другие продукты и услуги Adobe
   1. Работа с графическим объектом Illustrator в Photoshop
   2. Работа с файлами Photoshop в InDesign
      
   3. Материалы Substance 3D для Photoshop
   4. Photoshop и Adobe Stock
   5. Работа со встроенным расширением Capture в Photoshop
   6. Библиотеки Creative Cloud Libraries
   7. Библиотеки Creative Cloud в Photoshop
   8. Работа в Photoshop с использованием Touch Bar
   9. Сетка и направляющие
   10. Создание операций
   11. Отмена и история операций
4. Photoshop на iPad
   1. Photoshop на iPad | Общие вопросы
   2. Знакомство с рабочей средой
   3. Системные требования | Photoshop на iPad
   4. Создание, открытие и экспорт документов
   5. Добавление фотографий
   6. Работа со слоями
   7. Рисование и раскрашивание кистями
   8. Выделение участков и добавление масок
   9. Ретуширование композиций
   10. Работа с корректирующими слоями
   11. Настройка тональности композиции с помощью слоя «Кривые»
   12. Применение операций трансформирования
   13. Обрезка и поворот композиций
   14. Поворот, панорамирование, масштабирование и восстановление холста
   15. Работа с текстовыми слоями
   16. Работа с Photoshop и Lightroom
   17. Получение отсутствующих шрифтов в Photoshop на iPad
   18. Японский текст в Photoshop на iPad
   19. Управление параметрами приложения
   20. Сенсорные ярлыки и жесты
   21. Комбинации клавиш
   22. Изменение размера изображения
   23. Прямая трансляция творческого процесса в Photoshop на iPad
   24. Исправление недостатков с помощью восстанавливающей кисти
   25. Создание кистей в Capture и их использование в Photoshop
   26. Работа с файлами Camera Raw
   27. Создание и использование смарт-объектов
   28. Коррекция экспозиции изображений с помощью инструментов «Осветлитель» и «Затемнитель»
5. Бета-версия веб-приложения Photoshop
   1. Часто задаваемые вопросы | Бета-версия веб-приложения Photoshop 
   2. Общие сведения о рабочей среде
   3. Системные требования | Бета-версия веб-приложения Photoshop
   4. Комбинации клавиш | Бета-версия веб-приложения Photoshop
   5. Поддерживаемые форматы файлов | Бета-вервия веб-приложения Photoshop
   6. Открытие облачных документов и работа с ними
   7. Совместная работа с заинтересованными сторонами
   8. Ограниченные возможности редактирования облачных документов
6. Облачные документы
   1. Облачные документы Photoshop | Часто задаваемые вопросы
   2. Облачные документы Photoshop | Вопросы о рабочем процессе
   3. Работа с облачными документами и управление ими в Photoshop
   4. Обновление облачного хранилища для Photoshop
   5. Не удается создать или сохранить облачный документ
   6. Устранение ошибок с облачными документами Photoshop
   7. Сбор журналов синхронизации облачных документов
   8. Общий доступ к облачным документам и их редактирование
   9. Общий доступ к файлам и комментирование в приложении
7. Рабочая среда
   1. Основные сведения о рабочей среде
   2. Более быстрое обучение благодаря панели «Новые возможности» в Photoshop
   3. Создание документов
   4. Работа в Photoshop с использованием Touch Bar
   5. Галерея инструментов
   6. Установки производительности
   7. Использование инструментов
   8. Сенсорные жесты
   9. Возможности работы с сенсорными жестами и настраиваемые рабочие среды
   10. Обзорные версии технологии
   11. Метаданные и комментарии
   12. Комбинации клавиш по умолчанию
   13. Возможности работы с сенсорными жестами и настраиваемые рабочие среды
   14. Помещение изображений Photoshop в другие приложения
   15. Установки
   16. Комбинации клавиш по умолчанию
   17. Линейки
   18. Отображение или скрытие непечатных вспомогательных элементов
   19. Указание колонок для изображения
   20. Отмена и история операций
   21. Панели и меню
   22. Помещение файлов
   23. Позиционирование элементов с привязкой
   24. Позиционирование с помощью инструмента «Линейка»
   25. Наборы настроек
   26. Настройка комбинаций клавиш
   27. Сетка и направляющие
8. Разработка содержимого для Интернета, экрана и приложений
   1. Photoshop для дизайна
   2. Монтажные области
   3. Просмотр на устройстве
   4. Копирование CSS из слоев
   5. Разделение веб-страниц на фрагменты
   6. Параметры HTML для фрагментов
   7. Изменение компоновки фрагментов
   8. Работа с веб-графикой
   9. Создание веб-фотогалерей
9. Основные сведения об изображениях и работе с цветом
   1. Изменение размера изображений
   2. Работа с растровыми и векторными изображениями
   3. Размер и разрешение изображения
   4. Импорт изображений из камер и сканеров
   5. Создание, открытие и импорт изображений
   6. Просмотр изображений
   7. Ошибка «Недопустимый маркер JPEG» | Открытие изображений
   8. Просмотр нескольких изображений
   9. Настройка палитр цветов и образцов цвета
   10. HDR-изображения
   11. Подбор цветов на изображении
   12. Преобразование между цветовыми режимами
   13. Цветовые режимы
   14. Стирание фрагментов изображения
   15. Режимы наложения
   16. Выбор цветов
   17. Внесение изменений в таблицы индексированных цветов
   18. Информация об изображениях
   19. Фильтры искажения недоступны
   20. Сведения о цвете
   21. Цветные и монохромные коррекции с помощью каналов
   22. Выбор цветов на панелях «Цвет» и «Образцы»
   23. Образец
   24. Цветовой режим (или режим изображения)
   25. Цветовой оттенок
   26. Добавление изменения цветового режима в операцию
   27. Добавление образцов из CSS- и SVG-файлов HTML
   28. Битовая глубина и установки
10. Слои
    1. Основные сведения о слоях
    2. Обратимое редактирование
    3. Создание слоев и групп и управление ими
    4. Выделение, группировка и связывание слоев
    5. Помещение изображений в кадры
    6. Непрозрачность и наложение слоев
    7. Слои-маски
    8. Применение смарт-фильтров
    9. Композиции слоев
    10. Перемещение, упорядочение и блокировка слоев
    11. Маскирование слоев при помощи векторных масок
    12. Управление слоями и группами
    13. Эффекты и стили слоев
    14. Редактирование слоев-масок
    15. Извлечение ресурсов
    16. Отображение слоев с помощью обтравочных масок
    17. Формирование графических ресурсов из слоев
    18. Работа со смарт-объектами
    19. Режимы наложения
    20. Объединение нескольких фрагментов в одно изображение
    21. Объединение изображений с помощью функции «Автоналожение слоев»
    22. Выравнивание и распределение слоев
    23. Копирование CSS из слоев
    24. Загрузка выделенных областей на основе границ слоя или слоя-маски
    25. Просвечивание для отображения содержимого других слоев
    26. Слой
    27. Сведение
    28. Совмещенные изображения
    29. Фон
11. Выделения
    1. Рабочая среда «Выделение и маска»
    2. Быстрое выделение областей
    3. Начало работы с выделениями
    4. Выделение при помощи группы инструментов «Область»
    5. Выделение при помощи инструментов группы «Лассо»
    6. Выбор цветового диапазона в изображении
    7. Настройка выделения пикселей
    8. Преобразование между контурами и границами выделенной области
    9. Основы работы с каналами
    10. Перемещение, копирование и удаление выделенных пикселей
    11. Создание временной быстрой маски
    12. Сохранение выделенных областей и масок альфа-каналов
    13. Выбор областей фокусировки в изображении
    14. Дублирование, разделение и объединение каналов
    15. Вычисление каналов
    16. Выделение
    17. Ограничительная рамка
12. Коррекции изображений
    1. Деформация перспективы
    2. Уменьшение размытия в результате движения камеры
    3. Примеры использования инструмента «Восстанавливающая кисть»
    4. Экспорт таблиц поиска цвета
    5. Корректировка резкости и размытия изображения
    6. Общие сведения о цветокоррекции
    7. Применение настройки «Яркость/Контрастность»
    8. Коррекция деталей в тенях и на светлых участках
    9. Корректировка «Уровни»
    10. Коррекция тона и насыщенности
    11. Коррекция сочности
    12. Настройка насыщенности цвета в областях изображения
    13. Быстрая коррекция тона
    14. Применение специальных цветовых эффектов к изображениям
    15. Улучшение изображения при помощи корректировки цветового баланса
    16. HDR-изображения
    17. Просмотр гистограмм и значений пикселей
    18. Подбор цветов на изображении
    19. Кадрирование и выпрямление фотографий
    20. Преобразование цветного изображения в черно-белое
    21. Корректирующие слои и слои-заливки
    22. Корректировка «Кривые»
    23. Режимы наложения
    24. Целевая подготовка изображений для печатной машины
    25. Коррекция цвета и тона с помощью пипеток «Уровни» и «Кривые»
    26. Коррекция экспозиции и тонирования HDR
    27. Фильтр
    28. Размытие
    29. Осветление или затемнение областей изображения
    30. Избирательная корректировка цвета
    31. Замена цветов объекта
13. Adobe Camera Raw
    1. Системные требования Camera Raw
    2. Новые возможности Camera Raw
    3. Введение в Camera Raw
    4. Создание панорам
    5. Поддерживаемые объективы
    6. Виньетирование, зернистость и удаление дымки в Camera Raw
    7. Комбинации клавиш по умолчанию
    8. Автоматическая коррекция перспективы в Camera Raw
    9. Обратимое редактирование в Camera Raw
    10. Инструмент «Радиальный фильтр» в Camera Raw
    11. Управление настройками Camera Raw
    12. Обработка, сохранение и открытие изображений в Camera Raw
    13. Совершенствование изображений с улучшенным инструментом «Удаление точек» в Camera Raw
    14. Поворот, обрезка и изменение изображений
    15. Корректировка цветопередачи в Camera Raw
    16. Краткий обзор функций | Adobe Camera Raw | Выпуски за 2018 г.
    17. Обзор новых возможностей
    18. Версии обработки в Camera Raw
    19. Внесение локальных корректировок в Camera Raw
14. Исправление и восстановление изображений
    1. Удаление объектов с фотографий с помощью функции «Заливка с учетом содержимого»
    2. Заплатка и перемещение с учетом содержимого
    3. Ретуширование и исправление фотографий
    4. Коррекция искажений изображения и шума
    5. Основные этапы устранения неполадок для решения большинства проблем
15. Преобразование изображений
    1. Трансформирование объектов
    2. Настройка кадрирования, поворотов и холста
    3. Кадрирование и выпрямление фотографий
    4. Создание и редактирование панорамных изображений
    5. Деформация изображений, фигур и контуров
    6. Перспектива
    7. Использование фильтра «Пластика»
    8. Масштаб с учетом содержимого
    9. Трансформирование изображений, фигур и контуров
    10. Деформация
    11. Трансформирование
    12. Панорама
16. Рисование и живопись
    1. Рисование симметричных орнаментов
    2. Варианты рисования прямоугольника и изменения обводки
    3. Сведения о рисовании
    4. Рисование и редактирование фигур
    5. Инструменты рисования красками
    6. Создание и изменение кистей
    7. Режимы наложения
    8. Добавление цвета в контуры
    9. Редактирование контуров
    10. Рисование с помощью микс-кисти
    11. Наборы настроек кистей
    12. Градиенты
    13. Градиентная интерполяция
    14. Заливка и обводка выделенных областей, слоев и контуров
    15. Рисование с помощью группы инструментов «Перо»
    16. Создание узоров
    17. Создание узора с помощью фильтра «Конструктор узоров»
    18. Управление контурами
    19. Управление библиотеками узоров и наборами настроек
    20. Рисование при помощи графического планшета
    21. Создание текстурированных кистей
    22. Добавление динамических элементов к кистям
    23. Градиент
    24. Рисование стилизованных обводок с помощью архивной художественной кисти
    25. Рисование с помощью узора
    26. Синхронизация наборов настроек на нескольких устройствах
17. Текст
    1. Добавление и редактирование текста
       
    2. Универсальный текстовый редактор
    3. Работа со шрифтами OpenType SVG
    4. Форматирование символов
    5. Форматирование абзацев
    6. Создание эффектов текста
    7. Редактирование текста
    8. Интерлиньяж и межбуквенные интервалы
    9. Шрифт для арабского языка и иврита
    10. Шрифты
    11. Поиск и устранение неполадок, связанных со шрифтами
    12. Азиатский текст
    13. Создание текста
    14. Ошибка Text Engine при использовании инструмента «Текст» в Photoshop | Windows 8
18. Видео и анимация
    1. Видеомонтаж в Photoshop
    2. Редактирование слоев видео и анимации
    3. Общие сведения о видео и анимации
    4. Предварительный просмотр видео и анимации
    5. Рисование кадров в видеослоях
    6. Импорт видеофайлов и последовательностей изображений
    7. Создание анимации кадров
    8. 3D-анимация Creative Cloud (предварительная версия)
    9. Создание анимаций по временной шкале
    10. Создание изображений для видео
19. Фильтры и эффекты
    1. Использование фильтра «Пластика»
    2. Использование эффектов группы «Галерея размытия»
    3. Основные сведения о фильтрах
    4. Справочник по эффектам фильтров
    5. Добавление эффектов освещения
    6. Использование фильтра «Адаптивный широкий угол»
    7. Фильтр «Масляная краска»
    8. Эффекты и стили слоев
    9. Применение определенных фильтров
    10. Растушевка областей изображения
20. Сохранение и экспорт
    1. Сохранение файлов в Photoshop
       
    2. Экспорт файлов в Photoshop
    3. Поддерживаемые форматы файлов
       
    4. Сохранение файлов в других графических форматах
    5. Перемещение проектов между Photoshop и Illustrator
    6. Сохранение и экспорт видео и анимации
    7. Сохранение файлов PDF
    8. Защита авторских прав Digimarc
21. Печать
    1. Печать 3D-объектов
    2. Печать через Photoshop
    3. Печать и управление цветом
    4. Контрольные листы и PDF-презентации
    5. Печать фотографий в новом макете раскладки изображений
    6. Печать плашечных цветов
    7. Дуплексы
    8. Печать изображений на печатной машине
    9. Улучшение цветной печати в Photoshop
    10. Устранение неполадок при печати | Photoshop
22. Автоматизация
    1. Создание операций
    2. Создание изображений, управляемых данными
    3. Сценарии
    4. Обработка пакета файлов
    5. Воспроизведение операций и управление ими
    6. Добавление условных операций
    7. Сведения об операциях и панели «Операции»
    8. Запись инструментов в операциях
    9. Добавление изменения цветового режима в операцию
    10. Набор средств разработки пользовательского интерфейса Photoshop для внешних модулей и сценариев
23. Управление цветом
    1. Основные сведения об управлении цветом
    2. Обеспечение точной цветопередачи
    3. Настройки цвета
    4. Работа с цветовыми профилями
    5. Управление цветом документов для просмотра в Интернете
    6. Управление цветом при печати документов
    7. Управление цветом импортированных изображений
    8. Выполнение цветопробы
24. Подлинность контента
    1. Подробнее об учетных данных для содержимого
    2. Идентичность и происхождение токенов NFT
    3. Подключение учетных записей для творческой атрибуции
25. 3D-объекты и технические изображения
    1. 3D в Photoshop | Распространенные вопросы об упраздненных 3D-функциях
    2. 3D-анимация Creative Cloud (предварительная версия)
    3. Печать 3D-объектов
    4. 3D-рисование
    5. Усовершенствование панели «3D» | Photoshop
    6. Основные понятия и инструменты для работы с 3D-графикой
    7. Рендеринг и сохранение 3D-объектов
    8. Создание 3D-объектов и анимаций
    9. Стеки изображений
    10. Процесс работы с 3D-графикой
    11. Измерения
    12. Файлы формата DICOM
    13. Photoshop и MATLAB
    14. Подсчет объектов на изображении
    15. Объединение и преобразование 3D-объектов
    16. Редактирование 3D-текстур
    17. Коррекция экспозиции и тонирования HDR
    18. Настройки панели «3D»

Научитесь создавать фигуры на холсте и использовать функцию «Свойства интерактивной формы» для взаимодействия с фигурами.

В Photoshop предусмотрена удобная функция рисования и редактирования векторных фигур. Также можно преобразовать векторную фигуру в растровую или пиксельную. Прочитайте полную статью, чтобы узнать больше.

• Создание фигур
• Рисование произвольной фигуры
• Доступ к устаревшим пользовательским фигурам

• Заливка и обводка фигур
• Рисование звезды с помощью инструмента «Многоугольник»

Выполните эти быстрые действия для создания фигур в Photoshop:

1. Выберите инструмент «Фигура»

   На панели инструментов, нажмите и удерживайте значок группы инструментов Фигура (), чтобы вызвать различные варианты инструмента «Фигура» — Прямоугольник, Эллипс, Треугольник, Многоугольник, Линия и Произвольная фигура. Выберите инструмент для рисования нужной фигуры.
   

2. Настройка параметров инструментов группы «Фигура»

   На панели параметров инструментов группы «Фигура» можно задать следующие настройки:

   • Режим: задайте режим для инструмента «Фигура» — Фигура, Контур и Пиксели.
     
   • Заливка: выберите цвет заливки фигуры.
   • Обводка: выберите цвет, ширину и тип обводки фигуры.
   • Ш и В: вручную задайте ширину и высоту фигуры.
   • Операции с контуром: используйте операции с контуром для настройки взаимодействия фигур друг с другом.
     
   • Выравнивание контура: используйте этот параметр для выравнивания и распределения компонентов фигуры.
   • Упорядочение контура: используйте этот параметр для настройки порядка расположения создаваемых фигур.
   • Дополнительные параметры фигур и контуров: щелкните значок шестеренки () для доступа к дополнительным параметрам фигур и контуров, чтобы задать такие атрибуты, как ширина и цвет отображаемого на экране контура, и параметры соблюдения пропорций при рисовании фигур.

3. Рисование фигуры

   Чтобы нарисовать фигуру, выберите нужный инструмент группы «Фигура», затем щелкните кнопку мыши и перетащите указатель мыши на холсте. При этом автоматически создается новый слой-фигура на панели «Слои».

   • Удерживайте клавишу Shift во время рисования, чтобы сделать фигуры пропорциональными.
     
   • Выбрав слой-фигуру, используйте инструмент Перемещение, чтобы перемещать фигуру и менять ее расположение на холсте.
   • Чтобы легко масштабировать, трансформировать или поворачивать фигуру, выберите Редактирование > Свободное трансформирование или нажмите клавиши Control+T (Win) / Command+T (Mac).

4. Редактирование свойств фигуры

   Можно легко редактировать свойства фигуры прямо с помощью элементов управления на холсте или с помощью раздела Свойства фигуры на панели Свойства. Элементы управления на холсте позволяют взаимодействовать с фигурами на более интуитивном уровне.

   Можно использовать элементы управления трансформированием и скруглением на холсте для коррекции внешнего вида фигуры. Модификаторы клавиатуры будут управлять трансформированием на холсте так же, как при использовании инструмента Трансформирование в Photoshop. Можно изменять радиус всех углов прямоугольника одновременно: удерживайте клавишу Alt (Win) или Option (Mac) во время перетаскивания для изменения радиуса одного угла. У треугольников изменяются все углы, даже если перетащить только один из них. С легкостью поворачивайте фигуру с помощью маркера поворота на холсте, который появляется при наведении курсора мыши на фигуру.

   Щелкните значок сброса () на панели «Свойства», чтобы сбросить сразу все изменения.

   Нарисуйте фигуру и используйте элементы управления на холсте, чтобы легко редактировать ее свойства.

   Нарисовав фигуру, можно щелкнуть любую точку холста, чтобы вызвать всплывающее диалоговое окно Создание фигуры и изменить параметры фигуры.
   

Выполните эти быстрые действия для заливки и обводки фигур: 

1. На панели Слои выберите слой-фигуру, который необходимо залить или обвести.

2. Для выбора типа заливки или обводки фигуры выполните одно из следующих действий.

   • Выберите любой инструмент группы «Фигура» (нажмите «U») из панели инструментов. На панели параметров инструментов выберите Заливка или Обводка.
   • На панели Свойства щелкните нужный тип заливки или обводки.  

3. Во всплывающем меню выберите вариант заливки или обводки: Чистый цвет, Градиент или Узор.
   

   Чистый цвет: заполняет или обводит слой-фигуру текущим основным цветом. Для выбора другого цвета используйте палитру цветов или стили цвета.

   Градиент: для отображения диалогового окна «Редактор градиентов» выберите стиль градиента или щелкните градиент. Настройте дополнительные параметры градиента.

   • Значение параметра «Угол» определяет угол, под которым будет накладываться градиент.
     
   • Параметр «Инверсия» изменяет ориентацию цветов градиента.
     
   • Форма градиента определяется стилем.
   • Параметр «Масштаб» изменяет размер градиента.
   • Параметр «Выровнять по слою» использует ограничительную рамку слоя для расчета заполнения градиентом. Можно перетащить ее в окне изображения, чтобы переместить центр градиента.

   Узор: выберите узор в раскрывающемся меню и задайте дополнительные параметры.

   • Значение параметра «Угол» определяет угол, под которым будет накладываться узор. В средстве выбора угла можно указать определенный угол или вручную ввести нужную величину.
   • Параметр «Масштаб» задает размер узора. Введите значение в текстовое поле или с помощью ползунка.

Улучшение в выпуске Photoshop на компьютере за февраль 2021 года (22.2).

Рисовать произвольные фигуры можно, выбрав фигуры в раскрывающейся панели «Произвольная фигура». Можно также сохранить фигуру или контур и использовать их в дальнейшем как произвольную фигуру.

1. Выберите инструмент Произвольная фигура в группе инструментов «Фигура» на панели инструментов.

2. Чтобы просмотреть все произвольные фигуры, предусмотренные в Photoshop, щелкните значок шестеренки справа от палитры «Произвольная фигура» на панели параметров группы инструментов «Фигура». Появится список доступных фигур. Выберите любую произвольную фигуру на свое усмотрение.

3. Если вы не нашли нужную фигуру, щелкните значок шестеренки на палитре «Произвольная фигура» и выберите Импорт фигур для импорта нужной фигуры из сохраненных файлов. Также можно создать и сохранить произвольную фигуру в своей библиотеке.

4. Можно легко редактировать свойства инструмента «Произвольная фигура» прямо в разделе Свойства фигуры на панели Свойства. Кроме того, можно использовать элементы управления преобразованием на холсте для преобразования произвольной фигуры без изменения ее свойств. 
   

5. Щелкните и перетащите в любом месте холста, чтобы нарисовать произвольную фигуру.

Улучшенная панель свойств для инструмента «Произвольная фигура»

Кроме того, набор параметров инструмента «Произвольная фигура» можно настроить прямо на панели Окна > Фигура. При выборе произвольной фигуры на панели Окна > Фигура этот набор также обновится на палитре Инструмент «Произвольная фигура» > Произвольная фигура.  

Доступ к свойствам можно получить только для произвольных фигур, нарисованных с помощью инструмента «Произвольная фигура». Для контура, преобразованного в фигуру, такой возможности нет. 

1. Выберите контур на панели Контуры — векторную маску для слоя-фигуры, рабочий контур или сохраненный контур.

2. Выберите меню Редактирование > Определить произвольную фигуру и введите имя для новой произвольной фигуры в диалоговом окне Имя фигуры. Новая фигура появится на всплывающей панели Фигура на панели параметров.

3. Для сохранения новой произвольной фигуры в новой библиотеке выберите пункт Сохранить произвольные фигуры в меню раскрывающейся панели.

   Дополнительные сведения см. в разделе Работа со средством «Управление наборами».

Одна из основных фигур, которые мы учимся рисовать в детстве — пятиконечная звезда.

Выполните эти три простых действия, чтобы нарисовать звезду с помощью инструмента «Многоугольник».

1. На панели инструментов щелкните и удерживайте значок группы инструментов «Фигура», чтобы вызвать различные варианты инструмента «Фигура». Выберите инструмент Многоугольник.

2. Перетащите инструмент на холст, чтобы нарисовать многоугольник.
   

3. Щелкните в любом месте холста, чтобы вызвать диалоговое окно Создание многоугольника и задайте следующие атрибуты.

   • Ширина и высота: вручную задайте ширину и высоту фигуры.
   • Симметричный: установите флажок для сохранения симметрии в многоугольнике.
   • Количество сторон: вручную введите желаемое количество сторон многоугольника. Например, задайте количество сторон до 5, если требуется нарисовать пятиконечную звезду.
   • Радиус скругления: вручную задайте радиус, чтобы получить скругленные углы у многоугольника.
   • Пропорции звезды: настройте процент пропорции, чтобы получить звезду идеальной формы.
   • Сглаживание внутренних углов звезды: установите флажок, чтобы скруглить внутренние углы звезды.
   • От центра: установите флажок, чтобы выровнять звезду от центра.
   Создание звезды с помощью инструмента «Многоугольник»

Если вы использовали устаревшие пользовательские фигуры из старых версий Photoshop и хотите добавить их в текущую версию, выполните следующие действия.

1. В главном окне выберите Окно > Фигуры
   

2. В правом верхнем углу панели «Фигуры» нажмите значок меню () и выберите Фигуры прежней версии и др.
   

Больше по теме

• Сообщество Photoshop | Рисовать фигуры в Photoshop стало еще проще
• Сообщество Photoshop | Краткие советы: как найти и использовать устаревшие фигуры в текущей версии Photoshop
• Работа с инструментом «Линия»
• Сведения о рисовании
• Рисование с помощью инструмента «Перо»
• Добавление векторных фигур в дизайны | Учебное пособие

 

Вход в учетную запись

Войти

Управление учетной записью

Учебный проект Геометрия вокруг нас

Проектно-исследовательская деятельность «Геометрия в природе»

В настоящее время большое внимание в образовательном процессе общеобразовательных учреждений и учреждений дополнительного образования детей уделяется гармоничному развитию личности обучающегося. Одна из составляющих этого процесса развития – приобщение детей к познанию, исследованию изучаемых явлений. Для этого в образовательных учреждениях создаются благоприятные условия, способствующие реализации творческих идей обучающихся и их педагогов.Предлагаю вашему вниманию проект ученицы 7 класса.

Просмотр содержимого документа
«Проектно-исследовательская деятельность «Геометрия в природе»»

Геометрия в природе

Руководитель:

Волкова Е.А.

Цель проекта : исследовать и выделить основные геометрические фигуры в природе, поиск их в природных объектах

Задачи проекта:

— выделить основные геометрические фигуры;

-провести исследования природных объектов с целью определения их геометрических форм.

Объект проблемного наблюдения: геометрические фигуры в природе

Гипотеза: Основные геометрические формы, окружающие человека, берут своё начало в природе.

Природа говорит языком математики : буквы этого языка – круги, треугольники и иные математические фигуры. Галилей

Математика всегда сопровождала человека в жизни. Математика настолько практична, что немногое из окружающего нас может без нее функционировать.

Геометрические фигуры в природе

Кристаллы горного хрусталя напоминают отточенный карандаш. Кристалл соли имеет форму куба.

А снежинки – это одна из самых красивых геометрических фигур.

Обычная горошина, капельки росы – имеют форму шара.

Фигура, близкая к кругу, получится, если разрезать пополам апельсин, арбуз.

Дугу можно увидеть после дождя на небе — радугу.

Некоторые деревья, одуванчики, отдельные виды кактусов имеют сферическую форму.

В природе многие ягоды имеют форму шара, например, смородина, крыжовник, черника.

Алоэ Polyphylla — приковывает к себе взгляд своими правильными линиями, геометрическими формами, симметричным рисунком и другими внешними признаками.

Крассула «Храм Будды»,

Ураган закручивается по спирали

Спирально плетёт свою паутину паук

Другими интересными фигурами, которые мы можем повсеместно увидеть в природе, являются фракталы. Фракталы — это фигуры, составленные из частей, каждая из которых подобна целой фигуре.

Молния, трещины на камне имеют фрактальную форму

Геометрические фигуры у животных

Многие птицы — воробьи, крапивники, лирохвосты — строят свои гнёзда в форме полушара.

рыба колюшка строит свое гнездо в форме шара

Но самые искусные геометры — пчёлы. Они строят соты из шестиугольников.

Целью данной работы являлось исследование и выделение основных геометрических фигур, поиск их в природных объектах.

Для достижения поставленной цели, были выделены основные геометрические фигуры, проведены наблюдения природных объектов с целью определения их геометрической формы, проведены исследования на установление связи между геометрическими фигурами и природными объектами.

В ходе проекта была выдвинута гипотеза о том, что основные геометрические формы, окружающие человека, берут своё начало в природе.

Источник

Учебный проект «Геометрия вокруг нас»

Одной из главных целей школьного образования становится формирование у учащихся умения учиться, то есть развитие способности самостоятельно ставить учебные цели, проектировать пути их реализации, контролировать и оценивать свои достижения.

Воспитать такого ученика может учитель, владеющий современными образовательными технологиями, инновационными формами и методами обучения.

Одним из путей повышения мотивации и эффективности учебной деятельности в основной школе является включение обучающегося в учебно-исследовательскую и проектную деятельность.

Применение метода проектов в обучении геометрии помогает формированию и развитию устойчивого интереса к предмету, развитию активности учащихся, способствующей формированию навыков самообразования, творчества, инициативы. Деятельность учащихся в рамках проекта опирается на предыдущий жизненный опыт учащихся, доступные для них формы деятельности. Сейчас актуально развитие способности переноса знаний и навыков, полученных в одной области, в любую другую сферу человеческой деятельности.

Метод проектов – мощное дидактическое средство для обучения проектированию – умению находить решения различных проблем, которые возникают в жизни человека, занимающего активную жизненную позицию.

Метод проектов универсален, поэтому я применяю его и на уроках математики, и во внеурочной деятельности по предмету.

Учащиеся отмечают, что работа над проектом способствует проявлению самостоятельности, независимости, творчества. Их привлекает активная, равноправная позиция в учебном процессе.

Геометрический материал является составляющей содержания курса математики, начиная с 5 класса основной школы. Способ его изложения опирается на предыдущий жизненный и геометрический опыт учащихся, доступные для детей формы деятельности, и особую роль при этом играет принцип наглядности. Считаю целесообразным привлекать учащихся к исследовательской работе, в частности, проектной деятельности.

Настоящая работа – результат моего педагогического опыта, практической реализации метода учебного проекта.

Учебный проект “Геометрические кружева”

1. Введение.
2. Методический паспорт проекта.
3. Работа над проектом.

1. Введение.

Идея этого проекта пришла ко мне во время изучения с семиклассниками темы “Деление окружности на равные части”. Они обратили внимание, что в природе, окружающих нас предметах, зданиях много элементов, в основе которых лежит принцип деления окружности на равные части. Мои ученики привели примеры фрагментов ворот, ограды парка, окон в городах Ликино-Дулево и Орехово-Зуево, показали рисунки и фотографии в учебнике истории, попытались воспроизвести эти узоры. Так как геометрические построения сами по себе интересны учащимся, я решила реализовать эту тему для создания орнаментов и узоров в учебном проекте “Геометрические кружева”.

В ходе проекта учащиеся получили новые знания по геометрии, истории математики, познакомились с традициями в архитектуре. Практические навыки пригодятся им на уроках геометрии и технической графики. Проект дал возможность каждому ученику применить свои знания и умения, раскрыть свои способности и возможности.

Общим итогом стали композиции, созданные учащимися на основе приближенных способов построения правильных многоугольников; памятка-чертеж “Деление окружности на равные части”, подборка задач на построение (Приложение 1).

Источник

Презентация по теме: «Геометрия в природе и искусстве. Золотое сечение»

презентация к уроку (алгебра, 7 класс) на тему

«Золотым сечением» называется деление целого на две неравные части, при котором большая часть так относится к целому, как меньшая к большей. В геометрии «золотым сечением» называют также деление отрезка в среднем и крайнем отношении. АС:АВ=СВ:АС Точка С производит «золотое сечение» отрезка.

Части «золотого сечения» составляют приблизительно 62% и 38% С золотой пропорцией тесно связан ряд чисел Фибоначчи 1,1,2,3,5,8. 13,21,34,55,89 и т.д.. В этом ряду каждое последующее число является суммой двух предыдущих чисел.

Замечательный пример «золотого сечения» — правильный пятиугольник -выпуклый и звёздчатый. Звёздчатый пятиугольник называется пентаграммой. Пифагорейцы выбрали её в качестве талисмана. Она считалась символом здоровья. Пифагор

Пентаграмму никто не изобретал, её скопировали с натуры Мефистофель сначала послал черного пуделя отгрызть кончик двери с частью пентаграммы Морские звёзды

Вездесущий филлотаксис Гёте считал спиральность одним из характерных признаков всех организмов, проявлением самой сущности жизни. Носители информации –молекулы ДНК скручены в спираль.

Закономерность расположения листьев, чешуек, семян называют филлотаксисом. В корзинках подсолнечника расположены по двум спиралям. Чешуйки на поверхности шишки расположены по двум спиралям Условная спираль соединяет места расположения листьев на побеге. В формулах листорасположения встречаются числа Фибоначчи

Ритмы сердца Работа сердца в отношении временных циклов, изменения давления крови и объёмов желудочков оптимизировано по одному и тому же принципу – по правилу золотой пропорции

Загадки египетских пирамид Отношения сторон в треугольнике пирамиды равно Ф. Отношение поверхности граней к площади основания также равно золотой пропорции.

«Золотое сечение» в скульптуре Основу скульптуры составляла теория пропорций. Отношения частей человеческого тела связывались с формулой «золотого сечения». Поликлет. «Доридоф». Фидий.» Аполлон Бельведерский».

«Золотое сечение» в архитектуре Золотая пропорция использовалась при создании Парфенона и Пантеона в Древней Греции

Известный русский архитектор М.Казаков в своём творчестве широко использовал «золотое сечение». «Золотое сечение» можно обнаружить в архитектуре здания сената в Кремле. Архитектурный шедевр Москвы – Дом Пашкова архитектора В.Баженова. В.Баженов говорил: «Архитектура – главнейшие имеет три предмета: красоту, спокойность и прочность здания…К достижению сего служит руководством знание пропорции…»

«Золотое сечение»в живописи Портрет Моны Лизы (Джаконды) Леонардо да Винчи долгие годы привлекает внимание исследователей, которые обнаружили, что композиция рисунка основана на золотых треугольниках, являющихся частями правильного звёздчатого пятиугольника.

Алгебра музыки Наиболее обширное исследование проявлений золотого сечения в музыке было предпринято Л.Сабанеевым. Им было изучено 2000 произведений различных композиторов.

Моцарт 91% Гайдн 97% Бетховен 97% Шуберт 91% Шопен 92% Аренский 95% Скрябин 90%

Музыка стихов Совпадение кульминационных моментов в произведениях А.С. Пушкина с золотой пропорцией удивительно близкое, в пределах 1-3 строк. Чувство гармонии у него было развито необыкновенно, что объективно подтверждает гениальность великого поэта и писателя.

Принцип «золотого сечения» — высшее проявление структурного и функционального совершенства целого и его частей в искусстве, науке, технике и природе

По теме: методические разработки, презентации и конспекты

Презентация «Золотое сечение в природе»: история золотого сечения, золотое сечение в живой и неживой природе, золотое сечение тела человека, филлотаксис, числа Фибоначчи в природе. Применяется на урок.

Материалы к внеклассному мероприятию по математике в 6-7 классах «Геометрия в природе и искусстве. Золотое сечение»»

Материалы к внеклассному мероприятию по математике в 6-7 классах «Геометрия в природе и искусстве. Золотое сечение».

Презентация на тему: «Геометрия вокруг нас»

Презентация подготовлена учениками 7 класса для знакомства учащихся начальной школы с началными геометрическими сведениями.Задача этой презентации — мотивировать необходимость изучать геометрию.

Презентация к уроку (Золотое сечение и гармония форм природы и искусства) (8класс).

Конспект урока (Золотое сечение и гармония форм природы и искусства) (8 класс).

Интегрированный урок «Золотое сечение в природе и искусстве»

Интегрировааный урок «Золотое сечение в природе и искусстве» можно провести в рамках декады предметов естественно-математического цикла. Урок с использованием игровых методик, выполнением пр.

Презентация к занятию «Человек и природа в искусстве»

Источник



Стенгазета «Веселая геометрия»

Наши дети в рамках проекта «Геометрия повсюду» полюбили занимательную науку геометрию. Геометрические головоломки любимое занятие вечерами и в любую свободную минутку!

Решили мы свои любимые головоломки в стенгазету поместить. Раскрасили буквы в названии, затем поместили юных геометриков, которых сами раскрасили и вырезали с заданиями.

Газета получилась яркой и занимательной!

Поместили ее на мольберт! Каждую минутку, дети пытаются посчитать фигуры, отгадать сколько квадратов спряталось в прямоугольнике и отгадать – сколько треугольников? Каждая головоломка вырезана детьми, приклеена клеем карандашом! Дети аккуратно работали над стенгазетой! Посмотрите, какие милые у нас Геометрики — веселые, умные и симпатичные!

Возникают споры, развивается внимание. Оцените наши старания!

«Веселая ярмарка — Свистунья». Сценарий музыкального развлечения для детей старшего возраста «Веселая ярмарка — Свистунья». Разработка сценария: воспитатель Шурыгина Наталья.

Фотоотчет «Веселая масленица» Праздник масленица- веселый, яркий,весенний праздник. Она имеет свои традиции и обряды проведения. Этот праздник означает проводы Зимы и.

Фотоотчет «Веселая весна» Дорогие девочки! От всего сердца хочу поздравить вас с наступающим праздником-8 марта. Пожелать вам здоровья,счастья,семейного благополучия.

Конспект НОД по математике «Страна геометрия» Тема: «Страна Геометрия». Программное содержание: дать начальное представление об объемных геометрических телах «пирамида», «шар», «цилиндр»;.

Педагогический проект по ФЭМП для детей средней группы «Страна Геометрия» Проект направлен на решение вопросов развития интереса к игре и к математике в соответствии с новыми требованиями (ФГОС). Помимо интересных.

Программа «Веселая логика» Цель-развитие интеллектуальных способностей дошкольников. Задачи:Развитие способности к планомерной интеллектуальной деятельности; Формирование.

Сценарий турнира по решению геометрических задач «Криминальная геометрия, или Дело принципа» Криминальная геометрия, или Дело принципа. (Использован материал из журнала «Квант» «Методическое пособие в одном акте» Д. В. ФОМИН) Ведущий:.

Веселая артикуляционная гимнастика В работе логопеда артикуляционная гимнастика имеет большое значение. Звуки речи образуются в результате сложного комплекса движений артикуляционных.

Веселая масленица! (фотоотчет) Масленица в нашем детском саду прошла очень весело и шумно! Дети прощались с Зимой и встречали Весну. Все ребята с нетерпением ждали этот.

Веселая зарядка (фотоотчет) Зарядка — архиважный и архинужный процесс формирования гармонично развитой личности, особенно это актуально для жителей крупного мегаполиса,.

Источник

Волшебная геометрия в природе

Приветствую Вас, дорогие читатели. Геометрия сопровождает человека с древних времен, достаточно вспомнить таких древних ученых геометров: Евклида, Пифагора, Рене Декарта и других. Но все — таки самым идеальным геометром является природа — и об ее геометрических фигурах пойдет в нашей статье пойдет речь. Об геометрических фигурах в природе я уже писал в другой своей статье, но в ней больше посвящено все треугольникам: Изучаем с ребёнком треугольники (периметр, виды треугольников) с помощью цветной бумаги .

Основной геометрической фигурой природы являются многоугольники, которые на самом деле присутствуют практически везде. Многоугольники в природе в первую очередь представлены в снежинках , которые имеют разнообразные геометрические фигуры (см. фото 2) .

Как мы с вами наблюдаем по фотографии 2 снежинки в природе действительно имеют различные геометрические фигуры, которые мы с вами изучаем. Но мы изучаем основные геометрические фигуры (квадрат, прямоугольник, треугольники и т.д.).

Еще одними природными геометрами являются растения и цветы (даже те, которые находятся у нас в домах). А в некоторых случаях мы можем разглядеть даже куб (смотрите фото 3).

Некоторые растения используют геометрию для того, чтобы продолжать свой род, но при этом красиво отцветают и радуют глаз (Смотрите фото 4).

Как мы с вами видим, наш одуванчик цветет в виде круга — который он использует для продолжения рода.

Однако существует растение, которое применяет геометрическую форму круга для того, чтобы осуществлять охоту — жирянка (см. фото 5).

Жирянка, представленная на фото 5, хищник, который использует сладковатую сахарную слизь для того, чтобы ловить насекомых. Лепестки жирянки расположены по кругу, формируя круглую коробочку для поимки насекомых.

Конечно, это не весь спектр геометрии, которую применяют именно растения. Сейчас мы с вами поговорим о животных, которые также применяют геометрию .

В мире насекомых основное предпочтение отдадим паукам — именно они умеют правильно плести свою паутину и использовать ее для поимки еды. (См. фото 6)

Паучья паутина создана таким образом, что жертва запутываясь в ней создают вибрации по которым паук и определяет в каком месте паутины запуталась его жертва. При этом используются математические принципы построения паутины и объясняют поведение паука.

Среди животных также в их окрасе наблюдается симметрия, например в окрасе тигров или морских звезд . Даже наши мяукающие любимцы и те обладают геометрической симметрией. (См. фото 7.)

Кроме животных и растений, геометрия присутствует даже в такой важной науке как геммология (науке, изучающей камни и минералы) — в ней также наблюдается геометрическая симметрия . Например, флюорит имеет кубическую (квадратную) форму кристаллов, которая представлена на фотографии 8.

Из всех увиденных нами фотографий можно сделать следующие выводы, что: геометрия является неотъемлемой частью нашего мира и ее геометрические фигуры присутствуют и в снежинках, и в растениях, и в животных и даже в кристаллах. Поэтому изучение геометрии — это важный этап в учебном процессе.

Источник

КОМПОЗИЦИЯ ИЗ ГЕОМЕТРИЧЕСКИХ ТЕЛ НА ВСТУПИТЕЛЬНЫХ ЭКЗАМЕНАХ В МАРХИ • СПЛАЙН

На рис. 6.1 изображены простые геометрические тела, из которых должна состоять экзаменационная композиция. Кроме уже знакомых вам тел здесь представлены плашки и палочки. Плашки – дополнительные плоские квадратные, круглые и шестиугольные элементы, высота которых равна одной восьмой ребра куба. Палочки – линейные элементы композиции, длина которых равна ребру куба. Кроме того в композиции могут быть использованы тела одних пропорций, но разных размеров. Это так называемые композиции с масштабированием (поскольку на листе в таком случае присутствуют одинаковые тела, но как бы взятые в разном масштабе). Рассмотрите композиции, выполненные абитуриентами в последние годы (рис. 6.2-6.20).

Форма экзаменационной композиции, ее размер, размещение на листе, степень и характер взаимодействия геометрических тел уже давно сложились. Все эти позиции в той или иной степени отражены в экзаменационном задании. Конечно, следует сразу оговориться, что речь пойдет о том экзаменационном задании, которое существует на сегодняшний день – оно, возможно, будет изменено на тот момент, когда вы будете читать этот раздел пособия. Однако будем надеяться, что суть задания будет сохранена, и вы сможете воспользоваться нашими советами и рекомендациями.

Прежде всего, перечислим те критерии, по которым будут оценивать ваши композиции:

• соответствие выполненного рисунка заданию;

• композиционная идея в целом, гармоничность композиционного решения и сложность композиции;

• композиция листа;

• грамотное изображение отдельных элементов композиции, правильность перспективы и врезок;

• графика, тональное решение;

• завершенность работы.

Теперь остановимся подробнее на каждой из перечисленных позиций. Казалось бы, обязательность соответствия композиции экзаменационному заданию несомненна. Однако порой в процессе подготовки к экзамену в работах учеников случаются не только ошибки в пропорциях и относительных размерах геометрических тел, но и осознанное их изменение. Это, как правило, объясняют тем, что заданные условиями экзамена геометрические тела имеют некрасивые пропорции и соотношения – шестигранник, мол, слишком длинный, а шар маловат. Это верно, но вы уже знаете, что в экзаменационном задании пропорции и соотношения выражаются простыми пропорциями 1:1 или 1:1,5 – и это неслучайно -их просто изобразить и просто проверить. Изменять их нельзя. Это – задание, если вы изменили задание – вы сдаете какой-то другой экзамен. Для большей убедительности этого утверждения представьте, что на экзамене по математике вы умножаете не 2 на 2, как этого требует задание, а 3 на 3, потому что это гармоничнее, интереснее и выразительнее.

Если рассуждать об общем композиционном замысле, то экзамен в традиционно сложился таким образом, что от абитуриента не требуют составить композицию, отвечающую каким-то условиям, девизам (статика, динамика, погашенное движение, тяжесть, устойчивость и пр.), как это делается в некоторых других архитектурных вузах нашей страны. Хорошо это или плохо – это совершенно другой разговор. Важно то, что такая свобода многими абитуриентами воспринимается как узаконенный произвол, когда можно игнорировать все законы композиции, законы гармонии. Зачастую экзаменационные работы превращаются в навал предметов, которые хотя и взаимодействуют друг с другом, но не создают ничего, кроме некоего сложного хаоса. Из всех возможных путей составления композиции этот представляется наихудшим. Архитектурная композиция – вещь многообразная, точнее, может быть таковой, поскольку путей обретения гармонии множество. Но композиция – не хаос. Гармония может быть парадоксальной, но никогда она не возникает из хаоса. Хаос – энтропия, рассеяние, смешение всего. Гармония всегда закономерна, упорядочена, она противостоит энтропии, борется с ней, и цель человека разумного – победа гармонии над хаосом. Композиция там, где гармония.

В своей работе выберите сами близкую вам тему. Это может быть массивная устойчивость или легкое, устремленное в некую условную даль или ввысь движение. Движение может быть закольцовано или погашено, остановлено. Масса может быть плотной или разряженной. Композиция может строиться на метрических, равномерных закономерностях или же, наоборот – на простом или сложном ритме. В ней может присутствовать равномерное распространение массы или резкие, выделенные акценты. Перечисленные свойства могут комбинироваться (кроме тех, конечно, которые исключают друг друга в одной работе). Следует помнить, что ощущение сложности композиции возникает от восприятия сложной гармонии некоего нетривиального замысла, а не только от сложности врезок и уж точно не от нагромождения множества тел.

Композиция листа – очень важный критерий при оценке работы. Помните, что в конце экзамена вы сдаете в приемную комиссию не композицию из геометрических тел, а лист. Лист не просто носитель информации. В рисунке лист есть произведение искусства, ибо вне листа произведение не существует, как фильм не существует вне экрана. В Японии, когда детей начинают учить каллиграфии, обязательно говорят им, примерно, следующее: «Посмотрите, как прекрасен лист белой бумаги. Задача рисующего заключается в том, чтобы с каждой линией лист становился лучше, а не хуже». Из сказанного следует, что композиция листа столь же важна, как и композиция на листе. Лист надо плотно, но не переуплотнено. Силуэт композиции из геометрических тел должен быть живым и певучим как линия в рисунке, выражая общий замысел работы. Все свободные, незанятые телами поля должны быть уравновешены, красивы по пятну и по пропорциям. Вообще, понятия «композиция на листе» и «композиция самого листа» связаны так плотно, что совершенно невозможно определить, где заканчивается одно и начинается другое. Лист – это условное пространство, композиция тоже занимает пространство (иллюзорное). Эти два пространства не только должны находиться в одном месте, но и гармонично существовать, взаимно учитывая характер друг друга. Лист (имеется в виду формат А-3) имеет определенные границы – вертикали и горизонтали. Эти линии вместе с диагоналями задают основные направления, по которым развивается пространство листа. Кроме того это пространство имеет глубину, причем неоднородную: наибольшую – в центре, наименьшую – по краям, самые плоские участки листа – в его углах (стремление убрать эти плоские места привело к арочной и овальной формам изобразительных поверхностей). Композиция из геометрических тел должна учитывать эти особенности и некоторым образом подчиняться им. Так, композиция, учитывающая в своей структуре прежде всего края листа, имеет прямоугольные очертания. В такой композиции, когда лист заполнен почти до предела, лучше не размещать в углах листа геометрические тела, имеющие наибольшие объемные характеристики, например, шары. Такие прямоугольные композиции – корпусные, массивные, уравновешенные, но, как правило, не очень интересные – они часто вызывают ощущение, что автор старался не создать композицию, а просто равномерно заполнить лист. Лучше, когда в композиции на листе остается больше поля, которое взаимодействует с пространством между геометрическими телами внутри самой композиции. Так, например, композиция в форме овала, как правило, хорошо гармонирует с пространством листа, располагаясь в наиболее глубоком месте, оставляя незанятыми «плоские» углы. «Х»-образная композиция подчинена диагоналям листа. Эти направления могут быть равными по силе и, таким образом, уравновешивать друг друга, а в другом случае одна из диагоналей может доминировать. Возможны также Б и Л – образные композиции, которые строятся на особо сложном, как правило, непогашенном движении, или погашенном, но не до конца. Иногда встречаются интересные композиции в виде восьмерки, совсем редко – построенные в виде «бублика» (кольцеобразные). Возможны и другие принципы компоновки, но перечислять их все нет смысла, поскольку композиция листа рождается совместно с общим замыслом – он вам и должен подсказать наиболее интересное, грамотное, выигрышное решение. Запомните одно главное правило: не может быть хорошей экзаменационной работы, если сам лист некрасив, если он перекошен массами тел, неравномерно и бессмысленно перегружен в отдельных местах и пуст – в других.

Правильная перспектива – обязательное условие хорошей композиции. Вы, наверное, уже заметили, что когда ваша композиция состоит всего из нескольких геометрических тел, сохранить правильную перспективу на листе достаточно сложно. Даже если в основе работы практически идеально построенный куб, прибавление каждого нового тела ведет к постепенному нарастанию искажений. Отследить их и поправить достаточно сложно, особенно в первых композициях, когда опыт и практические навыки еще невелики. Именно поэтому для верного определения раскрытия всех граней и направления всех линий на листе используют различные способы упорядочения всех этих взаимосвязанных позиций, приведения их в единую систему. Одна из таких систем подробно описана в следующем задании. Это так называемая сетка – пространственная структура, определяющая раскрытие граней геометрических тел и направление линий в перспективе по всему листу. В процессе подготовки к экзамену «сетка» поможет вам собрать воедино все многообразие задач, связанных с процессом построения композиции, и разом, легко решить их. Безусловно, «сетка» – вещь полезная, но и в ней, конечно, есть свои плюсы и минусы. С одной стороны, изображая композиции на основе «сетки», вы, конечно, тратите некоторое (порой довольно значительное) время на подготовительный этап (рисунок самой «сетки»), тем самым уменьшая время работы над собственно композицией. С другой стороны, «сетка» может значительно сократить время на решение чисто технических задач, связанных с определением направлений горизонтальных прямых и раскрытием различных поверхностей. Конечно, определенный навык позволит вам свести к минимуму временные затраты на «сетку», но если в «сетке» будет допущена ошибка (что в стрессовых условиях экзамена вполне вероятно), то заметить эту ошибку вы сможете, только нарисовав первое геометрическое тело. Что делать в таком случае – исправлять сетку или отказаться от нее вовсе, чтобы наверстать упущенное время? Очевидно лишь то, что начинать работу над экзаменационной композицией с «сетки» следует, только если к экзамену вы научились делать «сетку» быстро и качественно, доведя этот процесс почти до автоматизма, и легко строите композицию на ее основе.

Еще один вопрос, который часто волнует абитуриента – вопрос о врезках: какие врезки стоит делать, насколько сложными они должны быть, и даже стоит ли их делать вообще? Начнем с того, что врезки в экзаменационной композиции можно и не делать – в экзаменационном задании использование врезок лишь рекомендовано и не является обязательным условием, однако следует понимать, что композиция без врезок значительно уступает в сложности и художественной выразительности. Не забывайте, что вашу композицию будут оценивать в ряду других, а следовательно, делая композицию без врезок, вы заведомо снижаете конкурентоспособность собственной (заботы. Конечно, год от года уровень экзаменационной композиции растет, и это диктует включение в композицию сложных врезок, которые делают экзаменационную работу выразительнее и интереснее. Однако их выполнение требует дополнительного времени, которое в условиях экзамена ограничено. В этой ситуации все зависит от вашего опыта – если вы усердно готовились к экзамену по композиции, скорее всего у вас уже есть свои любимые врезки, которые могут быть достаточно сложными, но, обрисованные много раз, они изображаются легко и, следовательно, быстро. Но не стоит увлекаться сложными врезками, переусложнить работу – помните, что даже композиция, выполненная с применением простых врезок, может быть достаточно сложной и выразительной. Важно также сказать о том, насколько геометрические тела должны врезаться друг в друга. Порой в композициях геометрические тела врезаны так незначительно, что создается ощущение, будто они не врезаны друг в друга, а лишь едва соприкасаются. Такие композиции, как правило, вызывают ощущение нестабильности, неустойчивости и незавершенности. У зрителя появляется непреодолимое желание сделать такую композицию плотнее, глубже врезать друг в друга геометрические тела. Анализируя такую работу, трудно говорить о ней как о композиции – группе гармонично соподчиненных объемов. В других композициях тела так глубоко врезаны друг в друга, что уже непонятно – какие же это тела? Такая композиция, как правило, похожа на сложную массу с торчащими из нее частями геометрических тел и не создает у зрителя ощущения гармонии. Тела в ней перестают существовать как самостоятельные объекты, превращаясь в геометрическую смесь. Если не рассматривать такие крайние случаи (когда геометрические тела почти не врезаются друг в друга или когда они превращаются в единую плотную массу), для создания композиции средней плотности следует придерживаться следующего правила: геометрическое тело должно врезаться в другое (или другие) геометрические тела не более чем наполовину, лучше – на одну треть. Кроме того, желательно, чтобы зритель всегда мог определить основные размеры геометрического тела по его видимой части. Иными словами, если в какое-либо тело врезается конус, на рисунке должна остаться видимой его вершина, значительная часть боковой поверхности и окружности основания. Если в какое-либо тело врезается цилиндр, то видимыми должны остаться части боковой поверхности цилиндра и окружностей его оснований. Особо следует сказать о врезках кубов и четырехгранников – в композиции эти геометрические тела составляют фон или, своего рода, каркас для расположения и врезки других, более сложных в построении геометрических тел. Поэтому допускаются врезки, когда видимые части кубов и четырехгранников составляют менее половины их объемов.

Сложность композиции, конечно же, связана не только с вопросом врезок, но и с вопросом количества геометрических тел. Как правило, условия экзаменационного задания особо оговаривают это количество – не менее 5 и не более 12. Как видите, даже этот диапазон достаточно широк для творчества. Определяя количество геометрических тел в композиции, помните, что чем меньше тел в композиции, тем крупнее они должны быть, тем сложнее их организовать по законам гармонии и красоты, так как каждая связка должна быть обрисована очень точно. Когда количество тел возрастает и уменьшаются их размеры, значительно упрощается задача создания красивых и гармоничных сочетаний геометрических тел вследствие больших возможностей по перемещению отдельных элементов относительно друг друга. Особую роль могут сыграть в композиции плашки. Композиция, в которую включены плашки, выглядит сложнее, интереснее и богаче по сравнению с композицией, где плашек нет. Плашки могут выполнять в композиции самые разнообразные функции. Так, при помощи плашек можно создавать различные объемы. Например, когда необходимо дополнить композицию каким-нибудь геометрическим телом, но все предлагаемые кубы, шестигранники, цилиндры и пр. либо слишком крупны и массивны для этого, либо слишком сложны и нарушают композиционный замысел, привлекая к себе излишнее внимание. В этом случае следует использовать плашки. Одинарная плашка является наименьшим объемом, участвующим в композиции – варьируя количество плашек и их взаимное расположение, можно создавать объемы, самые разные по массе, конфигурации, плотности и сложности.

Плашки могут организовать движение геометрических масс в композиции. Так, например, квадратные плашки останавливают движение, создают на листе ощущение стабильности и завершенности. Квадратные плашки, лежащие в трех взаимно перпендикулярных плоскостях, активно подчеркивают пространственную структуру композиции, фиксируют ее в плоскости листа. Круглые плашки, особенно вертикальные – похожи на колеса создают ощущение движения, неустойчивости, а иногда просто растаскивают композицию в разные стороны.

Плашками можно усилить в композиции какую-либо плоскость. Например, если композиция почти фронтально, т. е. в ней практически не выражена глубина пространства, развернутую на зрителя поверхность хорошо поддержат дополнительные фронтальные плашки. Если есть необходимость усилить движение в глубину композиции, с этим хорошо справятся включенные в композицию парные плашки, перпендикулярные фронтальной плоскости.

При помощи плашек можно создать тему. Одинаковые плашки, повторенные в разных местах композиции, объединяют различные геометрические тела в единую гармоничную структуру. Тема плашек может быть самостоятельной или поддерживать тему, заданную большими геометрическими телами (например, шестиугольные плашки поддержат включенные в композицию шестигранные призмы). Плашки могут «спасти» не очень красивую врезку геометрических тел, добавив в нее дополнительные членения.

Плашки могут создать красивый, динамичный абрис композиции. Выразительность контура композиции является важным моментом в процессе восприятия композиции зрителем. Иногда на край композиции выходит длинное ребро призмы или образующая цилиндра. Плашки, врезанные в геометрическое тело, могут усложнить объем и разрушить монотонность абриса в данном месте композиции.

В хороших композициях плашки выполняют сразу несколько функций. Умело включенные в вашу работу, плашки способны сделать ее яркой и выразительной, что, безусловно, очень важно. Однако всегда следует помнить о второстепенной роли плашек по отношению к крупной геометрии. Не стоит создавать при помощи плашек слишком значительные объемы. Помните, что основная масса композиции должна набираться из больших геометрических тел (кубов, четырехгранных и шестигранных призм, пирамид, конусов и т. д.), а плашки выступают только как дополнительные элементы.

Создавая композицию, внимательно следите за красивым балансом крупных объемов и плашек. Плашек не должно быть очень много (тем более, что их количество входит в общее число геометрических тел), иначе такая композиция будет напоминать семейство опят на старом пне или изоляторы на линии высоковольтных передач.

Не включайте в композицию большое количество разных плашек, ограничьтесь одним, максимум, двумя видами. В противном случае плашки будут не объединять, а наоборот вносить в вашу композицию хаос.

В тот год, когда эта книга была почти завершена, на экзамене по рисунку композиции плашек не было вовсе. Таким образом, задание значительно усложнилось. Создать красивую и гармоничную композицию только из больших геометрических тел не так просто. Вместо плашек в экзаменационное задание были введены геометрические тела двух разных размеров. Наряду с уже известными вам телами (кубом, четырехгранной и шестигранной призмами, цилиндром, конусом и шаром), в композиции можно было использовать те же геометрические тела в полтора раза большего (или меньшего) размера. При этом пропорции тел сохраняются прежними (1:1,5).

Графика в композиции заслуживает отдельного разговора. В экзаменационном задании говорится о линейном рисунке и легком введении тона. О том, какая линия должна быть на вашем рисунке, уже говорилось и не раз: четкая, красивая, разнообразная, выразительная. Скажем только, что графически линией всегда следует выделять и подчеркивать объем каждого геометрического тела, усиливая на рисунке видимые и невидимые ребра, а также общий объем всей композиции, усиливая ее контур. Что касается тона, то в реальной ситуации насколько легким или, напротив, насыщенным будет тон вашей композиции, определяется, прежде всего, ее сложностью. Сильный или слабый тон – не цель, а лишь средство выявления объемных характеристик композиции. Если композиция проста, тогда, действительно, хватит и легкого тона, но для создания сложного объема тональная шкала должна быть шире, а максимальный тон – соответственно, сильнее. Не увлекайтесь сильным тоном, помните, что сильный тон потребует большего времени для его технического выполнения, хотя таким тоном проще смоделировать сложный объем. Слабый тон, напротив, требует меньше времени на техническую работу, но моделировать сложный объем таким тоном не просто. Как видите, и в этом случае следует искать «золотую середину». Вообще создание красивой графики на листе требует долгой, кропотливой, внимательной и настойчивой работы. Не все получается сразу, часто ученик делает линейную композицию, затем наносит тон и видит, что линия «ушла», затерлась. Тогда ученик «поднимает линию», вновь критически оценивает свою работу и понимает, что теперь тон слабоват, и его необходимо усилить…, затем опять линию и опять – тон. В конце концов, когда вполне довольный результатом ученик приносит свою работу на консультацию педагогу или сравнивает ее с работами других учеников – его удовлетворенность куда-то исчезает. Если вам знакома такая ситуация – не отчаивайтесь, она абсолютно нормальна. Постепенно с опытом придет понимание не только того, какую силу тона и линии необходимо создать на вашем листе, но вы также научитесь чувствовать материал, работать им, и уж конечно тогда из вашего рисунка уйдут эти изнуряющие стадии приближения к идеалу. И если этого пока не произошло, позвольте дать еще один совет: не бойтесь делать ошибки – с ними приходит опыт и приобретаются навыки.

Еще несколько слов необходимо сказать об эскизе экзаменационной композиции. В эскизе можно решить основные композиционные вопросы: найти общие пропорции будущего изображения, размеры отдельных его частей и их место на листе, определить положение линии горизонта, а также направления горизонтальных линий, уходящих в точки схода. Однако найденную в небольшом эскизе гармонию не всегда удается полностью сохранить при переносе замысла на полный лист – так стоит ли вообще делать эскиз композиции?

Ответ на этот вопрос зависит от задачи, которую ставит перед собой рисовальщик, и от его опыта. Упорной работой, желанием и трудолюбием приобретается опыт, следовательно, возрастает сложность задачи. В своих первых работах, когда необходимо просто создать на листе перспективное изображение объема из врезанных друг в друга геометрических тел, занять геометрией весь лист и, по возможности, не допустить серьезных ошибок, вы можете обойтись и без эскиза. Когда опыт позволит вам не только грамотно и стабильно изображать геометрические тела и сложные врезки, но и размышлять о сложной пространственной структуре, движении масс, общем композиционном замысле, эскиз станет необходимым. В эскизе уже на первом этапе работы вы можете сформулировать основную идею, отобрать то, что необходимо включить в композицию, отбросив все лишнее.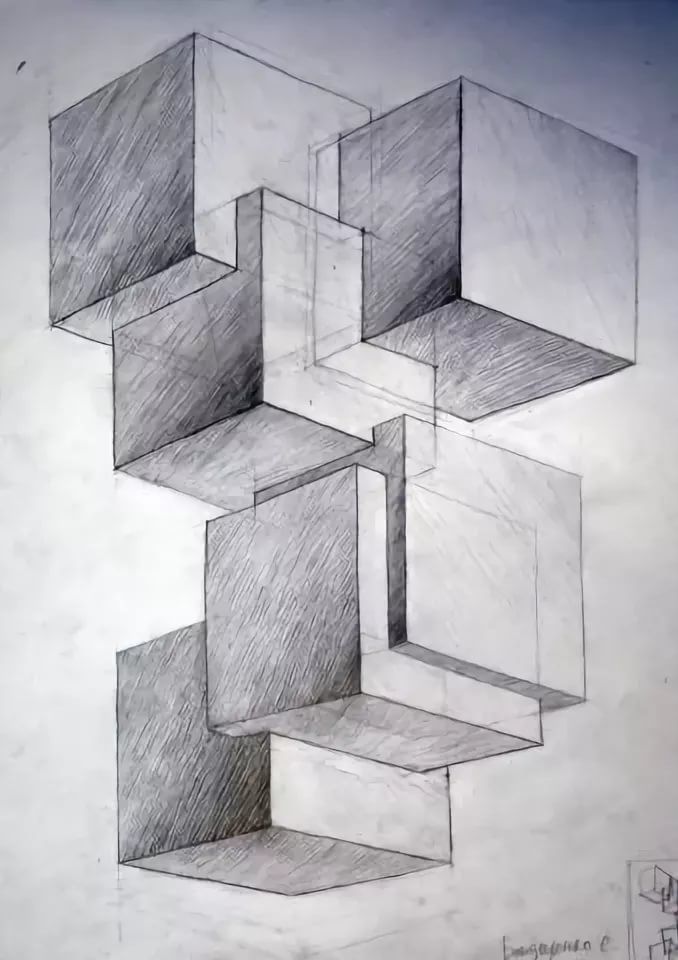 Постепенно рисовальщик формирует свои собственные представления о том, как должна выглядеть композиция, выявляет и определяет любимые связки геометрических тел, наиболее выразительные и эффектные врезки и композиционные приемы. Тогда опыт позволяет обходиться и без стадии предварительного эскизирования. Рисовальщик, достигший такого уровня, получив исходное экзаменационное задание, строит композицию, опираясь на многократно отработанные блоки и элементы.

Некоторые абитуриенты «идут дальше» и всерьез рассуждают о том, чтобы заранее подготовить хорошую композицию, запомнить, заучить ее, а затем просто повторить на экзамене, или «еще дальше», чтобы не утруждать себя изучением геометрических тел, не отрабатывать технику рисунка, не упражняться в выполнении различных врезок, а потратить отведенное на подготовку к вступительным экзаменам время на тупое зазубривание одной эффектной композиции. Пожалуй, мысль эта не нуждается в подробном комментарии. Экзаменационная работа является, прежде всего, проверкой уровня ваших знаний и умений, их соответствия высоким требованиям, предъявляемым к студенту первого курса. И пытаясь таким образом обмануть приемную комиссию, абитуриент обманывает, прежде всего, самого себя. Кроме того, каждый год экзаменационное задание хоть и незначительно, но меняется. Вводятся новые элементы (например, буквы или геометрические тела другого масштаба), задаются определенный ракурс (сверху или снизу) и точка зрения, определяются обязательные геометрические тела или их связки. Как правило, эти изменения становятся известны только на экзамене. И если вы пришли на экзамен с готовой, окончательно сложившейся композицией, эти новые вводные в лучшем случае не позволят вам реализовать «домашнюю заготовку», а в худшем – выведут вас из рабочего состояния, заставляя судорожно перекраивать вашу композицию под новые условия.

Некоторые абитуриенты испытывают трудности в «придумывании» композиции. Жалуясь на то что, Идея не рождается, а Муза не прилетает, они боятся, что окажутся в подобной ситуации на экзамене и не смогут или не успеют справиться с заданием. Есть простое решение этой проблемы. Создавая новую композицию, воспользуйтесь как основой предыдущей работой. Наверняка, заканчивая ее, вы сокрушались, что не смогли «дотянуть» композицию, не подвинули то или иное геометрическое тело, не исправили слишком поздно замеченные ошибки во врезках, не довели до совершенства графику и т. д. Это обычная практика. Идея может быть зафиксирована в рисунке на определенный момент ее существования, но остановить ее невозможно, она живет и развивается дальше. Когда же рисунок закончен, часто оказывается, что он хуже, чем идея, лежащая в его основе. В таком случае браться за принципиально новую композицию преждевременно. Следует нарисовать новую работу на ту же тему. В ней вы сможете осуществить все, что не удалось сделать в предыдущей работе.

Для исправления композиционных недостатков удобно пользоваться калькой. Отрежьте лист кальки на несколько сантиметров больше чем размер вашего рисунка. Положите кальку на уже нарисованную композицию и перенесите на неё те геометрические тела и связки, место которых вы хотели бы сохранить. Другие тела перемещайте в соответствии с вашим замыслом, двигая кальку по композиции, или же меняйте их на другие. Если за один раз вам не удастся внести в композицию все задуманные изменения, возьмите следующий лист кальки. Так продолжайте до тех пор, пока вы не будете удовлетворены результатом. Окончательный вариант изобразите на листе бумаги, предварительно перенеся на него с кальки место и основные габариты всех геометрических тел. Такая последовательная работа очень похожа на процесс архитектурного проектирования, когда архитектор шаг за шагом улучшает, уточняет, совершенствует свой замысел, пока не достигнет идеала. Так и вы улучшайте и совершенствуйте свою композицию, не бросая ее, разрабатывая тему до конца, как золотую жилу пока она не иссякнет. Скорее всего, в этот момент у вас появится новая идея. Она появится сама, рожденная вашими усердием, прилежанием и опытом. Со временем новые идеи потекут потоком, одна интереснее другой. Вы едва будете успевать выбирать лучшие композиции, чтобы их нарисовать.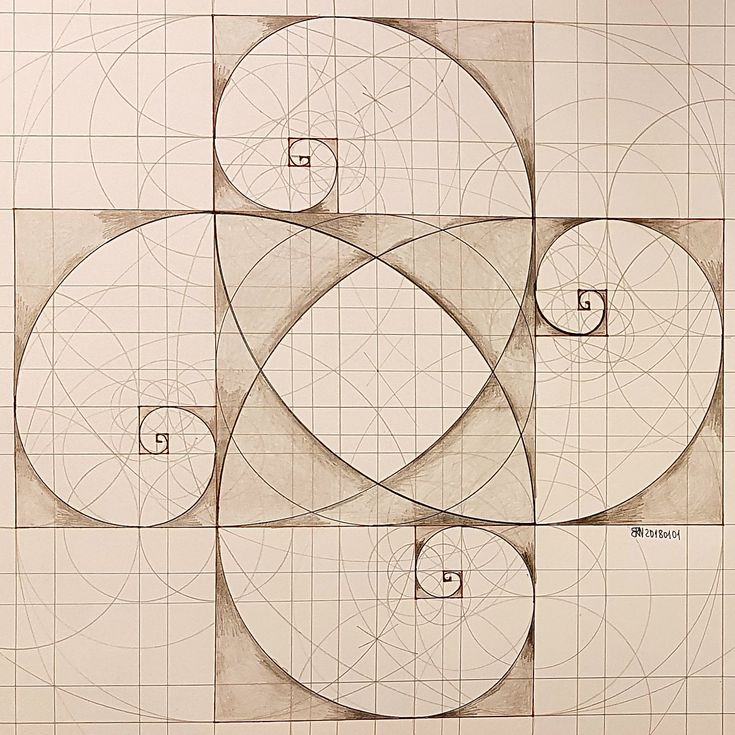 Тогда и вступительный экзамен не застанет вас врасплох, у вас сразу найдется достойный ответ на экзаменационное задание – красивый и выразительный. Но помните, чтобы это было именно так, необходимо упорно и старательно готовиться.

Вы не просто должны рисовать композиции по представлению, но тщательно анализировать каждую свою работу. Внимательно отбирайте красивые врезки, интересные связки геометрических тел, различные варианты общей структуры композиции, определенную графику (линию и штрих), формируя, таким образом, своеобразный личный «арсенал». Такой «арсенал» на экзамене не только сокращает время на подготовительную и техническую работу, но и увеличивает время на решение творческих задач.

Геометрия в ландшафтном дизайне

Идея использовать геометрические формы как источник вдохновения и выразительного средства в изобразительном искусстве и дизайне не нова. Первыми в этом направлении стали продвигаться художники, основавшие направление «кубизм». Известен и «супрематизм» К. Малевича с его квадратами, кругами, прямыми и ломаными линиями.

В ландшафтном дизайне геометрические фигуры стали использовать в давние времена. В качестве примера можно привести регулярный сад (парк) Версаля, созданные искусными садовниками эпохи французской монархии. Ровные дорожки, квадратные цветники, шарообразные и конусовидные топиары очевидно доминируют в садовых композициях в это время.

Сегодня такие мотивы способны стать основополагающими в дизайне сада, могут выступать в роли небольших и эффектных акцентов.

Планировка

Какой бы ни была планировка сада, она так или иначе будет связана с геометрией. Сами очертания участка, который обычно имеет прямые углы, задают ритм всему проекту. Сегодня встречаются участки неправильной формы, наполнить их гармонией может именно грамотная геометрия. Достаточно расположить дом и хозпостройки под нужными углами к сторонам участка, добиться равновесия за счет продуманной посадки деревьев, кустарников, цветников и других садовых объектов.

Опишем пример грамотного планирования на основе комплекса прямоугольников, дуги и шаров. Сейчас популярны дома в виде буквы П, которые имеют два крыла. Такой подход позволяет построить дом большой площади, ограничив его одним этажом, и при этом сделать разные его части достаточно удаленными друг от друга, что очень целесообразно, если люди любят уединение. Внутренний дворик, выделенный в общей композиции особым покрытием (брусчатка, плиты, доски и т.п.), строят на основании полукруга между двумя крыльями здания, в его центре. Саму дугу или ее концы можно обыграть шарообразными топиарами или светильниками.

В планировке дизайнер ландшафтной компании «Гринтэк» отталкивается от композиционного центра – жилого дома. Трехскатная крыша дает возможность повторения пирамидальных, конусовидных и треугольных форм. Стоит разделить стандартный четырехугольный цветник диагональю из цветов контрастного цвета – он войдет в резонанс с постройками.

Четкая геометрия

Кто-то тяготеет к природным формам, желает создать сад в эко-стиле, а кому-то милее четкость и строгость линий, авангардные решения и футуризм. Регулярность подразумевает общее стремление к упорядоченности и организованности, что придется по вкусу педантичным натурам.

Возможны дизайнерские решения, где вся концепция построена на обыгрывании пространственных и плоскостных фигур. Средствами будет все: от планировки до конкретных элементов (дорожек, бордюров, ограждений, зеленых насаждений и т.п.). Абсолютно любой объект вашего сада возможно соотнести с тем или иным фактом геометрии. Как уже говорилось, дом задает настроение в этом длинном ряду множащихся форм. Следующим важным звеном являются кроны деревьев и кустарников. Они сами по себе, без всякой обработки, уже тяготеют к шару, параболоиду, конусу. Их можно подвергнуть фигурной стрижке, которая либо доведет естественные очертания до идеальных соответствий этим фигурам, либо создадут совершенно несвойственные изначально ребристые формы куба, пирамиды и т.п.

Значимы плоскости и их оформление:

• коротко стриженными газонами разных видов;
• цветниками, покрытыми посадками одной высоты;
• ограждениями из досок, металлических листов и других плоских материалов.

На плоскостях линиями бордюров и дорожек выводятся любые композиции.

Используя все перечисленные элементы в комплексе, создаются разнообразны и органичные образы. Можно выделить два подхода:

• Построение всего проекта на обыгрывании однотипных форм (шара, круга, овала или прямоугольников, квадратов, кубов, прямых). В этом случае разнообразия добиваются с помощью использования разных по размеру объектов. Эффектно будет смотреться композиция из топиаров-шаров, где самым большим будет дерево-крупномер, поменьше – несколько кустарников, а шарообразные карликовые породы на штаммах завершат эту группу.
• Сочетание противоположных по своему звучанию объектов, добиваясь контрастных решений. Примером может быть декорирование прямоугольного или квадратного газона шарообразными кустами самшита, расположенными в его углах.

В любом случае цель дизайнера компании «Гринтэк» – добиться читаемости ландшафтного рисунка, сделать визуальный ряд нарядным и ненавязчивым.

Единичные декоративные акценты

Если вам по вкусу шары или конусы, совсем не обязательно погружать ландшафтный дизайн сада в стихию геометрии. Вы можете использовать любимые фигуры или линейные изображения как небольшие аккуратные акценты. Этот способ декора отлично работает в проекте практически любого стиля. Можно оформить таким образом входную группу, беседку, перголу, скамью и т.п. Пара шарообразных или конусовидных деревьев выделят зону входа. Актуальны и растения в кадках. Традиционно используют самшит, тую, ель. Такое обрамление подчеркнет композиционную роль элемента, выделит его вектор.

Еще один вариант включения шаров в ландшафт – их пунктирное расположение по ходу дорожки. Особенно эффектно они будут выглядеть, если тропинка проходит по открытому участку газона. Такого же результата можно добиться с помощью светильников круглой формы общей системы освещения сада.

В ландшафтном дизайне многое строится на геометрических конструкциях. Геометрия линий и форм отлично работает во всем, начиная с общей планировки пространства и введения отдельных акцентов и заканчивая тем, что дизайнер в целом делает ставку на эффектность кубических, шарообразных, линейных и т. п. элементов.

Геометрия форм и планировка

Планировка участка обязательно опирается на геометрические построения. Еще на этапе проектирования ландшафтный дизайнер смотрит на форму участка, на то, как в нее вписан дом и остальные постройки и размещает садовые элементы в соответствии с общей концепцией участка. Обычно участок бывает квадратной или прямоугольной формы, а дом сегодня может иметь самые замысловатые очертания на плане. Традиционные квадрат и прямоугольник, конечно, встречаются, но вообще проектировщики не скупятся на разнообразие. Например, если дом выстроен буквой П, то пространство между двумя крыльями строения уместно будет обыграть полукругом внутреннего дворика, несколько выступающим за общие очертания дома. Такое сочетание прямоугольных форм и дуги будет смотреться очень органично, а для законченности его можно дополнить шарообразными элементами декора, расположенными по окружности: светильниками или мелкими кустарниками.

Еще один интересный вариант, который успешно используют современные архитекторы – это трехскатная крыша в форме пирамиды.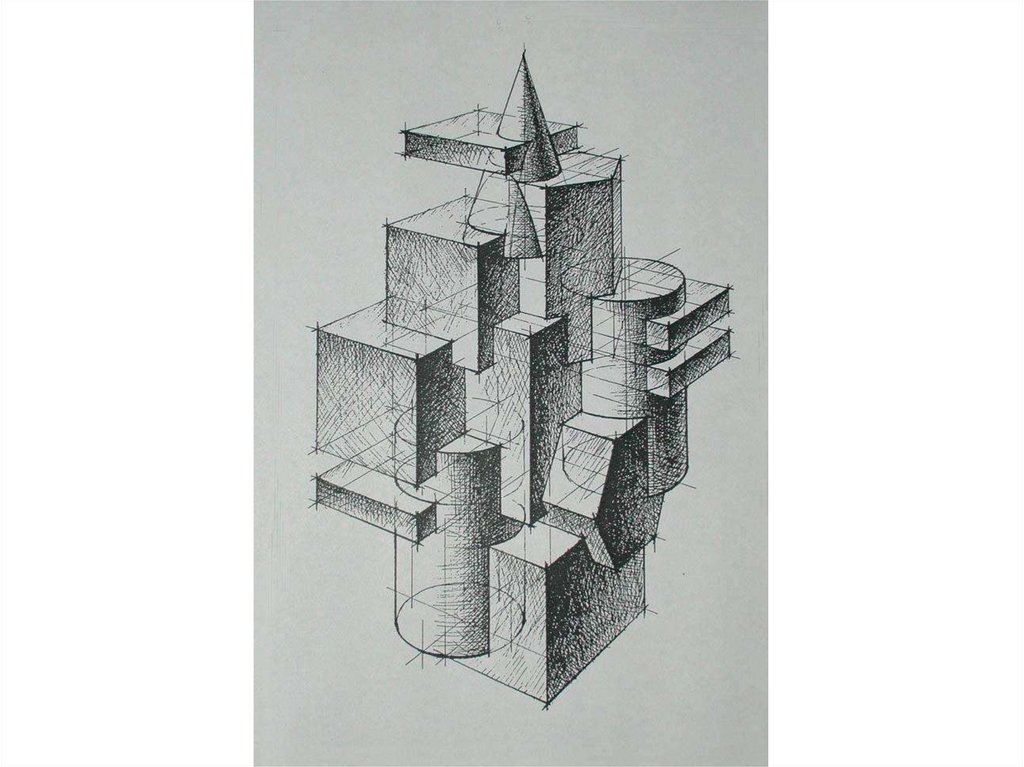 Такую конструкцию будет уместно обыгрывать треугольными формами и конусовидными объемными элементами в дальнейшем озеленении участка. Например, цветник перед домом может быть выполнен как разделенный от угла к углу квадрат или четырехугольник. Таким образом, фактически правильная и симметричная фигура будет зрительно соотноситься с треугольником.

Следует отметить, что разнообразие геометрических форм начинает звучать в нужном ключе лишь если эти формы имеют четкие очертания. Для воплощения геометрии плана в реальность изобразительными средствами для ландшафтного дизайна и озеленения служат мощеные и песчаные дорожки сада, бордюры и ограждения, живые изгороди.

Использование геометрических форм как концептуальный принцип

Кто-то старается создать в своем саду эффект дикой и нетронутой природы, а кто-то тяготеет к авангарду, кубизму, четкости линий. Стремление к регулярности и геометричности форм, симметричности и строгости вписывается в так называемый формальный стиль. Общее ощущение порядка и организованности подойдет педантичным натурам.

Если вам особо интересны правильные геометрические формы, и вы хотели бы любоваться их четкими очертаниями постоянно, то весь ландшафтный дизайн участка можно построить на обыгрывании кубов, шаров, пирамид и конусов.

При благоустройстве и озеленении в работе с геометрическими формами надо знать, что абсолютно все элементы композиции соотносятся с какой-либо плоскостной, линейной или объемной фигурой. Кроны кустарников и деревьев сами по себе тяготеют к форме шара, конуса или параболоида, но, кроме того, их можно довести до точного соответствия с любой объемной формой с помощью фигурной стрижки.

Линии на вашем участке могут быть представлены бордюрами, оградами, дорожками. Газоны и цветники с низко растущими, однотипными цветами воспринимаются глазом как плоскости.

Из всех этих компонентов составляются гармоничные, насыщенные и неизменно радующие взгляд композиции. Причем для нужного эффекта ландшафтные дизайнеры компании «ПозитивПроект» рекомендуют совмещать в одном контексте разные формы, создавая эффект контрастности. Начинающим следует основывать свою работу на какой-то одной форме, сочетая между собой либо шары, круги, овалы и дуги, либо кубы, квадраты, прямоугольники и прямые линии, либо пирамиды, конусы и треугольники и т.п. Разнообразия в таком случае можно достигать за счет совмещения фигур разных размеров. Так, хорошо будет смотреться круглая ваза или фонтан в центре округлого газона или цветника.

Однако грамотный и опытный профессионал работает более тонко и способен достигать потрясающих эффектов, выстраивая композиции на контрасте, совмещая не только крупные и мелкие, высокие и низкие элементы, но и самые противоположно звучащие формы.

Как это реализовать на практике? Приведем несколько примеров. Если у вас имеется прямоугольный или квадратный газон, то расположите в углах шарики мелкого кустарника, например, самшита.

Ландшафтный дизайн должен органично сочетать в себе противоположности или дополнять друг другом однородные формы, ведь в итоге необходимо достичь легкости восприятия основного рисунка участка.

Геометрия линий и форм в декоративных акцентах

По опыту дизайнеров компании «ПозитивПроект», геометрические акценты прекрасно работают на любом участке. Эти элементы могут присутствовать в разном количестве. Вариантов здесь множество. Так, чтобы акцентировать внимание на входе в дом или беседку можно расположить по обе стороны конусовидные деревья-солисты в горшках или кадках. Подходящими по форме будут туя или ель. Такой же прием можно использовать, подчеркивая композиционную значимость какой-либо малой архитектурной формы – скамьи, например. В районе входной группы вытянутым формам отдается приоритет в связи с тем, что они подчеркивают вертикальное положение двери, как бы повторяют ее вектор.

Небольшие самшитовые шары могут пунктиром располагаться вдоль дорожки, проходящей по открытому пространству газона. Так они дополнительно выделяют линию тропинки, что позволяет избежать ощущения пустоты на большой площади газонной травы.

Кстати, саму дорожку можно сделать не сплошной, а пунктиром: если квадратные плиты в траве положить на небольшом расстоянии друг от друга, то получится очень эффектный геометрический рисунок, напоминающий мозаику.

Осветительные приборы разных геометрических форм являются великолепным средством декора. Шарообразные светильники более современны, а светильники в форме параллелепипеда с крестообразным пересечением на каждой стороне создают атмосферу прошлых веков.

Компания “ПозитивПроект” предлагает

Для дошкольников и учеников 1-11 классов

16 предметов ОРГВЗНОС 25 Р.

Выбранный для просмотра документ Презентация.ppt

Описание презентации по отдельным слайдам:

Автор: Алмазова Марина Николаевна, обучающаяся 9 класса Т Руководитель: Гусева Ольга Николаевна, учитель математики

Памятник погибшим воинам

Проблема: Можно ли использовать геометрию в ландшафтном дизайне?

Цель: на примере озеленения памятника погибшим воинам показать связь геометрии с ландшафтным дизайном

ЗАДАЧИ: На основе литературных источников познакомиться с понятием «ландшафтный дизайн». Наглядно продемонстрировать использование геометрических фигур в ландшафтном дизайне. Привлечь жителей села к проблеме сохранения и благоустройства памятника, к его состоянию. Организовать практическую деятельность школьников.

Ландшафтный дизайн участка – особый вид деятельности, направленный на создание искусственной среды для жизнедеятельности человека путем активного использования природных компонентов.

Существуют 2 главных направления в садовом дизайне – регулярный и пейзажный

Парк в Петродворце

Этапы реализации проекта Подготовительный: мотивация, целеполагание проекта. Проектировочный: построение ориентировочной схемы деятельности. Практический: реализация проекта

Результаты 3 вопроса

Результаты 4 вопроса

Цветы в озеленении

Экономический расчет Наименование расходов Общая сумма Приобретение семян цветов для посадки в клумбах 300 Приобретение саженцев деревьев для посадки у памятника 500 Приобретение расходных материалов на изготовление листовок, афиш 100 Приобретение многолетних цветов (розы, папоротники и др.) 800

Выводы: Геометрия широко применяется в ландшафтном дизайне. Симметрия и геометрические фигуры придают ландшафту порядок, гармонию, закономерность, которые применяются в регулярном стиле. Благоустраиваемая территория пригодна для осуществления задуманного проекта; элементы дизайна, изображенные в эскизах, реально выполнимы.

Выбранный для просмотра документ геометрия в ландшафтном дизайне.doc

Филиал муниципального общеобразовательного учреждения

«Первомайская средняя общеобразовательная школа» в селе Старосеславино

Автор: Алмазова Марина Николаевна, обучающаяся 9 класса

Руководитель: Гусева Ольга Николаевна, учитель математики

Глава 1. Ландшафтный дизайн ……………………………………………..5

1.1. История развития ландшафтного дизайна ……………………..5

1.2. Современные представления о ландшафтном дизайне ……….7

1.3. Использование геометрии в ландшафтном дизайне ………….9

Глава 2. Этапы реализации проекта ………………………………………12

2.1. Подготовительный этап…………………………………………12

2.2. Проектировочный этап ………………………………………… 12

Глава 3.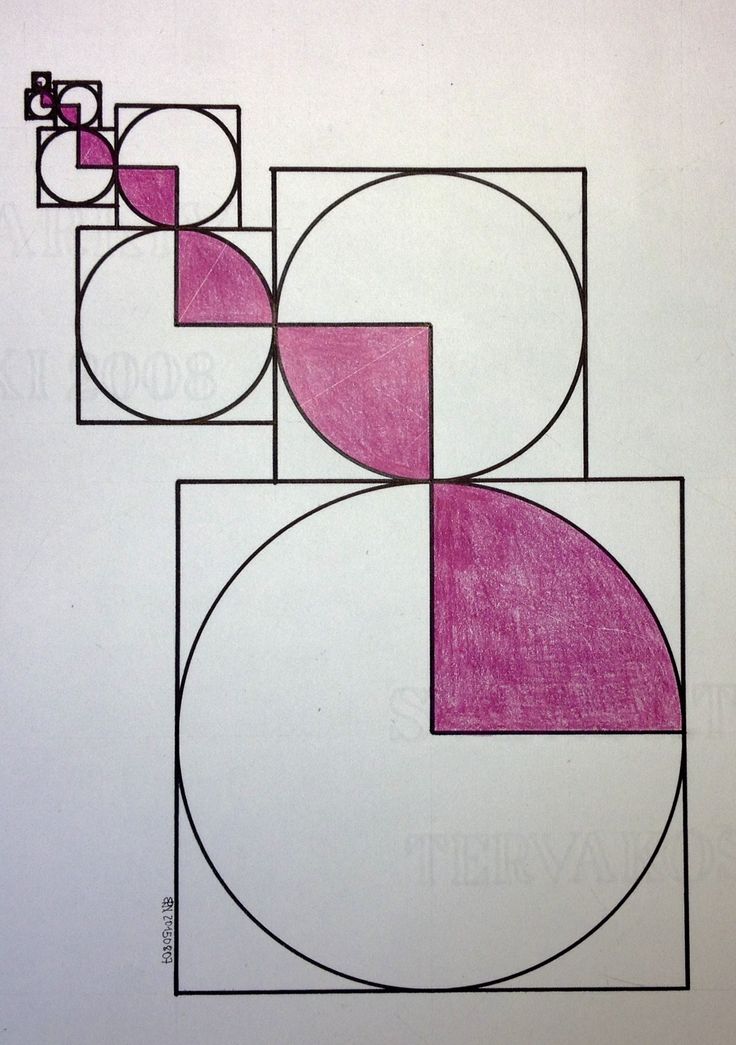 Результаты исследований…………………………………………15

3.1. Проведение социологического опроса жителей села…………15

3.2. Разработка идей, вариантов ……………………………………16

3.3. Экономический расчет …………………………………………19

В настоящее время можно с уверенностью сказать, что геометрическое образование является основным для многих профессий. Так в последние годы заметно проявился интерес ко всему, что связано с растениями и оформлением ими интерьеров. И это не мода на цветы, а желание сделать красивым то место, где живем, работаем, отдыхаем, воспитываем детей. Т акое место есть и у нас – это памятник воинам, погибшим в годы Великой Отечественной войны. Ни один житель села, а тем более – участники войны не могут пройти мимо этого святого места со спокойным сердцем. В ходе исследовательской деятельности мы выясним: действительно ли знание геометрии несет красоту в мир.

Именно поэтому нами была выдвинута проблема : можно ли использовать геометрию в ландшафтном дизайне?

Объектом исследования стала прилегающая к памятнику территория.

Предметом исследования являются геометрические фигуры и геометрические законы симметрии.

Цель нашего исследования заключается в том, чтобы на примере озеленения памятника погибшим воинам показать связь геометрии с ландшафтным дизайном.

Задачи, решаемые в данном проекте состоят в том, чтобы:

На основе литературных источников познакомиться с понятием «ландшафтный дизайн».

Наглядно продемонстрировать использование геометрических фигур в ландшафтном дизайне.

Привлечение жителей села к проблеме сохранения и благоустройства памятника, к его состоянию.

Организовать практическую деятельность школьников:

– Составление плана и эскиза благоустройства и озеленения памятника;

– Определение экологических условий озеленяемой территории памятника и элементов благоустройства;

– выращивание рассады цветочных культур для посадки в клумбы;

-организация экологических субботников с привлечением местных жителей.

5. Организовать массовую пропаганду среди населения благодаря:

– организации среди обучающихся школы конкурса детского рисунка – эскиза посадки растений у памятника;

– установке информационного щита, напоминающего жителям о бережном отношении к территории памятника (Приложение 1).

Таким образом, наш проект призван решить проблему эстетического оформления и озеленения территории памятника через геометрические законы симметрии, а также геометрические фигуры.

Глава 1 . ЛАНДШАФТНЫЙ ДИЗАЙН

1.1. История развития л андшафтного дизайна

Ландшафтный дизайн участка – особый вид деятельности, направленный на создание искусственной среды для жизнедеятельности человека путем активного использования природных компонентов (рельеф, вода, растительность и т. д.).

Ландшафтный дизайн участка – очень важный элемент благоустройства территории. Считается, что дизайн возник в начале прошлого века как «реакция на стихийное формирование визуальных и функциональных свойств предметной среды». И уже сегодня высокое искусство дизайна справедливо ассоциируется с красотой, комфортом и рациональностью, идет ли речь о полиграфическом дизайне, ландшафтном, флористическом и пр.

Что же такое стиль в ландшафтном дизайне ?

В ландшафтном дизайне – это определенная трактовка основных правил и приемов планировки, цветового решения малого сада, подбор растений и их сочетание. История развития человечества выдвинула два главных направления в садовом дизайне – регулярный и пейзажный. Каждая историческая эпоха вносила свои черты в эти направления. Не осталось в стороне и наше время. Пейзажный стиль пришел в Европу из Китая, где всегда абсолютизировалась красота природы. Здесь большое значение придавалось тому, чтобы здания органично вписывались в искусно обработанный природный ландшафт.

В Европе, точнее в Англии, первые пейзажные парки появились в XVIII в., обозначив появление нового отношения европейца к природе. Для пейзажного стиля характерны извилистые дорожки с низким плотным травяным покровом, либо покрытые песком, гравийным отсевом, дробленой щепой или кирпичной крошкой. Цветов в английском саду мало, и они высаживаются группами, чаще в миксбордерах. Растения используются с характерной фактурой листьев, естественной формой кроны, учитывается сочетание их формы и цвета, даже осенняя окраска листвы. Водоем имеет естественные, близкие к природным, очертания берегов. Модный нынче японский пейзажный сад невелик по площади, каждая его деталь – будь то мостик, фонарик или зонтик – несет сложный внутренний смысл. Для европейца японский сад излишне театрален, но очень привлекателен. Основной его принцип – ощущение спокойствия и отдыха, созерцания природы и миниатюризация.

Доминантой регулярного стиля всегда является здание, которому подчинен весь ландшафтный дизайн. В основу каждой садовой зоны заложены геометрические фигуры, законы симметрии и геометрии, что придает участку торжественность, парадность, которые скорее подавляют, чем располагают к отдыху. Характерным элементом регулярного стиля является партер, расположенный перед основным зданием и представляющий собой сочетание газона, цветников, воды, декоративных элементов, связанных между собой в сложном геометрическом рисунке. Обычно этот стиль применяют на небольших равнинных участках, где очень сложно создать уголки дикой природы, успокаивающе действующие на нервную систему. Для таких участков характерны прямые мощеные дорожки, кирпичные заборы, небольшие внутренние дворики, аккуратно подстриженные живые изгороди, посаженные по прямым линиям. Здесь редко можно встретить сооружения из натуральной необработанной древесины, природные валуны, альпийские горки, клумбы.

Регулярный стиль садового искусства находится в русле идей классицизма. Лейтмотив этого стиля – порядок. Четкость плана и строгость линий – это главное, что отличает парки регулярного стиля. Примером такого сада является роскошный парк в Петродворце с его знаменитыми фонтанами. Главный вход в парк располагается обычно в его нижней части, а центральная точка – в верхней, и входящего сразу подавляет величественность открывающейся перед ним картины. Впрочем, не менее величественно панорама парка выглядит и сверху.

В литературе мало уделяется внимания такому явлению, как русский пейзажный стиль. Некоторые исследователи даже утверждают, что такого стиля нет. Хотя русский сад XIX века имеет ярко выраженные индивидуальные черты. Это и большие пространства нетронутой, а лишь слегка прирученной природы, каскады копаных прудов, плодовые рощи, цветники, в которых сочетаются царственные лилии и полевые ромашки. Русский сад всегда удачно совмещал два направления – декоративное и утилитарное. Огороды в этих садах не в пример французским были красивы не изысканным оформлением, а богатым урожаем самых разнообразных овощей.

Казалось бы, еще недавно само понятие « ландшафтный дизайн » в нашей стране применялось исключительно к истории садово-паркового искусства. Сегодня ландшафтный дизайн шагнул из парковых комплексов в частные владения Уже есть примеры высококлассного оформления придомовой территории площадью менее сотки [1].

1.2. Современные представления о ландшафтном дизайне

Для современных стилей малого сада XX – X Х I вв. характерны усиление эстетической составляющей и расширение индивидуальности.

Высокую моду диктует, ежегодная выставка в Челси, которую организует Королевское садовое общество Великобритании с конца XIX века. В последние годы высокая мода делает акцент на экологизме ландшафтов. Все больше внимания уделяя не достижениям селекционеров, а дикоросам. Сегодня наивысшим достижением ландшафтного дизайнера может считаться сочетание геометрии форм цветников и таинственное волнение злаков, высокотехнологичных садовых изделий из стали и стекла с пришедшими в сады зарослями рогоза, бамбука. На пике моды нынче имитация старого заброшенного сада, воссоздание картины первозданной природы. Правда, создание атмосферы запущенности дело очень дорогое, а привнесение в сад наиболее эффектных дикоросов сопряжено с тем, что многие из них значатся в Красной книге.

Но может ли это остановить модников в области ландшафтного дизайна ? Конечно, нет. И европейские модные тенденции прорываются и в российские сады.

Что же сегодня популярно в российских садах? Постоянно растет интерес к традициям русской дворянской усадьбы. Тут вам и лирические березки, и романтический пруд, и лужайки с полевыми цветами, яблони, утопающие в цвету, заросли сирени и тонкий аромат чубушника (жасмина).

По-прежнему популярны восточные мотивы. Если японский стиль прослеживается лишь на небольшом участке, как правило, в приватной зоне сада, то элементы китайского сада порой пронизывают весь участок.

В нашей стране возвращается мода на солнечные часы. Вслед за Европой мы хотим иметь их в садах вовсе не для того, чтобы сверять время. Главное их достоинство – высокая декоративность.

Модным элементом сада является и зеленая скульптура. Это могут быть роскошные экземпляры стриженых вечнозеленых деревьев и кустарников, а могут быть выращенные на металлическом каркасе почвопокровные многолетники или плетистые растения.

В общем, модные тенденции вовсе не ставят дизайнера в жесткие рамки, а позволяют проявлять фантазию. Главное, чтобы владельцы участков доверяли выбранному дизайнеру, смелее шли на эксперименты и не ужасались экстравагантным предложениям специалистов. Сегодня это эксперимент, а завтра – модное течение [1,2,3].

Использование цветов в озеленении – это настоящее искусство. Оно существует с древних времен. Лучшим украшением каждого из них, как правило, становится цветник. Цветник из композиции различных цветочно-декоративных растений может включать газон, фонтан, беседку, скамейки, вазы и скульптуры.

1.3. Использование геометрии в ландшафтном дизайне

Происхождение термина « геометрия» , что буквально означает «землемерие», можно объяснить следующими словами, приписываемыми древнегреческому учёному Евдему Родосскому (4 в. до н. э.): « Геометрия была открыта египтянами и возникла при измерении Земли. Это измерение было им необходимо вследствие разлития реки Нил, постоянно смывавшего границы». Уже у древних греков геометрия означала математическую науку, в то время как для науки об измерении Земли был введён термин геодезия . Судя по сохранившимся отрывкам древнеегипетских сочинений, геометрия развилась не только из измерений Земли, но также из измерений объёмов и поверхностей при земляных и строительных работах и т.п.

Ландшафтный дизайн – понятие новое, в переводе с английского означает рисунок, чертеж, проект , но одновременно и сам процесс проектирования, а, кроме того, и его результат.

Геометрию также можно использовать в ландшафтном дизайне . Ведь для того, чтобы всё правильно сделать необходимо, знать, что каким будет по размеру и по форме. Так же нужно предполагать какой будет участок – симметричный или ассиметричный. В составлении плана тоже может помочь геометрия .

Для использования геометрии в ландшафтном дизайне необходимо знать несколько определений, используемых в архитектуре.

Перспектива. Перспективой называют зрительное изменение предметов по мере их удаления от наблюдателя. Законы перспективы были открыты мастерами Возрождения, разработавшими математически точную систему построения пространства. Леонардо да Винчи писал, что теория линейной перспективы разъясняет явления видимых форм, величины и цвета в зависимости от их положения в пространстве. Различают перспективу линейную и воздушную. Пространственные изменения цвета называют цветовой перспективой.

Линейная перспектива. И в природе, и на картине вы замечаете, как сходятся на горизонте уходящие от вас параллельные линии. При этом все вертикальные линии остаются вертикальными, уменьшаясь по величине,- чем дальше они от наблюдателя, тем меньше. Можно заметить и то, что невысокие растения на переднем плане могут казаться выше более высоких, расположенных вдали. Этот эффект носит название линейной перспективы.

Композиция. Под композицией (от лат. Compositio –связь, соединение) вообще понимается расположение различных форм в пространстве в сочетаниях, создающих гармоничное единство. При решении композиционных задач необходимо учитывать целый ряд свойств, которыми обладают пространственные формы. Сюда входят: геометрический вид формы, её величина, масса, фактура, положение в пространстве, цвет и освещенность.

Соотношение форм по геометрическому строению. Форму природных элементов можно обобщенно представить себе близкой к геометрической. Может быть линейная, плоскостная и объёмная форма в зависимости от соотношения её измерения. В линейной преобладает одно измерение над двумя другими, предельно малыми; в плоскостной – относительно равны два измерения при подчинённо малой величины третьего; в объёмной форме все измерения относительно близки по величине. Линейной формой, которая неизменно присутствует во многих элементах сада, можно считать дорожки, бордюры, ограждения сада.

Симметрия и асимметрия. Размещение отдельных элементов в саду и план сада в целом может быть симметричным и ассиметричным – по отношению к оси композиции, которой может быть линия взгляда либо дорога, а иногда ось садового домика.

Симметрия. В естественном ландшафте симметрия является редкостью. Поэтому там, где мы её наблюдаем, симметрия обыкновенно указывает на наличие порядка, наведенного человеком.

В Европе слово «симметрия» было синонимом слова «красивый» и означало приятную и изящную форму. Возможно, это объясняется тем, что симметрия подразумевает порядок и изящную форму. Так или иначе, но слово «симметрия» стало ассоциироваться с ясностью плана, с его равновесием, ритмом, единством и стабильностью.

Асимметрия. Асимметрия более утонченна, непреднамеренная и поэтому более интересна. Нас не ведут шаг за шагом вдоль жесткой композиции или сквозь неё. Напротив, нам предоставлена свобода самим исследовать и открывать в ландшафте то, что красиво, привлекательно или полезно, и, что особенно важно, асимметричная компоновка влечёт за собой меньше нарушений природы.

Что означает перевернутая буква T в математике? – Стратегии для родителей

Математика, кажется, время от времени бросает нам буквы, несмотря на то, что состоит в основном из цифр. Мы можем простить это в алгебре, но когда кажется, что эти буквы превращаются в странные символы, такие как перевернутая буква Т, многие из нас снова чувствуют себя потерянными.

Перевернутая буква T (или ⊥) относится к перпендикулярным линиям, которые представляют собой две линии, пересекающиеся под углом 90 градусов. Они должны быть прямыми линиями, а точка их пересечения также должна быть под прямым углом. Если линии волнистые или под любым другим углом, они не перпендикулярны. В геометрическом уравнении вы должны представлять перпендикулярные линии с помощью ⊥.

Этот перевернутый символ T относительно прост для понимания и применения, если вы знаете, что он представляет и как его использовать. Итак, чтобы стать знатоком геометрии, читайте дальше.

Что такое перпендикулярные линии?

Перпендикулярные линии пересекаются или пересекаются и соединяются под прямым углом (90 градусов). Таким образом, вы можете использовать перпендикулярные линии для многих математических уравнений и шаблонов, что служит существенной цели.

Мы видим вокруг себя перпендикулярные линии. Любой квадрат или прямоугольник имеет перпендикулярные углы. Вы можете измерить угол любой двери, и там тоже должны быть перпендикулярные линии.

Происхождение слова также говорит нам о его значении. Оно происходит от старофранцузского ( perpendiculer ), что означает формирование от прямого угла, которое они получили от латинского ( perpendiculum ), что означает «отвес» (источник).

«Отвес» означает прямую или вертикальную линию. Перпендикулярные линии требуют прямых линий, но они не обязательно должны быть вертикальными, поэтому смысл несколько изменился.

Теперь мы можем изучить, как вы можете использовать перпендикулярные линии в математике.

Что означает перпендикуляр в математике?

Как мы уже говорили выше, слово «перпендикуляр» означает то же самое в математике.

Перпендикулярные (или ортогональные) линии пересекаются друг с другом под прямым углом. Таким образом, эти линии должны быть прямыми и пересекаться под прямым углом (90 градусов). Существует несколько способов представления перпендикулярных линий (источник). Меньшая рамка представляет собой прямой угол на диаграмме.

Изображение Sona Digital Media

Линии R и S пересекаются друг с другом под прямым углом, состоящим из перпендикулярных линий. В геометрии вы бы написали это как R⊥S. Проще говоря, это означает, что там, где пересекаются R и S, возникает прямой угол.

Перпендикулярные линии могут пересекаться, идущие с любого направления.

Изображение Sona Digital Media

Несмотря на то, что линии пересекаются по диагонали, их угол по-прежнему прямой, и он по-прежнему будет R⊥S. В этих сценариях перпендикулярные линии создают крест. Тем не менее, края квадрата или прямоугольника также будут перпендикулярными линиями.

Изображение Sona Digital Media

В этом сценарии все углы являются перпендикулярными линиями, поскольку они встречаются под углом 90 градусов, и они будут A⊥B, B⊥C, C⊥D и D⊥A.

Другие фигуры также могут иметь перпендикулярные линии, но не на всех углах. Примером этого может быть треугольник, но он должен выглядеть как прямоугольник или квадрат, разрезанный пополам по диагонали.

Изображение от Sona Digital Media

Вы должны представить это как AB⊥BC. Есть много других примеров в формах, но главное, чтобы угол был прямым. Углы при А и С не перпендикулярны, так как они не равны 90 градусам. Мы обсудим это далее при рассмотрении теорем Пифагора.

Одним из важных моментов является то, что все перпендикулярные линии пересекаются (встречаются или пересекаются), но не все пересекающиеся прямые перпендикулярны.

Image by Kevin Mak via Unsplash

Что означает ⊥ в линейной алгебре?

Линейная алгебра ⊥ имеет аналогичное значение, но вы применяете ее по-другому. При использовании его в линейной алгебре математики называют его ортогональностью. Слово происходит от латинских слов «».орто , что означает вертикальный, и « гония », что означает угол. Следовательно, его значение очень похоже на перпендикуляр, но направленность другая.

Линейная алгебра

Прежде чем понять роль ⊥, нам нужно понять, что такое линейная алгебра. Несмотря на название, это не то же самое, что алгебра, которую вы изучали в школе.

Линейная алгебра — это изучение векторов и матриц, и многие знают ее как изучение данных. Линейные комбинации и декартовы плоскости создают информацию.

Линейная алгебра использует числа в столбцах, называемых векторами — они включают как величину, так и направление (источник). Матрицы используют числовые массивы, состоящие из набора чисел в квадратных скобках. Мы видим ⊥ в декартовых плоскостях.

Декартовы плоскости

Когда вы посмотрите на типы перпендикулярных линий в геометрии, вы увидите, что линии, пересекающиеся друг с другом, выглядят как декартова плоскость. Его двумерная форма представляет собой две пересекающиеся линии.

Декартова плоскость – это когда две числовые линии пересекаются перпендикулярно и образуют четыре квадранта. Горизонтальная линия — это ось x, а вертикальная линия — это ось y (источник).

Координаты указывают конкретное положение точки на числовой прямой или плоскости. Средняя точка плоскости равна 0, а ось x, идущая вправо, показывает положительные числа. Когда ось X движется влево, она показывает отрицательные числа.

Аналогично, ось Y, идущая вверх от нуля, показывает положительные числа, а линия оси Y, идущая вниз от нуля, указывает отрицательные числа. При связывании значений с декартовой плоскостью первое число указывает значение x, а второе число указывает значение y.

Изображение Sona Digital Media

Таким образом, [-3, -3] будет означать, что точка находится в нижнем левом квадранте, а [-3, 1] будет в верхнем левом квадранте.

Все точки на декартовой плоскости ортогональны или перпендикулярны из-за природы декартовых плоскостей, потому что все начинается с нулевой точки, которая является основанием прямого угла. Итак, вы можете выразить точку как 1, 1 ⊥ 0.

Теорема Пифагора

Любой уважающий себя студент-математик наверняка сталкивался с теорией Пифагора, но какое отношение она имеет к перевернутой букве T?

Когда мы ранее рассматривали перпендикулярные линии, одной из фигур, которые получились, был треугольник, у которого перпендикулярен только один угол. Теорема Пифагора устанавливает связь между длинами трех сторон.

Теория Пифагора показывает, что в треугольнике с перпендикулярным углом длина наибольшей стороны равна квадратному корню из суммы квадратов двух других сторон. Математически это можно выразить как ² + b ² = c ² .

Изображение Sona Digital Media

Из-за того, что сторона перпендикулярна, становится легче вычислить длину каждой стороны треугольника. Например, представьте, что вы знаете, что более короткие стороны треугольника имеют длину три и четыре дюйма соответственно.

Используя теорему Пифагора, вы должны заявить: 3 ² + 4 ² = 25, что делает самую длинную сторону = 5. Чтобы разбить это дальше, квадратный корень числа означает умножение самого себя. Итак, 3 х 3 = 9и 4 x 4 = 16. 9 + 16 равно 25, что является квадратным корнем из 5.

Что означает ⊥ в логике?

Несмотря на то, что ⊥ и 丄 выглядят как строчные и прописные версии одних и тех же символов, они имеют существенно разные значения и использование.

Меньший ⊥, который мы использовали, означает перпендикулярную линию. Больший 丄, который логики также называют символом вверх, встречается только в логике и указывает на то, что что-то всегда ложно (источник).

Примеры

Хотя значения истинности в математике и логике могут быть довольно сложными, давайте рассмотрим более простой пример. Представьте, что вы любите шоколад во всех его проявлениях. Таким образом, предложение «Я люблю шоколад» будет примером истинностного значения.

Напротив, если бы вы сказали «Я ненавижу шоколад», это было бы примером ложного значения, выраженного символом вверх: 丄.

Другим примером, более близким к математике, может быть очень простое уравнение: 1 + 1 = 2. Поскольку это верно и нет другого правильного ответа, это значение истинности. Напротив, 1 + 1 = 3 ложно, и никакое обсуждение не изменит этого, сделав его 丄.

Есть способы отличить истинные утверждения от ложных. Например, предложение «все женатые люди состоят в браке» совершенно точно благодаря характеру его формулировки. Если кто-то не женат, он не может называть себя женатым человеком.

Если в логике что-то верно, вы напишите это с большой буквы. Вы бы выразили эту мысль так: «Все женатые люди женаты = Т».

Однако мнение «все женатые люди счастливы» не может быть верным. Все женатые люди не могут быть счастливы, даже если вы счастливы в своем собственном браке. Вы бы представили это как «все женатые люди счастливы» = 丄.

Иногда логики заявляют, что символ 丄 означает «фальшь» и «абсурд». Оба являются латинскими терминами, которые означают, что что-то полностью ложно и не соответствует действительности.

Различные типы линий

Мы уже разобрали перпендикулярные линии, но другие линии обычно встречаются в геометрии.

Есть шутка о линиях в математике, представляющих разные истории любви. Параллельные линии никогда не должны пересекаться, касательные линии — это линии, которые когда-то были вместе, но никогда больше не сойдутся, а асимптоты сближаются, но никогда не сойдутся.

Параллельные линии — это две линии, идущие рядом друг с другом, но не соприкасающиеся и не пересекающиеся, какой бы длины они ни были.

Изображение Sona Digital Media

Далее у нас есть касательные линии. Касательные линии появляются на графиках с кривой. Они показывают, когда определенная точка касается кривой, но сразу после этого дуга отклоняется от линии, и они больше не встречаются.

Изображение Sona Digital Media

На приведенной выше диаграмме фиолетовая линия является касательной и касается кривой данных лишь на короткое время. Красная точка указывает на это.

Наконец, у нас есть асимптоты. В геометрии они появляются на декартовой плоскости и работают с кривой линии данных. Линия постоянно приближается к линии, но никогда не может коснуться линии.

Изображение Sona Digital Media

На приведенном выше рисунке линия асимптоты (выделена красным) следует за кривой данных, но не соприкасается с ней.

Это, конечно, не единственные линии в геометрии, а лишь несколько основных. В этом смысле перпендикулярные линии — это положительная история любви. Две линии, идущие с разных сторон, судьбой суждено встретиться всегда в «нужное» время.

Image by Dan-Cristian Paduret via Unsplash

Другие T-символы

Мы уже знаем о меньшем символе ⊥, обозначающем перпендикулярные линии, и о большем 丄 символе прихватки вверх. Однако это не единственные символы, которые используют Т-образную форму. Давайте посмотрим на несколько других.

В математике маленькая t указывает на измерение времени. Вы можете использовать его в ряде уравнений, чтобы показать, сколько секунд, минут или часов прошло или нужно учитывать.

Например, формула для времени: Время = Расстояние ÷ Скорость. В сокращении вы бы выразили это как t = d ÷ s. Допустим, в гипотетической ситуации нам нужно рассчитать, сколько времени потребуется, чтобы пройти 30 миль, если вы идете со скоростью 5 миль в час.

30 ÷ 5 = 6

T = 6 часов.

Как указывалось ранее, заглавная T говорит правду в логическом сценарии по сравнению с большим 丄, что означает ложь.

Наконец, ⫫ 9Символ 0006 (двойная закрепка) также присутствует в математике и логике. Он представляет собой независимую случайную величину. Случайная величина не влияет на расчет или эксперимент. Следовательно, вы бы не приняли это во внимание.

Например, если бы вы экспериментировали, чтобы найти лучший шоколадный торт в мире, количество яиц, которое вы использовали в каждом рецепте, было бы примером независимой случайной величины. Хотя яйца повлияют на вкус самого торта, они не повлияют на вкус других тортов.

Перевернутые символы в математике, логике и геометрии

В математике, логике и геометрии есть много символов, состоящих из букв, которые часто перевернуты. Такие символы позволяют математикам и логикам представлять сложные отношения в упрощенном формате.

Чтобы узнать больше о перевернутом символе «А», ознакомьтесь с разделом «Что означает перевернутый символ «А» в математике?» Эта статья была написана для Strategyforparents.com.

В качестве символов можно использовать не только буквы, но и цифры. Например, чтобы узнать больше об обратном числе 3, которое мы также называем «эпсилон», прочитайте «Что означает символ «обратное 3»?»

Заключительные мысли

Символ ⊥ является важной частью геометрии. При измерении фигур и вычислении площади перпендикулярные линии точно говорят нам, с чем мы имеем дело на фигуре. Хотя маловероятно, что вы встретите символ ⊥, если только вы не занимаетесь геометрией, всегда полезно знать, что вы ищете.

Математические символы (неофициальное справочное руководство LaTeX2e (май 2022 г.))

LaTeX предоставляет практически любые математические или технические символы, которые кто-нибудь использует. Например, если вы включаете $\pi$ в вашем исходнике, вы получите символ пи π. См. «Полный Список символов LaTeX» на https://ctan.org/pkg/comprehensive.

Вот список часто используемых символов. Он ни в коем случае не является исчерпывающим. Каждый символ описывается короткой фразой и его классом символа. который определяет интервал вокруг него, указан в скобках. Пока не иначе говоря, команды для этих символов могут использоваться только в математике режим. Чтобы переопределить команду, чтобы ее можно было использовать независимо от текущей режим см. \ensuremath .

\| ¶

∥ Параллельно (отношение). Синоним: \параллельно .

\ алеф ¶

ℵ Алеф, трансфинитный кардинал (обычный).

\альфа ¶

α Строчная греческая буква альфа (обычная).

\амальг ¶

⨿ Непересекающееся объединение (двоичное)

\ угол ¶

∠ Геометрический угол (обычный). Аналогично: меньше чем знак < и угловая скобка \langle .

\ приблизительно ¶

≈ Почти равно (отношение).

\ ¶

* Оператор звездочки, свертка, шестиконечная (двоичный). Синоним:  * , что часто является надстрочным индексом или нижний индекс, как у звезды Клини. Аналогично:  \star , т.е. пятиконечная и иногда используется как общая бинарная операция, и иногда зарезервированы для взаимной корреляции.

\асимп ¶

≍ Асимптотически эквивалентно (отношение).

\обратная косая черта ¶

\ Обратная косая черта (обычная). Аналогично: установите минус \setminus и \textbackslash для обратной косой черты вне математического режима.

\бета ¶

β Строчная греческая буква бета (обычная).

\bigcap ¶

⋂ Переменное или n-арное пересечение (оператор). Похожий: бинарное пересечение \заглушка .

\bigcirc ¶

⚪ Круг, больший (двоичный). Аналогично: функция состав \circ .

\bigcup ¶

⋃ Переменное, или n-арное, объединение (оператор). Аналогично: двоичный соединение \чашка .

\bigodot ¶

⨀ Оператор с переменным размером или n-значной точкой в ​​кружке (оператор).

\bigoplus ¶

⨁ Переменный размер или n-значный, обведен плюс оператор (оператор).

\bigotimes ¶

⨂ Переменный размер, или n-значный, обведенный кружком оператор времени (оператор).

\bigtriangledown ¶

▽ Переменный размер или n-значный открытый треугольник вершиной вниз (оператор).

\bigtriangleup ¶

△ Переменный размер или n-значный открытый треугольник, направленный вверх (оператор).

\bigqcup ¶

⨆ Переменное или n-арное квадратное объединение (оператор).

\biguplus ¶

⨄ Оператор объединения переменного размера или n-арного оператора с плюсом (оператор). (Обратите внимание, что имя имеет только одну букву.)

\bigvee ¶

⋁ Переменный размер, или n-значный, логическое-или (оператор).

\большой клин ¶

⋀ Переменного размера, или n-арное, логическое-и (оператор).

\bot ¶

⊥, закрепка вверх, низ, наименьший элемент частично упорядоченного множество, или противоречие (обычное). См. также  \top .

\бабочка ¶

⋈ Естественное соединение двух отношений (relation).

\Коробка ¶

□ Модальный оператор по необходимости; квадратная открытая коробка (обычный). Недоступно в простом TeX. В LaTeX вам нужно загрузить пакет amssymb .

\пуля ¶

• Пуля (бинарная). Аналогично: умножение точка \cdot .

\крышка ¶

∩ Пересечение двух множеств (бинарный). Аналогично: переменный размер оператор \bigcap .

\cdot ¶

⋅ Умножение (двоичное). Аналог: Пуля точка  \ маркер .

\чи ¶

χ Строчный греческий хи (обычный). 9{\mathsf{c}}$ или $\bar{S}$ .

\ соединение ¶

≅ конгруэнтны (отношение).

\coprod ¶

∐ Копроизведение (оператор).

\стакан ¶

∪ Объединение двух наборов (бинарный). Аналогично: переменный размер оператор \bigcup .

\ кинжал ¶

† Связь кинжала (бинарная).

\dashv ¶

⊣ Приборная панель с вертикальным перевернутым турникетом (связь). Похожий: турникет \vdash .

\ddagger ¶

‡ Отношение двойного кинжала (бинарное).

\Дельта ¶

Δ Греческая заглавная дельта, используемая для приращения (обычный).

\дельта ¶

δ Греческая строчная дельта (обычный).

\Алмаз ¶

◇ Крупный алмазный оператор (рядовой). Недоступно в простом TeX. В LaTeX вам нужно загрузить пакет amssymb .

\ алмаз ¶

⋄ Алмазный оператор (двоичный). Похожие: большие ромб \ ромб , круглая пуля \ пуля .

\алмазный костюм ¶

♢ Алмазная карточная масть (обычная).

\дел ¶

÷ Знак деления (двоичный).

\ doteq ¶

≐ Приближается к пределу (отношению). Подобные: геометрически равные до  \Doteq .

\вниз ¶

↓ Стрелка вниз, сходится (отношение). Похожий: \Downarrow двойная стрелка вниз.

\Вниз ¶

⇓ Двойная стрелка вниз (отношение). Похожий: \downarrow однострочная стрелка вниз.

\ell ¶

ℓ Строчная прописная буква l (обычная).

\пустой набор ¶

∅ Символ пустого набора (обычный). Вариант формы \varничего .

\эпсилон ¶

ϵ Строчный полулунный эпсилон (обычный). Похожий на Греческая текстовая буква. Более широко в математике используется сценарий small буква эпсилон \ varepsilon  ε. Связанный: установленное отношение принадлежности \in  ∈.

\экв ¶

≡ Эквивалентность (отношение).

\ эта ¶

η Строчная греческая буква (обычная).

\существует ¶

∃ Квантор существования (обычный).

плоский ¶

♭ Музыкальная квартира (обычная).

\ для всех ¶

∀ Универсальный квантификатор (обычный).

\хмуриться ¶

⌢ Изогнутая дуга вниз (обычная).

\Гамма ¶

Γ заглавная греческая буква (обычная).

\ гамма ¶

γ Строчная греческая буква (обычная).

\ge ¶

≥ Больше или равно (отношение). это синоним для \geq .

\geq ¶

≥ Больше или равно (отношение). это синоним для \ge .

\получает ¶

← Присваивается значение (отношение). Синоним:  \leftarrow .

\gg ¶

≫ Гораздо больше, чем (отношение). Аналогично: гораздо меньше чем \ll .

\hbar ¶

ℏ Постоянная Планка более двух пи (обычный).

\костюм ¶

♡ Карточная масть (обычная).

\hookleftarrow ¶

↩ Загнутая стрелка влево (отношение).

\hookrightarrow ¶

↪ Загнутая стрелка вправо (отношение).

\ тогда и только тогда, когда ¶

⟷ Если и только если (отношение). Это \Longleftrightarrow с \thickmuskip с обеих сторон.

\Im ¶

ℑ Мнимая часть (обычная). См.: реальная часть  \Re .

\имат ¶

Без точки i; используется, когда вы ставите ударение на i (см. Математические ударения).

\в ¶

∈ Элемент множества (отношение). Смотрите также: полумесяц в нижнем регистре epsilon  \epsilon ϵ и строчные буквы эпсилон \варэпсилон .

\ infty ¶

∞ Бесконечность (обычный).

\целое ¶

∫ Интеграл (оператор).

\йота ¶

ι Строчная греческая буква (обычная).

\Присоединить ¶

⨝ Сжатый символ галстука-бабочки (отношение). Недоступно в обычной версии ТеХ.

\jmath ¶

без точки j; используется, когда вы ставите ударение на j (см. Математические ударения).

\ каппа ¶

κ Строчная греческая буква (обычная).

\лямбда ¶

Λ заглавная греческая буква (обычная).

\лямбда ¶

λ Строчная греческая буква (обычная).

\ земля ¶

∧ Логическое и (двоичное). Синоним:  \клин . См. также логическое или  \ или .

\ угол ¶

⟨ Левый угол, или последовательность, скобка (отверстие). Похожий: меньше < . Соответствует  \rangle .

\lbrace ¶

{ Левая фигурная скобка (открытие). Синоним:  \{ . Соответствует \rbrace .

\lbrack ¶

[ Левая квадратная скобка (открывающаяся). Синоним:  [ . Соответствует \rbrack .

\lceil ¶

⌈ Левый потолочный кронштейн, как квадратный кронштейн, но с нижней сбрить (отверстие). Соответствует \rceil .

\ле ¶

≤ Меньше или равно (отношение). это синоним для \leq .

\ ведет к ¶

⇝ Волнистая стрелка вправо (отношение). Чтобы получить этот символ вне математического режима, вы можете поставить \newcommand*{\Leadsto}{\ensuremath{\leadsto}} в преамбулу, а затем используйте \ приводит к вместо этого.

\Стрелка влево ¶

⇐ Подразумевается двухстрочной стрелкой влево (отношение). Похожий: однострочная стрелка влево  \leftarrow .

\leftarrow ¶

← Однострочная стрелка влево (отношение). Синоним:  \получает . Аналогично: двойная линия слева стрелка  \стрелка влево .

\leftharpoondown ¶

↽ Гарпун однолинейный левый, шип под планкой (отношение).

\leftharpoonup ¶

↼ Однолинейный левый гарпун, зазубрина над перекладиной (отношение).

\Leftrightarrow ¶

⇔ Биимпликация; двухстрочная двунаправленная стрелка (отношение). Аналогично: однострочная двунаправленная стрелка \leftrightarrow .

\leftrightarrow ¶

↔ Однострочная двунаправленная стрелка (отношение). Похожий: двухлинейная двунаправленная стрелка \Стрелка влево .

\leq ¶

≤ Меньше или равно (отношение). это синоним для \le .

\ lэтаж ¶

⌊ Левый напольный кронштейн (отверстие). Совпадения:  \этаж .

\левый ¶

◁ Наконечник, то есть треугольник, указывающий влево (двоичный). Для обычного символа подгруппы вы должны загрузить amssymb и используйте \vartriangleleft (это отношение и так дает лучший интервал).

\ll ¶

≪ Гораздо меньше, чем (отношение). Аналогично: гораздо больше чем \gg .

\lне ¶

¬ Логическое отрицание (обычное). Синоним:  \neg .

\longleftarrow ¶

⟵ Длинная однострочная стрелка влево (отношение). Похожие: длинные двойная стрелка влево \Длинная левая стрела .

\longleftrightarrow ¶

⟷ Длинная однострочная двунаправленная стрелка (отношение). Похожие: длинные двухстрочная двунаправленная стрелка  \Longleftrightarrow .

\longmapsto ¶

⟼ Длинная однострочная стрелка влево, начинающаяся с вертикальной черты (связь). Аналогично: более короткая версия  \mapsto .

\longrightarrow ¶

⟶ Длинная однострочная стрелка вправо (отношение). Похожие: длинные двойная стрелка вправо  \длинная правая стрелка .

\или ¶

∨ Логическое или (двоичное). Синоним: \vee . См. также логические и \land .

\mapsto ¶

↦ Однострочная стрелка влево, начинающаяся с вертикальной черты (связь). Аналогично: более длинная версия  \longmaps to .

\mho ¶

℧ Проводимость, заглавная омега с полукругом (обычный).

\ середина ¶

∣ Однострочная вертикальная полоса (отношение). Типичное использование \mid для набора \{\, x \mid x\geq 5 \,\} .

Аналогично: \vert и | производят такие же однострочные символ вертикальной черты, но без интервала (они относятся к классу обычные), и вы не должны использовать их как отношения, а только как порядковые номера, т. е. символы сносок. Абсолютное значение см. в записи за 9 0225 \vert и норму см. в записи для  \vert .

\модели ¶

⊨ Предполагает или удовлетворяет; двойной турникет, короткая двойная черта (связь). Аналогично: длинное двойное тире \vDash .

\mp ¶

∓ Минус или плюс (отношение).

\mu ¶

μ Строчная греческая буква (обычная).

\набла ¶

∇ Дель Гамильтона, или дифференциальный оператор (обычный).

\ натуральный ¶

♮ Нотная натуральная запись (обычная).

\ne ¶

≠ Не равно (отношение). Синоним:  \neq .

¶

↗ Северо-восточная стрелка (отношение).

\neg ¶

¬ Логическое отрицание (обычное). Синоним:  \lnot . Иногда вместо этого используется отрицание:  \sim .

\neq ¶

≠ Не равно (отношение). Синоним:  \ne .

\ni ¶

∋ Эпсилон отраженного членства; имеет член (связь). Синоним:  \владеет . Аналогично: является членом из \в .

\ не ¶

    Длинный солид или косая черта, используемый для перечеркивания следующий оператор (отношение).

Доступно множество операторов с отрицанием, для которых не требуется \ не , особенно с пакетом amssymb . Например, \не типографически предпочтительнее \не\в .

\ не в ¶

∉ Не является элементом (отношения). Аналогично: не подмножество из  \nподмножество .

\nu ¶

ν Строчная греческая буква (обычная).

\nварроу ¶

↖ Стрелка северо-запад (отношение).

\одот ¶

⊙ Точка внутри круга (двоичная). Аналогично: переменный размер оператор \bigodot .

\ ¶

∮ Контурный интеграл, интеграл с окружностью посередине (оператор).

\Омега ¶

Ω заглавная греческая буква (обычная).

\омега ¶

ω Строчная греческая буква (обычная).

\оминус ¶

⊖ Знак минус или тире внутри круга (двоичный).

+ ¶

⊕ Знак плюс внутри круга (двоичный). Аналогично: переменный размер оператор \bigoplus .

\ослеш ¶

⊘ Солидус, или косая черта, внутри круга (бинарный).

\раз ¶

⊗ Знак времени или крестик внутри круга (двоичный). Похожий: оператор переменного размера \bigotimes .

\владеет ¶

∋ Эпсилон отраженного членства; имеет член (связь). Синоним:  \ni . Аналогично: является членом из \в .

\параллельно ¶

∥ Параллельно (отношение). Синоним:  \| .

\частичный ¶

∂ Частичный дифференциал (обычный).

\ перп ¶

⟂ Перпендикуляр (отношение). Аналогично:  \bot использует тот же глиф, но интервал другой, потому что он находится в классе обычный.

\Phi ¶

Φ Прописная греческая буква (обычная).

\фи ¶

ϕ Строчная греческая буква (обычная). Вариант формы \varphi φ.

\Pi ¶

Π заглавная греческая буква (обычная).

\pi ¶

π Строчная греческая буква (обычная). Вариант формы \варпи ϖ.

об/мин ¶

± Плюс или минус (двоичный).

\prec ¶

≺ предшествует (отношение). Аналогично: меньше < .

\preceq 9{\prime\prime\prime}$ , но использует гораздо меньше печатание. Вы можете использовать только \prime в математическом режиме. Использование права одинарная кавычка ' в текстовом режиме дает другой символ (апостроф).

\продукт ¶

∏ Продукт (оператор).

\propto ¶

∝ Пропорционально (отношению)

\пси ¶

Ψ заглавная греческая буква (обычная).

\psi ¶

ψ Строчная греческая буква (обычная).

\ угол ¶

⟩ Прямой угол, или последовательность, скобка (закрывающая). Аналогично: больше > . Совпадения: \langle .

\rbrace ¶

} Правая фигурная скобка (закрытие). Синоним:  \} . Соответствует \lbrace .

\rbrack ¶

] Правая квадратная скобка (закрытие). Синоним:  ] . Соответствует \lbrack .

\rceil ¶

⌉ Правый потолочный кронштейн (закрытие). Соответствует \lceil .

\Re ¶

ℜ Действительная часть, действительные числа, заглавная буква R (обычный). Связанный: двойная линия или полужирный шрифт, R  \mathbb{R} ; получить доступ это, загрузите пакет amsfonts .

\ ограничение ¶

↾, Ограничение функции (отношения). Синоним: \upharpoonright . Недоступно в простом TeX. В LaTeX вам нужно загрузить пакет amssymb .

\reemptyset ¶

⦰, Перевернутый символ пустого набора (обычный). Связанный: \varничего . Недоступно в простом TeX. В LaTeX вам нужно загрузить пакет stix .

\rэтаж ¶

⌋ Правый напольный кронштейн, правый квадратный кронштейн с верхним вырезом выключение (закрытие). Соответствует \lfloor .

\ правый ¶

◁ Наконечник, то есть треугольник, указывающий вправо (двоичный). Вместо обычного символа подгруппы вы должны загрузите amssymb и используйте \vartriangleright (который является отношение и, таким образом, дает лучший интервал).

\ро ¶

ρ Строчная греческая буква (обычная). Вариант формы \varrho ϱ.

\Стрелка вправо ¶

⇒ Подразумевает двойную стрелку, указывающую вправо. (связь). Аналогично: однострочная стрелка вправо \стрелка вправо .

\rightarrow ¶

→ Однострочная стрелка, указывающая вправо (отношение). Синоним: \to .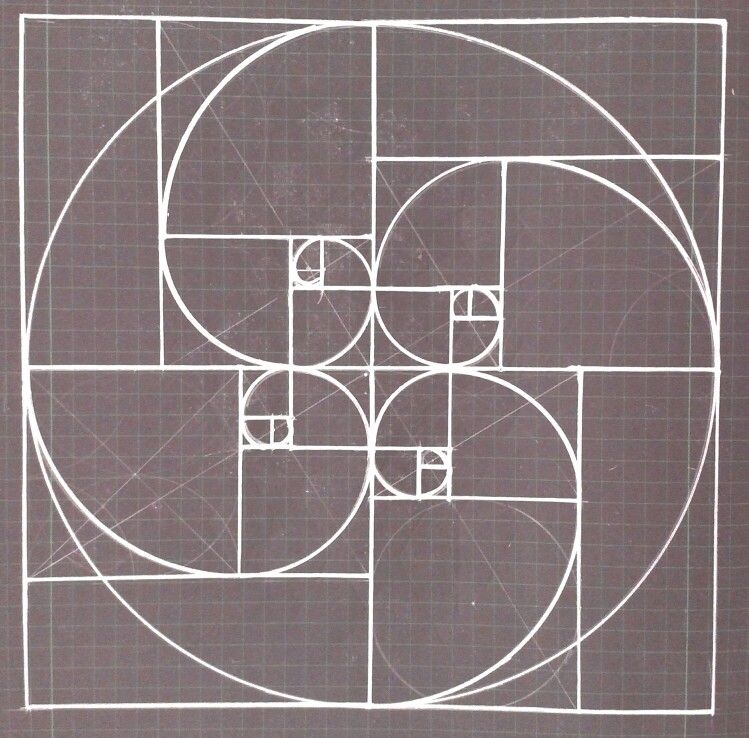 Аналогично: правая двойная линия стрелка \стрелка вправо .

\rightharpoondown ¶

⇁ Направленный вправо гарпун с зубцом внизу линия (отношение).

\rightharpoonup ¶

⇀ Направленный вправо гарпун с зубцом над линия (отношение).

\правыйлевыйгарпуны ¶

⇌ Правый гарпун вверх над левым гарпуном вниз (связь).

\серроу ¶

↘ Стрелка указывает на юго-восток (отношение).

\setminus ¶

⧵ Установить разность, обратную солидус или обратную косую черту, как \ (двоичный). Аналогично: обратная косая черта \обратная косая черта а также \textbackslash вне математического режима.

\ острый ¶

♯ Музыкальный диез (обыкновенный).

\Сигма ¶

Σ заглавная греческая буква (обычная).

\сигма ¶

σ Строчная греческая буква (обычная). Вариант формы \varsigma ς.

\sim ¶

∼ Подобный, в отношении (отношении).

\simeq ¶

≃ Подобный или равный, в отношении (отношении).

\маленький ¶

∫ Знак интеграла, который не меняется в большую сторону в дисплей (оператор).

\смайл ¶

⌣ Изогнутая вверх дуга, улыбка (обычная).

\пиджак ¶

♠ Пиковая масть (обычная).

\sqcap ¶

⊓ Символ пересечения квадратов (двоичный). Похожий: пересечение крышка .

\sqcup ¶

⊔ Символ объединения квадратов (двоичный). Похожий: штуцер чашка . Связанный: переменный размер оператор \bigsqcup .

\sqsubset ¶

⊏, Квадратный символ подмножества (отношение). Похожий: подмножество \подмножество . Недоступно в простом TeX. В LaTeX вам нужно загрузить 9Пакет 0225 amsymb .

\sqsubseteq ¶

⊑ Квадратное подмножество или символ равенства (двоичный). Аналогично: подмножество или равно \subseteq .

\sqsupset ¶

⊐, Квадратный символ надмножества (отношение). Похожий: надмножество \ надмножество . Недоступно в простом TeX. В LaTeX вам нужно загрузить пакет amssymb .

\sqsupseteq ¶

⊒ Квадратный надмножество или символ равенства (двоичный). Аналогично: надмножество или равное \supseteq .

\звезда ¶

⋆ Пятиконечная звезда, иногда используется как двойная. операция, но иногда зарезервированная для взаимной корреляции (бинарная). Аналогично: синонимы звездочка * и \ast , которые являются шестиконечными и чаще появляются в виде надстрочного или нижнего индекса, как со звездой Клини.

\ подмножество ¶

⊂ Подмножество (иногда подразумевается) (отношение).

\подмножество ¶

⊆ Подмножество или равно (отношение).

\succ ¶

≻ Приходит после, достигает успеха (отношение). Аналогично: меньше чем > .

\ успех ¶

⪰ Выполняется или равно (отношение). Аналогично: меньше больше или равно  \leq .

\сумма ¶

∑ Суммирование (оператор). Аналог: греческая столица сигма \ сигма .

\ смещение ¶

⊃ Надмножество (отношение).

\supseteq ¶

⊇ Надмножество или равно (отношение).

\сурд ¶

√ Радикальный символ (обычный). Команда LaTeX \sqrt{...} набирает квадратный корень аргумента с чертой который распространяется на аргумент.

\ ворона ¶

↙ Стрелка, указывающая на юго-запад (отношение).

\ тау ¶

τ Строчная греческая буква (обычная).

\тета ¶

θ Строчная греческая буква (обычная). Вариант формы \vartheta ϑ.

х ¶

× Знак умножения в начальной школе (двоичный). Видеть также \cdot .

\к ¶

→ Однострочная стрелка, указывающая вправо (отношение). Синоним:  \rightarrow .

\верх ¶

⊤ Вершина, наибольший элемент частично упорядоченного множества (обычный). См. также  \bot .

\ треугольник ¶

△ Треугольник (обычный).

\треугольник влево ¶

◁ Незаполненный треугольник, направленный влево (двоичный). Похожие: \левый . Для обычного символа подгруппы вы следует загрузить amssymb и использовать \vartriangleleft (который является отношением и поэтому дает лучший интервал).

\правый треугольник ¶

▷ Незакрашенный треугольник, направленный вправо (двоичный). Вместо обычного символа подгруппы вы должны загрузить amssymb и используйте \vartriangleright (это отношение и, таким образом, дает лучший интервал).

= unlhd ¶

⊴ Указывающая влево незаполненная подчеркнутая стрелка, т.е. треугольник с чертой под (бинарный). Для нормальная загрузка символа подгруппы amssymb и используйте \vartrianglelefteq (что является отношением и поэтому дает лучший интервал).

\ без правого колеса ¶

⊵ Указывающая вправо незаполненная подчеркнутая стрелка, т.е. треугольник с чертой под (бинарный). Для нормальная загрузка символа подгруппы amssymb и использовать \vartrianglerighteq (что является отношением и поэтому дает лучший интервал).

\Вверх ¶

⇑ Двойная стрелка, указывающая вверх (связь). Аналогично: однострочный, направленный вверх стрелка \вверхстрелка .

\стрелка вверх ¶

↑ Однострочная стрелка вверх, расходится (связь). Аналогично: двойная линия вверх стрелка  \ВверхСтрелка .

\Стрелка вверх вниз ¶

⇕ Двойная стрелка, указывающая вверх и вниз (связь). Аналогично: однострочный, направленный вверх и вниз стрелка \updownстрелка .

\updownarrow ¶

↕ Однострочная стрелка вверх и вниз (связь). Аналогично: двойная линия, направленная вверх и вниз. стрелка  \вверхстрелка .

\upharpoonright ¶

↾, Гарпун вверх, с зубцом справа (связь). Синоним: \ограничение . Недоступно в простом TeX. В LaTeX вам нужно загрузить пакет amssymb .

+ ¶

⊎ Multiset union, символ объединения со знаком плюс в средний (бинарный). Аналогично: союз \чашка . Связанный: оператор переменного размера \biguplus .

\Ипсилон ¶

Υ заглавная греческая буква (обычная).

\ипсилон ¶

υ Строчная греческая буква (обычная).

\varepsilon ¶

ε Эпсилон строчной буквы (обычный). Это более широко используется в математике, чем невариантная форма лунного эпсилона \эпсилон  ε. Связанный: установить членство \в .

\ничего ¶

∅, символ пустого набора. Аналогично: \emptyset . Связанный: \reemptyset . Недоступно в простом TeX. В LaTeX вам нужно загрузить 9Пакет 0225 amsymb .

\varphi ¶

φ Вариант строчной греческой буквы (обычный). Невариантная форма: \phi  ϕ.

\varpi ¶

ϖ Вариант строчной греческой буквы (обычный). Невариантная форма: \pi  π.

\варро ¶

ϱ Вариант строчной греческой буквы (обычный). Невариантная форма \ро р.

\варсигма ¶

ς Вариант строчной греческой буквы (обычный). Невариантная форма \сигма σ.

\vartheta ¶

ϑ Вариант строчной греческой буквы (обычный). Невариантная форма \ тета  θ.

\vdash ¶

⊢ Доказуемый; турникет, вертикальный и штриховой (связь). Аналогично: турникет повернулся полукруг \dashv .

¶

∨ Логическое или; нисходящая v-образная форма (бинарная). Связанный: логический и \клин . Аналогично: переменный размер оператор \bigvee .

\Верт ¶

‖ Вертикальная двойная перекладина (обычная). См. Разделители, как использовать пакет mathtools для создания символы норм.

\верт ¶

| Однострочная вертикальная полоса (обычная). Для «таких что», как и в определении множества, используйте  \mid потому что это является отношением. См. Разделители, чтобы узнать, как использовать математические инструменты . пакет для создания символов абсолютного значения гибкого размера.

\ клин ¶

∧ Логическое и (двоичное). Синоним:  \land . Смотрите также логический или \vee . Аналогично: переменный размер оператор \bigwedge .

\wp ¶

℘ Weierstrass p (обычный).

Вт ¶

≀ Сплетение (бинарный).

\Xi ¶

Ξ заглавная греческая буква (обычная).

\xi ¶

ξ Строчная греческая буква (обычная).

\дзета ¶

ζ Строчная греческая буква (обычная).

Следующие символы чаще всего используются в обычном тексте, но LaTeX предоставляет версии для использования в математическом тексте.

Что такое геометрия? — Определение Факты и примеры

Что такое геометрия

Геометрия — это раздел математики, изучающий размеры, формы, положения, углы и размеры объектов.

2D-фигуры в геометрии

Плоские фигуры, такие как квадраты, круги и треугольники, являются частью плоской геометрии и называются 2D-фигурами. Эти формы имеют только 2 измерения: длину и ширину.

Примеры двумерных фигур в плоской геометрии показаны ниже.

2D-формы могут быть дополнительно классифицированы как открытые и закрытые формы. Открытые формы могут быть определены как формы или фигуры, чьи отрезки линий и/или кривые не пересекаются. Они не начинаются и не заканчиваются в одной и той же точке. Замкнутые фигуры — это геометрические фигуры, которые начинаются и заканчиваются в одной и той же точке.

Трехмерные фигуры в геометрии

В геометрии трехмерная фигура может быть определена как сплошная фигура, объект или форма, имеющая три измерения: длину, ширину и высоту. В отличие от двумерных фигур трехмерные фигуры имеют толщину или глубину.

Атрибутами трехмерной фигуры являются грани, ребра и вершины. Три измерения составляют края трехмерной геометрической формы.

Куб, прямоугольная призма, сфера, конус и цилиндр — основные трехмерные формы, которые мы видим вокруг себя.

Угол

В геометрии угол можно определить как фигуру, образованную двумя лучами, сходящимися в одной точке. Угол обозначается символом ∠. Углы измеряются в градусах (°) с помощью транспортира. Например, 45 градусов представляются как 45°.

Углы классифицируются в зависимости от их размеров как:

1. Острый угол меньше 90°.
2. Тупой угол составляет от 90° до 180°.
3. Прямой угол точно равен 90°.
4. Угол, равный точно 180°, является прямым углом.
5. Угол рефлекса составляет от 180° до 360°.
6. Полный угол равен 360°.

Вершина фигуры, где два ребра встречаются, образуя угол. Различные фигуры в геометрии имеют разные меры угла.

Например, :

• Треугольник — это трехсторонняя фигура, а сумма трех его внутренних углов равна 180˚
• Квадрат, прямоугольник или четырехугольник — это четырехсторонние фигуры, и сумма их четырех внутренних углов составляет 360˚
• Другие многоугольники, такие как пятиугольник, шестиугольник, семиугольник, восьмиугольник, имеют соответственно 5, 6, 7, 8 сторон и различные углы.

Примеры различных многоугольников с их углами и сторонами показаны ниже.

Мы изучаем различные аспекты форм, такие как измерение углов, длины сторон, площади, объема и т. д. в геометрии. Подобие и конгруэнтность — два важных аспекта геометрии.

Сходство : Сходство — это когда две формы одинаковы, но их размеры могут различаться.

Конгруэнтность : Конгруэнтность — это когда две фигуры совершенно одинаковы по форме и размеру.

Координатная плоскость:

• Координатная плоскость — это двумерная поверхность, образованная с помощью двух числовых линий, которые пересекают друг друга под прямым углом.
• Горизонтальная числовая линия — это ось x, а вертикальная числовая линия — ось y.
• Пересечение двух осей — это координата (0,0).
• Используя координатную плоскость, мы рисуем точки, линии и т. д. Соединяя различные точки на координатной плоскости, мы можем создавать формы.

Мы используем формулу и теорему для решения задач по геометрии.

Формула — это математическое уравнение для решения задачи геометрии, а теорема — это утверждение, которое доказывается с использованием ранее известных фактов.

Например, « Теорема Пифагора » доказала, что a2+b2=c2 для прямоугольного треугольника, где a и b — стороны прямоугольного треугольника, а c — гипотенуза.

Однако, a2+b2=c2 — это формула для нахождения гипотенузы прямоугольного треугольника.

Забавные факты

— Слово «геометрия» образовано от греческих слов «гео», означающих «земля», и «метрия», означающих «измерение».

Решенные примеры

1. Является ли данная фигура примером простой замкнутой кривой, которая также является многоугольником?

Решение:

Замкнутая фигура, которая не пересекает сама себя, является простой замкнутой кривой. Многоугольники — это замкнутые формы, образованные только прямыми линиями, такие как треугольники, прямоугольники, пятиугольники и т. д.

Данная фигура изогнута и состоит не только из прямых линий, это не многоугольник.

2. В треугольнике ABC с прямым углом в точке B, если ∠C=45°, какова мера ∠A?  

Решение: △ ABC — заданный прямоугольный треугольник с ∠B=90°.

Сумма углов треугольника = 180°

∠A+∠B+∠C=180°

∠A+∠C=180°-90°=90°

Но, ∠C=45° отсюда ∠A =90°-45°=45°

3. Определите плоские поверхности в данной призме.  

Решение:

Плоские поверхности призмы представлены ниже:

Прямоугольник AECB, прямоугольник DCEF, прямоугольник ABDF образуют прямоугольные грани призмы.

△ BCD и △ AEF образуют треугольные грани призмы.

Практические задачи

A

B

C

D

Правильный ответ: B
Замкнутая фигура, которая не пересекает сама себя, является простой замкнутой кривой. У него одинаковые начальная и конечная точки.

A

B

C

D

Правильный ответ: D
Данная фигура является трехмерной и называется кубом.

10 сторон и 10 углов

12 сторон и 10 углов

5 сторон и 5 углов

18 сторон и 5 углов

Правильный ответ: 10 сторон и 10 углов
Звездообразная фигура 0 состоит из 1 прямых линий . Таким образом, у него 10 сторон и 10 углов.

Часто задаваемые вопросы

Какая связь между математикой и геометрией?

Математика — это общий термин для различных дисциплин, в которых основное внимание уделяется логике и абстрактным понятиям. Геометрия — один из разделов математики, изучающий формы и размеры фигур и их свойства.

Каковы некоторые приложения геометрии?

Геометрия может применяться во многих областях, таких как архитектура, электроника, машиностроение и строительство. Его также можно использовать в таких областях, как наука, для разработки проектов или программ по исследованию космоса.

В чем основное различие между 2D и 3D формами?

Основное различие между 2D- и 3D-фигурами заключается в отсутствии глубины или высоты в 2D-фигурах. Это плоские фигуры. Трехмерные формы существуют в трех измерениях с длиной, шириной и высотой и не кажутся плоскими.

В чем разница между алгеброй и геометрией?

Алгебра — это раздел математики, в котором переменные в виде букв используются в качестве чисел или величин в уравнениях и формулах. Геометрия — это раздел математики, изучающий размеры, формы, положение, углы и размеры вещей.

геометрия | Определение, история, основы, отрасли и факты

математики греко-римского мира

Смотреть все СМИ

Ключевые люди:

Блез Паскаль Евклид Птолемей Пьер де Ферма Бернхард Риманн

Похожие темы:

топология Евклидова геометрия аналитическая геометрия дифференциальная геометрия проективная геометрия

Просмотреть весь связанный контент →

геометрия , раздел математики, изучающий форму отдельных объектов, пространственные отношения между различными объектами и свойства окружающего пространства. Это одна из старейших областей математики, возникшая в ответ на такие практические задачи, как геодезия, и ее название происходит от греческих слов, означающих «измерение Земли». В конце концов стало понятно, что геометрия не должна ограничиваться изучением плоских поверхностей (геометрия плоскостей) и жестких трехмерных объектов (геометрия тел), но что даже самые абстрактные мысли и образы могут быть представлены и развиты в геометрических терминах.

Эта статья начинается с краткого описания основных разделов геометрии, а затем переходит к обширному историческому анализу. Для получения информации о конкретных разделах геометрии см. Евклидова геометрия, аналитическая геометрия, проективная геометрия, дифференциальная геометрия, неевклидовы геометрии и топология.

Основные разделы геометрии

В некоторых древних культурах была разработана форма геометрии, приспособленная к отношениям между длинами, площадями и объемами физических объектов. Эта геометрия была систематизирована Евклидом в Элементы около 300 г. до н.э. на основе 10 аксиом или постулатов, из которых несколько сотен теорем были доказаны дедуктивной логикой. Элементов олицетворяли аксиоматико-дедуктивный метод на протяжении многих веков.

Аналитическая геометрия была инициирована французским математиком Рене Декартом (1596–1650), который ввел прямоугольные координаты для определения местоположения точек и для того, чтобы линии и кривые могли быть представлены алгебраическими уравнениями. Алгебраическая геометрия — это современное расширение предмета на многомерные и неевклидовы пространства.

Викторина по Британике

Дайте определение: математические термины

Вот ваша миссия, если вы решите ее принять: Дайте определение следующим математическим терминам до того, как истечет время.

Проективная геометрия была создана французским математиком Жираром Дезаргом (1591–1661) для изучения тех свойств геометрических фигур, которые не изменяются при проецировании их изображения или «тени» на другую поверхность.

Немецкий математик Карл Фридрих Гаусс (1777–1855) в связи с практическими задачами съемки и геодезии положил начало дифференциальной геометрии. Используя дифференциальное исчисление, он охарактеризовал внутренние свойства кривых и поверхностей. Например, он показал, что внутренняя кривизна цилиндра такая же, как у плоскости, в чем можно убедиться, разрезав цилиндр вдоль его оси и сплющив, но не такая, как у сферы, которую нельзя сплющить без искажение.

Оформите подписку Britannica Premium и получите доступ к эксклюзивному контенту. Подпишитесь сейчас

Начиная с 19-го века, различные математики заменяли альтернативами постулат параллельности Евклида, который в его современной форме гласит: «данные линия и точка, не лежащие на прямой, можно провести ровно одну прямую через данная точка параллельна прямой». Они надеялись показать, что альтернативы логически невозможны. Вместо этого они обнаружили, что существуют непротиворечивые неевклидовы геометрии.

Топология

Топология, самый молодой и сложный раздел геометрии, фокусируется на свойствах геометрических объектов, которые остаются неизменными при непрерывной деформации — сжатии, растяжении и складывании, но не разрыве. Непрерывное развитие топологии началось с 1911 г., когда голландский математик Л.Э.Й. Брауэр (1881–1966) представил методы, обычно применимые к этой теме.

История геометрии

Самые ранние известные недвусмысленные примеры письменных источников — датируемые Египтом и Месопотамией около 3100 г. до н. контейнеры. Начиная примерно с VI века до н.0019 гео («Земля») и метрон («мера») для измерения Земли.

В дополнение к описанию некоторых достижений древних греков, в частности логического развития геометрии Евклидом в Элементах , в этой статье рассматриваются некоторые приложения геометрии в астрономии, картографии и живописи от классической Греции до средневекового ислама и Европы эпохи Возрождения. . Он завершается кратким обсуждением расширений неевклидовой и многомерной геометрии в современную эпоху.

Древняя геометрия: практическая и эмпирическая

Происхождение геометрии лежит в заботах повседневной жизни. Традиционное описание, сохранившееся в «Истории » Геродота (5 век до н. э.), приписывает египтянам изобретение геодезии для восстановления стоимости собственности после ежегодного разлива Нила. Точно так же стремление узнать объемы твердых цифр проистекало из необходимости оценивать дань, хранить нефть и зерно, строить плотины и пирамиды. Даже три непонятные геометрические задачи древности — удвоить куб, разделить угол на три части и возвести в квадрат круг, все из которых будут обсуждаться позже — вероятно, возникли из практических вопросов, из религиозного ритуала, хронометража и строительства, соответственно, в догреческих обществ Средиземноморья. И главный предмет позднейшей греческой геометрии, теория конических сечений, обязан своим общим значением, а может быть, и своим происхождением, своему применению к оптике и астрономии.

Хотя многие древние люди, известные и неизвестные, внесли свой вклад в эту тему, никто не мог сравниться с влиянием Евклида и его Элементов геометрии, книги, которой уже 2300 лет и которая является объектом столь же болезненного и кропотливого изучения, как Библия. Однако о Евклиде известно гораздо меньше, чем о Моисее. На самом деле, единственное, что известно с достаточной степенью достоверности, это то, что Евклид преподавал в Александрийской библиотеке во времена правления Птолемея I (323–285/283 до н. э.). Евклид писал не только по геометрии, но и по астрономии и оптике, а может быть, и по механике и музыке. Только Элементы , которые были тщательно скопированы и переведены, сохранились нетронутыми.

Элементы Евклида были настолько полны и ясно написаны, что буквально стерли работу его предшественников. То, что известно о греческой геометрии до него, исходит главным образом из фрагментов, цитируемых Платоном и Аристотелем, а также более поздними математиками и комментаторами. Среди других ценных предметов они сохранили некоторые результаты и общий подход Пифагора ( c. 580– в. 500 до н.э.) и его последователи. Пифагорейцы убедили себя, что все вещи являются числами или обязаны своими отношениями числам. Учение придавало математике первостепенное значение в исследовании и понимании мира. Платон развил подобный взгляд, и философы, находившиеся под влиянием Пифагора или Платона, часто восторженно писали о геометрии как о ключе к толкованию вселенной. Таким образом, древняя геометрия ассоциировалась с возвышенным, дополняя свое земное происхождение и свою репутацию образца точного рассуждения.

Нахождение прямого угла

Древние строители и геодезисты должны были уметь строить прямые углы в полевых условиях по требованию. Метод, применяемый египтянами, принес им в Греции прозвище «дергальщики каната», по-видимому, потому, что они использовали веревку для выкладки своих строительных инструкций. Один из способов, которым они могли использовать веревку для построения прямоугольных треугольников, заключался в том, чтобы пометить веревку с петлями узлами, чтобы, если ее удерживать за узлы и туго натягивать, веревка образовывала прямоугольный треугольник. Самый простой способ выполнить трюк — взять веревку длиной 12 звеньев, завязать 3 звена с одного конца и еще 5 звеньев с другого конца, а затем связать концы вместе, чтобы получилась петля. Однако египетские писцы не оставили нам указаний об этих процедурах, а тем более намеков на то, что они знали, как их обобщить, чтобы получить теорему Пифагора: квадрат на прямой, противоположной прямому углу, равен сумме квадратов на двух других. стороны. Точно так же ведические писания древней Индии содержат разделы, называемые sulvasutra s, или «правила веревки», для точного расположения жертвенных алтарей. Требуемые прямые углы были сделаны из веревок, размеченных для получения триад (3, 4, 5) и (5, 12, 13).

В вавилонских глиняных табличках ( ок. 1700–1500 гг. до н. э.) современные историки обнаружили задачи, решения которых указывают на то, что теорема Пифагора и некоторые специальные триады были известны более чем за тысячу лет до Евклида. Однако случайный прямоугольный треугольник вряд ли будет иметь все стороны, измеряемые одной и той же единицей измерения, то есть каждая сторона будет целым числом, кратным некоторой общепринятой единице измерения. Этот факт, который был шокирован, когда его обнаружили пифагорейцы, породил концепцию и теорию несоизмеримости.

Обнаружение недоступного

Согласно древней традиции, Фалес Милетский, живший до Пифагора в 6 веке до н.э., изобрел способ измерения недоступных высот, таких как египетские пирамиды. Хотя ни одно из его сочинений не сохранилось, Фалес, возможно, хорошо знал о вавилонском наблюдении, что для подобных треугольников (треугольников, имеющих одинаковую форму, но не обязательно одинаковый размер) длина каждой соответствующей стороны увеличивается (или уменьшается) на одно и то же кратное число. Древние китайцы пришли к измерению недоступных высот и расстояний другим путем, используя «дополнительные» прямоугольники, как показано на следующем рисунке, который, как можно показать, дает результаты, эквивалентные результатам греческого метода с использованием треугольников.

Оценка богатства

Вавилонская клинописная табличка, написанная около 3500 лет назад, посвящена проблемам плотин, колодцев, водяных часов и раскопок. В нем также есть упражнение с круглыми ограждениями с подразумеваемым значением π = 3. Подрядчик бассейна царя Соломона, который построил пруд 10 локтей в поперечнике и 30 локтей вокруг (3 Царств 7:23), использовал то же значение. Однако евреи должны были взять свое π у египтян до того, как переплыли Красное море, ибо папирус Райнда ( с. 2000 г. до н.э.; наш основной источник древнеегипетской математики) подразумевает π = 3,1605.

Знание площади круга имело практическое значение как для чиновников, следивших за данью фараона, так и для строителей алтарей и бассейнов. Ахмес, писец, скопировавший и комментировавший папирус Райнда ( ок. 1650 гг. до н. э.), может многое сказать о цилиндрических зернохранилищах и пирамидах, целых и усеченных. Он мог вычислить их объемы, и, как следует из того, что он взял египетские секед , горизонтальное расстояние, связанное с вертикальным подъемом в один локоть, как определяющая величина для наклона пирамиды, он кое-что знал о подобных треугольниках.

Требования к теме (A-G) | Приемная комиссия Калифорнийского университета

Чтобы соответствовать минимальным требованиям для поступления, вы должны пройти 15 летних курсов средней школы с буквенной оценкой C или выше — не менее 11 из них до вашего последнего года обучения в средней школе.

Имейте в виду, что посещение утвержденных курсов средней школы (A-G) — не единственный способ выполнить эти требования. Вы также можете встретить их, закончив курсы в колледже или набрав определенные баллы на различных приемлемых экзаменах.

A) История 

Утвержденные UC курсы средней школы

Два года истории, в том числе:

• один год всемирной истории, культуры или исторической географии (может быть один годичный курс или два односеместровых курса ), и
• один год истории США или полтора года истории США и полтора года гражданского общества или американского правительства

Экзамен AP или IB

История США: 3, 4 или 5 баллов на экзамене AP по истории США; оценка 5, 6 или 7 на экзамене IB History of the Americas HL.

Правительство США: 3, 4 или 5 баллов на экзамене AP соответствуют полугодовому обучению.

Всемирная история/культура/география: 3, 4 или 5 баллов на экзамене AP по европейской истории, всемирной истории (2020 г. и ранее), современной всемирной истории (2021 г. и позже) или географии человека; оценка 5, 6 или 7 на экзамене IB History HL или Geography HL

Курсы колледжа

История США: оценка C или выше за переносимый курс из 3 или более семестров (4 или более четвертей) единиц по истории США; оценка C или выше по переводному курсу из 3 или более семестров (4 или более четвертей) единиц по гражданскому праву или американскому правительству соответствует требованиям на один семестр.

Всемирная история/культура/география: оценка C или выше по переводному курсу из 3 или более семестров (4 или более четверти) по всемирной истории, культуре и географии

B) английский язык

средняя школа, утвержденная UC курсы

Четыре года подготовки к колледжу английского языка, которые включают в себя частое письмо, от мозгового штурма до итоговой работы, а также чтение классической и современной литературы. Для выполнения этого требования можно использовать не более одного года курсов типа ESL.

 

Экзамен по предмету SAT

Литература: 560 баллов удовлетворяют требованиям первых трех лет.

Экзамен AP или IB

Оценка 3, 4 или 5 на экзамене AP по английскому языку и сочинению или по английской литературе и сочинению; 5, 6 или 7 баллов на экзамене IB HL English: Literature (ранее IB HL English A1)

Курсы колледжа

За каждый год, необходимый до 11-го класса, оценка C или выше по курсу колледжа, который не подлежит переводу из 3 или более семестровых (4 или более квартальных) единиц по английскому сочинению, литературе (американской или английской) или иностранной литературе в переводе. Курсы, используемые для удовлетворения четвертого года обучения и/или всего требования, должны быть переносимыми. Для перевода в более низкий дивизион все курсы должны быть переводными. Курсы литературы должны включать существенную работу по композиции.

C) Математика

Утвержденные UC курсы средней школы

Три года подготовки к колледжу по математике, которые включают темы, охватываемые элементарной и продвинутой алгеброй, а также двумерной и трехмерной геометрией. Должен быть пройден курс геометрии или интегрированный курс математики с достаточным объемом содержания геометрии. Утвержденные интегрированные математические курсы могут использоваться для выполнения части или всего этого требования, как и математические курсы, изучаемые в седьмом и восьмом классах, если средняя школа признает их эквивалентными своим собственным курсам; также приемлемы курсы, посвященные ранее упомянутым областям содержания и включающие или объединяющие вероятность, статистику или тригонометрию. Курсы, предназначенные для 11-го и/или 12-го класса, могут удовлетворять требуемому третьему или рекомендуемому четвертому году предметного требования, если они утверждены как углубленный курс математики.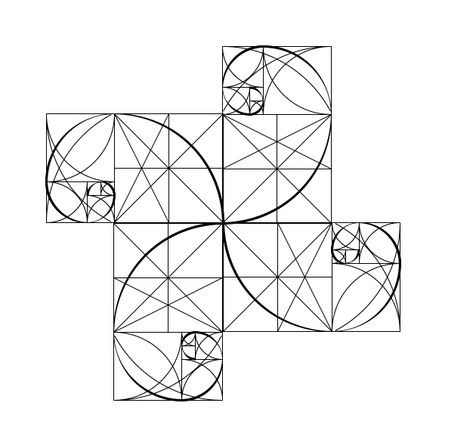

 

Экзамен AP или IB

Оценка 3, 4 или 5 на статистическом экзамене AP соответствует элементарной и промежуточной алгебре.

Оценка 3, 4 или 5 на экзамене AP по исчислению AB или исчислению BC соответствует двухлетнему требованию (но не геометрии).

Оценка 5, 6 или 7 на экзамене IB Mathematics HL соответствует двухлетнему требованию (но не геометрии).

Курсы колледжа

Три семестра (4 четверти) непереводимых курсов колледжа по элементарной алгебре, геометрии, промежуточной алгебре или тригонометрии с оценкой C или выше удовлетворяют одному году требований по математике.

Оценка C или выше по переводному курсу математики, состоящему не менее чем из 3 семестров (4 четверти), который включает в себя промежуточную алгебру в качестве предварительного условия, удовлетворяет двухлетнему требованию (но не геометрии).

ПРИМЕЧАНИЕ. Все учащиеся должны пройти курс геометрии или интегрировать математику с содержанием геометрии. Один переводной курс колледжа не будет соответствовать требованиям по математике за три года.

D) Наука

Утвержденные UC курсы средней школы

Два года подготовки к поступлению в колледж, включая или объединяя темы, которые дают фундаментальные знания по двум из этих трех предметов: биологии, химии или физике. Один год утвержденной междисциплинарной курсовой работы или курсовой работы по наукам о Земле и космосе может соответствовать одному году требований. Курсы информатики, инженерии, прикладных наук можно использовать в области D в качестве дополнительных наук (т. е. третий год и далее).

Экзамен AP или IB

Оценка 3, 4 или 5 на любых двух экзаменах AP по биологии, химии, физике (B, C, 1 или 2) и науке об окружающей среде; 5, 6 или 7 баллов за любые два экзамена IB HL по биологии, химии или физике

Курсы колледжа

За каждый год выполнения требования оценка C или выше по переводному курсу, состоящему не менее чем из 3 семестров (4 четверти) по естественным (физическим или биологическим) наукам с не менее 30 часами лабораторных работ ( не «демонстрация»)

E) Язык, отличный от английского

Утвержденные UC курсы средней школы

Требуется два года или эквивалент 2-го уровня обучения в средней школе на том же языке, кроме английского. (Рекомендуется три года/3-й уровень обучения в средней школе). Курсы должны подчеркивать разговорную речь и понимание, а также включать обучение грамматике, лексике, чтению, сочинению и культуре. Допустимы американский язык жестов и классические языки, такие как латынь и греческий, а также языки коренных американцев. Курсы, пройденные в седьмом и восьмом классах, могут использоваться для выполнения части или всего этого требования, если средняя школа признает их эквивалентными своим собственным курсам.

Экзамен по предмету SAT

Следующие баллы удовлетворяют всем требованиям:

• Китайский язык с аудированием: 520
• Французский/Французский с аудированием: 540
• Немецкий/немецкий с аудированием: 510
• Современный иврит: 470
• Итальянский: 520
• Японский с аудированием: 510
• Корейский с прослушиванием: 500
• Латинский: 530
• Испанский/Испанский с прослушиванием: 520

Экзамен AP или IB

Оценка 3, 4 или 5 на экзамене AP по китайскому языку и культуре, французскому языку и культуре, немецкому языку и культуре, итальянскому языку и культуре, японскому языку и культуре, испанскому языку, испанскому языку и культуре, испанской литературе и Культура или латынь; 5, 6 или 7 баллов на экзамене IB Language A2 HL.

Курсы колледжа

Оценка C или выше по любому переводному(ым) курсу(ам) (за исключением разговорной речи), проводимому колледжем, приравнивается к двум годам изучения языка в средней школе. Многие колледжи перечисляют обязательные условия для второго языкового курса как «Язык 1 в этом колледже или два года изучения языка в средней школе». В этом случае язык 1 очищает оба года требования.

F) Изобразительное и исполнительское искусство

Утвержденные UC курсы средней школы

Один годичный курс изобразительного и исполнительского искусства, выбранный из следующих дисциплин: танец, музыка, театр, изобразительное искусство или междисциплинарное искусство — или два одно- также допустимы семестровые курсы по той же дисциплине.

Экзамен AP или IB

Оценка 3, 4 или 5 на экзамене AP History of Art, Studio Art или Music Theory;
баллов из 5, 6 или 7 на любом экзамене IB HL по танцам, кино, музыке, театральному искусству или изобразительному искусству

Курсы колледжа

Оценка C или выше по любому переводному курсу из 3 семестров (4 четверти), который явно относится к одной из четырех дисциплин изобразительного/исполнительского искусства: танец, драма/театр, музыка или изобразительное искусство

G) Подготовительный к колледжу факультатив

Утвержденные UC курсы средней школы

Один год (два семестра) выбираются из курсов, относящихся к факультативной (G) предметной области, или курсов, выходящих за рамки тех, которые используются для удовлетворения требований предметов AF.

Предметный экзамен SAT

История США: 550 баллов

Всемирная история: 540 баллов

Письмо/английское сочинение или литература: 560 баллов

Математика Уровень 2: 520 баллов Требование категории «D»): те же тесты и баллы, что и в разделе «D» выше

Французский/Французский с аудированием: 590

немецкий/немецкий с аудированием: 570

Современный иврит: 500

Итальянский: 570

Японский с аудированием: 570

Корейский с аудированием: 550

Латинский: 580

Испанский/Испанский с прослушиванием: 570

Второй язык, кроме английского: те же тесты и баллы, что и в разделе «E» Психология, правительство США или сравнительное правительство; 5, 6 или 7 баллов на любом экзамене IB HL по экономике, философии, психологии, социальной и культурной антропологии или информатике

Курсы колледжа

Оценка C или выше по переводным курсам колледжа продолжительностью не менее 3 семестров (4 четверти) сверх тех, что перечислены выше, как соответствующие любому из требований «A-F».

Цифровые переходы #2: Математические действия сетки

«Наши классы становятся безбумажными». Это утверждение ходит по классам, но что оно означает для учащихся с нарушениями зрения и слепоты? Как мы можем помочь нашим учащимся с VIB осуществить этот цифровой переход, особенно когда речь идет о математических концепциях? Традиционно математика предоставляется в тактильном формате для учащихся K-12, умеющих читать по Брайлю; тем не менее, материалы о карьере в колледже и STEM обычно представлены только в цифровом формате. Как мы готовим наших студентов к этому цифровому переходу — переходу от бумажных материалов к цифровым материалам? Как только учащиеся поймут основную концепцию использования тактильных материалов, как мы можем научить этих академических студентов применять те же самые основополагающие концепции для доступа к цифровым математическим материалам?

Давайте начнем с того, что более подробно рассмотрим, как традиционно обучать базовым математическим навыкам «сетки» и как перенести концепции сетки с тактильных материалов на цифровые материалы.

Определения

• Числовая линия: — это прямая линия, отмеченная цифрами, которая часто используется для ответов на вопросы о сложении и вычитании.
• Сетка:  равномерно разделенных и расположенных на равном расстоянии друг от друга квадратов на фигурной или плоской поверхности.
• Математическая сетка: — это другое название координатной плоскости, состоящей из пространства маленьких квадратов, иногда с осью X и осью Y.
• Координатная сетка: Координатная сетка состоит из двух перпендикулярных линий или осей, помеченных как числовые линии. Горизонтальная ось называется осью x . Вертикальная ось называется осью Y . Точка пересечения оси x и оси y называется началом координат . Числа на координатной сетке используются для определения местоположения точек. Каждая точка может быть идентифицирована упорядоченной парой чисел; то есть число по оси x называется координатой x, а число по оси y называется координатой y. Упорядоченные пары записываются в скобках (координата x, координата y).

Упорядоченные пары обычно вводятся в классах 3 ^rd или 4 ^th , а графические уравнения — в классах 4 ^th или 5 ^th .

Традиционные образовательные ресурсы тактильной сетки

• Бумага с сеткой: APH Bold Line Tactile Graph Sheets Артикул 1-04080-00
• Графическое пособие APH Grid для математики (резиновый коврик в рамке с тиснением в виде сетки 34 X 30 из квадратов размером ½ дюйма.  В комплект входят три плоских пружинных провода, 14 нажимных штифтов и резиновые ленты.  Номер изделия: 1-00460-01
• Наклейки с номерами для настольных компьютеров APH Advanced Номер позиции 1-03482-00; (Также доступны расходуемые числовые строки как с крупным шрифтом, так и шрифтом Брайля/тактильным шрифтом.)

Дополнительные ресурсы тактильной сетки

• Настольная игра «Морской бой» — это классическая тактильная игра, в которой есть сетка, боевые корабли и колышки, которые используются для обозначения того, где игрок пытался найти/потопить боевой корабль. Игроки называют номер строки и столбца, пытаясь найти спрятанный линкор противника.
• Сетка Lego: учителя могут создавать быстрые тактильные представления сеток, используя основу Lego и блоки Lego. Вместо того, чтобы использовать буквы, как в кроссворде, предложите учащимся найти определенные символы/блоки Lego и определить их координаты. Попросите учащихся поместить персонажа в определенное место.
• Тактильно-кроссворд Брайля Используя деревянную доску и кусочки букв Брайля, создавайте слова в формате вверх-вниз или из стороны в сторону. В комплект входит деревянная доска с 10 рядами, 13 столбцами и 99 пластиковых плиток с буквами Брайля. Этот кроссворд предназначен для игры в слова. Однако игровая доска на самом деле представляет собой сетку, которую можно использовать для обучения концепциям сетки. Обязательно используйте номера строк и столбцов при обсуждении точек на сетке. Тактильное обозначение строк и столбцов может быть полезным для многих учащихся.
• Кроссворды часто являются забавным способом для учащихся выучить словарные слова, правописание слов и другие занятия по языковым искусствам. Когда классу дают печатный или цифровой кроссворд, научите своего ученика отвечать на кроссворд, сначала используя бумажные сетки, где вы можете быстро тактильно отметить пустые места. Не забудьте указать номера строк и столбцов. При необходимости используйте тактильный маркер (например, крошечную пенопластовую точку на липкой основе), чтобы обозначить начало слова.
• Традиционный кроссворд: в большинстве кроссвордов для обозначения строк или столбцов используются четные и нечетные числа. Студент, изучающий шрифт Брайля, должен иметь только одно слово, начинающееся в строке или строке. Пример. Если строки состоят из нечетных чисел, а слово начинается в строке 3, то соответствующее определение слова будет помечено цифрой 3. Учащийся будет знать, что первая буква его ответа будет начинаться с первого свободного места в строке 3. . Вторая буква будет справа от первой, все еще в строке 3. Если ответ представляет собой четное число 2, учащийся найдет первое свободное место в столбце 2, а вторая буква ответа будет добавлена ​​ниже первое письмо.
• Для младших школьников используйте наклейки Feel ‘n Peel от APH (буквы Брайля, артикул 1-08846-00) или используйте буквы Брайля, созданные учителем, чтобы учащиеся могли «приклеить» букву в правильном месте, а не пытаться выровнять и напечатать шрифт Брайля. письмо в кроссворде.
• Модифицированный кроссворд: измените кроссворд вашего ученика, используя «строка, столбец» (два числа, например «3,4», обозначающие 3 ^rd row, 4 ^th столбец) вместо четных и нечетных чисел.

Дополнительные кроссворды

• Попросите вашего ученика поместить определенную букву в определенное место. Пример: поместите букву D в 2,3.
• Расшифруй слова. Пример: Поместите букву D в 2,3. Поместите букву О в 2,4. Поместите букву G в 2,5. Что это значит?
• Составляйте слова по буквам, находя буквы, случайно расположенные на доске. Пример. Разместите 10 букв, разбросанных по доске. Дайте студенту координаты и пусть он найдет письмо. Поместите буквы, чтобы написать загадочное слово.
• Учитель кладет букву в определенное место. Студента просят назвать координаты.

Советы по обучению

• В частности, научите, что ряды перемещаются (вправо или влево) по прямой линии, а столбцы перемещаются вверх и вниз. Координаты строки перечислены первыми, за которыми следуют координаты столбца.
• Всегда вводите макет сетки — сколько строк и столбцов? Учащимся нужно предложить сначала изучить макет, назвав количество строк и столбцов. При использовании цифровых сеток программа чтения с экрана всегда должна сначала вводить макет сетки. (Обычно замещающий текст для изображения сетки должен предоставлять макет сетки, как только она появляется.  Если вы — учитель — создаете цифровую сетку, обязательно включите макет сетки в письменное описание сетки или в альтернативный текст, если сетка является изображением.)
• При создании сетки обязательно удалите неиспользуемые строки или столбцы. Пример. Если вы используете бумажную сетку 4 × 5, отрежьте дополнительные строки и столбцы. Для физических досок закройте области, которые не используются, так как это поможет учащимся развить представление о размере. Учащиеся узнают, что доска 4×5 намного меньше, чем доска 10×12.
• Если сетка 4×5, учащийся должен сразу распознать координаты четырех углов. 1,1 (вверху слева), 4,1 (внизу слева), 1,5 (вверху справа), 4,5 (внизу справа).
• Определите цель занятия, а затем обязательно научите/подчеркните эту цель на протяжении всего занятия. Целью может быть обучение макету сетки и отношениям внутри этого макета сетки, например координатам четырех углов.
• Обучая учащихся концепциям сетки, начинайте с очень простых, конкретных действий, соответствующих возрасту. Учащиеся детского сада должны быть представлены числовой прямой перед сеткой. Представляя сетку, учащиеся могут найти символ в определенном месте на доске Lego и назвать соответствующие номера строк и столбцов. Затем учащийся может поместить фигурку на доску Lego и назвать числа, и/или учитель может назвать числа, а учащийся помещает фигурку на это место. Следующий шаг может состоять в том, чтобы учащиеся разгадывали очень простой кроссворд с пятью просматриваемыми словами. Учащимся не следует знакомить с сетками, когда они изучают алгебру и должны рисовать уравнения!
• Обязательно обсудите со студентами, что координатная сетка часто начинается с обозначения оси Y снизу вверх, а координаты расположены в порядке «x, y». Между тем, таблицы и другие сетки часто начинают маркировку сверху вниз, и программы чтения с экрана объявляют строку, а затем столбец.
• Учащимся должно быть удобно читать письменную разметку сетки и координаты, а также слушать разметку сетки с координатами; учащиеся должны быть в состоянии разработать мысленную карту сетки. Помните, что цель состоит в том, чтобы обеспечить прочную основу решеток с помощью конкретных тактильных действий И научить учащегося слушать и понимать информацию решеток!
• Свяжите сетку с функциональными маршрутами и действиями O&M; изначально можно использовать тактильные карты. Пример. Район имеет размеры 3 на 4 квартала. Школа находится в верхнем левом углу. Заправка находится в правом верхнем углу. Сколько улиц вам нужно пересечь?
• Концепции сетки аналогичны концепциям таблиц. Студенты, которые понимают сетки, должны быть в состоянии перенести эти навыки на концепции таблиц. Таблицы в основном организованы как сетки, но включают заголовки строк и заголовки столбцов.

Цифровые игры, включающие грид-концепции

• Боулинг с завязанными глазами: приложение для iOS – это бесплатное приложение для iOS, которое обучает/развивает пространственные концепции и ментальную картографию. Вместо квадратной/прямоугольной сетки, как в обычных сетках, в этой игре используется сетка треугольной формы. (Кегли для боулинга имеют треугольную форму и пронумерованы.) Дополнительную информацию о боулинге с завязанными глазами, включая тактильные упражнения для обучения пространственному расположению, см. в публикации Боулинг с завязанными глазами: Приложение iOS Spatial Concepts.
• Приложение Blindfold Connect – это бесплатное приложение для iOS, похожее на популярную игру Connect Four. Эта игра укрепляет/обучает пространственным концепциям/ментальному картированию. Blindfold Connect использует сетку (обычно сетка 7 × 6). Проведите пальцем вправо или влево, чтобы перемещаться по столбцам. Нажмите дважды, чтобы поместить красную шашку в столбец. Цель состоит в том, чтобы получить линию из красных шашек в один столбец до того, как ваш компьютерный противник создаст линию из черных шашек.
• 3D Крестики-нолики с завязанными глазами от Blindfold Games — это бесплатное приложение для iOS, похожее на классическую игру «Крестики-нолики», за исключением того, что это приложение выполнено в 3D. Теперь доступно!
• Blindfold Sea Battle от Blindfold Games – бесплатное приложение для iOS, похожее на классическую игру Морской бой.
• Игры с кодированием . Есть несколько замечательных концептуальных игр по программированию для младших школьников; однако эти игры обычно недоступны для программ чтения с экрана. В «Пути к технологии» есть множество постов о программировании. Swift Playgrounds, бесплатная игра Apple по программированию, доступна; однако Swift Playgrounds немного более продвинутый и не предназначен для обучения основным понятиям сетки.

Многие из этих игр с кодированием включают в себя «путь», и игроки дают команды для перемещения влево, вправо, вверх или вниз по квадратам на этом пути. Эти игры часто имеют сетку. Создание тактильных сеток с отправной точкой и пунктом назначения, включающих пути, стены, препятствия, поможет разработать мысленную концепцию этих игр с кодированием. Учащиеся должны определить, на сколько квадратов нужно двигаться в каждом направлении. Lego — отличный ресурс для быстрого воссоздания таких игр по кодированию, чтобы учащиеся могли изучить основные концепции кодирования.

• CodeQuest , созданный командой студентов Университета Северной Каролины, теперь представляет собой бесплатное, полностью доступное концептуальное приложение для iOS, предназначенное для молодых студентов, доступное через APH. Узнайте больше о CodeQuest здесь.

• Sonokids apps — несколько приложений, которые будут включать в себя концепции памяти/пространства, сетки, таблицы и многое другое! ОБНОВЛЕНИЕ 27.10.17: Sonokids только что выпустила Ballyland Sound Memory — приложение для сопоставления iOS, которое включает основные концепции сетки со строками и столбцами! Для получения дополнительной информации перейдите к сообщению Paths to Technology, Ballyland Sound Memory Game: Matching & Grids.

ЭиТО Подсказка: учащиеся уже применяют пространственные навыки, мысленное картирование и другие «математические» навыки ежедневно, путешествуя по маршрутам ЭиТО. Обязательно соедините уроки O&M с этими уроками математики/сетки!

 Смотри вперед! Какие более высокие математические навыки потребуются вашим ученикам в старшей школе, колледже и в областях STEM? Подумайте о навыках построения графиков, которые потребуются вашим учащимся для изучения алгебры, — заложите основу прямо сейчас с помощью понятий сетки, ментального картографирования и пространственных понятий.

No related posts.