Шпаргалка: площадь многоугольников для геометрии 8 класса, формулы нахождения площади треугольника, квадрата, ромба, параллелограмма
31 августа, 2022
1 мин
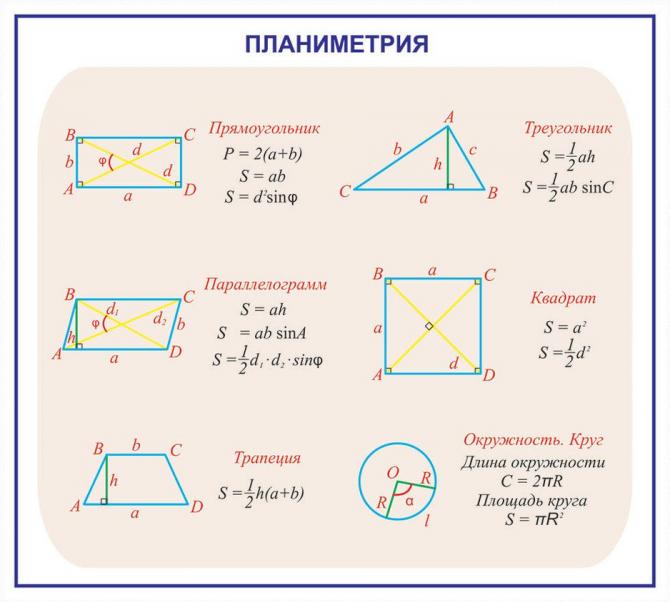
Треугольник
- Площадь треугольника по основанию и высоте: S=1/2 a⋅h
- Площадь треугольника по двум сторонам и углу между ними: S=1/ a⋅b⋅sinα
- Площадь треугольника по радиусу описанной окружности и трём сторонам: S = 4R/a⋅b⋅c
- Площадь треугольника по формуле Герона: S = √p(p — a)(p — b)(p — c). Где p — полупериметр, a,b,c — стороны треугольника.
- Площадь равностороннего треугольника по стороне: S = √3/4a²
- Площадь прямоугольного треугольника по двум катетам: S= ½ a • b
- Площадь прямоугольного треугольника по отрезкам, на которые делит гипотенузу вписанная окружность: S = d • e. Где d и e — отрезки гипотенузы.
Параллелограмм
- Площадь параллелограмма по основанию и высоте: S = a • h
- Площадь параллелограмма по двум сторонам и углу между ними: S = a⋅b⋅sinα
Ромб (он же параллелограмм, у которого все стороны равны и в который можно вписать окружность)
- Площадь ромба по вписанной окружности и стороне: S = 2 • a • r
Прямоугольник и квадрат
- Площадь прямоугольника через две стороны: S = a • b
- Площадь квадрата: S = a²
Если вы нашли ошибку, пожалуйста, выделите фрагмент текста и нажмите Ctrl+Enter. Мы обязательно поправим!
Мы обязательно поправим!
Редакция Без Сменки
Честно. Понятно. С душой.
44 подписчиков
+ Подписаться
Редакция Без Сменки
15 июня, 2022
1 мин
Физ 🔬
Угловая скорость
Каждая точка вращающегося вокруг оси тела, проходящей через точку О, движется по окружности, и. ..
..
Редакция Без Сменки
13 июня, 2022
1 мин
Био 🦠
Что здесь происходит? Давайте всмотримся детально в рисунок: 1️⃣ Солнышко в углу — значит…
Редакция Без Сменки
15 июня, 2022
1 мин
Инф 💻
Дел
📌 Необходимо найти наименьшее А при котором следующее неравенство будет истинно: (Дел(х, А)/\Дел…
Редакция Без Сменки
01 июля, 2022
1 мин
Лит 📚
Как отличить ямб от хорея?
Жили-были два потомственных котика 🐈🐈: старый, пожилой, очень знаменитый котик Иван и совсем ещё.
Подпишитесь на еженедельную рассылку полезных материалов про ЕГЭ, высшее образование и вузы и получите скидку на курсы Вебиума
Домашняя работа по геометрии за 9 класс к учебнику «Геометрия. 7-9 класс» А.В.Погорелов§14. Площади фигур
Решебники и ГДЗ
Начните вводить часть условия (например, могут ли, чему равен или найти):
- № 1. Докажите, что сумма площадей квадратов, построенных на катетах прямоугольного треугольника, равна площади квадрата, построенного на гипотенузе.
- № 2. Стороны двух участков земли квадратной формы равны 100 ми 150 м. Найдите сторону квадратного участка, равновеликого им.
- № 3. Найдите площадь квадрата S по его диагонали а.
- № 4. Во сколько раз площадь квадрата, описанного около окружности, больше площади квадрата, вписанного в ту же окружность?
- № 5. Как изменится площадь квадрата, если каждую его сторону увеличить в 3 раза?
- № 6.
 Во сколько раз надо уменьшить стороны квадрата, чтобы его площадь уменьшилась в 25 раз?
Во сколько раз надо уменьшить стороны квадрата, чтобы его площадь уменьшилась в 25 раз? - № 7. Чему равны стороны прямоугольника, если они относятся как 4:9, а его площадь 144 м2?
- № 8. Чему равны стороны прямоугольника, если его периметр 74 дм, а площадь 3 м2 ?
- № 9. Параллелограмм и прямоугольник имеют одинаковые стороны. Найдите острый угол параллелограмма, если площадь его равна половине площади прямоугольника.
- № 10. Квадрат и ромб имеют одинаковые периметры. Какая из фигур имеет большую площадь? 0бъясните ответ.
- № 11. Найдите площадь ромба, если его высота 10 см, а острый угол 30°.
- № 12. Найдите площадь ромба, если его высота 12 см, а меньшая диагональ 13 см.
- № 13. Докажите, что площадь ромба равна половине произведения диагоналей.
- № 14. Найдите, стороны ромба, зная, что его диагонали относятся как 1:2, а площадь ромба равна 12 см2.
- № 15. Разделите данный треугольник на три равновеликие части прямыми, проходящими через одну вершину.

- № 16*. Решите предыдущую задачу, взяв вместо треугольника параллелограмм.
- № 17. Чему равна площадь равнобедренного треугольника, если его основание 120 м, а боковая сторона 100 м? ΔАВС — равнобедренный, АВ = ВС = 100 м, АС = 120 м.
- № 18. Найдите площадь равнобедренного прямоугольного треугольника с гипотенузой а. Рассмотрим ΔАВС, ∠С = 90°, ВС = АС, АВ = а — гипотенуза.
- № 19. У треугольника со сторонами 8 см и 4 см проведены высоты к этим сторонам. Высота, проведенная к стороне 8 см, равна 3 см. Чему равна высота, проведенная к стороне 4 см?
- № 20. Докажите, что стороны треугольника обратно пропорциональны его высотам, т.е.:
- № 21. Найдите площадь равностороннего треугольника со стороной а.
- № 22. Найдите площадь правильного треугольника, вписанного вкруг радиуса 5.
- № 23. Найдите площадь прямоугольного треугольника, если его высота делит гипотенузу на отрезки 32 см и 18 см.
- № 24.
 Чему равны катеты прямоугольного треугольника, если его гипотенуза равна 73 см, а площадь равна 1320 см2?
Чему равны катеты прямоугольного треугольника, если его гипотенуза равна 73 см, а площадь равна 1320 см2? - № 25. У треугольника ABС АС = а, ВС = E. При каком угле С площадь треугольника будет наибольшей?
- № 26. Найдите площадь равнобедренного треугольника, у которого боковые стороны равны 1 м, а угол между ними равен 70°.
- № 27. Найдите площадь параллелограмма, если его стороны 2 ми 3 м, а один из углов равен 70°.
- № 28*. Найдите площадь треугольника по стороне a и прилежащим к ней углам а и b.
- № 29. Выведите формулу Герона для площади треугольника:
- № 30. Найдите площадь треугольника по трем сторонам:
- № 31. Стороны треугольника а, b, с. Найдите высоту треугольника, опущенную на сторону с.
- № 32. Боковые стороны треугольника 30 см и 25 см. Найдите высоту треугольника, опущенную на основание, равное: 1) 25 см; 2) 11 см.
- № 33. Периметр равнобедренного треугольника равен 64 см, а его боковая сторона на 11 см больше основания.
 Найдите высоту треугольника, опущенную на боковую сторону.
Найдите высоту треугольника, опущенную на боковую сторону. - № 35. Найдите высоту треугольника со сторонами
- № 36. Найдите наименьшую высоту треугольника со сторонами: 1) 5, 5, 6; 2) 17,65, 80 и наибольшую высоту
- № 37. Найдите площадь трапеции, у которой параллельные стороны 60 см и 20 см, а непараллельные — 13 см и 37 см.
- № 38. В равнобокой трапеции основания равны 10 см и 24 см, боковая сторона 25 см. Найдите площадь трапеции.
- № 39. В равнобокой трапеции большее основание равно 44 м, боковая сторона 17 ми диагональ 39 м. Найдите площадь трапеции.
- № 41*. Докажите, что среди всех параллелограммов сданными диагоналями наибольшую площадь имеет ромб.
- № 42. Выведите следующие формулы для радиусов описанной (R) и вписанной (r) окружностей треугольника:
- № 43. Найдите радиусы описанной (5) и вписанной (г) окружностей для треугольника со сторонами: 1) 13, 14, 15; 2) 15, 13, 4; 3) 35, 29, 8; 4) 4, 5, 7.
 1) а = 13, b = 14, с = 15. Полупериметр треугольника:
1) а = 13, b = 14, с = 15. Полупериметр треугольника: - № 44. Боковая сторона равнобедренного треугольника 6 см, высота, проведенная к основанию, 4 см. Найдите радиус описанной окружности. Пусть АВС — равнобедренный треугольник, АВ = ВС =
- № 45. Найдите радиусы окружностей описанной около равнобедренного треугольника с основанием а и боковой стороной b и вписанной в него.
- № 46. Найдите радиус г вписанной и радиус 5 описанной окружностей для равнобедренного треугольника с основанием 10 см и боковой стороной 13 см.
- № 47. Докажите, что в прямоугольном треугольнике радиус вписанной окружности равен половине разности между суммой катетов и гипотенузой.
- № 48. Катеты прямоугольного треугольника равны 40 см и 42 см. Найдите радиусы описанной и вписанной окружностей.
- № 49. Докажите, что площадь многоугольника, описанного около окружности, равна половине произведения периметра многоугольника на радиус окружности.
- № 50.
 Через середину высоты треугольника проведена перпендикулярная к ней прямая. В каком отношении она делит площадь треугольника? Пусть ΔАВС, ВН — высота, ВО = ОН.
Через середину высоты треугольника проведена перпендикулярная к ней прямая. В каком отношении она делит площадь треугольника? Пусть ΔАВС, ВН — высота, ВО = ОН. - № 51. Прямая, перпендикулярная высоте треугольника, делит его площадь пополам. Найдите расстояние от этой прямой до вершины треугольника, из которой проведена высота, если она равна А.
- № 52. Периметры правильных n-угольников относятся как а:b. Как относятся их площади?
- № 53. Найдите площадь круга, если длина окружности l.
- № 54. Найдите площадь кругового кольца, заключенного между двумя окружностями с одним и тем же центром и радиусами: 1) 4 см и 6 см; 2) 5,5 ми 6,5 м; 3) а и b, а > b.
- № 55. Во сколько раз увеличится площадь круга, если его диаметр увеличить: 1) в 2 раза; 2) в 5 раз; 3) в m раз? Если диаметр увеличить в n раз, то радиус увеличится тоже в n раз, тогда площадь увеличится в n2 раз.
- № 56. Найдите отношение площади круга к площади вписанного в него: 1) квадрата; 2) правильного треугольника; 3) правильного шестиугольника.
 1) Пусть ABCD — квадрат, вписанный вкруг.
1) Пусть ABCD — квадрат, вписанный вкруг. - № 57. Найдите отношение площади круга, вписанного в правильный треугольник, к площади круга, описанного около него.
- № 58. Найдите отношение площади круга, описанного около квадрата, к площади круга,вписанного в него.
- № 59. Найдите площадь сектора круга радиуса R, если соответствующий этому сектору центральный угол равен: 1) 40°; 2) 90°; 3) 150°; 4) 240°; 5) 300°; 6) 330°.
- № 60. Дана окружность радиуса 5. Найдите площадь сектора, соответствующего дуге с длиной, равной: 1) R, 2) l.
- № 61*. Найдите площадь кругового сегмента с основанием a√3 и высотой — a/2.
- № 62. Найдите площадь той части круга, которая расположена вне вписанного в него: 1) квадрата; 2) правильного треугольника; 3) правильного шестиугольника. Радиус круга 5. 1)
Поиск по сайту
Геометрия Часть 7: Площадь и периметр
Автор: cindyelkins
C. Elkins, OK Math and Reading Lady
Сегодняшняя тема — измерение площади и периметра.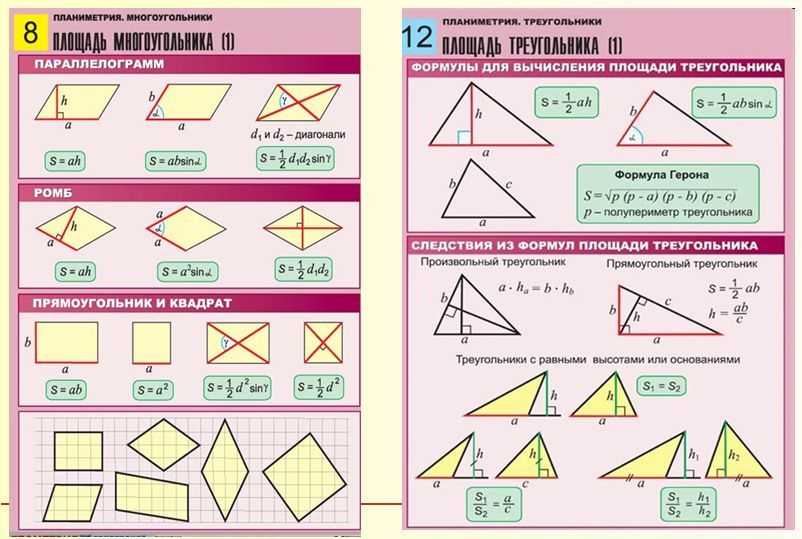 Хотя их можно считать стандартами измерения, они тесно связаны с геометрией (например, атрибуты прямоугольника). Прочтите предыдущие посты в моей серии «Геометрия» (составление и разложение), чтобы узнать о других упоминаниях площади и периметра.
Хотя их можно считать стандартами измерения, они тесно связаны с геометрией (например, атрибуты прямоугольника). Прочтите предыдущие посты в моей серии «Геометрия» (составление и разложение), чтобы узнать о других упоминаниях площади и периметра.
Неправильные представления открывают окно в детское мышление. Если мы заранее узнаем о неправильных представлениях, мы можем направить наше обучение и направления, чтобы помочь студентам избежать их. Я рассмотрю несколько неправильных представлений и некоторые стратегии и/или уроки, которые могут их исправить. Заблуждения № 1-2 появляются в этом посте. Заблуждения № 3-5 будут представлены в посте на следующей неделе.
Заблуждение №1: Учащийся слышит это: «Мы используем площадь для измерения внутри фигуры и периметр для измерения вокруг фигуры».
- Проблема: Учащийся не знает, как применить это определение к реальным ситуациям, требующим измерения площади и/или периметра.
- Проблема: Учащийся может подумать: «Поскольку периметр измеряет внешний край, то площадь означает измерение внутреннего края».

- Проблема: Учащиеся путают два термина.
Идеи:
Заблуждение № 2 : Учащийся слышит это: «Чтобы найти площадь, умножьте длину на ширину».
- Проблема: Учащийся не знает правила умножения.
- Проблема: Учащийся не знает, какие размеры являются длиной и шириной.
Идеи:
- Хорошее руководство: длина l — это l верхняя сторона. Ширина — самая короткая сторона.
- Длина и ширина равны двум , примыкающих к сторонам (не противоположным сторонам).
- Покажите, как разбить прямоугольник на квадраты. Если прямоугольник имеет размер 4″ x 2″, покажите им, как сделать 4 столбца и 2 строки. Смотрите, как они это делают. Многие ученики рисовали внутри 4 вертикальные линии, чтобы получились столбцы, и 2 горизонтальные линии, чтобы получились строки. Это, очевидно, приведет к набору квадратов 5 x 3, но учащиеся не всегда проверяют.
 Знают ли они — «Чтобы разделить прямоугольник на 4 столбца, мне нужно провести всего 3 линии». Теперь подсчет квадратов — не самый эффективный метод, но он может помочь учащимся, которые борются с концепцией или фактами умножения.
Знают ли они — «Чтобы разделить прямоугольник на 4 столбца, мне нужно провести всего 3 линии». Теперь подсчет квадратов — не самый эффективный метод, но он может помочь учащимся, которые борются с концепцией или фактами умножения. - Некоторые прямоугольники слишком велики, чтобы в них можно было рисовать квадраты. Если учащиеся не знают фактов умножения, прямоугольник можно разделить на 2 (или более) меньших прямоугольника, используя известные им факты. Затем площадь каждого меньшего прямоугольника складывается вместе, чтобы найти общую площадь. Для примера см. изображение под . Опять же, учащиеся должны подключиться к геометрии, чтобы понять, что противоположные стороны прямоугольника равны.
- Пример. Прямоугольник имеет размеры 8 x 7. Используя более известные факты, разбейте одно из измерений на 2 слагаемых (например, разбейте 7 на 5 + 2). Разделите прямоугольник на 2 прямоугольника и используйте 5 + 2, чтобы обозначить одну сторону (вместо 7). Используя концепцию распределительного свойства, учащийся вычисляет следующее: 8 x 7 = 8 (5 + 2) = (8 x 5) + (8 x 2) = 40 + 16 = 56 кв.
 единиц.
единиц.
- Пример. Прямоугольник имеет размеры 8 x 7. Используя более известные факты, разбейте одно из измерений на 2 слагаемых (например, разбейте 7 на 5 + 2). Разделите прямоугольник на 2 прямоугольника и используйте 5 + 2, чтобы обозначить одну сторону (вместо 7). Используя концепцию распределительного свойства, учащийся вычисляет следующее: 8 x 7 = 8 (5 + 2) = (8 x 5) + (8 x 2) = 40 + 16 = 56 кв.
Заблуждение №3: Учащийся видит только 2 заданных числа на изображении прямоугольника и не знает, складывать их или умножать.
- Проблема: Учащийся не знает свойств прямоугольника, применимых к этой ситуации, — что противоположные стороны равны по размеру.
- Проблема: Учащийся не понимает, как подсчет квадратов может помочь в вычислении площади и периметра.
Заблуждение № 4: Учащийся слышит следующее: «Запишите размер площади как квадратных дюймов , а размер периметра как дюймов». Примечание. Это относится к использованию таких единиц измерения, как см, футы, метры, ярды, мили и т. д.
- Проблема: Учащийся не понимает разницы между квадратными и неквадратными измерениями.
Заблуждение №5: Учащиеся думают, что между площадью и периметром может существовать связь. Они могут думать, что все фигуры с одинаковой площадью имеют одинаковый периметр.
Они могут думать, что все фигуры с одинаковой площадью имеют одинаковый периметр.
- Проблема. Это означает, что если одна фигура имеет площадь 12 квадратных дюймов и периметр 16 дюймов, они могут подумать, что все фигуры с площадью 12 имеют периметр 16 дюймов.
Следующее сообщение: Идеи по устранению заблуждений № 3, 4 и 5 и ссылки на действия в области и по периметру!! Оставайтесь с нами
Рубрика: Площадь и периметр, Геометрия / Измерение, Математика
Tagged площадь, геометрия, математические заблуждения, измерение, периметр
· 16 февраля
Базовая геометрия – Как найти площадь сложных фигур – Complete Test Preparation Inc.
- Сообщение от Брайан Стокер
- Дата 9 октября 2017 г.
Как найти площадь сложных фигур
Сложные фигуры можно разделить на несколько меньших фигур, для которых известна формула периметра или площади, а затем сложить их.
Пример.
 Составные двухмерные фигуры
Составные двухмерные фигуры
Чтобы определить площадь любой составной фигуры, просто введите ADD площади каждой составной базовой фигуры. Обязательно запишите свой окончательный ответ в квадратных единицах.
Определить площадь заданной фигуры.
Исходную форму можно перерисовать как прямоугольник и треугольник. У прямоугольников противоположные стороны конгруэнтны (совершенно одинаковые).
Площадь Составной = Площадь Треугольник + Площадь Прямоугольник
Площадь Треугольник = (1/2)(Основание)(Высота) = (1/2)(3м)(1,5м) = 2,25 м 2
Площадь Прямоугольник = (Основание)(Высота) = (3 м)(1,5 м) = 4,5 м 2
Площадь Композит = (2,25 м 2 ) + (4,5 м 2 ) = 6,75 м
06 2 Как найти площадь сложной фигуры Чтобы определить площадь поверхности любого составного тела, просто добавьте площадей поверхности каждого составного основного тела. Вы также должны вычесть площадь любой внутренней грани. Обязательно запишите свой окончательный ответ в квадратных единицах.
Вы также должны вычесть площадь любой внутренней грани. Обязательно запишите свой окончательный ответ в квадратных единицах.
Пример. Определить площадь поверхности данной фигуры. Оставьте окончательный ответ в терминах числа пи.
Исходная форма может быть перерисована в виде цилиндра и конуса. Нам придется вычесть площадь круга, где встречаются фигуры, из каждого уравнения площади поверхности, потому что они находятся «внутри» твердого тела.
SurfaceArea Composite = S.Area Конус + S.Area Цилиндр
S.Area Cone = (Basic Area)+(1/2)(ightPerimeter) )(dπ)(h) = (1/2)(6π)(2) = 6π футов 2
S. Площадь Цилиндр = 2(Площадь основания)+(Периметр)(Высота) = (πr 2 )+(dπ)(h) = (π3 2 )+(6π)( 5) = 39π FT 2
S.Area Композит = (6π FT 2 ) + (39π FT 2 ) = 45π FT 2
.
 вопросы по геометрии на стандартизированных тестах:
вопросы по геометрии на стандартизированных тестах: - Решить недостающий угол или сторону
- Нахождение площади или периметра различных фигур (например, треугольников, прямоугольников, кругов)
- Задачи с использованием теоремы Пифагора
- Расчет свойств геометрических фигур, таких как углы, прямые углы или параллельные стороны
- Расчет объема или площади поверхности сложных форм, например сфер, цилиндров или конусов
- Решение геометрических преобразований, таких как вращение, перемещение или отражение
Самые популярные вопросы по геометрии
Общие вопросы по геометрии в стандартизированных тестах:
- Найдите недостающий угол или сторону
- Нахождение площади или периметра различных фигур (например, треугольников, прямоугольников, кругов)
- Задачи с использованием теоремы Пифагора
- Расчет свойств геометрических фигур, таких как углы, прямые углы или параллельные стороны
- Расчет объема или площади поверхности сложных форм, например сфер, цилиндров или конусов
- Решение геометрических преобразований, таких как вращение, перемещение или отражение
Автор: , Брайан Стокер, Массачусетс, Complete Test Preparation Inc.

 Во сколько раз надо уменьшить стороны квадрата, чтобы его площадь уменьшилась в 25 раз?
Во сколько раз надо уменьшить стороны квадрата, чтобы его площадь уменьшилась в 25 раз?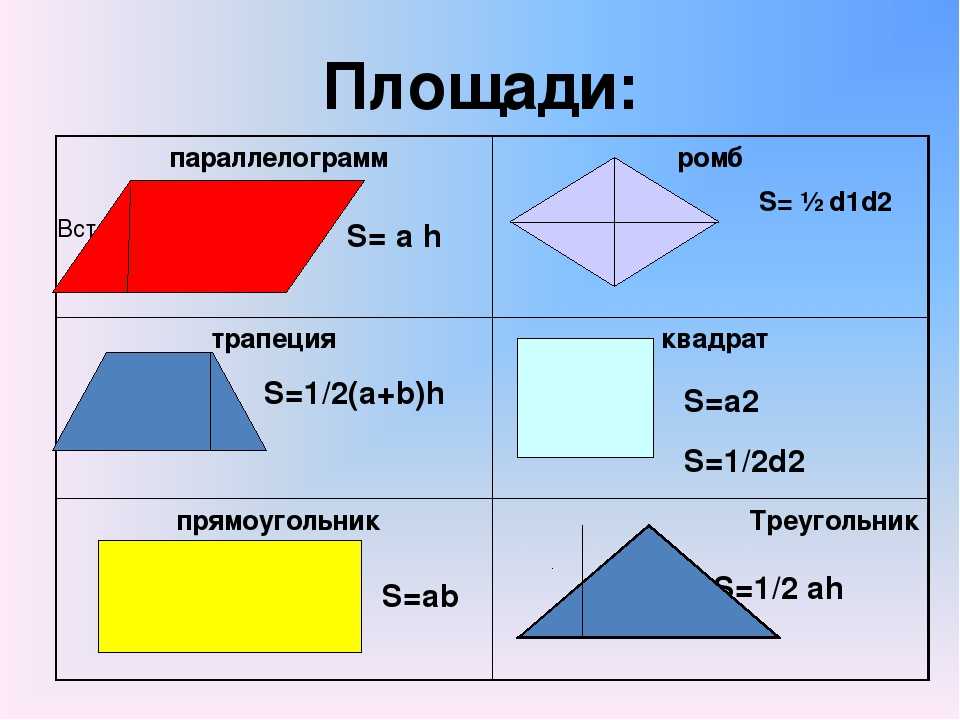
 Чему равны катеты прямоугольного треугольника, если его гипотенуза равна 73 см, а площадь равна 1320 см2?
Чему равны катеты прямоугольного треугольника, если его гипотенуза равна 73 см, а площадь равна 1320 см2? Найдите высоту треугольника, опущенную на боковую сторону.
Найдите высоту треугольника, опущенную на боковую сторону.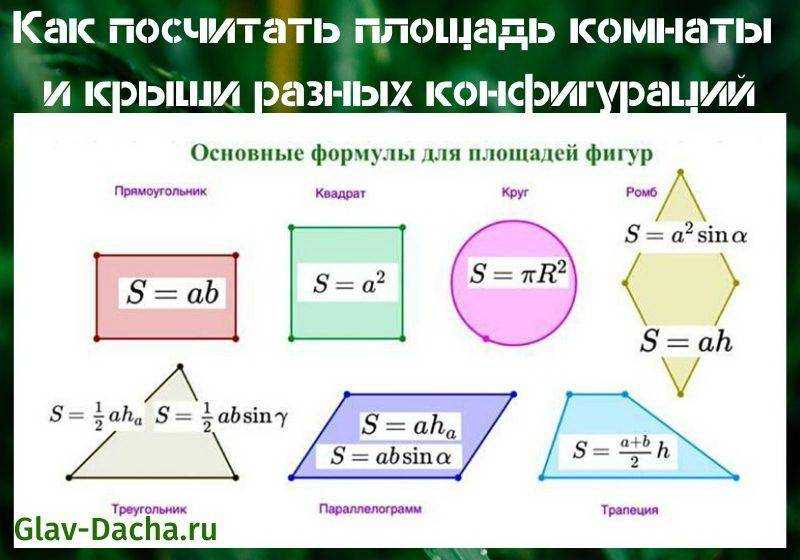 1) а = 13, b = 14, с = 15. Полупериметр треугольника:
1) а = 13, b = 14, с = 15. Полупериметр треугольника: Через середину высоты треугольника проведена перпендикулярная к ней прямая. В каком отношении она делит площадь треугольника? Пусть ΔАВС, ВН — высота, ВО = ОН.
Через середину высоты треугольника проведена перпендикулярная к ней прямая. В каком отношении она делит площадь треугольника? Пусть ΔАВС, ВН — высота, ВО = ОН.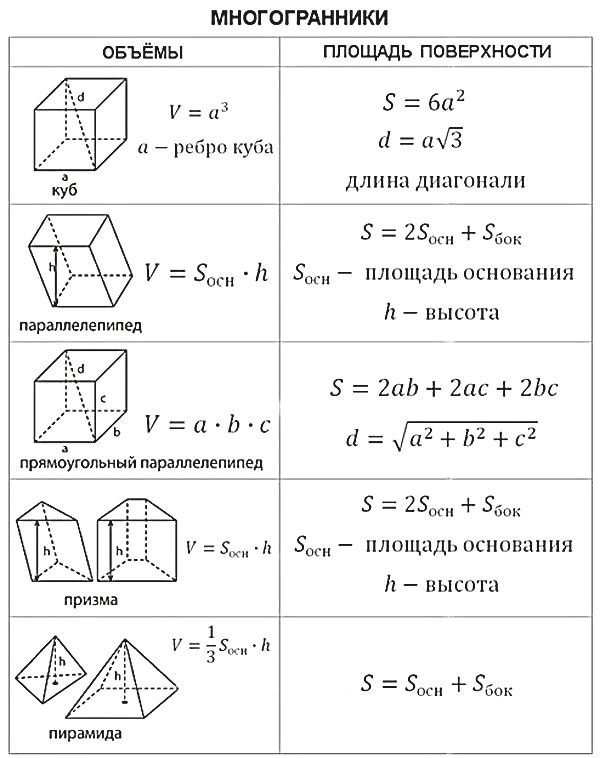 1) Пусть ABCD — квадрат, вписанный вкруг.
1) Пусть ABCD — квадрат, вписанный вкруг.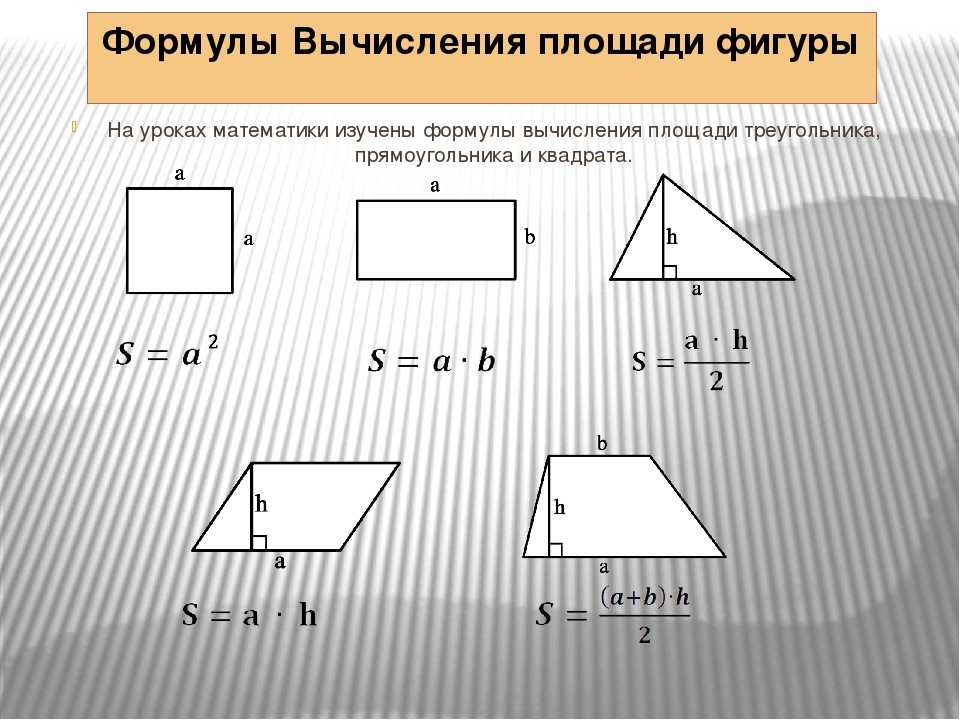
 Знают ли они — «Чтобы разделить прямоугольник на 4 столбца, мне нужно провести всего 3 линии». Теперь подсчет квадратов — не самый эффективный метод, но он может помочь учащимся, которые борются с концепцией или фактами умножения.
Знают ли они — «Чтобы разделить прямоугольник на 4 столбца, мне нужно провести всего 3 линии». Теперь подсчет квадратов — не самый эффективный метод, но он может помочь учащимся, которые борются с концепцией или фактами умножения. единиц.
единиц.