Совместные и несовместные события. Противоположные события. Полная группа событий
События называют несовместными, если в одном и том же испытании появление одного из событий исключает появление других событий. Простейшим примером несовместных событий является пара противоположных событий. Событие, противоположное данному, обычно обозначается той же латинской буквой с чёрточкой наверху:
– в результате броска монеты выпадет орёл;
– в результате этого же броска выпадет решка.
Совершено ясно, что в отдельно взятом испытании появление орла исключает появление решки (и наоборот), поэтому данные события и называются несовместными.
Противоположные события легко формулируются из соображений элементарной логики:
– в результате броска игрального кубика выпадет 5 очков;
– в результате этого же броска выпадет число очков, отличное от пяти.
Либо 5, либо не 5, т.е. данные события несовместны и противоположны.
Аналогично:
– из колоды будет извлечена карта трефовой масти, либо:
– извлечена пика, черва или бубна.
Множество несовместных событий образуют полную группу, если в результате отдельно взятого испытания обязательно появится одно и только одно из этих событий. Очевидно, что любая пара противоположных событий, например, и (выпадение / невыпадение «пятёрки») образует полную группу. Но, разумеется, полную группу могут образовывать не только противоположные события:
– в результате броска игрального кубика выпадет 1 очко;
– … 2 очка;
– … 3 очка;
– … 4 очка;
– … 5 очков;
– … 6 очков.
События несовместны (поскольку появление какой-либо грани исключает одновременное появление других) и образуют полную группу (так как в результате испытания обязательно появится одно из этих шести событий).
И из этих двух примеров вытекает ещё одно важное понятие, которое нам потребуется в дальнейшем – это элементарность
исхода (события). Если совсем просто, то элементарное событие нельзя «разложить на другие события». Например, события элементарны, но событие не является таковым, так как подразумевает выпадение 1, 2, 3, 4 или 6 очков (включает в себя 5 элементарных исходов).
Если совсем просто, то элементарное событие нельзя «разложить на другие события». Например, события элементарны, но событие не является таковым, так как подразумевает выпадение 1, 2, 3, 4 или 6 очков (включает в себя 5 элементарных исходов).
В примере с картами события (извлечение трефы, пики, червы или бубны соответственно) несовместны и образуют полную группу, но они неэлементарны. Если считать, что в колоде 36 карт, то каждое из перечисленных выше событий включает в себя 9 элементарных исходов. Аналогично – события (извлечение шестёрки, семёрки, …, короля, туза) несовместны, образуют полную группу и неэлементарны (каждое включает в себя 4 исхода).
Таким образом, элементарным исходом здесь считается лишь извлечение какой-то конкретной карты, и 36 несовместных элементарных исходов тоже образуют полную группу событий.
И коротко о событиях совместных. События называются совместными, если в отдельно взятом испытании появление одного из них не исключает появление другого. Например:
Например:
– из колоды карт будет извлечена трефа;
– из колоды карт будет извлечена семёрка.
– данные события совместны, т.к. при излечении семёрки треф одновременно имеют место оба события.
Понятие совместности охватывает и бОльшее количество событий:
– завтра в 12.00 будет дождь;
– завтра в 12.00 будет гроза;
– завтра в 12.00 будет солнце.
Ситуация, конечно, редкая, но совместное появление всех трёх событий, не исключено. Следует отметить, что перечисленные события совместны и попарно.
1.2.3. Сложение и умножение событий
1.2.1. Виды событий
| Оглавление |
Полную и свежую версию этой книги в pdf-формате,
а также курсы по другим темам можно найти здесь.
Также вы можете изучить эту тему подробнее – просто, доступно, весело и бесплатно!
С наилучшими пожеланиями, Александр Емелин
Элементы теории вероятности с примерами и образцами решения
Содержание:
- Случайные опыты и события
- Элементарные события
- Частота события
- Формула классической вероятности
- Комбинаторные методы решения вероятностных задач
- Геометрическая вероятность
- Операции над событиями
- Несовместные события.
 Формула сложения вероятностей
Формула сложения вероятностей - Совместные события. Формула сложения вероятностей
- Независимые события. Формула умножения вероятностей
- Сложение и умножение вероятностей
- Повторение испытаний. Формула Бернулли
| Элементы теории вероятности |
Элементы теории вероятностей
Теория вероятностей (ТВ) — раздел математики, изучающий вероятности событий. ТВ разрабатывает методы, с помощью которых можно вычислить вероятности одних событий, зная вероятности других. ТВ изучает также случайные величины и их распределения.
Случайные опыты и события
То или иное событие может осуществиться только при определенных условиях.
Определение. Случайное событие -событие, которое может наступить в ходе некоторого опыта, а может не наступить.
Например, при бросании игральной кости невозможно предсказать, какая из шести граней выпадет.
Определение. Те условия и действия, при которых может осуществиться случайное событие, называют случайным опытом (экспериментом, испытанием).
Например, в опыте «подбрасывание симметричной монеты» возможно случайное событие «появление орла».
По этой ссылке вы найдёте полный курс лекций по теории вероятности:
| Предмет теория вероятности |
Элементарные события
В каждом опыте можно выделить такие элементарные события, из которых состоят все остальные события.
Определение. События, которые нельзя разбить на более простые, называют элементарными событиями (исходами, случаями).
- Например, событие «выпало четное число очков» при бросании игральной кости состоит из трех элементарных событий: «выпало два очка», «выпало четыре очка», «выпало шесть очков».

Определение. Элементарные события, при которых наступает событие А, называют элементарными событиями, благоприятствующими (благоприятными) событию А.
Например, событию «сумма очков на обеих костях равна 7» при двойном бросании игральной кости благоприятствуют только шесть элементарных событий (1;6), (2;5), (3;4), (4;3), (5;2), (6;1).
Определение. Элементарные события, шансы наступления которых одинаковы, называют равновозможными событиями.
Примером может служить опыт, состоящий в бросании правильной игральной кости. В этом опыте шесть элементарных событий, и все они равновозможны.
Возможно вам будут полезны данные страницы:
Как решать задачи на вероятность |
Элементы комбинаторики: примеры решения |
| Найдите вероятность что случайно |
Бросили кость найти вероятность: пример решения |
Частота события
Пусть при проведении п случайных опытов событие А наступило к раз.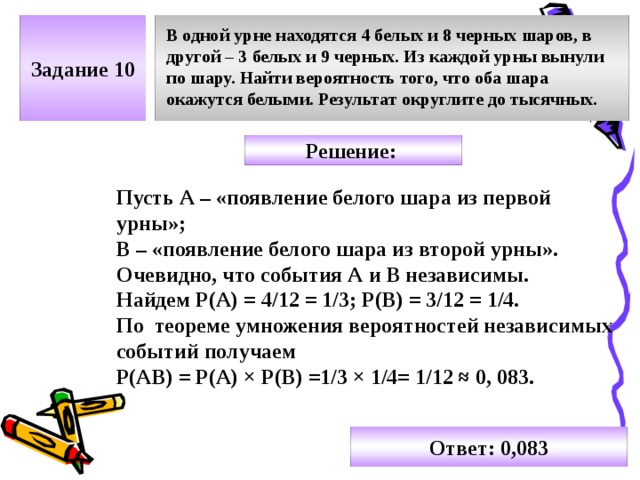 Частотой события А называют отношение
Частотой события А называют отношение
Сумма частот всех элементарных событий случайного опыта равна единице.
Пример 10.
Наблюдения показывают, что в среднем среди 1000 новорожденных детей 515 мальчиков. Найдите частоту рождения мальчика в такой серии наблюдений.
Решение:
Определим событие А -«рождение мальчика». Из условия задачи имеем . Тогда частота события А в данной серии наблюдений равна
Ответ: 0,515.
Формула классической вероятности
Вероятность — есть число, характеризующее возможность наступления события.
Определение. Вероятностью Р события А называют отношение числа т исходов, благоприятных этому событию, к общему числу л исходов
Сумма вероятностей всех элементарных событий случайного эксперимента равна 1.
Пример 11.
Из колоды в 36 карт одну за другой вытягивают две карты, не возвращая карту обратно. Какова вероятность того, что они одного цвета?
Решение:
Обозначим через А событие «обе карты одного цвета». Подсчитаем общее количество исходов, используя правило умножения « = 36-35 (для первой карты 36 вариантов, для второй — 35 вариантов). Количество благоприятствующих исходов m =36 17(для первой карты 36 вариантов, для второй — 17 вариантов). Искомая вероятность
Подсчитаем общее количество исходов, используя правило умножения « = 36-35 (для первой карты 36 вариантов, для второй — 35 вариантов). Количество благоприятствующих исходов m =36 17(для первой карты 36 вариантов, для второй — 17 вариантов). Искомая вероятность
Ответ:
Комбинаторные методы решения вероятностных задач
Умение находить число перестановок, размещений, сочетаний по формулам позволяет также решать задачи на вычисление вероятности.
Пример 12.
В классе 7 мальчиков и 14 девочек. 1 сентября случайным образом определяют двух дежурных на 2 сентября, которые должны приготовить класс к занятиям. Найдите вероятность того, что будут дежурить два мальчика.
Решение:
Обозначим через А событие «будут дежурить два мальчика». Общее число исходов (число сочетаний из 21 по
2) Число благоприятных исходов (число сочетаний из 7 по
2) . Согласно определению вероятности имеем
Ответ: 0,1.
Геометрическая вероятность
Если число исходов некоторого опыта бесконечно, то классическое определение вероятности не может служить характеристикой степени возможности наступления того или иного события. В этом случае пользуются геометрическим подходом к определению вероятности. При этом вероятность события А есть отношение меры А (длины, площади, объема и т.д.) к мере О пространства элементарных событий.
Пример 13.
В круг радиуса R наудачу брошена точка. Найдите вероятность того, что эта точка окажется внутри данного вписанного правильного треугольника.
Решение:
Искомая вероятность равна отношению площади треугольника к площади круга:
Ответ: =0,4137.
Операции над событиями
Действия над случайными событиями определяют по аналогии с действиями в теории множеств.
Определение. Суммой (объединением) событий А и В называют событие (обозначение ), состоящее в появлении либо только события А, либо только события В. либо и события А и события В одновременно.
либо и события А и события В одновременно.
Фразу «наступит или событие А или событие В или оба события А и В» обычно заменяют фразой «наступит хотя бы (по крайней мере) одно из данных событий».
Пример 14.
Если событие А — попадание в цель при первом выстреле, событие В — попадание в цель при втором выстреле, то событие С = А + В есть попадание в цель вообще (или только при первом выстреле, или только при втором выстреле, или при 1-м и при 2-м выстрелах).
Определение. Событием, противоположным событию А, называют событие (обозначение ), которому благоприятствуют все элементарные события, не благоприятствующие событию А.
Выпадение герба и выпадение решки при одном бросании монеты, попадание и промах при одном выстреле — события противоположные.
Определение. Произведением (пересечением) двух событий А и В называется событие (обозначение АВ или ), состоящее в совместном выполнении события А и события В .
Пример 15.

Если событие А — попадание в цель при первом выстреле, событие В — попадание в цель при втором выстреле, то событие С = АВ есть попадание при обоих выстрелах (и при первом выстреле и при втором выстрелах).
Несовместные события. Формула сложения вероятностей
Рассмотрим теоремы, при помощи которых по вероятностям одних случайных событий вычисляют вероятности других случайных событий.
Определение. События называют несовместными, если они не могут происходить одновременно в одном и том же испытании.
Например, выигрыш, ничейный исход и проигрыш одного игрока в одной партии в шахматы — три несовместных события.
Теорема. Вероятность суммы двух несовместных событий А и В (появления хотя бы одного события) равна сумме вероятностей этих событий:
Теорема обобщается на любое число попарно несовместных событий.
Следствие. Сумма вероятностей противоположных событий А и равна 1:
Пример 16.
Зачет по стрельбе курсант сдаст, если получит оценку не ниже 4. Какова вероятность сдачи зачета, если известно, что курсант получает за стрельбу оценку 5 с вероятностью 0,3 и оценку 4 с вероятностью 0,6?
Какова вероятность сдачи зачета, если известно, что курсант получает за стрельбу оценку 5 с вероятностью 0,3 и оценку 4 с вероятностью 0,6?
Решение:
Данный опыт состоит в том, что проведены стрельбы и по ним курсант получил оценку. В этом опыте обозначим через А событие «по стрельбе курсант получил оценку 5» и через В событие «по стрельбе курсант получил оценку 4». Эти события несовместны. Событие С «зачет сдан» является их суммой С = А + В . Из условия задачи следует, что вероятности и . По формуле сложения вероятностей несовместных событий имеем:
Ответ: 0,9.
Пример 17.
Наудачу берется трехзначное число. Какова вероятность того, что хотя бы две его цифры совпадают?
Решение:
Данный опыт состоит в том, что наудачу берется натуральное число из чисел от 100 до 999 и смотрят, есть ли в нем одинаковые цифры. Очевидно, что исходы «взяли наудачу трехзначное число» равновероятны, число этих исходов т = 900 . Введем событие А «у выбранного числа совпадают хотя бы две цифры». Проще подсчитать вероятность противоположного события А «у выбранного числа все цифры различны». Количество благоприятных событий равно .
Введем событие А «у выбранного числа совпадают хотя бы две цифры». Проще подсчитать вероятность противоположного события А «у выбранного числа все цифры различны». Количество благоприятных событий равно .
Тогда и
Ответ: 0,28.
Совместные события. Формула сложения вероятностей
Рассмотрим формулу для вероятности суммы двух событий в общем случае (не обязательно несовместных).
Определение. События называют совместными, если они могут происходить одновременно. Например, при бросании двух монет выпадение решки на одной не исключает появления решки на другой монете.
Теорема. Вероятность суммы двух совместных событий А и В (появления хотя бы одного события) равна сумме их вероятностей без вероятности их совместного появления, то есть
Частным случаем приведенной формулы является формула сложения вероятностей для несовместных событий, так как их совместное наступление есть невозможное событие и Р(АВ) = 0.
Для случая трех совместных событий формула имеет вид:
Пример 18.
Прибор, состоящий из двух блоков, выходит из строя, если выходят из строя оба блока. Вероятность безотказной работы за определенный промежуток времени первого блока составляет 0,9, второго — 0,8, обоих блоков — 0,75. Найти вероятность безотказной работы прибора в течение указанного промежутка.
Решение:
Обозначим через А событие «первый блок работает безотказно в течение определенного промежутка времени», через В событие «второй блок работает безотказно в течение определенного промежутка времени», через АВ событие «оба блока работают безотказно в течение определенного промежутка времени». Событие С «прибор работает безотказно в течение определенного промежутка времени» является суммой событий А и В: С = А + В . Из условия задачи известны вероятности Р( А) = 0,9,
. По формуле сложения вероятностей имеем:
Ответ: 0,95.
Рассмотрим обратную задачу.
Пример 19.
Школьнику надо сдать зачет по математике. В каждом билете — по два вопроса. Всего 25 билетов. Из них 5 билетов школьник вообще не учил. В каждом из оставшихся 20 билетов он хотя бы один вопрос выучил, причем в 18 билетах школьник выучил первый вопрос и в 15 билетах — второй вопрос. Школьник может получить удовлетворительную оценку, если вытащит такой билет, оба вопроса которого он знает. Какова вероятность того, что школьник сдаст зачет, если он первый тянет билет?
Решение:
Обозначим через А событие «школьнику достанется билет, первый вопрос которого он знает», через В событие «школьнику достанется билет, второй вопрос которого он знает», тогда событие А + В означает, что «школьник знает хотя бы один вопрос из 20».
Надо определить Р(АВ), где событие АВ означает, что «школьник ответит на 2 вопроса билета». Событию АВ благоприятствуют 20 вопросов из 25, поэтому
Так как из условия задачи имеем вероятности , то из формулы сложения вероятностей получаем:
Ответ: 0,52.
Независимые события. Формула умножения вероятностей
Часто возникает вопрос о том, как влияет на возможность осуществления некоторого события В наступление некоторого другого события А.
Определение. Два случайных события называют независимыми, если наступление одного из них не изменяет вероятность наступления другого. В противном случае события называют зависимыми.
Теорема. Вероятность произведения (совместного появления)двух независимых событий равна произведению вероятностей этих событий:
Теорема обобщается на любое число попарно независимых событий.
Следствие. Вероятность появления хотя бы одного события из л попарно независимых событий равна разности между 1 и произведением вероятностей событий, противоположных данным, то есть
Пример 20.
Вероятность того, что потребитель увидит рекламу определенного продукта по телевидению, равна 0,04. Вероятность того, что потребитель увидит рекламу того же продукта на рекламном стенде, равна 0,06. Чему равна вероятность того, что:
Чему равна вероятность того, что:
а) потребитель увидит обе рекламы;
б) потребитель увидит хотя бы одну рекламу?
Решение:
Обозначим через А событие «потребитель увидит рекламу продукта по телевидению», через В событие «потребитель увидит рекламу продукта на рекламном стенде». События А и В независимые.
а) Событие С «потребитель увидит обе
рекламы» является произведением событий . Из условия задачи известны вероятности и
По формуле умножения вероятностей независимых событий имеем:
б) Определим событие D «потребитель увидит хотя бы одну рекламу». Тогда получаем:
Ответ: а) 0,0024; б) 0,0976.
Зависимые события. Формула умножения вероятностей
В теории вероятностей характеристикой связи событий служит так называемая условная вероятность.
Определение. Условной вероятно-С7ль/о(обозначение ) называют вероятность события В, вычисленную в предположении, что событие А уже наступило.
Теорема. Вероятность произведения (совместного появления) двух зависимых событий равна произведению вероятности одного из них на условную вероятность второго, вычисленную при условии, что первое событие произошло, то есть
Теорему умножения легко распространить на любое конечное число событий. Например, для трех событий формула имеет вид
Пример 21.
В урне 6 шаров — 2 белых и 4 черных. Без возвращения выбираем два шара. Найти вероятность того, что оба шара белые.
Решение:
Пусть событие Бх состоит в том, что первый шар белый, а событие Б2 — второй шар белый. Из условия задачи имеем вероятность
После того, как мы вынули один шар и знаем, что он белый, мы имеем 5 шаров и среди них 1 белый. Тогда получаем . По теореме умножения зависимых событий находим
Ответ:
Рассмотрим обратную задачу.
Пример 22.
В рекламной фирме 21% работников получают высокую заработную плату. Известно также, что 40% работников фирмы — женщины, а 6,4% работников — женщины, получающие высокую заработную плату. Можно ли утверждать, что на фирме существует дискриминация женщин в оплате труда?
Известно также, что 40% работников фирмы — женщины, а 6,4% работников — женщины, получающие высокую заработную плату. Можно ли утверждать, что на фирме существует дискриминация женщин в оплате труда?
Решение:
Переформулируем задачу: какова вероятность того, что случайно выбранный работник будет женщиной, имеющей высокую заработную плату?
Определим событие А — «случайно выбранный работник — женщина», событие В — «случайно выбранный работник имеет высокую заработную плату».
Имеем
Так как 0,16 меньше, чем 0,21, то можно заключить, что женщины, работающие в этой рекламной фирме, имеют меньше шансов получить высокую заработную плату по сравнению с мужчинами.
Сложение и умножение вероятностей
Рассмотрим задачи, в которых используют обе теоремы: сложения вероятностей и умножения вероятностей.
Пример 23.
С первого станка на сборку поступает 40% , со второго — 30% и с
третьего — 30% всех деталей. Вероятности изготовления бракованной детали равны для каждого станка соответственно 0,01, 0,03 и 0,05. Найти вероятность того, что наудачу взятая деталь, поступившая на сборку, бракованная.
Найти вероятность того, что наудачу взятая деталь, поступившая на сборку, бракованная.
Решение:
Обозначим через события, состоящие в том, что деталь изготовлена соответственно на первом станке, втором станке и третьем станке. Пусть события означают, что деталь, изготовленная соответственно на первом станке, втором станке и третьем станке, бракованная. Из условия задачи следует, что вероятности . Событие «наудачу взятая деталь, поступившая на сборку, бракованная» является суммой трех несовместных событий
По формуле сложения вероятностей несовместных событий, а затем по формуле умножения вероятностей зависимых событий имеем:
Ответ: 0,028.
Повторение испытаний. Формула Бернулли
В одном опыте нас интересует один вопрос, произойдет или не произойдет некоторое событие. В серии опытов (испытаний) важен вопрос, сколько раз произойдет или не произойдет данное событие.
Например, игральный кубик бросили 10 раз подряд. Какова вероятность того, что «пятерка» выпадет ровно три раза?
Математик Я. Бернулли объединил такие примеры в единую вероятностную задачу (схему).
Бернулли объединил такие примеры в единую вероятностную задачу (схему).
Рассматривают независимые повторения одного и того же испытания с двумя возможными исходами, которые условно называют «успех» и «неудача». Какова вероятность того, что при n таких повторениях произойдет ровно к «успехов»?
Эту вероятность можно найти по формуле Бернулли
где вероятность появления события А в одном опыте равна р, а его непоявления равна
Пример 24.
В части А Единого государственного экзамена по математике в 2005 году было 10 заданий с выбором ответа. К каждому из них предлагается 4 варианта ответа, из которых только один верный. Если ученик не знает предмет и отвечает наугад, то с вероятностью он выберет правильный ответ, а с вероятностью — ошибется. Для получения положительной оценки за экзамен необходимо правильно ответить минимум на 6 заданий. Какова вероятность того, что нерадивый ученик сдаст экзамен?
Решение:
Из условия задачи имеем
Тогда получаем по формуле Бернулли
Ответ: 0,016.
Совместные, предельные и условные вероятности — Веб-сайт статистического обзора ENV710
Вероятности могут быть маргинальными, совместными или условными. Понимание их различий и того, как ими манипулировать, является ключом к успеху в понимании основ статистики.
Предельная вероятность : вероятность наступления события (p(A)), ее можно рассматривать как безусловную вероятность. Это не обусловлено другим событием. Пример: вероятность того, что вытянутая карта будет красной (p(red) = 0,5). Другой пример: вероятность того, что вынутая карта равна 4 (p(четыре)=1/13).
Совместная вероятность : p(A и B). Вероятность события A и события B. Это вероятность пересечения двух или более событий. Вероятность пересечения A и B можно записать как p(A ∩ B). Пример: вероятность того, что на карте четыре и красное = p(четыре и красное) = 2/52=1/26. (В колоде из 52 карт две красные четверки: 4 черви и 4 бубны).

Условная вероятность : p(A|B) – это вероятность наступления события A при условии, что событие B произошло. Пример: учитывая, что вы вытащили красную карточку, какова вероятность того, что это четверка (p(четыре|красная))=2/26=1/13. Таким образом, из 26 красных карточек (учитывая красную карточку) есть две четверки, поэтому 2/26 = 1/13.
Приведенное ниже уравнение является средством манипулирования совместными, условными и пограничными вероятностями. Как вы можете видеть в уравнении, условная вероятность A при данном B равна совместной вероятности A и B, деленной на маргинал B. Давайте используем наш пример с картой для иллюстрации. Мы знаем, что условная вероятность четверки при красной карточке равна 2/26 или 1/13. Это должно быть эквивалентно совместной вероятности красного и четырех (2/52 или 1/26), деленной на предельное P(красное) = 1/2. И низко и вот, это работает! Так как 1/13 = 1/26 разделить на 1/2.
 Для диагностического экзамена вы должны уметь манипулировать совместными, пограничными и условными вероятностями.
Для диагностического экзамена вы должны уметь манипулировать совместными, пограничными и условными вероятностями.
Теорема Байеса: уравнение, которое позволяет нам манипулировать условными вероятностями. Для двух событий, A и B, теорема Байеса позволяет нам перейти от p(B|A) к p(A|B), если мы знаем
предельных вероятностей исходов A и вероятность B при заданных исходах of A. Вот уравнение теоремы Байеса для двух событий с двумя возможными исходами (A и не A).
Предположим, мы знаем, что 1% женщин старше 40 лет имеют рак молочной железы.
[p(рак)=0,01]
Предположим, что у 90% женщин с раком груди будет
положительный результат на рак молочной железы на маммограмме.
[p(положительный тест|рак)=0,9]
Восемь процентов женщин, у которых нет рака, также будут иметь положительный результат.
[p(положительный тест|нет рака)=0,08]
Какова вероятность того, что у женщины рак, если у нее положительный результат [p(рак|положительный тест)]?
Будем называть p(рак) = P(A), а P(положительный тест) = P(B).
 Мы хотим знать P(A|B) – вероятность заболевания раком, если у вас положительный тест.
Мы хотим знать P(A|B) – вероятность заболевания раком, если у вас положительный тест.
Используя теорему Байеса, мы вычисляем, что вероятность того, что женщина больна раком молочной железы, при положительном результате теста равна примерно 0,10. Это имеет интуитивно понятный смысл, поскольку (1) этот результат превышает 1% (процент рака молочной железы среди населения в целом).
Следите за Элизабет А. Олбрайт, доктором философии, в Twitter @enviro_prof. Если вы нашли эту страницу полезной, пожалуйста, дайте ссылку или поделитесь ею через Facebook или Twitter. Спасибо!
Фото предоставлено Мэтью Дж. Киди, Тринидад и Тобаго.
20.1 — Две непрерывные случайные величины
До сих пор наше внимание в этом уроке было направлено на совместное распределение вероятностей двух или более дискретных случайных величин. Теперь обратим внимание на непрерывные случайные величины. Попутно, всегда в контексте непрерывных случайных величин, мы рассмотрим формальные определения совместных функций плотности вероятности, маргинальных функций плотности вероятности, математического ожидания и независимости. Мы также применим каждое определение к конкретному примеру. 9\infty f(x,y)dxdy=1\) \(P[(X,Y) \in A]=\int\int_A f(x,y)dxdy \) где {(
Теперь обратим внимание на непрерывные случайные величины. Попутно, всегда в контексте непрерывных случайных величин, мы рассмотрим формальные определения совместных функций плотности вероятности, маргинальных функций плотности вероятности, математического ожидания и независимости. Мы также применим каждое определение к конкретному примеру. 9\infty f(x,y)dxdy=1\) \(P[(X,Y) \in A]=\int\int_A f(x,y)dxdy \) где {(
Первое условие, конечно, просто говорит нам, что функция должна быть неотрицательной. Имея в виду, что \(f(x,y)\) — это некоторая двумерная поверхность, плавающая над плоскостью \(xy\), второе условие говорит нам, что объем, определяемый опорой, поверхностью и \ (xy\) — плоскость должна быть 1. Третье условие говорит нам, что для определения вероятности события \(A\) необходимо проинтегрировать функцию \(f(x,y)\) по пространство, определяемое событием \(A\). То есть точно так же, как поиск вероятностей, связанных с одной непрерывной случайной величиной, включает в себя поиск площадей под кривыми, поиск вероятностей, связанных с двумя непрерывными случайными величинами, включает в себя поиск объемов твердых тел, которые определяются событием \(A\) в \(xy\) -плоскость и двумерная поверхность \(f(x,y)\).
Пусть \(X\) и \(Y\) имеют совместную функцию плотности вероятности:
\(f(x,y)=4xy\)
для \(0 Перед попыткой убедиться, что \(f(x,y)\) является допустимой функцией PDF, полезно получить представление о том, как выглядит функция. Вот моя попытка наброска функции: Красный квадрат — это совместная опора \(X\) и \(Y\), которая лежит в плоскости \(xy\). Синяя поверхность в форме палатки — это мое представление поверхности \(f(x,y)\). Теперь, чтобы убедиться, что \(f(x,y)\) является корректной функцией распределения вероятности, нам сначала нужно показать, что \(f(x,y)\) всегда неотрицательна. Ясно, что это так, так как он полностью лежит над плоскостью \(xy\). Если вы все еще не убеждены, вы можете видеть, что при подстановке любого значения \(x\) и \(y\) в совместной опоре в функцию \(f(x,y)\) вы всегда получаете положительный ценность. Теперь нам просто нужно показать, что объем твердого тела, определяемый опорой, плоскостью \(xy\) и поверхностью, равен 1: Что такое \(P(Y Чтобы найти желаемую вероятность, нам снова нужно найти объем твердого тела, определяемый поверхностью, плоскостью \(xy\) и опорой. Однако на этот раз объем не определяется в плоскости \(xy\) единичным квадратом. Вместо этого область в \(xy\)-плоскости ограничивается только той частью единичного квадрата, для которой \(y Итак, нам нужно найти объем твердого тела между поверхностью \(f(x,y)\) и синим треугольником. То есть, чтобы найти искомый объем, то есть искомую вероятность, нам нужно проинтегрировать от \(y=0\) до Учитывая симметрию твердого тела относительно плоскости \(y=x\), возможно, нам не следует удивляться, обнаружив, что рассчитанная нами вероятность равна \(\frac{1}{2}\)! , где \(S_1\) и \(S_2\) — соответствующие опоры \(X\) и \(Y\). Пусть \(X\) и \(Y\) имеют совместную функцию плотности вероятности: \(f(x,y)=4xy\) для \(0 Чтобы найти маргинальную п.п.ф. \(X\), нам нужно проинтегрировать совместную п.ф.ф. \(f(x,y)\) над \(0 Пусть \(X\) и \(Y\) имеют совместную функцию плотности вероятности: \(f(x,y)=4xy\ ) для \(0 Ожидаемое значение \(X\) равно \(\frac{2}{3}\), как показано здесь: Мы предоставим вам показать, что неудивительно, что ожидаемое значение \(Y\) также равно \(\frac{2}{3}\). Определение. Непрерывные случайные величины \(X\) и \(Y\) являются независимыми тогда и только тогда, когда совместная p.d.f. множителей \(X\) и \(Y\) в произведение их маргинальных Ф.Р., а именно: \(f(x,y)=f_X(x)f_Y(y), \qquad x\in S_1, \qquad y\in S_2\) Пусть \(X\) и \(Y\) имеют совместную функцию плотности вероятности: \(f(x,y)=4xy\) для \(0 Решение
Решение
Пример (продолжение)
Решение
Пример (продолжение)
Решение
Пример (продолжение)

 Формула сложения вероятностей
Формула сложения вероятностей