Основные геометрические фигуры
Каждый из нас — и взрослый, и ребенок — замечал, как много геометрических фигур существует вокруг нас. Мы встречаемся с ними везде, во всех окружающих нас предметах. Где же встречаются геометрические фигуры в нашей жизни?
Где встречаются геометрические фигуры в нашей жизни?
Каждый из нас — и взрослый, и ребенок — замечал, как много геометрических фигур существует вокруг нас. Мы встречаемся с ними везде, во всех окружающих нас предметах.
Люди давно заинтересовались разнообразием геометрических фигур. Ещё для первобытных людей важную роль играла форма окружавших их предметов. Овладевая миром, люди знакомились с простейшими геометрическими формами. Сначала они изготавливали орудия труда относительно правильной формы, потом научились их совершенствовать. Специальных названий для геометрических фигур тогда, конечно, не было. Их придумали значительно позже. Когда люди стали строить дома, им пришлось ещё глубже разбираться в особенностях разных фигур, чтобы понять, какую форму следует придавать стенам и крыше, какой формы должны быть брёвна или каменные глыбы.
Сам того не зная, человек всё время занимался изучением фигур: женщины, изготавливая одежду, охотники — наконечники для копий или бумеранги сложной формы, рыболовы, делая такие крючки из кости, чтобы рыба с них не срывалась.
И в современном мире без этих знаний не прожить.
Где же встречаются геометрические фигуры в нашей жизни?
Возможно, кто-то считает, что различные линии фигуры «водятся» только в книгах учёных математиков. Однако, если посмотреть вокруг, становится понятно, что многие предметы имеют форму, похожую на основные геометрические фигуры. Просто мы не всегда это замечаем. Немало замечательных геометрических фигур встречается в окружающей нас природе. Поле имеет форму прямоугольника, река — кривой линии, озеро — круга, кристалл соли — форму куба, обычная горошинка, капелька росы — форму шара. Красивы и разнообразны многогранники — кристаллы горного хрусталя. Но и в привычной жизни основные геометрические фигуры тоже повсюду. Это здания, строения, транспорт, интерьер квартиры, даже посуда и предметы одежды.
К примеру, женская юбка — это трапеция, тарелка — круг, дом — квадрат и треугольник, а в трубе — цилиндр.
Знать все фигуры, их виды, названия и свойства очень важно. Систематизирует знания о геометрических фигурах и изучает их свойства математическая наука — геометрия. Наука эта очень важная, её применение просто бесценно во все времена и независимо от профессии. Без знаний геометрии не обходится ни рабочий, ни инженер, ни архитектор, ни художник. И очень важно начать осваивать эту науку в раннем возрасте.
Прекрасным помощником ребёнку в этом станет образовательная платформа iSmart. Основные виды геометрических фигур, их свойства, задачи на нахождение площади фигур и многое другое есть на платформе в разделе «Математика». Тут собраны несколько тысяч заданий на освоение этих тем, не повторяющиеся при многократной отработке. Занимаясь на , школьники начальных классов досконально разберутся в основах геометрии. Это даст им хорошую базу по предмету для учёбы в средних и старших классах.
Кроме того, интерактивные задания красочные, интересные, увлекательные.
Итак,
Простейшие виды фигур
Две основные фигуры — это точка и линия. Скопление точек и линий образует различные геометрические фигуры. Каждая из них индивидуальна, отличается своими параметрами, их формы очень разнообразны. Фигуры бывают простыми и сложными, плоскими и объёмными.
Точка
Точка — это самый минимальный, но в то же время самый главный объект в геометрии. Это самая малая геометрическая фигура, но именно она необходима для построения других фигур на плоскости и является основой для всех других фигур. Она не содержит таких свойств, как длина, высота, объём, площадь, не имеет измерительных особенностей и характеристик. Важно только то, где она расположена. Обозначается точка заглавной буквой латинского алфавита либо числом. Например, A, B, C или 1, 2, 3.
Всякая более сложная геометрическая фигура — это множество точек, которые обладают определенным свойством, характерным только для этой фигуры.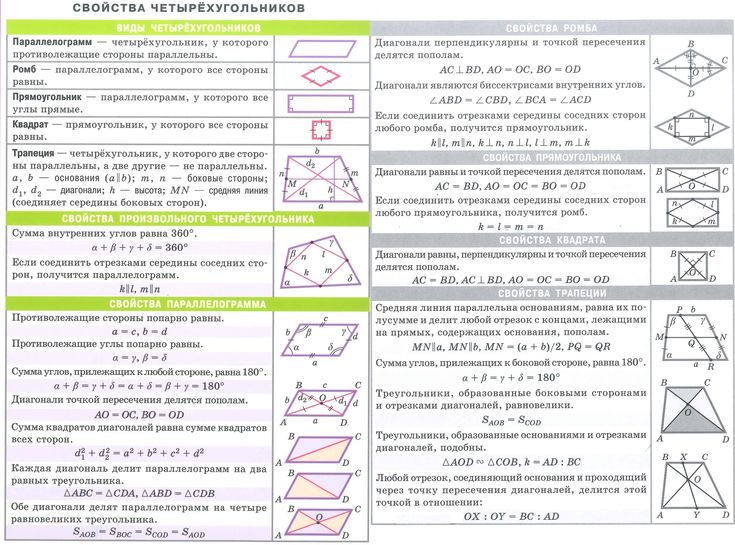
Самыми простейшими фигурами являются луч и отрезок.
- Луч — часть прямой, у которой есть начальная точка, но нет конца. Это продолжение в одну сторону.
- Отрезок — составная часть прямой, которая ограничена двумя точками. Он имеет начало и конец, поэтому измеряется. Длину отрезка можно определить, измерив расстояние между его концами.
Линия
Линия образуется из множества точек, последовательно расположенных друг за другом и соединённых между собой. Линии бывают замкнутыми и разомкнутыми, прямыми и кривыми, а также ломаными.
- Замкнутая — когда в одной точке расположена начальная и конечная часть направления. Из незамкнутой линии получают обратный вариант.
- Разомкнутая — когда начало и окончание линии не соединены.
- Прямая — непрерывная линия без изменений.
- Кривая — отличная от прямой линии.
- Ломаная — когда соединены отрезки не под углом 180 градусов.
Через одну точку можно провести бесконечное число линий, а через две — только одну прямую и множество кривых.
Основные геометрические фигуры
Соединённые между собой точки образуют линии, а соединённые между собой линии — основные геометрические фигуры на плоскости.
Геометрические фигуры бывают плоские или двухмерные (2D) и объёмные пространственные, или трёхмерные (3D). Они ограничены замкнутой поверхностью своей наружной границы.
Если все точки фигуры находятся в одной плоскости, значит, она является плоской. Плоские фигуры, которые знают все: точка, квадрат, прямоугольник, треугольник, круг, полукруг, окружность, овал, ромб, трапеция.
А если у геометрической фигуры все точки не находятся в одной плоскости, то она объёмная. К ним относятся шар, конус, цилиндр, сфера, пирамида и др.
Разберём плоские фигуры.
Треугольник
Треугольник — это фигура, которая образуется, когда три отрезка соединяют три точки, не лежащие на одной прямой. Эти три точки называются вершинами, а отрезки — сторонами.
Есть три вида треугольников:
- Прямоугольный — когда один угол прямой, другие два меньше 90 градусов.
- Остроугольный — когда градус его углов больше 0, но меньше 90 градусов.
- Тупоугольный — когда один угол тупой, то есть больше 90 градусов, а два других — острые.
Треугольники имеют следующие свойства:
- в треугольнике напротив большего угла лежит большая сторона и наоборот;
- сумма углов треугольника всегда равна 180 градусам;
- все углы равностороннего треугольника равны 60 градусам;
- в прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов катетов (но это изучается уже в старших классах).
Вершины треугольников обозначаются заглавными буквами латинского алфавита: A, B, C и др.
Примеры треугольников:
Окружность
Окружность — геометрическая фигура, образованная замкнутой кривой линией, все точки которой находятся на одинаковом от центра расстоянии.
Круг
Часть плоскости, находящаяся внутри окружности, называется кругом. То есть, окружность — это граница круга. А расстояние от центра окружности до любой точки на ней называется радиусом. Диаметр круга — это отрезок, который соединяет две точки на окружности и проходит через её центр. Диаметр круга равен двум его радиусам.
Прямоугольник
Прямоугольник — это фигура, состоящая из четырёх сторон и четырёх прямых углов, у которой:
- противоположные стороны равны между собой;
- диагонали равны и делятся в точке пересечения пополам;
- около прямоугольника можно описать окружность с центром в точке пересечения его диагоналей и радиусом, который равен половине диагоналей.
Квадрат
Квадрат — это тот же прямоугольник, у которого:
- все стороны равны;
- все углы равны и составляют 90 градусов;
- диагонали равны и перпендикулярны;
- центры вписанной и описанной окружности совпадают и находятся в точке пересечения его диагоналей.
Трапеция
Четырёхугольник, у которого две стороны параллельны, а две — нет, называется трапецией. Если сумма длин оснований трапеции равна сумме длин боковых сторон, в неё можно вписать окружность.
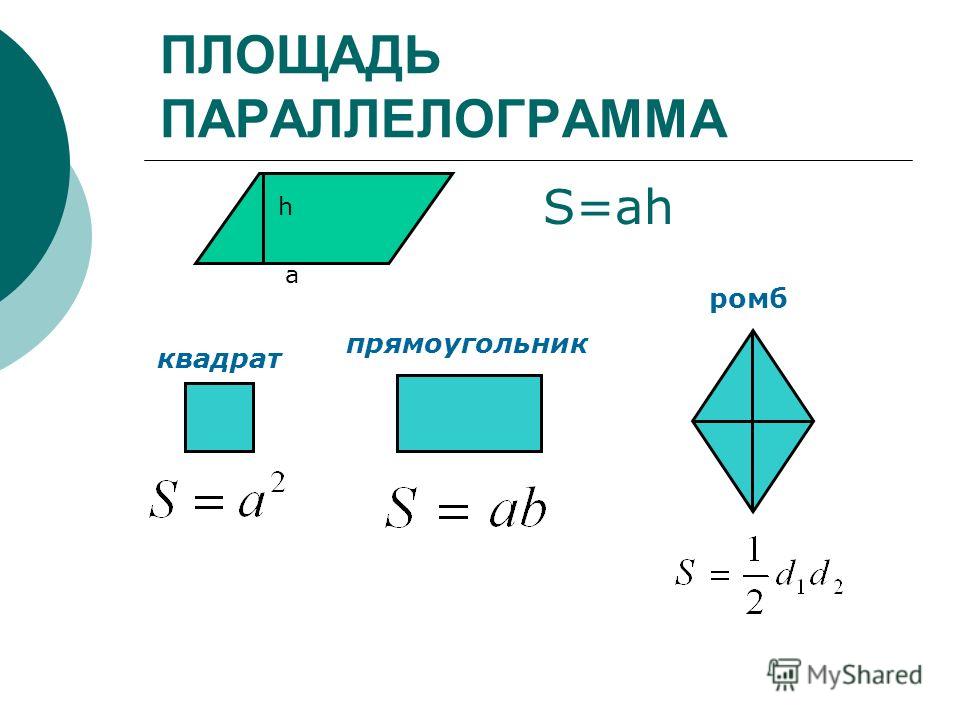
Параллелограмм и ромб
Параллелограмм — четырёхугольник, противоположные стороны которого попарно параллельны.
Ромб — это параллелограмм с равными сторонами.
Параллелограмм имеет следующие свойства:
- противоположные стороны и углы равны;
- сумма двух любых соседних углов равна 180 градусам;
- диагонали пересекаются и точкой пересечения делятся пополам;
- каждая диагональ делит фигуру на два равных треугольника.
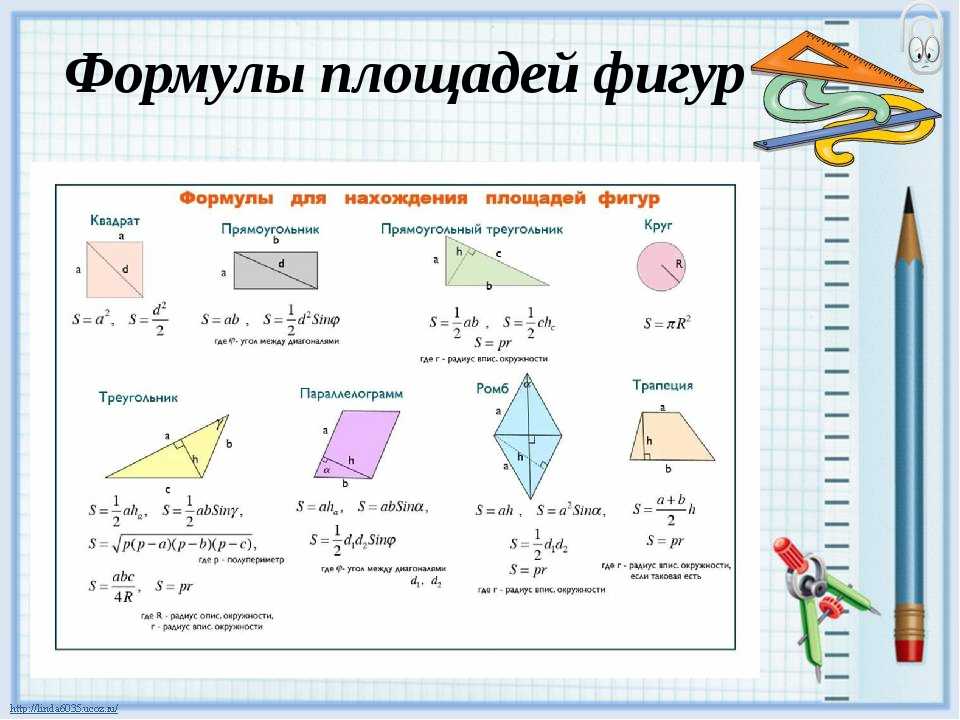
Основные величины и их формулы
Все геометрические фигуры имеют свои характеристики и собственную величину. Самыми распространёнными являются такие величины как площадь и периметр. Они используются в повседневной жизни, в строительстве и в других областях. Например, во время ремонта или нового строительства, количество необходимых материалов и объём работ не определить, не вычислив заранее площадь и периметр.
Периметр
Периметром называется замкнутая граница плоской геометрической фигуры, которая отделяет её внутреннюю область от внешней. Периметр есть у любой замкнутой геометрической фигуры:
На рисунке периметры выделены красной линией. Периметр окружности часто называют длиной.
Периметр измеряется в единицах измерения длины: мм, см, дм, м, км.
Обозначается заглавной латинской P.
Площадь
Площадь — это часть плоскости, занимаемая замкнутой плоской геометрической фигурой, то есть та часть плоскости, которая находится внутри периметра.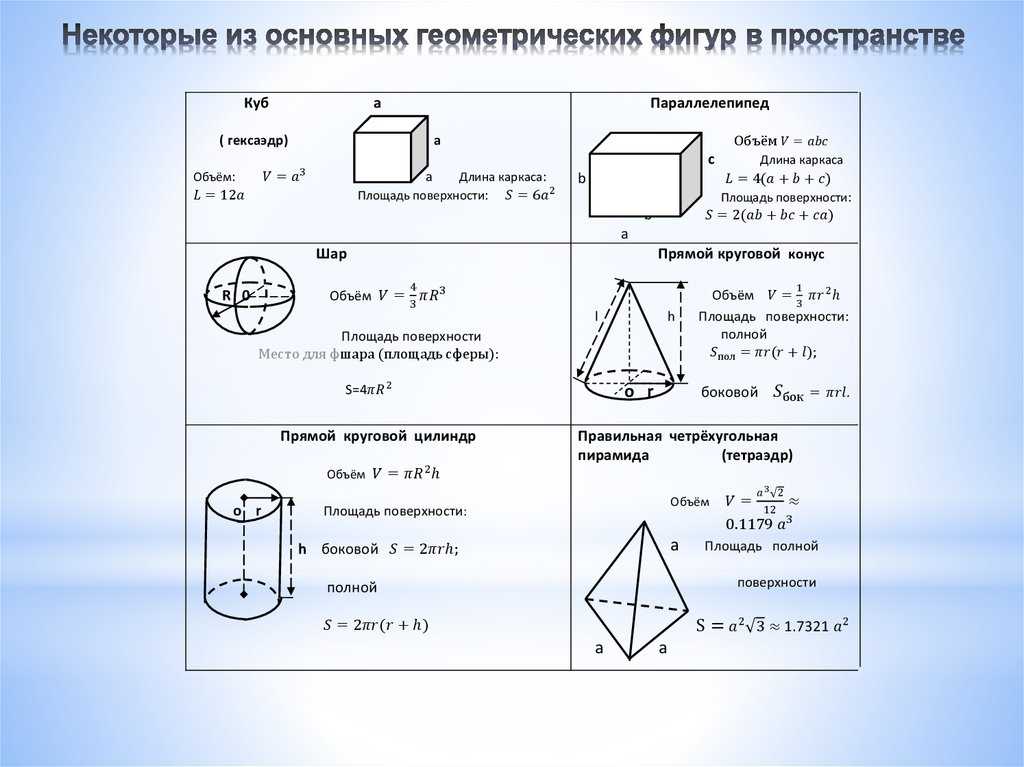
Именно она даёт нам основную информацию о её размере. Любая плоская замкнутая геометрическая фигура имеет определённую площадь.
На рисунке площади фигур окрашены различными цветами.
Измерить площадь фигуры — значит найти, сколько раз в данной фигуре помещается другая фигура, принятая за единицу измерения. Площадь измеряется в квадратных единицах измерения длины. К единицам измерения площади относятся: мм2, см2, м2, км2 и т. д. S (square) — знак площади.
Вычисление периметра и площади
Периметр — это длина замкнутого контура геометрической фигуры. Можно, конечно, измерить линейкой длины всех сторон и сложить их. Но лучше воспользоваться специальными формулами для вычисления периметра, это значительно упростит задачу.
- Квадрат: периметр = 4 * сторона.
- Треугольник: периметр = сторона 1 + сторона 2 + сторона 3.
- Неправильный многоугольник: периметр = сумме всех сторон многоугольника.
- Круг: длина окружности = 2 * π * радиус = π * диаметр (где π – это число пи (константа, примерно равная 3,14), радиус – это длина отрезка, соединяющего центр окружности и любую точку, лежащую на этой окружности, диаметр – это длина отрезка, проходящего через центр окружности и соединяющего любые две точки, лежащие на этой окружности).
Для вычисления площади фигуры также потребуется соответствующая формула. К разным фигурам применяются разные формулы. Для вычисления площади стандартных геометрических фигур можно воспользоваться следующими формулами:
- Параллелограмм: площадь = основание * высота
- Квадрат: площадь = сторона 1 * сторона 2
- Треугольник: площадь = ½ * основание * высота
- Круг: площадь = π * радиус² (где радиус – это длина отрезка, соединяющего центр окружности и любую точку, лежащую на этой окружности. Квадрат радиуса – это значение радиуса, умноженное само на себя).
Итак, мы перечислили основные и самые распространённые геометрические фигуры и их свойства. Образовательная платформа iSmart поможет вашему ребёнок изучить основные геометрические фигуры, их виды, названия и свойства с помощью увлекательных заданий. Преимущества занятий на умных тренажёрах iSmart:
- интерактивные задания больше похожи на игру;
- их можно отрабатывать многократно и они не будут повторяться;
- платформа сформирует индивидуальную траекторию обучения на основе диагностики знаний;
- достаточно всего 20 минут занятий в день, чтобы в короткий срок увидеть прогресс в обучении.
Кроме того, занятия помогут вам освободить своё время, ведь ребёнок сможет заниматься самостоятельно, а родитель — получать отчёты и наблюдать за динамикой обучения. Метод обучения iSmart основан на последних научных практиках: микрообучение и поведенческий анализ.
Образовательная платформа iSmart предлагает подготовку к контрольным работам, тестам, ВПР, олимпиадам, а также изучение дополнительных предметов, не вошедших в школьную программу.
Площадь (в геометрии) | это… Что такое Площадь (в геометрии)?
Площадь, одна из основных величин, связанных с геометрическими фигурами. В простейших случаях измеряется числом заполняющих плоскую фигуру единичных квадратов, т. е. квадратов со стороной, равной единице длины. Вычисление П. было уже в древности одной из важнейших задач практической геометрии (разбивка земельных участков). За несколько столетий до нашей эры греческие учёные располагали точными правилами вычисления П., которые в «Началах» Евклида облечены в форму теорем. При этом П. многоугольников определялись теми же приёмами разложения и дополнения фигур, какие сохранились в школьном преподавании. Для вычисления П. фигур с криволинейным контуром применялся предельный переход в форме исчерпывания метода.
Теория П. плоских фигур, ограниченных простыми (т. е. не пересекающими себя) контурами, может быть построена следующим образом. Рассматриваются всевозможные многоугольники, вписанные в фигуру F, и всевозможные многоугольники, описанные вокруг фигуры F.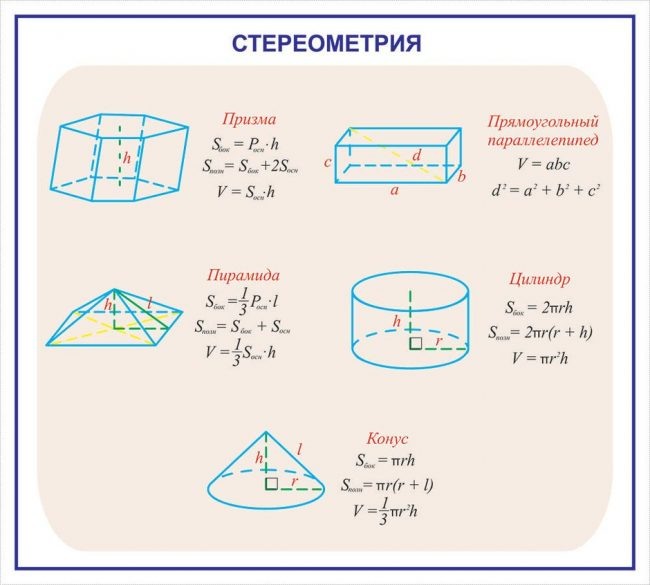
(Вычисление П. многоугольника сводится к вычислению П. равновеликого ему квадрата, который может быть получен посредством надлежащих прямолинейных разрезов и перекладывания полученных частей.) Пусть {Si} ‒ числовое множество П. вписанных в фигуру многоугольников, a {Sd} ‒ числовое множество П. описанных вокруг фигуры многоугольников. Множество {Si} ограничено сверху (площадью любого описанного многоугольника), а множество {Sd} ограничено снизу (например, числом нуль). Наименьшее из чисел , ограничивающее сверху множество {Si}, называется нижней площадью фигуры F, а наибольшее из чисел , ограничивающее снизу множество {Sd}, называется верхней площадью фигуры F. Если верхняя П. фигуры совпадает с её нижней П., то число S =
называется площадью фигуры, а сама фигура ‒ квадрируемой фигурой. Для того чтобы плоская фигура была квадрируемой, необходимо и достаточно, чтобы для любого положительного числа e можно было указать такой описанный вокруг фигуры многоугольник и такой вписанный в фигуру многоугольник, разность Sd‒Si площадей которых была бы меньше e.
Аналитически П. плоской фигуры может быть вычислена с помощью интегралов. Пусть фигура F ‒ т. н. криволинейная трапеция (рис. 1) ‒ ограничена графиком заданной на сегменте [a, b] непрерывной и неотрицательной функции f (x), отрезками прямых х = а и х = b и отрезком оси Ox между точками (а, 0) и (b, 0). П. такой фигуры может быть выражена интегралом
.
П. фигуры, ограниченной замкнутым контуром, который встречается с параллелью к оси Оу не более чем в двух точках, может быть вычислена как разность П. двух фигур, подобных криволинейной трапеции. П. фигуры может быть выражена в виде двойного интеграла:
,
где интегрирование распространяется на часть плоскости, занятой фигурой.
Теория П. фигур, расположенных на кривой поверхности, может быть определена следующим образом. Пусть F ‒ односвязная фигура на гладкой поверхности, ограниченная кусочно гладким контуром. Фигура F разбивается кусочно гладкими кривыми на конечное число частей Фi, каждая из которых однозначно проектируется на касательную плоскость, проходящую через точку Mi, принадлежащую части Фi, (рис.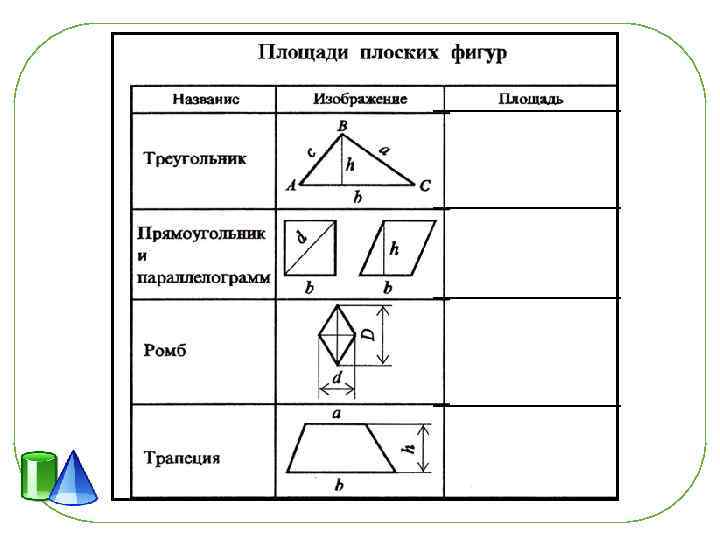
2). Предел сумм площадей этих проекций (если он существует), взятых по всем элементам разбиения, при условиях, что максимум диаметров этих элементов стремится к нулю и что он не зависит от выбора точек Mi, называется площадью фигуры F. Фигура на поверхности, для которой этот предел существует, называется квадрируемой. Квадрируемыми являются кусочно гладкие ограниченные полные двусторонние поверхности. П. всей поверхности слагается из П. составляющих её частей.
Аналитически П. фигуры F на поверхности, заданной уравнением z = f (x, у), где функция f однозначна и имеет непрерывные частные производные, может быть выражена следующим образом
.
Здесь G ‒ замкнутая область, являющаяся проекцией фигуры F на плоскость Оху, ds ‒ элемент площади на поверхности.
Об обобщении понятия П. см. Мера множеств.
Лит.: Фихтенгольц Г. М., Курс дифференциального и интегрального исчисления, 7 изд., т. 2, М., 1969; Кудрявцев Л. Д., Математический анализ, т.
1‒2, М., 1970; Ильин В. А., Позняк Э. Г., Основы математического анализа, 3 изд., ч. 1‒2, М., 1971‒73.
Solid Geometry on SAT Math: The Complete Guide
Геометрия — это раздел математики, который имеет дело с точками, линиями, формами и углами. Вопросы по геометрии SAT проверят ваши знания о формах, размерах и объемах различных фигур, а также об их положении в пространстве.
25-30% математических задач SAT будут включать геометрию , в зависимости от конкретного теста.
Поскольку геометрия в целом охватывает так много различных математических понятий, существует несколько различных подразделов геометрии (включая плоскую, объемную и координатную). Мы рассмотрим каждую область геометрии в отдельных руководствах с пошаговым подходом к вопросам и примерам задач.
Эта статья будет вашим исчерпывающим руководством по объемной геометрии на SAT . Мы познакомим вас со значением объемной геометрии, формулами и пониманием, которые вам необходимо знать, и как решить некоторые из самых сложных задач объемной геометрии, связанных с кубами, сферами и цилиндрами на SAT.
Прежде чем продолжить, имейте в виду, что обычно на каждом SAT будет только 1-2 вопроса по объемной геометрии, , поэтому вам следует в первую очередь изучать планарную (плоскую) геометрию и координатную геометрию. Оставьте изучение этого руководства напоследок с точки зрения подготовки к SAT по математике.
Прежде чем опуститься в царство объемной геометрии, убедитесь, что вы хорошо разбираетесь в планиметрии и координатной геометрии!
Что такое объемная геометрия?
Объемная геометрия — это название геометрии, выполненной в трех измерениях. Это означает, что к планарной (плоской) геометрии, которая использует только высоту и длину, добавляется еще одно измерение — объем.
Вместо плоских фигур, таких как круги, квадраты и треугольники, объемная геометрия имеет дело со сферами, кубами и пирамидами (наряду с любыми другими трехмерными формами).
И вместо того, чтобы использовать периметр и площадь для измерения плоских форм, твердотельная геометрия использует площадь поверхности и объем для измерения своих трехмерных форм.
Круг – это плоский объект. Это плоскостная геометрия.
Сфера представляет собой трехмерный объект. Это сплошная геометрия.
В SAT большинство задач по твердотельной геометрии расположены в конце каждого раздела. Это означает, что задачи по объемной геометрии считаются одними из самых сложных вопросов (или теми, которые занимают больше всего времени, поскольку их часто нужно решать несколькими частями). Используйте эти знания, чтобы сосредоточить свое внимание на обучении на наиболее продуктивных направлениях.
Если вы неправильно ответили на несколько вопросов в начале и в середине каждого раздела по математике, возможно, вам будет более продуктивно потратить время на то, чтобы сначала обновить свое общее понимание математических концепций, охватываемых SAT.
Вы также можете узнать, как улучшить свой балл по математике или обновить свое понимание всех формул, которые вам понадобятся.
Примечание: большинство формул SAT Math по объемной геометрии даются вам на тесте либо в поле формул, либо в самом вопросе. Если вы не уверены, какие формулы даны, а какие нет в математическом разделе, освежите свои знания о формулах.
Это поле с формулой, которое вы получите на всех математических разделах SAT. Вам даны формулы для объема прямоугольного тела и объема цилиндра. Другие формулы часто будут даваться вам в самом вопросе.
Но хотя многие формулы уже даны, вам все же важно понять, как они работают и почему . Так что не беспокойтесь о том, чтобы их запомнить, но do обратите на них внимание, чтобы углубить свое понимание принципов пространственной геометрии на SAT.
В этом руководстве я разделил подход к SAT по объемной геометрии на три категории:
№1: Типичные вопросы SAT по объемной геометрии
№2: Типы геометрических тел и их формулы
#3: Как решить задачу SAT по объемной геометрии с помощью наших математических стратегий SAT
Приключения по объемной геометрии, вот и мы!
Типичные вопросы по объемной геометрии на SAT
Прежде чем мы рассмотрим формулы, которые вам понадобятся для изучения твердотельной геометрии, важно ознакомиться с видами вопросов, которые SAT задаст вам о твердых телах.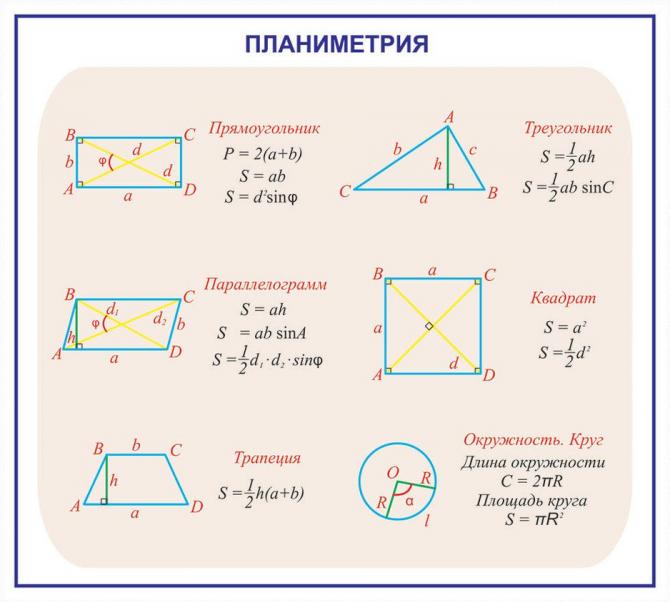
Вопросы SAT по объемной геометрии будут представлены в двух форматах: вопросы, в которых вам дается диаграмма, и вопросы со словами.
Независимо от формата, каждый тип вопросов SAT по объемной геометрии существует для проверки вашего понимания объема и/или площади поверхности фигуры. Вас спросят, как найти объем или площадь поверхности фигуры, или вас попросят определить, как смещаются и изменяются размеры фигуры.
Задачи с диаграммами
Задачи на диаграмму объемной геометрии предоставят вам рисунок геометрического тела и попросят вас найти недостающий элемент изображения. Иногда вас попросят найти объем фигуры, площадь поверхности фигуры или расстояние между двумя точками на фигуре. Вас также могут попросить сравнить объемы, площади поверхности или расстояния между несколькими разными фигурами.
Это типичный вопрос SAT о сравнении твердых веществ. Мы рассмотрим, как решить это позже в руководстве.
Сложные задачи
Сложные задачи по геометрии обычно требуют сравнения площади поверхности или объема двух фигур.
Они часто дают вам размеры одного твердого тела, а затем просят сравнить его объем или площадь поверхности с твердым телом с другими размерами.
На сколько кубических футов ящик высотой 2 дюйма, шириной 6 дюймов и глубиной 1 дюйм больше, чем цилиндр высотой 4 дюйма и диаметром 6 дюймов?
Это типичный вопрос со словами, который может появиться в разделе таблицы SAT по математике. Это просто еще один способ заставить вас задуматься об объеме фигуры и способах его измерения.
Каков минимально возможный объем куба в кубических дюймах, в который можно вписать сферу радиусом 3 дюйма?
A) 12√3$ (приблизительно 20,78$)
B) 24√3$ (приблизительно 41,57$)
C) 36√3$ (примерно 62,35$)
D) 216$
E) 1728$ Мы рассмотрим, как решить это позже в руководстве.
Текстовые задачи по объемной геометрии могут сбивать с толку многих людей, потому что без картинки сложно представить вопрос.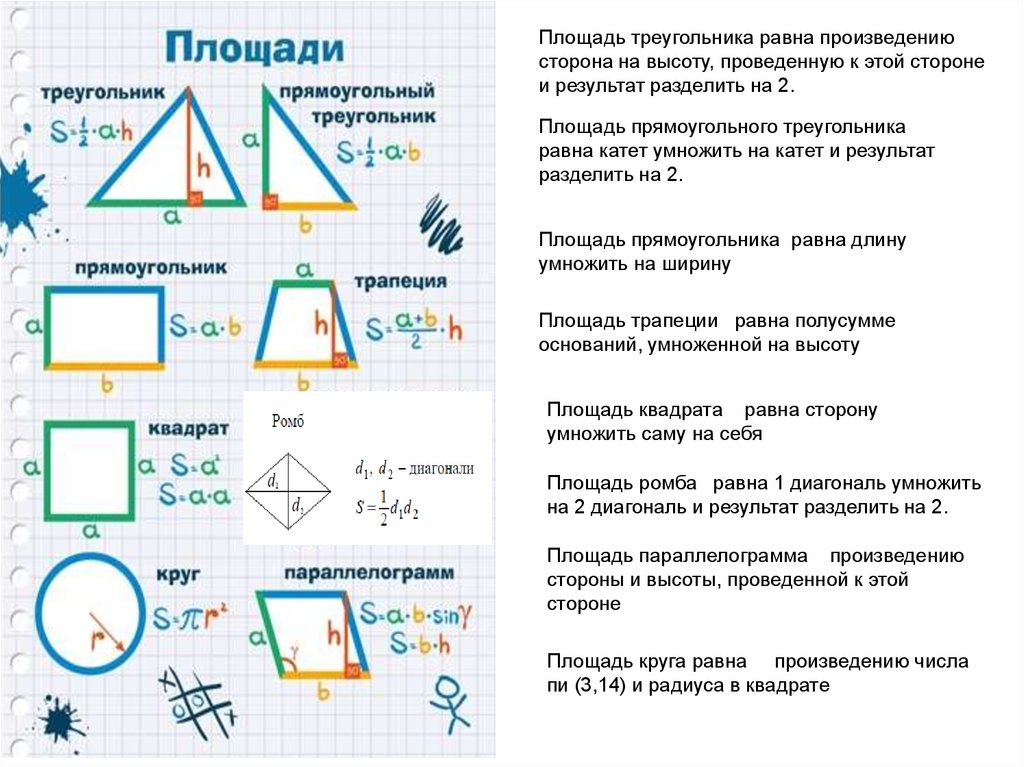
Как всегда со словесными задачами, описывающими формы или углы, рисуйте сами! Простое видение того, что описывает вопрос, может творить чудеса, помогая прояснить вопрос.
Общий стиль вопросов по объемной геометрии
Каждый вопрос по объемной геометрии в SAT связан либо с объемом, либо с площадью поверхности фигуры, либо с расстоянием между двумя точками на фигуре. Иногда вам придется комбинировать площадь поверхности и объем, иногда вам придется сравнивать два твердых тела друг с другом, но в конечном итоге все вопросы по геометрии твердого тела сводятся к этим понятиям.
Итак, теперь давайте рассмотрим, как найти объемы, площади поверхности и расстояния для всех различных геометрических тел на SAT.
Прекрасный пример геометрических тел в дикой природе
Призмы
Призма представляет собой трехмерную форму, которая имеет (как минимум) два конгруэнтных параллельных основания. По сути, вы можете взять призму и носить ее, прижав противоположные стороны к ладоням.
Некоторые из множества различных видов призм.
Прямоугольные тела
Прямоугольное тело по существу представляет собой коробку. Он имеет три пары противоположных сторон, которые конгруэнтны и параллельны.
Объем
$\Объем = lwh$
Объем фигуры есть мера ее внутреннего пространства.
- $l$ длина фигуры
- $w$ — ширина фигуры
- $h$ — высота цифры
Обратите внимание, что эта формула аналогична нахождению площади квадрата ($A = lw$) с добавленным измерением высоты, поскольку это трехмерная фигура
Сначала определите тип вопроса — он запрашивает объем или площадь поверхности? Вопрос касается внутреннего пространства твердого тела, поэтому это вопрос объема.
Теперь нам нужно найти прямоугольный объем, но этот вопрос несколько сложен.
$V = lwh$ => $(4)(3)(1) = 12\кубических\футов$
(Почему мы умножили футы и ширину на 1 вместо 2? Потому что вода доходит только до 1 фут; он не заполняет все 2 фута высоты резервуара)
Теперь мы собираемся налить эти 12 кубических футов воды во второй резервуар. Этот второй бак имеет общий объем:
$V = lwh$ => $(3)(2)(4) = 24\кубических\фута$
Хотя второй бак может вместить 24 кубических фута воды, мы кладут только 12. Так что 12/24 = 1/2$.
Вода будет подниматься ровно на половину высоты второго резервуара, что означает ответ D , 2 фута.
В любом случае, эти рыбы не будут очень счастливы в половине аквариума с водой
Площадь поверхности
найдите площадь поверхности прямоугольной призмы, вы найдете площади всех плоских прямоугольников на поверхности фигуры (граней), а затем сложите эти площади вместе.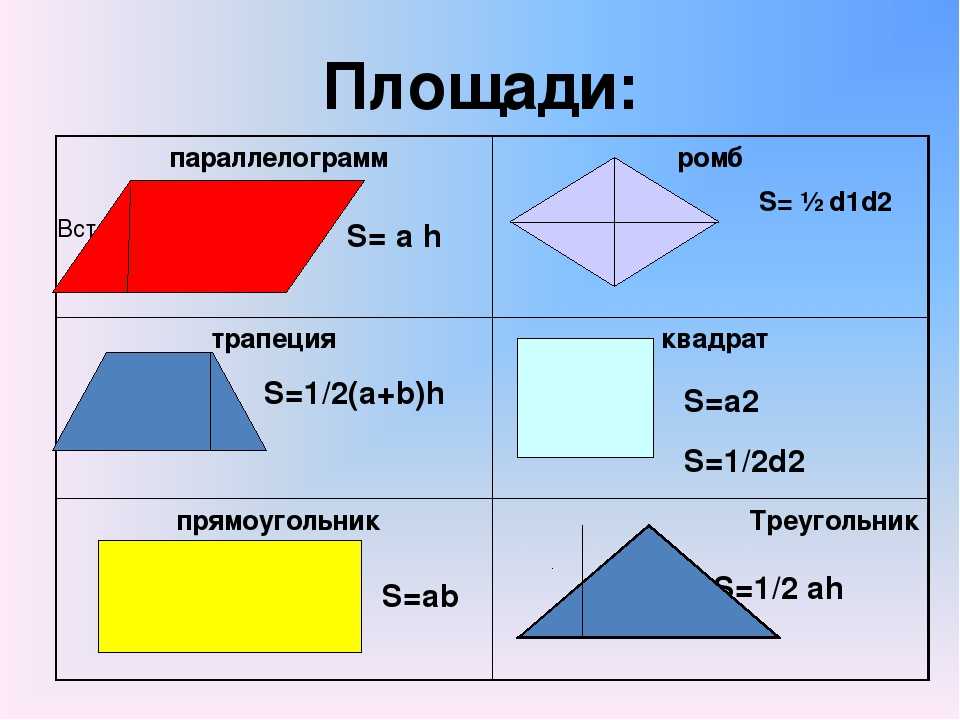
У прямоугольного твердого тела снаружи фигуры шесть граней. Они разделены на три конгруэнтные пары противоположных сторон.
Если вам трудно изобразить площадь поверхности, помните, что у игральной кости шесть граней.
Итак, вы находите площади трех комбинаций длины, ширины и высоты (lw, lh и wh), которые затем умножаете на два, потому что у каждой из этих комбинаций есть две стороны. Полученные площади затем складываются вместе, чтобы получить площадь поверхности. 92]$
Диагональ прямоугольного тела – это самая длинная внутренняя линия тела. Он касается от угла одной стороны призмы до противоположного угла другой.
Вы можете найти эту диагональ, либо используя приведенную выше формулу, либо разбив фигуру на два плоских треугольника и применив теорему Пифагора для обоих. Вы всегда можете это сделать, если не хотите запоминать формулу или боитесь неправильно запомнить формулу в день экзамена.
93 = 216$
Или вы можете использовать формулу, чтобы найти объем любого прямоугольного тела:
$\Volume = lwh$ => $(6)(6)(6) = 216$
Теперь найдите объем одного из меньших прямоугольных тел:
$\Volume = lwh$ => $(3)(2)(1) = 6$
И разделите большее прямоугольное тело на меньшее, чтобы узнать, сколько меньших прямоугольные тела могут поместиться внутри большего:
$216/6 = 36$
Итак, ваш окончательный ответ D , 36 92$
Длина диагонали
$\Diagonal = s√3$
Как и в случае с прямоугольным телом, вы можете разбить куб на два плоских треугольника и использовать теорему Пифагора для обоих в качестве альтернативы формула.
Это точно такой же процесс, как нахождение диагонали прямоугольного тела.
Сначала найдите длину диагонали (гипотенузы) основания тела, используя теорему Пифагора.
Затем используйте эту длину как одну из меньших сторон нового треугольника с диагональю прямоугольного тела в качестве новой гипотенузы.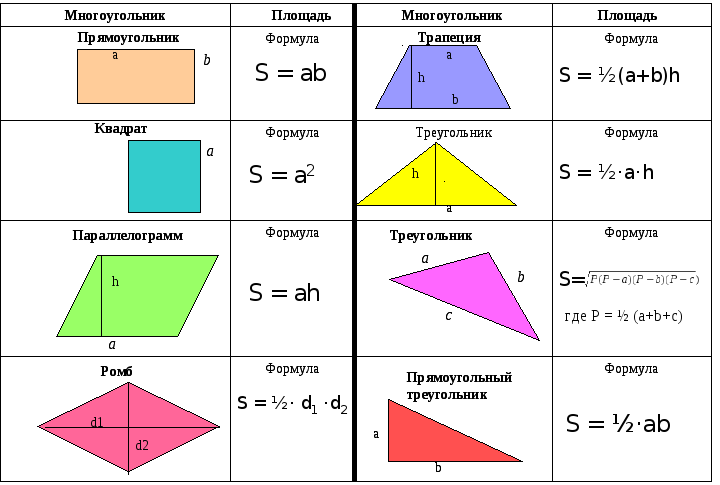
Найдите диагональ, снова используя теорему Пифагора.
Цилиндры
Цилиндр представляет собой призму с двумя круглыми основаниями на противоположных сторонах Нарисуйте фигуру, которую они описывают.
Если диаметр его круглых оснований равен 4, это означает, что его радиус равен 2. Теперь у нас есть две длины сторон прямоугольного треугольника. Используя теорему Пифагора, найдите длину гипотенузы. 92h$
- $π$ — универсальная константа, также представленная как 3,14(159)
- $r$ — радиус круглого основания. Это любая прямая линия, проведенная от центра круга к окружности круга.
- $h$ — высота круга. Это прямая линия, соединяющая два круглых основания.
Эта задача требует, чтобы вы поняли, как получить объем прямоугольного тела и объем цилиндра, чтобы сравнить их. 92)(4) = 16π$ или $50,27$
Объемы прямоугольных тел находятся по формуле:
$V = lwh$
Таким образом, объем тела A равен $(3)(3)(3) = 27$
Тело B имеет объем $(4)(3)(3) = 36$
Тело C имеет объем $(5)(4)(3) = 60$
Тело D имеет объем объем $(4)(4)(4) = 64$
И твердый E имеет объем $(4)(4)(3) = 48$
Таким образом, ответ равен E , 48
Поверхность трубы также можно записать как $SA = πdh$, потому что диаметр в два раза больше радиуса. Другими словами, поверхность трубы — это формула длины окружности с дополнительным измерением высоты.
Твердые тела без призмы
Твердые тела без призмы – это фигуры в трех измерениях, не имеющие параллельных конгруэнтных сторон. Если вы возьмете эти фигуры рукой, максимум одна сторона (если таковая имеется) будет плоско прилегать к вашей ладони.
Конусы
Конус похож на цилиндр, но имеет только одно круглое основание вместо двух. Его противоположный конец заканчивается точкой, а не кругом.
Есть два вида конусов — прямые конусы и косые конусы. Для целей SAT вам нужно заботиться только о правильных конусах. Наклонные конусы ограничены предметными тестами по математике I и II.
Правильный конус имеет вершину (конечная точка сверху), которая находится непосредственно над центром круглого основания конуса.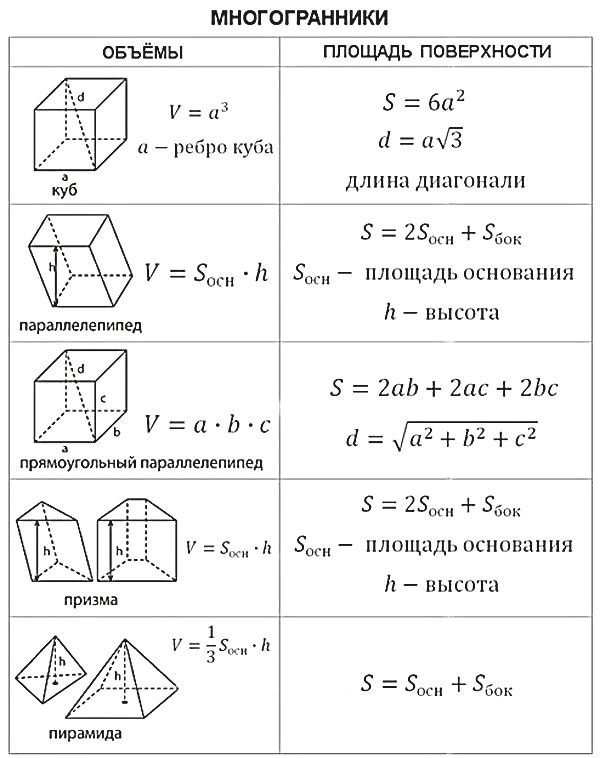
92h$
- $π$ — константа, записанная как 3.14(159)
- $r$ — радиус круглого основания
- $h$ — высота, проведенная под прямым углом от вершины конуса к центру круглого основания
Объем конуса составляет $1/3$ объема цилиндра. Логически это имеет смысл, поскольку конус — это, по сути, цилиндр с одним основанием, свернутым в точку. Таким образом, объем конуса будет меньше объема цилиндра.
Площадь поверхности 92$) и площадь боковой поверхности ($πrl$)
Поскольку прямые конусы образуют прямоугольный треугольник с длинами сторон: $h$, $l$ и $r$, вы часто можете использовать теорему Пифагора для решения задач .
Пирамиды
Пирамиды представляют собой геометрические тела, похожие на конусы, за исключением того, что они имеют многоугольник в основании и плоские треугольные стороны, сходящиеся в вершине.
Существует много типов пирамид, определяемых формой их основания и углом их вершины, но ради SAT вам нужно заботиться только о правильных квадратных пирамидах.
92h$, так как основание квадратное, поэтому длины сторон одинаковы.
Сферы
Сфера представляет собой трехмерный круг. В круге любая прямая линия, проведенная из центра в любую точку на окружности, будет равноудалена. Это расстояние является радиусом (r). В сфере этот радиус может простираться в трех измерениях, поэтому все линии от поверхности сферы до центра сферы равноудалены.
Том 93$
Вписанные тела
Наиболее распространенными вписанными телами на SAT будут: куб внутри сферы и сфера внутри куба. Вы можете получить совершенно другую форму, но основные принципы работы с вписанными формами все равно будут применяться. Чаще всего этот вопрос является тестом Вам часто приходится знать принципы и формулы твердотельной геометрии для каждой формы в отдельности, чтобы иметь возможность собрать их вместе.
При работе с вписанными фигурами рисуйте на схеме, которую они вам дают.
если они не давать вам схему, сделайте свою! Рисуя свои собственные линии, вы сможете лучше преобразовать трехмерные объекты в серию двухмерных объектов, которые чаще всего приведут вас к вашему решению.
Поймите, что когда вам дают тело внутри другого тела, это не просто так. Это может показаться вам запутанным, но SAT всегда даст вам достаточно информации для решения проблемы.
Например, одна и та же линия будет иметь разное значение для каждой фигуры, и это часто является ключом к решению проблемы.
Итак, у нас есть вписанное тело и нет рисунка. Итак, первым делом сделайте свой рисунок!
Теперь, поскольку у нас есть сфера внутри куба, вы можете видеть, что радиус сферы всегда равен половине длины любой стороны куба (поскольку у куба по определению все стороны равны). Итак, $2r$ — это длина всех сторон куба. Теперь подставьте $2r$ в формулу нахождения объема куба.
Вы можете использовать формулу объема куба: 93$.
Для подавляющего большинства вопросов о вписанных телах радиус (или диаметр) круга будет ключом к решению вопроса. Радиус сферы будет равен половине длины стороны куба, если куб находится внутри сферы (как в вопросе выше). Это означает, что диаметр сферы будет равен одной стороне куба, потому что диаметр в два раза больше радиуса. .
Но что произойдет, если у вас есть сфера внутри куба? В этом случае диаметр сферы фактически становится диагональ куб.
Каков максимально возможный объем куба в кубических дюймах, который можно вписать внутрь сферы радиусом 3 дюйма?
A) 12√3$ (приблизительно 20,78$)
B) 24√3$ (приблизительно 41,57$)
C) 36√3$ (приблизительно 62,35$)
9002D) 9002$ $Сначала нарисуйте фигуру.
Вы можете видеть, что, в отличие от случая, когда сфера была вписана в куб, сторона куба не в два раза больше радиуса круга, потому что между сторонами куба и окружностью сферы есть зазоры.
Единственная прямая линия куба, которая касается двух противоположных сторон сферы, является диагональю куба.
93 = 12√12 = 24√3$
Хотя поначалу объемная геометрия может показаться запутанной, практика и внимание к деталям помогут вам найти правильный ответ
Выводы
2 Вопросы по объемной геометрии на SAT всегда будут касаться объема, площади поверхности или расстояния между точками на фигуре. Они усложняют задачу, заставляя вас сравнивать элементы разных фигур или заставляя выполнять несколько шагов для каждой задачи.
Но вы всегда можете разбить любой вопрос SAT на более мелкие части.
Этапы решения задачи объемной геометрии
#1: Определите, что задача просит вас найти.
Задача спрашивает о кубах или сферах? Оба? Вас просят найти объем или площадь поверхности фигуры? Оба?
Убедитесь, что вы понимаете, какие формулы вам понадобятся и с какими элементами геометрического тела (тел) вы имеете дело.
#2: Нарисуйте
Нарисуйте изображение в любое время, когда они описывают твердое тело, не предоставляя вам изображения. Это часто позволяет легче увидеть, какая именно информация у вас есть, и как вы можете использовать эту информацию, чтобы найти то, что вопрос просит вас предоставить.
#3: Используйте свои формулы
После того, как вы определили формулы, которые вам понадобятся, часто достаточно просто ввести предоставленную информацию.
Если вы не можете вспомнить свои формулы (например, формулу для диагонали), используйте альтернативные методы, чтобы найти ответ, например, теорему Пифагора.
№ 4. Следите за чистотой информации и дважды проверяйте свою работу
Обязательно ли вы маркировали свою работу? Создатели теста знают, что учащиеся легко могут стать неряшливыми в условиях высокого стресса, и соответственно подбрасывают ответы-приманки.
Поэтому убедитесь, что объем вашего цилиндра и объем вашего куба помечены соответствующим образом.
И не забудьте перепроверить свой ответ, если у вас есть время! Имеет ли смысл говорить, что ящик высотой 20 футов может поместиться в ящик объемом 15 кубических футов? Точно нет! Убедитесь, что все элементы вашего ответа и вашей работы находятся в правильном месте, прежде чем вы закончите.
Следуйте инструкциям по решению задач по объемной геометрии, и вы получите это золото. это просто плоская геометрия, перенесенная в третье измерение. Если вы сможете понять, как каждая из этих форм меняется и соотносится друг с другом, вы сможете справиться с этим разделом SAT с большей легкостью, чем когда-либо прежде.
Что дальше?
Теперь, когда вы сделали свои шаги по объемной геометрии, может быть хорошей идеей просмотреть все математические темы, протестированные на SAT, чтобы убедиться, что вы хорошо их усвоили. Хотите получить высший балл? Ознакомьтесь с нашей статьей о том, как получить 800 баллов по математике SAT идеальным оценщиком SAT.
Сейчас средний результат? Не хватает времени на математический раздел? Не читайте дальше наших статей о том, как улучшить свой балл, если в настоящее время ваш балл ниже диапазона 600 и как остановить нехватку времени на SAT по математике.
Хотите улучшить свой результат SAT на 160 баллов?
Ознакомьтесь с нашей лучшей в своем классе онлайн-программой подготовки к SAT. Мы гарантируем возврат ваших денег, если вы не улучшите свой результат SAT на 160 или более баллов.
Наша программа полностью онлайн, и она настраивает то, что вы изучаете, в соответствии с вашими сильными и слабыми сторонами. Если вам понравилось это руководство по математической стратегии, вам понравится и наша программа. Наряду с более подробными уроками вы получите тысячи практических задач SAT Math, организованных по отдельным навыкам, чтобы вы могли учиться наиболее эффективно. Мы также дадим вам пошаговую программу, чтобы вы никогда не запутались в том, что изучать дальше.
Ознакомьтесь с нашей 5-дневной бесплатной пробной версией:
Геометрические формулы | Superprof
В этой статье мы составили список геометрических формул, которые весьма полезны при решении вопросов, связанных с площадями, объемами и периметрами геометрических фигур. Итак, давайте начнем.
Формулы площади и периметра
В этом разделе мы составили список формул площади и периметра различных геометрических фигур.
Площадь геометрической фигуры – это площадь в квадратных единицах длины, занимаемая поверхностью геометрической фигуры. С другой стороны, периметр относится к расстоянию вокруг замкнутой геометрической фигуры или формы.
Треугольник
Треугольник — одна из самых фундаментальных геометрических фигур, состоящая из трех сторон и трех вершин. Сумма внутренних углов треугольника равна 180 градусов. Треугольники бывают равносторонними, равнобедренными и разносторонними.
Формула площади треугольника:
Площадь =
Формулы периметра равностороннего, равнобедренного и разностороннего треугольника немного отличаются.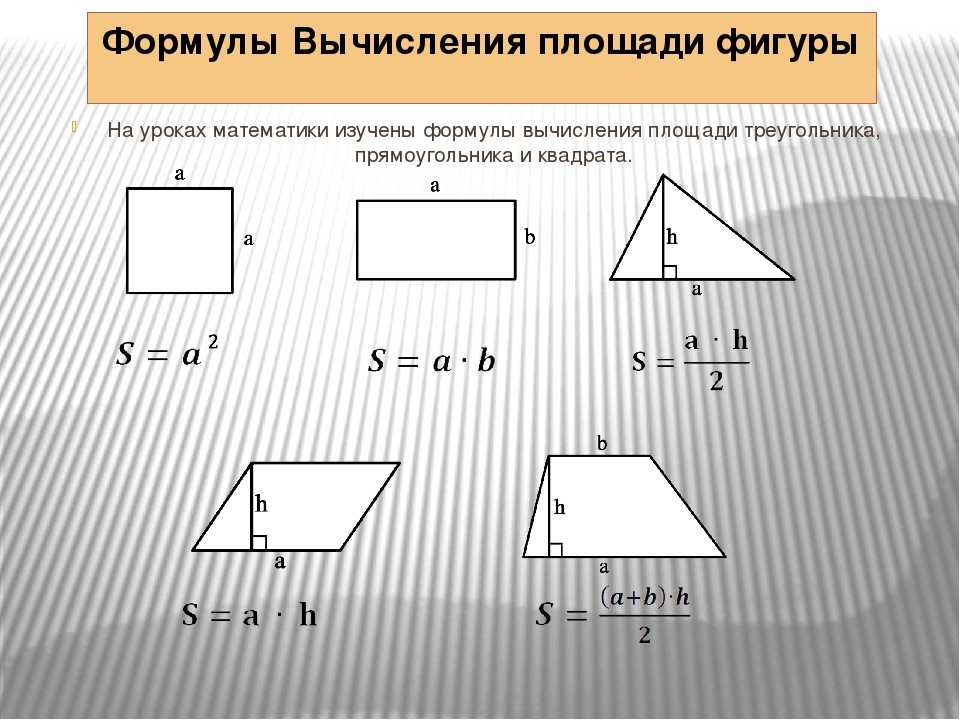
По сути, все они включают сложение длин трех сторон треугольника.
Периметр равностороннего треугольника = 3 x длина его стороны
Периметр равнобедренного треугольника = 2 x длина + основание
Периметр разностороннего треугольника = P = a + b + c
Квадрат
Квадрат относится к правильному четырехугольнику, который имеет четыре равные стороны и углы. Это означает, что все стороны квадрата имеют одинаковую длину и все углы равны.
Формула площади квадрата:
Площадь = l x l
Формула для вычисления периметра квадрата:
Периметр = 4 x длина стороны
Прямоугольник
четырехугольник с четырьмя прямыми углами. Противоположные стороны прямоугольника имеют одинаковую длину и параллельны друг другу.
Формула площади прямоугольника:
Площадь = l x w, где l — длина прямоугольника, а w — его ширина
Формула периметра прямоугольника:
Периметр = 2 (l + w)
Ромб
Ромбом называется параллелограмм с четырьмя равными сторонами и противоположными равными углами.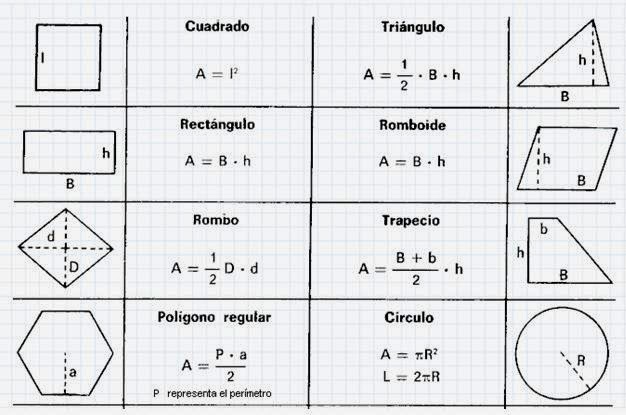
Это означает, что все четыре стороны ромба имеют одинаковую длину и противоположные углы равны.
Формула для вычисления площади ромба:
Площадь = , здесь D и d представляют собой диагонали ромба
Формула для расчета периметра ромба:
Периметр = 4 x длина стороны ромба параллелограмма, у которого смежные стороны имеют разную длину, а углы не равны 90 градусам.
Формула для вычисления площади ромба:
Площадь = основание x высота
Формула для вычисления периметра ромба:
Периметр = 2 . (a + b), где a и b — стороны ромба
Площадь трапеции
Трапеция — это четырехугольник с одной парой параллельных сторон, как показано на рисунке ниже:
Формула для расчета площади трапеция:
Площадь =
Площадь правильного многоугольника
В геометрии правильный многоугольник — это равносторонний и равноугольный многоугольник. Это означает, что все стороны правильного многоугольника имеют одинаковую длину и все его углы имеют одинаковую величину.
Формула для вычисления площади правильного многоугольника:
Площадь =
Формула для вычисления периметра правильного многоугольника:
Периметр = n x l, где n обозначает количество сторон многоугольника
Многоугольник
Если у вас есть неправильный многоугольник, похожий на рисунок, приведенный ниже, то вы можете рассчитать площадь путем триангуляции многоугольника и добавления площади этих треугольников.
Круг
Окружность – это геометрическая фигура, все точки которой расположены на равном расстоянии от ее центра.
Вместо периметра у круга есть окружность. Формула для расчета длины окружности:
, где имеет фиксированное значение, а «r» — радиус окружности
Так как радиус окружности равен половине ее диаметра, значит, мы также можем написать формулу длины окружности круга, как показано ниже:
Формула для расчета площади круга:
, где r — радиус окружности
Сектор окружности
Сектор окружности, также называемый центром диска или центром окружности, представляет собой часть окружности, заключенную в дугу и два радиуса окружности.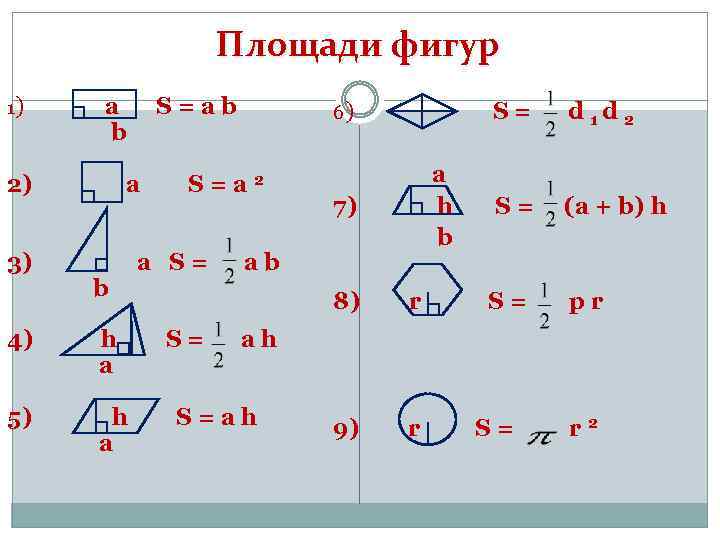
Формула для вычисления площади кругового сектора приведена ниже:
Формула для вычисления длины дуги кругового сектора:
Круговой сегмент
«отрезается» от остальной окружности хордой или секущей.
Формула для расчета площади сегмента окружности:
Площадь сегмента окружности AB = площадь сектора окружности AOB — площадь треугольника AOB
Луна Гиппократа
по двум дугам окружности. Вы можете прочитать нашу статью здесь, чтобы узнать больше об этой концепции.
Площадь луночки = площадь полукруга − площадь кругового сегмента.
Площадь лунки = Площадь прямоугольного треугольника
Круговая трапеция
В двух заданных концентрических окружностях круговая трапеция относится к области, лежащей между двумя непересекающимися хордами окружности.
Формула вычисления площади круглой трапеции приведена ниже:
Площадь, заключенная между двумя концентрическими окружностями
Формула вычисления площади между двумя концентрическими окружностями приведена ниже:
Лучшие математики доступно
Поехали
Формулы площади и объема
В этом разделе статьи мы составили список формул площади поверхности и объема различных геометрических фигур.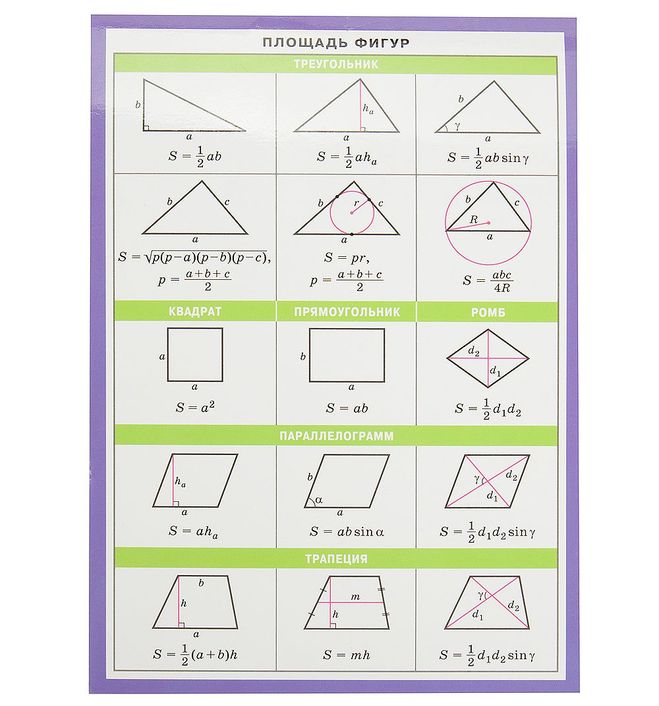
Тетраэдр
Тетраэдром называется твердое тело, содержащее четыре плоские треугольные грани
Формула для расчета площади тетраэдра:
Формула для расчета объема тетраэдра:
Октаэдр
Октаэдр относится к трехмерной форме, которая имеет восемь плоских граней.
Формула для вычисления площади октаэдра:
Формула для вычисления объема октаэдра:
Икосаэдр
Икосаэдр относится к объемной фигуре, которая содержит 20 плоских граней.
Формула вычисления площади икосаэдра:
Формула вычисления объема тетраэдра:
Додекаэдр
Додекаэдр — это трехмерная фигура с двенадцатью плоскими гранями.
Формула вычисления площади додекаэдра:
Формула вычисления объема додекаэдра:
Куб
Трехмерная фигура, содержащая шесть равных квадратов, называется кубом.
Формула для расчета объема куба:
Формула для расчета площади поверхности куба:
Прямоугольный параллелепипед
Трехмерная геометрическая фигура, содержащая шесть прямоугольных граней, известна как прямоугольный параллелепипед.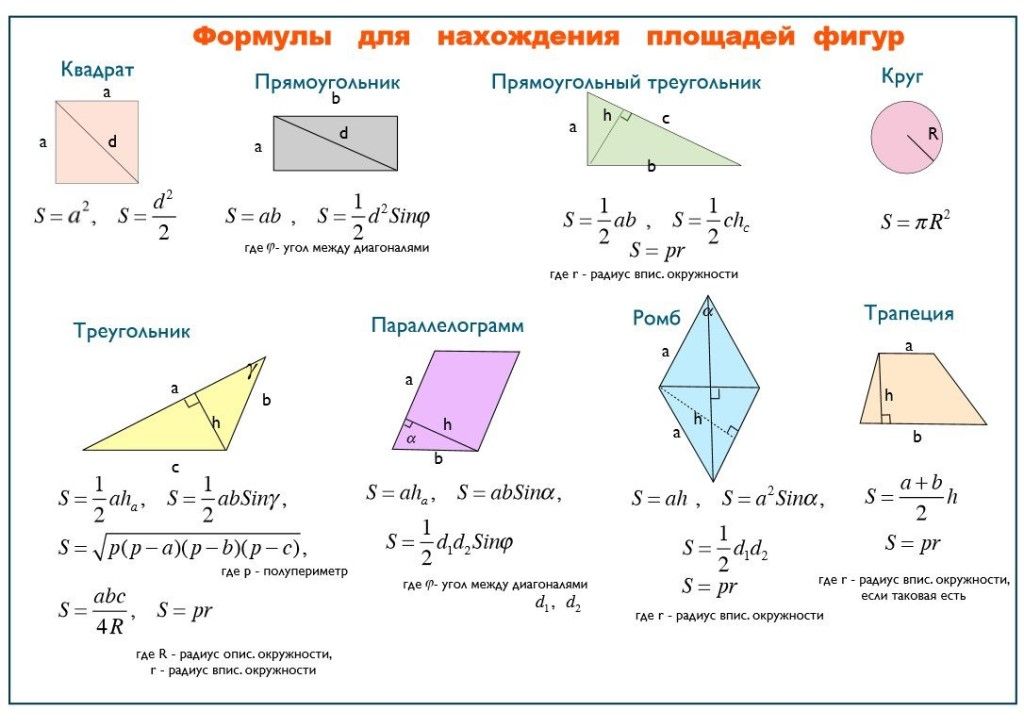
Призма
Под призмой понимается объемная геометрическая фигура, два конца которой равны, подобны и параллельны прямолинейным фигурам, а стороны представляют собой параллелограммы, как показано на рисунке ниже:
= Периметр основания
Пирамида
В геометрии пирамидой называется многогранник, образованный соединением многоугольника с точкой, известной как вершина
= Периметр основания
Ap = апофема вершины пирамида
ap = апофема основания
Усеченная пирамида
Усеченная пирамида получается в результате разрезания пирамиды плоскостью, параллельной основанию, и частями.
P = Периметр большего основания
P’ = Периметр меньшего основания
A = Площадь большего основания
A’ = Площадь меньшего основания
Циндер 3 цилиндр, как показано ниже, относится к поверхности, которая содержит все точки на всех линиях, которые параллельны данной линии и проходят через фиксированную плоскую кривую в плоскости, не параллельной данной линии.