Урок геометрии в 7 классе по теме «Медиана, биссектриса, высота треугольника»
Урок геометрии в 7 классе
Тема: Медиана, биссектриса, высота треугольника.
Автор: Григорян Жанна Виктори,
учитель математики высшей квалификационной категории
2016г.
Тема: Медиана, биссектриса, высота треугольника.
Тип урока: «Исследовательская работа»
Цели урока:
— дидактическая:
сформировать понятия «медиана треугольника», «биссектриса треугольника», «высота треугольника»;
— психологическая:
обучать умению математически грамотно проводить рассуждения; развивать творческое мышление учащихся;
— воспитательная:
активизировать умственную деятельность учащихся.
Оборудование:
1. Интерактивная доска
2. Компьютеры у учащихся
3. Линейка, транспортир, угольник.
4. Карточки для работы готовыми чертежами.
5. Бланк практической работы.
План урока.
I. Мотивация. Постановка учебной задачи.
II. Решение учебной
части.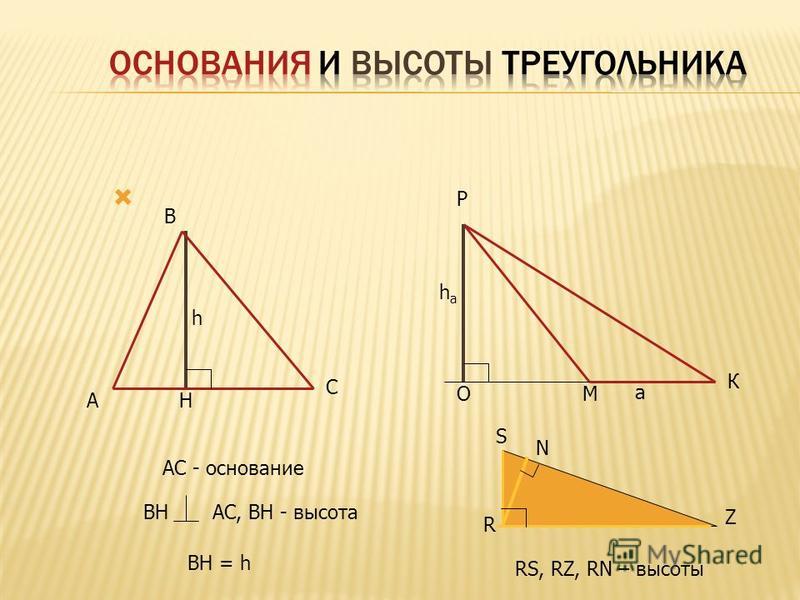
Задание 1.
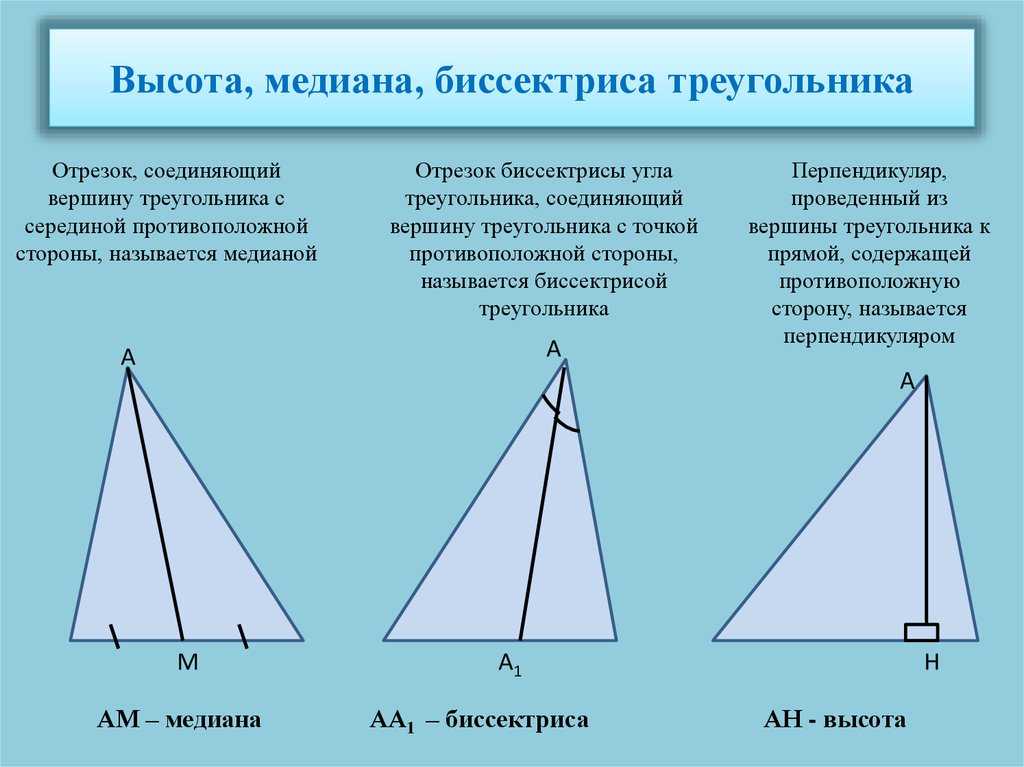
Установить понятие «высота треугольника».
Задание 2.
Установить понятие «биссектриса треугольника».
Задание 3.
Установить понятие «медиана треугольника».
Задание 4.
Сформулировать свойства высот, биссектрис, медиан треугольника.
III. Обобщение урока. Домашнее задание.
Содержание урока.
I. Ориентировочно-мотивационный этап. 10 минут.
1) Выравнивание знаний.
Что такое треугольник?
Из каких элементов он состоит?
Первый признак равенства треугольников?
Что такое отрезок?
Что такое середина отрезка?
Что такое биссектриса угла?
2) Постановка цели урока.
Кроме названных вами элементов треугольника в этой фигуре есть еще
линии, которые очень важны для дальнейшего изучения геометрии.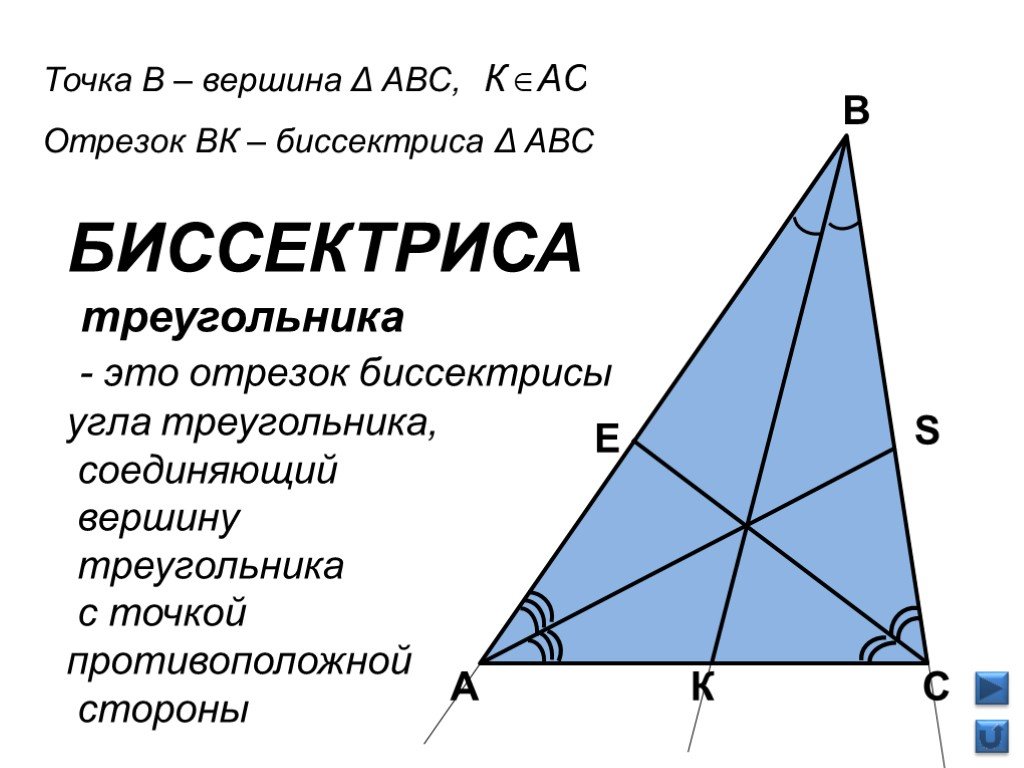 Важны до такой
степени, что их даже называют Замечательные линии треугольника. Какая у нас
сегодня цель на уроке? (Формулировка учащимися цели урока)
Важны до такой
степени, что их даже называют Замечательные линии треугольника. Какая у нас
сегодня цель на уроке? (Формулировка учащимися цели урока)
3) Задание на формулировку темы урока
Распределить треугольники на три группы.
Почему так распределили. В первой группе в треугольнике проведен отрезок, который называется медианой треугольника, во второй группе – биссектриса треугольника. И в третьей группы – высота треугольника.
Историческая справка.
Эти слова пришли к нам из латинского языка. Например, слово «биссектриса» означает «бис» — дважды и «сектио» — рассечение, т.е.«рассекающая надвое». Слово «перпендикуляр» означает «пендула» — маятник, отвес. Таким образом, перпендикуляром называли когда-то просто вертикальное направление. Оно образует прямой угол с земной поверхностью.
Сегодня мы сформулируем определения: «высота
треугольника», «медиана треугольника», «биссектриса треугольника» и совместно
составим алгоритмы их построения.
II. Операционально-исполнительский этап.
Попробуйте дать определение медианы, глядя на рисунок. Давайте дадим определение медианы треугольника, биссектрисы треугольника, высоты треугольника.
Запоминалки:
Биссектриса — это крыса, которая бегает по углам и делит угол пополам.
Медиана – обезьяна, она идет по сторонам и делит стороны пополам.
Выстота похожа на кота, который выгнет спину и под прямым углом соединит вершину со стороной хвостом.
Задание 1.
Построить отрезок, соединяющий вершину треугольника с серединой противоположной стороны. Сформулировать определение медианы треугольника. Составить алгоритм ее построения.
Самооценка.
Алгоритм построения медианы треугольника.
1. Построить ∆АВС.
2. Построить середину стороны АС и обозначить буквой М.
3.
Соединить вершину
треугольника В с построенной точкой М.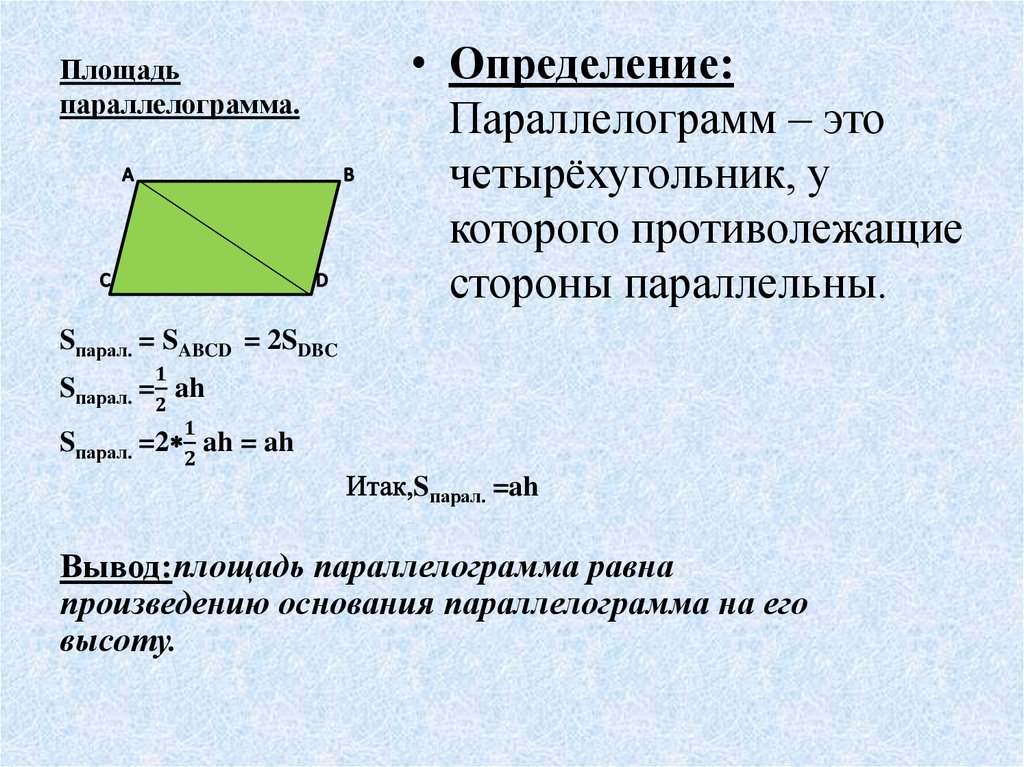
4. Считать отрезок BМ медианой треугольника.
Медиана может быть обозначена буквой m.
Поочередно вывешиваются алгоритмы построения медианы, биссектрисы, высоты треугольника.
Задание 2.
Построить отрезок биссектрисы угла треугольника, соединяющий вершину треугольника с точкой противоположной стороны. Сформулировать определение биссектрисы треугольника. Составить алгоритм ее построения.
Самооценка.
Алгоритм построения биссектрисы треугольника.
1. Построить ∆АВС.
2. Провести биссектрису угла треугольника при вершине В.
3. Обозначить точку пересечения биссектрисы угла с противолежащей стороной буквой D.
4. Считать отрезок BD биссектрисой треугольника.
Биссектриса может быть обозначена буквой b.
Задание 3.
Провести перпендикуляр из вершины треугольника к
прямой, содержащей противоположную сторону. Сформулировать определение высоты
треугольника. Составить алгоритм ее построения.
Сформулировать определение высоты
треугольника. Составить алгоритм ее построения.
Самооценка.
Алгоритм построения высоты треугольника.
1. Построить ∆АВС.
2. Опустить перпендикуляр из вершины В к прямой, содержащей противоположную сторону АС.
3. Основание перпендикуляра обозначить точкой К.
4. Считать отрезок ВК высотой треугольника.
Высота может быть обозначена буквой h.
Задание 4. Компьютерная лаборатория
Учащиеся выполняют практическую работу в среде «Живая математика» (задание1, задание 2).
На основании полученных результатов делают вывод:
· Медианы любого треугольника пересекаются в одной точке, расположенной внутри треугольника.
· Биссектрисы любого треугольника пересекаются в одной точке, расположенной внутри треугольника.
Учащиеся на листах с готовыми чертежами
остроугольного, прямоугольного, тупоугольного треугольников, пользуясь
алгоритмом, проводят высоты в каждом треугольнике.
Возникает проблемная ситуация: В тупоугольном треугольнике высоты не пересекаются внутри треугольника. Обращаются к программе «Живая математика». Провот эксперимент.
На основании полученных результатов делают вывод:
· Высоты в остроугольном треугольнике пересеклись в точке, находящейся внутри треугольника.
· Высоты в прямоугольном треугольнике пересеклись в вершине прямого угла.
· Высоты в тупоугольном треугольнике пересеклись в точке, расположенной вне треугольника.
Озвучивание выводов
· Медианы любого треугольника пересекаются в одной точке, расположенной внутри треугольника. Эта точка называется центром тяжести треугольника.
· Биссектрисы любого треугольника пересекаются в одной точке, расположенной внутри треугольника. Эта точка называется центром вписанной окружности.
· Высоты любого
треугольника пересекаются в одной точке. Эта точка называется ортоцентром
треугольника.
Эта точка называется ортоцентром
треугольника.
· Высоты в остроугольном треугольнике пересеклись в точке, находящейся внутри треугольника.
· Высоты в прямоугольном треугольнике пересеклись в вершине прямого угла.
· Высоты в тупоугольном треугольнике пересеклись в точке, расположенной вне треугольника.
Историческая справка.
В «Началах» Евклида указывается, что три биссектрисы внутренних углов треугольника пересекаются в одной точке – центре вписанной окружности, но не говорится о том, что высоты пересекаются водной точке (ортоцентре). «Ортос» — греческое слово (прямой, правильный).
Об этом знали Архимед, Прокл. Архимед доказал, что
точка пересечения медиан треугольника является центром тяжести (барицентр). На
эти точки было обращено внимание, начиная с XVIII века они были названы «замечательными» или
«особенными» точками треугольника. Исследование свойств треугольника, связанных
с этими точками и другими, послужило началом для создания новой ветви
элементарной математики «геометрии треугольника», родоначальником которой был
Леонард Эйлер.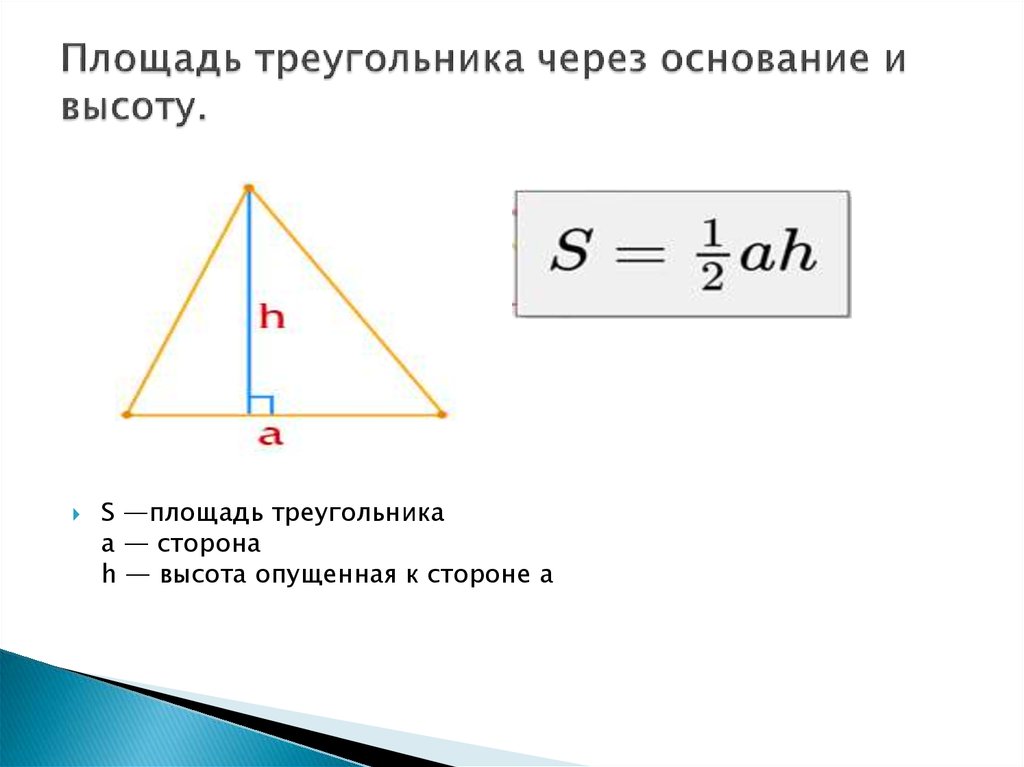 В 1765 году Эйлер доказал, что в любом треугольнике ортоцентр,
барицентр, центр описанной окружности лежат на одной прямой, названной «прямой
Эйлера».
В 1765 году Эйлер доказал, что в любом треугольнике ортоцентр,
барицентр, центр описанной окружности лежат на одной прямой, названной «прямой
Эйлера».
Задание 5.
Составить графическую модель усвоенного материала.
III. Рефлексивно – оценочный этап.
1) Какие цели были поставлены на уроке?
2) Что узнали на уроке?
3) Какие выводы сделали на уроке?
4) Закрыть записи. Проговорить вслух и про себя понятия медианы, биссектрисы, высоты треугольника. Проговорить алгоритмы построения этих элементов треугольника.
5) А сейчас каждый из вас подойдет к доске и покажет свое настроение после урока.
I. Домашнее задание.
1) По учебнику: п. 17, №103, №104;
2) На творческое применение знаний:
· «Головоломка со спичками».
Шесть спичек
образуют два равных треугольника. Нужно эти спички расположить так, чтобы они
образовали четыре таких же треугольника.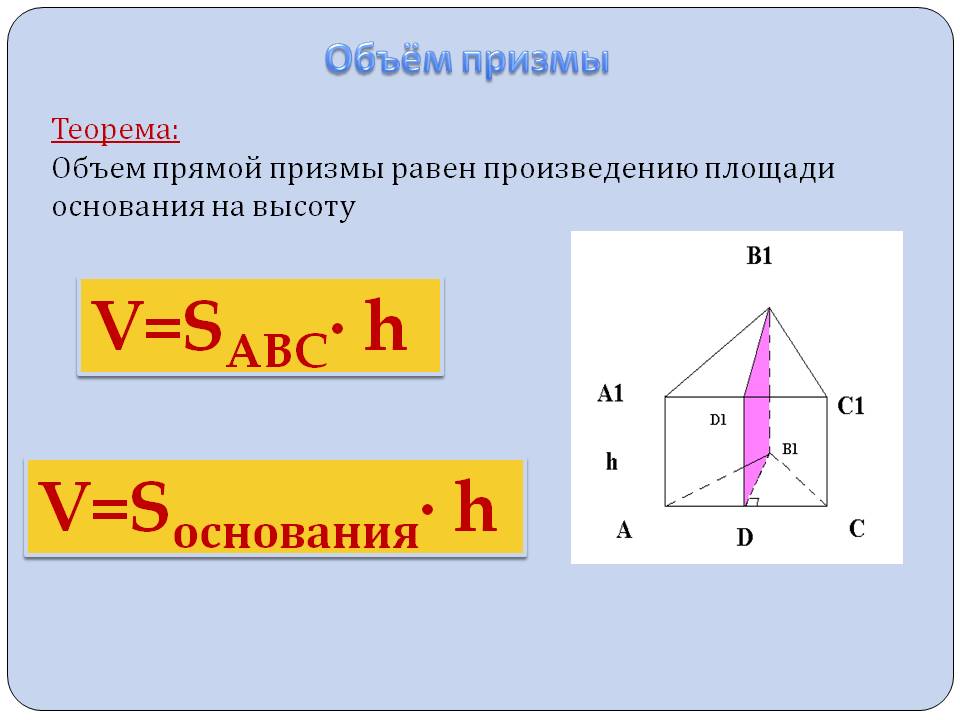
· Подготовить реферат на тему «Замечательные линии и точки треугольника».
Элементы треугольника. Высоты, медианы, биссектрисы
Высоты, медианы и биссектрисы треугольника постоянно встречаются нам в задачах по геометрии. Мы начнем с таблицы, в которой показано, что такое высоты, медианы и биссектрисы, и какими свойствами они обладают. Затем — подробные объяснения и решение задач.
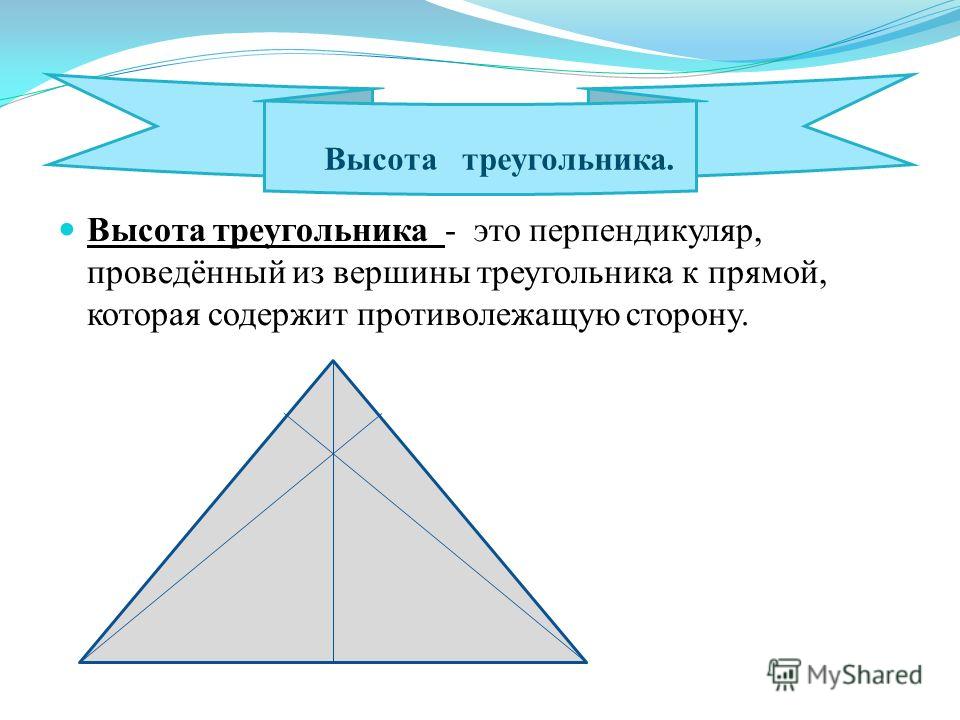
Напомним, что высота треугольника — это перпендикуляр, опущенный из его вершины на противоположную сторону.
Три высоты треугольника всегда пересекаются в одной точке. Вот как это выглядит в случае остроугольного треугольника.
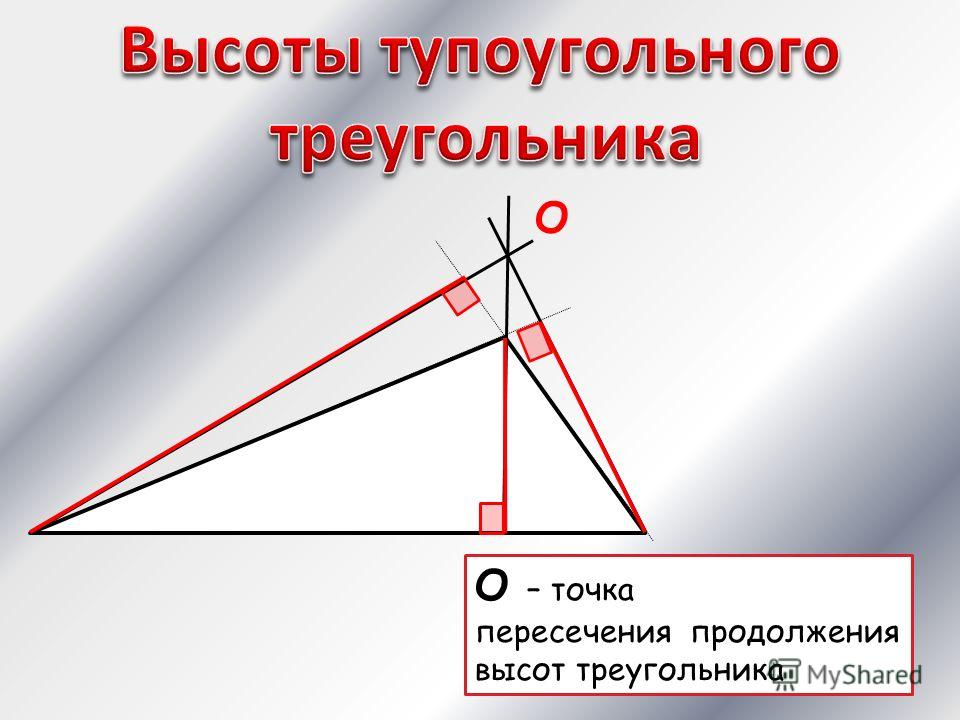
Попробуйте
провести три высоты в тупоугольном
треугольнике. Получилось? Да, редкий
выпускник справляется с этим заданием.
Действительно, мы не можем опустить
перпендикуляр из точки А
на отрезок ВС,
зато можем опустить его на прямую ВС —
то есть на продолжение стороны
ВС.
В этом случае в одной точке пересекаются не сами высоты, а их продолжения.
А как выглядят три высоты в прямоугольном треугольнике? В какой точке они пересекаются?
Медиана треугольника — отрезок, соединяющий его вершину с серединой противоположной стороны.
Три медианы треугольника пересекаются в одной точке и делятся в ней в отношении 2:1, считая от вершины.
Биссектриса треугольника — отрезок, соединяющий вершину треугольника с точкой на противоположной стороне и делящий угол треугольника пополам.
У биссектрисы
угла есть замечательное свойство —
точки, принадлежащие ей, равноудалены
от сторон угла. Поэтому три биссектрисы
треугольника пересекаются в одной
точке, равноудаленной от всех сторон
треугольника. Эта точка является центром
окружности, вписанной в треугольник.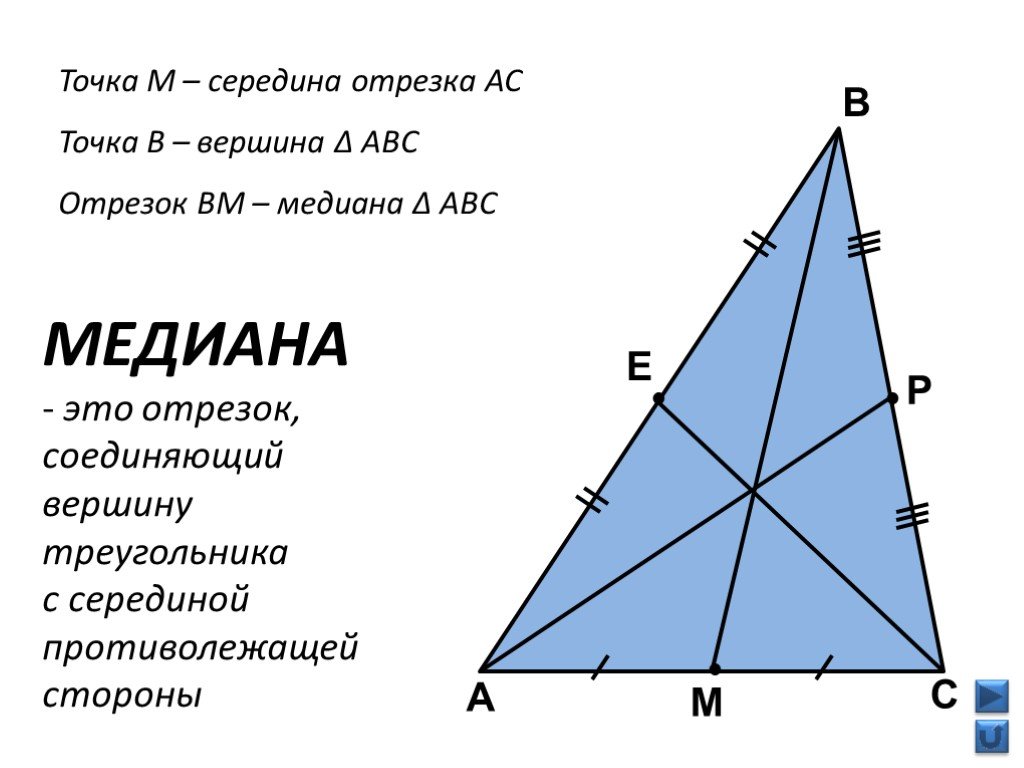
Еще одно свойство биссектрисы пригодится тем, кто собирается решать задачу С4. Биссектриса треугольника делит противоположную сторону в отношении длин прилежащих сторон.
Разберем несколько задач, в которых речь идет о высотах, медианах и биссектрисах треугольника. Все задачи взяты из Банка заданий ФИПИ.
1. Найдите острый угол между биссектрисами острых углов прямоугольного треугольника. Ответ дайте в градусах.
Пусть биссектрисы треугольника АВС ( в котором угол С равен 90°) пересекаются в точке М.
Рассмотрим треугольник АВМ.
∠ МАВ = ∠ ВАС,
∠ АВМ = ∠ АВС, тогда ∠ АМВ = 180° — ∠ МАВ — ∠ АВМ = 180° — (∠ АВС + ∠ ВАС).
Острый угол между биссектрисами на рисунке обозначен φ.
Угол
φ смежный
с углом АМВ,
следовательно, φ
=
(∠
АВС + ∠
ВАС).
Поскольку треугольник АВС — прямоугольный, то ∠ АВС + ∠ ВАС = 90°.
Тогда φ = (∠ АВС + ∠ ВАС) = 90° : 2 = 45°.
Ответ: 45.
2. Острые углы прямоугольного треугольника равны 29º и 61º. Найдите угол между высотой и биссектрисой, проведенными из вершины прямого угла. Ответ дайте в градусах.
Пусть СН — высота, проведенная из вершины прямого угла С, СК — биссектриса угла С.
Тогда ∠ АСН = ∠ АВС = 61°, ∠ АСК = 90° : 2 = 45°.
Угол между высотой и биссектрисой — это угол КСН.
∠ КСН = ∠ АСН — ∠ АСК = 61° — 45° = 16°
Ответ: 16.
3. Два угла треугольника равны 58º и 72º. Найдите тупой угол, который образуют высоты треугольника, выходящие из вершин этих углов. Ответ дайте в градусах.
Из треугольника
АВН
(угол Н —
прямой) найдем угол ВАН. Он равен 18°.
Он равен 18°.
Из треугольника АВК (угол К — прямой) найдем угол АВК. Он равен 32°.
В треугольнике АОВ известны два угла. Найдем третий, то есть угол АОВ, который и является тупым углом между высотами треугольника АВС:
∠ АОВ = 180° — 18° — 32° = 130°.
Ответ: 130.
4. В треугольнике ABC угол C равен 58º, AD и BE — биссектрисы, пересекающиеся в точке O. Найдите угол AOB. Ответ дайте в градусах.
Пусть в треугольнике АВС угол ВАС равен А, угол АВС равен В.
Рассмотрим треугольник АОВ.
∠ ОАВ = ∠ А
∠ АВО = ∠ В, тогда ∠ АОВ = 180° — (∠ А + ∠ В). Из треугольника АВС получим, что ∠ А + ∠ В = 180° — 58° = 122°.
Тогда ∠ АОВ = 180° — (∠ А + ∠ В) = 180° — 61° = 119°.
Ответ:
119°.
5. В треугольнике ABC угол A равен 60º, угол B равен 82º. AD, BE и CF — биссектрисы, пересекающиеся в точке O. Найдите угол AOF. Ответ дайте в градусах.
Найдем угол АСВ. Он равен 38°.
Тогда ∠ АСF = ∠ ACB = 19°.
Из треугольника АСF найдем угол AFC. Он равен 101°.
Рассмотрим треугольник АОF.
∠ AFО = 101°, ∠ FAO = ∠ ВАС = 30°. Значит, ∠ AOF = 49°.
Ответ: 49.
6. В треугольнике АВС СD — медиана, угол ACB равен 90º, угол B равен 58º. Найдите угол ACD. Ответ дайте в градусах.
Как решать эту задачу? У медианы прямоугольного треугольника, проведенной из вершины прямого угла, есть особое свойство. Мы докажем его в теме «Прямоугольник и его свойства».
Подсказка:
Сделайте чертеж, найдите на нем
равнобедренные треугольники и докажите,
что они равнобедренные.
Правильный ответ: 22.
Разница между длиной и высотой (со сравнительной таблицей)
Представьте твердый объект, такой как куб, прямоугольный параллелепипед, пирамида и т. д., которые имеют три измерения: длину, ширину и высоту. Длина относится к экстенту объекта, т. е. определяет длину объекта. С другой стороны, высота подразумевает высоту объекта; это говорит о том, насколько высока сущность?
Есть много студентов-математиков, которые сомневаются в длине и высоте объекта, для них эти два измерения — одно и то же. Но, это не так, у них только общие характеристики, есть тонкие различия между длиной и высотой.
Прочтите статью, чтобы понять концепцию двух измерений.
Содержание: длина и высота
- Сравнительная таблица
- Определение
- Ключевые отличия
- Сходства
- Заключение
Сравнительная таблица
| Основание для сравнения | Длина | Высота |
|---|---|---|
| Значение | Длина описывается как измерение объекта от одной точки до другой. | Рост относится к измерению человека или объекта сверху вниз. |
| Определяет | Какой длины объект? | На какой высоте находится объект? |
| Расстояние | Горизонтальное | Вертикальное |
| Размер | Максимальный размер объекта. | Размер, который был бы вверху в обычной ориентации. |
Определение длины
Размер объекта, который является самым длинным, называется его длиной. Это горизонтальная протяженность, которая измеряется вдоль плоскости X на графике и измеряет расстояние между двумя концами. Единицами измерения длины являются метр, сантиметр, километр, дюйм, фут, миля и т. д.
Длина относится к размеру объекта, независимо от размеров. Он устанавливает степень, в которой что-то длинно или далеко от одной точки до другой.
Определение высоты
Высота в математике определяется как мера расстояния от низа до верха, т.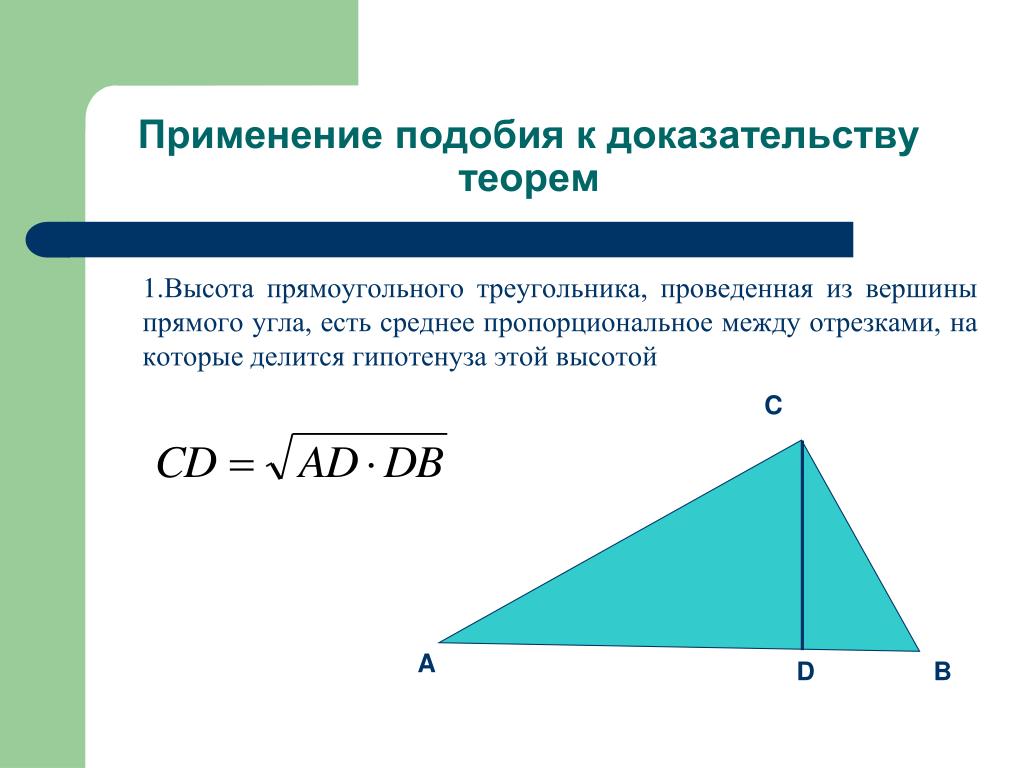 е. от эталонного уровня до определенной точки.
е. от эталонного уровня до определенной точки.
Высота обозначается как высота, когда мы говорим о том, насколько трехмерный объект, такой как горы, деревья или здания, высок или высок относительно уровня моря. Он измеряет расстояние по вертикали от самой низкой до самой высокой точки. Рост человека показывает, насколько он высок.
Ключевые различия между длиной и высотой
Пункты, приведенные ниже, являются существенными, поскольку речь идет о разнице между длиной и высотой:
- Длина в основном является измерением объекта от начала до конца. Напротив, высота — это измерение расстояния объекта от основания до вершины.
- Длина определяет, насколько что-то длинное, тогда как высота является показателем того, насколько кто-то или что-то высокое.
- В то время как длина измеряется по оси X, по сути, это горизонтальная сторона чего-либо, высота выровнена по оси Y, которая представляет собой вертикальную сторону чего-либо.
- Длина — это не что иное, как самая длинная грань объекта.
 И наоборот, высота — это та сторона объекта, которая была бы вверху при нормальной ориентации.
И наоборот, высота — это та сторона объекта, которая была бы вверху при нормальной ориентации.
Аналоги
- Длина и высота являются линейными измерениями.
- Они измеряются в единицах расстояния.
- Выражается в футах, дюймах, метрах, ярдах и т. д.
Заключение
Таким образом, из приведенного выше обсуждения становится ясно, что это два разных понятия геометрии, которые часто понимаются вместе, но это не делает их одним целым. Положение объекта играет решающую роль в определении того, какое измерение является высотой, а какое — длиной, потому что измерения меняются с изменением положения, по сути, высота объекта становится его длиной, а длина превращается как его высота.
Разница между длиной и высотой
Чтобы понять, что такое длина и высота, давайте рассмотрим несколько примеров трехмерных геометрических объектов, таких как куб, квадрат, прямоугольный параллелепипед, пирамида и т. д. Эти объекты измеряются с точки зрения трех измерений, а именно длины.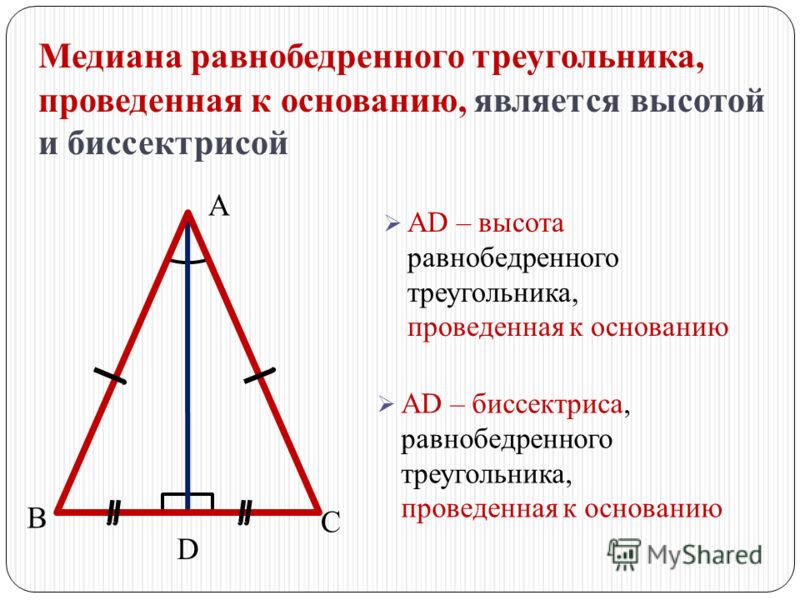 , ширина и высота. Длина — это мера протяженности объекта или параметр, определяющий длину объекта. Принимая во внимание, что параметр «высота» относится к высоте объекта и измеряет высоту объекта. Среди студентов и фасилитаторов распространена тенденция делать правильный выбор между длиной и высотой. Существует общее неверное представление о том, что длина и высота — это одно и то же. Однако, хотя длина и высота имеют много общего, математически они по определению являются двумя разными параметрами. Разница между длиной и шириной тоже есть. Эта статья поможет вам проанализировать сходства и различия между длиной и высотой.
, ширина и высота. Длина — это мера протяженности объекта или параметр, определяющий длину объекта. Принимая во внимание, что параметр «высота» относится к высоте объекта и измеряет высоту объекта. Среди студентов и фасилитаторов распространена тенденция делать правильный выбор между длиной и высотой. Существует общее неверное представление о том, что длина и высота — это одно и то же. Однако, хотя длина и высота имеют много общего, математически они по определению являются двумя разными параметрами. Разница между длиной и шириной тоже есть. Эта статья поможет вам проанализировать сходства и различия между длиной и высотой.
В чем разница между длиной и высотой?
Длина и высота — это величины в математике, которые до сих пор считаются одними и теми же многими изучающими и даже экспертами в этой области. Несмотря на ряд сходств между этими двумя, между длиной и высотой есть тонкая разница. В таблице ниже описано сравнение длины и высоты.
Сравнение длины и высоты
Описание | Длина | Высота |
Значение | Измерением длины объекта называется его длина от одной точки плоскости до другой в одной и той же плоскости. | Высота — это измерение объекта сверху вниз. |
Что он измеряет? | Определяет длину объекта. | Это представление высоты объекта. |
Направление измерения | Длина измеряется по горизонтали. | Высота измеряется по вертикали. |
Измерение | Это наиболее протяженное измерение объекта. | Это измерение, которое было бы вверху в обычной ориентации. |
Определение длины
Наибольшее измерение объекта называется его длиной. Это горизонтальное расширение объекта, которое обычно измеряется по оси X графика декартовых координат. Это дает расстояние между двумя концами. Длину можно измерять в метрах (сантиметрах, миллиметрах, километрах), дюймах, футах, милях и т.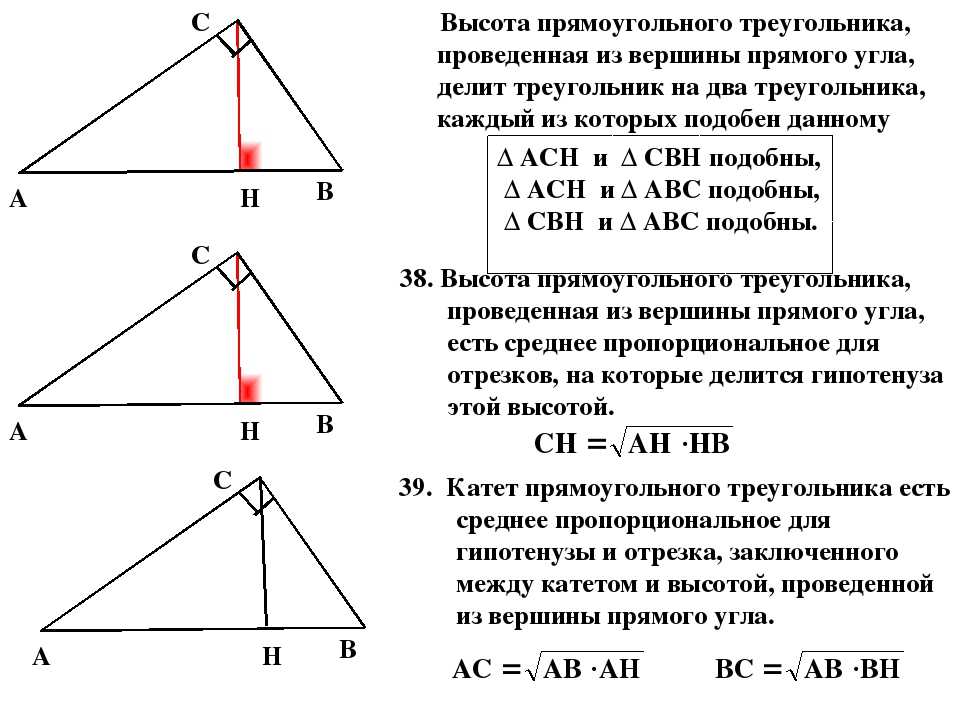 д.
д.
Независимо от размеров, длина относится к размеру объекта. Он представляет собой степень расширения между любыми двумя точками на горизонтальной плоскости.
Определение высоты
Высота также является мерой расстояния. Однако это не то же самое, что измеряется в случае длины. Высота – это мера вертикального расстояния до объекта. то есть мера объекта сверху вниз. Высота объекта обычно называется высотой. В случае трехмерных объектов, таких как деревья, здания и горы, измерение их высоты является одним из ключевых факторов, придающих им большее значение. Его также можно определить как измерение вертикального расстояния объекта от его нижней точки до самой высокой точки. Рост также является одной из величин, измеряемых для определения физической подготовки человека. Высота имеет те же единицы измерения, что и длина. Измеряется в метрах, дюймах, футах и милях.
Разница между длиной и высотой
Длина — это измерение расстояния объекта от одного конца до другого.
 Высота – это мера расстояния между основанием и вершиной объекта.
Высота – это мера расстояния между основанием и вершиной объекта.Высота определяет степень высоты объекта, а длина является индикатором длины объекта.
Длина измеряется по горизонтали и обозначается по оси X в декартовой плоскости, тогда как высота измеряется по вертикали и обозначается по оси Y в декартовой плоскости.
Длина — это самая длинная грань объекта, тогда как высота — это сторона объекта в нормальной ориентации, но направленная вверх.
Сходство длины и высоты
И длина, и высота имеют одни и те же единицы измерения.
Длина и высота измеряются в единицах измерения расстояния.
Единицы измерения длины и роста: футы, дюймы, ярды, метры.

Забавные факты
Длина слова происходит от слова lengthe в среднеанглийском языке, что буквально означает свойство быть длинным или вытянутым в определенном направлении.
Длина также считается свойством времени, потому что определенное количество времени имеет тенденцию иметь длину.
Метрическая система измерения длины впервые была принята во Франции.
Международная система единиц предписала «метр» в качестве стандартной единицы, принятой во всем мире для измерения длины и высоты или любого вида расстояния.
Рост человека равен размаху рук, вытянутых в стороны.
Высота над уровнем моря называется высотой.

Разница между длиной и шириной заключается в том, что длина — это самая длинная сторона объекта, а ширина — более короткая сторона. Например, в прямоугольнике со сторонами 4 см и 9 см ширина равна 4 см, а длина равна 9 см.
Веданту стремится сделать будущее своих учеников ярким и полным возможностей. Предоставляя бесплатный доступ к огромному количеству учебных материалов, Vedantu позволяет учащимся просматривать различные предметы и помогает лучше понять сложные темы. Он разбивает сложные понятия на гораздо более простое и увлекательное содержание, так что учащемуся становится легко понять его, а также не терять концентрацию во время учебы. Будь то решение сомнений, постановка вопросов или пересмотр содержания, Веданту гарантирует, что академические потребности студента будут удовлетворены, предоставляя им доступ к множеству услуг, таких как виртуальное обучение в присутствии опытного преподавательского состава, решение сомнений с помощью экспертов.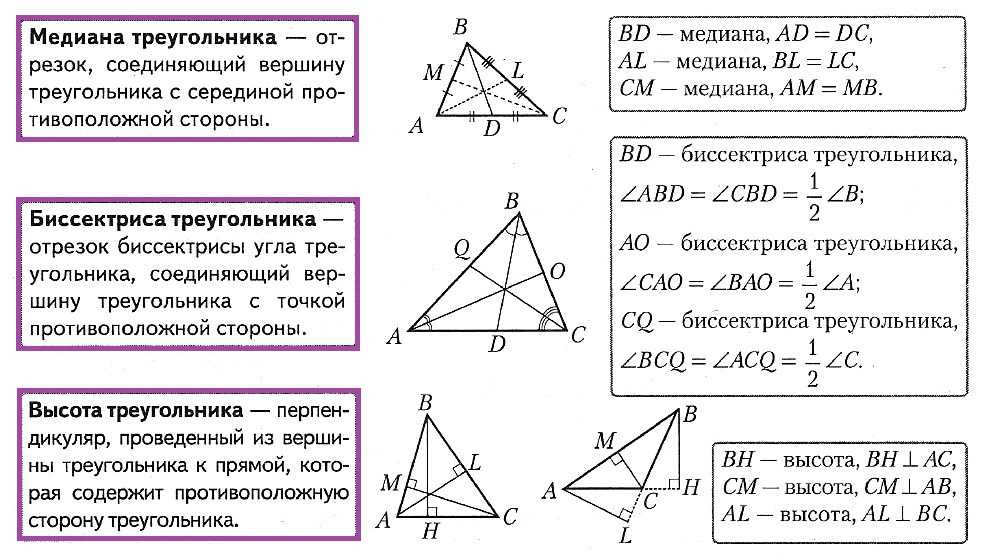

 И наоборот, высота — это та сторона объекта, которая была бы вверху при нормальной ориентации.
И наоборот, высота — это та сторона объекта, которая была бы вверху при нормальной ориентации.
 Высота – это мера расстояния между основанием и вершиной объекта.
Высота – это мера расстояния между основанием и вершиной объекта.