Методы решения геометрических задач. Планиметрия
Похожие презентации:
Решение задач С4. Планиметрия
Решение геометрических задач при подготовке к ГИА
Решение геометрических задач при подготовке к ЕГЭ
Подготовка к ОГЭ. Методы, способствующие решению геометрических задач
Особенности решения геометрических задач второй части ОГЭ
Алгебраические методы решения геометрических задач
Методы решения задач повышенной сложности по геометрии (ЕГЭ). Семинар с практической частью
Решение задач несколькими способами. Равнобедренный треугольник
Треугольники. Решение задач
Геометрические построения. Графический способ решения геометрических задач
Методы
решения геометрических задач
(планиметрия)
2. Основные методы решения геометрических задач
Метод дополнительных построенийМетод геометрических преобразований
Метод подобия
Метод площадей
Метод вспомогательной окружности
Метод геометрического видения
Метод координат
Векторный метод
3.
 Метод дополнительных построенийРазновидности:
Метод дополнительных построенийРазновидности:Продолжение отрезка (отрезков) на
определенное расстояние или до пересечения
с заданной прямой (прямыми).
Проведение прямой через две заданные точки.
Проведение через заданную точку прямой,
параллельной данной прямой, или
перпендикулярной данной прямой.
4. Метод геометрических преобразований
Разновидности:центральная симметрия,
осевая симметрия,
параллельный перенос,
поворот.
5. Метод площадей
Один из алгоритмов решения многихгеометрических задач основан на
использовании свойств площадей фигур.
6. Метод вспомогательной окружности
«Окружность – душа геометрии.Познайте окружность, и вы не
только познаете душу геометрии,
но и возвысите душу свою».
И.Ф. Шарыгин
7. Метод геометрического видения
Основывается на умениях видеть исопоставлять геометрические факты.
Обычно при решении не нужно выполнять
дополнительные построения и вычислений.
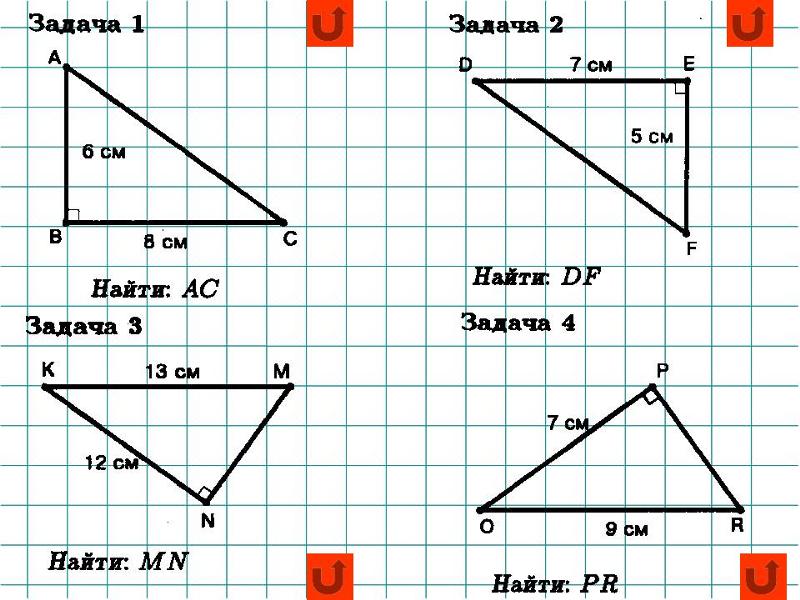
8. Метод координат
и векторный метод самые универсальные методы геометрии.Главное — удачно выбрать систему координат.
• I тип – задачи на нахождение зависимости
между элементами данной фигуры;
• II тип – задачи на составление уравнения
данной фигуры, если известны
характеристические свойства точек данной
фигуры.
9. Векторный метод
Типы задач, решаемых с помощьювекторного метода:
I тип – задачи, связанные с использованием
операций сложения векторов и умножения
вектора на число;
II тип – задачи с использованием операций
скалярного умножения векторов и
разложения вектора по базису.
«Лучше решить
задачу десятью
способами,
чем десять задач
одним».
Дьёрдь Пойя
В треугольнике АВС биссектриса BЕ и медиана
АD перпендикулярны и имеют одинаковую
длину, равную 4. Найти стороны треугольника
АВС.
12. Метод дополнительных построений
В равнобедренном ∆ABDBO – биссектриса и
высота, значит,
AO=OD=2,
AD – медиана ∆ABС,
тогда BC=2AB.

BE – биссектриса ∆ABС,
следовательно, EC=2AE.
Проведем среднюю линию DF ∆BCE. DF=2.
Тогда OE=1 как средняя линия ∆ADF. BO=3.
∆AOB прямоугольный.
По теореме Пифагора
AB= AO 2 OB 2
AB= 2 2 32 13
BC= 2 13
AC=3AE.
AC=3 AO 2 OE 2 3 2 2 12 3 5
14. Метод геометрических преобразований
Построим точку F,симметричную точке
С относительно BE:
F AB DE
∆ FBC равнобедренный,
Е – точка пересечения медиан ∆ FBC.
2
2
2
FE=EC= AC = FH EH 2 5, AC= 3 5.
3
BH=6, AD – средняя линия, значит BO=3. AB= 13
BC=2 13 .
15. Метод площадей
1AO·BE=S ABE
2
S BDE 4 SCDE
Тогда S ABC 12, а S ABD 6.
1
6= 2 AD·BO, AD=4,
откуда BO=3.
Далее воспользуемся теоремой Пифагора для
отыскания сторон треугольника АВС.
16. Координатный метод
Уравнение прямойx 4
y b
АС:
2 4
0 b
b
b
или y x 6
3
Е АС, поэтому
b
Е(0; ). ВЕ=4.
3
2
16
b
4b
2
4 0
9
3
b=3.
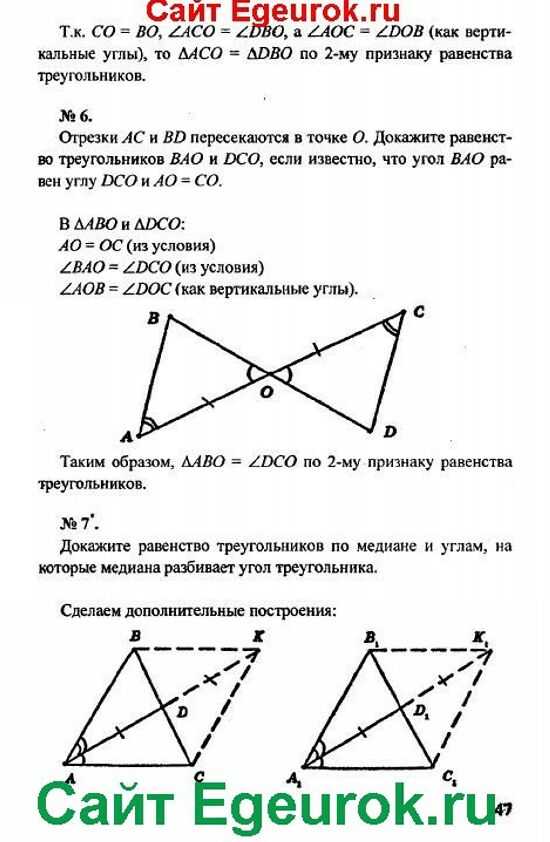 Остается найти стороны по теореме Пифагора.
Остается найти стороны по теореме Пифагора.17. Векторный метод
2a cBE=4, BE
3
1
AD=4, AD с a
2
36 2а a c
2
16 2a a c
2
a 13 , c 2 13
AC c a
2
2
( AC ) (c a )
2
2
2
AC c 2a c a
2
5a 2a c 5 13 20 45
AC 3 5.
English Русский Правила
Геометрия средней школы онлайн в Excel High School
Описание:
Этот предмет начинается с рассмотрения и введения определений основных элементов геометрии. Студенты разрабатывают прочную основу для работы с определениями, постулатами и аксиомами. Они будут изучать логику, как она связана с математикой, рассуждениями и доказательствами. Содержание курса помогает учащимся развить сильное чувство работы с фигурами и формами всех форм, а также расширить их представления о реальных проблемах. В процессе изучения различных свойств фигур и форм, включая конгруэнтность, площадь, периметр, объем, площадь поверхности и подобие, у учащихся формируются сильные навыки пространственного мышления. Эти новые идеи дают учащимся возможность постоянно применять накопленные знания и навыки по алгебре. Курс завершается изучением многочисленных свойств, связанных с окружностями, и введением в тригонометрию.
Эти новые идеи дают учащимся возможность постоянно применять накопленные знания и навыки по алгебре. Курс завершается изучением многочисленных свойств, связанных с окружностями, и введением в тригонометрию.
Учебник: Концепции геометрии — Excel Education Systems, Inc. 2019©
Цели курса:
На протяжении всего курса вы будете решать следующие задачи:
- Понимать точки, прямые и плоскости — основные строительные блоки геометрии
- Распознавать постулаты, теоремы и свойства, и как они используются в геометрии
- Определите двумерные и трехмерные фигуры и связанные с ними формулы
- Понимать и применять теорему Пифагора для решения задач на правильный треугольник
- Понимать геометрию окружности и термины, используемые для определения ее частей
- Изучите основные инструменты тригонометрии и научитесь применять их для измерения углов
Содержание:
Семестр А
Раздел 1: Основы геометрии
Раздел 2: Логика/рассуждения в геометрии
Раздел 3: Фигуры и параллельные прямые
Раздел 4: Конгруэнтность треугольника
Раздел 5: Площадь и периметр
Семестр B
Раздел 6: Объем и площадь поверхности
Раздел 7: Подобие фигур
Раздел 8: Геометрия окружностей
Раздел 9: Введение в тригонометрию
Шкала оценок
A = 90-100%
B = 80-89%
C = 70-79%
D = 60-69%
F = менее 59%
Взвешивание оценок
Контрольные работы. …………………… 70%
…………………… 70%
Итоговый экзамен ………………. 30%
100%
Нужны дополнительные онлайн-курсы для средней школы(Нажмите здесь)
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Решение геометрических задач – Mike’s Math Page
mjlawler Без категории 1 минута
[короткая заметка во время обеда]
За последние пару дней я нашел в Интернете две очень интересные задачи по геометрии для моего сына. Первая проблема, которую я увидел (она была второй), возникла из-за вопроса Майкла Першана в Твиттере:
.Что приходит вам в голову, когда вы пытаетесь решить эту проблему? Что вы пытаетесь сделать? Какие подсказки вы бы дали ребенку? pic.twitter.com/cvGiywOyjQ
— Майкл Першан (@mpershan) 10 марта 2015 г.
Обычно я плохо понимаю, как ребенок подойдет к решению проблемы, но мне нравится видеть, что происходит лично. В этом случае подход моего сына отличался от моего:
youtube.com/embed/uWDzd43IMR0?version=3&rel=1&showsearch=0&showinfo=1&iv_load_policy=1&fs=1&hl=en&autohide=2&wmode=transparent» allowfullscreen=»true» sandbox=»allow-scripts allow-same-origin allow-popups allow-presentation»>
Вторая задача была опубликована в твиттере Five Triangles.
https://twitter.com/Five_Triangles/status/575091153072226304
Как упоминалось выше, мой сын действительно сначала решил эту проблему (вчера днем). Он добился интересного прогресса, но не смог дойти до конца. В первом видео показан прогресс, которого он добился, а во втором показано, как мы работаем до конца проблемы.

 com ожидают решения.
com ожидают решения.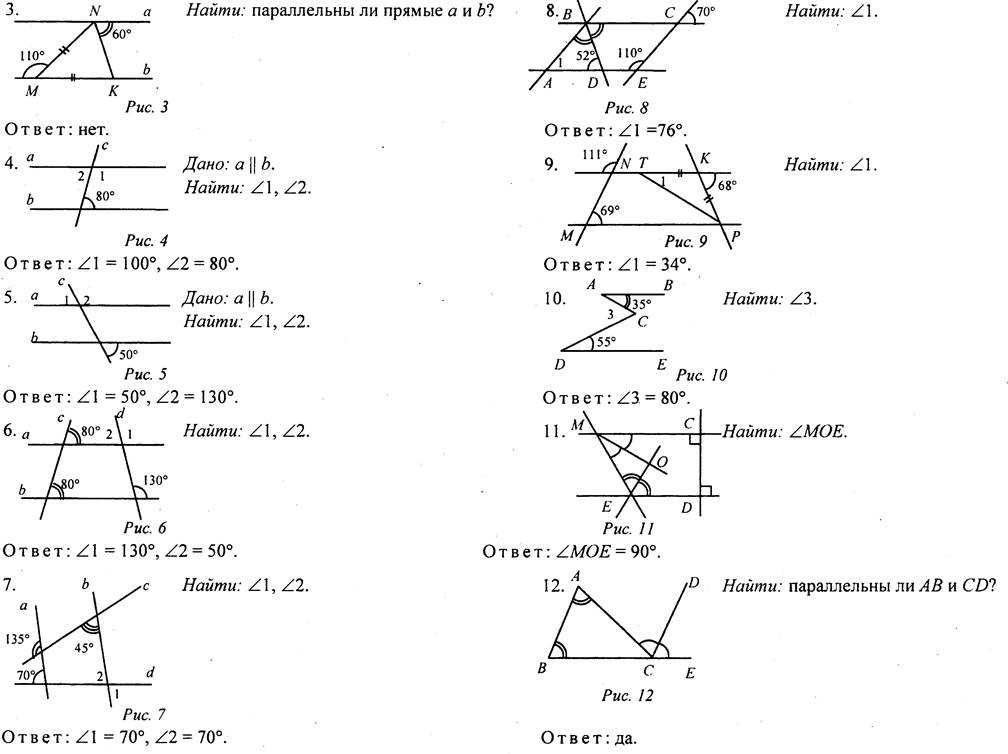

 Уровень сложности: средняя школа.
Уровень сложности: средняя школа.



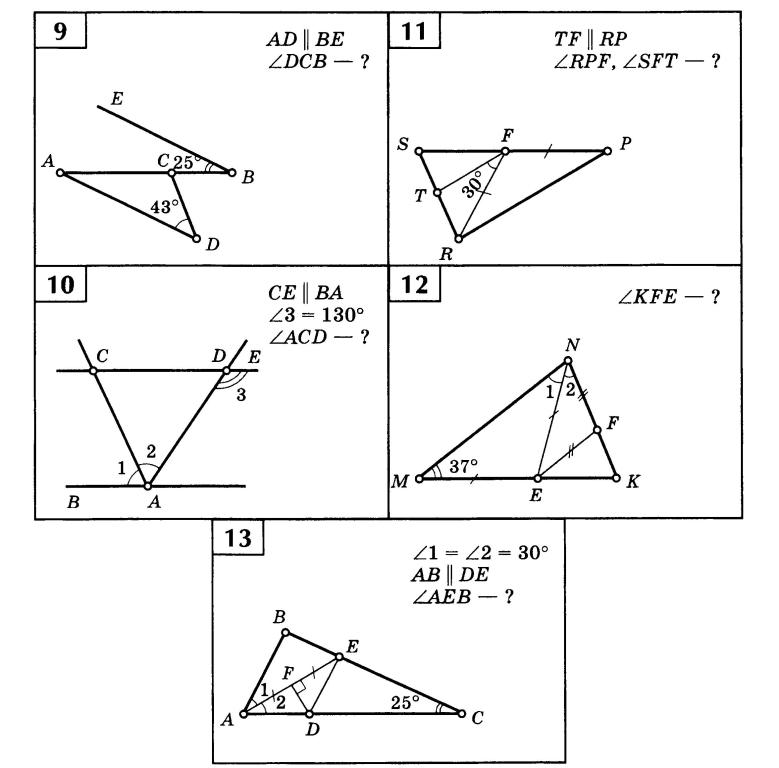


 ГеоГебра,
iPad.
ГеоГебра,
iPad.