Прямая и обратная пропорциональность. Коэффициент и формулы
- Прямая пропорциональность
- Формула прямой пропорциональности
- Обратная пропорциональность
- Формула обратной пропорциональности
Пропорциональность — это зависимость одной величины от другой, при которой изменение одной величины приводит к изменению другой во столько же раз.
Пропорциональность величин может быть прямой и обратной.
Прямая пропорциональность
Прямая пропорциональность — это зависимость двух величин, при которой одна величина зависит от второй величины так, что их отношение остаётся неизменным. Такие величины называются прямо пропорциональными или просто пропорциональными.
Рассмотрим пример прямой пропорциональности на формуле пути:
s = vt,
где s — это путь, v — скорость, а t — время.
При равномерном движении путь пропорционален времени движения. Если взять скорость v равной 5 км/ч, то пройденный путь s будет зависеть только от времени движения t:
Если взять скорость v равной 5 км/ч, то пройденный путь s будет зависеть только от времени движения t:
| Скорость v = 5 км/ч | |||||
|---|---|---|---|---|---|
| Время t (ч) | 1 | 2 | 4 | 8 | 16 |
| Путь s (км) | 5 | 10 | 20 | 40 | 80 |
Из примера видно, что во сколько раз увеличивается время движения t, во столько же раз увеличивается пройденное расстояние s. В примере мы увеличивали время каждый раз в 2 раза, так как скорость не менялась, то и расстояние увеличивалось тоже в два раза.
В данном случае скорость (v = 5 км/ч) является коэффициентом прямой пропорциональности, то есть отношением пути ко времени, которое остаётся неизменным:
| s | = v, |
| t |
следовательно,
| 5 | = | 10 | = | 20 | = | 40 | = | 80 | = 5. |
| 1 | 2 | 4 | 8 | 16 |
Если время движения остаётся неизменным, то при равномерном движении расстояние будет пропорционально скорости:
| Время t = 2 ч | ||||
|---|---|---|---|---|
| Скорость v (км/ч) | 5 | 15 | 45 | 90 |
| Расстояние s (км) | 10 | 30 | 90 | 180 |
В этом примере коэффициентом прямой пропорциональности, то есть, отношением пути к скорости, которое остаётся неизменным, является время (t = 2 ч):
| s | = t, |
| v |
следовательно,
| 10 | = | 30 | = | 90 | = | 180 | = 2. |
| 5 | 15 | 45 | 90 |
Из данных примеров следует, что две величины называются прямо пропорциональными, если при увеличении (или уменьшении) одной из них в несколько раз другая увеличивается (или уменьшается) во столько же раз.
Формула прямой пропорциональности
Формула прямой пропорциональности:
y = kx,
где y и x — это переменные величины, а k — это постоянная величина, называемая коэффициентом прямой пропорциональности.
Коэффициент прямой пропорциональности — это отношение любых соответствующих значений пропорциональных переменных y и x равное одному и тому же числу.
Формула коэффициента прямой пропорциональности:
| y | = k. |
| x |
Обратная пропорциональность
Обратная пропорциональность — это зависимость двух величин, при которой увеличение одной величины приводит к пропорциональному уменьшению другой. Такие величины называются обратно пропорциональными.
Рассмотрим пример обратной пропорциональности на формуле пути:
s = vt,
где s — это путь, v — скорость, а t — время.
| Путь s = 120 км | ||||
|---|---|---|---|---|
| Скорость v (км/ч) | 10 | 20 | 40 | 80 |
| Время t (ч) | 12 | 6 | 3 | 1,5 |
Из примера видно, что во сколько раз увеличивается скорость движения v, во столько же раз уменьшается время t. В примере мы увеличивали скорость движения каждый раз в 2 раза, а так как расстояние, которое нужно преодолеть, не менялось, то количество времени на преодоление данного расстояния сокращалось тоже в два раза.
В данном случае путь (s = 120 км) является коэффициентом обратной пропорциональности, то есть произведением скорости на время:
s
= vt,следовательно,
10 · 12 = 20 · 6 = 40 · 3 = 80 · 1,5 = 120.
Из данного примера следует, что две величины называются обратно пропорциональными, если при увеличении одной из них в несколько раз другая уменьшается во столько же раз.
Формула обратной пропорциональности
Формула обратной пропорциональности:
| y = | k | , |
| x |
где y и x — это переменные величины, а k — это постоянная величина, называемая коэффициентом обратной пропорциональности.
Коэффициент обратной пропорциональности — это произведение любых соответствующих значений обратно пропорциональных переменных y и x, равное одному и тому же числу.
Формула коэффициента обратной пропорциональности:
xy = k.
Коэффициент пропорциональности седьмого класса Математика, Математика, золото, материал png
Коэффициент пропорциональности седьмого класса Математика, Математика, золото, материал pngтеги
- золото,
- материал,
- константа,
- площадь,
- пропорция,
- пропорциональность,
- отношение,
- школа,
- среднее,
- седьмой класс,
- шестой класс,
- статистика,
- символ,
- понимание,
- вероятность И статистика,
- вероятность,
- значок,
- шар,
- круг,
- восьмой класс,
- дробь,
- геометрия,
- линия,
- математика,
- средняя школа,
- процент,
- желтый,
- png,
- прозрачный png,
- без фона,
- бесплатная загрузка
 02KB )
02KB )- Размер изображения
- 512x512px
- Размер файла
- 76.02KB
- MIME тип
- Image/png
изменить размер PNG
ширина(px)
высота(px)
Некоммерческое использование, DMCA Contact Us
- Математика Расчет Начальная школа, Математика, текст, начальная школа png 668x682px 111.27KB
- Liber Abaci Золотое сечение Золотая спираль, Математические с, угол, текст png 942x638px 31.22KB
- Число Фибоначчи Золотая спираль Золотое сечение Последовательность, спираль, угол, белый png 1600x1012px 47.16KB org/ImageObject»> Золотая спираль числа Фибоначчи Золотое сечение Либера Абачи, Математика, угол, белый png 800x524px 18.2KB
- Евклидово изображение, золотое знамя, корона и лента иллюстрация, CDR, этикетка png 800x800px 151.53KB
- Математика Orange Middle School Математическая запись Алгебра Число, падение креатив, лист, текст png 844x797px 98.24KB
- фейс арт, золотое сечение лицо, математика, лицо, лицо, угол, белый png 603x800px 94.68KB
- Общественные науки США Средняя школа World Learning, мультфильм глобус, глобус, класс png 456x596px 92.6KB
- Веб-баннер Лента Евклидова, Золотая лента, баннерная лента, партия золотой ленты, другие, текст png
3085x5498px
1.
 74MB
74MB - Золотая спираль Золотое сечение число Фибоначчи, другие, разное, угол png 2400x1697px 34.32KB
- Теория вероятностей Математика Вероятность и статистика Независимость, Кости, угол, белый png 2000x1500px 165.45KB
- Знак процента Компьютерная Иконка Процент, Хорошее Чтение, текст, другие png 512x512px 13.4KB
- Неделя Школьного духа Восьмого класса Одежда, Звезда, текст, спорт png 600x451px 135.91KB
- Математика Математические науки Седьмой класс Информатика, Математика, фиолетовый, текст png 724x511px 294.81KB org/ImageObject»> Фи Золотое сечение Символ Пи Математика, символ, разное, текст png 628x768px 19.7KB
- математическое уравнение, математика для младших классов средней школы Евклидово обучение, рисованная формула математики для младших классов средней школы, угол, текст png 1540x1546px 104.69KB
- Витрувианский Человек Золотое сечение Лицо Математика, Лицо, белый, люди png 1206x1600px 324.7KB
- золотая звезда, звезда золото, песочная звезда, коричневый, звезды png 600x500px 252.71KB
- Математическая нотация Математический символ Арифметика, Предварительный расчет с, умножение, сложение png 1600x1329px 226.87KB org/ImageObject»> Золотое сечение Золотая спираль число Фибоначчи, Математика, угол, белый png 2000x1268px 39.15KB
- Фракция математика 1/4 балла, математика, угол, число png 600x600px 16.54KB
- числовые иллюстрации, евклидово число, элемент PPT, текст, прямоугольник png 12454x13187px 3.86MB
- логотип белой птицы, логотип Kementerian Pendidikan dan Kebudayaan Индонезия Министерство образования и культуры Южной Джакарты, Tut wuri handayani, CDR, логотип png 800x445px 175.84KB
- умножение и буквы, математика, милая маленькая математика, текст, прямоугольник png 2917x2917px 697.11KB
- Круг Золотая спираль Золотое сечение число Фибоначчи, круг, угол, белый png 2000x1237px 40.91KB
- Иррациональное число Математика Иррациональность, Математика, угол, белый png 500x500px 39.98KB
- Logo Средняя школа Начальная школа Эмблема, школа, эмблема, текст png 1261x1262px 89.21KB
- Школа образования Icon, Образование детей, инфографика, ребенок png 2000x2000px 1.5MB
- Число Фибоначчи Золотое сечение Золотая спираль Золотой прямоугольник, круг, угол, белый png
2000x1266px
79.
 55KB
55KB - Число Фибоначчи Золотое сечение Золотая спираль Математика, Математика, угол, спираль png 1024x755px 612.7KB
- Дети, сидящие на стуле, Студенческий вопрос Компьютерный файл, Студенты отвечают на вопросы в классе, Разное, угол png 1157x1443px 125.24KB
- коричневая строка искусства, рамка золотой узор, золотой узор, рамка, угол png 1114x586px 134.37KB
- математическое уравнение, математическая формула, евклидова формула, эссе для средней школы, рисованная математическая формула для средней школы, угол, текст png
2029x1547px
63.
 03KB
03KB - Bas de casse Математика, золотые буквы, текст, другие png 1271x1280px 190.18KB
- Scripps National Spelling Bee Ученик средней школы, школа, текст, логотип png 897x900px 817.02KB
- Школа математики Formula School Графический дизайн, творческая формула математики для младших классов средней школы, угол, белый png 1600x1225px 80.62KB
- Фракции, Десятичные числа, Проценты 1/4 Половина процента, BB-8, фиолетовый, угол png 717x538px 20.1KB
- Круглый круг Пирог Фракция Одна половина, Круговая диаграмма, угол, оранжевый png
1024x512px
38.
 68KB
68KB - Иллюстрация монеты четыре золотых доллара, икона, золотые монеты, еда, золотая монета png 2312x1936px 599.44KB
- Золотой угол Круг Геометрия Точка Правильный многоугольник, красный круг, угол, белый png 2785x2525px 86.26KB
- круглый желтый и белый логотип, желтый круг, рамка желтого круга, рамка, золотая рамка png 3001x2743px 464.88KB
- желтая шестерня, Университет Уилфрида Лорье Образовательные технологии Школа Преподаватель, инновации, угол, класс png 550x550px 78.51KB
- Золотое сечение Золотая спираль Золотой прямоугольник, квадраты, угол, белый png
1280x838px
31.
 12KB
12KB - дети, занимающиеся спортом икона, физкультура, 61 милый мультфильм дети играют, мультипликационный персонаж, ребенок png 1673x1320px 274.82KB
- красный и коричневый номер шесть, добыча золота в Папуа-Новой Гвинее, золотой и красный номер шесть, золото, цвет png 2775x4140px 3.14MB
- белый баннер с воздушными шарами, веб-баннер ленты материал воздушного шара, праздничный баннер ленты воздушный шар, баннер, лента Лук png 1800x1800px 158.67KB
- Золотая рамка, золотая икона, мультфильм Золотой круг, мультипликационный персонаж, золотая рамка png 2001x1871px 496.43KB org/ImageObject»> 6 иллюстраций, номер, золотой деко номер шесть, цвет, шрифт png 3032x4110px 1.57MB
Пропорциональные символы—ArcGIS Pro | Документация
Пропорциональные символы используются для отображения относительных различий в количестве элементов. Пропорциональная символика аналогична символике градуированных символов в том, что обе рисуют символы, размер которых соответствует величине атрибута объекта. Но там, где градуированные символы распределяют функции по отдельным классам, пропорциональные символы представляют количественные значения в виде серии неклассифицированных символов, размер которых соответствует каждому конкретному значению.
Пропорциональные символы могут быть определены для точечных, линейных или полигональных векторных слоев. При применении к точечным или линейным символам размер объекта изменяется напрямую. При применении к полигональным объектам точечный символ пропорционального размера рисуется в центре полигона. Для справки вы можете указать единый фоновый символ для многоугольников, которые рисуются под точками.
Пропорциональные символы могут быть основаны на поле атрибута в наборе данных, или вы можете написать выражение Arcade, на основе которого будут генерироваться числовые значения для обозначения.
Предупреждение:
Когда пропорциональные символы основаны на одном поле, символы рисуются в отсортированном порядке, где более крупные объекты отображаются первыми, а более мелкие — выше. Когда символы основаны на выражении, такой сортировки не происходит, и некоторые меньшие символы могут быть скрыты более крупными.
Относительный размер
Если значения атрибута представляют количество (например, население или количество добытых бушелей), а не измеримое количество, или если единица измерения неизвестна, можно указать минимальный и максимальный размер символа. Все символы отображаются между этими двумя размерами, и вы можете использовать гистограмму для интерактивной установки значений данных, соответствующих минимальному и максимальному размерам. Значения, находящиеся ниже или за пределами этого диапазона, отображаются с наименьшими и наибольшими символами соответственно.
Значения, находящиеся ниже или за пределами этого диапазона, отображаются с наименьшими и наибольшими символами соответственно.
Или вы можете установить Максимальный размер на Нет. В этом случае Минимальный размер соответствует наименьшему значению в данных, а все остальные символы имеют размер пропорционально этому минимальному размеру. Если оставить диапазон открытым, не определив максимальный размер символа, диапазон символов будет действительно относительного размера, но это может привести к тому, что некоторые символы будут слишком большими, если существует большой разброс значений.
Погружение:
Читатели карт склонны недооценивать размер пропорциональных кругов на картах, особенно в верхней части диапазона размеров. Чтобы противодействовать этому восприятию, вы можете проверить компенсацию внешности (Фланнери). Компенсация внешнего вида использует алгоритм, определенный Джеймсом Флэннери, в котором более крупные символы масштабируются, чтобы компенсировать это восприятие. Вы можете использовать компенсацию внешнего вида, только если у вас есть пропорциональные символы относительного размера (пропорциональные символы без указания единицы измерения) и не указан Максимальный размер. Поскольку исследование Флэннери относится именно к восприятию кругов, компенсацию внешнего вида следует использовать только с круглыми символами.
Вы можете использовать компенсацию внешнего вида, только если у вас есть пропорциональные символы относительного размера (пропорциональные символы без указания единицы измерения) и не указан Максимальный размер. Поскольку исследование Флэннери относится именно к восприятию кругов, компенсацию внешнего вида следует использовать только с круглыми символами.
Фактический размер
Если символизируемый атрибут напрямую связан с фактическим значением с известной единицей измерения, вы можете использовать пропорциональные символы для рисования символов, размер которых точно соответствует этим размерам. Например, у вас может быть точечный слой отдельных деревьев, который включает атрибут радиуса кроны дерева, измеряемый в футах, и вы хотите представить каждое дерево в виде круга, используя его реальный размер кроны.
Задайте для свойства Unit единицу измерения, которую представляют ваши данные. Значение атрибута умножается на эту единицу для определения размера каждого символа. Вы также должны указать, должно ли это значение соответствовать площади, радиусу (половина ширины в случае квадрата) или высоте символа в свойстве «Данные представляют». Высота может быть указана только тогда, когда вы работаете в сцене.
Вы также должны указать, должно ли это значение соответствовать площади, радиусу (половина ширины в случае квадрата) или высоте символа в свойстве «Данные представляют». Высота может быть указана только тогда, когда вы работаете в сцене.
При выборе Area значение атрибута умножается на квадрат значения Unit. В случае линейной геометрии вы выбираете, представляют ли данные ширину или расстояние от центра. Затем вы можете отформатировать основные свойства выбранной фигуры, такие как цвет и контур. Пропорциональные символы, нарисованные с реальным размером, ограничены только кругами или квадратами.
Поскольку размер символа представляет собой измеряемую единицу, карта должна быть в системе координат проекции или сцена должна быть в режиме локального просмотра с использованием системы координат проекции. Для получения точных изображений следует использовать равновеликую проекцию, особенно если вы наносите на карту большую географическую область.
Нарисуйте слой с пропорциональными символами относительного или фактического размера
Вкладка Основные символы имеет две подвкладки для установки градуированных символов:
- На вкладке Классы вы устанавливаете количество легенд и управляете нулевыми и исключенными значениями.

- На вкладке «Гистограмма» можно просматривать и редактировать диапазоны данных символов. Дополнительные сведения см. в разделе Использование гистограмм символов.
Чтобы отобразить количественные данные с пропорциональными символами, выполните следующие действия:
- Выберите векторный слой на панели Содержание.
- На вкладке Векторный слой в группе Рисование щелкните Символы и щелкните Пропорциональные символы.
Появится панель Символы.
- На панели Символы на вкладке Первичные символы выберите числовое поле для данных, которые необходимо сопоставить, или напишите выражение.
Чтобы использовать выражение, щелкните Задать выражение, чтобы открыть диалоговое окно Построитель выражений. Напишите выражение и нажмите «Проверить», чтобы подтвердить его. Обратите внимание, что хотя выражение допустимо, оно может не возвращать допустимое числовое значение. Вы можете отфильтровать диалоговое окно Expression Builder, чтобы отображались только числовые поля, чтобы предотвратить это.

- Чтобы нормализовать данные, выберите поле в меню «Нормализация» или выберите процент от общего числа, чтобы разделить значение данных для создания соотношений, или выберите логарифм для обозначения логарифма каждого значения. Это может быть эффективным способом создания меньшего диапазона значений, если набор данных содержит значительные выбросы. Нормализация доступна, только если пропорциональные символы основаны на поле. Если он символизируется в выражении, поле Нормализация недоступно.
- Решите, следует ли отображать данные фактическими или относительными пропорциональными символами. Обратитесь к разделам выше для получения дополнительной информации. При желании установите минимальный и максимальный размеры символа, представляющего ваши данные.
- Чтобы использовать пропорциональные символы относительного размера, выберите Unknown для Unit. Установите Минимальный размер и Максимальный размер символа, представляющего ваши данные.
 Или установите для параметра Максимальный размер значение Нет. При необходимости отрегулируйте шаблон и фоновые символы.
Или установите для параметра Максимальный размер значение Нет. При необходимости отрегулируйте шаблон и фоновые символы. - Для отображения пропорциональными символами реального размера выберите единицу измерения для представления данных. Установите элемент управления «Данные представляют» на «Площадь», «Радиус» (1/2 ширины), «Высота» (только 3D), «Ширина» (только линии) или «Расстояние от центра» (только линии). При необходимости отрегулируйте форму символа, его заливку и фоновый символ.
- Чтобы использовать пропорциональные символы относительного размера, выберите Unknown для Unit. Установите Минимальный размер и Максимальный размер символа, представляющего ваши данные.
Изменить пропорциональные символы
На вкладке Основные символы на вкладке Классы можно выполнить следующие действия:
- их или выбрать другие.
- Если исходные данные были изменены или обновлены, нажмите «Дополнительно» и нажмите «Обновить значения», чтобы обновить диапазон значений.
- Чтобы отобразить нулевые значения, нажмите «Дополнительно» и выберите «Показать нулевые значения».
 На вкладке «Классы» разверните «Нулевые значения», чтобы указать символ, метку легенды и описание легенды. Если поле атрибута, используемое для определения символов пропорционального размера, содержит нулевые значения, символы для этих объектов не будут отображаться, если только вы явно не выберете их отображение с помощью выделенного символа.
На вкладке «Классы» разверните «Нулевые значения», чтобы указать символ, метку легенды и описание легенды. Если поле атрибута, используемое для определения символов пропорционального размера, содержит нулевые значения, символы для этих объектов не будут отображаться, если только вы явно не выберете их отображение с помощью выделенного символа.
На вкладке Дополнительные параметры символов можно выполнить следующие действия:
- По умолчанию размер выборки, используемый для расчета статистики и диапазонов классов, составляет 10 000 записей. Чтобы изменить максимальный размер выборки, разверните Размер выборки и измените значение Максимальный размер выборки. Ограничение размера выборки повышает производительность, но может непреднамеренно пропустить важные выбросы в наборе данных. Как правило, чем больше набор данных, тем больший размер выборки следует использовать.
- Чтобы настроить маскирование для отдельных объектов, разверните Маскирование на уровне объектов.

- Чтобы исключить значения данных из схемы символов и при необходимости определить альтернативный символ для исключенных значений, разверните Исключение данных, чтобы определить запрос. Чтобы прекратить отображение исключенных значений, на вкладке Основные символы щелкните Дополнительно и снимите флажок Показать исключенные значения.
Изменение пропорциональных символов с помощью прозрачности, поворота или цвета
В дополнение к указанию величины объектов с пропорциональными символами вы также можете отображать дополнительные атрибуты, изменяя прозрачность, поворот и цвет символов. Хотя все эти обработки можно применять одновременно, имейте в виду, что слишком большое количество визуальных вариаций затрудняет интерпретацию слоя. Рекомендуется экономно применять вторичные символы.
Узнайте больше о концепциях символов
- На панели Символы щелкните вкладку Изменение символов по атрибуту .
- Расширение прозрачности, поворота или цвета.

Публикация слоя с пропорциональными символами
Когда вы публикуете слой с пропорциональными символами в ArcGIS Online или ArcGIS Enterprise в качестве векторного веб-слоя или слоя веб-сцены, слой отображается с неклассифицированными символами градуированного размера и может выглядеть иначе, чем слой в ArcGIS Pro.
Если указана единица измерения, она не учитывается в результирующем слое веб-карты, но учитывается в слое веб-сцены. В веб-сцене единицы могут представлять высоту и ширину. Значение максимального размера, установленное на None, также не учитывается. Применяется максимальное значение, и все символы имеют размер в пределах этого диапазона.
Слой с пропорциональными символами может быть опубликован как веб-слой листов только в том случае, если для параметра Максимальный размер установлено значение Нет. Слой веб-листов выглядит так же, как слой в ArcGIS Pro.
Похожие темы
Отзыв по этой теме?
Сегменты Середины и лучи
Концепция линий проста, но большая часть геометрии связана с частями линий. Некоторые из этих частей настолько особенные, что имеют собственные имена и символы.
Некоторые из этих частей настолько особенные, что имеют собственные имена и символы.
Линейный сегмент
Отрезок представляет собой соединенный кусок линии. Он имеет две конечные точки и называется по своим конечным точкам. Иногда для обозначения сегмента используется символ – написанный поверх двух букв. Это отрезок CD (рис. 1).
Рисунок 1 Сегмент линии.
пишется CD (Технически CD относится к точкам C и D и всем точкам между ними, а CD без относится к расстоянию от C до D . ) Обратите внимание, что CD является частью .
Постулат 7 (Постулат линейки): Каждая точка на линии может быть соединена ровно с одним действительным числом, называемым ее координата . Расстояние между двумя точками равно положительной разности их координат (рис.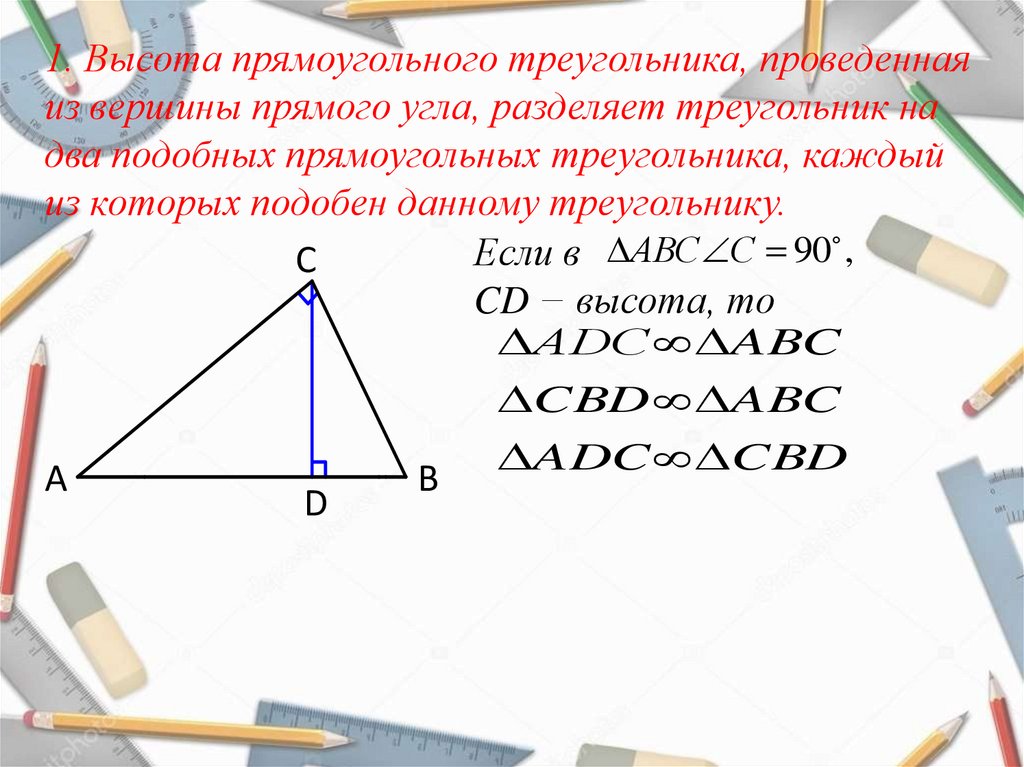 2).
2).
Пример 1 : На рисунке 3 найдите длину QU .
Рисунок 3 Длина сегмента линии.Постулат 8 (Постулат сложения сегментов): Если B лежит между A и C в строке, то AB + BC = AC (рисунок 4).
Рисунок 4 Сложение длин отрезков.
Пример 2 : На рисунке 5 A находится между C и T . Найдите CT , если CA = 5 и AT = 8.
Рисунок 5 Сложение длин отрезков.
Поскольку A лежит между C и T , постулат 8 говорит вам, что
Средняя точка
Середина отрезка прямой является средней точкой или точкой, равноудаленной от конечных точек (рис. 6).
6).
Рисунок 6 Середина отрезка.
R является средней точкой QS , потому что QR = RS или потому что QR = ½ QS или RS = ½ QS
Пример 3: На рисунке 7 найдите середину KR .
Рисунок 7 Середина отрезка прямой.Середина KR будет равна ½ (24) или 12 пробелам либо от K , либо от R . Поскольку координата K равна 5, и она меньше, чем координата R (которая равна 29), чтобы получить координату средней точки, вы можете либо прибавить 12 к 5, либо вычесть 12 из 29. В любом случае вы определить, что координата середины равна 17. Это означает, что точка O является средней точкой KR , потому что KO = ИЛИ .
Другой способ получить координату средней точки — найти среднее значение координат конечной точки.

 74MB
74MB 55KB
55KB 03KB
03KB 68KB
68KB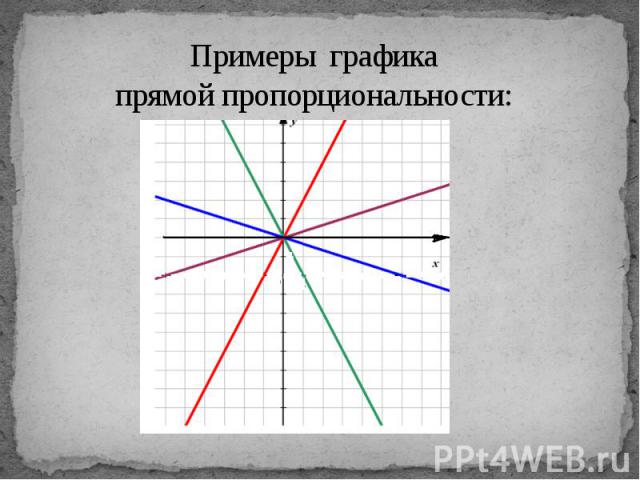 12KB
12KB

 Или установите для параметра Максимальный размер значение Нет. При необходимости отрегулируйте шаблон и фоновые символы.
Или установите для параметра Максимальный размер значение Нет. При необходимости отрегулируйте шаблон и фоновые символы. На вкладке «Классы» разверните «Нулевые значения», чтобы указать символ, метку легенды и описание легенды. Если поле атрибута, используемое для определения символов пропорционального размера, содержит нулевые значения, символы для этих объектов не будут отображаться, если только вы явно не выберете их отображение с помощью выделенного символа.
На вкладке «Классы» разверните «Нулевые значения», чтобы указать символ, метку легенды и описание легенды. Если поле атрибута, используемое для определения символов пропорционального размера, содержит нулевые значения, символы для этих объектов не будут отображаться, если только вы явно не выберете их отображение с помощью выделенного символа.
