Знак подобия в геометрии: «Как выглядит знак подобия в геометрии?» — Яндекс Кью

Подобные треугольники. Признаки подобия | Геометрия

• Первый признак подобия треугольников
• Второй признак подобия треугольников
• Третий признак подобия треугольников

Подобные треугольники — это треугольники, у которых все три угла равны, а все стороны одного треугольника в одно и то же число раз длиннее (или короче) сторон другого треугольника, то есть треугольники подобны если их углы равны, а сходственные стороны пропорциональны.

Сходственные стороны — это стороны двух треугольников, лежащие против равных углов.

Рассмотрим два треугольника  ABC  и  A₁B₁C₁,  у которых  ∠A = ∠A₁,  ∠B = ∠B₁,  ∠C = ∠C₁:

Стороны  AB  и  A₁B₁,  BC  и  B₁C₁,  CA  и  C₁A₁

,  лежащие напротив равных углов, называются сходственными сторонами. Следовательно, отношения сходственных сторон равны:

AB	=	BC	=	AC	= k,
A1B1		B1C1		A1C1

k  — это коэффициент подобия ( число, равное отношению сходственных сторон подобных треугольников). Если  k = 1,  то треугольники равны, то есть равенство треугольников – это частный случай подобия.

Подобие треугольников обозначается знаком  ~:  ABC ~ A₁B₁C₁.

Отношение площадей подобных треугольников равно квадрату коэффициента подобия. Если обозначить площади двух подобных треугольников буквами 

S  и  S₁,  то:

S	= k2.
S1

Первый признак подобия треугольников

Если два угла одного треугольника равны двум углам другого, то треугольники подобны.

Если  ∠A = ∠A₁,  ∠C = ∠C₁,

то  ABC ~ A₁B₁C₁.

Второй признак подобия треугольников

Если две стороны одного треугольника пропорциональны двум сторонам другого треугольника и углы, заключённые между этими сторонами, равны, то треугольники подобны.

Если	AB	=	AC	,  ∠A = ∠A1,
	A1B1		A1C1
то  ABC ~ A1B1C1.

Третий признак подобия треугольников

Если три стороны одного треугольника пропорциональны трём сходственным сторонам другого, то треугольники подобны.

Если	AB	=	BC	=	AC	,
	A1B1		B1C1		A1C1
то  ABC ~ A1B1C1.

Таблица знаков в геометрии и их значения: пересечение, подобие

Sign in

Password recovery

Восстановите свой пароль

Ваш адрес электронной почты

MicroExcel.ru Математика Знаки и символы в геометрии

Ниже представлена таблица с основными математическими символами и знаками, которые используются в геометрии с 7 класса и старше.

00″ data-percent-format=»10.00%» data-date-format=»DD.MM.YYYY» data-time-format=»HH:mm» data-features=»["after_table_loaded_script"]» data-search-value=»» data-lightbox-img=»» data-head-rows-count=»1″ data-pagination-length=»50,100,All» data-auto-index=»off» data-searching-settings=»{"columnSearchPosition":"bottom","minChars":"0"}» data-lang=»default» data-override=»{"emptyTable":"","info":"","infoEmpty":"","infoFiltered":"","lengthMenu":"","search":"","zeroRecords":"","exportLabel":"","file":"default"}» data-merged=»[]» data-responsive-mode=»2″ data-from-history=»0″>

Знак	Название	Значение/описание	Пример
∠	угол	фигура, состоящая из двух лучей и вершины	∠ABC = 30°
ru/wp-content/uploads/2020/01/ostr-ugol.png" class="stbSkipLazy aligncenter size-full" width="40" height="40" data-full="https://microexcel.ru/wp-content/uploads/2020/01/ostr-ugol.png" />» data-order=»<img src="https://microexcel.ru/wp-content/uploads/2020/01/ostr-ugol.png" class="stbSkipLazy aligncenter size-full" width="40" height="40" data-full="https://microexcel.ru/wp-content/uploads/2020/01/ostr-ugol.png" />»>	острый угол	угол от 0 до 90 градусов	∠AOB = 60°
ru/wp-content/uploads/2020/01/pryamoy-ugol.png" class="stbSkipLazy aligncenter size-full" width="40" height="40" data-full="https://microexcel.ru/wp-content/uploads/2020/01/pryamoy-ugol.png" />» data-order=»<img src="https://microexcel.ru/wp-content/uploads/2020/01/pryamoy-ugol.png" class="stbSkipLazy aligncenter size-full" width="40" height="40" data-full="https://microexcel.ru/wp-content/uploads/2020/01/pryamoy-ugol.png" />»>	прямой угол	угол, равный 90 граусам	∠AOB = 90°
ru/wp-content/uploads/2020/01/tupoy-ugol.png" class="stbSkipLazy aligncenter size-full" width="40" height="40" data-full="https://microexcel.ru/wp-content/uploads/2020/01/tupoy-ugol.png" />» data-order=»<img src="https://microexcel.ru/wp-content/uploads/2020/01/tupoy-ugol.png" class="stbSkipLazy aligncenter size-full" width="40" height="40" data-full="https://microexcel.ru/wp-content/uploads/2020/01/tupoy-ugol.png" />»>	тупой угол	угол от 90 до 180 градусов	∠AOB = 120°
ru/wp-content/uploads/2020/01/razvernuty-ugol-1.png" class="stbSkipLazy aligncenter size-full" width="80" height="240" data-full="https://microexcel.ru/wp-content/uploads/2020/01/razvernuty-ugol-1.png" />» data-order=»<img src="https://microexcel.ru/wp-content/uploads/2020/01/razvernuty-ugol-1.png" class="stbSkipLazy aligncenter size-full" width="80" height="240" data-full="https://microexcel.ru/wp-content/uploads/2020/01/razvernuty-ugol-1.png" />»>	развернутый угол	угол, равный 180 градусам	∠AOB = 180°
° (или deg)	градус	единица измерения угла, равна 1/360 окружности	45°
′	минута	единица измерения угла, 1° = 60′	α = 70°59′
″	секунда	единица измерения угла, 1′ = 60″	α = 70°59′59″
ru/wp-content/uploads/2020/01/line-exc.png" class="stbSkipLazy aligncenter size-full" width="30" height="30" data-full="https://microexcel.ru/wp-content/uploads/2020/01/line-exc.png" />» data-order=»<img src="https://microexcel.ru/wp-content/uploads/2020/01/line-exc.png" class="stbSkipLazy aligncenter size-full" width="30" height="30" data-full="https://microexcel.ru/wp-content/uploads/2020/01/line-exc.png" />»>	линия	бесконечная прямая без начала и конца
ru/wp-content/uploads/2020/01/line-segment-exc.png" class="stbSkipLazy aligncenter size-full" width="30" height="30" data-full="https://microexcel.ru/wp-content/uploads/2020/01/line-segment-exc.png" />» data-order=»<img src="https://microexcel.ru/wp-content/uploads/2020/01/line-segment-exc.png" class="stbSkipLazy aligncenter size-full" width="30" height="30" data-full="https://microexcel.ru/wp-content/uploads/2020/01/line-segment-exc.png" />»>	отрезок	участок на прямой между точками A и B
ru/wp-content/uploads/2020/01/ray-exc.png" class="stbSkipLazy aligncenter size-full" width="35" height="35" data-full="https://microexcel.ru/wp-content/uploads/2020/01/ray-exc.png" />» data-order=»<img src="https://microexcel.ru/wp-content/uploads/2020/01/ray-exc.png" class="stbSkipLazy aligncenter size-full" width="35" height="35" data-full="https://microexcel.ru/wp-content/uploads/2020/01/ray-exc.png" />»>	луч	бесконечная прямая, имеющая начало в точке A, но не имеющая конца
ru/wp-content/uploads/2020/01/arc-exc.png" class="stbSkipLazy aligncenter size-full" width="30" height="30" data-full="https://microexcel.ru/wp-content/uploads/2020/01/arc-exc.png" />» data-order=»<img src="https://microexcel.ru/wp-content/uploads/2020/01/arc-exc.png" class="stbSkipLazy aligncenter size-full" width="30" height="30" data-full="https://microexcel.ru/wp-content/uploads/2020/01/arc-exc.png" />»>	дуга	дуга, образованная между точками A и B
⊥	перпендикулярность	линии (прямые), расположенные под углом 90° по отношению друг к другу	AC ⊥ BC
||	параллельность	непересекающиеся прямые (линии)	AB || CD
∩	пересечение	множество одинаковых элементов, принадлежащих как множеству A, так и B	A ∩ B
∈ / ∉	принадлежность/ непринадлежность	элемент является/не является элементом заданного множества	a ∈ S
≅	конгуэнтность	эквивалентность геометрических форм и размеров	∆ABC ≅ ∆XYZ
~	подобие	та же форма, но разные размеры	∆ABC ~ ∆XYZ
Δ	треугольник	фигура треугольника	ΔABC ≅ ΔBCD
|x-y|	дистанция	дистанция между точками X и Y	| x-y | = 5
π	константа «Пи»	отношение длины окружности к диаметру круга, π = C/d	141592654…</nobr>» data-order=»<nobr>π = 3.141592654…</nobr>»>π = 3.141592654…
рад (rad) или c	радиан	единица измерения угла	360° = 2π c

microexcel. ru

ЧАЩЕ ВСЕГО ЗАПРАШИВАЮТ

Таблица знаков зодиака

Нахождение площади трапеции: формула и примеры

Нахождение длины окружности: формула и задачи

Римские цифры: таблицы

Таблица синусов

Тригонометрическая функция: Тангенс угла (tg)

Нахождение площади ромба: формула и примеры

Нахождение объема цилиндра: формула и задачи

Тригонометрическая функция: Синус угла (sin)

Геометрическая фигура: треугольник

Нахождение объема шара: формула и задачи

Тригонометрическая функция: Косинус угла (cos)

Нахождение объема конуса: формула и задачи

Таблица сложения чисел

Нахождение площади квадрата: формула и примеры

Что такое тетраэдр: определение, виды, формулы площади и объема

Нахождение объема пирамиды: формула и задачи

Признаки подобия треугольников

Нахождение периметра прямоугольника: формула и задачи

Формула Герона для треугольника

Что такое средняя линия треугольника

Нахождение площади треугольника: формула и примеры

Нахождение площади поверхности конуса: формула и задачи

Что такое прямоугольник: определение, свойства, признаки, формулы

Разность кубов: формула и примеры

Степени натуральных чисел

Нахождение площади правильного шестиугольника: формула и примеры

Тригонометрические значения углов: sin, cos, tg, ctg

Нахождение периметра квадрата: формула и задачи

Теорема Фалеса: формулировка и пример решения задачи

Сумма кубов: формула и примеры

Нахождение объема куба: формула и задачи

Куб разности: формула и примеры

Нахождение площади шарового сегмента

Что такое окружность: определение, свойства, формулы

Похожие фигурки

Горячая математика

Говорят, что две фигуры похожий если они одинаковой формы. Говоря более математическим языком, две фигуры подобны, если их соответствующие углы равны конгруэнтный , а отношения длин их соответствующих сторон равны.

Это обычное отношение называется масштаб .

Символ ∼ используется для обозначения сходства.

Пример 1:

На рисунке ниже пятиугольник А Б С Д Е ∼ пятиугольник В Вт Икс Д Z .

(Обратите внимание, что порядок, в котором вы пишете вершины, имеет значение; например, пятиугольник А Б С Д Е является нет похоже на пятиугольник В Z Д Икс Вт .)

Пример 2:

Два цилиндра похожи. Найдите масштабный коэффициент и радиус второго цилиндра.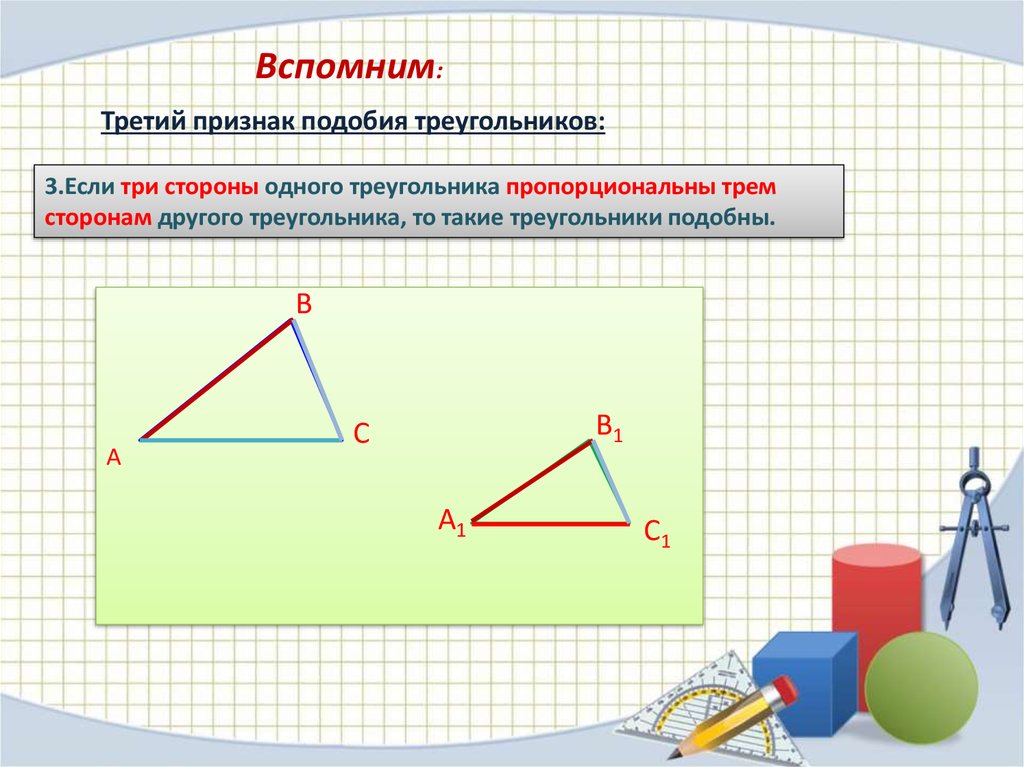

Высота цилиндра справа 1 3 высота цилиндра слева. Итак, масштабный коэффициент 1 3 .

Чтобы получить радиус меньшего цилиндра, разделите 1,8 к 3 .

1,8 ÷ 3 «=» 0,6

Значит, радиус меньшего цилиндра 0,6 см.

Заметим, что двумерная фигура подобна другой, если вторая может быть получена из первой последовательностью вращения , размышления , переводы , и расширения .

Пример 3:

На рисунке выше шестиугольник А 1 Б 1 С 1 Д 1 Е 1 Ф 1 переворачивается горизонтально, чтобы получить А 2 Б 2 С 2 Д 2 Е 2 Ф 2 .

Затем шестиугольник А 2 Б 2 С 2 Д 2 Е 2 Ф 2 переводится как получить А 3 Б 3 С 3 Д 3 Е 3 Ф 3 .

Шестиугольник А 3 Б 3 С 3 Д 3 Е 3 Ф 3 расширяется на масштабный коэффициент 1 2 получить А 4 Б 4 С 4 Д 4 Е 4 Ф .

Обратите внимание, что

А 1 Б 1 С 1 Д 1 Е 1 Ф 1 ∼ А 2 Б 2 С 2 Д 2 Е 2 Ф 2 ∼ А 3 Б 3 С 3 Д 3 Е 3 Ф 3 ∼ А 4 Б 4 С 4 Д 4 Е 4 Ф 4 .

То есть все четыре шестиугольника подобны. (На самом деле, первые три конгруэнтны.)

Пример 4:

Рассмотрим пятиугольник п Вопрос р С Т на координатной плоскости.

Ротация на 180 ° о происхождении отводит пятиугольник к п ‘ Вопрос ‘ р ‘ С ‘ Т ‘ .

Теперь расширение относительно начала координат с помощью масштабного коэффициента 2 берет пятиугольник п ‘ Вопрос ‘ р ‘ С ‘ Т ‘ к п ‘ ‘ Вопрос ‘ ‘ р ‘ ‘ С ‘ ‘ Т ‘ ‘ .

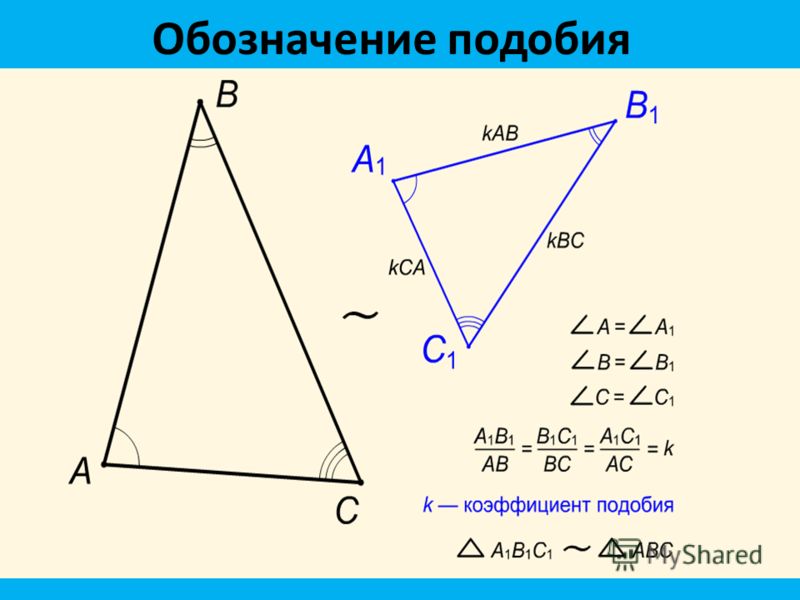
Обратите внимание, что п Вопрос р С Т ∼ п ‘ Вопрос ‘ р ‘ С ‘ Т ‘ ∼ п ‘ ‘ Вопрос ‘ ‘ р ‘ ‘ С ‘ ‘ Т ‘ ‘ . То есть все три пятиугольника подобны. (И первые два совпадают.)

Символы в геометрии

Символы экономят время и место при написании. Вот наиболее распространенные геометрические символы:

.

Символ	Значение	Пример	Словами
△	Треугольник	△ABC имеет 3 равные стороны	Треугольник ABC имеет три равные стороны
∠	Угол	∠ABC равно 45°	Угол, образованный треугольником ABC, равен 45 градусам.
⊥	Перпендикуляр	АВ⊥CD	Линия AB перпендикулярна линии CD
∥	Параллельный	EF∥GH	Линия EF параллельна линии GH
°	градусов	360°	360 градусов (полный оборот!)
∟	Прямоугольный (90°)	∟ равно 90°	Прямой угол равен 90 градусов
	Линейный сегмент «AB»	АБ	Отрезок между А и В
	Линия «АВ»		Бесконечная линия, включающая A и B
	Рэй «АБ»		Линия, которая начинается в A, проходит через B и продолжается
≅	Конгруэнтные (одинаковая форма и размер)	△ABC ≅ △DEF	Треугольник ABC равен треугольнику DEF
~	Аналогичные (такой же формы, разного размера)	△DEF∼△MNO	Треугольник DEF подобен треугольнику MNO
∴	Поэтому	а=б б=а	a равно b, поэтому b равно a

Пример: В △ABC, ∠BAC равно ∟

Действительно говорится: «В треугольнике ABC угол BAC прямой»

Именование углов

Для углов центральная буква находится там, где находится угол.