Этап урока Методы и приемы | Хроно- Метраж | Содержание урока | Формируемые УУД | |
Деятельность учителя, формы деятельности учащихся | Деятельность ученика | |||
I. Психологический настрой Наглядный: демонстрация слайдов | 2 мин | Фронтальная форма работы — Здравствуйте, дети! — Присаживайтесь на свои места. — Сядьте, как должны сидеть ученики. Спинку депржим ровно, ноги на полу. — Посмотрите на экран. Прочитайте девиз нашего урока. Учение – путь к умению. — Скажите, как вы понимаете это выражение? — Все верно. Молодцы. | -Здравствуйте Слушают учителя. Читают девиз -Если мы будем обладать полезными знаниями, то всегда с легкостью можем использовать их в жизни. | Л: восприятие речи учителя непосредственно обращенную к учащимся; формирование желания выполнять учебные действия К: планирование учебного сотрудничества с учителем и сверстниками |
II. Практический: диктант Словесный: беседа | 8 мин | Фронтальная форма работы -Откройте ваши тетради отступите от последней работы четыре клеточки, посередине строчки запишите число – 10 апреля ниже на следующей строке напишите «Классная работа». — В ваших тетрадях написано число, пропишите его в строчку. Устный счет. -Проведем небольшую разминку, проверим, как хорошо вы знаете таблицу умножения. Пропишите в строчку через запятую ответы на эти примеры: 2*9, 9*4, 4*6, 6*5, 7*3, 1*8, 10*1, 8*7, 3*5, 5*2, 0*3 — А сейчас проверим ваши ответы. | Записывают число в тетради. Прописывают число в строчку Записывают ответы в тетрадь
| П: осознанное и произвольное построение речевого высказывания К: умение выражать свои мысли с достаточной полнотой и точностью Р: осуществление подведения под понятие; |
III. Постановка учебной задачи Наглядный: демонстрация слайдов Словесный: беседа | 3 мин | Фронтальная форма работы — Ребята, посмотрите на слайд, назовите, как называется каждое выражение? 25 + 5 25 – 5 25 * 5 25 : 5 — А теперь давайте назовем компоненты для каждого действия. — Как называются числа при сложении? — Как называются числа при вычитании? — Как называются числа при умножении? — Кто может назвать, как называются числа при делении? — Как вы думаете, о чем мы будем сегодня говорить? Как будет звучать тема нашего урока? — Какие цели поставим? | — Сумма. — Разность. — Произведение. — Частное. — Слагаемое, слагаемое, сумма. — Уменьшаемое, вычитаемое, разность. -Множитель, множитель, произведение. — Сегодня мы узнаем, как называются числа при делении. — «Делимое и делитель» — Ставят цели. | Р: целеполагание – постановка учебной задачи; К: планирование учебного сотрудничества – определение цели; |
IV. Открытие нового знания Словесный: беседа Наглядный: демонстрация слайдов Практический: выполнение упражнений Словесный: беседа | 6 мин | Фронтальная форма работы. — Откройте учебник на странице 92 упражнение 1. — Посмотрите на рисунок, что вы видите? — Как будет выглядеть запись частного 12 и 4? — Какой знак используется для записи частного 12 и 4? — Посмотрите на первое число в выражении. — Прочитайте на странице 92 первую рамку. Прочитайте ее. — Какое число является делимым, подчеркните его? — Как вы думаете, почему оно его так называют? — Совершенно верно, а кто теперь прочитает вторую рамку? — Подчеркните делитель в выражении. Как вы думаете, почему оно так называется? — Хорошо, а чем является частное? Вопрос непонятен — Давайте выполним задание 2. Кто прочитает задание? — Что нам нужно найти? — А что нам известно? — Что стоит первым в частном? — Назовите делимое. — А что должно стоять вторым? — Назовите делитель. — Как должно выглядеть выражение? — Что является частным? — Хорошо. | — 12 яблок разделили по тарелкам по 4. — 12:4 — Деление. Отвечают на вопрос. — Первое число в частном – это делимое. — 12 — Потому что это число делят. — Второе число в частном – это делитель. — Потому на это число делят. — Значение частного – это результат действия. — Составь и запиши частное, если делитель равен 3, а делимое 9. — Значение частного. — Делимое и делитель. — Делимое. — 9. — Делитель. -3. — 9:3 — 3 | К: умение выражать свои мысли с достаточной полнотой и точностью П.: анализ П.: извлечение необходимой информации |
V. Первичное закрепление Словесный: беседа Практический: выполнение упражнений Словесный: беседа | 10 мин | Фронтальная форма работы. — На странице 93 выполните упражнение 3.Прочитайте задание. Что нужно сделать? — Что называют делимым? — Выписывайте в строчку, через запятую, не забывайте пропускать клетку после каждого выражения. — Итак, назовите мне выражение, которое вы не выписали. — Почему? — Хорошо, теперь выполните 4 упражнение. Прочитайте задание. Что нужно сделать? — Что является делителем в частном? — Записывать упражнение будете, как предыдущее, в строчку через запятую. Можете приступать. — Кто назовет частные, которые вы не выписали? — Почему вы их не выписали? — Теперь у вас будет творческое задание. Составьте и запишите пять частных. Делимое подчеркните в каждом — красным, а делитель – синим. Записывайте частные в столбик. Можете приступать. — Давайте посмотрим, что у вас получилось. | — Первое число в частном. Выполняют задания. — 48:24 — Потому что 24 в этом частном является делителем. — Выписать частные, в которых делитель 6. — Второе число в частном. Выполняют задание. — 6:2, 6:3 — Потому 6 является делимым. Выполняют задание. Проверяют задание. | К: умение выражать свои мысли с достаточной полнотой и точностью; П: соотнесение ранее изученного материала для выполнения задания; П: осуществление поиска и выделение необходимой информации; П: осуществление поиска и выделение необходимой информации; |
Динамическая пауза | 1м | -А сейчас давайте немного разомнемся. Посмотрите на экран. | Выполняют движения. | |
VI. Самостоятельная работа с самопроверкой Практический: работа с карточками Наглядный: демонстрация слайдов с эталоном | 7 мин | Индивидуальная форма работа — Теперь вы поработаете самостоятельно, перед вами лежат таблица, ваша задача – соединить линией равенство и название компонента равенства. Есть ли у вас вопросы? Можете приступать к заданию. — Итак, давайте проверим. Посмотрите на эталон. Если у вас нет ошибок, то оценка «5», если у вас 1-2 ошибки, то оценка «4», а если ошибок больше, то вам нужно еще потренироваться. | Слушают задание. Выполняют задание самостоятельно. Проверка по эталону. | Р: самостоятельное планирование и выполнение свои действий на знакомом учебном материале. П: осуществление контроля и оценки процесса и результатов деятельности; |
VII. Включение в систему знаний, повторение Словесный: беседа Практический: выполнение упражнений | 6 мин | — Теперь вы поработаете в парах, перед вами лежат таблица, ваша задача — записать частные в нужный столбик. — Если у вас нет вопросов, можете приступать к заданию. Давайте проверим. | Слушают указания. — Выполняют задание. Проверяют задание. | Р: самостоятельное планирование и выполнение свои действий на знакомом учебном материале |
VIII.Рефлексия деятельности | 2 мин | Фронтальная форма работы. — Итак, ребята, наш урок подходит к концу. — Посмотрите на экран. Это цели, которые мы ставили в начале урока. — Ребята, достаньте ваши цветные карандаши. Поднимите руку с зеленым карандашом, если сегодня вы собой довольны. Поднимите руку с красным карандашом, если что-то у вас сегодня не получилось. | Поднимают руку | П: построение речевого высказывания Р: осуществление итогового контроля |
Этап самоопределения к деятельности
Актуализация знаний и мотивация
Что с ним делают?
Приступайте.
В Математике: Делимое В Дроби 9 Букв
Решение этого кроссворда состоит из 9 букв длиной и начинается с буквы Ч
Ниже вы найдете правильный ответ на В математике: делимое в дроби 9 букв, если вам нужна дополнительная помощь в завершении кроссворда, продолжайте навигацию и воспользуйтесь нашей функцией поиска.
ответ на кроссворд и сканворд
ЧИСЛИТЕЛЬ
предыдущий следующий
ты знаешь ответ ?
ответ:
связанные кроссворды
- Числитель
- Делимое в дроби
- Дробная вершина
похожие кроссворды
- Делимое в дроби
- Делимое в дроби 9 букв
- Число, на которое- в действии деления- делят делимое (в математике) 8 букв
- В математике: делитель в дроби 11 букв
- В математике: повторяющаяся группа цифр в записи бесконечной дроби 6 букв
- Группа повторяющихся цифр в бесконечной десятичной дроби (в математике) 6 букв
- Часть дроби, стоящая под чертой (в математике) 11 букв
- Делимое без остатка
- Число или величина, на которую делится делимое 8 букв
- Делимое, делитель, 7 букв
- Сорт дроби на птиц
- Знак препинания в десятичной дроби
- Рассеивание дроби или пуль при стрельбе из конкретного ружья
- Делитель в дроби
- Часть дроби (математическое)
- Очистка деталей струей дроби
- Вместилище для хранения и ношения дроби
- Мешочек или коробка для ружейной дроби
Что такое остаток в математике?
Написано
Malcolm McKinsey
Проверка по фактам
Пол Маццола
Определение оставшихся
Остальные-часть дивиденда, которая не может быть достоверной дивизионной. После деления целых чисел, чтобы найти частное, вы можете получить часть остатка дивиденда; это остаток. Он представляет собой долю дивиденда и может быть записан в виде десятичной или дробной части.
Деление с остатком
Решением или ответом на задачу деления является частное, которое может включать остаток.
Что такое остаток в математике?При делении мы делим отдельные предметы, например торт, и наборы предметов, например кексы, между группами, надеясь, что каждый получит справедливую долю. Любая сумма дивиденда, которая не делится на делитель, является остатком.
Предположим, мы отмечаем 19-летие школьного математического клуба. У нас есть большой, вкусный листовой пирог, чтобы поделиться со всеми 43 членов. Как мы будем резать торт, чтобы поровну поровну досталось всем?
Мы могли бы разрезать торт разными способами, составляя равные части, но нет способа отрезать ровно 43 частей от прямоугольника.
Как бы мы ни разрезали торт, чтобы дать каждому по кусочку, что-то останется. остаток будет останется .
Если мы разрежем торт на 5 строк и 9 столбцов, у нас будет 45 ломтиков, которые можно разделить между 43 человек; каждый получает 1 фрагментов, и у нас остается 2 фрагментов.
Первое число, 1 , является частным. 2 это остаток, объедки, часть пирога, которую нельзя разумно разделить между всеми 45 членами Математического клуба.
Деление с остатком примерКак найти остаток в делении
Шаги к делению в длинное с остатком легко вспомнить с помощью мнемоники (трюка с памятью): D oes M cDonald’s S ell C heese B urgers D aily? :
D OES = D IVIDE (Разделение дивиденда от Divisor)
M CDONALD’0003
S ell = S вычесть (вычесть произведение из первых цифр делимого)
C heese = C разность сравнить с делителем; меньше)
Б ургерс Д айлы = Б кольцо Д собственный (сбей следующую цифру своего дивиденда и начни сначала)
Если останется разница после выполнения всех шагов все цифры делимого, эта разница равна остаток .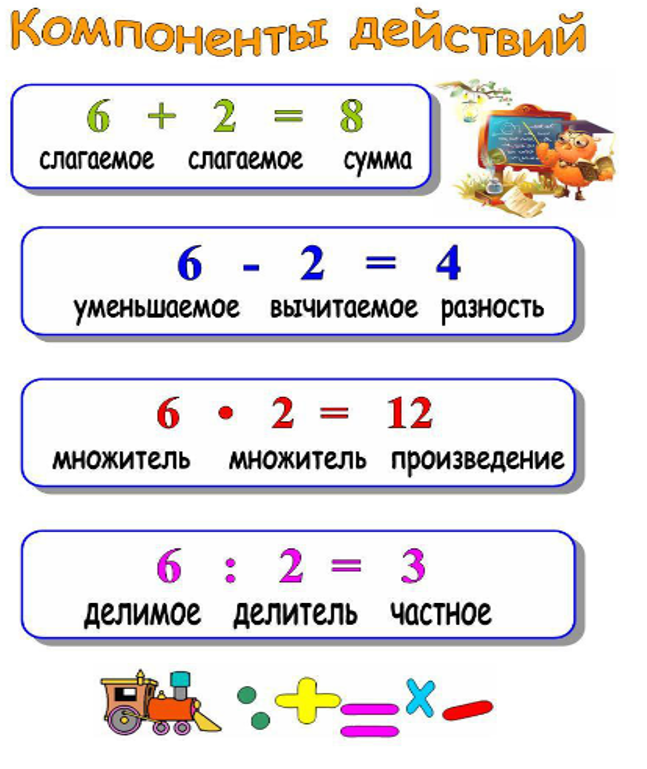
Символ остатка
Чтобы обозначить, что в вашем ответе есть остаток, вы пишете заглавную букву R после частного, за которой следует число, обозначающее остаток. Ответ, или частное, представляет собой целое число, а остаток обозначается буквой R .
Символ остаткаЧтобы интерпретировать остаток, вы должны посмотреть на единицы делимого, делителя и частного. Если дивидендом являются кексы, а делитель представляет членов Математического клуба. Затем частное — это кексы на участника, а остаток — это кексы, которые нельзя было справедливо разделить между участниками.
Вот как это выглядит в словесной задаче:
48 кексы доступны для справедливого распределения между 7 членами Математического клуба. Сколько получит каждый участник и сколько останется?
В виде уравнения это выглядит так:
48 кексов, разделенных между 7 участниками, равно 6 кексов на каждого члена, при этом остается 6 кексов.
Как написать остаток
Существуют разные способы записи остатка в задаче на деление. Остаток может быть целым числом или дробью. Вы всегда пишете остаток после заглавной буквы R, чтобы показать, что это остаток.
Если вы хотите выразить остаток как нечто иное, чем остаточное целое число, вы можете сделать его частью делимого.
Научиться записывать остаток в виде дроби очень просто. Остаток становится числителем, а делитель — знаменателем. Единица для частного и остатка называется делимым и делителем (дивиденд на делитель). Упростите дробь, если это возможно.
Как написать остатокОстаток примеры задач
Вот пример листа пирожных, нарезанных на 44 отдельные пирожные. Вы раздаете их 7 членам Математического клуба, если каждый член подпишет нового члена из класса первокурсников. Все 7 членов соответствуют требованиям. Как будут делиться пирожные 44 ?
Сначала выполните деление в большую сторону:
44 ÷ 7 = 6 пирожных на члена, при этом осталось 2 пирожных (остаток от 2 )
Затем поместите остаток в числитель дроби и используйте делитель в качестве знаменателя:
2 пирожных, которые нужно разделить между 7 участниками, 2/7
дробное количество пирожных на члена нельзя упростить, поэтому окончательный ответ — 6 пирожных.
Дробные остатки также работают с членами множества. Предположим, у вас есть 190 лотерейных билетов, которые нужно справедливо разделить между 14 участниками – 77 ветеранов-членов и 77 новобранцев — Математического клуба для продажи в качестве сбора средств.
Сколько билетов должен получить каждый участник и какая часть будет остатком?
Каждый участник должен продать 13 билетов!
На самом деле ни один участник не будет пытаться продать примерно половину билета, но оставшаяся часть дает каждому участнику цель: каждый должен попытаться продать 14 билетов, зная, что некоторые продадут только 13 и другие продадут больше.
Математические навыки: как сделать деление
| Группировка объектов |
Деление можно считать обратным или обратным умножению.
Если мы вернемся к 12 собакам в умножении, мы можем разделить их на 3 равные группы. Сколько будет в каждой группе?
Всего 12 собак, разделенных на 3 группы по 4:
| Группа 1 | Группа 2 | Группа 3 |
| 4 собаки | 4 собаки | 4 собаки |
Итак, теперь мы можем сказать, что 12 собак, разделенных на 3 группы, составляют по 4 собаки в группе. Мы можем записать это как —
12 3 = 4 (здесь мы используем символ деления)
ИЛИ
12 / 3 = 4 (косая черта означает «делится на»)
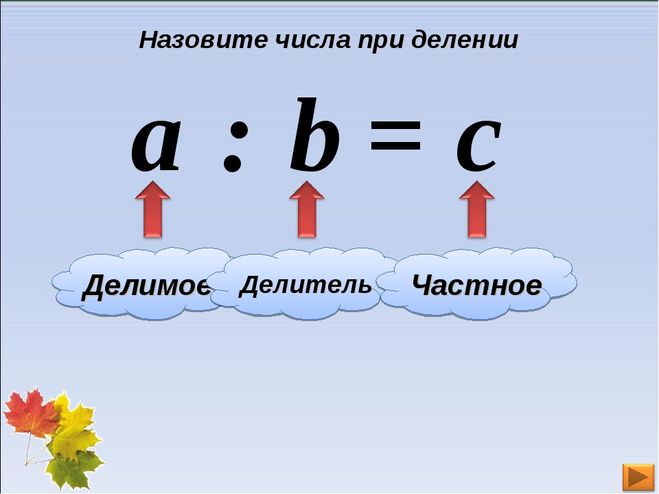
| Условия – делитель, дивиденд, частное, остаток |
Есть четыре основных термина для описания частей деления.
Если у нас есть задача 23 5 = 4 R 3 , мы имеем делимое 23, делитель 5, частное 4 и остаток 3, потому что 23 нельзя разделить поровну на 5 групп. Когда вы разделите его на 5 групп, вы получите по 4 предмета в каждой группе и 3 предмета в запасе.
| Факты отдела |
Деление становится быстрее и проще, если вы знаете и запоминаете основные факты. Факты деления обратны фактам умножения. Например, если 9 x 6 = 54, то 54 9 = 6.
Флэш-карточки очень помогают в изучении фактов деления.
| Деление на ноль — не определено |
Деление определяется как действие, обратное умножению.
Если 2 х 9= 18, тогда 18 9 = 2 и 18 2 = 9.
Деление на ноль было бы обратным умножению на ноль. 7 x 0 = 0. Это соответствует 0/7 = 0 или 0 7 = 0. Однако 0 0 не равно 7. Это не вычисляется. Таким образом, деление на ноль не определено, поскольку оно не работает с нашим определением.
Деление нуля считается неопределенным. Невозможно ничего разделить на группы ничего.
| Элемент идентификации умножения – один |
Элемент идентичности — это определенное число, которое при соединении с любым другим числом определенным образом дает исходное число. Одним из них является мультипликативный элемент или элемент идентичности умножения. Это также элемент идентификации подразделения. Один раз любое число является исходным числом; исходное число, деленное на единицу, является исходным числом.
х 1 =
5 х 1 = 5 и 25 х 1 = 25
А 1 = а
5 1 = 5 и 25 1 = 25
| Мультипликативный обратный |
Мультипликативное обратное или обратное число (например, а) обозначается 1/а так, что число а и его обратное число 1/а дают 1 при умножении.
Хотите узнать больше? Пройдите онлайн-курс по базовой математике.
Например, мультипликативное обратное число 8 равно 1/8. Когда вы умножаете 8 х 1/8, ответ будет 8/8, что равно 1 или 1 целому.
Для мультипликативной обратной или обратной величины любого числа разделите 1 на это число.
| Деление с одноразрядным делителем |
Когда мы действительно делаем деление, мы должны использовать так называемое длинное деление. Разделим 46 на 2.
Мы можем спросить: сколько раз 2 переходит в 4 или 4 делится на то, что равно 2. Мы знаем, что 2 x 2 = 4. Поэтому мы ставим 2 над 4, затем умножаем это 2 на 2 в делителе. и получить 4, которые мы кладем под 4 и вычитаем.
Когда мы вычитаем, ответ всегда должен быть меньше делителя. Если это не так, вы знаете, что цифру, которую вы использовали в частном, можно увеличить хотя бы на единицу.
Также проверьте свое умножение и вычитание.
Теперь мы опускаем 6 и спрашиваем, что получится, если мы разделим 6 на 2. Это будет 3. Итак, мы поместим 3 над 6 и умножим его на 2 в делителе, чтобы получить 6, а затем вычтем.
Чтобы проверить ответ, умножьте частное на делитель. Если дивиденд — это ваш ответ, ваше частное верно. 2 х 23 = 46,
Это довольно простая задача, которая решается равномерно. Давайте попробуем решить задачу, которая не так проста. Давайте разделим 3749 на 3.
3 входит в 3 (3000) один раз, поэтому поставьте 1 над 3 и умножьте 1 x 3, чтобы получить 3, и вычтите. Затем запишите следующую цифру.
Сколько раз 3 входит в 7? Мы знаем, что 3 x 2 = 6 и 3 x 3 = 9. Мы не можем превысить 7, поэтому ставим 2 выше 7 и умножаем, помещая 6 под 7 и вычитая, чтобы получить 1.
Затем опустим 4.
Теперь нам нужно число, которое при умножении на 3 дает нам самое близкое к 14 число без перебора. 3 х 5 = 15, так что это слишком много. 3 x 4 = 12, поэтому мы используем 4 над 4, кладем 12 под 14 и вычитаем, чтобы получить 2. Затем мы уменьшаем 9.
Сколько раз 3 будет 29? 3 x 9 = 27. Итак, мы поставим 9 над 9, умножим и снова вычтем. Поскольку у нас больше нет цифр, которые нужно записать, у нас будет остаток 2.
В реальных жизненных ситуациях остаток работает не очень хорошо. Когда вы начнете делать десятичные дроби, вы будете использовать другой метод для работы с остатками.
Чтобы проверить ответ, умножьте частное на делитель, затем прибавьте остаток:
1249 x 3 = 3747 + 2 = 3749
| Деление с кратным делителем | 2
Иногда ваш делитель состоит из двух или трех цифр.
С этим действительно несложно работать; это просто требует немного больше размышлений. Давайте посмотрим на 2 892 12.
Теперь вам нужно начать с первых двух цифр делимого (иногда вам нужно смотреть сразу на три). Сколько раз 12 можно превратить в 28, не превысив 28? 2 x 12 = 24 и 3 x 12 = 36. Следовательно, мы поставим 2 над 8 и умножим 2 x 12 = 24, поместим 24 под 28 и вычтем, чтобы получить 4. Затем мы опустим следующую цифру. что такое 9.
Мы знаем, что 4 x 12 равно 48, поэтому мы кладем 4 выше 9. Затем мы умножаем и кладем 48 ниже 49, вычитаем, чтобы получить 1, и опускаем 2 вместе с ним.
Это то же число, что и наш делитель, поэтому мы помещаем 1 (элемент мультипликативной идентичности) над 2, умножаем и вычитаем, чтобы получить 0.
**Помните, что при вычитании полученное число всегда должно быть меньше делителя. Если это не так, то нужно увеличить цифру в частном на 1 и снова умножить.