| 1 | Найти объем | сфера (5) | |
| 2 | Найти площадь | окружность (5) | |
| 3 | Найти площадь поверхности | сфера (5) | |
| 4 | Найти площадь | окружность (7) | |
| 5 | Найти площадь | окружность (2) | |
| 6 | Найти площадь | окружность (4) | |
| 7 | Найти площадь | окружность (6) | |
| 8 | сфера (4) | | |
| 9 | Найти площадь | окружность (3) | |
| 10 | Вычислить | (5/4(424333-10220^2))^(1/2) | |
| 11 | Разложить на простые множители | 741 | |
| 12 | Найти объем | сфера (3) | |
| 13 | Вычислить | 3 квадратный корень из 8*3 квадратный корень из 10 | |
| 14 | Найти площадь | окружность (10) | |
| 15 | Найти площадь | окружность (8) | |
| 16 | Найти площадь поверхности | сфера (6) | |
| 17 | Разложить на простые множители | 1162 | |
| 18 | Найти площадь | окружность (1) | |
| 19 | Найти длину окружности | окружность (5) | |
| 20 | Найти объем | сфера (2) | |
| 21 | Найти объем | сфера (6) | |
| 22 | Найти площадь поверхности | сфера (4) | |
| 23 | Найти объем | сфера (7) | |
| 24 | Вычислить | квадратный корень из -121 | |
| 25 | Разложить на простые множители | 513 | |
| 26 | Вычислить | квадратный корень из 3/16* квадратный корень из 3/9 | |
| 27 | Найти объем | прямоугольный параллелепипед (2)(2)(2) | |
| 28 | Найти длину окружности | окружность (6) | |
| 29 | Найти длину окружности | окружность (3) | |
| 30 | Найти площадь поверхности | сфера (2) | |
| 31 | Вычислить | ||
| 32 | Найти объем | прямоугольный параллелепипед (5)(5)(5) | |
| 33 | Найти объем | прямоугольный параллелепипед (10)(10)(10) | |
| 34 | Найти длину окружности | окружность (4) | |
| 35 | Перевести в процентное соотношение | 1. 2-4*-1+2 | |
| 45 | Разложить на простые множители | 228 | |
| 46 | Вычислить | 0+0 | |
| 47 | Найти площадь | окружность (9) | |
| 48 | Найти длину окружности | окружность (8) | |
| 49 | Найти длину окружности | окружность (7) | |
| 50 | Найти объем | сфера (10) | |
| 51 | Найти площадь поверхности | сфера (10) | |
| 52 | Найти площадь поверхности | сфера (7) | |
| 53 | Определить, простое число или составное | 5 | |
| 54 | 3/9 | ||
| 55 | Найти возможные множители | 8 | |
| 56 | Вычислить | (-2)^3*(-2)^9 | |
| 57 | Вычислить | 35÷0. 2 | |
| 60 | Преобразовать в упрощенную дробь | 2 1/4 | |
| 61 | Найти площадь поверхности | сфера (12) | |
| 62 | Найти объем | сфера (1) | |
| 63 | Найти длину окружности | окружность (2) | |
| 64 | Найти объем | прямоугольный параллелепипед (12)(12)(12) | |
| 65 | Сложение | 2+2= | |
| 66 | Найти площадь поверхности | прямоугольный параллелепипед (3)(3)(3) | |
| 67 | Вычислить | корень пятой степени из 6* корень шестой степени из 7 | |
| 68 | Вычислить | 7/40+17/50 | |
| 69 | Разложить на простые множители | 1617 | |
| 70 | Вычислить | 27-( квадратный корень из 89)/32 | |
| 71 | Вычислить | 9÷4 | |
| 72 | Вычислить | 2+ квадратный корень из 21 | |
| 73 | Вычислить | -2^2-9^2 | |
| 74 | Вычислить | 1-(1-15/16) | |
| 75 | Преобразовать в упрощенную дробь | 8 | |
| 76 | Оценка | 656-521 | |
| 77 | Вычислить | 3 1/2 | |
| 78 | Вычислить | -5^-2 | |
| 79 | Вычислить | 4-(6)/-5 | |
| 80 | Вычислить | 3-3*6+2 | |
| 81 | Найти площадь поверхности | прямоугольный параллелепипед (5)(5)(5) | |
| 82 | Найти площадь поверхности | сфера (8) | |
| 83 | Найти площадь | окружность (14) | |
| 84 | Преобразовать в десятичную форму | 11/5 | |
| 85 | Вычислить | 3 квадратный корень из 12*3 квадратный корень из 6 | |
| 86 | Вычислить | (11/-7)^4 | |
| 87 | Вычислить | (4/3)^-2 | |
| 88 | Вычислить | 1/2*3*9 | |
| 89 | Вычислить | 12/4-17/-4 | |
| 90 | Вычислить | 2/11+17/19 | |
| 91 | Вычислить | 3/5+3/10 | |
| 92 | Вычислить | 4/5*3/8 | |
| 93 | Вычислить | 6/(2(2+1)) | |
| 94 | Упростить | квадратный корень из 144 | |
| 95 | Преобразовать в упрощенную дробь | 725% | |
| 96 | Преобразовать в упрощенную дробь | 6 1/4 | |
| 97 | Вычислить | 7/10-2/5 | |
| 98 | Вычислить | 6÷3 | |
| 99 | Вычислить | 5+4 | |
| 100 | Вычислить | квадратный корень из 12- квадратный корень из 192 |
Как использовать математические функции IM.
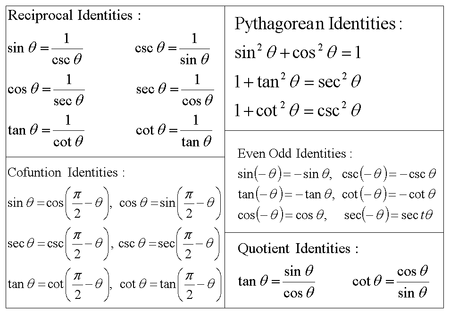SEC и IM.SECH в ExcelПриложения
0 292 3 минут на чтение
Когда вы используете Excel , у нас под рукой так много возможностей, что зачастую мы не знаем об имеющихся инструментах. Их можно выполнить с помощью очень простых работ, таких как таблицы с данными , для сложных вычислений с очень большими и большими переменными.
Примером этого являются функции IM.SEC и IM.SECH , для вычисления секущих комплексных чисел в тригонометрии. Важно иметь предварительные знания об этой области знаний, чтобы понять, на чем основан соответствующий расчет.
Обратите особое внимание на то, что мы объясним ниже относительно функций IM.SEC и IM.SECH в Excel.
Приложения и использование функции IM.SEC в Excel
Когда вы хотите вычислить секанс комплексного числа в Excel, функция ИМ.СЕК идеально. Это функция, которая является частью категории инженерных инструментов программы Excel.
Это в текстовом формате x + yi или x + yj за понимание функций и программ. Это очень полезная тригонометрическая функция, которая помогает получить секущие значений, заданных для того же самого объяснения.
Требуется обязательный аргумент Число работать, потому что это представление обрабатываемого значения. Это комплексное число, поэтому IM.SEC относится к этому типу очень специфических функций.
Чтобы эта функция работала правильно, Inumber не может иметь логического значения , потому что она будет генерировать просчет. С другой стороны, важно, чтобы это было комплексное число, а действительные и мнимые числа можно было преобразовать с помощью COMPLEX.
Точное представление строки формул: = ИМ.СЕК , заключив значение Innumber в скобки после. Также следует использовать кавычки, так как это протокол программирования, который требует функции для его математического распознавания.
Excel — настолько всеобъемлющий инструмент, что его также можно использовать для создания список расходов для семейного бюджета.
Он содержит как графические элементы и математика необходима для решения этой задачи без больших проблем и очень быстро.
Также возможно использование функций TINV и TINV.2C кто статистические функции в Excel просто и важно. Они используются для определения распределений Стьюдента левого и правого хвостов сформулированных данных.
Всегда используйте функция ИМ.СЕК для вычисления значения секанса при работе с комплексными числами в тригонометрии.
Приложения и использование функции IM.SECH в Excel
Для функции ИМ.СЕЧ , также определяется значение секанса, но в данном случае это гиперболический тип. Отличие от секущей функции состоит в том, что она основана на экспоненциальных функциях для ее расширения и правильного вычисления.
Также работает с текстовым форматом. x + yi или x + yj это важно помнить. Он также работает с обязательным аргументом Inumber для вычисления гиперболического секанса, необходимого для любой важной задачи.
Логическое значение использовать нельзя при определении числа, потому что будет сгенерирована ошибка вычисления. Следовательно, важно соблюдать все характеристики, необходимые для правильного расчета.
Если у вас нет сложных значений, а есть реальные или мнимые, вы можете использовать функция СЛОЖНЫЙ . Он помогает преобразовывать обычные числовые значения в комплексные для использования в этих типах тригонометрических функций.
Он представлен = ИМ.СЕЧ в строке формул Excel и должен сопровождаться числом в скобках. Также необходимо использовать кавычки, чтобы программная обработка могла понять выполняемые вычисления.
Последняя деталь Excel, которую следует выделить, — это возможность опубликовать интерактивный файл этой программы в Интернете. Это очень полезный помощник для передавать информацию без использования других более сложных и труднодоступных инструментов.
На нашей страничке Посмотрите, как это делается, у нас есть множество справочных статей, которые нужно изучить.
Сегодня нам известны важные вопросы, и необходимо решить многие общие вопросы.
Подобные предметы
Сек Тета — определение, формулы, значения и примеры
Функция секанса «или» Sec Theta является одной из тригонометрических функций помимо синуса, косинуса, тангенса, косеканса и котангенса. В прямоугольной тригонометрии функция секущей определяется как отношение гипотенузы к прилежащему катету.
Математическое обозначение функции секущей:
\(\sec(\theta) = \frac{\text{Сторона гипотенузы}}{\text{Смежная сторона}}\)
Подробнее о секте тета
Производная от \(\sec(\theta)\) в исчислении равна \(\sec(\theta) \tan(\theta)\), а интеграл от нее равен \(\ln|\sec(\theta) ) + \тан(\тета)|\). Обратная величина \(\sec(\theta)\) равна \(\cos(\theta)\).
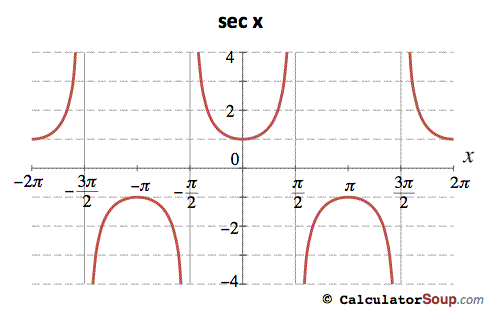
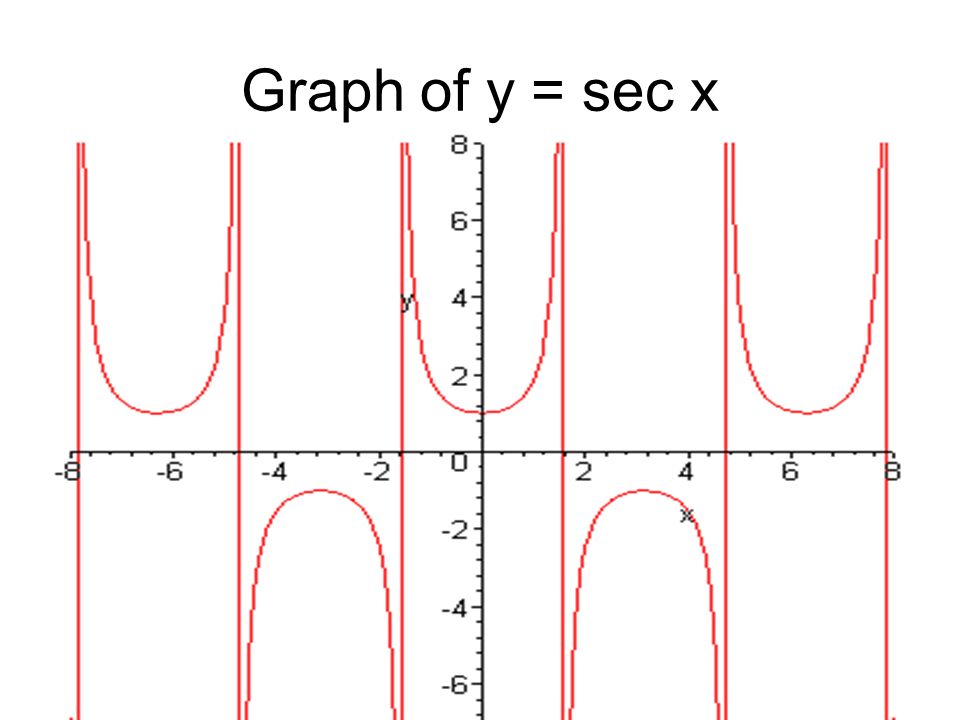
График функции sec thetaНиже приведена таблица значений sec theta для различных градусов и радиан.
| Радианы | Градусы | Значение тангенса |
| 2 0 0° | 1 | |
| \(\frac{\pi}{6}\) | 30° | \(\frac{2}{\sqrt{3}}\) |
| \( \frac{\pi}{4}\) | 45° | \(\sqrt{2}\) |
| \(\frac{\pi}{3}\) | 60° | 2 |
| \(\frac{\pi}{2}\) | 90° | \(\infty\) |
| \(\pi\) | 180° | -1 |
| \(\frac{3\pi}{2}\) | 270° 92(x)\)
Вопрос 1. Раствор. Используя тригонометрическое тождество, \(\sec(x) = \frac{1}{\cos(x)} = \frac{1}{3/5}\) \(∴ \sec(x) = \frac{5}{3}\) Вопрос 2. Если \(\tan(\frac{x}{2}) = \frac{5}{8}\), вычислите значение \( \сек(х)\). 92\\ Вопрос 3. Докажите \(\sec(x + y) = \frac{\sec(x) \sec(y)}{1 — \tan(x) \tan(y)}\) Раствор. Как мы знаем, \(\sec(x) = \frac{1}{\cos(x)}\) и \(\tan(x) = \frac{\sin(x)}{\cos (x)}\) Учитывая правую часть данного уравнения, \( & = \frac{1}{\cos(x + y)} \\ & = \sec(x + y)\\ \end{align} \) Следовательно, LHS = RHS … Доказано Часто задаваемые вопросы Объясните, почему sec(-x) = sec(x ). Как мы знаем, угол (-x) лежит в 4-м квадранте графика, а секанс в этом квадранте положителен. Следовательно, sec(-x) = sec(x). Что такое сек тета ? Секунда тета угла в прямоугольном треугольнике определяется как отношение гипотенузы к прилежащей стороне. В каких квадрантах секущая функция положительна, а в каких отрицательна? Из приведенного выше графика видно, что sec(x) положительна в 1-м и 4-м квадрантах и отрицательна во 2-м и 3-м квадрантах. Узнать больше Тригонометрическая функция Секанс (сек), косеканс (csc) и котангенс (cot)Перейти к содержимому В этом разделе показано, как тригонометрические функции, такие как котангенс, секанс и косеканс, связаны с другими тригонометрическими функциями синуса, косинуса и тангенса. Тригонометрические функцииТригонометрические функции, функции углов, широко распространены в реальном мире и в математике. Звук, который выходит из динамиков компьютеров, генерируется тригонометрическими волнами или звуковыми волнами, передаваемыми из динамиков, которые видны в виде синусоидальной волны. К этому моменту вы уже знакомы с функциями синуса, косинуса и тангенса. Это всего лишь три основные функции тригонометрии. Все остальные тригонометрические функции полностью основаны на этих трех функциях, которые вы увидите. Знаете ли вы функции синуса, косинуса и тангенса? Если нет, то вспомните его с их тремя противолежащими сторонами, гипотенузой и прилежащими сторонами. Посмотрите на прямоугольный треугольник, вы помните, как мы определили эти три функции? Функция синуса определяется как противолежащая сторона/гипотенуза, а косинус определяется как прилежащая сторона/гипотенуза, а тангенс – это отношение противолежащей стороны/прилегающей стороны. КотангенсПрежде всего, у нас есть функция котангенса, которая определяется как величина, обратная обратной функции тангенса. В математике мы записываем это как cot θ = 1 / tan θ. Все наши тригонометрические функции сокращаются до трех букв при написании функции во время вычисления. Теперь, поскольку котангенс является обратной функцией тангенса, мы также определяем его как обратную функцию тангенса. Если касательная является противоположной/прилежащей стороной, то функция котангенса является обратной ей стороной – примыкающей/противоположной. Мы можем записать всю такую информацию следующим образом: Функция котангенса вычисляется как: Cot θ = 1 / tan θ = соседняя сторона / противоположная сторона Функция секанса Теперь у нас есть функция секанса. Мы можем определить его как обратную функцию косинуса. Сек θ = 1 / cos θ = гипотенуза / прилежащая сторона. Функция косекансаТеперь у нас есть функция косеканса. Эта функция является обратной функцией синуса, которая имеет короткую форму cosec или CSC. Поскольку это функция, обратная синусоидальной функции, а синусоидальная функция определяется как противолежащая сторона/гипотенуза, мы можем альтернативно определить функцию косеканса как: иметь четкое представление о концепции всех трех тригонометрических функций. Изучите следующую диаграмму: Пример 1: Чему равно csc x? A — противолежащая сторона, B — прилежащая сторона, C — гипотенуза. Так как csc = гипотенуза /противоположная, csc x = C/A Пример 2: Чему равна сек x? Опять же, A — это противоположная сторона, B — прилежащая сторона, а C — гипотенуза. |
Если \(\cos(x) = \frac{3}{5}\), вычислите значение \(\sec(x)\). 
Теперь, когда мы рассмотрели эти три функции тригонометрии, давайте посмотрим на другие три функции тригонометрии котангенса, секанса и косеканса.
Три буквы или, скажем, краткая форма секанса — сек. Вы знаете, как определяется косинус? Да, косинус записывается как прилежащий катет/гипотенуза. Тогда секанс является обратной величиной функции косинуса, которая является обратной величиной функции косинуса –