Что в математике означает log: Функция LOG — ONLYOFFICE

4, равный 16. Когда мы берем логарифм 16 с базовым значением 2, мы получаем ответ 4.

В Python мы используем другой метод для решения математических задач: функцию log(). Функция math.log() использует математическую библиотеку для вычисления натурального логарифма определенного числа. Он принимает 2 значения: включая число и основание (необязательно), для вычисления натурального логарифма.

Содержание

1. Пример 1
2. Пример 2
3. Пример 3
4. Пример 4
5. Пример 5
6. Пример 6
7. Пример 7
8. Заключение

Пример 1

В примере 1 мы находим логарифм значения с основанием, таким как log(x,(base)). Эта функция использует два параметра: число, которое равно x, а другое является основанием. Он вычисляет журнал базы аргумента x, выраженный как log(x)/log(base).

import math
print («logarithm of 17 is : «, end=«»)
print (math.log(17)
# Printing the log base 3 of 8
print («Logarithm base 3 of 8 is : «, end=«»)
print (math. log(8,3))

Как мы видим, результат работы метода math.log().

Пример 2

В примере 2 мы берем число в качестве ввода от пользователя и сохраняем его в переменной «число», а другое значение (базу) в качестве ввода от пользователя храним в его переменной «x». Передайте число и значение x в параметре math.log() и получите вывод через оператор печати на языке python.

import math
#Take input from user
number = int(input(«Enter the number:»))
x = int(input(«Enter the base:»))
print(«log of number is:», math.log(number))
print(«log of number is:», math.log(number, x))

Когда мы выполняем код, мы получаем следующий результат:

Пример 3

В логарифме с пользовательским базовым примером мы создали функцию с именем logarithm() и передали базовое значение и переменную в виде числа в ее параметре. Внутри функции мы инициализировали две переменные, «x» и «y», которые хранят метод math.log() и возвращают переменную. Выведите результат функции в виде логарифма (x, y) на последнем шаге.

import math
def logarithm(base,number):
x = math.log(number)
y = math.log(base)
return x/
# log with custom base:  
#                 base    number
print(logarithm(  4 ,   17    )  )
print(logarithm(  2 ,   100   )  )

Этот пример показывает результат написанного выше кода.

Пример 4

В примере 4 мы реализовали оператор if/else, чтобы проверить, является ли число отрицательным или нет. Мы никогда не получаем ошибок математической области из-за условных операторов.

Ошибка значения: ошибка MathDomain возникает, когда мы передаем нулевые или отрицательные числа, которые невозможно вычислить.

Если мы вычисляем логарифм нуля, также возникают ошибки математической области.

import math
value = —23
if int(value) >= :
math.log(value)
else:
print(«We can’t calculate the negative logrithm value»)

Вывод представлен здесь:

Другой пример кода без условия if-else, чтобы показать ошибку математической области:

import math

value = 

math. log(value)

Вывод представлен здесь:

Пример 5

Метод numpy.log() — это математическая функция, которая позволяет вам вычислять журнал, где a — это сумма чисел во входном массиве. Обратная функция exp() — это журнал, поэтому log(exp(a)) = а. В примере 5 мы инициализируем переменную «x» и сохраняем в ней массив из 5 индексов. Затем инициализируйте другую переменную «y» и сохраните значение функции np.log(x).

import numpy as nump
x = [7, 11, 17, 3**9]
print («Array with different values : «, x)
y = numpy.log(x)
print («Result, «y)

Получим результат после выполнения:

Пример 6

Метод log1p() — это встроенная функция Python, которая принимает натуральный логарифм 1+x (по основанию x) при получении значения. Он принимает значение и возвращает натуральное значение логарифма 1+ по основанию x.

Когда мы вводим другое значение, отличное от числа, функция возвращает TypeError, указывающую, что «требуется число с плавающей запятой».

В примере 6 мы берем входное значение от пользователя; затем мы вычисляем логарифм (1+a) числа 13.

import math
#  positive integer
number = int(input(«Enter number: «))
#  Log(1+x)
print(«Log of the value is: «, math.log1p(number))

После выполнения этого кода результат приведен ниже.

Пример 7

Функция использует одно значение в качестве параметра и вычисляет журнал с основанием 2. Причина использования значения основания 2 заключается в том, что мы получаем более точный результат, и если мы не передаем параметр в функцию, отображается сообщение об ошибке типа. Мы решаем приведенный ниже пример с базовым значением 2.

Мы печатаем два утверждения, одно показывает, какая функция содержит значение параметра, мы получаем требуемый результат с помощью этого утверждения, а другое указывает, какая функция не содержит значения параметра (без передачи аргумента). Итак, в этом случае мы получаем сообщение об ошибке типа.

import math

print(«Log of the value is: «,math.log2(37))

print(«Log of the value is: «,math.log2())

Когда мы выполнили программу, появились два разных результата, которые кратко объясняются в верхнем абзаце.

В математической функции мы изучили множество различных логарифмических методов. Если мы используем какие-либо функции журнала с отрицательным значением, мы получим ошибку математической области. Он содержит значение метода журнала и использует библиотечную «математику», позволяющую нам вычислять журналы с помощью всего одной строки кода. В первом примере мы просто передали значение в качестве параметра в math.log() и получили простой результат. Во втором примере мы принимаем данные от пользователя во время компиляции, чтобы получить желаемый результат. В примере 3 мы используем функцию для проверки того, как работают пользовательские базы в программе на python. В четвертом примере мы использовали оператор условия, чтобы преодолеть проблему ошибки и заменить его условием if/else. В примере 5 мы использовали numpy.log(), чтобы проверить, как массивы работают с логарифмами. В шестом примере мы проверили натуральный логарифм с помощью функции log1p(), равной log(1+x). В последнем примере мы использовали функцию math.log2(). Мы надеемся, что вы поймете функцию журнала Python из всех объясненных выше примеров.

Что означает ln в математике?

Людям часто трудно понять разницу между ln и log.. Это потому, что они похожи по своему смыслу, но разные по способу написания.

ln означает натуральный логарифм, в то время как журнал представляет собой степенную функцию, такую ​​как степень возведения одной величины в n-ю степень.

ln можно записать как = 1/x, а log можно записать как = x или = xlog.(Икс).

пер (натуральный логарифм) математическая функция, вычисляющая натуральный логарифм действительного числа. Обозначается греческим символом или 𝜃, что выглядит так:

Функция преобразует все положительные числа в отрицательные и представляет собой функцию, обратную tan. . Аналогичная функция называется “е” определен для комплексных чисел и имеет вид

Определение ln в математике

Натуральный логарифм (пер) является функцией, обратной экспоненциальной функции. В этой секции, вы узнаете, как применять натуральный логарифм в математике.

Натуральный логарифм (пер) — ключевая концепция математики, определяющая, что записывает натуральное число.. В этой секции, Сначала мы исследуем некоторые важные концепции, чтобы понять, что означает ln и его важность в математике..

Натуральные логарифмы (пер) используются для аппроксимации значений, которые не являются точными числами, такими как пи или е, но есть числовые значения, такие как 1/3 а также 2/5. Это также полезно для аппроксимации значений показателей.

Основание натурального логарифма равно 10.

Функция натурального логарифма — это функция, которая возвращает логарифм числа.. Натуральный логарифм x, обозначается ln(Икс), — показатель степени, до которого необходимо возвести e, чтобы получить x. Другими словами, пер(Икс) = х – х ** и

пер(Икс) является натуральным логарифмом числа x по основанию e. Это означает, что ln(Икс) определяется как,

пер (Икс) = х.

ln используется во многих областях, включая

* математические операции, относящиеся к логарифмам и экспоненциальным функциям,

* решение дифференциальных уравнений и их символическая интерпретация,

* геология, где это полезно для расчета площадей фигур, состоящих из одинаковых треугольников и квадратов, и более.

Определение логарифма и натурального логарифма

Логарифм — это степень числа, до которого мы возводим 10. Его можно рассматривать как показатель степени при умножении или делении.. Натуральный логарифм — это величина, обратная этой степени., или сила, до которой мы поднимаем 2.

Натуральный логарифм (обозначается ln) определяется как функция, обратная логарифму (обозначается журналом). Натуральный логарифм x равен e x, где e = 2,71828182845904…

Логарифм — это математическая функция, которая дает показатель степени основному числу.. Натуральный логарифм — это величина, обратная логарифму..

Натуральный логарифм, также известный как “обратный” натурального логарифма (лог-инверсия), определяется как:

Это можно показать, сравнив его определение с определением производной:

и его можно использовать для расчета производных.

В чем разница между неравенством и уравнением?

Уравнения представляют собой равенство, не неравенство.

Неравенство — это линия или точка, в которой одно число больше другого.. Например, 4>2. У уравнения есть две стороны, левая сторона и правая сторона. Например, 2+х = 5 или х-1 = 0.

Разные люди используют термины неравенство и уравнение как синонимы.. Там есть, тем не мение, разница между двумя.

Уравнение — это математическое утверждение, которое можно использовать для моделирования неравенства. . Не всегда удается составить уравнение равенства. Например:

$$х гидроразрыв{2}{3}= и $$

Невозможно преобразовать это в уравнение, так как это не будет иметь смысла без y в нем..

Неравенство — это математическое утверждение, которое не обязательно всегда верно для некоторых значений x и y, но его противоположное может быть верным для других значений x и y.. Например:

В этом случае, неравенство имеет два решения: х = 2/3 и х = 1/3.

Что такое логарифмы и экспоненты?

Когда COVID-19 обрушился на Соединенные Штаты, цифры просто взорвались. Во-первых, было всего один или два случая. Потом было 10. Потом 100. Потом тысячи, потом сотни тысяч. Такие увеличения трудно понять. Но экспоненты и логарифмы могут помочь понять эти резкие увеличения.

Ученые часто описывают тенденции резкого увеличения очень как экспоненциальные. Это означает, что вещи не увеличиваются (или не уменьшаются) с постоянной скоростью или скоростью. Это означает, что скорость изменяется с некоторой возрастающей скоростью.

Примером может служить шкала децибел, которая измеряет уровень звукового давления. Это один из способов описать силу звуковой волны. Это не совсем то же самое, что громкость с точки зрения человеческого слуха, но близко. На каждые 10 децибел звуковое давление увеличивается в 10 раз. Таким образом, звук в 20 децибел имеет не удвоенное звуковое давление 10 децибел, а 10 раз этого уровня. А уровень звукового давления шума в 50 децибел в 10 000 раз выше, чем шепот в 10 децибел (потому что вы умножили 10 х 10 х 10 х 10).

Показатель степени — это число, указывающее, сколько раз нужно умножить некоторое базовое число само на себя. В приведенном выше примере основание равно 10. Таким образом, используя показатели степени, вы можете сказать, что 50 децибел в 10 ⁴ раз громче, чем 10 децибел. Показатели отображаются в виде надстрочного индекса — небольшого числа справа вверху от основного числа. И эта маленькая 4 означает, что вы должны умножить 10 раз на четыре раза. Опять же, это 10 х 10 х 10 х 10 (или 10 000).

Логарифмы обратны показателям степени. Логарифм (или log) — это математическое выражение, используемое для ответа на вопрос: сколько раз нужно умножить одно «основное» число само на себя, чтобы получить какое-то другое конкретное число?

Например, сколько раз нужно умножить число 10 само на себя, чтобы получить 1000? Ответ: 3 (1000 = 10 × 10 × 10). Таким образом, логарифм по основанию 10 от 1000 равен 3. Он записывается с помощью нижнего индекса (маленького числа) в правом нижнем углу числа по основанию. Таким образом, выражение будет выглядеть так: log ₁₀ (1000) = 3.

Сначала идея логарифма может показаться незнакомой. Но вы, вероятно, уже мыслите логарифмически о числах. Вы просто этого не осознаете.

Давайте подумаем, сколько цифр в числе. Число 100 в 10 раз больше числа 10, но в нем всего на одну цифру больше. Число 1 000 000 в 100 000 раз больше 10, но в нем всего пять цифр. Количество цифр в числе растет логарифмически. Размышление о числах также показывает, почему логарифмы могут быть полезны для отображения данных. Вы можете себе представить, если бы каждый раз, когда вы записываете число 1 000 000, вам приходилось бы записывать миллион счетных знаков? Ты будешь там всю неделю! Но используемая нами «система значений разрядов» позволяет нам записывать числа гораздо более эффективным способом.

Зачем описывать вещи как журналы и экспоненты?

Логарифмические шкалы могут быть полезны, поскольку некоторые типы человеческого восприятия являются логарифмическими. Что касается звука, мы воспринимаем разговор в шумной комнате (60 дБ) чуть громче, чем разговор в тихой комнате (50 дБ). При этом уровень звукового давления голосов в шумном помещении может быть в 10 раз выше.

На этих графиках представлена ​​одна и та же информация, но несколько по-разному. График слева линейный, справа логарифмический. Крутая кривая на левом графике выглядит более плоской на правом графике. Канадский журнал политических наук, 14 апреля 2020 г., стр. 1–6/ (CC BY 4.0)

Другая причина использования логарифмической шкалы заключается в том, что она позволяет ученым легко отображать данные. Было бы трудно уместить на листе миллиметровой бумаги 10 миллионов линий, которые потребуются для построения разностей от тихого шепота (30 децибел) до звука отбойного молотка (100 децибел). Но они легко поместятся на странице, используя логарифмическую шкалу. Это также простой способ увидеть и понять большие изменения, такие как темпы роста (для щенка, дерева или экономики страны). Каждый раз, когда вы видите фразу «порядок величины», вы видите ссылку на логарифм.

Логарифмы широко используются в науке. рН — мера того, насколько кислым или щелочным является раствор — логарифмический. Так же как и шкала Рихтера для измерения силы землетрясений.

В 2020 году термин логарифмический стал наиболее известен общественности благодаря его использованию для описания распространения нового пандемического коронавируса (SARS-CoV-2). Пока каждый заразившийся распространяет вирус не более чем на одного человека, размер инфекции останется прежним или вымрет. Но если бы число было больше 1, оно бы увеличивалось «по экспоненте», а это значит, что логарифмическая шкала могла бы быть полезна для его построения.

Основные основания

Основание логарифма может быть практически любым числом. Но есть три основания, которые особенно распространены в науке и других целях.

1. Двоичный логарифм: Это логарифм, в котором основание равно двум. Двоичные логарифмы лежат в основе двоичной системы счисления, которая позволяет людям считать, используя только числа ноль и единицу. Двоичные логарифмы важны в информатике. Они также используются в теории музыки. Двоичный логарифм описывает количество октав между двумя музыкальными нотами.
2. Натуральный логарифм: Так называемый «натуральный» логарифм — записывается как в — используется во многих областях математики и естественных наук. Здесь базовое число — это иррациональное число, называемое e , или число Эйлера. (Математик Леонард Эйлер не собирался называть его своим именем. Он писал математическую работу, используя буквы для представления чисел, и случайно использовал e для этого числа.) Это e равно примерно 2,72 (хотя вы никогда не сможете написать это полностью в десятичных дробях). Число e обладает особыми математическими свойствами, которые делают его полезным во многих областях математики и естественных наук, включая химию, экономику (изучение богатства) и статистику. Исследователи также использовали натуральный логарифм для определения кривой, которая описывает, как возраст собаки соотносится с человеческим.
3. Десятичный логарифм: Это логарифм, основание которого равно 10. Это логарифм, используемый при измерениях звука, pH, электричества и света.

Силовые слова

Подробнее о сильных словах

кислотный : Прилагательное для материалов, содержащих кислоту. Эти материалы часто способны разъедать некоторые минералы, такие как карбонат, или вообще предотвращать их образование.

по основанию : (в математике) Число, которое нужно умножить само на себя в логарифмическом выражении (и показано в виде нижнего индекса справа внизу от основного числа) или на количество раз, требуемое показателем степени (показывается как верхний индекс справа вверху от этого основного числа). (в химии) Химическое вещество, которое производит ионы гидроксида (ОН-) в растворе. Основные растворы также называют щелочными. (в генетике) Сокращенный вариант термина азотистое основание. Эти основания являются строительными блоками молекул ДНК и РНК.

двоичный : Что-то, состоящее из двух частей. (в математике и информатике) Система счисления, в которой значения представлены двумя символами 1 (включено) или 0 (выключено).

химия : Область науки, изучающая состав, структуру и свойства веществ и то, как они взаимодействуют. Ученые используют эти знания для изучения незнакомых веществ, для воспроизведения большого количества полезных веществ или для разработки и создания новых и полезных веществ.

Информатика : Научное изучение принципов и использования компьютеров. Ученые, работающие в этой области, известны как компьютерщики.

коронавирус

: семейство вирусов, названных в честь короновидных шипов на их поверхности (corona означает «корона» на латыни). Коронавирусы вызывают простуду. В семейство также входят вирусы, вызывающие гораздо более серьезные инфекции, включая атипичную пневмонию.

COVID-19 : название, данное коронавирусу, вызвавшему массовую вспышку потенциально смертельного заболевания, начавшуюся в декабре 2019 года.. Симптомы включали пневмонию, лихорадку, головные боли и проблемы с дыханием.

данные : Факты и/или статистические данные, собранные вместе для анализа, но не обязательно организованные таким образом, чтобы придать им смысл. Для цифровой информации (тип, хранящийся в компьютерах) эти данные обычно представляют собой числа, хранящиеся в двоичном коде, отображаемом в виде строк нулей и единиц.

децибел : Шкала измерения интенсивности звуков, воспринимаемых человеческим ухом. Он начинается с нуля децибел (дБ), звук едва слышим для людей с хорошим слухом. Звук в 10 раз громче будет на 10 дБ. Поскольку шкала логарифмическая, звук в 100 раз громче 0 дБ будет 20 дБ; тот, который в 1000 раз громче 0 дБ, будет описан как 30 дБ.

цифра : (в математике) Индивидуальное число (от 0 до 9), используемое для представления числа или части числа.

e : математическая константа, которая никогда не меняется. Это примерно 2,718281828459. e — это число Эйлера, математика, который его открыл. Это основание натурального логарифма.

землетрясение : Внезапное и иногда сильное сотрясение земли, иногда вызывающее большие разрушения, в результате движения земной коры или вулканического действия.

экономика

: Социальная наука, изучающая производство, распределение и потребление товаров и услуг, а также теорию и управление экономикой или экономическими системами. Человек, изучающий экономику, является экономистом.

экономика : Термин для совокупного богатства и ресурсов (например, люди, рабочие места, земля, леса и полезные ископаемые) нации или региона. Его часто измеряют с точки зрения рабочих мест и доходов или с точки зрения производства и использования товаров (например, продуктов) и услуг (например, ухода за больными или доступа в Интернет).

электричество : Поток заряда, обычно возникающий в результате движения отрицательно заряженных частиц, называемых электронами.

показатель степени : число, отображаемое в виде надстрочного индекса (крошечное число справа вверху от какого-либо другого «базового» числа или математического выражения). Показатель степени определяет, сколько раз это базовое число или выражение должно быть умножено само на себя.

выражение : (в математике) Утверждение, включающее комбинации цифр и/или букв (которые обозначают числа, которые могут различаться) и включает указания (или правила) о том, что делать с этими числами (например, складывать или делить их). , возьмем их логарифм или приравняем их комбинации друг к другу).

инфекция : Болезнь, которая может передаваться от одного организма к другому. Обычно это вызвано каким-то микробом.

обратное : Что-то, что является противоположностью или противоположностью другой вещи, или что движется в направлении, противоположном чему-то.

иррациональный : (в математике) Число, которое нельзя записать как целое или дробное. При записи в виде десятичного числа его цифры никогда не заканчиваются и не повторяются. Примеры: π (пи), отношение диаметра круга к его длине окружности (3,14159…), а

e — число Эйлера (2,71828…).

log : (в математике) Аббревиатура для логарифма.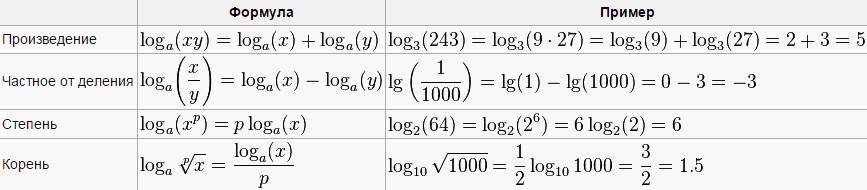

логарифм : Степень (или показатель), в которую нужно возвести одно базовое число — умножить само на себя — чтобы получить другое число. Например, в системе с основанием 10 10 нужно умножить на 10, чтобы получить 100. Таким образом, логарифм 100 в системе с основанием 10 равен 2. В системе с основанием 10 логарифм 1000 будет равен 3, логарифм 10000 будет 4 и так далее.

магнитуда : (в геологии) Число, используемое для описания относительной силы землетрясения. Он варьируется от 1 до более чем 8 и рассчитывается по пиковым колебаниям грунта, зарегистрированным сейсмографами. Существует несколько шкал величин. Один из наиболее часто используемых сегодня известен как величина момента. Он основан на размере разлома (трещины в земной коре), степени смещения (движения) разлома во время землетрясения и силе энергии, необходимой для обеспечения этого движения. При каждом увеличении магнитуды землетрясение вызывает в 10 раз большее движение грунта и высвобождает примерно в 32 раза больше энергии.

В перспективе землетрясение магнитудой 8 может высвободить энергию, эквивалентную взрыву 6 миллионов тонн тротила.

числовой : Имеющий отношение к числам.

октава : (в музыке) Интервал между одной нотой и нотой с удвоенной частотой. На самом деле в октаве 12 полутонов одинакового размера. Октавы — это образец звуковой дифференциации, типичный для северной и западной музыки.

пандемия : Эпидемия, затрагивающая большую часть населения страны или мира.

восприятие : Состояние осознания чего-либо — или процесс осознания чего-либо — посредством использования органов чувств.

pH : Мера кислотности или щелочности раствора. pH 7 абсолютно нейтрален. Кислоты имеют рН ниже 7; чем дальше от 7, тем сильнее кислота. Щелочные растворы, называемые основаниями, имеют рН выше 7; опять же, чем выше 7, тем прочнее основание.

разрядная система значений : (в математике) Числа выражаются с помощью 10 символов — от 0 до 9 — известных как цифры.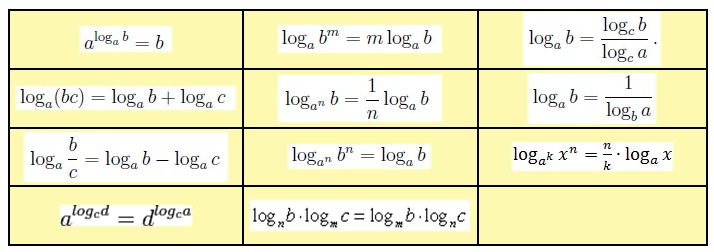 Когда число достигает 10 или выше, новые символы не используются. Вместо этого мы начинаем новый столбец цифр слева, который описывает, сколько десятков в этом числе. После этого мы пишем цифру, указывающую, сколько единиц следует за ней. Таким образом, число десять записывается как 10 (для одной десятки и нуля единиц). Двадцать семь записывается как 27, потому что в нем две десятки и семь единиц. Когда число превышает 99, новый столбец необходим для определения количества 100, за которым следует количество 10 и 1. И каждый раз, когда число превышает доступное пространство, добавляется новый столбец, позволяющий нам отображать 1000, 10 000, 100 000, миллионы и более.

излучение : (в физике) Один из трех основных способов передачи энергии. (Двумя другими являются проводимость и конвекция.) При излучении электромагнитные волны переносят энергию из одного места в другое. В отличие от проводимости и конвекции, которым для передачи энергии нужен материал, излучение может передавать энергию через пустое пространство.

SARS-CoV-2 : коронавирус, появившийся в Ухане, Китай, в конце декабря 2019 года. Он будет вызывать широко распространенные, а иногда и смертельные заболевания в Китае и многих других странах. Его название отражает его близкое сходство с исходным коронавирусом, известным как SARS (тяжелый острый респираторный синдром). Этот вирус атипичной пневмонии вызвал глобальную вспышку заболевания в 2003 году.

звуковая волна : Волна, передающая звук. Звуковые волны имеют чередующиеся полосы высокого и низкого давления.

статистика : Практика или наука о сборе и анализе числовых данных в больших количествах и интерпретации их значения. Большая часть этой работы связана с уменьшением ошибок, которые могут быть связаны со случайными вариациями. Профессионал, работающий в этой области, называется статистиком.

сейсмическая волна : Волна, проходящая через землю, вызванная землетрясением или другими причинами.

теория : (в науке) Описание некоторых аспектов мира природы, основанное на обширных наблюдениях, тестах и ​​рассуждениях. Теория также может быть способом организации обширной совокупности знаний, применимых в широком диапазоне обстоятельств для объяснения того, что произойдет. В отличие от общепринятого определения теории, теория в науке — это не просто догадка. Идеи или выводы, основанные на теории, но еще не на достоверных данных или наблюдениях, называются теоретическими. Ученые, которые используют математику и/или существующие данные для прогнозирования того, что может произойти в новых ситуациях, известны как теоретики.

вирус : Крошечные инфекционные частицы, состоящие из РНК или ДНК, окруженные белком. Вирусы могут размножаться, только внедряя свой генетический материал в клетки живых существ. Хотя ученые часто называют вирусы живыми или мертвыми, на самом деле ни один вирус не является по-настоящему живым. Он не ест, как животные, и не готовит себе пищу, как растения. Он должен захватить клеточный механизм живой клетки, чтобы выжить.

волна : Возмущение или изменение, которое распространяется в пространстве и материи регулярным, колебательным образом.

Бетани Брукшир долгое время работала штатным корреспондентом в Science News Explores . У нее есть докторская степень. по физиологии и фармакологии и любит писать о неврологии, биологии, климате и многом другом. Она считает поргов инвазивным видом.

5.4: Логарифмы и логарифмические функции

1. Последнее обновление

2. Сохранить как PDF

Идентификатор страницы

38598

• Рупиндер Секон и Роберта Блум
• Колледж Де Анза

Цели обучения

В этом разделе вы узнаете

1. определение логарифмической функции как обратной экспоненциальной функции
2. для записи эквивалентных логарифмических и экспоненциальных выражений 9Икс . \nonumber \]

   Пока мы настроили экспоненциальные модели и использовали их для прогнозирования, вы, возможно, заметили, что решение экспоненциальных уравнений еще не упоминалось. Причина проста: ни один из обсуждавшихся до сих пор алгебраических инструментов недостаточен для решения экспоненциальных уравнений. Рассмотрим уравнение 2 ^x = 10 выше. Мы знаем, что 2 ³ = 8 и 2 ⁴ = 16, поэтому ясно, что x должно быть некоторым значением между 3 и 4, поскольку г ( х ) = 2 ^х увеличивается. Мы могли бы использовать технологию для создания таблицы значений или графика, чтобы лучше оценить решение, но мы хотели бы найти алгебраический способ решения уравнения.

   Нам нужна операция, обратная возведению в степень, чтобы найти переменную, если переменная находится в степени. Как мы узнали на уроке алгебры (необходимое условие для этого конечного курса математики), обратная функция для экспоненциальной функции является логарифмической функцией.

   Мы также узнали, что экспоненциальная функция имеет обратную функцию, потому что каждое выходное значение (y) соответствует только одному входному значению (x). Имя, данное этому свойству, было «один к одному».

   Источник: материалы в этом разделе учебника получены от Дэвида Липпмана и Мелони Расмуссен, книжного магазина Open Text, Precalculus: An Investigation of Functions, «Chapter 4: Exponential and Logarithmic Functions», под лицензией Creative Commons CC BY-SA. 3.0 лицензия. Материал здесь основан на материале, содержащемся в этом учебнике, но был изменен Робертой Блум, как разрешено этой лицензией. 9{\log_{b}(x)}=x \nonumber \]

   Поскольку log — это функция, наиболее правильно записать ее как log _b ( c ), используя круглые скобки для обозначения вычисления функции, просто как и с f(c) . Однако, когда вход представляет собой одну переменную или число, часто можно увидеть, что круглые скобки опущены, а выражение записано как log _b c .

   Пример \(\PageIndex{1}\)

   Запишите эти экспоненциальные уравнения в виде логарифмических уравнений: 9{2}=9\)

Установив взаимосвязь между экспоненциальной и логарифмической функциями, теперь мы можем решать основные логарифмические и экспоненциальные уравнения путем перезаписи.

Пример \(\PageIndex{3}\)

Журнал решения ₄ ( x ) = 2 для x .

Решение

Переписав это выражение в виде экспоненты, 4 ² = x , поэтому x = 16

Пример \(\PageIndex{4}\)

Решить 2 ^x = 10 для x .

Решение

Переписав это выражение в виде логарифма, мы получим x = log ₂ (10)

Хотя это и определяет решение, вы можете найти его несколько неудовлетворительным, поскольку его трудно сравнивать. выражение к десятичной оценке, которую мы сделали ранее. Кроме того, давать точное выражение для решения не всегда полезно — часто нам действительно нужна десятичная аппроксимация решения. К счастью, с этой задачей хорошо справляются калькуляторы и компьютеры. К несчастью для нас, большинство калькуляторов и компьютеров вычисляют логарифмы только по двум основаниям: по основанию 10 и по основанию 9.0217 и . К счастью, в конечном итоге это не проблема, так как мы скоро увидим, что можем использовать формулу «изменения основания» для вычисления логарифмов для других оснований.

Обычный и натуральный логарифмы

Обычный логарифм представляет собой логарифм с основанием 10 и обычно записывается как \(\log (x)\), а иногда и как \(\log_{10} (x)\). Если основание не указано в логарифмической функции, то используемое основание b равно \(b=10\).

Натуральный логарифм представляет собой логарифм по основанию \(e\) и обычно записывается как \(\ln (x)\).

Обратите внимание, что для любого другого основания b, отличного от 10, основание должно быть указано в обозначении \(\log_b (x)\).

Пример \(\PageIndex{5}\)

Вычислить \(\log(1000)\) с помощью определения общего журнала.

Решение

В таблице приведены значения общего журнала

номер	число экспоненциальное	журнал (номер )
1000	10 3	3
100	10 2	2
10	10 1	1
1	10 0	0
0,1	10 -1	-1
0,01	10 -2	-2
0,001	10 -3	-3

Чтобы вычислить log(1000), мы можем сказать

\[ x = \log(1000) \nonumber \]

Затем перепишем уравнение в экспоненциальной форме, используя общую логарифмическую базу 10

9{1 / 2}\right)=1 / 2 \nonumber \]

Пример \(\PageIndex{8}\)

Оцените с помощью калькулятора или компьютера следующее:

1. \(\log 500\)
2. \(\ln 500\)

Раствор

а. Используя клавишу LOG на калькуляторе для вычисления логарифмов по основанию 10, мы вычисляем LOG(500)

Ответ: \(\log 500 \приблизительно 2,69897\)

b. Использование клавиши LN на калькуляторе для вычисления натуральных логарифмов , 9{x}=\log _{c} A\).

Теперь, используя свойство экспоненты для бревен с левой стороны,
\[x \log _{c} b=\log _{c} A \nonumber \]

Разделив, мы получим \(x=\frac{ \log _{c}(A)}{\log _{c}(b)}\), что является изменением базовой формулы.

Вычисление логарифмов

С изменением основной формулы \(\log _{b}(A)=\frac{\log _{c}(A)}{\log _{c}(b)}\ ) для любых базисов \(b\), \(c >0\), мы можем, наконец, найти десятичное приближение к нашему вопросу из начала раздела. 9х = 10\) для \(х\).

Решение

Перепишите показательное уравнение 2 ^x = 10 в виде логарифмического уравнения

\[x=\log _{2}(10) \nonumber \]

, мы можем переписать логарифм по основанию 2 как логарифм любого другого основания. Поскольку наши калькуляторы могут вычислять натуральный логарифм, мы можем использовать натуральный логарифм, который является основанием логарифма e :

Используя наши калькуляторы для вычисления этого, \(\frac{\ln (10)}{\ln ( 2)}=\mathrm{LN}(10) / \mathrm{LN}(2) \приблизительно 3,3219\)

Это, наконец, позволяет нам ответить на наш первоначальный вопрос, поставленный в начале этого раздела:
Для популяции из 50 мух, которая удваивается каждую неделю, потребуется приблизительно 3,32 недели, чтобы вырасти до 500 мух.

Пример \(\PageIndex{10}\)

Вычислить \(\log_{5}(100)\), используя формулу изменения базы.

Решение

Мы можем переписать это выражение, используя любое другое основание.

Метод 1: Мы можем использовать натуральный логарифм по основанию e с изменением базовой формулы

\[\log _{5}(100)=\frac{\ln (100)}{\ln (5)}=\mathrm{LN}(100) / \ mathrm{LN}(5) \приблизительно 2.861 \nonumber \]

Метод 2: Мы можем использовать десятичный логарифм с основанием 10 с заменой базовой формулы,

\[\log _{5}(100)=\frac{ \log (100)}{\log (5)}=\operatorname{LOG}(100) / \mathrm{LOG}(5) \приблизительно 2,861 \nonumber \]

Подытожим взаимосвязь между экспоненциальной и логарифмической функциями

Логарифмы

9{q}\right)=q \log _{b}(A) \nonumber\)

Свойства журналов: Изменение базы: \(\log _{b}(A)=\frac{\log _{c}(A)}{\log _{c}(b)} \text { для любого основания } b, c>0 \nonumber\)

Обратное, экспоненциальное и изменение основных свойств выше позволит нам решать уравнения, возникающие в задачах, с которыми мы сталкиваемся в этом учебнике. Для полноты приведем еще несколько свойств логарифмов

Сумма логарифмов Свойство: \(\log _{b}(A)+\log _{b}(C)=\log _{b}(A C )\)

Различие журналов Свойство: \(\log _{b}(A)-\log _{b}(C)=\log _{b}\left(\frac{A}{C} \right)\)

Логи обратных величин: \(\log _{b}\left(\frac{1}{C}\right)=-\log _{b}(C)\)

Взаимные основания: \(\log _{1 / b} C=-\log _{b}(C)\)

Источник: Материал в этом разделе учебника взят у Дэвида Липпмана и Мелони Расмуссен, Open Text Bookstore, Precalculus: An Investigation of Functions, «Глава 4: Экспоненциальные и логарифмические функции», под лицензией Creative Commons CC BY-SA 3.0. Материал здесь основан на материале, содержащемся в этом учебнике, но был изменен Робертой Блум, как разрешено этой лицензией.

---

Эта страница под названием 5.4: Логарифмы и логарифмические функции распространяется под лицензией CC BY 4.0 и была создана, изменена и/или курирована Рупиндером Секоном и Робертой Блум с использованием исходного контента, который был отредактирован в соответствии со стилем и стандартами платформы LibreTexts.

No related posts.