Что в математике значит log: Функция LOG — ONLYOFFICE

3 равно e×e×e и т. д. все, что имеет степень 1, равно самому себе .

Каково значение журнала 2? Таблица журнала с 1 по 10 для базы журнала 10

Десятичный логарифм числа (log10 x)	Значения журнала
Журнал 2	0.3010
Журнал 3	0.4771
Журнал 4	0.6020
Журнал 5	0.6989

Дополнительно Чему равно LNE? Натуральный логарифм числа – это его логарифм относительно основание математической константы e, которое является иррациональным и трансцендентным числом, примерно равным 2.718281828459. Натуральный логарифм x обычно записывается как ln x, log_e x, а иногда, если основание e неявно, просто log x.

Что такое e в математике? Число e, также известное как число Эйлера, равно математическая константа, приблизительно равная 2.71828, и может быть охарактеризован многими способами.

Это основание натуральных логарифмов. Это предел (1 + 1/n)ⁿ когда n приближается к бесконечности, это выражение возникает при изучении сложных процентов.

Что это значит ∑?

Символ ∑ указывает суммирование и используется как сокращенное обозначение суммы терминов, следующих за шаблоном.

Что значит е 10? Е10 означает переместите десятичную дробь вправо на 10 разрядов. Если число 1-9 является целым числом, то десятичная дробь может не отображаться, но для целей перемещения десятичной дроби после каждого целого числа стоит невидимая десятичная дробь.

Что такое e в калькуляторе? На дисплее калькулятора E (или e) означает для показателя степени 10, и за ним всегда следует другое число, которое является значением показателя степени. Например, калькулятор покажет число 25 триллионов как 2.5E13 или 2.5E13. Другими словами, E (или e) — это сокращенная форма научного обозначения.

Как найти log2 без калькулятора?

Также Как вы берете журнал 2? Поскольку основание также равно 10, мы получаем log(2) = 3*0.1. знак равно 0.3. Это очень точное значение, так как значение, которое мы получаем с помощью калькулятора, составляет 0.301. Мы можем использовать формулу разложения натурального логарифма, чтобы найти значение ln(2).

Как сделать log2 на научном калькуляторе?

Как упростить LNE?

Как переписать e 2x?

Помните, что натуральные логарифмы имеют основание e. n, когда n бесконечно, и добавляя к ряду 1 + 1/1! + 1/2!

Как найти число Эйлера?

1. Значение e примерно равно e=2.718.
2. e математически представляется как e=limn→∞(1+1n)n.
3. Эйлер ввел число e применительно ко многим математическим вычислениям. Например, для расчета сложных процентов мы используем A=Pert A = Pert. Решаемые примеры.

Что такое странное е в математике?

Символ ∈ указывает установить членство и означает «является элементом», так что утверждение x∈A означает, что x является элементом множества A. Другими словами, x является одним из объектов в коллекции (возможно, многих) объектов в множестве A.

Что значит в Тик Ток? Смайлы для мозга, которые вы видите повсюду в TikTok, на самом деле код для орального секса.

Для чего нужен сленг Hammer?

переходный глагол. Если вы говорите, что кто-то бьет другого человека, вы имеете в виду, что они атаковать, критиковать, или строго наказать другого человека. 10.

Что такое e5 в математике?

Что означает e в статистике? В статистике символ представляет собой математическую константу, приблизительно равную 2.71828183. … 2.3e-5, значит 2.3 умножить на десять в минус пятую степень, или 0.000023. 4.5e6 означает 4.5 умножить на десять в шестой степени, или 4500000, что равно 4,500,000.

Что означает E 4 на калькуляторе? е^—4 часть означает, что десятичную точку в числе 4.3 следует переместить на четыре позиции влево, что требует добавления дополнительных нулей. Длинное описание.

Логарифм и его свойства

Логарифм и его свойства

Итак, давайте рассмотрим степенную функцию. Например, что значит 4² = 16? 2 — это показатель степени, который показывает, сколько раз необходимо умножить число 4 само на себя, чтобы получить 16. Иными словами, в какую степень следует возвести 4, чтобы получить 16. Если нам необходимо получить число 36 из числа 6, это значит, что мы число 6 должны возвести во вторую степень.

В общем виде рассматриваемые случаи можно записать следующим образом:

a^x = N.

Стоит обратить внимание, что в качестве «а» мы можем использовать все положительные числа, кроме числа 1. Более того, если число «а» больше нуля, то и N не может иметь отрицательные значения при любых показателях степеней.

Корнем некоторого уравнения a^x = N, где «а» может принимать положительные значения, отличные от нуля и единицы, является логарифмом некоторого N при основании «а». Иными словами,

ОПРЕДЕЛЕНИЕ: Логарифм — это степень, в которую необходимо возвести число «а», чтобы получить N.

Логарифм записывается словом log.

Например, 4³ = 64 можно записать иначе: log₄64 = 3.

Число 4 в данном логарифме называется его основанием. Данное выражение читается, как логарифм 64 по основанию 4 равен 3.

То есть для a^x = N, при «а» больше нуля и не равном единице, получим: log_aN = x.

На графике логарифм имеет вид, симметричный показательной функции.

Свойство логарифмов для положительного «а», не равного единице

Логарифм имеет любое положительное число, отличное от единицы. Если число отрицательное, то оно не может иметь логарифма.

Обратите внимание на график, функция может принимать положительные, отрицательные значения, а также число ноль, но при этом х только стремится к нулю, не достигая его.

Свойства для функций, у которых «а» строго больше единицы

1. Если некоторое число N₁  N₂, то и log_aN₁  log_aN₂. То есть, чем больше число логарифма с одинаковыми основаниями, тем больше и значение логарифма.

2.  Если логарифм записан для N  1, то значение логарифма положительное число. Если же N лежит в пределах от нуля до 1, то значение логарифма будет отрицательным числом.

3. При возрастании числа под логарифмом с одинаковым основанием должно возрастать и значение логарифма.

4. Если значения числа приближается к нулю, это значит, что значение логарифма убывает и может быть отрицательным. Чем больше модуль отрицательного значения логарифма, тем меньше число, и тем ближе оно к нулю.

Свойства для логарифмов, для которых «а» находится в пределе от нуля до единицы

1. Если некоторое число N растет, то значение логарифма падает.

2. Если число N больше единицы, то значение такого логарифма при заданном «а» будет числом отрицательным. Если же число N меньше единицы, то значение такого логарифма положительно.

3. Если число при заданном «а» возрастает до бесконечности, то значение такого логарифма падает до минус бесконечности.

Основное логарифмическое тождество

Среди всех остальных формул существует основное тождество, которое приводит к получению остальных свойств:

Свойства логарифмов

1. Если имеется логарифм произведения двух чисел больших нуля, то данный логарифм можно записать в виде суммы:

Данное свойство вытекает из основного свойства степени — при умножении степеней их показатели складываются.

2. Логарифм частного двух чисел равен разности двух логарифмов:

Данное свойство было получено из свойства деления степеней — при делении степеней, показатели вычитаются.

3. Если некоторое число в степени находится под знаком логарифма, то показатель степени можно вынести вперед, тем самым, умножив логарифм на показатель:

Данное свойство вытекает из одного из основных свойств степенной функции — при возведении степени в степень показатели степеней перемножаются.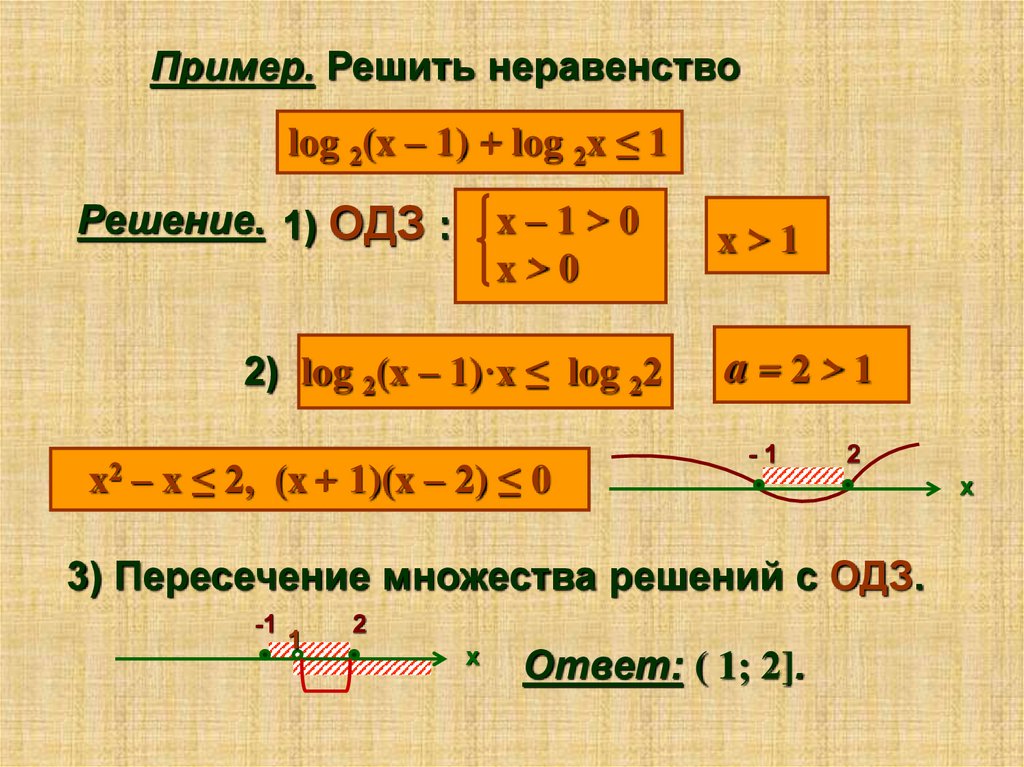

4. Если число и основание логарифма совпадает, то значение такого логарифма равно единице:

5. Логарифм по любому основанию равен нулю, если число равно единице:

6. При любом логарифме можно перейти от одного основания к другому. Для этого необходимо просто воспользоваться формулами:

Десятичный и натуральный логарифмы, число е

Одним из самых распространенных логарифмов является десятичный логарифм. Данная функция имеет в основании число 10.

Десятичный логарифм используется для стандартной записи числа, ведь именно при данной записи число 10 возводится в некоторую положительную или отрицательную степень.

Десятичный логарифм записывается, как lg. 

Например, log₁₀100 = lg100 = 2.

Одним из основных видов логарифмов считается натуральный логарифм, который имеет в качестве основания иррациональное число, которое называется числом Эйлера. Данное число равно: е ≈ 2,718.

Если логарифм имеет основание «е», то такой логарифм называется натуральным или неперовым. Записывается он как ln.

Первая буква обозначения говорит о том, что это логарифм, а вторая — что он натуральный.

Наиболее распространенные натуральные логарифмы:

ln 2 = 0, ln 3 = 1,098, ln 10 = 2,303.

Все свойства, которые рассматривались в предыдущих вопросах для логарифмов, справедливы для десятичного и натурального логарифмов.

Общие основания логарифмов и значения, где логарифмы не определены — Криста Кинг Математика

10 и e — специальные основания логарифма.

Помните, что в данном случае число ???8??? называется «базой».

Есть базы, которые мы используем гораздо чаще, чем все остальные, поэтому им нужно уделить особое внимание.

Привет! Я Криста.

Я создаю онлайн-курсы, чтобы помочь вам в учебе по математике. Прочитайте больше.

Логи по базе 10

Но иногда вы увидите логи, написанные вообще без базы, примерно так:

???\log{(100)}=2???

Если в журнале нет основания, это означает, что вы имеете дело с

десятичным логарифмом , основание которого всегда равно ???10???. ???\log_{10}??? настолько часто используемый журнал в реальном мире, что мы решили сэкономить время и просто упростить ???\log_{10}??? чтобы просто ???\log???, и понять что база-???10??? подразумевается. Это означает, что мы можем переписать ???\log{(100)}=2??? как 92=100???

Логарифмы по основанию e

Возможно иметь логарифм, основание которого называется «e». e  на самом деле число Эйлера, и это константа, равная примерно ???2,71???. Вот еще несколько цифр ???e???.

???е\ок2.7182818284590452353602874713527…???

Как ???\pi???, ???e??? является иррациональным числом, так что его цифры продолжаются вечно и не повторяются. Любой логарифм с основанием ???e??? представляет собой

натуральных логарифмов 94\ок54.598???

Определение журналов по основанию 10, журналов по основанию e и случаев, когда эти функции журнала не определены

Пройти курс

Хотите узнать больше об Алгебре 2? У меня есть пошаговый курс для этого. 🙂

Учить больше

Решение логарифмического уравнения по основанию 10

Пример

Решите логарифм для ???x???. 9х=1000???

???х=3???

Если в журнале нет основания, это означает, что вы имеете дело с десятичным логарифмом , основание которого всегда равно 10. x=y???, соответствующий логарифм равен ???\log_a{(y)}=x??? , наоборот.

Логарифм в виде ???\log_a{(y)}=x???, основание ???a??? должен быть положительным и не равен ???1???, и поэтому аргумент ???y??? также будет положительным

Если мы не будем следовать этим правилам, мы можем столкнуться с проблемами и получить неверные уравнения.

Получить доступ к полному курсу Алгебра 2

Начать

Изучайте математикуКриста Кинг 7 марта 2020 г. математика, выучить онлайн, онлайн-курс, онлайн-математика, алгебра 2, алгебра II, логарифмы, журналы, натуральные логарифмы, натуральные логарифмы, общие основания, ограниченные значения, основание 10, основание e, десятичные логарифмы, десятичные логарифмы

0 лайков

Основание логарифма: примеры и формулы

Логарифм — это показатель степени, определяющий, сколько раз можно умножить число, чтобы получить другое число. Это степень, в которую возводят число (основание), чтобы получить другое число. Говоря о логарифмах, вам нужно помнить и уметь различать такие термины, как показатель степени и основание.

Мы больше сосредоточимся на основаниях логарифмов. Следовательно, мы должны быть в состоянии идентифицировать базу, когда мы ее видим. Давайте познакомимся с основной формулой, связанной с логарифмами, а затем определим основание.

b — основание, y — показатель степени, в которую возводится основание и X — полученный результат.

Также записывается как:

, где log — это сокращение от логарифма.

Если у вас есть , 2 — основание, 3 — показатель степени и 8 — полученный результат. Его также можно записать как . Если мы можем идентифицировать основание в логарифмическом выражении, мы можем вывести значение основания.

Основание логарифма означает

Основание логарифма — это нижний индекс символа логарифма (log). Можно сказать, что это число, которое несет или повышает показатель степени в зависимости от формы выражения ( или ). Давайте возьмем несколько примеров, чтобы укрепить наше понимание определения базы.

Определите базу в следующем.

Решение

1. Основание здесь равно 3. Это индекс логарифмического символа log.
2. Основание здесь равно 5. Это число, которое повышает показатель степени 4.

Популярными формами логарифмов являются десятичный логарифм и натуральный логарифм. Двойной логарифм по основанию 10 записывается как или просто, а натуральный логарифм по основанию е записывается как или . При решении десятичных логарифмов лучше всего использовать калькулятор. Калькулятор имеет кнопку журнала, которая даст вам ответ. Вы можете попробовать сделать это без калькулятора, если числа маленькие и их легко вычислить, но в противном случае воспользуйтесь калькулятором.

Дайте ответы на следующие вопросы.

Решение Мы видим, что все вопросы относятся к основанию 10.a. Получить ответ можно с помощью калькулятора. Просто нажмите кнопку журнала и введите 1000, и вы получите ответ.

Это означает, что если умножить 10 в трех местах, получится 1000, то есть .

Это также возможно сделать без калькулятора, потому что мы можем вычислить, что = 1000.b. log 20 = 1,3010с. журнал 8 = 0,9031

Натуральный логарифм по основанию e называется числом Эйлера, равным 2,71828. Когда вы хотите решить это, вы используете кнопку в вашем калькуляторе, чтобы получить ответ.

Давайте посмотрим еще несколько примеров.

Дайте ответы на следующие

a.

б.

в.

Решение

1. Чтобы получить ответ на вопрос , вам понадобится калькулятор. Вам нужно будет нажать кнопку на калькуляторе, а затем 7. 3. После этого появится ответ.

б. Используя калькулятор,

c. Используя калькулятор,

Помимо десятичного логарифма и натурального логарифма с основанием 10 и e, логарифмы также могут иметь любое основание. Основание может быть любым числом. Например, и являются логарифмами с разными основаниями.

Решение логарифмов с разными основаниями

Если у вас есть логарифмы с разными основаниями, это означает, что у вас есть логарифмическое уравнение или выражение, в котором основания имеют разные числа. Способ сделать это — использовать формулу, называемую изменение базовой формулы. Цель состоит в том, чтобы сделать разные базы равными. Таким образом, вы сможете легко получить решение. Давайте посмотрим, как выглядит изменение базовой формулы.

Логарифмические правила, которые мы обычно используем, это те же самые правила для решения логарифмического основания. Давайте посмотрим на некоторые из этих правил.

Нам нужны эти формулы, чтобы помочь нам, потому что наши калькуляторы могут вычислять логарифмы только по основанию «10» и по основанию «е». Давайте посмотрим, как используется замена базовой формулы в следующих примерах.

Упрощение

Решение

Первым делом необходимо изменить основание, используя формулу изменения основания. Вы можете изменить основание на любое число, включая основание 10 и натуральный логарифм. Вам просто нужно убедиться, что они оба являются одной и той же базой. Делая это, мы будем иметь:

Мы будем использовать калькулятор, чтобы найти числитель и знаменатель, чтобы получить:

Давайте посмотрим больше примеров.

Решить

Решение

Вы заметите, что задействованы разные основания, поэтому мы будем использовать формулу замены основания. Мы можем изменить оба основания на 3 или 9, и вы все равно получите тот же ответ. Помните, что цель состоит в том, чтобы убедиться, что обе базы равны.

Мы будем использовать формулу замены основания в правой части. Это означает, что мы делаем основания 3.

Имеется закон логарифмирования в виде . Применим этот закон к присутствующему знаменателю и получим:

Подставим результат «2» в уравнение и продолжим решение.

Существует еще один закон логарифмирования в виде . Если мы применим это, мы получим:

Используя правило, что если , то наш окончательный ответ будет:

Решить

Решение

Первое, что нужно сделать, это сделать основания одинаковыми. Мы можем сделать их обоих равными 9 или 3. В любом случае мы придем к одному и тому же ответу. Давайте сделаем их обоих 3.

Формула замены основания:

Мы воспользуемся формулой замены основания для первого члена выражения и получим:

Если вы понаблюдаете, то увидите, что можно упростить знаменатель с помощью калькулятор или вручную. Вы можете сказать, что результат равен 2, потому что 3 в квадрате равно 9. Итак, теперь у нас будет:

Давайте умножим каждый член на 2

Мы можем использовать правило логарифмической степени для второго выражения, которое равно

Теперь у нас будет

Здесь мы можем использовать правило сложения, которое равно

Следовательно,

Теперь мы возьмем антилогарифм, чтобы получить

Здесь мы упростили, возведя основание 3 в степень 6.

Следующим и последним шагом является нахождение x

Извлечение квадратного корня из обеих сторон

Логарифмы иногда выражаются в графической форме, и основание логарифмической функции может повлиять на результат графика . Дело в том, что чем больше основание, тем меньше кривая. Другими словами, чем больше основание, тем ближе кривая подходит к оси Y.

Возьмем пример

Постройте логарифмические выражения и посмотрите на график.

и

Решение

Вам нужно составить таблицу для обоих выражений и построить график.

No related posts.