Формулы по математике сложные: Сложные математические формулы в программировании

Формулы в математике — презентация онлайн

Похожие презентации:

Элементы комбинаторики ( 9-11 классы)

Применение производной в науке и в жизни

Проект по математике «Математика вокруг нас. Узоры и орнаменты на посуде»

Знакомство детей с математическими знаками и монетами

Тренажёр по математике «Собираем урожай». Счет в пределах 10

Методы обработки экспериментальных данных

Лекция 6. Корреляционный и регрессионный анализ

Решение задач обязательной части ОГЭ по геометрии

Дифференциальные уравнения

Подготовка к ЕГЭ по математике. Базовый уровень Сложные задачи

1. «У математиков существует свой язык-это ФОРМУЛЫ»

С. В. КОВАЛЕВСКАЯ
(1850-1891)

2. История создания страны формул:

Диофант
Александрийский
(III век н. э.) —
древнегреческий
математик.
Еще в глубокой древности было
замечено, что некоторые
многочлены можно умножать
быстрее, чем все остальные. Так,
древнегреческими
математиками еще до нашей эры
(более 2000 лет назад)
геометрическим способом были
выведены некоторые формулы,
которые получили название
формулы сокращенного
умножения.

3. Устная работа

1. Выполнить умножение многочленов
(c+5)(b+2).
Как можно назвать полученное
выражение?

4. Устная работа

2. Найти квадрат выражения
y

5. Устная работа

2. Найти квадраты выражений
8xy

6. Устная работа

2. Найти квадрат выражения
2/3

7. Устная работа

2. Найти квадрат выражения
3m

8. Устная работа

2. Найти квадрат выражения
5

9. Устная работа

2. Найти квадрат выражения
3

10. Устная работа

3.Найти произведение одночленов
6x и 5h
Чему равно их удвоенное произведение?

11. Устная работа

3.Найти произведение одночленов
3а и b
Чему равно их удвоенное произведение?

12. Устная работа

3.Найти произведение одночленов
tи k
Чему равно их удвоенное произведение?

13.

Устная работа4. Найти соответствие:
а) m2 — n2
б) (m+n)2
квадрат разности
разность квадратов
в) m2+n2
удвоенное произведение
г) 2mn
квадрат суммы
д)
(m-n)2
сумма квадратов

14. Формулы сокращенного умножения

15. Формулы сокращенного умножения

16. Формулы сокращенного умножения

Квадрат суммы
и
квадрат разности
двух выражений

17. ОТКРЫТИЕ № 1

ФОРМУЛА
КВАДРАТ СУММЫ ДВУХ ЧИСЕЛ:
(а +
2
b) =
2
а
+ 2аb +
2
b

18. Открытие № 2

1
(m — n) (m -n) =
=
2
(c — d) (c -d) =
=
3
(p — q) (p — q) =
=

19. Исследование № 2

1
(m — n) (m — n) =
=m2 — 2 m n + n2
2
(c — d) (c -d) =
=c2 -2 c d + d2
3
(p — q) (p — q) =
= p2 — 2qp + q2

20. Исследование № 2

1
(m — n) (m — n) = (m — n)2
=m2 — 2 m n + n2
2
(c — d) (c -d) =
(c — d) 2
=c2 -2 c d + d2
3
(p — q) (p — q) =
(p — q)2
= p2 — 2qp + q2

21.

ОТКРЫТИЕ № 2ФОРМУЛА
КВАДРАТ РАЗНОСТИ ДВУХ
ЧИСЕЛ:
(а —
2
b) =
2
а
— 2аb +
2
b

23. Найти ошибку

(b —
2
у)
= b – 2bу +
2
у

24. Найти ошибку

(р —
2
10) =
2
р —
20р + 10

25. Найти ошибку

English     Русский Правила

дело не в числах, а в том, чтобы учиться думать / Хабр

Недавно по сети пробежал твит, содержание которого было следующим: в одной из кулинарий Питтсбурга появилась загадочная табличка со следующим обращением к посетителям: «Пожалуйста, откажитесь от обсуждения математики в очереди к кассе».

Жители Питтсбурга не смогли найти нашумевший магазин, потому что на самом деле он находится в Коннектикуте. Впрочем, это не помешало юмористам принять новость за чистую монету и поверить, что это настоящая табличка, якобы действительно помещенная в заведении кассиром, которому надоело, что какие-то всезнайки спорят с ним по поводу итоговой суммы.

А так все и было?

На самом деле нет, ничего подобного (в качестве подтверждения можете почитать про эту историю). Но в целом это объяснение вполне правдоподобно. Кассиры в наши дни не умеют делать расчеты в уме, не так ли?

С другой стороны, кто вообще сегодня умеет считать? Математика слишком сложна. Только те, кто работает с числами умеют производить вычисления в уме.

Это утверждение, опять же, неверно. Неверно, но популярно? Что ж, вполне может быть.

Во всяком случае Дениз Легран регулярно сталкивается с его подтверждением в ресторанах и магазинах. Например, во время тусовок с друзьями, в моменты, когда нужно скинуться на оплату счета или дать на чаевые. «Людей пугает любая необходимость решать какие-либо задачи, — говорит она.

Еще до того как кассовые аппараты превратили вычисление скидок в нажатие на несколько иконок, она часто помогала торговому персоналу с подсчетом итоговой суммы покупок. И делая это, она всякий раз задавалась вопросом: «Как они считают свои деньги? Как планируют бюджет?».

Но Легран — как раз одна из тех самых людей, которые работают с числами. Она руководит Центром помощи по обучению математике Арканзасского университета в Литл-Роке и преподает математический анализ на факультете математики и статистики университета. И она, к слову, часто остается обескуражена реакцией людей, узнающих о ее профессии: «Вы учитель математики? Никогда не любил(а) математику».

«Не думаю, что я вообще хоть когда-то встречала человека, который признался бы мне, что ему нравится математика», — грустно сообщает она.

Сэм Лохорн, молодой выпускник Арканзасского университета в Литл-Роке со степенью бакалавра по математике, недоумевает от того, что отсутствие навыков для работы с числами вызывает в обществе уважительную реакцию: люди едва ли не хвастаются друг перед другом по этому поводу.

«Как часто вы слышите, что люди говорят «Не умею читать, ненавижу читать»?» — спрашивает он.

«При этом говорить «ненавижу математику» — вполне приемлемая для социума вещь», — соглашается Легран

Тем временем спрос на профессионалов в области точных и естественных наук по всему миру растет.

Вот где появляются новые рабочие места. Чтобы удовлетворить потребность в квалифицированных кадрах «многие правительства и частные организации совершенствуют подходы к преподаванию точных наук и продвигают обучение, направленное на улучшение математических навыков и навыков научной работы среди студентов и рабочих», — пишут исследователи из Университета Чикаго в своем отчете, опубликованном в февральском выпуске журнала Current Directions in Psychological Science.

Подобные усилия, пишут они, как правило, направлены на ускорение и улучшение подачи большего количества математического и научного материала. Однако в результате анализа данных Международной программы по оценке образовательных достижений учащихся в 64 странах, в рамках которой 15-летние учащиеся сдавали тесты по математике, естествознанию и навыкам чтения, исследователи пришли к выводу, что обеспокоенность по поводу решения математических задач — «страх перед математикой» — оказывает довольно большое влияние на способность учащихся осваивать точные науки и с этим необходимо что-то делать.

В ходе других исследований было выявлено, что необходимость сдавать тесты в целом усиливает переживания студентов, однако волнения по поводу математики стоят особняком. К примеру, некоторые исследования показали, что пульс испытуемых учащался при упоминании математики, тогда как с другими предметами подобная реакция не наблюдалась.

Даже преуспевающие в математике ученики оказываются подвержены этому страху в достаточной степени, чтобы совершать ошибки. Тревога по поводу математики приводит к снижению успеваемости в ее освоении, говорят исследователи.

Поиск решений

Работа с подобными страхами — одна из миссий Легран в качестве директора Центра помощи по обучению математике, который предоставляет студентам любого уровня и любых кафедр индивидуальные и групповые занятия. Выступающие в роли преподавателей центра студенты предлагают другим обучающимся помощь с домашним заданием, улучшением навыков обучения, подготовкой к тестам и в целом работают над популяризацией математики.

Эта лаборатория на четвертом этаже здания инженерных технологий и науки университета в Литтл-Роке — набор освещенных флуоресцентными лампами и оснащенных компьютерами комнат. В центре есть как «громкая часть» для групповых занятий, так и «тихая сторона» для работы или игр в тишине. Здесь есть зал для отдыха, игрушки, диваны, белые лекционные доски и вдохновляющие слоганы.

Вот примеры некоторых из них:

• Неудача случается, только когда человек опускает руки.
• Пример Тетриса учит нас тому, что ошибки скапливаются горой, а достижения исчезают.
• Разница между гениальностью и глупостью в том, что у любой гениальности есть свои пределы.
• Ты уникален, прямо как и все остальные.

«Некоторые из них надо стереть», — делится своими мыслями по этому поводу Легран.

Лохорн вызвался работать преподавателем-волонтером в центре во время своего обучения в университете. Кроме того, он также преподавал на платной основе в нескольких центрах Mathnasium. Он и Легран видят определенные закономерности в мышлении взрослых людей, которым математика пришлась не по душе. Вот некоторых из них:

• Ошибка равносильна глупости.
• Математика — это запоминание формул.
• Люди делятся на тех, у кого «математический склад ума», то есть у которых хорошо получается работать с числами, и всех остальных.
• Успех означает получение правильного ответа. Есть только один верный способ получить правильный ответ.

Все эти установки очень вредны, считают математики, и предлагают перестать мыслить таким образом.

Неудача — тоже хорошо

Преподаватели центра дают студентам советы по поводу способов расслабления и успокоения, таких, как глубокое дыхание. Они подчеркивают, что при решении задач полезно не откладывать их до последнего момента, делать работу сразу, вкладывать в нее время.

Они также выступают за правильные психологические установки:

«Вам необходимо потерпеть неудачу, — говорит Лохорн. — Неудачные попытки — часть процесса обучения. Очень полезно оказаться в ситуации, когда Вам нужно спросить себя: «Блин, что я сделал не так?» Вот тогда вы собираетесь с мыслью и получается что-нибудь в духе: «Ага, я не видел всю ситуацию целиком, не заметил того нюанса, не имел целостного представления о том, что происходит»».

Неудачи — это инструмент. Освободите свой разум от предубеждений чтобы научиться на своих ошибках.

Кроме того, «запоминание — не есть цель математики, — говорит Легран. — Главное — понять процесс». Конечно, знание или, по крайней мере, способность узнать формулу может помочь, однако как только студенты начинают понимать почему формулы работают, они могут начать переделывать их по собственному усмотрению.

Запоминание формул не поможет Вам начать мыслить логичнее.

«Люди вполне естественно ассоциируют математику с числами, — говорит Лохорн. — Они думают, что это наука о числах. Однако на деле это скорее наука о закономерностях. Я считаю, что человеческий мозг создан для математики.

Например, мы не могли бы ходить, если бы не приспособленность мозга к поиску закономерностей. Мы созданы для того, чтобы искать закономерности. Мы любим их и не любим хаос».

И кстати, по словам Легран, ни она, ни Лохорн не были рождены с «математическим складом ума». Им также нужно изучать предмет и думать головой. Она, в частности, проводит самые тщательные проверки материала, перед тем как давать урок. Однако главная идея здесь в том, что необходимость работать над своим уровнем математики не делает из них неудачников. Они научились получать удовольствие от прилагаемых усилий.

«Пообщавшись с большинством математиков, — говорит Лохорн, — вы увидите, что если перед Вами не зациклившийся на самом себе человек, то он всегда скажет Вам что-нибудь вроде «Мне надо поработать над тем-то или тем-то»».

Как и другие предметы, у математики есть свой особый словарь и грамматика, отличная от стандартной. Легран подчеркивает, что хорошая успеваемость в ней требует терпеливого чтения, также как и в других предметах.

Но математика отличается от других предметов в том смысле, что одни ее концепции строятся на других. Студенту исторического факультета совсем необязательно знать историю Арканзаса чтобы иметь возможность прочитать об истории Литтл-Рока. В математике, напротив, научиться тригонометрии, не научившись сначала считать пальцы на руках и ногах, и сдачу с доллара, невозможно. Каждая новая тема добавляет в вашу копилку набор навыков, который потребуется в дальнейшем.

Легран не определяет успех как получение правильного ответа. Успех заключается в озарении от понимания того, как получается этот ответ.

«Люди говорят: «Алгебра мне никогда не пригодится!», но дело вовсе не в этом, — говорит она. — Смысл в том, чтобы научиться мыслить. Вы учитесь обрабатывать информацию».

И кстати, как отмечает Лохорн:

«Одна из вещей, которую я говорю посетителям лаборатории: «Вам вовсе не обязательно запоминать абсолютно все, чему Вас когда-либо учили». Да, мы надеемся, что вы запомните все эти нюансы, но этого не случится, если Вы не будете пользоваться ими регулярно.

Вы читаете все время, ведь так? Нам постоянно приходится читать. Даже если вы не берете в руки книги, вы все равно читаете меню, знаки дорожного движения, инструкции, субтитры, и прочие самые разные виды текстов. Но как часто Вам приходится производить какие-либо сложные математические операции для решения задач? Среднестатистический человек делает это нечасто».

Из этого следуют два умозаключения:

• Проблемы с запоминанием формулы квадратного уравнения не означает, что у вас нет способностей к «работе с числами».
• Для закрепления математических навыков, используйте их чаще.

Отличный способ сделать это — использовать игровые методы.

Обучение всегда должно быть в радость

Пользуйтесь приложениями для игры в математические игры, даже предназначенными для детей. Играйте на компьютере, смартфоне или любых других мобильных девайсах.

• Бесплатное приложение Bedtime Math (bedtimemath.org) предлагает увлекательный формат представления фактов с последующими проверочными вопросами разного уровня сложности. Одна из задачек рассказывала об использовании козлов вместо газонокосилки. Приложение предлагало Вам посмотреть видео о том, как 800 козлов выщипывали лужайку Национальной лаборатории им. Лоуренса в Беркли.
• Посложнее будет Euclidea Geometric Constructions (euclidea.xyz) — другое бесплатное приложение с собственной веб-версией. Его задания основаны на классических задачах построения с помощью линейки и циркуля и поделены на 120 уровней сложности от простых до очень, очень сложных.
• Книги-раскраски с мандалами позиционируются как хорошее средство успокоения для взрослых. «Вы можете создавать собственные варианты мандал с помощью линейки для рисования и циркуля, — говорит Лохорн. — Это очень полезная вещь, если вы расстроены или обеспокоены».
• Khan Academy (khanacademy.org) ­— бесплатный обучающий веб-сайт с видео и интерактивными играми для обучающихся разных уровней — от детского сада до колледжа.
• Легран отмечает, что танцы и музыка — математика в движении. Поэтому танцуйте, играйте на музыкальном инструменте.
• Судоку, КенКен, магические квадраты, шахматы и шашки можно назвать математикой для отдыха, этакие головоломки, требующие применения навыков уровня продвинутой математики без необходимости знания продвинутой математики как таковой.
• В газете The Wall Street Journal есть еженедельная колонка Varsity Math, где публикуются развлекательные математические задачи
• Другую интересную колонку с аналогичными задачками довольно долго вел Мартин Гарднер для Scientific American. На сайте Martin Gardner Puzzles собраны некоторые лучшие из них.
• А еще поищите на YouTube видео об оригами «гексафлексагонах» Гарднера. Вот классный пример.

Если со всем остальным у Вас не получилось, просто вернитесь к баловству со сворачиванием и разворачиванием гексафлексагонов.

Таблицы Google: создание сложных формул

Урок 13. Создание сложных формул

/en/googlespreadsheets/creating-simple-formulas/content/

Введение

У вас может быть опыт работы с формулами, которые содержат только один оператор, например 7+9 . Более сложные формулы могут содержать несколько математических операторов , например 5+2*8 . Если в формуле более одной операции, порядок операций сообщает Google Таблицам, какую операцию следует вычислить в первую очередь. Чтобы написать формулы, которые дадут вам правильный ответ, вам нужно понять порядок операций.

Посмотрите видео ниже, чтобы узнать, как создавать сложные формулы.

Порядок операций

Google Sheets вычисляет формулы на основе следующего порядка операций :

1. Операции, заключенные в скобки
2. 0 E

   92, например)

3. M Ultiplication и Division , в зависимости от того, что наступит первые
4. A DDITY и Вычитание , какой бы ни был первый

А. P аренда E извините M y D ухо A unt S союзник.

Нажмите на стрелки в слайд-шоу ниже, чтобы узнать, как порядок операций используется для расчета формул в Google Таблицах. 92=4.

Далее мы решим любое умножение и деление слева направо. Поскольку операция деления предшествует умножению, она вычисляется первой: 3/4=0,75.

Теперь решим оставшуюся операцию умножения: 0,75*4=3.

Далее мы вычислим любое сложение или вычитание, снова работая слева направо. Сначала идет сложение: 10+3=13.

Наконец, у нас осталась одна операция вычитания: 13-1=12.

Теперь у нас есть ответ: 12. И это точно такой же результат, который вы получите, если введете формулу в Excel.

Создание сложных формул

В приведенном ниже примере мы покажем, как Google Sheets решает сложную формулу, используя порядок операций. Сложная формула в ячейке D6 рассчитывает налог с продаж путем сложения цен и умножения на налоговую ставку 5,5% (которая записывается как 0,055).

Google Таблицы следуют порядку операций и сначала добавляют значения в скобках: (D3+D4+D5) = 274,10 $ . Затем он умножается на налоговую ставку: 274,10$*0,055 . Результат покажет, что налог равен $15,08 .

Особенно важно соблюдать порядок операций при создании формулы. В противном случае Google Sheets не сможет точно рассчитать результаты. В нашем примере, если круглых скобок не включены, сначала вычисляется умножение, и результат неверен. Круглые скобки часто являются лучшим способом определить, какие вычисления будут выполняться в первую очередь в Google Таблицах.

Чтобы создать сложную формулу с использованием порядка операций:

В приведенном ниже примере мы будем использовать ссылок на ячейки вместе с числовыми значениями , чтобы создать сложную формулу, которая будет вычислять промежуточный итог для счета за питание. . Формула сначала рассчитает стоимость каждого пункта меню, а затем добавит эти значения.

1. Выберите ячейку , которая будет содержать формулу. В нашем примере мы выберем ячейку C 5 .
2. Введите формулу . В нашем примере мы введем =B3*C3+B4*C4 . Эта формула будет следовать порядку операций, сначала выполняя умножение: 2,79 * 35 = 97,65 и 2,29 * 20 = 45,80 . Затем он добавит эти значения для расчета суммы: 97,65+45,80 .
3. Еще раз проверьте формулу на точность, затем нажмите Введите на клавиатуре. Формула рассчитает и отобразит результат . В нашем примере результат показывает, что промежуточная сумма заказа составляет 143,45 $ .

Google Sheets не всегда сообщит вам , если ваша формула содержит ошибку, поэтому вы должны проверить все свои формулы. Чтобы узнать, как это сделать, прочитайте нашу статью о том, почему вы должны перепроверять свои формулы.

Вызов!

1. Откройте файл нашего примера. Убедитесь, что вы вошли в Google, затем нажмите Файл > .Сделайте копию .
2. Выберите лист Challenge . Допустим, мы хотим сравнить две скидки. Первая скидка составляет 20% от общей суммы, а вторая скидка — 30 долларов США от общей суммы.
3. В ячейке D6 создайте формулу , которая вычисляет общую сумму, используя скидку 20%.
   Подсказка: Так как у нас скидка 20%, останется 80% от общей суммы. Чтобы вычислить это, умножьте 0,80 на сумму итогов строк.
4. В ячейке D7 , создайте формулу , которая вычитает 30 из общей суммы.
5. Когда вы закончите, ваша электронная таблица должна выглядеть так:

Продолжать

Предыдущий: Создание простых формул

Далее:Типы ссылок на ячейки

/en/googlespreadsheets/types-of-cell-references/content/

обозначение — Обучение чтению сложных математических формул

спросил 9 лет, 8 месяцев назад

Изменено 4 года, 11 месяцев назад

Просмотрено 28 тысяч раз

$\begingroup$

кто-нибудь может указать мне книгу или статью, где я мог бы научиться читать такие формулы:

Я понятия не имею, что это значит.

• обозначение

$\endgroup$

5

$\begingroup$

Следующие пункты могут быть полезны:

1. $i$ используется для индексации различных числовых значений $x_i$, которые у вас есть. Обычно, если не указано иное, подразумевается, что $i$ находится в диапазоне от $1$ до некоторого конечного значения $n$.

   Таким образом, в вашем примере у вас есть $n$ наблюдений, каждое из которых обозначается $x_i$.

2. $\bar{x}$ обозначает среднее значение из $n$ наблюдений, т. е.

   $$\bar{x} = \frac{x_1+x_2+\ldots+x_n}{n}$$

   Такая же интерпретация справедлива для $y_i$ и $\bar{y}$.

3. $\Sigma$ означает сумму, поэтому мы могли бы переписать среднее значение следующим образом:

   $$\bar{x} = \frac{x_1+x_2+\ldots+x_n}{n}=\frac{\Sigma_i{x_i}}{n}$$

Надеюсь, это поможет понять, что происходит в уравнении.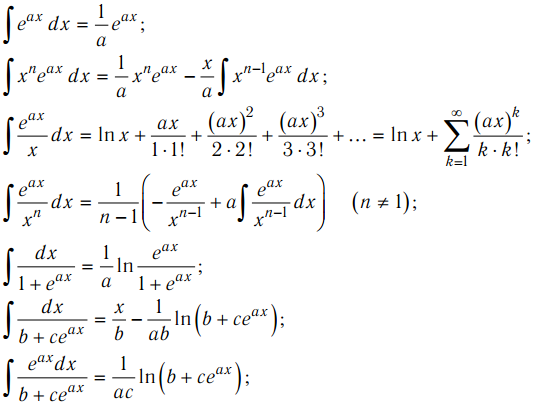

$\endgroup$

$\begingroup$

Для этой формулы хорошим началом будет любая вводная книга по статистике. Вероятно, у вас не будет предыстории этой книги, и тогда вам придется вернуться назад.

В частности, для ответа на этот вопрос вы можете поискать «обозначение сигма-суммирования», так как это единственный действительно странный символ здесь. Другие символы, такие как $\bar x $, должны быть определены. Формула, о которой вы спрашивали, оказалась формулой для расчета коэффициента корреляции Пирсона, измеряющего, насколько изменение одной переменной соответствует изменению другой. В этом случае значения берутся из точек данных на плоскости, а наличие полосы означает среднее значение (так что $\bar x$ означает среднее значение всех $x$).

$\endgroup$

1

$\begingroup$

Этот исчерпывающий PDF-файл может быть полезен: Справочник по разговорной математике

В нем представлены математические символы и объясняется, как их читать.