Как обозначается объем в математике: Урок 11. понятие объема — Геометрия — 11 класс

Содержание

Урок 11. понятие объема — Геометрия — 11 класс

Геометрия, 11 класс

Урок №11

Понятие объёма

Перечень вопросов, рассматриваемых на уроке:

Понятие объёма.

Свойства объёмов.

Объём прямоугольного параллелепипеда.

Формула объёма прямоугольного параллелепипеда.

Тезаурус

Объём тела– величина, характеризующая часть пространства, занимаемую телом, и определяемая формой и линейными размерами этого тела.

Основные свойства объёма:

— равные тела имеют равные объёмы;

— если тело составлено из нескольких тел, то его объём равен сумме объёмов этих тел.

Основная литература:

Атанасян Л. С. и др. Математика: алгебра и начала математического анализа, геометрия. Геометрия. 10–11 классы [текст]: учеб. для общеобразоват. организаций: базовый и углубл. уровни – М.: Просвещение, 2014. – 255 с. С. 130–133.

Теоретический материал для самостоятельного изучения

С понятием объёмного тела, отличающегося от плоской фигуры, мы познакомились ещё в начальной школе.

Объёмом принято называть положительную величину, характеризующую часть пространства, занимаемую телом, и определяемую формой и линейными размерами этого тела.

Мы можем вычислить объём тела точно так же, как ранее находили площадь фигуры. Объём принято измерять в единицах измерения объёма (единицах измерения размера пространства, занимаемого телом), то есть в кубических метрах, сантиметрах, миллиметрах и так далее. За единицу измерения объёма можно принять куб с ребром 1 см, то есть, кубический сантиметр (обозначение: см³). По аналогии, можно за единицу измерения объёма принять кубический миллиметр (1 мм³), кубический метр (1 м³) и тому подобное.

Объём выражается в положительных числах. Это число показывает, сколько единиц измерения содержится в теле. Например, сколько кубических миллиметров в аквариуме, сколько кубических метровв бассейне и так далее.

Объём обозначается заглавной латинской буквой V.

Пример:

Объём книги400 кубических сантиметров запишут: V = 400см³.

Рассмотрим свойства объёмов.

Свойство № 1. Равные тела имеют равные объёмы. Это означает, что если два тела идентичны, то есть имеют равное количество единиц измерения и частей, то равны и их объёмы. Например, 2 одинаковых пакета молока равны в объёме.

Свойство № 2. Если тело составлено из нескольких тел, то его объём равен сумме объёмов этих тел.

Следствие из основных свойств объёмов.

Объём куба с ребром 1/n равен 1/n³

Доказательство. Рассмотрим куб, объём которого принят за единицу измерения объёмов, тоесть равный некоторому числукубических сантиметров. Его ребро равно единице измерения отрезков. Разобьём каждое ребро этого куба на произвольное количество частей – nтак, чтобы провести плоскости, перпендикулярные к этому ребру.

По второму свойству объёмов, сумма объёмов всех кубиков равна объёму всего куба (1 см³). Следовательно, поскольку мы разбили каждое ребро на n частей, то каждый маленький куб внутри большого куба будет иметь ребро

Объём каждого из маленьких кубиков при этом будет равен 1/n³.

Объём прямоугольного параллелепипеда

Теорема

Объём прямоугольного параллелепипеда равен произведению трёх его измерений.

Доказательство

Обозначимизмеренияпрямоугольного параллелепипеда P буквами a,b,c, его объём буквой V, и докажем, что V = a ∙ b ∙ c.

Рассмотрим два возможных случая.

Случай первый. Измерения a, b и c представляют собой конечные десятичные дроби, у которых число знаков после запятой не превосходит n (можно считать, что n больше или равно 1). В этом случае числа a ∙10

n, b∙10ⁿ, c∙10ⁿ, являются целыми. Разобьём каждое ребро параллелепипеда на равные части длины: 1/10ⁿ и через точки разбиения проведём плоскости, перпендикулярные к этому ребру. Параллелепипед P разобьётся на abc∙10³ⁿ равных кубов с ребром 1/10ⁿ. Так как объём каждого куба равен 1/10³ⁿ, что мы доказали ранее, то объём всего параллелепипеда P = abc, что и требовалось доказать.

Случай второй.

Хотя бы одно из измерений a, b, c представляет собой бесконечную десятичную дробь. Рассмотрим конечные десятичные дроби: a_n, b_n, c_n, которые получаются из чисел a, b, c, если отбросить в каждом из них все цифры после запятой, начиная с n + 1. Очевидно, a

n ≤ a ≤ a_n’, где a_n’= a_n+1 : 10ⁿ. Аналогичные неравенства справедливы для b и c. Перемножив эти неравенства, получим произведение a_nb_nc_n ≤ abc ≤ a_n’b_n’c_n’, где b_n’= b_n+1 : 10ⁿ, c_n’ = c_n+1 : 10ⁿ

По доказанному в первом случае, левая часть неравенства представляет собой объём V_n прямоугольного параллелепипеда P_nс измерениями a_n, b_n, c_n, а правая часть – это объём V_n’прямоугольного параллелепипеда P_n’ с измерениями a_n’, b_n’, c_n’.

Так как параллелепипед P содержит в себе параллелепипед P_n, а сам содержится в параллелепипеде P_n’, то объём V параллелепипеда P заключён между V_n, = a_nb_nc_n и V_n’= a_n’b_n’c_n’. Будем неограниченно увеличивать n. Тогда 1/10ⁿ будет становиться сколь угодно малым, и поэтому произведение a_n’b_n’c_n’будет сколь угодно мало отличаться от числа, выраженного произведением a_nb_nc_n. Отсюда следует, что число V сколь угодно мало отличается от числа, выраженного произведением a_nb_nc_n, а значит, они равны.V = abc, что и требовалось доказать.

Примеры и разбор решения заданий тренировочного модуля.

№1.Длины сторон основания прямоугольного параллелепипеда равны 15 см и 20 см. Высота параллелепипеда равна диагонали основания. Найдите объём этого параллелепипеда.

Решение:

Найдём длину диагонали основания, для этого воспользуемся теоремой Пифагора:

А теперь найдём объём параллелепипеда:

V = 15 ∙ 20 ∙ 25 = 7500 см³

Ответ: V = 7500 см³.

№2.

Найдите площадь закрашенной фигуры, если объём прямоугольного параллелепипеда равен 960 см³, AB = 8 см, АА₁₌20 см.

Варианты ответов:

220 см²

100 см²

400 см²

200 см²

Решение.

Найдём длину АD:

AD = 960 : 8 : 20 = 6 см

Найдём АС, воспользовавшись теоремой Пифагора:

Закрашенная фигура – прямоугольник. Вычислим его площадь: 10∙20= 200 см².

Ответ: площадь закрашенной фигуры 200 см².

Верный ответ: 200 см²

Как найти Объем Параллелепипеда?

Понятие объема

Чтобы без труда вычислить объём любой фигуры, нужно разобраться с определениями.

Объём — это количественная характеристика пространства, занимаемого телом или веществом.

Другими словами, это то, сколько места занимает предмет.

Объём измеряется в единицах измерения объема (единицах измерения размера пространства, занимаемого телом), то есть в кубических метрах, сантиметрах, миллиметрах.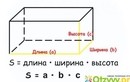

За единицу измерения объёма можно принять куб с ребром 1 см, то есть, кубический сантиметр (см3), кубический миллиметр (1 мм3), кубический метр (1 м3).

Объём всегда выражается в положительных числах. Это число показывает, какое именно количество единиц измерения есть в теле. Например, сколько воды в бассейне, вина в бочке, земли в клумбе.

Два свойства объёма

У равных тел равные объёмы. Если два тела одинаковы, и имеют равное количество единиц измерения — их объёмы равны. Например, у двух одинаковых пакетов сока равные объемы.

Если геометрическое тело состоит из нескольких геометрических тел, то его объём равен сумме объёмов этих тел.

Любое объемное тело имеет объем. Получается, при желании мы можем вычислить объем кружки, смартфона, вазы, кота — чего угодно.

Объем прямоугольного параллелепипеда

Давайте вспомним, какие виды параллелепипедов бывают.

Параллелепипедом называется призма, основаниями которой являются параллелограммы. Другими словами, параллелепипед — это многогранник с шестью гранями. Каждая грань которой называется параллелограмм.

Призма — это многогранник, в основаниях которого лежат равные многоугольники, а его боковые грани — это параллелограммы.

Какие бывают призмы:

Прямой параллелепипед — это параллелепипед, у которого боковые ребра перпендикулярны основанию.

Прямоугольным параллелепипедом называют параллелепипед, у которого основание — прямоугольник, а боковые ребра перпендикулярны основанию.

Формула объема прямоугольного параллелепипеда

Чтобы вычислить объем прямоугольного параллелепипеда, найдите произведение его длины, ширины и высоты:

V = a * b * h

Чтобы не запутаться в формулах, запоминайте табличку с условными обозначениями.

a	длина параллелепипеда
b	ширина параллелепипеда
h	высота параллелепипеда
P (осн)	периметр основания
S (осн)	площадь основания
S (бок)	площадь боковой поверхности
S (п.п.)	площадь полной поверхности
V	объем

Пример 1. Чему равен объем параллелепипеда со сторонами 9 см, 6 см, 3 см.

a = 9 см

b = 6 см

h = 3 см

V = a * b * h

V = 9 * 6 * 3 = 162 см3.

Ответ: объем прямоугольного параллелепипеда равен 162 см3.

Следствие 1

Объем параллелепипеда равен произведению площади основания на высоту.

V = S осн * h

Из этого следствия выведем формулу нахождения площади основания параллелепипеда.

S осн = V : h

Пример 2. Найдите площадь основания параллелепипеда, если его объем равен 82 см3, а высота 8 см.

V = 82 см3

h = 8 см

V = S осн * h

S осн = V : h

S осн = 82 см3: 8 см = 10,25 см2.

Ответ: площадь основания параллелепипеда равна 10,25 см2.

Следствие 2

Объём прямой призмы, основанием которой является прямоугольный треугольник, равен произведению площади основания на высоту.

V = S осн * h

Пример 3. Основанием прямой призмы служит прямоугольный треугольник с катетами 6 и 8 см. Боковое ребро равно 5. Найдем объем призмы.

V = S * h = 12* a * b * h

a = 6

b = 8

h = 5

V = 1/2 * 6 * 8 * 5 = 120 см3.

Ответ: объём прямой призмы, основанием которой является прямоугольный треугольник, равен 120 см3.

С каждым годом геометрия становится все более объемной. Формулы множатся, а задачки усложняются. В детской онлайн-школе Skysmart ваш ребенок сможет заполнить пробелы, разобрать сложные темы и научиться доказывать любые теоремы.

Записывайтесь на бесплатный вводный урок и знакомьтесь с устройством учебной платформы лично.

Вычисление площади

Как вы уже поняли, вычисление объёма параллелепипеда напрямую зависит от вычисления его площади. Давайте разберемся, сколько всего площадей можно найти в параллелепипеде.

Чтобы найти площадь боковой поверхности параллелепипеда, вычислите по отдельности площадь каждой боковой грани, а затем найдите сумму получившихся значений.

Чтобы вычислить площадь полной поверхности параллелепипеда, сложите площадь боковой поверхности и две площади основания.

S п.п. = 2 (ab + ac + bc)

Пример 4. Найдем площадь поверхности параллелепипеда, если длина основания равна 6 сантиметров, ширина — 4 см соответственно, а высота — 3 см.

S п.п. = 2 (ab + ac + bc)

S п.п. = 2(6 * 4 + 6 * 3 + 4 * 3) = 2 * (24 + 18 + 12) = 2 * 54 = 108 см2.

Ответ: площадь поверхности параллелепипеда — 108 см2.

Как видите, вычислить объём и найти площадь параллелепипеда совсем не трудно. В интернете есть много онлайн-калькуляторов, которые помогут вам быстро вычислить объем:

Задачи на самопроверку

Пользоваться онлайн-калькуляторами можно, когда вы уже натренировались в решении задачек и с закрытыми глазами можете вычислить объем любого параллелепипеда. Давайте разберем еще несколько примеров.

Задачка 1. Найдите объём параллелепипеда со сторонами 18 см, 10 см, 7 см.

Как решаем:

a = 18 см

b = 10 см

h = 7 см

Формула нахождения объема параллелепипеда:

V = a * b * h

Подставляем наши числа:

V = 18 * 10 * 7 = 1260 см3.

Ответ: объём параллелепипеда = 1260 см3.

Задачка 2. Найдите площадь основания параллелепипеда, если его объём = 120 см3, а высота — 15 см.

Как решаем:

V = 120 см3

h = 15 см

V = S осн * h

S осн = V : h

S осн = 120 см3: 15 см = 8 см2.

Ответ: площадь основания параллелепипеда = 8 см2.

Задачка 3. Найдите площадь полной поверхности прямоугольного параллелепипеда, если длина основания = 30 сантиметров, ширина = 12 см, а высота = 5 см.

Как решаем:

S п.п. = 2 (ab + ac + bc)

S п.п. = 2(30 * 12 + 30 *5 + 12 * 5) = 2 * (360 + 150 + 60) = 2 * 570 = 1140 см2.

Ответ: площадь полной поверхности параллелепипеда = 1140 см2.

Пусть все необходимые формулы будут под рукой в нужный момент. Сохраняйте табличку-шпаргалку на гаджет или распечатайте ее и храните в учебнике.

V параллелепипеда	V = a * b * h
	V = S осн * h
S боковой поверхности	S б. п. = 2(ac + bc)
S полной поверхности	S п.п. = 2 (ab + ac + bc)
Диагональ параллелепипеда	d2 = a2+ b2 + c2

На уроках математики в современной школе Skysmart нет скучных учебников, надоевших задачек и неинтересных тетрадей. Ученики занимаются по интерактивному учебнику, чертят на настоящей онлайн-доске и решают занимательные примеры.

Математика может быть по-настоящему увлекательной. Записывайтесь на бесплатный вводный урок, чтобы проверить, так ли это на самом деле.

Урок математики 4 класс тема ««Объем. Единицы объема»

Государственное бюджетное общеобразовательное учреждение

«Средняя общеобразовательная школа №45

с углублённым изучением испанского языка»

Учитель: Болотина Е.В.

Класс: 4-Б

Тема урока: «Объем. Единицы объема»

Тип урока: урок изучения нового материала.

Цели урока:

1. Формировать представления детей об объёме через практическую исследовательскую деятельность.

2. Совершенствовать вычислительные навыки, умение классифицировать, сравнивать: числа, геометрические фигуры и тела.

3. Развивать внимание, пространственное и конструктивное мышление, математическую речь.

4. Воспитывать творческую активность, чувство взаимопомощи в совместной

деятельности.

5. Повторить знания учащихся о величинах , изученных ранее

6.Учить решать геометрические задачи.

Мыслительные операции: анализ, аналогия, сравнение, синтез, обобщение.

Технические средства обучения: компьютер, мультимедийная система.

Демонстрационный материал: презентация «Объём. Единицы объёма», геометрические фигуры и тела.

Раздаточный материал: карточки для индивидуальной и групповой работы.

Ход урока.

1.Орг. момент (Слайд2)

Сегодня мы откроем тайну –

Секрет математических чудес необычайных

Орешек знанья тверд, но все же

Мы начинаем наш урок

И я хочу, чтобы каждый из вас

В конце урока мог сказать:

«Сегодня я искал, творил.

И знания новые открыл,

И то, что мне пришлось узнать,

могу теперь я применять»

2.Актуализация знаний (Слайд 3)

Прочитайте выражения и найдите их значения

И (10 + 8) ·10

Н 900 –(3 ·100)

В 60 · 10 : 6

И (700:100) · 10

Л (30:3) · 5

Е 100 — 800 :10

Ы 7 · 8 · 10

Ч (200 +80) :1

Взаимопроверка тетрадей. Проверьте результаты. (На слайде появляются буквы)

Расположите значение выражений в порядке убывания и расшифруйте слово. Слайд 4

Расшифруйте слово: ВЕЛИЧИНА

Что мы называем величиной?

Величина – это то, что можно измерить и результат измерения выразить числом. Всё, что можно измерить и исчислить (мат. физ., Словарь Ушакова.)

Какие способы измерения величин вы знаете (на глаз, с помощью измерения)

Что надо знать, чтобы измерить величину? (Чтобы измерить величину, надо знать единицы измерения этой величины.)

Назовите величины, которые вы знаете и их единицы измерения.

Индивидуальная работа на карточках.

Соотнесите величину и единицу измерения этой величины

Масса г кг

Длина мм см дм м км

Площадь мм ² см ² дм² м² а га

Назовите единицы площади? Длины? Массы?

3.Открытие новых знаний

Что это? ( Учитель показывает квадрат и куб, используя конструктор)

Что можете рассказать об этих предметах.

Что у них общего и различного?

Какие величины мы можем измерить?

Назовите геометрическую фигуру, геометрическое тело.

Сегодня познакомимся с новой геометрической величиной. Подберите однокоренное слово к слову объёмная, это слово имя существительное. С какой величиной мы познакомимся? (С ОБЪЕМОМ. ) Слайд 5

Как вы думаете, где мы сможем находить объем?

Конечно, объем находим только в объемных (геометрических) телах.

Сегодня мы не только узнаем, что такое объем, но и научимся его измерять и узнаем единицы измерения объема. В этом нам поможет учебник.

4. Работа с учебником стр.32 №118,119.

Слайд 6

Посмотрите на первый рисунок и расскажите о паре, пользуясь, планом.

Что изображено?

Что является меркой? Что измеряет мерка? (отрезок)

Как она называется? (сантиметр) Назовите величину. (длина)

Посмотрите на второй рисунок.

Что измеряет мерка? (большой квадрат)

Как она называется? (квадратный сантиметр) Назовите величину (площадь)

Посмотрите на третий рисунок.

Что измеряет мерка? (большой кубик)

Как она называется? (мы не знаем) Назовите величину (объём).

Поразмышляем (с опорой на слайды №8, 9)

Как называется мерка, которой можно измерить объемное тело (кубический см) (учитель показывает мерку из пластилина.)

Как появилась эта мерка? Если затрудняетесь, найдите ответ в правиле. Объясните (учебник стр.33).

Длину 1см умножили на ширину 1 см, умножили на высоту 1 см

1см · 1 см · 1 см = 1 см ³

Таким образом, мы познакомились с новым понятием объем, который обозначается латинской буквой V.

№119 Догадайтесь, чему равен объём данного куба. Что для этого надо сделать? Надо измерить длину ребра куба. Она равна 1дм. Значит объём этого куба равен 1 кубическому дециметру ( 1дм³ )

5. Работа по закреплению знаний

Работа в парах. Решение задачи №120

Найдите объём фигуры, если ребро каждого куба равно 1 см.

12 см³ 2) 13 см³ 3) 14 см³ 4) 16 см³

6. Физминутка.

7. Объём параллелепипеда. Слайд 13.

Как называется эти многогранники? (параллелепипед и куб)

Фигуры сложили из мерок — 1см³ . Как сосчитать мерки, чтобы узнать объём каждой фигуры? Слайд 14.

Покажите, что мы можем найти и измерить в этом геометрическом теле?

Покажите длину, ширину, высоту. Эти измерения нам нужны для нахождения объема. Как вычислить объём прямоугольного параллелепипеда? Что для этого мы должны сделать? Слайд 15.

Если это куб, сколько надо выполнить измерений. (Всего одно, так как все мерки будут одинаковы, так как куб состоит из граней — одинаковых квадратов.)

Запись на доске:

Задача №1

а= 5 см V= а · в · с

в=3см V= 5 · 3 · 4= 60см³

с=4см

Найти V-?

Ответ: V= 60см³

8. Работа в группах.

Заполните таблицу и прочтите, как вы сегодня работали.

9. Творческая работа в парах.

Составить свою задачу на нахождение объёма параллелепипеда.

10.Итог урока.

Блиц-опрос Слайд 18.

Проверим, как это поняли.

Выбери правильное рассуждение, и обведите букву правильного ответа

1.Объём – это…

А) величина

Б) геометрическая фигура

В) единица измерения

2.Найди формулу нахождения объема

А) V= а · в

Б) V= а · в · с

В) V= а · в · с · d

3.Назови единицу измерений объема

А) см

Б) см²

В) см³

11.Рефлексия.

Слайд 20 Мы сегодня, узнавая новое, тоже заполняли объем своих знаний. Нарисуй солнышко, если на уроке ты узнал новое и тебе было всё понятно. Нарисуй тучку, если на уроке было много непонятного и ты устал. Нарисуй звёздочку, если ты ещё хочешь узнать что-нибудь новое об объёме.

Приложение.

КАРТОЧКА № 1

Соотнесите величину и

единицу измерения этой величины

МАССА см ²

см

кг

ПЛОЩАДЬ дм²

м²

км

дм

ДЛИНА м

мм ²

мм

Блиц – опрос

А Б В

А Б В

А Б В

^{_______________________________________________}

Оцени свою работу на уроке

1 группа

2 группа

ил

3 группа

4 группа

5 группа

ыл

Какой буквой обозначается объём? | Полезная информация для всех

Объм обозначается всегда буквой V.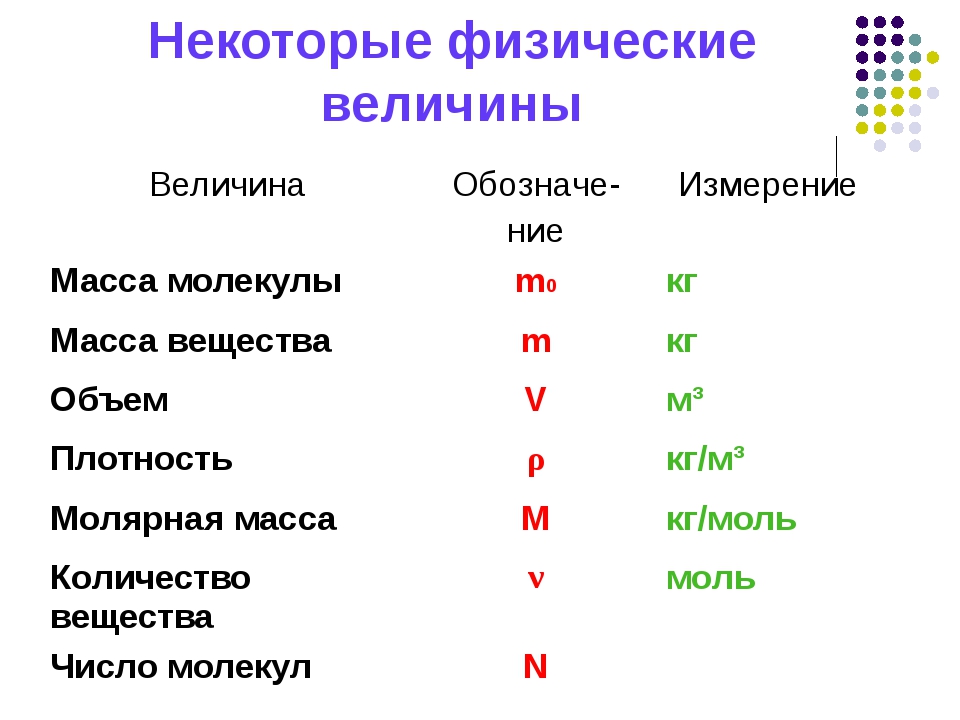

А измеряется в кубических метрах (м3), в кубических сантиметрах (см3) и т.д.

Ниже приведена формула объма куба и запоминается она легко.

Как найти объм цилиндра, конуса и шара тоже показано на рисунке.

Объем — это пространство, занимаемое определенным телом.

В различных формулах (например, физических или математических) объем всегда обозначают заглавной латинской буквой V. В переводе с латыни volume обозначает quot;объемquot;, именно поэтому объем принято обозначать как V.

Объем в химических, математических, физических формулах принято обозначать заглавной латинской буквой V.

Единица измерения объема в системе СИ — это кубический метр, другие единицы измерения — это кубические сантиметры, кубические миллиметры, литры (кубические дециметры), пинта, баррель, галлон, кубический дюйм и другие.

Обозначение объема в физике

В физике и других науках за величину объема принята буква quot;Vquot;.

В химии, математике и остальных науках принят этот же символ.

Объем везде измеряется в таких величинах как: куб.метр(СИ), куб.см, куб.мм, куб.км.

Для начала поймм что же это такое объм. По существу — это вместимость геометрческого тела, которое ограничено замкнутой поверхностью. Буква же, которая обозначает его пишется V. А измеряется объм в м3 и естественно всех производных от него.

в стандартной системе обозначений величина объема обозначается латинской буквой V. иногда можно встретить и маленькую букву v. это тоже объем, но другого толка — маленькой буквой обозначается номинальный объем.

Наиболее частое обозначение объема в задачах по физике, химии и по другим подобным дисциплинам — буква quot;Vquot;. Такое обозначение принято у всех, сложилось историчски, хоть и является весьма условным символом.

Объемом обладает любое тело, которое имеет три измерения, то есть является плоской фигурой. Определить можно объем любого тела, простого по математическим формулам, образованного кривой линией по интегралам, а реального произвольного тела по методу Архимеда или вычислив плотность тела и его массу. Обозначают объем латинской буквой V, и измеряют в кубических метрах, сантиметрах или миллиметрах. Впрочем есть внесистемные единицы объема — литр, ведро, пинта, галлон. Интересно, что тела одного объема могут весить абсолютно по разному, в зависимости от их плотности. Вот какую массу будут иметь кубический сантиметр разного вещества:

По моему (если я точно помню) объм всегда обозначался буквой quot;Vquot;.

Насколько я помню из школьного курса геометрии, объем обозначается буквой V всегда. Кроме того, объем требовался на физике и химии и везде объем обозначался именно этой буквой. Кстати, для справки или для напоминания, единицы измерения объема = метры кубические

Для того, что бы количественно охарактеризовать пространство, которое занимает вещество или тело, используется объм.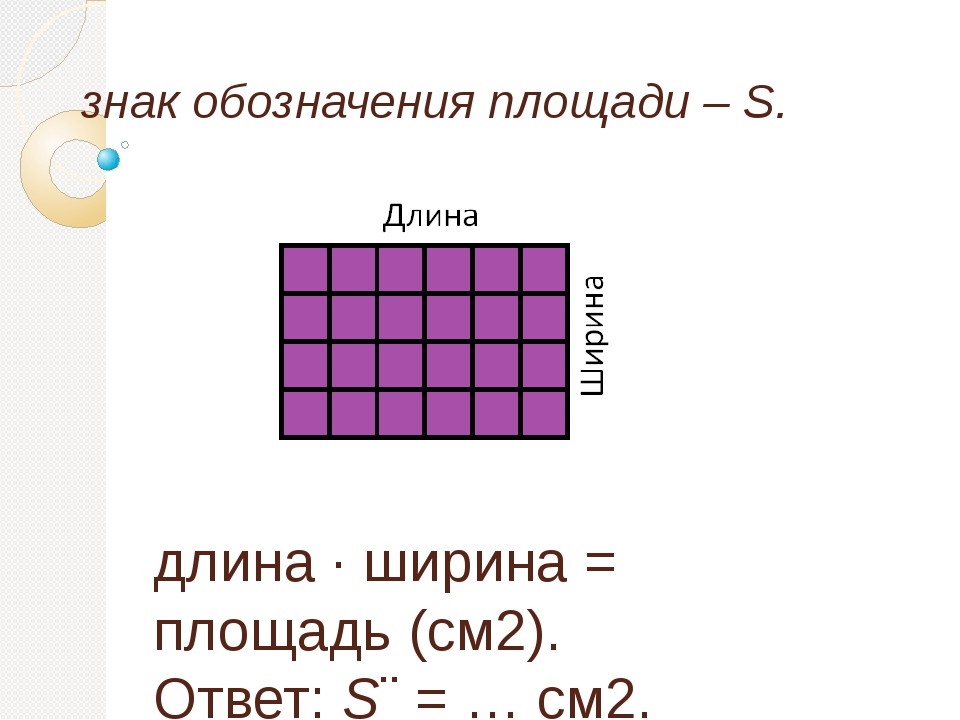 Эту величина в физике и других науках принято обозначать буквой V. В системе СИ е измеряют с помощью метра кубического и его производных. Есть ещ и внесистемные единицы измерения: баррель, галлон.

Периметр, площадь и объем

Данный материал содержит геометрические фигуры с измерениями. Приведённые измерения являются приблизительными и могут не совпадать с измерениями в реальной жизни.

Периметр геометрической фигуры

Периметр геометрической фигуры — это сумма всех её сторон. Чтобы вычислить периметр, нужно измерить каждую сторону и сложить результаты измерений.

Вычислим периметр следующей фигуры:

Это прямоугольник. Детальнее мы поговорим об этой фигуре позже. Сейчас просто вычислим периметр этого прямоугольника. Длина его равна 9 см, а ширина 4 см.

У прямоугольника противоположные стороны равны. Это видно на рисунке. Если длина равна 9 см, а ширина равна 4 см, то противоположные стороны будут равны 9 см и 4 см соответственно:

Найдём периметр.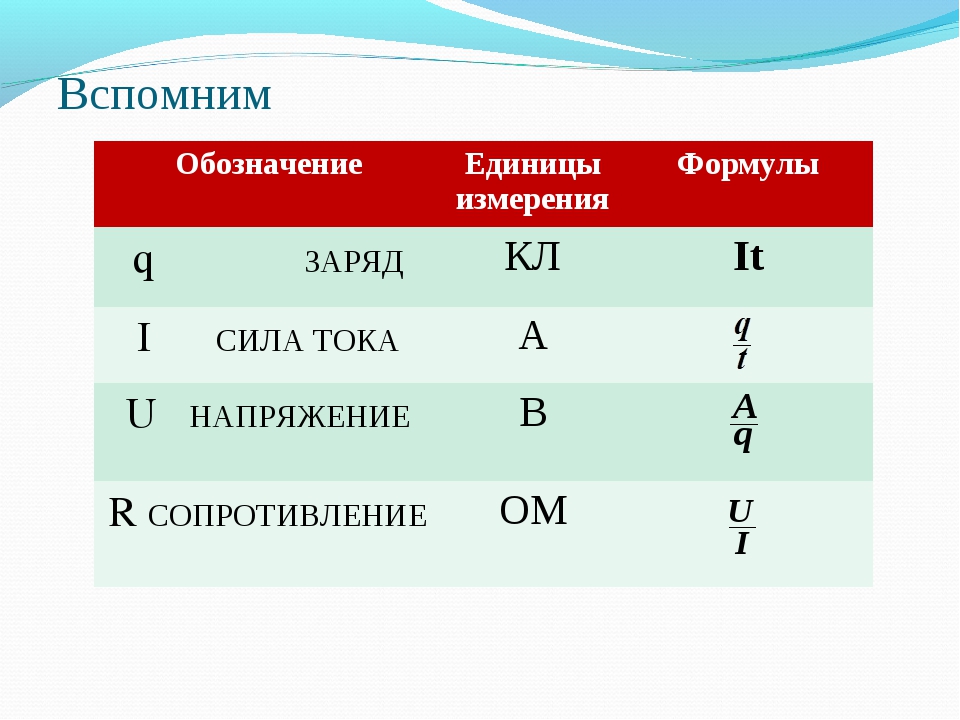 Для этого сложим все стороны. Складывать их можно в любом порядке, поскольку от перестановки мест слагаемых сумма не меняется. Периметр часто обозначается заглавной латинской буквой P (англ. perimeters). Тогда получим:

P = 9 см + 4 см + 9 см + 4 см = 26 см.

Поскольку у прямоугольника противоположные стороны равны, нахождение периметра записывают короче — складывают длину и ширину, и умножают её на 2, что будет означать «повторить длину и ширину два раза»

P = 2 × (9 + 4) = 18 + 8 = 26 см.

Квадрат это тот же прямоугольник, но у которого все стороны равны. Например, найдём периметр квадрата со стороной 5 см. Фразу «со стороной 5 см» нужно понимать как «длина каждой стороны квадрата равна 5 см»

Чтобы вычислить периметр, сложим все стороны:

P = 5 см + 5 см + 5 см + 5 см = 20 см

Но поскольку все стороны равны, вычисление периметра можно записать в виде произведения. Сторона квадрата равна 5 см, и таких сторон 4. Тогда эту сторону, равную 5 см нужно повторить 4 раза

P = 5 см × 4 = 20 см

Площадь геометрической фигуры

Площадь геометрической фигуры — это число, которое характеризует размер данной фигуры.

Следует уточнить, что речь в данном случае идёт о площади на плоскости. Плоскостью в геометрии называют любую плоскую поверхность, например: лист бумаги, земельный участок, поверхность стола.

Площадь измеряется в квадратных единицах. Под квадратными единицами подразумевают квадраты, стороны которых равны единице. Например, 1 квадратный сантиметр, 1 квадратный метр или 1 квадратный километр.

Измерить площадь какой-нибудь фигуры означает выяснить сколько квадратных единиц содержится в данной фигуре.

Например, площадь следующего прямоугольника равна трём квадратным сантиметрам:

Это потому что в данном прямоугольнике содержится три квадрата, каждый из которых имеет сторону, равную одному сантиметру:

Справа представлен квадрат со стороной 1 см (он в данном случае является квадратной единицей).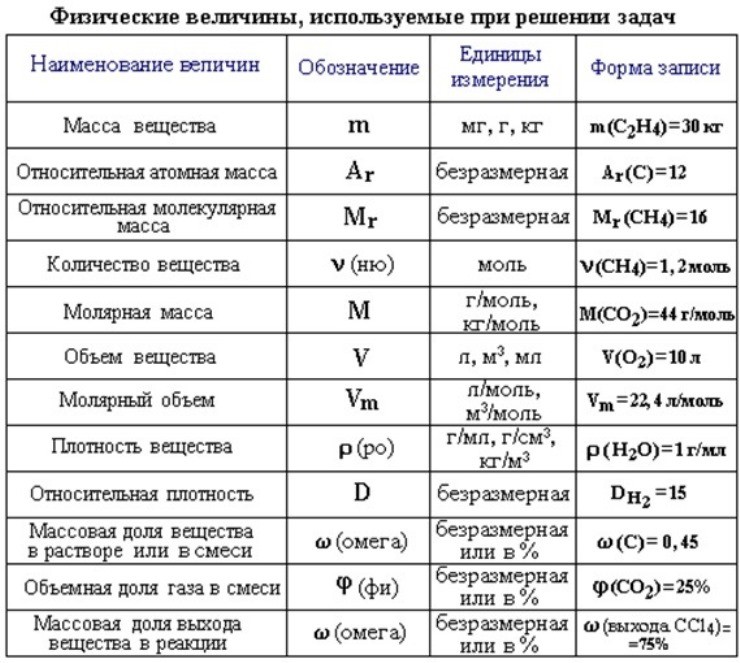 Если посмотреть сколько раз этот квадрат входит в прямоугольник, представленный слева, то обнаружим, что он входит в него три раза.

Следующий прямоугольник имеет площадь, равную шести квадратным сантиметрам:

Это потому что в данном прямоугольнике содержится шесть квадратов, каждый из которых имеет сторону, равную одному сантиметру:

Допустим, потребовалось измерить площадь следующей комнаты:

Определимся в каких квадратах будем измерять площадь. В данном случае площадь удобно измерить в квадратных метрах:

Итак, наша задача состоит в том, чтобы определить сколько таких квадратов со стороной 1 м содержится в исходной комнате. Заполним этим квадратом всю комнату:

Видим, что квадратный метр содержится в комнате 12 раз. Значит, площадь комнаты составляет 12 квадратных метров.

Площадь прямоугольника

В предыдущем примере мы вычислили площадь комнаты, последовательно проверив сколько раз в ней содержится квадрат, сторона которого равна одному метру. Площадь составила 12 квадратных метров.

Комната представляла собой прямоугольник. Площадь прямоугольника можно вычислить перемножив его длину и ширину.

Чтобы вычислить площадь прямоугольника, нужно перемножить его длину и ширину.

Вернёмся к предыдущему примеру. Допустим, мы измерили длину комнаты рулеткой и оказалось, что длина составила 4 метра:

Теперь измерим ширину. Пусть она составила 3 метра:

Умножим длину (4 м) на ширину (3 м).

4 × 3 = 12

Как и в прошлый раз получаем двенадцать квадратных метров. Это объясняется тем, что измерив длину, мы тем самым узнаём сколько раз можно уложить в эту длину квадрат со стороной, равной одному метру. Уложим четыре квадрата в эту длину:

Затем мы определяем сколько раз можно повторить эту длину с уложенными квадратами. Это мы узнаём, измерив ширину прямоугольника:

Площадь квадрата

Квадрат это тот же прямоугольник, но у которого все стороны равны. Например, на следующем рисунке представлен квадрат со стороной 3 см. Фраза «квадрат со стороной 3 см» означает, что все стороны равны 3 см

Площадь квадрата вычисляется таким же образом, как и площадь прямоугольника — длину умножают на ширину.

Вычислим площадь квадрата со стороной 3 см. Умножим длину 3 см на ширину 3 см

3 × 3 = 9

В данном случае требовалось узнать сколько квадратов со стороной 1 см содержится в исходном квадрате. В исходном квадрате содержится девять квадратов со стороной 1 см. Действительно, так оно и есть. Квадрат со стороной 1 см, входит в исходный квадрат девять раз:

Умножив длину на ширину, мы получили выражение 3 × 3, а это есть произведение двух одинаковых множителей, каждый из которых равен 3. Иными словами выражение 3 × 3 представляет собой вторую степень числа 3. А значит процесс вычисления площади квадрата можно записать в виде степени 3².

Поэтому вторую степень числа называют квадратом числа. При вычислении второй степени числа a, человек тем самым находит площадь квадрата со стороной a. Операцию возведения числа во вторую степень по другому называют возведением в квадрат.

Обозначения

Площадь обозначается заглавной латинской буквой S (англ. Square — квадрат). Тогда площадь квадрата со стороной a см будет вычисляться по следующему правилу

S = a²

где a — длина стороны квадрата. Вторая степень указывает на то, что происходит перемножение двух одинаковых сомножителей, а именно длины и ширины. Ранее было сказано, что у квадрата все стороны равны, а значит равны длина и ширина квадрата, выраженные через букву a.

Если задача состоит в том, чтобы определить сколько квадратов стороной 1 см содержится в исходном квадрате, то в качестве единиц измерения площади нужно указывать см². Это обозначение заменяет словосочетание «квадратный сантиметр».

Например, вычислим площадь квадрат со стороной 2 см.

Значит, квадрат со стороной 2 см, имеет площадь, равную четырём квадратным сантиметрам:

Если задача состоит в том, чтобы определить сколько квадратов со стороной 1 м содержится в исходном квадрате, то в качестве единиц измерения нужно указывать м². Это обозначение заменяет словосочетание «квадратный метр».

Вычислим площадь квадрата со стороной 3 метра

Значит, квадрат со стороной 3 м, имеет площадь равную девяти квадратным метрам:

Аналогичные обозначения используются при вычислении площади прямоугольника. Но длина и ширина прямоугольника могут быть разными, поэтому они обозначаются через разные буквы, например a и b. Тогда площадь прямоугольника, длиной a и шириной b вычисляется по следующему правилу:

S = a × b

Как и в случае с квадратом, единицами измерения площади прямоугольника могут быть см², м², км². Эти обозначения заменяют словосочетания «квадратный сантиметр», «квадратный метр», «квадратный километр» соответственно.

Например, вычислим площадь прямоугольника, длиной 6 см и шириной 3 см

Значит, прямоугольник длиной 6 см и шириной 3 см имеет площадь, равную восемнадцати квадратным сантиметрам:

В качестве единицы измерения допускается использовать словосочетание «квадратных единиц». Например, запись S = 3 кв.ед означает, что площадь квадрата или прямоугольника равна трём квадратам, каждый из которых имеет единичную сторону (1 см, 1 м или 1 км).

Перевод единиц измерения площади

Единицы измерения площади можно переводить из одной единицы измерения в другую. Рассмотрим несколько примеров:

Пример 1. Выразить 1 квадратный метр в квадратных сантиметрах.

1 квадратный метр это квадрат со стороной 1 м. То есть все четыре стороны имеют длину, равную одному метру.

Но 1 м = 100 см. Тогда все четыре стороны тоже имеют длину, равную 100 см

Вычислим новую площадь этого квадрата. Умножим длину 100 см на ширину 100 см или возведём в квадрат число 100

S = 100² = 10 000 см²

Получается, что на один квадратный метр приходится десять тысяч квадратных сантиметров.

1 м² = 10 000 см²

Это позволяет в будущем умножить любое количество квадратных метров на 10 000 и получить площадь, выраженную в квадратных сантиметрах.

Чтобы перевести квадратные метры в квадратные сантиметры, нужно количество квадратных метров умножить на 10 000.

А чтобы перевести квадратные сантиметры в квадратные метры, нужно наоборот количество квадратных сантиметров разделить на 10 000.

Например, переведём 100 000 см² в квадратные метры. Рассуждать в этом случае можно так: «если 10 000 см² это один квадратный метр, то сколько раз 100 000 см² будут содержать по 10 000 см²»

100 000 см² : 10 000 см² = 10 м²

Другие единицы измерения можно переводить таким же образом. Например, переведём 2 км² в квадратные метры.

Один квадратный километр это квадрат со стороной 1 км. То есть все четыре стороны имеют длину, равную одному километру. Но 1 км = 1000 м. Значит, все четыре стороны квадрата также равны 1000 м. Найдём новую площадь квадрата, выраженную в квадратных метрах. Для этого умножим длину 1000 м на ширину 1000 м или возведём в квадрат число 1000

S = 1000² = 1 000 000 м²

Получается, что на один квадратный километр приходится один миллион квадратных метров:

1 км² = 1 000 000 м²

Это позволяет в будущем умножить любое количество квадратных километров на 1 000 000 и получить площадь, выраженную в квадратных метрах.

Чтобы перевести квадратные километры в квадратные метры, нужно количество квадратных километров умножить на 1 000 000.

Итак, вернёмся к нашей задаче. Требовалось перевести 2 км² в квадратные метры. Умножим 2 км² на 1 000 000

2 км² × 1 000 000 = 2 000 000 м²

А чтобы перевести квадратные метры в квадратные километры, нужно наоборот количество квадратных метров разделить на 1 000 000.

Например, переведём 3 500 000 м² в квадратные километры. Рассуждать в этом случае можно так: «если 1 000 000 м² это один квадратный километр, то сколько раз 3 500 000 м² будут содержать по 1 000 000 м²»

3 500 000 м² : 1 000 000 м² = 3,5 км²

Пример 2. Выразить 7 м² в квадратных сантиметрах.

Умножим 7 м² на 10 000

7 м² = 7 м² × 10 000 = 70 000 см²

Пример 3. Выразить 5 м² 13 см² в квадратных сантиметрах.

5 м² 13 см² = 5 м² × 10 000 + 13 см² = 50 013 см²

Пример 4. Выразить 550 000 см² в квадратных метрах.

Узнаем сколько раз 550 000 см² содержит по 10 000 см². Для этого разделим 550 000 см² на 10 000 см²

550 000 см² : 10 000 см² = 55 м²

Пример 5. Выразить 7 км² в квадратных метрах.

Умножим 7 км² на 1 000 000

7 км² × 1 000 000 = 7 000 000 м²

Пример 6. Выразить 8 500 000 м² в квадратных километрах.

Узнаем сколько раз 8 500 000 м² содержит по 1 000 000 м². Для этого разделим 8 500 000 м² на 1 000 000 м²

8 500 000 м² × 1 000 000 м² = 8,5 км²

Единицы измерения площади земельных участков

Площади небольших земельных участков удобно измерять в квадратных метрах.

Площади более крупных земельных участков измеряются в арах и гектарах.

Ар (сокращённо: a) — это площадь равная ста квадратным метрам (100 м²). В виду частого распространения такой площади (100 м²) она стала использоваться, как отдельная единица измерения.

Например, если сказано что площадь какого-нибудь поля составляет 3 а, то нужно понимать, что это три квадрата площадью 100 м² каждый, то есть:

3 а = 100 м² × 3 = 300 м²

В народе ар часто называют соткой, поскольку ар равен квадрату, площадью 100 м². Примеры:

1 сотка = 100 м²

2 сотки = 200 м²

10 соток = 1000 м²

Гектар (сокращенно: га) — это площадь, равная 10 000 м². Например, если сказано что площадь какого-нибудь леса составляет 20 гектаров, то нужно понимать, что это двадцать квадратов площадью 10 000 м² каждый, то есть:

20 га = 10 000 м² × 20 = 200 000 м²

Прямоугольный параллелепипед и куб

Прямоугольный параллелепипед — это геометрическая фигура, состоящая из грáней, рёбер и вершин. На рисунке показан прямоугольный параллелепипед:

Желтым цветом показаны грáни параллелепипеда, чёрным цветом — рёбра, красным — вершины.

Прямоугольный параллелепипед обладает длиной, шириной и высотой. На рисунке показано где длина, ширина и высота:

Параллелепипед, у которого длина, ширина и высота равны между собой, называется кубом. На рисунке показан куб:

Объём геометрической фигуры

Объём геометрической фигуры — это число, которое характеризует вместимость данной фигуры.

Объём измеряется в кубических единицах. Под кубическими единицами подразумевают кубы длиной 1, шириной 1 и высотой 1. Например, 1 кубический сантиметр или 1 кубический метр.

Измерить объём какой-нибудь фигуры означает выяснить сколько кубических единиц вмещается в данную фигуру.

Например, объём следующего прямоугольного параллелепипеда равен двенадцати кубическим сантиметрам:

Это потому что в данный параллелепипед вмещается двенадцать кубов длиной 1 см, шириной 1 см и высотой 1 см:

Объём обозначается заглавной латинской буквой V. Одна из единиц измерения объема это кубический сантиметр (см³). Тогда объём V рассмотренного нами параллелепипеда равен 12 см³

V = 12 см³

Объём любого параллелепипеда вычисляют следующим образом: перемножают его длину, ширину и высоту .

Объём прямоугольного параллелепипеда равен произведению его длины, ширины и высоты.

V = abc

где, a — длина, b — ширина, c — высота

Так, в предыдущем примере мы визуально определили, что объём параллелепипеда равен 12 см³. Но можно измерить длину, ширину и высоту данного параллелепипеда и перемножить результаты измерений. Мы получим тот же результат

Объём куба вычисляется таким же образом, как и объём прямоугольного параллелепипеда — перемножают длину, ширину и высоту.

Например, вычислим объём куба, длина которого 3 см. У куба длина, ширина и высота равны между собой. Если длина равна 3 см, то равны этим же трём сантиметрам ширина и высота куба:

Перемножаем длину, ширину, высоту и получаем объём, равный двадцати семи кубическим сантиметрам:

V = 3 × 3 × 3 = 27 см³

Действительно, в исходный куб вмещается 27 кубиков длиной 1 см

При вычислении объёма данного куба мы перемножили длину, ширину и высоту. Получилось произведение 3 × 3 × 3. Это есть произведение трёх сомножителей, каждый из которых равен 3. Иными словами, произведение 3 × 3 × 3 является третьей степенью числа 3 и может быть записано в виде 3³.

V = 3³ = 27 см³

Поэтому третью степень числа называют кубом числа. При вычислении третьей степени числа a, человек тем самым находит объём куба, длиной a. Операцию возведения числа в третью степень по другому называют возведением в куб.

Таким образом, объём куба вычисляется по следующему правилу:

V = a³

Где a — длина куба.

Кубический дециметр. Кубический метр

Не все объекты нашего мира удобно измерять в кубических сантиметрах. Например, объём комнаты или дома удобнее измерять в кубических метрах (м³). А объём бака, аквариума или холодильника удобнее измерять в кубических дециметрах (дм³).

Другое название одного кубического дециметра – один литр.

1 дм³ = 1 литр

Перевод единиц измерения объёма

Единицы измерения объёма можно переводить из одной единицы измерения в другую. Рассмотрим несколько примеров:

Пример 1. Выразить 1 кубический метр в кубических сантиметрах.

Один кубический метр это куб со стороной 1 м. Длина, ширина и высота этого куба равны одному метру.

Но 1 м = 100 см. Значит, длина, ширина и высота тоже равны 100 см

Вычислим новый объём куба, выраженный в кубических сантиметрах. Для этого перемножим его длину, ширину и высоту. Либо возведём число 100 в куб:

V = 100³ = 1 000 000 см³

Получается, что на один кубический метр приходится один миллион кубических сантиметров:

1 м³ = 1 000 000 см³

Это позволяет в будущем умножить любое количество кубических метров на 1 000 000 и получить объём, выраженный в кубических сантиметрах.

Чтобы перевести кубические метры в кубические сантиметры, нужно количество кубических метров умножить на 1 000 000.

А чтобы перевести кубические сантиметры в кубические метры, нужно наоборот количество кубических сантиметров разделить на 1 000 000.

Например, переведём 300 000 000 см³ в кубические метры. Рассуждать в этом случае можно так: «если 1 000 000 см³ это один кубический метр, то сколько раз 300 000 000 см³ будут содержать по 1 000 000 см³»

300 000 000 см³ : 1 000 000 см³ = 300 м³

Пример 2. Выразить 3 м³ в кубических сантиметрах.

Умножим 3 м³ на 1 000 000

3 м³ × 1 000 000 = 3 000 000 см³

Пример 3. Выразить 60 000 000 см³ в кубических метрах.

Узнаем сколько раз 60 000 000 см³ содержит по 1 000 000 см³. Для этого разделим 60 000 000 см³ на 1 000 000 см³

60 000 000 см³ : 1 000 000 см³ = 60 м³

Вместимость бака, банки или канистры измеряют в литрах. Литр это тоже единица измерения объема. Один литр равен одному кубическому дециметру.

1 литр = 1 дм³

Например, если вместимость банки составляет 1 литр, это значит что объём этой банки составляет 1 дм³. При решении некоторых задач может быть полезным умение переводить литры в кубические дециметры и наоборот. Рассмотрим несколько примеров.

Пример 1. Перевести 5 литров в кубические дециметры.

Чтобы перевести 5 литров в кубические дециметры, достаточно умножить 5 на 1

5 л × 1 = 5 дм³

Пример 2. Перевести 6000 литров в кубические метры.

Шесть тысяч литров это шесть тысяч кубических дециметров:

6000 л × 1 = 6000 дм³

Теперь переведём эти 6000 дм³ в кубические метры.

Длина, ширина и высота одного кубического метра равны 10 дм

Если вычислить объём этого куба в дециметрах, то получим 1000 дм³

V = 10³= 1000 дм³

Получается, что одна тысяча кубических дециметров соответствует одному кубическому метру. А чтобы определить сколько кубических метров соответствуют шести тысячамл кубических дециметров, нужно узнать сколько раз 6 000 дм³ содержит по 1 000 дм³

6 000 дм³ : 1 000 дм³ = 6 м³

Значит, 6000 л = 6 м³.

Таблица квадратов

В жизни часто приходиться находить площади различных квадратов. Для этого каждый раз требуется возводить исходное число во вторую степень.

Квадраты первых 99 натуральных чисел уже вычислены и занесены в специальную таблицу, называемую таблицей квадратов.

Первая строка данной таблицы (цифры от 0 до 9) это единицы исходного числа, а первый столбец (цифры от 1 до 9) это десятки исходного числа.

Например, найдём квадрат числа 24 по данной таблице. Число 24 состоит из цифр 2 и 4. Точнее, число 24 состоит из двух десятков и четырёх единиц.

Итак, выбираем цифру 2 в первом столбце таблицы (столбце десятков), а цифру 4 выбираем в первой строке (строке единиц). Затем, двигаясь вправо от цифры 2 и вниз от цифры 4, найдём точку пересечения. В результате окажемся на позиции, где располагается число 576. Значит, квадрат числа 24 есть число 576

24² = 576

Таблица кубов

Как и в ситуации с квадратами, кубы первых 99 натуральных чисел уже вычислены и занесены в таблицу, называемую таблицей кубов.

Куб числа по таблице определяется таким же образом, как и квадрат числа. Например, найдём куб числа 35. Это число состоит из цифр 3 и 5. Выбираем цифру 3 в первом столбце таблицы (столбце десятков), а цифру 5 выбираем в первой строке (строке единиц). Двигаясь вправо от цифры 3 и вниз от цифры 5, найдём точку пересечения. В результате окажемся на позиции, где располагается число 42875. Значит, куб числа 35 есть число 42875.

35³ = 42875

Задания для самостоятельного решения

Задача 1. Длина прямоугольника составляет 6 см, а ширина 2 см. Найдите периметр.

Решение

P = 2(a + b)

a = 6, b = 2
P = 2(6 + 2) = 12 + 4 = 16 см

Ответ: периметр прямоугольника равен 16 см.

Задача 2. Длина прямоугольника составляет 6 см, а ширина 2 см. Найдите площадь.

Решение

S = ab
a = 6, b = 2
S = 6 × 2 = 12 см²

Ответ: площадь равна 12 см².

Задача 3. Площадь прямоугольника составляет 12 см². Длина составляет 6 см. Найдите ширину прямоугольника.

Решение

S = ab
S = 12, a = 6, b = x
12 = 6 × x
x = 2

Ответ: ширина прямоугольника составляет 2 см.

Задача 4. Вычислите площадь квадрата со стороной 8 см

Решение

S = a²
a = 8
S = 8²= 64 см²
Ответ: площадь квадрата со стороной 8 см равна 64 см²

Задача 5. Вычислите объем прямоугольного параллелепипеда, длина которого 6 см, ширина 4 см, высота 3 см.

Решение

V = abc
a = 6, b = 4, c = 3
V = 6 × 4 × 3 = 72 см³.

Ответ: объем прямоугольного параллелепипеда, длина которого 6 см, ширина 4 см, высота 3 см равен 72 см³

Задача 6. Объем прямоугольного параллелепипеда составляет 200 см³. Найдите высоту параллелепипеда, если его длина равна 10 см, а ширина 5 см

Решение

V = abc
V = 200, a = 10, b = 5, c = x
200 = 10 × 5 × x
200 = 50x
x = 4

Ответ: высота прямоугольного параллелепипеда равна 4 см.

Задача 7. Площади земельного участка, засеянные пшеницей и льном, пропорциональны числам 4 и 5. На какой площади засеяна пшеница, если под льном засеяно 15 га

Решение

Число 4 отражает площадь, засеянную пшеницей. А число 5 отражает площадь, засеянную льном.
Сказано что площади, засеянные пшеницей и льном пропорциональны этим числам.

Проще говоря, во сколько раз изменяются числа 4 или 5, во сколько же раз изменится и площадь, которая засеяна пшеницей или льном. Льном засеяно 15 га. То есть число 5, которое отражает площадь, засеянную льном, изменилось в 3 раза.

Тогда число 4, которое отражает площадь засеянную пшеницей, нужно увеличить в три раза

4 × 3 = 12 га

Ответ: пшеницей засеяно 12 га.

Задача 8. Длина зернохранилища 42 м, ширина составляет длины, а высота – 0,1 длины. Определите сколько тонн зерна вмещает зернохранилище, если 1 м³ его весит 740 кг.

Решение

a — длина
b — ширина
c — высота

a = 42 м
b = м
c = 42 × 0,1 = 4,2 м

Определим объем зернохранилища:

V = abc = 42 × 30 × 4,2 = 5292 м³

Определите сколько тонн зерна вмещает зернохранилище:

5292 × 740 = 3916080 кг

Переведём килограммы в тонны:

Ответ: зернохранилище вмещает 3916,08 тонн зерна.

Задача 9. 12. Бассейн имеет форму прямоугольного параллелепипеда, длина которого равна 5,8 м, а ширина – 3,5 м. Две трубы наполняют его водой в течение 13 ч 32 мин., причём через одну из них вливается 25 л/мин, а через вторую – 0,75 этого количества. Определите высоту (глубину) бассейна.

Решение

Определим сколько литров в минуту вливается через вторую трубу:

25 л/мин × 0,75 = 18,75 л/мин

Определим сколько литров в минуту вливается в бассейн через обе трубы:

25 л/мин + 18,75 л/мин = 43,75 л/мин

Определим сколько литров воды будет залито в бассейн за 13 ч 32 мин

43,75 × 13 ч 32 мин = 43,75 × 812 мин = 35 525 л

1 л = 1 дм³

35 525 л = 35 525 дм³

Переведём кубические дециметры в кубические метры. Это позволит вычислит объем бассейна:

35 525 дм³ : 1000 дм³ = 35,525 м³

Зная объём бассейна можно вычислить высоту бассейна. Подставим в буквенное уравнение V=abc имеющиеся у нас значения. Тогда получим:

V = 35,525
a = 5.8
b = 3.5
c = x

35,525 = 5,8 × 3,5 × x
35,525 = 20,3 × x
x = 1,75 м

с = 1,75

Ответ: высота (глубина) бассейна составляет 1,75 м.

Понравился урок?
Вступай в нашу новую группу Вконтакте и начни получать уведомления о новых уроках

Возникло желание поддержать проект?
Используй кнопку ниже

Навигация по записям

Объём прямоугольного параллелепипеда — урок. Математика, 5 класс.

Уже известны единицы измерения длины, например:

мм,см,дм,м,км… — и другие.

Для фигур на плоскости измеряют площадь в соответствующих квадратных единицах измерения:

мм2,см2,дм2,м2,км2…

Для геометрических тел измеряют объём, и для этого необходимы единицы измерения.

Единицей измерения объёма служит объём куба, у которого все грани равны $1$ единице измерения длины:

мм3,см3,дм3,м3,км3…

Это кубический миллиметр, кубический сантиметр, кубический дециметр, кубический метр или даже кубический километр:

1км3=1000000000м3;1м3=1000дм3=1000000см3;1дм3=1000см3;1см3=1000мм3.

Часто для измерения объёма жидкости используют единицу измерения $1$ литр: 1 л =1000см3=1дм3.

Если измерять объём прямоугольного параллелепипеда, то можно представить, как маленькие кубики перекрывают прямоугольник в основании прямоугольного параллелепипеда.

Длины сторон прямоугольника определяют, сколько кубиков в ряду и сколько рядов с кубиками будет.

Если стороны равны, например, $3$ см и $4$ см, то прямоугольник перекрывается $3·4 = 12$ кубиками.

Высота параллелепипеда определяет, сколько таких слоёв с кубиками можно поставить.

Если высота прямоугольного параллелепипеда равна $3$ см, то всего получится $3$ слоя с кубиками. Итак, всего $3·3·4 = 36$ кубиков, или объём равен $36$ см³.

Значит, три измерения прямоугольного параллелепипеда позволяют посчитать, сколько всего кубиков поместилось в геометрическом теле, то есть вычислить объём прямоугольного параллелепипеда.

Пусть измерения прямоугольного параллелепипеда будут a, b и c единиц измерения.

Тогда объём $V = a·b·c$ кубических единиц измерения.

Как обозначается длина и ширина

Высота ширина длина — латинские обозначения: как правильно пишутся размеры и чем отличаются величины

Решая геометрические задачи, ученики сталкиваются с вопросом: как правильно обозначить те или иные части чертежа? Например, высоту треугольника, ширину прямоугольника, размеры бассейна. Подобные обозначения мы найдем и в физических задачах: длина маятника, высота, с которой тело начинает падать… Поэтому следует знать некоторые правила….

Как обозначаются различные параметры

В единой системе измерения используется обозначение латинскими буквами:

длину буквой l, если речь идет об одной прямой линии: маятнике, рычаге, отрезке, прямой. Но если речь идет о геометрической фигуре, например, прямоугольнике, то используется А,
высоту или глубину – h,
ширину – В.

Что такое система СИ, ученики узнают лишь в средней школе, поэтому обычно в младших классах специального обозначениям для этих величин не вводят.

Как обозначить глубину?

Почему же для высоты и глубины применяется одна и та же буква? Если вы построите чертеж параллелепипеда, то здесь вы отметите высоту фигуры.

А если составить чертеж прямоугольного бассейна того же размера, что и параллелепипед, то обозначается глубина. Таким образом, можно сказать, высота и глубина в этом случае будут одной величиной.

Внимание! Высота и глубина – две величины, которые обозначают один и тот же перпендикуляр, соединяющий две противоположные плоскости.

Понятие «глубина» встречается и в географии. На картах она отображается цветом. Если речь идет о водных просторах, то чем темнее синий, цвет, тем больше глубина, а если речь идет о суше, то низменности обозначаются темно-зеленым цветом.

В черчении эта величина обозначается литерой S. Она позволяет создать полное восприятие объекта иногда даже с одним видом.

Что бывает длинным

Что же такое длина и как обозначается этот показатель? Она указывает расстояние от точки до точки, то есть размер отрезка. В геометрических задачах его принято обозначать как А. В стереометрии ее могут обозначать и А, и l (например, в задачах, где встречается прямая, пересекающая плоскость).

В физике же длина маятника, плеча рычага и т.д. в «Дано» обозначается буквой l, так как речь идет об отдельной прямой.

Отличие длины от высоты

Длина – это величина, которая характеризует протяженность линии.

А высота – это перпендикуляр, опущенный на противолежащую плоскость.

То есть можно сделать вывод, что длина от высоты отличается тем, что является частью фигуры, совпадая с ее гранью, а высота получается в результате дополнительного построения на чертеже.

Высоту проводят для того, чтобы получить новые данные для решения задач, а также новых фигур в составе исходной.

Вот такой ширины

Ширина предмета необходима для того, чтобы понять форму как двумерного, так и трехмерного объекта. Как правило, она обозначается буквой В.

Измеряется ширина в метрах (по СИ). Но если предмет слишком мал, то для удобства используют более мелкие единицы измерения:

дециметры,
сантиметры,
миллиметры,
микрометры и т.д.

А если предмет слишком крупный, то пишутся такие приставки:

Кило- (10³),
Мега- (106),
Гига- (109),
Тера- (1012) и т.д.

Разумеется, такие крупные единицы измерения необходимы, например, для астрономии. Также они применяются в квантовой физике, микробиологии и так далее.

Как называются стороны прямоугольника?

В отличие от квадрата, стороны прямоугольника попарно равны и параллельны.

Это значит, что стороны, образующие углы различны.

Как правило, более длинную сторону прямоугольника называют длиной, а ширина прямоугольника это его короткая сторона.

Важно! Зная такие данные, как длина и ширина прямоугольника, можно найти его периметр, площадь, длину диагоналей и угол между ними. Вокруг прямоугольника всегда можно описать окружность. Эти свойства работают и в обратном направлении.

В чем измеряются размеры длины, ширины и высоты по СИ

По единой системе измерения длина, высота и ширина измеряются в метрах. Но иногда, если это дробное или многозначное число, для удобства в вычислениях используют кратные единицы измерения.

Для того чтобы знать, как правильно переводить единицы измерения в более крупные или же наоборот мелкие, необходимо знать значения приставок.

Дека 101,
Гекто 102,
Кило 103,
Мега 106,
Гига 109,
Деци – 10-1,
Санти – 10-2,
Милли – 10-3,
Микро 10-6,
Нано – 10-9.

После подсчетов эти единицы должны быть переведены в метры.

Существуют также внесистемные единицы, но они встречаются очень редко:

миля – 1,6 км,
фут – 12 дюймов – 0,3048 м,
ярд – 36 дюймов – 91,44 мм,
дюйм – 25,4 мм и т.д.

При решении задач такие единицы должны быть переведены в метры.

При выполнении геометрических заданий единицам измерения не уделяют особого внимания, главное, чтобы они были сопоставимы

(если вы производите подсчеты в сантиметрах, значит, все величины необходимо перевести в сантиметры).

А при решении физических задач ответ должен быть дан в метрах в соответствии с единой системой измерения.

Обозначения длины, ширины, высоты в геометрии

Измеряем геометрические параметры

Вывод

Теперь вы знаете, какой буквой обозначается длина, в чем измеряется ширина прямоугольника, и сможете сами объяснить любому, как обозначаются различные параметры.

Это интересно! Легкие правила округления чисел после запятой

tvercult.ru

Обозначение: высота, ширина, длина. Ширина

Построение чертежей — дело непростое, но без него в современном мире никак. Ведь чтобы изготовить даже самый обычный предмет (крошечный болт или гайку, полку для книг, дизайн нового платья и подобное), изначально нужно провести соответствующие вычисления и нарисовать чертеж будущего изделия. Однако часто составляет его один человек, а занимается изготовлением чего-либо по этой схеме другой.

Чтобы не возникло путаницы в понимании изображенного предмета и его параметров, во всем мире приняты условные обозначения длины, ширины, высоты и других величин, применяемых при проектировании. Каковы они? Давайте узнаем.

Величины

Площадь, длина, ширина, высота и другие обозначения подобного характера являются не только физическими, но и математическими величинами.

Единое их буквенное обозначение (используемое всеми странами) было уставлено в середине ХХ века Международной системой единиц (СИ) и применяется по сей день. Именно по этой причине все подобные параметры обозначаются латинскими, а не кириллическими буквами или арабской вязью. Чтобы не создавать отдельных трудностей, при разработке стандартов конструкторской документации в большинстве современных стран решено было использовать практически те же условные обозначения, что применяются в физике или геометрии.

Любой выпускник школы помнит, что в зависимости от того, двухмерная или трехмерная фигура (изделие) изображена на чертеже, она обладает набором основных параметров. Если присутствуют два измерения — это ширина и длина, если их три – добавляется еще и высота.

Итак, для начала давайте выясним, как правильно длину, ширину, высоту обозначать на чертежах.

Ширина

Как было сказано выше, в математике рассматриваемая величина является одним из трех пространственных измерений любого объекта, при условии что его замеры производятся в поперечном направлении. Так чем знаменита ширина? Обозначение буквой «В» она имеет. Об этом известно во всём мире. Причем, согласно ГОСТу, допустимо применение как заглавной, так и строчной латинских литер. Часто возникает вопрос о том, почему именно такая буква выбрана. Ведь обычно сокращение производится по первой букве латинского, греческого или английского названия величины. При этом ширина на английском будет выглядеть как «width».

Вероятно, здесь дело в том, что данный параметр наиболее широкое применение изначально имел в геометрии. В этой науке, описывая фигуры, часто длину, ширину, высоту обозначают буквами «а», «b», «с». Согласно этой традиции, при выборе литера «В» (или «b») была заимствована системой СИ (хотя для других двух измерений стали применять отличные от геометрических символы).

Большинство полагает, что это было сделано, дабы не путать ширину (обозначение буквой «B»/«b») с весом. Дело в том, что последний иногда именуется как «W» (сокращение от английского названия weight), хотя допустимо использование и других литер («G» и «Р»). Согласно международным нормам системы СИ, измеряется ширина в метрах или кратных (дольных) их единицах. Стоит отметить, что в геометрии иногда также допустимо использовать «w» для обозначения ширины, однако в физике и остальных точных науках такое обозначение, как правило, не применяется.

Длина

Как уже было указано, в математике длина, высота, ширина – это три пространственных измерения. При этом, если ширина является линейным размером в поперечном направлении, то длина — в продольном. Рассматривая ее как величину физики можно понять, что под этим словом подразумевается численная характеристика протяжности линий.

В английском языке этот термин именуется length. Именно из-за этого данная величина обозначается заглавной или строчной начальной литерой этого слова — «L». Как и ширина, длина измеряется в метрах или их кратных (дольных) единицах.

Высота

Наличие этой величины указывает на то, что приходится иметь дело с более сложным — трехмерным пространством. В отличие от длины и ширины, высота численно характеризует размер объекта в вертикальном направлении.

На английском она пишется как «height». Поэтому, согласно международным нормам, ее обозначают латинской литерой «Н»/«h». Помимо высоты, в чертежах иногда эта буква выступает и как глубины обозначение. Высота, ширина и длина – все все эти параметры измеряются в метрах и их кратных и дольных единицах (километры, сантиметры, миллиметры и т. п.).

Радиус и диаметр

Помимо рассмотренных параметров, при составлении чертежей приходится иметь дело и с иными.

Например, при работе с окружностями возникает необходимость в определении их радиуса. Так именуется отрезок, который соединяет две точки. Первая из них является центром. Вторая находится непосредственно на самой окружности. На латыни это слово выглядит как «radius». Отсюда и общепринятое сокращение: строчная или заглавная «R»/«r».

Чертя окружности, помимо радиуса часто приходится сталкиваться с близким к нему явлением – диаметром. Он также является отрезком, соединяющим две точки на окружности. При этом он обязательно проходит через центр.

Численно диаметр равен двум радиусам. По-английски это слово пишется так: «diameter». Отсюда и сокращение – большая или маленькая латинская буква «D»/«d». Часто диаметр на чертежах обозначают при помощи перечеркнутого круга – «Ø».

Хотя это распространенное сокращение, стоит иметь в виду, что ГОСТ предусматривает использование только латинской «D»/«d».

Толщина

Большинство из нас помнят школьные уроки математики. Ещё тогда учителя рассказывали, что, латинской литерой «s» принято обозначать такую величину, как площадь. Однако, согласно общепринятым нормам, на чертежах таким способом записывается совсем другой параметр – толщина.

Почему так? Известно, что в случае с высотой, шириной, длиной, обозначение буквами можно было объяснить их написанием или традицией. Вот только толщина по-английски выглядит как «thickness», а в латинском варианте — «crassities». Также непонятно, почему, в отличие от других величин, толщину можно обозначать только строчной литерой. Обозначение «s» также применяется при описании толщины страниц, стенок, ребер и так далее.

Периметр и площадь

В отличие от всех перечисленных выше величин, слово «периметр» пришло не из латыни или английского, а из греческого языка. Оно образовано от «περιμετρέο» («измерять окружность»). И сегодня этот термин сохранил свое значение (общая длина границ фигуры). Впоследствии слово попало в английский язык («perimeter») и закрепилось в системе СИ в виде сокращения буквой «Р».

Площадь — это величина, показывающая количественную характеристику геометрической фигуры, обладающей двумя измерениями (длиной и шириной). В отличие от всего перечисленного ранее, она измеряется в квадратных метрах (а также в дольных и кратных их единицах). Что касается буквенного обозначения площади, то в разных сферах оно отличается. Например, в математике это знакомая всем с детства латинская литера «S». Почему так – нет информации.

Некоторые по незнанию думают, что это связано с английским написанием слова «square». Однако в нем математическая площадь – это «area», а «square» — это площадь в архитектурном понимании. Кстати, стоит вспомнить, что «square» — название геометрической фигуры «квадрат». Так что стоит быть внимательным при изучении чертежей на английском языке. Из-за перевода «area» в отдельных дисциплинах в качестве обозначения применяется литера «А». В редких случаях также используется «F», однако в физике данная буква означает величину под названием «сила» («fortis»).

Другие распространенные сокращения

Обозначения высоты, ширины, длины, толщины, радиуса, диаметра являются наиболее употребляемыми при составлении чертежей. Однако есть и другие величины, которые тоже часто присутствуют в них. Например, строчное «t». В физике это означает «температуру», однако согласно ГОСТу Единой системы конструкторской документации, данная литера — это шаг (винтовых пружин, заклепочных соединений и подобного). При этом она не используется, когда речь идет о зубчатых зацеплениях и резьбе.

Заглавная и строчная буква «A»/«a» (согласно все тем же нормам) в чертежах применяется, чтобы обозначать не площадь, а межцентровое и межосевое расстояние. Помимо различных величин, в чертежах часто приходится обозначать углы разного размера. Для этого принято использовать строчные литеры греческого алфавита. Наиболее применяемые — «α», «β», «γ» и «δ». Однако допустимо использовать и другие.

Какой стандарт определяет буквенное обозначение длины, ширины, высоты, площади и других величин?

Как уже было сказано выше, чтобы не было недопонимания при прочтении чертежа, представителями разных народов приняты общие стандарты буквенного обозначения. Иными словами, если вы сомневаетесь в интерпретации того или иного сокращения, загляните в ГОСТы. Таким образом вы узнаете, как правильно обозначается высота, ширины, длина, диаметр, радиус и так далее.

Для Российской Федерации таким нормативным документом является ГОСТ 2.321-84. Он был внедрен еще в марте 1984 г. (во времена СССР), взамен устаревшего ГОСТа 3452—59.

fb.ru

Длина — Википедия

Материал из Википедии — свободной энциклопедии

Измерения:
L — длина,
B — ширина,
H — высота, толщина, глубина

Длина — физическая величина, числовая характеристика протяжённости линий.

В большинстве систем измерений единица длины — одна из основных единиц измерения, через которые определяются другие (производные) единицы. В международной системе единиц (СИ) за единицу длины принят метр.

В узком смысле под длиной понимают линейный размер предмета в продольном направлении (обычно это направление наибольшего размера), то есть расстояние между его двумя наиболее удалёнными точками, измеренное горизонтально, в отличие от высоты, которая измеряется в вертикальном направлении, а также ширины или толщины, которые измеряются поперёк объекта (под прямым углом к длине).

В физике термин «длина» обычно используется как синоним «расстояния» и обозначается L{\displaystyle L} или l{\displaystyle l} от нем. länge (длина). Символ размерности длины — dim l = L. В ряду других пространственных величин длина — это величина единичной размерности, тогда как площадь — двухмерная, объём — трёхмерная.

Метрическая система[править | править код]

Метрическая система считается самой удобной из всех придуманных из-за своей простоты. В основе метрической системы лежит единица измерения метр. Все остальные единицы измерения являются кратными степеням десяти от метра (например, километр — это 10³ метров и т. п.), что позволяет облегчить подсчёты. До 1960 года у метра был специальный эталон, ныне хранящийся в Международном бюро мер и весов, расположенном в городе Севр (предместье Парижа, Франция). Сегодня, по определению, метр равен расстоянию, которое проходит свет в вакууме за 1/299 792 458 долю секунды.

Британская/американская система[править | править код]

Исходными английскими мерами длины были миля, ярд, фут и дюйм. Миля пришла в Англию из Древнего Рима, где она определялась как тысяча двойных шагов вооружённого римского воина.

Старорусская система[править | править код]

В Древней Руси мерой длины, веса и т. п. являлся человек. На это указывают названия мер длины: локоть (расстояние от конца вытянутого среднего пальца руки или сжатого кулака до локтевого сгиба), пядь (расстояние между вытянутым большим и указательным пальцами руки), сажень (расстояние от конца пальцев одной руки до конца пальцев другой) и другие^[1].

В частности, аршин был связан с длиной человеческого шага. Однако необходимость унификации систем измерений с британской в связи с развитием международной торговли потребовала введения во времена Петра I так называемого «казённого аршина». Это была мерная линейка с металлическими наконечниками с государственным клеймом. Казённый аршин равнялся 28 английским дюймам и делился на 16 вершков.^[2]

Относительные размеры
объектов, м

-20 —

–

-18 —

–

-16 —

–

-14 —

–

-12 —

–

-10 —

–

-8 —

–

-6 —

–

-4 —

–

-2 —

–

0 —

–

2 —

–

4 —

–

6 —

–

8 —

–

10 —

–

12 —

–

14 —

–

16 —

–

18 —

–

20 —

–

22 —

–

24 —

–

26 —

–

28 —

–

30 —

См. также[править | править код]

Древнегреческая система[править | править код]

Мусульманская система[править | править код]

Типографическая система[править | править код]

Морская система[править | править код]

Морская система измерения длины привязана к размеру планеты Земля. В качестве основной единицы измерения принята морская миля, равная длине одной минуты (1/60 градуса) дуги меридиана земного эллипсоида. Длина морской мили является величиной переменной, зависящей от широты. Её численное значение составляет от 1843 метров на экваторе до 1861,6 метров на полюсах.

Международная морская миля составляет 1852 м, в отличие от морской мили британской системы (1853,184 м). Для измерения меньших размеров применяют кабельтов — 1/10 морской мили, или 185,2 м (округлённо — 185 м)^[4].

Единицы, применяемые в астрономии[править | править код]

Измерительные инструменты и меры[править | править код]

Измерительные приборы[править | править код]

Другие средства[править | править код]

Большие расстояния в навигации определяются при помощи средств радионавигационных систем или спутниковых систем
Очень маленькие расстояния измеряются с помощью измерительных микроскопов

Расстояния и размеры объектов, доступных наблюдению[править | править код]

Основной источник: ^[5]

Наблюдаемые объекты	Размер, м
Расстояние от Земли до самого далекого видимого объекта во Вселенной	1,0×1026{\displaystyle 1{,}0\times 10^{26}}
Расстояние от Земли до галактики в созвездии Андромеды	2,0×1022{\displaystyle 2{,}0\times 10^{22}}
Диаметр нашей Галактики	1,0×1021{\displaystyle 1{,}0\times 10^{21}}
Расстояние от Земли до ближайшей звезды в созвездии Центавра	4,0×1016{\displaystyle 4{,}0\times 10^{16}}
Расстояние от Земли до Солнца	1,5×1011{\displaystyle 1{,}5\times 10^{11}}
Диаметр Солнца	1,4×109{\displaystyle 1{,}4\times 10^{9}}
Расстояние от Земли до Луны	3,8×108{\displaystyle 3{,}8\times 10^{8}}
Диаметр Земли	1,3×107{\displaystyle 1{,}3\times 10^{7}}
Самая глубокая впадина на поверхности Земли	1,1×104{\displaystyle 1{,}1\times 10^{4}}
Самая высокая гора на поверхности Земли	9,0×103{\displaystyle 9{,}0\times 10^{3}}
Длина синего кита — самого большого животного на Земле	35{\displaystyle 35}
Рост самого высокого человека	2,85{\displaystyle 2{,}85}
Размеры амебы	5,0×10−4{\displaystyle 5{,}0\times 10^{-4}}
Толщина человеческого волоса	1,0×10−4{\displaystyle 1{,}0\times 10^{-4}}
Диаметр красного кровяного шарика	1,0×10−5{\displaystyle 1{,}0\times 10^{-5}}
Диаметр вируса гриппа	8,0×10−8{\displaystyle 8{,}0\times 10^{-8}}
Длина молекулы гемоглобина	1,5×10−8{\displaystyle 1{,}5\times 10^{-8}}
Расстояние между атомами в твердом теле	1,0×10−10{\displaystyle 1{,}0\times 10^{-10}}
Диаметр ядра атома урана	1,0×10−14{\displaystyle 1{,}0\times 10^{-14}}
Диаметр протона	1,6×10−15{\displaystyle 1{,}6\times 10^{-15}}
Минимальные размеры областей внутри элементарных частиц, доступных экспериментальному изучению с помощью современных ускорителей	1,0×10−17{\displaystyle 1{,}0\times 10^{-17}}

ru.wikipedia.org

Как правильно написать размеры длина ширина высота

Размеры длина, ширина, высота

Производство асбоцементных профилей организовано в соответствии госстандартами: 3034095 для волновых и 1812495 для плоских.

Волновые АЦЛ

Хотя состав стройматериала одинаковый, по размерам изделия могут разниться. Это также касается толщины изделия. Как правило, она изменяется в промежутке от 5 до 9 мм. Что же касается ширины, то она определяется количеством волн.

Профиль АЦЛ зависит от формы поперечного сечения и расстояния между волнами. Форма поперечного сечения бывает двух типов – 40 на 150 и 54 на 200. Первое число этого показателя (40 или 54) указывает на высоту волны, а второе (150 или 200), соответственно, на ее шаг. Высота шифера есть не что иное, как длина отрезка, связывающее верх волны и низ без учета толщины профиля.

Вариант шифера	Высота	Ширина	Длина	Шаг волны
7-ми волн.	8-ми волн.	6-ти волн.
40/150/1750	40	980	1130		1750	150
54/200/1750	54			1125	1750	200

На заметку
Отечественные производители имеют право на производство нестандартных АЦЛ на основе собственных ТУ.

Листы с различными профилями классифицируют в три группы:

ВО – обычный профиль;
УВ – унифицированный;
ВУ – усиленный.

для обычных – 1,2 на 0,68 м;
для унифицированных – 1,75 на 1,125 м;
для усиленных длина шифера равна 2,80 м.
волн современных асбоцементных листов – шесть, семь и восемь. К примеру, стандартный шифер 8 ми волнового – 1,75х1,13 м при толщине – 5,2 или 5,8 мм, величина площади – 1,977 кв. м. У 7-ми и 8-ми — одинаковая высота, ширина же отличается, поскольку количество волн не совпадает.

Плоские АЦЛ

Определенные качества плоских и волновых профилей схожи, тем не менее между ними есть определенные различия. К примеру, плоские могут быть непрессованными, а это значит, что они будут отличаться по своим техническим характеристикам. Следует отметить, что плоские АЦЛ более прочные по сравнению с волновыми. К примеру, их прочность на сжатие и изгиб достигает, соответственно, 90-130 и 20-50 Мпа.

Главное достоинство этого материала, скорее всего, в разнообразии его использования. Всего несколько примеров:

достаточно малый вес позволяет использовать плоские профили при устройстве перекрытия, причем дополнительные элементы укрепления при этом не используют.
довольно часто используется в качестве внутренней и внешней отделки зданий;
с их помощью возводят перегородки различного типа и вертикальные ограждения.

длина может быть 2,5, 3,0 и 3,5 м;
ширина – 1,2 и 1,5 м;
толщина – 0,6, 0,8 и 1,0 см.

На строительном рынке можно встретить также плоские листы промышленного производства меньших габаритов (длина – 0,6 м, ширина – 0,4 м), которые подходят для устройства кровли.

Следует отметить, что производители изготавливают на заказ профили других габаритов и оттенков. Разработанные красители отличаются устойчивостью не только к воздействиям атмосферы, но и к выгоранию.

2019 stylekrov.ru

Как правильно пишутся размеры высота, ширина, длина обозначения латинскими буквами

Решая геометрические задачи, ученики сталкиваются с вопросом: как правильно обозначить те или иные части чертежа? Например, высоту треугольника, ширину прямоугольника, размеры бассейна. Подобные обозначения мы найдем и в физических задачах: длина маятника, высота, с которой тело начинает падать… Поэтому следует знать некоторые правила.

Как обозначаются различные параметры

В единой системе измерения используется обозначение латинскими буквами:

длину — буквой l, если речь идет об одной прямой линии: маятнике, рычаге, отрезке, прямой. Но если речь идет о геометрической фигуре, например, прямоугольнике, то используется А,
высоту или глубину – h,
ширину – В.

Как обозначить глубину?

Что бывает длинным

Что же такое длина и как обозначается этот показатель? Она указывает расстояние от точки до точки, то есть размер отрезка. В геометрических задачах его принято обозначать как А. В стереометрии ее могут обозначать и А, и l (например, в задачах, где встречается прямая, пересекающая плоскость).

Отличие длины от высоты

Длина – это величина, которая характеризует протяженность линии.

А высота – это перпендикуляр, опущенный на противолежащую плоскость.

Вот такой ширины

дециметры,
сантиметры,
миллиметры,
микрометры и т.д.

А если предмет слишком крупный, то пишутся такие приставки:

Как называются стороны прямоугольника?

В отличие от квадрата, стороны прямоугольника попарно равны и параллельны.

Это значит, что стороны, образующие углы различны.

Как правило, более длинную сторону прямоугольника называют длиной, а ширина прямоугольника — это его короткая сторона.

В чем измеряются размеры длины, ширины и высоты по СИ

Для того чтобы знать, как правильно переводить единицы измерения в более крупные или же наоборот мелкие, необходимо знать значения приставок.

Дека — 10 1 ,
Гекто — 10 2 ,
Кило — 10 3 ,
Мега — 10 6 ,
Гига — 10 9 ,
Деци – 10 -1 ,
Санти – 10 -2 ,
Милли – 10 -3 ,
Микро — 10 -6 ,
Нано – 10 -9 .

После подсчетов эти единицы должны быть переведены в метры.

Существуют также внесистемные единицы, но они встречаются очень редко:

миля – 1,6 км,
фут – 12 дюймов – 0,3048 м,
ярд – 36 дюймов – 91,44 мм,
дюйм – 25,4 мм и т.д.

При решении задач такие единицы должны быть переведены в метры.

При выполнении геометрических заданий единицам измерения не уделяют особого внимания, главное, чтобы они были сопоставимы

(если вы производите подсчеты в сантиметрах, значит, все величины необходимо перевести в сантиметры).

А при решении физических задач ответ должен быть дан в метрах в соответствии с единой системой измерения.

Обозначения длины, ширины, высоты в геометрии

Измеряем геометрические параметры

Это интересно! Легкие правила округления чисел после запятой

ОСНОВНЫЕ ПОЛОЖЕНИЯ

1.1. Определенная величина обозначается буквой латинского или греческого алфавита без индексов или с индексами, служащими для уточнения различных характеристик этой величины.

1.2. Прописные и строчные буквы «О, о» латинского алфавита не должны употребляться в обозначениях. Буквы греческого алфавита следует принимать по табл. 1.

1.3. Буквенные обозначения необходимых величин, не приведенных в настоящем стандарте СЭВ, устанавливают по принципу, указанному в табл. 2.

Сила, произведение силы на длину, длина в степени, не равной единице

Прописные латинского алфавита

Длина, отношение длины ко времени в какой-либо степени, отношением усилия к единице длины или площади

Строчные латинского алфавита

Строчные греческого алфавита

1.4. Индексы подразделяются на цифровые и буквенные. Буквенные дополнительно подразделяются на одно-, двух- и трехбуквенные. Для обозначения цифровых индексов используются арабские цифры, а для обозначения буквенных индексов — буквы латинского алфавита.

1.5. Цифровые индексы применяются для выражения порядкового номера данного обозначения.

1.6. Однобуквенные индексы применяются для обозначения осей координат, расположения, вида материала, напряженного состояния, действующей нагрузки и других характеристик.

1.7. Двухбуквенные и трехбуквенные индексы применяются в том случае, когда использование однобуквенных индексов может привести к неясностям. Они отделяются от однобуквенных индексов запятыми.

1.8. Индексы располагаются с правой стороны букв внизу. При печатании на пишущей машинке букву и индекс допускается печатать на одной строчке.

1.9. Если в настоящем стандарте отсутствует необходимый индекс, его следует устанавливать из строчных букв латинского алфавита.

1.10. Обозначение, выражающее геометрическую величину, допускается дополнять вертикальным штрихом справа, если необходимо обозначить, что имеется ввиду сжатая часть сечения или элемента.

ГОСТ 4541-70. Машины электрические вращающиеся. Обозначения буквенные установочно-присоединительных и габаритных размеров

(текст документа с изменениями и дополнениями на ноябрь 2014 года)

Утвержден и введен в действие Постановлением Госстандарта СССР от 26 февраля 1970 г. N 235

Взамен ГОСТ 4541-48

Срок введения с 1 января 1971 года

Постановлением Комитета стандартов, мер и измерительных приборов при Совете Министров СССР от 26 февраля 1970 г. N 235. Проверен в 1984 г.

Переиздание (ноябрь 1984 г.) с Изменением N 1, утвержденным в сентябре 1984 г. (ИУС 12-84).

1. Настоящий стандарт распространяется на вновь проектируемые и модернизируемые вращающиеся электрические машины и преобразовательные агрегаты и устанавливает буквенные обозначения установочно-присоединительных и габаритных размеров.

2. Номера чертежей с примерами буквенных обозначений установочно-присоединительных и габаритных размеров электрических машин и концов валов указаны в табл. 1.

(Измененная редакция, Изм. N 1).

3. Буквенные обозначения установочно-присоединительных и габаритных размеров отдельных видов электрических машин и агрегатов с иными конструктивными разновидностями монтажных поверхностей и форм исполнения, не предусмотренных табл. 1, рекомендуется устанавливать аналогично приведенным в настоящем стандарте.

4. Для обозначений установочно-присоединительных и габаритных размеров электрических машин и преобразовательных агрегатов следует применять строчные буквы латинского и греческого алфавитов с подстрочными индексами:

b — для ширины (в направлении, перпендикулярном к оси вала),

d — для диаметров,

l — для длины (в направлении оси вала),

r — для радиусов,

t — для размеров в шпоночных соединениях,

— для угловых размеров.

Примечание. Высоту оси вращения (h) проставляют без подстрочного индекса.

5. Подстрочные индексы к буквенным обозначениям следует устанавливать в зависимости от следующего их назначения:

1 — 9 — для концов валов,

10 — 19 — для размеров лап и фундаментных плит (рам),

20 — 29 — для размеров фланца,

30 — 80 — для остальных установочно-присоединительных размеров,

80 и более — для размеров агрегатов и специальных машин.

6. Буквенные обозначения установочно-присоединительных и габаритных размеров должны соответствовать указанным на черт. 1 — 12 и в табл. 2.

Электрическая машина группы 1М1

Электрическая машина группы 1М2

Электрическая машина группы 1М3

Электрическая машина группы 1М4

Электрическая машина группы 1М5

Электрическая машина группы 1М6

Электрическая машина группы 1М7

Агрегаты преобразовательные двухмашинные

Агрегаты преобразовательные трехмашинные

Выступающий конец вала электрической машины

Второй выступающий конец вала электрической машины

Участок вала под посадку шкива

В чертежах и каталогах проставлять один из размеров или , или .

Чертежи служат лишь для пояснения размеров, приведенных в табл. 2.

Количество размеров, проставляемых в чертежах конкретных исполнений машин, устанавливается применительно к каждому исполнению.

(Измененная редакция, Изм. N 1).

7. При простановке обозначений размеров на рабочих чертежах и в каталогах следует избегать образования замкнутых размерных цепочек, например (см. черт. 8) один из размеров , или должен быть опущен.

8. В случае одинаковых по форме и размерам обоих выступающих концов вала следует устанавливать обозначения, принятые для первого выступающего конца вала.

9. Буквенные обозначения размеров вентиляционных каналов настоящим стандартом не устанавливаются.

10. Буквенные обозначения на чертежах следует выполнять с наклоном. Допускается применение в обозначениях прямых букв и цифр. Форма и размеры букв латинского и греческого алфавитов и арабских цифр должны соответствовать ГОСТ 2.304-81.

Достоинства и недостатки асбоцементных листов

Свою неизменную популярность асбоцементные листы заслужили благодаря широкому набору преимуществ. Отметим лишь некоторые из них.

Это достаточно прочный и долговечный материал.
Наличие открытого огня не представляет угрозы, абсолютно пожаробезопасен. Более того, даже будучи расположенным в очаге возгорания не выделяет вредных веществ.
Устойчив к резким температурным перепадам. Прессованные образцы в состоянии выдерживать до 50 циклов замораживание/оттаивание.
Высокая ремонтопригодность кровли: ее достаточно просто отремонтировать, установив заплатку или заменив целые листы.
Материалу не грозят такие негативные явления как гниение и коррозия, его легко обрабатывать, используя самые простые инструменты.
Устройство кровли при стандартных размерах листа шифера достаточно простое, позволяет сократить время монтажа и сэкономить на профессионализме кровельщиков.

недостаточно высокая прочность на изгиб и механическое воздействие;
относительно высокий уровень удельного веса – порядка 20 кг/кв. м;
проблема образования мха, который негативно сказывается на прочности профиля и его внешней привлекательности.

Габаритные размеры

Авиация: Энциклопедия. — М.: Большая Российская Энциклопедия . Главный редактор Г.П. Свищев . 1994 .

Смотреть что такое «Габаритные размеры» в других словарях:

габаритные размеры — Рис. 1. Габаритные размеры самолёта. габаритные размеры самолёта, вертолёта предельные значения длины и высоты, полного размаха крыла (у самолёта), диаметра несущего винта (у вертолёта) и т. п. (см. рис. 1, 2). Г. р. летательного аппарата… … Энциклопедия «Авиация»

габаритные размеры — Номинальные наружные размеры (включая при необходимости положительные допуски): длина, ширина и высота, измеряемые вдоль наружных кромок контейнера. Примечание Допуски к диагоналям, приемлемые для всех шести граней контейнера, даны в ИСО 668 95.… … Справочник технического переводчика

ГАБАРИТНЫЕ РАЗМЕРЫ — (в антропометрии) наибольшие размеры тела в разных его положениях и позах, ориентированные в разных плоскостях (размеры рук, наибольший поперечный диаметр тела, горизонтальная и вертикальная досягаемость руки и т. п.). Г. р. измеряются по… … Энциклопедический словарь по психологии и педагогике

габаритные размеры электроагрегата (электростанции) в транспортном положении — габаритные размеры Расстояние между крайними по длине, ширине и высоте точками электроагрегата (электростанции). Тематики электроагрегаты генераторные Синонимы габаритные размеры … Справочник технического переводчика

габаритные размеры пакетированной авиационной грузовой единицы — Предельные наружные размеры пакетированной авиационной грузовой единицы, включающие в себя любые ручки или другие выступающие элементы на ее поверхности. Тематики авиационные грузовые перевозки EN external dimensionsULD… … Справочник технического переводчика

габаритные размеры тары — Максимальные наружные размеры тары, включая выступающие части и детали. Тематики упаковка, упаковывание Обобщающие термины параметры и характеристики тары и упаковки EN overall dimensions of a container DE Grossmasse der… … Справочник технического переводчика

mr-build.ru

Буквенные обозначения на чертежах

ГОСТ 2.321 – 84

Для оформления конструкторских документов предусмотрены основные буквенные обозначения, которые отражают следующие условные величины:

Высота и глубина

Для обозначения габаритных и суммарных размеров рекомендуется применять прописные буквы.

Если в одном и том же документе используется одинаковые буквы, для различных величин, применяются цифровые или буквенные индексы, например:

d, d₁, d₂, d_n, d_n1, d_n2.

Расстояние между осями или центрами

Обозначение ширины

Указание диаметра

Обозначение высоты или глубины

Обозначение длины

Радиус элемента детали

Толщина листа

Шаг витка пружины

Углы

gk-drawing.ru

Как пишутся размеры длина ширина высота – габариты как правильно указывать

Как правильно пишутся размеры: высота, ширина, длина обозначения латинскими буквами

Как обозначаются различные параметры

В единой системе измерения используется обозначение латинскими буквами:

длину буквой l, если речь идет об одной прямой линии: маятнике, рычаге, отрезке, прямой. Но если речь идет о геометрической фигуре, например, прямоугольнике, то используется А,
высоту или глубину – h,
ширину – В.

Как обозначить глубину?

Что бывает длинным

Отличие длины от высоты

Длина – это величина, которая характеризует протяженность линии.

А высота – это перпендикуляр, опущенный на противолежащую плоскость.

Вот такой ширины

дециметры,
сантиметры,
миллиметры,
микрометры и т.д.

А если предмет слишком крупный, то пишутся такие приставки:

Как называются стороны прямоугольника?

В отличие от квадрата, стороны прямоугольника попарно равны и параллельны.

Это значит, что стороны, образующие углы различны.

В чем измеряются размеры длины, ширины и высоты по СИ

Дека 101,
Гекто 102,
Кило 103,
Мега 106,
Гига 109,
Деци – 10-1,
Санти – 10-2,
Милли – 10-3,
Микро 10-6,
Нано – 10-9.

После подсчетов эти единицы должны быть переведены в метры.

Существуют также внесистемные единицы, но они встречаются очень редко:

миля – 1,6 км,
фут – 12 дюймов – 0,3048 м,
ярд – 36 дюймов – 91,44 мм,
дюйм – 25,4 мм и т.д.

При решении задач такие единицы должны быть переведены в метры.

(если вы производите подсчеты в сантиметрах, значит, все величины необходимо перевести в сантиметры).

А при решении физических задач ответ должен быть дан в метрах в соответствии с единой системой измерения.

Обозначения длины, ширины, высоты в геометрии

Измеряем геометрические параметры

Вывод

Это интересно! Легкие правила округления чисел после запятой

X Y Z

Казалось бы, что сложного в правильном расположении пары слов на картинке или рядом с фотогрфаией. Но нет.

Нередко редакторы в статьях не сопоставляют присланный текст копирайтера и фотоколлаж от дизайнера. А если они сами и текст пишут и фотографии подбирают, тогда это совсем странно:

В дизайне это тоже встрачается. Например, почти на каждой второй обложке имена располагают напротив чужого актера. И даже женщины с мужскими именами и мужики с женскими дизайнеров совсем не смущают:

А еще можно перепутать длину и ширину. Чаще всего это встрачается на картинках с размерами фотографий. Правильно в таких случаях сначала подписывать ось Х, затем ось Y:

Найдете фейл в распечатанных фотографиях на стене?

Ниже в комментариях еще один был найден

Тут ребята из музея в комментарии пожаловали и они не согласны. Оказывается, у них там свое государство со своими законами. Поэтому, если надо написать картину маслом, то Y x X. А если ее нужно напечатать на принтере, то X x Y. К слову, рамки для фото/картин в магазинах продают для дизайнеров, а не для художников. Ну тоже Х х Y. И так как мы дизайнеры с маслом не дружим, то пример менять не буду. Всем спасибо, расходимся

Легко можно запомнить легко по последним буквам английского алфавита:

X (длина), Y (ширина/высота), Z (глубина/толщина)

Добавь к ответу свадебное фото прямо над девушкой (40×60)

Что-то пошло не так))
Принято (по крайней мере в нашей стране (РФ)) писать «ШВД», расшифровывается как Ширина Высота Длина (она же Глубина, она же Толщина).
Ширина всегда указывается первой, Высота — вторая ну и третий параметр зависит от ситуации (2D/3D).

ШВД — это спел в Харстоуне: Shadow Word Death. А писать надо сначала длину (по горизонтали Х), потом ширину (по вертикали Y), потом глубину (по оси Z).

Ширина Высота Длина (она же Глубина, она же Толщина) — это те же XYZ. Только названия неподходящие.

Длина (она же Глубина, она же Толщина)

Очевидно же, что «длина» — по длинной стороне, а не по короткой. А глубина/толщина — как правило, самые маленькие значения.

В теме «Найдете фейл?» Фейлом является всё, кроме 80х90.
В художественной живописи, в галереях, музеях и т.д., сначала указывают высоту, а затем ширину. Надо же быть в теме, прежде чем что-то кому-то объяснять.
И потом вы путаете понятие Ширина (Y) — это высота.

В теме «Найдете фейл?» Фейлом является всё, кроме 80х90.

В художественной живописи, в галереях, музеях и т.д., сначала указывают высоту, а затем ширину.

Почти везде правосторонее движение, а где-то с левой стороны дороги ездят. Возможно, в живописи так принято, значит, пример мой не подходит, и надо бы его поменять на такой же, но без багета, чтобы получить не картины на стене, а печать фото на документы. Но он взят с сайта художника, а не дизайнера. Уж он то в курсе

Не хватает только мебельщиков. Ждем))

Проблема в другом. Речь о дизайне, а не о музеях. Я дизайнер и пишу дизайнерам о дизайне. В полиграфии принят такой порядок: X x Y.

Сначала Х, потом Y. Если не доверяете Вики, откройте любой сайт типографии. Хотя любой — это я погорячился. Вот уже сайт одного из художников открыл на свою голову

И потом вы путаете понятие Ширина (Y) — это высота.

Ширина это и есть высота, смотря в какой плоскости расположить измеряемый предмет. Если нужно сделать принт на пол, то у него нет никакой высоты: только длина и ширина. С потолками, например, тоже самое: натяжные потолки с фото — для подготовки рисунка нужна длина и его ширина. А выражение «высота потолков» — это как раз расстояние от пола до потолка. Если же печатаем картину на стену, то ширина трансформируется в высоту. А глубина/толщина холста, соответственно, третье измерение.

Надо же быть в теме, прежде чем что-то кому-то объяснять.

А вот с этим как раз-таки и не поспоришь. Долгое время работал в типографии и даже был техническим специалистом отдела дизайна: ну т.е. подготовка файлов, смик/ргб, размеры и вот это все.

А значит, если надо написать картину маслом, то Y x X. А если ее нужно напечатать на принтере, то X x Y. К слову, рамки для фото/картин в магазинах продают для дизайнеров, а не для художников. Ну т.е. тоже Х х Y. И так как мы, дизайнеры, с маслом не дружим, то пример менять не буду. Тем более, добавив перед ним фразу «…в распечатанных фотографиях на стене», все стало на свои места, верно?)

В любом случае, в конце статьи добавил сноску про музей. Спасибо

Запись габаритных размеров

15 сообщений в этой теме

Создайте аккаунт или авторизуйтесь, чтобы оставить комментарий

Комментарии могут оставлять только зарегистрированные пользователи

Создать аккаунт

Зарегистрировать новый аккаунт.

Общие правила нанесения размеров на чертежах

Стандарт (ГОСТ 2.307-68) устанавливает правила нанесения размеров на чертежах.

Линейные размеры на чертежах проставляются в миллиметрах без обозначения единиц измерения (мм). При других единицах измерения (сантиметрах, метрах) размерные числа записываются с обозначением единиц измерения (см, mi). Угловые размеры указывают в градусах, минутах, секундах с обозначением единиц измерения. Общее количество размеров на чертежах должно быть минимальным, но достаточным для изготовления и контроля изделия.

Существуют строго определенные правила нанесения размеров. При нанесении размера прямолинейного отрезка размерную линию проводят параллельно этому отрезку, а выносные линии — перпендикулярно размерным (рис. 40, б). Выносные линии выходят за размерные на 1-3 мм. Расстояние от размерной линии до контура изображения должно быть не менее 10 мм, а расстояние между двумя близлежащими размерными линиями — не менее 7 мм (рис. 40, б).

На концах размерных линий наносят стрелки. Форма и размеры стрелки показаны на рис. 40, а. Величина стрелок должна быть одинаковой на всем чертеже. Стрелки при недостатке места могут заменяться засечками или точками (рис. 41, б, в). Допускается проставлять размеры так, как показано на рис. 41, г.

Размерные числа наносят над размерной линией ближе к середине (рис. 42).

При нанесении нескольких параллельных или концентрических размерных линий размерные числа над ними располагают в шахматном порядке (рис. 43).

На чертежах необходимо избегать пересечения размерных и выносных линий. Если для нанесения размерного числа недостаточно места над размерной линией, то размеры проставляются так, как показано на рис. 44.

В местах нанесения размерного числа осевые, центровые линии и линии штриховки прерывают (рис. 45, а, б).

При нанесении размеров дуг перед размерным числом помещают знак радиуса — R. Высота знака радиуса и размерного числа должна быть одинаковой (рис. 46, а). При проведении нескольких радиусов из одного центра размерные линии любых двух радиусов не располагают на одной прямой (рис. 46, б). При большой величине радиуса центр разрешается приближать к дуге. В таких случаях размерную линию показывают с изломом (рис. 46, в).

При нанесении размеров окружностей перед размерным числом ставят знак диаметра — 0 (рис. 47). При недостатке места на чертеже размеры диаметра проставляют так, как показано на рис. 47, б.

Размеры нескольких одинаковых элементов изделия наносят один раз с указанием их количества на полке-выноске, рис. 48.

Размеры квадрата или квадратного отверстия наносятся, как показано на рис. 49.

Толщина плоской детали обозначается буквой S с последующим указанием размерного числа (рис. 50).

Длина изделия обозначается малой буквой латинского алфавита — I (рис. 51).

Нанесение размеров фаски — скошенной кромки стержня, бруска, отверстия — осуществляется либо простановкой двух линейных размеров (рис. 52, б), либо линейным и угловым размерами (рис. 52, в, г).

Если на чертеже встречается несколько одинаковых фасок, то размер наносят один раз так, как показано на рис. 52, в. Эта надпись означает, что снято две фаски размером 2 мм под углом 45°.

На чертежах необходимо проставлять габаритные размеры.

Габаритными размерами называют размеры, определяющие предельные величины внешних очертаний изделий. К габаритным размерам относятся размеры длины, ширины, высоты изделия.

Габаритные размеры всегда больше других, поэтому их на чертеже располагают дальше от изображения, чем остальные.

На рис. 53 (валик) — габаритными являются размеры 75 мм и 40 мм.

На рис. 53 (полуцилиндр) — к габаритным относятся размеры 80 мм, 50 мм.

На чертежах иногда наносят справочные размеры. Размеры, нанесенные на чертеже, но не подвергающиеся контролю, называют справочными. На чертеже они отмечаются знаком * (рис. 54). На месте расположения технических требований (над основной надписью) делают запись: * — размер для справок.

Не нашли то, что искали? Воспользуйтесь поиском:

Лучшие изречения: Да какие ж вы математики, если запаролиться нормально не можете. 8358 — | 7290 — или читать все.

188.64.169.166 © studopedia.ru Не является автором материалов, которые размещены. Но предоставляет возможность бесплатного использования. Есть нарушение авторского права? Напишите нам | Обратная связь.

Отключите adBlock!
и обновите страницу (F5)
очень нужно

Обозначение: высота, ширина, длина. Ширина — обозначение буквой. Обозначение ширины на чертежах

Величины

Итак, для начала давайте выясним, как правильно длину, ширину, высоту обозначать на чертежах.

Ширина

Длина

Высота

Радиус и диаметр

Помимо рассмотренных параметров, при составлении чертежей приходится иметь дело и с иными.

Толщина

Периметр и площадь

Другие распространенные сокращения

Какой стандарт определяет буквенное обозначение длины, ширины, высоты, площади и других величин?

iv-proect.ru

какой буквой в геометрии обозначается ширина

В принципе, любой. В формуле площади прямоугольника S = a*b одна из величин длина, другая ширина. Какая где — безразлично.

Нет конкретного обозначения ширины.

а-длина, б-ширина, но это условно.. . а так любой буквой…

согласно Буквенные обозначения ГОСТ 2.321-68, ширина обозначается буквой B, b

touch.otvet.mail.ru

Главные размерения — Википедия

Материал из Википедии — свободной энциклопедии

Главные размерения судна (основные размерения судна или корабля) — совокупность конструктивных, расчётных, наибольших и габаритных линейных размеров судна: длины, ширины, осадки и высоты борта. Главные размерения характеризуют мореходные качества корабля (судна) и определяют возможность его проводки в узкостях (каналах, бухтах, проливах), шлюзах, на мелководье, определяют возможность размещения на стапеле (слипе) или постановки в корабельный док^[1].

Высота борта — вертикальное расстояние, измеряемое в плоскости мидель-шпангоута от основной плоскости до бортовой линии верхней палубы — линии пересечения теоретических поверхностей борта и верхней палубы или их продолжения при закруглённом соединении палубы с бортом. Для подводной лодки высота борта определяется как расстояние по вертикали между крайними точками наружного корпуса в районе мидель-шпангоута, но без учёта высоты ограждения рубки^[2].

Осадка — расстояние от горизонтальной плоскости, проходящей через нижнюю точку в середине длины корпуса (без учёта выступающих частей) до поверхности спокойной воды. Различают осадку носом, кормой и среднюю осадку, как среднеарифметическое значение кормовой и носовой осадки^[1].

Длина судна — расстояние между его носовыми и кормовыми конструктивными элементами^[2]. Различают длину судна: по конструктивной ватерлинии, между перпендикулярами, наибольшую и габаритную. Для подводных лодок дополнительно различают: длину непроницаемого корпуса и длину прочного корпуса^[1].

Длина корабля по конструктивной (расчётной) ватерлинии — расстояние между точками пересечения носовой и кормовой частей конструктивной ватерлинии с диаметральной плоскостью. Длина между перпендикулярами — расстояние между носовым и кормовым перпендикулярами корабля. Наибольшая длина корабля — расстояние между крайними точками теоретической поверхности корпуса корабля в носовой и кормовой оконечностях. Габаритная длина судна — расстояние между крайними точками носовой и кормовой оконечностей корпуса с учётом выступающих частей. Длина непроницаемого корпуса подводной лодки — расстояние между концевыми поперечными переборками (чаще всего концевых цистерн главного балласта). Длина прочного корпуса — расстояние между крайними точками концевых переборок прочного корпуса^[1].

Длина гражданского судна — расстояние, измеряемое на уровне летней грузовой ватерлинии от передней кромки форштевня до оси баллера руля или 96 % длины судна, измеряемой на уровне этой ватерлинии от передней кромки форштевня до крайней кромки кормовой оконечности судна^[1].

Ширина судна — расстояние между различными конструктивными точками корабля, расположенными на его правом и левом бортах. Различают наибольшую ширину, ширину по конструктивной ватерлинии, по расчётной ватерлинии, на мидель-шпангоуте, габаритную, ширину по стабилизаторам (для подводных лодок)^[1].

Наибольшей шириной корабля называют расстояние, измеряемое перпендикулярно диаметральной плоскости, между крайними точками теоретической поверхности корпуса корабля. Шириной корабля по конструктивной ватерлинии называют наибольшую ширину конструктивной ватерлинии. Шириной корабля по расчётной ватерлинии называют наибольшую ширину расчётной ватерлинии. Шириной корабля на мидель-шпангоуте называют ширину конструктивной ватерлинии на мидель-шпангоуте. Габаритной шириной корабля называют расстояние, измеряемое перпендикулярно диаметральной плоскости между крайними точками корпуса корабля (судна), с учётом выступающих частей. Под шириной подводной лодки по стабилизаторам подразумевают размах стабилизаторов подводной лодки, то есть расстояние между крайними точками стабилизаторов^[1].

Главные размерения корабля // Военно-морской словарь / Чернавин В. Н. — М.: Воениздат, 1990. — С. 107—108. — 511 с. — ISBN 5-203-00174-X.
Лобач-Жученко М. Б. Основные элементы кораблей и судов. — М.: издательство ДОСААФ, 1955. — 80 с. — 10 000 экз.

ru.wikipedia.org

Список обозначений в физике — Википедия

Символ	Значение и происхождение
A{\displaystyle A}	Площадь (лат. area), векторный потенциал^[1], работа (нем. Arbeit), амплитуда (лат. amplitudo), параметр вырождения, Работа выхода (нем. Austrittsarbeit), коэффициент Эйнштейна для спонтанного излучения, массовое число
a{\displaystyle a}	Ускорение (лат. acceleratio), амплитуда (лат. amplitudo), активность (лат. activitas), коэффициент температуропроводности, вращательная способность, радиус Бора, натуральный показатель поглощения света
B{\displaystyle B}	Вектор магнитной индукции^[1], барионный заряд (англ. baryon number), удельная газовая постоянная, вириальний коэффициент, функция Бриллюэна (англ. Brillion function), ширина интерференционной полосы (нем. Breite), яркость, постоянная Керра, коэффициент Эйнштейна для вынужденного излучения, коэффициент Эйнштейна для поглощения, вращательная постоянная молекулы
b{\displaystyle b}	Вектор магнитной индукции^[1], красивый кварк (англ. beauty/bottom quark), постоянная Вина, ширина распада (нем. Breite)
C{\displaystyle C}	Электрическая ёмкость (англ. capacitance), теплоёмкость (англ. heatcapacity), постоянная интегрирования (лат. constans), очарование (чарм, шарм; англ. charm), коэффициенты Клебша — Гордана (англ. Clebsch-Gordan coefficients), постоянная Коттона — Мутона (англ. Cotton-Mouton constant), кривизна (лат. curvatura)
c{\displaystyle c}	Скорость света (лат. celeritas), скорость звука (лат. celeritas), Теплоёмкость (англ. heat capacity), очарованный кварк (англ. charm quark), концентрация (англ. concentration), первая радиационная постоянная, вторая радиационная постоянная, удельная теплоёмкость
D{\displaystyle D}	Вектор электрической индукции^[1] (англ. electric displacement field), Коэффициент диффузии (англ. diffusion coefficient), Оптическая сила (англ. dioptric power), коэффициент прохождения, тензор квадрупольного электрического момента, угловая дисперсия спектрального прибора, линейная дисперсия спектрального прибора, коэффициент прозрачности потенциального барьера, D-мезон (англ. D meson), Диаметр (лат. diametros, др.-греч. διάμετρος)
d{\displaystyle d}	Расстояние (лат. distantia), Диаметр (лат. diametros, др.-греч. διάμετρος), дифференциал (лат. differentia), нижний кварк (англ. down quark), дипольный момент (англ. dipole moment), период дифракционной решётки, толщина (нем. Dicke)
E{\displaystyle E}	Энергия (лат. energīa), напряжённость электрического поля^[1] (англ. electric field), Электродвижущая сила (англ. electromotive force), магнитодвижущая сила, освещенность (фр. éclairement lumineux), излучательная способность тела, модуль Юнга
e{\displaystyle e}	Основание натуральных логарифмов (2,71828…), электрон (англ. electron), элементарный электрический заряд (англ. elementaty electric charge), константа электромагнитного взаимодействия
F{\displaystyle F}	Сила (лат. fortis), постоянная Фарадея (англ. Faraday constant), свободная энергия Гельмгольца (нем. freie Energie), атомный фактор рассеяния, тензор электромагнитного поля, магнитодвижущая сила, модуль сдвига, фокусное расстояние (англ. focal length)
f{\displaystyle f}	Частота (лат. frequentia), функция (лат. functia), летучесть (нем. Flüchtigkeit), сила (лат. fortis), фокусное расстояние (англ. focal length), сила осциллятора, коэффициент трения
G{\displaystyle G}	Гравитационная постоянная (англ. gravitational constant), тензор Эйнштейна, свободная энергия Гиббса (англ. Gibbs free energy), метрика пространства-времени, вириал, парциальная мольная величина, поверхностная активность адсорбата, модуль сдвига, полный импульс поля, Глюон (англ. gluon), константа Ферми, квант проводимости, электрическая проводимость, Вес (нем. Gewichtskraft)
g{\displaystyle g}	Ускорение свободного падения (англ. gravitational acceleration), Глюон (англ. gluon), фактор Ланде, фактор вырождения, весовая концентрация, Гравитон (англ. graviton), метрический тензор
H{\displaystyle H}	Напряжённость магнитного поля^[1], эквивалентная доза, энтальпия (англ. heat contents или от греческой буквы «эта», H — ενθαλπος^[2]), гамильтониан (англ. Hamiltonian), функция Ганкеля (англ. Hankel function), функция Хевисайда (англ. Heaviside step function), бозон Хиггса (англ. Higgs boson), экспозиция, полиномы Эрмита (англ. Hermite polynomials)
h{\displaystyle h}	Высота (нем. Höhe), постоянная Планка (нем. Hilfsgröße^[3]), спиральность (англ. helicity)
I{\displaystyle I}	сила тока (фр. intensité de courant), интенсивность звука (лат. intēnsiō), интенсивность света (лат. intēnsiō), сила излучения, сила света, момент инерции, вектор намагниченности
i{\displaystyle i}	Мнимая единица (лат. imaginarius), единичный вектор (координатный орт)
J{\displaystyle J}	Плотность тока (также 4-вектор плотности тока), момент импульса, функция Бесселя, момент инерции, полярный момент инерции сечения, вращательное квантовое число, сила света, J/ψ-мезон
j{\displaystyle j}	Мнимая единица (в электротехнике и радиоэлектронике), плотность тока (также 4-вектор плотности тока), единичный вектор (координатный орт)
K{\displaystyle K}	Каона (англ. kaons), термодинамическая константа равновесия, коэффициент электронной теплопроводности металлов, модуль всестороннего сжатия, механический импульс, постоянная Джозефсона, кинетическая энергия
k{\displaystyle k}	Коэффициент (нем. Koeffizient), постоянная Больцмана, теплопроводность, волновое число, единичный вектор (координатный орт)
L{\displaystyle L}	Момент импульса, дальность полёта, удельная теплота парообразования и конденсации, индуктивность, функция Лагранжа (англ. Lagrangian), классическая функция Ланжевена (англ. Langevin function), число Лоренца (англ. Lorenz number), уровень звукового давления, полиномы Лагерра (англ. Laguerre polynomials), орбитальное квантовое число, энергетическая яркость, яркость (англ. luminance)
l{\displaystyle l}	Длина (англ. length), длина свободного пробега (англ. length), орбитальное квантовое число, радиационная длина
M{\displaystyle M}	Момент силы, масса (лат. massa, от др.-греч. μᾶζα, кусок теста), вектор намагниченности (англ. magnetization), крутящий момент, число Маха, взаимная индуктивность, магнитное квантовое число, молярная масса
m{\displaystyle m}	Масса, магнитное квантовое число (англ. magnetic quantum number), магнитный момент (англ. magnetic moment), эффективная масса, дефект массы, масса Планка
N{\displaystyle N}	Количество (лат. numerus), постоянная Авогадро, число Дебая, полная мощность излучения, увеличение оптического прибора, концентрация, мощность, сила нормальной реакции
n{\displaystyle n}	Показатель преломления, количество вещества, нормальный вектор, единичный вектор, нейтрон (англ. neutron), количество (англ. number), основное квантовое число, частота вращения, концентрация, показатель политропы, постоянная Лошмидта
O{\displaystyle O}	Начало координат (лат. origo)
P{\displaystyle P}	Мощность (лат. potestas), давление (лат. pressūra), полиномы Лежандра, вес (фр. poids), сила тяжести, вероятность (лат. probabilitas), поляризуемость, вероятность перехода, импульс (также 4-импульс, обобщённый импульс; лат. petere)
p{\displaystyle p}	Импульс (также 4-импульс, обобщённый импульс; лат. petere), протон (англ. proton), дипольный момент, волновой параметр, давление, число полюсов, плотность.
Q{\displaystyle Q}	Электрический заряд (англ. quantity of electricity), количество теплоты (англ. quantity of heat), объёмный расход, обобщённая сила, хладопроизводительность, энергия излучения, световая энергия, добротность (англ. quality factor), нулевой инвариант Аббе, квадрупольный электрический момент (англ. quadrupole moment), энергия ядерной реакции
q{\displaystyle q}	Электрический заряд, обобщённая координата, количество теплоты (англ. quantity of heat), эффективный заряд, добротность
R{\displaystyle R}	Электрическое сопротивление (англ. resistance), универсальная газовая постоянная, постоянная Ридберга (англ. R ydberg constant), постоянная фон Клитцинга, коэффициент отражения, сопротивление излучения (англ. resistance), разрешение (англ. resolution), светимость, пробег частицы, расстояние
r{\displaystyle r}	Радиус (лат. radius), радиус-вектор, радиальная полярная координата, удельная теплота фазового перехода, удельная рефракция (лат. rēfractiō), расстояние
S{\displaystyle S}	Площадь поверхности (англ. surface area), энтропия^[4], действие, спин (англ. spin), спиновое квантовое число (англ. spin quantum number), странность (англ. strangeness), главная функция Гамильтона, матрица рассеяния (англ. scattering matrix), опера

ru.wikipedia.org

Нанесение размеров на чертежах ✏️ как правильно обозначать длину, ширину, толщину, высоту, виды размеров, проставление по ГОСТу, допуски и посадки

Как правило, проекты составляют целые конструкторские бюро, после этого чертежи переходят на сборочные участки для изготовления. Чтобы не было расхождений в их чтении, есть специальные стандарты, называемые ГОСТами. Они дают чёткие рекомендации, как верно проставлять размеры и какими условными знаками можно обозначить те или иные элементы.

Основные величины

Существуют несколько геометрических параметров, которые характеризуют любой объект. Это:

длина;
ширина;
высота;
глубина;
межцентровое и межосевое расстояние;
площадь и т. д.

Данные характеристики могут быть как физическими, так и математическими. Единое буквенное обозначение, которое употребляется на всей планете, появилось в середине ХХ столетия и вошло в Международную систему единиц (СИ). За основу взяты латинские буквы, таким образом начертание кириллицей при проектировании не допускается.

В конструкторских документах пишутся в основном символы, применяемые в физике или геометрии.

Существуют двухмерные и трёхмерные изображения. На плоскости присутствуют два измерения, для ширины обозначение буквой В было взято из геометрии. Она измеряется в поперечном направлении. При очерчивании фигур чаще всего пользуются латинским алфавитом: а, b, с. Длина измеряется в продольном разрезе. Это численная характеристика протяжённости линий. В английском языке она звучит как length. Собственно благодаря этому изначально применяемая буква L была взята за основу и внесена в ГОСТ. Стандарт разрешает как заглавное, так и строчное начертание.

Длину и ширину в международной системе измеряют в метрах или других производных от него кратных 10 единицах. Всем известны сантиметры, миллиметры, микроны и др.

Если работа с построением идёт в трёхмерном пространстве, то добавляется ещё и высотный параметр H, в отдельных случаях ещё и толщина. Эта величина характеризует величину объекта по вертикали. Обозначение толщины — буква S. А при работе с круглыми и сферическими объектами появляется такое понятие, как радиус: это отрезок, соединяющий соединяет центр со второй точкой, расположенной на окружности. В международной практике его принято обозначать как R или r, от латинского слова radius. Нередко применяется понятие диаметра. Это отрезок, проходящий через центр и соединяющий две точки на окружности.

Угловые величины принято обозначать греческими буквами.

Цифровые значения на чертёжных документах наносятся над размерными линиями заканчивающихся с двух сторон стрелками. Выносные линии показывают, к какому именно элементу относится то или иное число. Размеры стрелок подбираются в зависимости от толщины основных линий контура и прорисовываются примерно одинаковыми. На рисунке приведены ГОСТированные параметры стрелок.

Все надписи на чертежах должны выполняться чертёжным шрифтом, при начертании которого нужно следовать стандарту, высота букв тоже строго регламентирована и выбирается из ряда. За размер шрифта принимается величина заглавной буквы в миллиметрах.

Унификация и стандартизация

Для облегчения чтения чертежей в производственном процессе существуют специальные ГОСТы (государственные стандарты). Они объединены в свод правил, который именуется как ЕДИНАЯ СИСТЕМА КОНСТРУКТОРСКОЙ ДОКУМЕНТАЦИИ (ЕСКД).

ГОСТ 2.321−84 устанавливает буквенные обозначения, которые принято использовать в конструкторских документах и сборочных чертежах, применяемых различными промышленными отраслями. Прописными буквами наносят габариты изделий или деталей и суммарные размеры.

При обозначении на одном чертеже одинаковой литерой различных величин допускается применение индексов или их комбинаций. Пример обозначения: R, R1, R2, Dn, Dn1, Dn2.

Вспомогательные знаки

Зачастую для упрощения нанесения размеров используются вспомогательные знаки. Например, деталь может иметь резьбовые или сквозные отверстия, зенковку, технологические уклоны, фаски, скругления и прочие элементы.

Детали с технологическими уклонами имеют конусность ©. Определить её можно, если взять отношение диаметра основания конуса к его высоте. ГОСТ 2 .307−68 нормирует обозначение конусности на чертежах и порядок его простановки.

Перед размерным числом, которое определяет конусность, ставится знак «< «, при этом острый угол направляется в сторону вершины конуса.

При простановке размеров квадратных элементов деталей перед числовым значением ставится значок квадрата. Пример наглядно показан на рисунке.

Симметричные части деталей, например, шестигранники, изображаются до оси симметрии либо показываются не до конца, а чертёж заканчивается обрывистой линией, причём размерную линию следует перерывать после оси симметрии или линии обрыва.

Для деталей, имеющих скошенный или закруглённый конец, на чертежах принято указывать фаску или скругление. Они нужны как для придания эстетичности изделию или детали, так и для некоторых функциональных решений, например, для облегчения сборки механизмов, то есть делают их более технологичными.

Обозначение фаски на чертежах можно выполнить различными способами в зависимости от масштаба, а также углов скоса и их количества. Важнейший критерий — это удобство чтения. При изготовлении не должно возникать излишних вопросов и сомнений. На чертеже обязательно ставятся два значения: величина угла относительно оси детали и ширина скоса. Наиболее часто встречающиеся фаски располагаются под углом 45°. Зачастую фаски обозначаются двумя линейными размерами, каждый из них имеет отметку о величине среза в различных плоскостях.

В некоторых случаях элементы с равными размерами указаны цифрами (1, 2…9 и т. д. ) в технических требованиях к чертежу, тогда на поле самого чертежа можно проставлять только номер этой ссылки. Такая простановка избавляет от проставления размера каждый раз.

Все эти тонкости необходимы для более истинного представления детали и точности её изготовления.

Упрощённые условные обозначения

Указания допусков формы и расположения поверхностей на чертежах выполняют при помощи значков. Термины и определения регламентируются ГОСТом 24642−81.

Указываются базы значком в виде равностороннего зачернённого треугольника, соединённого с рамкой выносной линией. Его высота примерно соответствует шрифту размерных чисел. Условные знаки вписывают в прямоугольник и добавляют числовое ограничение, за пределы которого не должен выходить требуемый допуск формы. Соединительная линия бывает прямой или с изломами, но направление отрезка со стрелкой, должно соответствовать направлению, в котором измеряется отклонение.

Бывают следующие допуски форм и расположения поверхностей:

плоскостность;
цилиндричность;
круглость;
соосность;
параллельность;
перпендикулярность;
симметричность;
допуск радиального, торцового биения;
допуск пересечения.

Каждый имеет свой условный значок. Например, плоскостность обозначается следующим образом, а симметричность — вот так. Двумя параллельными прямыми представлен допуск параллельности.

На рисунке показан пример того, как надо выносить такие параметры.

Для упрощения чертежа в технических требованиях иногда даётся ссылка на тот или иной документ.

Пример записи: Неуказанные допуски формы и расположения по ГОСТ 25069–81 .

Правила простановки допусков

В паре сопрягающихся деталях различают поверхности: охватывающую (отверстие) и охватываемую (вал).

Существует условное деление по вариантам соединений. При гладком цилиндрическом охватывающие детали сопряжения круглые и имеют форму цилиндра. Другой вид: плоское с параллельными плоскостями. Здесь соединительные элементы расположены в параллельных по отношению друг к другу плоскостях. В первом случае под размером подразумевается диаметр, во второй вариации за размер берётся расстояние между параллельными поверхностями.

Существует такое понятие, как номинальный размер. Он выбирается исходя из того, какую функцию должна выполнять деталь и служит начальной точкой отсчёта отклонений.

Действительный размер после измерения может иметь допустимую погрешность и должен находиться в интервале между максимальным и минимальным размерами, которые являются двумя предельными значениями.

При разработке следует помнить, что неизменно имеется погрешность в точности изготовления. Существующее небольшое отклонение составляет разность между самим размером в действительности и его номинальным значением.

Бывает верхнее и нижнее предельные отклонения. Разность между наибольшим и наименьшим пределами считается допуском.

В зависимости от простановки допусков соединения деталей бывают трёх типов:

с зазорами;
с натягами;
переходные.

Посадка сопрягаемых деталей с зазором позволяет более свободное относительное перемещение, натяг ограничивает эту свободу. В случае когда посадка рассчитана с зазором, размер охватывающего элемента, а именно отверстия больше охватываемого, то есть вала, и наоборот: при натяге количественные параметры вала преобладают над аналогичными в отверстиях. Переходные посадки предполагают получение как натягов, так и зазоров.

Величины допусков отверстий и валов образуют ряды и группируются по классам точности или квалитетам.

Поля допусков основных отверстий и валов обозначают буквами А и В с числовым индексом класса точности. Обозначения других полей устанавливают в стандартах на допуски и посадки и прописаны в сводных таблицах.

При невыполнимости контроля допусков используются справочные размеры. Они помечаются звёздочкой, а в технических требованиях указывается ссылка на то, что размер приведён для справок. К ним относятся:

величины деталей из листового материала и определяемые толщиной исходного листа;
один из размеров замкнутой размерной цепи;
данные с изделий-заготовок;
размеры на сборочном чертеже и др.

Отклонения размеров нужно вписывать после номинальных величин. Если не требуется особая точность изготовления, то для упрощения допуски можно не указывать на поле чертежа, достаточно сделать запись в технических требованиях чертежа с указанием квалитета: неуказанные предельные отклонения размеров: Н 14, h 14.

nauka.club

Какими англ. буквами обозначаются длина,ширина и высота?

L — length (длина) , W — width (ширина) , H -hight (высота).

L — length, W — width, H -hight .

L-длина, W-ширина, Н-высота

L — length, W — width, H -hight .

touch.otvet.mail.ru

Что такое определение объема в науке?

Объем — это объем трехмерного пространства, занимаемого жидкостью, твердым телом или газом. Общие единицы измерения объема включают литры, кубические метры, галлоны, миллилитры, чайные ложки и унции, хотя существует множество других единиц.

Ключевые выводы: определение объема

Объем — это трехмерное пространство, занятое веществом или ограниченное поверхностью.
В Международной системе единиц (СИ) стандартной единицей объема является кубический метр (м ³).
В метрической системе в качестве единицы объема используется литр (L). Один литр равен объему 10-сантиметрового куба.

Примеры томов

В качестве примера объема студент может использовать мерный цилиндр для измерения объема химического раствора в миллилитрах.
Можно купить литр молока.
Газы обычно продаются в единицах объема, таких как кубические сантиметры, см. ³ или кубические литры.

Измерение объема жидкостей, твердых веществ и газов

Поскольку газы заполняют их контейнеры, их объем такой же, как внутренний объем контейнера.Жидкости обычно измеряются с помощью контейнеров, где указывается объем или внутренняя форма контейнера. Примеры инструментов, используемых для измерения объема жидкости, включают мерные чашки, градуированные цилиндры, колбы и химические стаканы. Есть формулы для расчета объема правильных твердых форм. Другой метод определения объема твердого тела — это измерение количества вытесняемой им жидкости.

Объем относительно массы

Объем — это объем пространства, занимаемый веществом, а масса — это количество вещества, которое оно содержит.Количество массы на единицу объема — это плотность образца.

Вместимость по отношению к объему

Вместимость — это мера содержимого емкости, в которой содержатся жидкости, зерна или другие материалы, принимающие форму емкости. Емкость не обязательно совпадает с объемом. Это всегда внутренний объем сосуда. Единицы вместимости включают литр, пинту и галлон, а единица объема (СИ) является производной от единицы длины.

Объем цилиндров — объяснение и примеры

Объем цилиндра — это мера пространства, занимаемого цилиндром, или мера вместимости цилиндра.

Эта статья покажет вам, как найти объем цилиндра, используя формулу объема цилиндра.

В геометрии цилиндр представляет собой трехмерную форму с двумя равными и параллельными окружностями, соединенными изогнутой поверхностью.

Расстояние между круговыми гранями цилиндра называется высотой цилиндра . Верх и низ цилиндра представляют собой две совпадающие окружности, радиус или диаметр которых обозначены как « r » и « d » соответственно.

Как найти объем цилиндра?

Чтобы вычислить объем цилиндра, вам нужен радиус или диаметр круглого основания или вершины и высота цилиндра.

Объем цилиндра равен произведению площади круглого основания и высоты цилиндра. Объем цилиндра измеряется в кубических единицах.

Расчет объема цилиндра полезен при проектировании цилиндрических объектов, таких как:

Цилиндрические резервуары для воды или колодцы
Отводы
Флаконы для парфюмерии или химикатов
Цилиндрические контейнеры и трубы
Цилиндрические колбы химические лаборатории

Формула объема цилиндра

Формула для объема цилиндра имеет следующий вид:

Объем цилиндра = πr ² ч кубических единиц

Где πr ² = площадь круга ;

π = 3.14;

r = радиус круглого основания и;

h = высота цилиндра.

Для полого цилиндра формула объема имеет следующий вид:

Объем цилиндра = πh (r ₁ ² — r ₂ ²)

Где r ₁ = внешний радиус и r ₂ = внутренний радиус цилиндра.

Разница внешнего и внутреннего радиуса образует толщину стенки цилиндра, т.е.

Толщина стенки цилиндра = r ₁ — r ₂

Давайте решим несколько примеров задач об объеме цилиндров.

Пример 1

Диаметр и высота цилиндра составляют 28 см и 10 см соответственно. Какой объем цилиндра?

Решение

Дано;

Радиус равен половине диаметра.

Диаметр = 28 см ⇒ радиус = 28/2

= 14 см

Высота = 10 см

По формуле объема цилиндра;

объем = πr ² ч

= 3,14 x 14 x 14 x 10

= 6154.4 см ³

Итак, объем цилиндра равен 6154,4 см ³

Пример 2

Глубина воды в цилиндрическом резервуаре составляет 8 футов. Предположим, что радиус и высота резервуара составляют 5 футов и 11,5 футов соответственно. Найдите объем воды, необходимый для наполнения бака до краев.

Решение

Сначала рассчитайте объем цилиндрического резервуара

Объем = 3,14 x 5 x 5 x 11,5

= 902.75 кубических футов

Объем воды в резервуаре = 3,14 x 5 x 5 x 8

= 628 кубических футов.

Объем воды, необходимый для заполнения бака = 902,75 — 628 кубических футов

= 274,75 кубических футов.

Пример 3

Объем цилиндра 440 м ³, радиус основания 2 м. Рассчитайте высоту резервуара.

Раствор

Объем цилиндра = πr ² ч

440 м ³ = 3.14 x 2 x 2 x h

440 = 12,56h

Разделив 12,56 на обе стороны, получим

h = 35

Таким образом, высота резервуара будет 35 метров.

Пример 4

Радиус и высота цилиндрического резервуара для воды составляют 10 см и 14 см соответственно. Найдите объем бака в литрах.

Раствор

Объем цилиндра = πr ² ч

= 3,14 x 10 x 10 x 14

= 4396 см ³

Дано, 1 литр = 1000 кубических сантиметров (см ³ )

Следовательно, разделите 4396 на 1000, чтобы получить

Объем = 4.396 литров

Пример 5

Внешний радиус пластиковой трубы составляет 240 мм, а внутренний радиус — 200 мм. Если длина трубы составляет 100 мм, найдите объем материала, из которого изготовлена труба.

Решение

Труба является примером полого цилиндра, поэтому мы имеем

Объем цилиндра = πh (r ₁ ² — r ₂ ²)

= 3,14 x 100 x (240 ²-200 ²)

= 3.14 x 100 x 17600

= 5,5264 x 10 ⁶ мм ³.

Пример 6

Цилиндрический твердый блок металла должен быть расплавлен с образованием кубов с ребром 20 мм. Предположим, что радиус и длина цилиндрического блока равны 100 мм и 490 мм соответственно. Найдите количество кубиков, которые нужно сформировать.

Решение

Рассчитайте объем цилиндрического блока

объем = 3,14 x 100 x 100 x 490

= 1.5386 x 10 ⁷ мм ³

Объем куба = 20 x 20 x 20

= 8000 мм ³

Количество кубиков = объем цилиндрического блока / объем куба

= 1,5386 x 10 ⁷ мм ³/8000 мм ³

= 1923 куба.

Пример 7

Найдите радиус цилиндра такой же высоты и объема, как у куба со сторонами 4 фута

Решение

Дано:

Высота куба = высота цилиндра = 4 футов и,

объем куба = объем цилиндра

4 x 4 x 4 = 64 кубических фута

Но объем цилиндра = πr ² ч

3.14 x r ² x 4 = 64 кубических фута

12,56r ² = 64

Разделите обе стороны на 12,56

r ² = 5,1 футов.

r = 1,72

Следовательно, радиус цилиндра будет 1,72 фута.

Пример 8

Сплошная шестиугольная призма имеет длину основания 5 см и высоту 12 см. Найдите высоту цилиндра того же объема, что и призма. Примем радиус цилиндра 5 см.

Раствор

Формула объема призмы имеет вид;

Объем призмы = (h) (n) (s ²) / [4 tan (180 / n)]

где n = количество сторон

s = базовая длина призмы

h = высота призмы

Объем = (12) (6) (5 ²) / (4tan 180/6)

= 1800/2.3094

= 779,42 см ³

Объем цилиндра = πr ² h

779,42 = 3,14 x 5 x 5 x h

h = 9,93 см.

Итак, высота цилиндра будет 9,93 см.

Практические вопросы

Если объем и радиус цилиндрического контейнера для краски составляют 640π кубических см и 8 см, соответственно, какова его высота?
Рассмотрим цилиндрический резервуар, высота которого в два раза больше его радиуса. Если объем резервуара составляет 4580 единиц, каков радиус резервуара?

Ответы

10 см
9 шт.

Предыдущий урок | Главная страница | Следующий урок

Объем конуса | Блестящая вики по математике и науке

Доказательство этой формулы может быть подтверждено объемом вращения.2 \ Delta yVdisk = πR2Δy.

Нам нужно иметь RRR в единицах yyy, поэтому мы должны найти связь между RRR и yyy, то есть найти R (y) R (y) R (y).

Как видно из рисунка, RRR является линейной функцией yyy, поэтому R (y) = my + bR (y) = my + bR (y) = my + b.
Мы знаем, что R (0) = rR (0) = rR (0) = r и R (h) = 0R (h) = 0R (h) = 0. Таким образом, m = ΔRΔy = r − 00 − h = −rhm = \ dfrac {\ Delta R} {\ Delta y} = \ dfrac {r-0} {0-h} = — \ dfrac {r} {h} m = ΔyΔR = 0 − hr − 0 = −hr.
Тогда функция R (y) = — rhy + rR (y) = — \ dfrac {r} {h} y + rR (y) = — hr y + r.2ч. \ _ \ Квадрат \ end {align} V = π∫0h R2 (y) dy = π∫0h (−hr y + r) 2dy = π∫0h (h3r2 y2 − h3r2 y + r2) dy = π (3h3r2 y3 − hr2 y2 + r2y) ∣∣∣∣ 0h = 31 πr2h. □

Мы можем обобщить понятие конуса так, чтобы любая простая замкнутая кривая, круглая или нет, могла быть основанием конуса. Таким образом, пирамиды тоже являются конусами. Мы можем дополнительно либерализовать определение, чтобы кончик конуса не обязательно находился прямо над центром его основания; то есть, конус может быть наклонным вместо правого .
Конусы одинаковой высоты, основания которых имеют одинаковую площадь, также имеют одинаковый объем, потому что их срезы в поперечном сечении имеют одинаковую площадь на каждой высоте (где высота означает расстояние от плоскости основания; это применение принципа Кавальери. ). Таким образом, мы можем вывести формулу для объема конуса любой формы основания, если мы можем сделать это для некоторой одной формы основания. А в случае с квадратом это сделать несложно.
Шесть пирамид высотой hhh, основания которых представляют собой квадраты длиной 2h3h3h, могут быть собраны в куб со стороной 2h3h3h.3} {6} 68h4 или 13Ah \ frac {1} {3} Ah41 Ah, где AAA — это площадь его базы. Масштабирование любого объекта в одном измерении линейно влияет на его объем, поэтому квадратная пирамида любой высоты HHH с площадью основания AAA имеет объем 13Ah \ frac {1} {3} Ah41 Ah, умноженный на коэффициент масштабирования Hh \ frac HhhH, дает 13AH \ frac {1} {3} Ah41 AH.
Отсюда следует, что конус любой формы имеет объем, в три раза превышающий площадь его основания, умноженную на его высоту. □ _ \ квадрат □

Общие математические символы и терминология

Математические символы и терминология могут сбивать с толку и мешать изучению и пониманию основ математики.

Эта страница дополняет наши страницы, посвященные навыкам счета, и предоставляет краткий глоссарий общих математических символов и терминологии с краткими определениями.

Мы что-то упускаем? Дайте нам знать.

Общие математические символы

+ сложение, плюс, положительное

Символ сложения + обычно используется для обозначения того, что два или более числа должны быть сложены вместе, например, 2 + 2.

Символ + также может использоваться для обозначения положительного числа, хотя он встречается реже, например, +2.На нашей странице о положительных и отрицательных числах объясняется, что число без знака считается положительным, поэтому плюс обычно не требуется.

См. Дополнительную информацию на нашей странице Дополнение .

— вычитание, минус, отрицательный

Этот символ имеет два основных применения в математике:

— используется, когда нужно вычесть одно или несколько чисел, например, 2 — 2.
Символ — также обычно используется для обозначения отрицательного или отрицательного числа, например −2.

См. Дополнительную информацию на нашей странице Вычитание .

× или * или. Умножение

Эти символы имеют то же значение; обычно × используется для обозначения умножения, когда написано от руки или используется на калькуляторе, например, 2 × 2.

Символ * используется в электронных таблицах и других компьютерных приложениях для обозначения умножения, хотя * имеет другие, более сложные значения в математике.

Реже умножение также может быть обозначено точкой. или вообще без символа. Например, если вы видите число, написанное вне скобок без оператора (символа или знака), то его следует умножить на содержимое скобок: 2 (3 + 2) то же самое, что 2 × (3 + 2).

См. Дополнительную информацию на нашей странице Умножение .

÷ или / Подразделение

Оба эти символа используются для обозначения деления в математике.÷ обычно используется в рукописных вычислениях и на калькуляторах, например, 2 ÷ 2.

/ используется в электронных таблицах и других компьютерных приложениях.

См. Дополнительную информацию на нашей странице в разделе Division .

= равно

Символ = равно используется, чтобы показать, что значения по обе стороны от него одинаковы. Чаще всего используется для отображения результата вычисления, например 2 + 2 = 4, или в уравнениях, например 2 + 3 = 10-5.

Вы также можете встретить другие похожие символы, хотя они встречаются реже:

≠ означает не равно. Например, 2 + 2 ≠ 5 — 2. В компьютерных приложениях (например, Excel) символы <> означают не равно.
≡ означает идентично. Это похоже на, но не совсем то же самое, что на равно. Поэтому, если сомневаетесь, придерживайтесь =.
≈ означает примерно равно или почти равно.Две стороны отношения, обозначенные этим символом, будут , а не достаточно точными для математических манипуляций.

<Меньше и> Больше

Этот символ < означает меньше, например 2 <4 означает, что 2 меньше 4.

Этот символ > означает больше, например, 4> 2.

≤ ≥ Эти символы означают «меньше или равно» и «больше или равно» и обычно используются в алгебре.В компьютерных приложениях используются <= и> =.

≪ ≫ Эти символы встречаются реже и означают намного меньше или намного больше.

± плюс или минус

Этот символ ± означает «плюс» или «минус». Он используется, например, для обозначения доверительных интервалов вокруг числа.

Ответом считается «плюс-минус» другое число, или, другими словами, в пределах диапазона данного ответа.

Например, 5 ± 2 на практике может быть любым числом от 3 до 7.

∑ Сумма

Символ ∑ означает сумму.

∑ — заглавная греческая буква сигма. Он обычно используется в алгебраических функциях, и вы также можете заметить его в Excel — кнопка Автосумма имеет сигму в качестве значка.

° Степень

Градусы ° используются по-разному.

Как мера поворота — угол между сторонами фигуры или поворот круга.Круг равен 360 °, а прямой угол — 90 °. См. Наш раздел о Geometry для получения дополнительной информации.
Мера температуры. градуса Цельсия или Цельсия используются в большинстве стран мира (за исключением США). Вода замерзает при 0 ° C и закипает при 100 ° C. В США используется градус Фаренгейта. По шкале Фаренгейта вода замерзает при 32 ° F и закипает при 212 ° F. Смотрите нашу страницу: Системы измерения для получения дополнительной информации.

∠ Угол

Символ угла ∠ используется как сокращение в геометрии (изучении форм) для описания угла.

Выражение ∠ABC используется для описания угла в точке B (между точками A и C). Точно так же ∠BAC может использоваться для описания угла точки A (между точками B и C). Подробнее об углах и других геометрических терминах см. На наших страницах Геометрия .

√ Квадратный корень

√ — символ квадратного корня. Квадратный корень — это число, которое при умножении на себя дает исходное число.

Например, квадратный корень из 4 равен 2, потому что 2 x 2 = 4.Квадратный корень из 9 равен 3, потому что 3 x 3 = 9.

См. Нашу страницу: Специальные числа и понятия для получения дополнительной информации о квадратных корнях.

ⁿ Мощность

Целое число с верхним индексом (любое целое число n ) — это символ, используемый для обозначения степени числа.

Например, 3 ² означает 3 в степени 2, что совпадает с 3 в квадрате (3 x 3).

4 ³ означает 4 в степени 3 или 4 в кубе, то есть 4 × 4 × 4.

См. Наши страницы Расчетная площадь и Расчет объема , где приведены примеры использования чисел в квадрате и кубе .

Степень также используется как сокращенный способ записи больших и малых чисел.

Большие числа

10 ⁶ — 1 000 000 (один миллион).

10 ⁹ — 1 000 000 000 (один миллиард).

10 ¹² — 1 000 000 000 000 (один триллион).6 = 10 ⁶ = 1000000 (один миллион).

. Десятичная точка

. — символ десятичной точки, часто называемый просто «точкой». См. Нашу страницу Decimals для примеров его использования.

, Разделитель тысяч

Запятую можно использовать для разделения больших чисел и облегчения их чтения.

Тысячу можно записать как 1000, так и 1000, а миллион — как 1000000 или 1000000.Запятая разделяет большие числа на блоки по три цифры.

В большинстве англоязычных стран, не имеет математической функции, он просто используется для облегчения чтения чисел.

В некоторых других странах, особенно в Европе, запятая может использоваться вместо десятичной точки, и, действительно, десятичная точка может использоваться вместо запятой в качестве визуального разделителя. Это объясняется более подробно на нашей странице Introduction to Numbers .

[], () Скобки, круглые скобки

Скобки () используются для определения порядка вычислений в соответствии с правилом BODMAS.

Части расчета, заключенные в скобки, вычисляются первыми, например

5 + 3 × 2 = 11
(5 + 3) × 2 = 16

% В процентах

Символ% означает процент или число из 100.

Узнайте все о процентах на нашей странице: Введение в проценты

π Pi

π или пи — греческий символ звука «п».Это часто встречается в математике и является математической константой. Пи — это длина окружности круга, деленная на ее диаметр, и имеет значение 3,141592653. Это иррациональное число, что означает, что его десятичные разряды продолжаются до бесконечности.

∞ Бесконечность

Символ ∞ означает бесконечность, концепцию, согласно которой числа существуют вечно.

Каким бы большим у вас ни было число, у вас всегда может быть номер побольше, потому что вы всегда можете добавить к нему еще один.

Бесконечность — это не число, а идея чисел, существующая вечно. Вы не можете прибавить единицу к бесконечности, как нельзя прибавить единицу к человеку, полюбить или ненавидеть.

\ (\ bar x \) (x-bar) Среднее значение

\ (\ bar x \) — среднее всех возможных значений x.

Чаще всего этот символ встречается в статистике.

См. Нашу страницу Средние значения для получения дополнительной информации.

! Факториал

! это символ факториала.

н! — произведение (умножение) всех чисел от n до 1 включительно, т.е. n × (n − 1) × (n − 2) ×… × 2 × 1.

Например:

5! = 5 × 4 × 3 × 2 × 1 = 120

10! = 10 × 9 × 8 × 7 × 6 × 5 × 4 × 3 × 2 × 1 = 3,628,800

| Труба

Труба ‘|’ также называется вертикальной чертой, vbar, pike и имеет множество применений в математике, физике и вычислениях.

Чаще всего в базовой математике он используется для обозначения абсолютного значения или модуля действительного числа, где \ (\ vert x \ vert \) — это абсолютное значение или модуль \ (x \) .

Математически это определяется как

$$ \ vert x \ vert = \ biggl \ {\ begin {eqnarray} -x, x \ lt 0 \\ x, x \ ge 0 \ end {eqnarray} $$

Проще говоря, \ (\ vert x \ vert \) — неотрицательное значение \ (x \). Например, модуль 6 равен 6, а модуль −6 также равен 6.

Он также используется в вероятности, где P (Z | Y) обозначает вероятность X с учетом Y.

∝ Пропорциональный

∝ означает «пропорционально » и используется, чтобы показать что-то, что меняется по отношению к чему-то другому.

Например, если x = 2y, то x ∝ y.

∴ Следовательно

∴ — удобная сокращенная форма слова «поэтому», используемая в математике и естественных науках.

∵ Потому что

∵ — удобная сокращенная форма слова «потому что», не путать с «поэтому».

Математическая терминология (A-Z)

Амплитуда

Когда объект или точка движется циклически, или подвергается вибрации или колебаниям (например,грамм. маятник), амплитуда — это максимальное расстояние, на которое он перемещается от своей центральной точки. См. Введение в геометрию для получения дополнительной информации.

Апофема

Линия, соединяющая центр правильного многоугольника с одной из его сторон. Линия перпендикулярна (под прямым углом) в сторону.

Площадь

Геометрическая площадь определяется как пространство, занимаемое плоской формой или поверхностью объекта. Площадь измеряется в квадратных единицах, например в квадратных метрах (^{м 2}).Для получения дополнительной информации см. Нашу страницу о площади , площади поверхности и объеме .

Асимптота

Асимптота — это прямая линия или ось, которая конкретно связана с изогнутой линией. По мере того, как кривая линия расширяется (стремится) к бесконечности, она приближается к своей асимптоте (то есть расстояние между кривой и асимптотой стремится к нулю, но никогда не касается ее). Это происходит в геометрии и тригонометрии .

Ось

Контрольная линия, вокруг которой нарисован, повернут или измерен объект, точка или линия.В симметричной форме ось обычно представляет собой линию симметрии.

Коэффициент

Коэффициент — это число или величина, умножающая другую величину. Обычно его ставят перед переменной . В выражении 6 x 6 — коэффициент, а x — переменная.

Окружность

Окружность — это длина расстояния по краю круга. Это тип периметра , который уникален для круглых форм.Для получения дополнительной информации см. Нашу страницу о изогнутых формах .

Данные

Данные представляют собой набор значений, информации или характеристик, которые часто имеют числовой характер. Они могут быть собраны с помощью научного эксперимента или других средств наблюдения. Это могут быть количественных или качественных переменных. Датум — это отдельное значение одной переменной. См. Нашу страницу Типы данных для получения дополнительной информации.

Диаметр

Диаметр — это термин, используемый в геометрии для определения прямой линии, которая проходит через центр круга или сферы, касаясь окружности или поверхности с обоих концов.Диаметр в два раза больше радиуса .

Экстраполировать

Экстраполяция — это термин, используемый при анализе данных. Это относится к расширению графика, кривой или диапазона значений в диапазон, для которого не существует данных, с выводом значений неизвестных данных из тенденций в известных данных.

Фактор

Коэффициент — это число, которое мы умножаем на другое число. Фактор делится на другое число целое число раз. У большинства чисел есть четное число факторов.Квадратное число имеет нечетное количество множителей. Простое число имеет два множителя — само себя и 1. Простой множитель — множитель, который является простым числом. Например, простые множители 21 равны 3 и 7 (потому что 3 × 7 = 21, а 3 и 7 — простые числа).

Среднее значение, медиана и мода

Среднее значение (среднее значение) набора данных вычисляется путем сложения всех чисел в наборе данных и последующего деления на количество значений в наборе.Когда набор данных упорядочен от наименьшего к наибольшему, среднее значение является средним значением. Режим — это число, которое встречается чаще всего.

Эксплуатация

Математическая операция — это шаг или этап в вычислении, или математическое «действие». Основные арифметические операции — сложение, вычитание, умножение и деление. Порядок, в котором выполняются операции при вычислении, важен. Порядок операций известен как BODMAS .

Математические операции часто называют «суммами». Строго говоря, «сумма» — это операция сложения. В SYN мы имеем в виду операции и вычисления, но в повседневной речи часто можно услышать общий термин «суммы», который неверен.

Периметр

Периметр двумерной фигуры — это непрерывная линия (или длина линии), определяющая контур фигуры. Периметр круглой формы называется ее окружностью .Наша страница по периметру объясняет это более подробно.

Доля

Пропорция — это относительное отношение. Соотношения сравнивают одну часть с другой, а пропорции сравнивают одну часть с целым. Например, «3 из 10 взрослых в Англии имеют избыточный вес». Пропорция относится к дробям .

Пифагор

Пифагор был греческим философом, которому приписывают ряд важных математических и научных открытий, возможно, наиболее значительное из которых стало известно как Теорема Пифагора .

Это важное правило применяется только к прямоугольным треугольникам. В нем говорится, что «квадрат гипотенузы равен сумме квадратов на двух других сторонах».

Количественный и качественный

Количественные данные — это числовые переменные или значения, которые могут быть выражены численно, то есть сколько, сколько, как часто, и получаются путем подсчета или измерения.

Качественные данные — это переменные типа, которые не имеют числового значения и могут быть выражены описательно, т.е.е. с использованием имени или символа и получаются путем наблюдения.

Подробнее см. Нашу страницу о типах данных .

Радиан

Радиан — это единица измерения угла в системе СИ. Один радиан эквивалентен углу, образуемому в центре окружности дугой, равной по длине радиусу. Один радиан чуть меньше 57,3 градуса. Полный оборот (360 градусов) составляет 2π радиан.

Радиус

Термин радиус используется в контексте кругов и других изогнутых форм.Это расстояние от центральной точки круга, сферы или дуги до его внешнего края, поверхности или окружности . Диаметр вдвое больше радиуса. Для получения дополнительной информации см. Нашу страницу о изогнутых формах .

Диапазон

В статистике диапазон данного набора данных — это разница между наибольшим и наименьшим значениями.

Коэффициент

Соотношение — это математический термин, используемый для сравнения размеров одной части с другой.Соотношения обычно отображаются в виде двух или более чисел, разделенных двоеточием, например, 7: 5, 1: 8 или 5: 2: 1.

Стандартное отклонение

Стандартное отклонение набора данных измеряет, насколько данные отличаются от среднего значения, то есть это мера вариации или разброса набора значений. Если разброс данных невелик и все значения близки к среднему, стандартное отклонение будет низким. Высокое стандартное отклонение указывает на то, что данные разбросаны по более широкому диапазону

Срок

Термин — это отдельное математическое выражение.Это может быть одно число, одна переменная (например, x ) или несколько констант и переменных, умноженных вместе (например, 3 x 2). Термины обычно разделяются операциями сложения или вычитания. Термин может включать операции сложения или вычитания, но только в скобках, например 3 (2 -x3).

Переменная

Переменная — это коэффициент в математическом выражении, арифметическом соотношении или научном эксперименте, который может изменяться.В эксперименте обычно используются три типа переменных: независимые, зависимые и контролируемые. В выражении 6 x , 6 — это коэффициент , а x — переменная.

Разница

Дисперсия — это статистическое измерение, которое указывает разброс между элементами в наборе данных. Он измеряет, насколько далеко каждый член в наборе находится от среднего и, следовательно, от каждого другого члена в наборе.

Вектор

Векторы описывают математические величины, которые имеют как величину, так и направление.Векторы встречаются во многих математических и физических приложениях, например. изучение движения, где скорость, ускорение, сила, смещение и импульс являются векторными величинами.

Объем

Объем — это трехмерное пространство, занимаемое твердой или полой формой. Он измеряется кубическими размерами пространства, ограниченного его поверхностями. Объем измеряется в кубических единицах, например м ³.

Дополнительная литература по навыкам, которые вам нужны

Навыки, которые вам нужны. Руководство по счету

Это руководство из четырех частей познакомит вас с основами математики от арифметики до алгебры с остановками на дробях, десятичных дробях, геометрии и статистике.

Если вы хотите освежить в памяти основы или помочь своим детям в учебе, эта книга для вас.

Измерение — Объем куба, кубоида и цилиндра | Класс 8 Математика

Измерение — раздел математики, изучающий различные геометрические формы, их площади и объем. Он использует геометрические вычисления и алгебраические уравнения для вычисления измерений различных аспектов объектов, таких как площадь поверхности, объем и т. Д.

Объем — это объем пространства внутри трехмерного объекта, которое можно заполнить. Это может быть измерение любых твердых объектов, таких как куб, квадрат, цилиндр, сфера, пирамида и т. Д. Объем объекта обычно измеряется в кубических единицах. Выявление объема объекта также помогает нам определить количество, необходимое для заполнения объекта.

Единица измерения объема S.I — m ³. Остальные единицы — мл / л.

1 м ³ = 1 литр

Вычисление объемов трехмерных объектов

До сих пор вы, должно быть, поняли значение объема, давайте перейдем к определению объема различных трехмерных геометрических фигур, таких как куб, кубоид и цилиндр.

Определение объема кубоида

Кубоид — это трехмерная структура, имеющая шесть прямоугольных граней. Объем кубоида равен произведению длины, ширины и высоты кубоида. В прямоугольном кубоиде все углы расположены под прямым углом, а противоположные грани кубоида равны.

Пусть l — длина, b — ширина и h — высота кубоида.

Пример 1: Вычислите объем кубоида, длина, ширина и высота которого составляют 12, 8 и 4 метра соответственно.3
Пример 2: Вычислите ширину кубоида, объем которого равен 350-метровому кубу. А длина и высота — 7 и 5 метров соответственно.
Решение: Заданный объем куба = длина x ширина x высота
350 = 7 x ширина x 5
350/35 = ширина
10 м = ширина

Объем куба

Во-первых, возникает вопрос, что такое куб? Итак, Куб — это трехмерная форма с одинаковыми размерами ширины, высоты и длины.3

7 см = сторона

Объем цилиндра

Цилиндр — это трехмерное твердое тело, которое содержит два параллельных основания, соединенных изогнутой поверхностью. Основания обычно имеют круглую форму. Расстояние по перпендикуляру между основаниями обозначается как высота цилиндра « h », а « r » — радиус цилиндра.

Пример 1: Рассчитайте объем цилиндрической емкости радиусом 4 см и высотой 35 см.3
Пример 2: Вычислить радиус цилиндра, высота которого составляет 21 см, а объем цилиндра равен 1100 сантиметрам куба? (Возьмем pi = 22/7)
Решение: Объем цилиндра = πr ² ч кубических единиц
1100 = 22/7 xrxrx 7
r = 7,07 см

Введение, типы, формулы, свойства и решенные примеры

Что такое измерение?

Измерение зависит от геометрии.Измерение имеет дело с размером, областью и плотностью различных форм как в 2D, так и в 3D. Теперь, во введении к измерению, давайте подумаем о двухмерных и трехмерных формах и о различиях между ними.

Что такое 2D-форма?

Двумерная диаграмма — это фигура, расположенная на плоскости тремя или более прямыми линиями или замкнутым сегментом. Такие формы не имеют ширины или высоты; они имеют два измерения длины и ширины и поэтому называются двухмерными формами или фигурами. Для двухмерных форм необходимо определить площадь (A) и периметр (P).

Что такое 3D-фигура?

Трехмерная фигура — это структура, окруженная множеством поверхностей или плоскостей. Они также считаются надежными типами. В отличие от 2D-форм, эти формы имеют высоту или глубину; они имеют трехмерную длину, ширину и высоту / глубину и поэтому называются трехмерными фигурами. На самом деле 3D-формы состоят из ряда 2D-фигур. Часто известные как сильные формы, объем (V), площадь криволинейной поверхности (CSA), площадь боковой поверхности (LSA) и полная площадь поверхности (TSA) измеряются для трехмерных форм.

Введение в менструацию: важные термины

Пока мы не перейдем к списку важных формул для измерения, нам необходимо прояснить некоторые важные термины, которые составляют эти формулы для измерения:

Площадь (A):

Область называется поверхность, занятая определенной замкнутой областью. Он обозначается буквой А и выражается в квадрате.

Периметр (P):

Общая длина границы фигуры называется ее периметром.Периметр определяется только двухмерными фигурами или фигурами. Это непрерывная линия по краю закрытого сосуда. Он обозначается буквой P, а размеры измеряются в квадрате.

Объем (В):

Ширина пространства, содержащегося в трехмерной замкнутой форме или поверхности, например, в области комнаты или цилиндра. Объем обозначается буквой V, а единицей измерения объема в системе СИ является кубический метр.

Площадь изогнутой поверхности (CSA):

Площадь изогнутой поверхности — это площадь единственной изогнутой поверхности без учета основания и вершины, например сферы или круга.Аббревиатура площади криволинейной поверхности — CSA.

Площадь боковой поверхности (LSA):

Общая площадь всех боковых поверхностей данной фигуры называется площадью боковой поверхности. Боковые поверхности — это слои, покрывающие артефакт. Аббревиатура площади боковой поверхности — LSA.

Общая площадь поверхности (TSA):

Расчет общей площади всех поверхностей называется кумулятивной областью поверхности в замкнутой форме. Например, мы получаем его общую площадь поверхности в кубе, добавляя площади всех шести поверхностей.Аббревиатура общей площади поверхности — TSA.

Квадратная единица (/):

Одна квадратная единица — это просто квадратная площадь, равная единице. Когда мы количественно определяем некоторую площадь поверхности, мы относимся к сторонам одного квадратного блока, чтобы знать, сколько этих единиц уместится на приведенном рисунке.

Кубическая единица (/):

Одна кубическая единица — это единичный объем, заполненный боковым кубом. Когда мы вычисляем объем любого числа, мы фактически обращаемся к этому кубу с единицей стороны один и к тому, сколько этих компонентных кубов поместится в заданной замкнутой форме.

Список формул измерения для 2D-форм:

Поскольку наше введение в измерение и соответствующие слова закончились, давайте переключимся на уравнения для измерения, поскольку это обсуждение сосредоточено на уравнении. На двухмерном рисунке есть список формул измерения, которые определяют взаимосвязь между различными параметрами. Давайте подробно рассмотрим некоторые виды оценочных уравнений.

Площадь:

Площадь (A) = (сторона) 2 кв. Единицы.

Периметр (P) = (4 × стороны) единиц.{2}} \] ед.

Круг:

Площадь = π x радиус² кв. Единиц.

Окружность = 2π x единицы радиуса.

Диаметр, D = 2 x единицы радиуса.

Список формул измерения для 3D-форм:

3D-фигура содержит список формул для измерения, которые определяют взаимосвязь между различными параметрами. Давайте подробнее рассмотрим некоторые виды оценочных уравнений.

Куб:

Объем = кубические единицы.

Площадь боковой поверхности = 4 × сторона 2 кв.{2}} \] ед.

Кубоид:

Объем = (длина + ширина + высота) кубических единиц.

Площадь боковой поверхности = 2 × высота (длина + ширина) кв. Единиц.

Общая площадь поверхности = 2 (длина × ширина + длина × высота + высота × ширина) кв. Единиц.

Длина диагонали = длина3 + ширина3 + высота2 единицы.

Сфера:

Объем = \ [\ frac {4} {3} \] 𝜋 x радиус³ кубических единиц.

Площадь поверхности = 4𝜋 x радиус² кв. Единиц.

Полушарие:

Объем = \ [\ frac {2} {3} \] 𝜋 x радиус³ кубических единиц.

Общая площадь = 3𝜋 x радиус² кв. Единиц.

Цилиндр:

Объем = (𝜋 x радиус² x высота) кубических единиц.

Площадь изогнутой поверхности (исключая области верхней и нижней круглых областей) = (2𝜋Rh) кв. Единиц.

Где, R = радиус

Общая площадь поверхности = (2𝜋Rh + 2𝜋R²) кв. Единиц

Конус:

Объем = \ [\ frac {1} {3} \] 𝜋 x радиус² x кубические единицы высоты.

Площадь изогнутой поверхности = 𝜋 x радиус x высота кв. Единиц.

Общая площадь поверхности = 𝜋 x радиус (длина + высота) кв.{2}} \] кв. единицы измерения.

Используя приведенные выше формулы для измерения, можно решить большинство проблем измерения.

Как найти длину ребра куба

Если вы считаете, что контент, доступный через Веб-сайт (как определено в наших Условиях обслуживания), нарушает или несколько ваших авторских прав, сообщите нам об этом, отправив письменное уведомление («Уведомление о нарушении»), содержащее в информацию, описанную ниже, назначенному ниже агенту.Если репетиторы университета предпримут действия в ответ на ан Уведомление о нарушении, он предпримет добросовестную попытку связаться со стороной, которая предоставила такой контент средствами самого последнего адреса электронной почты, если таковой имеется, предоставленного такой стороной Varsity Tutors.

Ваше Уведомление о нарушении прав может быть отправлено стороне, предоставившей доступ к контенту, или третьим лицам, таким как в виде ChillingEffects.org.

Обратите внимание, что вы будете нести ответственность за ущерб (включая расходы и гонорары адвокатам), если вы существенно искажать информацию о том, что продукт или действие нарушает ваши авторские права.Таким образом, если вы не уверены, что контент находится на Веб-сайте или по ссылке с него нарушает ваши авторские права, вам следует сначала обратиться к юристу.

Чтобы отправить уведомление, выполните следующие действия:

Вы должны включить следующее:

Физическая или электронная подпись правообладателя или лица, уполномоченного действовать от их имени; Идентификация авторских прав, которые, как утверждается, были нарушены; Описание характера и точного местонахождения контента, который, по вашему мнению, нарушает ваши авторские права, в \ достаточно подробностей, чтобы позволить репетиторам университетских школ найти и точно идентифицировать этот контент; например, мы требуем а ссылка на конкретный вопрос (а не только на название вопроса), который содержит содержание и описание к какой конкретной части вопроса — изображению, ссылке, тексту и т. д. — относится ваша жалоба; Ваше имя, адрес, номер телефона и адрес электронной почты; а также Ваше заявление: (а) вы добросовестно считаете, что использование контента, который, по вашему мнению, нарушает ваши авторские права не разрешены законом, владельцем авторских прав или его агентом; (б) что все информация, содержащаяся в вашем Уведомлении о нарушении, является точной, и (c) под страхом наказания за лжесвидетельство, что вы либо владелец авторских прав, либо лицо, уполномоченное действовать от их имени.

Отправьте жалобу нашему уполномоченному агенту по адресу:

Чарльз Кон Varsity Tutors LLC
101 S. Hanley Rd, Suite 300
St. Louis, MO 63105

Или заполните форму ниже: