Вычислительные навыки 5 класс Вариант 1
| Вычислительные навыки 5 класс Вариант 2
|
Вычислительные навыки 5 класс Вариант 1
| Вычислительные навыки 5 класс Вариант 2
|
Вычислительные навыки 5 класс Вариант 1
| Вычислительные навыки 5 класс Вариант 2
|
Вычислительные навыки 5 класс Вариант 1
| Вычислительные навыки 5 класс Вариант 2
|
Вычислительные навыки 5 класс Вариант 1
| Вычислительные навыки 5 класс Вариант 2
|
Фамилия ______________________________ 2. Сравни 6,31 и 17,28 3. Реши уравнение 2,8 : х = 0,8 4. Округли 45,1254 до сотых 5. Вычисли 4,125 ∙ 1,6 – 5,7 | Ответы: 1 |
Фамилия ______________________________ | Ответы: 1. |
Фамилия ______________________________ 4. Округли 45,94 до целых 5. Вычисли 5,8 ∙ 0,1 + 5,7 : 10 | Ответы: 1. |
Фамилия ______________________________ | Ответы: 1. |
Фамилия ______________________________ | Ответы: 1. |
Фамилия ______________________________ | Ответы: 1. |
Фамилия ______________________________ | Ответы: 1. |
Фамилия ______________________________ | Ответы: 1. |
Фамилия ______________________________ | Ответы: 1. 3. 15 4. 0,33 5. 20,635 |
Фамилия ______________________________ | Ответы: 1. |
Фамилия ______________________________ 4. Округли 0,9458 до целых 5. Вычисли 0,06 ∙ 0,1 + 12 : 0,1 | Ответы: 1. |
Фамилия ______________________________ | Ответы: 1. |
Фамилия ______________________________ | Ответы: 1. |
Фамилия ______________________________ | Ответы: 1. |
Фамилия ______________________________ | Ответы: 1. 3. 8,5 4. 0,9 5. 547,725 |
Фамилия ______________________________ | Ответы: 1. |
Фамилия ______________________________ | Ответы: 1. 4. 235,1 5. 31,333 |
Фамилия ______________________________ | Ответы: 1. |
Фамилия ______________________________ | Ответы: 1. 5. 43,164 |
Фамилия ______________________________ | Ответы: 1. |
Фамилия ______________________________ | Ответы: 1. 4. 1,236 5. 2344,87 |
Фамилия ______________________________ | Ответы: 1. |
Фамилия ______________________________ | Ответы: 1. |
Фамилия ______________________________ | Ответы: 1. |
Achievethecore.org :: Дроби
Многочисленные исследования говорят нам о том, что гибкость и точность работы с дробями являются одними из наиболее важных элементов успеха учащихся в математике. Одна из самых важных задач учителей начальных классов средних классов состоит в том, чтобы помочь всем детям опираться на свое понимание целых чисел и концептуализировать дроби как часть системы счисления, чтобы полностью рассуждать, вычислять и применять понимание дробей.
На этой странице есть что-то для всех — классного руководителя, тренера, руководителя и директора, — которым нужны большие ресурсы и поддержка для их собственного изучения дробей, а также для преподавания и изучения дробей с учениками. . Используйте меню навигации, чтобы найти исследования и обоснования, примеры задач на дроби для использования со студентами и профессиональные учебные ресурсы для создания сообщества и обучения с коллегами.
Почему дроби?
Преподавание и изучение концепций дроби часто бывает довольно сложным. Многие учителя сами не были обучены критическим математическим понятиям, лежащим в основе дробей, когда они были студентами. (Помните приемы?) Даже во время своей профессиональной подготовки многие учителя не имели возможности заниматься глубоким обучением, посвященным исключительно дробям. Хотя понимание и овладение дробями имеет решающее значение для математических навыков, эти концепции и навыки не всегда являются приоритетными при подготовке учителей или профессиональном развитии.
Кроме того, мир вокруг нас бомбардирует наших учеников изображениями и словами о фракциях, которые работают против наших усилий. Вы когда-нибудь слышали, как кто-то говорит, разделяя угощение: «Я хочу большую половину!»? Однако по определению половинки равны. Представьте, насколько сбивает с толку этот язык для учащихся, которые начинают понимать дроби. Они видят рисунки фруктовых пирогов и пирогов с пиццей, и их просят несколько раз заштриховать части этих пирогов. Помогает ли это им понять, что дробь сама по себе является числом, или укрепляет ошибочное убеждение, что дробь — это всего лишь часть числа, всего лишь числовой кусочек целого пирога?
Многие учащиеся борются с дробями, но цветные учащиеся, учащиеся из бедных семей и изучающие английский язык с меньшей вероятностью будут иметь доступ к эффективным методам обучения, соответствующей индивидуальной поддержке или методам обучения и материалам, отражающим их идентичность. Чтобы реализовать изучение дробей более справедливо, мы должны учитывать студентов, поддерживающих , культурно значимое содержание и практику и согласованные учебные материалы . Это означает, что преподаватели должны иметь глубокие знания о фракционном содержании и обучать таким образом, чтобы ценить все учащиеся, их происхождение, языки, культуры, точки зрения, знания и навыки. В этом сборнике вы найдете эти важные элементы обучения дробям.
Чтобы реализовать изучение дробей более справедливо, мы должны учитывать студентов, поддерживающих , культурно значимое содержание и практику и согласованные учебные материалы . Это означает, что преподаватели должны иметь глубокие знания о фракционном содержании и обучать таким образом, чтобы ценить все учащиеся, их происхождение, языки, культуры, точки зрения, знания и навыки. В этом сборнике вы найдете эти важные элементы обучения дробям.
Поддержка социального, эмоционального и академического развития в области математики . Ясно, что внимание должно быть направлено не только на понимание дробей и академическое развитие учащихся, но и на их социальные и эмоциональные потребности. В этом документе вы найдете более подробное описание того, как это сделать, включая примеры действий для поддержки студенческого агентства, личности и принадлежности.
Карта когерентности . Карта когерентности оказалась невероятно полезной при разработке опыта обучения этой фракции. Вот короткое видео, созданное Washington Core Advocates, в котором карта согласованности рассматривается как инструмент.
Карта когерентности оказалась невероятно полезной при разработке опыта обучения этой фракции. Вот короткое видео, созданное Washington Core Advocates, в котором карта согласованности рассматривается как инструмент.
Карта когерентности Дробная активность . Используйте это задание, чтобы просмотреть стандарты для разных классов. В рамках каждого стандарта потратьте некоторое время на чтение основного стандарта, выдержек из документа «Прогресс», относящихся к этому стандарту, и задач, подпадающих под этот стандарт. Учтите: Какова связь между стандартами и последующими последствиями понимания учащимися значения дроби на основе единичного мышления?
Фракция Руководство для преподавателей . Преподавание фракционного содержания в отдельных классах и школах может сильно различаться. Если ваши ученики спотыкаются при работе с дробями, возможно, им не хватает некоторых основных концепций дробей. Это руководство предназначено для того, чтобы помочь вам определить некоторые традиционные практики, которые могут мешать обучению учащихся, и предложить альтернативные подходы.
Дроби как числа
Если задать вопрос: « Являются ли дроби числами, и как узнать? » вы можете быть удивлены ответами и обоснованиями, которые вы получите. Неправильные представления, которые вы найдете в этих ответах, указывают на то, что усложняет как понимание, так и преподавание дробей. В следующих коллекциях заданий для каждого класса вы найдете ресурсы, которые помогут вам мыслить уверенно (и точно) в ответах.
Да, дробь — это число, потому что ее можно поставить в числовой строке.
По мере того, как разворачивается история фракций, важно оставаться на связи с прогрессом, изложенным в самих стандартах, копать глубже и позволять исследованиям и осмыслению. Доля единиц играет решающую роль в этом обучении и занимает видное место в каждой коллекции на уровне класса. Коллекции на уровне классов намеренно выделяют числовую линию над моделями стержней и круговыми моделями, чтобы подчеркнуть дроби по сравнению с предшествующей работой с целыми числами, и не включают все стандарты NF или полностью учитывают аспект строгости в одном классе.
Задания для 3 класса
Как бы вы описали длину показанного отрезка?Это вводное задание является одним из семи примеров из этой коллекции для классов. Он служит связующим звеном между предыдущей работой учащихся с целыми числами и введением 3-го класса в дроби как числа. Он обеспечивает отправную точку для работы с дробями, которая пытается пробудить любопытство учащихся к ответу на вопрос: «Зачем нам вообще нужны числа, отличные от целых чисел?»
В 3 классе основное внимание уделяется дробям как числам и , расширяя представление учащихся о числовой прямой, чтобы включить дроби, а также целые числа .
Задания на части для 3 класса . В этом ресурсе используются примеры задач, чтобы выделить основные идеи дробями для 3-го класса. Здесь представлены образцы работ учащихся (иногда в письменной форме, а иногда в виде видео), дополнительные ресурсы для учебной поддержки и вопросы для продвижения идентичности учащихся, свободы действий и принадлежности к ним как к учащимся и деятели математики.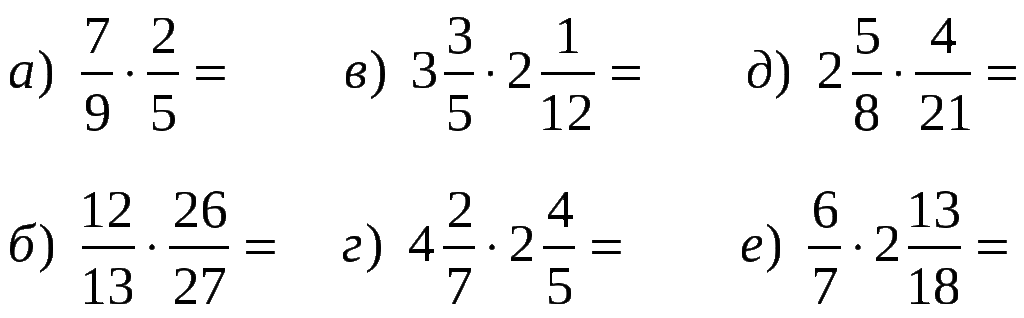
Задания для 4 класса
Какая дробь больше: 3 / 7 или 6 / 13 ?Это вводное задание показывает рост по сравнению с работой 3-го класса, где учащиеся сравнивают дроби с , как числители , или , как знаменатели , с работой 4-го класса, где учащиеся сравнивают дроби с , в отличие от числителей , и , в отличие от . знаменатели. Это один из девяти примеров, которые вы найдете в коллекции для классов.
В 4 классе основное внимание уделяется тому, чтобы учащиеся применяли свои знания о дробях к сравнению дробей и сложению и вычитанию дробей . Кроме того, домен поднимает его на ступеньку выше, поскольку учащихся знакомят с десятичными дробями и рассуждают об их размере по сравнению с долями десятых и сотых.
Задания на части для 4 класса . В этом ресурсе используются примеры задач, чтобы выделить основные идеи дробями для 4 класса. Здесь представлены образцы работ учащихся (иногда в письменной форме, иногда в виде видео), дополнительные ресурсы для учебной поддержки и вопросы, призванные повысить самобытность учащихся, свободу действий и принадлежность к ним как к учащимся и деятели математики.
Здесь представлены образцы работ учащихся (иногда в письменной форме, иногда в виде видео), дополнительные ресурсы для учебной поддержки и вопросы, призванные повысить самобытность учащихся, свободу действий и принадлежность к ним как к учащимся и деятели математики.
Задания для 5 класса
Какова сумма этих дробей?Это вступительное задание служит связующим звеном между навыками учащихся 4-го класса по составлению эквивалентных дробей и сложению дробей со знаменателями , например , и ожиданием 5-го класса по сложению дробей и дробей более единицы с в отличие от знаменателей. Далее приводится описание этой задачи вместе с семью дополнительными примерами, чтобы подчеркнуть содержание оценки.
В 5 классе основное внимание уделяется учащимся расширить свои навыки работы с целыми числами — сложения, вычитания, умножения и деления — до дробей .
Дробные задачи 5 класса . В этом ресурсе используются примеры задач, чтобы дробно выделить основные идеи для 5-го класса. Здесь представлены образцы работ учащихся (иногда в письменном виде, а иногда в виде видео), дополнительные ресурсы для учебной поддержки и вопросы для продвижения идентичности учащихся, их свободы действий и принадлежности к учащимся и ученикам. деятели математики.
Здесь представлены образцы работ учащихся (иногда в письменном виде, а иногда в виде видео), дополнительные ресурсы для учебной поддержки и вопросы для продвижения идентичности учащихся, их свободы действий и принадлежности к учащимся и ученикам. деятели математики.
Задания для 6 класса и выше
В то время как предмет «Числа и операции — дроби» охватывает 3–5 классы, изучение дробей и их применения выходит далеко за рамки начальных классов.
Как бы вы написали числа в точках A и B?Это задание предназначено для того, чтобы учащиеся использовали свое понимание дробей как чисел, полученных в 3-5 классах, и расширили их известную систему счисления, включив в нее рациональные числа.
6 класс и выше Дробные задания . В этом ресурсе используются примеры задач, чтобы выделить большие идеи дробями для 6-го класса и старшей школы. Есть образцы студенческих работ в письменной и / или видеоформе, дополнительные ресурсы для учебной поддержки и вопросы для продвижения студенческой идентичности, свободы действий и принадлежности к учащимся и тем, кто занимается математикой.
Дела для 6 класса . По мере того, как учащиеся проходят начальные и средние классы, важно знакомить их с содержанием на уровне класса таким образом, чтобы подтверждать знания, которыми они уже владеют. Ресурсы Do Now предназначены для использования в начале урока, чтобы познакомить учащихся с содержанием 6-го класса «Отношения и пропорциональное мышление». Ресурсы объединяют страницу работы ученика с руководством для учителя, которое содержит учебные вопросы и языковую поддержку, а также аннотированные работы учеников.
Тренеры и руководители инструкторов
Тренеры и руководители инструкторов выполняют важную работу по поддержке учителей и учащихся, занимающихся содержанием фракций. Приведенные ниже ресурсы предназначены для обеспечения высококачественного профессионального обучения и коучинга.
Вопрос к изображению Дробная активность . Используйте это профессиональное учебное задание, чтобы изучить и обсудить возможные изображения и визуальные эффекты, с которыми вы и ваши ученики можете столкнуться в учебных единицах. Помогают ли учащимся изображения фрагментов, которые им показывают, или мешают их пониманию?
Помогают ли учащимся изображения фрагментов, которые им показывают, или мешают их пониманию?
5frac — Математические укладчики
ТЭКС
5.1 Стандарты математических процессов. Студент использует математические процессы, чтобы приобрести и продемонстрировать математическое понимание. Студент должен:
A. Применять математику к проблемам, возникающим в повседневной жизни, обществе и на рабочем месте;
B. Использовать модель решения проблем, которая включает анализ имеющейся информации, формулирование плана или стратегии, определение решения, обоснование решения и оценку процесса решения проблемы и обоснованности решения;
C. Выбрать инструменты, в том числе реальные объекты, манипуляции, бумагу и карандаш, а также соответствующие технологии, а также методы, в том числе математические расчеты в уме, оценку и чувство числа, для решения задач;
D.
 Излагать математические идеи, рассуждения и их последствия, используя различные представления, включая символы, диаграммы, графики и соответствующий язык;
Излагать математические идеи, рассуждения и их последствия, используя различные представления, включая символы, диаграммы, графики и соответствующий язык;E. Создавать и использовать представления для организации, записи и передачи математических идей;
F. Анализировать математические отношения для связи и передачи математических идей;
G. Отображать, объяснять и обосновывать математические идеи и аргументы, используя точный математический язык в письменной или устной речи.
5.3 Количество и операции. Учащийся применяет стандарты математического процесса для разработки и использования стратегий и методов вычисления положительных рациональных чисел для эффективного и точного решения задач. Ожидается, что учащийся:
H. Представлять и решать сложение и вычитание дробей с неравными знаменателями, относящимися к одному и тому же целому, используя предметы и графические модели и свойства операций; Стандарт поддержки.

I. Представлять и решать умножение целого числа на дробь, относящуюся к одному и тому же целому, с использованием предметов и графических моделей, включая модели площадей; Стандарт поддержки.
K. Свободно складывать и вычитать положительные рациональные числа; Стандарт готовности.
L. Разделить целые числа на дроби и дроби на целые числа.
Common Core
Число и операции — дроби:
Используйте эквивалентные дроби в качестве стратегии для сложения и вычитания дробей.
5.NF.A.1 Складывать и вычитать дроби с разными знаменателями (включая смешанные числа) путем замены данных дробей эквивалентными дробями таким образом, чтобы получить эквивалентную сумму или разность дробей с одинаковыми знаменателями. Например, 2/3 + 5/4 = 8/12 + 15/12 = 23/12. (В общем, a/b + c/d = (ad + bc)/bd.)
5.NF.A.2 Решите текстовые задачи на сложение и вычитание дробей, относящихся к одному и тому же целому, включая случаи в отличие от знаменателей, например, с использованием визуальных моделей дробей или уравнений для представления проблемы.
 Используйте эталонные дроби и числовой смысл дробей для мысленной оценки и оценки обоснованности ответов. Например, распознайте неверный результат 2/5 + 1/2 = 3/7, заметив, что 3/7 < 1/2 .
Используйте эталонные дроби и числовой смысл дробей для мысленной оценки и оценки обоснованности ответов. Например, распознайте неверный результат 2/5 + 1/2 = 3/7, заметив, что 3/7 < 1/2 .
Применить и расширить прежнее понимание умножения и деления.
5.NF.B.3 Интерпретировать дробь как деление числителя на знаменатель ( a / b = a ÷ b ). Решайте текстовые задачи на деление целых чисел, чтобы получить ответы в виде дробей или смешанных чисел, например, используя визуальные модели дробей или уравнения для представления задачи. Например, интерпретируйте 3/4 как результат деления 3 на 4, заметив, что 3/4, умноженное на 4, равно 3, и что, когда 3 целого делятся поровну между 4 людьми, каждый человек получает долю размером 3/4. Если 9 человек хотят разделить 50-фунтовый мешок риса поровну по весу, сколько фунтов риса должен получить каждый? Между какими двумя целыми числами лежит ваш ответ?
5.
 NF.B.4 Применение и расширение предыдущего понимания умножения для умножения дроби или целого числа на дробь.
NF.B.4 Применение и расширение предыдущего понимания умножения для умножения дроби или целого числа на дробь.5.NF.B.4.A Интерпретировать произведение ( a / b ) × q как a частей разделения q 909 0 03, равных 03 на части; эквивалентно, в результате последовательности операций a × q ÷ b . Например, используйте модель визуальной дроби, чтобы показать (2/3) × 4 = 8/3, и создайте контекст истории для этого уравнения. Сделайте то же самое с (2/3) × (4/5) = 8/15. (В общем случае (a/b) × (c/d) = (ac)/(bd).
5.NF.B.5 Интерпретировать умножение как масштабирование (изменение размера) на:
использование моделей визуальных фракций или уравнений для представления проблемы.
5.NF.B.7 Применить и расширить прежнее понимание деления, чтобы разделить дробные единицы на целые числа и целые числа на дробные единицы.


 7 • 1,4
7 • 1,4 7 • 1,4
7 • 1,4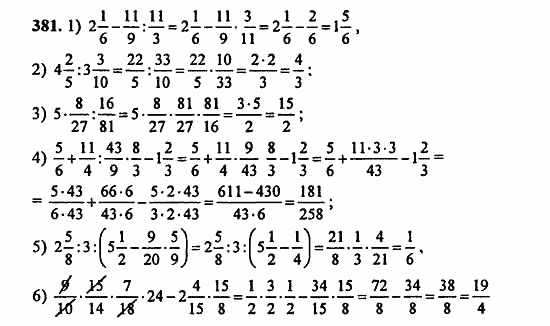 5-й класс
5-й класс

 Сравни 6,001 и 6,01
Сравни 6,001 и 6,01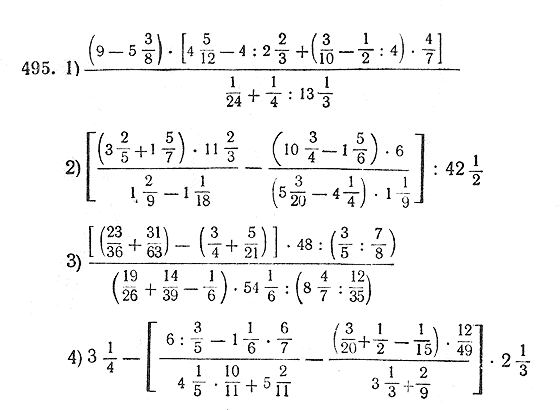
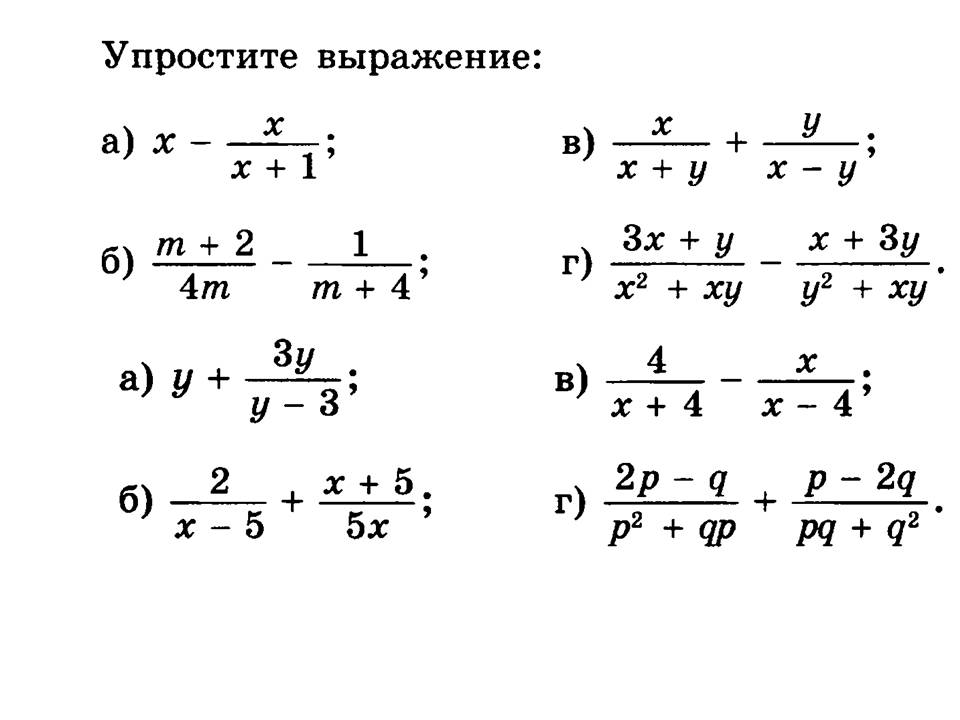

 Как разделить десятичную дробь на натуральное число? Приведи пример.
Как разделить десятичную дробь на натуральное число? Приведи пример. Округли 1,23012 до десятых
Округли 1,23012 до десятых 14,1
14,1 Как разделить десятичную дробь на 0,1; 0,01; 0,001; …? Приведи пример.
Как разделить десятичную дробь на 0,1; 0,01; 0,001; …? Приведи пример. Излагать математические идеи, рассуждения и их последствия, используя различные представления, включая символы, диаграммы, графики и соответствующий язык;
Излагать математические идеи, рассуждения и их последствия, используя различные представления, включая символы, диаграммы, графики и соответствующий язык;
 Используйте эталонные дроби и числовой смысл дробей для мысленной оценки и оценки обоснованности ответов. Например, распознайте неверный результат 2/5 + 1/2 = 3/7, заметив, что 3/7 < 1/2 .
Используйте эталонные дроби и числовой смысл дробей для мысленной оценки и оценки обоснованности ответов. Например, распознайте неверный результат 2/5 + 1/2 = 3/7, заметив, что 3/7 < 1/2 . NF.B.4 Применение и расширение предыдущего понимания умножения для умножения дроби или целого числа на дробь.
NF.B.4 Применение и расширение предыдущего понимания умножения для умножения дроби или целого числа на дробь.