Помогаю с учёбой — Преподаватель Анна Евкова
Рада видеть вас на моем сайте. Если вы здесь – значит, вам необходима помощь с учебой. |
Я, Анна Евкова, бывший преподаватель Самарского института информатики и вычислительной техники и моя команда преподавателей поможем вам справиться с трудностями в заданиях. Мы поможем с любым заданием от простого заказа в одну формулу, или если у вас будет заказ на написание большой работы примерно на 198 страниц — мы это тоже умеем!
Я всегда в вашем смартфоне, заказывайте где удобно и когда удобно — просто прислав файлы в Telegram!
Все заказы выполняются качественно, профессионально и высылаются раньше срока. Каждый выполненный заказ проходит проверку на плагиат, вы не сдадите на проверку одинаковую с кем-то работу. Ваш заказ будет уникальным!
Ваш заказ будет уникальным!
Подготовимся онлайн совместно со мной или с преподавателем из моей команды, проработаем базовые темы, освоим сложные разделы, отработаем экзаменационные задания и подойдём к сдаче любого предмета максимально подготовленным и расскажем все секреты.
Лучшие университеты мира: МГУ и MIT
Моя видео презентация:
Пять простых шагов и всё будет на ❝отлично❞
Шаг 1. Сфотографируйте задание так, чтобы изображение было максимально четким. В чат прикрепите необходимые для выполнения вашей работы, лекции, учебники, методички и т. д. (если имеются). При необходимости напишите дополнительные пояснения.
Шаг 2. Все файлы пришлите мне в чат в Telegram.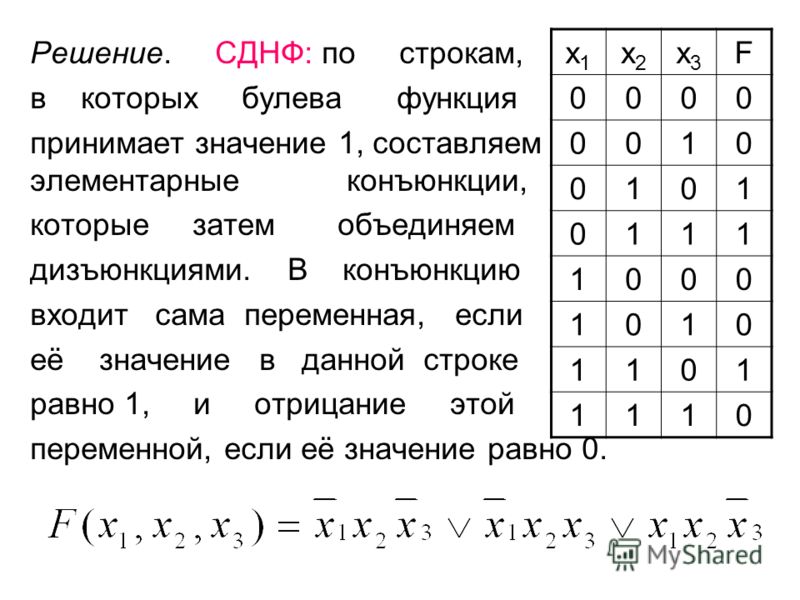
После этого я изучу и оценю. (Не забывайте чем больше времени, тем меньше цена!)
Шаг 3. Если всё понравится — оплатите. Оплатить можно с помощью баланса мобильного телефона, картой Visa и MasterCard, а также через Apple Pay и Google Pay.
Шаг 4. Приступаю к работе. Все необходимые требования и сроки будут соблюдены. Более 78% заказов отправляются в чат раньше указанного времени.
Шаг 5. Получаете заказ в чат. Если у вас возникнут вопросы, я подробно отвечу. Гарантия на заказ действует 1 год. В течение этого времени ошибки в заказе будут исправлены.
ТОП 5 ответов на ваши вопросы
Как вы работаете?
Для того, чтобы разобраться с этим вопросом, предлагаю ознакомиться с простым алгоритмом:
- Вы присылаете необходимые файлы с описанием в Telegram.
- Я знакомлюсь с файлами, и оцениваю заказ.

- Вы оплачиваете заказ.
- Я, или преподаватель, начинаем работу над заказом.
- В согласованный срок, или раньше, Вы получаете свою работу файлом в чат.
Какая будет цена?
Невозможно ответить на этот вопрос не изучив файлы. Стоимость определяется исходя из нескольких важных факторов: уровень сложности задания, определенные требования к оформлению.
Для точной оценки стоимости присылайте файлы в чат в Telegram. Например: лекции, методички, учебники (если такие имеются).
Какой срок выполнения?
Минимальный срок выполнения заказа варьируется от 2 до 4 дней. Главное помнить, что для срочных заказов цена будет увеличиваться, а срок выполнения сокращаться.
Как происходит оплата?
Оплатить можно с помощью баланса мобильного телефона, картой Visa и MasterCard, а также через Apple Pay и Google Pay.
Какие гарантии?
Любые ошибки, допущенные мной или преподавателем в заказе, исправим в течении 1 года.
Что обо мне говорят студенты и школьники
Разместила отзывы с Ютуба и чуть ниже с Вконтакте, остальные отзывы на моём ютуб канале и социальных сетях.
youtube.com/embed/YPUfikF82Bo»> youtube.com/embed/gaOdLZkyy6E»>
Правовые документы:
Условия использования
Политика конфиденциальности
Помогаю с учёбой — Преподаватель Анна Евкова
Рада видеть вас на моем сайте. Если вы здесь – значит, вам необходима помощь с учебой. |
Я, Анна Евкова, бывший преподаватель Самарского института информатики и вычислительной техники и моя команда преподавателей поможем вам справиться с трудностями в заданиях. Мы поможем с любым заданием от простого заказа в одну формулу, или если у вас будет заказ на написание большой работы примерно на 198 страниц — мы это тоже умеем!
Я всегда в вашем смартфоне, заказывайте где удобно и когда удобно — просто прислав файлы в Telegram!
Все заказы выполняются качественно, профессионально и высылаются раньше срока. Каждый выполненный заказ проходит проверку на плагиат, вы не сдадите на проверку одинаковую с кем-то работу. Ваш заказ будет уникальным!
Каждый выполненный заказ проходит проверку на плагиат, вы не сдадите на проверку одинаковую с кем-то работу. Ваш заказ будет уникальным!
Подготовимся онлайн совместно со мной или с преподавателем из моей команды, проработаем базовые темы, освоим сложные разделы, отработаем экзаменационные задания и подойдём к сдаче любого предмета максимально подготовленным и расскажем все секреты.
Лучшие университеты мира: МГУ и MIT
Моя видео презентация:
Пять простых шагов и всё будет на ❝отлично❞
Шаг 1. Сфотографируйте задание так, чтобы изображение было максимально четким. В чат прикрепите необходимые для выполнения вашей работы, лекции, учебники, методички и т.
Шаг 2. Все файлы пришлите мне в чат в Telegram.
После этого я изучу и оценю. (Не забывайте чем больше времени, тем меньше цена!)
Шаг 3. Если всё понравится — оплатите. Оплатить можно с помощью баланса мобильного телефона, картой Visa и MasterCard, а также через Apple Pay и Google Pay.
Шаг 4. Приступаю к работе. Все необходимые требования и сроки будут соблюдены. Более 78% заказов отправляются в чат раньше указанного времени.
Шаг 5. Получаете заказ в чат. Если у вас возникнут вопросы, я подробно отвечу. Гарантия на заказ действует 1 год. В течение этого времени ошибки в заказе будут исправлены.
ТОП 5 ответов на ваши вопросы
Как вы работаете?
Для того, чтобы разобраться с этим вопросом, предлагаю ознакомиться с простым алгоритмом:
- Вы присылаете необходимые файлы с описанием в Telegram.

- Я знакомлюсь с файлами, и оцениваю заказ.
- Вы оплачиваете заказ.
- Я, или преподаватель, начинаем работу над заказом.
- В согласованный срок, или раньше, Вы получаете свою работу файлом в чат.
Какая будет цена?
Невозможно ответить на этот вопрос не изучив файлы. Стоимость определяется исходя из нескольких важных факторов: уровень сложности задания, определенные требования к оформлению.
Для точной оценки стоимости присылайте файлы в чат в Telegram. Например: лекции, методички, учебники (если такие имеются).
Какой срок выполнения?
Минимальный срок выполнения заказа варьируется от 2 до 4 дней. Главное помнить, что для срочных заказов цена будет увеличиваться, а срок выполнения сокращаться.
Как происходит оплата?
Оплатить можно с помощью баланса мобильного телефона, картой Visa и MasterCard, а также через Apple Pay и Google Pay.
Какие гарантии?
Любые ошибки, допущенные мной или преподавателем в заказе, исправим в течении 1 года.
Что обо мне говорят студенты и школьники
Разместила отзывы с Ютуба и чуть ниже с Вконтакте, остальные отзывы на моём ютуб канале и социальных сетях.
youtube.com/embed/vtUKcvDOhBs»> youtube.com/embed/cBeKupGTino»>
Правовые документы:
Условия использования
Политика конфиденциальности
Помогаю с учёбой — Преподаватель Анна Евкова
Рада видеть вас на моем сайте. Если вы здесь – значит, вам необходима помощь с учебой. |
Я, Анна Евкова, бывший преподаватель Самарского института информатики и вычислительной техники и моя команда преподавателей поможем вам справиться с трудностями в заданиях. Мы поможем с любым заданием от простого заказа в одну формулу, или если у вас будет заказ на написание большой работы примерно на 198 страниц — мы это тоже умеем!
Я всегда в вашем смартфоне, заказывайте где удобно и когда удобно — просто прислав файлы в Telegram!
Все заказы выполняются качественно, профессионально и высылаются раньше срока. Каждый выполненный заказ проходит проверку на плагиат, вы не сдадите на проверку одинаковую с кем-то работу. Ваш заказ будет уникальным!
Каждый выполненный заказ проходит проверку на плагиат, вы не сдадите на проверку одинаковую с кем-то работу. Ваш заказ будет уникальным!
Подготовимся онлайн совместно со мной или с преподавателем из моей команды, проработаем базовые темы, освоим сложные разделы, отработаем экзаменационные задания и подойдём к сдаче любого предмета максимально подготовленным и расскажем все секреты.
Лучшие университеты мира: МГУ и MIT
Моя видео презентация:
Пять простых шагов и всё будет на ❝отлично❞
Шаг 1. Сфотографируйте задание так, чтобы изображение было максимально четким. В чат прикрепите необходимые для выполнения вашей работы, лекции, учебники, методички и т. д. (если имеются). При необходимости напишите дополнительные пояснения.
д. (если имеются). При необходимости напишите дополнительные пояснения.
Шаг 2. Все файлы пришлите мне в чат в Telegram.
После этого я изучу и оценю. (Не забывайте чем больше времени, тем меньше цена!)
Шаг 3. Если всё понравится — оплатите. Оплатить можно с помощью баланса мобильного телефона, картой Visa и MasterCard, а также через Apple Pay и Google Pay.
Шаг 4. Приступаю к работе. Все необходимые требования и сроки будут соблюдены. Более 78% заказов отправляются в чат раньше указанного времени.
Шаг 5. Получаете заказ в чат. Если у вас возникнут вопросы, я подробно отвечу. Гарантия на заказ действует 1 год. В течение этого времени ошибки в заказе будут исправлены.
ТОП 5 ответов на ваши вопросы
Как вы работаете?
Для того, чтобы разобраться с этим вопросом, предлагаю ознакомиться с простым алгоритмом:
- Вы присылаете необходимые файлы с описанием в Telegram.

- Я знакомлюсь с файлами, и оцениваю заказ.
- Вы оплачиваете заказ.
- Я, или преподаватель, начинаем работу над заказом.
- В согласованный срок, или раньше, Вы получаете свою работу файлом в чат.
Какая будет цена?
Невозможно ответить на этот вопрос не изучив файлы. Стоимость определяется исходя из нескольких важных факторов: уровень сложности задания, определенные требования к оформлению.
Для точной оценки стоимости присылайте файлы в чат в Telegram. Например: лекции, методички, учебники (если такие имеются).
Какой срок выполнения?
Минимальный срок выполнения заказа варьируется от 2 до 4 дней. Главное помнить, что для срочных заказов цена будет увеличиваться, а срок выполнения сокращаться.
Как происходит оплата?
Оплатить можно с помощью баланса мобильного телефона, картой Visa и MasterCard, а также через Apple Pay и Google Pay.
Какие гарантии?
Любые ошибки, допущенные мной или преподавателем в заказе, исправим в течении 1 года.
Что обо мне говорят студенты и школьники
Разместила отзывы с Ютуба и чуть ниже с Вконтакте, остальные отзывы на моём ютуб канале и социальных сетях.
youtube.com/embed/vtUKcvDOhBs»> youtube.com/embed/cBeKupGTino»>
Правовые документы:
Условия использования
Политика конфиденциальности
Дискретная математика
1.1. Цели курса
В колледже Джорджии Гвиннетт студенты, успешно окончившие курс дискретной математики,
Рассуждайте математически и используйте математический язык соответствующим образом, чтобы продемонстрировать понимание понимания и построения математических аргументов.
Выполняйте комбинаторный анализ для решения задач подсчета и анализа алгоритмов.
Продемонстрировать понимание дискретных структур, включая множества, перестановки, отношения, графы и деревья.

Демонстрируйте алгоритмическое мышление, используя математическое творчество и критическое мышление, определяя алгоритмы, проверяя их работу и анализируя время, необходимое для выполнения определенных алгоритмов.
Используйте соответствующие технологии для оценки, анализа и синтеза информации в ситуациях решения проблем.
Эти цели курса помогают структурировать содержание этого класса, который направлено на студентов г. информационные технологии, информатика и прикладная математика. Основное внимание уделяется применению методы дискретной математики из двух широких составляющих областей дискретного математика, а именно комбинаторика или методы перечисления, а также теория графов.
С этой целью алгоритмическое мышление фигурирует
видное место в этом курсе.
Разработка алгоритмов, особенно алгоритмов
применительно к сетям, предполагает использование методов теории графов. Реализация алгоритмов
требует тщательного понимания логических структур и, как правило, реализации сверху вниз
подход, начиная с описания спецификаций, а затем продолжая
к реализации псевдокода и, наконец, к кодированию, зависящему от языка
реализация. Более того, анализ сложности алгоритмов требует знания функций,
рост функций и методы подсчета из комбинаторного анализа. Точно так же математическая индукция и рекурсия
определения используются связным образом для понимания алгоритмов и вариантов их реализации.
рекурсивно против итеративно.
Реализация алгоритмов
требует тщательного понимания логических структур и, как правило, реализации сверху вниз
подход, начиная с описания спецификаций, а затем продолжая
к реализации псевдокода и, наконец, к кодированию, зависящему от языка
реализация. Более того, анализ сложности алгоритмов требует знания функций,
рост функций и методы подсчета из комбинаторного анализа. Точно так же математическая индукция и рекурсия
определения используются связным образом для понимания алгоритмов и вариантов их реализации.
рекурсивно против итеративно.
Подход, который мы используем, заключается в интегративном включении программирования и алгоритмы в курс. Цель состоит в том, чтобы помочь улучшить успехи учащихся с их широкими учебными планами по программированию в таких курсах, как промежуточное и продвинутое программирование.
1.2. Приложения дискретной математики
Дискретная математика применяется во многих областях, включая физическую, инженерную и, во все большей степени,
социальные науки.
1.2.1. Приложения к прикладной математике
Большинство задач, связанных с вычислительными методами, необходимо решить с помощью ЭВМ. Вместо того, чтобы решить для карту температуры всей плоской области, мы решаем для температура с использованием дискретного набора сетки или сетки точек на репрезентативное подмножество плоской области.
Рис. 1. Непрерывный температурный профиль в сравнении с дискретным сеточным представлением на компьютере
1.2.2. Приложения к информационным технологиям и информатике
Дискретная математика необходима для информатики, поскольку информация и данные хранятся в цифровом виде. Цифровой представленные данные по своей сути дискретны и обрабатываются с использованием дискретных методов. Например, дискретная сетка курса представление двумерного распределения температуры с пластины выше может быть:
\( \left(\begin{matrix}1&1&1\\2&4&8\\3&9&27\\4&16&64\\5&25&125\\\end{matrix}\right) \)
В базе данных реестра избирателей могут быть избиратели, доступные из списка:
\(
\left(\begin{matrix}Джон\ Смит\\Рахим\ Джонсон\\. \\.\\.\\Сара\ Мюллер\\\end{matrix}\right)
\)
\\.\\.\\Сара\ Мюллер\\\end{matrix}\right)
\)
К которым может потребоваться доступ и сортировка, скажем, по географическому или алфавитному принципу.
1.2.3. Приложения к науке о данных
В решениях многих проблем, связанных с наукой о данных, используются алгоритмы машинного обучения, которые носят дискретный характер. Информация, которая нуждается в обработке, является дискретной, так же как и основные проблемы науки о данных, такие как проблемы классификации или кластеризации. Особенно
Информация, состоящая из наборов данных, представляется с использованием различных данных структуры, включая графические структуры, такие как деревья. Методы и алгоритмы науки о данных включают процедуры, которые манипулировать этими графическими структурами, например, в сети, деревья классификации и деревья решений.
Проблемы классификации носят дискретный характер.
 Классификация опухолей как злокачественных или доброкачественных предполагает попытку предсказать
если переменная \(Y\), о которой мы можем думать, что она принимает два значения либо \(0\), либо \(1\)
либо злокачественные, либо доброкачественные. Существуют различные
алгоритмы, используемые в задачах классификации, таких как бинарная опухоль
классификация, в том числе методы от вероятности.
Классификация опухолей как злокачественных или доброкачественных предполагает попытку предсказать
если переменная \(Y\), о которой мы можем думать, что она принимает два значения либо \(0\), либо \(1\)
либо злокачественные, либо доброкачественные. Существуют различные
алгоритмы, используемые в задачах классификации, таких как бинарная опухоль
классификация, в том числе методы от вероятности.
Рисунок 2. Алгоритм бинарной классификации («1» злокачественное, «0» доброкачественное)
1.2.4. Приложения к инженерии
Цифровая обработка сигнала включает в себя съемку видео, звук или другой сигнал, такой как температура, давление, положение и скорость, которые являются непрерывными, оцифровывая их, а затем математическая обработка цифрового сигнала.
Рис. 3. Непрерывный и дискретный временной сигнал
1.2.5. Приложения комбинаторики
Комбинаторика включает в себя частично изучение подсчета числа
объектов, удовлетворяющих заданному условию, из наборов
переменный размер. Перечисление и комбинаторика важны во многих
области и примеры, включая:
Перечисление и комбинаторика важны во многих
области и примеры, включая:
1.2.6. Приложения теории графов
Теория графов , который изучает структуры, построенные с узлами и ребра, соединяющие их, имеют приложения во многих областях, в том числе,
Рисунок 4. Теория графов и молекулярные связи
Рисунок 5. Ранжирование страниц с использованием модели теории графов.
Пример задачи о кратчайшем туре показан ниже. с помощью программного решения.
Рисунок 6. Использование программного обеспечения, такого как Mathematica, для решения задачи оптимизации сети, такой как поиск кратчайшего тура.
1.2.7. Приложения вероятности и статистики
Многие назначения вероятностей основаны на счетных и комбинаторных методах.
Если предположить, что вероятность дождя одинакова в любой день в сентябре нас может интересовать вероятность того, что дождь идет \(0\) дней, идет дождь ровно \(1\) день, ровно \(2\) день и т.
 д.
Такие распределения вероятностей называются дискретными распределениями.
в отличие от непрерывных распределений, таких как кривая нормального распределения.
д.
Такие распределения вероятностей называются дискретными распределениями.
в отличие от непрерывных распределений, таких как кривая нормального распределения.Также в науке о данных часто используются вероятностные и статистические методы. Проблема бинарной классификации, например, классификация опухоли как злокачественные или доброкачественные, использует метод статистического моделирования, называемый регрессия, в частности логистическая регрессия для определения силы связи между независимой переменной и зависимой переменная неоднородность. В примере классификации опухоли независимые переменная будет \((x_1,x_2 )\) (упругая неоднородность, нелинейная упругость), и зависимая переменная будет \(Y\), классифицируется как \(0\) или \(1\), (злокачественные или доброкачественные).
Дискретные математические методы важны для понимания и
анализ социальных сетей, в том числе социальных сетей.
Математика голосования – это процветающая область исследований, в том числе математический анализ манипулирование избирательными округами в пользу и / или не одобряют конкурирующие политические партии. Следующий пример иллюстрирует некоторые из основные идеи, связанные с джерримендерингом.
1.3. Понимание непрерывных и дискретных наборов
Наборы объектов дискретный если есть зазор между каждым из элементов. Неформально мы имеем в виду, что элементы нет постоянно подключен чтобы там значения элементов множества не попадают в континуум. Практически говоря, множества дискретны, если они могут быть подсчитано.
Конечное множество всегда дискретно, так как его можно сосчитать. |
1.3.1. Примеры дискретных наборов
Существуют различные типы дискретных множеств.
1.4. Упражнения
Задайте множество всех отношений из множества \(\{A, B \}\) в множество, \(\{0, 1, 2\}\) и объясните, почему множество дискретно.
Попробуйте дважды бросить шестигранный кубик. Возможные результаты имеют вид \((2, 3)\), что соответствует прокатке a \(2\), за которым следует бросок \(3\) или \(((3,2)\), что соответствует прокатке \(3\), за которым следует бросок \(2\).
Перечислите все возможные исходы.
Объясните, почему множество всех возможных исходов дискретно.
Дискретная математика Приложение C | University of Wisconsin River Falls
Все курсы содержания профессионального образования, ведущие к сертификации, должны включать преподавание и оценку Стандартов содержания штата Висконсин в области содержания.
В этом столбце перечислите стандарты штата Висконсин, которые включены в этот курс. Стандарты для каждой области контента можно найти в документе Wisconsin Content Standards. | В этой колонке укажите характер оценок успеваемости, используемых в этом курсе для оценки уровня владения учащимися каждым стандартом. |
|---|---|
Структуры внутри дисциплины, исторические корни и развивающаяся природа математики, а также взаимодействие между технологией и дисциплиной. | Домашние задания по схемам Эйлера и путям Гамильтона относятся к историческим корням предмета. Задания по различным алгоритмам касаются взаимодействия техники и предмета. |
Содействие формированию у учащихся концептуального и процедурного понимания. | Используются обсуждения в классе в сочетании с домашними заданиями. |
Помощь всем учащимся в формировании понимания дисциплины, включая: . Уверенность в своих способностях использовать математические знания. . Осознание полезности математики. . Экономические последствия тонкой математической подготовки. | Большинство тем, затронутых в курсе, связаны с приложениями математики. Каждое задание используется для оценки знаний учащихся об этих приложениях. |
Исследование, предположения, изучение и тестирование всех аспектов решения проблем. | При обсуждении в классе задач на счет применяются различные стратегии решения задач. |
Формулирование и постановка математических задач, решение проблем с использованием нескольких стратегий, оценка результатов, обобщение решений, эффективное использование подходов к решению проблем и применение математического моделирования к реальным ситуациям. | Задачи подсчета сначала тщательно ставятся, а затем решаются с помощью прямых и косвенных методов, таких как соотношения включения-исключения и рекуррентные соотношения. Способность студентов сделать это затем оценивается на экзамене. |
Создание убедительных математических аргументов, постановка математических вопросов и предположений, формулирование контрпримеров, построение и оценка аргументов, а также использование интуитивного, неформального исследования и формального доказательства. | Ожидается, что учащиеся продемонстрируют на заданиях и экзаменах, что они могут строить доказательства, используя прямые и косвенные методы, методы противоречия и индукции. Также ожидается, что они будут знать, когда и как приводить контрпримеры. |
Выражение идей устно, письменно и визуально с использованием математического языка, обозначений и символов; перевод математических идей между контекстами и между ними. | Ожидается, что учащиеся примут участие в обсуждениях в классе по темам, а затем напишут решения упражнений, используя правильный математический язык. |
Соединение понятий и процедур математики, установление связей между математическими направлениями, между математикой и другими дисциплинами, а также с повседневной жизнью. | Взаимодействие между теорией графов и счетными темами и задачами из повседневной жизни подчеркивается в дискуссиях и на экзаменах. |
Выбор подходящих представлений для облегчения решения математических задач и перевод между представлениями для разъяснения ситуаций решения задач. | Ожидается, что учащиеся продемонстрируют различные способы представления графов и выберут наилучшее представление для данного приложения. |
Математические процессы в том числе: . . Коммуникация. . Рассуждения и формальные и неформальные аргументы. . Математические связи. . Представительства. . Технологии. | Каждый экзамен и домашнее задание используются для оценки этих навыков в контексте различных тем курса. |
Числовые операции и отношения как с абстрактной, так и с конкретной точек зрения, идентифицирующие приложения реального мира, а также представляющие и связывающие математические концепции и процедуры, включая: . Чувство числа. . Теория множеств. . Количество и действие. . Составление и разложение чисел, включая разрядное значение, простые числа, множители, кратные, обратные значения и распространение этих понятий на всю математику. . Системы счисления через действительные числа, их свойства и отношения. . Вычислительные процедуры. . Пропорциональное рассуждение. . Теория чисел. | Выполняя задания, учащиеся должны продемонстрировать свою способность работать с элементарной теорией множеств, элементарной теорией чисел, включая алгоритм Евклида, и работать с альтернативной системой счисления модульной арифметики. |
Математические понятия и процедуры, а также связи между ними для обучения числовым операциям и отношениям верхнего уровня, включая: . Расширенные процедуры подсчета, включая объединение и пересечение наборов, а также операции со скобками. . Алгебраические и трансцендентные числа. . Комплексная система счисления, включая полярные координаты. . Приближенные методы как основа для численного интегрирования, фракталов и численных доказательств. . Ситуации, в которых числовые аргументы представлены в различных ситуациях в классе и в реальном мире (например, политических, экономических, научных, социальных), могут быть созданы и подвергнуты критическому анализу. . Возможности, с помощью которых можно оценить допустимые пределы погрешности (например, оценка стратегий, проверка обоснованности результатов и использование технологий для выполнения вычислений). | Учащиеся работают с расширенными процедурами подсчета, включая включение-исключение в заданиях. Эти методы также оцениваются на экзаменах. |
Геометрия и измерения как с абстрактной, так и с конкретной точки зрения, а также для определения реальных приложений, а также математических концепций, процедур и связей между ними, включая: . Формальный и неформальный спор. . Названия, свойства и взаимосвязи двух- и трехмерных фигур. . Пространственное чувство. . Пространственное мышление и использование геометрических моделей для представления, визуализации и решения проблем. . Преобразования и способы, которыми вращение, отражение и перемещение фигур могут иллюстрировать понятия, свойства и отношения. . Системы координатной геометрии, включая отношения между координатной и синтетической геометрией, а также обобщение геометрических принципов от двухмерной системы к трехмерной системе. . Понятия измерения, включая измеримые атрибуты, стандартные и нестандартные единицы измерения, точность и правильность, а также использование соответствующих инструментов. . Структура систем измерения, включая разработку и использование систем измерения и отношения между различными системами. Измерение, включая длину, площадь, объем, размер углов, вес и массу, время, температуру и деньги. . Измерение, оценка и использование измерений для описания и сравнения геометрических явлений. . Косвенное измерение и его использование, включая разработку формул и процедур для определения меры для решения проблем. | Не оценивается в этом курсе. |
Математические понятия, процедуры и связи между ними для обучения геометрии и измерениям верхнего уровня, включая: . . Преобразования, координаты и векторы и их использование при решении задач. Трехмерная геометрия и ее обобщение на другие измерения. Топология, включая топологические свойства и преобразования. . Возможность представить убедительные аргументы посредством демонстрации, неформального доказательства, контрпримеров или других логических средств, чтобы показать истинность утверждений и/или обобщений. | Не оценивается в этом курсе |
Статистика и вероятность как с абстрактной, так и с конкретной точек зрения, а также для определения реальных приложений, а также математических концепций, процедур и связей между ними, включая: . Использование данных для изучения реальных проблем. . Процесс исследования, включающий постановку проблемы, разработку плана сбора данных, а также сбор, запись и организацию данных. . Представление данных в виде графиков, таблиц и сводной статистики для описания распределения данных, центральной тенденции и дисперсии. . Анализ и интерпретация данных. . Случайность, выборка и вывод. . Вероятность как способ описания шансов или риска в простых и сложных событиях. . Прогнозирование результатов на основе экспериментов или теоретических вероятностей. | Приемы решения задач на счет применяются к элементарным вероятностным вопросам в заданиях и на экзаменах. |
Математические понятия, процедуры и связи между ними для обучения статистике и вероятности верхнего уровня в том числе: . Использование случайной величины при генерации и интерпретации вероятностных распределений. . Описательная и выводная статистика, показатели выплат, включая достоверность и надежность, и корреляция. . Теория вероятностей и ее связь со статистикой вывода. . Дискретные и непрерывные распределения вероятностей как основы для вывода. . Ситуации, в которых учащиеся могут анализировать, оценивать и критиковать методы и выводы статистических экспериментов, о которых сообщается в журналах, журналах, средствах массовой информации, рекламе и т. д. | Не оценивается в этом курсе. |
Функции, алгебра и основные понятия, лежащие в основе исчисления как с абстрактной, так и с конкретной точки зрения, и для определения реальных приложений, а также математические понятия, процедуры и связи между ними, включая: . Узоры. . Функции, используемые для описания отношений и моделирования реальных ситуаций. . Представления ситуаций, которые включают переменные величины с выражениями, уравнениями и неравенствами и которые включают алгебраические и геометрические отношения. . Множественные представления отношений, сильные стороны и ограничения каждого представления и преобразование из одного представления в другое. . Атрибуты полиномиальных, рациональных, тригонометрических, алгебраических и экспоненциальных функций. . Операции над выражениями и решение уравнений, систем уравнений и неравенств конкретными, неформальными и формальными методами. . Основные концепции исчисления, включая скорость изменения, пределы и приближения для неправильных областей. | Основное понятие функции исследуется в заданиях. Затем это понятие применяется для выявления закономерностей в задачах подсчета и анализа эффективности алгоритмов. |
Математические понятия, процедуры и связи между ними для обучения функциям верхнего уровня, алгебре и понятиям исчисления, включая: . Понятия исчисления, включая пределы (эпсилон-дельта) и касательные, производные, интегралы, последовательности и ряды. . Моделирование для решения проблем. . Методы исчисления, включая нахождение пределов, производных, интегралов и использование специальных правил. . Приложения для вычислений, включая моделирование, оптимизацию, скорость и ускорение, площадь, объем и центр масс. . Численные и приближенные методы, включая правило Симпсона, правило трапеций, приближение Ньютона и линеаризацию. . Многомерное исчисление. . Дифференциальные уравнения. | Не оценивается в этом курсе. |
Дискретные процессы как с абстрактной, так и с конкретной точки зрения, а также для определения реальных приложений, а также математических концепций, процедур и связей между ними, включая: . Техники счета. . Представление и анализ задач дискретной математики с использованием последовательностей, теории графов, массивов и сетей. . Итерация и рекурсия. | Понимание учащимися всех этих тем оценивается на протяжении всего курса при выполнении заданий, обсуждении в классе и на экзаменах. |
Математические понятия, процедуры и связи между ними для обучения дискретной математике верхнего уровня в том числе: . . Матрицы как математическая система, а матрицы и матричные операции как средства записи информации и решения задач. . Разработка и анализ алгоритмов. | Понимание учащимися вводной логики, математической индукции, конечных графов, матриц как метода представления графов и анализа алгоритмов оценивается на заданиях, в обсуждениях в классе и на экзаменах |
7 основных разделов дискретной математики
Математика делает четкое различие между обычно синонимичными терминами «элементарный» и «простой», где «элементарный» означает, что для чтения работы не требуется очень много математических знаний, а «простой» означает, что не очень много математических знаний. нужна способность понимать это. – Юлиан Гавел
Дискретная математика — это раздел математики, включающий дискретные элементы, использующие алгебру и арифметику. Он постоянно применяется во многих областях математики и информатики. Это считается очень эффективным подходом к развитию силы и решению проблем.
Он постоянно применяется во многих областях математики и информатики. Это считается очень эффективным подходом к развитию силы и решению проблем.
Дискретная математика фокусируется на систематическом изучении математических структур , которые по своей природе дискретны и не требуют веры в непрерывность.
Иногда ее также называют математикой принятия решений или конечной математикой, она работает с объектами, которые могут иметь различные отдельные значения. Объекты, которые изучаются в рамках этой части математики, поддаются исчислению на огромном уровне, таком как формальный язык, целые числа, конечные графы и т. д.
, разработка программного обеспечения, криптография, алгоритмы и т. д. Он включает в себя различные темы, такие как теория графов, теория множеств, теория вероятностей и многие другие.
И, следовательно, этот учебник объясняет концепции и функции различных тем (ветвей) под навесом дискретной математики.
Содержание
1. Что такое математика?
2. Что такое дискретная математика?
3. Разделы дискретной математики
4. Заключение
Давайте начнем с небольшого обсуждения простой концепции математики. объекты. Справляется с логическими рассуждениями и количественными расчетами.
Однако его эволюция включает в себя растущую степень идеализации и осмысления его предмета.
В целом математику можно разделить на две категории:
1. Непрерывная математика − В зависимости от непрерывной числовой прямой или действительных чисел, непрерывная математика может характеризоваться тем фактом, что среди любых двух чисел всегда существует бесконечное количество чисел.
- Например, непрерывную математическую функцию можно изобразить непрерывной кривой без разрывов.
- Вдобавок к этому непрерывная математика дает превосходные методы и инструменты для изучения изменений явлений реального мира с течением времени, таких как движение планет вокруг Солнца.
2. Дискретная математика − Включая дискретные (различные) значения между любыми двумя точками, существует счетное количество точек.
- Для конечного набора объектов функция может быть определена в терминах упорядоченных пар списка, содержащего эти объекты, которые могут быть отображены как полный список этих пар.
- Вдобавок к этому дискретная математика дает соответствующие инструменты и процедуры для интерпретации неожиданно трансформирующихся явлений реального мира.
- Практикуется от компьютеров до преобразования телефонных звонков и от личных заданий до приложений генетики .

(Обязательно к прочтению: Введение в байесовскую статистику)
Что такое дискретная математика ?
Дискретная математика — это раздел математики, работающий с объектами, который рассматривает только отдельные, разделенные значения. В отличие от непрерывной математики, дискретная математика может быть охарактеризована целыми числами. Это математический язык компьютерных наук, который можно применять в практических областях математики.
Проще говоря, дискретная математика дает человеку возможность понимать математический язык, который можно изучить с помощью различных его ветвей. Кроме того;
Считается отличным инструментом для улучшения мышления и способности решать проблемы. Таким образом, его важность в последние годы значительно возросла с ростом цифровых устройств.

Комбинации, теория графов и логические утверждения широко используются как структуры в дискретной математике наряду с конечными или бесконечными числами.
Он используется при разработке повседневно используемых приложений и программ в области информатики.
Это важно для цифровых устройств, хотя мир технологий постоянно развивается, исследования и исследования в области дискретной математики могут стать для нас ценным развитием.
В частности, дискретная математика не ограничивается только целыми числами, она также охватывает математические структуры или разнообразные методы, состоящие из отдельных частей, которые можно объяснить в терминах конечных последовательностей символов с компьютерной клавиатуры.

В широком смысле дискретная математика — это исследование методов, идей и средств рассуждения, необходимых в различных прикладных дисциплинах, таких как компьютерные науки или информационные технологии.
Являясь порталом в области продвинутой теоретической математики, он помогает понять разницу между аналоговыми и дискретными системами.
Математика — это не осторожное шествие по расчищенной дороге, а путешествие в неведомую дикую местность, где путешественники часто теряются. Строгость должна быть сигналом для историка, что карты были сделаны, а настоящие исследователи ушли куда-то еще. — В. С. Энглин
Дискретная математика включает различные области исследований: теорию графов и гиперграфов, теорию кодирования, блочные конструкции, комбинаторику, теорию множеств, теорию матроидов, дискретную геометрию, матрицы, дискретную вероятность и части криптографии.
(рекомендуйте прочитать: что такое граф знаний?)
. в соответствующем исследовании, которое обсуждается в этом разделе. Однако большинство из этих математических тем связаны с информатикой.
Основные темы (разделы) дискретной математики
- Комбинаторика
Комбинаторика — это специальная математика счета и организации. Он применяет математические операции для подсчета вещей (больших по количеству) и их упорядочения соответствующим образом.
Будучи полезным приложением в информатике, методы комбинаторики полезны при разработке и измерении количества операций, требуемых компьютерным алгоритмом. Это жизненно важная тема в изучении дискретной математики.
Поскольку это связано с упорядочиванием (группировкой) вещей, его можно рассматривать для подсчета возможных исходов при однородном вероятностном событии.
Фундаментальные правила, связанные с группировкой вещей, — это правило произведения и правило суммы, которые управляют актом расположения посредством операций умножения и сложения соответственно.
Комбинаторика имеет дело с возможным расположением или конфигурацией объектов в наборе, эти комбинаторные задачи бывают трех типов:
Экзистенциальная комбинаторика: изучает существование или отсутствие определенных конфигураций.
Перечислительная комбинаторика: занимается подсчетом количества конфигураций определенного типа.
Конструктивная комбинаторика: имеет дело с методами, которые идентифицируют определенные конфигурации, которые противоположны отражению их существования.

- Теория графов
Теория графов — это систематическое изучение различных видов графов, которые, возможно, представляют собой совокупность связанных узлов. Проще говоря, граф — это набор точек, известных как узлы или вершины, которые связаны между собой серией линий, называемых ребрами.
Изучение графов или теории графов является важной частью ряда дисциплин в области математики, инженерии и компьютерных наук.
Графики особенно удобны для представления всех типов реальных проблем. Как правило, график (G) включает в себя две вещи;
- Набор V=V(G), где компоненты, связанные с набором, известны как вершины, точки или узлы G.
- Множество E = E(G) неорганизованной пары непохожих вершин, называемых ребрами G.
(Аналогичный блог: Что такое теория групп?)
- Теория чисел
Теория чисел — это изучение натуральных чисел и особенно их свойств делимости. Натуральные числа охватывают коммутативные и ассоциативные операции сложения и умножения, где каждое имеет тождество, а умножение распространяется на сложение. И никакое натуральное число не имеет аддитивной или мультипликативной инверсии, за исключением единичных элементов 0 и 1.
Натуральные числа охватывают коммутативные и ассоциативные операции сложения и умножения, где каждое имеет тождество, а умножение распространяется на сложение. И никакое натуральное число не имеет аддитивной или мультипликативной инверсии, за исключением единичных элементов 0 и 1.
Делимость: Если для заданных чисел a и b возможно, что (a÷b) дает целое число, то в этом случае можно сказать, что b делит a, символически b | а. И если это верно, то b является делителем или множителем a, а a кратно b. Другими словами, если б | a, то a= bk для некоторого целого числа k. Некоторые ценные факты о делимости;
Если д | м и г | п, затем д | (м + п). Пусть m = ad и n = bd, тогда (m + n) = (a + b)d.
Если д | n и n ≠ 0, то d ≤ n. Предположим, что n = k, d ≠ 0 означает, что k ≥ 1 означает, что n = kd ≥ d.
Для всех d, d | 0.
 Пусть 0 · d = 0.
Пусть 0 · d = 0. Если d|m или d|n, то d|mn. Предположим, что m = kd, тогда mn = (nk)d или, наоборот, если n = kd, то mn = (mk)d.
Также иногда встречается несоответствие между определением натурального числа N (которое включает 0) и определением, данным теоретиками чисел (которое не включает). Как правило, теоретики чисел хотели бы исключить 0, так как многие теоремы о числах требуют оговорки «кроме 0».
- Теория вероятностей
Вероятность можно определить как идентификацию возможности возникновения события, с точки зрения математики, это подробное описание случайных процессов и их соответствующих результатов.
Чтобы представить вероятность события, оно отображается числом от 0 до 1 включительно. Несколько законов вероятности имеют широкое применение в самых разных областях, таких как генетика, прогнозирование погоды, фондовые рынки и т. д. Кроме того,
д. Кроме того,
Дискретная вероятность — это вероятность, основанная на дискретном наборе исходов.
Наиболее фундаментальным типом вероятности является равномерная вероятность. Кроме того, если исходы в наборе равновероятны, то вероятность каждого события эквивалентна отношению мощностей.
Законы произведения, суммы и дополнения вероятности действуют аналогично законам комбинаторики. Кроме того, структура принципа включения и исключения (ПИС) вероятности также такая же, как ПИС для наборов.
(Статья по теме: Введение в распределение вероятностей)
- Теория множеств
Будучи разделом математики, теория множеств занимается сбором объектов. Наборы могут быть дискретными или непрерывными; и на начальном уровне теория множеств связана с тем, почему и как эти множества могут быть организованы, интегрированы и подсчитаны. Это включает в себя;
Это включает в себя;
Мощность конечного множества — это, в частности, количество элементов в этом множестве. Для данного множества A его мощность может быть выражена как |A|.
Дополнением множества является множество элементов, не входящих в это множество. Кроме того, изучение дополнений множества предоставляет различное количество методов для вычисления мощностей конечных множеств.
Объединение и пересечение предлагают несколько способов объяснить, как можно консолидировать любую комбинацию множеств.
Законы Де Моргана обеспечивают тождества/выражения для дополнений союзов и пересечений.
Принцип включения и исключения (PIE) способствует процессам идентификации либо объединения, либо пересечения между двумя или более наборами.
(Предлагаемый блог: Что такое описательный анализ?)
- Булева алгебра
Булева алгебра описывает операции, определенные над переменными, которые учитывают значение true (1) или false (0). Это реализовано для разработки компьютерных или цифровых схем с помощью логических вентилей, которые принимают сигналы на вход и выдают сигналы на выходе.
Это реализовано для разработки компьютерных или цифровых схем с помощью логических вентилей, которые принимают сигналы на вход и выдают сигналы на выходе.
Ниже приведены свойства булевой алгебры;
Коммутативные свойства: (i)a+b = b+a и (ii)a*b=b *a
Распределительные свойства: (i) a+(b*c)=(a+b)*(a+c) и (ii)a*(b+c)=(a*b)+(a* в)
Идентификационные свойства: (i) a+0=a и (ii) a *1=a
Дополненные законы: (i) a+a’=1 и (ii)a * a’=0
- Бинарные деревья
Граф, не имеющий цикла, называется ациклическим графом. Дерево — это ациклический граф или граф, не имеющий циклов. Дерево — это просто ациклический граф или граф, не имеющий цикла, а общее дерево — это непустой конечный набор компонентов, известных как вершины или узлы, которые обладают свойством, состоящим в том, что каждый узел может иметь минимальную степень, равную 1, и максимальную. степень как н.
Дерево — это просто ациклический граф или граф, не имеющий цикла, а общее дерево — это непустой конечный набор компонентов, известных как вершины или узлы, которые обладают свойством, состоящим в том, что каждый узел может иметь минимальную степень, равную 1, и максимальную. степень как н.
Если указать двоичное дерево, то в условиях, когда исходящая степень каждого узла меньше или эквивалентна 2 в направленном дереве, дерево называется двоичным деревом. И дерево, которое включает в себя узлы, такие как пустое дерево, является бинарным деревом.
Некоторые из основных терминов и определений бинарных деревьев:
Корень: Двоичное дерево имеет единственный узел, известный как корень дерева.
Левый потомок: Левый узел корня называется его левым потомком.
Правый потомок: Правый узел корня называется его правым потомком.

Родительский узел: Родительский узел — это тот, у которого есть левый дочерний или правый дочерний узел, или оба.
Братья и сестры: Два узла дерева, имеющие одного родителя, называются братьями и сестрами.
Лист: Узел, не имеющий дочерних элементов, называется листом. Однако количество листьев на дереве может варьироваться от минимума, равного одному, до максимума, равного половине числа вершин в дереве.
Заключение
Завершая блог, можно сказать, что дискретная математика — это раздел математики, который занимается различными наборами объектов, принимая во внимание только различные, разделенные объекты.
Математика не является дедуктивной наукой, это клише.




 Классификация опухолей как злокачественных или доброкачественных предполагает попытку предсказать
если переменная \(Y\), о которой мы можем думать, что она принимает два значения либо \(0\), либо \(1\)
либо злокачественные, либо доброкачественные. Существуют различные
алгоритмы, используемые в задачах классификации, таких как бинарная опухоль
классификация, в том числе методы от вероятности.
Классификация опухолей как злокачественных или доброкачественных предполагает попытку предсказать
если переменная \(Y\), о которой мы можем думать, что она принимает два значения либо \(0\), либо \(1\)
либо злокачественные, либо доброкачественные. Существуют различные
алгоритмы, используемые в задачах классификации, таких как бинарная опухоль
классификация, в том числе методы от вероятности. д.
Такие распределения вероятностей называются дискретными распределениями.
в отличие от непрерывных распределений, таких как кривая нормального распределения.
д.
Такие распределения вероятностей называются дискретными распределениями.
в отличие от непрерывных распределений, таких как кривая нормального распределения.
 Решение проблем.
Решение проблем.


 Системы геометрии, включая евклидову, неевклидову, координатную, трансформационную и проективную геометрию.
Системы геометрии, включая евклидову, неевклидову, координатную, трансформационную и проективную геометрию.


 Темы, включая символическую логику, индукцию, линейное программирование и конечные графы.
Темы, включая символическую логику, индукцию, линейное программирование и конечные графы.



