Задачи по математике как решать: примеры и способы решения математических задач для родителей

примеры и способы решения математических задач для родителей

На протяжении всего обучения школьникам приходится решать задачи — в начальной школе по математике, а затем по алгебре, геометрии, физике и химии. И хотя условия задач в разных науках отличаются, способы решения основаны на одних и тех же логических принципах. Понимание того, как устроена простая задача по математике, поможет ребёнку разработать алгоритмы для решения задач из других областей науки. Поэтому учить ребёнка решать задачи необходимо уже с первого класса. 

Нередки случаи, когда точные науки вызывают у детей сопротивление. Видя это, учителя и родители записывают таких детей в «гуманитарии», из-за чего они только укрепляются во мнении, что точные науки — это не для них. Преподаватель математики Анна Эккерман уверена, что проблемы с математикой часто имеют исключительно психологический характер:

‍Детям вбивают в голову, что математика — это сложно. К длинным нудным параграфам в учебнике сложно подступиться. Учитель ставит на ребёнке клеймо «троечника» или «двоечника». Если не внушать детям, что они глупые и у них ничего не получится, у них получится ровно всё.

Чтобы ребёнку было интересно учить математику, он должен понимать, как эти знания пригодятся ему, даже если он не собирается становиться программистом или инженером.

Математика ежедневно помогает нам считать деньги, без умения вычислять периметр и площадь невозможно сделать ремонт, а навык составления пропорций незаменим в кулинарии — используйте это. Превращайте ежедневные бытовые вопросы в математические задачи для ребёнка: пусть польза математики станет для него очевидна. 

Конечно, найти в быту применение иррациональным числам или квадратным уравнениям не так просто. И если польза этих знаний вызывает у подростка вопросы, объясните ему, что с их помощью мы тренируем память, развиваем логическое мышление и остроту ума — навыки, в равной степени необходимые как «технарям», так и «гуманитариям». 

<<Форма демодоступа>>

Как правильно научить ребёнка решать задачи

Если ребёнок только начинает осваивать навык решения задач, приучите его придерживаться определённого алгоритма.    

1. Внимательно читаем условия  

Лучше вслух и несколько раз. После того как ребёнок прочитал задачу, задайте ему вопросы по тексту и убедитесь, что ему понятно, что вычислять нужно количество грибов, а не огурцов. Старайтесь не нервничать, если ребёнок упустил что-то из вида. Дайте ему разобраться самостоятельно. Если в условиях упоминаются неизвестные ребёнку реалии — объясните, о чём идёт речь.

Особую сложность представляют задачи с косвенным вопросом, например:

«Один динозавр съел 16 деревьев, это на 3 меньше, чем съел второй динозавр. Сколько деревьев съел второй динозавр?». Невнимательно прочитав условия, ребёнок посчитает 16−3, и получит неправильный ответ, ведь эта задача на самом деле требует не вычитания, а сложения.        

2. Делаем описание задачи

В решении некоторых задач поможет представление данных в виде схемы, графика или рисунка. Чем ярче сложится образ, тем проще будет его осмыслить. Наглядная запись позволит ребёнку не только быстро разобраться в условиях задачи, но и поможет увидеть связь между ними. Часто план решения возникает уже на этом этапе. 

Ребёнок должен чётко понимать значения словесных формул и знать, какие математические действия им соответствуют.  

Формы краткой записи условий задач / shkola4nm.ru
‍

3. Выбор способа решения

Наглядно записанное условие должно подтолкнуть ребёнка к нахождению решения. Если этого не произошло, попробуйте задать наводящие вопросы, проиллюстрировать задачу при помощи окружающих предметов или разыграть сценку. Если один из способов объяснения не сработал — придумайте другой. Многократное повторение одного и того же вопроса неэффективно. 

Все, даже самые сложные, математические задачи сводятся к принципу «из двух известных получаем неизвестное». Но для нахождения этой пары чисел часто требуется выполнить несколько действий, то есть разложить задачу на несколько более простых. 

Ребёнок должен знать способы получения неизвестных данных из двух известных:

• слагаемое = сумма − слагаемое
• вычитаемое = уменьшаемое − разность
• уменьшаемое = вычитаемое + разность
• множитель = произведение ÷ множитель
• делитель = делимое ÷ частное
• делимое = делитель × частное
  

После того как план действий найден, подробно запишите решение. Оно должно отражать всю последовательность действий — так ребёнок сможет запомнить принцип и пользоваться им в дальнейшем. 

4. Формулировка ответа

Ответ должен быть полным и точным. Это не просто формальность: обдумывая ответ, ребёнок привыкает серьёзно относиться к результатам своего труда. А главное — из описания должна быть понятна логика решения.

Задание из базового курса алгебры домашней онлайн-школы «Фоксфорда», 7 класс
‍

Одна из самых распространённых ошибок — представление в ответе не тех данных, о которых спрашивалось изначально. Если такая проблема возникает, нужно вернуться к первому пункту.   

5. Закрепление результата

Не стоит думать, что выполнив задание один раз, ребёнок сразу научится решать задачи. Полученный результат нужно зафиксировать. Для этого подумайте над решённой задачей ещё немного: предложите ребёнку поискать другой способ решения или спросите, как изменится ответ при изменении того или иного параметра в условии.

Важно, чтобы у ребёнка сложился чёткий алгоритм рассуждений и действий в каждом из вариантов.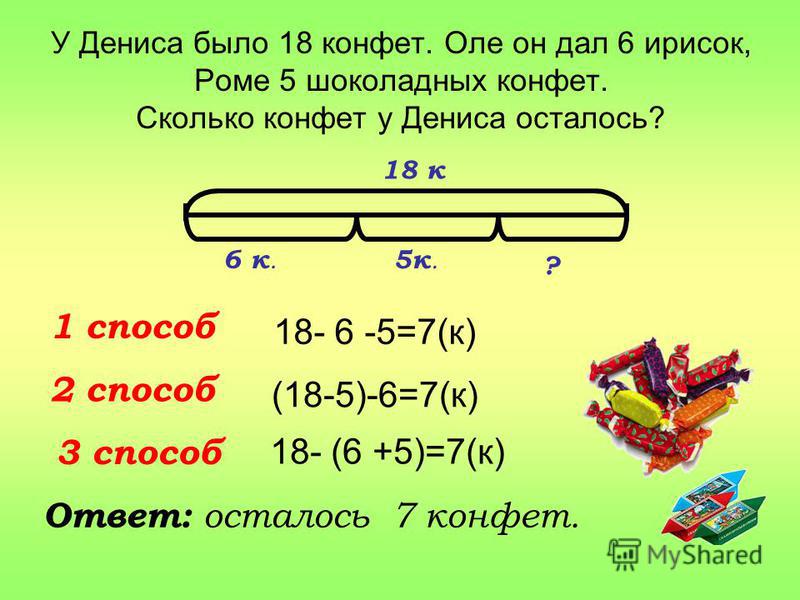  

В нашей онлайн-школе, помимо уроков, ученики могут закреплять  свои знания на консультациях в формате открытых часов, где учителя разбирают темы, вызвавшие затруднения, показывают необычные задачи и различные способы их решения. 

<<Форма курс 5-11>>

Что поможет ребёнку решать задачи  

В заключение расскажем о том, как сделать процесс решения задач проще и интереснее:

• Для того чтобы решать задачи, необходимо уметь считать. Следует выучить с ребёнком таблицу умножения, освоить примеры с дробями и простые уравнения.
• Чтобы решение задач не превратилось для ребёнка в рутину, проявите фантазию. Меняйте текст задания в соответствии с интересами ребёнка. Например, решать задачи на движение будет куда интереснее, если заменить банальные поезда трансформерами, летящими навстречу друг другу в эпической схватке. 
• Дети с развитой логикой учатся решать задачи быстрее. Советуем разбавлять чисто математические задания логическими. Задачи «с подвохом» избавят ребёнка от шаблонного мышления, а задания с большим количеством лишних данных научат выделять главное из большого количества условий.   

<<Блок перелинковки>>

После того как ребёнок решит достаточно задач одного типа, предложите ему самому придумать задачу. Это позволит ему не только закрепить материал, но и проявить творческие способности.

Как легко решать сложные задачи — 5 полезных советов от профессора-математика

Валерий Иванович Опойцев — математик, просветитель, профессор МФТИ, всю жизнь занимался наукой и преподаванием. Он издал 16-томник «Лекции по математике»*, а в последние годы создал крупный онлайн-проект «Школа Опойцева», который развивается до сих пор — хотя автора уже нет с нами. Сын ученого Сергей Опойцев выбрал 5 видеоуроков своего отца, которые будут полезны всем.

Если набрать в поисковике запрос «школьная математика», лекции моего отца до сих пор будут на первой-второй странице в выдаче. Мне кажется, все дело в том, что у отца был особый дар: он умел объяснять сложные вещи простым языком. А в своих лекциях доходчиво и доступно разъяснял те разделы математики и физики, которые вызывают наибольшие трудности у школьников и студентов.

«Это [лекции Опойцева] продукт нового поколения. Те же колеса, тот же руль, та же математическая суть — но по-другому» — так он сам описывал свой подход. Мой отец был убеждён, что «в условиях информационного наводнения инструменты вчерашнего дня перестают работать». Сегодня нужно учить иначе.

Сейчас на канале «Школы Опойцева» в YouTube размещено более 270 лекций. Для того чтобы составить представление о методике моего отца, я выбрал пять интересных лекций — они посвящены вопросам преподавания в целом и могут быть интересны и учителям, и школьникам, и их родителям.

1. Преамбула

Некоторые говорят, отмечает Опойцев, что математика — трудный и ненужный предмет. Музыкантам и ветеринарам математика, считается, не нужна. Но математика, полагает Валерий Иванович, — это язык высокого уровня, часть мира. Если исключить математику из багажа знаний, будет потеряна часть Вселенной.

Главная сложность, по мнению Опойцева, в том, что математику учат умом, а не нутром. Но как создать среду, где изучение математики было бы необходимой потребностью? Первое — убрать строгость изложения. Остальные принципы — в этой лекции.

2. «Не боги горшки обжигают!»

Этот видеоурок отвечает на часто задаваемые родителями вопросы: почему учебники написаны так, что детям ничего не понятно, и как объяснить материал, чтобы ребенок все же понял.

Профессор рассказывает истории из своего преподавательского опыта и пытается дать ответ на вопрос, почему даже современные учебные пособия перегружены информацией и очень запутанны. По мнению Опойцева, это зачастую происходит потому, что авторы при написании учебников все время думают, как их будет оценивать комиссия при Минобразовании. Именно страх перед комиссией подталкивает авторов вывалить на учеников все темы сразу.

Как переломить этот паттерн? Ответ на этот и другие вопросы Валерий Опойцев дает в этом видео.

3. Опасно ли клиповое мышление?

Изменился мир, изменилось то, как люди потребляют информацию и общаются. Валерий Опойцев считает, что клиповое мышление сейчас не только у школьников, но и у всех людей вокруг. Люди меньше читают толстые книги. В метро сегодня большинство людей листают страницы в социальных сетях или ищут информацию в интернете и лишь у единиц можно увидеть в руках книгу. Стоит ли с этим бороться? Нет. А вот преподавать точные науки с учетом новых вводных — пожалуй.

4. Как искать пути решения?

В этом уроке Опойцев размышляет, как правильно решать сложные задачи. «Для решения некоторых задач нужно выйти за пределы стандартного мышления», — говорит он. Стандартные решения — взять длину, умножить на ширину, и получится площадь — тут не работают. На людей находит ступор, они толпятся вокруг стеклянного забора, а решение лежит за его пределами.

Как научиться хитро решать задачи? Рецепт такой: нужно решать их, и решать, и решать. Не надо торопиться и искать сразу подсказку в ответах. Надо думать и думать, и все эти раздумья даром не проходят. Причем это может быть не только решение задач, это могут быть игры в слова и другие головоломки.

5. «Корабли Колумба» в системе образования

В этой лекции Опойцев рассказывает легенду о том, что индейцы не видели кораблей Колумба, когда те приблизились к берегам Америки. Некоторые не верят в это. Но сам Опойцев считает, что это вполне закономерно: люди часто просто не хотят видеть новое и незнакомое, как бы закрываются от этой информации.

Эффект «кораблей Колумба», по мнению Опойцева, довольно часто встречается и в процессе обучения. И при обучении математике в том числе — но и эту ситуацию можно исправить.

---

* Лекции выпущены под псевдонимом Валерий Босс.

Факторирование многочлена или выражения с помощью программы «Пошаговое решение математических задач»

Процесс факторизации необходим для упрощения многих алгебраических выражений и является полезным инструментом при решении уравнений высших степеней. На самом деле процесс факторизации настолько важен, что очень мало алгебры, кроме этого пункта, можно выполнить без его понимания.

В предыдущих главах подчеркивалось различие между терминами и факторами . Вы должны помнить, что члены складываются или вычитаются, а множители умножаются. Далее следуют три важных определения.

Термины встречаются в указанной сумме или разнице. Факторы встречаются в указанном продукте.

Выражение находится в факторизованной форме , только если все выражение является указанным произведением.

Обратите внимание, что в этих примерах мы всегда должны учитывать выражение целиком.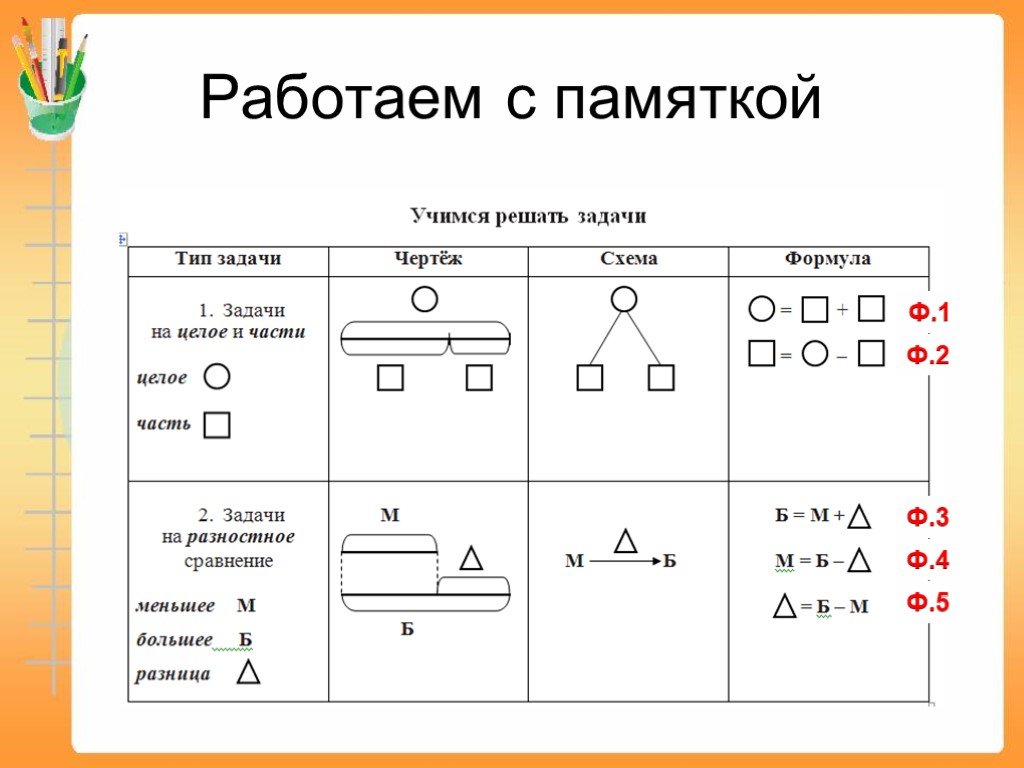 Факторы могут состоять из терминов, а термины могут содержать факторы, но факторизованная форма

должна соответствовать приведенному выше определению.

Факторинг — это процесс преобразования выражения из суммы или разности терминов в произведение факторов.

Обратите внимание, что в этом определении подразумевается, что значение выражения не изменяется — только его форма.

УДАЛЕНИЕ ОБЩИХ ФАКТОРОВ

ЦЕЛИ

По завершении этого раздела вы сможете:

1. Определите, какие факторы являются общими для всех терминов в выражении.
2. Фактор общих факторов.

В предыдущей главе мы умножили такое выражение, как 5(2x + 1), чтобы получить 10x + 5. Обычно факторизация «отменяет» умножение. Каждый член 10x + 5 имеет множитель 5, а 10x + 5 = 5 (2x + 1).

Чтобы разложить выражение на множители, удалив общие множители, действуйте, как в примере 1.

3x — наибольший общий множитель всех трех членов.

Затем найдите факторы, общие для всех терминов, и отыщите наибольший из них. Это самый большой общий фактор. В этом случае наибольший общий делитель равен 3x.

Продолжайте, поставив 3x перед скобками.

Члены в скобках находятся путем деления каждого члена исходного выражения на 3x.

Обратите внимание, что это свойство распределения. Это обратный процесс, который мы использовали до сих пор.

Исходное выражение теперь преобразуется в факторизованную форму. Чтобы проверить факторинг, имейте в виду, что факторинг изменяет форму, но не значение выражения. Если ответ правильный, то должно быть верно, что . Умножьте, чтобы увидеть, что это правда. Вторая проверка также необходима для факторинга — мы должны быть уверены, что выражение было полностью факторизовано. Другими словами: «Удалили ли мы все общие факторы? Можем ли мы еще добавить факторы?»

Если бы мы удалили только множитель «3» из 3x ² + 6xy + 9xy ² , ответ был бы

3(x ² + 2xy + 3xy ² ).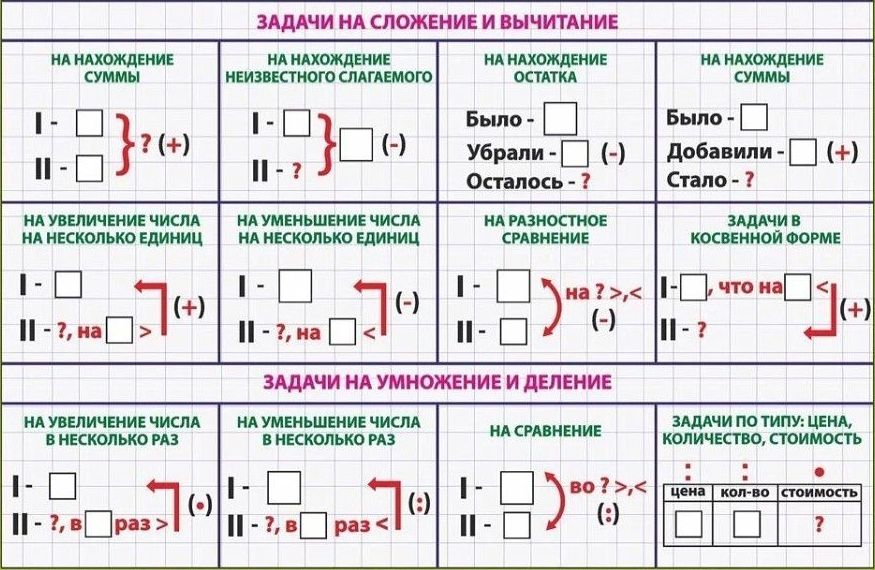

Умножая для проверки, мы находим, что ответ на самом деле равен исходному выражению. Однако фактор x по-прежнему присутствует во всех терминах. Следовательно, выражение не является полностью факторизованным.

Это выражение факторизовано, но не полностью.

Чтобы факторинг был правильным, решение должно соответствовать двум критериям:

1. Должна быть возможность умножить факторизованное выражение и получить исходное выражение.
2. FВыражение должно быть полностью разложено на .

Пример 2 Коэффициент 12x ³ + 6x ² + 18x.

Решение

На данный момент нет необходимости перечислять факторы каждого термина. Вы должны быть в состоянии мысленно определить наибольший общий множитель. Хорошей процедурой для подражания является продумывание элементов по отдельности. Другими словами, не пытайтесь сразу получить все общие множители, а сначала получите число, а затем каждую соответствующую букву. Например, 6 — это множитель 12, 6 и 18, а x — множитель каждого члена. Отсюда 12x ³ + 6x ² + 18x = 6x(2x ² + x + 3). Умножая, мы получаем оригинал и видим, что члены в скобках не имеют другого общего множителя, поэтому мы знаем, что решение правильное.

Спросите себя: «Каков наибольший общий делитель чисел 12, 6 и 18?»

Затем «Каков наибольший общий делитель x 3 , x 2 и x?»

Помните, это проверка, чтобы убедиться, что мы правильно рассчитали.

Снова умножьте в качестве чека.

Снова найдите наибольший общий делитель чисел и каждой буквы в отдельности.

Если выражение нельзя разложить на множители, говорят, что оно простое .

Помните, что 1 всегда является множителем любого выражения.

ФАКТОРИЗАЦИЯ ПО ГРУППИРОВКЕ

ЦЕЛИ

После завершения этого раздела вы сможете:

1. Факторные выражения, когда общий фактор включает более одного термина.
2. Фактор по группировке.

Расширение идей, представленных в предыдущем разделе, относится к методу факторинга, который называется группировкой .

Во-первых, мы должны отметить, что общий множитель не обязательно должен быть одним термином. Например, в выражении 2y(x + 3) + 5(x + 3) есть два члена. Это 2y(x + 3) и 5(x + 3). В каждом из этих терминов у нас есть множитель (x + 3), состоящий из термов. Этот множитель (x + 3) является общим множителем.

Иногда, когда имеется четыре или более терминов, мы должны вставить один или два промежуточных шага для факторизации.

Решение

Во-первых, обратите внимание, что не все четыре члена в выражении имеют общий делитель, но некоторые из них имеют. Например, мы можем разложить первые два члена на 3, что даст 3(ax + 2y). Если мы разложим a из оставшихся двух членов, мы получим a (ax + 2y). Теперь выражение равно 3(ax + 2y) + a(ax + 2y), и у нас есть общий множитель (ax + 2y), и мы можем разложить как (ax + 2y)(3 + a). Умножая (ax + 2y)(3 + a), мы получаем исходное выражение 3ax + 6y + a ² x + 2ay и убедитесь, что факторинг правильный.

Это пример разложения на множители путем группировки , поскольку мы «сгруппировали» термины по два за раз.

Умножьте (x — y)(a + 2) и посмотрите, получится ли исходное выражение. Опять умножить как чек.

Иногда члены должны быть сначала переупорядочены, прежде чем можно будет выполнить разложение по группам.

Пример 7 Коэффициент 3ax + 2y + 3ay + 2x.

Решение

Первые два члена не имеют общего делителя, но первый и третий члены имеют, поэтому мы переставим члены так, чтобы третий член располагался после первого. Всегда смотрите вперед, чтобы увидеть порядок, в котором термины могут быть расположены.

Во всех случаях важно убедиться, что коэффициенты в скобках абсолютно одинаковы. Это может потребовать факторизации отрицательного числа или буквы.

Помните, свойство коммутативности позволяет нам переставлять эти термины. Умножить как чек.

Пример 8 Коэффициент ax — ay — 2x + 2y.

Решение

Обратите внимание, что если мы разложим a из первых двух членов, мы получим a(x — y). Глядя на последние два члена, мы видим, что разложение на множители +2 даст 2(-x + y), но разложение на множители «-2» дает -2(x — y). Мы хотим, чтобы члены в круглых скобках были (x — y), поэтому мы действуем таким образом.

ФАКТОРИЗАЦИЯ ТРЕХНОМОВ

ЦЕЛИ

По завершении этого раздела вы должны уметь:

1. Умножьте в уме два двучлена.
2. Разложите трехчлен с коэффициентом первого члена, равным 1.
3. Найдите делители любого факторизуемого трехчлена.

Большое количество будущих задач будет связано с разложением на множители трехчленов как произведений двух двучленов. В предыдущей главе вы научились умножать многочлены. Теперь мы хотим рассмотреть частный случай умножения двух двучленов и разработать шаблон для этого типа умножения.

Поскольку этот тип умножения очень распространен, полезно иметь возможность найти ответ, не выполняя так много шагов. Давайте посмотрим на образец для этого.

Из примера (2x + 3)(3x — 4) = 6x ² + x — 12 обратите внимание, что первый член ответа (6x ² ) получен из произведения двух первых членов множители, то есть (2x)(3x).

Также обратите внимание, что третий член (-12) получен из произведения вторых членов факторов, то есть (+ 3)(-4).

Теперь у нас есть следующая часть шаблона:

Теперь снова взглянув на пример, мы видим, что средний член (+x) получен из суммы двух произведений (2x)(-4) и (3)(3x).

Теперь для любых двух биномов у нас есть следующие четыре произведения:

1. Первый срок за первым сроком
2. Внешние условия
3. Внутренние условия
4. Последний срок за последним сроком

Эти продукты показаны этим шаблоном.

Когда произведения внешних членов и внутренних членов дают одинаковые члены, их можно объединить, и решение будет трехчленным.

Этот метод умножения двух двучленов иногда называют методом FOIL. FOIL расшифровывается как First, Outer, Inner, Last. Это быстрый метод умножения двух двучленов, и его полезность будет видна, когда мы разложим трехчлены.

Вы должны запомнить эту схему.

Опять же, возможно, запоминание слова ФОЛЬГА поможет.

Этот образец следует не только запомнить, но и научиться переходить от задачи к ответу без каких-либо письменных шагов. Этот умственный процесс умножения необходим, если мы хотим достичь мастерства в факторинге.

Работая над следующими упражнениями, попытайтесь найти правильный ответ, ничего не записывая, кроме самого ответа. Чем больше вы практикуете этот процесс, тем лучше у вас будет факторинг.

Теперь, когда мы установили схему умножения двух двучленов, мы готовы разложить трехчлены на множители. Сначала мы рассмотрим разложение на множители только тех трехчленов, у которых коэффициент первого члена равен 1.

Решение

Поскольку это трехчлен и не имеет общего делителя, мы будем использовать схему умножения для факторизации.

На самом деле мы будем работать в обратном порядке по сравнению с предыдущим упражнением.

Сначала напишите круглые скобки под задачей.

Теперь мы хотим заполнить термины так, чтобы шаблон давал исходный трехчлен при умножении. Первый член прост, поскольку мы знаем, что (x)(x) = x ² .

Помните, произведение первых двух членов двучлена дает первый член трехчлена.

Теперь мы должны найти числа, которые при умножении дают 24 и в то же время складывают, чтобы получить средний член. Обратите внимание, что в каждом из следующих у нас будет правильный первый и последний термин.

Только последний продукт имеет средний член 11x, и правильное решение

Этот метод факторинга называется методом проб и ошибок — по понятным причинам.

Здесь могут быть полезны некоторые числовые факты из арифметики. Произведение двух нечетных чисел нечетно. Произведение двух четных чисел четно. Произведение нечетного и четного числа равно четному. Сумма двух нечетных чисел четна. Сумма двух четных чисел четна. Сумма нечетного и четного числа нечетна. Следовательно, когда мы факторизуем такое выражение, как x 2 + 11x + 24, мы знаем, что произведение двух последних членов бинома должно быть 24, что является четным, а их сумма должна быть равна 11, что является нечетным. Таким образом, будет работать только нечетное и четное число. Нам даже не нужно пробовать такие комбинации, как 6 и 4 или 2 и 12 и так далее.

Решение

Здесь проблема немного другая. Мы должны найти числа, которые при умножении дают 24 и при этом при сложении дают — 11. Всегда нужно помнить о закономерности. Последний член получается строго путем умножения, а средний член получается, наконец, из суммы. Зная, что произведение двух отрицательных чисел положительно, а сумма двух отрицательных чисел отрицательна, мы получаем

Решение

Здесь мы сталкиваемся с отрицательным числом для третьего слагаемого, и это несколько усложняет задачу. трудный. Поскольку -24 может быть только произведением положительного числа и отрицательного числа, а средний член должен исходить из суммы этих чисел, мы должны мыслить в терминах различия. Мы должны найти числа, произведение которых равно 24 и которые отличаются на 5. Кроме того, большее число должно быть отрицательным, потому что, когда мы складываем положительное и отрицательное число, ответ будет иметь знак большего. Учитывая все это, получаем

Порядок факторов не важен. по коммутативному закону умножения.

Следующие пункты помогут разложить трехчлены на множители:

1. Когда знак третьего члена положителен, оба знака в множителях должны быть одинаковыми — и они должны быть подобны знаку среднего члена.
2. Когда знак последнего члена отрицательный, знаки в множителях должны быть разными, а знак большего члена должен быть подобен знаку среднего члена.

В предыдущем упражнении коэффициент каждого из первых слагаемых был равен 1. Когда коэффициент первого слагаемого не равен 1, проблема факторинга значительно усложняется, поскольку число возможностей значительно увеличивается.

Выполнив предыдущий набор упражнений, вы теперь готовы попробовать еще несколько сложных трехчленов.

Обратите внимание, что есть двенадцать способов получить первый и последний члены, но только один из них имеет 17x в качестве среднего члена.

Вы, конечно, могли бы попробовать каждое из них мысленно вместо того, чтобы записывать их.

Есть только один способ получить все три термина:

В этом примере одна из двенадцати возможностей верна. Таким образом, проб и ошибок может занять очень много времени.

Несмотря на то, что используемый метод представляет собой метод угадывания, это должно быть «обоснованное угадывание», в котором мы применяем все наши знания о числах и упражняемся в умственной арифметике. В предыдущем примере мы бы сразу отбросили многие комбинации. Поскольку мы ищем 17x в качестве среднего члена, мы не будем пытаться использовать те возможности, которые умножают 6 на 6, или 3 на 12, или 6 на 12 и т. д., поскольку эти произведения будут больше 17. Кроме того, поскольку 17 нечетно, мы знаем, что это сумма четного числа и нечетного числа. Все эти вещи помогают сократить количество возможных попыток.

Сначала найдите числа, которые дают правильный первый и последний члены трехчлена. Затем добавьте внешний и внутренний продукт, чтобы проверить правильность среднего члена.

Решение

Сначала мы должны проанализировать проблему.

1. Последний член положительный, поэтому два одинаковых знака.
2. Средний член отрицательный, поэтому оба знака будут отрицательными.
3. Множители 6×2 равны x, 2x, 3x, 6x. Делители 15 равны 1, 3, 5, 15.
4. Исключить как слишком большое произведение 15 на 2x, 3x или 6x. Попробуйте несколько разумных комбинаций.

Это автоматически дало бы слишком большой средний член.

Посмотрите, как сокращается количество возможностей.

Раствор

Анализ:

1. Последний член отрицательный, поэтому отличается от знаков.
2. Мы должны найти произведения, отличающиеся на 5 с большим отрицательным числом.
3. Мы исключаем произведение 4x и 6 как возможно слишком большое.
4. Попробуйте несколько комбинаций.

Помните, мысленно попробуйте различные возможные комбинации, которые являются разумными. Это процесс факторинга методом проб и ошибок. Вы станете более опытным в этом процессе благодаря практике.

(4x — 3)(x + 2): Здесь средний член равен + 5x, что является правильным числом, но неправильным знаком. Будьте осторожны, чтобы не принять это как решение, а поменяйте знаки так, чтобы большее произведение совпадало по знаку со средним членом.

К тому времени, когда вы закончите следующий набор упражнений, вы должны чувствовать себя намного более комфортно, разлагая трехчлен на множители.

ОСОБЫЕ СЛУЧАИ ФАКТОРИНГА

ЦЕЛИ

По завершении этого раздела вы должны уметь:

1. Определите и разложите на множители разности двух идеальных квадратов.
2. Определите и разложите на множители совершенный квадратный трехчлен.

В этом разделе мы хотим рассмотреть некоторые частные случаи факторинга, которые часто встречаются в задачах. Если эти особые случаи признаются, факторинг значительно упрощается.

Первый частный случай, который мы обсудим, это разность двух полных квадратов .

Напомним, что при умножении двух двучленов на шаблон средний член получается из суммы двух произведений.

Из нашего опыта работы с числами мы знаем, что сумма двух чисел равна нулю только в том случае, если эти два числа являются отрицательными по отношению друг к другу.

Когда сумма двух чисел равна нулю, одно из чисел называется аддитивным обратным другого. Например: ( + 3) + (-3) = 0, поэтому + 3 является аддитивным, обратным к — 3, а также -3 является аддитивным, обратным к +3.

В каждом примере средний член равен нулю. Обратите внимание, что если два двучлена умножаются, чтобы получить двучлен (средний член отсутствует), они должны быть в форме (a — b) (a + b).

Правило можно записать как = (a — b)(a + b). Это форма, которую вы найдете наиболее полезной в факторинге.

Чтение этого правила справа налево говорит нам, что если у нас есть проблема для факторизации и если она имеет форму , факторы будут (a — b)(a + b).

Решение

Здесь оба члена являются полными квадратами и разделены знаком минус.

Где a = 5x и b = 4.

Особые случаи действительно облегчают факторинг, но не забудьте признать, что особый случай является именно таким особенным. В этом случае оба члена должны быть полными квадратами, а знак должен быть отрицательным, отсюда «разность двух полных квадратов».

Сумма двух квадратов не разлагается.

Вы также должны быть осторожны, чтобы распознать правильные квадраты. Помните, что совершенные квадратные числа — это числа, квадратные корни которых являются целыми числами. Кроме того, совершенные квадратные показатели четны.

Студенты часто упускают из виду тот факт, что (1) является полным квадратом. Таким образом, такое выражение, как x 2 — 1, представляет собой разность двух полных квадратов и может быть разложено по этому методу.

Другим частным случаем факторинга является совершенный квадратный трехчлен. Заметьте, что возведение бинома в квадрат приводит к этому случаю.

Мы узнаем этот случай, отмечая особенности. Три вещи очевидны.

1. Первый член — полный квадрат.
2. Третий член — полный квадрат.
3. Средний член равен удвоенному произведению квадратного корня из первого и третьего членов.

Для целей факторинга удобнее записать отчет как

Решение

1. 25x ² — это совершенный квадратный главный квадратный корень = 5x.
2. 4 — это совершенный квадратный главный квадратный корень = 2.
3. 20x — удвоенное произведение квадратных корней из 25x ² и
4. 20х = 2(5х)(2).

Чтобы разложить на множители идеальный квадратный трехчлен , сформируйте двучлен из квадратного корня из первого члена, квадратного корня из последнего члена и знака среднего члена и укажите квадрат этого двучлена.

Таким образом, 25x ² + 20x + 4 = (5x + 2) ²

Всегда возводите бином в квадрат, чтобы убедиться, что средний член правильный.

Не частный случай совершенного квадратного трехчлена.

15 ≠ 2(2x)(3)

ДОПОЛНИТЕЛЬНЫЕ КОРРЕКТЫ ДЛЯ ФАКТОРИНГА ПРОБ И ОШИБОК

ЦЕЛИ

По завершении этого раздела вы сможете:

1. Найдите ключевое число трехчлена.
2. Используйте номер ключа для факторизации трехчлена.

В этом разделе мы хотим обсудить некоторые упрощения метода проб и ошибок. Они необязательны по двум причинам. Во-первых, некоторые могут предпочесть пропустить эти методы и просто использовать метод проб и ошибок; во-вторых, эти сокращения не всегда практичны для больших чисел. Однако они увеличат скорость и точность для тех, кто их освоит.

Первым шагом в этих сочетаниях клавиш является поиск номер ключа . После того, как вы нашли номер ключа, его можно использовать более чем одним способом.

В разлагаемом на множители трехчлене ключевое число является произведением коэффициентов первого и третьего членов.

Произведение этих двух чисел является «ключевым числом».

Первое использование номера ключа показано в примере 3.

Решение
Шаг 1 Найдите номер ключа. В этом примере (4)(-10)=-40.
Шаг 2 Найдите множители ключевого числа (-40), которые в сумме дадут коэффициент среднего члена ( + 3). В этом случае (+8)(-5)=-40 и (+8)+(-5)=+3.
Шаг 3 Множители ( + 8) и ( — 5) будут перекрестными произведениями в схеме умножения.

Произведение этих двух чисел является «ключевым числом».

Шаг 4 Используя только внешнее перекрестное произведение, найдите множители первого и третьего членов, которые при умножении дают произведение. В этом примере мы должны найти множители 4×2 и -10, которые при умножении дают +8x. Это 4x от 4×2 и (+2) от (-10).
Поместите эти множители на первую и последнюю позиции в шаблоне

Есть только один способ сделать это правильно.

Шаг 5 Забудьте номер ключа на этом этапе и вернитесь к исходной проблеме. Поскольку первая и последняя позиции заполнены правильно, теперь необходимо заполнить только две другие позиции.

Опять же, это можно сделать только одним способом.

Мы знаем, что произведение двух первых слагаемых должно давать 4×9.0077 2 и 4x уже на месте. Нет другого выбора, кроме х.

Обратите внимание, что на шаге 4 мы могли бы начать с внутреннего продукта вместо внешнего продукта. Мы получили бы те же коэффициенты. Наиболее важным является систематический процесс факторинга.

Мы знаем, что произведение двух вторых членов должно быть (-10) и (+2) уже на месте. У нас нет другого выбора, кроме как (- 5).

Помните, что если трехчлен можно разложить на множители, то существует только один возможный набор множителей.

Если не удается найти делителей ключевого числа, сумма которых является коэффициентом при средних членах, то трехчлен является простым и не делит.

Второе использование номера ключа в качестве ярлыка включает факторинг путем группирования. Работает как в примере 5.

Решение
Шаг 1 Найдите число ключа (4)(-10) = -40.
Шаг 2 Найдите множители (-40), которые в сумме дадут коэффициент среднего члена (+3).

Шаги 1 и 2 в этом методе такие же, как и в предыдущем методе.

Шаг 3 Перепишите исходную задачу, разбив средний член на две части, найденные в шаге 2. 8x — 5x = 3x, поэтому мы можем записать

Шаг 4 метод группировки, изученный в разделе 8-2

Теперь это становится обычной задачей факторизации по группировке.

907:40 Следовательно,

Опять же, существует только одна возможная пара множителей, которые можно получить из данного трехчлена.

Помните, что если шаг 2 невозможен, трехчлен является простым и не может быть разложен на множители.

ПОЛНАЯ ФАКТОРИЗАЦИЯ

ЦЕЛИ

По завершении этого раздела вы сможете разложить трехчлен на множители, выполнив следующие два шага:

1. Сначала найдите общие факторы.
2. Разложите на множители оставшийся трехчлен, применяя методы, описанные в этой главе.

Итак, мы изучили все обычные методы факторизации, встречающиеся в элементарной алгебре. Однако вы должны знать, что для решения одной проблемы может потребоваться более одного из этих методов. Помните, что существует две проверки правильности факторинга.

1. Будут ли множители умножаться, чтобы дать исходную задачу?
2. Все ли множители простые?

Как только общий множитель найден, вы должны проверить, является ли полученный трехчлен факторизуемым.

Если у трехчлена есть какие-либо общие делители, обычно проще сначала разложить их на множители.

При разложении на множители рекомендуется всегда сначала удалять наибольший общий множитель, а затем, если возможно, факторизовать то, что осталось.

SUMMARY

Ключевые слова

• Выражение находится в факторизованной форме, только если все выражение является указанным произведением.
• Факторинг — это процесс, который превращает сумму или разность условий в произведение факторов.
• Простое выражение нельзя разложить на множители.
• Наибольший общий делитель — это наибольший общий делитель всех терминов.
• Выражение является полностью разложенным на множители , когда дальнейшее разложение на множители невозможно.
• Возможность факторизации путем группировки существует, когда выражение содержит четыре или более членов.
• Метод FOIL можно использовать для умножения двух двучленов.
• Особые случаи факторинга включают разность двух квадратов и трехчленов с совершенными квадратами .
• Ключевое число является произведением коэффициентов первого и третьего членов трехчлена.

Процедуры

• Чтобы удалить общие делители, найдите наибольший общий делитель и разделите на него каждый член.
• Трехчлены можно разложить на множители методом проб и ошибок. При этом используется шаблон для умножения, чтобы найти множители, которые дадут исходный трехчлен.
  
• Чтобы разложить на множители разность двух квадратов, используйте правило
  
• Чтобы разложить на множители идеальный квадратный трехчлен, сформируйте двучлен с квадратным корнем из первого члена, квадратным корнем из последнего члена и знаком среднего члена и укажите квадрат этого двучлена.
• Используйте ключевое число для помощи в определении факторов, сумма которых является коэффициентом среднего члена трехчлена.

  No related posts.