Проект «Методы решения заданий С1 ЕГЭ по математике»
Слайд 1
Методы решения заданий С1 ЕГЭ по математике Автор: Иримиа Регина , ученица 11 «А» класса МБОУ г.Астрахани «СОШ №57»Слайд 2
Формулы записи решений простейших тригонометрических уравнений. В большинстве учебников для записи решений простейших уравнений используются следующие формулы:
Слайд 3
При повторении формул решения уравнений следует обратить внимание на то, что формулы задают множества чисел, которые образованы по закону арифметической прогрессии с разностью 2 π или π . С другой стороны использование общей формулы серий решений не всегда является удобной при отборе корней, в частности, на числовой окружности. В этом случае как раз удобнее не объединять серии решений тригонометрических уравнений, а представлять их совокупностью, выделяя разность 2 π соответствующих прогрессий.
Слайд 4
sin x
Слайд 5
cos x
Слайд 6
tg x и ctg x
Слайд 7
Для тригонометрических уравнений применимы общие методы решения (разложение на множители, замена переменной, функционально-графические) и равносильные преобразования общего характера. Решение тригонометрических уравнений
Слайд 8
В данном пункте рассмотрим уравнения, содержащие синус, косинус, тангенс и котангенс степени не выше первой. Уравнения данного вида сводятся к простейшим путем замены f(x)=t . Часто задача осложняется тем, что требуется найти все решения уравнения, принадлежащие указанному промежутку.
Слайд 9
Решение . Положив 4x=t , будем искать корни уравнения cost =3 , принадлежащие другому промежутку [0;4 π ] . Решения задаются формулами: В тех случаях, когда промежутки привязаны к четвертям тригонометрической окружности, для отбора корней удобно использовать модель тригонометрической окружности. Так как и то неравенство справедливо при k=0 и k=1 . Соответственно, неравенство , справедливо при k=1 и k=2 . Возвращаясь к исходной переменной, получим:
Слайд 10
На числовой окружности (см. Рис. 21) получаем два числа, удовлетворяющие условию задачи: В некоторых простых случаях замена не обязательна.
Слайд 11
Решение. Используя нечетность синуса, перепишем уравнение в виде Последнее равенство выполняется в двух случаях: Отсюда получаем
Слайд 12
Тренировочные упражнения 1. Найдите корни уравнения удовлетворяющие условию 2. Найдите корни уравнения принадлежащие промежутку 3. Найдите корни уравнения удовлетворяющие условию
Слайд 13
Тренировочные упражнения 4. Найдите корни уравнения удовлетворяющие условию 5. Найдите корни уравнения удовлетворяющие условию 6. Найдите корни уравнения удовлетворяющие условию
Слайд 19
Решение. Среди значений x , для которых cos x = 0 , корней уравнения нет (если cos x = 0 , то из уравнения следует, что и sin x = 0 , а одновременно эти два равенства выполняться не могут). Значит, деление обеих частей уравнения на cos x не приведет к потере корней. Разделив, получим уравнение:
Слайд 20
Решение. Разделим обе части уравнения на Уравнение примет вид
Слайд 21
Cos x
Слайд 22
Тренировочные упражнения Решите уравнения: 1. 2. 3. Дано уравнение а) Решите уравнение. б) Укажите корни, принадлежащие отрезку 4 . Найдите корни уравнения принадлежащие отрезку [0; 4]. 5. Найдите корни уравнения на отрезке
Слайд 23
Тригонометрические уравнения, сводящиеся к алгебраическим уравнениям с помощью замены В тех случаях, когда исходное уравнение может быть приведено к виду то заменой уравнение сводится к решению уравнения Далее для каждого полученного корня необходимо решить уравнение
Слайд 24
В тех случаях, когда множество значений функции g ( x ) известно, то пишется ограничение на новую переменную.
Слайд 25
Иногда при решении уравнений часть «посторонних» решений возникающих в результате замены могут быть удалены по причине несоответствия их области определения или множеству значений тригонометрических и обратных тригонометрических функций. Напомним их и покажем на примерах как ограничение, связанное с новой переменной, позволяет проводить проверку на промежуточном этапе решения.
Слайд 26
Решение. Обозначим где Полученное квадратное уравнение имеет корни (не удовлетворяет
Слайд 27
Решение. Положим arccosx =t . Так как множество значений функции arccosx – отрезок [0; π ] , найдем решения уравнения удовлетворяющие условию Такой корень один: Если , то , откуда
Слайд 28
Сведение тригонометрических уравнений к алгебраическим путем замены переменной — одна из наиболее плодотворных идей, используемая для решения тригонометрических уравнений. Рассмотрим несколько типичных ситуаций введения новой переменной. Уравнения, сводящиеся к многочлену от одной тригонометрической функции. Рассмотрим уравнения, сводящиеся к квадратным относительно синуса, косинуса, тангенса или котангенса. Решение. Используя основное тригонометрическое тождество, приведем уравнение к виду:
Слайд 29
Заметим, что все решения можно представить одной формулой:
Слайд 30
Решение. Воспользовавшись основным тригонометрическим тождеством, перепишем уравнение в виде:
Слайд 31
Решение. Если записать условие sin 2x
Слайд 32
Решение уравнений, однородных относительно синуса и косинуса в которых сумма показателей степеней у sinx и cosx (степень уравнения) во всех членах уравнения одинакова. Например,
Слайд 34
В частности, уравнения вида приводятся к однородным путем представления правой части в виде:
Слайд 35
Решение. Преобразуем обе части уравнения, воспользовавшись тождествами: Заметим, что среди значений x , для которых cos x=0 , корней уравнения нет, поскольку, если cos x=0 , то из уравнения следует, что и sinx=0 , а одновременно эти два равенства выполняться не могут. Значит, можно разделить обе части уравнения на , не опасаясь потери корней. После деления получим уравнение Последовательно имеем: Решив его как квадратное относительно tgx , найдем: tg x=0,5 , tgx=3 , откуда
Слайд 36
Симметрические уравнения Рассмотрим тригонометрические уравнения f ( x )=0 , левая часть которых представляет собой рациональное выражение от переменных t= sinx+cosx (или t= sinx-cosx ) и v= sinx * cosx . Поскольку Следовательно, исходное уравнение сводится к алгебраическому относительно переменной t . Так как то поиск корней алгебраического уравнения можно ограничить промежутком
Слайд 37
Решение. Введем новую переменную С учетом равенства перепишем уравнение в виде или Последнее уравнение имеет два корня из которых только первый удовлетворяет условию Вернемся к переменной x . Получим или откуда
Слайд 38
Решение . Воспользовавшись формулой разности кубов Положим Тогда и, значит, Таким образом, после замены получим уравнение
Слайд 39
Отсюда Условию удовлетворяет только одно из найденных значений: Возвратимся к исходной переменной. Получим или Откуда или Таким образом, исходное уравнение имеет две серии решений:
Слайд 40
Уравнения f ( x ) =0, левая часть которых может быть представлена как многочлен от tg x+ctg x , сводятся к алгебраическим заменой t g x +ct g x=t . Решение. Положим t g x + ctg x=t . Заметим, что Последнее уравнение имеет два корня t=1 и t =2 , из которых только второй удовлетворяет условию t ≥ 2 . Если t=2 , то tg x + ctg x =2 , или sin 2 x =1 , откуда
Слайд 41
Применение универсальной тригонометрической подстановки Так как выражаются через , то уравнение вида подстановкой часто удается свести к алгебраическому уравнению. При этом следует иметь в виду, что замена на и на ведет к сужению области определения уравнения, поскольку из рассмотрения исключаются значения x , при которых т.е. при которых
Слайд 42
Поэтому при применении универсальной тригонометрической подстановки необходимо дополнительно выяснить, являются или нет исключаемые из рассмотрения значения x корнями исходного уравнения.
Слайд 43
Решение. Преобразовав уравнение к виду введем новую переменную Так как исходное уравнение не определено для то такая замена не может привести к потере корней. Заменив на получим уравнение которое равносильно каждому следующему уравнению: Получаем и, возвращаясь к переменной x , решаем уравнение
Слайд 44
Тренировочные упражнения Решите уравнение: 1. 2. 3. 4. 5. 6. 7. 8.
Слайд 45
Тренировочные упражнения Решите уравнение: 1. 2. 3. 4. 5.
Слайд 46
Метод разложения на множители Один из основных подходов к решению тригонометрических уравнений состоит в их последовательном упрощении с целью сведения к одному или нескольким простейшим. Для упрощения используются тригонометрические формулы. Универсального ответа на вопрос, какие формулы следует применить в том или ином случае, нет, однако есть ряд приемов, которые полезно иметь в виду при поиске решения.
Слайд 47
Довольно часто в результате преобразований удается привести уравнение к виду В этом случае дальнейшее решение сводится к поиску корней уравнений и дальнейшему отбору тех из них, которые принадлежат области определения исходного уравнения. Такой подход к решению уравнений, известный как метод разложения на множители, является универсальным (его применяют при решении рациональных, иррациональных, показательных и логарифмических уравнений).
Слайд 48
Решение. Воспользуемся формулой синуса двойного аргумента Так как то последнее уравнение равносильно системе
Слайд 49
Решение. Так как общий наименьший период функций tg x и sin x равен 2 π , то отбор корней удобно проводить на промежутке [0;2 π ) . Проведем равносильные преобразования: На промежутке [0;2 π ) из трех корней 0, π /2, π исключаем число π /2, поэтому множество корней данного уравнения задается формулой
Слайд 50
Решение. Перепишем уравнение в виде Функции, входящие в последнее уравнение, определены при всех x , кроме На этом множестве последнее уравнение равносильно совокупности уравнений t g x =0 и cos 8 x =1 , решения которых определяются формулами
Слайд 51
Теперь необходимо отобрать из полученных значений x те, которые удовлетворяют условию cos x≠0 , т.е., Для первой серии корней условие cos x≠0 выполняется. Для отбора корней второй серии воспользуемся следующим. Представим число n в виде а p принимает значения 0, 1, 2 и 3. Тогда при разных значениях p корни второй серии будут иметь вид:
Слайд 52
Значит при p=2 получаются «запрещенные» значения, а все оставшиеся решения можно задать, например, как совокупность серий: причем вторая из этих серий была получена ранее.
Слайд 53
В случае тригонометрических уравнений проблема преобразования исходного уравнения к виду уравнения к виду решается, главным образом, путем использования тригонометрических формул. Рассмотрим, как это делается на примерах.
Слайд 54
Решение. Так как то данное уравнение равносильно следующим: Полученное уравнение в свою очередь равносильно совокупности уравнений
Слайд 56
Если уравнение содержит выражения то для разложения на множители можно попробовать применить формулы преобразования этих сумм (разностей) в произведения.
Слайд 57
Решение. Перепишем уравнение в виде Далее преобразуем это уравнение, используя формулу Получим
Слайд 58
Последнее уравнение распадается на три:
Слайд 59
Пример 54. Найти наибольший отрицательный корень уравнения Решение. Последовательно имеем
Слайд 60
Продемонстрируем применение различных способов для отбора наибольшего отрицательного корня данного уравнения. Алгебраический способ . Для каждой серии корней решим неравенства относительно соответствующего параметра n , k и l . а) Для первой серии корней имеем Отсюда получаем а наибольшее целое отрицательное значение и корень
Слайд 61
б) Второе неравенство выполняется, если или и В) тогда или Выбираем наибольший отрицательный корень уравнения
Слайд 62
Арифметический способ. Выполнив перебор значений параметров n , k и l , найдем значения для переменной х.
Слайд 63
Геометрический способ. На тригонометрическом круге изобразим точками числа, соответствующие найденным сериям решений (рис. 22). При обходе по тригонометрической окружности в отрицательном направлении первое встретившееся число есть
Слайд 64
Тренировочные упражнения 1. Найдите все решения уравнения принадлежащие промежутку 2. Найдите все корни уравнения удовлетворяющие неравенству 3 . Решите уравнение 4. Решите уравнение 5. Найдите сумму корней уравнения Принадлежащие промежутку 6. Найдите сумму корней уравнения Принадлежащие промежутку
Слайд 65
Источники информации http://www.bymath.net/studyguide/tri/sec/tri6.htm http://eahmath.ru/algebsc/alabspr.php?i=1 «МАТЕМАТИКА, ЕГЭ. Тригонометрические уравнения: методы решений и отбор корней (типовые задания С1)» Корянов А.Г., Прокофьев А.А.
nsportal.ru
13 Задание (2016) (C1) – Репетитор по математике
13 Задание (2016) (C1)14 Задание (2016) (C2)Диагностические работы
Задание 13.
а) Решите уравнение
б) Найдите все корни этого уравнения, принадлежащие отрезку [].
Решение.
показать
Дробь равна нулю, когда числитель равен нулю, а знаменатель не равен нулю.
Получим систему:
первое уравнение:
:
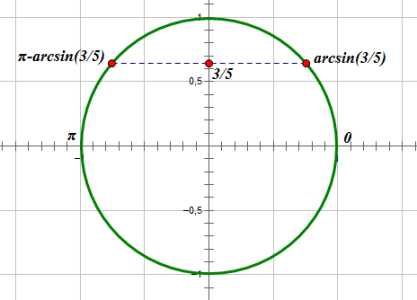
Второе условие:
Заметим, что , поэтому :
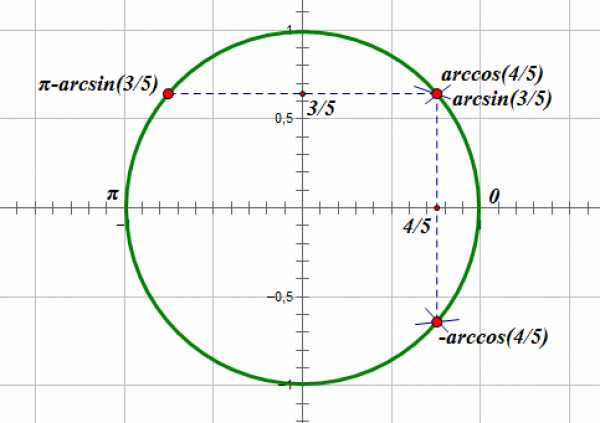
Остался единственный корень:
б) Отберем корни, принадлежащие отрезку []:
Мы видим, что отрезку [] принадлежит корень :
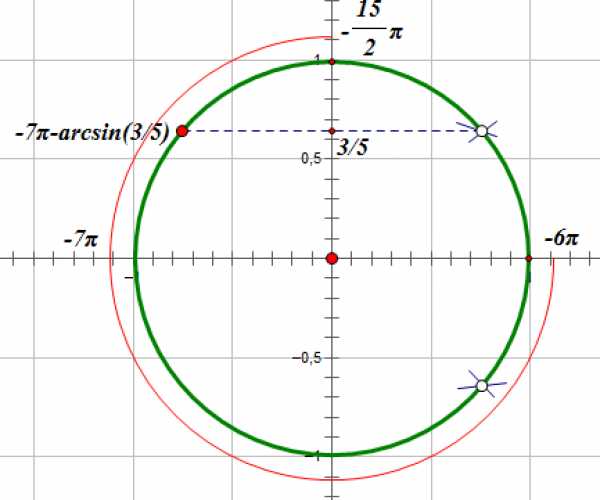
Ответ: а)
б)
Задание 14.
В основании правильной треугольной пирамиды лежит треугольник со стороной, равной 6. Боковое ребро пирамиды равно 4. Через такую точку ребра , что , параллельно прямым и проведена плоскость.
а) Докажите, что сечение пирамиды указанной плоскостью является прямоугольником.
б) Найдите площадь сечения.
Решение.
показать
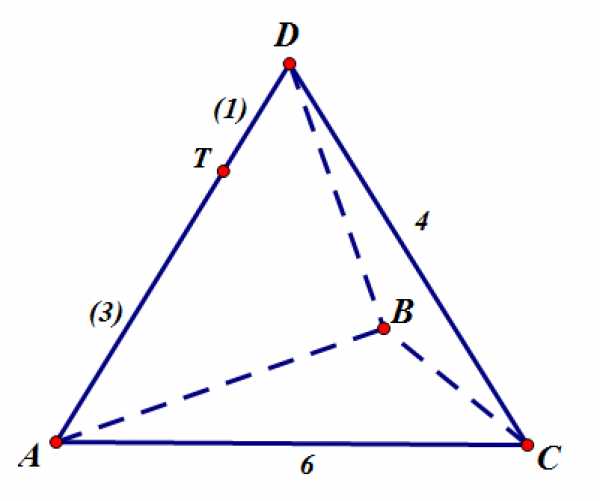
Построим сечение.
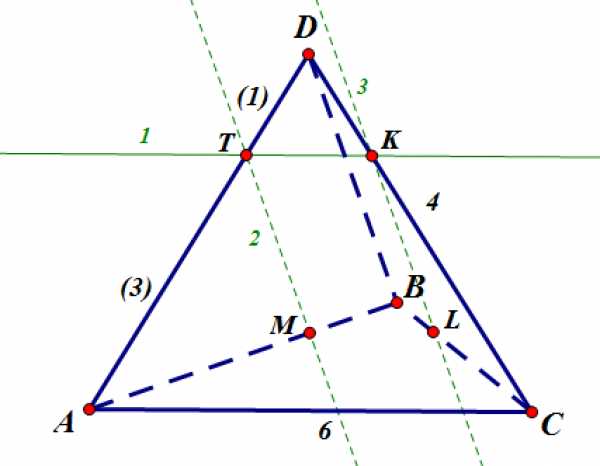
— Проведем прямую №1 () параллельно .
Через точку проведем прямую №2 () параллельно .
Через точку проведем прямую №3 () параллельно .
Получили сечение — четырехугольник :
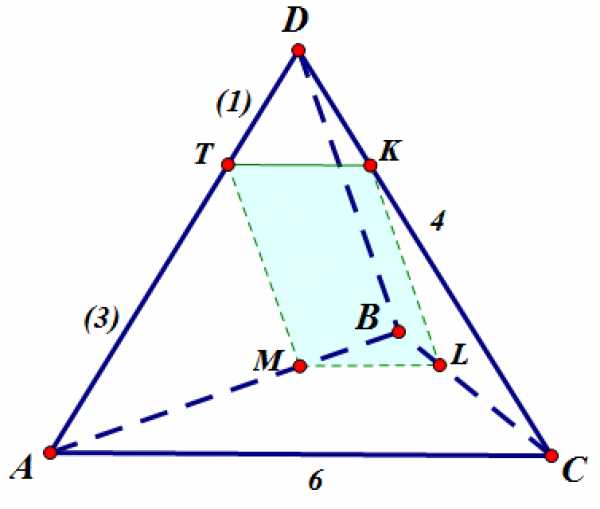
Данное сечение удовлетворяет всем условиям задачи:
- — по построению, следовательно (по теореме о параллельности прямой и плоскости).
- — по построению, следовательно (по теореме о параллельности прямой и плоскости).
Докажем, что четырехугольник — прямоугольник.
, так как — линия пересечения плоскости и плоскости , , следовательно линии пересечения плоскости сечения с плоскостями и (соответственно и ) параллельны.
, так как и параллельны . Следовательно, противоположные стороны четырехугольника попарно параллельны и он является параллелограммом.
Докажем, что . Проведем высоту пирамиды:
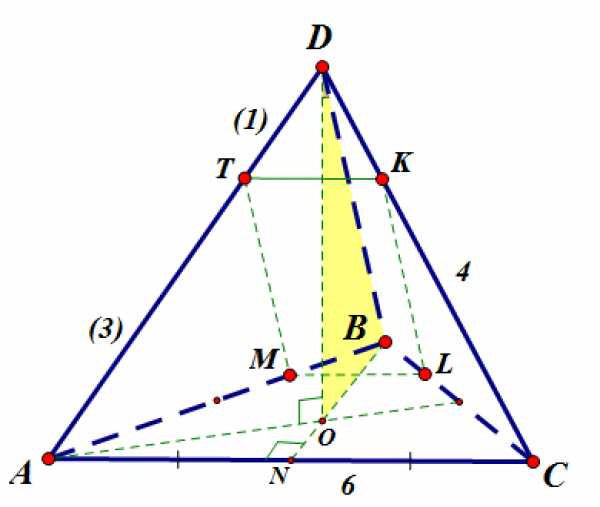
Вершина правильной пирамиды проецируется в точку , ортоцентр основания, то есть в точку пересечения медиан, высот и биссектрис треугольника .
, следовательно, по теореме о трех перпендикулярах . , , следовательно .
Найдем длины сторон прямоугольника .
(из подобия треугольников и )
;
(из подобия треугольников и )
ege-ok.ru
Задание №1 ЕГЭ по математике базовый уровень
Элементарные математические вычисления
Описание задания
В задании №1 ЕГЭ по математике базового уровня необходимо провести элементарные вычисления — сложение, вычитание, деление и умножение дробей. Ответом в первом задании является целое число или конечная десятичная дробь.
Тематика заданий: элементарные математические вычисления
Бал: 1 из 20
Сложность задания: ♦◊◊
Примерное время выполнения: 3 мин.
Разбор типовых вариантов заданий №1 ЕГЭ по математике базового уровня
Во всех заданиях необходимо найти значение выражения.
Вариант 1МБ1
Алгоритм решения:
- Определить порядок действий.
- Выполнить действия в скобках.
- Преобразовать смешанное число в неправильную дробь.
- Привести дроби в скобках к наименьшему общему знаменателю.
- Произвести действия в числителе.
- Знаменатель оставить наименьший общий.
- Умножить числитель получившейся дроби на 9.
- Полученный результат сократить и преобразовать в десятичную дробь.
Решение в общем виде:
Пояснения к решению:
Первым всегда выполняется действие в скобках, в данном случае вычитание.
Преобразуем смешанное число
в неправильную дробь. Для этого умножим целую часть на знаменатель, и прибавим числитель
3 • 15 + 1 = 46
Запишем результат в числитель, знаменатель оставим без изменения.
Действие в скобках примет вид:
Ищем наименьший общий знаменатель для дробей 4/9 и 46/15. 15 не делится на 9, удвоим наибольший знаменатель. 30 не делится на 9. утроим наибольший знаменатель, 45 делится на 9. Следовательно, 45 делится одновременно и на 15, и на 9. То есть 45 – наименьший общий знаменатель дробей 4/9 и 46/15.
Приводим дроби к общему знаменателю – 45. Для этого по основному свойству дроби необходимо и числитель и знаменатель дроби умножить на одно и то же число, чтобы дробь не изменилась. Это число называется дополнительным множителем. Дополнительный множитель к первой дроби — 5 (9*5=45). Чтобы получить в знаменателе первой дроби 45 необходимо умножить на 5 и числитель и знаменатель.
Вторую дробь умножим на 3 (15 • 3=45)
Действие в скобках после преобразования будет выглядеть так:
Произведем вычитание дробей с одинаковыми знаменателями. Для этого в числителе запишем вычитание числителей, а знаменатель оставим без изменений.
Выполним действие за скобками, в данном случае умножение на целое число. Для этого умножим числитель дроби на 9, а знаменатель оставим без изменений. Числитель и знаменатель полученной дроби сократим на 9, то есть разделим и числитель и знаменатель дроби на 9. По основному свойству дроби дробь не изменится.
Минус в числителе выносится за дробную черту.
Полученную дробь преобразуем в десятичную, поделив в столбик.
Не забудьте о знаке «минус» в ответе.
Ответ: 23,6
Вариант 1МБ2
Алгоритм решения:
- Определить порядок действий.
- Выполнить действие в скобках.
- Привести дроби в скобках к наименьшему общему знаменателю.
- Выполнить вычитание числителей, знаменатель оставить без изменений.
- Выполнить деление. Для этого числитель первой дроби нужно умножить на знаменатель второй, результат записать в числитель; знаменатель первой дроби умножить на числитель второй, результат записать в знаменатель.
Решение в общем виде:
Пояснения к решению:
Первым ВСЕГДА выполняют действия в скобках, в данном случае вычитание.
Для того чтобы выполнить вычитание дробей с разными знаменателями, необходимо привести их к наименьшему общему знаменателю. Сделаем это путем подбора. Необходимо найти число, которое одновременно делится и на 4, и на 9. 9 на 4 не делится. Удвоим больший знаменатель: 18 не делится на 4. Утроим больший знаменатель: 27 не делится на 4. Увеличим больший знаменатель в 4 раза: 36 делится и на 9, и на 4 одновременно. Следовательно, 36 – наименьший общий знаменатель для дробей 1/4 и 2/9.
Примечание. Метод подбора удобен, если числа небольшие. В противном случае нужно искать НОК по алгоритму.
Найдем дополнительные множители для дробей 1/4 и 2/9. По основному свойству дроби, если и числитель, и знаменатель дроби умножить на одно и то же число, то дробь не изменится. Дробь 1/4 нужно умножить на 9(и числитель, и знаменатель), чтобы в знаменателе получился наименьший общий знаменатель 36. Дробь 2/9 нужно умножить на 4 (и числитель, и знаменатель), чтобы в знаменателе получился наименьший общий знаменатель 36.
В результате получим:
Действие в скобках примет вид:
Выполним вычитание дробей с одинаковыми знаменателями. Для этого вычтем из числителя первой дроби числитель второй, результат запишем в числитель. Знаменатель оставим прежним.
Выполним действие за скобками. Для этого числитель первой дроби нужно умножить на знаменатель второй, результат записать в числитель; знаменатель первой дроби умножить на числитель второй, результат записать в знаменатель.
Сократим (разделим и числитель и знаменатель) полученную дробь на 12.
Ответ: 21
Вариант 1МБ3
Алгоритм решения:
- Определить порядок действий.
- Первым ВСЕГДА выполняют действия в скобках, в данном случае сложение.
- Перевести смешанное число в неправильную дробь.
- Привести полученные дроби к наименьшему общему знаменателю.
- Выполните сложение дробей с одинаковыми знаменателями. Для этого сложить числители, результат записать в числитель, знаменатель оставить без изменений.
- Выполнить деление.
- Перевести смешанное число в неправильную дробь. Для этого целую часть умножить на знаменатель и прибавить числитель, результат записать в числитель, а знаменатель оставить прежним.
- Числитель первой дроби умножить на знаменатель второй – записать в числитель. Знаменатель первой дроби умножить на числитель второй результат записать в знаменатель.
- Сократить получившуюся дробь.
- Привести результат к десятичному виду.
Решение в общем виде:
Пояснения к решению:
Первым ВСЕГДА выполняют действия в скобках, в данном случае сложение.
Нужно сложить смешанное число и правильную дробь. Для этого целую часть умножить на знаменатель и прибавить числитель, результат записать в числитель, а знаменатель оставить прежним. Переведем смешанное число в неправильную дробь:
Действие в скобках примет вид:
Для того, чтобы выполнить сложение дробей с разными знаменателями, необходимо привести их к наименьшему общему знаменателю. Сделаем это путем подбора. Необходимо найти число, которое одновременно делится и на 5, и на 7. 7 на 5 не делится. Удвоим больший знаменатель: 14 не делится на 5. Утроим больший знаменатель: 21 не делится на 5. Увеличим больший знаменатель в 4 раза: 28 не делится 5. Увеличим больший знаменатель в 5 раз: 35 делится одновременно и на 5, и на 7. Следовательно, 35 – наименьший общий знаменатель для дробей 9/5 и 3/7.
Примечание. Метод подбора удобен, если числа небольшие. В противном случае нужно искать НОК по алгоритму.
Найдем дополнительные множители для дробей 9/5 и 3/7. По основному свойству дроби, если и числитель, и знаменатель дроби умножить на одно и то же число, то дробь не изменится. Дробь 9/5 нужно умножить на 7(и числитель, и знаменатель), чтобы в знаменателе получился наименьший общий знаменатель 35. Дробь 3/7 нужно умножить на 5 (и числитель, и знаменатель), чтобы в знаменателе получился наименьший общий знаменатель 35.
В результате получим:
Действие в скобках примет вид:
Выполним сложение дробей с одинаковыми знаменателями. Для этого сложим числители, результат запишем в числитель. Знаменатель оставим прежним.
Выполним действие за скобками. Переведем смешанное число в неправильную дробь, для этого целую часть нужно умножить на знаменатель и прибавить числитель, результат записать в числитель, а знаменатель оставить прежним.
Выполнить деление дробей. Числитель первой дроби нужно умножить на знаменатель второй, результат записать в числитель; знаменатель первой дроби умножить на числитель второй, результат записать в знаменатель.
Сократим (разделим и числитель, и знаменатель на одно и то же число) полученную дробь на 39.
Переведем полученную дробь в десятинную.
Ответ: 8,75
Вариант 1МБ4
(6,7 − 3,2) ⋅ 2,4
В данном случае первым действием мы выполняем вычитание в скобках, а затем производим умножение:
6,7 − 3,2 = 3,5
3,5⋅ 2,4 = 8,4
Отдельно остановлюсь на последнем действии. Его можно вычислить умножением в столбик, либо посчитать устно, воспользовавшись следующими логическими операциями:
2,4 ⋅ 3 + 2,4 ⋅ 0,5 = 2 ⋅ 3 + 0,4 ⋅ 3 + 2,4/2 = 6 + 1,2 +1,2 = 8,4
Ответ: 8,4
Вариант 1МБ5
В данном случае необходимо выполнить сложение обыкновенных дробей. Общий знаменатель для дробей в скобках — 15 (если вы забыли как определять общий знаменатель, смотрите здесь). Первую дробь домножаем на 5, вторую на 3. Получаем:
(5 + 3)/15
После сложения:
8/15
Теперь выполняем умножение:
8•6/15 = 48/15
В таком варианте дробь в ответ записать мы не можем, выделяем сначала целую часть, это 3 (45/15=3), в остатке получим:
3/15
После сокращения на 3:
1/5
и перевода в десятичный вид:
1/5 = 20/100 = 2/10 = 0,2
Не забываем про целую часть и получаем ответ:
3,2
Ответ: 3,2
Вариант 1МБ6
- Если представить черту дроби в виде знака деления, то получим выражение: (2,7+5,8):6,8. Отсюда получаем приоритет действий: 1) сложение в скобках; 2) деление. Поэтому сначала выполняем действие в числителе.
- Избавляемся от десятичных запятых в числителе и знаменателе. Для этого применяем основное свойство дроби и умножаем числитель и знаменатель на 10.
- Делим 85 на 68 в столбик.
Решение

Ответ: 1,25
Вариант 1МБ7
- Учитываем приоритетность операций. Здесь 1-м действием выполняется умножение, а затем вычитание.
- При умножении числа записываем друг под другом, выровняв их по последней цифре. В результирующем числе отделяем столько знаков после запятой, сколько имеется суммарно в обоих множителях. В данном случае нужно отделить 2 знака.
- При выполнении вычитания в столбик числа располагают так, чтобы десят.запятые располагались на друг под другом.
Решение
Ответ: 26,7
Вариант 1МБ8
- Умножаем 1/5 на 5,5. При этом 5,5 переходит в числитель дроби.
- Выполняем сокращение полученной дроби на 5. Получаем десят.дробь
- Находим конечную разность.
Решение
Ответ:0,1
Вариант 1МБ9
- Находим разность в скобках. Для этого находим НОК (25, 38) и приводим дроби к общему знаменателю.
- Делим результат в скобках на дробь 6/19. Для этого переходим к умножению дробей, перевернув 9/16 и получив 16/9. Далее сокращаем множители в числителе и знаменателе и находим результирующую дробь.
- Полученную дробь записываем в десят.виде.
Решение
spadilo.ru
Разбор и решение задания №1 ОГЭ по математике
Числа и вычисления
Описание задания
Первое задание проверяет наши умения проведения вычислений. Это самое простое задание из всего модуля и требует от нас только знания арифметики. В первом задании арифметические действия будут самыми простыми. В демонстрационном варианте ОГЭ предлагается сложить две дроби: обыкновенную и десятичную. Тем не менее, в соответствии с документами о проведении ОГЭ, учащиеся должны быть готовы и к выполнению некоторых других несложных заданий. Ответом в первом задании является целое число или конечная десятичная дробь.
Тематика заданий: числа и вычисления
Первичный бал: 1
Сложность задания: ♦◊◊
Примерное время выполнения: 3 мин.
Теория к заданию №1
Итак, для успешного выполнения необходимо помнить:
- порядок проведения арифметических операций — сначала производятся действия в скобках, затем возведение в степень или извлечение корня, затем умножения и деления, а затем вычитания и сложения.
- правила умножения и деления в столбик
- правила вычисления обыкновенных дробей
Напоминаем правила операций с обыкновенными дробями:

Рекомендуем вычислить отдельно числитель и знаменатель, а затем разделить числитель на знаменатель. Остальные рекомендации смотрите ниже при разборе типовых вариантов первого задания ОГЭ по математике. 🙂
Разбор типовых вариантов задания №1 ОГЭ по математике
Первый вариант задания
Найдите значение выражения:
или:
9 / (4,5 • 2,5)
Решение:
Задачу можно решать разными путями, а именно менять последовательность действий, но этот вариант решения рекомендуется для тех, кто уверен в своих возможностях и знает математику на отлично. Для остальных мы рекомендуем выполнить последовательно действия в числителе и знаменателе, а затем разделить числитель на знаменатель. Числитель вычислять в данном примере нет необходимости, это число 9.
Вычислим значение знаменателя:
4,5 • 2,5
Можно произвести вычисления в столбик, тогда получим:
4,5 • 2,5 = 11,25
Либо перевести дробь к простому виду:
4,5 • 2,5 = 4½ • 2 ½ = 9 / 2 • 5 / 2 = 45 / 4
Последний случай предпочтительней, так как для дальнейшей операции — деления числителя на знаменатель задача упрощается. Делим числитель на знаменатель, умножая числитель на перевернутую дробь в знаменателе:
9 / ( 45 / 4 ) = ( 9 / 1 ) • ( 4 / 45 ) = ( 9 • 4 ) / (1 • 45 )
9 и 45 можно сократить на 9:
( 9 • 4 ) / (1 • 45 ) = ( 1 • 4 )/ (1 • 5 ) = 4 / 5 = 8 / 10 = 0,8
Получаем ответ: 0,8
Подводя итог, сделаем выводы:
Удобней сразу переходить к дробям простого вида. Надежней производить вычисления последовательно в числителе и знаменателе.
Второй вариант задания
Найдите значение выражения:
или:
6 • (1/3)² — 17 • 1/3
Решение:
Можно решать задачу напрямую — вычисляя значения последовательно, это не должно составить труда, однако решение будет долгим и с большими вычислениями. Здесь можно заметить, что 1/3 присутствует как в уменьшаемом — 6 • (1/3)², так и в вычитаемом — 17 • 1/3, поэтому её можно легко вынести за скобку.
1/3 • (6 • (1/3) — 17 )
Проведя вычисления в скобках, получим:
1/3 • ( 6 • (1/3) — 17 ) = 1/3 • (6 /3 — 17 ) = 1/3 • ( 2 — 17 ) = 1/3 • ( -15 )
Теперь умножим полученное значение -15 на 1/3:
1/3 • ( -15 ) = -5
Ответ: -5
Какие выводы можно сделать: не всегда стоит стараться решить задачу «в лоб», даже в ОГЭ.
Третий вариант задания
Найдите значение выражения:
Решение:
Аналогично предыдущим заданиям вычисляем знаменатель: для этого приводим дроби к общему знаменателю — это 84. Для этого первую дробь умножаем на 4, а вторую на 3, получим:
1/21 + 1/28 = 4/84 + 3/84
Затем складываем:
4/84 + 3/84 = 7/84
Итак, мы получили в знаменателе 7/84, теперь делим числитель на знаменатель — это все равно что умножить 1 на обратную 7/84 дробь:
1 / ( 7 / 84 ) = 1 •84/7 = 84/7
Далее остается поделить 84 на 7:
84 / 7 = 12
Ответ: 12
Демонстрационный вариант ОГЭ 2019
Найдите значение выражения: ¼ + 0,07
Решение:
К данному заданию, как и к большинству заданий 1 модуля Алгебры, подход к решению заключается в переводе дроби от одного вида к другому. В нашем случае это переход от обыкновенной дроби к десятичной.
Переводим ¼ из обыкновенной дроби в десятичную. Делим 1 на 4, получаем 0,25. Затем переписываем выражение с использованием только десятичных дробей и вычисляем:
0,25 + 0,07 = 0,32
Ответ: 0,32
Четвертый вариант задания
Найдите значение выражения:
–0,3·(–10)4+4·(–10)2–59
Решение:
Для получения результата необходимо последовательно выполнить математические действия в соответствии с их приоритетом.
–0,3·(–10)4+4·(–10)2–59 =
Выполняем возведение в степень. Получаем числа, состоящие из единицы и следующего за ней количества нулей, равного показателю степени. При этом знаки «–» в скобках исчезают, поскольку показатели степеней четные. Получаем:
= –0,3·10000+4·100–59 =
Выполняем умножение. Для этого в числе 0,3 переносим десятичную запятую на 4 знака вправо (так как в 10000 четыре нуля), а к 4 дописываем, соответственно, 2 нуля. Получаем:
= –3000+400–59 =
Выполняем сложение –3000+400. Поскольку это числа с разными знаками, то вычитаем из большего модуля меньший и перед результатом ставим «–», поскольку число с большим модулем отрицательное. Получаем:
= –2600–59 =
Так как оба числа отрицательные, то складываем их модули и перед результатом ставим «–». Получаем:
= –(2600+59) = –2659
Ответ: –2659
Пятый вариант задания
Найдите значение выражения:
–13·(–9,3)–7,8
Решение:
Это задание требует простого умения выполнять арифметические действия с десятичными дробями.
–13·(–9,3)–7,8 =
Сначала выполняем умножение. Умножаем –13 и –9,3 в столбик без учета знаков «–» перед сомножителями. В полученном произведении отделяем одну – последнюю – цифру десятичной запятой:
Знак произведения будет положительным, поскольку умножаются два отрицательных числа. Получаем:
= 120,9–7,8 =
Эту разность можно вычислить в столбик, но можно и устно. Выполним это действие в уме: вычитаем отдельно целые части и десятичные. Получаем:
= 113,1
Ответ: 113,1
spadilo.ru
Задания по профильной математике ЕГЭ с разбором решений
Минимальный порог — 27 баллов.
Экзаменационная работа состоит из двух частей, которые различаются по содержанию, сложности и числу заданий.
Определяющим признаком каждой части работы является форма заданий:
- часть 1 содержит 8 заданий (задания 1-8) с кратким ответом в виде целого числа или конечной десятичной дроби;
- часть 2 содержит 4 задания (задания 9-12) с кратким ответом в виде целого числа или конечной десятичной дроби и 7 заданий (задания 13–19) с развернутым ответом (полная запись решения с обоснованием выполненных действий).
 Панова Светлана Анатольевна, учитель математики высшей категории школы, стаж работы 20 лет:
Панова Светлана Анатольевна, учитель математики высшей категории школы, стаж работы 20 лет:
Задание № 1 — проверяет у участников ЕГЭ умение применять навыки, полученные в курсе 5 — 9 классов по элементарной математике, в практической деятельности. Участник должен владеть вычислительными навыками, уметь работать с рациональными числами, уметь округлять десятичные дроби, уметь переводить одни единицы измерения в другие.
Пример 1. В квартире, где проживает Петр, установили прибор учета расхода холодной воды (счетчик). Первого мая счетчик показывал расход 172 куб. м воды, а первого июня — 177 куб. м. Какую сумму должен заплатить Петр за холодную воду за май, если цена 1 куб. м холодной воды составляет 34 руб 17 коп? Ответ дайте в рублях.
1) Найдем количество потраченной воды за месяц:
177 — 172 = 5 (куб м)
2) Найдем сколько денег заплатят за потраченную воду:
34,17 · 5 = 170,85 (руб)
Ответ: 170,85.
Задание № 2 —является одним из простейших заданий экзамена. С ней успешно справляется большинство выпускников, что свидетельствует о владении определением понятия функции. Тип задания № 2 по кодификатору требований — это задание на использования приобретённых знаний и умений в практической деятельности и повседневной жизни. Задание № 2 состоит из описания с помощью функций различных реальных зависимостей между величинами и интерпретация их графиков. Задание № 2 проверяет умение извлекать информацию, представленную в таблицах, на диаграммах, графиках. Выпускникам нужно уметь определять значение функции по значению аргумента при различных способах задания функции и описывать поведение и свойства функции по её графику. Также необходимо уметь находить по графику функции наибольшее или наименьшее значение и строить графики изученных функций. Допускаемые ошибки носят случайный характер в чтении условия задачи, чтении диаграммы.
Чтобы продолжить чтение, авторизуйтесь на сайте.
rosuchebnik.ru
ЕГЭ
Задачи ЕГЭ по математике
На этой странице вы можете ознакомиться с задачами из части «В» Единого государственного экзамена. Открыв какое-либо задание (В1, или В2, или В3 и т.д.), вы увидите сразу несколько условий задач, соответствующих этому типу задания ЕГЭ. Их можно решать в любом порядке и в течение любого времени.
Решив задачу, можно проверить себя, щёлкнув по ссылке «Показать ответ». Если решение не получилось – всегда можно посмотреть наш вариант, пройдя по ссылке «Показать решение». Свои комментарии можно оставить в «Обсуждении задачи».
Наш раздел ориентирован в первую очередь не на педагогов, а на самих учеников. Именно для них написаны подробные решения. Яркие, красочные рисунки, многочисленные пометки и пояснения, в том числе раскрывающие, как надо думать на том или ином этапе, – вот то, что отличает их от большинства пояснений и комментариев к заданиям ЕГЭ, представленных в Интернете. Думайте, решайте, наслаждайтесь красотой решения задач вместе с нами!
- B1 Целые, рациональные и дробные числа
- B2 Проценты
- B3 Графическое представление данных. Анализ данных
- B4 Табличное представление данных. Прикладные задачи на нахождение наибольшего и наименьшего значения
- B5 Площадь треугольника, параллелограмма, трапеции, круга, сектора. Декартовы координаты на плоскости
- B6 Элементы теории вероятностей
- B7 Уравнения
- B8 Планиметрия. Треугольник, трапеция, параллелограмм, ромб, прямоугольник, квадрат. Окружность и круг. Угол. Нахождение элементов и величин в различных геометрических фигурах
- B9 Графики функции, производных функций. Исследование функций
- B10 Многогранники. Измерение геометрических величин
- B11 Числа, корни и степени. Основы тригонометрии. Логарифмы. Преобразования выражений
- B12 Прикладные задачи. Осуществление практических расчетов по формулам
- B13 Многогранники. Тела вращения. Прямые и плоскости в пространстве. Измерение геометрических величин
- B14 Составление уравнений и неравенств по условию задач. Их решение
- B15 Исследование функций. Применение производной функции
- 1 Квадратный корень
- 2 Линейные уравнения
- 3 Неполные квадратные уравнения
- 4 Полные квадратные уравнения
- 5 Теорема Виета
- 6 Дробные рациональные уравнения
- 7 Уравнения высоких степеней
- 8 Числовые неравенства и их свойства
- 9 Неравенства с одной переменной
- 10 Системы неравенств
- 11 Совокупности неравенств
- 12 Расщепление неравенств
- 13 Неравенства с модулями
- 14 Разные неравенства
- 15 Неравенства второй степени. Рациональные неравенства
- 16 Степень с целым показателем
- 17 Область определения и область значений функции
- 18 Свойства функций: монотонность, чётность, нечётность
- 19 Обратные функции
- 20 Построение графиков функций
- 21 Системы линейных уравнений и системы, сводящиеся к ним
- 22 Нелинейные системы уравнений. Метод подстановки и алгебраического сложения
- 23 Нелинейные системы уравнений. Метод почленного умножения и деления уравнений системы
- 24 Нелинейные системы уравнений. Замена неизвестной. Симметрические системы
- 25 Нелинейные системы уравнений. Системы однородных уравнений и приводящиеся к ним системы
- 27 Разные системы
- 28 Корень n-ой степени
- 29 Степень с рациональным показателем
- 30 Иррациональные уравнения
- 31 Иррациональные неравенства
- 32 Числовые последовательности
- 33 Арифметическая прогрессия
- 34 Геометрическая прогрессия
- 35 Комбинированные задачи на арифметическую и геометрическую прогрессии
- 36 Бесконечная геометрическая прогрессия
- 37 Простейшие текстовые задачи
- 38 Задачи на проценты
- 39 Задачи на целые числа
- 40 Задачи на смеси и сплавы
- 41 Задачи на движение
- 42 Задачи на работу
- 43 Понятие угла LIGHT
- 44 Радианная мера угла LIGHT
- 45 Определение синуса и косинуса угла LIGHT
- 46 Основные формулы для синуса и косинуса угла LIGHT
- 47 Тангенс и котангенс угла LIGHT
- 48 Основные задачи тригонометрии LIGHT
- 49 Зависимость между функциями одного аргумента. Формулы приведения LIGHT
- 50 Тригонометрический круг
- 51 Определение синуса, косинуса, тангенса и котангенса. Радианная мера угла
- 52 Зависимость между функциями одного аргумента. Формулы приведения
- 53 Теоремы сложения
- 54 Формулы двойного и половинного аргумента
- 55 Преобразование суммы тригонометрических функций в произведение и обратно
© 2017-2019 Математушка
matematushka.ru
 Задача С1 традиционно посвящена решению тригонометрических уравнений. Как правило это несложные задачи со стандартным решением. Традиционно данное задание ЕГЭ по математике состоит из двух частей, в первой надо найти общее решение, во второй выбрать решения, принадлежащие некоторому интервалу. Эксперт оценивает данное задание в 0, 1 или 2 балла. Приведем критерии оценки данного задания.
Задача С1 традиционно посвящена решению тригонометрических уравнений. Как правило это несложные задачи со стандартным решением. Традиционно данное задание ЕГЭ по математике состоит из двух частей, в первой надо найти общее решение, во второй выбрать решения, принадлежащие некоторому интервалу. Эксперт оценивает данное задание в 0, 1 или 2 балла. Приведем критерии оценки данного задания.
Критерии оценки задания C1
2 балла – Обоснованно получены верные ответы в обоих пунктах
1 балл – Обоснованно получен верный ответ в пункте а) или б)
0 баллов – Решение не соответствует ни одному из критериев, перечисленных выше
Поясним критерии на примере. В работе квадратное уравнение относительно синуса сведено к простейшему тригонометрическому уравнению, например, sin x=-0,5, при этом оно вообще не решено или имеется неточность или ошибка, но отбор корней, например, на отрезке произведен правильно. В этом случае в соответствии с параметрами эксперт должен поставить 1 балл.
Примеры решений ЕГЭ с обсуждением возможных ошибок
1. а) Решите уравнение
б) Найдите все корни уравнения, принадлежащие промежутку
Решение
а)
. Если будет не верно вычислено или указан другой период, то за эту часть задания уже не получить 1 балл.
б)
. Учитывая, что – целое число, получаем, что оно принимает значения -2, -3, -4. Следовательно получаем следующие значения
2. Решить уравнение
Решение.
или . Отсюда получаем два набора значений:
Замечание. Буква n и k надо писать разными, кроме этого обязательно писать, что они целые.
3. Пример очень обидной арифметической ошибки.
. Такая ошибка приводит к 0 баллов. Поэтому будьте внимательны и не делайте досадных ошибок.
Такое задание есть во всех вариантах ЕГЭ по математике, оно конечно же будет и в ЕГЭ по математике 2013 года.
Связанные статьи
mathi.ru
