Проанализируем первый график:
Исходная прямая y = x – 1 превращается в ломаную y = |x – 1|, «отражается» в точке (1; 0) в положительную полуплоскость y > 0.
Далее, ломаная y = |x – 1| опускается на 1 вниз y = |x – 1| – 1.
Наконец, области y = |x – 1| – 1 с отрицательными Y снова отражаются в положительную полуплоскость y > 0.
Второй график – окружность с центром (1; 0), радиусом 1.
Получаем три пары решений.
Ответ: {(0; 0) (1; 1) (2; 0)}.
Пример 2. Решите графически систему неравенств:
a) \( \left\{ \begin{array}{ l } \mathrm{|x-2|+|y-4|\leq 2} & \\ \mathrm{y\leq \frac{1}{x-2}+4} & \end{array}\right. \)
|x – 2| + |y – 4| ≤ 2 – внутренняя область и стороны квадрата с точкой пересечения диагоналей (2; 4), длиной диагоналей 4.
\( \mathrm{y\leq \frac{1}{x-2}+4} \) – область под гиперболой с асимптотами x = 2, y = 4.
Решение – точка A(1; 3) и треугольник BCD, заданный системой трех неравенств:
\)б) \( \left\{ \begin{array}{ l } \mathrm{1\leq |x+y|\leq 3} & \\ \mathrm{2\leq |x-y|\leq 5} & \end{array}\right. \)
Первое неравенство: \( \mathrm{1\leq |x+y|\leq 3\Rightarrow -3\leq x+y\leq -1\cup 1\leq x+y\leq 3\Rightarrow} \)
\( \mathrm{\Rightarrow -x-3\leq y\leq -x-1\cup -x+1\leq y\leq -x+3} \) – две полосы, параллельные y = –x.
Второе неравенство: \( \mathrm{2\leq |x-y|\leq 5\Rightarrow -5\leq x-y\leq -2\cup 2\leq x-y\leq 5\Rightarrow} \)
\( \mathrm{\Rightarrow -x-5\leq -y\leq -x-2\cup -x+2\leq -y\leq -x+5\Rightarrow} \)
\( \mathrm{\Rightarrow x+2\leq y\leq x+5\cup x-5\leq y\leq x-2} \) – две полосы, параллельные y = x.
Решение – четыре прямоугольника, образованные пересечением полос.
\( \left\{ \begin{array}{ l } \mathrm{-x-3\leq y\leq -x-1\cup -x+1\leq y \leq -x+3} & \\ \mathrm{x+2\leq y\leq x+5\cup x-5\leq y\leq x -2} & \end{array}\right. \)
Пример 3. Найдите значения параметра a, при которых система имеет ровно два решения:
\( \left\{ \begin{array}{ l } \mathrm{y=x^2-5|x|+4} & \\ \mathrm{y\leq a} & \end{array}\right.
\)
y = x2 – 5|x| + 4 – парабола y = x2 – 5x + 4 = (x – 1)(x – 4), x > 0, отраженная в отрицательную полуплоскость x < 0 относительно оси Y.
Осью симметрии параболы при x > 0 является прямая \( \mathrm{x_0=\frac{x_1+x_2}{2}=\frac{1+4}{2}=2,5} \)
Вершина лежит на оси. Ордината вершины: y0 = 2,52 – 5 · 2,5 + 4 = –2,25.
В полуплоскости x < 0 вершина расположена симметрично относительно оси Y и имеет ту же ординату.
Значит, при a = –2,25 система имеет два решения:
При a < –2,25 решений нет, при a > –2,25 решений бесконечное множество (отрезки кривой).
Ответ: a = –2,25.
Презентация на тему: Неравенства с модулем.
Неравенства с модулями
11 класс презентация
Неравенства вида |f(x)| a при a ≤ 0 имеют решением всю область определения функции f(x) . При a 0 исходное неравенство равносильно двум неравенствам : f(x) a и f(x) , при этом решения обоих неравенств являются решениями исходного. Это справедливо и для нестрогих неравенств. «
Неравенства вида |f(x)| при a ≤ 0 решений не имеют, а при a 0 равносильны двойному неравенству –a . Заметим, что если неравенство нестрогое |f(x) |≤ a , то при а=0 оно равносильно уравнению f(x)=0.
Неравенства вида |f(x)| a при a ≤ 0 имеют решением всю область определения функции f(x) . При a 0 исходное неравенство равносильно двум неравенствам : f(x) a и f(x) , при этом решения обоих неравенств являются решениями исходного. Это справедливо и для нестрогих неравенств.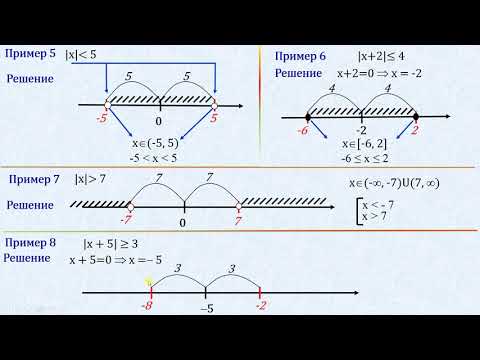
Решить неравенство :
|3 — 8x 2 | -3
Решение.
Поскольку модуль всегда заведомо больше отрицательного числа, решением этого неравенства является область определения функции, стоящей под знаком модуля, т.е. любое рациональное число.
Ответ : x (-∞;∞)
Решить неравенство: |x 2 — 2x| ≤ 0
Решение.
Решением этого неравенства будут корни уравнения x 2 -2x=0 ,т.е. x 1 =0 и x 2 =2 .
Ответ : x ϵ {0} ᴜ {2}
Решить неравенство : |7x 2 + 8| ≤ -3
Решение.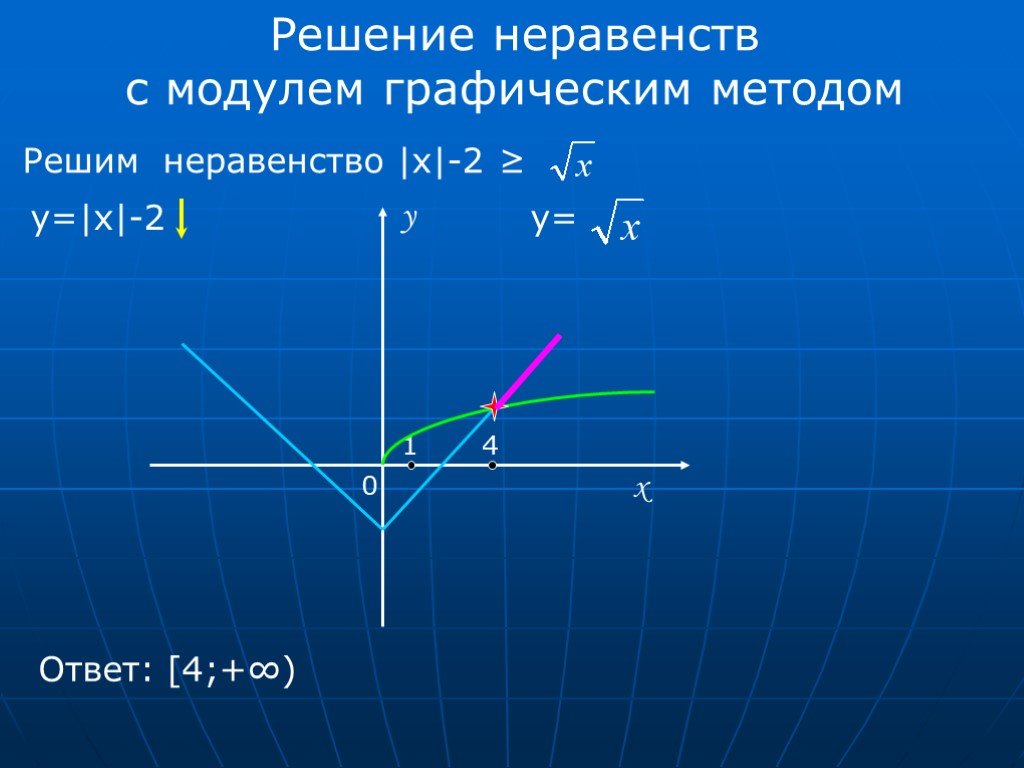
Неравенство решений не имеет, так как модуль всегда положителен.
Ответ : x ϵ
Решить неравенство : |x 2 — 7x| ≥ 12
- Решение.
Равносильные неравенства x 2 — 7x ≥ 12 и x 2 — 7x ≤ -12 сводятся к квадратным x 2 — 7x -12 ≥ 0 и x 2 — 7x + 12 ≤ 0 .
Решаем первое неравенство.
Корни уравнения 😡 1 = и x 2 = ; решением этого неравенства будут два полубесконечных интервала : (-∞;] и [ ;∞)
Решаем второе неравенство.
Корни уравнения: x 1 = 3 и x 2 = 4 ; решением этого неравенства будет интервал: x
Следовательно, решением исходного неравенства будут три интервала решений квадратных неравенств.
Ответ : x
Решить неравенство : | ≤ 3
- Решение.
Данное неравенство равносильно двойному : -3 ≤ ≤ 3.
≥ 0
+ 3 ≥ 0
≥ -3
≤ 3
≤ 0
— 3 ≤ 0
(6x – 8)(x – 3) ≥ 0
≥ 0
x ϵ ( -∞ ; ] ᴜ ( 3 ; ∞)
x ≠ 3
x ϵ ( — ∞ ; 3 )
≤ 0
x – 3
Ответ : x ϵ ( — ∞ ; )
Неравенства вида |f(x)|≤ g(x) сводятся к равносильной системе:
- f(x) ≤ g(x) f(x) ≥ -g(x) ,
а неравенства вида |f(x)|≥ g(x) – к аналогичной равносильной системе:
f(x) ≥ g(x) f(x) ≤ -g(x) .
Решить неравенство : |x 2 — 8x + 15|
Решение .
Равносильная система неравенств
x 2 — 8x + 15 x 2 — 8x + 15 3 — x
сводится к решению двух равносильных неравенств :
x 1 = 3 x 2 = 6
x ϵ ( 3 ; 6 ) x ϵ ( -∞ ; 3) ᴜ ( 4 ; ∞ )
x 2 — 9x + 18 x 2 — 7x + 12 0
6
3
x 1 = 3 x 2 = 4
4
3
Ответ : x ϵ ( 4 ; 6 )
Решить неравенство : |x 2 – 2x — 3| 3x — 3
Решение .
Равносильная система неравенств
x 2 – 2x – 3 3x – 3 x 2 – 2x – 3
как и в предыдущем примере, сводится к системе квадратных неравенств :
x 1 = 0 x 2 = 5
x ϵ ( -∞ ; 0 ) ᴜ ( 5 ; ∞ ) x ϵ ( -3 ; 2 )
x 2 –5x 0 x 2 + x – 6
0
5
x 1 = -3 x 2 = 2
2
-3
Ответ : x ϵ ( -3 ; 0 )
Неравенства вида F(|f(x)|) v 0 заменой y=|f(x)| сводятся к равносильной системе :
F(y) v 0 y ≥ 0
Решать его нужно методом интервалов для рациональных и дробно-рациональных неравенств, предварительно разложив левую часть на множители. Корень у=1 кубического трехчлена угадывается сразу. Поэтому, деля y 3 + y — 2 на у – 1 или применяя метод неопределенных коэффициентов с использованием теоремы Безу, разложим выражение на два сомножителя – линейный и квадратный. Решить неравенство : |x — 4| 3 + |x — 4| 2 Решение . Заменой y=|x — 4| исходное неравенство сводится к равносильной системе : y 3 + y 2 y ≥ 0 y — 1 y 2 + y + 2 y 3 + y – 2 y 3 – y 2 — y 2 + y y 2 – y — 2у – 2 2у – 2 — 0 «
Первое неравенство y 3 + y — 2 0 – рациональное. Решать его нужно методом интервалов для рациональных и дробно-рациональных неравенств, предварительно разложив левую часть на множители. Корень у=1 кубического трехчлена угадывается сразу. Поэтому, деля y 3 + y — 2 на у – 1 или применяя метод неопределенных коэффициентов с использованием теоремы Безу, разложим выражение на два сомножителя – линейный и квадратный.
Решить неравенство : |x — 4| 3 + |x — 4| 2
Решение .
Заменой y=|x — 4| исходное неравенство сводится к равносильной системе :
y 3 + y 2 y ≥ 0
y — 1 y 2 + y + 2
y 3 + y – 2 y 3 – y 2
—
y 2 + y y 2 – y
—
2у – 2 2у – 2
—
0
Таким образом,
y 3 + y – 2 = (у – 1)(y 2 + y + 2)
Итак, равносильная система приняла вид :
(у – 1)(y 2 + y + 2)0 y≥0 ,
откуда у1
Переходя к переменной х, получаем простейшее неравенство |х — 4| 1 , которое разбивается на два равносильных : х – 4 1 , или х 5 , и х – 4 , или х .
Таким образом, x ϵ ( -∞ ; 3) ᴜ ( 5; ∞ ) .
Ответ : x ϵ ( -∞ ; 3) ᴜ ( 5 ; ∞ )
- Неравенства вида F ( ϕ (x) ; | f(x) | ) v 0 сводятся к двум равносильным системам :
f(x) ≥ 0
f(x) 0 F( ϕ (x) ; -f(x)) v 0
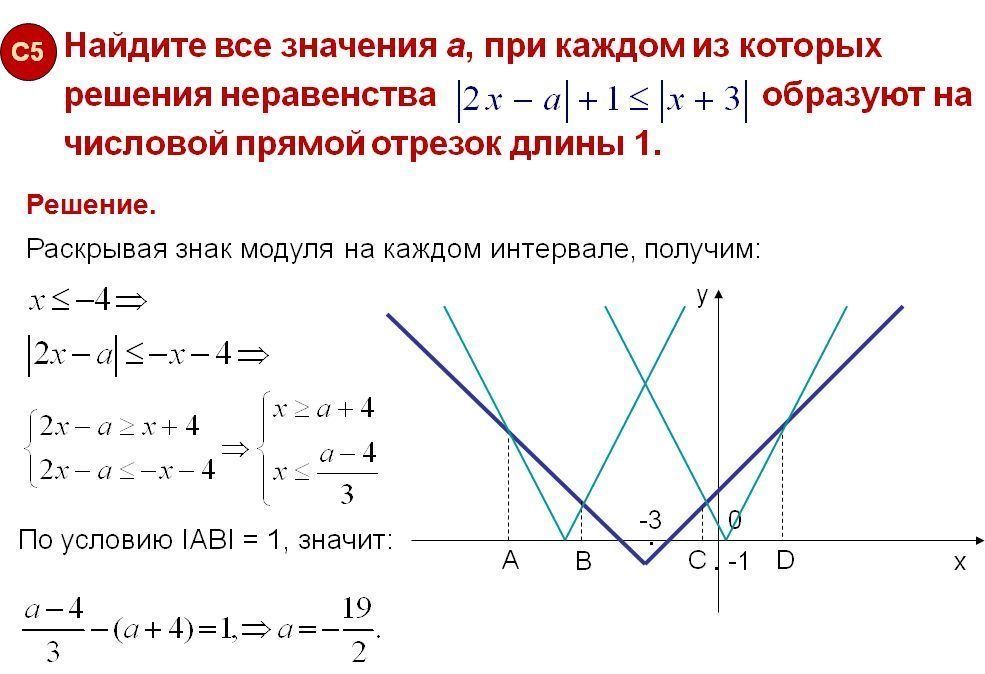
Решить неравенство : x 2 + 2|x + 3| — 10 ≤ 0
Решение .
Равносильные системы :
x ≥ -3 x 1 = -1 + x 2 = -1 —
x ≥ -3 x 2 + 2x – 4 ≤ 0
x + 3 ≥ 0 x 2 + 2(x + 3) – 10 ≤ 0
x ϵ [-3 ; -1 +
и
x x 1 = 1 + x 2 = 1 —
x + 3 x 2 — 2(x + 3) – 10 ≤ 0
x x 2 — 2x – 16 ≤ 0
x ϵ [1 — ; -1 + ]
Ответ : x ϵ [ 1 — ; -1 + ]
«
Неравенства вида |f(x)||g(x)| , как и соответствующие уравнения, сводятся к равносильному [ f(x) ] 2 [ g(x) ] 2 .
Решить неравенство : |2x — 5| — |4x + 7|≥ 0
Решение .
Приводим исходное неравенство к виду
|2x — 5| ≥ |4x + 7|
и возводим в квадрат :
(2x – 5) 2 ≥ (4x + 7) 2
Решением неравенства является интервал [ -6 ; — ] , он же – решением исходного неравенства с модулями.
Раскрывая скобки и приводя подобные члены, получаем квадратное неравенство :
3x 2 + 19x + 6 ≤ 0
x 1 = — 6 x 2 = —
3x 2 + 19x + 6 = 0
Ответ : x ϵ [ -6 ; — ]
Не следует путать этот метод с методом интервалов, применяемым для решения рациональных и дробно-рациональных неравенств.
Внимание!
Неравенства вида |f 1 (x)|±|f 2 (x)|±…±|f n (x)| v a решаются тем же самым методом интервалов, что и уравнения с модулем. Разница лишь в том, что в данном случае в каждом интервале решается не уравнение, а неравенство и из решений неравенства выбираются те, которые принадлежат данному интервалу. В остальном метод интервалов остается тем же, что и при решении уравнений с модулем.
Решить неравенство : |x|- 2|x + 1|+ 3|x + 2|≥ 4
Решение .
Найдем сначала все x i , разбивающие числовую ось на интервалы и получающиеся как решения уравнений f j (x i )=0 : х=0; х + 1=0 ; х + 2=0 .
Таким образом, границами интервалов являются числа x 1 =0, x 2 =-1 и x 3 =-2. Отметим эти значения на числовой оси для каждого из полученных интервалов определим знаки выражений, стоящих под знаком модуля :
III
IV
II
I
-2
-1
0
x x + 1 x + 2
x x + 1 x + 2 0
x x + 1 0 x + 2 0
x0 x + 1 0 x + 2 0
Раскроем модули на интервале I (x≤-2) :
-x + 2( + 1) – 3(x + 2) ≥ 4
После преобразования получаем
-2х – 4 ≥ 4 ,
откуда х ≤ -4
Этот интервал входит в интервал I и является решением исходного неравенства.
II интервал ( -2≤ х ≤-1 ) :
-х+ 2(х + 1) + 3(х + 2) ≥ 4
4х + 8 ≥ 4 ,
откуда х≥-1
Решением в этом интервале является точка х=-1
III интервал ( -1≤ х ≤0 ) :
-х – 2(х + 1) + 3(х + 2) ≥ 4
4 ≥ 4
В результате мы получили истинное неравенство ( заметим, что, если бы неравенство было строгим, оно становилось бы ложным).
Следовательно, весь интервал III является решением исходного неравенства.
IV интервал ( х≥0 )
х – 2(х + 1) + 3( + 2) ≥ 4
2х + 4 ≥ 4 ,
откуда х≥0
Таким образом, весь интервал IV является решением исходного неравенства. Заметим, что решения, полученные в интервалах II , III и IV , «сливаются» по граничным точкам x 1 =-1 и x 2 =0 в единый интервал [-1 ; ∞).
Ответ : ( -∞ ; -4 ] ᴜ [ -1 ; ∞ )
6.4 – Линейные неравенства и системы линейных неравенств с двумя переменными
Цели обучения
- (6.4.1) – Определить решение линейного неравенства с двумя переменными
- (6.4.2) – График решения набора линейного неравенства с двумя переменными
- (6.4.3) – Построить график системы линейных неравенств и определить область решений
- (6.4.4) – Определить, является ли точка решением системы неравенств
- (6. 4.5) – Определите, когда система неравенств не имеет решения
- (6.4.6) – Приложения систем линейных неравенств
4.5) – Определите, когда система неравенств не имеет решенияРаньше мы учились решать неравенства только с одной переменной. Теперь мы узнаем о неравенствах, содержащих две переменные. В частности, мы рассмотрим линейных неравенств с двумя переменными, которые очень похожи на линейные уравнения с двумя переменными.
Линейные неравенства с двумя переменными имеют множество применений. Например, если вы управляете бизнесом, вы хотели бы, чтобы ваши доходы превышали ваши расходы, чтобы ваш бизнес приносил прибыль.
Линейное неравенство с двумя переменными
A линейное неравенство с двумя переменными – это неравенство, которое может быть записано в одной из следующих форм:
[latex]Ax+By < 0[/latex] [latex]Ax+ By>0[/latex] [latex]Ax+By \leq 0[/latex] [latex]Ax+By \geq 0[/latex]
, где [latex]A[/latex] и [latex]B[ /latex] не равны нулю.
Напомним, что неравенство с одной переменной имело много решений. Например, решением неравенства [латекс]x > 3[/латекс] является любое число больше 3. Мы показали это на числовой прямой, заштриховав числовую строку справа от 3 и поставив открытую скобку на 3.
Аналогично линейные неравенства с двумя переменными имеют множество решений. Любая упорядоченная пара [латекс](х,у)[/латекс], которая делает неравенство верным при подстановке значений, является решением линейного неравенства.
Решение линейного неравенства с двумя переменными
Упорядоченная пара [латекс](х,у)[/латекс] является решением линейного неравенства , если неравенство верно, когда мы подставляем значения [латекс] x[/латекс] и [латекс]у[/латекс].
ПРИМЕР
Определите, является ли каждая упорядоченная пара решением неравенства [latex]y>x+4[/latex].
a)[латекс](0,0)[/латекс]
б)[латекс](1,6)[/латекс]
Показать ответ
Наборы решений неравенств
На приведенном ниже графике показана область значений, которая делает неравенство [латекс]3x+2y\leq6[/латекс] верным (заштрихована красным), граничная линия [латекс]3x+2y=6[ /латекс], а также несколько заказанных пар.
Граница сплошная, потому что точки на граничной линии [latex]3x+2y=6[/latex] делают неравенство [latex]3x+2y\leq6[/latex] истинным.
Вы можете подставить значения [latex]x[/latex]– и [latex]y[/latex] – в каждую из упорядоченных пар [latex](x,y)[/latex] в неравенство найти решения. Иногда имеет смысл составить таблицу значений для более сложных неравенств.
| Заказная пара | Делает неравенство [латекс]3x+2y\leq6[/латекс] верное утверждение | Делает неравенство [латекс]3x+2y\leq6[/латекс] ложное утверждение |
|---|---|---|
| [латекс](−5, 5)[/латекс] | [латекс]\begin{array}{r}3\left(−5\right)+2\left(5\right)\leq6\\−15+10\leq6\\−5\leq6\end{array }[/латекс] | |
| [латекс](−2,−2)[/латекс] | [латекс]\begin{array}{r}3\left(−2\right)+2\left(–2\right)\leq6\\−6+\left(−4\right)\leq6\\ –10\leq6\end{массив}[/латекс] | |
| [латекс](2,3)[/латекс] | [латекс]\begin{array}{r}3\left(2\right)+2\left(3\right)\leq6\\6+6\leq6\\12\leq6\end{array}[/ латекс] | |
| [латекс](2,0)[/латекс] | [латекс]\begin{array}{r}3\left(2\right)+2\left(0\right)\leq6\\6+0\leq6\\6\leq6\end{array}[/ латекс] | |
| [латекс](4,−1)[/латекс] | [латекс]\begin{массив}{r}3\влево(4\вправо)+2\влево(-1\вправо)\leq6\\12+\влево(-2\вправо)\leq6\\10\ leq6\end{массив}[/латекс] |
Если подстановка [латекс](х,у)[/латекс] в неравенство дает верное утверждение, тогда упорядоченная пара является решением неравенства, и точка будет нанесена в заштрихованную область или точку будет частью сплошной граничной линии.
Ложное утверждение означает, что упорядоченная пара не является решением, и точка будет находиться вне заштрихованной области или будет частью пунктирной граничной линии.
В следующем видео показан пример определения того, является ли упорядоченная пара решением неравенства.
В следующем видео показан еще один пример определения того, является ли упорядоченная пара решением неравенства.
Так как же перейти от алгебраической формы неравенства, например [латекс]у>3х+1[/латекс], к графику этого неравенства? Построить неравенство довольно просто, если вы выполните пару шагов.
Графические неравенства
Чтобы построить график неравенства:
- Нарисуйте соответствующую линию границы. Замените знак <, >, ≤ или ≥ в неравенстве на =, чтобы найти уравнение граничной линии.
- Определите хотя бы одну упорядоченную пару по обе стороны от линии границы и подставьте эти значения [латекс](х,у)[/латекс] в неравенство. Закрасьте область, содержащую упорядоченные пары, которые делают утверждение неравенства верным.
- Если точки на граничной линии являются решениями, используйте сплошную линию для рисования граничной линии. Это произойдет для ≤ или ≥ неравенств.
- Если точки на граничной линии не являются решениями, используйте пунктирную линию для граничной линии. Это произойдет для < или > неравенств.
Построим график неравенства [латекс]х+4у\leq4[/латекс].
Чтобы построить граничную линию, найдите не менее двух значений, лежащих на линии [latex]x+4y=4[/latex]. Вы можете использовать точки пересечения x и y для этого уравнения, подставив сначала 0 вместо x и найдя значение y ; затем подставьте 0 вместо y и найдите x .
| х | у |
| 0 | 1 |
| 4 | 0 |
Нанесите точки [латекс](0,1)[/латекс] и [латекс](4,0)[/латекс] и проведите линию через эти две точки в качестве граничной линии. Линия сплошная, потому что ≤ означает «меньше или равно», поэтому все упорядоченные пары вдоль линии включаются в набор решений.
Следующий шаг — найти область, содержащую решения. Это выше или ниже границы? Чтобы определить область, в которой справедливо неравенство, вы можете протестировать пару упорядоченных пар, по одной с каждой стороны от граничной линии.
Если заменить [латекс](−1,3)[/латекс] на [латекс]x+4y\leq4[/латекс]:
[латекс]\begin{array}{r}−1+4\ left(3\right)\leq4\\−1+12\leq4\\11\leq4\end{array}[/latex]
Это неверное утверждение, поскольку 11 не меньше или равно 4.
С другой стороны, если вы замените [латекс](2,0)[/латекс] на [латекс]x+4y\leq4[/латекс]:
[латекс]\begin{array}{r}2 +4\left(0\right)\leq4\\2+0\leq4\\2\leq4\end{массив}[/latex]
Это правда! Область, включающая [латекс](2,0)[/латекс], должна быть заштрихована, так как это область решений.
Вот и все — график множества решений для [latex]x+4y\leq4[/latex].
Небольшое примечание к описанной выше проблеме — обратите внимание, что вы можете использовать точки [латекс](0,−3)[/латекс] и [латекс](2,1)[/латекс] для построения линии границы , но что эти точки не входят в область решений, так как область не включает граничную линию!
Рассмотрим график неравенства [latex]y<2x+5[/latex].
Пунктирная линия: [латекс]у=2х+5[/латекс]. Каждая упорядоченная пара в заштрихованной области под линией является решением [латекс]y<2x+5[/латекс], так как все точки под линией сделают неравенство верным.
Если вы сомневаетесь в этом, попробуйте подставить в неравенство координаты [latex]x[/latex] и [latex]y[/latex] точек A и B — вы увидите, что они работают. Итак, заштрихованная область показывает все решения этого неравенства.
Линия границы делит координатную плоскость пополам. В данном случае она показана пунктирной линией, так как точки на прямой не удовлетворяют неравенству. Если бы неравенство было [латекс]y\leq2x+5[/латекс], то граница была бы сплошной.
Нарисуем другое неравенство: [латекс]у>-х[/латекс]. Вы можете проверить пару точек, чтобы определить, какую сторону линии границы следует заштриховать. Проверка точек M и N дает верные утверждения. Итак, заштриховываем область над линией. Линия пунктирная, так как точки на прямой не соответствуют действительности.
Чтобы создать систему неравенств, вам нужно построить график двух или более неравенств. Давайте использовать [латекс]y<2x+5[/латекс] и [латекс]у>-х[/латекс], так как мы уже построили график каждого из них.
Фиолетовая область показывает, где перекрываются решения двух неравенств. Эта область является решением системы неравенств . Любая точка в этой фиолетовой области будет верна как для [латекс]у>-х[/латекс], так и для [латекс]у<2x+5[/латекс].
В следующих видео-примерах показано, как построить график системы линейных неравенств и определить область решения.
В следующем разделе мы увидим, что точки могут быть решениями систем уравнений и неравенств. Алгебраически проверим, является ли точка решением линейного уравнения или неравенства.
На приведенном выше графике вы можете видеть, что точки B и N являются решениями для системы, потому что их координаты делают оба утверждения неравенства верными.
Напротив, точки M и A лежат вне области решения (фиолетовый). Хотя точка M является решением неравенства [latex]y>−x[/latex], а точка A является решением неравенства [latex]y<2x+5[/latex], ни одна из точек не является решением система . В следующем примере показано, как проверить точку, чтобы увидеть, является ли она решением системы неравенств.
Вот график системы в приведенном выше примере. Обратите внимание, что [латекс](2,1)[/латекс] находится в фиолетовой области, которая является областью перекрытия двух неравенств.
Вот график этой системы. Обратите внимание, что [латекс](2, 1)[/латекс] не находится в фиолетовой области, которая является перекрывающейся областью; это решение одного неравенства (красная область), но не решение второго неравенства (синяя область).
В следующем видео мы покажем еще один пример определения того, входит ли точка в решение системы линейных неравенств.
Как показано выше, решение системы неравенств можно найти, изобразив каждое неравенство в виде графика и определив область, которую они разделяют.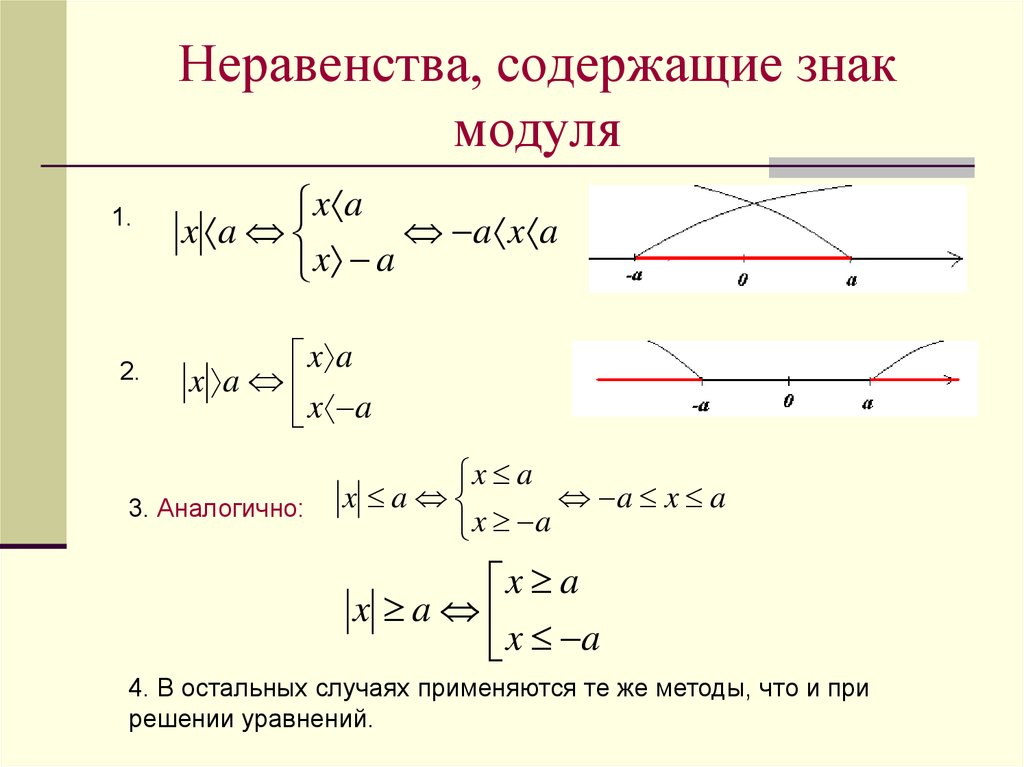
Ниже приведены дополнительные примеры, показывающие весь процесс определения области решений на графе для системы двух линейных неравенств. Общие шаги описаны ниже:
- Изобразите каждое неравенство в виде линии и определите, будет ли она сплошной или пунктирной
- Определите, какая сторона каждой граничной линии представляет решения неравенства, проверив точку на каждой стороне
- Закрасьте область, представляющую решения для обоих неравенств
В следующем примере мы покажем решение системы двух неравенств, граничные линии которых параллельны друг другу. Когда графики системы двух линейных уравнений параллельны друг другу, мы обнаружили, что система не имеет решения. Аналогичный результат мы получим для следующей системы линейных неравенств.
Примеры
Граф системы [латекс]\начало{массив}{с}у\ге2х+1\\у\lt2x-3\конец{массив}[/латекс]
Показать решение
В следующих примерах мы продолжим практиковаться в построении графика области решения для систем линейных неравенств.
Мы также построим графики решений системы, включающей сложное неравенство.
Пример
Закрасьте область графика, которая представляет решения для обоих неравенств. [латекс]x+y\geq 1[/латекс] и [латекс]y -x\geq 5[/латекс].
Показать решение
В следующих видеороликах показано больше примеров построения графика множества решений системы линейных неравенств.
Система в нашем последнем примере включает составное неравенство. Мы увидим, что сложное неравенство можно рассматривать как две линии, когда вы рисуете их на графике.
Пример
Найдите решение системы [латекс]3x + 2y < 12[/латекс] и [латекс]−1\leq y \leq 5[/латекс].
Показать ответ
В следующем видео мы покажем, как решить еще одну систему неравенств.
В нашем первом примере мы покажем, как написать и построить график системы линейных неравенств, которая моделирует объем продаж, необходимый для получения определенной суммы денег.
Пример
Кэти продает рожки мороженого на школьном благотворительном мероприятии. Она продает два размера: маленький (с 1 мерной ложкой) и большой (с 2 мерными ложками). Она знает, что может получить максимум 70 шариков мороженого из своего запаса. Она берет 3 доллара за маленький конус и 5 долларов за большой.
Кэти хочет заработать как минимум 120 долларов, чтобы отдать их школе.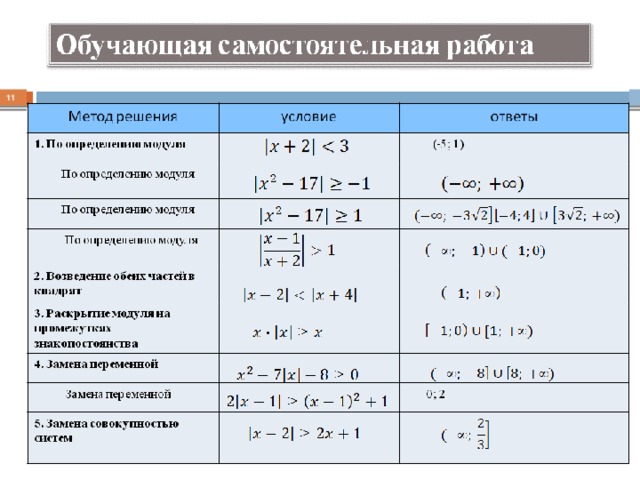
Напишите и начертите систему неравенств, моделирующую эту ситуацию.
Показать ответ
В предыдущем примере для поиска решения системы линейных уравнений мы ввели уравнения затрат и доходов производителя:
Стоимость: [латекс]y=0,85x+35 000[/латекс]
Доход: [латекс] y=1,55x[/latex]
Уравнение затрат показано синим цветом на графике ниже, а уравнение дохода показано оранжевым цветом. Точка, в которой пересекаются две линии, называется точкой безубыточности, мы узнали, что это решение системы линейных уравнений, которые в данном случае составляют уравнения затрат и доходов.
Заштрихованная область справа от точки безубыточности представляет объемы, при которых компания получает прибыль. Область слева представляет количества, по которым компания несет убытки.
В следующем примере вы увидите, как информацию, которую вы узнали о системах линейных неравенств, можно применить для ответов на вопросы о затратах и доходах.
Обратите внимание, что заштрихованная синим цветом область между уравнениями «Затраты» и «Доход» помечена как «Прибыль». Это «золотое пятно», которого компания хочет достичь, когда они производят достаточно велосипедных рам с минимальными затратами, чтобы зарабатывать деньги. Они не хотят, чтобы уходило больше денег, чем приходило!
Пример
Определите область прибыли для бизнеса по производству скейтбордов, используя неравенства, учитывая систему линейных уравнений: 1,55x[/latex]
Показать раствор
В следующем видео вы увидите пример того, как найти точку безубыточности для небольшого бизнеса по производству сноу-конуса.
А вот еще один видео пример решения задачи с помощью системы линейных неравенств.
Мы видели, что системы линейных уравнений и неравенств могут помочь определить рыночное поведение, которое очень полезно для бизнеса. Пересечение уравнений затрат и доходов дает точку безубыточности, а также помогает определить регион, в котором компания будет получать прибыль.
Примеры решения линейных неравенств
Введение и форматирование Более сложные примеры
Purplemath
Помните, линейные неравенства с одной переменной решаются почти так же, как линейные уравнения с одной переменной. (Да, есть одно отличие. Мы вернемся к этому далее на этой странице.)
Так что, как всегда, сделайте то же самое с обеих сторон, и вы будете золотыми!
Содержание продолжается ниже
MathHelp.com
Решение неравенств
- Решить 2 x ≤ 9.
Если бы мне дали уравнение «2 x = 9», я бы разделил по 2 с каждой стороны. Я могу сделать то же самое здесь:
Я мог бы записать решение в десятичной форме (то есть как 4,5), но они, вероятно, предпочитают дроби, поэтому мой ответ:
x ≤ 9 / 2
- Solve x / 4 > 1 / 2
Если бы мне дали уравнение
x / 4 = 1 / 2 , я бы умножил обе части на 4, чтобы найти решение. Я могу сделать то же самое с неравенством, которое они мне дали:
Да, я мог бы сделать это в уме (я имею в виду четверти и половинки? Легко!), но тогда у меня не было бы никакой работы, которую можно было бы показать.
И им нравится смотреть на работу.
Мой ответ:
x > 2
- Решить −2 x < 5.
Помните, я сказал, что решение линейных неравенств *почти* точно такое же, как решение линейных уравнений? Ну, это единственное место, где все по-другому. Чтобы объяснить, что я собираюсь сделать, рассмотрим следующее верное утверждение о неравенстве:
3 > 2
Что произойдет с приведенным выше неравенством, если я умножу его на −1? Возникает соблазн сказать, что ответ будет «−3 > −2». Но -3 не больше , чем -2; на самом деле меньше , чем -2. То есть правильное неравенство после замены всех знаков на самом деле будет следующим:
−3 < −2
Как видите, умножение на минус (в данном случае −1) меняет знак неравенства с « больше чем» до «меньше чем». Это новая проблема для решения неравенств; Вот почему решение линейных неравенств лишь *почти* похоже на решение линейных уравнений.
Чтобы решить -2 x < 5, мне нужно разделить на минус (в данном случае -2), поэтому мне нужно перевернуть неравенство:
Примечание.
Рисунок ниже анимирован в оригинале («живая») версия веб-страницы.
Тогда мой ответ:
x > −5 / 2
Вы можете задаться вопросом, почему мы должны переворачивать символ неравенства при делении (или умножении) на минус, когда не было речи о переворачивании чего-либо, когда вы были работа с линейными уравнениями. Но если подумать, какая разница, если перевернуть знак «равно», верно?
Если вы хотите избежать проблем с переворачиванием знаков, переместите все так, чтобы любой коэффициент переменной больше не был отрицательным. В приведенном выше упражнении это означало бы, что первым шагом будет:
−2 x < 5
+2 x − 5 < −5 + 2 x
Делая сложение и вычитание вместо деления, коэффициент при переменной теперь плюс, и деление насквозь не потребует ничего переворачивать.
Если вам так удобнее обращаться с минусовым коэффициентом, сделайте так. Это может быть немного нестандартно, но это совершенно верная математика.
В любом случае всегда помните:
При решении неравенств, если вы умножаете или делите на минус, вы также должны перевернуть знак неравенства.
- Решить (2 x − 3) / 4 ≤ 2
Хм… это более грязно, чем другие. Но я могу использовать свои знакомые инструменты решения линейных уравнений, так что это выполнимо.
Сначала я умножу на 4. Поскольку 4 положительное число, мне не нужно менять знак неравенства:
(2 x − 3) / 4 ≤ 2
(4) × (2 x − 3) / 4 ≤ (4)(2)
2 x − 3 ≤ 8
2 x ≤ 11
Это потребовало больше шагов, чем в предыдущих упражнениях, но каждый шаг я выучил, когда решал линейные уравнения, поэтому весь процесс был на самом деле довольно простым.
Мой ответ:
x ≤ 11 / 2 = 5,5
Вы можете использовать виджет Mathway ниже, чтобы попрактиковаться в решении линейных неравенств. Попробуйте введенное упражнение или введите свое собственное упражнение. Затем нажмите кнопку и выберите один из вариантов «Решить для», чтобы сравнить свой ответ с ответом Mathway. (Или пропустите виджет и продолжите урок.)
Пожалуйста, примите «предпочтительные» файлы cookie, чтобы включить этот виджет.
(Нажав «Нажмите, чтобы просмотреть шаги» на экране ответов виджета, вы перейдете на сайт Mathway для платного обновления.)
До сих пор мы имели дело с неравенствами, решения которых занимают половину числовой прямой. Но неравенства могут быть более сложными, включающими более одного отношения неравенства.
Что такое составное неравенство?
Составное неравенство — это неравенство, в котором есть два или более символов неравенства; другими словами, будет два или более неравенства, над которыми нужно работать как над набором.
Число является решением составного неравенства, если оно «удовлетворяет» (то есть работает) любой части составного неравенства.
- Решите 10 ≤ 3 x + 4 ≤ 19
Это так называемое «сложное неравенство». Оно работает так же, как обычное неравенство, за исключением того, что оно имеет три стороны вместо обычных двух. Так, например, когда я собираюсь вычесть 4, мне придется вычесть его со всех трех сторон.
10 ≤ 3 x + 4 ≤ 19
−4 −4 −4
6 ≤ 3 x ≤ 15
2 ≤ x ≤ 5
2 ≤ x ≤ 5
2 ≤ x ≤ 5
0022Это трехчастное неравенство и есть ответ, который они ищут. В нем говорится, что x может быть любым значением от двух до пяти. Мой ответ:
2 ≤ x ≤ 5
Составные неравенства также могут быть совершенно отдельными неравенствами, но с ними вам придется иметь дело вместе. Их пространство решений (то есть множество всех значений, удовлетворяющих хотя бы одной части неравенства) может быть совершенно отдельными интервалами.
Конечно, так как нет х -значение может находиться внутри двух разных интервалов одновременно, эти неравенства будут соединены словом «или». Это отличается от приведенного выше составного неравенства, где неравенство из трех частей также можно было бы сформулировать как «10 ≤ 3 x + 4 * и* 3 x + 4 ≤ 19».
Любое составное неравенство, в котором неравенства соединены знаком «и», будет составлено, как в приведенном выше примере: одно неравенство, состоящее из трех частей, с переменной, ограниченной двумя действительными числами (то есть бесконечности не задействованы). Любое составное неравенство, в котором неравенства соединены знаком «или», будет представлять собой два (или более) совершенно отдельных интервала. Решение будет иметь два или более полностью отдельных интервала решения.
- Решите 3 x + 2 ≤ −4 или 5 x -3 ≥ 17
Чтобы решить это составное неравенство, мне придется решить каждое из двух неравенств по отдельности.
Вот решение первого:
3 x + 2 ≤ -4
3 x ≤ -6
x ≤ -2
Хорошо, это решило одно из неравенств. Теперь решу другую:
5 x − 3 ≥ 17
5 x ≥ 20
x ≥ 4
Интервалы для этих двух неравенств не перекрываются (то есть их наборы точек решения не пересекаются), поэтому решение представляет собой два неравенства с «или» между ними. Почему «или»? Потому что ни одно значение x не может находиться в двух разных интервалах одновременно. Значение будет находиться в одном интервале или в другом, но не в обоих. Так что эти неравенства нельзя брать вместе с «и»; они должны быть разделены с помощью «или».
Итак, мой ответ:
x ≤ −2 или x ≥ 4
Вы можете использовать виджет Mathway ниже, чтобы попрактиковаться в решении интервального неравенства. Попробуйте введенное упражнение или введите свое собственное упражнение. Затем нажмите кнопку «бумажный самолетик», чтобы сравнить свой ответ с ответом Mathway.