Перевод десятичных чисел в дробь: онлайн калькулятор
Говоря сухим математическим языком, дробь — это число, которое представляется в виде части от единицы. Дроби широко используются в жизни человека: при помощи дробных чисел мы указываем пропорции в кулинарных рецептах, выставляем десятичные оценки на соревнованиях или используем их для подсчета скидок в магазинах.
Представление дробей
Существует минимум две формы записи одного дробного числа: в десятичной форме или в виде обыкновенной дроби. В десятичной форме числа выглядят как 0,5; 0,25 или 1,375. Любое из этих значений мы может представить в виде обыкновенной дроби:
- 0,5 = 1/2;
- 0,25 = 1/4;
- 1,375 = 11/8.
И если 0,5 и 0,25 мы без проблем конвертируем из обыкновенной дроби в десятичную и обратно, то в случае с числом 1,375 все неочевидно. Как быстро преобразовать любое десятичное число в дробь? Существует три простых способа.
Избавляемся от запятой
Самый простой алгоритм подразумевает умножение числа на 10 до тех пор, пока из числителя не исчезнет запятая. Такое преобразование осуществляется в три шага:
Шаг 1: Для начала десятичное число запишем в виде дроби «число/1», то есть мы получим 0,5/1; 0,25/1 и 1,375/1.
Шаг 2: После этого умножим числитель и знаменатель новых дробей до тех пор, пока из числителей не исчезнет запятая:
- 0,5/1 = 5/10;
- 0,25/1 = 2,5/10 = 25/100;
- 1,375/1 = 13,75/10 = 137,5/100 = 1375/1000.
Шаг 3: Сокращаем полученные дроби до удобоваримого вида:
- 5/10 = 1 × 5 / 2 × 5 = 1/2;
- 25/100 = 1 × 25 / 4 × 25 = 1/4;
- 1375/1000 = 11 × 125 / 8 × 125 = 11/8.
Число 1,375 пришлось три раза умножать на 10, что уже не очень удобно, а что нам придется делать в случае, если понадобится преобразовать число 0,000625? В этой ситуации используем следующий способ преобразования дробей.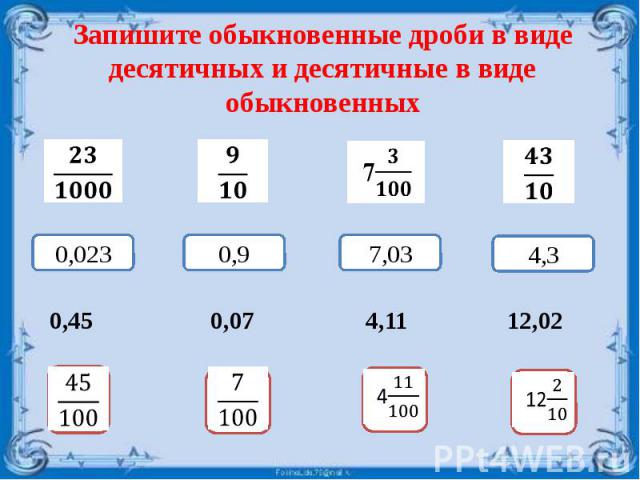
Избавляемся от запятой еще проще
Первый способ детально описывает алгоритм «удаления» запятой из десятичной дроби, однако мы можем упростить этот процесс. И вновь мы выполняем три шага.
Шаг 1: Считаем, сколько цифр стоит после запятой. К примеру, у числа 1,375 таких цифр три, а у 0,000625 — шесть. Это количество мы обозначим буквой n.
Шаг 2: Теперь нам достаточно представить дробь в виде C/10n, где C – это значимые цифры дроби (без нулей, если они есть), а n – количество цифр после запятой. К примеру:
- для числа 1,375 C = 1375, n = 3, итоговая дробь согласно формуле 1375/103 = 1375/1000;
- для числа 0,000625 C = 625, n = 6, итоговая дробь согласно формуле 625/106 = 625/1000000.
По сути, 10n – это 1 с количеством нулей, равным n, поэтому вам не нужно заморачиваться с возведением десятки в степень — достаточно указать 1 с n нулей. После этого столь богатую на нули дробь желательно сократить.
Шаг 3: Сокращаем нули и получаем итоговый результат:
- 1375/1000 = 11 × 125 / 8 × 125 = 11/8;
- 625/1000000 = 1 × 625/ 1600 × 625 = 1/1600.
Дробь 11/8 — это неправильная дробь, так как числитель у нее больше знаменателя, а значит, мы можем выделить целую часть. В этой ситуации мы вычитаем из 11/8 целую часть 8/8 и получаем остаток 3/8, следовательно, дробь выглядит как 1 и 3/8.
Преобразование на слух
Для тех, кто умеет правильно читать десятичные дроби, проще всего их преобразовать на слух. Если вы читаете 0,025 не как «ноль, ноль, двадцать пять», а как «25 тысячных», то у вас не будет никаких проблем с конвертацией десятичных чисел в обыкновенные дроби.
0,025 = 25/1000 = 1/40
Таким образом, правильное прочтение десятичного числа позволяет сразу же записать ее как обыкновенную дробь и сократить в случае необходимости.
Примеры использования дробей в повседневной жизни
На первый взгляд обыкновенные дроби практически не используются в быту или на работе и трудно представить ситуацию, когда вам понадобится перевести десятичную дробь в обычную за пределами школьных задач.
Рассмотрим пару примеров.
Работа
Итак, вы работаете в кондитерском магазине и продаете халву на развес. Для простоты реализации продукта вы разделяете халву на килограммовые брикеты, однако мало кто из покупателей готов приобрести целый килограмм. Поэтому вам приходится каждый раз разделять лакомство на кусочки. И если очередной покупатель попросит у вас 0,4 кг халвы, вы без проблем продадите ему нужную порцию.
0,4 = 4/10 = 2/5
Быт
К примеру, необходимо сделать 12 % раствор для покраски модели в нужный вам оттенок. Для этого нужно смешать краску и растворитель, но как правильно это сделать? 12 % — это десятичная дробь 0,12. Преобразовываем число в обыкновенную дробь и получаем:
0,12 = 12/100 = 3/25
Зная дроби, вы сможете правильно смешать компоненты и получить нужный цвет.
Заключение
Дроби широко используются в повседневной жизни, поэтому если вам часто необходимо преобразовывать десятичные значения в обыкновенные дроби, вам пригодится онлайн-калькулятор, при помощи которого можно мгновенно получить результат в виде уже сокращенной дроби.
Калькулятор дробей
Этот калькулятор дробей выполняет базовые и расширенные операции с дробями, выражения с дробями в сочетании с целыми, десятичными и смешанными числами. Он также показывает подробную пошаговую информацию о процедуре расчета дроби. Калькулятор помогает найти значение из операций с несколькими дробями. Решайте задачи с двумя, тремя и более дробями и числами в одном выражении.
Правила выражения с дробями:
Дроби — используйте косую черту для деления числителя на знаменатель, т.е. для пятисотых введите 5/100 . Если вы используете смешанные числа, оставьте пробел между целой и дробной частями.
Смешанные числа (смешанные числа или дроби) сохраняют один пробел между целым числом и дробью
и используют косую черту для ввода дробей, например, 1 2/3 . Пример отрицательной смешанной дроби: -5 1/2 .
Поскольку косая черта одновременно является знаком дробной строки и деления, используйте двоеточие (:) в качестве оператора деления дробей, т.
е. 1/2 : 1/3 .
Decimals (десятичные числа) вводятся с десятичной точкой . и они автоматически преобразуются в дроби — т.е. 1,45 .
Математические символы
| Символ | Название символа | Символ Значение | Пример |
|---|---|---|---|
| + | плюс | 0046 | 1/2 + 1/3 |
| — | знак минус | вычитание | 1 1/2 — 2/3 |
| * | звездочка | умножение | 2/3 * 3/4 9 | знак умножения | умножение | 2 /3 × 5/6 |
| : | знак деления | деление | 1/2 : 3 |
| 4 деления 4 деления 6 | деление | 1/3 / 5 1/2 • сложение дробей и смешанных чисел: 8/5 + 6 2/7 • деление целых чисел и дробей: 5 ÷ 1/2 • сложные дроби: 5/8 : 2 2/3 • десятичная дробь: 0,625 • Преобразование дроби в десятичную: 1/4 • Преобразование дроби в процент: 1/8 % • сравнение дробей: 1/4 2/3 • умножение дроби на целое число: 6 * 3/4 • квадратный корень дроби: sqrt(1/16) • уменьшение или упрощение дроби (упрощение) — деление числителя и знаменателя дроби на одно и то же ненулевое число — эквивалентная дробь: 4/22 • выражение со скобками: 1/3 * (1/2 — 3 3/8) • составная дробь: 3/4 от 5/7 • кратные дроби: 2/3 от 3/5 • разделить, чтобы найти частное: 3/5 ÷ 2/3 Калькулятор следует известным правилам для порядка операций .
больше задач по математике 8  .. все математические калькуляторыПреобразование процентов, десятичных дробей и дробейУрок 5. Преобразование процентов, десятичных дробей и дробей/en/fractions/multipliing-and-dividing-fractions/content/ Преобразование дробей, десятичных знаков и процентовКогда мы говорим, мы часто используем разные слова для выражения одного и того же. Например, мы можем описать один и тот же автомобиль как крошечный или маленький или маленький . Все эти слова означают, что машина не большая. Дроби, десятичные числа и проценты похожи на слова крошечный , маленький и маленький . Это всего лишь разные способы выражения части из всего . На этом изображении в каждой мерной чашке одинаковое количество сока. Иногда полезно преобразовать один вид числа в другой. Например, гораздо проще сложить 1/4 и 0,5, если превратить 0,5 в дробь. Изучение того, как преобразовывать дроби, десятичные числа и проценты, также поможет вам в изучении более сложной математики. Дроби и десятичные числаКаждая дробь может быть записана как десятичная и наоборот. Возможно, вы не будете делать это очень часто, но преобразование десятичных и дробных чисел может помочь вам в математике. Например, проще вычесть 1/6 из 0,52, если сначала превратить 1/6 в десятичную дробь. Преобразование дроби в десятичную Преобразуем дробь в десятичную. Мы будем использовать математический навык, который вы уже изучили: длинное деление. Щелкните слайд-шоу, чтобы узнать, как преобразовать дробь в десятичную.
Попробуйте!Преобразуйте каждую из этих дробей в десятичное число . Преобразование десятичного числа в дробьТеперь сделаем это в обратном порядке. Преобразуем десятичную дробь в дробь. Щелкните слайд-шоу, чтобы узнать, как преобразовать десятичную дробь в дробь.
Уменьшение дроби может показаться ненужным при преобразовании десятичной дроби. Но это важно, если вы собираетесь использовать дробь в математической задаче. Попробуй!Преобразуйте эти десятичные дроби в дроби. Не забудьте привести каждую дробь к простейшей форме! Проценты и десятичные дробиЗнание того, как преобразовывать проценты и десятичные дроби, поможет вам рассчитать такие вещи, как налог с продаж и скидки. Чтобы узнать, как это сделать, ознакомьтесь с нашим уроком «Проценты в реальной жизни». Преобразование процентов в десятичные числаПреобразование процентов в десятичные числа на удивление легко. Это займет всего несколько простых шагов. Щелкните слайд-шоу, чтобы узнать, как преобразовать проценты в десятичные дроби.
Почему это работает? Преобразование процентов в десятичные дроби настолько просто, что вам может показаться, что вы что-то упустили. Но не волнуйтесь — это действительно так просто! Вот почему метод, который мы вам показали, работает. Когда мы превращаем процент в десятичную дробь, мы фактически делаем два шага. Сначала мы конвертируем наш процент в дробь. Поскольку все проценты выходят за пределы 100, мы просто помещаем проценты больше 100, например: 78% = 78/100 На втором этапе мы преобразуем 78/100 в десятичное число. Вы уже знаете, что это означает, что мы разделим числитель на знаменатель , например: 78 ÷ 100 = 0,78 Так почему же мы не показали вам эти шаги в слайд-шоу? Потому что вы можете получить ответ и без них. Вы знаете, что все проценты не равны 100, поэтому можете не превращать проценты в дроби. Вы должны разделить процент на 100, чтобы получить десятичную дробь, но есть быстрый способ сделать это. Просто переместите запятую на две позиции влево! Таким образом, вы можете получить тот же ответ всего за один простой шаг. Попробуй!Преобразуйте эти проценты в десятичные дроби. Преобразование десятичной дроби в проценты Теперь обратим то, что вы только что узнали. Щелкните слайд-шоу, чтобы узнать, как преобразовать десятичную дробь в проценты.
Попробуйте!Вычислить эти десятичные дроби в процентах. Проценты и дробиУмение записывать проценты в виде дробей и наоборот может помочь вам в повседневной жизни. Например, предположим, что вы получили оценку 80% на тесте. Вы можете преобразовать 80% в дробь, чтобы узнать, сколько из ваших ответов были правильными. Когда ваш учитель оценивает тест, он может поступить наоборот. Если учащийся правильно ответил на 8 из 10 вопросов, учитель может преобразовать 8/10 в проценты, чтобы поставить учащемуся оценку. Преобразование процентов в дроби При преобразовании процентов в дроби полезно помнить, что проценты всегда выходят за пределы 100. Щелкните слайд-шоу, чтобы узнать, как преобразовать проценты в дроби.
Попробуйте! Запишите эти проценты в виде дробей. Преобразование дроби в процентыПреобразование дроби требует двух навыков, которые вы только что изучили: записи дроби в виде десятичной дроби и записи десятичной дроби в виде процентов . Давайте посмотрим, как мы можем использовать эти навыки для преобразования дроби в проценты. Щелкните слайд-шоу, чтобы узнать, как преобразовать дробь в проценты.
|
Наиболее распространенные мнемоники для запоминания этого порядка операций: 
Но мы выразили эту сумму тремя способами: в виде дроби, в процентах и в виде десятичной дроби. Поскольку они выражают одно и то же количество, мы знаем, что 1/2, 50% и 0,5 равны друг другу. Каждый раз, когда мы видим 1/2, мы знаем, что это также может означать 50% или 0,5.
Чтобы освежить в памяти этот навык, вы можете просмотреть наш урок «Длинная дивизия».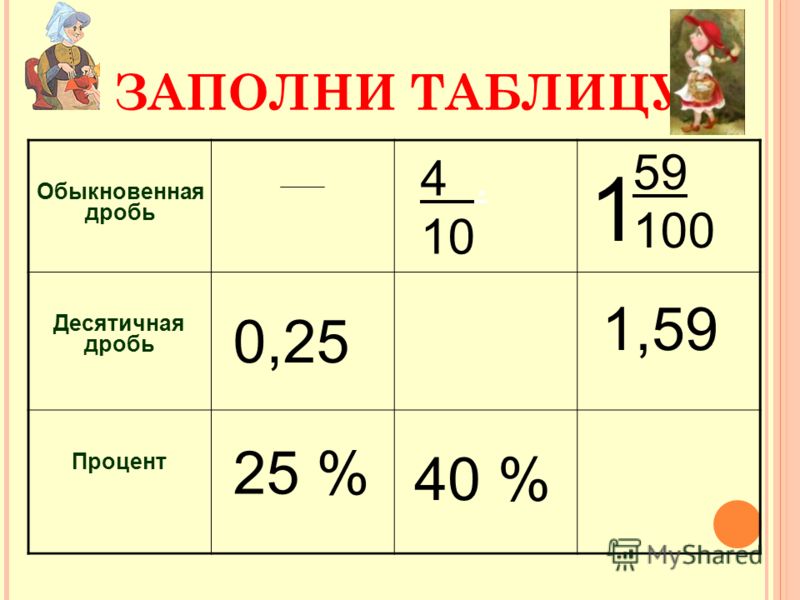
Мы добавим еще один 0 после запятой и уменьшим его.
Если вы добавляете две дроби, вам может даже понадобиться уменьшить или изменить обе дроби, чтобы они имели общий знаменатель .
.. и превратим его в десятичную точку.
Преобразуем десятичную дробь в проценты.
Вы можете попрактиковаться с процентами в нашем уроке «Введение в проценты».
Убедитесь, что уменьшите каждую дробь до простейшей формы.