| 1 | Найти объем | сфера (5) | |
| 2 | Найти площадь | окружность (5) | |
| 3 | Найти площадь поверхности | сфера (5) | |
| 4 | Найти площадь | окружность (7) | |
| 5 | Найти площадь | окружность (2) | |
| 6 | Найти площадь | окружность (4) | |
| 7 | Найти площадь | окружность (6) | |
| 8 | сфера (4) | | |
| 9 | Найти площадь | окружность (3) | |
| 10 | Вычислить | (5/4(424333-10220^2))^(1/2) | |
| 11 | Разложить на простые множители | 741 | |
| 12 | Найти объем | сфера (3) | |
| 13 | Вычислить | 3 квадратный корень из 8*3 квадратный корень из 10 | |
| 14 | Найти площадь | окружность (10) | |
| 15 | Найти площадь | окружность (8) | |
| 16 | Найти площадь поверхности | сфера (6) | |
| 17 | Разложить на простые множители | 1162 | |
| 18 | Найти площадь | окружность (1) | |
| 19 | Найти длину окружности | окружность (5) | |
| 20 | Найти объем | сфера (2) | |
| 21 | Найти объем | сфера (6) | |
| 22 | Найти площадь поверхности | сфера (4) | |
| 23 | Найти объем | сфера (7) | |
| 24 | Вычислить | квадратный корень из -121 | |
| 25 | Разложить на простые множители | 513 | |
| 26 | Вычислить | квадратный корень из 3/16* квадратный корень из 3/9 | |
| 27 | Найти объем | прямоугольный параллелепипед (2)(2)(2) | |
| 28 | Найти длину окружности | окружность (6) | |
| 29 | Найти длину окружности | окружность (3) | |
| 30 | Найти площадь поверхности | сфера (2) | |
| 31 | Вычислить | ||
| 32 | Найти объем | прямоугольный параллелепипед (5)(5)(5) | |
| 33 | Найти объем | прямоугольный параллелепипед (10)(10)(10) | |
| 34 | Найти длину окружности | окружность (4) | |
| 35 | Перевести в процентное соотношение | 1. 2-4*-1+2 2-4*-1+2 | |
| 45 | Разложить на простые множители | 228 | |
| 46 | Вычислить | 0+0 | |
| 47 | Найти площадь | окружность (9) | |
| 48 | Найти длину окружности | окружность (8) | |
| 49 | Найти длину окружности | окружность (7) | |
| 50 | Найти объем | сфера (10) | |
| 51 | Найти площадь поверхности | сфера (10) | |
| 52 | Найти площадь поверхности | сфера (7) | |
| 53 | Определить, простое число или составное | 5 | |
| 54 | 3/9 | ||
| 55 | Найти возможные множители | 8 | |
| 56 | Вычислить | (-2)^3*(-2)^9 | |
| 57 | Вычислить | 35÷0.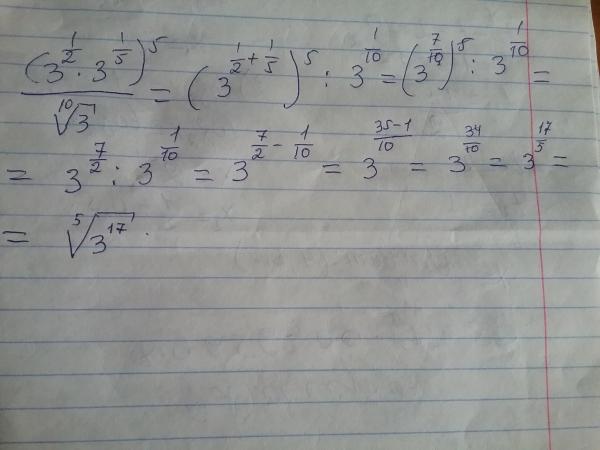 2 2 | |
| 60 | Преобразовать в упрощенную дробь | 2 1/4 | |
| 61 | Найти площадь поверхности | сфера (12) | |
| 62 | Найти объем | сфера (1) | |
| 63 | Найти длину окружности | окружность (2) | |
| 64 | Найти объем | прямоугольный параллелепипед (12)(12)(12) | |
| 65 | Сложение | 2+2= | |
| 66 | Найти площадь поверхности | прямоугольный параллелепипед (3)(3)(3) | |
| 67 | Вычислить | корень пятой степени из 6* корень шестой степени из 7 | |
| 68 | Вычислить | 7/40+17/50 | |
| 69 | Разложить на простые множители | 1617 | |
| 70 | Вычислить | 27-( квадратный корень из 89)/32 | |
| 71 | Вычислить | 9÷4 | |
| 72 | Вычислить | 2+ квадратный корень из 21 | |
| 73 | Вычислить | -2^2-9^2 | |
| 74 | Вычислить | 1-(1-15/16) | |
| 75 | Преобразовать в упрощенную дробь | 8 | |
| 76 | Оценка | 656-521 | |
| 77 | Вычислить | 3 1/2 | |
| 78 | Вычислить | -5^-2 | |
| 79 | Вычислить | 4-(6)/-5 | |
| 80 | Вычислить | 3-3*6+2 | |
| 81 | Найти площадь поверхности | прямоугольный параллелепипед (5)(5)(5) | |
| 82 | Найти площадь поверхности | сфера (8) | |
| 83 | Найти площадь | окружность (14) | |
| 84 | Преобразовать в десятичную форму | 11/5 | |
| 85 | Вычислить | 3 квадратный корень из 12*3 квадратный корень из 6 | |
| 86 | Вычислить | (11/-7)^4 | |
| 87 | Вычислить | (4/3)^-2 | |
| 88 | Вычислить | 1/2*3*9 | |
| 89 | Вычислить | 12/4-17/-4 | |
| 90 | Вычислить | 2/11+17/19 | |
| 91 | Вычислить | 3/5+3/10 | |
| 92 | Вычислить | 4/5*3/8 | |
| 93 | Вычислить | 6/(2(2+1)) | |
| 94 | Упростить | квадратный корень из 144 | |
| 95 | Преобразовать в упрощенную дробь | 725% | |
| 96 | Преобразовать в упрощенную дробь | 6 1/4 | |
| 97 | Вычислить | 7/10-2/5 | |
| 98 | Вычислить | 6÷3 | |
| 99 | Вычислить | 5+4 | |
| 100 | Вычислить | квадратный корень из 12- квадратный корень из 192 |
Лучший ответ по мнению автора | ||||||||||||||||||||||||||||||||||||||||||||||||||||||
| |||||||||||||||||
|
|
| |||||||||||||||||||||||||||||||||||||||||||||||||||
Посмотреть всех экспертов из раздела Учеба и наука > Математика
Пользуйтесь нашим приложением
| 1 | Найдите количество возможностей | ||
| 2 | Найдите количество возможностей | 8 выбрать 3 | |
| 3 | Найдите количество возможностей | 5 выбрать 2 | |
| 4 | Найдите количество возможностей | 4 выбрать 2 | |
| 5 | Найдите количество возможностей | 8 выбрать 4 | |
| 6 | Найдите количество возможностей | 10 выбрать 3 | |
| 7 | Найдите количество возможностей | 7 выбрать 4 | |
| 8 | Найдите количество возможностей | 6 выбрать 3 | |
| 9 | Найдите количество возможностей | 9 выбрать 3 | |
| 10 | Найдите количество возможностей | 3 выбрать 2 | |
| 11 | Найдите количество возможностей | 6 выбрать 4 | |
| 12 | Найдите количество возможностей | 5 выбрать 4 | |
| 13 | Найдите количество возможностей | 7 переставить 3 | |
| 14 | Найдите количество возможностей | 7 выбрать 2 | |
| 15 | Найдите количество возможностей | 10 выбрать 5 | |
| 16 | Найдите количество возможностей | 10 выбрать 6 | |
| 17 | Найдите количество возможностей | 13 выбрать 5 | |
| 18 | Найдите количество возможностей | 3 выбрать 3 | |
| 19 | Найдите количество возможностей | 4 выбрать 1 | |
| 20 | Найдите количество возможностей | 4 выбрать 4 | |
| 21 | Найдите количество возможностей | 5 выбрать 1 | |
| 22 | Найдите количество возможностей | 6 переставить 3 | |
| 23 | Найдите количество возможностей | 8 выбрать 5 | |
| 24 | Найдите количество возможностей | 9переставить 4 | |
| 25 | Найдите количество возможностей | 13 выбрать 3 | |
| 26 | Найдите количество возможностей | 12 выбрать 2 | |
| 27 | Найдите количество возможностей | 12 выбрать 4 | |
| 28 | Найдите количество возможностей | 12 выбрать 3 | |
| 29 | Найдите количество возможностей | 9 выбрать 5 | |
| 30 | Найдите количество возможностей | 9 выбрать 2 | |
| 31 | Найдите количество возможностей | 7 выбрать 5 | |
| 32 | Найдите количество возможностей | 6 переставить 6 | |
| 33 | Найдите количество возможностей | 8 переставить 5 | |
| 34 | Найдите количество возможностей | 8 переставить 3 | |
| 35 | Найдите количество возможностей | 7 переставить 5 | |
| 36 | Найдите количество возможностей | 52 выбрать 5 | |
| 37 | Найдите количество возможностей | 5 переставить 3 | |
| 38 | Найдите количество возможностей | 12 выбрать 5 | |
| 39 | Найдите количество возможностей | 3 выбрать 1 | |
| 40 | Найдите количество возможностей | 11 выбрать 5 | |
| 41 | Найдите количество возможностей | 10 выбрать 2 | |
| 42 | Найдите количество возможностей | 15 выбрать 3 | |
| 43 | Найдите количество возможностей | 52 выбрать 4 | |
| 44 | Найдите количество возможностей | 9 выбрать 4 | |
| 45 | Найдите количество возможностей | 9 переставить 3 | |
| 46 | Найдите количество возможностей | 7 переставить 4 | |
| 47 | Найдите количество возможностей | 7 переставить 2 | |
| 48 | Найдите количество возможностей | 11 выбрать 4 | |
| 49 | Найдите количество возможностей | 11 выбрать 2 | |
| 50 | Найдите количество возможностей | 11 выбрать 3 | |
| 51 | Найдите количество возможностей | 10 переставить 5 | |
| 52 | Найдите количество возможностей | 5 выбрать 5 | |
| 53 | Найдите количество возможностей | 6 выбрать 1 | |
| 54 | Найдите количество возможностей | 8 переставить 4 | |
| 55 | Найдите количество возможностей | 8 выбрать 6 | |
| 56 | Найдите количество возможностей | 13 выбрать 4 | |
| 57 | Оценить | и | |
| 58 | Найти любое уравнение, перпендикулярное прямой | -7x-5y=7 | |
| 59 | Найдите количество возможностей | 13 выбрать 2 | |
| 60 | Найдите количество возможностей | 10 переставить 2 | |
| 61 | Найдите количество возможностей | 10 переставить 3 | |
| 62 | Найдите количество возможностей | 10 выбрать 7 | |
| 63 | Найдите количество возможностей | 20 выбрать 4 | |
| 64 | Найдите количество возможностей | 6 переставить 4 | |
| 65 | Найдите количество возможностей | 5 переставить 4 | |
| 66 | Найдите количество возможностей | 6 выбрать 5 | |
| 67 | Найдите количество возможностей | 52 выбрать 3 | |
| 68 | Найдите количество возможностей | 4 выбрать 0 | |
| 69 | Найдите количество возможностей | 9переставить 7 | |
| 70 | Найдите количество возможностей | 6 выбрать 2 | |
| 71 | Найдите количество возможностей | 5 переставить 5 | |
| 72 | Найдите количество возможностей | 5 переставить 2 | |
| 73 | Найдите количество возможностей | 6 выбрать 6 | |
| 74 | Найдите количество возможностей | 7 выбрать 6 | |
| 75 | Найдите количество возможностей | 8 переставить 6 | |
| 76 | Найдите количество возможностей | 7 переставить 7 | |
| 77 | Найдите количество возможностей | 9 переставить 5 | |
| 78 | Найдите количество возможностей | 2 переставить 2 | |
| 79 | Найдите количество возможностей | 10 выбрать 8 | |
| 80 | Найдите количество возможностей | 12 выбрать 7 | |
| 81 | Найдите количество возможностей | 15 выбрать 5 | |
| 82 | Найдите обратное | [[1,0,1],[2,-2,-1],[3,0,0]] | |
| 83 | Найти диапазон | 1/4x-7 | |
| 84 | Найдите количество возможностей | 10 переставить 7 | |
| 85 | Найдите количество возможностей | 12 выбрать 6 | |
| 86 | Найдите количество возможностей | 2 выбрать 1 | |
| 87 | Найдите количество возможностей | 30 выбрать 3 | |
| 88 | Найдите количество возможностей | 9 выбрать 6 | |
| 89 | Найдите количество возможностей | 8 переставить 2 | |
| 90 | Найдите количество возможностей | 7 выбрать 1 | |
| 91 | Найдите количество возможностей | 6 перестановка 2 | |
| 92 | Найдите количество возможностей | 4 переставить 2 | |
| 93 | Найдите количество возможностей | 4 переставить 3 | |
| 94 | Найдите количество возможностей | 3 переставить 3 | |
| 95 | Найдите количество возможностей | 46 выбрать 6 | |
| 96 | Найдите количество возможностей | 5 переставить 1 | |
| 97 | Найдите количество возможностей | 52 выбрать 7 | |
| 98 | Найдите количество возможностей | 52 переставить 5 | |
| 99 | Найдите количество возможностей | 9выбрать 1 | |
| 100 | Найдите количество возможностей | 9 переставить 6 |
Эволюция
252. Эволюция противоположна инволюции. Один находит степень количества, умножая его на себя. Другой — найти корень, разложив количество на равные множители. Количество разлагается на любое количество равных множителей путем деления его индекс на столько же равных частей ; (Статья 241.)
Эволюция противоположна инволюции. Один находит степень количества, умножая его на себя. Другой — найти корень, разложив количество на равные множители. Количество разлагается на любое количество равных множителей путем деления его индекс на столько же равных частей ; (Статья 241.)
Таким образом, эволюция может осуществляться по следующему общему правилу;
Разделите индекс количества на число, выражающее искомый корень.
Или поставьте над количеством знак корня, принадлежащий нужному корню.
1. Таким образом, кубический корень из 6 равен 2 . Для 2 .a 2 .a 2 = a 6 .
Здесь 6, индекс данного количества, делится на 3, число, выражающее кубический корень.
2. Кубический корень из a или a 1 равен 1/3 или 3 √a.
Для 1/3 .a 1/3 .a 1/3r или 3 √a. 3 √а. 3 √а = а. (статьи 239, 242).
3 √а. 3 √а = а. (статьи 239, 242).
3. Корень 5-й степени из числа ab равен (ab) 1/5 или 5 √ab.
4. n-й корень из 2 — это 2/n или n √a 2 5. Седьмой корень из 2d — x равен (2d — x) 1/7 или 7 √2d — x.
6. Кубический корень из 1/2 равен 1/6 . (Статья 160.)
7. Корень четвертой степени из -1 равен -1/4 .
8. Кубический корень из 2/3 равен 2/9 .
9. Корень n из x m равен x m/n .
253. По только что приведенному правилу кубический корень из квадратного находится делением показателя 1/2 на 3, как в примере 6-м. Но вместо деления на 3 мы можем умножить на 1/3. Для (1/2):3 = (1/2):(3/1) = (1/2).(1/3). (Статья 159.)
Итак, (1/m):n = (1/m).(1/n). Следовательно, корневой корень n-го корня a равен a (1/n). (1/m) .
(1/m) .
То есть (a 1/n ) 1/m = a (1/n).(1/m) = a 1/mn .
Здесь два дробных индекса сводятся к одному путем умножения.
Иногда необходимо отменить этот процесс; чтобы преобразовать индекс в два фактора .
Таким образом, х 1/8 = х (1/4).(1/2) = (х 1/4 ) 1/2 . То есть корень восьмой степени из х равен квадратному корню из корня четвертой степени.
Итак, (а + b) 1/mn = (a + b) (1/m).(1/n) = [(a + b) 1/m ] 1/n .
Возможно, необходимо заметить, что разложение индекса на множители — это не то же самое, что разложение количества на множители. Последнее осуществляется делением индекса на частей .
254. Правило ст. 252, может применяться к каждому случаю эволюции. Но когда величина, корень которой нужно найти, состоит из нескольких множителей , часто бывает выгодно брать корень из каждого из множителей в отдельности .
Это делается по принципу, что корень произведения разъединенных множителей равен произведению их корней .
Таким образом, √ab = √a.√b. Для каждого члена уравнения, если он участвует, будет давать одинаковую мощность.
Квадрат √ab равен ab. (Статья 237.)
Квадрат √a.√b равен √a.√a.√b.√b. (Статья 99).
Но √а.√а = а. (Статья 237.) И √b.√b = b.
Следовательно, квадрат √a.√b = √a.√a.√b.√b = ab, который также является √ab.
По тому же принципу (ab) 1/n =a 1/n .b 1/n .
Поэтому, когда количество состоит из нескольких факторов, мы можем либо извлечь корень из целого вместе; или мы можем найти корень множителей по отдельности, а затем перемножить их друг с другом.
Бывший. 1. Кубический корень из xy равен (xy) 1/3 или x 1/3 .y 1/3 .
2. Корень пятой степени из 3y равен 5 √3y или 5 √3. 5 √г.
3. Корень 6-го числа abh равен (abh) 1/6 или a 1/6 b 1/6 h 1/6 .
4. Кубический корень из 8b равен (8b) 1/3 или 2b 1/3 .
5. Корень n из x n y равен (x n y) 1/n или xy 1/n .
255. Размер дроби равен корню из числителя, деленному на корень из знаменателя.
1. Таким образом, квадратный корень из a/b = a 1/2 /b 1/2 . Для (a 1/2 /b 1/2 ).(a 1/2 /b 1/2 ) = a/b.
2. Квадратный корень из x/ay, √x/√ay.
3. √ах/ху = √ах/√ху
256. Для определения чего знак для приставки к корню, важно отметить, что
Нечетный корень любой величины имеет тот же знак, что и сама величина.
Даже ботинок утвердительного количества неоднозначен.
Четный корень из отрицательной величины невозможен.
Что 3-й, 5-й, 7-й или любой другой нечетный корень количества должен иметь тот же знак, что и само количество, видно из ст. 215.
257. Но даже корень из положительное количество может быть как утвердительным, так и отрицательным. Ибо количество может быть произведено как из одного, так и из другого. (Статья 215.)
Таким образом, квадратный корень из 2 равен +a или -a.
Поэтому четный корень положительного количества называется двусмысленным и обозначается как +, так и -.
Таким образом, квадратный корень из 3b равен ±√3b.
Корень четвертой степени из x равен ±x 1/4 .
Двусмысленности, однако, не существует, когда из природы случая или предшествующего умножения известно, действительно ли мощность была произведена из положительной или из отрицательной величины.
258. Но четного корня из отрицательной величины найти нельзя. Квадратный корень из -а 2 не является ни -а, ни +а.
Для +а.+а = +а 2 .
И -а.-а = +а 2 также.
Поэтому четный корень из отрицательной величины называется невозможным или мнимым .
Однако есть цели, на которые нужно ответить, применяя знак радикала к отрицательным величинам. Выражение √-a часто можно встретить в алгебраических процессах. Ибо, хотя мы не можем присвоить ему ранг ни среди положительных, ни среди отрицательных величин; однако мы знаем, что при умножении на себя его произведение равно -а, потому что √-а по обозначению равно корень из -а, т. е. количество, умноженное само на себя, дает -а.
На первый взгляд может показаться, что это исключение из общего правила, согласно которому произведение двух отрицаний является утвердительным. Но следует учитывать, что √-a сама по себе не является отрицательной величиной, а является корнем отрицательной величины.
Знак вычитания здесь не следует путать с тем, что предшествует перед корневым знаком. Выражение √-a не эквивалентно -√a. Первый является корнем -а; но последний является корнем +a:
Выражение √-a не эквивалентно -√a. Первый является корнем -а; но последний является корнем +a:
Для -√a.-√a = √aa = a.
Однако корень -a может быть неоднозначным. Это может быть либо +√-a, либо -√-a.
Одно из употреблений воображаемых выражений — указание на невозможное или абсурдное предположение в постановке задачи. Предположим, требуется разделить число 14 на две такие части, что их произведение будет равно 60. Если одна из частей будет х, то другая будет 14 — х. И по предположению,
х.(14 — х) = 60, или 14х — х 2 = 60.
Это, уменьшенное по правилам следующего раздела, даст
х = 7 ± √-11.
Поскольку значение х здесь содержит мнимое выражение, мы заключаем, что в постановке задачи есть несоответствие: число 14 нельзя разделить на любые две части, произведение которых должно быть 60.
259. Методы извлечения корней соединения в количествах будут рассмотрены в следующем разделе. Но есть один их класс, квадраты биномиальные и остаточные величины, на которые будет уместно обратить внимание в этом месте. Было показано (ст. 210,), что квадрат биномиальной величины состоит из трех слагаемых , два из которых — полные степени, а другой — двойное произведение корней этих степеней. Например, квадрат a + b равен
Было показано (ст. 210,), что квадрат биномиальной величины состоит из трех слагаемых , два из которых — полные степени, а другой — двойное произведение корней этих степеней. Например, квадрат a + b равен
а 2 + 2аб + б 2 ,
, два члена которого, а 2 и b 2 , являются полными степенями, а 2ab есть удвоенное произведение a на b, то есть корень из 2 в корень b 2 .
Следовательно, всякий раз, когда мы встречаемся с величиной, соответствующей этому описанию, мы можем знать, что ее квадратный корень является двучленом; и это можно найти, взяв корень двух терминов, являющихся полными силами, и соединив их знаком +. Другой член исчезает в корне. Таким образом, чтобы найти квадратный корень из
x 2 + 2xy + y 2 ,
взять корень x 2 и корень y 2 и соедините их знаком +. Биномиальный корень тогда будет x + y.
В остаточном количестве двойное произведение имеет знак — вместо префикса +. Квадрат a — b, например, равен a 2 — 2ab + b 2 (ст. 210). полные полномочия, и соедините их знаком -. Таким образом, квадратный корень из x 2 -2xy + y 2 равен x — y. Следовательно,
Квадрат a — b, например, равен a 2 — 2ab + b 2 (ст. 210). полные полномочия, и соедините их знаком -. Таким образом, квадратный корень из x 2 -2xy + y 2 равен x — y. Следовательно,
260. Чтобы извлечь биномиальный или остаточный квадратный корень, возьмите корни двух членов, которые являются полными степенями, и соедините их знаком, который стоит перед другим членом.
Бывший. 1. Найти корень из х 2 + 2х + 1.
Два слагаемых, которые представляют собой полные степени, это x 2 и 1.
Корни равны х и 1. (Статья 244.)
Следовательно, биномиальный корень равен x + 1.
2. Квадратный корень из 2 + а + 1/4 равен а + 1/2. (Статья 220.)
3. Квадратный корень из 2 + ab + b 2 /4 равен a + b/2.
4. Квадратный корень из a 2 + 2ab/c + b 2 /c 2 , a + b/c.
261. Корень, значение которого не может быть точно выражено в числах, называется сурдом .

 07.15
07.15