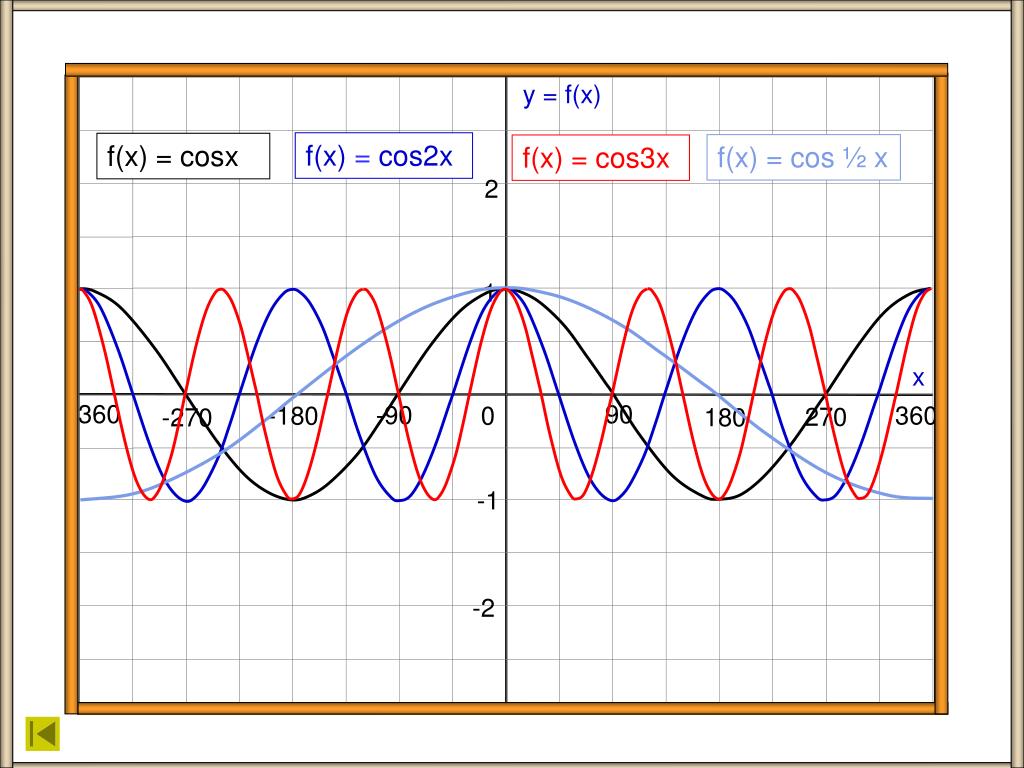
исчисление — Сумма ряда $ \cos(x)-\cos(2x)+\cos(3x)-…$
$\begingroup$
В книге «Дух математического анализа» Мартина Ома автор приводит пример дифференцирования бесконечного ряда и получения абсурдного результата (стр. 2)
Из ряда
$\frac{x}{2 }=\sin(x)-\frac{1}{2}\sin2x+\frac{1}{3}\sin(3x)-…$ (1)
Если дифференцировать слагаемое по слагаемому, то получается этот ряд
$\frac{1}{2}=\cos(x)-\cos(2x)+\cos(3x)-…$ (2)
Автор сказал, что последний ряд расходится, поэтому этот результат не имеет смысла.
Мой вопрос: как получить первую серию? Какое преобразование нужно выполнить, чтобы получить $\frac{x}{2}$ в левой части.
Мой второй вопрос, как мы можем доказать, что второй ряд расходится?
- исчисление
$\endgroup$
14
$\begingroup$ 9{k-1}\sin(kx)$$
Они кажутся коррелированными плюс-минус дивергенции. Если вы хотите утверждать, что эту функцию можно интегрировать со строгостью (что, как я где-то читал, возможно [возможно, в брошюре Харди о рядах Фурье]), я думаю, вы должны доказать, что эти «коррелированные» положительные и отрицательные расхождения каким-то образом компенсируют друг друга в процессе интеграции.В $x=\pi/2$ у вас есть ряд.
$$\frac{1}{2}=1-1+1-1+…$$
Доказательство серии (1) находится здесь, и вы сможете доказать свою серию аналогичным образом. переходя к экспоненциальной форме.
$\endgroup$
1
$\begingroup$
Первый ряд есть не что иное, как ряд Фурье $2\pi$-периодической нечетной функции
$$
y=\frac{x}{2},\quad\pi $\endgroup$ 1 $\begingroup$ Правая часть первого уравнения имеет вид $\Im\ln(1+\exp ix)$. БАНСАЛЬНЫЕ ПРЕДЕЛЫ И ПРОИЗВОДНЫЕ-Все вопросы РЕКЛАМА Аб Падхай каро бина адс ке Хариэдо Д.Н. Про и дехо сари видео бина киси ад ки рукаават ке! Войти, если уже приобретено
Правая часть второго уравнения может иметь сходящиеся частичные суммы только в том случае, если $\lim_{n\to\infty}\cos nx=0$, но это явно не работает при рациональном $x/\pi$. Известный, но менее очевидный результат состоит в том, что другие действительные $x$ также не достигают такого предела. 92)
Пусть f(x)=|[cosx, sinx, cosx],[cos2x,sin2x,2cos2x],[cos3x,sin3x,3cos3x]|. Найти f'(pi/2)
230746
07:33
Решить: cos3x+cosx−cos2x=0
34799136
03:38
IF COS3X+COSX-COS2X = 0, затем
95420009
02:15
हल करें COS3X+COSX-COS2X = 0
104443665
03:32
COSX+COS2X+COS3X+2
03:32
COSX+COS2X+COS2X+COS3X+40004 03:32
COSX 2X3669
03:32
COSX3665
03:32
.
127291102
03:16
IF: y = sinx [1cosx> cos2x+1cos2xcot3x+1cos3x> cos4x], затем: dydx at x = π4
141180009
08:57
→ 00004 41180009
08:57
0009
08:57
−cos2x)(3+cosx)xtan4x равно-
234810147
03:52
সমাধান করোcosx+cos2x+cos3x=0
39530358503:55
(lim)x→0cos2x−1cosx−1
571220264
04:00
Evaluate the following limit: (lim)x→0cos3x−cos7xx2
642576892
02: 07
Evaluate the following limit: (lim)x→0cos3x−cos5xx2
642576912
05:57
Evaluate the following limit: (lim)x→01−cos2xcos2x−cos8x
642576915
02:04
Найдите общее решение следующих уравнений:
COS3X+COSX — COS2X = 0
642772376
02:54
COSX> COS2X> ਦਾ ਦੇ ਦੇ ਬਾਬਤ ਡੈਰੀਵੇਟਿਵ ਪਤਾ ਕਰੋ ਕਰੋ ਕਰੋ ਕਰੋ ਕਰੋ ਕਰੋ ਕਰੋ ਕਰੋ ਕਰੋ ਕਰੋ ਕਰੋ
642815439
03:04
Если f(x)=⎡⎢⎣cosxsinxcosxcos2xsin2x2cos2xcos3xsin3x3cos3x⎤⎥⎦
найти f'(pi/2).