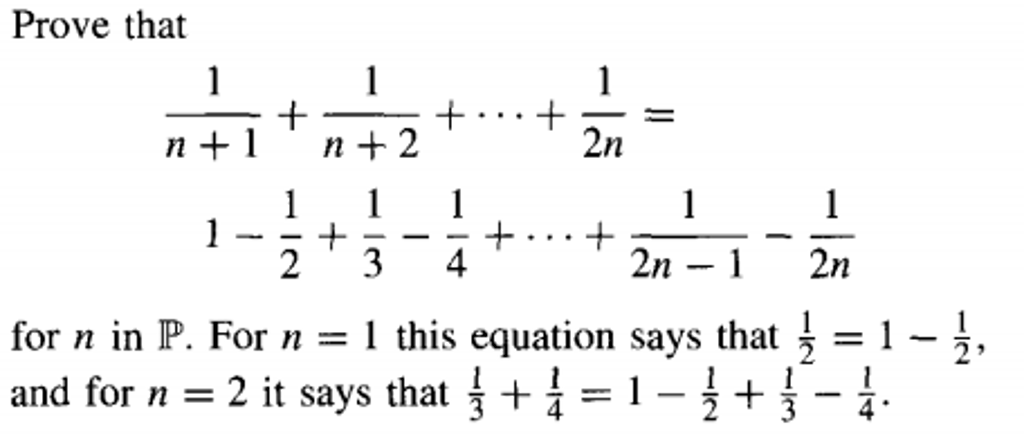— Доказательство $\frac{1}{n+1} + \frac{1}{n+2}+\cdots+\frac{1}{2n} > \frac{13}{24}$ для $n >1,n\in\Bbb N$ по индукции
спросил
Изменено 4 года, 9 месяцев назад
Просмотрено 17 тысяч раз
$\begingroup$
Доказательство $\frac{1}{n+1} + \frac{1}{n+2}+\cdots+\frac{1}{2n} > \frac{13}{24}$ для $n>1 ,n\in\Bbb N$
Чтобы решить его, я использовал индукцию, но она никуда меня не привела. Моя попытка была следующей:
Предположим, что неравенство верно для $n = k$, тогда нам нужно доказать, что оно верно верно для $k+1$
поэтому нам нужно доказать $\frac1{k+2} + \frac1{k+3}+\cdots+\frac1{2(k+1)} > 13/24$
Я не знаю, куда идти отсюда, пожалуйста, помогите.
- суммирование
- индукция
- номера гармоник
$\endgroup$
7
$\begingroup$
Используя индукцию, мы сначала покажем, что это верно для $n=2$:
$\frac{1}{2+1}+\frac{1}{2+2}=\frac{1}{3} +\frac{1}{4}=\frac{7}{12}=\frac{14}{24}\gt\frac{13}{24}$
Следовательно, это действительно верно для $n=2 $.
Теперь предположим, что это верно для некоторого $n=k$, следовательно:
$S_k=\frac{1}{k+1}+\frac{1}{k+2}+…+\frac{1}{2k}\gt\frac{13}{24}$
Наконец, нам нужно доказать, что из этого следует, что верно и для $n=k+1$:
$S_{k+1}=\frac{1}{(k+1)+1}+\frac {1}{(k+1)+2}+…+\frac{1}{2(k+1)-2}+\frac{1}{2(k+1)-1}+\ frac{1}{2(k+1)}$
$\qquad=\frac{1}{k+2}+\frac{1}{k+3}+…+\frac{1}{ 2k}+\frac{1}{2k+1}+\frac{1}{2(k+1)}$
$\qquad=-\frac{1}{k+1}+\frac{1} {k+1}+\frac{1}{k+2}+\frac{1}{k+3}+.
по определенным интегралам Реймана, и это предельная сумма и для всех членов, сумма меньше $\log(2)$
и $$\log(2)> \frac{13}{24}$$
$\endgroup$
0
$\begingroup$
$$f(n)=\frac{1}{n+1}+\frac{1}{n+2}+\ldots+\frac{1}{2n}=H_{2n}-H_n $$ является возрастающей функцией, так как $$ f(n+1)-f(n) = \frac{1}{(2n+1)(2n+2)}>0. $$ Отсюда следует, что $\для всех n>
$\endgroup$
комбинаторика — Докажите, что ${2n \выберите n}= 2{2n-1 \выберите n}$
Задать вопрос
спросил
Изменено 3 года, 9 месяцев назад
Просмотрено 1к раз
$\begingroup$
Итак, я совершенно новичок в этом, и у меня есть очень базовое понимание того, как это работает.
${2n \выбрать n}$
=$\frac{(2n)!}{(n)!(2n-n)!}$
=$\frac{(2n)!}{2(n)!}$
и затем
${2n-1 \выберите n}$
=$\frac{(2n-1)!} {(н)! (2n-1-n)!}$
=$\frac{(2n-1)!}{(n)! (n-1)!}$
Я понятия не имею, является ли этот метод доказательством этой проблемы, и даже правильно ли я делал это до этого момента. Я попал в блок, пытаясь получить ${2n \choose n}$, эквивалентный ${2n-1 \choose n}$.
Здесь я действительно начинающий, поэтому, если бы вы могли объяснить свои шаги, было бы здорово! 92}=\binom{2n}{n}$.
$\endgroup$
4
$\begingroup$
$$\text{Из треугольника Паскаля мы знаем, что }\binom m k=\binom{m−1}{k−1}+\binom{m−1}{k}.$$ $$\следовательно\binom{2n}n=\binom{2n−1}{n−1}+\binom{2n−1}n=2\binom{2n−1}n$$
$$\text {так как }\binom{2n-1}{n-1}=\binom{2n-1}n\text{ так как } (2n-1)-(n-1)=n. $$
$$
$\endgroup$
1
$\begingroup$
С очень небольшим количеством вычислений :
Мы можем использовать рекуррентное соотношение $$\binom nk=\frac nk\binom{n-1}{k-1}, $$ что лежит в основе доказательства формулы с факториалами. Особенно, $$\binom{2n}n= 2\binom{2n-1}{n-1}=2\binom{2n-1}n,\quad\text {так как}\quad n=(2n-1)- (n-1).$$
$\endgroup$
2
$\begingroup$
Заметив $2n-n=n, $ имеем $${2n \choose n}=\frac{\color{red}{(2n)!}}{\color{green}{(n)!}(n) !}.$$
Также, учитывая $(2n-1)-n=n-1, $ имеем $${2n-1 \choose n}=\frac{(2n-1)!}{(n )!(n-1)!}.$$
Наконец, обратите внимание, что $\color{red}{(2n)!}=2n\times(2n-1)!$ и $\color{green}{n !}=n\times(n-1)!$ и $\frac {2n}n=2$ и готово.