График y x 2 4x. Алгоритм построения квадратичной функции
«Преобразование функций» — Качелями. Сдвиг по оси y вверх. Включи полную громкость – увеличишь a (амплитуду) колебаний воздуха. Сдвиг по оси x влево. Задачи урока. 3 балла. Музыкой. Постройте график функции и определите D(f), E(f) и T: Сжатие по оси x. Сдвиг по оси y вниз. Добавь красного цвета в палитру – уменьшишь k (частоту) электромагнитных колебаний.
«Функции нескольких переменных» — Производные высших порядков. Функцию двух переменных можно изобразить графически. Дифференциальное и интегральное исчисления. Внутренние и граничные точки. Определение предела функции 2-х переменных. Курс математического анализа. Берман. Предел функции 2-х переменных. График функции. Теорема. Ограниченная область.
«Понятие функции» — Способы построение графиков квадратичной функции. Изучение разных способов задания функции – важный методический прием. Особенности изучения квадратичной функции. Генетическая трактовка понятия «функция».
Функции и графики в школьном курсе математики. Представление о линейной функции выделяется при построении графика некоторой линейной функции.
«Тема Функция» — Анализ. Нужно выяснить не то, что ученик не знает, а то, что он знает. Заложение основ для успешной сдачи ЕГЭ и поступление в ВУЗы. Синтез. Если ученики работают по-разному, то и учитель должен с ними работать по-разному. Аналогия. Обобщение. Распределение заданий ЕГЭ по основным блокам содержания школьного курса математики.
«Преобразование графиков функций» — Повторить виды преобразований графиков. Сопоставить каждому графику функцию. Симметрия. Цель урока: Построение графиков сложных функций. Рассмотрим примеры преобразований, объясним каждый вид преобразования. Преобразование графиков функций. Растяжение. Закрепить построение графиков функций с использованием преобразований графиков элементарных функций.
«Графики функций» — Функция вида. Область значений функции – все значения зависимой переменной у. Графиком функции является парабола.
С нами легко в режиме онлайн строить графики различной сложности. Построение производится мгновенно. Сервис востребован для нахождения точек пересечения функций, для изображения графиков для дальнейшего их перемещения в Word документ в качестве иллюстраций при решении задач, для анализа поведенческих особенностей графиков функций. Оптимальным браузером для работы с графиками на данной странице сайта является Google Chrome. При использовании других браузеров корректность работы не гарантируется.
Разберем как строить график с модулем.
Найдем точки при переходе которых знак модулей меняется.
Каждое выражения, которое под модулем приравниваем к 0. У нас их два x-3 и x+3.
x-3=0 и x+3=0
x=3 и x=-3
У нас числовая прямая разделится на три интервала (-∞;-3)U(-3;3)U(3;+∞). На каждом интервале нужно определить знак под модульных выражений.
1. Это сделать очень просто, рассмотрим первый интервал (-∞;-3). Возьмем с этого отрезка любое значение, например, -4 и подставим в каждое под модульное уравнение вместо значения х.
х=-4
x-3=-4-3=-7 и x+3=-4+3=-1
У обоих выражений знаки отрицательный, значит перед знаком модуля в уравнении ставим минус, а вместо знака модуля ставим скобки и получим искомое уравнение на интервале (-∞;-3).
y=— (x-3)-(— (x+3))=-х+3+х+3=6
На интервале (-∞;-3) получился график линейной функции (прямой) у=6
2. Рассмотрим второй интервал (-3;3). Найдем как будет выглядеть уравнение графика на этом отрезке. Возьмем любое число от -3 до 3, например, 0. Подставим вместо значения х значение 0.
х=0
x-3=0-3=-3 и x+3=0+3=3
У первого выражения x-3 знак отрицательный получился, а у второго выражения x+3 положительный.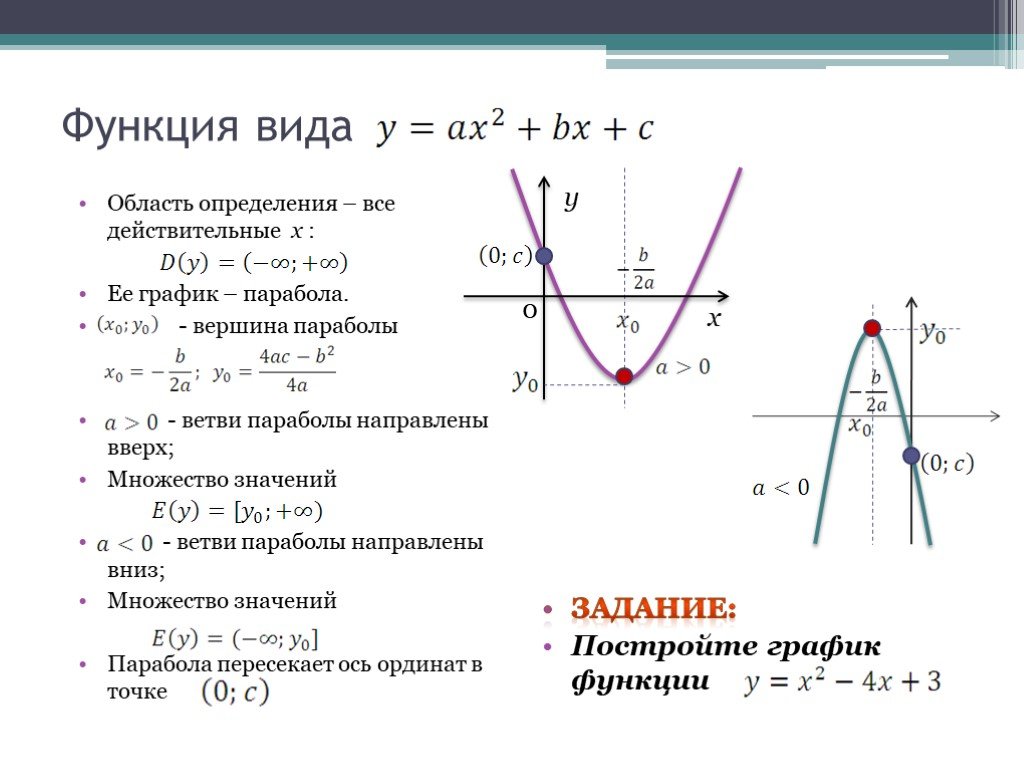
Следовательно, перед выражением x-3 запишем знак минус, а перед вторым выражением знак плюс.
y=— (x-3)-(+ (x+3))=-х+3-х-3=-2x
На интервале (-3;3) получился график линейной функции (прямой) у=-2х
3.Рассмотрим третий интервал (3;+∞). Возьмем с этого отрезка любое значение, например 5, и подставим в каждое под модульное уравнение вместо значения х.
х=5
x-3=5-3=2 и x+3=5+3=8
У обоих выражений знаки получились положительными, значит перед знаком модуля в уравнении ставим плюс, а вместо знака модуля ставим скобки и получим искомое уравнение на интервале (3;+∞).
y=+ (x-3)-(+ (x+3))=х-3-х-3=-6
На интервале (3;+∞) получился график линейной функции (прямой) у=-6
4. Теперь подведем итог.Постоим график y=|x-3|-|x+3|.
На интервале (-∞;-3) строим график линейной функции (прямой) у=6.
На интервале (-3;3) строим график линейной функции (прямой) у=-2х.
Чтобы построить график у=-2х подберем несколько точек.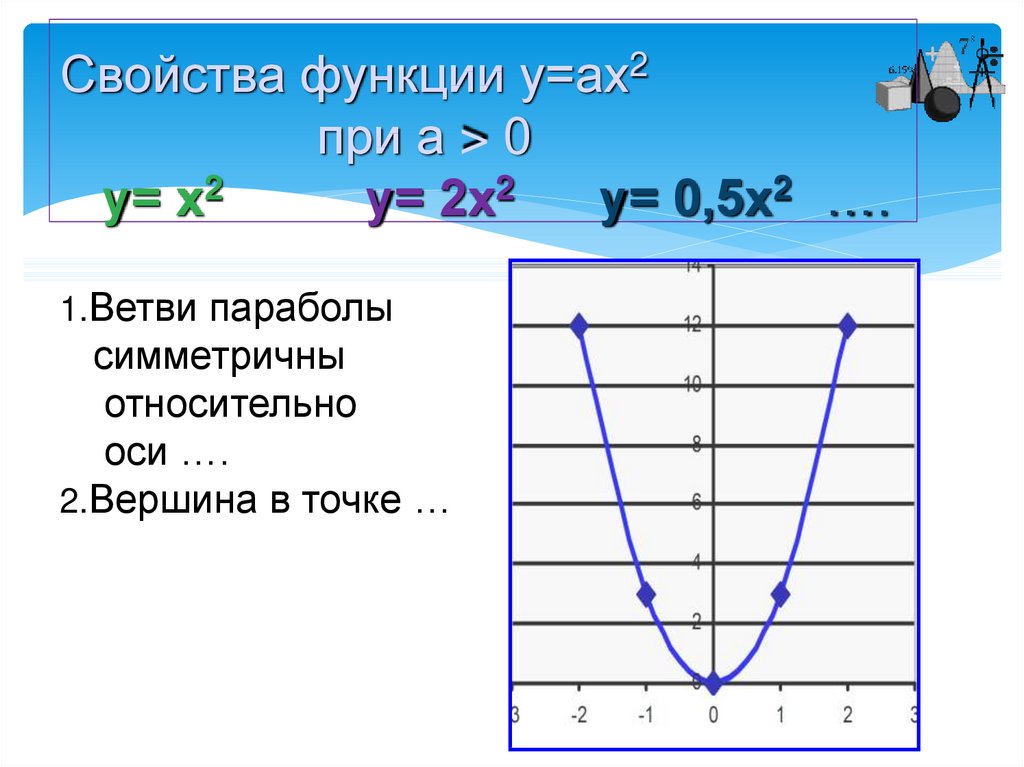
x=-3 y=-2*(-3)=6 получилась точка (-3;6)
x=0 y=-2*0=0 получилась точка (0;0)
x=3 y=-2*(3)=-6 получилась точка (3;-6)
На интервале (3;+∞) строим график линейной функции (прямой) у=-6.
5. Теперь проанализируем результат и ответим на вопрос задания найдем значение k, при которых прямая y=kx имеет с графиком y=|x-3|-|x+3| данной функции ровно одну общую точку.
Прямая y=kx при любом значении k всегда будет проходить через точку (0;0). Поэтому мы можем изменить только наклон данной прямой y=kx, а за наклон у нас отвечает коэффициент k.
Если k будет любое положительное число, то будет одно пересечение прямой y=kx с графиком y=|x-3|-|x+3|. Этот вариант нам подходит.
Если k будет принимать значение (-2;0), то пересечений прямой y=kx с графиком y=|x-3|-|x+3| будет три.Этот вариант нам не подходит.
Если k=-2, решений будет множество [-2;2], потому что прямая y=kx будет совпадать с графиком y=|x-3|-|x+3| на данном участке. Этот вариант нам не подходит.
Если k будет меньше -2, то прямая y=kx с графиком y=|x-3|-|x+3| будет иметь одно пересечение.Этот вариант нам подходит.
Если k=0, то пересечений прямой y=kx с графиком y=|x-3|-|x+3| также будет одно.Этот вариант нам подходит.
Ответ: при k принадлежащей интервалу (-∞;-2)U; график f(х) = х + 2 – это прямая, параллельная прямой f(х) = х, но сдвинутая на две единицы вверх и поэтому проходящая через точку с координатами (0,2) (потому что постоянная равна 2).
Построение графика сложной функции
- формирование у учащихся умения строить график квадратичной функции в соответствии со схемой, приведенной в учебнике на с.41 учебника “Алгебра, 9 класс” под редакцией Теляковского А.С.;
- научить учащихся определять основные свойства квадратичной функции.
Найдите нули функции. Нули функции – это значения переменной «х», при которых у = 0, то есть это точки пересечения графика с осью Х. Имейте в виду, что нули имеют не все функции, но это первый шаг процесса построения графика любой функции. Чтобы найти нули функции, приравняйте ее к нулю. Например:
Найдите и отметьте горизонтальные асимптоты. Асимптота – это прямая, к которой график функции приближается, но никогда не пересекает ее (то есть в этой области функция не определена, например, при делении на 0).
На втором промежутке \(\left({ — 2, — 1} \right)\) переменная \(x\) возрастает от \(x\left({ — 2} \right) = — 2\)
до \(x\left({ — 1} \right) = 1,\) а переменная \(y\) убывает от \(y\left({ — 2} \right) = 8\) до
\(y\left({ — 1} \right) = 5.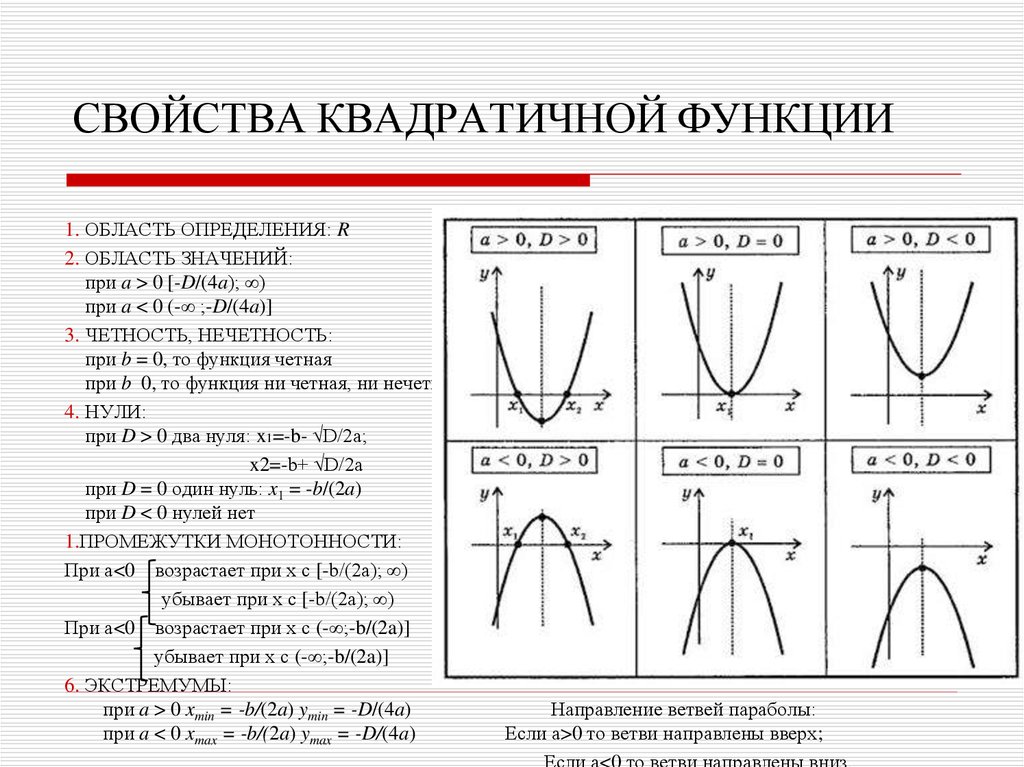
На третьем интервале \(\left({ — 1,\large\frac{1}{3}\normalsize} \right)\) обе переменные убывают. Значение \(x\) изменяется от \(x\left({ — 1} \right) = 1\) до \(x\left({\large\frac{1}{3}\normalsize} \right) = — \large\frac{5}{{27}}\normalsize.\) Соответственно, значение \(y\) уменьшается от \(y\left({ — 1} \right) = 5\) до \(y\left({\large\frac{1}{3}\normalsize} \right) = — \large\frac{29}{{27}}\normalsize.\) Кривая \(y\left(x \right)\) при этом пересекает начало координат.
На четвертом интервале \(\left({\large\frac{1}{3}\normalsize,\large\frac{2}{3}\normalsize} \right)\)
переменная \(x\) возрастает от \(x\left({\large\frac{1}{3}\normalsize} \right) = — \large\frac{5}{{27}}\normalsize\)
до \(x\left({\large\frac{2}{3}\normalsize} \right) = \large\frac{2}{{27}}\normalsize,\)
а переменная \(y\) убывает от \(y\left({\large\frac{1}{3}\normalsize} \right) = — \large\frac{29}{{27}}\normalsize\)
до \(y\left({\large\frac{2}{3}\normalsize} \right) = — \large\frac{40}{{27}}\normalsize.
Исследуем также выпуклость данной кривой. Вторая производная
\(y»»\left(x \right)\) имеет вид:
\[
y»»\left(x \right) = {y»»_{xx}} = \frac{{{{\left({{y»_x}} \right)}»_t}}}{{{x»_t}}}
= \frac{{{{\left({\frac{{3{t^2} + 4t — 4}}{{3{t^2} + 2t — 1}}} \right)}^\prime }}}{{{{\left({{t^3} + {t^2} — t} \right)}^\prime }}}
= \frac{{\left({6t + 4} \right)\left({3{t^2} + 2t — 1} \right) — \left({3{t^2} + 4t — 4} \right)\left({6t + 2} \right)}}{{{{\left({3{t^2} + 2t — 1} \right)}^3}}}
= \frac{{18{t^3} + 12{t^2} + 12{t^2} + 8t — 6t — 4 — \left({18{t^3} + 24{t^2} — 24t + 6{t^2} + 8t — 8} \right)}}{{{{\left({3{t^2} + 2t — 1} \right)}^3}}}
= \frac{{\cancel{\color{blue}{18{t^3}}} + \color{red}{24{t^2}} + \color{green}{2t} — \color{maroon}{4} — \cancel{\color{blue}{18{t^3}}} — \color{red}{30{t^2}} + \color{green}{16t} + \color{maroon}{8}}}{{{{\left({3{t^2} + 2t — 1} \right)}^3}}}
= \frac{{ — \color{red}{6{t^2}} + \color{green}{18t} + \color{maroon}{4}}}{{{{\left({3{t^2} + 2t — 1} \right)}^3}}}
= \frac{{ — 6\left({t — \frac{{9 — \sqrt {105} }}{6}} \right)\left({t — \frac{{9 + \sqrt {105} }}{6}} \right)}}{{{{\left({t + 1} \right)}^3}{{\left({3t — 1} \right)}^3}}}.
\]
Следовательно, вторая производная меняет свой знак на противоположный при переходе через следующие точки (рис.\(15с\)):
\[
{{t_1} = — 1:\;\;x\left({ — 1} \right) = 1,}\;\;
{y\left({ — 1} \right) = 5;}
\]
\[
{{t_2} = \frac{{9 — \sqrt {105} }}{6}:}\;\;
{x\left({\frac{{9 — \sqrt {105} }}{6}} \right) \approx 0,24;}\;\;
{y\left({\frac{{9 — \sqrt {105} }}{6}} \right) \approx 0,91;}
\]
\[
{{t_3} = \frac{1}{3}:}\;\;
{x\left({\frac{1}{3}} \right) = — \frac{5}{{27}},}\;\;
{y\left({\frac{1}{3}} \right) = — \frac{{29}}{{27}};}
\]
\[
{{t_4} = \frac{{9 + \sqrt {105} }}{6}:}\;\;
{x\left({\frac{{9 + \sqrt {105} }}{6}} \right) \approx 40,1;}\;\;
{y\left({\frac{{9 + \sqrt {105} }}{6}} \right) \approx 40,8.}
\]
Поэтому указанные точки представляют собой точки перегиба кривой \(y\left(x \right).\)
Схематический график кривой \(y\left(x \right)\) показан выше на рисунке \(15b.\)
Построение графика квадратичной функции. 9-й класс
“Мало иметь хороший ум, главное – уметь его
применять”.
Рене Декарт
Цели урока:
Задачи урока.
обучающие:
знать: алгоритм построения графика квадратичной функции;
уметь: строить график любой квадратичной функции, определять основные свойства функции по графику.
развивающие: развивать навыки самостоятельной работы, самоконтроля и взаимоконтроля.
воспитательные: воспитывать
самостоятельность, настойчивость для достижения
конечных результатов, способствовать развитию
интереса к математике через различные формы
работы.
Оборудование: мультимедийный проектор, интерактивная доска, презентация Power Point, тетрадь с печатной основой.
Ход урока
1. Организационный момент.
2. Устная работа. Повторение ранее изученного материала.
1) Повторить, как найти координаты вершины параболы, что является осью симметрии параболы, куда направлены ветви параболы, что такое нули функции.
(Вопросы задаются всему классу, после ответов к доске приглашаются три ученика работать по карточкам)
Карточка №1.
Найти координаты вершины параболы:
a) x2-8x+7=0; б) 9x2-6x+1=0; в) 7x-2x2=0
Карточка №2.
Найти нули функции:
a) x2-8x+7=0; б) 9x2-6x+1=0; в) 7x-2x2=0
Карточка №3.
Найдите координаты вершины параболы:
а)y=5(x-7)2+9 x0=______, y0= ______
б)y=-4(x+3)2-5 x0=______, y0= ______
в)y=x2— 16 x0=______, y0= ______
г)y=(x-4)2 +10 x0=______, y0= ______
2) запись темы урока (Слайд 2), сообщение целей и задач урока (Слайд 3-4).
3) проверка домашнего задания с помощью тестового задания (учащиеся выполняют задание по вариантам в течение 5 минут, у каждого ученика на столе текст задания и чистый лист). Текст задания на экране (Слайд 5-6).
Учитель в это время проверяет работы учащихся у доски. Затем проверка тестовых заданий (взаимопроверка — ученики обменялись вариантами). (Слайд 7)
Работы сданы учителю для выставления оценок.
4) а) повторение (устно) преобразований графика квадратичной функции с помощью слайдов, учащиеся при этом комментируют свои ответы (Слайды 9-13):
График функции, симметричен оси Оу;
График функции симметричен оси Ох;
Сжатие или растяжение;
График функции y=|f(x)|;
График функции у =f(x)+A, y=f(x)-A.
Итак, можно показать, что любую квадратичную функцию у =ax2+вх +с
с помощью выделения полного квадрата можно записать в виде у = a(x-x0)2 +y0 , где х0= — b/(2a) , y0= y(x0)= — (b2-4ac)/(4a).
Графиком функции у =a(x-x0)2 +y0 является парабола, получаемая сдвигом параболы у = ax2:
вдоль оси абсцисс вправо на x0, если x0
> 0,влево на |x0|, если х0 < 0.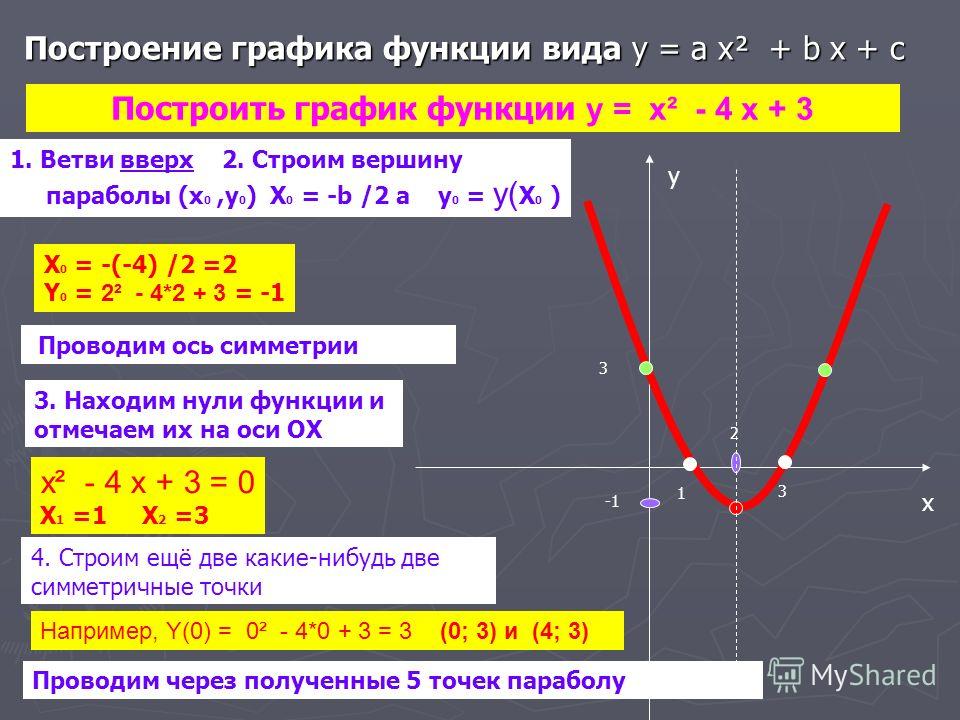
вдоль оси ординат вверх на y0, если y0 >0, вниз на |y0|, если y0 < 0.
(Слайды 14-15)
б) Рассмотрим несколько примеров, как определить координаты вершины параболы, заданной уравнением у = (х – а)2+в и у = ( х +а)2-в. (Слайд 16)
в) найти координаты вершины параболы: (Слайд 17), учащиеся записывают и называют координаты вершин заданных графиков параболы (красная, синяя, фиолетовая, желтая, зеленая) и проверка ответов из слайда.
Выставление оценок за устно — письменную работу на уроке на данном этапе.
5) Повторить этапы построения параболы, заданной уравнениями:
y = (x+7)2 -6; y= (x-4)2 +3. (Слайд 18-19)
Затем построить график у = (х-4)2 -8 в тетради
с помощью шаблона y = x2 с последующей
проверкой (Слайд 21).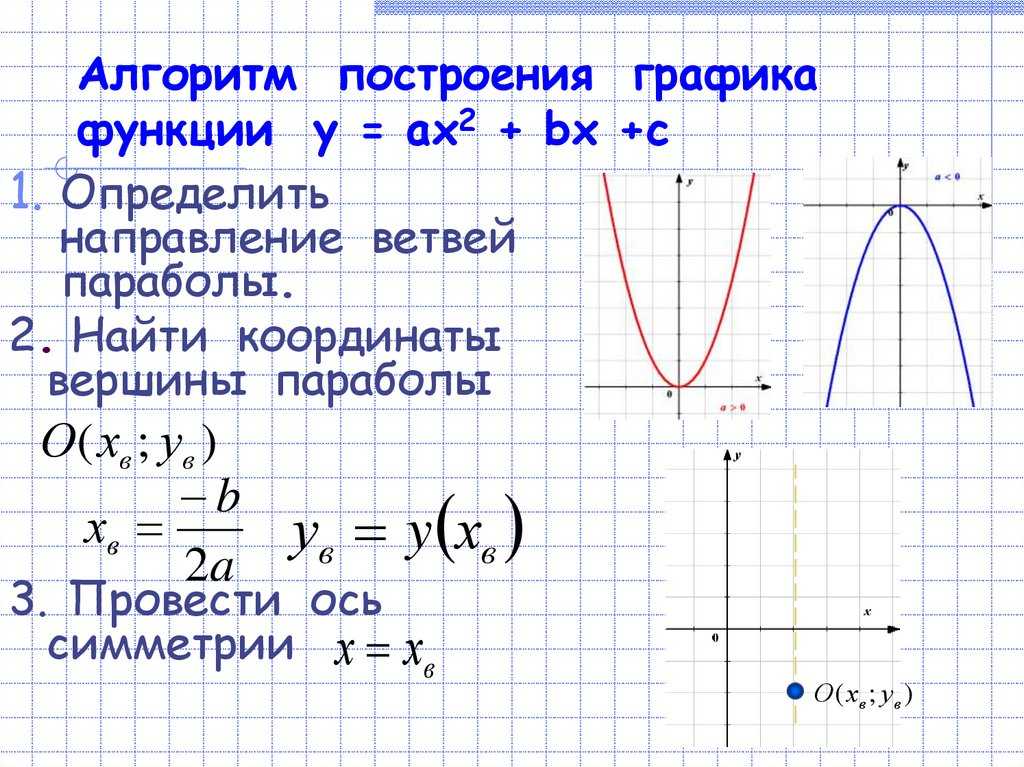
(Выставление оценок за устно-письменную работу)
3. Объяснение нового материала.
Беседа. Изучение поведения функций и
построение их графиков является важным разделом
математики. Свободное владение техникой
построения графиков часто помогает решать
многие задачи, и порой является единственным
средством их решения. Кроме того, умение строить
графики функций представляет большой
самостоятельный интерес. Находясь на выставке
картин, мы рассматриваем произведения искусств и
обращаем внимание на то, сумел ли художник
передать глубину, завершенность образного
содержания. Картина является итогом длительных
наблюдений и размышлений художника над жизнью.
Представьте, что мы находимся на выставке картин,
выполненных с помощью компьютера. В компьютерном
“изобразительном искусстве” мы можем увидеть
не что иное, как графики функций. Чтобы научиться
видеть в таких картинах действительно графики
функций, научиться создавать самим такие
картины, необходимо знать основные функции их
свойства.
Можно привести множество примеров, как
важно уметь строить графики и описывать их
свойства.
Ученый-сейсмолог, анализируя сейсмограмму, узнает, когда было землетрясение, где оно произошло, определяет силу и характер толчков. Врач, исследующий больного, может по кардиограмме судить о нарушениях сердечной деятельности: изучение кардиограммы помогает правильно поставить диагноз заболевания. Инженер- радиоэлектроник по характеристике полупроводникового элемента выбирает наиболее подходящий режим его работы. Более того, по мере развития математики растет проникновение графического метода в самые различные области
жизни человека. В частности, использование функциональных зависимостей и построение графиков широко применяется в экономике. Значит, растет и важность изучения рассматриваемого раздела математики в школе, в вузе, и особенно - важности самостоятельной работы над ним. (Слайд 22)
Итак, тема урока: “Построение графика
квадратичной функции” (Слайд 23-24).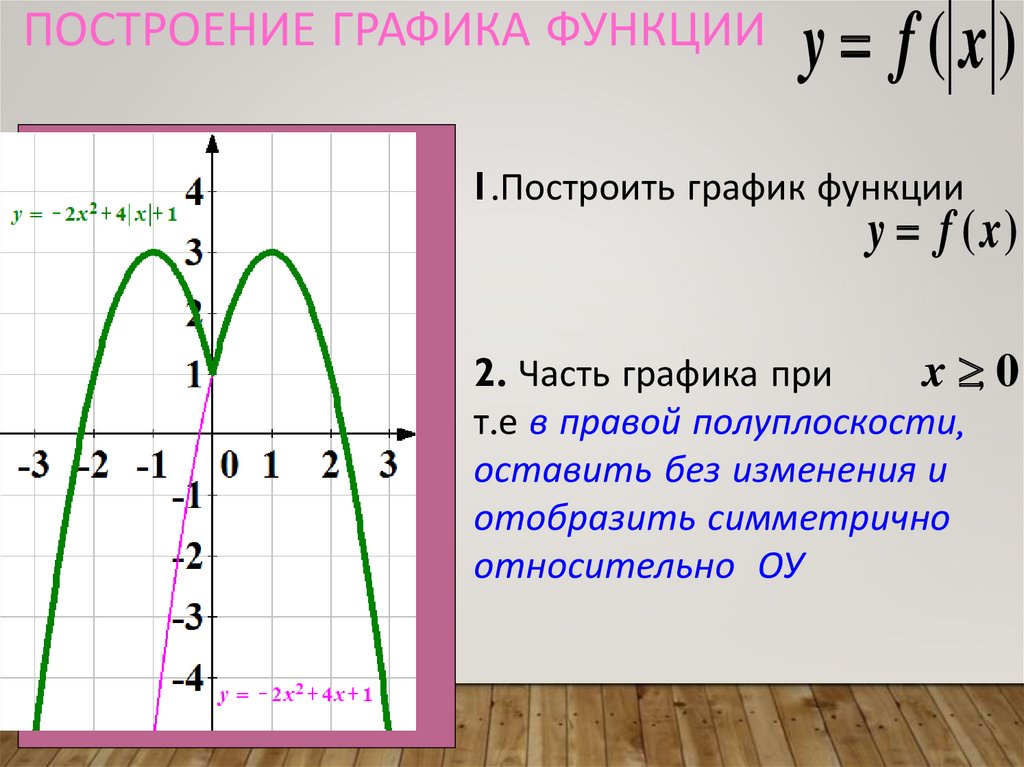
Работа
учеников в тетради по заданному алгоритму.
В результате выполнения работы, учащиеся приходят к выводу, что для построения любой квадратичной функции необходимо использовать схему: (Слайд 25)
4. Закрепление учебного материала.
Ученики работают в рабочих тетрадях с печатной основой самостоятельно, используя полученные знания, затем тетради сдают на проверку учителю. (Тетрадь с печатной основой прилагается)
5. Подведение итогов урока. Выставление оценок.
Домашнее задание: п.7, №125 (в), 126 (б, в), 132 (а, б). (Слайды 26-27)
Приложение
Алгоритм и блок-схема для нахождения всех корней квадратного уравнения
Квадратные уравнения представляют собой полиномиальные уравнения степени 2 от одной переменной типа: f(x) = ax 2 + bx + c, где a, b, c, ∈ R и a ≠ 0. Это общая форма квадратного уравнения, где «a» называется старшим коэффициентом, а «c» называется абсолютным членом f (x).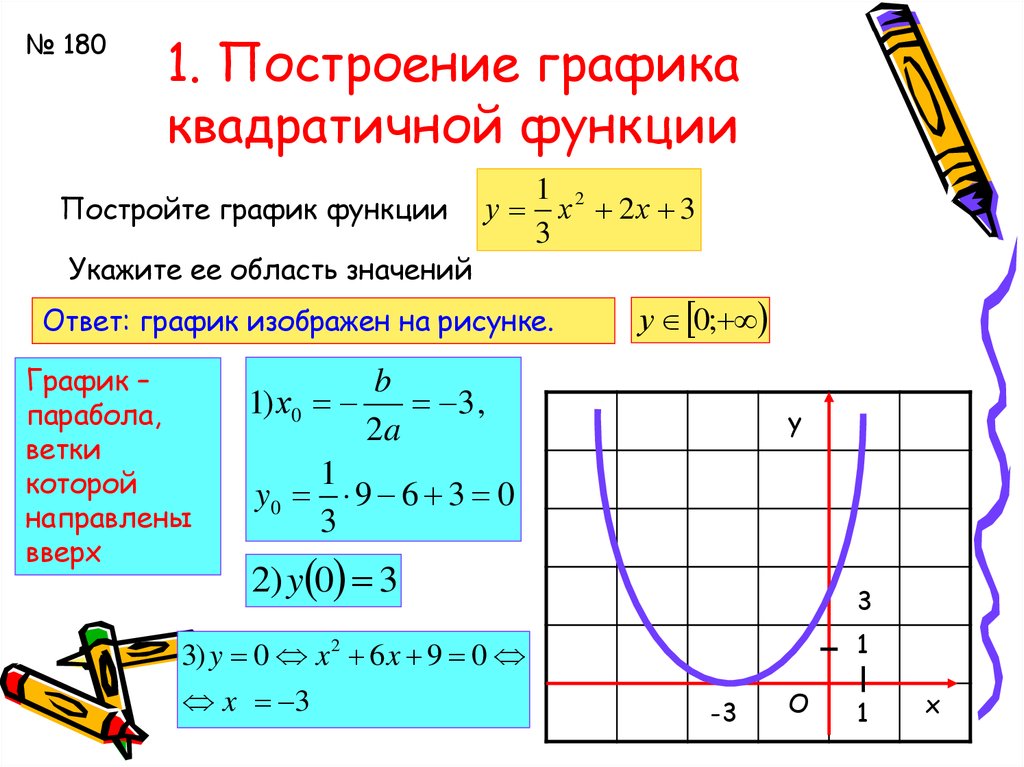
Квадратное уравнение всегда будет иметь два корня. Природа корней может быть как реальной, так и мнимой.
Общая форма квадратного уравнения: топор 2 + бх + с
Пример: 4x 2 + 6x + 12
Корни квадратного уравнения находятся по квадратной формуле:
Член b 2 — 4ac известен как дискриминант квадратного уравнения. Это говорит о природе корней.
| Если дискриминант > 0 | |
| Если дискриминант = 0 | |
| Если дискриминант |
Мы собираемся использовать приведенную выше логику для решения этой проблемы.
Давайте взглянем на алгоритм и блок-схему, чтобы лучше понять.
Алгоритм поиска всех корней квадратного уравнения:
Шаг 1. Начните Шаг 2. Считайте коэффициенты уравнения, a, b и c от пользователя. Шаг 3. Вычислить дискриминант = (b * b) – (4 * a * c) Шаг 4. Если дискриминант > 0: 4.1: Вычислить root1 = (-b + sqrt(дискриминант)) / (2 * a) 4.2: Вычислить root2 = (-b — sqrt(дискриминант)) / (2 * a) 4.3: Дисплей «Корни настоящие и разные» 4.4: Показать root1 и root2 Шаг 5: В противном случае, если дискриминант = 0: 5.1: Вычислить root1 = -b / (2 *a) 5.2: корень2 = корень1 5.3: Отображение «Корни действительны и равны» 5.4: Показать root1 и root2 Шаг 6. Еще: 6.1: Вычисление реального = -b / (2 * a) 6.2: Вычислить мнимую = sqrt (-дискриминант) / (2 * a) 6.3: Дисплей «Корни мнимые» 6.4: Отображение реального, «±», мнимого, «i» Шаг 7. Остановка
Объяснение:
Алгоритм начинается с получения от пользователя коэффициентов уравнения a, b и c. После этого по заданной формуле вычисляется дискриминант.
Теперь проверим, больше ли дискриминант 0. Если да, то корни уравнения действительны и различны. Если дискриминант равен 0, то корни вещественные и равные. Если дискриминант меньше 0, то корни мнимые и разные.
Мы сравним вычисленный дискриминант с каждым из условий и в зависимости от того, какое из них выполнено, мы вычислим два корня по соответствующей формуле, а затем отобразим это.
Примечание. Пожалуйста, обратитесь к таблице в начале, чтобы увидеть соответствующую формулу.
Например: Рассмотрим уравнение: 6x² + 11x — 35 = 0,
.
Здесь дискриминант = 961
Следовательно, дискриминант > 0; корни настоящие и разные.
Итак, root1 = 938, root2 = -81?
Блок-схема для нахождения всех корней квадратного уравнения:
Удалить водяной знак сверху Блок-схема
Алгоритм решения квадратного уравнения — Блок-схема | Математика | Схемы программного обеспечения 92+бх+с=0
, где x представляет собой неизвестное, а a, b и c являются константами, где a не равно 0.
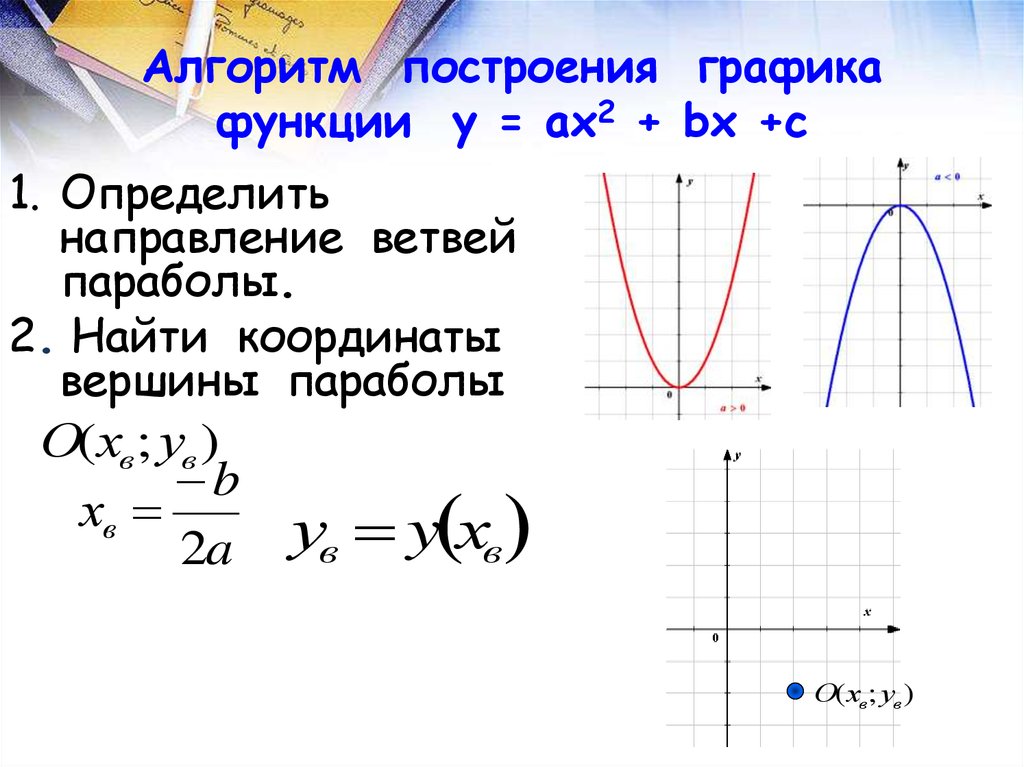Если a = 0, то уравнение является линейным, а не квадратичным. Константы a, b и c называются соответственно квадратичным коэффициентом, линейным коэффициентом и постоянным или свободным членом. Поскольку квадратное уравнение содержит только одно неизвестное, оно называется одномерным. Квадратное уравнение содержит только степени x, которые являются неотрицательными целыми числами, и, следовательно, это полиномиальное уравнение, и, в частности, это полиномиальное уравнение второй степени, поскольку наибольшая степень равна двум.
Квадратные уравнения могут быть решены с помощью процесса, известного в американском английском как факторинг, а в других вариантах английского языка как факторизация, путем завершения квадрата, использования квадратной формулы или построения графика». [Квадратное уравнение. Википедия]
Пример блок-схемы «Решение алгоритма квадратного уравнения» был создан с использованием программного обеспечения ConceptDraw PRO для построения диаграмм и векторного рисования, дополненного решением Mathematics из раздела «Наука и образование» ConceptDraw Solution Park.
Блок-схема решения квадратного уравнения
Используемые решения
Наука и образование >
Математика
Математическое решение дополняет программу ConceptDraw PRO шаблонами, образцами и библиотеками векторных трафаретов для рисования математических иллюстраций, диаграмм и графиков.
Проектируйте и документируйте разработку проектов, используя широкий спектр предварительно нарисованных форм и интеллектуальных соединителей. Разрабатывайте решения для визуализации с помощью встроенного языка сценариев.
ConceptDraw PRO — идеальный инструмент для задач проектирования и планирования; Разработка решений для визуализации; Планирование проекта (диаграммы Ганта, временные шкалы, графики проектов).
ConceptDraw PRO — мощный инструмент для рисования идей и концепций делового общения, простого визуального представления числовых данных в среде Mac.