как найти общий знаменатель | Математика
Как найти общий знаменатель, что такое общий знаменатель и конечно же нахождение общего знаменателя онлайн на нашем калькуляторе. И если вам требуется наименьший общий знаменатель, то он тут.
Скопировать ссылку
Что такое общий знаменатель?
Кроме понятия «общий знаменатель«, есть еще такое понятие как — «Наименьший общий знаменатель (НОЗ)» — это… тоже самое, что и «НОК». Поэтому, мы не будем это разбирать здесь второй раз.Но что такое общий знаменатель простыми словами?
Общий знаменатель — это любое целое число, которое делится без остатка на первый и второй знаменатель.
Количество чисел, которые могут быть общим знаменателем стремится к бесконечности, но обычно общим знаменателем принимают НОЗПример общего знаменателя :
Для того, чтобы понять, «что такое общий знаменатель» нам нужен пример двух дробей и какое-то действие(иначе смысла в этом нет), пусть это будут две дроби 1/2 и 1/3 и действие сложение — «+».
Для таких маленьких чисел, как 2 и 3 — «нок» будет равен 6. Для этого нам никакие инструменты не понадобятся, наверняка вы это тоже смогли посчитать в уме.
Т.е. 6 делится на 2 без остатка 6 : 2 = 3, и 6 делится на 3 без остатка 6 : 3 = 2.
Мы получили два числа, первую дробь 1/2 надо умножить на 3, чтобы привести её к общему знаменателю 6 — 1*3/2*3 = 3/6.
А вторую дробь нужно умножить на 2, чтобы привести и её к общему знаменатель 6, 1*2/3*2 = 2/6.
После того, как мы нашли общий знаменатель, мы можем произвести действие, в нашем случае — «+» — 3/6 + 2/6 = (3 + 2)/6 = 5/6.
Когда мы нашли «общий знаменатель» мы смогли выполнить необходимое действие с дробями.
1*32*3 + 1*23*2 =
36 + 26 =
3 + 2 6 =
5 6
В каком случае ноз двух дробей будет являться произведением знаменателей?
Отличный поисковый запрос — «в каком случае ноз двух дробей будет являться произведением знаменателей?«, что выше не было озвучено.
Когда ноз двух дробей равен произведению знаменателей?
Как минимум, когда знаменатели будут простыми числами, т.е. в качестве примера, это выше приведенные дроби со знаменателями 2 и 3. Эти числа являются простыми, т.е. делятся на себя и на 1.И общий знаменатель двух чисел 2 и 3 будет равен произведению 2 * 3 = 6.
Скопировать ссылку
Формула общего знаменателя
Как вы знаете. что если умножить и числитель и знаменатель на одно число, то результат дроби не изменится! Поэтому мы можем вывести формулу общего знаменателя буквами :Первую дробь умножаем на знаменатель второй дроби.
А вторую дробь умножаем на знаменатель первой дроби
AB + CD =A*DB*D + C*BD*B =
Нахождение общего знаменателя с помощью нок.
Для того чтобы найти общий знаменатель, можно воспользоваться правилом «НОК» для двух чисел, которые здесь — знаменатели.
Пример нахождения общего знаменателя методом разложения на множители
Это тоже самое. что и выше приведенный «НОК» — только может называться по другому…смайлы
Этот способ может называться как «нахождение общего знаменателя методом разложения на множители»
Либо «метод нахождения наименьшего общего знаменателя» или просто «НОЗ»
Рассмотрим два знаменателя 8 и 6, к примеру это могут быть две дроби 1/8 и 1/6 и нам нужно найти их общий знаменатель.
Надо расположить в первую строчку наибольший знаменатель — это 8 и разложить его на множители:
8 = 2 * 2 * 2Ниже раскладываем меньший знаменатель :
6 = 2 * 3Далее нам нужно исключить все множители, которые повторяются в меньшем знаменателе… это 2 и у нас остается 3. далее эту тройку надо умножить на больший знаменатель :
8 * 3 = 24Итого получаем общий знаменатель = 24.
Пример номер 2 подбора общего знаменателя
Чтобы у вас не возникало сомнений, давайте разберем второй пример подбора общего знаменателя, пусть это будут 4 и 10.
Берем больший знаменатель раскладываем его на множители :
10 = 2 * 5Раскладываем меньший знаменатель :
4 = 2 * 2Виртуально исключаем повторяющиеся множители из второго знаменателя — это 2. И во втором знаменателе остается вторая 2. Умножаем больший знаменатель на 2 :
10 * 2 = 20Итого получаем общий знаменатель 20, двух чисел 4 и 10.
Скопировать ссылку
Как найти общий знаменатель дробей онлайн
У нас есть калькулятор, который в том числе умеет находитьПрежде чем приступать к поиску общего знаменателя, давайте найдем общий знаменатель для двух знаменателей, а потом проверим данное решение на калькуляторе.
Пусть это будут два знаменателя 20 и 6.
Раскладываем больший знаменатель на множители :
20 = 2 * 2 * 5Раскладываем на множители второй знаменатель :
8 = 2 * 2 * 2Исключаем повторяющиеся множители во втором знаменателе и у нас остается одна двойка.
Умножаем больший знаменатель на 2 :
20 * 2 = 40Итого получаем их общий знаменатель 40.
Переходим к нахождению общего знаменателя онлайн
Открываем наш калькулятор.Вводим первый знаменатель 20.
Нажимаем кнопку «НОК»
Набираем второй знаменатель 8.
Нажимаем равно — «=»
Получаем результат нахождения общего знаменателя онлайн :
Далее вы можете сравнить два результата нахождения общего знаменателя.Скопировать ссылку
Что такое
наименьший общий знаменатель? Разница между «общим знаменателем«(1) и «наименьшим общим знаменателем«(2) в том, что первое может быть бесконечное количество… а второе «НОЗ», только один!Но, что же такое «наименьший общий знаменатель»
НОЗ — это абсолютно тоже самое, что и «НОК».Определение, что же такое «наименьший общий знаменатель»
Наименьший общий знаменатель двух знаменателей — это самое маленькое целое число, которое делится без остатка на первый и второй знаменатель.
Скопировать ссылку
Формула наименьшего общего кратного
Для нахождения «наименьшего общего знаменателя» двух знаменателей, нужно эти два знаменателя разложить на множители. Больший знаменатель записываем в первую строчку, второй знаменатель раскладываем на множители и записываем во вторую строчку.
То число(если больше 1, то перемножаем между собой) умножаем на большее число.
Для пониманияформулы наименьшего общего кратного нам нужен пример!
Предположим, что у нас есть два знаменателя 10 и 6 и нужно найти наименьший общий знаменатель :
Разложим больший знаменатель на множители :
10 = 2 * 5Разложим второй знаменатель на множители :
6 = 2 * 3Теперь, нам нужно исключить повторяющеюся цифру 2 из второй строчки, остается цифра 3.
Умножаем больший знаменатель на 3.
Итого получаем, что наименьший общий знаменатель двух знаменателей 10 и 5 равно 30.
Скопировать ссылку
Как найти
наименьший общий знаменатель на калькуляторе Для понимания процесса получения наименьшего общего знаменателя на калькуляторе нам потребуются два знаменателя, например 18 и 12 из дробей 1/18 и 1/12Прежде чем приступать к нахождению «нок» двух чисел на калькуляторе, давайте найдем наименьшее общее кратное, как мы делали это выше :
Раскладываем большее число на множители :
18 = 2 * 3 * 3Раскладываем меньшее число на множители :
12 = 2 * 2 * 3Исключаем повторяющиеся цифры — это одна 2 и 3, остается 2.
Умножаем большее число на 2.
18 * 2 = 36
Итого получаем, что наименьшее общее кратное двух чисел 18 и 12 = 36.
Теперь проверим правильность нахождения «нок» на калькуляторе.
Набираем первое число – пусть это будет число 12
Нажимаем «нок» на калькуляторе – для этого есть специальная кнопка.
После нажатия на кнопку нок – нам нужно добавить втрое число –пусть это будет 18.
И нам отсеется нажать кнопку равно!
И видим результат нахождения наименьшего общего кратного на калькуляторе…
Скопировать ссылку
Как найти общий знаменатель трех дробей
Для того чтобы найти общий знаменатель сразу трех дробей нужно подряд найти нок между этими тремя знаменателями!
Для подтверждения данного тезиса — давайте решим задачку/пример.
Задача/пример найдите общий знаменатель для трех дробей.
У нас даны три дроби и у них у всех три разных знаменателя :
Для такой простой задачи можно в уме посчитать. .. перебором…, а потом подтвердим наше решение через «НОК».
.. перебором…, а потом подтвердим наше решение через «НОК».
5 — не подходит — не делится на 3.
10 — не подходит — не делится на 3.
15 — не подходит, не делится на 2.
20 — не подходит, не делится на 3.
25 — не подходит, не делится на 2.
30 — подходит, делится на все без остатка… мы нашли общий знаменатель для трех дробей, методом перебора
Найдем общий знаменатель для трех дробей на калькуляторе через НОК.
Набираем первый знаменатель — 2.
Нажимаем кнопку — «НОК».
Набираем второй знаменатель — 3.
Нажимаем равно — «=».
Далее опять нажимаем — «НОК».
Набираем третий знаменатель — 6.
Нажимаем равно — «=».
Получаем общий знаменатель для трех дробей посчитанный онлайн на калькуляторе.
Скопировать ссылку
Как найти общий знаменатель дробей с разными знаменателями
Если говориться о том, чтобы найти общий знаменатель, то логично предположить, что у дробей изначально разные знаменатели — иначе, зачем искать общий знаменатель — ведь знаменатели одинаковые.
Вариант разложения знаменателей на множители.
Вариант нахождения общего знаменателя с помощью НОК и т.д
Теги :
как найти общий знаменатель
как найти наименьший общий знаменатель
как найти общий знаменатель дробей с разными
как найти общий знаменатель у дробей
как найти наименьший общий знаменатель дробей
найдите общий знаменатель дробей
найти общий знаменатель онлайн
найти общий знаменатель чисел
найдите наименьшее общее кратное знаменателей
как быстро найти общий знаменатель
как найти общий знаменатель дробей класс
как найти наибольший общий знаменатель
найти общее кратное знаменателей дробей
найдите наименьший общий знаменатель дробей
найти общий знаменатель дробей онлайн
найдите наименьший общий знаменатель дробей
как найти общий знаменатель при сложении
калькулятор найти общий знаменатель
как найти общий знаменатель двух дробей
как быстро найти общий знаменатель у дроби с большим знаменателем
общий знаменатель дробей это такое простыми словами
общий знаменатель трех дробей онлайн
решение общего знаменателя
Как приводить к наименьшему общему знаменателю дроби.
 Приведение дробей к наименьшему общему знаменателю, правило, примеры, решения
Приведение дробей к наименьшему общему знаменателю, правило, примеры, решенияВ данной статье рассказывается, как привести дроби к общему знаменателю и как найти наименьший общий знаменатель. Приведены определения, дано правило приведения дробей к общему знаменателю и рассмотрены практические примеры.
Что такое приведение дроби к общему знаменателю?
Обыкновенные дроби состоят из числителя — верхней части, и знаменателя — нижней части. Если дроби имеют одинаковый знаменатель, говорят, что они приведены к общему знаменателю. Например, дроби 11 14 , 17 14 , 9 14 имеют одинаковый знаменатель 14 . Другими словами, они приведены к общему знаменателю.
Если же дроби имеют разные знаменатели, то их всегда можно привести к общему знаменателю при помощи нехитрых действий. Чтобы сделать это, нужно числитель и знаменатель умножить на определенные дополнительные множители.
Очевидно, что дроби 4 5 и 3 4 не приведены к общему знаменателю. Чтобы это сделать, нужно с использованием дополнительных множителей 5 и 4 привести их к знаменателю 20. Как именно сделать это? Умножим числитель и знаменатель дроби 4 5 на 4 , а числитель и знаменатель дроби 3 4 умножим на 5 . Вместо дробей 4 5 и 3 4 получим соответственно 16 20 и 15 20 .
Как именно сделать это? Умножим числитель и знаменатель дроби 4 5 на 4 , а числитель и знаменатель дроби 3 4 умножим на 5 . Вместо дробей 4 5 и 3 4 получим соответственно 16 20 и 15 20 .
Приведение дробей к общему знаменателю
Приведение дробей к общему знаменателю — это умножение числителей и знаменателей дробей на такие множители, что в результате получаются идентичные дроби с одинаковым знаменателем.
Общий знаменатель: определение, примеры
Что такое общий знаменатель?
Общий знаменатель
Общий знаменатель дробей — это любое положительное число, которое является общим кратным всех данных дробей.
Другими словами, общим знаменателем какого-то набора дробей будет такое натуральное число, которое без остатка делится на все знаменатели этих дробей.
Ряд натуральных чисел бесконечен, и поэтому, согласно определению, каждый набор обыкновенных дробей имеет бесконечное множество общих знаменателей. Иначе говоря, существует бесконечно много общих кратных для всех знаменателей исходного набора дробей.
Общий знаменатель для нескольких дробей легко найти, пользуясь определением. Пусть есть дроби 1 6 и 3 5 . Общим знаменателем дробей будет любое положительное общее кратное для чисел 6 и 5 . Такими положительными общими кратными являются числа 30, 60, 90, 120, 150, 180, 210 и так далее.
Рассмотрим пример.
Пример 1. Общий знаменатель
Можно ди дроби 1 3 , 21 6 , 5 12 привести к общему знаменателю, который равен 150 ?
Чтобы выяснить, так ли это, нужно проверить, является ли 150 общим кратным для знаменателей дробей, то есть для чисел 3 , 6 , 12 . Другими словами, число 150 должно без остатка делиться на 3 , 6 , 12 . Проверим:
150 ÷ 3 = 50 , 150 ÷ 6 = 25 , 150 ÷ 12 = 12 , 5
Значит, 150 не является общим знаменателем указанных дробей.
Наименьший общий знаменатель
Наименьшее натуральное число из множества общих знаменателей какого-то набора дробей называется наименьшим общим знаменателем.
Наименьший общий знаменатель
Наименьший общий знаменатель дробей — это наименьшее число среди всех общих знаменателей этих дробей.
Наименьший общий делитель данного набора чисел — это наименьшее общее кратное (НОК). НОК всех знаменателей дробей является наименьшим общим знаменателем этих дробей.
Как найти наименьший общий знаменатель? Его нахождение сводится к нахождению наименьшего общего кратного дробей. Обратимся к примеру:
Пример 2. Найти наименьший общий знаменатель
Нужно найти наименьший общий знаменатель для дробей 1 10 и 127 28 .
Ищем НОК чисел 10 и 28 . Разложим их на простые множители и получим:
10 = 2 · 5 28 = 2 · 2 · 7 Н О К (15 , 28) = 2 · 2 · 5 · 7 = 140
Как привести дроби к наименьшему общему знаменателю
Существует правило, которое объясняет, как привести дроби к общему знаменателю. Правило состоит из трех пунктов.
Правило приведения дробей к общему знаменателю
- Найти наименьший общий знаменатель дробей.
- Для каждой дроби найти дополнительный множитель. Чтобы найти множитель нужно наименьший общий знаменатель разделить на знаменатель каждой дроби.

- Умножить числитель и знаменатель на найденный дополнительный множитель.
Рассмотрим применение этого правила на конкретном примере.
Пример 3. Приведение дробей к общему знаменателю
Есть дроби 3 14 и 5 18 . Приведем их к наименьшему общему знаменателю.
По правилу, сначала найдем НОК знаменателей дробей.
14 = 2 · 7 18 = 2 · 3 · 3 Н О К (14 , 18) = 2 · 3 · 3 · 7 = 126
Вычисляем дополнительные множители для каждой дроби. Для 3 14 дополнительный множитель находится как 126 ÷ 14 = 9 , а для дроби 5 18 дополнительный множитель будет равен 126 ÷ 18 = 7 .
Умножаем числитель и знаменатель дробей на дополнительные множители и получаем:
3 · 9 14 · 9 = 27 126 , 5 · 7 18 · 7 = 35 126 .
Приведение нескольких дробей к наименьшему общему знаменателю
По рассмотренному правилу к общему знаменателю можно приводить не только пары дробей, но и большее их количество.
Приведем еще один пример.
Пример 4. Приведение дробей к общему знаменателю
Привести дроби 3 2 , 5 6 , 3 8 и 17 18 к наименьшему общему знаменателю.
Вычислим НОК знаменателей. Находим НОК трех и большего количества чисел:
Н О К (2 , 6) = 6 Н О К (6 , 8) = 24 Н О К (24 , 18) = 72 Н О К (2 , 6 , 8 , 18) = 72
Для 3 2 дополнительный множитель равен 72 ÷ 2 = 36 , для 5 6 дополнительный множитель равен 72 ÷ 6 = 12 , для 3 8 дополнительный множитель равен 72 ÷ 8 = 9 , наконец, для 17 18 дополнительный множитель равен 72 ÷ 18 = 4 .
Умножаем дроби на дополнительные множители и переходим к наименьшему общему знаменателю:
3 2 · 36 = 108 72 5 6 · 12 = 60 72 3 8 · 9 = 27 72 17 18 · 4 = 68 72
Если вы заметили ошибку в тексте, пожалуйста, выделите её и нажмите Ctrl+Enter
Материал этой статьи объясняет, как найти наименьший общий знаменатель и как привести дроби к общему знаменателю . Сначала даны определения общего знаменателя дробей и наименьшего общего знаменателя, а также показано, как найти общий знаменатель дробей. Дальше приведено правило приведения дробей к общему знаменателю и рассмотрены примеры применения этого правила. В заключение разобраны примеры приведения трех и большего количества дробей к общему знаменателю.
В заключение разобраны примеры приведения трех и большего количества дробей к общему знаменателю.
Навигация по странице.
Что называют приведением дробей к общему знаменателю?
Теперь мы можем сказать, что такое приведение дробей к общему знаменателю. Приведение дробей к общему знаменателю – это умножение числителей и знаменателей данных дробей на такие дополнительные множители, что в результате получаются дроби с одинаковыми знаменателями.
Общий знаменатель, определение, примеры
Теперь пришло время дать определение общего знаменателя дробей.
Иными словами, общим знаменателем некоторого набора обыкновенных дробей является любое натуральное число, которое делится на все знаменатели данных дробей.
Из озвученного определения следует, что данный набор дробей имеет бесконечно много общих знаменателей, так как существует бесконечное множество общих кратных всех знаменателей исходного набора дробей.
Определение общего знаменателя дробей позволяет находить общие знаменатели данных дробей. Пусть, к примеру, даны дроби 1/4
и 5/6
, их знаменатели равны 4
и 6
соответственно. Положительными общими кратными чисел 4
и 6
являются числа 12
, 24
, 36
, 48
, … Любое из этих чисел является общим знаменателем дробей 1/4
и 5/6
.
Пусть, к примеру, даны дроби 1/4
и 5/6
, их знаменатели равны 4
и 6
соответственно. Положительными общими кратными чисел 4
и 6
являются числа 12
, 24
, 36
, 48
, … Любое из этих чисел является общим знаменателем дробей 1/4
и 5/6
.
Для закрепления материала рассмотрим решение следующего примера.
Пример.
Можно ли дроби 2/3 , 23/6 и 7/12 привести к общему знаменателю 150 ?
Решение.
Для ответа на поставленный вопрос нам нужно выяснить, является ли число 150 общим кратным знаменателей 3 , 6 и 12 . Для этого проверим, делится ли 150 нацело на каждое из этих чисел (при необходимости смотрите правила и примеры деления натуральных чисел , а также правила и примеры деления натуральных чисел с остатком): 150:3=50 , 150:6=25 , 150:12=12 (ост. 6) .
Итак, 150 не делится нацело на 12 , следовательно, 150 не является общим кратным чисел 3 , 6 и 12 . Следовательно, число 150 не может быть общим знаменателем исходных дробей.
Ответ:
Нельзя.
Наименьший общий знаменатель, как его найти?
В множестве чисел, являющихся общими знаменателями данных дробей, существует наименьшее натуральное число , которое называют наименьшим общим знаменателем. Сформулируем определение наименьшего общего знаменателя данных дробей.
Определение.
Наименьший общий знаменатель – это наименьшее число, из всех общих знаменателей данных дробей.
Осталось разобраться с вопросом, как найти наименьший общий делитель.
Так как является наименьшим положительным общим делителем данного набора чисел, то НОК знаменателей данных дробей представляет собой наименьший общий знаменатель данных дробей.
Таким образом, нахождение наименьшего общего знаменателя дробей сводится к знаменателей этих дробей. Разберем решение примера.
Пример.
Найдите наименьший общий знаменатель дробей 3/10 и 277/28 .
Решение.
Знаменатели данных дробей равны 10
и 28
. Искомый наименьший общий знаменатель находится как НОК чисел 10
и 28
. В нашем случае легко : так как 10=2·5
, а 28=2·2·7
, то НОК(15, 28)=2·2·5·7=140
.
В нашем случае легко : так как 10=2·5
, а 28=2·2·7
, то НОК(15, 28)=2·2·5·7=140
.
Ответ:
140 .
Как привести дроби к общему знаменателю? Правило, примеры, решения
Обычно обыкновенные дроби приводят к наименьшему общему знаменателю. Сейчас мы запишем правило, которое объясняет, как привести дроби к наименьшему общему знаменателю.
Правило приведения дробей к наименьшему общему знаменателю состоит из трех шагов:
- Во-первых, находится наименьший общий знаменатель дробей.
- Во-вторых, для каждой дроби вычисляется дополнительный множитель, для чего наименьший общий знаменатель делится на знаменатель каждой дроби.
- В-третьих, числитель и знаменатель каждой дроби умножается на ее дополнительный множитель.
Применим озвученное правило к решению следующего примера.
Пример.
Приведите дроби 5/14 и 7/18 к наименьшему общему знаменателю.
Решение.
Выполним все шаги алгоритма приведения дробей к наименьшему общему знаменателю.
Сначала находим наименьший общий знаменатель, который равен наименьшему общему кратному чисел 14 и 18 . Так как 14=2·7 и 18=2·3·3 , то НОК(14, 18)=2·3·3·7=126 .
Теперь вычисляем дополнительные множители, с помощью которых дроби 5/14 и 7/18 будут приведены к знаменателю 126 . Для дроби 5/14 дополнительный множитель равен 126:14=9 , а для дроби 7/18 дополнительный множитель равен 126:18=7 .
Осталось умножить числители и знаменатели дробей 5/14 и 7/18 на дополнительные множители 9 и 7 соответственно. Имеем и .
Итак, приведение дробей 5/14 и 7/18 к наименьшему общему знаменателю завершено. В итоге получились дроби 45/126 и 49/126 .
Изначально я хотел включить методы приведения к общему знаменателю в параграф «Сложение и вычитание дробей». Но информации оказалось так много, а важность ее столь велика (ведь общие знаменатели бывают не только у числовых дробей), что лучше изучить этот вопрос отдельно.
Итак, пусть у нас есть две дроби с разными знаменателями. А мы хотим сделать так, чтобы знаменатели стали одинаковыми. На помощь приходит основное свойство дроби, которое, напомню, звучит следующим образом:
А мы хотим сделать так, чтобы знаменатели стали одинаковыми. На помощь приходит основное свойство дроби, которое, напомню, звучит следующим образом:
Дробь не изменится, если ее числитель и знаменатель умножить на одно и то же число, отличное от нуля.
Таким образом, если правильно подобрать множители, знаменатели у дробей сравняются — этот процесс называется приведением к общему знаменателю. А искомые числа, «выравнивающие» знаменатели, называются дополнительными множителями.
Для чего вообще надо приводить дроби к общему знаменателю? Вот лишь несколько причин:
- Сложение и вычитание дробей с разными знаменателями. По-другому эту операцию никак не выполнить;
- Сравнение дробей. Иногда приведение к общему знаменателю значительно упрощает эту задачу;
- Решение задач на доли и проценты. Процентные соотношения являются, по сути, обыкновенными выражениями, которые содержат дроби.
Есть много способов найти числа, при умножении на которые знаменатели дробей станут равными. Мы рассмотрим лишь три из них — в порядке возрастания сложности и, в некотором смысле, эффективности.
Мы рассмотрим лишь три из них — в порядке возрастания сложности и, в некотором смысле, эффективности.
Умножение «крест-накрест»
Самый простой и надежный способ, который гарантированно выравнивает знаменатели. Будем действовать «напролом»: умножаем первую дробь на знаменатель второй дроби, а вторую — на знаменатель первой. В результате знаменатели обеих дробей станут равными произведению исходных знаменателей. Взгляните:
В качестве дополнительных множителей рассмотрим знаменатели соседних дробей. Получим:
Да, вот так все просто. Если вы только начинаете изучать дроби, лучше работайте именно этим методом — так вы застрахуете себя от множества ошибок и гарантированно получите результат.
Единственный недостаток данного метода — приходится много считать, ведь знаменатели умножаются «напролом», и в результате могут получиться очень большие числа. Такова расплата за надежность.
Метод общих делителей
Этот прием помогает намного сократить вычисления, но, к сожалению, применяется он достаточно редко. Метод заключается в следующем:
Метод заключается в следующем:
- Прежде, чем действовать «напролом» (т.е. методом «крест-накрест»), взгляните на знаменатели. Возможно, один из них (тот, который больше), делится на другой.
- Число, полученное в результате такого деления, будет дополнительным множителем для дроби с меньшим знаменателем.
- При этом дробь с большим знаменателем вообще не надо ни на что умножать — в этом и заключается экономия. Заодно резко снижается вероятность ошибки.
Задача. Найдите значения выражений:
Заметим, что 84: 21 = 4; 72: 12 = 6 . Поскольку в обоих случаях один знаменатель делится без остатка на другой, применяем метод общих множителей. Имеем:
Заметим, что вторая дробь вообще нигде ни на что не умножалась. Фактически, мы сократили объем вычислений в два раза!
Кстати, дроби в этом примере я взял не случайно. Если интересно, попробуйте сосчитать их методом «крест-накрест». После сокращения ответы получатся такими же, но работы будет намного больше.
В этом и состоит сила метода общих делителей, но, повторюсь, применять его можно лишь в том случае, когда один из знаменателей делится на другой без остатка. Что бывает достаточно редко.
Метод наименьшего общего кратного
Когда мы приводим дроби к общему знаменателю, мы по сути пытаемся найти такое число, которое делится на каждый из знаменателей. Затем приводим к этому числу знаменатели обеих дробей.
Таких чисел очень много, и наименьшее из них совсем не обязательно будет равняться прямому произведению знаменателей исходных дробей, как это предполагается в методе «крест-накрест».
Например, для знаменателей 8 и 12 вполне подойдет число 24, поскольку 24: 8 = 3; 24: 12 = 2 . Это число намного меньше произведения 8 · 12 = 96 .
Наименьшее число, которое делится на каждый из знаменателей, называется их наименьшим общим кратным (НОК).
Обозначение: наименьшее общее кратное чисел a и b обозначается НОК(a ; b ) . Например, НОК(16; 24) = 48 ; НОК(8; 12) = 24 .
Если вам удастся найти такое число, итоговый объем вычислений будет минимальным. Посмотрите на примеры:
Задача. Найдите значения выражений:
Заметим, что 234 = 117 · 2; 351 = 117 · 3 . Множители 2 и 3 взаимно просты (не имеют общих делителей, кроме 1), а множитель 117 — общий. Поэтому НОК(234; 351) = 117 · 2 · 3 = 702.
Аналогично, 15 = 5 · 3; 20 = 5 · 4 . Множители 3 и 4 взаимно просты, а множитель 5 — общий. Поэтому НОК(15; 20) = 5 · 3 · 4 = 60.
Теперь приведем дроби к общим знаменателям:
Обратите внимание, насколько полезным оказалось разложение исходных знаменателей на множители:
- Обнаружив одинаковые множители, мы сразу вышли на наименьшее общее кратное, что, вообще говоря, является нетривиальной задачей;
- Из полученного разложения можно узнать, каких множителей «не хватает» каждой из дробей. Например, 234 · 3 = 702 , следовательно, для первой дроби дополнительный множитель равен 3.
Чтобы оценить, насколько колоссальный выигрыш дает метод наименьшего общего кратного, попробуйте вычислить эти же примеры методом «крест-накрест». Разумеется, без калькулятора. Думаю, после этого комментарии будут излишними.
Разумеется, без калькулятора. Думаю, после этого комментарии будут излишними.
Не думайте, что таких сложных дробей в настоящих примерах не будет. Они встречаются постоянно, и приведенные выше задачи — не предел!
Единственная проблема — как найти этот самый НОК. Иногда все находится за несколько секунд, буквально «на глаз», но в целом это сложная вычислительная задача, требующая отдельного рассмотрения. Здесь мы не будем этого касаться.
Наименьшим общим знаменателем (НОЗ) данных несократимых дробей является наименьшее общее кратное (НОК) знаменателей этих дробей. ( см. тему «Нахождение наименьшего общего кратного» :
Чтобы привести дроби к наименьшему общему знаменателю, надо: 1) найти наименьшее общее кратное знаменателей данных дробей, оно и будет наименьшим общим знаменателем. 2) найти для каждой из дробей дополнительный множитель, для чего делить новый знаменатель на знаменатель каждой дроби. 3) умножить числитель и знаменатель каждой дроби на ее дополнительный множитель.
Примеры. Привести следующие дроби к наименьшему общему знаменателю.
Находим наименьшее общее кратное знаменателей: НОК(5; 4)=20, так как 20 — самое меньшее число, которое делится и на 5 и на 4. Находим для 1-й дроби дополнительный множитель 4 (20: 5=4). Для 2-й дроби дополнительный множитель равен 5 (20: 4=5). Умножаем числитель и знаменатель 1-й дроби на 4, а числитель и знаменатель 2-й дроби на 5. Мы привели данные дроби к наименьшему общему знаменателю (20 ).
Наименьший общий знаменатель этих дробей — число 8, так как 8 делится на 4 и на само себя. Дополнительного множителя к 1-й дроби не будет (или можно сказать, что он равен единице), ко 2-й дроби дополнительный множитель равен 2 (8: 4=2). Умножаем числитель и знаменатель 2-й дроби на 2. Мы привели данные дроби к наименьшему общему знаменателю (8 ).
Данные дроби не являются несократимыми.
Сократим 1-ю дробь на 4, а 2-ю дробь сократим на 2. (см. примеры на сокращение обыкновенных дробей: Карта сайта → 5.4.2. Примеры сокращения обыкновенных дробей
). Находим НОК(16; 20)=2 4 · 5=16· 5=80. Дополнительный множитель для 1-й дроби равен 5 (80: 16=5). Дополнительный множитель для 2-й дроби равен 4 (80: 20=4). Умножаем числитель и знаменатель 1-й дроби на 5, а числитель и знаменатель 2-й дроби на 4. Мы привели данные дроби к наименьшему общему знаменателю (80 ).
(см. примеры на сокращение обыкновенных дробей: Карта сайта → 5.4.2. Примеры сокращения обыкновенных дробей
). Находим НОК(16; 20)=2 4 · 5=16· 5=80. Дополнительный множитель для 1-й дроби равен 5 (80: 16=5). Дополнительный множитель для 2-й дроби равен 4 (80: 20=4). Умножаем числитель и знаменатель 1-й дроби на 5, а числитель и знаменатель 2-й дроби на 4. Мы привели данные дроби к наименьшему общему знаменателю (80 ).
Находим наименьший общий знаменатель НОЗ(5; 6 и 15)=НОК(5; 6 и 15)=30. Дополнительный множитель к 1-й дроби равен 6 (30: 5=6), дополнительный множитель ко 2-й дроби равен 5 (30: 6=5), дополнительный множитель к 3-ей дроби равен 2 (30: 15=2). Умножаем числитель и знаменатель 1-й дроби на 6, числитель и знаменатель 2-й дроби на 5, числитель и знаменатель 3-ей дроби на 2. Мы привели данные дроби к наименьшему общему знаменателю (30 ).
Правило приведения дробей к общему знаменателю.
 Записи с меткой «приведение к наименьшему общему знаменателю»
Записи с меткой «приведение к наименьшему общему знаменателю»Чтобы привести дроби к наименьшему общему знаменателю, надо: 1) найти наименьшее общее кратное знаменателей данных дробей, оно и будет наименьшим общим знаменателем. 2) найти для каждой из дробей дополнительный множитель, для чего делить новый знаменатель на знаменатель каждой дроби. 3) умножить числитель и знаменатель каждой дроби на ее дополнительный множитель.
Примеры. Привести следующие дроби к наименьшему общему знаменателю.
Находим наименьшее общее кратное знаменателей: НОК(5; 4)=20, так как 20 — самое меньшее число, которое делится и на 5 и на 4. Находим для 1-й дроби дополнительный множитель 4 (20: 5=4). Для 2-й дроби дополнительный множитель равен 5 (20: 4=5). Умножаем числитель и знаменатель 1-й дроби на 4, а числитель и знаменатель 2-й дроби на 5. Мы привели данные дроби к наименьшему общему знаменателю (20 ).
Наименьший общий знаменатель этих дробей — число 8, так как 8 делится на 4 и на само себя. Дополнительного множителя к 1-й дроби не будет (или можно сказать, что он равен единице), ко 2-й дроби дополнительный множитель равен 2 (8: 4=2). Умножаем числитель и знаменатель 2-й дроби на 2. Мы привели данные дроби к наименьшему общему знаменателю (8 ).
Дополнительного множителя к 1-й дроби не будет (или можно сказать, что он равен единице), ко 2-й дроби дополнительный множитель равен 2 (8: 4=2). Умножаем числитель и знаменатель 2-й дроби на 2. Мы привели данные дроби к наименьшему общему знаменателю (8 ).
Данные дроби не являются несократимыми.
Сократим 1-ю дробь на 4, а 2-ю дробь сократим на 2. (см. примеры на сокращение обыкновенных дробей: Карта сайта → 5.4.2. Примеры сокращения обыкновенных дробей ). Находим НОК(16; 20)=2 4 · 5=16· 5=80. Дополнительный множитель для 1-й дроби равен 5 (80: 16=5). Дополнительный множитель для 2-й дроби равен 4 (80: 20=4). Умножаем числитель и знаменатель 1-й дроби на 5, а числитель и знаменатель 2-й дроби на 4. Мы привели данные дроби к наименьшему общему знаменателю (80 ).
Находим наименьший общий знаменатель НОЗ(5; 6 и 15)=НОК(5; 6 и 15)=30. Дополнительный множитель к 1-й дроби равен 6 (30: 5=6), дополнительный множитель ко 2-й дроби равен 5 (30: 6=5), дополнительный множитель к 3-ей дроби равен 2 (30: 15=2). Умножаем числитель и знаменатель 1-й дроби на 6, числитель и знаменатель 2-й дроби на 5, числитель и знаменатель 3-ей дроби на 2. Мы привели данные дроби к наименьшему общему знаменателю (30 ).
Умножаем числитель и знаменатель 1-й дроби на 6, числитель и знаменатель 2-й дроби на 5, числитель и знаменатель 3-ей дроби на 2. Мы привели данные дроби к наименьшему общему знаменателю (30 ).
Страница 1 из 1 1
Схема приведения к общему знаменателю
- Нужно определить, какое будет наименьшее общее кратное для знаменателей дробей. Если Вы имеете дело со смешанным или целым числом, то его нужно сначала превратить в дробь, а уже потом определять наименьшее общее кратное. Чтобы целое число превратить в дробь, нужно в числителе записать само это число, а в знаменателе — единицу. Например, число 5 в виде дроби будет выглядеть так: 5/1. Чтобы смешанное число превратить в дробь, нужно целое число умножить на знаменатель и прибавить к нему числитель. Пример: 8 целых и 3/5 в виде дроби = 8×5+3/5 = 43/5.
- После этого необходимо найти дополнительный множитель, который определяется делением НОЗ на знаменатель каждой дроби.
- Последний шаг — умножение дроби на дополнительный множитель.

Важно запомнить, что приведение к общему знаменателю нужно не только для сложения или вычитания. Для сравнения нескольких дробей с разными знаменателями также необходимо сначала привести каждую из них к общему знаменателю.
Приведение дробей к общему знаменателю
Для того чтобы понять, как привести к общему знаменателю дробь, необходимо разобраться в некоторых свойствах дробей. Так, важным свойством, используемым для приведения к НОЗ, является равенство дробей. Другими словами, если числитель и знаменатель дроби умножается на число, то в результате получает дробь, равная предыдущей. В качестве примера приведём следующий пример. Для того чтобы привести дроби 5/9 и 5/6 к наименьшему общему знаменателю, нужно выполнить следующие действия:
- Сначала находим наименьшее общее кратное знаменателей. В данном случае для чисел 9 и 6 НОК будет равно 18.
- Определяем дополнительные множители для каждой из дробей. Делается это следующим образом. Делим НОК на знаменатель каждой из дробей, в результате получаем 18: 9 = 2, а 18: 6 = 3.
 Эти числа и будут дополнительными множителями.
Эти числа и будут дополнительными множителями. - Приводим две дроби к НОЗ. Умножая дробь на число, нужно умножить и числитель, и знаменатель. Дробь 5/9 можно умножить на дополнительный множитель 2, в результате чего получится дробь, равная данной, — 10/18. То же самое делаем со второй дробью: 5/6 умножаем на 3, в результате чего получаем 15/18.
Как видим из представленного выше примера, обе дроби были приведены к наименьшему общему знаменателю. Чтобы окончательно разобраться в том, как найти общий знаменатель, необходимо освоить еще одно свойство дробей. Оно заключается в том, что числитель и знаменатель дроби можно сократить на одно и то же число, которое называется общим делителем. Например, дробь 12/30 можно сократить до 2/5, если разделить ее на общий делитель — число 6.
На этом уроке мы рассмотрим приведение дробей к общему знаменателю и решим задачи по этой теме. Дадим определение понятию общего знаменателя и дополнительного множителя, вспомним о взаимно простых числах. Дадим определение понятию наименьший общий знаменатель (НОЗ) и решим ряд задач на его нахождение.
Дадим определение понятию наименьший общий знаменатель (НОЗ) и решим ряд задач на его нахождение.
Тема: Сложение и вычитание дробей с разными знаменателями
Урок: Приведение дробей к общему знаменателю
Повторение. Основное свойство дроби.
Если числитель и знаменатель дроби умножить или разделить на одно и то же натуральное число, то получится равная ей дробь.
Например, числитель и знаменатель дроби можно разделить на 2. Получим дробь . Эту операцию называют сокращением дроби. Можно выполнить и обратное преобразование, умножив числитель и знаменатель дроби на 2. В этом случае говорят, что мы привели дробь к новому знаменателю. Число 2 называют дополнительным множителем.
Вывод. Дробь можно привести к любому знаменателю кратному знаменателю данной дроби. Для того чтобы привести дробь к новому знаменателю, ее числитель и знаменатель умножают на дополнительный множитель.
1. Приведите дробь к знаменателю 35.
Число 35 кратно 7, то есть 35 делится на 7 без остатка. Значит, это преобразование возможно. Найдем дополнительный множитель. Для этого разделим 35 на 7. Получим 5. Умножим на 5 числитель и знаменатель исходной дроби.
2. Приведите дробь к знаменателю 18.
Найдем дополнительный множитель. Для этого разделим новый знаменатель на исходный. Получим 3. Умножим на 3 числитель и знаменатель данной дроби.
3. Приведите дробь к знаменателю 60.
Разделив 60 на 15, получим дополнительный множитель. Он равен 4. Умножим числитель и знаменатель на 4.
4. Приведите дробь к знаменателю 24
В несложных случаях приведение к новому знаменателю выполняют в уме. Принято только указывать дополнительный множитель за скобочкой чуть правее и выше исходной дроби.
Дробь можно привести к знаменателю 15 и дробь можно привести к знаменателю 15. У дробей и общий знаменатель 15.
Общим знаменателем дробей может быть любое общее кратное их знаменателей. Для простоты дроби приводят к наименьшему общему знаменателю. Он равен наименьшему общему кратному знаменателей данных дробей.
Для простоты дроби приводят к наименьшему общему знаменателю. Он равен наименьшему общему кратному знаменателей данных дробей.
Пример. Привести к наименьшему общему знаменателю дроби и .
Сначала найдем наименьшее общее кратное знаменателей данных дробей. Это число 12. Найдем дополнительный множитель для первой и для второй дроби. Для этого 12 разделим на 4 и на 6. Три — это дополнительный множитель для первой дроби, а два — для второй. Приведем дроби к знаменателю 12.
Мы привели дроби и к общему знаменателю, то есть мы нашли равные им дроби, у которых один и тот же знаменатель.
Правило. Чтобы привести дроби к наименьшему общему знаменателю, надо
Во-первых, найти наименьшее общее кратное знаменателей этих дробей, оно и будет их наименьшим общим знаменателем;
Во-вторых, разделить наименьший общий знаменатель на знаменатели данных дробей, т. е. найти для каждой дроби дополнительный множитель.
В-третьих, умножить числитель и знаменатель каждой дроби на ее дополнительный множитель.
а) Привести к общему знаменателю дроби и .
Наименьший общий знаменатель равен 12. Дополнительный множитель для первой дроби — 4, для второй — 3. Приводим дроби к знаменателю 24.
б) Привести к общему знаменателю дроби и .
Наименьший общий знаменатель равен 45. Разделив 45 на 9 на 15, получим, соответственно, 5 и 3. Приводим дроби к знаменателю 45.
в) Привести к общему знаменателю дроби и .
Общий знаменатель — 24. Дополнительные множители, соответственно, — 2 и 3.
Иногда бывает трудно подобрать устно наименьшее общее кратное для знаменателей данных дробей. Тогда общий знаменатель и дополнительные множители находят с помощью разложения на простые множители.
Привести к общему знаменателю дроби и .
Разложим числа 60 и 168 на простые множители. Выпишем разложение числа 60 и добавим недостающие множители 2 и 7 из второго разложения. Умножим 60 на 14 и получим общий знаменатель 840. Дополнительный множитель для первой дроби — это 14. Дополнительный множитель для второй дроби — 5. Приведем дроби к общему знаменателю 840.
Дополнительный множитель для второй дроби — 5. Приведем дроби к общему знаменателю 840.
Список литературы
1. Виленкин Н.Я., Жохов В.И., Чесноков А.С. и др. Математика 6. — М.: Мнемозина, 2012.
2. Мерзляк А.Г., Полонский В.В., Якир М.С. Математика 6 класс. — Гимназия, 2006.
3. Депман И.Я., Виленкин Н.Я. За страницами учебника математики. — Просвещение, 1989.
4. Рурукин А.Н., Чайковский И.В. Задания по курсу математика 5-6 класс. — ЗШ МИФИ, 2011.
5. Рурукин А.Н., Сочилов С.В., Чайковский К.Г. Математика 5-6. Пособие для учащихся 6-х классов заочной школы МИФИ. — ЗШ МИФИ, 2011.
6. Шеврин Л.Н., Гейн А.Г., Коряков И.О. и др. Математика: Учебник-собеседник для 5-6 классов средней школы. Библиотека учителя математики. — Просвещение, 1989.
Можно скачать книги, указанные в п.1.2. данного урока.
Домашнее задание
Виленкин Н.Я., Жохов В.И., Чесноков А.С. и др. Математика 6. — М.: Мнемозина, 2012. (ссылка см. 1.2)
Домашнее задание: №297, №298, №300.
Другие задания: №270, №290
В данной статье рассказывается, как привести дроби к общему знаменателю и как найти наименьший общий знаменатель. Приведены определения, дано правило приведения дробей к общему знаменателю и рассмотрены практические примеры.
Что такое приведение дроби к общему знаменателю?
Обыкновенные дроби состоят из числителя — верхней части, и знаменателя — нижней части. Если дроби имеют одинаковый знаменатель, говорят, что они приведены к общему знаменателю. Например, дроби 11 14 , 17 14 , 9 14 имеют одинаковый знаменатель 14 . Другими словами, они приведены к общему знаменателю.
Если же дроби имеют разные знаменатели, то их всегда можно привести к общему знаменателю при помощи нехитрых действий. Чтобы сделать это, нужно числитель и знаменатель умножить на определенные дополнительные множители.
Очевидно, что дроби 4 5 и 3 4 не приведены к общему знаменателю. Чтобы это сделать, нужно с использованием дополнительных множителей 5 и 4 привести их к знаменателю 20.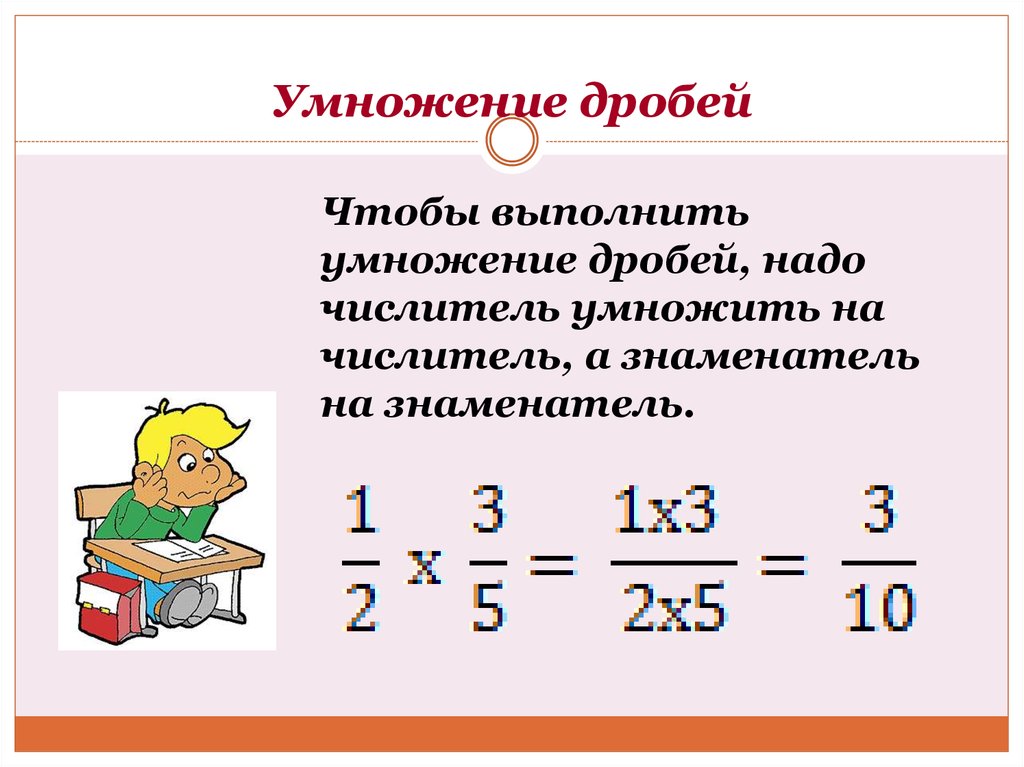 Как именно сделать это? Умножим числитель и знаменатель дроби 4 5 на 4 , а числитель и знаменатель дроби 3 4 умножим на 5 . Вместо дробей 4 5 и 3 4 получим соответственно 16 20 и 15 20 .
Как именно сделать это? Умножим числитель и знаменатель дроби 4 5 на 4 , а числитель и знаменатель дроби 3 4 умножим на 5 . Вместо дробей 4 5 и 3 4 получим соответственно 16 20 и 15 20 .
Приведение дробей к общему знаменателю
Приведение дробей к общему знаменателю — это умножение числителей и знаменателей дробей на такие множители, что в результате получаются идентичные дроби с одинаковым знаменателем.
Общий знаменатель: определение, примеры
Что такое общий знаменатель?
Общий знаменатель
Общий знаменатель дробей — это любое положительное число, которое является общим кратным всех данных дробей.
Другими словами, общим знаменателем какого-то набора дробей будет такое натуральное число, которое без остатка делится на все знаменатели этих дробей.
Ряд натуральных чисел бесконечен, и поэтому, согласно определению, каждый набор обыкновенных дробей имеет бесконечное множество общих знаменателей. Иначе говоря, существует бесконечно много общих кратных для всех знаменателей исходного набора дробей.
Общий знаменатель для нескольких дробей легко найти, пользуясь определением. Пусть есть дроби 1 6 и 3 5 . Общим знаменателем дробей будет любое положительное общее кратное для чисел 6 и 5 . Такими положительными общими кратными являются числа 30, 60, 90, 120, 150, 180, 210 и так далее.
Рассмотрим пример.
Пример 1. Общий знаменатель
Можно ди дроби 1 3 , 21 6 , 5 12 привести к общему знаменателю, который равен 150 ?
Чтобы выяснить, так ли это, нужно проверить, является ли 150 общим кратным для знаменателей дробей, то есть для чисел 3 , 6 , 12 . Другими словами, число 150 должно без остатка делиться на 3 , 6 , 12 . Проверим:
150 ÷ 3 = 50 , 150 ÷ 6 = 25 , 150 ÷ 12 = 12 , 5
Значит, 150 не является общим знаменателем указанных дробей.
Наименьший общий знаменатель
Наименьшее натуральное число из множества общих знаменателей какого-то набора дробей называется наименьшим общим знаменателем.
Наименьший общий знаменатель
Наименьший общий знаменатель дробей — это наименьшее число среди всех общих знаменателей этих дробей.
Наименьший общий делитель данного набора чисел — это наименьшее общее кратное (НОК). НОК всех знаменателей дробей является наименьшим общим знаменателем этих дробей.
Как найти наименьший общий знаменатель? Его нахождение сводится к нахождению наименьшего общего кратного дробей. Обратимся к примеру:
Пример 2. Найти наименьший общий знаменатель
Нужно найти наименьший общий знаменатель для дробей 1 10 и 127 28 .
Ищем НОК чисел 10 и 28 . Разложим их на простые множители и получим:
10 = 2 · 5 28 = 2 · 2 · 7 Н О К (15 , 28) = 2 · 2 · 5 · 7 = 140
Как привести дроби к наименьшему общему знаменателю
Существует правило, которое объясняет, как привести дроби к общему знаменателю. Правило состоит из трех пунктов.
Правило приведения дробей к общему знаменателю
- Найти наименьший общий знаменатель дробей.
- Для каждой дроби найти дополнительный множитель. Чтобы найти множитель нужно наименьший общий знаменатель разделить на знаменатель каждой дроби.

- Умножить числитель и знаменатель на найденный дополнительный множитель.
Рассмотрим применение этого правила на конкретном примере.
Пример 3. Приведение дробей к общему знаменателю
Есть дроби 3 14 и 5 18 . Приведем их к наименьшему общему знаменателю.
По правилу, сначала найдем НОК знаменателей дробей.
14 = 2 · 7 18 = 2 · 3 · 3 Н О К (14 , 18) = 2 · 3 · 3 · 7 = 126
Вычисляем дополнительные множители для каждой дроби. Для 3 14 дополнительный множитель находится как 126 ÷ 14 = 9 , а для дроби 5 18 дополнительный множитель будет равен 126 ÷ 18 = 7 .
Умножаем числитель и знаменатель дробей на дополнительные множители и получаем:
3 · 9 14 · 9 = 27 126 , 5 · 7 18 · 7 = 35 126 .
Приведение нескольких дробей к наименьшему общему знаменателю
По рассмотренному правилу к общему знаменателю можно приводить не только пары дробей, но и большее их количество.
Приведем еще один пример.
Пример 4. Приведение дробей к общему знаменателю
Привести дроби 3 2 , 5 6 , 3 8 и 17 18 к наименьшему общему знаменателю.
Вычислим НОК знаменателей. Находим НОК трех и большего количества чисел:
Н О К (2 , 6) = 6 Н О К (6 , 8) = 24 Н О К (24 , 18) = 72 Н О К (2 , 6 , 8 , 18) = 72
Для 3 2 дополнительный множитель равен 72 ÷ 2 = 36 , для 5 6 дополнительный множитель равен 72 ÷ 6 = 12 , для 3 8 дополнительный множитель равен 72 ÷ 8 = 9 , наконец, для 17 18 дополнительный множитель равен 72 ÷ 18 = 4 .
Умножаем дроби на дополнительные множители и переходим к наименьшему общему знаменателю:
3 2 · 36 = 108 72 5 6 · 12 = 60 72 3 8 · 9 = 27 72 17 18 · 4 = 68 72
Если вы заметили ошибку в тексте, пожалуйста, выделите её и нажмите Ctrl+Enter
Правила приведение к наименьшему общему. Как привести к общему знаменателю? Правило приведения дробей к наименьшему общему знаменателю
Как привести алгебраические (рациональные) дроби к общему знаменателю?
1) Если в знаменателях дробей стоят многочлены, нужно попытаться одним из известных способов.
2) Наименьший общий знаменатель (НОЗ) состоит из всех множителей, взятых в наибольшей степени.
Наименьший общий знаменатель для чисел устно ищем как наименьшее число, которое делится на остальные числа.
3) Чтобы найти дополнительный множитель к каждой дроби, надо новый знаменатель разделить на старый.
4) Числитель и знаменатель первоначальной дроби умножаем на дополнительный множитель.
Рассмотрим примеры приведения алгебраических дробей к общему знаменателю.
Чтобы найти общий знаменатель для чисел, выбираем большее число и проверяем, делится ли оно на меньшее. 15 на 9 не делится. Умножаем 15 на 2 и проверяем, делится ли полученное число на 9. 30 на 9 не делится. Умножаем 15 на 3 и проверяем, делится ли полученное число на 9. 45 на 9 делится, значит, общий знаменатель для чисел равен 45.
Наименьший общий знаменатель состоит из всех множителей, взятых в наибольшей степени. Таким образом, общий знаменатель данных дробей равен 45 bc (буквы принято записывать в алфавитном порядке).
Чтобы найти дополнительный множитель к каждой дроби, надо новый знаменатель разделить на старый. 45bc:(15b)=3c, 45bc:(9c)=5b. Умножаем числитель и знаменатель каждой дроби на дополнительный множитель:
45bc:(15b)=3c, 45bc:(9c)=5b. Умножаем числитель и знаменатель каждой дроби на дополнительный множитель:
Сначала ищем общий знаменатель для чисел: 8 на 6 не делится, 8∙2=16 на 6 не делится, 8∙3=24 на 6 делится. Каждую из переменных нужно включить в общий знаменатель один раз. Из степеней берем степень с большим показателем.
Таким образом, общий знаменатель данных дробей равен 24a³bc.
Чтобы найти дополнительный множитель к каждой дроби, нужно новый знаменатель разделить на старый: 24a³bc:(6a³c)=4b, 24a³bc:(8a²bc)=3a.
Дополнительный множитель умножаем на числитель и знаменатель:
Многочлены, стоящие в знаменателях данных дробей, нужно . В знаменателе первой дроби — полный квадрат разности: x²-18x+81=(x-9)²; в знаменателе второй — разность квадратов: x²-81=(x-9)(x+9):
Общий знаменатель состоит из всех множителей, взятых в наибольшей степени, то есть равен (x-9)²(x+9). Находим дополнительные множители и умножаем их на числитель и знаменатель каждой дроби:
- Сложение и вычитание дробей с одинаковыми знаменателями
- Сложение и вычитание дробей с разными знаменателями
- Понятие о НОК
- Приведение дробей к одному знаменателю
- Как сложить целое число и дробь
1 Сложение и вычитание дробей с одинаковыми знаменателями
Чтобы сложить дроби с одинаковыми знаменателями, надо сложить их числители, а знаменатель оставить тот же, например:
Чтобы вычесть дроби с одинаковыми знаменателями, надо из числителя первой дроби вычесть числитель второй дроби, а знаменатель оставить тот же, например:
Чтобы сложить смешанные дроби, надо отдельно сложить их целые части, а затем сложить их дробные части, и записать результат смешанной дробью,
Пример 1:
Пример 2:
Если при сложении дробных частей получилась неправильная дробь, выделяем из нее целую часть и прибавляем ее к целой части, например:
2 Сложение и вычитание дробей с разными знаменателями.

Для того, чтобы сложить или вычесть дроби с разными знаменателями, нужно сначала привести их к одному знаменателю, а дальше действовать, как указано в начале этой статьи. Общий знаменатель нескольких дробей — это НОК (наименьшее общее кратное). Для числителя каждой из дробей находятся дополнительные множители с помощью деления НОК на знаменатель этой дроби. Мы рассмотрим пример позже, после того, как разберемся, что же такое НОК.
3 Наименьшее общее кратное (НОК)
Наименьшее общее кратное двух чисел (НОК) — это наименьшее натуральное число, которое делится на оба эти числа без остатка. Иногда НОК можно подобрать устно, но чаще, особенно при работе с большими числами, приходится находить НОК письменно, с помощью следующего алгоритма:
Для того, чтобы найти НОК нескольких чисел, нужно:
- Разложить эти числа на простые множители
- Взять самое большое разложение, и записать эти числа в виде произведения
- Выделить в других разложениях числа, которые не встречаются в самом большом разложении (или встречаются в нем меньшее число раз), и добавить их к произведению.

- Перемножить все числа в произведении, это и будет НОК.
Например, найдем НОК чисел 28 и 21:
4 Приведение дробей к одному знаменателю
Вернемся к сложению дробей с разными знаменателями.
Когда мы приводим дроби к одинаковому знаменателю, равному НОК обоих знаменателей, мы должны умножить числители этих дробей на дополнительные множители . Найти их можно, разделив НОК на знаменатель соответствующей дроби, например:
Таким образом, чтобы привести дроби к одному показателю, нужно сначала найти НОК (то есть наименьшее число, которое делится на оба знаменателя) знаменателей этих дробей, затем поставить дополнительные множители к числителям дробей. Найти их можно, разделив общий знаменатель (НОК) на знаменатель соответствующей дроби. Затем нужно умножить числитель каждой дроби на дополнительный множитель, а знаменателем поставить НОК.
5 Как сложить целое число и дробь
Для того, чтобы сложить целое число и дробь, нужно просто добавить это число перед дробью, при этом получится смешанная дробь, например:
Если мы складываем целое число и смешанную дробь, мы прибавляем это число к целой части дроби, например:
Тренажер 1
Сложение и вычитание дробей с одинаковыми знаменателями.

Лимит времени: 0
Навигация (только номера заданий)
0 из 20 заданий окончено
Информация
В этом тесте проверяется умение складывать дроби с одинаковыми знаменателями. При этом нужно соблюдать два правила:
- Если в результате получается неправильная дробь, нужно перевести ее в смешанное число.
- Если дробь можно сократить, обязательно сократите ее, иначе будет засчитан неправильный ответ.
Вы уже проходили тест ранее. Вы не можете запустить его снова.
Тест загружается…
Вы должны войти или зарегистрироваться для того, чтобы начать тест.
Вы должны закончить следующие тесты, чтобы начать этот:
Результаты
Правильных ответов: 0 из 20
Ваше время:
Время вышло
Вы набрали 0 из 0 баллов (0 )
- С ответом
- С отметкой о просмотре
Материал этой статьи объясняет, как найти наименьший общий знаменатель и как привести дроби к общему знаменателю . Сначала даны определения общего знаменателя дробей и наименьшего общего знаменателя, а также показано, как найти общий знаменатель дробей. Дальше приведено правило приведения дробей к общему знаменателю и рассмотрены примеры применения этого правила. В заключение разобраны примеры приведения трех и большего количества дробей к общему знаменателю.
Сначала даны определения общего знаменателя дробей и наименьшего общего знаменателя, а также показано, как найти общий знаменатель дробей. Дальше приведено правило приведения дробей к общему знаменателю и рассмотрены примеры применения этого правила. В заключение разобраны примеры приведения трех и большего количества дробей к общему знаменателю.
Навигация по странице.
Что называют приведением дробей к общему знаменателю?
Теперь мы можем сказать, что такое приведение дробей к общему знаменателю. Приведение дробей к общему знаменателю – это умножение числителей и знаменателей данных дробей на такие дополнительные множители, что в результате получаются дроби с одинаковыми знаменателями.
Общий знаменатель, определение, примеры
Теперь пришло время дать определение общего знаменателя дробей.
Иными словами, общим знаменателем некоторого набора обыкновенных дробей является любое натуральное число, которое делится на все знаменатели данных дробей.
Из озвученного определения следует, что данный набор дробей имеет бесконечно много общих знаменателей, так как существует бесконечное множество общих кратных всех знаменателей исходного набора дробей.
Определение общего знаменателя дробей позволяет находить общие знаменатели данных дробей. Пусть, к примеру, даны дроби 1/4 и 5/6 , их знаменатели равны 4 и 6 соответственно. Положительными общими кратными чисел 4 и 6 являются числа 12 , 24 , 36 , 48 , … Любое из этих чисел является общим знаменателем дробей 1/4 и 5/6 .
Для закрепления материала рассмотрим решение следующего примера.
Пример.
Можно ли дроби 2/3 , 23/6 и 7/12 привести к общему знаменателю 150 ?
Решение.
Для ответа на поставленный вопрос нам нужно выяснить, является ли число 150
общим кратным знаменателей 3
, 6
и 12
. Для этого проверим, делится ли 150
нацело на каждое из этих чисел (при необходимости смотрите правила и примеры деления натуральных чисел , а также правила и примеры деления натуральных чисел с остатком): 150:3=50
, 150:6=25
, 150:12=12 (ост. 6)
.
6)
.
Итак, 150 не делится нацело на 12 , следовательно, 150 не является общим кратным чисел 3 , 6 и 12 . Следовательно, число 150 не может быть общим знаменателем исходных дробей.
Ответ:
Нельзя.
Наименьший общий знаменатель, как его найти?
В множестве чисел, являющихся общими знаменателями данных дробей, существует наименьшее натуральное число , которое называют наименьшим общим знаменателем. Сформулируем определение наименьшего общего знаменателя данных дробей.
Определение.
Наименьший общий знаменатель – это наименьшее число, из всех общих знаменателей данных дробей.
Осталось разобраться с вопросом, как найти наименьший общий делитель.
Так как является наименьшим положительным общим делителем данного набора чисел, то НОК знаменателей данных дробей представляет собой наименьший общий знаменатель данных дробей.
Таким образом, нахождение наименьшего общего знаменателя дробей сводится к знаменателей этих дробей. Разберем решение примера.
Разберем решение примера.
Пример.
Найдите наименьший общий знаменатель дробей 3/10 и 277/28 .
Решение.
Знаменатели данных дробей равны 10 и 28 . Искомый наименьший общий знаменатель находится как НОК чисел 10 и 28 . В нашем случае легко : так как 10=2·5 , а 28=2·2·7 , то НОК(15, 28)=2·2·5·7=140 .
Ответ:
140 .
Как привести дроби к общему знаменателю? Правило, примеры, решения
Обычно обыкновенные дроби приводят к наименьшему общему знаменателю. Сейчас мы запишем правило, которое объясняет, как привести дроби к наименьшему общему знаменателю.
Правило приведения дробей к наименьшему общему знаменателю состоит из трех шагов:
- Во-первых, находится наименьший общий знаменатель дробей.
- Во-вторых, для каждой дроби вычисляется дополнительный множитель, для чего наименьший общий знаменатель делится на знаменатель каждой дроби.
- В-третьих, числитель и знаменатель каждой дроби умножается на ее дополнительный множитель.

Применим озвученное правило к решению следующего примера.
Пример.
Приведите дроби 5/14 и 7/18 к наименьшему общему знаменателю.
Решение.
Выполним все шаги алгоритма приведения дробей к наименьшему общему знаменателю.
Сначала находим наименьший общий знаменатель, который равен наименьшему общему кратному чисел 14 и 18 . Так как 14=2·7 и 18=2·3·3 , то НОК(14, 18)=2·3·3·7=126 .
Теперь вычисляем дополнительные множители, с помощью которых дроби 5/14 и 7/18 будут приведены к знаменателю 126 . Для дроби 5/14 дополнительный множитель равен 126:14=9 , а для дроби 7/18 дополнительный множитель равен 126:18=7 .
Осталось умножить числители и знаменатели дробей 5/14 и 7/18 на дополнительные множители 9 и 7 соответственно. Имеем и .
Итак, приведение дробей 5/14 и 7/18 к наименьшему общему знаменателю завершено. В итоге получились дроби 45/126 и 49/126 .
Схема приведения к общему знаменателю
- Нужно определить, какое будет наименьшее общее кратное для знаменателей дробей.
 Если Вы имеете дело со смешанным или целым числом, то его нужно сначала превратить в дробь, а уже потом определять наименьшее общее кратное. Чтобы целое число превратить в дробь, нужно в числителе записать само это число, а в знаменателе — единицу. Например, число 5 в виде дроби будет выглядеть так: 5/1. Чтобы смешанное число превратить в дробь, нужно целое число умножить на знаменатель и прибавить к нему числитель. Пример: 8 целых и 3/5 в виде дроби = 8×5+3/5 = 43/5.
Если Вы имеете дело со смешанным или целым числом, то его нужно сначала превратить в дробь, а уже потом определять наименьшее общее кратное. Чтобы целое число превратить в дробь, нужно в числителе записать само это число, а в знаменателе — единицу. Например, число 5 в виде дроби будет выглядеть так: 5/1. Чтобы смешанное число превратить в дробь, нужно целое число умножить на знаменатель и прибавить к нему числитель. Пример: 8 целых и 3/5 в виде дроби = 8×5+3/5 = 43/5. - После этого необходимо найти дополнительный множитель, который определяется делением НОЗ на знаменатель каждой дроби.
- Последний шаг — умножение дроби на дополнительный множитель.
Важно запомнить, что приведение к общему знаменателю нужно не только для сложения или вычитания. Для сравнения нескольких дробей с разными знаменателями также необходимо сначала привести каждую из них к общему знаменателю.
Приведение дробей к общему знаменателю
Для того чтобы понять, как привести к общему знаменателю дробь, необходимо разобраться в некоторых свойствах дробей. Так, важным свойством, используемым для приведения к НОЗ, является равенство дробей. Другими словами, если числитель и знаменатель дроби умножается на число, то в результате получает дробь, равная предыдущей. В качестве примера приведём следующий пример. Для того чтобы привести дроби 5/9 и 5/6 к наименьшему общему знаменателю, нужно выполнить следующие действия:
Так, важным свойством, используемым для приведения к НОЗ, является равенство дробей. Другими словами, если числитель и знаменатель дроби умножается на число, то в результате получает дробь, равная предыдущей. В качестве примера приведём следующий пример. Для того чтобы привести дроби 5/9 и 5/6 к наименьшему общему знаменателю, нужно выполнить следующие действия:
- Сначала находим наименьшее общее кратное знаменателей. В данном случае для чисел 9 и 6 НОК будет равно 18.
- Определяем дополнительные множители для каждой из дробей. Делается это следующим образом. Делим НОК на знаменатель каждой из дробей, в результате получаем 18: 9 = 2, а 18: 6 = 3. Эти числа и будут дополнительными множителями.
- Приводим две дроби к НОЗ. Умножая дробь на число, нужно умножить и числитель, и знаменатель. Дробь 5/9 можно умножить на дополнительный множитель 2, в результате чего получится дробь, равная данной, — 10/18. То же самое делаем со второй дробью: 5/6 умножаем на 3, в результате чего получаем 15/18.

Как видим из представленного выше примера, обе дроби были приведены к наименьшему общему знаменателю. Чтобы окончательно разобраться в том, как найти общий знаменатель, необходимо освоить еще одно свойство дробей. Оно заключается в том, что числитель и знаменатель дроби можно сократить на одно и то же число, которое называется общим делителем. Например, дробь 12/30 можно сократить до 2/5, если разделить ее на общий делитель — число 6.
Приведение дробей к общему знаменателю
Дроби И имеют одинаковые знаменатели. Говорят, что они имеют общий знаменатель 25. Дроби и имеют разные знаменатели, но их можно привести к общему знаменателю с помощью основного свойства дробей. Для этого найдем число, которое делится на 8 и на 3, например, 24. Приведем дроби к знаменателю 24, для этого умножим числитель и знаменатель дроби на дополнительный множитель 3. Дополнительный множитель обычно пишут слева над числителем:
Умножим числитель и знаменатель дроби на дополнительный множитель 8:
Приведем дроби и к общему знаменателю. Чаще всего дроби приводят к наименьшему общему знаменателю, который является наименьшим общим кратным знаменателей данных дробей. Так как НОК (8, 12) = 24, то дроби можно привести к знаменателю 24. Найдем дополнительные множители дробей: 24:8 = 3, 24:12 = 2. Тогда
Чаще всего дроби приводят к наименьшему общему знаменателю, который является наименьшим общим кратным знаменателей данных дробей. Так как НОК (8, 12) = 24, то дроби можно привести к знаменателю 24. Найдем дополнительные множители дробей: 24:8 = 3, 24:12 = 2. Тогда
К общему знаменателю можно приводить несколько дробей.
Пример. Приведем дроби к общему знаменателю. Так как 25 = 5 2 , 10 = 2 5, 6 = 2 3, то НОК (25, 10, 6) = 2 3 5 2 = 150.
Найдем дополнительные множители дробей и приведем их к знаменателю 150:
Сравнение дробей
На рис. 4.7 изображен отрезок АВ длины 1. Он разделен на 7 равных частей. Отрезок АС имеет длину , а отрезок AD имеет длину .
Длина отрезка AD больше длины отрезка AС т. е. дробь больше дроби
Из двух дробей с общим знаменателем больше та, у которой числитель больше, т. е.
Например, или
Чтобы сравнить любые две дроби, их приводят к общему знаменателю, а затем применяют правило сравнения дробей с общим знаменателем.
Пример. Сравнить дроби
Решение. НОК (8, 14) = 56. Тогда Так как 21 > 20, то
Если первая дробь меньше второй, а вторая меньше третьей, то первая меньше третьей.
Доказательство. Пусть даны три дроби. Приведем их к общему знаменателю. Пусть после этого они будут иметь вид Так как первая дробь меньше
второй, то r
Дробь называется правильной , если ее числитель меньше знаменателя.
Дробь называется неправильной , если ее числитель больше знаменателя или равен ему.
Например, дроби-правильные, а дроби -неправильные.
Правильная дробь меньше 1, а неправильная дробь больше или равна 1.
Читайте также…
- Научно-исследовательская работа на тему «Определение средней квадратичной скорости молекул воздуха» (10 класс)
- Учимся описывать картинку (ЕГЭ, ОГЭ)
- Практические рекомендации
- Говорение ЕГЭ: задание С6(44)
Как найти дополнительный знаменатель.
 Приведение дробей к новому знаменателю
Приведение дробей к новому знаменателюКак привести алгебраические (рациональные) дроби к общему знаменателю?
1) Если в знаменателях дробей стоят многочлены, нужно попытаться одним из известных способов.
2) Наименьший общий знаменатель (НОЗ) состоит из всех множителей, взятых в наибольшей степени.
Наименьший общий знаменатель для чисел устно ищем как наименьшее число, которое делится на остальные числа.
3) Чтобы найти дополнительный множитель к каждой дроби, надо новый знаменатель разделить на старый.
4) Числитель и знаменатель первоначальной дроби умножаем на дополнительный множитель.
Рассмотрим примеры приведения алгебраических дробей к общему знаменателю.
Чтобы найти общий знаменатель для чисел, выбираем большее число и проверяем, делится ли оно на меньшее. 15 на 9 не делится. Умножаем 15 на 2 и проверяем, делится ли полученное число на 9. 30 на 9 не делится. Умножаем 15 на 3 и проверяем, делится ли полученное число на 9. 45 на 9 делится, значит, общий знаменатель для чисел равен 45.
45 на 9 делится, значит, общий знаменатель для чисел равен 45.
Наименьший общий знаменатель состоит из всех множителей, взятых в наибольшей степени. Таким образом, общий знаменатель данных дробей равен 45 bc (буквы принято записывать в алфавитном порядке).
Чтобы найти дополнительный множитель к каждой дроби, надо новый знаменатель разделить на старый. 45bc:(15b)=3c, 45bc:(9c)=5b. Умножаем числитель и знаменатель каждой дроби на дополнительный множитель:
Сначала ищем общий знаменатель для чисел: 8 на 6 не делится, 8∙2=16 на 6 не делится, 8∙3=24 на 6 делится. Каждую из переменных нужно включить в общий знаменатель один раз. Из степеней берем степень с большим показателем.
Таким образом, общий знаменатель данных дробей равен 24a³bc.
Чтобы найти дополнительный множитель к каждой дроби, нужно новый знаменатель разделить на старый: 24a³bc:(6a³c)=4b, 24a³bc:(8a²bc)=3a.
Дополнительный множитель умножаем на числитель и знаменатель:
Многочлены, стоящие в знаменателях данных дробей, нужно . В знаменателе первой дроби — полный квадрат разности: x²-18x+81=(x-9)²; в знаменателе второй — разность квадратов: x²-81=(x-9)(x+9):
В знаменателе первой дроби — полный квадрат разности: x²-18x+81=(x-9)²; в знаменателе второй — разность квадратов: x²-81=(x-9)(x+9):
Общий знаменатель состоит из всех множителей, взятых в наибольшей степени, то есть равен (x-9)²(x+9). Находим дополнительные множители и умножаем их на числитель и знаменатель каждой дроби:
В данном материале мы разберем, как правильно приводить дроби к новому знаменателю, что такое дополнительный множитель и как его найти. После этого сформулируем основное правило приведения дробей к новым знаменателям и проиллюстрируем его примерами задач.
Понятие приведения дроби к другому знаменателю
Вспомним основное свойство дроби. Согласно ему, обыкновенная дробь a b (где a и b – любые числа) имеет бесконечное количество дробей, которые равны ей. Такие дроби можно получить, умножив числитель и знаменатель на одинаковое число m (натуральное). Иными словами, все обыкновенные дроби могут быть заменены другими вида a · m b · m . Это и есть приведение исходного значения к дроби с нужным знаменателем.
Это и есть приведение исходного значения к дроби с нужным знаменателем.
Привести дробь к другому знаменателю можно, умножив ее числитель и знаменатель на любое натуральное число. Главное условие – множитель должен быть одинаков для обоих частей дроби. В итоге получится дробь, равная исходной.
Проиллюстрируем это примером.
Пример 1
Привести дробь 11 25 к новому знаменателю.
Решение
Возьмем произвольное натуральное число 4 и умножим обе части исходной дроби на него. Считаем: 11 · 4 = 44 и 25 · 4 = 100 . В итоге получилась дробь 44 100 .
Все подсчеты можно записать в таком виде: 11 25 = 11 · 4 25 · 4 = 44 100
Выходит, любую дробь можно привести к огромному количеству разных знаменателей. Вместо четверки мы могли бы взять другое натуральное число и получить еще одну дробь, эквивалентную исходной.
Но не любое число может стать знаменателем новой дроби. Так, для a b в знаменателе могут стоять только числа b · m , кратные числу b . Вспомните основные понятия деления – кратные числа и делители. Если число не кратно b , но делителем новой дроби оно быть не может. Поясним нашу мысль примером решения задачи.
Вспомните основные понятия деления – кратные числа и делители. Если число не кратно b , но делителем новой дроби оно быть не может. Поясним нашу мысль примером решения задачи.
Пример 2
Вычислить, возможно ли приведение дроби 5 9 к знаменателям 54 и 21 .
Решение
54 кратно девятке, которая стоит в знаменателе новой дроби (т.е. 54 можно разделить на 9). Значит, такое приведение возможно. А 21 мы разделить на 9 не можем, поэтому такое действие для данной дроби выполнить нельзя.
Понятие дополнительного множителя
Сформулируем, что такое дополнительный множитель.
Определение 1
Дополнительный множитель представляет собой такое натуральное число, на которое умножают обе части дроби для приведения ее к новому знаменателю.
Т.е. когда мы выполняем это действие с дробью, мы берем для нее дополнительный множитель. Например, для приведения дроби 7 10 к виду 21 30 нам потребуется дополнительный множитель 3 . А получить дробь 15 40 из 3 8 можно с помощью множителя 5 .
Соответственно, если мы знаем знаменатель, к которому необходимо привести дробь, то мы можем вычислить для нее и дополнительный множитель. Разберем, как это сделать.
У нас есть дробь a b , которую можно привести к некоторому знаменателю c ; вычислим дополнительный множитель m . Нам надо произвести умножение знаменателя исходной дроби на m . У нас получится b · m , а по условию задачи b · m = c . Вспомним, как связаны между собой умножение и деление. Эта связь подскажет нам следующий вывод: дополнительный множитель есть не что иное, как частное от деления c на b , иначе говоря, m = c: b .
Таким образом, для нахождения дополнительного множителя нам нужно разделить требуемый знаменатель на исходный.
Пример 3
Найдите дополнительный множитель, с помощью которого дробь 17 4 была приведена к знаменателю 124 .
Решение
Используя правило выше, мы просто разделим 124 на знаменатель первоначальной дроби – четверку.
Считаем: 124: 4 = 31 .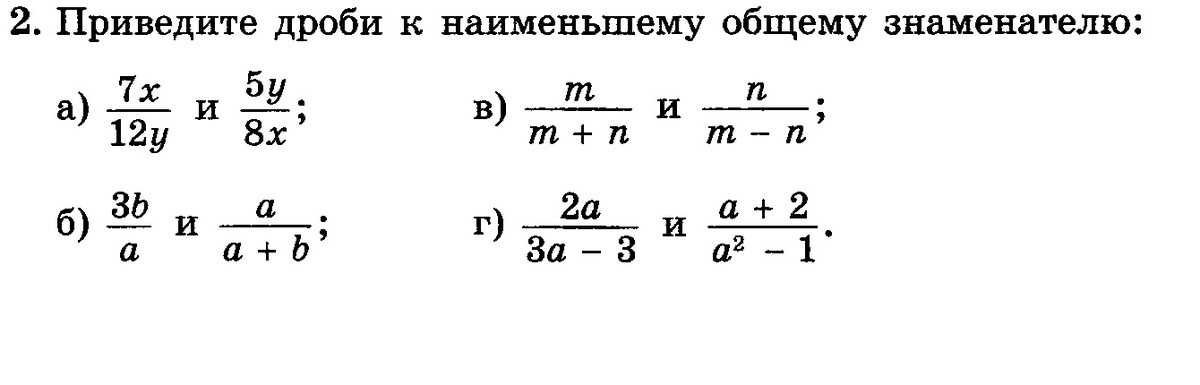
Выполнять расчеты такого типа часто требуется при приведении дробей к общему знаменателю.
Правило приведения дробей к указанному знаменателю
Перейдем к определению основного правила, с помощью которого можно привести дроби к указанному знаменателю. Итак,
Определение 2
Для приведения дроби к указанному знаменателю нужно:
- определить дополнительный множитель;
- умножить на него и числитель, и знаменатель исходной дроби.
Как применить это правило на практике? Приведем пример решения задачи.
Пример 4
Выполните приведение дроби 7 16 к знаменателю 336 .
Решение
Начнем с вычисления дополнительного множителя. Разделим: 336: 16 = 21 .
Полученный ответ умножаем на обе части исходной дроби: 7 16 = 7 · 21 16 · 21 = 147 336 . Так мы привели исходную дробь к нужному знаменателю 336 .
Ответ: 7 16 = 147 336 .
Если вы заметили ошибку в тексте, пожалуйста, выделите её и нажмите Ctrl+Enter
Схема приведения к общему знаменателю
- Нужно определить, какое будет наименьшее общее кратное для знаменателей дробей.
 Если Вы имеете дело со смешанным или целым числом, то его нужно сначала превратить в дробь, а уже потом определять наименьшее общее кратное. Чтобы целое число превратить в дробь, нужно в числителе записать само это число, а в знаменателе — единицу. Например, число 5 в виде дроби будет выглядеть так: 5/1. Чтобы смешанное число превратить в дробь, нужно целое число умножить на знаменатель и прибавить к нему числитель. Пример: 8 целых и 3/5 в виде дроби = 8×5+3/5 = 43/5.
Если Вы имеете дело со смешанным или целым числом, то его нужно сначала превратить в дробь, а уже потом определять наименьшее общее кратное. Чтобы целое число превратить в дробь, нужно в числителе записать само это число, а в знаменателе — единицу. Например, число 5 в виде дроби будет выглядеть так: 5/1. Чтобы смешанное число превратить в дробь, нужно целое число умножить на знаменатель и прибавить к нему числитель. Пример: 8 целых и 3/5 в виде дроби = 8×5+3/5 = 43/5. - После этого необходимо найти дополнительный множитель, который определяется делением НОЗ на знаменатель каждой дроби.
- Последний шаг — умножение дроби на дополнительный множитель.
Важно запомнить, что приведение к общему знаменателю нужно не только для сложения или вычитания. Для сравнения нескольких дробей с разными знаменателями также необходимо сначала привести каждую из них к общему знаменателю.
Приведение дробей к общему знаменателю
Для того чтобы понять, как привести к общему знаменателю дробь, необходимо разобраться в некоторых свойствах дробей. Так, важным свойством, используемым для приведения к НОЗ, является равенство дробей. Другими словами, если числитель и знаменатель дроби умножается на число, то в результате получает дробь, равная предыдущей. В качестве примера приведём следующий пример. Для того чтобы привести дроби 5/9 и 5/6 к наименьшему общему знаменателю, нужно выполнить следующие действия:
Так, важным свойством, используемым для приведения к НОЗ, является равенство дробей. Другими словами, если числитель и знаменатель дроби умножается на число, то в результате получает дробь, равная предыдущей. В качестве примера приведём следующий пример. Для того чтобы привести дроби 5/9 и 5/6 к наименьшему общему знаменателю, нужно выполнить следующие действия:
- Сначала находим наименьшее общее кратное знаменателей. В данном случае для чисел 9 и 6 НОК будет равно 18.
- Определяем дополнительные множители для каждой из дробей. Делается это следующим образом. Делим НОК на знаменатель каждой из дробей, в результате получаем 18: 9 = 2, а 18: 6 = 3. Эти числа и будут дополнительными множителями.
- Приводим две дроби к НОЗ. Умножая дробь на число, нужно умножить и числитель, и знаменатель. Дробь 5/9 можно умножить на дополнительный множитель 2, в результате чего получится дробь, равная данной, — 10/18. То же самое делаем со второй дробью: 5/6 умножаем на 3, в результате чего получаем 15/18.

Как видим из представленного выше примера, обе дроби были приведены к наименьшему общему знаменателю. Чтобы окончательно разобраться в том, как найти общий знаменатель, необходимо освоить еще одно свойство дробей. Оно заключается в том, что числитель и знаменатель дроби можно сократить на одно и то же число, которое называется общим делителем. Например, дробь 12/30 можно сократить до 2/5, если разделить ее на общий делитель — число 6.
Чтобы понять, как складывать дроби с разными знаменателями, сначала изучим правило, а затем рассмотрим конкретные примеры.
Чтобы сложить или вычесть дроби с разными знаменателями, надо:
1) Найти(НОЗ) данных дробей.
2) Найти дополнительный множитель к каждой дроби. Для этого новый знаменатель нужно разделить на старый.
3) Умножить числитель и знаменатель каждой дроби на дополнительный множитель и сложить или вычесть дроби с одинаковыми знаменателями.
4) Проверить, является ли полученная в результате дробь правильной и несократимой.
В следующих примерах надо сложить или вычесть дроби с разными знаменателями:
1) Чтобы вычесть дроби с разными знаменателями, сначала ищем наименьший общий знаменатель данных дробей. Выбираем большее из чисел и проверяем, делится ли оно на меньшее. 25 на 20 не делится. Умножаем 25 на 2. 50 на 20 не делится. Умножаем 25 на 3. 75 на 20 не делится. Умножаем 25 на 4. 100 на 20 делится. Значит, наименьший общий знаменатель равен 100.
2) Чтобы найти дополнительный множитель к каждой дроби, надо новый знаменатель разделить на старый. 100:25=4, 100:20=5. Соответственно, к первой дроби дополнительный множитель 4, ко второй — 5.
3) Умножаем числитель и знаменатель каждой дроби на дополнительный множитель и вычитаем дроби по правилу вычитания дробей с одинаковыми знаменателями.
4) Полученная дробь — правильная и несократимая. Значит, это — ответ.
1) Чтобы сложить дроби с разными знаменателями, сначала ищем наименьший общий знаменатель. 16 на 12 не делится. 16∙2=32 на 12 не делится. 16∙3=48 на 12 делится. Значит, 48 — НОЗ.
16∙2=32 на 12 не делится. 16∙3=48 на 12 делится. Значит, 48 — НОЗ.
2) 48:16=3, 48:12=4. Это — дополнительные множители к каждой дроби.
3) умножаем числитель и знаменатель каждой дроби на дополнительный множитель и складываем новые дроби.
4)Полученная в результате дробь — правильная и несократимая.
1) 30 на 20 не делится. 30∙2=60 на 20 делится. Значит, 60 — наименьший общий знаменатель этих дробей.
2) чтобы найти дополнительный множитель к каждой дроби, надо новый знаменатель поделить на старый: 60:20=3, 60:30=2.
3) умножаем числитель и знаменатель каждой дроби на дополнительный множитель и вычитаем новые дроби.
4) полученную дробьна 5.
1) 8 на 6 не делится. 8∙2=16 на 6 не делится. 8∙3=24 делится и на 4, и на 6. Значит, 24 — это и есть НОЗ.
2) чтобы найти дополнительный множитель к каждой дроби, нужно новый знаменатель разделить на старый. 24:8=3, 24:4=6, 24:6=4. Значит, 3, 6 и 4 — дополнительные множители к первой, второй и третьей дроби.
3) умножаем числитель и знаменатель каждой долби на дополнительный множитель. Складываем и вычитаем. Полученная дробь — неправильная, поэтому необходимо выделить целую часть.
LCM 10, 15 и 18
Калькуляторы Учебные материалы по математике
- Главная страница
- Математические функции
- Калькулятор LCM
- LCM 10, 15 и 18
LCM 10, 15 и 18 равно 90. Комплексная работа дает представление о том, как найти больше это lcm 10, 15 и 18 с использованием простых множителей и специальных методов деления, а также пример использования математики и реальных задач.
что такое lcm 10, 15 и 18?
lcm (10 15 18) = (?)
10 => 2 x 5
15 => 3 x 5
18 => 2 x 3 x 3
= 2 x 3 x 5 x 3
= 90
lcm (10, 15 и 18) = 90
90 — lcm числа 10, 15 и 18.
, где
10 — целое положительное число,
15 — целое положительное число,
90 — lcm числа 10. , 15 и 18,
, 15 и 18,
{2, 3, 5} в {2 x 5, 3 x 5, 2 x 3 x 3} — наиболее повторяющиеся множители 10, 15 и 18,
{3} в {2 x 5 , 3 x 5, 2 x 3 x 3} — другие оставшиеся множители 10, 15 и 18.
Использование в математике: НОК 10, 15 и 18
Ниже приведены некоторые математические приложения, в которых можно использовать МОК 10, 15 и 18:
- найти наименьшее число, которое точно делится на 10, 15 и 18.
- , чтобы найти общие знаменатели для дробей, имеющих 10, 15 и 18 в качестве знаменателей при сложении или вычитании разнородных дробей.
Использование в реальных задачах: 10, 15 и 18 lcm
В контексте задач реального мира lcm, lcm 10, 15 и 18 помогает найти точное время, когда три одинаковых и повторяющихся с разным графиком времени происходят вместе в одно и то же время. Например, задачи реального мира включают lcm в ситуациях, когда нужно определить, в какое время все колокола A, B и C звонят вместе, если колокол A звонит через 10 секунд, B звонит через 15 секунд и C многократно звонит через 18 секунд. Ответ заключается в том, что все колокола A, B и C звонят вместе через 90 секунд в первый раз, через 180 секунд во второй раз, через 270 секунд в третий раз и так далее.
Ответ заключается в том, что все колокола A, B и C звонят вместе через 90 секунд в первый раз, через 180 секунд во второй раз, через 270 секунд в третий раз и так далее.
Важные примечания: 10, 15 и 18 lcm
Ниже приведены важные примечания, которые следует помнить при решении lcm из 10, 15 и 18:
- Повторяющиеся и неповторяющиеся простые множители 10, 15 и 18 следует умножить, чтобы найти наименьшее общее кратное 10, 15 и 18 при решении lcm методом простых множителей.
- Результаты lcm 10, 15 и 18 идентичны, даже если мы изменим порядок заданных чисел в вычислении lcm, это означает, что порядок заданных чисел в вычислении lcm не повлияет на результаты.
Для значений, отличных от 10, 15 и 18, используйте этот инструмент ниже:
В приведенном ниже решенном примере с пошаговой работой показано, как найти lcm числа 10, 15 и 18, используя либо метод простых множителей, либо метод специального деления. .
.
Пример решения с использованием метода простых множителей:
Что такое НОК 10, 15 и 18?
шаг 1
Обратитесь к входным параметрам, значениям и посмотрите, что будет найдено:
Входные параметры и значения:
A = 10
B = 15
C = 18
Что нужно найти:
найти lcm числа 10, 15 и 18
шаг 5 и 10 числа 1: 1, 10
Простые множители 10 = 2 x 5
Простые множители 15 = 3 x 5
Простые множители 18 = 2 x 3 x 3
шаг 3 Определите повторяющиеся и неповторяющиеся простые множители 10, 15 и 18:
{2, 3, 5} — наиболее повторяющиеся факторы, а {3} — неповторяющиеся факторы 10, 15 и 18.
шаг 4 Найдите произведение повторяющихся и неповторяющихся простых множителей 10, 15 и 18:
= 2 x 3 x 5 x 3
= 90
lcm(20 и 30) = 90
Следовательно,
lcm 10, 15 и 18 равно 90
Пример решения с использованием специального метода деления:
Этот специальный метод деления является самым простым способом понять весь расчет того, что такое lcm для 10, 15 и 18.
шаг 1 Обратитесь к входным параметрам, значениям и посмотрите, что нужно найти:
Входные параметры и значения:
Целые числа: 10, 15 и 18
Что нужно найти:
lcm (10, 15, 18) = ?
шаг 2 Расположите заданные целые числа по горизонтали, разделяя их пробелами или запятыми:
10, 15 и 18
шаг 3 Выберите делитель, который делит каждое или большинство заданных целых чисел (10, 15 и 18), разделите каждое целое число отдельно и запишите частное в следующей строке прямо под соответствующими целыми числами. Перенесите целое число на следующую строку, если какое-либо целое число из 10, 15 и 18 не делится на выбранный делитель; повторяйте тот же процесс, пока все целые числа не будут равны 1, как показано ниже:
| 2 | 10 | 15 | 18 |
| 3 | 5 | 15 | 9 |
| 3 | 5 | 5 | 3 |
| 5 | 5 | 5 | 1 |
| 1 | 1 | 1 |
Шаг 4. = 90
= 90
НОК(10, 15, 18) = 90
Наименьшее общее кратное для трех чисел 10, 15 и 18 равно 90
Как найти наименьшее общее кратное
Все ресурсы SAT Math Resources
16 Диагностические тесты 660 практических тестов Вопрос дня Карточки Learn by Concept
← Предыдущая 1 2 Следующая →
SAT Math Help » Арифметика » Целые числа » Факторы / мультипликаторы » Наименьший общий множитель » Как найти наименьшее общее кратное
Сколько натуральных чисел меньше десяти тысяч, кратных как восьми, так и восемнадцати?
Возможные ответы:
138
70
555
72
139
Правильный ответ:
138
. Объяснение:
Чтобы найти все числа, кратные как 8, так и 18, нам нужно найти наименьшее общее кратное (НОК) 8 и 18. Самый простой способ сделать это — перечислить кратные из 8 и 18 и определить наименьший из них, общий для обоих.
Самый простой способ сделать это — перечислить кратные из 8 и 18 и определить наименьший из них, общий для обоих.
Сначала перечислим первые несколько чисел, кратных восьми:
8, 16, 24, 32, 40, 48, 56, 64, 72, 80, 88 . . .
Далее мы перечисляем несколько первых чисел, кратных восемнадцати:
18, 36, 54, 72, 90, 108, 126, 144 . . .
Сравнивая числа, кратные восьми и восемнадцати, мы видим, что наименьшее из них равно 72. Таким образом, НОК 8 и 18 равен 72.
Поскольку НОК равен 72, это означает, что каждое кратное 72 также кратно как 8, так и 18. Таким образом, чтобы найти все числа, кратные 8 и 18, кратные 8 и 18, нам просто нужно найти, сколько кратных 72 меньше 10000, и сделать это, все, что нам нужно сделать, это разделить 10000 на 72.
Когда мы делим 10000 на 72, мы получаем 138 с остатком 64; следовательно, 72 превратится в десять тысяч 138 раз, прежде чем превысит десять тысяч. Другими словами, существует 138 чисел, меньших 10000, которые кратны 72 и, соответственно, кратны как 8, так и 18.
Ответ: 138.
Сообщить об ошибке ?
Возможные ответы:
Правильный ответ:
Объяснение:
– это разные числа. У нас есть составное число и простое число соответственно. У них общий коэффициент . Поэтому мы просто умножаем оба числа, чтобы получить ответ .
Сообщить об ошибке
Чему равно наименьшее общее кратное ?
Возможные ответы:
Правильный ответ:
Объяснение:
Наименьшее общее кратное — это наименьшее число, которое делится на два или более множителя. Поскольку это простые числа, и их нельзя разбить на более мелкие множители, мы просто умножаем их, чтобы получить как наш ответ.
Сообщить об ошибке
Чему равно наименьшее общее кратное ?
Возможные ответы:
Правильный ответ:
Объяснение:
Мы склонны умножать числа, однако, если мы разделим оба числа на , мы получим остаток. Эти числа являются единичными и простыми числами соответственно и имеют общий коэффициент . Чтобы определить наименьшее общее кратное, мы умножаем множитель на оставшиеся числа. Наш ответ: просто или .
Эти числа являются единичными и простыми числами соответственно и имеют общий коэффициент . Чтобы определить наименьшее общее кратное, мы умножаем множитель на оставшиеся числа. Наш ответ: просто или .
Сообщить об ошибке
Чему равно наименьшее общее кратное ?
Возможные ответы:
Правильный ответ:
Объяснение:
Оба числа четные, поэтому мы можем разделить оба числа на , чтобы получить . У нас есть простое число и составное число соответственно. У них общий коэффициент . Чтобы определить наименьшее общее кратное, мы умножаем множитель на оставшиеся числа. Наш ответ: просто или .
Сообщить об ошибке
Чему равно наименьшее общее кратное ?
Возможные ответы:
Правильный ответ:
Объяснение:
Оба числа делятся на , поэтому остальные числа делятся . У нас есть простое число и составное число соответственно. У них общий коэффициент . Чтобы определить наименьшее общее кратное, мы умножаем множитель на оставшиеся числа. Наш ответ: просто или .
У нас есть простое число и составное число соответственно. У них общий коэффициент . Чтобы определить наименьшее общее кратное, мы умножаем множитель на оставшиеся числа. Наш ответ: просто или .
Сообщить об ошибке
Чему равно наименьшее общее кратное ?
Возможные ответы:
Правильный ответ:
Объяснение:
Если мы разделим на оба числа, мы получим . Делаем второй раз и получаем. Теперь у нас есть единица и простое число. Поэтому мы просто перемножаем множители и оставшиеся числа, чтобы получить или .
Сообщить об ошибке
Чему равно наименьшее общее кратное ?
Возможные ответы:
Правильный ответ:
Объяснение:
Оба числа делятся на , потому что сумма цифр делится на . Получаем как остальные числа. Мы можем разделить на , чтобы получить . У нас есть два простых числа. Теперь мы перемножаем множители и оставшиеся числа, чтобы получить или .
Получаем как остальные числа. Мы можем разделить на , чтобы получить . У нас есть два простых числа. Теперь мы перемножаем множители и оставшиеся числа, чтобы получить или .
Сообщить об ошибке
Чему равно наименьшее общее кратное ?
Возможные ответы:
Правильный ответ:
Объяснение:
Оба числа четные, поэтому мы можем разделить оба числа на , чтобы получить . У нас есть простое число и составное число соответственно. У них общий коэффициент . Чтобы определить наименьшее общее кратное, мы умножаем множитель на оставшиеся числа. Наш ответ: просто или .
Сообщить об ошибке
Чему равно наименьшее общее кратное ?
Возможные ответы:
Правильный ответ:
Объяснение:
Нам нужно убедиться, что все числа имеют общий делитель . даже так давайте разделим их на . Мы получаем остатки вместе с тем, что не делится поровну с . Теперь, когда все эти числа имеют общий делитель , мы умножаем их все, включая то, что мы разделили. Получаем или .
даже так давайте разделим их на . Мы получаем остатки вместе с тем, что не делится поровну с . Теперь, когда все эти числа имеют общий делитель , мы умножаем их все, включая то, что мы разделили. Получаем или .
Сообщить об ошибке
← Предыдущая 1 2 Следующая →
Уведомление об авторских правах 93-8
Наименьшие общие кратные
Обновлено 11 февраля 2017 г. | Infoplease Staff
| Infoplease Staff
Обыкновенные кратные — это кратные, которые имеют два общих числа. Это может быть полезно при работе с дробями и отношениями.
Пример:
Какие общие числа кратны 2 и 3?
Кратность 2: 2, 4, 6 , 8, 10, 12 , 14, 16, 18 , 20, 22, 24 …
Кратные 3: 3, 6 , 9, 12 , 15, 18 , 21, 24 , 27…
Общие кратные 2 и 3 включают 9,1342, 6 18, и 24 .
Пример:
Какие общие кратны числам 25 и 30?
Кратность 25: 25, 50, 75, 100, 125, 150 , 175, 200, 225, 250, 275, 300 , 325…
Кратность 30: 30, 61, 0, 90, 90, 90,
150 , 180, 210, 240, 270, 300 , 330…
Общие кратные 25 и 30 включают 150 и 300 .
Наименьшее общее кратное или наименьшее общее кратное — это наименьшее кратное двух общих чисел.
Есть два способа найти наименьшее общее кратное двух чисел.
Метод 1: перечисление кратных
Первый способ найти наименьшее общее кратное состоит в том, чтобы сделать то, что мы сделали выше: написать список наименьших кратных каждого числа и найти наименьшее кратное, общее для обоих чисел.
Пример:
Каково наименьшее общее кратное 2 и 3?
Кратные 2: 2, 4, 6 , 8…
Кратные 3: 3, 6 , 9…
Наименьшее общее кратное 2 и 3 равно 6 .
Пример:
Каково наименьшее общее кратное чисел 25 и 30?
Кратность 25: 25, 50, 75, 100, 125, 150 , 175…
Кратность 30: 30, 60, 90, 120, 150 , 180…
Наименьшее общее кратное чисел 25 и 30 равно 150 .
Метод 2: множители
Другой способ найти наименьшее общее кратное — перечислить простые множители для каждого числа. Удалите простые делители, которые являются общими для обоих чисел. Умножьте одно из чисел на оставшиеся простые множители другого числа. Результатом будет наименьшее общее кратное.
Результатом будет наименьшее общее кратное.
Пример:
Каково наименьшее общее кратное чисел 25 и 30?
Простые делители числа 25 равны 9.1342 5 x 5.
Простые множители числа 30 равны 2 x 3 x 5 .
Удалите 5 , которые являются общими для 25 и 30 в качестве простого множителя.
Умножьте 25 на оставшиеся простые делители 30.
25 x 2 x 3 = 150.
Наименьшее общее кратное 25 и 30 равно 150 .
Вы получите одинаковые результаты независимо от того, с каким числом вы работаете:
Пример:
Какое наименьшее общее кратное чисел 25 и 30?
Простые делители числа 25 равны 9.1342 5 x 5.
Простые множители числа 30 равны 2 x 3 x 5 .
Удалите 5 , которые являются общими для 25 и 30 в качестве простого множителя.
Умножьте 30 на оставшиеся простые делители 25.
30 x 5 = 150.
Наименьшее общее кратное 25 и 30 равно 150 .
Другой пример
Пример:
Какое наименьшее общее кратное 42 и 48?
Простые делители числа 42 равны 2 x 3 x 7,
Простые множители числа 48 равны 2 х 2 х 2 х 2 х 3 .
Удалите 2 x 3 , которые являются общими для 42 и 48 в качестве простых множителей.
Умножьте 48 на оставшиеся простые делители 42.
48 x 7 = 336.
Наименьшее общее кратное 42 и 48 равно 336 .
Что, если они не имеют общих простых делителей?
Пример:
Каково наименьшее общее кратное чисел 44 и 45?
Простые делители числа 44 равны 2 x 2 x 11,9.0019 Простые делители числа 45 равны 3 x 3 x 5.
44 и 45 не имеют общих простых делителей. 1980 11 = 1980.
Или:
44 x 45 = 1980.
Наименьшее общее кратное 44 и 45 равно 1980 .
Как показывает последний пример, если два числа не имеют общих простых делителей, наименьшее общее кратное будет равно произведению этих двух чисел.
Рассматривать простые числа как простые делители
Если одно число является простым, вы можете рассматривать его как собственный простой делитель.
Пример:
Каково наименьшее общее кратное 7 и 30?
7 — простое число.
Простые делители числа 30 равны 2 x 3 x 5.
7 и 30 не имеют общих простых делителей.
7 x 30 = 210.
Наименьшее общее кратное 7 и 30 равно 210 .
Пример:
Каково наименьшее общее кратное 2 и 3?
2 — простое число.
3 — простое число.
2 и 3 не имеют общих простых множителей.
2 x 3 = 6.
Наименьшее общее кратное 2 и 3 равно 6 .
Пример:
Каково наименьшее общее кратное 3 и 30?
3 — простое число.
Простые делители числа 30 равны 2 x 3 x 5.
Удалите 3 , которые являются общими для 3 и 30, в качестве простого делителя.
Либо:
Умножьте 3 на оставшиеся простые множители 30.
3 x 2 x 5 = 30
Или:
Обычно вы умножаете 30 на оставшиеся простые делители 3, но — это оставшихся простых делителей.
Наименьшее общее кратное равно 30.
Простые результаты
Как видно из приведенного выше, есть два сценария, если хотя бы одно число простое:
- Если одно число простое, а простые множители другого числа включают этого простого числа наименьшее общее кратное будет равно не простому числу.
- Если одно число простое, а простые делители другого числа не включают это простое число, наименьшее общее кратное будет равно произведению двух чисел.
(Второй сценарий также включает в себя случаи, когда оба числа являются основными.)
| Общие факторы | Факторы и фракции | Смешанные числа и неподходящие фракции |
 Неправильные дроби
Неправильные дроби.com/ipa/0/9/3/3/3/5/A0933352.html
Источники +
Наши общие источники
- Сокращение дробей до наименьших членов
LCM Наименьшее общее кратное или наименьшее общее кратное
Образование, Общее
22 октября 2016 г. | Местоположение Литтлтон
Многим пяти- и шестиклассникам (и их родителям!) трудно понять концепцию наименьшего общего кратного, часто называемого для краткости НОК. Если вы один из них, не волнуйтесь, мы здесь, чтобы помочь.
Понять значение слов
Наименьшее или наименьшее общее кратное означает все общие кратные, число, которое является наименьшим. Давайте начнем с рассмотрения одного слова и понятия за раз.
Число , умноженное на , является произведением умножения. К кратным 9 относятся: 9, 18, 27, 36 и так далее. Наименьшее кратное — это просто наименьшее кратное любого числа. Таким образом, наименьшее кратное любого числа равно этому числу, умноженному на 1. 1 x 9.= 9, поэтому 9 является наименьшим кратным 9. Становится интереснее, когда вы говорите общее кратное . Слово «общий» означает то же самое. Если у вас есть набор чисел, каждое число в наборе будет иметь разные кратные. В качестве примера возьмем набор чисел (3, 9 и 10).
1 x 9.= 9, поэтому 9 является наименьшим кратным 9. Становится интереснее, когда вы говорите общее кратное . Слово «общий» означает то же самое. Если у вас есть набор чисел, каждое число в наборе будет иметь разные кратные. В качестве примера возьмем набор чисел (3, 9 и 10).
Мультипликации 3 : 3, 6, , 12, 15, 18, 21, 24, 27 , 30 , 33, 36 , 39, 42, 45 , 48, 48 , 51, 54 , 57, 60 … 90 , 93 и так далее.
Мультипликации 9: , 18 , 27 , 36 , 45 , 54 , 63, 72, 81, 90 , 9944, 63, 72, 81, 90 , и так.
Кратность 10: 10, 20, 30, 40, 50, 60 , 70, 80, 90 , 100, 110, 120 и так далее.
Общие кратные 3 и 9 — это числа, которые входят в оба набора кратных, включая 9 , 18 , 27 , 36 , 45 , 54 и так далее.
Любое кратное 9 также кратно 3.
Общее кратное чисел 9 и 10 равно 90 (а также 900 и 9000).
Общие кратные набора (3 и 10) равны 30 , 60 , 90 , 120 и так далее. Только 30 является LCM, потому что это наименьшее возможное общее кратное .
Общие кратные от 3, 9 и 10 — это 90 , 900, 9000 и т. д., а из этих 90 — НОК, потому что это наименьшее возможное общее кратное для всех трех чисел в нашем наборе.
Поиск LCM
Следовательно, наименьшее общее кратное или НОК набора (3, 9 и 10) равно 90, потому что это наименьшее число, на которое без остатка делится каждое число в наборе.
Чтобы определить НОК, вы можете найти все кратные всех чисел в наборе (как мы сделали выше), а затем просто посмотреть, какое число является наименьшим общим кратным. Это очень хорошо работает с небольшими числами и небольшими наборами, такими как 3 и 5 9.0019
Кратность 3: 3, 6, 9, 15, 18
Кратные 5: 5, 10, 15, 20.
Уже через несколько секунд становится очевидным, что 15 является наименьшим общим кратным 3 и 5.
Нет ли лучшего метода?
Перечислять все кратные не всегда разумно, чтобы найти LCM. Это может стать слишком трудоемким и трудоемким. Есть несколько других методов. В этих методах используется «первичная факторизация». Эти стратегии отлично подходят для детей, которые имеют четкое представление о LCM и о том, почему стратегии простой факторизации работают. Но слишком быстрый переход к ярлыку может нанести ущерб пониманию.
Если вам (или вашему ребенку) нужна помощь в понимании простой факторизации или LCM, пригласите их в Mathnasium of Littleton на бесплатное пробное занятие. Для бесплатных пробных занятий необходима предварительная запись, поэтому, пожалуйста, позвоните заранее, чтобы убедиться, что мы готовы принять вас! 303-979-9077
Для бесплатных пробных занятий необходима предварительная запись, поэтому, пожалуйста, позвоните заранее, чтобы убедиться, что мы готовы принять вас! 303-979-9077
Эта статья была написана и принадлежит Cuttlefish Copywriting, www.cuttlefishcopywriting.com. Он защищен авторским правом. Mathnasium of Littleton имеет разрешение на его использование. В других местах Mathnasium следует связаться с Хизер по адресу [email protected], прежде чем использовать его.
Похожие статьи
Ваш ребенок борется с математикой; Вот что вы можете с этим поделать
29 апреля 2022 г. | Местоположение Литтлтон
У вашего ребенка проблемы с математикой? Один отец сказал: «Я ненавидел разочарование и чувство неполноценности моего сына, когда дело касалось математики». Это мнение разделяют многие родители. Как ваш ребенок успевает по математике? Существуют ли математические понятия, которые видят..
Это мнение разделяют многие родители. Как ваш ребенок успевает по математике? Существуют ли математические понятия, которые видят..
Почему математика проще для одних детей и сложнее для других?
26 апреля 2022 г. | Местоположение Littleton
Вы когда-нибудь замечали, что математика дается одним ученикам легко, в то время как другим ученикам приходится прилагать гораздо больше усилий, чтобы понять ее? Почему это? Чтобы найти ответ, мы должны обратиться к источнику… к гиппокампу. Гиппокамп представляет собой сложную структуру головного мозга, включающую
Чем больше, тем веселее: братья и сестры в Матназиуме
26 апреля 2022 г. | Местонахождение Littleton
| Местонахождение Littleton
Вызов всех занятых родителей!! Мы знаем, что вы водите детей на тренировки; посещение игр, конкурсов и представлений. Мы знаем, что вы планируете внеклассные мероприятия, игры, дни рождения и каникулы. И мы знаем, как Вам помочь! Ма..
10 лучших кулинарных книг осени 2022 года
Если вы покупаете что-то по ссылке Eater, Vox Media может получить комиссию. См. нашу политику этики.
Опять пришла осень, и нет, мы тоже не знаем, как это произошло. Что мы действительно знаем, так это то, что наряду с более низкими температурами (мы предполагаем? Но кто может сказать больше?) и промежуточными выборами, сезон предвещает новый и очень долгожданный урожай поваренных книг. Поскольку поваренные книги делают это надежно, эти последние дополнения к канону дают стимул обратиться внутрь себя и увидеть (или съесть) больше мира, попробовать что-то новое, ища утешения в историях со счастливым концом. Потому что рецепты, по крайней мере хорошие, именно таковы.
В поваренных книгах этой осени можно найти много счастливых концовок. На самом деле так много, что было чрезвычайно сложно выбрать всего 10 названий для освещения. Приведенный ниже список включает в себя множество кухонь и подходов к приготовлению пищи, но их общий знаменатель заключается в том, что все они заставляют нас хотеть бросить все, что мы делаем, и начать готовить. Есть книги, предназначенные для тех из нас, у кого мало времени, но много аппетита, и книги, которые позволяют глубоко погрузиться в кулинарию Пуэрто-Рико, Шри-Ланки и Великобритании. Есть книги, которые показывают нам изысканные слои, содержащиеся в веганской китайской и тайваньской американской кухне, а для пекарей есть долгожданный хлеб и долгожданная вторая книга от легендарного кондитера.
Зима близко, это правда, но когда она придет, эти книги будут вносить свой вклад в то, чтобы наши желудки и дух были сытыми.
Веганская китайская кухня
Ханна Че
Кларксон Поттер, 13 сентября
Своей первой кулинарной книгой Ханна Че, веганский шеф-повар, фотограф и блогер, внесла неоценимый вклад в канон веганской и вегетарианской домашней кухни. Как отмечает Че, растительная кухня — это традиция, которая существует в Китае более 2000 лет, и ее книга — ее главы, организованные по типам растений, — дает яркое представление о ее широте и сложности. Че вплетается в свою собственную историю как ребенка иммигрантов, которые изначально не понимали ее приверженности веганству, наряду с ее желанием воссоздать блюда своего детства. «Кажется, что мои китайско-американские друзья и я начали осознавать наследие домашней кухни наших родителей», — пишет она. С такими рецептами, как тушеная зимняя дыня, баклажаны с ароматом рыбы, вегетарианская курица с пятью специями, грибы кунг-пао и хор паровых булочек, Че предлагает блюда, которые уважительно кивают прошлому и указывают на ослепительное будущее.
Как отмечает Че, растительная кухня — это традиция, которая существует в Китае более 2000 лет, и ее книга — ее главы, организованные по типам растений, — дает яркое представление о ее широте и сложности. Че вплетается в свою собственную историю как ребенка иммигрантов, которые изначально не понимали ее приверженности веганству, наряду с ее желанием воссоздать блюда своего детства. «Кажется, что мои китайско-американские друзья и я начали осознавать наследие домашней кухни наших родителей», — пишет она. С такими рецептами, как тушеная зимняя дыня, баклажаны с ароматом рыбы, вегетарианская курица с пятью специями, грибы кунг-пао и хор паровых булочек, Че предлагает блюда, которые уважительно кивают прошлому и указывают на ослепительное будущее.
Дом там, где яйца
Молли Йе
Поваренные книги Уильяма Морроу, 27 сентября
Привлекательная вторая кулинарная книга звезды сериала «Девушка знакомится с фермой » была написана после рождения ее первого ребенка; его рецепты, как пишет Молли Йе, предназначены для «блюд, которые я нахожу удовлетворением, подавая своей семье в любой старый день». Еврейское и китайское происхождение Йе и скандинавские корни ее мужа на Среднем Западе повлияли на такие рецепты, как салями из мацы брей, курица му-шу и лефсе по будням; есть также звездная миска из коричневого риса с копченым лососем, в которой изобретательно используются крекеры Ritz.
Еврейское и китайское происхождение Йе и скандинавские корни ее мужа на Среднем Западе повлияли на такие рецепты, как салями из мацы брей, курица му-шу и лефсе по будням; есть также звездная миска из коричневого риса с копченым лососем, в которой изобретательно используются крекеры Ritz.
Хлебная голова: выпечка для менее проторенной дороги
Грег Уэйд с Рэйчел Хольцман
W.W. Norton & Company, 27 сентября
«Хлеб, который я научу вас печь, немного грубоват, чуть громче, чем нужно, и чертовски хорош», — пишет Грег Уэйд, главный пекарь чикагской кондитерской. Хлеб общественного качества. Зерновые культуры, выращенные на местной ферме, — «своенравные сестры и братья мягкой пшеницы» — являются предметом ревности Уэйда и строительными блоками его натуральной закваски, долго ферментированного хлеба. С простыми, доступными рецептами для всего, от багета из нескольких злаков до ржаного слоеного теста и исключительного кукурузного хлеба, это, верная своему названию, возможно, самая легкая кулинарная книга о хлебе, когда-либо написанная, а также чрезвычайно информативная.
Идем глубже: Таня Холланд стремится к удару
Шеф-повар из Окленда достигла своей жизненной цели по созданию сообщества — благодаря своему легендарному (но уже закрытому) ресторану, своей работе в СМИ и своей новейшей книге « Калифорнийская душа ». Но она только начинается.
Персиана Каждый день
Сабрина Гайур
Осьминог, 4 октября
Персия автор Сабрина Гайур, которая предлагает коллекцию рецептов авиронов, вечеринок и блюд Ближнего Востока. дружеская кулинария. Тем не менее, пишет она во введении к своей новой книге, «если вы ожидаете, что все эти рецепты займут 15 минут или будут состоять всего из 5 ингредиентов, то мне жаль, что я не та девушка». Гайур мало использует ограничительные правила других людей в отношении структуры рецептов и замен: она выступает за жареный перец в рассоле (для ее мухаммары, в которой также используется фундук вместо более традиционных грецких орехов), слоеное тесто, купленное в магазине, «дешево и сердито». консервированный нут и фасованные макароны, последняя из которых играет главную роль в ее так называемых ленивых мантах. Специи, такие как хлопья чили, тмин и кориандр, также используются разумно, добавляя слои к таким блюдам, как пикантный паштет из скумбрии, «читс дал», стейк из обжаренного перца и салат из помидоров. Это прекрасная, спокойная поваренная книга с выигрышным балансом практичности и творчества.
консервированный нут и фасованные макароны, последняя из которых играет главную роль в ее так называемых ленивых мантах. Специи, такие как хлопья чили, тмин и кориандр, также используются разумно, добавляя слои к таким блюдам, как пикантный паштет из скумбрии, «читс дал», стейк из обжаренного перца и салат из помидоров. Это прекрасная, спокойная поваренная книга с выигрышным балансом практичности и творчества.
Рамбутан: рецепты из Шри-Ланки
Синтия Шанмугалингам
Блумсбери, 11 октября
передать красоту и сложность еды и места, а письмо, которое надежно вызывает смех, слезы и более полное понимание мира. А вот Синтия Шанмугалингам, родившаяся в Англии у родителей, эмигрировавших туда из Шри-Ланки в начале 1970-х, справился (с помощью фотографа Алекса Лау). Описывает ли она воронки как «пикантное нижнее белье шри-ланкийской кухни», использует анекдот о сексизме, чтобы представить кулинарную технику, известную как темпер, или рассказывает, как дом ее детства наполнялся перемещенными родственниками в конце 80-х, когда «Шри-Ланка была быть разорванным насилием», Шанмугалингам попадает в неожиданные, часто захватывающие места. Еда, в том числе набор карри, пневматический пирог с манго и сочащийся бутерброд с самболом, яйцом и сыром, вызывает внезапный и сильный голод. Побольше всего этого, пожалуйста.
Еда, в том числе набор карри, пневматический пирог с манго и сочащийся бутерброд с самболом, яйцом и сыром, вызывает внезапный и сильный голод. Побольше всего этого, пожалуйста.
Британская кулинарная книга: аутентичные рецепты домашней кухни из Англии, Уэльса, Шотландии и Северной Ирландии
Бен Мервис
Файдон, 12 октября
«Что такое британская еда?» — спрашивает Бен Мервис в начале своего обширного, впечатляюще проработанного тома, на создание которого ушло девять лет. Ответ, конечно, лежит далеко за пределами простой категоризации. Британская кухня, пишет Мервис, «это не четко унифицированная кухня». Наоборот, оно имеет очень региональный характер и формируется такими несоизмеримыми силами, как модели иммиграции и то, какие культуры могут расти на местной почве. Таким образом, это кладезь деликатесов с великолепными названиями, от шотландского rumbledethumps (запеканка для завтрака) до stwnsh (валлийское корневое пюре) и вызывающего воспоминания, несколько жуткого пирога Stargazey, корнуоллского блюда, названного так за сардины, которые смотрят прямо в глаза.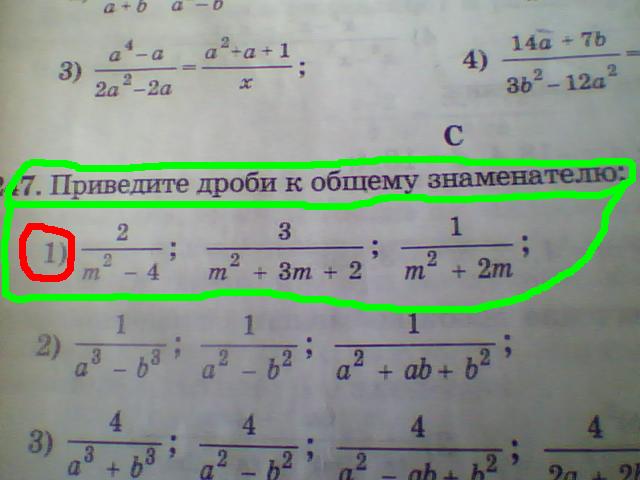 безжизненно от шелушащейся корки. Это одна из тех поваренных книг, которая подходит как для справки, так и для настоящей кулинарии, хотя одно только изобилие лепешек, пышек, буханок и булочек делает вескими доводами в пользу последней.
безжизненно от шелушащейся корки. Это одна из тех поваренных книг, которая подходит как для справки, так и для настоящей кулинарии, хотя одно только изобилие лепешек, пышек, буханок и булочек делает вескими доводами в пользу последней.
Diasporican: Пуэрто-риканская кулинарная книга
Illyanna Maisonet
Ten Speed Press, 18 октября
Illyanna Maisonet хочет, чтобы вы знали, что, вопреки названию, это не пуэрториканская кулинарная книга — это «поваренная книга Пуэрто-Рико». для диаспоры, — пишет она, — для 5,5 миллионов человек, живущих в Штатах, которые продолжают готовить еду на нашей родине». Так начинается ее увлекательная и самоуверенная ода кухне Пуэрто-Рико, которую, как и сам остров и его жителей, по-прежнему неправильно понимают. Рецепты таких блюд, как хамонилья гисада и арроз чино борикуа, напоминают о том, как колониализм и иммиграция сформировали Пуэрто-Рико, а преобладание мяса и жареных во фритюре блюд иллюстрирует важность продуктов, которые обладают как вкусом, так и долговременным питанием. Яркая, убедительная книга.
Яркая, убедительная книга.
Изысканная выпечка: сладкая и соленая выпечка
Клаудия Флеминг с Кэтрин Янг
Рэндом Хаус, 25 октября
Поклонники Клаудии Флеминг, легендарного кондитера, которая сделала себе имя в таверне Gramercy Tavern, ждали много лет за продолжение ее столь же легендарной первой книги, The Last Course . Ожидание того стоило: эти рецепты, продукты Флеминга во время изоляции от пандемии, являются фантазией домашнего пекаря. Между татином из кумквата, дьявольским пирогом с кремом Эрл Грей, песочным кленовым печеньем и целым садом овощных пирогов трудно понять, с чего начать. Я выбрал черничный, черничный, черничный пирог, повторение его названия служит подтверждением как фруктов, так и восклицательной радости от конечного результата.
Первое поколение: рецепты из моего тайваньско-американского дома
Фрэнки Гоу
Ten Speed, 25 октября
Посвящается своим родителям, азиатскому сообществу и ЛГБТК-сообществу, дебют блогера Little Fat Boy Фрэнки Гоу поваренная книга — это жизнерадостное, глубоко прочувствованное упражнение в памяти, идентичности и вкусе. Гоу, сын тайваньских иммигрантов, поселившихся в Цинциннати в середине 1980-х годов, «хотел написать эту книгу, чтобы отметить опыт американцев азиатского происхождения в первом поколении», — пишет он. «По мере того, как я рос, ориентируясь в своей идентичности, еда была в центре моего открытия как глубокого стыда, так и переполняющей гордости». Еда в поваренной книге Го свидетельствует о вкусе, сформированном едой Среднего Запада и блюдами, приготовленными его тайваньскими бабушками: есть рецепты корн-догов лапчхон («мечта» для «молодого азиатско-американского ребенка из пригорода Огайо»). ), жареный рисовый пирог болоньезе, перец чили из Цинциннати с мучной лапшой и биг-маки с головой льва, творение, которое Гоу описывает как «любовную записку к Среднему Западу, увиденную через призму моего наследия». Вы также найдете подробные руководства по приготовлению бао, пельменей и хот-пота — и, подчеркивая все это, вдумчивые, часто очень забавные дани Гау семье и еде, которые сделали его тем, кем он является сегодня.
Гоу, сын тайваньских иммигрантов, поселившихся в Цинциннати в середине 1980-х годов, «хотел написать эту книгу, чтобы отметить опыт американцев азиатского происхождения в первом поколении», — пишет он. «По мере того, как я рос, ориентируясь в своей идентичности, еда была в центре моего открытия как глубокого стыда, так и переполняющей гордости». Еда в поваренной книге Го свидетельствует о вкусе, сформированном едой Среднего Запада и блюдами, приготовленными его тайваньскими бабушками: есть рецепты корн-догов лапчхон («мечта» для «молодого азиатско-американского ребенка из пригорода Огайо»). ), жареный рисовый пирог болоньезе, перец чили из Цинциннати с мучной лапшой и биг-маки с головой льва, творение, которое Гоу описывает как «любовную записку к Среднему Западу, увиденную через призму моего наследия». Вы также найдете подробные руководства по приготовлению бао, пельменей и хот-пота — и, подчеркивая все это, вдумчивые, часто очень забавные дани Гау семье и еде, которые сделали его тем, кем он является сегодня.




 Эти числа и будут дополнительными множителями.
Эти числа и будут дополнительными множителями.


 Если Вы имеете дело со смешанным или целым числом, то его нужно сначала превратить в дробь, а уже потом определять наименьшее общее кратное. Чтобы целое число превратить в дробь, нужно в числителе записать само это число, а в знаменателе — единицу. Например, число 5 в виде дроби будет выглядеть так: 5/1. Чтобы смешанное число превратить в дробь, нужно целое число умножить на знаменатель и прибавить к нему числитель. Пример: 8 целых и 3/5 в виде дроби = 8×5+3/5 = 43/5.
Если Вы имеете дело со смешанным или целым числом, то его нужно сначала превратить в дробь, а уже потом определять наименьшее общее кратное. Чтобы целое число превратить в дробь, нужно в числителе записать само это число, а в знаменателе — единицу. Например, число 5 в виде дроби будет выглядеть так: 5/1. Чтобы смешанное число превратить в дробь, нужно целое число умножить на знаменатель и прибавить к нему числитель. Пример: 8 целых и 3/5 в виде дроби = 8×5+3/5 = 43/5.
 Если Вы имеете дело со смешанным или целым числом, то его нужно сначала превратить в дробь, а уже потом определять наименьшее общее кратное. Чтобы целое число превратить в дробь, нужно в числителе записать само это число, а в знаменателе — единицу. Например, число 5 в виде дроби будет выглядеть так: 5/1. Чтобы смешанное число превратить в дробь, нужно целое число умножить на знаменатель и прибавить к нему числитель. Пример: 8 целых и 3/5 в виде дроби = 8×5+3/5 = 43/5.
Если Вы имеете дело со смешанным или целым числом, то его нужно сначала превратить в дробь, а уже потом определять наименьшее общее кратное. Чтобы целое число превратить в дробь, нужно в числителе записать само это число, а в знаменателе — единицу. Например, число 5 в виде дроби будет выглядеть так: 5/1. Чтобы смешанное число превратить в дробь, нужно целое число умножить на знаменатель и прибавить к нему числитель. Пример: 8 целых и 3/5 в виде дроби = 8×5+3/5 = 43/5.

