Неполные также можно классифицировать на два вида: без свободного члена и с его наличием. К первому и второму типу применимы различные формулы сокращенного умножения. Например, первое решается только посредством вынесения общего множителя за скобку, а для решения второго используется соотношение разности квадратов.
Однако не во всех случаях можно рассчитывать на формулы, поскольку большинство сложных заданий требуют выполнения математических преобразований.
Формулы разложения на элементы
Для решения квадратного уравнения применяются соответствующие тождества, позволяющие понижать вторую степень. Запомнить их довольно просто, поскольку количество ограничено несколькими формулами разложения на множители (сокращенного умножения):
- (t+s)^2=t^2+2ts+s^2.
2+4t-8=0. Последнее уравнение нужно решать через дискриминант, а это еще дополнительные расчеты и ценное время, которое может быть потрачено с пользой на другие задачи.При решении равенства методом разложения на множители вычислительный процесс более оптимизирован, т. е. (5t-2)(2t+3)-(5t-2)(t-1)=(5t-2)(2t+3-t+1)=(5t-2)(t+4)=0. Чтобы решить последнее тождество, достаточно приравнять к нулю его множители, которые являются обыкновенными линейными уравнениями.
Корни уравнения
Перед использованием алгоритма необходимо разобрать, что означает решить уравнение. Если предположить, что существует некоторое тождество, состоящее из некоторых коэффициентов и переменных, то нужно посредством математических преобразований и формул вычислить значения неизвестных, при которых выражение принимает истинное значение. Например, 1=1 — истина.
Корни уравнения — допустимые значения переменных, если их подставить в исходное выражение, результат не изменяется.
Следует отметить, что в некоторых случаях могут возникать ложные величины. Это очень часто происходит при решении кубических, биквадратных и других сложных выражений. Однако они могут возникать при решении квадратных двучленов.Чтобы избавиться от ложных величин, необходимо выполнить единственное правило: подставить их в исходное тождество. Если решение получено графическим методом, то проверку можно не выполнять. Последний метод рекомендуется использовать также для проверки количества решений. Для этого достаточно схематичного построения графика функции, на котором и будут видны корни — точки пересечения с осями координат.
В алгебре можно также встретить задачи на эту тематику. Например, требуется найти точки пересечения двух или трех графических представлений. Однако у графического способа решения есть один существенный недостаток (при точном определении значений переменных) — только для целочисленных значений корней. Его рекомендуется использовать в различных онлайн-приложениях, позволяющих строить графики функций и точно определять точки пересечения.
Следует отметить, что для проверки правильности нахождения корней квадратного трехчлена или двучлена можно использовать также онлайн-калькуляторы, в поля которых вводятся коэффициенты при неизвестных и свободный член. После нажатия кнопки «вычислить» или «найти корни» программа мгновенно выдает результаты. Если какого-то члена в тождестве нет, то в соответствующем поле указывается нулевая величина.
Алгоритм операции
Любое сложное действие рекомендуется выполнять по определенной методике, которая называется алгоритмом. При решении уравнений методом разложения на множители используется такая последовательность действий:
- Написать уравнение.
- Проанализировать возможность нахождения корней (выбор метода решения).
- Упростить уравнение (разложить на множители по одной из формул сокращенного умножения).
- Выполнить математические преобразования при необходимости.
- Перенести 0 вправо, а все остальные части — влево.
- Приравнять каждый из множителей к 0.
- Найти корни для каждого элемента отдельно.
- Отсеять ложные значения.
- Записать окончательный результат.
Второй пункт алгоритма является очень важным, поскольку именно от него зависит правильность и скорость решения уравнения. Последнее должно раскладываться на множители. Вообще суть их решения сводится к их упрощению и приравниванию элементов в левой части к нулевому значению. В некоторых случаях требуется привести подобные слагаемые, а затем подвести результат к определенной формуле сокращенного умножения.
Следует отметить, что восьмой пункт методики — проверка. Однако ее специалисты рекомендуют новичкам выполнять на каждом этапе алгоритма, чтобы избежать ошибок при нахождении корней. Если учащиеся совершают много тренировок, то уже нет необходимости обращать внимание на пункты, поскольку постоянные тренировки делают вычислительный процесс автоматизированным.
2+28t+40=40-40=0 (+).
2+4t-8=0. Последнее уравнение нужно решать через дискриминант, а это еще дополнительные расчеты и ценное время, которое может быть потрачено с пользой на другие задачи.
Следует отметить, что в некоторых случаях могут возникать ложные величины. Это очень часто происходит при решении кубических, биквадратных и других сложных выражений. Однако они могут возникать при решении квадратных двучленов.
2+28t+40=40-40=0 (+).При решении получено два корня, но это не означает, что при подстановке в исходное тождество они превращают его в истину. Следовательно, t1=1 — ложный корень, поскольку 72 не равно 0.
Таким образом, для решения квадратных уравнений подойдет метод разложения выражения с неизвестными на множители, поскольку эта операция позволит существенно оптимизировать процесс нахождения корней, избежать ошибок и сократить время вычислений.
Как правильно разложить квадратный трёхчлен, формулы разложения множителей, уравнения и примеры
Мир погружён в огромное количество чисел. Любые исчисления происходят с их помощью.
Люди учат цифры для того, чтобы в дальнейшей жизни не попадаться на обман. Необходимо уделять огромное количество времени, чтобы быть образованным и рассчитать собственный бюджет.
…
Оглавление:
- Формула разложения квадратного трёхчлена на множители
- Дискриминант
- Теорема Виета
- Разложение трёхчлена с помощью скобки
Математика — это точная наука, которая играет большую роль в жизни. В школе дети изучают цифры, а после, действия над ними.
Действия над числами бывают совершенно разными: умножение, разложение, добавление и прочие. Помимо простых формул, в изучении математики используют и более сложные действия. Существует огромное количество формул, по которым узнают любые значения.
Это интересно: разность векторов, определение разности.
В школе, как только появляется алгебра, в жизнь школьника добавляются формулы упрощения. Бывают уравнения, когда неизвестных числа два, но найти простым способом не получится. Трёхчлен — соединение трёх одночленов, с помощью простого метода отнимания и добавления. Трёхчлен решается с помощью теоремы Виета и дискриминанта.
Существуют два правильных и простых решения примера:
- дискриминант;
- теорема Виета.
Квадратный трёхчлен имеет неизвестный в квадрате, а также число без квадрата. Первый вариант для решения задачи использует формулу Виета. Это простая формула, если цифры, что стоят перед неизвестным, будут минимальным значением.
Для других уравнений, где число стоит перед неизвестным, уравнение необходимо решать через дискриминант. Это более сложное решение, но используют дискриминант намного чаще, нежели теорему Виета.
Изначально, для нахождения всех переменных уравнения необходимо возвести пример к 0. Решение примера можно будет проверить и узнать правильно ли подстроены числа.
Это интересно: умножение на 0 — правило для любого числа.
Дискриминант
1. Необходимо приравнять уравнение к 0.
2. Каждое число перед х будет названо числами a, b, c. Так как перед первым квадратным х нет числа, то оно приравнивается к 1.
3. Теперь решение уравнения начинается через дискриминант:
4. Теперь нашли дискриминант и находим два х. Разница заключается в том, что в одном случае перед b будет стоять плюс, а в другом минус:
5. По решению два числа получилось -2 и -1. Подставляем под первоначальное уравнение:
6. В этом примере получилось два правильных варианта. Если оба решения подходят, то каждое из них является истинным.
Через дискриминант решают и более сложные уравнение. Но если само значение дискриминанта будет меньше 0, то пример неправильный. Дискриминант при поиске всегда под корнем, а отрицательное значение не может находиться в корне.
Это интересно: признак перпендикулярности прямой и плоскости, теория и практика.
Теорема Виета
Применяется для решения лёгких задач, где перед первым х не стоит число, то есть a=1. Если вариант совпадает, то расчёт проводят через теорему Виета.
Для решения любого трёхчлена необходимо возвести уравнение к 0.
Первые шаги у дискриминанта и теоремы Виета не отличаются.
2. Теперь между двумя способами начинаются отличия. Теорема Виета использует не только «сухой» расчёт, но и логику и интуицию. Каждое число имеет свою букву a, b, c. Теорема использует сумму и произведение двух чисел.
Запомните! Число b всегда при добавлении стоит с противоположным знаком, а число с остаётся неизменным!
Подставляя значения данные в примере, получаем:
Это интересно: что такое разность в математике?
3. Методом логики подставляем наиболее подходящие цифры. Рассмотрим все варианты решения:
- Цифры 1 и 2. При добавлении получаем 3, но если умножить, то не получится 4. Не подходит.
- Значение 2 и -2. При умножении будет -4, но при добавлении получается 0. Не подходит.
- Цифры 4 и -1. Так как в умножении стоит отрицательное значение, значит, одно из чисел будет с минусом. При добавлении и умножении подходит. Правильный вариант.
4. Остаётся только проверить, раскладывая числа, и посмотреть правильность подобранного варианта.
5. Благодаря онлайн-проверке мы узнали, что -1 не подходит по условию примера, а значит является неправильным решением.
При добавлении отрицательного значения в примере, необходимо цифру заносить в скобки.
В математике всегда будут простые задачи и сложные. Сама наука включает в себя разнообразие задач, теорем и формул. Если понимать и правильно применять знания, то любые сложности с вычислениями будут пустяковыми.
Математика не нуждается в постоянном запоминании. Нужно научится понимать решение и выучить несколько формул. Постепенно, по логическим выводам, можно решать похожие задачи, уравнения. Такая наука может с первого взгляда показаться очень тяжёлой, но если окунутся в мир чисел и задач, то взгляд резко изменится в лучшую сторону.
Технические специальности всегда остаются самыми востребованными в мире. Сейчас, в мире современных технологий, математика стала незаменимым атрибутом любой сферы.
Нужно всегда помнить о полезных свойствах математики.
Разложение трёхчлена с помощью скобки
Кроме решения привычными способами, существует ещё один — разложение на скобки. Используют с применением формулы Виета.
1. Приравниваем уравнение к 0.
ax 2 + bx+ c= 0
2. Корни уравнения остаются такими же, но вместо нуля теперь используют формулы разложения на скобки.
ax 2 + bx+ c = a ( x – x 1 ) ( x – x 2 )
3. Пример уравнения.
2 x 2 – 4 x – 6 = 2 ( x + 1 ) ( x – 3 )
4. Решение х=-1, х=3
Формулы разложения кубов. Формулы сокращенного умножения
Математические выражения (формулы) сокращённого умножения (квадрат суммы и разности, куб суммы и разности, разность квадратов, сумма и разность кубов) крайне не заменимы во многих областях точных наук.
Эти 7 символьных записей не заменимы при упрощении выражений, решении уравнений, при умножении многочленов, сокращении дробей , решении интегралов и многом другом. А значит будет очень полезно разобраться как они получаются, для чего они нужны, и самое главное, как их запомнить и потом применять. Потом применяя формулы сокращенного умножения на практике самым сложным будет увидеть, что есть х и что есть у. Очевидно, что никаких ограничений для a и b нет, а значит это могут быть любые числовые или буквенные выражения.
И так вот они:
Первая х 2 — у 2 = (х — у) (х+у) .Чтобы рассчитать разность квадратов двух выражений надо перемножить разности этих выражений на их суммы.
Вторая (х + у) 2 = х 2 + 2ху + у 2 . Чтобы найти квадрат суммы двух выражений нужно к квадрату первого выражения прибавить удвоенное произведение первого выражения на второе плюс квадрат второго выражения.
Третья (х — у) 2 = х 2 — 2ху + у 2 .
Чтобы вычислить квадрат разности двух выражений нужно от квадрата первого выражения отнять удвоенное произведение первого выражения на второе плюс квадрат второго выражения.
Четвертая (х + у) 3 = х 3 + 3х 2 у + 3ху 2
Пятая (х — у) 3 = х 3 — 3х 2 у + 3ху 2 — у 3 . Чтобы рассчитать куб разности двух выражений необходимо от куба первого выражения отнять утроенное произведение квадрата первого выражения на второе плюс утроенное произведение первого выражения на квадрат второго минус куб второго выражения.
Шестая х 3 + у 3 = (х + у) (х 2 — ху + у 2) Чтобы высчитать сумму кубов двух выражений нужно умножить суммы первого и второго выражения на неполный квадрат разности этих выражений.
Седьмая х 3 — у 3 = (х — у) (х 2 + ху + у 2) Чтобы произвести вычисление разности кубов двух выражений надо умножить разность первого и второго выражения на неполный квадрат суммы этих выражений.
Не сложно запомнить, что все формулы применяются для произведения расчетов и в противоположном направлении (справа налево).
О существовании этих закономерностей з нали еще около 4 тысяч лет тому назад. Их широко применяли жители древнего Вавилона и Египта. Но в те эпохи они выражались словесно или геометрически и при расчетах не использовали буквы.
Разберем доказательство квадрата суммы (а + b) 2 = a 2 +2ab +b 2 .
Первым эту математическую закономерность доказал древнегреческий учёный Евклид, работавший в Александрии в III веке до н.э., он использовал для этого геометрический способ доказательства формулы, так как буквами для обозначения чисел не пользовались и учёные древней Эллады. Ими повсеместно употреблялись не “а 2 ”, а “квадрат на отрезке а”, не “ab”, а “прямоугольник , заключенный между отрезками a и b”.
Формулы или правила сокращенного умножения используются в арифметике, а точнее — в алгебре, для более быстрого процесса вычисления больших алгебраических выражений. Сами же формулы получены из существующих в алгебре правил для умножения нескольких многочленов.
Использование данных формул обеспечивает достаточно оперативное решение различных математических задач, а также помогает осуществлять упрощение выражений. Правила алгебраических преобразований позволяют выполнять некоторые манипуляции с выражениями, следуя которым можно получить в левой части равенства выражение, стоящее в правой части, или преобразовать правую часть равенства (чтобы получить выражение, стоящее в левой части после знака равенства).
Удобно знать формулы, применяемые для сокращенного умножения, на память, так как они нередко используются при решении задач и уравнений. Ниже перечислены основные формулы, входящие в данный список, и их наименование.
Квадрат суммы
Чтобы вычислить квадрат суммы, необходимо найти сумму, состоящую из квадрата первого слагаемого, удвоенного произведения первого слагаемого на второе и квадрата второго.
В виде выражения данное правило записывается следующим образом: (а + с)² = a² + 2ас + с².
Квадрат разности
Чтобы вычислить квадрат разности, необходимо вычислить сумму, состоящую из квадрата первого числа, удвоенного произведения первого числа на второе (взятое с противоположным знаком) и квадрата второго числа. В виде выражения данное правило выглядит следующим образом: (а — с)² = а² — 2ас + с².
Разность квадратов
Формула разности двух чисел, возведенных в квадрат, равна произведению суммы этих чисел на их разность. В виде выражения данное правило выглядит следующим образом: a² — с² = (a + с)·(a — с).
Куб суммы
Чтобы вычислить куб суммы двух слагаемых, необходимо вычислить сумму, состоящую из куба первого слагаемого, утроенного произведения квадрата первого слагаемого и второго, утроенного произведения первого слагаемого и второго в квадрате, а также куба второго слагаемого. В виде выражения данное правило выглядит следующим образом: (а + с)³ = а³ + 3а²с + 3ас² + с³.
Сумма кубов
Согласно формуле, приравнивается к произведению суммы данных слагаемых на их неполный квадрат разности. В виде выражения данное правило выглядит следующим образом: а³ + с³ = (а + с)·(а² — ас + с²).
Пример. Необходимо вычислить объем фигуры, которая образована сложением двух кубов. Известны лишь величины их сторон.
Если значения сторон небольшие, то выполнить вычисления просто.
Если же длины сторон выражаются в громоздких числах, то в этом случае проще применить формулу «Сумма кубов», которая значительно упростит вычисления.
Куб разности
Выражение для кубической разности звучит так: как сумма третьей степени первого члена, утроенного отрицательного произведения квадрата первого члена на второй, утроенного произведения первого члена на квадрат второго и отрицательного куба второго члена. В виде математического выражения куб разности выглядит следующим образом: (а — с)³ = а³ — 3а²с + 3ас² — с³.
Разность кубов
Формула разности кубов отличается от суммы кубов лишь одним знаком.
Таким образом, разность кубов — формула, равная произведению разности данных чисел на их неполный квадрат суммы. В виде математического выражения разность кубов выглядит следующим образом: а 3 — с 3 = (а — с)(а 2 + ас + с 2).
Пример. Необходимо вычислить объем фигуры, которая останется после вычитания из объема синего куба объемной фигуры желтого цвета, которая также является кубом. Известна лишь величина стороны маленького и большого куба.
Если значения сторон небольшие, то вычисления довольно просты. А если длины сторон выражаются в значительных числах, то стоит применить формулу, озаглавленную «Разность кубов» (или «Куб разности»), которае значительно упростит вычисления.
В предыдущем уроке мы разобрались с разложением на множители. Освоили два способа: вынесение общего множителя за скобки и группировку. В этом уроке — следующий мощный способ: формулы сокращённого умножения . В краткой записи — ФСУ.
Формулы сокращённого умножения (квадрат суммы и разности, куб суммы и разности, разность квадратов, сумма и разность кубов) крайне необходимы во всех разделах математики.
Они применяются в упрощении выражений, решении уравнений, умножении многочленов, сокращении дробей, решении интегралов и т.д. и т.п. Короче, есть все основания разобраться с ними. Понять откуда они берутся, зачем они нужны, как их запомнить и как применять.
Разбираемся?)
Откуда берутся формулы сокращённого умножения?
Равенства 6 и 7 записаны не очень привычно. Как бы наоборот. Это специально.) Любое равенство работает как слева направо, так и справа налево. В такой записи понятнее, откуда берутся ФСУ.
Они берутся из умножения.) Например:
(a+b) 2 =(a+b)(a+b)=a 2 +ab+ba+b 2 =a 2 +2ab+b 2
Вот и всё, никаких научных хитростей. Просто перемножаем скобки и приводим подобные. Так получаются все формулы сокращённого умножения. Сокращённое умножение — это потому, что в самих формулах нет перемножения скобок и приведения подобных. Сокращены.) Сразу дан результат.
ФСУ нужно знать наизусть. Без первых трёх можно не мечтать о тройке, без остальных — о четвёрке с пятёркой.
)
Зачем нужны формулы сокращённого умножения?
Есть две причины, выучить, даже зазубрить эти формулы. Первая — готовый ответ на автомате резко уменьшает количество ошибок. Но это не самая главная причина. А вот вторая…
Кстати, у меня есть ещё парочка интересных сайтов для Вас.)
Можно потренироваться в решении примеров и узнать свой уровень. Тестирование с мгновенной проверкой. Учимся — с интересом!)
можно познакомиться с функциями и производными.
Формулы сокращенного умножения — Математика
Формулы сокращенного умножения
|
А именно — занеся минус в первые скобки и открыв крайние мы получим квадрат разности, который легко преобразуется в многочлен:
Далее применяя формулы сокращенного умножения получаем ответ:
2.2 Формула разложения числа по степеням основания
Пусть в десятичной системе задано некоторое число А(10)=3745. Каждая позиция, занимаемая цифрами, называется разрядом числа. Разряды имеют названия и номера: разряд единиц, разряд десятков, разряд сотен и т.д. Названия разрядов определяют их вес: единицы, десятки, сотни, тысячи. Поэтому количественный эквивалент цифры в записи числа равен произведению значения цифры на вес разряда, где она записана.
Заданное число, не изменяя его количества, можно записать следующими способами:
А(10)=3745;
А(10)=3000+700+40+5;
А(10)=31000+7100+410+5;
А(10)=3103+7102+4101+5100.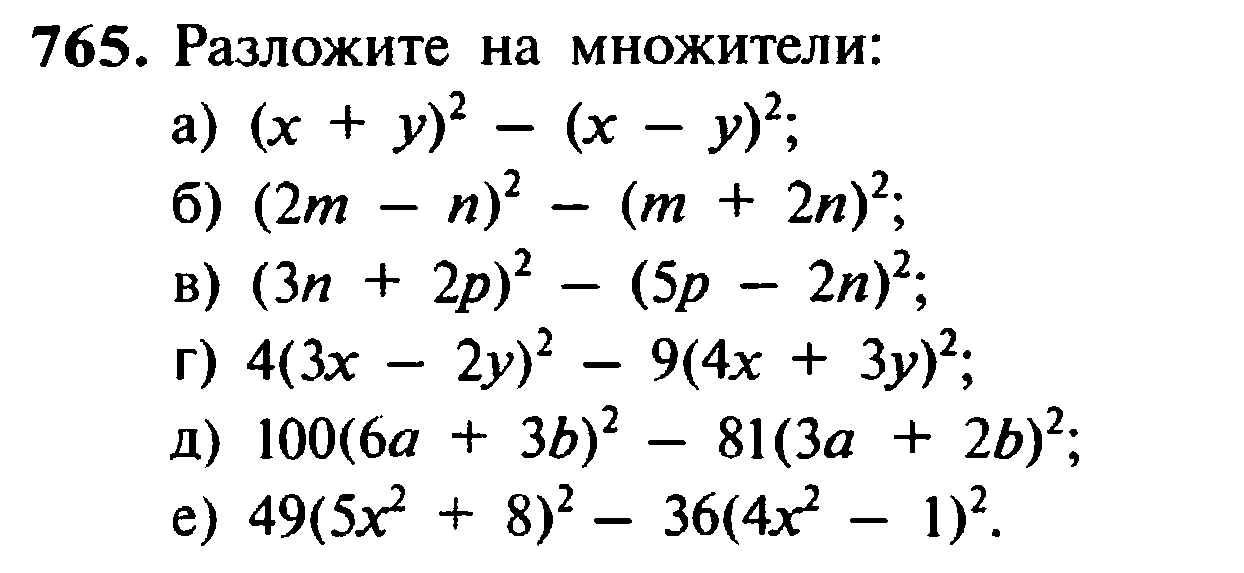
Последнюю запись называют разложением числа по степеням основания. Формула разложения показывает, что число в позиционной системе можно представить в виде суммы количественных эквивалентов цифр, которые в свою очередь равны произведению цифры на степень основания, т.е. на вес разряда.
Запишем целое четырехразрядное десятичное число и формулу его разложения в общем виде:
A(10)=a3a2a1a0= a3103+ a2102+ a1101+ a0100.
Заметим, что номера разрядов числа совпадают с показателями степени основания. Смешанная десятичная дробь, имеющая по четыре разряда в целой и дробной части, и формула его разложения запишется так (опустим знаки умножения):
A(10)=a3a2a1a0,a-1a-2a-3a-4= a3103+a2102+a1101+a0100+a-110-1 +
+a-210-2+a-310-3+a-4 10-4.
В принятых обозначениях формула количественного эквивалента цифры i-гo разряда в записи десятичного числа такая: Вi=аi10i.
Формула разложения смешанной дроби, имеющей n+1 разрядов в целой части и m разрядов в дробной, в позиционной системе с основанием р запишется так:
A(p)=anan-1…a3a2a1a0,a-1a-2a-3a-4…a-m+1a-m= anpn+ an-1pn-1+…+ a2p2+
+ a1p1+
a0p0+a-1p-1+a-2p-2+…+a-m+1p-m+1+a-mp-m.
2.3 Перевод чисел между системами счисления
2.3.1 Перевод с использованием формулы разложения
Наиболее простой способ перевода заключается в суммировании количественных эквивалентов цифр заданного числа. Действия при переводе выполняются в новой системе, поэтому способ удобно использовать для перевода чисел в десятичную систему. В основе способа лежит использование значений степеней основания чисел. Некоторые степени оснований 10, 2, 8 и 16 приведены в таблице 2. Часть клеток таблицы не заполнена ввиду значительной величины чисел.
Таблица 2 – Таблица степеней оснований pn
n | 7 | 6 | 5 | 4 | 3 | 2 | 1 | 0 | -1 | -2 | -3 | -4 |
p=10 | 107 | 107 | 107 | 107 | 107 | 107 | 107 | 1 | . | .01 | .001 | |
p=2 | 128 | 64 | 32 | 16 | 8 | 4 | 2 | 1 | 1/2 | 1/4 | 1/8 | 1/16 |
p=8 | 512 | 64 | 8 | 1 | 1/8 | 1/64 | 1/512 | |||||
p=16 | 256 | 16 | 1 | 1/16 | 1/256 |
1Пример 4
Дано: A(2)=1101.
Найти
A(10).
Решение. Записываем формулу разложения двоичного числа по степеням основания:
A(2)=a3a2a1a0= A(10)=a323+a222+a121+a020 =a38+a24+a12+a01.
Подставим в формулу значения разрядов заданного двоичного числа и выполним действия:
A(10)=18+14+02+11=13.
Воспользовавшись таблицей 1, убедимся, что получен правильный результат. Действительно, двоичному числу 1101(2) соответствует десятичное число 13(10) .
Ответ:A(10)=13.
Пример 5
Дано: A(2)=10111,101. Найти A(10).
Решение. Записываем формулу разложения двоичного числа по степеням основания:
A(2)=a4a3a2a1a0,a-1a-2a-3=A(10)=a424+a323+a222+a121+a020 + a-12-1+
+a-22-2+a-32-3=a416+a38+a24+a12+a01+a-1+a-2+
a-3.
Подставим в формулу значения разрядов заданного двоичного числа и выполним действия:
A(10)=116+08+14+12+11+1+0+1=23.
Ответ:A(10)=23.
Пример 6
Дано: A(8)=135,42. Найти A(10).
Решение. Записываем формулу разложения двоичного числа по степеням основания:
A(8)=a2a1a0,a-1a-2=A(10)=a282+a181+a080 + a-18-1+a-28-2.
Подставим в формулу значения разрядов заданного восьмеричного числа и выполним действия:
A(10)=164+38+5+4+2=93.
Ответ:A(10)= 93.
Пример 7
Дано: A(16)=2A,3E.
2
ChemTeam: Разложение
ChemTeam: РазложениеТипы реакций: Разложение
Вернуться в меню уравнений
Перейти к одиночной замене
Перейти к двойной замене
Перейти к синтезу
Перейти к сжиганию
Важно помнить: (1) НИ ОДНО из уравнений не сбалансировано!! и (2) убедитесь, что вы написали правильные формулы. НЕ копируйте индексы реагентов в продукты.
При разложении одно соединение распадается на две (или более) части. Эти части могут быть элементами или более простыми соединениями.
Записывается с использованием общих символов, обычно отображается как:
АВ —> А + В
Однако на самом деле это работает только для разделения на элементы, как в этих примерах.
HgO —> Hg + O 2
H 2 O —> H 2 + O 2
MgCl 2 —> Mg + Cl 2
Fe 90-S > Fe+S
Разложение также может разделить одно соединение на два более простых соединения (или соединение и элемент), как в этих примерах:
CaCO 3 —> CaO + CO 2
Na 2 CO 3 —> Na 2 O + CO 2
KCl 90 + O 3 — 3 2
Ba(ClO 3 ) 2 —> BaCl 2 + O 2
Обратите внимание, что до сих пор в каждом случае в левой (реагентной) части находится только одно вещество.
Это всегда имеет место в реакции разложения. Не забывайте об этом!!
Выяснить, какие продукты разлагаются, сложнее (может быть, вы думаете, что это проще!!), потому что вам придется распознавать несколько категорий реакций разложения. Вот ваши первые (да, есть еще!) три:
1) Все бинарные соединения (такие как четыре в первом примере, приведенном выше) распадаются на свои элементы.
2) Все карбонаты (как и первые два во втором приведенном выше примере) распадаются на оксид и углекислый газ.
3. Хлораты (например, KClO 3 и Ba(ClO 3 ) 2 в примере) будут распадаться на бинарную соль и кислород.
Вот еще одна категория реакций разложения:
Ca(OH) 2 —> CaO + H 2 O
NaOH —> Na 2 O + H 2 O
HNO 3 —> N 2 O O 5 + H 2 O
H 3 PO 4 —> P 2 O 5 + Н 2 О
Первые два вещества являются основаниями, а последние два – кислотами.
В каждом случае кислота или основание распадаются на оксид металла (в случае оснований) или оксид неметалла (в случае кислот) плюс вода.
Вот по одному примеру каждой категории, которые затем решаются ниже:
1) NaClO 3 —>
2) Li 2 CO 3 —>
3) KOH —>
4) NaCl —>
Пример №1
Как определить правую сторону (или сторону товара):
(1) Определите тип соединения, разлагающегося:
NaClO 3 представляет собой хлорат
Обратите внимание, что вы должны уметь «читать» формулу и определять составляющие ее части (катион и анион).
(2) Примените правило для этого типа:
хлораты разлагаются на бинарную соль и газообразный кислород
(3) Напишите две новые (ПРАВИЛЬНО!!) формулы, используя правило из шага два.
NaCl, так как Na положителен 1, а Cl минус один
O 2 поскольку кислород является двухатомным газом
Итак, окончательный ответ выглядит так:
NaClO 3 —> NaCl + O 2
Пример №2
Как определить правую сторону (или сторону товара):
(1) Определите тип соединения, разлагающегося:
Li 2 CO 3 представляет собой карбонат
(2) Примените правило для этого типа:
карбонаты разлагаются на бинарный оксид и углекислый газ
(3) Напишите две новые (ПРАВИЛЬНО!!) формулы, используя правило из шага два.
Li 2 O, так как Li положительный 1, а O минус два
CO 2 — формула углекислого газа
Итак, окончательный ответ выглядит так:
Li 2 CO 3 —> Li 2 O + CO 2
Пример №3
Как определить правую сторону (или сторону товара):
(1) Определите тип соединения, разлагающегося:
KOH является основой
(2) Примените правило для этого типа:
основания разлагаются на бинарный оксид и воду
(3) Напишите две новые (ПРАВИЛЬНО!!) формулы, используя правило из шага два.
K 2 O, так как K положительный 1, а O минус два
H 2 O — формула воды
Итак, окончательный ответ выглядит так:
КОН —> К 2 О + Н 2 О
Пример №4
Как определить правую сторону (или сторону товара):
(1) Определите тип соединения, разлагающегося:
NaCl — это бинарное соединение (это не кислота и не основание.
Я оставил этот вопрос до сих пор).(2) Примените правило для этого типа:
бинарные соединения разлагаются на элементы
(3) Напишите две новые (ПРАВИЛЬНО!!) формулы, используя правило из шага два.
Na — правильный символ
Cl 2 — правильный символ хлора, так как он двухатомный
Итак, окончательный ответ выглядит так:
NaCl —> Na + Cl 2
Пример №5
Существует другой тип кислоты, в которой нет кислорода. Примерами являются HCl, HBr и HI. Эти кислоты просто разлагаются на свои элементы:
HCl —> H 2 + Cl 2
Практические задачи
Обратите внимание, что ни одна из приведенных выше задач не сбалансирована. Это может потребоваться вашему учителю, но ChemTeam предоставит только некоторые из следующих сбалансированных ответов.
Остальное зависит от вас!!
Напишите правильные формулы продуктов этих реакций разложения. № 3 может быть жестким — не забудьте сохранить степень окисления азота.
1) Ni(ClO 3 ) 2 —>
2) Ag 2 O —>
3) HNO 2 —>
4) Fe(OH) 3 —>
5) ZnCO 3 —>
6) Cs 2 CO 3 —>
7) Al(OH) 3 —>
8) H 2 SO 4 —>
9) RbClO 3 —>
10) RaCl 2 —>
Перейти к ответам
Вернуться в меню уравнений
Перейти к одиночной замене
Перейти к двойной замене
Перейти к синтезу
Перейти к сжиганию
Реакция разложения: определение, примеры и применение
- Что такое реакция разложения?
- Что происходит во время реакции разложения?
- Характеристики реакции разложения
- Примеры реакции разложения
- Как сбалансировать реакцию разложения?
- Типы реакций разложения
- Примеры реакций разложения в реальной жизни
- Часто задаваемые вопросы
Что такое реакция разложения?
Реакция разложения — это тип химической реакции, при которой соединение распадается на два или более веществ.
Противоположна комбинированной реакции. Иногда сложный химический вид распадается на простые части. Исходное вещество называют реагентом, а полученные вещества — продуктами [1-5] .
Общее уравнение
Следующее уравнение представляет собой общую реакцию разложения.
AB → A + B
При написании фактической реакции реакция должна быть сбалансирована.
Реакция разложенияЧто происходит во время реакции разложения?
В ходе реакции разложения в исходном веществе разрываются связи между атомами. Затем атомы перестраиваются, образуя новые связи, в результате чего появляются новые вещества со свойствами, отличными от исходного материала.
Характеристики реакции разложения
- Один единственный реагент и два или более продуктов
- Требуется энергия
Примеры реакции разложения
Примером реакции разложения является разложение угольной кислоты (H 2 CO 3 ) на диоксид углерода (CO 2 ) и воду (H 6 902 О) [2] .
H 2 CO 3 (водн.) → CO 2 (г) + H 2 O (ж)
Эта реакция имеет большое значение и является причиной шипения соды. Ниже приведены еще несколько примеров:
Примеры реакции разложенияКак сбалансировать реакцию разложения?
Возьмем пример разложения хлората калия (KClO 3 ) на хлорид калия (KCl) и кислород (O 2 ).
KClO 3 (т) → KCl (т) + O 2 (г)
Это уравнение несбалансировано. Чтобы сбалансировать уравнение, мы проверяем количество атомов кислорода (O) в правой части уравнения и сравниваем его с левой. Заметим, что два атома кислорода справа и три слева. Итак, мы умножаем правый O на 3, а левый O на 2. Обратите внимание, что мы собираемся умножить все соединение KClO 3 на 2 и сбалансируйте кислород.
2 KClO 3 (т) → KCl (т) + 3 O 2 (г)
Теперь мы замечаем, что калий (К) и хлор (Cl) не сбалансированы.
В левой части уравнения два атома K и Cl, а в правой — только по одному атому каждого из них. Итак, умножаем соединение KCl на 2 и получаем окончательное уравнение.
2 KClO 3 (т) → 2 KCl (т) + 3 O 2 (г)
Типы реакции разложения
Существует три типа реакций разложения [1-3] .
1. Термическое разложение
В этой реакции для разрыва связей соединения требуется энергия в виде тепла. Реакция обычно эндотермическая, т. е. к реакции добавляется тепло.
Правила термического разложения
- Карбонаты разлагаются на углекислый газ и оксид.
- Хлораты разлагаются на газообразный кислород и хлорид.
- Гидроксиды разлагаются на воду и оксид.
- Кислоты, содержащие кислород, разлагаются на воду и молекулярный оксид.
- Оксиды разлагаются на кислород и другой элемент.
Примеры
- Карбонат кальция (CaCO 3 ) при нагревании разлагается на оксид кальция (CaO) и диоксид углерода (CO 2 ).
CaCO 3 (т) + тепло → CaO (т) + CO 2 (г)
- При высоких температурах карбонат магния (MgCO 3 ) разлагается на оксид магния (MgO) и диоксид углерода (CO 2 ).
CaCO 3 (т) + тепло → CaO (т) + CO 2 (г)
- Термическое разложение фосфорной кислоты (H 3 PO 4
6)
4 P 2 O 7 ) и вода (H 2 O).
2 H 3 Заказ на покупку 4 → H 4 P 2 O 7 + H 2 O
- Dichromate Ammonium (NH 4 ) 2 CR 2 O 7 2 CR 2 O 7 2 CR 2 O 7 2 CR 2 O 7 2 CR 2 , 7 2 CR 2 , 7 2 CR 2 7 2 Водяной пары и твердый хромий (III) оксид (CR 2 O 3 ) [6]
(NH 4 ) 2 CR 2 O 7 7 (S) +
+ (S) +(S) +(S) +(S) +(S) +(S) + (S).2. Электролитическое разложение
В этой реакции разложение происходит при пропускании электрического тока через водный раствор соединения.
Примеры
- Электролиз воды (H 2 O) с получением водорода (H 2 ) и кислорода (O 2 ) Газы
2 H 2 7 itpe H 2 (г) + O 2 (г)
- Электролиз раствора хлорида натрия (NaCl) дает расплавленный натрий (Na) и хлор (Cl 2 ) газ
2 NaCl (ж) → 2 Na (ж) + Cl 2 (г)
3. Фото или фотохимическое разложение
В этой реакции свет (фотоны) используется для разложения сложный.
Примеры
- Хлорид серебра (AgCl) разлагается на серебро (Ag) и хлор (Cl 2 ) в присутствии солнечного света + Cl 2 (г)
3
- В присутствии света перекись водорода (H 2 O 2 ) разлагается на воду (H 2 O) и кислород (O 2 ).
2 H 2 O 2 (л) → 2 H 2 O (л) + O 2 (г)
Другой тип реакции разложения этого типа
разложения, реакция происходит с помощью катализатора.
Пример
- Разложение перекиси водорода (H 2 O 2 ) в воду (H 2 O) и кислород (O 2 ) катализируется ферментом каталазой [7] .
2 H 2 O 2 (L) + Каталаза (фермент) → 2 H 2 O (L) + O 2 (G)
. Реакция разложения имеет несколько применений в промышленности и повседневной жизни.
Промышленность
- Производство оксида кальция или негашеной извести
- Производство оксида лития
- Получение кислорода и углекислого газа
- В металлургии для извлечения металлов из их оксидов и хлоридов электролитическим разложением
Повседневная жизнь
- кислота распадается с образованием воды и углекислого газа, что вызывает шипение.
- Во время переваривания пищи в нашем организме углеводы, жиры и белки расщепляются с образованием множества более простых веществ.
- Фотопленки имеют покрытие из бромида серебра, которое при воздействии света распадается на серебро и бром.
- Когда перекись водорода наносится на порез или рану, перекись разлагается и образует пузырьки кислорода и лопается.
- При выпечке пирога с разрыхлителем (гидрокарбонатом натрия) разложение приводит к образованию двуокиси углерода и гидроксида натрия.
- В пищевых продуктах наблюдаются многие органические разложения, такие как ферментация и обрастание. Гниение пищевых продуктов и кожуры овощей дает отличные питательные вещества и навоз для почвы.
Лаборатория
- В некоторых аналитических методах, таких как масс-спектрометрия, гравиметрический анализ и термогравиметрический анализ
Часто задаваемые вопросы
Q.
Ответ. Для большинства реакций разложения требуется энергия в виде тепла, света или электричества. Поглощение энергии вызывает разрыв связей, присутствующих в реагирующем веществе, которое разлагается с образованием продукта.
Q.2. Чем реакция соединения отличается от реакции разложения?
Ответ. В реакции соединения два или более веществ объединяются с образованием одного продукта. Однако в реакции разложения одно вещество распадается на два или более веществ. Следовательно, они противоположны друг другу. Как правило, комбинированные реакции в основном экзотермические, а реакции разложения эндотермические.
В.3. Является ли разложение окислительно-восстановительной реакцией?
Ответ.
Q.4. Является ли разложение аспирина реакцией разложения?
Ответ. Нет. Разложение аспирина — это реакция двойной замены.
Ссылки
- Amrita.olabs.edu.in
- Chem.libretexts.org
- Opentextbc.ca
- Cpanhd.sitehost.iu.edu
- Chem.wisc.edu
- Angelo.eduYork.ac.uk
Формула разложения Verlinde Sums
[1] Алексеев, Антон; Майнренкен, Экхард; Вудворд, Кристофер Формулы Верлинде как формулы с фиксированной точкой, J. Symplectic Geom., Volume 1 (2001) no. 1, стр. 1-46 | DOI | Г-Н | Збл
[2] Алексеев, Антон; Майнренкен, Экхард; Вудворд, Кристофер Дуистермаат-Хекман, меры и пространства модулей плоских расслоений над поверхностями, Geom.
[3] Бальдони, М. Велледа; Бек, Матиас; Коше, Чарльз; Vergne, Michele Вычисление объема для многогранников и статистические суммы для классических корневых систем, Discrete Comput. Геом., Том 35 (2006), нет. 4, стр. 551-595 | DOI | Г-Н | Збл
[4] Бальдони, М.
[5] Бойсал, Арзу; Vergne, Формула пересечения стены Мишель Парадан для статистических сумм и дифференциальный оператор Хованского-Пухликова, Ann. Инст. Фурье, Том 59 (2009), нет. 5, стр. 1715-1752.
[6] Бойсал, Арзу; Вернь, Множественный ряд Мишель Бернулли, формула Эйлера – Маклорена и пересечения стен, Ann. Инст. Фурье, Том 62 (2012) нет. 2, стр. 821-858 | DOI | Намдам | Г-Н | Збл
[7] Брион, Мишель; Вернь, Мишель Расположение гиперплоскостей, I: Рациональные функции и вычет Джеффри – Кирвана, Ann.
[8] Дамен, Вольфганг; Микчелли, Чарльз А. Число решений линейных диофантовых уравнений и многомерных сплайнов, Trans. Являюсь. Мат. Soc., Том 308 (1988) нет. 2, стр. 509-532 | DOI | Г-Н | Збл
[9] Гиймен, Виктор; Прато, Элиза Хекман, формулы Костанта и Стейнберга для симплектических многообразий, Adv.
[10] Гиймен, Виктор В.; Лерман, Юджин М.; Штернберг, Шломо О формуле кратности Костанта, J. Geom. Phys., Том 5 (1988) нет. 4, стр. 721-750 | DOI | Г-Н | Збл
[11] Лоизидес, Яннис локализация норм-квадрата для гамильтоновых LG-пространств, J.
[12] Майнренкен, Скрученные K-гомологии Экхарда и карты моментов с групповыми значениями, Int. Мат. Рез. Не., Том 2012 (2012) нет. 20, стр. 4563-4618 | DOI | Г-Н
[13] Парадан, Поль-Эмиль Локализация характера Римана-Роха, J.
[14] Парадан, Формулы пересечения стены Пола-Эмиля в гамильтоновой геометрии, Геометрические аспекты анализа и механики (Прогресс в математике), том 292, Биркхойзер, 2011, стр. 295-343. | DOI | Г-Н | Збл
[15] Szenes, András Проверка формул Verlinde для SU (2), Int.
[16] Сенеш, Андраш. Комбинаторика формулы Верлинде, Векторные расслоения в алгебраической геометрии (Дарем, 1993) (серия лекций Лондонского математического общества), том 208, издательство Кембриджского университета, 1995, стр. 241–253. | DOI | Г-Н | Збл
[17] Szenes, András Итерированные остатки и множественные многочлены Бернулли, Int.
[18] Сенеш, Андраш Теорема о вычетах для рациональных тригонометрических сумм и формула Верлинде, Duke Math. Дж., Том 118 (2003) нет. 2, стр. 189-227 | Г-Н | Збл
[19] Сенеш, Андраш; Вернь, Мишель Формулы вычетов для векторных разбиений и сумм Эйлера – Маклорена, Adv.
[20] Сенеш, Андраш; Вернь, Мишель [Q, R] = 0 и статистические суммы Костанта, Enseign. Матем., Том 63 (2017) нет. 3-4, стр. 471-516 | Г-Н | Збл
[21] Thaddeus, Michael Конформная теория поля и когомологии пространства модулей стабильных расслоений, J.
[22] Вернь, Мишель Множественные серии Бернулли и пересечение стен (слайды для встречи AMS в Сан-Франциско, 2010 г.) | Намдам | Збл
[23] Вернь, Мишель Формулы вычетов для сумм Верлинде и для числа целых точек в выпуклых рациональных многогранниках, Европейские женщины в математике (Мальта, 2001 г.
[26] Верлинде, Эрик Правила слияния и модульные преобразования в двумерной конформной теории поля, Nucl.
[27] Виттен, Эдвард О квантовых калибровочных теориях в двух измерениях, Commun. Мат. Phys., том 141 (1991), нет. 1, стр. 153-209. | DOI | Г-Н | Збл
Урок видео: Термическое разложение | Nagwa
Стенограмма видео
В этом видео мы узнаем, как описать и привести примеры реакций термического разложения.
Реакция разложения – это тип химическая реакция, при которой соединение распадается на более простые вещества. Реагент разложения реакция представляет собой соединение, а продукты реакции разложения могут быть элементы, соединения или и то, и другое. Самый распространенный тип реакция разложения называется термическим разложением.
Термическое разложение – это расщепление вещества при нагревании с образованием двух или более других веществ. Фактор, вызывающий химическая реакция происходит тепло. В химическом уравнении 𝛥 символ, который выглядит как треугольник, представляет добавление тепла.
Напротив, в термическом реакция разложения, нагревание вызывает химическое изменение. Образуются новые вещества, и мы могут наблюдать признаки того, что произошло химическое изменение, такое как образование газ, изменение цвета или запах. Множество различных типов соединений могут подвергаться реакциям термического разложения. Фактически, многие карбонаты металлов могут разлагаются при нагревании с образованием оксида металла и углекислого газа.
Карбонаты металлов химические соединения, состоящие из положительно заряженных катионов металлов и отрицательно заряженных карбонат-анионы. Карбонат-анион имеет химическое формула CO32−. Некоторые примеры карбонатов металлов подвергаются реакциям термического разложения: карбонат меди(II), свинец(II) карбонат и карбонат цинка.
В карбонате меди(II) медь ион имеет заряд два плюс, а ион карбоната имеет заряд два минус. Химические соединения нейтральны. Таким образом, общая сумма заряда должна равен нулю, что верно в данном случае. Поэтому химическая формула карбонат меди(II) – CuCO3. Как для карбоната свинца(II), так и карбоната цинка сумма зарядов ионов также равна нулю. Таким образом, химические формулы этими двумя соединениями являются PbCO3 и ZnCO3.
При нагревании карбоната металла и он разлагается, есть два продукта: оксид металла и углекислый газ. Допустим, твердый свинец(II) карбонат в пробирке нагревают горелкой Бунзена, в результате чего свинец (II) карбонат разлагаться.
Если сравнить массу твердого тела в пробирке до реакции на твердое вещество в пробирке после реакции, мы бы увидели, что масса уменьшилась. Мы ожидаем, что масса будет то же самое до и после реакции, потому что закон сохранения массовых состояний что масса продуктов должна равняться массе реагентов в химическом реакция. Проблема в том, что углерод газообразный диоксид, образовавшийся в результате реакции, вышел из пробирки до того, как мы смогли найти масса.
Теперь, когда мы знаем этот металл карбонаты могут быть разложены при нагревании с образованием оксида металла и диоксида углерода. газа, давайте узнаем, как эти реакции представлены с помощью химических уравнения. Карбонат цинка представляет собой карбонат металла который разлагается при нагревании. Напишем словесное уравнение представляют эту реакцию. Карбонат цинка является реагентом Реакция. Поэтому мы напишем это перед стрелка реакции. Над стрелкой реакции нам нужно чтобы использовать символ 𝛥 для обозначения нагрева. Есть два продукта компании реакция. Одним из продуктов является оксид цинка, который представляет собой оксид металла, а другой продукт — двуокись углерода. Углекислый газ всегда является одним из продукты термического разложения карбоната металла.
Вместо представления реакции, используя названия участвующих веществ, мы могли бы также написать химическую уравнения с использованием химических формул.
Как карбонат цинка, так и оксид цинка иметь похожий внешний вид; они оба представляют собой белые твердые вещества. Как определить, является ли химическое реакция произошла? Нам нужен способ обнаружения углерода образовавшийся диоксид. Один из аппаратов, используемых для обнаружения Для образования углекислого газа используются следующие детали: пробирка для нагрева, который содержит твердый карбонат цинка и закреплен на подставке, чтобы удерживать его в место.
Поскольку образуется двуокись углерода внутри пробирки, которая нагревается, она проходит через подающую трубку и в пробирку, наполненную известковой водой. Известковая вода представляет собой водный раствор гидроксид кальция. Как пузырьки углекислого газа через известковую воду раствор известковой воды начинает мутнеть. Этот полезный визуальный знак говорит нам что карбонат цинка действительно разложился на оксид цинка и углекислый газ.
Теперь нам нужно обсудить безопасность меры предосторожности, необходимые при проведении термического разложения в лаборатории. Прежде чем мы начнем наш эксперимент, мы должны надеть наши защитные очки; осмотрите стеклянную посуду, например, пробирки, на сколы или трещины; и очистите нашу рабочую зону от любых легковоспламеняющихся материалов.
После выключения Бунзена горелки, крайне важно, чтобы подающая трубка была отсоединена от пробирка с известковой водой. Если трубка доставки не отсоединяют от пробирки, наполненной известковой водой, затем по мере остывания оборудования вниз, известковая вода могла стекать обратно в нагреваемую пробирку, что стекло может треснуть или даже разбиться. Эффект известен как всасывание и можно предотвратить, удалив нагнетательную трубку, как только горелка Бунзена погаснет. был выключен. Нагрев химикатов в стеклянной посуде в лаборатория опасна. Обязательно соблюдайте технику безопасности меры предосторожности и инструкции вашего учителя.
Существуют и другие виды химических соединения, способные вступать в реакции термического разложения.
Давайте обсудим еще два тепловых реакции разложения. Оксид ртути(II) разлагается на нагревание с образованием элементарной ртути и газообразного кислорода. А нитрат натрия разлагается при нагревание с образованием нитрита натрия и газообразного кислорода.
Прежде чем мы подведем итог тому, что мы узнали о термическом разложении в этом видео, давайте посмотрим на вопрос.
Какой из следующих химических уравнения показывает термическое разложение карбоната цинка? (A) Твердый ZnCO3 реагирует с образованием ZnO твердое вещество плюс газ CO2. (B) Реакция твердого ZnO и газообразного CO2 образуют твердый ZnCO3. (C) ZnC2 плюс газообразный O2 реагируют с образованием два твердых ZnO плюс газообразный CO2.
В этом вопросе мы просят определить, какое из химических уравнений, представленных в вариантах ответа правильно представляет термическое разложение карбоната цинка. Термическое разложение определяется как расщепление вещества при нагревании с образованием двух или более других вещества. Поскольку процесс термического разложение образует новые вещества, это тип химической реакции и может быть представлен химическим уравнением.
Внимательно прочитав это определения, мы замечаем, что в ходе реакции термического разложения один реагент распадается с образованием двух и более продуктов. Имея в виду это определение, давайте посмотрим на варианты ответов, предоставленные нам.
Теперь давайте рассмотрим подробнее варианты ответов (C) и (D). В обоих этих химических уравнений, мы замечаем, что есть два реагента. По определению термальный Реакция разложения происходит, когда один реагент разрушается при нагревании. Поэтому эти два химических уравнения не могут представить термическое разложение карбоната цинка.
Таким образом, вариант ответа (А) должен быть правильный ответ. Но давайте обсудим немного больше почему это так.
При нагревании карбоната цинка он будет разлагаться с образованием оксида цинка, который является оксидом металла, и углекислого газа газ. Следовательно, химическое уравнение который показывает термическое разложение карбоната цинка, является выбором ответа (A). Твердый ZnCO3 реагирует с образованием ZnO твердое вещество плюс газ CO2.
Подытожим, что имеем узнал о термическом разложении. Во-первых, термическое разложение. является химическим изменением. Производятся новые вещества, и мы могут увидеть признаки химической реакции, такие как выделяющийся газ или цвет сдача. Реакция термического разложения происходит, когда вещество нагревается и распадается на два или более новых вещества. Когда карбонат металла термически разлагается, продукты реакции — оксид металла и углекислый газ газ. Наличие углекислого газа Произведенное вещество можно обнаружить, пропуская его через известковую воду. Известковая вода, представляющая собой водный раствор гидроксида кальция мутнеет в присутствии углекислого газа газ.
Нам нужно соблюдать технику безопасности меры предосторожности при нагревании химических веществ в лаборатории.
Общая формула декомпозиции для ценообразования ванильных опционов в стохастических моделях волатильности
Мы получаем декомпозицию цены колл-опциона для очень общей модели диффузии стохастической волатильности, расширяя предыдущую формулу декомпозиции для модели Хестона. Мы понимаем, что новый термин возникает, когда цена акций не следует экспоненциальной модели. Методы, используемые для этой цели, являются неупреждающими. В частности, мы также видим, что эквивалентные результаты могут быть получены с использованием функционального исчисления Ито.
1. Введение
Стохастические модели волатильности являются естественным расширением модели Блэка-Шоулза для управления перекосом и улыбкой, наблюдаемыми в реальных данных. Хорошо известно, что в этих моделях релевантной величиной является среднее значение будущей волатильности. См., например, [1, гл. 2]. К сожалению, добавление стохастической структуры волатильности усложняет ценообразование и калибровку, поскольку не всегда существуют закрытые формулы. См., например, [2] для первой ссылки на эту тему. Более того, даже когда эти формулы существуют, как, например, для модели Хестона (см. [3]), в общем случае они не позволяют провести быструю калибровку параметров.
В последние годы были опубликованы различные разработки по нахождению приближений к формулам ценообразования опционов в закрытой форме. Методы Маллявена, естественно, используются для решения этой проблемы в [4, 5], поскольку средняя будущая волатильность является упреждающей величиной. В противном случае для модели Хестона в [6] разработан неупреждающий метод получения аппроксимации формулы ценообразования. Метод основан на использовании адаптированной проекции средней будущей волатильности. В результате модель позволяет получить декомпозицию цены колл-опциона с точки зрения такой будущей волатильности.
В настоящей статье мы обобщаем [6] на общие стохастические модели диффузии волатильности. Точно так же, следуя тем же идеям, мы расширяем разложение, основанное на исчислении Маллявена, полученное в [4, 5]. Это важно, поскольку модель Хестона не является единственной стохастической моделью волатильности, используемой в настоящее время на практике, а некоторые из них, например модель SABR, не относятся к экспоненциальному типу.
Основные идеи, развитые в этой статье, следующие: (i) Общая декомпозиция цены опциона колл находится без указания структуры волатильности. (ii) Новый термин появляется, когда цены опциона на акции не следуют экспоненциальной модели. , как, например, в случае SABR. (iii) Формула Фейнмана-Каца является ключевым элементом в разложении. Это позволяет выразить новые термины, возникающие в новой структуре (т. е. стохастическую волатильность), как поправки к формуле Блэка-Шоулза. (iv) Разложение, полученное с помощью функционального исчисления Ито, похоже, такое же, как разложение, полученное с помощью наших методов. (v) Дано общее выражение производной подразумеваемой волатильности как для неупреждающего, так и упреждающего случаев.
2. Обозначения
Пусть — строго положительный ценовой процесс при выбранной рынком нейтральной к риску вероятности, которая следует модели, где и — независимые броуновские движения, , , , и — положительный интегрируемый с квадратом процесс, адаптированный к фильтрации .
О существовании и единственности решения в случае Хестона см., например, [8, раздел 2.2]. Для моделей CEV и SABR см. [9] и ссылки в ней.
Во всей статье будут использоваться следующие обозначения: (i) Мы будем обозначать ценой простого ванильного европейского колл-опциона в рамках классической модели Блэка-Шоулза с постоянной волатильностью, текущей ценой акции, временем до погашения, ценой исполнения , и процентная ставка . В этом случае, где обозначает кумулятивную функцию вероятности стандартного нормального закона и (ii) Мы используем во всей статье обозначение , где естественная фильтрация .
3. Формула разложения с использованием исчисления Ито
В этом разделе, следуя идеям из [6], мы распространяем формулу разложения на общий процесс диффузии стохастической волатильности. Отметим, что новую формулу можно расширить без указания основного процесса волатильности, получив более гибкую формулу декомпозиции. Когда цена акции не следует экспоненциальному процессу, появляется новый термин. Формула, доказанная в [6], является частным случаем.
Хорошо известно, что если процесс стохастической волатильности независим от ценового процесса, то формула ценообразования простого ванильного европейского колла задается формулой где есть так называемая средняя будущая дисперсия и определяется она, естественно, называется средней будущая волатильность. См. [1, стр. 51].
Идея, использованная в [6], заключается в рассмотрении адаптированной проекции средней будущей дисперсии для получения разложения по .
Теорема 1 (формула разложения). Для всех имеем где .
Доказательство. Обратите внимание на это. Как мартингал, мы можем написать Наша идея состоит в том, чтобы применить формулу Ито к процессу
Поскольку производные не ограничены, мы должны использовать приближение к тождеству, изменяющемуся на где для некоторых таких, что для всех и для всех , и через , где , и, наконец, применить теорему о мажорируемой сходимости. Для простоты мы опускаем этот успокаивающий аргумент в статье.
Итак, применяя формулу Ито, используя тот факт, что и оператор Фейнмана-Каца (7), мы выводим Взяв условное математическое ожидание и умножив на , мы имеемЗамечание 2. В [6] определены следующие операторы для :(i)(ii)(iii)
Заметим следующее: (i)(ii)(iii).Замечание 3. Мы распространили формулу разложения из [6] на СДУ общего положения (1). Когда мы применяем исчисление Ито, мы понимаем, что формула Фейнмана-Каца поглощает некоторые из возникающих терминов. Важно отметить, что этот метод работает для любого выигрыша или любой диффузионной модели, удовлетворяющей формуле Фейнмана-Каца.
Примечание 4. Обратите внимание, что когда (т. е. цена акций следует экспоненциальному процессу), тогда и член исчезает.
Действительно, мы показываем, что благодаря использованию формулы Фейнмана-Каца, где используется в формуле Фейнмана-Каца и4. Основные элементы функционального исчисления Ито
Исчисление Ито разработано в [10–13].
Пусть — процесс Ито, т. е. непрерывный семимартингал, определенный на фильтрованном вероятностном пространстве, который допускает стохастическое интегральное представление где — броуновское движение и — непрерывные процессы соответственно в и .
Определим пространство кадлаг-функций.
В этой структуре у нас есть следующие определения производной.
Определение 5 (горизонтальная производная). Горизонтальная производная функционала at определяется как
Определение 6 (вертикальная производная). Вертикальная производная функционала at определяется как Конечно, мы можем рассматривать повторяющиеся производные как .
У нас также есть следующая формула Ито, которая работает для неупреждающих функционалов:
Теорема 7 (Функциональная формула Ито). Для любого неупреждающего функционала и любого , имеем при условии, что , и принадлежат .
Доказательство. См. [11, 12].
5. Общая декомпозиция с использованием функционального исчисления Ито
В этом разделе мы применяем функциональное исчисление Ито к проблеме нахождения декомпозиции для цены опциона колл. Проблема декомпозиции является упреждающей задачей, зависящей от пути. Используя разумный выбор процесса волатильности в формуле Блэка-Шоулза, мы можем преобразовать его в неупреждающий. Естественно задаться вопросом, не привнесет ли Функциональное исчисление Ито в проблему что-то новое.
Рассмотрим функционал где – зависящий от пути процесс, а – неупреждающий функционал.
В соответствии с этой структурой мы вычисляем производные с использованием функционального исчисления Ито по отношению к дисперсии. Затем мы записываем их в терминах классических производных Блэка-Шоулза. Мы должны понимать, что для простоты новые производные рассчитываются относительно дисперсии, а не изменчивости процесса.
Замечание 8.
Теорема 9 (формула разложения). Для всех , , и имеем
Доказательство. Обратите внимание, что . Как и в случае мартингала, мы можем написать Наша идея состоит в том, чтобы применить приближение к аргументу тождества, как в теореме 1, а затем использовать функциональную формулу Ито, чтобы вывести это. Обратите внимание, что (i) поскольку это не зависит от пути, мы имеем это ; (ii) так как и является неупреждающим функционалом, то .
Итак, мы имеем Мы заключаем, что Взяв теперь условные математические ожидания, используя (15) и умножив на , мы получим, чтоЗамечание 10. Заметим, что функциональная формула Ито, доказанная в [11], справедлива для семимартингалов, а в [12] также доказана для процесса Дирихле. В обоих случаях гипотеза выполняется по определению и дифференцируемости производных функции Блэка-Шоулза при .
Замечание 11. Заметим, что теорема 9 совпадает с теоремой 1 при выборе функции волатильности в качестве . Мы обнаружили эквивалентность идей, развитых в [6, 10–13], в задаче о декомпозиции. Обе формулы исходят из разных точек зрения; идеи [10–13] основаны на распространении на функционалы работы [14], а основная идея [6] состоит в изменении процесса его ожиданием. Поймите, что стандартное исчисление Ито также может быть применено к процессам Дирихле (дополнительную информацию см. в [14]).
Замечание 12. Поймите, что теорема 9 верна для любого неупреждающего . Нетривиально найти другой неупреждающий процесс, отличный от выбранного в [6].
6. Основные элементы исчисления Маллявена
В следующем разделе мы представляем краткое введение в основные факты исчисления Маллявена. Для получения дополнительной информации см. [15].
Рассмотрим броуновское движение, заданное на полном вероятностном пространстве.
Мы будем использовать следующую формулу Ито для упреждающих процессов.
Предложение 13. Рассмотрим процессы , где . Кроме того, рассмотрим также процесс , для некоторых . Позвольте быть дважды непрерывно дифференцируемой функцией такой, что существует положительная постоянная такая, что для всех и ее производных, оцененных в, ограничены .
Доказательство. См. [4].
Следующее предложение полезно, когда мы хотим вычислить производную Маллявена.
Предложение 14. Пусть и — непрерывно дифференциальные функции на с ограниченными производными. Рассмотрим решение стохастического дифференциального уравнения: Тогда имеем , где .
Доказательство. См. [15, раздел 2.2].
7. Формула декомпозиции с использованием исчисления Маллявена
В этом разделе мы используем исчисление Маллявена для расширения декомпозиции цены колл-опциона в упреждающей структуре. На этот раз в формуле разложения на один член меньше, чем в формуле Ито.
Напомним определение будущей средней волатильности как
Теорема 15 (формула разложения). Для всех имеем где
Доказательство. Обратите внимание, что . Как мартингал, мы можем написать Так, используя приближение к тождественному аргументу и применяя формулу Ито, представленную в предложении 13, чтобы вывести, используя (15) и (7), что Взяв условное математическое ожидание и умножив на , мы имеем
Замечание 16.
Замечание 17. В частности, при раздел формулы.
Замечание 18. Заметим, что в случае детерминированной функции все формулы разложения равны.
Замечание 19. Когда , имеем В частности, когда , Разница между двумя подходами определяется объемом опциона.
8. Выражение для производной подразумеваемой волатильности
В этом разделе мы даем общее выражение для производной подразумеваемой волатильности в рамках исчисления Ито и исчисления Маллявена. Предыдущее вычисление этой производной в случае экспоненциальных моделей с использованием исчисления Маллявена дано в [5].
Обозначим процесс подразумеваемой волатильности, который по определению удовлетворяет . Мы вычисляем производную подразумеваемой волатильности в стандартном случае Ито.
Предложение 20. В соответствии с (1), для каждого фиксированного и предполагая, что п.
Доказательство. Взяв частные производные по от выражения , получим С другой стороны, из теоремы 1 выводим то, что следует, что Используя тот факт, что , можно проверить, что корректно определено и конечно п.н. Таким образом, используя тот факт, что , (59) и (61), получаем Из [16] мы знаем, что , где – подразумеваемая волатильность в случае , значит, имеем, что С другой стороны, имеем, что где – стандартная гауссова плотность. Затем
Теперь мы получаем подразумеваемую волатильность, используя исчисление Маллявена. Это сделано в [5] для случая .
Предложение 21. В соответствии с (1) для каждого фиксированного и предполагая, что п.н., имеем где
Доказательство. См. [5] или предыдущее доказательство.
Замечание 22. Отметим, что это обобщение формулы, доказанной в [5]. В таком случае и .
9. Примеры
В этом разделе мы приводим некоторые приложения формулы декомпозиции к известным моделям в финансах.
9.1. Heston Model
Мы считаем, что цена акций соответствует модели Heston (1). Используя теорему 1 или теорему 9, мы имеем
. Используя теорему 15, мы имеем, что где
9.2. Модель SABR
Мы считаем, что цена акции соответствует модели SABR (3). Используя теорему 1 или теорему 9, имеем, где
. Используя теорему 15, имеем, что где .
10. Заключение
В этой статье мы отмечаем, что идея, использованная в [6], может быть использована для общего стохастического дифференциального уравнения (СДУ). Нет необходимости указывать процесс волатильности. Необходимы только существование и единственность решения СДУ, что обеспечивает гораздо большую гибкость формулы разложения. Мы наблюдаем, каков эффект предположения, что цена акций следует экспоненциальному процессу, и как в общей структуре возникает новый термин. Кроме того, мы вычислили разложение, используя три различных метода: формулу Ито, функциональное исчисление Ито и исчисление Маллявена.
Конфликт интересов
Авторы заявляют об отсутствии конфликта интересов в связи с публикацией данной статьи.
Copyright © 2015 Рауль Мерино и Хосеп Вивес. Это статья с открытым доступом, распространяемая в соответствии с лицензией Creative Commons Attribution License, которая разрешает неограниченное использование, распространение и воспроизведение на любом носителе при условии надлежащего цитирования оригинальной работы.
Руководство по изучению реакции разложения | Inspirit
Реакция разложения — это химическая реакция, при которой из одного реагента получаются два или более продуктов.
ВВЕДЕНИЕ
Мы изучали химические реакции, в которых участвует один или несколько реагентов, в результате которых образуются продукты. Одно из основных правил состоит в том, что левая сторона — это реагенты, а правая — продукты. Однако химические реакции можно разделить на различные типы, из которых реакции разложения являются основным типом.
Источник
ЧТО ТАКОЕ РЕАКЦИЯ РАЗЛОЖЕНИЯ?
Если в результате химической реакции два или более продуктов получаются с использованием только одного реагента, то такая химическая реакция называется реакцией разложения. Общая форма любой реакции разложения будет следующей:
АВ → А + ВИсточник
Уравнения разложения также можно назвать реакциями анализа или даже химическими разложениями. Противоположностью реакции разложения будет синтез, при котором более одного реагента объединяются с образованием сложного продукта. Реакции разложения можно легко распознать, ища отдельные реагенты с более чем одним продуктом.
ПРИМЕРЫ РЕАКЦИЙ РАЗЛОЖЕНИЯ
Если вы обратите внимание, реакции разложения происходят каждый день в вашей жизни. Одним из них был бы электролиз воды с образованием газообразного водорода и кислорода.
2 H₂O → 2 H₂ + O₂Другим примером может служить разложение перекиси водорода с образованием воды и кислорода.
2 H₂O₂ → 2 H₂O + O₂Другим примером реакции разложения может быть нагревание зеленого карбоната меди; он разлагается с образованием оксида меди, а также двуокиси углерода.
CuCO₃ → CuO + CO₂(г)Соединение изменит цвет со светло-зеленого на черный.
ТИПЫ РЕАКЦИЙ РАЗЛОЖЕНИЯ
Существуют три типа реакций разложения, в основном:
Термическое разложение: Реакция термического разложения активируется теплом. Этот тип реакции разложения является эндотермическим. Ярким примером реакции термического разложения может быть разложение карбоната кальция с образованием диоксида углерода и оксида кальция.
CaCO₃ → CaO + CO₂Электролитическое разложение: Чтобы реагенты разлагались более чем на один продукт, электрическая энергия снабжает эту реакцию энергией активации. Электролиз воды, как упоминалось выше, является ярким примером.
Фотолитическое разложение: Реагент поглощает энергию фотонов, чтобы разорвать химические связи и затем сформировать продукты. Примером такой реакции разложения может быть разложение озона с образованием кислорода.
O₃ hv → O₂ + OЕсли катализатор способствует какой-либо реакции разложения, то ее можно назвать реакцией каталитического разложения.
Применение:
Источник
- Реакция разложения используется для получения негашеной извести для цемента.
- Используется для сварки термитной реакцией.
- Чтобы облегчить кислотное расстройство желудка.
- Для идентификации любого образца на основе реакции разложения и полученных продуктов.
- Другим важным применением этой реакции может быть извлечение чистых металлов из их хлоридов, оксидов, а также руд.
ЗАКЛЮЧЕНИЕ
- Реакция разложения – это химическая реакция, при которой из одного реагента получаются два или более продуктов.
- Простой способ определить реакцию разложения — посмотреть на количество продуктов.
- Реакции разложения бывают трех типов: термическое разложение, фотолитическое разложение, электролитическое разложение.
Часто задаваемые вопросы
1. Как происходит разложение карбоната меди?
Это реакция термического разложения, при которой нагревая зеленый карбонат меди, он разлагается с образованием оксида меди, а также двуокиси углерода.
2. Каково сбалансированное уравнение для карбоната меди?
Сбалансированное уравнение для карбоната меди будет следующим:
CuCO₃ → CuO + CO₂(г)
Мы надеемся, что вам понравился этот урок, и вы узнали что-то интересное о Реакция разложения ! Присоединяйтесь к нашему сообществу Discord, чтобы получить ответы на любые вопросы и пообщаться с другими студентами, такими же, как и вы! Не забудьте загрузить наше приложение, чтобы испытать наши веселые классы виртуальной реальности — мы обещаем, это делает учебу намного веселее! 😎
ИСТОЧНИКИ
- Реакция разложения: https://www.
плавка → Cr 2 O 3 (с) + N 2 (г) + 4 H 2 O (г)
1. Почему реакции разложения носят в основном эндотермический характер? 
Нет. Не все разложения являются окислительно-восстановительными реакциями.
Функц. Анал., Том 12 (2002), нет. 1, стр. 1-31
|
DOI
|
Г-Н
|
Збл
Велледа; Бойсал, Арзу; Вернь, Мишель Кратные ряды Бернулли и объемы пространств модулей плоских расслоений над поверхностями, J. Symb. вычисл., том 68 (2015) нет. 2, стр. 27-60
|
DOI
|
Г-Н
|
Збл
|
DOI
|
Намдам
|
Г-Н
|
Збл
науч. Эк. Норма. Super., Том 32 (1999) нет. 5, стр. 715-741
|
DOI
|
Намдам
|
Г-Н
|
Збл
Матем., Том 82 (1990), нет. 2, стр. 160-179
|
DOI
|
Г-Н
|
Збл
Geom. Phys., Том 114 (2017), стр. 420-449.
|
DOI
|
Г-Н
|
Збл
Funct. Анал., Том 187 (2001), нет. 2, стр. 442-509
|
DOI
|
Г-Н
|
Збл
Мат. Рез. Не., Том 1991 (1991) нет. 7, стр. 93-98
|
DOI
|
Г-Н
|
Збл
Мат. Рез. Не., Том 18 (1998), стр. 937-956
|
DOI
|
Г-Н
|
Збл
заявл. Матем., Том 30 (2003) нет. 1-2, стр. 295-342
|
DOI
|
Г-Н
|
Збл
Differ. Геом., Том 35 (1992) нет. 1, стр. 131-149
|
Г-Н
|
Збл
), World Scientific, 2003 г., стр. 225-285.
|
DOI
|
Збл
9-класс, сплайны и кратности индекса трансверсально эллиптических операторов, Изв. Росс. акад. наук, сер. Матем., Том 80 (2016) нет. 5, стр. 157-192
|
Г-Н
|
Збл
Phys., B, том 300 (1988), стр. 360-376.
|
DOI
|
Збл
Мы объясним, почему тепловой
разложение — это химическое изменение, используйте химические уравнения, чтобы представить их
реакций, а также показать меры предосторожности, связанные с выполнением термических
разложение в лаборатории.
Мы знаем, что тепло можно добавить к
вещество изменить свое состояние, например, растопить лед, и что это было бы
считается физическим изменением.
Карбонат калия является еще одним
пример карбоната металла, но для его разложения требуется гораздо больше тепла, чем
к другим перечисленным карбонатам. Химические формулы металла
карбонаты всегда пишутся сначала с катионами металлов, а с анионами карбонатов.
второй.
Карбонат свинца(II), представляющий собой
белое твердое вещество, является реагентом реакции термического разложения. После реакции остается твердое вещество
в пробирке, но твердое вещество желтого цвета. Это изменение цвета является признаком того, что
произошла химическая реакция. Желтое твердое вещество известно как
оксид свинца (II) и имеет химическую формулу PbO. Но оксид свинца(II) является лишь одним из
продукты реакции. Другой продукт — углерод
диоксид.
Химическая формула цинка
карбонат ZnCO3. Карбонат цинка представляет собой твердое вещество, поэтому мы
также может включать символ состояния «s». Оксид цинка также является
твердый и имеет химическую формулу ZnO. И химическая формула углерода
двуокись, с которой мы хорошо знакомы, — это CO2. Углекислый газ — это газ, поэтому мы будем
используйте здесь символ состояния «g».
Горелка Бунзена с регулируемым
Синее пламя используется для непрерывного нагревания карбоната цинка в пробирке.
После того, как мы увидим поворот известковой воды
мутно, реакция завершена.
Например, гидроксид меди(II)
разлагается при нагревании с образованием оксида меди (II) и воды. А сульфат меди(II) разлагается
путем нагревания с получением оксида меди (II) и газообразного триоксида серы. Эти две реакции очень
похожий. Оба они производят оксид меди (II),
который представляет собой оксид металла. При нагревании гидроксида меди образуется
водяной пар, при нагревании сульфата меди(II) образуется газообразный триоксид серы. Если сравнить эти две реакции
к термическому разложению карбоната меди(II), мы увидим, что все три
реакции производят оксид меди (II), но в процессе образуются разные газы.
каждой реакции.
Мы замечаем, что в обоих этих
реакции разложения, кислород газообразный является одним из продуктов. В лаборатории мы не можем увидеть
образуется газообразный кислород. Однако, если мы зажжем деревянную
шину, а затем осторожно задуйте пламя так, чтобы шина светилась, затем, когда
мы помещаем светящуюся деревянную шину в пробирку, шина снова загорается и
ярко гореть, если выделяется газообразный кислород.
(D) Два твердых ZnO плюс твердый C
реагируют с образованием двух твердых частиц Zn и газообразного CO2. (E) Реакция двух твердых частиц Zn и газообразного O2
с образованием двух твердых ZnO.
Во всех вариантах ответа
кроме вариантов ответа (B) и (E), образуется два или более продуктов. В варианте ответа (B) твердый ZnCO3
образуется единственный продукт. И в варианте ответа (E), ZnO твердый
образуется единственный продукт. Поскольку эти два химических
уравнения имеют только один продукт, они не могут представлять термическое разложение
реакции. Так что мы можем их устранить.
Карбонат цинка является разновидностью
соединение, называемое карбонатом металла. Когда карбонаты металлов подвергаются
реакция термического разложения, они производят оксид металла и углекислый газ
газ. Карбонаты металлов состоят из
положительно заряженные ионы металлов и отрицательно заряженные ионы карбоната. Одна единица карбоната цинка составляет
состоит из одного цинка два плюс иона и карбонат-иона. Сумма зарядов этих двух
ионов равно нулю. Поэтому химическая формула
карбонат цинка можно записать как ZnCO3.
Мы всегда должны носить очки
и осмотрите стеклянную посуду на наличие сколов или трещин, прежде чем использовать ее в эксперименте. И очень важно избегать
всасывать обратно, что может привести к ситуации, когда горячая пробирка, полная химикатов,
мог разбиться. Наконец, мы также узнали, что
кроме карбонатов металлов термическому разложению подвергаются и другие вещества
реакции, такие как гидроксид меди, сульфат меди, нитрат натрия и ртуть
окись.
Используя те же обобщающие идеи, мы также распространяем на неэкспоненциальные модели формулу декомпозиции цены альтернативного колл-опциона, записанную в терминах производной Маллявена процесса волатильности. Наконец, мы даем общее выражение для производной подразумеваемой волатильности как в упреждающем, так и в неупреждающем случаях.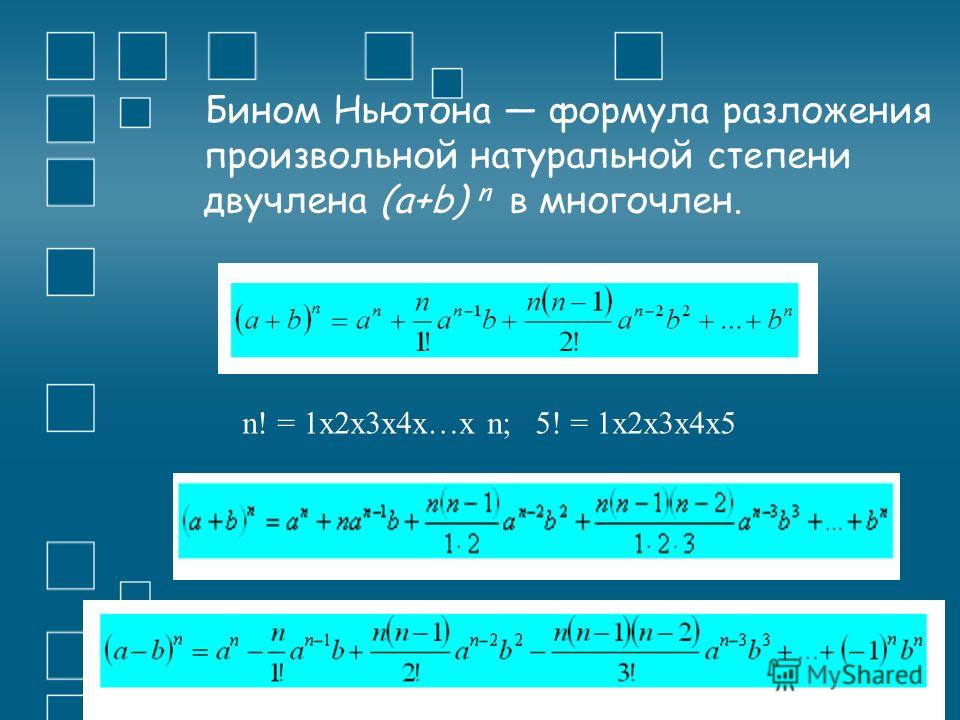
Общее обсуждение моделей стохастической волатильности на практике см. в [7].
Предположим, что и достаточные условия, обеспечивающие существование и единственность решения уравнения (1). Обратите внимание, что мы не предполагаем никакой конкретной структуры волатильности. Таким образом, наши разложения могут быть адаптированы ко многим различным моделям. В частности, мы рассматриваем следующие модели: (i) модель Блэка-Шоулза: , , , и . (ii) модель CEV: , с , , , и . (iii) модель Хестона: , , , , и где , , и положительные константы, удовлетворяющие условию Феллера .(iv)Модель SABR: , с , , , и с
(iii) В наших условиях цена опциона колл определяется как ( iv) Вспоминая, что из формулы Фейнмана-Каца оператор удовлетворяет . (v) Мы также будем использовать следующие определения для :
Эта идея переключает упреждающую проблему, связанную с упреждающим процессом, на неупреждающую проблему с адаптированным процессом. Мы применяем эту технику к нашему общему стохастическому дифференциальному уравнению (1).