| 1 | Найти точное значение | sin(30) | |
| 2 | Найти точное значение | sin(45) | |
| 3 | Найти точное значение | sin(30 град. ) | |
| 4 | Найти точное значение | sin(60 град. ) | |
| 5 | Найти точное значение | tan(30 град. ) | |
| 6 | Найти точное значение | arcsin(-1) | |
| 7 | Найти точное значение | sin(pi/6) | |
| 8 | cos(pi/4) | ||
| 9 | Найти точное значение | sin(45 град. ) ) | |
| 10 | Найти точное значение | sin(pi/3) | |
| 11 | Найти точное значение | arctan(-1) | |
| 12 | Найти точное значение | cos(45 град. ) | |
| 13 | Найти точное значение | cos(30 град. ) | |
| 14 | Найти точное значение | tan(60) | |
| 15 | Найти точное значение | csc(45 град. ) | |
| 16 | Найти точное значение | tan(60 град. ) | |
| 17 | Найти точное значение | sec(30 град. ) ) | |
| 18 | Найти точное значение | cos(60 град. ) | |
| 19 | Найти точное значение | cos(150) | |
| 20 | Найти точное значение | sin(60) | |
| 21 | Найти точное значение | cos(pi/2) | |
| 22 | Найти точное значение | tan(45 град. ) | |
| 23 | Найти точное значение | arctan(- квадратный корень из 3) | |
| 24 | Найти точное значение | csc(60 град. ) | |
| 25 | Найти точное значение | sec(45 град. ) ) | |
| 26 | Найти точное значение | csc(30 град. ) | |
| 27 | Найти точное значение | sin(0) | |
| 28 | Найти точное значение | sin(120) | |
| 29 | Найти точное значение | cos(90) | |
| 30 | Преобразовать из радианов в градусы | pi/3 | |
| 31 | Найти точное значение | tan(30) | |
| 32 | Преобразовать из градусов в радианы | 45 | |
| 33 | Найти точное значение | cos(45) | |
| 34 | Упростить | sin(theta)^2+cos(theta)^2 | |
| 35 | Преобразовать из радианов в градусы | pi/6 | |
| 36 | Найти точное значение | cot(30 град. ) ) | |
| 37 | Найти точное значение | arccos(-1) | |
| 38 | Найти точное значение | arctan(0) | |
| 39 | Найти точное значение | cot(60 град. ) | |
| 40 | Преобразовать из градусов в радианы | 30 | |
| 41 | Преобразовать из радианов в градусы | (2pi)/3 | |
| 42 | Найти точное значение | sin((5pi)/3) | |
| 43 | Найти точное значение | sin((3pi)/4) | |
| 44 | Найти точное значение | tan(pi/2) | |
| 45 | Найти точное значение | sin(300) | |
| 46 | Найти точное значение | cos(30) | |
| 47 | Найти точное значение | cos(60) | |
| 48 | Найти точное значение | cos(0) | |
| 49 | Найти точное значение | cos(135) | |
| 50 | Найти точное значение | cos((5pi)/3) | |
| 51 | Найти точное значение | cos(210) | |
| 52 | Найти точное значение | sec(60 град. ) ) | |
| 53 | Найти точное значение | sin(300 град. ) | |
| 54 | Преобразовать из градусов в радианы | 135 | |
| 55 | Преобразовать из градусов в радианы | 150 | |
| 56 | Преобразовать из радианов в градусы | (5pi)/6 | |
| 57 | Преобразовать из радианов в градусы | (5pi)/3 | |
| 58 | Преобразовать из градусов в радианы | 89 град. | |
| 59 | Преобразовать из градусов в радианы | 60 | |
| 60 | Найти точное значение | sin(135 град. ) ) | |
| 61 | Найти точное значение | sin(150) | |
| 62 | Найти точное значение | sin(240 град. ) | |
| 63 | Найти точное значение | cot(45 град. ) | |
| 64 | Преобразовать из радианов в градусы | (5pi)/4 | |
| 65 | Найти точное значение | sin(225) | |
| 66 | Найти точное значение | sin(240) | |
| 67 | Найти точное значение | ||
| 68 | Найти точное значение | tan(45) | |
| 69 | Вычислить | sin(30 град. ) ) | |
| 70 | Найти точное значение | sec(0) | |
| 71 | Найти точное значение | cos((5pi)/6) | |
| 72 | Найти точное значение | csc(30) | |
| 73 | Найти точное значение | arcsin(( квадратный корень из 2)/2) | |
| 74 | Найти точное значение | tan((5pi)/3) | |
| 75 | Найти точное значение | tan(0) | |
| 76 | Вычислить | sin(60 град. ) | |
| 77 | Найти точное значение | arctan(-( квадратный корень из 3)/3) | |
| 78 | Преобразовать из радианов в градусы | (3pi)/4 | |
| 79 | Найти точное значение | sin((7pi)/4) | |
| 80 | Найти точное значение | arcsin(-1/2) | |
| 81 | Найти точное значение | sin((4pi)/3) | |
| 82 | Найти точное значение | csc(45) | |
| 83 | Упростить | arctan( квадратный корень из 3) | |
| 84 | Найти точное значение | sin(135) | |
| 85 | Найти точное значение | sin(105) | |
| 86 | Найти точное значение | sin(150 град. ) ) | |
| 87 | Найти точное значение | sin((2pi)/3) | |
| 88 | Найти точное значение | tan((2pi)/3) | |
| 89 | Преобразовать из радианов в градусы | pi/4 | |
| 90 | Найти точное значение | sin(pi/2) | |
| 91 | Найти точное значение | sec(45) | |
| 92 | Найти точное значение | cos((5pi)/4) | |
| 93 | Найти точное значение | cos((7pi)/6) | |
| 94 | Найти точное значение | arcsin(0) | |
| 95 | Найти точное значение | sin(120 град. ) ) | |
| 96 | Найти точное значение | tan((7pi)/6) | |
| 97 | Найти точное значение | cos(270) | |
| 98 | Найти точное значение | sin((7pi)/6) | |
| 99 | Найти точное значение | arcsin(-( квадратный корень из 2)/2) | |
| 100 | Преобразовать из градусов в радианы | 88 град. |
Программируем бегущего человечка
Вы уже познакомились с кодами программы «Бегущего человечка». И вы уже знаете, что в программе есть несколько строк кодов, которые вычисляют координаты точек ног человечка. Для удобства мы приняли, что траекторией движения «ступней» ног человечека будет окружность. Эти коды следующие:
Для удобства мы приняли, что траекторией движения «ступней» ног человечека будет окружность. Эти коды следующие:
Xlega1 = 0
Ylega1 = 0
Xlega2 = — R*sin(alpha)
Ylega2 = -R*cos(alpha)
Xlegb1 = 0
Ylegb1 = 0
Xlegb2 = R*sin(alpha)
Ylegb2 = -R*cos(alpha)
Наверное, многие из вас здесь впервые столкнулись с выражениями R*cos(alpha) и R*sin(alpha). Что это такое?
Если отвечать кратко, то это функции, являющейся произведением двух сомножителей. Первый сомножитель- это переменная R – радиус окружности. Второй сомножитель- так называемые тригонометрические функции синус угла альфа и косинус угла альфа.
В математике эти функции записали бы так: R*cos(α) и R*sin(α). Значения обеих функций зависят от переменной R и переменной α. R- как мы сказали, это радиус окружности. Но в общем случае, это может быть длина некоторого отрезка, длиной R. Переменная α — это угол. Мы назвали его альфа, но могли бы назвать его и любой другой буквой. В математике для обозначения углов принято использовать буквы греческого алфавита. Например, это могла бы быть и тэта : θ.
Например, это могла бы быть и тэта : θ.
Ниже, в таблице приведены буквы греческого алфавита, и как они произносятся по русски.
Эти же буквы с произношением по английски приведены ниже:
Как видите, русский алфавит ближе к греческому, чем английский. Ведь кириллица использует почти все те же буквы. Только одна буква θ не имеет аналога в современном русском языке.
Итак, функции R*cos(α) и R*sin(α) берут переменные R и α , и преобразуют их. Во что же они их преобразуют, и вообще, для чего придумали эти функции? Их придумали для вычисления координаты точек окружности и сторон прямоугольного треугольника. Позже, вы увидите, что это два взаимосвязанных вычисления. Пока же начнем с прямоугольного треугольника.
Пусть нам дан произвольный прямоугольный треугольник. Например, как на верхнем рисунке на Рис.1. В прямоугольном треугольнике самая длинная сторона называется гипотенузой. Она всегда лежит напротив прямого угла треугольника. Две другие стороны прямоугольного треугольника называются катетами. Еще раз подчеркну: все это верно только для прямоугольных треугольников.
Еще раз подчеркну: все это верно только для прямоугольных треугольников.
Пусть в этом треугольнике один из углов равен θ. Чему именно? θ может быть равен любому углу больше ноля и меньше 90 градусов. Тогда, длина катета прилежащего к углу θ равна R*cos(θ ). А длина катета лежащего напротив угла θ будет равна R*sin(θ ).
В нашем случае, мы используем эти функции, чтобы найти Х и Y координаты ступней человечка. Траектория движения ступней в виде штриховой окружности, и нога человечка изображены на изображены на Рис.1. В этом случае, нога изображена как отрезок R, который равен радиусу окружности. Если построим проекции точки ступни на оси координат, то как видно из рисунка, мы построим два прямоугольных треугольника. И тогда пользуясь свойством тригонометрических функций в прямоугольных треугольниках, можно легко найти, что произведение -R*sin(alpha) вычисляет Х координату ступни, где радиус R их гипотенуза, а угол α — это угол между ногой и осью OY (Рис.1).
Рис. 1. Вверху, справа нарисован прямоугольный треугольник. В нем, длина стороны противолежащая прямому углу, (она называется гипотенузой) равна R. Пусть в этом прямоугольном треугольнике мы знаем, чему равен один из двух других углов. Например, мы его измерили и он оказался равен θ градусов (переменные для обозначения величины углов в геометрии обычно записывают греческими буквами, а не словами, как в программировании). Переменная θ может означать любое число большее 0 градусов, но меньшее 90градусов, или, если мы будем мерить в радианах, то более 0 и менее π/2. Тогда длина прилежащей к углу θ стороны прямоугольного треугольника (сторона называется катетом) будет равна R*cos(θ ). А длина катета лежащего напротив угла θ будет равна R*sin(θ ). Внимание: всё это верно только для прямоугольного треугольника!!!
1. Вверху, справа нарисован прямоугольный треугольник. В нем, длина стороны противолежащая прямому углу, (она называется гипотенузой) равна R. Пусть в этом прямоугольном треугольнике мы знаем, чему равен один из двух других углов. Например, мы его измерили и он оказался равен θ градусов (переменные для обозначения величины углов в геометрии обычно записывают греческими буквами, а не словами, как в программировании). Переменная θ может означать любое число большее 0 градусов, но меньшее 90градусов, или, если мы будем мерить в радианах, то более 0 и менее π/2. Тогда длина прилежащей к углу θ стороны прямоугольного треугольника (сторона называется катетом) будет равна R*cos(θ ). А длина катета лежащего напротив угла θ будет равна R*sin(θ ). Внимание: всё это верно только для прямоугольного треугольника!!!
Рисунок внизу показывает, как зная значения угла и радиуса для любой точки на окружности, можно найти её Декартовы координаты с помощью функций синус и косинус. Как вы видите, эти вычисления аналогичны тем, что используются в прямоугольном треугольнике, только угол обозначен другой буквой.
Аналогично вычисляется координата Y. Но здесь используется функция: -R*cos(alpha).
В подписи к рисунку говорится, что угол может измеряться или в градусах, что вы обычно делаете, когда измеряете транспортиром, или в радианах, что часто делают в компьютерных программах. Здесь число π — это тоже буква греческого алфавита, но она обозначает не переменную. Так называется математическая константа, равная отношению половины длины окружности, к её радиусу.
На первый взгляд, кажется, что длину окружности и её радиус можно легко измерить, а затем легко посчитать их отношение. Но ни длину окружности, ни половину её длины точно измерить нельзя. Поэтому точного значения числа π никто не знает. Первые три знака в числе π следующие: 3.14 .Полная же запись числа будет содержать бесконечное число цифр. При этом все цифры всегда будут образовывать все новые и новые комбинации. Если бы кто-то смог точно вычислить это число, то в его записи вы смогли бы найти любую комбинацию из цифр. Например 1111234, или 1111111, или 123443212344321 и т.д.. Более того если мы зашифруем с помощью цифр наш алфавит (например пусть буква А это 1, Б- 2 , В-3 , и так далее до Я-33), и затем запишем число π с помощью букв (для этого правда надо сначала записать число π в 33-значной системе), то в этой записи рано или поздно вы сможете прочитать любой из написанных на Земле текстов, включая любой роман или рассказ, или любую из текстовых записей на вашем телефоне. Существуют и другие подобные числа. Например число e. Такие числа называются иррациональными. Значения числа π или е, с максимально возможным количеством знаков после запятой для вашего компьютера, вы легко можете посмотреть в таблицах OpenOffice записав в ячейку =pi(), или =e . Только не забудьте изменить для этого еще и формат ячейки: правая клавиша->Format Cells, затем увеличьте Decimal Places до максимально возможного. Также увеличьте ширину самой ячейки, чтобы число поместилось в неё. Например, у вас может получиться число 3.
Например 1111234, или 1111111, или 123443212344321 и т.д.. Более того если мы зашифруем с помощью цифр наш алфавит (например пусть буква А это 1, Б- 2 , В-3 , и так далее до Я-33), и затем запишем число π с помощью букв (для этого правда надо сначала записать число π в 33-значной системе), то в этой записи рано или поздно вы сможете прочитать любой из написанных на Земле текстов, включая любой роман или рассказ, или любую из текстовых записей на вашем телефоне. Существуют и другие подобные числа. Например число e. Такие числа называются иррациональными. Значения числа π или е, с максимально возможным количеством знаков после запятой для вашего компьютера, вы легко можете посмотреть в таблицах OpenOffice записав в ячейку =pi(), или =e . Только не забудьте изменить для этого еще и формат ячейки: правая клавиша->Format Cells, затем увеличьте Decimal Places до максимально возможного. Также увеличьте ширину самой ячейки, чтобы число поместилось в неё. Например, у вас может получиться число 3. 14159265358979000000. Оно на самом деле означает, что ваш компьютер смог посчитать только число 3.14159265358979. Более точное значение можете получить с помощью программы на Basic или калькулятора на компьютере: 3.141592653589793238462643. Но и это, конечно, не бесконечно длинное число, а очень короткая его часть.
14159265358979000000. Оно на самом деле означает, что ваш компьютер смог посчитать только число 3.14159265358979. Более точное значение можете получить с помощью программы на Basic или калькулятора на компьютере: 3.141592653589793238462643. Но и это, конечно, не бесконечно длинное число, а очень короткая его часть.
Несмотря на такую неопределенность с точным значением, число π часто используется в программировании и в физике. Ведь для большинства практических применений нам достаточна та точность, которая уже достигнута. Переход от углов к радианам тоже очень простой. Угол 180 градусов равен π радиан. Вместо слова градусы можно использовать условное обозначение, значок «о». Например: 90 градусов = 90о .
Давайте теперь немного подробнее познакомимся с функциями синус и косинус: sin и cos угла, и с функцией R*cos(α) и R*sin(α). Более детально вы изучите их в старших классах. А сейчас вы познакомитесь с тем минимумом, который вам понадобиться при написании программы.
Во-первых, не надо пугаться слов синус и косинус. Это всего лишь названия двух специальных функций, с помощью которых легко найти координаты точек окружности. Вы уже многократно сталкивались с разными функциями. Что делает любая функция? Она осуществляет преобразования.
Это всего лишь названия двух специальных функций, с помощью которых легко найти координаты точек окружности. Вы уже многократно сталкивались с разными функциями. Что делает любая функция? Она осуществляет преобразования.
С различными функциями вы часто встречаетесь в повседневной жизни. Например, вам надо купить мороженое. Сколько денег вам надо будет заплатить за него? Это зависит от сорта мороженого и веса порции, которую вы купите. В данном примерe стоимость мороженого есть функция его веса и сорта. То есть, вы говорите продавцу какой сорт мороженного вы хотите купить и сколько хотите купить по весу. А продавец выполняет роль функции и преобразует эти данные в цену, которую вам сообщает. Иногда вместо веса в граммах, вы говорите сколько шариков мороженного вам положить в стаканчик, Тогда можно сказать, что вес измеряется не в граммах, а в шариках мороженного. Или можно сказать, что вместо веса вы пользуетесь объёмом, и измеряете объём купленного мороженного в шариках. В данном случае, это не изменит окончательную цену покупки. Ведь вес мороженного и его объём взаимосвязаны: вес мороженного прямо пропорционален его объёму, и ваша функция-продавец легко учтет это.
Ведь вес мороженного и его объём взаимосвязаны: вес мороженного прямо пропорционален его объёму, и ваша функция-продавец легко учтет это.
Рассмотрим пример по сложнее. Пусть вам надо купить провода для пайки вашего электронного устройства. Вы заходите на сайт McMaster-Car (www.mcmaster.com), и после недолгого поиска electrical wire, перед вами будет такая страница (Рис.2)
Рис.2. Веб страница McMaster-Car (в малиновой рамке) на которой вы можете выбрать и заказать провода. Существует множество разных проводов. Они отличаются внешним диаметром (OD), диаметром металлической сердцевины провода, которая непосредственно проводит ток (Wire Gauge), длиной провода. Эти и другие параметры указаны в левой колонке (в зеленой рамке). К другим параметрам относятся материал сердцевины провода, материал и цвет изолятора провода, гибкость провода. Суммарная таблица для покупки провода обведена оранжевой рамкой. На рисунке также приведено увеличенное изображение колонки с параметрами и таблицы.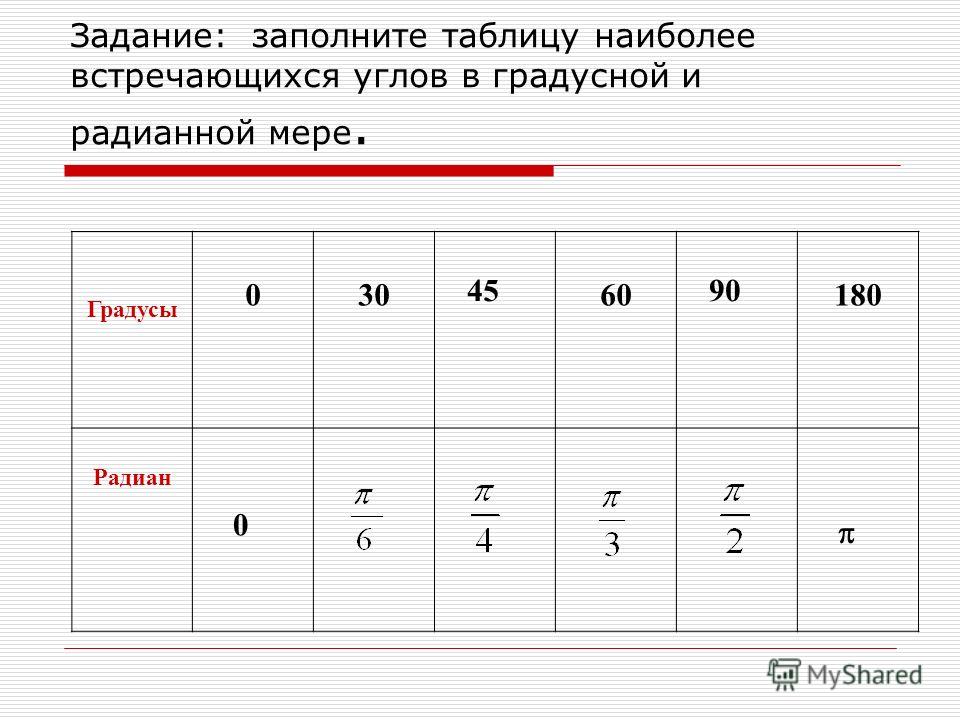 Увеличенные изображения обведены рамками с соответствующим цветом. Итоговая стоимость провода, который вы хотите купить, на математическом языке и на языке компьютерной программы, может быть записана как функция WirePrice. Эту функцию можно записать тоже в виде произведения функции WirePricePerLength и переменной Length. Функция WirePricePerLength будет выдавать цену провода единичной длины в зависимости от диаметра металлической жилы провода WireGauge , внешнего диаметра провода OD, и минимальной длины, которую надо купить по данной цене MinLength. MinLength — это единица измерения длины. Как видно из таблицы эта единица длины может быть равна 10, 25 или 50 футам. Т.е. в случае единичного отрезка длиной 10 футов мы можем купить провода длиной 10, 20, 30, и т. д. футов. В случае единичного отрезка длиной 50 футов, мы можем купить провода с длиной кратной 50 футам. Например 50, 100, 150, или 200 футов, но не сможем купить 10 футов, или 30футов.
Увеличенные изображения обведены рамками с соответствующим цветом. Итоговая стоимость провода, который вы хотите купить, на математическом языке и на языке компьютерной программы, может быть записана как функция WirePrice. Эту функцию можно записать тоже в виде произведения функции WirePricePerLength и переменной Length. Функция WirePricePerLength будет выдавать цену провода единичной длины в зависимости от диаметра металлической жилы провода WireGauge , внешнего диаметра провода OD, и минимальной длины, которую надо купить по данной цене MinLength. MinLength — это единица измерения длины. Как видно из таблицы эта единица длины может быть равна 10, 25 или 50 футам. Т.е. в случае единичного отрезка длиной 10 футов мы можем купить провода длиной 10, 20, 30, и т. д. футов. В случае единичного отрезка длиной 50 футов, мы можем купить провода с длиной кратной 50 футам. Например 50, 100, 150, или 200 футов, но не сможем купить 10 футов, или 30футов.
Также обратите внимание, что задав WireGauge вы задаете диаметр металлической жилы провода. Только учтите, что численные значения WireGauge -это коды диаметров. С помощью Google, вы можете найти по этим кодам величины самих диаметров.
Только учтите, что численные значения WireGauge -это коды диаметров. С помощью Google, вы можете найти по этим кодам величины самих диаметров.
Из этой страницы, вы видите, что цена провода зависит, от того, какой диаметр металлической жилы (сердцевины) WireGauge , какой внешний диаметр провода OD, и какая длина провода вам нужны. Ещё, провода могут различаться материалами из которых сделана металлическая жила и изолятор провода, гибкостью провода. Но в данном случае у вас большого выбора нет: Это только медные гибкие провода с изолятором из пластика. Бывает, что вам нужен провод, который должен проходить через отверстия в плате. Поэтому вы знаете какой диаметр OD должен быть у вашего провода. Но чаще, провода покупают в зависимости от величины электрического тока, который будет по ним протекать. Для большего тока нужны провода с большим диаметром металлической жилы. У вас есть выбор цвета провода, но от него цена не зависит. Величины WireGauge, OD, материал, гибкость, цвет провода, являются переменными от которых зависит конечная цена.
Также, стоимость вашей покупки будет сильно зависеть от длины провода. Чем длиннее провод, тем он дороже. Длина провода- это тоже переменная. В самом простом случае, можно сказать, что цена провода прямо пропорциональна его длине. Т.е. во сколько раз провод длиннее, во столько раз его цена больше. Например, пусть 10 футов стоят $14, а вам нужен провод длиной 40 футов. 40 футов длиннее 10 футов в 4 раза. Тогда цена провода будет $14*4= $56.
В нашем случае зависимость цены от длины провода сложнее. Причина тому- желание продавца продать побольше. Поэтому он предлагает вам скидку в цене, если вы купите провод подлиннее. Например из таблицы следует, что провод калибра (переменная WireGauge) 36, длиной 10 футов стоит $14.05, или это $14.05/10=$1.405 за один фут. А тот же провод длиной 50 футов стоит $53.22. Теперь цена стала менее $1.065 за один фут. Скажем, вам хотите купить 100 футов провода. Вы можете попросить отмерить 10 раз по 10 футов, и тогда 100 футов провода будут стоить 10*$14. 05=$140.5. Или можете попросить отмерить 2 раза по 50 футов. И тогда те же 100футов провода стоят 2*$53.22=$106.44. Получается продавец предлагает вам скидку $33.54, за покупку провода длиной 100 футов. Обратите внимание, за 50 футов предлагается скидка, но в этом случае вы должны покупать провод длиной кратной 50 футам: 50 футов, 100 футов, 150 футов и так далее. Например, вы не сможете купить 140 футов по этой цене. Вам надо будет брать или 100футов, или 150 футов. И минимальная длина провода по этой цене может быть только 50 футов.
05=$140.5. Или можете попросить отмерить 2 раза по 50 футов. И тогда те же 100футов провода стоят 2*$53.22=$106.44. Получается продавец предлагает вам скидку $33.54, за покупку провода длиной 100 футов. Обратите внимание, за 50 футов предлагается скидка, но в этом случае вы должны покупать провод длиной кратной 50 футам: 50 футов, 100 футов, 150 футов и так далее. Например, вы не сможете купить 140 футов по этой цене. Вам надо будет брать или 100футов, или 150 футов. И минимальная длина провода по этой цене может быть только 50 футов.
На математическом языке, вычисление стоимости вашей покупки, как всегда, может быть записано с помощью функции. Назовем эту функцию «WirePrice». Очевидно, чтобы посчитать стоимость проводов, надо сначала определить стоимость провода единичной длины, а затем умножить её на длину провода, который хотите купить, но измеренной в этих единицах. На языке математики это можно сказать так: Функция WirePrice будет произведением функции WirePricePerLength и переменной Length.
Функция WirePricePerLength будет выдавать вам стоимость провода в зависимости от минимальной единичной длины (минимальная единичная длина- это переменная MinLength), внешнего диаметра провода (это переменная OD), и диаметра металлической жилы (переменная WireGauge). Задать такую функцию можно с помощью таблиц или графиков, как вы уже делали. В нашем случае, эту функцию задаёт таблица на веб странице. На Рис.2 она обведена оранжевым цветом.
Переменная Length обозначает длину провода.
Что делает функция WirePrice? Она выдаёт стоимость вашей покупки. Для этого вам надо задать значения переменных OD, MinLength, WireGauge, и Length , и функция WirePrice посчитает итоговую стоимость. На языке математики, функция WirePrice берет значения OD, MinLength, WireGauge, и Length и преобразует их в стоимость покупки.
Повторю ещё раз. В нашем случае функция WirePrice задаётся таблицей, но может быть задана и графиком или формулой (т. е. аналитически). После того, как функция задана, её значения могут вычислены с помощью компьютера.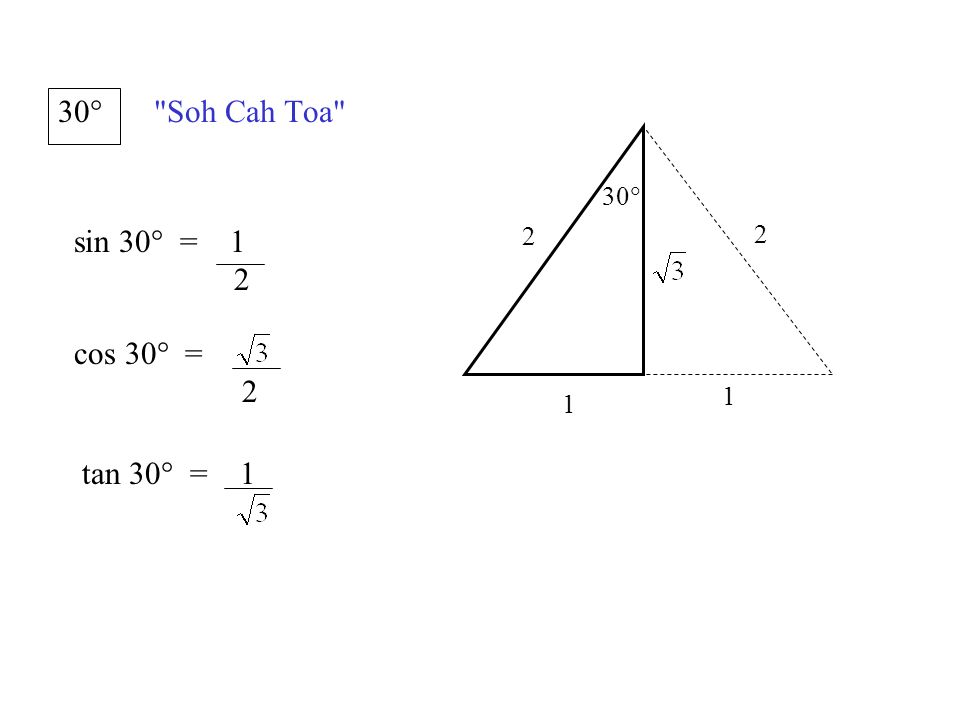 Именно так и определяется стоимость покупки на вебстранице. В этом случае, компьютер выполняет функцию WirePrice.
Именно так и определяется стоимость покупки на вебстранице. В этом случае, компьютер выполняет функцию WirePrice.
Эту же функцию WirePrice может выполнять не компьютер, а работник отдела продаж, которому вы можете позвонить по телефону. Вы должны будете ему сообщить значения OD, MinLength, WireGauge, и Length, которые вам нужны, а продавец вычислит вам итоговую цену.
Задание: Допустим вам надо купить 60 футов провода с WireGauge=29. Тогда вам выгоднее купить 50 футов по цене $42.30 за 50 футов, и 10 футов по цене $11.17. Итого вам надо заплатить $42.30+$11.17= $53.47. Как вам дешевле всего купить 170 футов этого провода? А как вам дешевле купить 49 футов? А как вам дешевле купить провод длиной 40 футов?
Произведение R*sin(θ )- это тоже функция. Только она вычисляет длину катета лежащего напротив угла θ (Рис.1), а не стоимость покупки. Эта функция тоже произведение переменной длины (в данном случае это длина гипотенузы прямоугольного треугольника), и функции sin(θ ).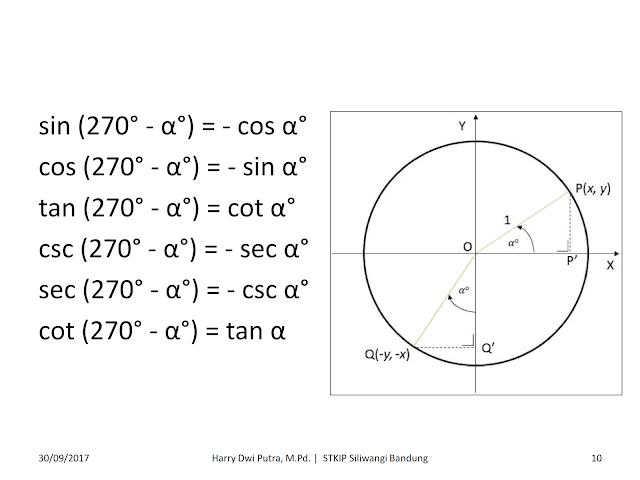
Аналогична ей и функция R*cos(θ ), которая вычисляет длину другого катета прямоугольного треугольника, который соприкасается с углом θ. Эта функция тоже произведение переменной длины ( длины гипотенузы прямоугольного треугольника), и другой функции (теперь это функция cos(θ )).
Для обеих функций, R*sin(θ ) и R*cos(θ ), переменными будут длина R и угол θ. Нам, как и в случае с WirePrice, надо только задать эти переменные, а функции R*cos(θ ) и R*sin(θ ) вычислят необходимые длины катетов. Ну и конечно, все это вычислит компьютер, который знает приблизительные значения функций cos(θ ) и sin(θ ), и умеет вычислять произведения.
Как компьютер вычисляет значения cos(θ ) и sin(θ ) ? Раньше, когда компьютеры не были распространены, инженеры сами вычисляли значения функций. Оказывается эти значения можно найти, зная некоторые свойства функций синус и косинус. Ниже, вы познакомитесь с некоторыми из них. Для удобства, на основе этих вычислений были составлены таблицы. Вы их можете найти на Google: Bradis Table of Sines and Cosines. Также поступает и компьютер. Во многих компьютерных языках и программах есть блоки, содержащие алгоритмы вычисления значений функций cos(θ ) и sin(θ ).
Также поступает и компьютер. Во многих компьютерных языках и программах есть блоки, содержащие алгоритмы вычисления значений функций cos(θ ) и sin(θ ).
Поговорим теперь немного об этих загадочных свойствах функций cos(θ ) и sin(θ ), которые используются и для вычисления значений тригонометрических функций. Вы знаете, что многие устройства используют полярные, а не Декартовы координаты. Например, полярные координаты используют радиолокаторы. Полярные координаты очень часто применяются в инженерных расчетах и в программировании. Но для нас более привычны Декартовы. На рисунке 3, показаны 3-ех мерные Декартовы координаты, и цилиндрические, которые тоже используют полярные координаты; и как они описывают одно и тоже движение точки в пространстве.
Как зная координаты точки в полярных координатах, найти координаты этой же точки в Декартовых?
Рис.3 Движение точки в Декартовых и цилиндрических координатах. В обоих случаях, у точки есть только 3 координаты. В декартовых , это проекции точки на координатные оси (Px, Py, Pz), В цилиндрических- это угол, радиус и высота точки: (R, α , Pz).
Пусть у нас есть множество точек, лежащих на окружности. Назовем эти точки, как T1, T2, T3…..Tn …. . А их координаты обозначим так (X1 ,Y1), (X2 ,Y2), (X3 ,Y3), ……, (Xn ,Yn)….. Вы уже знаете, что для любой точки лежащей на окружности с радиусом R , её координаты всегда удовлетворяют уравнению
Yn*Yn+ Xn*Xn= R*R
или тоже самое можно записать в таком виде:
Yn2+ Xn2= R2
, где n любое целое число.
С помощью этого уравнения, для точки на окружности, зная её Х координату можно найти её Y координату. Для этого перепишем это уравнение в таком виде:
Yn2 = R2— Xn2
Чтобы найти значение Yn , надо вычислить квадратный корень из выражения R2 — Yn2 . Но квадратный корень может давать два решения, отличающихся знаком + и — , для одного и того же значения Yn2 .
Но квадратный корень может давать два решения, отличающихся знаком + и — , для одного и того же значения Yn2 .
Эта неоднозначность и громоздкость решения неудобны в вычислениях. Чтобы упростить эти вычисления и были придуманы функции cos(θ ) и sin(θ ).
Функции cos(α ) и sin(α ) определяются следующим образом. Возьмем произвольную точку Tn на окружности с радиусом R и соединим её с центром окружности (Рис.4). У вас получился прямоугольный треугольник ОTnXn . Как мы уже говорили, длину катета этого треугольника OХn можно вычислить зная его гипотенузу OTn и угол прилежащий к этому катету. В обозначениях рисунка это длина R и угол αn. Тогда длина
OХn = R*cos( αn ).
А для катета TnXn верно
TnXn = R*sin( αn ).
Но длина OХn равна величине координаты Хn точки Tn. А длина катета TnXn равна величине координаты Yn точки Tn. Поэтому
Если же взять точки лежащие на единичной окружности (R=1 ), то получим
Это и есть определение функций синус sin( α ) и косинус cos( α ):
Синус угла α равен Y координате точки единичной окружности, лежащей на угле α, а косинус угла α равен Х координате этой точки. При этом угол всегда откладывается против часовой стрелки от оси ОХ.
При этом угол всегда откладывается против часовой стрелки от оси ОХ.
Случай же с треугольником является следствием этого определения.
Рис.4. Для произвольной точки Tn окружности можно построить ее проекции Yn и Xn, на оси OY и OX. Также можно соединить точку Tn с центром окружности и измерить угол между отрезком OТn и осью ОХ. Пусть этот угол равен α градусам. Тогда координата Xn ( или длина OXn) равна Хn = R*cos( αn ). А координата Yn ( или длина OYn) равна Yn = R*sin( αn ). Если бы у нас была единичная окружность, когда R=1, то координата Хn была бы просто равна косинусу угла: Хn = cos( αn ), а координата Yn равна синусу угла: Yn = sin( αn ).
Это полное определение синуса и косинуса угла верно для самых разных углов от минус бесконечности, до плюс бесконечности. В то время, как для вычисления катетов прямоугольного треугольника используются углы только первого квадранта, причем более 0, но менее 90 градусов.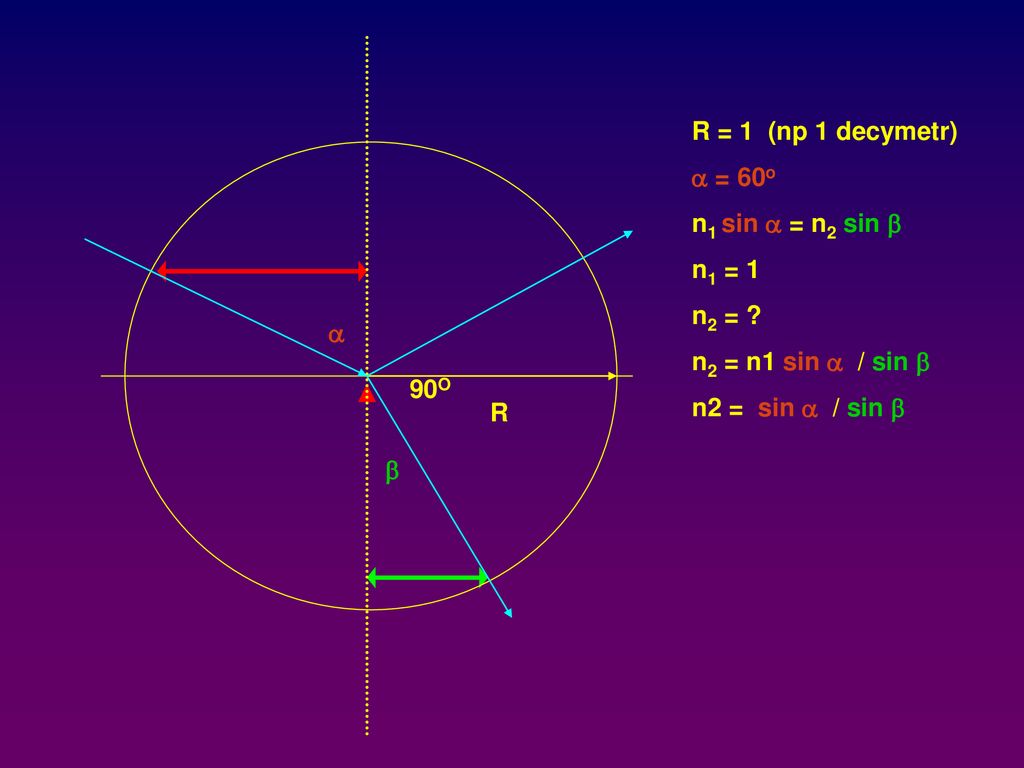
Рисунок 5 показывает расположение четырёх квадрантов на координатной плоскости.
Рис.5. Расположение четырех квадрантов плоскости.
Задание: проведите радиус окружности образующий угол с осью ОХ равный 720 градусам. А где расположена точка окружности лежащая на угле 900 градусов? А где расположена точка окружности лежащая на угле равном 6*π радиан?
С помощью функций R*sin( α ) и R*cos( α ) можно найти координаты любой точки плоскости. Для этого надо соединить эту точку с центром координат. Это будет радиус окружности. Расстояние от точки до центра координат даст длину радиуса R. Затем надо измерить угол между ОХ и проведенным радиусом. И тогда координата Х для любой точки будет равна
Х = R*cos( α )
, а её Y координата равна
Y = R*sin( α )
Примеры разных точек окружности радиусом R и произвольного угла показаны на рисунке 6.
Рис.6. Примеры разных точек окружности и их углов и соответствующих значений функций
R*sin( α ) и R*cos( α ).
Значения косинуса и синуса определены для любых углов. Но оказывается, что эти значения всегда можно выразить, через значения синуса и косинуса углов первого квадранта, т. е. через углы от 0 до 90 градусов. Посмотрим например, как это делается для шестой точки на Рис. 6. Этот случай показан на Рис.7.
Рис.7. Точка окружности Т6 лежащая в третьем квадранте. В этом случае угол α больше 180 градусов, но меньше 270 градусов.
Для любой точки третьего квадранта можно найти точку первого квадранта центрально симметричную ей относительно начала координат. Для этого надо продолжить радиус соединяющий эту точку с началом координат до повторного пересечения окружности (Рис.8). Т.е. из радиуса OТ6 получится диаметр окружностиТ6 Т’6 . Точка Т’6 будет центрально симметрична точке Т6 . Т.е. если окружность повернуть относительно ее центра на 180 градусов, то точка Т6 перейдет в точку Т’6 , а точка Т’6 перейдет в точку Т6 . При этом ОТ’6 образует угол β с осью ОХ, а ОТ6 образует угол β с отрицательным направлением оси ОХ. В этом случае угол α в градусах можно записать, как α = 180 + β. А если записывать в радианах, то будет α = π + β . Можно также заметить, что треугольник Т6 ОХ6 и треугольник Т’6 ОХβ одинаковы. Ведь они оба прямоугольные. У обоих гипотенуза равна радиусу окружности R. И у них есть одинаковый угол β . Поэтому расстояние ОХ6 равно расстоянию ОХβ, ведь ОХ6 = ОХβ= R*cos(β). Значит координата Х6 = -Хβ . Но по определению функции косинуса, координата Х6 равна R*cos(180+β), координата Хβ равна R*cos(β). Отсюда получается, что
В этом случае угол α в градусах можно записать, как α = 180 + β. А если записывать в радианах, то будет α = π + β . Можно также заметить, что треугольник Т6 ОХ6 и треугольник Т’6 ОХβ одинаковы. Ведь они оба прямоугольные. У обоих гипотенуза равна радиусу окружности R. И у них есть одинаковый угол β . Поэтому расстояние ОХ6 равно расстоянию ОХβ, ведь ОХ6 = ОХβ= R*cos(β). Значит координата Х6 = -Хβ . Но по определению функции косинуса, координата Х6 равна R*cos(180+β), координата Хβ равна R*cos(β). Отсюда получается, что
R*cos(180+β) = — R*cos(β).
После деления обеих сторон равенства на радиус, получаем:
Рассмотрев аналогично другие катеты ОY6 и ОYβ можно показать, что
Таким образом мы нашли, что значения косинуса и синуса углов третьего квадранта можно выразить через значения косинуса и синуса углов первого квадранта.
Рис.8. Рисунок показывает, как значения функций R*cos(α) и R*sin(α) углов третьего, квадранта могут быть выражены через значения этих функций углов первого квадранта.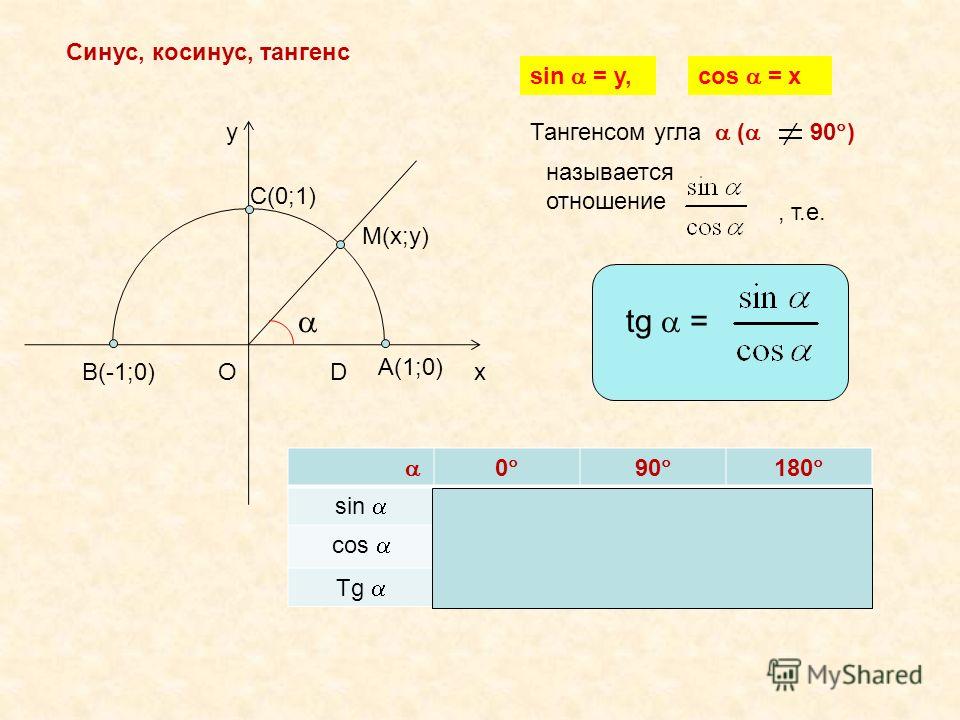 Для этого находим для произвольной точки третьего квадранта Т6 центрально симметричную ей точку первого квадранта Т’6 . Эта точки будут лежать на пересечении окружности и прямой Т6Т’6 , поскольку и прямая и окружность переходят сами в себя при повороте на 180 градусов относительно центра окружности (говорят, что они центрально симметричны). Также при таком повороте перейдет в сама в себя и ось ОХ (она только изменит направление при таком повороте). Поэтому угол Х6 ОТ6 перейдет в угол ХβОТ’6 . Значит величины этих углов одинаковы ےХ6 ОТ6= ےХβОТ’6 = β
Для этого находим для произвольной точки третьего квадранта Т6 центрально симметричную ей точку первого квадранта Т’6 . Эта точки будут лежать на пересечении окружности и прямой Т6Т’6 , поскольку и прямая и окружность переходят сами в себя при повороте на 180 градусов относительно центра окружности (говорят, что они центрально симметричны). Также при таком повороте перейдет в сама в себя и ось ОХ (она только изменит направление при таком повороте). Поэтому угол Х6 ОТ6 перейдет в угол ХβОТ’6 . Значит величины этих углов одинаковы ےХ6 ОТ6= ےХβОТ’6 = β
Используя свойство, что все точки окружности второго квадранта симметричны относительно оси OY точкам окружности первого квадранта, можно выразить значения sin и cos углов второго квадранта через значения значения sin и cos углов первого квадранта.
А используя свойство, что все точки окружности четвертого квадранта симметричны относительно оси OХ точкам окружности первого квадранта, можно выразить значения sin и cos углов четвертого квадранта через значения значения sin и cos углов первого квадранта.
Запишется это так:
Значит, чтобы компьютеру подсчитать значения sin и cos любых углов, достаточно знать значения sin и cos углов только первого квадранта.
Также можно заметить, что катеты прямоугольного треугольника можно вычислить зная гипотенузу и один из двух острых углов. Например, рассмотрим треугольник на Рисунке 8.
Если мы возьмем гипотенузу R и угол α, то его катеты равны:
длина синего катета равна R*cos(α)
длина зеленого катета равна R*sin(α).
Если же мы возьмем гипотенузу R и угол θ, то его катеты равны:
длина синего катета равна R*sin(θ)
длина зеленого катета равна R*cos(θ).
Т.е. мы получили, что R*cos(α)= R*sin(θ), и R*sin(α)=R*cos(θ). Опять сокращаем обе стороны уравнений на R и получаем:
Рис.9. Два способа вычислить длину одного и того же катета с помощью функций sin и cos.
Учтем теперь, что сумма углов любого треугольника равна 180 градусам. Значит для нашего прямоугольного треугольника
α + θ + 90o =180o
Отсюда
α + θ = 90o
Или
θ = 90o — α
Тогда
Получается, что достаточно вычислить значения только например cos от углов первого квадранта.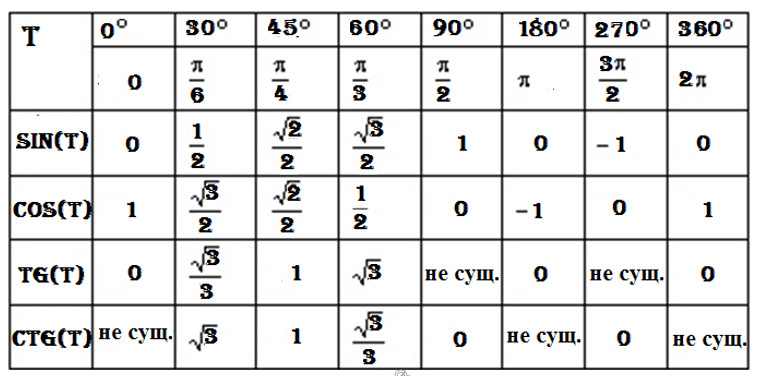 Тогда значения cos углов первого квадранта уже можно найти через значения sin. Более того достаточно вычислить значения sin углов от 0 до 45 градусов. Все остальные значения функций sin и cos для любых углов можно вычислить через них. Как конкретно вычислять значения этих функций углов от 0 до 45 градусов, мы сейчас не будем. Для этого надо будет найти правило, как вычислять значения этих функций от суммы двух углов. Еще полезно знать, что для углов менее 10 градусов=π/18 радиан значения sin такого угла приблизительно равно значению угла выраженному в радианах. Т.е. если α измерено в радианах, и при этом α < π/18, то sin( α) ~ α. Причем чем меньше угол, тем точнее это приближение.
Тогда значения cos углов первого квадранта уже можно найти через значения sin. Более того достаточно вычислить значения sin углов от 0 до 45 градусов. Все остальные значения функций sin и cos для любых углов можно вычислить через них. Как конкретно вычислять значения этих функций углов от 0 до 45 градусов, мы сейчас не будем. Для этого надо будет найти правило, как вычислять значения этих функций от суммы двух углов. Еще полезно знать, что для углов менее 10 градусов=π/18 радиан значения sin такого угла приблизительно равно значению угла выраженному в радианах. Т.е. если α измерено в радианах, и при этом α < π/18, то sin( α) ~ α. Причем чем меньше угол, тем точнее это приближение.
Задание: До сих пор мы определяли тригонометрические функции словами и аналитически с помощью уравнений. А теперь посмотрим, как выглядит графическое представление этих функций. С помощью OpenOffice SpreadSheets постройте графики y=cos(α) и y=sin(α )для α от -720 градусов до 720 градусов.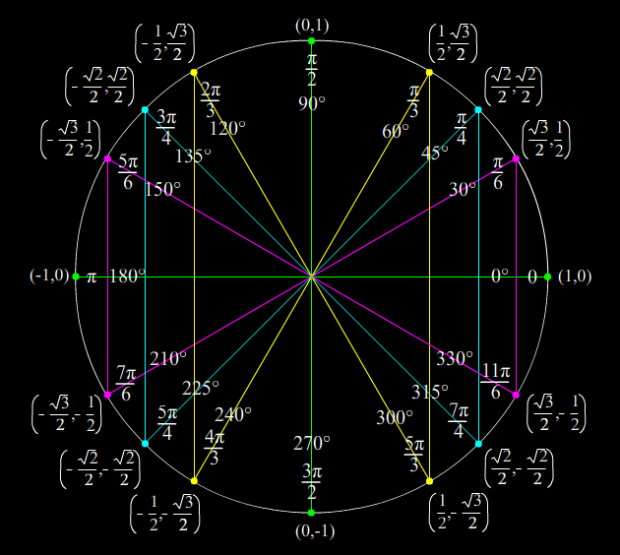 Подсказка: вы строите графическое представление функций cos(α) и sin(α ) в декартовых координатах. Поэтому в этих графиках y=cos(α) и y=sin(α ), а x=α .
Подсказка: вы строите графическое представление функций cos(α) и sin(α ) в декартовых координатах. Поэтому в этих графиках y=cos(α) и y=sin(α ), а x=α .
Итак, вы познакомились с функциями R*cos(α) и R*sin(α). Посмотрим теперь, как с помощью этих функций можно запрограммировать движение человечка на месте. Когда вы делали gif файл с мультяшкой движущегося на месте человечка, вы рисовали несколько слайдов. Эти слайды были аналогичны рисунку 10.
Рис.10. Отдельно взятый кадр из мультяшки «человечек движущейся на месте».
Всего было 5 кадров-слайдов, похожих на кадр рисунка 10. Угол гол наклона ног α менялся от слайда к слайду. Когда человечек раздвигал ноги, то угол наклона α рос. Когда человечек наоборот сдвигал ноги, то угол наклона уменьшался. Всего мы делали 4 таких кадра. Но их может быть и 6, и 10, и 100. За их число в программе отвечает переменная m. Получившаяся мультяшка представлена на Рис.11.
Рис.11. Человечек шагающий на месте.
Обратите внимание, что в этом случае координаты самого тела человечка не меняются. Двигаются только ноги.
Посмотрим теперь, как сделать, чтобы человечек пошел. Очевидно, что в этом случае тело должно начать двигаться, и его координаты должны начать тоже меняться. А вот ступня человечка, на которую он опирается при шаге, не должна двигаться относительно Земли. Но после того как он сделал шаг, т. е. раздвинул ноги на максимальную ширину, другая ступня должна коснуться земли. И когда человечек будет сдвигать ноги, уже эта ступня будет покоиться относительно Земли. В тот момент, когда человечек окончательно сдвинет ноги, он переместиться на один шаг. Далее он будет повторять эту же последовательность движений.
Мы пока не будем программировать такую последовательность. Для начала мы упростим нашу задачу, и не будем различать какая ступня коснулась земли. Мы просто начнем перемещать человечка вдоль оси ОХ со скоростью один шаг за один цикл из 4 кадров
(как уже сказали, цикл может содержать любое число кадров-слайдов. В программе они задаются числом m).
В программе они задаются числом m).
А чтобы было проще программировать это движение, мы разобьём его на два независимых движения. Первое движение- это движение ног человечка относительно его тела. И хотя тело движется, но ноги никуда не уходят от тела и только ступни движутся циклически по круговой траектории. Поэтому их движение относительно тела будет то самое движение на месте, которое мы только что рассмотрели. Для описания этого движения мы используем Декартову систему координат XY связанную с телом (Рис. 12). За начало координат, как и ранее , примем верхнюю точку ног. Эта система координат XY будет двигаться относительно Земли так же, как и тело . Но тело относительно неё будет стоять на месте и только двигать ногами.
Второе движение- это движение тела относительно Земли. Для описания этого движения мы введем систему координат X’Y’, которая покоится относительно Земли. За её начало отсчета примем точку касания земли опорной ступней, в первый момент времени. Это наша покоящаяся система отсчета.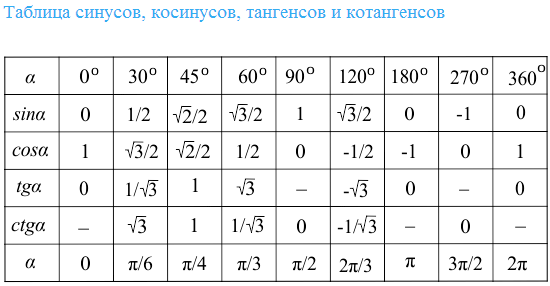 Система координат XY будет двигаться относительно неё. Поэтому система XY будет называться движущейся системой координат.
Система координат XY будет двигаться относительно неё. Поэтому система XY будет называться движущейся системой координат.
Рис.12. Покоящаяся X’Y’ и движущаяся XY системы координат. Верхний рисунок показывает положение тела и ног в первый момент времени. Нижний рисунок показывает положение ног и тела в момент наибольшего расстояния между ступнями и наибольшего угла между ногами.
Обратите внимание. В движущейся системе (верхний Рисунок 12), координаты опорной ступни координат равны:
Х
1= -R*sin(α), Y1= -R*cos(α), а координаты основания ног/низа тела (0,0).
Эти же точки в покоящейся системе координат :
координата опорной ступни теперь стала (0,0),
а координаты основания ног/низа тела:
Х’
1= R*sin(α), Y’1= R*cos(α)Если мы примем, что в начальный момент α =0, то координата начала отсчета движущейся системы координат в неподвижной системе будет:
Х’1= 0, Y’1= R.
В нашем случае один шаг является циклом из 4 движений/слайдов. Логично принять, что величина перемещения человечка за один такой цикл будет равна максимальному расстоянию между ступнями (Рисунок справа на Рис. 12) . Это расстояние, мы примем за длину шага. Поэтому примем, что в каждом слайде, тело человечка будет смещаться на ¼ от длины шага. Рис.13 показывает движение человечка, которое получится в этом случае.
Рис.13. Двигающийся человечек.
Видно, что координаты начала отсчета движущейся системы меняются следующим образом:
Y1 =R , и не меняется во время движения.
X1= (Шаг/4)*(число шагов).
Мы теперь знаем как меняются координаты ступней относительно начала отсчета движущейся системы координат. И знаем как меняются координаты этой точки начала отсчета относительно начала отсчета покоящейся системы координат. Этого достаточно, чтобы написать функцию описывающую движение ступней и тела относительно начала отсчета покоящейся системы координат, и использовать эту функцию в наше программе. Делается это с помощью преобразований Галилея. Они проиллюстрированы на Рис.14.
Делается это с помощью преобразований Галилея. Они проиллюстрированы на Рис.14.
Наиболее просто их можно записать в векторной форме:
P = A+ a
, где вектор P указывает на положение предмета в покоящихся координатах,
вектор A дает положение начала отсчета движущихся координат в покоящихся координатах,
и вектор a указывает на положение предмета в движущихся координатах.
Запись через координаты аналогична. В нашем случае это будет:
Xp= X’1+X1
Yp=Y’1+Y1
Рис.14. Преобразования Галилея. Показаны разные варианты применения преобразований Галилея.
Или то же самое после подстановки значений ХY и X’Y’ координат для n слайда:
Только не забывайте, изменятся не только координаты ног, но и координаты тела. В покоящейся системе координат они станут такими:
X’body1 = 0+(Шаг/4)*n
Y’body1 = 0 + R
X’body2 = 0+(Шаг/4)*n
Y’body2 =4 + R
Определите значение sin L,cos L, tg L.
 если L=90°.1020°,-1… -reshimne.ru
если L=90°.1020°,-1… -reshimne.ru
Новые вопросы
Ответы
Похожие вопросы
Е. 30/48 и 36/56,ж.56/84 и82/108,з.121/77 и 45/21,и.49/63 и 34 /85…
Чему равна 1/4 часть веревки, 2/5 которой равны 24 м…
1158 упражнение помогите решить пожалуйста
…
При каком значении а значения 13а является простым число
1 1
2 2
3 3
4 4…
Помогите решить задачу от куска ситуации отрезали 1,5 часть что составляет 14 м. Какова длинна всего куска ситца.
Со 100 кг. свеклы получили 7 кг. сахара. Сколько сахара можно получить с 3 тон свеклы)))…
Математика
Литература
Алгебра
Русский язык
Геометрия
Английский язык
Химия
Физика
Биология
Другие предметы
История
Обществознание
Окружающий мир
География
Українська мова
Українська література
Қазақ тiлi
Беларуская мова
Информатика
Экономика
Музыка
Право
Французский язык
Немецкий язык
МХК
ОБЖ
Психология
Что запрещает принцип Паули? / Хабр
Принцип запрета Паули с однозначной многочастичной волновой функцией эквивалентен требованию, чтобы волновая функция была антисимметричной по отношению к обмену частицами. Как это объяснить на пальцах? Легко — ткните пальцем в стол, в монитор, во что-нибудь твердое. Глубоко пронзили материю? Удалось достичь перекрывания атомных электронных облаков пальца и стола? Нет? Не удивительно. Читайте дальше, если хотите узнать, почему так.
Как это объяснить на пальцах? Легко — ткните пальцем в стол, в монитор, во что-нибудь твердое. Глубоко пронзили материю? Удалось достичь перекрывания атомных электронных облаков пальца и стола? Нет? Не удивительно. Читайте дальше, если хотите узнать, почему так.
Спин
Цитата из Википедии: Принцип исключения Паули (принцип запрета Паули или просто принцип запрета) — это квантово-механический принцип, который гласит, что два или более идентичных фермиона (частицы с полуцелым спином) не могут одновременно находиться в одном и том же квантовом состоянии в квантовой системе.
Волновая функция вращающейся частицы.Что-то про спин. Начнём с того, что такое спин, в частности, полуцелый спин. Пускай частица движется по окружности длины , а через мы обозначим позицию частицы. Частица будет описываться волновой функцией. Для простоты положим, что это самая обычная бегущая волна.
Частица будет описываться волновой функцией. Для простоты положим, что это самая обычная бегущая волна.
Волновая функция должна однозначно определяться на окружности, а поворот на
радиан никак не должен её изменять, то есть:
Экспонента в мнимой степени это тригонометрическая функция, как синус или косинус, по сути мы записали, что волновая функция периодическая. Это возможно только если произведение
, где n — обязательно целое число. Вспомнив, что произведение ничто иное как момент импульса, для нашей частицы мы получаем условие:
Та самая открытка Нильсу Бору от Отто Штерна и Вальтера Герлаха.Всё это хорошо, но Отто Штерн и Вальтер Герлах установили, что электрон может так вращаться, что совершив полный оборот он не придёт в тоже самое состояние, что и раньше. А вот если два оборота сделает, тогда всё хорошо. В его случае n=1/2 и он может крутиться с периодичностью . Если Вы тоже задали себе этот вопрос: а что, черт возьми, курили эти ученые, то вам поможет удовлетворить любопытство эта статья — Stern and Gerlach: How a Bad Cigar Helped Reorient Atomic Physics.
Хорошие новости — в трехмерном пространстве есть такой тип вращения. Забавная особенность — такое вращение не перекручивает подсоединенные к телу верёвки. Попробуйте этот трюк в баре с кружкой пива — Вы сможете её постоянно поворачивать не перекручивая свою руку.
Антисимметричность по отношению к обмену электронов
Перестановка двух связанных друг с другом объектов трехмерного пространства эквивалентна повороту одного из них на 360 градусов. Значит, если периодичность вращения объекта — то перестановка приводит к смене его волновой функции. Две смены знака: .
Обязательную смену знака волновой функции при перестановке двух частиц со спином можно трактовать как требование не перекручивать связывающее их пространство [См. Pauli principle in Euclidean geometry]. Эта лента гибкая, но до определенных пределов. Давайте установим предел гибкости нашего пространства-времени на скручивание.
Следующий пример описывается в статье Вайскопф, В. Современная физика в элементарном изложении. УФН 103(1) (1971) 155-179. Пусть есть два электрона с волновыми функциями:
Современная физика в элементарном изложении. УФН 103(1) (1971) 155-179. Пусть есть два электрона с волновыми функциями:
Забудем пока об электростатическом отталкивании, просто летят два электрона с импульсами
на встречу друг другу. Расстояние между ними . Волновая функция этой системы электронов:
однако, она в таком виде еще не обладает свойством антисимметрии. Легко поправить дело:
тогда перепишем её как:
Плотность вероятности имеет вид:
где — волновое число. Для всех возможных импульсов со средним значением плотность вероятности есть интеграл по всем волнам с различными значениями k. После интегрирования получаем, что имеет вид ступени.
Черная кривая — плотность вероятности для некоего среднего значения импульса.Плотность вероятности встречи электронов на расстоянии менее стремится к нулю. Минимальное возможное расстояние между ними, как видно, имеет порядок их средней длины волны, т.е. . Именно так получается характерный объём пространства, занимаемый электроном. Как будто электрон — упругий шарик.
Как будто электрон — упругий шарик.
Принцип запрета Паули
Плотная упаковка электронов в атоме.Расположим шарики-электроны плотной упаковкой, т.к. положительно заряженное ядро стягивает их к себе, а принцип Паули и кулоновское отталкивание мешают подходить им близко друг к другу. В полученной структуре шарики расположены слоями — наружный слой, средний, внутренний. Места в пространстве у шариков однозначно задаются адресами из трех целых чисел. (Подробнее см. в Stevens, P.S. A Geometric Analogue of the Electron Cloud. Proceedings of the National Academy of Sciences 56(3) (1966) 789-793.) Смотрите на картинку.
Оболочечная структура атома: главное квантовое число, орбитальное число и магнитное число.Если считать, что четвертое число — окраска шара (черная/белая, спин +1/2 или -1/2), получим, что принцип запрета Паули (нет двух электронов в атоме с одинаковым набором четырех квантовых чисел) эквивалентен однозначности адресации шара в плотной упаковке.
В свою очередь, атомы в веществе, как правило, стремятся плотно заполнить пространство. Пустого места нет, и метафора с электронными облаками, а облака могут проникать друг в друга, здесь неуместна. Материя плотная и мы это чувствуем физически.
Октет Льюиса, двойной квартет Линнета
Стремление к заполнению оболочки (правило 8 электронов, правило 18 электронов) есть ничто иное, как попытка электронов атома выстроить максимально плотную и симметричную структуру. Более того, октет Льюиса как раз исторически произошёл от кубической модели атома. С появлением квантовой механики о кубе забыли, но правило октета осталось в школьных учебниках.
В 1961 году Линнет выдвинул интересную модификацию правила октета Льюиса (см. Дей К., Селбин Д. Теоретическая неорганическая химия. М.: «Химия» 1976. Стр. 197). Он предположил, что ключевым принципом построения оболочки должно быть максимальное отталкивание электронов одного спина. Учитывая, что они же стягиваются к ядру атома, получается плотная упаковка — тетраэдр. Устойчивой оболочкой Линнет считал ориентацию двух тетраэдров, обеспечивающую их максимальное отталкивание, т.е. 4+4=8, куб. Пока мы не рассматриваем спин, его правило не отличается от правила октета, однако, оно приводит к геометрической трактовке связи. Например, отличие однократной, двойной и тройной связей выглядит так:
Устойчивой оболочкой Линнет считал ориентацию двух тетраэдров, обеспечивающую их максимальное отталкивание, т.е. 4+4=8, куб. Пока мы не рассматриваем спин, его правило не отличается от правила октета, однако, оно приводит к геометрической трактовке связи. Например, отличие однократной, двойной и тройной связей выглядит так:
Интересно, что предсказываемые соотношения для длин связей находятся в прекрасном согласии с наблюдаемой геометрией молекул. Более того, его принцип позволяет объяснить электронную структуру молекулы кислорода, для которой основное состояние — триплет, два неспаренных электрона. Правило октета в данном случае бессильно.
Триплетное состояние кислорода.Долгое время было загадкой, почему две молекулы NO (свободные радикалы) не образуют устойчивый димер, в отличие от циана CN, который димеризуются в дициан C2N2. С позиции теории двойного квартета, структура O=N-N=O потребовала бы пространственного совмещения тетраэдров электронов разного спина, что невыгодно из-за электростатического отталкивания, тогда как дициан позволяет минимизировать отталкивание электронов. Принцип плотной упаковки электронов описывает все типы химических связей: ковалентную с кратными связями, ионную, а также металлическую связь.
Принцип плотной упаковки электронов описывает все типы химических связей: ковалентную с кратными связями, ионную, а также металлическую связь.
! Используем программу GAMESS US $CONTRL SCFTYP=UHF MULT=3 LOCAL = BOYS RUNTYP=ENERGY NZVAR=0 $END ! PRTLOC = a flag to control supplemental printout. The ! extra output is the rotation matrix to the ! localized orbitals, and, for the Boys method, ! the orbital centroids, for the Ruedenberg ! method, the coulomb and exchange matrices, ! for the population method, atomic populations. ! (default=.FALSE.) $LOCAL PRTLOC=.T. $END $SYSTEM TIMLIM=100 MWORDS=5 $END $BASIS GBASIS=STO NGAUSS=3 $END $GUESS GUESS=HUCKEL $END $DATA Cnv 4 O 8.0 0.0 0.0 0.000 O 8.0 0.0 0.0 1.210 $ENDОрбитали Бойса. Связь C-H, двойная связь, тройная связь.
Орбитали Бойса, как видно из картинки выше, отличаются от «традиционных» представлений о различии связей π-типа и σ-типа. Моё мнение — концепция Линнета куда как больше подходит к школьному курсу химии, чем существующий набор разрозненных представлений — правило Льюиса, гибридизация, орбитали… Электроны и ядра, связанные классическими механическими силами, выстраивают атомы и связи, последние, в свою очередь, образуют механическую молекулярную систему — появляется понятие о конформации молекул.
Моё мнение — концепция Линнета куда как больше подходит к школьному курсу химии, чем существующий набор разрозненных представлений — правило Льюиса, гибридизация, орбитали… Электроны и ядра, связанные классическими механическими силами, выстраивают атомы и связи, последние, в свою очередь, образуют механическую молекулярную систему — появляется понятие о конформации молекул.
Потенциал Гейзенберга
Соотношение неопределённости , как и принцип Паули, также интерпретируется с позиций механики. Рассмотрим атом водорода. Запишем импульс электрона — , а радиус его орбиты — . Имеем: . Полная энергия атома (в системе атомных единиц):
Тогда c учётом соотношения неопределенности имеем:
В точке минимума энергия атома водорода как и должно быть по законам квантовой механики. Вид потенциала аналогичен таковому у шарика на упругой пружинке. Воспользуемся найденным потенциалом для поиска кривой потенциальной энергии молекулярного иона.
Пусть электрон в молекулярном ионе находится на линии связи H-H, на расстояниях от центров , . Тогда статическое равновесие сил записывается как:
Тогда статическое равновесие сил записывается как:
Решим систему уравнений и найдем зависимость полной энергии иона от межядерного расстояния.
Сессия MAXIMA решения системы уравнений.Решение системы не требует каких-то нешкольных навыков, просто MAXIMA удобна, чтобы не запутаться в выкладках. Результаты на картинке ниже.
Кривая потенциальной энергии молекулярного иона водорода.Мы видим, что молекулярный ион термодинамически стабилен относительно распада на протон и атом водорода. Энергия разрыва связи составляет 1/16 (164 кДж/моль), а длина связи — R=8/3 (1.41 Å). Экспериментальные значения — 255 кДж/моль энергия связи, расстояние — 1.07 Å. Для такой простой модели это более чем хорошее согласие.
Заключение
Сведение квантовомеханической задачи к молекулярной механике фермионов открывает в перспективе легкий и очень быстрый способ моделирования свойств материалов и химических реакций. Простые аппроксимации потенциалов Паули и Гейзенберга, к сожалению, не позволяют добиться высокой точности в предсказании свойств. Пока. Тем не менее, сам подход хорош уже тем, что не требует сложнейшего аппарата квантовой механики для понимания различных химических и физических явлений. Возможно, что кому то следующая мысль покажется крамолой, но я уверен в том, что основы химии можно объяснить без отсылок к квантовой физике. Без разбора уравнения Шредингера, гибридизации, теории резонанса, перекрывания орбиталей и прочего.
Пока. Тем не менее, сам подход хорош уже тем, что не требует сложнейшего аппарата квантовой механики для понимания различных химических и физических явлений. Возможно, что кому то следующая мысль покажется крамолой, но я уверен в том, что основы химии можно объяснить без отсылок к квантовой физике. Без разбора уравнения Шредингера, гибридизации, теории резонанса, перекрывания орбиталей и прочего.
Наши серверы можно использовать для разработки и просчета научных экспериментов.
Зарегистрируйтесь по ссылке выше или кликнув на баннер и получите 10% скидку на первый месяц аренды сервера любой конфигурации!
Найдите значения синуса. косинуса и тангенса угла, равного 135 градусов
Математика, 2020-12-11 17:20:06, bochkova123Алеся
Ответ
Ответ разместил: verymam
∠135°=∠180°-∠45°
по формулам приведения:
sin 135= sin (180 — 45) =√2/2
cos 135 = cos (180 – 45) = — cos 45 =- √2/2
tg 135 =sin 135 /cos 135 = -1
Ответ
Ответ разместил: suv1612
Ответ
Ответ разместил: sempai1
sin 150 градусов= sin 30 градусов=1/2
косинус 150 градусов= — cos 30 градусов= — корень из 3/2
тангенс 150 градусов= sin 30 градусов/ -cos 30 градусов= — корень из 3/ 3
Ответ
Ответ разместил: qwerty882
синус 30=
синус 45=
синус 60=
косинус 30=
косинус 45=
косинус 60=
тангенс 30=
тангенс 45=1
тангенс 60=
Ответ
Ответ разместил: Цыпленочка
синус 35⁰= 0,5736
косинус=-0,9063
тангенс= 0,7002
Ответ
Ответ разместил: worldteawithlemon
Sin -660
Sin -300
Sin 60=корень3/2
Cos 60=1/2
Tg 60 = корень 3
Ctg 60=1/корень3
Ответ
Ответ разместил: ХипХоп11
Sin(-660)=-sin660=-sin(720-60)=sin60=√3/2
cosx=√1-3/4=√1/4=1/2
tgx=√3/2/1/2=√3
ctgx=1/2/√3/2=1/√3
Ответ
Ответ разместил: sssmak1
Sin(-660°)=-Sin660°=-Sin(2*360-60)=
-(-Sin60°)=Sin60°=√3/2;
Cos(-660°)=Cos660°=Cos(2*360-60)=Cos60°=1/2;
tg(-660°)=Sin(-660°)/Cos(-660°)=
√3/2 : 1/2=√3;
ctg(-660°)=1/tg(-660°)= 1/√3=√3/3;
Другие вопросы по: Математика
Автобус выехал в 8 часов утра и ехал три часа со скоростью 60км/ч. за это время было пройдено 3/4 всего расстояния. с какой скоростью автобусу надо проехать оставшуюся часть пути,…
за это время было пройдено 3/4 всего расстояния. с какой скоростью автобусу надо проехать оставшуюся часть пути,…
Опубликовано: 28.02.2019 20:00
Ответов: 1
Вавтопарке было в 1,5 раза больше грузовых машин, чем легковых. после того как автопарк получил ещё 45 легковых машин, а 12 грузовых передал фермерам, в нем стало легковых машин на…
Опубликовано: 01.03.2019 05:20
Ответов: 3
Муравей выбежал из муравейника и вернулся кокае растояние он пробежал? решить по рисунку прямоугольник длина 3дм высота 2дм….
Опубликовано: 01.03.2019 13:10
Ответов: 1
Диагональ осевого сечения цилиндра равна d и наклонена к плоскости основания под углм альфа .найдите диаметр основания…
Опубликовано: 03.03.2019 07:20
Ответов: 1
Преобразуйте данную схему в уравнение реакции, расставте коэффициенты методом электронного : p+h3o2+> nah3po4. ..
..
Опубликовано: 03.03.2019 15:10
Ответов: 3
Скратким ответом. записать адрес файла program. exe, хранящегося на компьюторе, зарегистрированном в домене верхнего уровня ru, домене второго уровня schools и имеющем собственное…
Опубликовано: 03.03.2019 18:50
Ответов: 1
Популярные вопросы
.(Реши ! зарание ! дуремару для разведения пиявок нужен аквариум, вмещающий не менее 390 л воды. в магазине есть аквариум с измерениями 90 см,60см и 75 см. подойдет лион аптекарю?…
Опубликовано: 27.02.2019 19:50
Ответов: 2
Фарамант приказал доставить во дворец корзины с фруктами и сладостями. масса каждой корзины с фруктами 15кг, а масса каждой корзины со сладостями 20 кг. доставили 3 корзины. чему м…
Опубликовано: 02.03.2019 03:10
Ответов: 1
3,3-диметилпентан охарактеризовать хс и мп. ..
..
Опубликовано: 02.03.2019 05:40
Ответов: 3
Плоскость α и β параллельны причем плоскость α пересекает прямую а. докажите, что и плоскость β пересекает прямую а….
Опубликовано: 02.03.2019 23:10
Ответов: 1
Составьте уравнение реакции горения в избытке кислорода этана c2h6.рассчитайте массу (г) образовавшейся воды , если сгорело 34 г…
Опубликовано: 03.03.2019 09:00
Ответов: 2
Деловое эссе на тему загрязнение воздуха…
Опубликовано: 03.03.2019 12:00
Ответов: 2
1) могут ли углы треугольника относиться как числа 1,2,3? 2) найдите cos и tg, если sinα= 3в корне/2 люди надеюсь есть такие на белом свете?…
Опубликовано: 03.03.2019 13:30
Ответов: 3
1целая 1/2, 2целых 7/10,12 целых 3/4, 8 целых 7/20, 9 целых 1/10 запишите в виде неправильной дроби.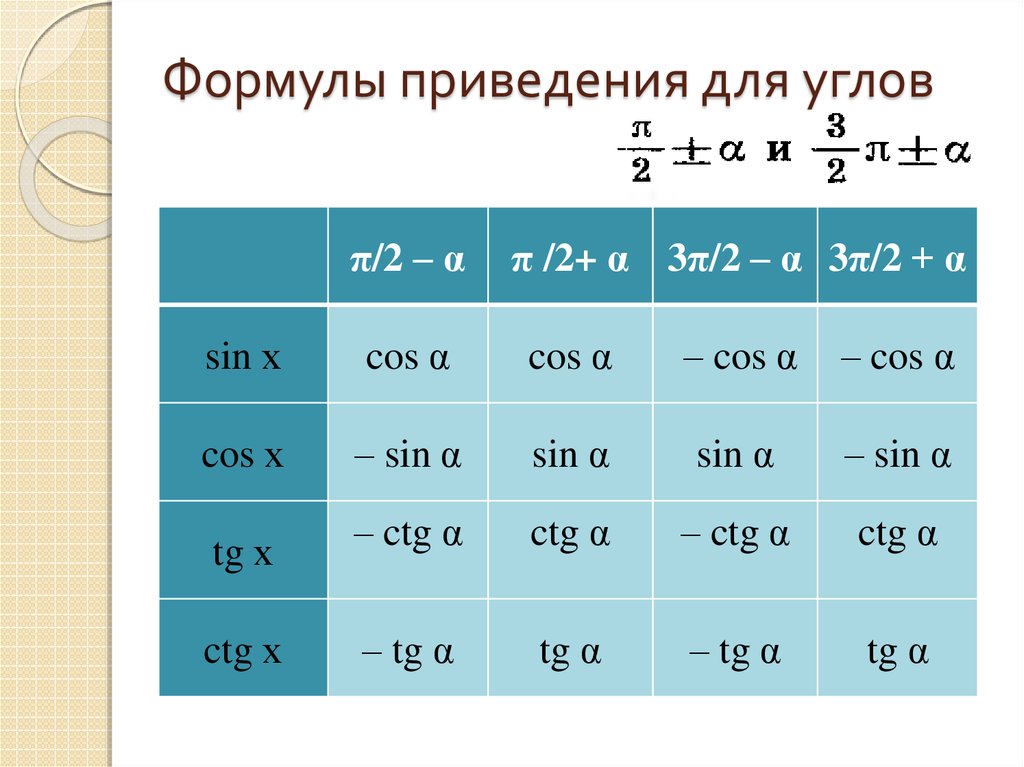 …
…
Опубликовано: 03.03.2019 22:20
Ответов: 2
Твір роздум чому я люблю бувати біля річки…
Опубликовано: 04.03.2019 04:00
Ответов: 1
Выполни деление с остатком 17: 19= 60: 16= 50: 17= 49: 3=…
Опубликовано: 04.03.2019 08:50
Ответов: 2
Больше вопросов по предмету: Математика Случайные вопросы
Ответы | ||||||||||||||||||||||||||||||||||||||||||||||||||||||
| ||||||||||||
|
|
| |||||||||||||||||||||||||||||||||||||||||||||||||||
Посмотреть всех экспертов из раздела Учеба и наука
| Похожие вопросы |
Поезд выехал из Алматы 19 мая в 15 50 мин прибыл в Актобе 21 мая в 10 30 мин сколько времени поезд находился в пути
Заряд на обкладках конденсатора меняется по закону q=0,03cos10^5пt(Кл). Определите значение заряда на обкладках конденса)дайте решение пожалуйста
Определите значение заряда на обкладках конденса)дайте решение пожалуйста
В Волшебной стране каждому дождливому дню обязательно предшествуют три солнечных дня, а через неделю после каждого солнечного дня снова наступает…
В двуз бочках 725л бензина…
Решено
Обществознание
Пользуйтесь нашим приложением
Sin 720 градусов — Найдите значение Sin 720 градусов
LearnPracticeDownload
Значение sin 720 градусов равно 0 . Sin 720 градусов в радианах записывается как sin (720° × π/180°), т. е. sin (4π) или sin (12,566370…). В этой статье мы обсудим способы нахождения значения sin 720 градусов на примерах.
- Sin 720°: 0
- Грех (-720 градусов): 0
- Sin 720° в радианах: грех (4π) или грех (12,5663706 .
 . . .)
. . .)
Каково значение греха 720 градусов?
Значение sin 720 градусов равно 0. Sin 720 градусов также может быть выражено с помощью эквивалента заданного угла (720 градусов) в радианах (12,56637 . . .).
Используя преобразование градусов в радианы, мы знаем, что θ в радианах = θ в градусах × (pi/180°)
⇒ 720 градусов = 720° × (π/180°) рад = 4π или 12,5663. . .
∴ sin 720° = sin(12,5663) = 0
Объяснение:
Для sin 720° угол 720° > 360°. Учитывая периодическое свойство синусоидальной функции, мы можем представить ее как sin(720° mod 360°) = sin(0°). Угол 720°, котерминальный углу 0°, лежит на положительной оси x.
Таким образом, значение sin 720 градусов = 0
Точно так же sin 720 ° также может быть записан как sin 720 градусов = (720 ° + n × 360 °), n ∈ Z.
⇒ sin 720° = sin 1080° = sin 1440° и так далее.
Примечание: Поскольку синус является нечетной функцией, значение sin(-720°) = -sin(720°) = 0,
Методы определения значения sin 720 градусов
Значение sin 720° принимается равным 0.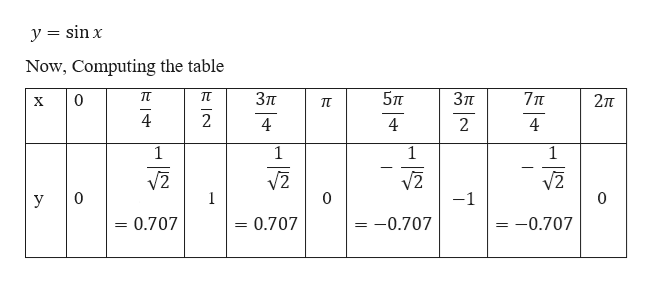 Мы можем найти значение sin 720 градусов следующим образом:
Мы можем найти значение sin 720 градусов следующим образом:
- Используя тригонометрические функции
- Использование единичного круга
Sin 720° в терминах тригонометрических функций
Используя формулы тригонометрии, мы можем представить sin 720 градусов как:
- ± √(1-cos²(720°))
- ± тангенс 720°/√(1 + тангенс²(720°))
- ± 1/√(1 + раскладушка²(720°))
- ± √(сек²(720°) — 1)/сек 720°
- 1/косек 720°
Примечание. Поскольку 720° лежит на положительной оси x, окончательное значение sin 720° будет равно 0.
Мы можем использовать тригонометрические тождества для представления sin 720° как ) = sin(-540°)
Sin 720 градусов с использованием единичного круга
Чтобы найти значение sin 720 градусов с помощью единичной окружности, представьте 720° в виде (2 × 360°) + 0° [∵ 720°>360°] ∵ синус — периодическая функция, sin 720° = sin 0°.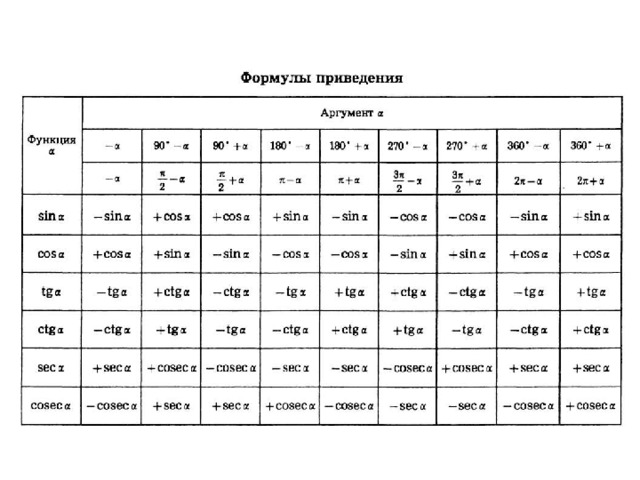
- Поверните ‘r’ против часовой стрелки, чтобы образовать угол 720° или 0° с положительной осью x.
- Синус 720 градусов равен координате y(0) точки пересечения (1, 0) единичной окружности и r.
Отсюда значение sin 720° = y = 0
☛ Также проверьте:
- грех 90 градусов
- грех 2 градуса
- грех 1 градус
- грех 17 градусов
- грех 130 градусов
- грех 7 градусов
Примеры использования Sin 720 градусов
Пример 1. Найдите значение 5 sin(720°)/7 cos(0°).
Решение:
Используя тригонометрические формулы, мы знаем, что sin(720°) = 0 и cos(0°) = 1,
⇒ Значение 5 sin(720°)/7 cos(0°) = 0Пример 2: Используя значение sin 720°, решите: (1-cos²(720°)).
Решение:
Мы знаем, (1-cos²(720°)) = (sin²(720°)) = 0
⇒ (1-cos²(720°)) = 0Пример 3.
 Найдите значение sin(-540°), если sin 720° = 0.
Найдите значение sin(-540°), если sin 720° = 0. Решение:
Так как sin(720°) = sin(-540°)
⇒ sin(540°) = 0
перейти к слайдуперейти к слайдуперейти к слайду
Готовы увидеть мир глазами математика?
Математика лежит в основе всего, что мы делаем. Наслаждайтесь решением реальных математических задач на живых уроках и станьте экспертом во всем.
Запишитесь на бесплатный пробный урок
Часто задаваемые вопросы о Sin 720 Degrees
Что такое Sin 720 Degrees?
Sin 720 градусов — значение тригонометрической функции синуса для угла, равного 720 градусам. Значение sin 720° равно 0.
Каково точное значение sin 720 градусов?
Точное значение sin 720 градусов равно 0.
Каково значение Sin 720 градусов в терминах Tan 720°?
Мы знаем, что, используя тригонометрические тождества, мы можем записать sin 720° как tan 720°/√(1 + tan²(720°)).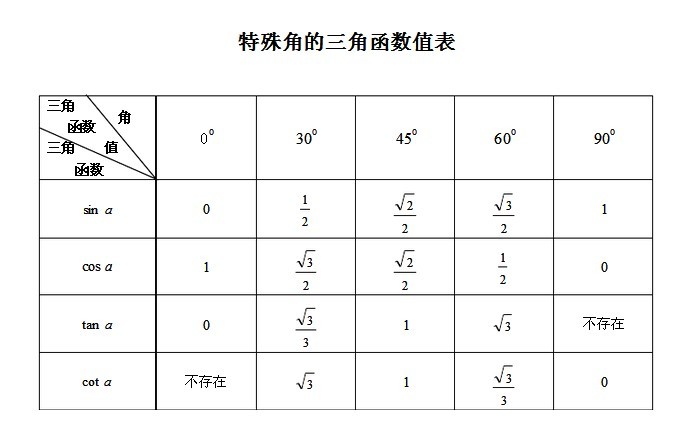 Здесь значение tan 720° равно 0.
Здесь значение tan 720° равно 0.
Как найти значение Sin 720 градусов?
Значение sin 720 градусов можно вычислить, построив угол 720° с осью x и затем найдя координаты соответствующей точки (1, 0) на единичной окружности. Значение sin 720° равно координате y (0). ∴ sin 720° = 0,
Как найти Sin 720° в терминах других тригонометрических функций?
Используя формулу тригонометрии, значение sin 720° может быть выражено через другие тригонометрические функции следующим образом:
- ± √(1-cos²(720°))
- ± тангенс 720°/√(1 + тангенс²(720°))
- ± 1/√(1 + раскладушка²(720°))
- ± √(сек²(720°) — 1)/сек 720°
- 1/косек 720°
☛ Также проверьте: Тригонометрическая таблица
Скачать БЕСПЛАТНЫЕ учебные материалы
Тригонометрия
Рабочие листы по математике и
визуальные учебные программы
| 1 | Найти точное значение | грех(30) | |
| 2 | Найти точное значение | грех(45) | |
| 3 | Найти точное значение | грех(30 градусов) | |
| 4 | Найти точное значение | грех(60 градусов) | |
| 5 | Найти точное значение | загар (30 градусов) | |
| 6 | Найти точное значение | угловой синус(-1) | |
| 7 | Найти точное значение | грех(пи/6) | |
| 8 | Найти точное значение | cos(pi/4) | |
| 9 | Найти точное значение | грех(45 градусов) | 902:30|
| 10 | Найти точное значение | грех(пи/3) | |
| 11 | Найти точное значение | арктический(-1) | |
| 12 | Найти точное значение | cos(45 градусов) | |
| 13 | Найти точное значение | cos(30 градусов) | |
| 14 | Найти точное значение | желтовато-коричневый(60) | |
| 15 | Найти точное значение | csc(45 градусов) | |
| 16 | Найти точное значение | загар (60 градусов) | |
| 17 | Найти точное значение | сек(30 градусов) | |
| 18 | Найти точное значение | cos(60 градусов) | |
| 19 | Найдите точное значение | соз(150) | |
| 20 | Найти точное значение | грех(60) | |
| 21 | Найти точное значение | cos(pi/2) | |
| 22 | Найти точное значение | загар (45 градусов) | |
| 23 | Найти точное значение | arctan(- квадратный корень из 3) | |
| 24 | Найти точное значение | csc(60 градусов) | |
| 25 | Найти точное значение | сек(45 градусов) | |
| 26 | Найти точное значение | csc(30 градусов) | |
| 27 | Найти точное значение | грех(0) | |
| 28 | Найти точное значение | грех(120) | 902:30|
| 29 | Найти точное значение | соз(90) | |
| 30 | Преобразовать из радианов в градусы | пи/3 | |
| 31 | Найти точное значение | желтовато-коричневый(30) | |
| 35 | Преобразовать из радианов в градусы | пи/6 | |
| 36 | Найти точное значение | детская кроватка(30 градусов) | |
| 37 | Найти точное значение | арккос(-1) | 902:30|
| 38 | Найти точное значение | арктический(0) | |
| 39 | Найти точное значение | детская кроватка(60 градусов) | |
| 40 | Преобразование градусов в радианы | 30 | |
| 41 | Преобразовать из радианов в градусы | (2 шт. )/3 )/3 | |
| 42 | Найти точное значение | sin((5pi)/3) | |
| 43 | Найти точное значение | sin((3pi)/4) | |
| 44 | Найти точное значение | желтовато-коричневый (пи/2) | |
| 45 | Найти точное значение | грех(300) | |
| 46 | Найти точное значение | соз(30) | |
| 47 | Найдите точное значение | соз(60) | |
| 48 | Найти точное значение | соз(0) | |
| 49 | Найти точное значение | соз(135) | |
| 50 | Найти точное значение | cos((5pi)/3) | |
| 51 | Найти точное значение | соз(210) | |
| 52 | Найти точное значение | сек(60 градусов) | |
| 53 | Найти точное значение | грех(300 градусов) | |
| 54 | Преобразование градусов в радианы | 135 | |
| 55 | Преобразование градусов в радианы | 150 | |
| 56 | Преобразовать из радианов в градусы | (5 дюймов)/6 | 902:30|
| 57 | Преобразовать из радианов в градусы | (5 дюймов)/3 | |
| 58 | Преобразование градусов в радианы | 89 градусов | |
| 59 | Преобразование градусов в радианы | 60 | |
| 60 | Найти точное значение | грех(135 градусов) | |
| 61 | Найти точное значение | грех(150) | |
| 62 | Найти точное значение | грех(240 градусов) | |
| 63 | Найти точное значение | детская кроватка(45 градусов) | |
| 64 | Преобразовать из радианов в градусы | (5 дюймов)/4 | |
| 65 | Найти точное значение | грех(225) | |
| 66 | Найдите точное значение | грех(240) | |
| 67 | Найти точное значение | cos(150 градусов) | |
| 68 | Найти точное значение | желтовато-коричневый(45) | |
| 69 | Оценить | грех(30 градусов) | |
| 70 | Найти точное значение | сек(0) | |
| 71 | Найти точное значение | cos((5pi)/6) | |
| 72 | Найти точное значение | КСК(30) | 902:30|
| 73 | Найти точное значение | arcsin(( квадратный корень из 2)/2) | |
| 74 | Найти точное значение | желтовато-коричневый ((5pi)/3) | |
| 75 | Найти точное значение | желтовато-коричневый(0) | |
| 76 | Оценить | грех(60 градусов) | |
| 77 | Найти точное значение | arctan(-(квадратный корень из 3)/3) | |
| 78 | Преобразовать из радианов в градусы | (3 пи)/4 | |
| 79 | Найти точное значение | sin((7pi)/4) | |
| 80 | Найти точное значение | угловой синус(-1/2) | |
| 81 | Найти точное значение | sin((4pi)/3) | |
| 82 | Найдите точное значение | КСК(45) | |
| 83 | Упростить | арктан( квадратный корень из 3) | |
| 84 | Найти точное значение | грех(135) | |
| 85 | Найти точное значение | грех(105) | |
| 86 | Найти точное значение | грех(150 градусов) | |
| 87 | Найти точное значение | sin((2pi)/3) | |
| 88 | Найти точное значение | желтовато-коричневый ((2pi)/3) | |
| 89 | Преобразовать из радианов в градусы | пи/4 | |
| 90 | Найти точное значение | sin(pi/2) | |
| 91 | Найти точное значение | сек(45) | 902:30|
| 92 | Найти точное значение | cos((5pi)/4) | |
| 93 | Найти точное значение | cos((7pi)/6) | |
| 94 | Найти точное значение | угловой синус(0) | |
| 95 | Найти точное значение | грех(120 градусов) | |
| 96 | Найти точное значение | желтовато-коричневый ((7pi)/6) | |
| 97 | Найти точное значение | соз(270) | |
| 98 | Найдите точное значение | sin((7pi)/6) | |
| 99 | Найти точное значение | arcsin(-( квадратный корень из 2)/2) | |
| 100 | Преобразование градусов в радианы | 88 градусов |
Калькулятор — sin(720) — Solumaths
Sin, расчет онлайн
Резюме:
Тригонометрическая функция sin для вычисления синуса угла в радианах,
градусов или градианов.
sin online
Описание:
Калькулятор позволяет использовать большинство из тригонометрических функций , есть возможность вычислить синус , косинус и касательная угла через одноименные функции.
Тригонометрическая функция синус отметил синус , позволяет вычислить синус угла онлайн , можно использовать разные угловые единицы: градус, градус и радианы, которые по умолчанию являются угловыми единицами.
- Расчет синуса
- Таблица специальных синусоидальных значений
- Основные свойства
Вычисление синуса угла в радианах
Калькулятор синуса позволяет через функцию sin вычислить онлайн синус синус угла в радианах, сначала нужно
выберите нужную единицу, нажав на кнопку параметров расчетного модуля.
После этого можно приступать к расчетам.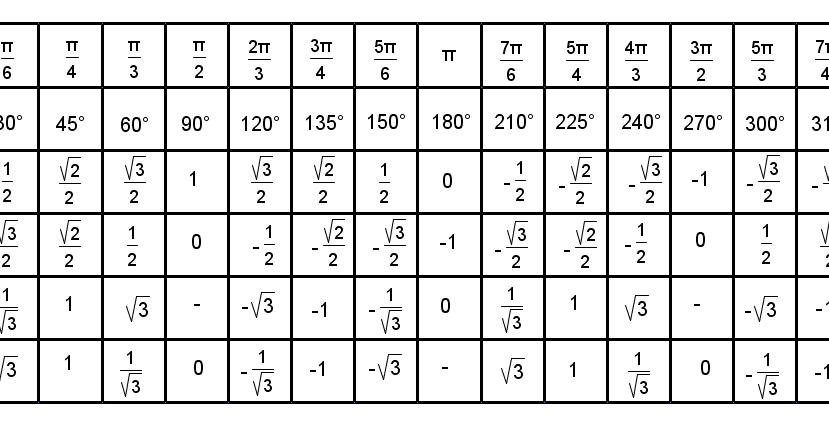
Чтобы вычислить синус онлайн от `pi/6`, введите sin(`pi/6`), после вычисления результат `1/2` возвращается.
Обратите внимание, что функция синуса способна распознавать некоторые специальные углы и делать расчеты со специальными связанными значениями в точной форме.
Вычислить синус угла в градусах
Чтобы вычислить синус угла в градусах, необходимо сначала выбрать нужную единицу измерения нажав на кнопку модуля расчета параметров. После этого можно приступать к вычислениям.
Чтобы вычислить синус 90, введите sin(90). результат 1 возвращается.
Вычислить синус угла в градусах
Чтобы вычислить синус угла в градианах, необходимо сначала выбрать нужную единицу измерения нажав на кнопку модуля расчета параметров. После этого можно приступать к вычислениям.
Чтобы вычислить синус 50, введите sin(50), после вычисления,
возвращается результат `sqrt(2)/2`.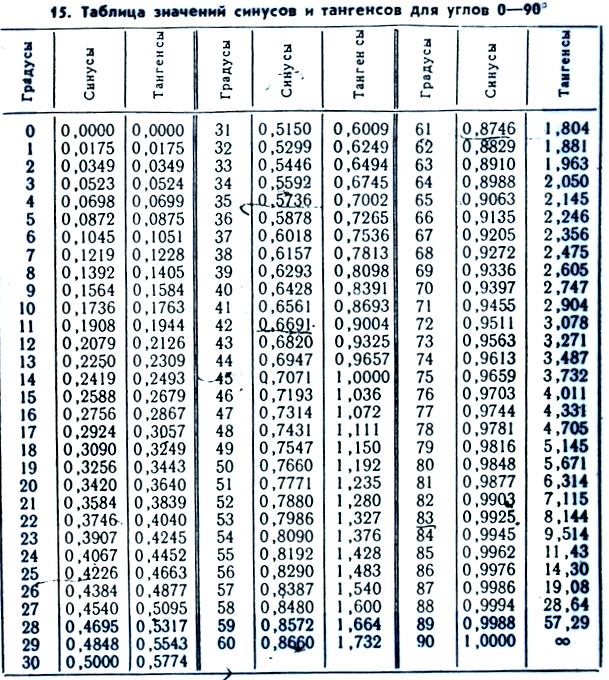
Обратите внимание, что функция синуса способна распознавать некоторые специальные углы и выполнять исчисление со специальными ассоциированными точными значениями.
Синус допускает некоторые специальные значения, которые калькулятор может определить в точных формах. Вот таблица значений общего синуса :
| sin(`2*pi`) | `0` | ||
| sin(`pi`) | `0` | ||
| sin(`2 `2 `2`) | 5 | ||
| sin(`pi/4`) | `sqrt(2)/2` | ||
| sin(`pi/3`) | `sqrt(3)/2` | ||
| sin(`pi/6`) | `1/2` | ||
| sin(`2*pi/3`) | `sqrt(3) /2` | ||
| sin(`3*pi/4`) | `sqrt(2)/2` | ||
| sin(`5*pi/6`) | `1/2` | ||
| sin(`0`) | `0` | ||
| sin(`-2*pi`) | `0` | ||
| sin(`-pi`) 2 3 9025 `1`290 | sin(`pi/2`) | `-1` | |
| sin(`-pi/4`) | `-sqrt(2)/2` | ||
| sin(`-pi/3`) | `-sqrt(3)/2` | ||
| sin(`-pi/6`) | `-1/2` | ||
| sin(`-2*pi/3`) | `-sqrt(3)/2` | ||
| sin( `-3*pi/4`) | `-sqrt(2)/2` | ||
| sin(`-5*pi/6`) | `-1/2` |
`AA x в RR, k в ZZ`,
- `sin(-x)= -sin(x)`
- `sin(x+2*k*pi)=sin(x)`
- `sin(pi-x)=sin(x)`
- `sin(pi+x)=-sin(x)`
- `sin(pi/2-x)=cos(x)`
- `sin(pi/2+x)=cos(x)`
Производная синуса равна cos(x).
Первообразная синуса равна -cos(x).
Функция sine является нечетной функцией, для каждого действительного x `sin(-x)=-sin(x)`. Следствием для кривой, представляющей синусоидальную функцию, является то, что она допускает начало отсчета как точку симметрии.
Калькулятор имеет решатель, который позволяет решать уравнение с синусом вида cos(x)=a . Расчеты для получения результата детализированы, поэтому можно будет решать уравнения типа `грех(х)=1/2` или же `2*sin(x)=sqrt(2)` с этапами расчета.
Синтаксис:
sin(x), где x — мера угла в градусах, радианах или градах.
Примеры:
sin(`0`), возвращает 0
Производный синус:
можно использовать калькулятор производной, который позволяет вычислить производную функции синуса
производная sin(x) является производной(`sin(x)`)=`cos(x)`
Синус первообразной :
Калькулятор первообразных позволяет вычислить первообразную функции синуса.
Первопроизводная sin(x) есть первопроизводная(`sin(x)`)=`-cos(x)`
Предел синуса :
Калькулятор предела позволяет вычислять пределы функции синуса.
предел sin(x) is limit(`sin(x)`)
Обратная функция синуса :
обратная функция синуса представляет собой функцию арксинуса, обозначенную как arcsin.
График синуса :
Графический калькулятор может отображать синусоидальную функцию в заданном интервале.
Свойство функции синуса:
Функция синуса является нечетной функцией.
Расчет онлайн с синусом (sine)
См. также
Список связанных калькуляторов:
- Арккосинус : arccos.
 Функция arccos позволяет вычислять арккосинус числа.
Функция arccos является обратной функцией функции косинуса.
Функция arccos позволяет вычислять арккосинус числа.
Функция arccos является обратной функцией функции косинуса. - Арксинус : арксинус. Функция arcsin позволяет вычислить арксинус числа. Функция arcsin является обратной функцией функции синуса.
- Арктангенс: арктангенс. Функция арктангенса позволяет вычислить арктангенс числа. Функция арктангенса является обратной функцией функции тангенса.
- Тригонометрический калькулятор: simple_trig. Калькулятор, который использует тригонометрическую формулу для упрощения тригонометрического выражения.
- Косинус: cos. Кос-тригонометрическая функция вычисляет косинус угла в радианах, градусов или градианов.
- Косеканс: косеканс Тригонометрическая функция sec позволяет вычислить секанс угла, выраженного в радианах, градусах или градусах.
- Котангенс: котан. Тригонометрическая функция котана для вычисления котана угла в радианах, градусов или градианов.
- Тригонометрическое расширение: expand_trigo.
 Калькулятор позволяет получить тригонометрическое разложение выражения.
Калькулятор позволяет получить тригонометрическое разложение выражения. - Тригонометрическая линеаризация : linearization_trigo. Калькулятор, позволяющий линеаризовать тригонометрическое выражение.
- Упростить калькулятор: упростить. Калькулятор, который может упростить алгебраическое выражение онлайн.
- Секанс : сек. Тригонометрическая функция sec позволяет вычислить секанс угла, выраженного в радианах, градусах или градусах.
- Синус : грех. Тригонометрическая функция sin для вычисления греха угла в радианах, градусов или градианов.
- Тангенс: коричневый. Тригонометрическая функция тангенса для вычисления тангенса угла в радианах, градусов или градианов.
Напоминания о курсах, калькуляторы, упражнения и игры: Тригонометрические функции, Вещественные функции
Симметрии 360 и 720 градусов – Чтение Фейнмана
Мой предыдущий пост был ужасно длинный, так что я должен предположить, что многие из моих читателей, возможно, начали читать его, но… Ну… бросили на полпути или даже раньше.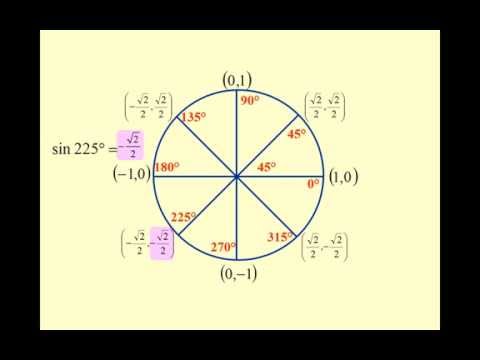 🙂 Однако я добавил сноску, над которой интересно поразмыслить. Кроме того, я знаю, что многие из моих читателей не интересуются математикой, даже если они понимают, что без математики нельзя по-настоящему оценить квантовую теорию. Но да. Возможно, я оставил некоторых читателей позади. Поэтому позвольте мне подобрать самую интересную часть всех историй в моих последних сообщениях настолько простым языком, насколько я смогу найти.
🙂 Однако я добавил сноску, над которой интересно поразмыслить. Кроме того, я знаю, что многие из моих читателей не интересуются математикой, даже если они понимают, что без математики нельзя по-настоящему оценить квантовую теорию. Но да. Возможно, я оставил некоторых читателей позади. Поэтому позвольте мне подобрать самую интересную часть всех историй в моих последних сообщениях настолько простым языком, насколько я смогу найти.
У нас есть эта странная симметрия 360/720° в квантовой физике или, если быть точным, она есть у элементарных частиц материи (вспомните, например, электроны). Надеюсь, чтобы помочь вам понять, о чем идет речь, мне пришлось объяснить часто путающиеся, но существенно отличающиеся концепции системы отсчета и репрезентативной базы (или репрезентации tout court ). Я не буду повторять это объяснение, но подумайте о следующем.
Если мы просто повернем системы отсчета на 360°, мы просто используем одну и ту же систему отсчета и поэтому видим одно и то же: какой-то объект, который мы смутно описываем некоторой функцией.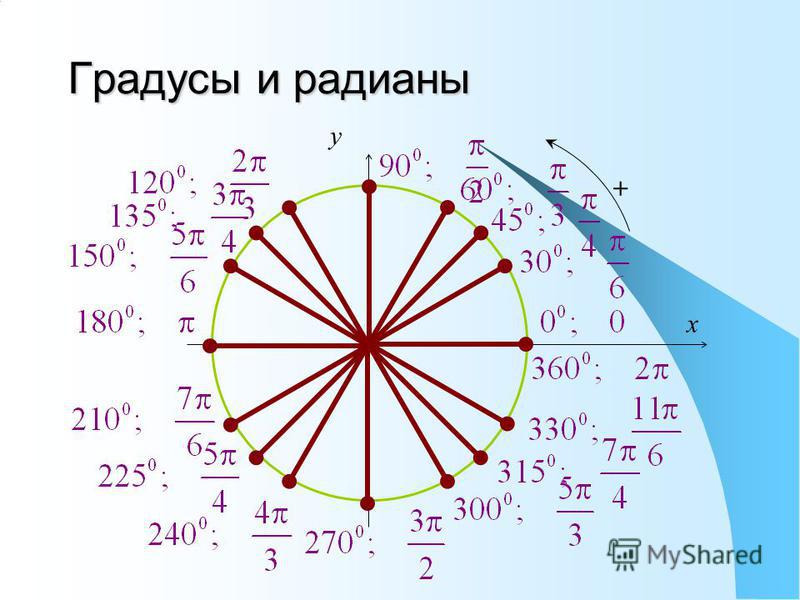 Подумайте о каком-нибудь вращающемся объекте. В своей собственной системе отсчета он будет просто вращаться вокруг некоторого центра или, в нашей, он будет вращаться, двигаясь вдоль некоторой оси в своей собственной системе отсчета, или, если смотреть из нашей, как движущийся в каком-то направлении во время своего вращения, как показано ниже.
Подумайте о каком-нибудь вращающемся объекте. В своей собственной системе отсчета он будет просто вращаться вокруг некоторого центра или, в нашей, он будет вращаться, двигаясь вдоль некоторой оси в своей собственной системе отсчета, или, если смотреть из нашей, как движущийся в каком-то направлении во время своего вращения, как показано ниже.
Чтобы быть точным, я должен сказать, что мы описываем его некоторой Фурье суммой таких функций. Теперь, если его направление вращения… Ну… В другом направлении, то мы опишем его какой-нибудь функцией e − i ·θ (опять же следует читать: сумма Фурье таких функций). Странно следующее: если мы повернем сам объект на те же 360°, мы получим другой объект: наш e I · θ и E — I · θ Функция (опять -таки: мыслите · θ (опять же: мыслите · θ (опять же: придумайте · θ (снова: придумайте · θ , так: «Подумайте о · θ ».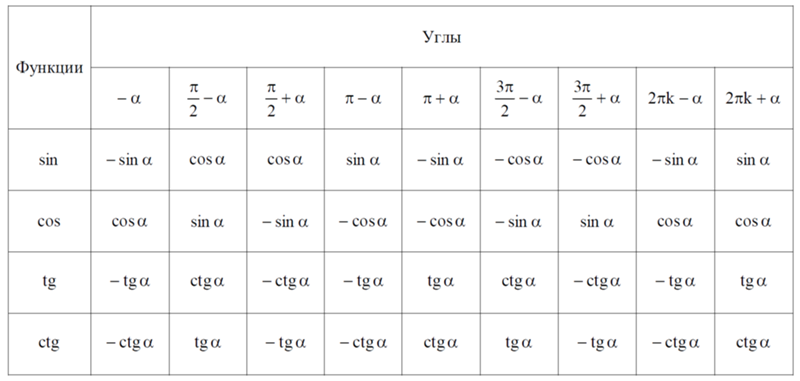 e ± i ·θ вещь. Перед ним появляется знак минус . Так что же здесь произошло? Какая разница, на самом деле ?
e ± i ·θ вещь. Перед ним появляется знак минус . Так что же здесь произошло? Какая разница, на самом деле ?
Ну… не знаю. Это очень глубоко. Думайте о нас с вами как о двух электронах, которые наблюдают друг за другом. Если я ничего не сделаю, а ты продолжишь смотреть на меня при повороте вокруг меня на полные 360° (так что это поворот вашей системы отсчета на 360°), то вы окажетесь там, где были в начале, и, что важно, вы увидите то же самое: мне . 🙂 То есть… Вы увидите ровно то же самое: если бы я был волновым пакетом e + i · θ , я все еще
7 7 +
+ · волновой пакет θ сейчас. Или если бы я был e − i · θ волновой пакет, то я все еще e − i · θ волновой пакет сейчас. Легкий. Логичный. Очевидно , верно? Но теперь мы попробуем кое-что другое: я оборачиваюсь, совершая полный 360-градусный поворот, и вы остаетесь на месте и смотрите на меня , пока я поворачиваюсь.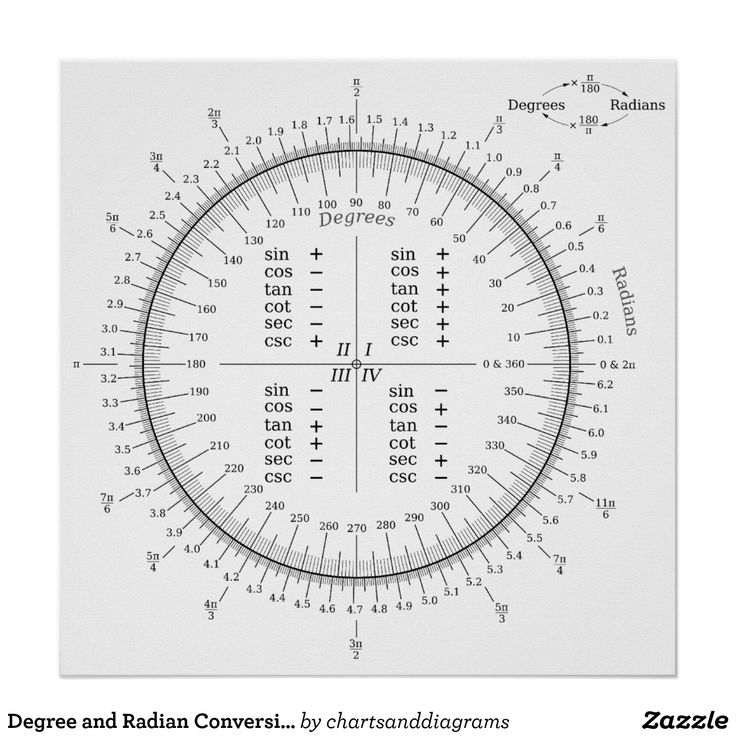 Что случается? В классическом понимании ничего не должно происходить, но… Ну… Это странный мир квантовой механики: когда я снова там, где был, — так сказать, снова смотрю на вас — тогда… Ну… Я уже не совсем тот. Или… Ну… Может, я, но ты видишь меня иначе. Если я был e + i · θ волновым пакетом, то теперь я стал − e + i · θ волновым пакетом
Что случается? В классическом понимании ничего не должно происходить, но… Ну… Это странный мир квантовой механики: когда я снова там, где был, — так сказать, снова смотрю на вас — тогда… Ну… Я уже не совсем тот. Или… Ну… Может, я, но ты видишь меня иначе. Если я был e + i · θ волновым пакетом, то теперь я стал − e + i · θ волновым пакетом
Не сильно отличается от , но… Ну… Этот знак минус имеет значение, верно? Или если я был волновым пакетом, составленным из элементарных a · e − i · θ волн, то я стал − e − i ·θ волновой пакет сейчас. Что случилось?
Это заставляет меня думать о парадоксе близнецов в специальной теории относительности. Мы знаем, что это парадокс — так что это только кажущееся противоречие: мы знаем, какой из близнецов остался на Земле, а какой путешествовал из-за гравитационных сил, действующих на путешествующего близнеца. Тот, кто остается на Земле, не испытывает ни ускорения, ни замедления. Здесь то же самое? Я имею в виду… Тот, кто оборачивается, должен испытать что-то сила .
Тот, кто остается на Земле, не испытывает ни ускорения, ни замедления. Здесь то же самое? Я имею в виду… Тот, кто оборачивается, должен испытать что-то сила .
Можем ли мы связать это с парадоксом близнецов? Может быть. Обратите внимание, что знак минус перед функциями e −± i · θ представляет собой знак минус перед компонентами синуса и косинуса. Итак… Ну… Отрицательное значение синуса и косинуса — это синус и косинус, но со сдвигом по фазе на 180°: θ ± π). Теперь, добавляя или вычитая общий фазовый фактор в/из аргумента волновой функции составляет изменение начала отсчета времени. Итак… Ну… я действительно думаю, что парадокс близнецов и эта довольно странная история с 360° и 720° симметриями, по сути, связаны. 🙂
Post scriptum : Google отмечает сегодня 135 лет со дня рождения Макса Борна. 🙂 Я думаю, что это отличное совпадение в свете того, о чем я писал в последнее время (возможные интерпретации волновой функции). 🙂
🙂
Функция косеканса
Функция косеканса является тригонометрической функцией, одной из трех обратных функций , которые мы рассматриваем на этих страницах, а двумя другими являются функция секанса и функция котангенса . Обратная функция — это функция, которая является обратной (или мультипликативной обратной ) другой функции (см. ниже). Функция косеканса (обычно сокращенно csc) является обратной функцией функция синуса . Как и в случае с другими тригонометрическими функциями, используемыми в современном мире, функция косеканса, безусловно, была известна арабским ученым, а таблицы значений косеканса, как известно, существовали к десятому веку нашей эры. Чтобы прояснить, как именно связаны функция косеканса и функция синуса, рассмотрите диаграмму ниже.
Косеканс как отрезок единичной окружности
Как и другие тригонометрические функции, косеканс можно представить в виде отрезка, связанного с единичный круг . На диаграмме показан косеканс для угла поворота θ от на сорок пять градусов (измерено против часовой стрелки от положительной оси x ). Отрезок AF лежит на линии, касательной к окружности в точке A. Отрезок OF (показан красным) представляет собой косеканс и является продолжением отрезка OP . Помните, что точка P — это точка на окружности, чьи x и 9Координаты 1458 y
На диаграмме показан косеканс для угла поворота θ от на сорок пять градусов (измерено против часовой стрелки от положительной оси x ). Отрезок AF лежит на линии, касательной к окружности в точке A. Отрезок OF (показан красным) представляет собой косеканс и является продолжением отрезка OP . Помните, что точка P — это точка на окружности, чьи x и 9Координаты 1458 y
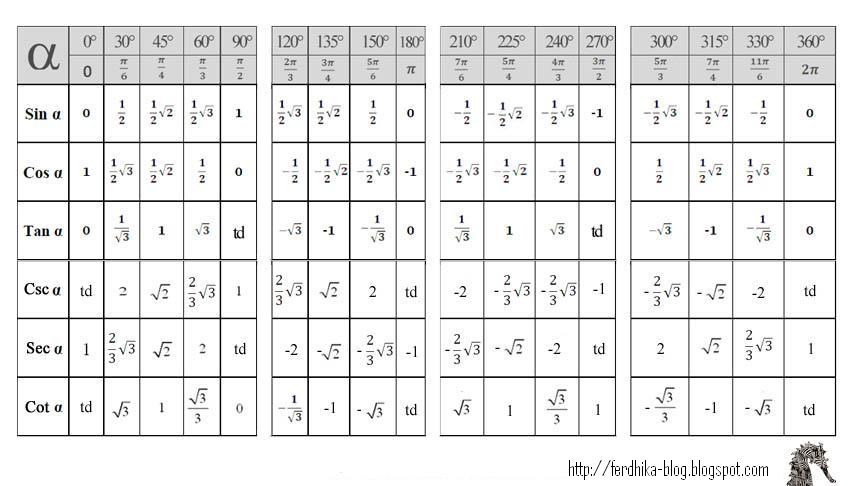 Однако по мере того, как значение sin ( θ ) приближается к нулю, значение csc ( θ ) стремится к бесконечности. Таким образом, значение csc ( θ ), когда sin ( θ ) равно нулю, называется undefined .
Однако по мере того, как значение sin ( θ ) приближается к нулю, значение csc ( θ ) стремится к бесконечности. Таким образом, значение csc ( θ ), когда sin ( θ ) равно нулю, называется undefined .Очевидно, поскольку функция косеканса является обратной величиной функции синуса, ее можно выразить через функцию синуса следующим образом:
| csc ( θ ) = | 1 | |||||
| sin ( θ ) | 231
| csc ( θ ) = | 1 |
| y |
Мы также можем определить косеканс в терминах прямоугольного треугольника. Если вы читали страницы этого раздела, посвященные трем основным тригонометрическим функциям ( синус , косинус и тангенс ), вы уже знакомы с приведенной ниже диаграммой.
Если вы читали страницы этого раздела, посвященные трем основным тригонометрическим функциям ( синус , косинус и тангенс ), вы уже знакомы с приведенной ниже диаграммой.
В треугольнике ABC csc ( θ ) = c / a
В прямоугольном треугольнике АВС синус угла θ — это частное против и гипотенузы (т. Поскольку функция косеканса есть , обратная функции синуса, то косеканс угла θ будет частным гипотенузы и противоположного . Это дает нам:
| csc ( θ ) = | 1 | = | hypotenuse | = | c |
| sin ( θ ) | opposite | a |
Для тех, кто интересуется такими вещами, мы использовали Microsoft Excel для создания собственной таблицы значений косеканса для углов в диапазоне от ноль градусов (0°) до триста шестьдесят градусов (360°) с приращением одна десятая градуса.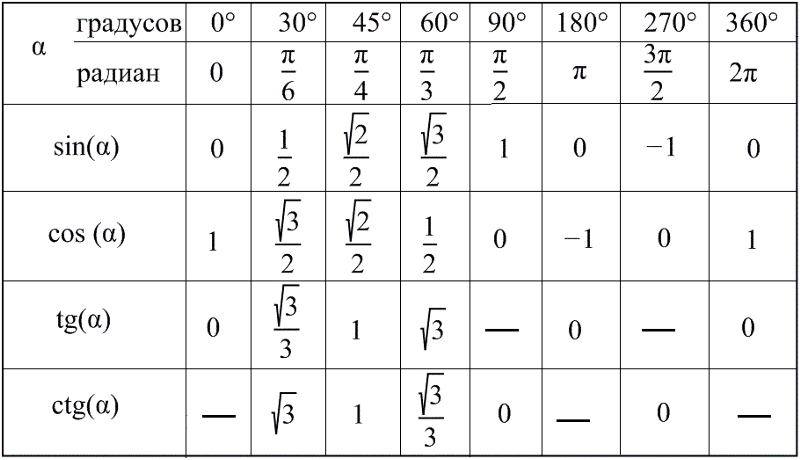 Чтобы увидеть таблицу, нажмите здесь .
Чтобы увидеть таблицу, нажмите здесь .
Если вы изучите таблицу, то увидите, что существует значительный диапазон углов с центром около девяноста градусов, для которых значение, возвращаемое функцией косеканса, довольно мало и изменяется относительно медленно. Однако для углов, близких к ноль градусов (0°) или сто восемьдесят градусов (180°), значение, возвращаемое функцией косеканса, намного больше. Этого и следовало ожидать, поскольку значение sin ( θ ) будет очень мал для этих углов, поэтому его обратное будет соответственно большим. На самом деле, значение, возвращаемое функцией косеканса для угла либо в ноль градусов, либо в сто восемьдесят градусов, считается равным undefined , поскольку уравнение csc ( θ ) = 1 / sin ( θ ) будет включать деление на ноль. То же верно и для угла триста шестьдесят градусов (360°). На самом деле, это будет применяться к любому углу, для которого значение синуса равно нулю. Ниже мы приводим график функции косеканса для углов в диапазоне ноль градусов до семьсот двадцать градусов (720°).
Ниже мы приводим график функции косеканса для углов в диапазоне ноль градусов до семьсот двадцать градусов (720°).
График функции косеканса для углов в диапазоне от 0° до 720°
Поскольку абсолютное значение синуса угла никогда не превысит на , обратная величина синуса угла никогда не будет меньше единицы. Итак, точно так же, как значение косеканса не определено для любого угла, для которого синус равен ноль всегда будет один для любого угла, для которого синус равен единице, и минус один (-1) для любого угла, для которого синус равен минус единице. На самом деле, как видно из таблицы значений косеканса и графика функции косеканса, значение косеканса отрицательно для всех углов, для которых синус отрицателен. Как и график функции тангенса, график функции косеканса может включать несколько очень больших положительных и отрицательных пиков, так как значение sin ( θ ) стремится к нулю. Однако, в отличие от функции тангенса, период функции косеканса составляет триста шестьдесят градусов (360°), или 2π. Как и функция синуса, функция косеканса возвращает положительные значения углов в квадрантах I и II и отрицательные значения углов в квадрантах III и IV .
Однако, в отличие от функции тангенса, период функции косеканса составляет триста шестьдесят градусов (360°), или 2π. Как и функция синуса, функция косеканса возвращает положительные значения углов в квадрантах I и II и отрицательные значения углов в квадрантах III и IV .
Если вы читали страницу, озаглавленную «Функция касательной» (или, возможно, даже если не читали), вы знаете, что вертикальные красные линии на графике равны асимптот . Асимптота кривой — это такая линия, что по мере приближения расстояния между кривой и линией к нулю значение кривой стремится к бесконечности. В этом случае асимптотами можно считать «пробелы» на графике, где значение csc ( θ ) не определено. Обратите также внимание на то, что по мере того, как график пересекает асимптоту, значение csc ( θ ) переходит от своего максимального положительного значения к максимальному отрицательному значению (или наоборот). Вы также можете увидеть, как значения различаются по обе стороны от асимптоты, изучив таблицу значений косеканса.
Вы также можете увидеть, как значения различаются по обе стороны от асимптоты, изучив таблицу значений косеканса.
Как и в случае с другими тригонометрическими функциями, которые мы рассмотрели, нам не нужно использовать таблицы для нахождения косеканса угла (или угла, соответствующего заданному значению косеканса), так как любой современный научный калькулятор может сделать это за нас, даже хотя в большинстве калькуляторов нет специальной кнопки для функции косеканса. Нахождение косеканса угла с помощью встроенного калькулятора, предусмотренного в Microsoft Windows , по-прежнему относительно просто. Предположим, мы хотим найти косеканс угла восемьдесят пять градусов (85°). Вы можете найти встроенный калькулятор Microsoft Windows, нажав кнопку «Пуск» в Windows 7 и выбрав «Все программы»> «Стандартные»> «Калькулятор» (в других версиях Windows может потребоваться другая последовательность нажатий клавиш). Научную версию калькулятора можно выбрать в меню View приложения.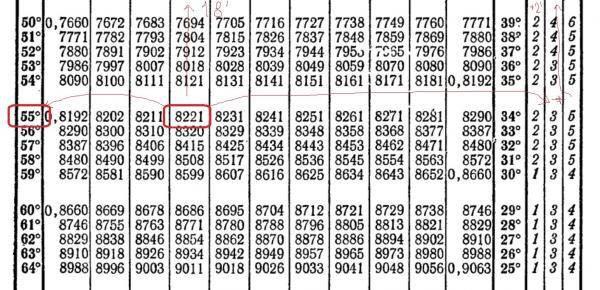 Чтобы найти косеканс восьмидесяти пяти градусов с помощью калькулятора Windows, введите следующие нажатия клавиш (если у вас нет калькулятора Windows, используйте любой доступный калькулятор, который может выполнять триггерные функции):
Чтобы найти косеканс восьмидесяти пяти градусов с помощью калькулятора Windows, введите следующие нажатия клавиш (если у вас нет калькулятора Windows, используйте любой доступный калькулятор, который может выполнять триггерные функции):
Введите эти нажатия клавиш, чтобы найти косеканс 85°.
Поскольку функция косеканса является обратной функцией синуса, все, что мы сделали здесь, это использовали кнопку функции синуса на калькуляторе, а затем применили встроенную кнопку обратной функции калькулятора (обычно обозначенную как 1/ x ). к результату. Кстати, убедитесь, что калькулятор настроен на градусов .режиме (если только вы не планируете вводить значение угла в радианах или градах). Если вы правильно ввели нажатия клавиш, вы должны увидеть следующий экран:
Калькулятор отображает значение csc(85°)
Все идет нормально. Теперь давайте предположим, что вы хотите найти размер острого угла в прямоугольном треугольнике, сначала найдя частное гипотенузы и противоположной части (то есть косеканс угла). Если у вас есть значения длин сторон треугольника, вы можете достаточно легко найти значение косеканса угла. Нахождение угла не так просто, как для трех основных тригонометрических функций, поскольку в большинстве калькуляторов нет специальной кнопки для 9Функция арккосеканса 1458 (обратная функция косеканса ). К счастью, есть относительно простой способ обойти это. Найдем значение угла θ для прямоугольного треугольника, показанного ниже.
Теперь давайте предположим, что вы хотите найти размер острого угла в прямоугольном треугольнике, сначала найдя частное гипотенузы и противоположной части (то есть косеканс угла). Если у вас есть значения длин сторон треугольника, вы можете достаточно легко найти значение косеканса угла. Нахождение угла не так просто, как для трех основных тригонометрических функций, поскольку в большинстве калькуляторов нет специальной кнопки для 9Функция арккосеканса 1458 (обратная функция косеканса ). К счастью, есть относительно простой способ обойти это. Найдем значение угла θ для прямоугольного треугольника, показанного ниже.
Мы хотим найти величину угла θ
Для угла θ стороны c и a являются гипотенузой и противоположной стороной соответственно. На самом деле мы можем найти размер угла за одну операцию на калькуляторе Windows. Мы делаем это, используя скобки во введенной последовательности клавиш, чтобы заставить калькулятор сначала найти обратное значение частного гипотенузы и противоположное (то есть косеканс угла). Затем мы применяем функцию арксинуса к результату. Вот последовательность клавиш для использования:
Затем мы применяем функцию арксинуса к результату. Вот последовательность клавиш для использования:
Введите эти нажатия клавиш, чтобы найти размер угла θ
Возможно, вы уже поняли, что здесь мы находили синус угла, взяв обратное косеканса . Затем мы просто применили к результату функцию арксинуса . Мы могли бы, конечно, просто изменить порядок, в котором мы вводим значения (т.е. напротив / гипотенуза ), и в этом случае нам не нужно использовать ответную кнопку. На этом этапе вы должны начать понимать, что все тригонометрические функции очень тесно взаимосвязаны и что мы часто можем заменить выражение, включающее одну тригонометрическую функцию, эквивалентным выражением, включающим другую тригонометрическую функцию. Иногда это может быть очень полезно. Если вы правильно ввели нажатия клавиш, вы должны увидеть следующий экран:
Калькулятор отображает значение угла θ
Функция косеканса, как и другие тригонометрические функции, может быть представлена в виде бесконечного ряда . Как мы упоминали в другом месте, значение, возвращаемое тригонометрической функцией для заданного угла, не может быть вычислено с помощью простой алгебраической формулы. Для большинства углов точное значение можно получить только как сумму бесконечного числа слагаемых, чего, очевидно, достичь невозможно. Достаточно точное приближение значения находится с использованием суммы ограниченного числа членов из бесконечного ряда функции. Чем больше число включенных терминов, тем выше точность результата. Количество используемых терминов будет зависеть от требуемой точности и доступных вычислительных ресурсов. Бесконечный ряд, часто упоминаемый для функции косеканса, выглядит следующим образом:
Как мы упоминали в другом месте, значение, возвращаемое тригонометрической функцией для заданного угла, не может быть вычислено с помощью простой алгебраической формулы. Для большинства углов точное значение можно получить только как сумму бесконечного числа слагаемых, чего, очевидно, достичь невозможно. Достаточно точное приближение значения находится с использованием суммы ограниченного числа членов из бесконечного ряда функции. Чем больше число включенных терминов, тем выше точность результата. Количество используемых терминов будет зависеть от требуемой точности и доступных вычислительных ресурсов. Бесконечный ряд, часто упоминаемый для функции косеканса, выглядит следующим образом:
| csc ( x ) = x -1 + | 1 | x + | 7 | x 3 + | 31 | x 5 +· · · · |
| 6 | 360 | 15,120 |
Тригонометрические функции — Justin Skycak
95TRIGONOMETRIC — Justin Skycak
9.
Существуют три основные «триггерные» функции: синус, косинус и тангенс, а для запоминания того, что они представляют, часто используется мнемоника SohCahToa:
- • СИНУС угла — это отношение длин ПРОТИВОПОЛОЖНОЙ стороны. и ГИПОТЕНУЗА.
- • КОСИНУС угла – это отношение длин СМЕЖНОЙ стороны и ГИПОТЕНУЗЫ.
- • ТАНГЕНТ угла – это отношение длин ПРОТИВОПОЛОЖНОЙ стороны и СМЕЖНОЙ стороны.
Чтобы найти оставшуюся сторону, мы можем использовать любой из трех методов: теорему Пифагора, косинус или тангенс.
Независимо от того, какой метод мы используем, мы получим один и тот же результат (хотя, если мы используем нашу аппроксимацию $c \ приблизительно 23,66$, мы можем немного ошибиться из-за ошибки округления).
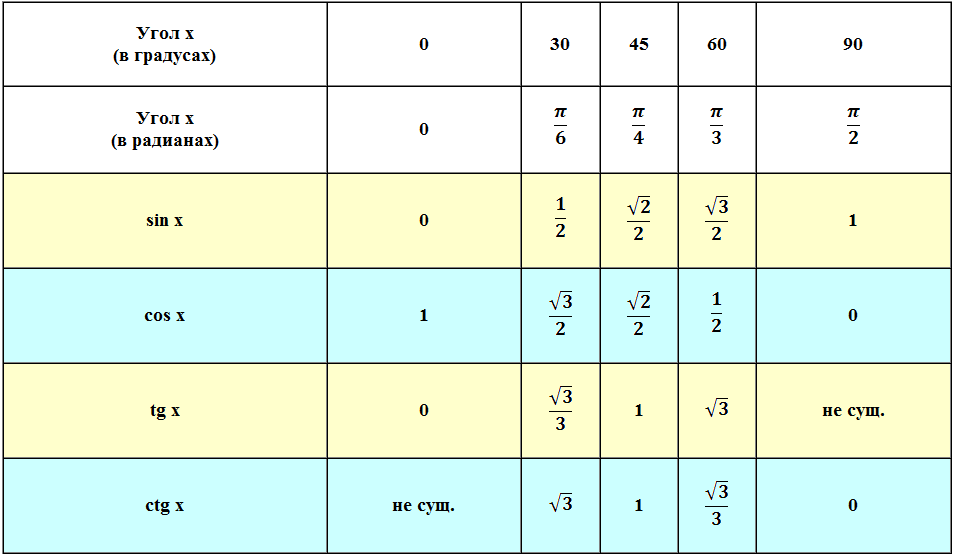 \circ \end{align*}$ 9\circ \end{align*}$
\circ \end{align*}$ 9\circ \end{align*}$
Чтобы лучше понять триггерные функции, мы можем представить себе треугольник внутри круга на координатной плоскости.
Координаты угловой точки $(x,y)$ на окружности сообщают нам две другие стороны треугольника: горизонтальная сторона имеет длину $x$, а вертикальная сторона имеет длину $y$. Если мы сделаем окружность радиусом $1$, то гипотенуза треугольника равна $1$, и мы получим
Чтобы получить касательную, мы можем просто взять отношение координаты y к координате x.
Используя симметрию, мы можем обозначить углы в трех других квадрантах окружности.
Вывод специальных углов
Вам может быть интересно, где значения $\frac{1}{2}$, $\frac{\sqrt{2}}{2}$ и $\frac{\sqrt {3}}{2}$ поступают в первую очередь.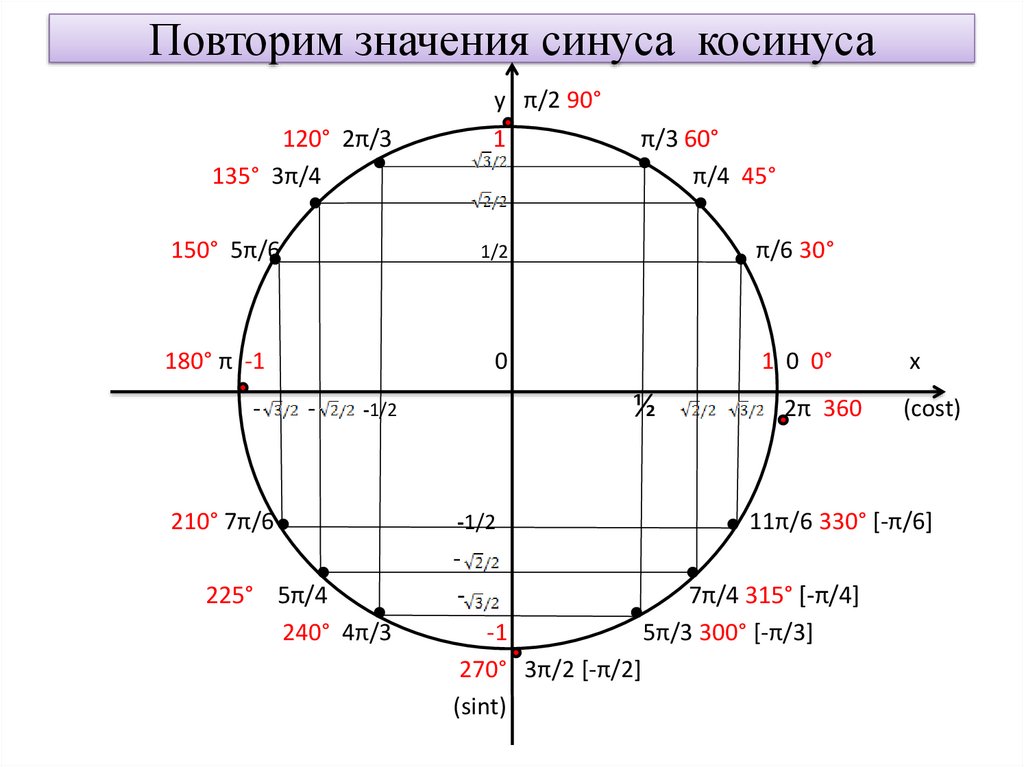
Кратчайшие стороны двух треугольников вместе составляют сторону равностороннего треугольника, длина которого, как мы знаем, равна $1$, поэтому каждая из кратчайших сторон двух треугольников должна быть равна $\frac{1}{2}$. Используя теорему Пифагора, находим, что длина другой ноги равна $\frac{\sqrt{3}}{2}$.
Чтобы понять формы графиков, попробуйте проследить значения триггерной функции, следуя по единичному кругу.
Радианы
Стандартный способ измерения углов на самом деле не в градусах, а в радианах . Один радиан эквивалентен углу, дуга которого равна одному радиусу окружности. 9\circ$ по кругу эквивалентен $2\pi$ радианам.
9\circ$ по кругу эквивалентен $2\pi$ радианам.
Ниже приведена копия единичного круга, в которой вместо градусов используются радианы.
Ниже приведены триггерные функции в радианах. Ничего не меняется, кроме единиц измерения по оси x.
Обратные тригонометрические функции
Существуют еще три тригонометрические функции: секанс, косеканс и котангенс. Это просто обратные величины косинуса, синуса и тангенса.
9\circ$Решение:
$-\frac{1}{2}$ $18) \hspace{.5cm} \cos \frac{\pi}{3}$
Решение:
$\frac{ 1}{2}$ $19) \hspace{.5cm} \sin \frac{5\pi}{6}$
Решение:
$\frac{1}{2}$ $20) \hspace{.5cm } \tan \frac{2\pi}{3}$
Решение:
$-\sqrt{3}$ $21) \hspace{.5cm} \cos \pi$
Решение:
$-1 $ $22) \hspace{.5cm} \tan \frac{7\pi}{6}$
Решение:
$\frac{ \sqrt{3}}{3}$ $23) \hspace{.5cm} \sin 2\pi$
Решение:
$0$ $24) \hspace{.


 03.14
03.14 . . .)
. . .)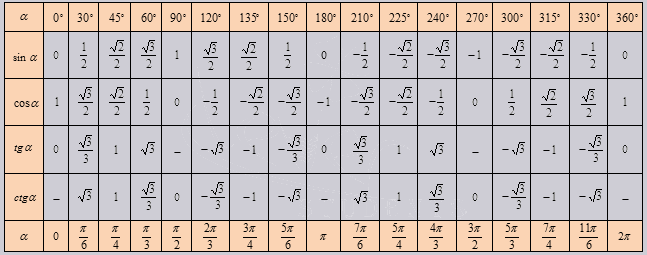 Найдите значение sin(-540°), если sin 720° = 0.
Найдите значение sin(-540°), если sin 720° = 0.  Функция arccos позволяет вычислять арккосинус числа.
Функция arccos является обратной функцией функции косинуса.
Функция arccos позволяет вычислять арккосинус числа.
Функция arccos является обратной функцией функции косинуса.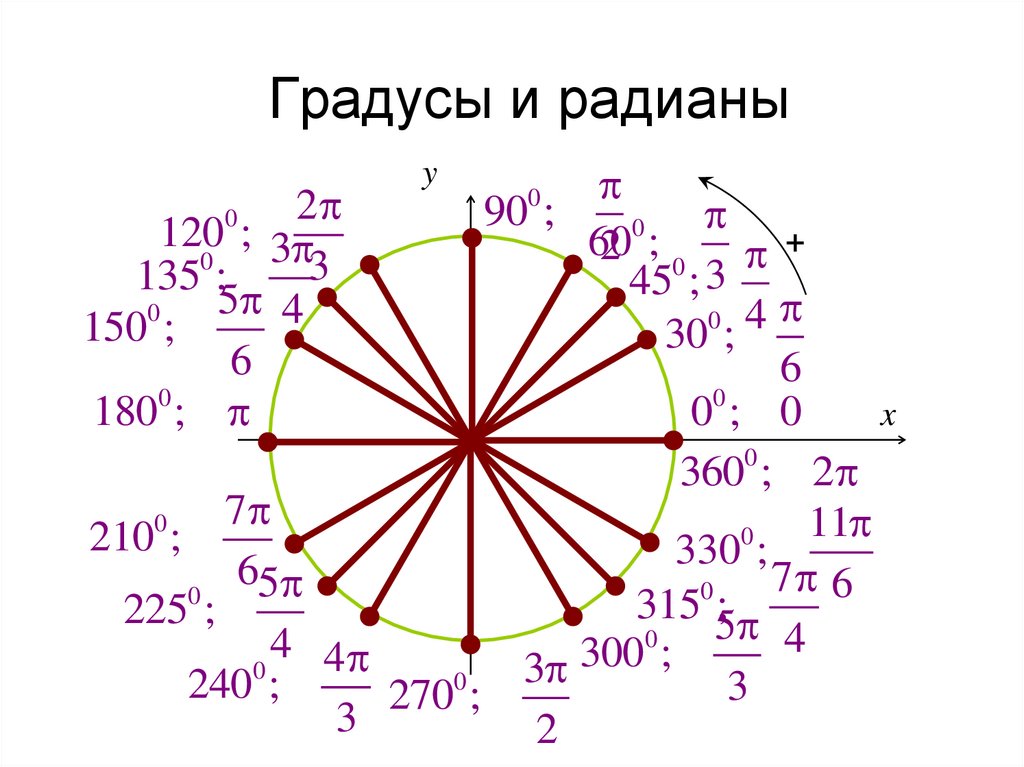 Калькулятор позволяет получить тригонометрическое разложение выражения.
Калькулятор позволяет получить тригонометрическое разложение выражения.