10 умножить на 4: Mathway | Популярные задачи

Содержание

Умножение на 4 | Таблица умножения

На этой странице представлены примеры, описывающие умножение на 4 и умножение числа 4, деление, некоторые способы произношения и записи, таблица умножения на 4 без ответов, в конце статьи — картинки для скачивания, с помощью которых можно распечатать часть таблицы. Умножение на 4:
1 x 4 = 4
2 x 4 = 8
3 x 4 = 12
4 x 4 = 16
5 x 4 = 20
6 x 4 = 24
7 x 4 = 28
8 x 4 = 32
9 x 4 = 36
10 x 4 = 40

Первый вариант произношения:
1 x 4 = 4 (1 умножить на 4, равно 4)
2 x 4 = 8 (2 умножить на 4, равно 8)
3 x 4 = 12 (3 умножить на 4, равно 12)
4 x 4 = 16 (4 умножить на 4, равно 16)
5 x 4 = 20 (5 умножить на 4, равно 20)
6 x 4 = 24 (6 умножить на 4, равно 24)
7 x 4 = 28 (7 умножить на 4, равно 28)
8 x 4 = 32 (8 умножить на 4, равно 32)
9 x 4 = 36 (9 умножить на 4, равно 36)
10 x 4 = 40 (10 умножить на 4, равно 40)

Второй вариант произношения:

1 x 4 = 4 ( по 1 взять 4 раза, получится 4)
2 x 4 = 8 ( по 2 взять 4 раза, получится 8)
3 x 4 = 12 ( по 3 взять 4 раза, получится 12)
4 x 4 = 16 ( по 4 взять 4 раза, получится 16)
5 x 4 = 20 ( по 5 взять 4 раза, получится 20)
6 x 4 = 24 ( по 6 взять 4 раза, получится 24)
7 x 4 = 28 ( по 7 взять 4 раза, получится 28)
8 x 4 = 32 ( по 8 взять 4 раза, получится 32)
9 x 4 = 36 ( по 9 взять 4 раза, получится 36)
10 x 4 = 40 ( по 10 взять 4 раза, получится 40)

От перемены мест множителей значение произведения не меняется, поэтому, зная результаты умножения на 4, можно легко найти результаты умножения числа 4. В качестве знака умножения в разных источниках используют разные символы. Выше был показан пример с (x), в этот раз сделаем запись с помощью приподнятой точки ( ∙ )

Умножение числа 4:

4 ∙ 1 = 4
4 ∙ 2 = 8
4 ∙ 3 = 12
4 ∙ 4 = 16
4 ∙ 5 = 20
4 ∙ 6 = 24

4 ∙ 7 = 28
4 ∙ 8 = 32
4 ∙ 9 = 36
4 ∙ 10 = 40

Варианты произношения:
4 ∙ 1 = 4 (по 4 взять 1 раз, получится 4)
4 ∙ 2 = 8 (по 4 взять 2 раза, получится 8)
4 ∙ 3 = 12 (по 4 взять 3 раза, получится 12)
4 ∙ 4 = 16 (по 4 взять 4 раза, получится 16)
4 ∙ 5 = 20 (по 4 взять 5 раз, получится 20)
4 ∙ 6 = 24 (по 4 взять 6 раз, получится 24)
4 ∙ 7 = 28 (по 4 взять 7 раз, получится 28)
4 ∙ 8 = 32 (по 4 взять 8 раз, получится 32)
4 ∙ 9 = 36 (по 4 взять 9 раз, получится 36)
4 ∙ 10 = 40 (по 4 взять 10 раз, получится 40)

4 ∙ 1 = 4 (4 умножить на 1, равно 4)
4 ∙ 2 = 8 (4 умножить на 2, равно 8)
4 ∙ 3 = 12 (4 умножить на 3, равно 12)
4 ∙ 4 = 16 (4 умножить на 4, равно 16)
4 ∙ 5 = 20 (4 умножить на 5, равно 20)
4 ∙ 6 = 24 (4 умножить на 6, равно 24)
4 ∙ 7 = 28 (4 умножить на 7, равно 28)
4 ∙ 8 = 32 (4 умножить на 8, равно 32)
4 ∙ 9 = 36 (4 умножить на 9, равно 36)
4 ∙ 10 = 40 (4 умножить на 10, равно 40)

Деление на 4:

4 ÷ 4 = 1
8 ÷ 4 = 2
12 ÷ 4 = 3
16 ÷ 4 = 4
20 ÷ 4 = 5
24 ÷ 4 = 6
28 ÷ 4 = 7
32 ÷ 4 = 8
36 ÷ 4 = 9
40 ÷ 4 = 10

4 ÷ 4 = 1 (4 разделить на 4, равно 1)
8 ÷ 4 = 2 (8 разделить на 4, равно 2)
12 ÷ 4 = 3 (12 разделить на 4, равно 3)
16 ÷ 4 = 4 (16 разделить на 4, равно 4)
20 ÷ 4 = 5 (20 разделить на 4, равно 5)
24 ÷ 4 = 6 (24 разделить на 4, равно 6)
28 ÷ 4 = 7 (28 разделить на 4, равно 7)
32 ÷ 4 = 8 (32 разделить на 4, равно 8)
36 ÷ 4 = 9 (36 разделить на 4, равно 9)
40 ÷ 4 = 10 (40 разделить на 4, равно 10)

Картинка:

Деление.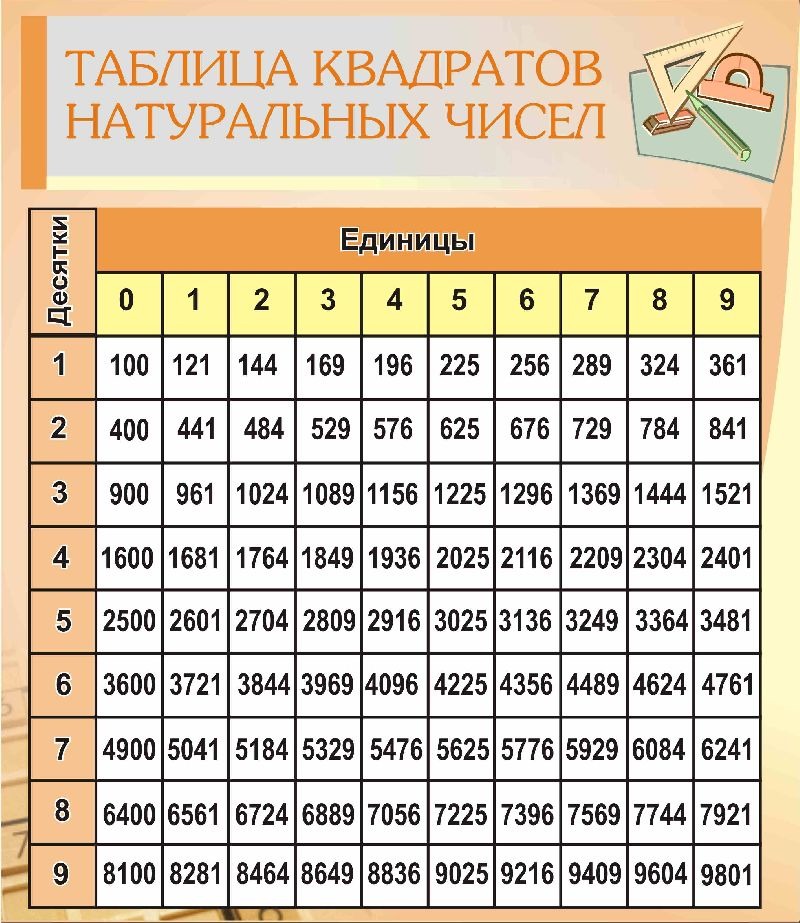 Картинка:

Таблица умножения и деления на 4 без ответов (по порядку и вразброс):

1 ∙ 4 =	3 ∙ 4 =	4 ÷ 4 =	36 ÷ 4 =
2 ∙ 4 =	6 ∙ 4 =	8 ÷ 4 =	32 ÷ 4 =
3 ∙ 4 =	1 ∙ 4 =	12 ÷ 4 =	28 ÷ 4 =
4 ∙ 4 =	4 ∙ 4 =	16 ÷ 4 =	24 ÷ 4 =
5 ∙ 4 =	2 ∙ 4 =	20 ÷ 4 =	16 ÷ 4 =
6 ∙ 4 =	7 ∙ 4 =	24 ÷ 4 =	20 ÷ 4 =
7 ∙ 4 =	10 ∙ 4 =	28 ÷ 4 =	12 ÷ 4 =
8 ∙ 4 =	5 ∙ 4 =	32 ÷ 4 =	8 ÷ 4 =
9 ∙ 4 =	9 ∙ 4 =	36 ÷ 4 =	4 ÷ 4 =
10 ∙ 4 =	8 ∙ 4 =	40 ÷ 4 =	40 ÷ 4 =

Способы записи таблицы умножения на 4:

x	Приподнятая точка	*	Знак не указан
1 x 4 = 4	1 ∙ 4 = 4	1 * 4 = 4	1 __ 4 = 4
2 x 4 = 8	2 ∙ 4 = 8	2 * 4 = 8	2 __ 4 = 8
3 x 4 = 12	3 ∙ 4 = 12	3 * 4 = 12	3 __ 4 = 12
4 x 4 = 16	4 ∙ 4 = 16	4 * 4 = 16	4 __ 4 = 16
5 x 4 = 20	5 ∙ 4 = 20	5 * 4 = 20	5 __ 4 = 20
6 x 4 = 24	6 ∙ 4 = 24	6 * 4 = 24	6 __ 4 = 24
7 x 4 = 28	7 ∙ 4 = 28	7 * 4 = 28	7 __ 4 = 28
8 x 4 = 32	8 ∙ 4 = 32	8 * 4 = 32	8 __ 4 = 32
9 x 4 = 36	9 ∙ 4 = 36	9 * 4 = 36	9 __ 4 = 36
10 x 4 = 40	10 ∙ 4 = 40	10 * 4 = 40	10 __ 4 = 40

Способы записи таблицы деления на 4:

/	:	÷	Знак не указан
4 / 4 = 1	4 : 4 = 1	4 ÷ 4 = 1	4 __ 4 = 1
8 / 4 = 2	8 : 4 = 2	8 ÷ 4 = 2	8 __ 4 = 2
12 / 4 = 3	12 : 4 = 3	12 ÷ 4 = 3	12 __ 4 = 3
16 / 4 = 4	16 : 4 = 4	16 ÷ 4 = 4	16 __ 4 = 4
20 / 4 = 5	20 : 4 = 5	20 ÷ 4 = 5	20 __ 4 = 5
24 / 4 = 6	24 : 4 = 6	24 ÷ 4 = 6	24 __ 4 = 6
28 / 4 = 7	28 : 4 = 7	28 ÷ 4 = 7	28 __ 4 = 7
32 / 4 = 8	32 : 4 = 8	32 ÷ 4 = 8	32 __ 4 = 8
36 / 4 = 9	36 : 4 = 9	36 ÷ 4 = 9	36 __ 4 = 9
40 / 4 = 10	40 : 4 = 10	40 ÷ 4 = 10	40 __ 4 = 10

Умножение на:

‹ Умножение на 3 Вверх Умножение на 5 ›

Умножить на 0,5.

Умножение дроби на число. Умножение дробей на целое число.

Альфашкола
Статьи
Как легко умножить на 0,5

В этой статье ты узнаешь как легко умножить любое число на \(0,5\), для этого тебе даже не понадобится калькулятор. \(0,5-\) это десятичная дробь, приведём её к виду обыкновенной дроби:

При умножении на \(0,5\) можно заменить умножением на \(\frac{1}{2}\). Обратная дробь одной пятой \(-2\) То есть для того чтобы умножить на \(0,5\) надо разделить на \(2.\) Легко не так ли?

Пример 1. Умножьте \(10\) на \(0,5\).

Решение: \(10*0,5=10*\frac{1}{2}=10:2=5\)

Ответ: \(5\).

Пример 2. Умножьте \(30\) на \(0,5\).

Решение: \(30*0,5=30*\frac{1}{2}=30:2=15\)

Ответ: \(15\).

Пример 2. Умножьте \(34\) на \(0,5\).

Решение: \(34*0,5=34*\frac{1}{2}=34:2=17\)

Ответ: \(17\).

Больше уроков и заданий по математике вместе с преподавателями нашей онлайн-школы «Альфа». Запишитесь на пробное занятие уже сейчас!

Запишитесь на бесплатное тестирование знаний!

Нажимая кнопку «Записаться» принимаю условия Пользовательского соглашения и Политики конфиденциальности

Наши преподаватели

Ольга Викторовна Пятаева

Репетитор по математике

Стаж (лет)

Образование:

Ташкентский ордена Дружбы народов гос.

педагогический институт

Проведенных занятий:

Форма обучения:

Дистанционно (Скайп)

Репетитор по математике 5-9 класса. Математику, я люблю за то, что это стройная система с четкими правилами. Которая охватывает огромное количество других наук, учит мыслить критически, закаляет характер, математика всегда пригодится в быту и приводит ум в порядок. Большой опыт по подготовке к ОГЭ, ВПР и другим диагностическим работам по математике. Мои ученики — активные участники различных конкурсов, олимпиад, (Всероссийская олимпиада школьников, «Кенгуру», и т.д.), но не только участники, но и победители и призёры. К каждому учащемуся стараюсь найти индивидуальный подход, в занятиях ориентируюсь на интересы ребенка и помогаю полюбить математику, показывая, как и где её можно применять в жизни.

Создаю ситуацию успеха с учеником. Также есть опыт работы с детьми с особенностями развития. Мои достижения в преподавательской деятельности — это успехи моих учеников. Это и высокие баллы на экзаменах (от 60 и выше), экзамены пишем без двоек.

Вера Александровна Бондаренко

Репетитор по математике

Стаж (лет)

Образование:

Ульяновский государственный педагогический университет имени ИН Ульянова

Проведенных занятий:

Форма обучения:

Дистанционно (Скайп)

Я считаю, что знать русский язык, грамотно писать и говорить на нём – это гражданский долг каждого человека, проживающего в Российской Федерации.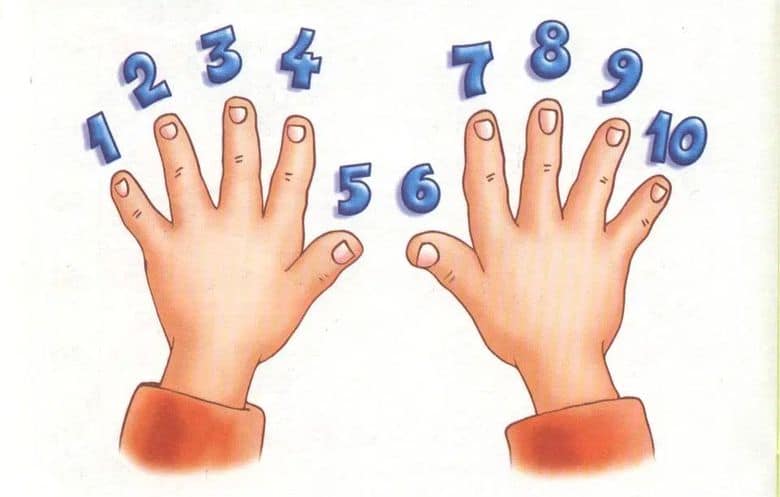 Тем самым мы проявляем уважение к языку и сохраняем его для будущих поколений. Беру в работу как начальные, так и средние классы; осуществляю подготовку детей в ВПР, ОГЭ, олимпиадам, проектам; даю консультации. Методы преподавания, которые используются в работе с учеником, направлены на определение целей и задач обучения русскому языку как родному и их результативность.

Евгений Борисович Царенков

Репетитор по математике

Стаж (лет)

Образование:

Брестский государственный университет им. А.С. Пушкина

Проведенных занятий:

Форма обучения:

Дистанционно (Скайп)

Репетитор 6-9 классов. Буду рад помочь разобраться с предметом, успешно усвоить материал школьной программы по математике. Устраню пробелы в пройденном материале, подниму текущий уровень знаний по математике. Доношу материал понятно и грамотно, акцентирую внимание на важных и значимых вещах. Не оставляю материал непонятым. В отличии от школы мы никуда не торопимся — будем разбирать тему до тех пор, пока не сформируем компетенцию. Нет ничего сложного ни в каком предмете, если его преподают с любовью.

правила, примеры, решения, 1 умножить на 10

Имея общее представление об умножении натуральных чисел и их свойств, легче понять принцип выполнений действий над ними. Мы разберем правила, по которым производится умножение натуральных чисел. Весь материал имеет конкретные примеры и подробные объяснения. Совершим проверки результатов для того, чтобы сверить полученные на выходе числа.

Таблица умножения

Умножая два натуральных числа, получаем результат, который производится при умножении однозначных натуральных чисел. Произведение чисел 6 и 3 приравнивается к сумме, состоящей из трех слагаемых, равных числу 6. Иначе это запишем: 6·3=6+6+6=18. Таким же образом получены все результаты умноженных однозначных натуральных чисел. Все занесены в таблицу, приведенную ниже.

1·1=1	2·1=2	3·1=3
1·2=2	2·2=4	3·2=6
1·3=3	2·3=6	3·3=9
1·4=4	2·4=8	3·4=12
1·5=5	2·5=10	3·5=15
1·6=6	2·6=12	3·6=18
1·7=7	2·7=14	3·7=21
1·8=8	2·8=16	3·8=24
1·9=9	2·9=18	3·9=27

4·1=4	5·1=5	6·1=6
4·2=8	5·2=10	6·2=12
4·3=12	5·3=15	6·3=18
4·4=16	5·4=20	6·4=24
4·5=20	5·5=25	6·5=30
4·6=24	5·6=30	6·6=36
4·7=28	5·7=35	6·7=42
4·8=32	5·8=40	6·8=48
4·9=36	5·9=45	6·9=54

7·1=7	8·1=8	9·1=9
7·2=14	8·2=16	9·2=18
7·3=21	8·3=24	9·3=27
7·4=28	8·4=32	9·4=36
7·5=35	8·5=40	9·5=45
7·6=42	8·6=48	9·6=54
7·7=49	8·7=56	9·7=63
7·8=56	8·8=64	9·8=72
7·9=63	8·9=72	9·9=81

Это и есть таблица умножения. Все результаты сгруппированы для удобного дальнейшего применения. Таблица сложения натуральных чисел выглядит подобным образом. Она предоставлена ниже.

Чтобы выяснить, как пользоваться таблицей, приведем пример. Если необходимо найти произведение 6 и 8, необходимо отметить столбец верхней ячейки, где имеем 6 (8), и строку левой ячейки, где число 8 (6). Чтобы найти результат, следует найти их общую ячейку, то есть пересечение столбца и строки. На рисунке ниже изображен пример нахождения искомого умножения 6 и 8.

Умножение трех и более количества чисел

Мы дали определение понятию умножения двух чисел. Теперь поговорим об умножении трех и более имеющихся чисел. Таким образом, в такой ситуации применимо сочетательное свойство умножения натуральных чисел.

Сочетательное свойство умножения показывает равнозначность двух произведений a·(b·c) и (a·b)·c, где a, b и c могут быть любыми числами. Результат умножения данных чисел не будет зависеть от местоположения скобок. Поэтому чаще всего при произведении скобки отсутствуют, а запись имеет вид a·b·c. Данное выражение называют произведением трех чисел, причем все входящие в него числа – множители.

Сочетательное свойство умножения необходимо для того, чтобы легче было выявлять равные произведения. Это значит, что из приведенных (a·b)·(c·d), (a·(b·c))·d, ((a·b)·c)·d, a·(b·(c·d)) и a·((b·c)·d) можно сделать вывод, что они все равные. Положение скобок при умножении не играет роли. Это произведение может быть записано в виде a·b·c·d.

Обычно скобки опускаются при умножении. Произведение нескольких трех и более чисел без скобок приводит к последовательной замене двух соседних множителей до получения необходимого результата. Скобки могут быть расставлены произвольно, так как итог произведения не изменится.

Если взять пять натуральных чисел и записать их в виде произведения, то получим 2·1·3·1·8. Имеется два основных способы решения.

Первый способ заключается в том, что два множителя слева будут последовательно заменяться произведением. Тогда получим, что 2·1·3·1·8=2·3·1·8. Так как 2·3=6, то 2·3·1·8=6·1·8. Далее имеем, что 6·1=6, тогда в итоге получим результат 6·8=48. Умножение пяти заданных чисел будет равняться 48. Этот способ записывается, как (((2·1)·3)·1)·8.

Второй способ заключается в том, что скобки располагаются таким образом ((2·1)·3)·(1·8). Имеем, что 2·1=2 и 1·8=8, то ((2·1)·3)·(1·8)=(2·3)·8. При 2·3 равном 6 получим, что (2·3)·8=6·8. В итоге получим, что 6·8=48. Отсюда следует, что 2·1·3·1·8=48.

Порядок следования множителей не влияет на результат. Множители могут быть записаны в любом порядке. Это следует из свойств умножения натуральных чисел.

Пример 1

Даны четыре числа для умножения: 3, 9, 2, 1. Их произведение записывается в виде 3·9·2·1.

При замене произведения множителей 3 и 9 или 9 и 2 получим, что следующий этап необходимо будет произвести умножение двузначных чисел 27 и 18.

Чтобы избежать это, необходимо поменять слагаемые местами, иначе расставить скобки.

Тогда получим: 3·9·2·1=3·2·9·1=(3·2)·(9·1)=6·9=54.

При перемене мест множителей можно производить наиболее удобные комбинирования для вычисления. Рассмотрим задание, где решение приводит к умножению нескольких чисел.

Пример 2

Каждая коробка имеет по 3 предмета. В ящики положили 2 коробки. Какое количество предметов будет в 4 ящиках?

Решение

Нам дано, что в одном ящике 2 коробки, а в них соответственно по 3 предмета.

Тогда в одном ящике 3·2=6 предметов. Отсюда получим, что в 4 ящиках 6·4=24 предмета. Можно рассуждать иным образом. Один ящик вмещает в себя 2 коробки, отсюда в 4 ящиках 2·4=8 коробок. Каждая из коробок имеет 3 предмета, тогда имеем, что 8 коробок содержат 3·8=24 предмета.

Эти решения можно записать таким образом (3·2)·4=6·4=24 или 3·(2·4)=3·8=24.

Делаем вывод, что искомое количество предметов – это произведение 3,2,4, а значит, что 3·2·4=24.

Ответ: 24.

Подведем итоги.

При умножении трех и более чисел действия производятся последовательно. Используя переместительное и сочетательное свойства умножения, разрешается менять местами множителями и заменять их двумя другими умножаемыми числами.

Умножение суммы на натуральное число и наоборот

Благодаря распределительному свойству умножения сложение и умножение связаны. Это помогает в изучении сложения и умножения. Свойство способствует углубиться в изучение всех действий.

Если рассматривать распределительное свойство умножения относительно сложения, то получим такой вид записи с двумя слагаемыми: (a+b)·c=a·c+b·c, где a, b, c являются произвольными натуральными числами. Исходя из данного равенства при помощи метода математической индукции докажем справедливость предложенного (a+b+c)·d=a·d+b·d+c·d, (a+b+c+d)·h=a·h+b·h+c·h+d·h и т.д., где a, b, c, d, h являются натуральными числами.

Отсюда следует, что произведение суммы нескольких чисел и данного числа равна сумме произведений каждого из слагаемых с данным числом. Это правило применимо при умножении на заданное число.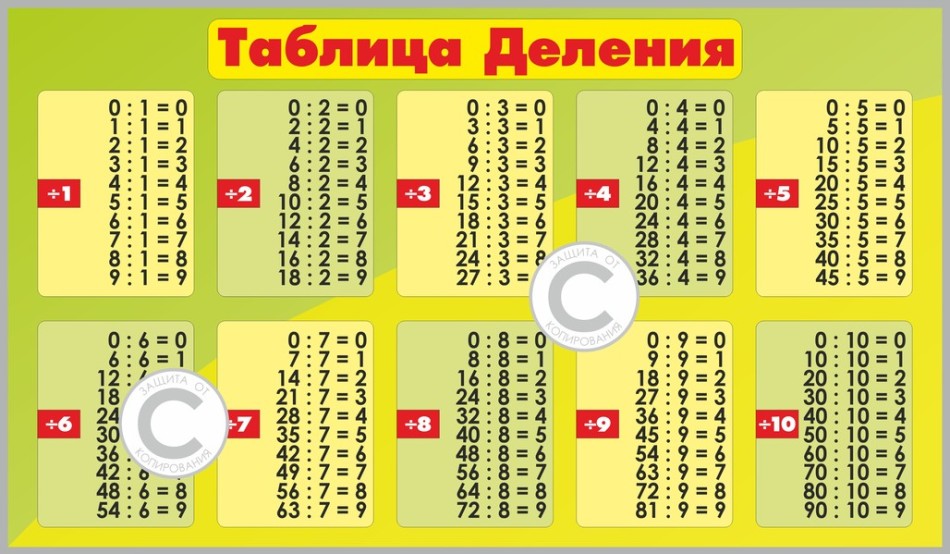

Если взять сумму из пяти чисел 7, 2, 3, 8, 8 на 3, получим, что (7+2+3+8+8)·3=7·3+2·3+3·3+8·3+8·3. Отсюда имеем, что 7·3=21, 2·3=6, 3·3=9, 8·3=24, то 7·3+2·3+3·3+8·3+8·3=21+6+9+24+24, после чего находим сумму чисел 21+6+9+24+24=84.

Можно было сделать вычисления иначе, тогда следовало посчитать сумму, после чего умножение. Этот случай менее удобен, так как умножение двухзначного числа 7+2+3+8+8=28 на 3 мы пока не выполняли. Умножение двухзначных чисел – это тема, показанная в разделе умножения многозначного и однозначного натуральных чисел.

Используя переместительное свойство, мы можем переформулировать правило умножения суммы чисел на заданное число таким образом: произведение данного числа и суммы нескольких чисел равняется сумме произведений данного числа и каждого из слагаемых. Это правило умножения данного числа на заданную сумму.

Например, 2·(6+1+3)=2·6+2·1+2·3=12+2+6=20. Здесь применяем правила умножения числа на сумму.

Рассмотрим конкретный пример, где умножение решение сводится к умножению суммы чисел на данное число.

Пример 3

В коробке находятся по 3 красных, 7 зеленых и 2 синих предмета. Какой количество предметов имеется во всех четырех коробках?

Решение

Для определения количества предметов в одной коробке, вычислим 3+7+2. Отсюда следует, что четыре коробки содержат в 4 раза больше, значит, (3+7+2)·4 предметов.

Находим произведение суммы на число, применив полученное правило, тогда (3+7+2)·4=3·4+7·4+2·4=12+28+8=48.

Ответ: 48 предметов.

Умножение натурального числа на 10, 100, 1000 и так далее

Чтобы получить правило произвольного умножения натурального числа на 10, рассмотрим подробно.

Натуральные числа вида 20, 30, 40, …, 90 соответствуют 2, 3, 4, …, 9 десяткам. Это значит, что 20=10+10, 30=10+10+10, … отсюда следует, что умножением двух натуральных чисел их смысл суммы должен быть идентичным, тогда получим 2·10=20, 3·10=30, …, 9·10=90.

Таким же образом можно прийти к следующим неравенствам:

2·100=200, 3·100=300, . .., 9·100=900; 2·1 000=2 000, 3·1 000=3 000, …, 9·1 000=9 000; 2·10 000=20 000, 3·10 000=30 000, …, 9·10 000=90 000; …

Выходит, что десяток десятков – это сотня, то 10·10=100;

что десяток сотен – это тысяча, тогда 100·10=1 000;
что десяток тысяч – это десять тысяч, то 1 000·10=10 000.
Исходя из рассуждений, получим 10 000·10=100 000, 100 000·10=1 000 000, …

рассмотрим пример для формулировки правила умножения произвольного натурального числа на 10.

Пример 4

Необходимо произвести умножение натурального числа 7032 на 10.

Решение

Чтобы быстрее подсчитать, необходимо представить число 7032 в виде суммы разрядных слагаемых.

Применим правило умножения суммы на число из предыдущего пункта, тогда получим 7 032·10=(7 000+30+2)·10=7 000·10+30·10+2·10. Число 7000 можно представить в виде произведения 7·1 000, число 30 произведением 3·10.

Отсюда получим, что сумма 7 000·10+30·10+2·10 будет равна сумме (7·1 000)·10+(3·10)·10+2·10. Тогда сочетательное свойство умножения можно зафиксировать, как (7·1 000)·10+(3·10)·10+2·10=7·(1 000·10)+3·(10·10)+2·10.

Отсюда получим, что 7·(1 000·10)+3·(10·10)+2·10=7·10 000+3·100+2·10=70 000+300+20. Сумма, полученная в результате, представляет собой разложение по рядам числа 70320: 70 000+300+20.

Ответ: 7 032·10=70 320.

Аналогичным способом мы можем умножить любое натуральное число на 10. В таких случаях запись всегда будет оканчиваться на 0.

Приведенные примеры и рассуждения дают возможность перейти к правилу умножения произвольного натурального число на 10. Если в конце записи дописать цифру 0, тогда заданное число будет служить результатом умножения на 10. Когда в записи натурального числа дописывают 0, то полученное число применяется как результат умножения на 10.

Приведем примеры: 4·10=40, 43·10=430, 501·10=5 010, 79 020·10=790 200 и так далее.

Основываясь на правиле умножения натурального числа на 10, можно получить умножение произвольного числа на 100, 1000 и выше.

Если 100=10·10,тогда умножение натурального числа на 100 приводит к умножению числа на 10 и еще одному умножению на 10.

Тогда получим:

17·100=17·10·10=170·10=1 700; 504·100=504·10·10=5 040·10=50 400; 100 497·100=100 497·10·10=1 004 970·10=10 049 700.

Если полученная запись имеет на 2 цифры 0 больше, тогда считается, что это результат умножения всего числа на 100. Это и называется правилом умножения числа на 100.

Произведение 1 000=100·10, тогда умножение любого натурального числа на 1000 приводит к умножению заданного числа на 100 и еще одному умножению на 10. Отсюда следует, что это правило умножения произвольного натурального числа на 1000. Когда в записи имеется 3 цифры 0, тогда считают, что это результат умножения числа на 1000.

Таким же образом производится умножение на 10000, 100000 и так далее. Идет дописывание нулей в конце числа.

В качестве примера запишем:

58·1 000=58 000; 6 032·1 000 000=6 032 000 000; 777·10 000=7 770 000.

Умножение многозначного и однозначного натуральных чисел

Имея навыки для выполнения умножения, разберем все правила на примере.

Пример 5

Найти произведение трехзначного числа 763 на 5.

Решение

Для начала представляем число в виде суммы разрядных слагаемых. Здесь получим, что 763=700+60+3. Отсюда получим, что 763·5=(700+60+3)·5.

Используя правило умножения суммы на число, получим, что:

(700+60+3)·5=700·5+60·5+3·5.

Произведения 700=7·100 и 60=6·10 и сумма 700·5+60·5+3·5 записывается, как (7·100)·5+(6·10)·5+3·5.

Применив переместительное и сочетательное свойство, получим (7·100)·5+(6·10)·5+3·5=(5·7)·100+(5·6)·10+3·5.

Так как 5·7=35, 5·6=30 и 3·5=15, то (5·7)·100+(5·6)·10+3·5=35·100+30·10+15.

Выполняем умножение на 100, на 10. После этого выполняем сложение 35·100+30·10+15=3 500+300+15=3 815

Ответ: произведение 763 и 5= 3815.

Чтобы закрепить материал, необходимо рассмотреть пример умножения.

Пример 6

Найти произведение 3 и 104558.

Решение

3·104 558=3·(100 000+4 000+500+50+8)==3·100 000+3·4 000+3·500+3·50+3·8==3·100 000+3·(4·1 000)+3·(5·100)+3·(5·10)+3·8==3·100 000+(3·4)·1 000+(3·5)·100+(3·5)·10+3·8==3·100 000+12·1 000+15·100+15·10+3·8==300 000+12 000+1 500+150+24=313 674.

Ответ: результат умножения 3 и 104558 = 313674.

Умножение двух многозначных натуральных чисел

Умножение двух многозначных натуральных чисел производится таким образом, что один из множителей раскладывается по разрядам, после этого применяют правило умножения на сумму. Изучение предыдущих статей позволит быстрее разобраться с имеющимся разделом.

Пример 7

Вычислить произведение 41 и 3806.

Решение

Необходимо произвести разложение числа 3806 по разрядам 3000+800+6, тогда 41·3 806=41·(3 000+800+6).

Правило умножения применимо для 41·(3 000+800+6)=41·3 000+41·800+41·6.

Так как 3 000=3·1 000 и 800=8·100, тогда справедливо равенство 41·3 000+41·800+41·6=41·(3·1 000)+41·(8·100)+41·6.

Сочетательное свойство способствует записи последней суммы (41·3)·1 000+(41·8)·100+41·6.

Вычисляя произведения 41·3, 41·8 и 41·6, представляем его в виде суммы

41·3=(40+1)·3=40·3+1·3=(4·10)·3+1·3=(3·4)·10+1·3=12·10+3=120+3=123; 41·8=(40+1)·8=40·8+1·8=(4·10)·8+1·8=(8·4)·10+1·8=32·10+8=320+8=328; 41·6=(40+1)·6=40·6+1·6=(4·10)·6+1·6=(6·4)·10+1·6=24·10+6=240+6=246

Получим, что

(41·3)·1 000+(41·8)·100+41·6=123·1 000+328·100+246=123 000+32 800+246

Вычислим сумму натуральных чисел:

123 000+32 800+246=156 046

Ответ: Произведение 41 и 3806 = 156046.

Теперь умеем умножать два любых натуральных числа.

Проверка результата умножения натуральных чисел

Умножение всегда требует проверки. Она производится при помощи деления по правилу: полученное произведение делят на один из множителей. Если полученное число равно одному из множителей, тогда вычисление произведено правильно. Если нет, то допущена ошибка.

Пример 8

Произвести умножение 11 на 13, равное 143. Необходимо выполнить проверку.

Решение

Проверка производится посредством деления 143 на 11. Тогда получим, что 143:11=(110+33):11=110:11+33:11=10+3=13.

Если получим число, равное одному из множителей, тогда задание решено верно.

Пример 9

Произведено умножение 37 на 14. Результат равен 528. Выполнить проверку.

Решение

Для выполнения проверки необходимо разделить 528 на 37. Должны получить число 14. Производится делением столбиком:

При делении мы выявили, что 528 делится на 37, но с остатком.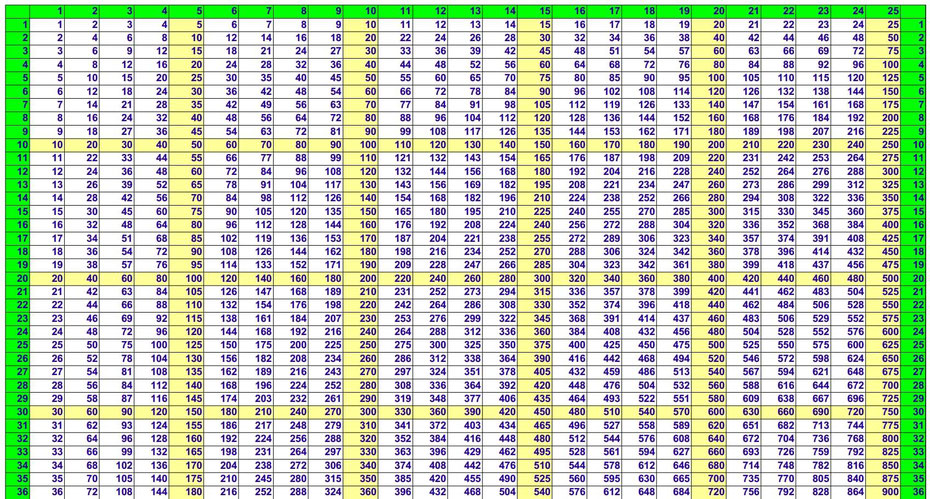 Отсюда следует, что умножение 37 на 14 было выполнено неверно.

Ответ: проверка показала, что умножение было выполнено неверно.

Пример 10

Вычислить произведение чисел 53 и 7, после чего выполнить проверку.

Решение

Представляем число в виде суммы 50+3. Применим свойство умножения суммы двух чисел на натуральное число. Получим, что 53·7=(50+3)·7=50·7+3·7=350+21=371.

Для выполнения проверки, разделим 371 на 7: 371:7=(350+21):7=350:7+21:7=50+3=53. Значит, умножение произведено верно.

Ответ: 53·7=371.

Решение задач от 1 дня / от 150 р. Курсовая работа от 5 дней / от 1800 р. Реферат от 1 дня / от 700 р.

Эффективный счёт в уме или разминка для мозга / Хабр

Эта статья навеяна топиком «Как и насколько быстро вы считаете в уме на элементарном уровне?» и призвана распространить приёмы С.А. Рачинского для устного счёта.
Рачинский был замечательным педагогом, преподававшим в сельских школах в XIX веке и показавшим на собственном опыте, что развить навык быстрого устного счёта можно. Для его учеников не было особой проблемой посчитать подобный пример в уме:

Используем круглые числа

Один из самых распространённых приёмов устного счёта заключается в том, что любое число можно представить в виде суммы или разности чисел, одно или несколько из которых «круглое»:

Т. к. на 10, 100, 1000 и др. круглые числа умножать быстрее, в уме нужно сводить всё к таким простым операциям, как 18 x 100 или 36 x 10. Соответственно, и складывать легче, «отщепляя» круглое число, а затем добавляя «хвостик»: 1800 + 200 + 190.
Еще пример:

31 x 29 = (30 + 1) x (30 - 1) = 30 x 30 - 1 x 1 = 900 - 1 = 899.

Упростим умножение делением

При устном счёте бывает удобнее оперировать делимым и делителем нежели целым числом (например, 5 представлять в виде 10:2, а 50 в виде 100:2):

68 x 50 = (68 x 100) : 2 = 6800 : 2 = 3400;
3400 : 50 = (3400 x 2) : 100 = 6800 : 100 = 68.

Аналогично выполняется умножение или деление на 25, ведь 25 = 100:4. Например,

600 : 25  = (600 : 100) x 4 = 6 x 4 = 24;
24 x 25 = (24 x 100) : 4 = 2400 : 4 = 600.

Теперь не кажется невозможным умножить в уме 625 на 53:

625 x 53 = 625 x 50 + 625 x 3 = (625 x 100) : 2 + 600 x 3 + 25 x 3 = (625 x 100) : 2 + 1800 + (20 + 5) x 3 = 
= (60000 + 2500) : 2 + 1800 + 60 + 15 = 30000 + 1250 + 1800 + 50 + 25 = 33000 + 50 + 50 + 25 = 33125. 2 = 17000 + 19000 + 2000 + 25 = 38025.

Хм, я бы не сказала, что это сильно легче, чем возведение в столбик, но, возможно, со временем можно приноровиться.
И начинать тренировки, конечно, следует с возведения в квадрат двузначных чисел, а там уже и до дизассемблирования в уме можно дойти.

Умножение двузначных чисел

Этот интересный приём был придуман 12-летним учеником Рачинского и является одним из вариантов добавления до круглого числа.
Пусть даны два двузначных числа, у которых сумма единиц равна 10:

M = 10m + n, K = 10a + 10 - n.

Составив их произведение, получим:

Например, вычислим 77 x 13. Сумма единиц этих чисел равна 10, т.к. 7 + 3 = 10. Сначала ставим меньшее число перед большим: 77 x 13 = 13 x 77.
Чтобы получить круглые числа, мы забираем три единицы от 13 и добавляем их к 77. Теперь перемножим новые числа 80 x 10, а к полученному результату прибавим произведение отобранных 3 единиц на разность старого числа 77 и нового числа 10:

13 x 77 = 10 x 80 + 3 x (77 - 10) = 800 + 3 x 67 = 800 + 3 x (60 + 7) = 800 + 3 x 60 + 3 x 7 = 800 + 180 + 21 = 800 + 201 = 1001.

У этого приёма есть частный случай: всё значительно упрощается, когда у двух сомножителей одинаковое число десятков. В этом случае число десятков умножается на следующее за ним число и к полученному результату приписывается произведение единиц этих чисел. Посмотрим, как элегантен этот приём на примере.
48 x 42. Число десятков 4, последующее число: 5; 4 x 5 = 20. Произведение единиц: 8 x 2 = 16. Значит,

48 x 42 = 2016.

99 x 91. Число десятков: 9, последующее число: 10; 9 x 10 = 90. Произведение единиц: 9 x 1 = 09. 2 = 10000 + 9500 x 2 + 9025 = 10000 + (90+5) x 2 x 100 + 9000 + 25 = = 10000 + 19000 + 1000 + 8000 + 25 = 38025.

Вместо заключения

Казалось бы, зачем уметь считать в уме в 21 веке, когда можно просто подать голосовую команду смартфону? Но если задуматься, что будет с человечеством, если оно будет взваливать на машины не только физическую работу, но и любую умственную? Не деградирует ли оно? Даже если не рассматривать устный счёт как самоцель, для закалки ума он вполне подходит.

Использованная литература:
«1001 задача для умственного счёта в школе С.А. Рачинского».

Как ребенку быстро и легко выучить таблицу умножения?

Таблицу умножения обычно начинают проходить уже во втором классе, когда дети уверенно освоили сложение. Педагоги обычно говорят, что таблицу нужно учить наизусть, чтобы «отлетала от зубов». Казалось бы, это не так уж и необходимо. Например, умножить 7 на 6 — это то же самое, что просто взять 6 раз по 7 и сложить, не запоминая лишних цифр… Но мало того, что эти сложные операции затянут выполнение контрольных работ, — в обычной жизни, за пределами школы, знание таблицы умножения требуется постоянно.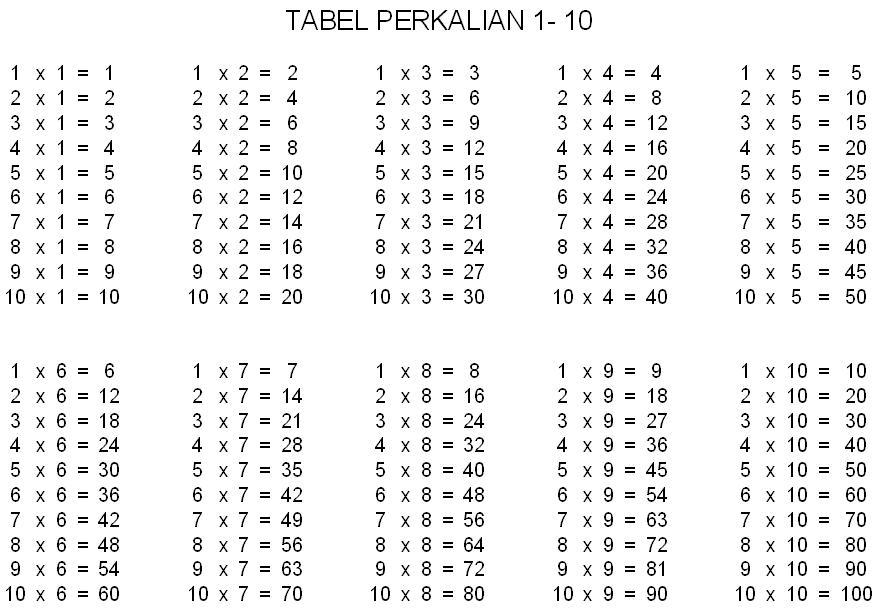 В магазине, дома, а в будущем — и на работе… Так что же, каждый раз строить длинные цепочки вычислений или доставать калькулятор? Нет, выучить таблицу все же придется — зато раз и навсегда.

Как помочь ребенку выучить таблицу умножения?

Помочь ребенку выучить таблицу умножения не так уж сложно, если правильно подойти к обучению. Вот несколько рекомендаций.

Заинтересуйте

У ребенка должна появиться мотивация. Не конфета и прогулка, хотя на усмотрение родителей можно использовать и эти методы, а что-то более значимое и долгосрочное. Сначала продемонстрируйте, в каких случаях, кроме урока в школе, таблица умножения необходима. Например, он хочет угостить пятерых друзей любимыми конфетами — каждому раздать по три, — и сколько же всего конфет принести? Или на день рождения к ребенку собираются три семьи, в каждой по три человека — сколько пар столовых приборов надо приготовить?

Нарисуйте школьнику печальную перспективу: вот в магазине его, доверчивого неуча, обманывает продавец. А вот он на работе не может умножить две цифры и достает калькулятор, а коллеги поднимают его на смех. Вот, в конце концов, он спустя годы решает в классе куда более длинные и сложные примеры, чем предлагают ему пока, и «плавает», потому что не знает основ. Без таблицы умножения в математике дальше не продвинуться! А без математики — не окончить школу и не пойти учиться на того, кем ребенок сейчас мечтает быть…

А чтобы избежать всех этих проблем, надо-то всего лишь взять и выучить эту таблицу! И уж с каким восхищением будут смотреть учителя и одноклассники, которым умножение пока не дается

Объясните суть таблицы умножения

В умножении второе число обозначает, сколько раз нужно сложить первое с самим собой. Это базовый момент, который должен усвоить ребенок, и заодно подстраховка, если он все-таки в ответственный момент забыл какой-то один результат в таблице умножения. Но, как мы уже заметили, постоянно на метод последовательного сложения вместо умножения полагаться не стоит.

Чтобы школьник лучше понял смысл, продемонстрируйте ему, что, например, 4 х 3 — это три ряда по 4 клеточки в каждом. Пусть сосчитает число клеточек — это и будет произведение цифр.

Успокойте и упростите

Наверняка ребенок ужаснется, увидев столбцы примеров на умножение сзади на обложке своей тетради: «И это все я должен знать назубок?!» Объясните, что все не так ужасно, как выглядит, ведь от перемены мест множителей произведение не меняется. То есть достаточно запомнить, сколько будет 3 х 4, чтобы понять, сколько — 4 х 3. А значит, учить придется не столь и много.

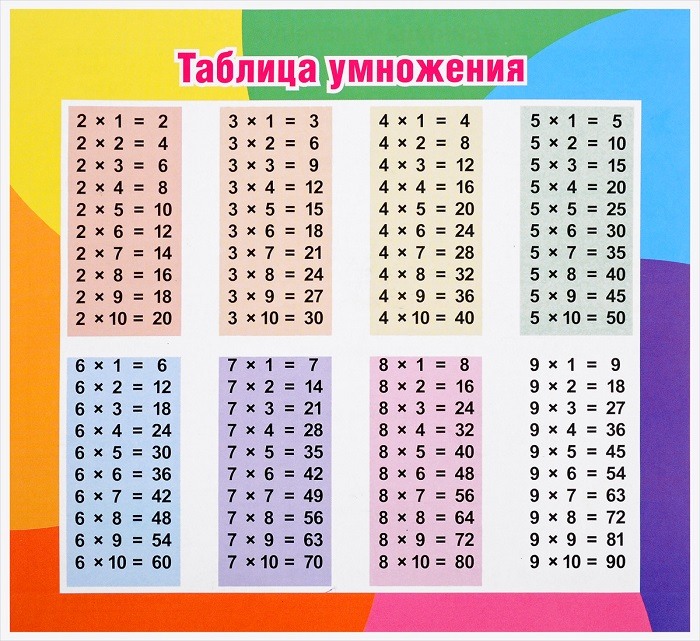
Используйте таблицу Пифагора

Вместо длинных рядов чисел продемонстрируйте таблицу Пифагора. В ее строках и столбцах — множители, а на пересечении — произведение. Покажите ребенку, как с ней работать, лучше всего — с карандашом: ищешь первое число по вертикали, второе — по горизонтали, а там, где они «встречаются», и есть значение произведения. Какую цифру искать в столбце, а какую — в строке, совершенно неважно, ведь перемена мест множителей роли не играет.

Эта таблица наглядна, и учиться по ней гораздо приятнее, особенно если у школьника хорошо развита визуальная память. Да и знания по ней можно проверить за пару секунд.

Чтобы заинтересовать ребенка, можно рассказать, что таблице умножения почти 4 тыс. лет, и нашли ее в Древнем Вавилоне. Только та таблица была гораздо более сложной и громоздкой — 60-ричной, а не десятичной, какую используют в России. Между прочим, в Великобритании таблица заканчивается не на 10 х 10, как у нас, а на 12 х 12, потому что там другие система мер длины и денежное обращение (фут равен 12 дюймам, шиллинг — 12 пенсам). И в английском образовании на изучение таблицы умножения ребенку дают время аж до 11 лет.

Не перегружайте

Дети хорошо усваивают информацию, в том числе для долговременной памяти. Но переутомлять ребенка не стоит. Выделите по одному-два дня на каждый кусок таблицы умножения — например, сегодня мы выучим таблицу на 2, завтра закрепим, послезавтра начнем — на 3, и так далее.

Важно начинать с простого. Разделавшись с таблицей на 3 и 4, младшеклассник уже усвоит основные принципы таблицы умножения, и дальше будет легче.

Повторяйте

Чем чаще, тем лучше: если учить таблицу умножения с разбросом в пять дней, толку не будет. Для создания нейронных связей в мозгу нужны регулярность и привычка. Пусть ребенок не только отвечает на ваши вопросы, но и регулярно натыкается на таблицу. Например, можно повесить красочный плакат в его комнате.

Проверяя знания ребенка, также двигайтесь от простого к более сложному: вначале, задавая ему вопрос «Сколько будет 3 х 2?», давайте ему больше времени на размышление. На первых порах следом за «3 х 2» спрашивайте «3 х 3», а со временем, когда школьник усвоит таблицу умножения лучше, предлагайте примеры вразнобой.

Укажите на закономерности

Некоторые принципы умножения помогут сократить время на лишние вычислительные операции:

Умножив на 0, мы получим 0, на 1 — то же число, а на 10 — то же число, но с ноликом на конце.
Умножить на 2 — это сложить число с самим собой.
Умножить на 4 — это умножить на 2 и еще раз на 2. Поскольку ребенок пока не научился умножать двузначные числа, но уже хорошо умеет складывать, ему будет проще умножить на 2 и прибавить к получившемуся числу такое же. Например, 6 х 4 = 6 х 2 + 6 х 2 = 12 + 12 = 24.
При умножении на 5 произведение (результат умножения) заканчивается на 5 или 0, причем поочередно — например, 1 х 5 = 5, 2 х 5 = 10, 3 х 5 = 15.
При умножении на 9 проще умножить на 10 (то есть приставить к исходному числу 0), а потом вычесть это исходное число: 9 х 9 = 9 х 10 — 9 = 81.
Кстати, когда ребенок чуть освоится с умножением и начнет решать примеры подлиннее, объясните: там, где есть умножение, сложение и вычитание, по умолчанию сначала выполняется умножение. Если только нет скобок — действие в них как раз должно быть совершено первым. Так, в примере 9 х (10 — 9) результат будет уже другой: сначала решается то, что в скобках, а потом уже выполняется умножение: 9 х 1 = 9.
При умножении на 11 (такие операции пригодятся ребенку чуть позже) изначальная цифра удваивается: 6 х 11 = 66, 8 х 11 = 88. Если речь о двухзначных числах, тоже можно обойтись без калькулятора: возьмите умножаемое число и между двумя его цифрами вставьте их сумму. Например: 12 х 11 = 132 (между 1 и 2 — 3).

Запоминание закономерностей таблицы умножения — еще один способ успокоить ребенка. Если он что-то и забудет, результат можно будет «вывести».

5 эффективных способов выучить таблицу умножения

Не ограничивайтесь одним методом объяснения и запоминания. Научить можно разными способами:

1. На пальцах и палочках

С этого стоит начинать знакомство с таблицей умножения. Легче всего показать «два раза по два» на пальцах или каких-то предметах. Правда, с более сложными вычислениями — например, с таблицей на 8 — будет труднее. муторнее.

Но при этом по пальцам легко освоить умножение на 9. Расположите руки вниз ладонями и мысленно пронумеруйте пальцы слева направо от 1 до 10. Загните палец, которому соответствует число, на которое нужно умножить 9. Например, если пример звучит как «9 х 5», это будет большой палец левой руки. Теперь считайте, что все пальцы слева (4) — десятки, а справа (5) — единицы. Таким образом, ответ — 45.

2. Через приложения на телефоне

Современным школьникам, возможно, больше понравится изучать таблицу умножения на экране любимого гаджета. Упражняться можно не только в учебное время, но и на каникулах или в транспорте по дороге в школу — скорее всего, такую тренировку ученик будет воспринимать скорее как игру, чем как домашнее задание, и ему самому будет интереснее.

Приложений немало: в некоторых ребенку одновременно предлагается решить пример, уложиться в предложенное время и накопить баллы/призы. Азарт, как известно, — отличный стимул.

3. По карточкам

Это более «древний», но тоже близкий к игровому способ запоминания. Распечатайте примеры из таблицы умножения на карточках: на одной стороне — пример, на другой — ответ (только проследите, чтобы цифры в ответе не просвечивали, лучше взять плотный картон). Разложите карточки в ряд и предложите ребенку выбрать пример. Если он отвечает верно, убирайте карточку с поля, если нет — перекладывайте ее в конец ряда. Игра заканчивается, когда карточек на столе не остается. Эту игру можно проводить и на время — пусть ребенок соревнуется сам с собой или с другими детьми.

4. По стихам

Стишки про таблицу умножения есть в интернете — в такой форме любая теория запоминается лучше. Например: «Осьминоги шли купаться: дважды восемь ног — шестнадцать», «Два атлета взяли гири, это — дважды два — четыре». Этот способ лучше использовать как вспомогательный, в дополнение к остальным — не будешь же придумывать стишок на каждый пример. Впрочем, были бы желание и фантазия.

5. По играм и мультикам

Одна из популярных игр — «Математическое лото». В нее стоит играть группой детей, находящихся примерно на одном уровне знаний таблицы умножения. Механика примерно та же, что с карточками, только на одних карточках пишутся примеры, на других — ответ. Раздайте детям те, что с ответами, — например, по 4 числа-ответа на каждой карточке, — а те, что с примерами, оставьте себе и поочередно показывайте группе. Пусть тот, кто найдет в карточке ответ, зачеркнет это число и назовет вслух. Например, ведущий говорит: «9 х 9». Тот, у кого в карточке есть число 81, зачеркивает его и называет вслух. Выигрывает тот, кто первым зачеркнул все числа в своей карточке и при этом решил примеры верно.

Еще больше ребенка может заинтересовать игра «Золотоискатели». У нее интересная «легенда»: искатели сокровищ нашли остров, где спрятан клад, но должны тщательно просчитывать ходы, чтобы первыми находить лучшие тайники. Для игры требуются поле — незаполненная таблица Пифагора (можно нарисовать квадрат с ячейками самостоятельно, десяток произвольно выбранных клеток раскрасьте желтым цветом), игровой кубик и ручка.

Первый игрок бросает кубик — сколько ему выпало, столько шагов от старта в любую сторону (но в одном направлении) он может сделать. В клетку, на которой остановился, игрок вписывает произведение чисел, на пересечении которых находится. Это будет количество монет, которые он нашел. Если удалось остановиться на желтой клетке — игрок нашел сундучок, и сумма удваивается. Причем если на этой клетке остановится потом другой игрок (а по правилам он имеет на это право), монет из сундучка он уже не получит.

Следующий игрок, бросая кубик, отсчитывает шаги уже от той клетки, где остановился соперник. Игра заканчивается, когда остается пять пустых клеток. Естественно, выигрывает тот, кто собрал больше монет.

Увлекательна и «Борьба прямоугольников». Это игра на двоих. Нужны только лист бумаги в клеточку, два фломастера, два кубика и по одному цветному карандашу для обоих участников. Каждый игрок по очереди бросает по два кубика. Выпавшие цифры — множители. Игрок рисует на листке со своей стороны прямоугольник или квадрат, стороны которого по количеству клеток равны числам на кубиках. В середине фигуры записывается ее площадь, то есть произведение чисел. Когда на листе не остается места для новых фигур, игру можно завершить. Выиграл тот, кому повезло заполнить фигурами больше клеточек на бумаге.

Другая, менее творческая игра, предлагает участникам из написанных на плакате чисел от 1 до 90 назвать те, что встречаются в таблице умножения на то или иное число. Можно устроить соревнование на время — раздать плакаты нескольким детям и предложить каждому вычеркивать или подчеркивать числа.

Можно заказать в интернете или найти в магазине уже готовые настольные игры на тему умножения — «Много-много» или «Цветариум».

Онлайн-игры для запоминания таблицы умножения, которые можно свободно отыскать в Сети, ничего не скачивая, схожи механикой с играми в мобильных приложениях. Ребенку даются все те же примеры на умножение, но в картинках (вместо 3 х 2 на «доске» рисуется три звездочки, а потом «х 2»), или тренажер на время с результатами: игрок решает сгенерированные компьютером примеры и видит в табличке, сколько дал правильных и неправильных ответов.

По тому же принципу построены развивающие «арифметические» мультфильмы: на экране появляется то или иное, меняющееся количество птичек/зверюшек/конфет, фоном идет веселая тематическая песенка. Но это, опять же, скорее для закрепления уже усвоенного материала, чем для его изучения.

Итак, ничего сложного и ужасного — чередуя разные методы освоения материала, вы постепенно достигнете успеха. Не настраивайтесь на быстрый результат — вероятно, до того, как школьник сможет уверенно отвечать на любой вопрос по таблице, пройдет не меньше месяца. Зато результат будет приносить плоды всю жизнь.

Математика и логика для детей 7-13 лет

Развиваем логическое мышление через решение сюжетных математических задач в интерактивном игровом формате

узнать подробнее

Калькулятор дробей

Этот калькулятор выполняет основные и расширенные операции с дробями, выражения с дробями в сочетании с целыми, десятичными и смешанными числами. Он также показывает подробную пошаговую информацию о процедуре расчета дроби. Калькулятор помогает найти значение из операций с несколькими дробями. Решайте задачи с двумя, тремя и более дробями и числами в одном выражении.

Правила выражения с дробями:

Дроби — используйте косую черту для деления числителя на знаменатель, т.е. для пятисотых введите 5/100 . Если вы используете смешанные числа, оставьте пробел между целой и дробной частями.

Смешанные числа (смешанные числа или дроби) сохраняют один пробел между целым числом и дробью
и используют косую черту для ввода дробей, например, 1 2/3 . Пример отрицательной смешанной дроби: -5 1/2 .
Поскольку косая черта является одновременно знаком дробной части и деления, используйте двоеточие (:) в качестве оператора деления дробей, т. е. 1/2 : 1/3 .
Decimals (десятичные числа) вводятся с десятичной точкой . и они автоматически преобразуются в дроби — т. е. 1,45 .

Math Symbols

Symbol

Symbol name

Symbol Meaning

Example

plus sign

addition

1/2 + 1/3

—

знак минус

вычитание

1 1/2 — 2/3

asterisk

multiplication

2/3 * 3/4 

times sign

multiplication

2 /3 × 5/6

division sign

division

1/2 : 3

division slash

division

1/3 / 5 1/2
• сложение дробей и смешанных чисел: 8/5 + 6 2/7
• деление целых чисел и дробей: 5 ÷ 1/2
• сложные дроби: 5/8 : 2 2/3
• десятичная дробь: 0,625
• Преобразование дроби в десятичную: 1/4
• Преобразование дроби в процент: 1/8 %
• сравнение дробей: 1/4 2/3
• умножение дроби на целое число: 6 * 3/4
• квадратный корень дроби: sqrt(1/16)
• уменьшение или упрощение дроби (упрощение) — деление числителя и знаменателя дроби на одно и то же ненулевое число — эквивалентная дробь: 4/22
• выражение со скобками: 1/3 * (1/2 — 3 3/8)
• составная дробь: 3/4 от 5/7
• кратные дроби: 2/3 от 3/5
• разделить, чтобы найти частное: 3/5 ÷ 2/3

Калькулятор следует известным правилам для порядка операций . Наиболее распространенные мнемоники для запоминания этого порядка операций:
PEMDAS — Скобки, Экспоненты, Умножение, Деление, Сложение, Вычитание.
BEDMAS — Скобки, Экспоненты, Деление, Умножение, Сложение, Вычитание
BODMAS — Скобки, Порядок, Деление, Умножение, Сложение, Вычитание.
GEMDAS — Символы группировки — скобки (){}, возведения в степень, умножение, деление, сложение, вычитание.
MDAS — Умножение и деление имеют тот же приоритет, что и сложение и вычитание. Правило MDAS является частью порядка операций правила PEMDAS.
Будьте осторожны; всегда выполняйте умножение и деление перед сложением и вычитанием . Некоторые операторы (+ и -) и (* и /) имеют одинаковый приоритет и должны оцениваться слева направо.

Использование денег
Из 550 000,00, переданных школе, было использовано 325 000,00. Какая часть от общей суммы была использована?
Дети 9
В комнате 11 детей. 6 детей — девочки. Какую часть детей составляют девочки?
Одна суббота
Однажды субботним вечером в кинотеатре 40 девушек, 25 юношей, 18 женщин и 17 мужчин. Какую часть составляют девочки?
Дробями
Муравей поднимается на 2/5 шеста за первый час и на 1/4 шеста за следующий час. Какую часть шеста преодолевает муравей за два часа?
У Макса 2
У Макса 13 пар носков. Отсюда шесть пар синих, три пары коричневых, две черных и две белых. Какая часть носков Макса коричневого или черного цвета?
Младенцы
В автобусе двое взрослых, двое детей и четверо младенцев. Какую часть населения составляют младенцы?
Marry
Marry хранит в холодильнике полторы дюжины яиц. Использовала 1/3 яйца. Какая часть яиц использовалась?
Вычислить выражение
Вычислить значение выражения z/3 — 2 z/9 + 1/6, для z = 2
Ферма 6
На ферме 20 животных. Есть четыре курицы. Какую часть животных составляют куры? Выразите ответ дробью в простейшей форме.
Значение Z
При x = -9, каково значение Z, где Z равно числителю дроби x минус 17 в знаменателе 6,5 конец дроби Дайте ответ с точностью до 2 знаков после запятой.
Мэтью
У Мэтью восемь карандашей. У трех из них нет ластика на конце. Какая часть карандашей не имеет ластика на конце?

Таблица умножения на 10 – Выучить таблицу из 10

LearnPracticeDownload

Таблица умножения на 10 – одна из самых простых для запоминания таблиц. Простой способ выучить таблицу 10 — добавить ноль после каждого числа, на которое вы умножаете, и вы получите ответ. Итак, давайте подробно узнаем и разберемся в удивительной таблице умножения 10 в этом плане мини-урока.

10 Таблица умножения Таблица умножения:

1.	Таблица умножения 10
2.	Советы по 10-кратному столу
3.	Часто задаваемые вопросы о таблице 10 Times

Таблица умножения 10

Изучение таблицы умножения 10 имеет преимущество при решении математических задач и понимании числовых закономерностей. Просмотрите приведенную ниже таблицу умножения на 10, чтобы быстрее решать математические задачи.

Таблица умножения на 10

Таблица умножения на 10 до 10
10 × 1 = 10	10 × 6 = 60
10 × 2 = 20	10 × 7 = 70
10 × 3 = 30	10 × 8 = 80
10 × 4 = 40	10 × 9 = 90
10 × 5 = 50	10 × 10 = 100

Вы можете распечатать или сохранить таблицу 10 в формате PDF, нажав на ссылку ниже.

☛ Таблица 10 раз

Советы по 10-кратному столу

Таблицу 10 легче всего запомнить. Цифра на месте единиц кратных 10 всегда равна 0.
Просто запишите натуральные числа, за которыми следует 0, чтобы получить таблицу умножения на 10.

Выделенные цифры — это не что иное, как натуральные числа, за которыми следует 0. Следующие десять кратных 10 показаны ниже. Видите ли вы аналогичную закономерность в числах, показанных ниже?

Таблица от 10 до 20

10 × 11 = 110	10 × 16 = 160
10 × 12 = 120	10 × 17 = 170
10 × 13 = 130	10 × 18 = 180
10 × 14 = 140	10 × 19 = 190
10 × 15 = 150	10 × 20 = 200

10 примеров таблицы умножения

Пример 1: В скольких наборах по 10 штук можно разложить 103 шоколадки, используя таблицу умножения на 10. Сколько шоколадок останется?
Решение:
Запишем таблицу 10, пока не получим 103. 10, 20, 30, 40, 50, 60, 70, 80, 90, 100, 110. Число 103 не входит в число 10. таблица умножения. Мы видим, что 100 является ближайшим кратным.
Таким образом, мы можем разместить 103 шоколадки в 10 наборах. Если мы это сделаем, останется 3 шоколада.
Пример 2: Используя таблицу 10, найдите значение 5 плюс 10 умножить на 6 на 2.
Решение:
Сначала мы математически запишем 5 плюс 10 умножить на 6 на 2.
Используя таблицу умножения на 10, мы имеем: 5 плюс 10 умножить на 6 на 2 = 5 + 10 × 6/2 = 5 + 10 × 3 = 5 + 30 = 35
Таким образом, 5 плюс 10 умножить на 6 на 2 равно 35
Пример 3: Используя таблицу умножения на 10, найдите 2 минус 10 умножить на 8 плюс 5.
Решение:
Во-первых, мы математически запишем 2 минус 10 умножить на 8 плюс 5.
Используя таблицу 10, мы имеем: 2 минус 10 умножить на 8 плюс 5 = 2 — 10 × 8 + 5 = 2 — 80 + 5 = -73
Таким образом, 2 минус 10 умножить на 8 плюс 5 равно -73.
Пример 4: Используя таблицу 10, найдите значение 10 умножить на 3 минус 8 умножить на 4?
Решение:
Во-первых, мы математически запишем 10 умножить на 3 минус 8 умножить на 4.
Из таблицы 10 имеем: 10 умножить на 3 минус 8 умножить на 4 = 10 × 3 — 8 × 4 = 30 — 32 = -2
Таким образом, 10 умножить на 3 минус 8 умножить на 4 равно -2.

перейти к слайдуперейти к слайдуперейти к слайдуперейти к слайду

Развивайте логическое мышление и укрепляйте его уверенность!

Благодаря гибкому учебному плану Куэмат выходит за рамки традиционных методов обучения. Мы делаем математику увлекательной. Проверьте, как!

Забронировать бесплатный пробный урок

Часто задаваемые вопросы о таблице 10 Times

Что такое все 10-кратные таблицы?

Таблица 10 раз состоит из кратных 10 и записывается как:

10 × 1 = 10	10 × 6 = 60
10 × 2 = 20	10 × 7 = 70
10 × 3 = 30	10 × 8 = 80
10 × 4 = 40	10 × 9 = 90
10 × 5 = 50	10 × 10 = 100

Как учить таблицу умножения на 10?

Таблицу умножения на 10 можно выучить, используя следующие пункты:

Таблица 10 строится путем подсчета чисел по десять.
Все числа заканчиваются нулем.
Чтобы умножить целое число на десять, поставьте в конце цифру ноль.

Как написать таблицу 10?

10 × 1 = 10	10
10 × 2 = 20	10 + 10 = 20
10 × 3 = 30	10 + 10 + 10 = 30
10 × 4 = 40	10 + 10 + 10 + 10 = 40
10 × 5 = 50	10 + 10 + 10 + 10 + 10 = 50
10 × 6 = 60	10 + 10 + 10 + 10 + 10 + 10 = 60
10 × 7 = 70	10 + 10 + 10 + 10 + 10 + 10 + 10 = 70
10 × 8 = 80	10 + 10 + 10 + 10 + 10 + 10 + 10 + 10 = 80
10 × 9 = 90	10 + 10 + 10 + 10 + 10 + 10 + 10 + 10 +10 = 90
10 × 10 = 100	10 + 10 + 10 + 10 + 10 + 10 + 10 + 10 + 10 + 10 = 100

Сколько будет 10 раз по 100?

10 умножить на 100 = 10 × 100 = 1000.

Таблицы умножения

Вы можете изучить математические таблицы чисел до 25 ниже:

Скачать БЕСПЛАТНО учебные материалы

Обозначение индекса — степень числа 10

Показатель степени (или индекс, или степень) числа говорит
сколько раз использовать число в умножении .

10 ² Средства 10 × 10 = 100

(IT написано 10 2 раз в умножении)

Пример: 10

³ = 10 × 10 = 1 000 .

Прописью: 10 ³ можно назвать «10 в третьей степени», «10 в степени 3» или просто «10 в кубе»

Пример: 10

⁴ = 10 × 10 × 10 × 10 = 10 000

Прописью: 10 ⁴ можно назвать «10 в четвертой степени», «10 в степени 4» или «от 10 до 4»

Вы можете умножать любое число само на себя столько раз , сколько хотите, используя это обозначение (см. Экспоненты), но степени 10 имеют особое применение . ..

Степени числа 10

«Степени числа 10» — очень удобный способ записи больших или малых чисел.

Вместо множества нулей вы показываете, сколько степеней из 10 получится столько-то нулей

Пример: 5000 = 5 × 1000 = 5 × 10

5 тысяч — это 5 раз по тысяче. А тысяча это 10 ³ . Итак, 5 умножить на 10 ³ = 5000

Видите ли, что 10 ³ — это удобный способ получить 3 нуля?

Ученые и инженеры (которые часто используют очень большие или очень маленькие числа) любят записывать числа Сюда.

Пример: Масса Солнца

Масса Солнца составляет 1,988 × 10 ³⁰ кг.

Слишком сложно написать 1 988 000 000 000 000 000 000 000 000 000 кг 94 = 3 × 10 × 10 × 10 × 10 = 30 000

Калькуляторы часто используют «E» или «e» следующим образом:

Пример:

6E+ 5 равно 6 × 10 ⁵

× 10 × 10 × 10 = 600 000

Пример:

3. 12E4 равно 3,12 × 10 ⁴

3,12E4 = 3,12 × 10 × 0 09 × 91, 208 3,12 × 10 × 10 × 91,208 10 × 100

Трюк

На первый взгляд это может показаться сложным, но есть простой «трюк»:

Индекс 10 говорит …

… на сколько знаков переместить десятичную точку Направо.

Пример: чему равно 1,35 × 10

⁴ ?
Вы можете рассчитать это как: 1,35 x (10 × 10 × 10 × 10) = 1,35 x 10 000 = 13 500
Но проще думать «переместить запятую на 4 знака вправо» следующим образом:
1 . 35 13 . 5 135 . 1350 . 13500 .
Отрицательные степени числа 10
Отрицательное? Что может быть противоположным умножению? Разделение!
Отрицательная степень означает сколько раз разделить на число.
Пример: 5 × 10
^-3 = 5 ÷ 10 ÷ 10 ÷ 10 = 0,005
Помните, что для отрицательных степеней 10:
Для отрицательных степеней 10 переместите запятую влево.
Таким образом, негативы просто идут другим путем.
Пример: Чему равно 7,1 × 10
^-3 ?
Действительно 7,1 х ( ¹ / ₁₀ × ¹ / ₁₀ × ¹ / ₁₀ ) = 7,01 × 0,00004
Но проще думать «переместить запятую на 3 знака от до » так:
7 . 1 0 . 71 0 . 071 0 . 0071
Попробуйте сами
Введите число и посмотрите его в научной записи:
Теперь попробуйте самостоятельно использовать научную запись:
Резюме
Индекс 10 указывает, на сколько разрядов переместить десятичную точку. Положительный означает переместить его вправо, отрицательный означает влево. Пример:
Номер
В научной нотации

Прописью
Положительные силы 5000 5 × 10 ³ 5 тысяч
Отрицательные силы 0,005 5 × 10 ^-3 5 тыс. тыс.
Фракции: Умножение и делятивные фракции
Урок 4: Умножение и разделение фракций
/EN/Фракции/Добавление и подключение фракций/Содержание/
. часть из целых . На прошлом уроке вы научились складывать и вычитать дроби. Но это не единственный вид математики, который вы можете делать с дробями. Бывают случаи, когда полезно будет умножать и дроби.
Щелкните слайд-шоу, чтобы узнать, как написать задачу на умножение с дробями.
Приведем пример умножения дробей. Предположим, вы выпиваете 2/4 чашки кофе каждое утро.
Но ваш врач только что сказал вам, что вам нужно сократить потребление кофе до 9 часов.0280 половина .
Теперь вам нужно выяснить, сколько стоит 1/2 от 2/4 кофейника.
Это может не выглядеть как задача на умножение. Но когда вы видите слово из с дробями, значит нужно умножать.
Чтобы настроить пример, мы просто заменим слово из знаком умножения.
Теперь наш пример готов к решению.
В отличие от обычного умножения, которое дает большее число …
В отличие от обычного умножения, которое дает на большее число . .. умножение дробей обычно дает на меньшее число .
Итак, когда мы умножаем 1/2 на 2/4…
Итак, когда мы умножаем 1/2 на 2/4… наш ответ будет меньше, чем 2/4.
Вот еще один пример. Допустим, у вас есть 3/5 чашки шоколадной начинки.
Вы хотите положить одинаковое количество начинки в каждый из этих 4 кексов.
Можно сказать, что вы хотите положить 1/4 от 3/5 стакана начинки в каждый кекс.
Как и раньше, мы изменим слово из на знак умножения.
Теперь наши дроби готовы к умножению.
Попробуйте!
Попробуйте решить приведенную ниже задачу на умножение. Пока не беспокойтесь о ее решении!
Рецепт требует 2/3 стакана молока. Вы хотите сократить рецепт вдвое.
Примечание : Хотя в нашем примере правильный ответ 2/3 x 1/2, помните, что порядок умножения не имеет значения. 1/2 х 2/3 тоже будет правильно.
Решение задач на умножение с дробями
Теперь, когда мы знаем, как решать задачи на умножение с дробями, давайте попрактикуемся в решении некоторых из них. Если вам удобно умножать целые числа, вы готовы к умножению дробей.
Щелкните слайд-шоу, чтобы научиться умножать две дроби.
Давайте умножим, чтобы найти 1/2 от 7/10.
Как и раньше, мы заменим слово из знаком умножения. Теперь мы готовы к умножению.
Сначала мы умножим числители: 1 и 7.
1 умножить на 7 равно 7, поэтому мы напишем 7 справа от числителей.
Когда мы добавили дроби, знаменатели остались прежними. Но когда мы умножаем, знаменатели тоже умножаются.
2 умножить на 10 равно 20, поэтому мы напишем 20 справа от знаменателя.
Теперь мы знаем, что 1/2 умножить на 7/10 равно 7/20.
Можно также сказать, что 1/2 от 7/10 равно 7/20.
Давайте попробуем другой пример: 3/5 умножить на 2/3.
Сначала умножим наши числители. 3 умножить на 2 равно 6.
Далее мы умножим наши знаменатели. 5 умножить на 3 равно 15.
Итак, 3/5 умножить на 2/3 равно 6/15.
Попробуйте!
Попробуйте решить приведенные ниже задачи на умножение.
Умножение дроби на целое число
Умножение дроби на целое число аналогично умножению двух дробей. Есть только один дополнительный шаг: прежде чем вы сможете умножать, вам нужно превратить целое число в дробь. Это слайд-шоу покажет вам, как это сделать.
Щелкните слайд-шоу, чтобы узнать, как умножать дробь и целое число.
Умножим 2 раза на 1/3. Помните, это всего лишь еще один способ спросить: «Сколько будет 1/3 от 2?»
Прежде чем мы начнем, нам нужно убедиться, что эти числа готовы к умножению.
Мы не можем умножить целое число на дробь, поэтому нам придется записать 2 в виде дроби.
Как вы узнали из раздела «Введение в дроби», мы также можем записать 2 как 2/1. Это потому, что 2 можно дважды разделить на 1.
Теперь мы готовы к умножению!
Сначала умножим числители : 2 и 1.
2 умножить на 1 равно 2. Выровняем 2 с числителями.
Далее мы умножим знаменатели числа : 1 и 3.
1 умножить на 3 равно 3. Выровняем 3 со знаменателем.
Итак, 2/1 умножить на 1/3 равно 2/3. Мы могли бы также сказать, что 1/3 от 2 равно 2/3.
Попробуем другой пример: 4 раза по 1/5.
Прежде чем мы начнем, нам придется записать 4 в виде дроби.
Мы перепишем 4 как 4/1. Теперь мы готовы к умножению.
Сначала умножим числители: 4 и 1.
4 умножить на 1 равно 4, поэтому числитель нашего ответа равен 4.
Далее умножим знаменатели: 1 и 5.
1 умножить на 5 равно 5, поэтому 5 — знаменатель нашего ответа.
Итак, 4/1 умножить на 1/5 равно 4/5.
Попробуйте!
Попробуйте решить приведенные ниже задачи на умножение.
Деление дробей
За последние несколько страниц вы узнали, как умножать дроби. Вы, наверное, уже догадались, что можно разделить и на дробь. Вы делите дроби, чтобы увидеть, сколько частей чего-то содержится в чем-то другом. Например, если вы хотите узнать, сколько четвертей дюйма составляет четыре дюйма, вы можете разделить 4 на 1/4.
Попробуем другой пример. Представьте, что рецепт требует 3 стакана муки, но ваш мерный стакан вмещает только 1/3, или одну треть , стакана. Сколько третей чашки нужно добавить?
Нам нужно выяснить, сколько третей чашки содержится в трех чашках. Другими словами, нам нужно разделить три на одну треть.
Мы бы написали задачу так:
3 ÷ 1/3
Попробуйте!
Попробуйте решить эти задачи на деление с дробями. Не беспокойтесь об их решении!
Рецепт требует 3/4 стакана воды. У вас есть только мерный стакан 1/8.
Решение задач на деление с дробями
Теперь, когда мы знаем, как писать задачи на деление, давайте потренируемся, решив несколько задач. Деление дробей очень похоже на умножение. Просто требуется один дополнительный шаг. Если вы можете умножать дроби, вы можете их и делить!
Просмотрите слайд-шоу, чтобы узнать, как разделить целое число на дробь.
Разделим 3 на 1/3. Помните, это всего лишь еще один способ спросить: «Сколько трети в 3?»
В нашем уроке о делении вы научились писать знак деления следующим образом (/). (÷) чтобы не ошибиться с дробью
Так же, как и с умножением, мы начнем с поиска любых целых чисел в нашей задаче. то же самое, что и 3/1.
Прежде чем мы сможем разделить, нам нужно сделать еще одно изменение.
Мы поменяем местами числитель и знаменатель дроби, на которую мы делим : 1/3 в этом примере.
Итак, 1/3 становится 3/1.
Это называется нахождением обратной или мультипликативной обратной , дроби.
Так как мы меняем нашу первоначальную дробь, мы также поменяем знак деления (÷) на умножение на знак (х).
Это потому, что умножение — это , обратное делению.
Теперь мы можем рассматривать это как обычную задачу на умножение.
Сначала мы умножим числители: 3 и 3.
3 умножить на 3 равно 9, поэтому мы напишем это рядом с числителями.
Далее умножим знаменатели: 1 и 1.
1 умножить на 1 равно 1, поэтому мы напишем 1 рядом со знаменателем.
Как видите, 3/1 х 1/3 = 9/1.
Помните, что любая дробь больше 1 также может быть выражена как целое число . Таким образом, 9/1 = 9.
3 ÷ 1/3 = 9. Другими словами, в 3 содержится 9 третей .
Давайте попробуем другой пример: 5 разделить на 4/7.
Как всегда, мы перепишем любые целые числа, чтобы 5 стало 5/1.
Далее мы найдем , обратное числа 4/7. Это дробь, на которую мы делим.
Для этого мы поменяем местами числитель и знаменатель, так что 4/7 станет 7/4.
Затем мы изменим знак деления (÷) на знак умножения (x).
Теперь мы можем умножать, как обычно. Сначала умножим числители: 5 и 7.
5 умножить на 7 равно 35, поэтому мы напишем это рядом с числителями.
Далее мы умножим знаменатели: 1 и 4.
1 умножить на 4 равно 4, поэтому мы напишем это рядом со знаменателями.
Итак, 5/1 х 4/7 = 35/4.
Как вы узнали ранее, мы можем преобразовать нашу неправильную дробь в смешанное число , чтобы наш ответ было легче читать.
35/4 = 8 3/4. Итак, 5 ÷ 4/7 = 8 3/4.
Попробуйте!
Попробуйте решить эти задачи на деление. Пока не беспокойтесь о сокращении ответа.
Деление двух дробей
Мы только что научились делить целое число на дробь . Вы можете использовать тот же метод, чтобы разделить на две части .
Просмотрите слайд-шоу, чтобы узнать, как делить на две дроби.
Давайте попробуем решить задачу с двумя дробями: 2/3 ÷ 3/4. Здесь мы хотим знать, сколько 3/4 в 2/3.
Сначала мы найдем , обратное дроби, на которую мы делим: 3/4.
Для этого мы поменяем местами числитель и знаменатель. Таким образом, 3/4 становится 4/3.
Далее мы изменим знак деления (÷) на знак умножения (x).
Теперь умножим числители. 2 x 4 = 8, поэтому мы напишем 8 рядом с верхними числами.
Далее мы умножим знаменатели. 3 x 3 = 9, поэтому мы напишем 9 рядом с нижними числами.
Итак, 2/3 х 4/3 = 8/9.
Мы могли бы также записать это как 2/3 ÷ 3/4 = 8/9.
Давайте попробуем другой пример: 4/7 разделить на 2/9.
Целых чисел нет, поэтому найдем обратное дроби, на которую мы делим. Это 2/9.
Для этого мы поменяем местами числитель и знаменатель. Таким образом, 2/9 становится 9/2.
Теперь мы изменим знак деления (÷) на знак умножения знак (x) и умножим как обычно.
Сначала умножим числители. 4 x 9 = 36.
Далее мы умножим знаменатели. 7 х 2 = 14,
Итак, 4/7 х 9/2 = 36/14. Как и раньше, вы можете преобразовать эту неправильную дробь в смешанное число.
Итак, 4/7 ÷ 2/9 = 2 8/14.
Попробуйте!
Попробуйте решить эти задачи на деление. Пока не беспокойтесь о сокращении ответа.
Умножение и деление смешанных чисел
Как бы вы решили подобную задачу?
Как вы узнали из предыдущего урока, всякий раз, когда вы решаете задачу с помощью смешанный число вам нужно сначала преобразовать его в неправильную дробь . Затем вы можете умножать или делить, как обычно.
Использование сокращения для упрощения задач
Иногда вам может понадобиться решить такие задачи:
Обе эти дроби включают больших чисел . Вы можете умножать эти дроби так же, как и любые другие дроби. Однако такие большие числа трудно понять. Можете ли вы представить 21/50 или двадцать одна пятидесятая , в голове?
21/50 x 25/14 = 525/700
Даже ответ кажется сложным. Это 525/700, или пятьсот двадцать пять семисотых . Какой глоток!
Если вам не нравится работать с большими числами, вы можете упростить подобную задачу, используя метод, называемый отменой . Когда вы отменяете дроби в задаче, вы сокращаете их обе одновременно.
Сначала отмена может показаться сложной, но мы покажем вам, как это сделать шаг за шагом. Давайте еще раз взглянем на пример, который мы только что видели.
Шаг 1
Во-первых, посмотрите на числитель первой дроби и знаменатель второй. Мы хотим посмотреть, можно ли разделить на одно и то же число.
В нашем примере похоже, что и 21, и 14 можно разделить на 7.
Шаг 2
Далее мы разделим 21 и 14 на 7. Сначала мы разделим наше верхнее число слева: 21.
21 ÷ 7 = 3
Затем разделим нижнее число справа: 14.
14 ÷ 7 = 2
Ответы на каждую задачу запишем рядом с числами, которые мы разделили. Поскольку 21 ÷ 7 равно 3, мы напишем 3 там, где было 21. 14 ÷ 7 равно 2, поэтому мы напишем 2 там, где было 14. Мы можем вычеркнуть или отменить , числа, с которых мы начали.
Теперь наша задача выглядит намного проще, не так ли?
Шаг 3
Давайте посмотрим на другие числа дроби. На этот раз мы рассмотрим знаменатель первой дроби и числитель второй. Можно ли разделить на одно и то же число?
Обратите внимание, что их можно разделить на 25! Вы могли также заметить, что они оба могут делиться на 5. Мы могли бы также использовать 5 , но обычно, когда вы отменяете, вы хотите найти наибольшее число , на которое можно разделить оба числа. Таким образом, вам не придется снова сокращать дробь в конце.
Шаг 4
Затем мы отменим так же, как мы делали это в шаге 2.
Мы разделим наше нижнее число слева: 50.
50 ÷ 25 = 2
Затем мы разделим верхнее число на справа: 25.
25 ÷ 25 = 1
Ответы на каждую задачу запишем рядом с числами, которые мы разделили.
Шаг 5
Теперь, когда мы отменили исходные дроби, мы можем умножить наши новые дроби, как обычно. Как всегда, сначала умножьте числители:
3 x 1 = 3
Затем умножьте знаменатели:
2 x 2 = 4
Итак, 3/2 x 1/2 = 3/4, или три четверти .
Шаг 6
Наконец, давайте еще раз проверим нашу работу. 525/700 был бы нашим ответом, если бы мы решили проблему без отмены. Если мы разделим и 525, и 700 на 175, то увидим, что 525/700 равно 3/4.
Можно также сказать, что мы уменьшаем 525/700 до 3/4. Помните, отмена — это еще один способ сократить дроби перед решением задачи. Вы получите один и тот же ответ, независимо от того, когда вы их уменьшите.
Продолжать
Предыдущий: Сложение и вычитание дробей
Next:Преобразование процентов, десятичных дробей и дробей
/ru/фракции/преобразование-процентов-десятичных-и-фракций/содержание/
Калькулятор времени | Сложение, вычитание, умножение, деление Время
Базовый калькулятор
Поделись этим калькулятором и страницей
Калькулятор
Используйте калькулятор времени
для сложения, вычитания, умножения и деления времени в днях, часах, минутах и секундах.
Калькулятор может складывать и вычитать отрезки времени или умножать и делить время на число или десятичную дробь. Ответы включают эквивалентное время в днях, часах, минутах или секундах.
Как рассчитать время
Ниже объясняется, как выполнять математические операции со временем. См. примеры сложения, вычитания, умножения и деления отрезков времени.
Как складывать время
Складывать дни, часы, минуты и секунды от наименьшей единицы времени к наибольшей.
Добавьте секунды
Если общее количество секунд больше 59, вычтите 60 из секунд и перенесите 1 в минуты
Добавьте минуты, включая все, что перенесено из расчета секунд
Если общее количество минут больше 59, вычтите 60 из минут и перенесите 1 в часы
Добавьте часы, включая перенесенные из расчета минут
Если общее количество часов больше 24, вычтите 24 из часов и перенесите 1 в дни
Добавьте дни, включая любые перенесенные из расчета часов
Добавление времени Пример задачи
Добавить 2 дня 21 час 45 минут 39 секунд к 5 дням 10 часов 45 минут 22 секунды

2 дня
21 час
45 минут
39 секунд
+плюс;
5 дней
10 часов
45 минут
22 секунды

39 секунд + 22 секунды = 61 секунда

2 дня
21 час
45 минут
39 секунд
+плюс;
5 дней
10 часов
45 минут
22 секунды
=
61 секунда

61 секунда — 60 = 1 секунда, перенос 1 в минуты
1 минута + 45 минут + 45 минут = 91 минута
перенос
1 минута

2 дня
21 час
45 минут
39 секунд
+ плюс;
5 дней
10 часов
45 минут
22 секунды
=
91 минута
1 секунда

91 минута — 60 = 31 минута, перенести 1 на часы
1 час + 21 час + 10 часов = 32 часа
нести
1 час
1 минута

2 дня
21 час
45 минут
39 секунд
4
4
5 дней
10 часов
45 минут
22 секунды
=
32 часа
31 минута
1 секунда

32 часа — 24 = 8 часов, перенести 1 на дни
1 день + 2 дня + 5 дней = 8 дней
Перенос
1 день
1 час
1 минута
2 дня
21 часа
45 минут
39 секунд
& Plus;
5 дней
10 часов
45 минут
22 секунды
=
8 дней
8 часов
31 минута
1 секунда

Завершено Добавление времени Математическая задача

2 дня
21 час
45 минут
39 секунд
+плюс;
5 дней
10 часов
45 минут
22 секунды
=
8 дней
8 часов
31 минута
1 секунда
Как вычесть время
Вычитание дней, часов, минут и секунд от наименьшей единицы времени к наибольшей.
Вычесть секунды
Если секунды, которые вы вычитаете, больше верхнего числа, заимствуйте 1 минуту из первых минут и добавьте 60 к первым секундам. Затем вычтите.
Вычесть минуты
Если количество минут, которое вы вычитаете, превышает максимальное число, заимствуйте 1 час от максимального количества часов и добавьте 60 к максимальному количеству минут. Затем вычтите.
Вычесть часы
Если часы, которые вы вычитаете, больше, чем верхнее число, заимствуйте 1 день из верхних дней и добавьте 24 к верхним часам. Затем вычтите.
Вычесть дни
Обратите внимание, что в любом случае, когда вам нужно заимствовать, если следующая по величине единица равна 0, то заимствование производится из 2-й по величине единицы. Так же, как и при длинном вычитании, берите взаймы со следующего по величине разряда.
Пример вычтения Пример задачи
Вычитание 2 дня 21 часа 56 минут 18 секунд с 5 дней 0 часов 10 минут 13 секунд
5 дней
0 часов
10 минут
13 Секунды
—
2. дней
21 час
56 минут
18 секунд

Вычесть секунды
13 секунд меньше 18 секунд, поэтому заимствуйте 1 из верхних минут
1 минута = 60 секунд, поэтому добавьте 60 секунд к 13, чтобы получить 73
.
73 секунды — 18 секунд = 55 секунд
Заимствование
1 минута
5 дней
0 часов
9000
73 секунды
—
2 Days
21 часы
56 минут
18 Seceld
и равные
56 минут
18 Secelds и равные;
55 секунд

Вычесть минуты
9 минут меньше 56 минут, поэтому заимствуйте 1 из часов
Есть 0 часов, поэтому займите 1 из дней
1 день = 24 часа и 1 час = 60 минут, поэтому добавьте 24 к часам, затем заимствуйте 1 из часов, чтобы получить 23
Добавьте 60 минут к 9, чтобы получить 69
69 минут — 56 минут = 13 минут
одолжить
1 день
1 час
1 минута
4 Дни
23 часа
69 минут
73 секунд
—
2 Дни
21 часы
56 минут
9000 2 180004
21 часы
56 минут 9000 21000 210004
21. =
13 минут
55 секунд

Вычесть часы
23 часа — 21 час = 2 часа
одолжить
1 день
1 час
1 минута
4 Дни
23 часа
69 минут
73 секунды
—
2 Days
21 часы
56 минут
18 секунд
& QUAL
56 минут
18 секунд
& Equals;
2 часа
13 минут
55 секунд

Вычесть дни
4 дня — 2 дня = 2 дня
одолжить
1 день
1 час
1 минута
4 Дни
23 часа
69 минут
73 секунды
—
2 Days
21 часы
56 минут
18 секунд
& QUAL
56 минут
18 секунд
& Equals;
2 дня
2 часа
13 минут
55 секунд

Математическая задача на время вычитания

5 дней
0 часов
10 минут
13 секунд
−
2 дня
21 час
56 минут
18 секунд
=
2 дня
2 часа
13 минут
55 секунд
Как умножить время
Умножьте дни, часы, минуты и секунды на множитель, работая от наименьшей единицы времени к наибольшей.
Умножить каждую единицу времени на кратное
Работая от наименьшей единицы времени к наибольшей, преобразовать лишние единицы времени в следующую более высокую единицу
Если секунды больше 59, разделите на 60, чтобы получить целое число и остаток
Оставьте остаток как общее количество секунд и добавьте целое число к минутам
Если минуты больше 59, разделите на 60, чтобы получить целое число и остаток
Сохраните остаток как общее количество минут и добавьте целое число к часам
Если часов больше 23, разделите на 24, чтобы получить целое число и остаток
Оставьте остаток как общее количество часов и добавьте целое число к дням
Пример умножения пример задачи
Умножение 2 дня 10 часов 32 минуты 16 секунд на 5
2 дня
10 часов
32 минуты
16 секунд

Умножение каждого блока на 5 9000 2 секунд

. Умножение.0208

2 дня
10 часов
32 минуты
16 секунд
=
10 дней
50 часов
160 минут
80 секунд

80 секунд больше 59, поэтому преобразуйте лишнее в минуты
80 разделить на 60 равно 1 с остатком 20
Сохранить 20 секунд и перенести 1 на минуты
160 + 1 = 161 минута
перенос
1 минута
=
10 дней
50 часов
161 минута
20 секунд

161 минута больше 59, поэтому преобразуйте лишнее в часы
161 разделить на 60 равно 2 с остатком 41
Держите 41 секунду и переносите 2 на часы
50 + 2 = 52 часа
перенос
2 часа
1 минута
=
10 дней
52 часа
41 минута
20 секунд

52 часа больше 24, поэтому преобразуйте лишнее в дни
52 разделить на 24 равно 2 с остатком 4
Держите 4 часа и носите 2 дня
10 + 2 = 12 дней
перенос
2 дня
2 часа
1 минута
=
12 дней
4 часа
41 минута
20 секунд

Завершенная математическая задача на умножение времени

2 дня
10 часов
32 минуты
16 секунд
=
12 дней
4 часа
41 минута
20 секунд

Как разделить время
Разделите дни, часы, минуты и секунды на делитель, работая от наименьшей единицы времени к наибольшей.
Разделите каждую единицу времени на делитель
Затем, работая от наибольшей единицы времени к наименьшей, преобразуйте любые десятичные значения в целые числа, сдвигая десятичную величину к меньшей единице времени
Если дни имеют десятичную дробь, сохраните целое число как общее количество дней и преобразуйте десятичную дробь в часы
Поскольку 1 день = 24 часа, умножьте десятичную дробь на 24 и прибавьте результат к часам
.
Если в часах есть десятичная дробь, сохраните целое число как общее количество часов и преобразуйте десятичную дробь в минуты
Поскольку 1 час = 60 минут, умножьте десятичную дробь на 60 и прибавьте результат к минутам
.
Если минуты имеют десятичную дробь, сохраните целое число как общее количество минут и преобразуйте десятичную дробь в секунды
Поскольку 1 минута = 60 секунд, умножьте десятичную дробь на 60 и прибавьте результат к секундам
Если в секундах есть десятичная дробь, вы обычно можете оставить это как окончательный ответ в зависимости от вашего приложения
Пример деления Пример задачи
Разделение 4 дня 10 часов 13 минут 16 секунд на 4
4 Дни
10 часов
13 минут
16 секунд

Разделение каждого блока на 4
208

4 дня
10 часов
13 минут
16 секунд
=
1 день
2,5 часа
3,25 минуты
4 секунды

Работа от наименьшей единицы времени к наибольшей Преобразование любых десятичных значений в целые числа
Часы — это не целое число, поэтому преобразуйте десятичную дробь в минуты
.
2,5 часа — это 2 часа плюс 0,5 часа
Поскольку 1 час = 60 минут, 0,5 от 1 часа равняется 0,5 от 60 минут = 30 минут
Хранить 2 часа и носить с собой 30 минут
30 + 3,25 = 33,25 минуты
перенос
30 минут
=
1 день
2 часа
33,25 минуты
4 секунды

Минуты не являются целым числом, поэтому преобразуйте десятичную дробь в секунды
33,25 минуты равно 33 минутам плюс 0,25 минуты
Так как 1 минута = 60 секунд, 0,25 от 1 минуты равняется 0,25 от 60 секунд = 15 секунд
Сохранить 33 минуты и перенести 15 секунд на
15 + 4 = 19 секунд
перенос
30 минут
15 секунд
=
1 дней
2 часа
33 минуты
19 секунд

Завершенная математическая задача на деление времени

4 дня
10 часов
13 минут
16 секунд
=
1 дня
2 часа
33 минуты
19 секунд

Время преобразования. 0004
3600 секунд
1 минута
60 секунд
1 секунда

Цитируйте этот контент, страницу или калькулятор как:
Фьюри, Эдвард «Калькулятор времени | Сложение, вычитание, умножение, деление времени» на https://www.calculatorsoup.com/calculators/time/time-calculator.php из КалькуляторСуп, https://www.calculatorsoup.com — Онлайн-калькуляторы
Подписаться на CalculatorSoup:
Почему я так много писаю и как часто я должен писать?
Если вы когда-нибудь задавались вопросом, как часто вы должны мочиться в день, вы не одиноки. То, как часто вы мочитесь, на самом деле является важным признаком вашего общего состояния здоровья, начиная с младенчества и продолжая на протяжении всей жизни. Продолжайте читать, чтобы узнать больше о мочеиспускании и о том, что частое мочеиспускание может сигнализировать о том, что вам нужно посетить врача.
Обычным считается мочеиспускание до семи раз в сутки, при этом большинство людей мочится от шести до семи раз. Но нет ничего необычного в том, чтобы мочиться больше или меньше в любой день. Сколько вы мочитесь, зависит от многих факторов, таких как:
возраст
сколько вы выпиваете в день
что вы пьете
заболевания, такие как диабет или инфекция мочевыводящих путей (ИМП)
прием лекарств
размер мочевого пузыря
более семи раз
мочеиспускание раз в день может быть нормальным для некоторых людей и может не быть признаком проблемы со здоровьем. Но Национальный институт старения рекомендует обратиться к врачу, если вы регулярно мочитесь восемь и более раз.
Причины, по которым вы можете чаще мочиться, включают:
Инфекция мочевыводящих путей (ИМП)
ИМП — это распространенное заболевание, которое может повлиять на частоту мочеиспускания. У любого человека может развиться ИМП, хотя они чаще встречаются у женщин. ИМП может вызвать у вас острую потребность в мочеиспускании, даже если вы недавно опорожняли мочевой пузырь.
Во время инфекции вы можете чаще мочиться, но в меньшем количестве. Вы также, вероятно, почувствуете жжение при мочеиспускании.
Существует множество возможных причин ИМП, поэтому при подозрении на инфекцию мочевыводящих путей лучше обратиться к врачу.
Беременность
Особые обстоятельства, такие как беременность и первые недели после родов, могут повлиять на частоту мочеиспускания. Во время беременности человек мочится чаще из-за гормональных изменений, а также из-за давления на мочевой пузырь от растущего плода. После рождения у них сохраняется повышенный диурез в течение нескольких недель. Это связано с дополнительными жидкостями, которые они могли получить во время родов через капельницу или лекарства, а также с естественной реакцией организма на мобилизацию и удаление жидкости после рождения.
Задержка мочи
Задержка мочи — это когда вы не можете полностью опорожнить мочевой пузырь. Это может вызвать постоянное ощущение потребности в мочеиспускании, боль в нижней части живота и частое мочеиспускание. Это может быть вызвано:
неврологическими факторами
инфекциями
дисфункцией мышц мочевого пузыря
обструкцией
лекарствами
диабетом
Более частое мочеиспускание — это способ организма избавиться от лишнего сахара в крови.
Гипокальциемия или гиперкальциемия
Если уровень кальция в организме слишком высок или слишком низок — состояния, известные как гипокальциемия или гиперкальциемия, — частота мочеиспускания может измениться.
Низкий уровень калия (гипокалиемия)
Низкий уровень калия может ухудшить способность почек концентрировать мочу и может привести к сильной жажде или чрезмерному мочеиспусканию.
Лекарства
Люди с проблемами сердца, высоким кровяным давлением или плохой функцией почек часто принимают лекарства, называемые диуретиками. Диуретики работают, помогая почкам отфильтровывать больше жидкости в мочу. Прием диуретиков может привести к более частому мочеиспусканию. Некоторые распространенные диуретики включают:
chlorothiazide (Diuril)
chlorthalidone (Thalitone)
hydrochlorothiazide (Microzide)
indapamide
metolazone
bumetanide (Bumex)
furosemide (Lasix)
torsemide (Demadex)
amiloride (Midamor)
эплеренон (Inspra)
спиронолактон (Aldactone)
триамтерен (Dyrenium)
Некоторые продукты и добавки
Некоторые продукты или добавки являются естественными диуретиками и могут увеличить количество жидкости, выводимой организмом. К ним относятся:
caffeine
dandelion
hawthorn
horsetail
juniper
green tea and black tea
parsley
hibiscus
watermelon
grapes
berries
celery
Sickle cell anemia
Sickle клеточная анемия может повлиять на функцию почек. Повреждение почек означает, что они также не могут выполнять свою работу, и вырабатывается больше мочи. Это вызывает потребность в более частом мочеиспускании
Застойная сердечная недостаточность
Застойная сердечная недостаточность может затруднить избавление организма от лишней жидкости, особенно в нижней части тела. Когда вы ложитесь ночью, ваше тело может производить больше мочи, чтобы попытаться избавиться от этой жидкости.
До половины людей с застойной сердечной недостаточностью страдают гиперактивным мочевым пузырем и недержанием мочи.
Тахикардия
Тахикардия — это аномально быстрое сердцебиение. Тахикардия-полиурия — увеличение диуреза вследствие тахикардии, определяемой как сердцебиение более 120 ударов в минуту в течение более 30 минут. Считается, что снижение уровня антидиуретического гормона и продукции предсердного натрийуретического пептида связано с увеличением диуреза.
Медицинские процедуры
Если вы недавно проходили тест, связанный с введением красителя в ваше тело, например компьютерную томографию, вы можете мочиться чаще, так как ваш организм выводит лишнюю жидкость.
Алкоголь и кофеин
Алкоголь и кофеин могут оказывать мочегонное действие, заставляя вас мочиться чаще, чем обычно. При употреблении этих веществ частое мочеиспускание, вероятно, не является признаком медицинской проблемы.
Кофеин содержится во многих пищевых продуктах и напитках, включая:
Coffee
TEA
SODA
Горячий шоколад
Энергетические напитки
Узнайте больше: воздействие кофеина на тело »
Увеличение водяного инкаляции
. ДЕЛА. диурез и частота мочеиспускания.
Гиперфункция щитовидной железы
Гиперфункция щитовидной железы может вызывать широкий спектр симптомов, включая частое мочеиспускание и постоянную жажду. Другие общие симптомы включают в себя:
проблемы со сном
повышенный аппетит
беспокойство
неспособность сконцентрироваться
Беспокойство
Беспокойство может привести к сокращению гладких мышц, окружающих мочевой пузырь, вызывая давление и стимулируя позывы к мочеиспусканию.
Интерстициальный цистит
Интерстициальный цистит — это состояние, вызывающее хроническое воспаление мочевого пузыря. Общие симптомы включают:
частое мочеиспускание
случайное подтекание мочи
тазовая или абдоминальная боль и давление
срочная потребность в мочеиспускании
Множественная миелома
Множественная миелома является редким типом рака крови. Одним из симптомов может быть высокий уровень кальция, который может вызвать учащение мочеиспускания.
Первичный альдостеронизм
Гиперальдостеронизм — это гиперпродукция гормона альдостерона надпочечниками. Перепроизводство этого гормона может привести к тому, что ваше тело будет удерживать натрий и терять больше калия. Низкий уровень калия может вызвать частое мочеиспускание.
Поликистоз почек
Поликистоз почек — это генетическое заболевание, при котором в почках растут кисты. Люди, как правило, не проявляют симптомы, пока им не исполнится от 30 до 50 лет. Частое мочеиспускание является одним из возможных ранних симптомов.
Камни в почках
Около 600 000 человек в США ежегодно сталкиваются с камнями в почках. Они могут вызывать сильную боль в боку и спине, которая может иррадиировать в живот или пах. Другие симптомы включают:
частое мочеиспускание
боль во время мочеиспускания
императивные позывы к мочеиспусканию
кровь в моче
мутная моча
лихорадка и озноб У мужчин это может быть связано с увеличением простаты. Увеличение предстательной железы часто вызвано доброкачественным увеличением предстательной железы (ДГПЖ), которое не является злокачественным или вызвано раком предстательной железы. Когда простата увеличивается, она может блокировать отток мочи из мочевого пузыря. Это может привести к тому, что вы не сможете полностью опорожнить мочевой пузырь даже после мочеиспускания.
Если вы мочитесь так много или так часто каждый день, что чувствуете, что это влияет на качество вашей жизни, поговорите с врачом. У вас может быть основное заболевание, такое как гиперактивный мочевой пузырь. Это можно лечить.
Вам также следует обратиться к врачу, если вы слишком редко мочитесь или чувствуете, что мочевой пузырь не полностью опорожняется даже во время мочеиспускания, особенно если вы пожилой мужчина. Другими симптомами, требующими обращения к врачу, являются:
лихорадка и боль в спине
кровь в моче
белая и мутная моча
обесцвеченная моча
сильный или ненормальный запах мочи
Ваше лечение может зависеть от того, какое состояние вызывает ваши симптомы. Например, если вы беременны, частое мочеиспускание будет продолжаться до тех пор, пока вы не родите.
Если ваши симптомы вызваны заболеванием, лечение этого состояния может помочь.
Если у вас диабет, контроль уровня сахара в крови должен уменьшить потребность в мочеиспускании.
Если частота мочеиспускания вызвана ИМП, после устранения ИМП диурез должен вернуться к норме.
Если у вас увеличенная простата, которая блокирует отток мочи, вам может потребоваться лекарство для увеличения оттока мочи или уменьшения размера простаты.
Если вы принимаете мочегонные препараты для лечения сердечной недостаточности или высокого кровяного давления, ваш врач может попытаться скорректировать дозу, чтобы облегчить ваши симптомы.
В дополнение к тому, что вы должны сообщить своему врачу о проблемах с мочеиспусканием, вот несколько советов по уменьшению раздражения половых органов и мочи:
Ешьте продукты, богатые пробиотиками, особенно лактобациллами, которые содержатся в йогурте и кефире. Ранние исследования показывают, что лактобациллы могут быть полезны женщинам с рецидивирующими ИМП.
Если вы используете мыло в области гениталий, используйте продукт без запаха, предназначенный для чувствительной кожи.
Носите свободное хлопковое нижнее белье.
Избегайте узких джинсов и леггинсов.
Старайтесь мочиться каждые 3-4 часа и старайтесь не задерживать мочу, когда вам нужно идти.
No related posts.
Навигация по записям
Предыдущая статьяЧему равен логарифм 0: Mathway | Популярные задачи
Следующая статьяКорень онлайн рассчитать: Калькулятор корней онлайн | umath.ru
Добавить комментарий Отменить ответ
Ваш адрес email не будет опубликован. Обязательные поля помечены *
Комментарий *
Имя *
Email *
Сайт

Найти:
Рубрики
Геометрия
Математика
Физика
Химия
Школьная жизнь
Разное
© 2015 - 2019 Муниципальное казённое общеобразовательное учреждение «Таловская средняя школа»
Карта сайта