Чему равен натуральный логарифм 0. Что такое логарифм? Решение логарифмов
Как известно, при перемножении выражений со степенями их показатели всегда складываются (a b *a c = a b+c). Этот математический закон был выведен Архимедом, а позже, в VIII веке, математик Вирасен создал таблицу целых показателей. Именно они послужили для дальнейшего открытия логарифмов. Примеры использования этой функции можно встретить практически везде, где требуется упростить громоздкое умножение на простое сложение. Если вы потратите минут 10 на прочтение этой статьи, мы вам объясним, что такое логарифмы и как с ними работать. Простым и доступным языком.
Определение в математике
Логарифмом называется выражение следующего вида: log a b=c, то есть логарифмом любого неотрицательного числа (то есть любого положительного) «b» по его основанию «a» считается степень «c», в которую необходимо возвести основание «a», чтобы в итоге получить значение «b». Разберем логарифм на примерах, допустим, есть выражение log 2 8. Как найти ответ? Очень просто, нужно найти такую степень, чтобы из 2 в искомой степени получить 8. Проделав в уме некоторые расчеты, получаем число 3! И верно, ведь 2 в степени 3 дает в ответе число 8.
Разберем логарифм на примерах, допустим, есть выражение log 2 8. Как найти ответ? Очень просто, нужно найти такую степень, чтобы из 2 в искомой степени получить 8. Проделав в уме некоторые расчеты, получаем число 3! И верно, ведь 2 в степени 3 дает в ответе число 8.
Разновидности логарифмов
Для многих учеников и студентов эта тема кажется сложной и непонятной, однако на самом деле логарифмы не так страшны, главное — понять общий их смысл и запомнить их свойста и некоторые правила. Существует три отдельных вида логарифмических выражений:
- Натуральный логарифм ln a, где основанием является число Эйлера (e = 2,7).
- Десятичный a, где основанием служит число 10.
- Логарифм любого числа b по основанию a>1.
Каждый из них решается стандартным способом, включающим в себя упрощение, сокращение и последующее приведение к одному логарифму с помощью логарифмических теорем. Для получения верных значений логарифмов следует запомнить их свойства и очередность действий при их решениях.
Правила и некоторые ограничения
В математике существует несколько правил-ограничений, которые принимаются как аксиома, то есть не подлежат обсуждению и являются истиной. Например, нельзя числа делить на ноль, а еще невозможно извлечь корень четной степени из отрицательных чисел. Логарифмы также имеют свои правила, следуя которым можно с легкостью научиться работать даже с длинными и емкими логарифмическими выражениями:
- основание «a» всегда должно быть больше нуля, и при этом не быть равным 1, иначе выражение потеряет свой смысл, ведь «1» и «0» в любой степени всегда равны своим значениям;
- если а > 0, то и а b >0, получается, что и «с» должно быть больше нуля.
Как решать логарифмы?
К примеру, дано задание найти ответ уравнения 10 х = 100. Это очень легко, нужно подобрать такую степень, возведя в которую число десять, мы получим 100. Это, конечно же, 10 2 =100.
А теперь давайте представим данное выражение в виде логарифмического. Получим log 10 100 = 2. При решении логарифмов все действия практически сходятся к тому, чтобы найти ту степень, в которую необходимо ввести основание логарифма, чтобы получить заданное число.
Получим log 10 100 = 2. При решении логарифмов все действия практически сходятся к тому, чтобы найти ту степень, в которую необходимо ввести основание логарифма, чтобы получить заданное число.
Для безошибочного определения значенияя неизвестной степени необходимо научиться работать с таблицей степеней. Выглядит она следующим образом:
Как видите, некоторые показатели степени можно угадать интуитивно, если имеется технический склад ума и знание таблицы умножения. Однако для больших значений потребуется таблица степеней. Ею могут пользоваться даже те, кто совсем ничего не смыслит в сложных математических темах. В левом столбце указаны числа (основание a), верхний ряд чисел — это значение степени c, в которую возводится число a. На пересечении в ячейках определены значения чисел, являющиеся ответом (a c =b). Возьмем, к примеру, самую первую ячейку с числом 10 и возведем ее в квадрат, получим значение 100, которое указано на пересечении двух наших ячеек. Все так просто и легко, что поймет даже самый настоящий гуманитарий!
Уравнения и неравенства
Получается, что при определенных условиях показатель степени — это и есть логарифм. Следовательно, любые математические численные выражения можно записать в виде логарифмического равенства. Например, 3 4 =81 можно записать в виде логарифма числа 81 по основанию 3, равному четырем (log 3 81 = 4). Для отрицательных степеней правила такие же: 2 -5 = 1/32 запишем в виде логарифма, получим log 2 (1/32) = -5. Одной из самых увлекательных разделов математики является тема «логарифмы». Примеры и решения уравнений мы рассмотрим чуть ниже, сразу же после изучения их свойств. А сейчас давайте разберем, как выглядят неравенства и как их отличить от уравнений.
Следовательно, любые математические численные выражения можно записать в виде логарифмического равенства. Например, 3 4 =81 можно записать в виде логарифма числа 81 по основанию 3, равному четырем (log 3 81 = 4). Для отрицательных степеней правила такие же: 2 -5 = 1/32 запишем в виде логарифма, получим log 2 (1/32) = -5. Одной из самых увлекательных разделов математики является тема «логарифмы». Примеры и решения уравнений мы рассмотрим чуть ниже, сразу же после изучения их свойств. А сейчас давайте разберем, как выглядят неравенства и как их отличить от уравнений.
Дано выражение следующего вида: log 2 (x-1) > 3 — оно является логарифмическим неравенством, так как неизвестное значение «х» находится под знаком логарифма. А также в выражении сравниваются две величины: логарифм искомого числа по основанию два больше, чем число три.
Самое главное отличие между логарифмическими уравнениями и неравенствами заключается в том, что уравнения с логарифмами (пример — логарифм 2 x = √9) подразумевают в ответе одно или несколько определенных числовых значений, тогда как при решении неравенства определяются как область допустимых значений, так и точки разрыва этой функции. Как следствие, в ответе получается не простое множество отдельных чисел как в ответе уравнения, а а непрерывный ряд или набор чисел.
Как следствие, в ответе получается не простое множество отдельных чисел как в ответе уравнения, а а непрерывный ряд или набор чисел.
Основные теоремы о логарифмах
При решении примитивных заданий по нахождению значений логарифма, его свойства можно и не знать. Однако когда речь заходит о логарифмических уравнениях или неравенствах, в первую очередь, необходимо четко понимать и применять на практике все основные свойства логарифмов. С примерами уравнений мы познакомимся позже, давайте сначала разберем каждое свойство более подробно.
- Основное тождество выглядит так: а logaB =B. Оно применяется только при условии, когда а больше 0, не равно единице и B больше нуля.
- Логарифм произведения можно представить в следующей формуле: log d (s 1 *s 2) = log d s 1 + log d s 2. При этом обязательным условием является: d, s 1 и s 2 > 0; а≠1. Можно привести доказательство для этой формулы логарифмов, с примерами и решением. Пусть log a s 1 = f 1 и log a s 2 = f 2 , тогда a f1 = s 1 , a f2 = s 2.
 Получаем, что s 1 *s 2 = a f1 *a f2 = a f1+f2 (свойства степеней), а далее по определению: log a (s 1 *s 2)= f 1 + f 2 = log a s1 + log a s 2, что и требовалось доказать.
Получаем, что s 1 *s 2 = a f1 *a f2 = a f1+f2 (свойства степеней), а далее по определению: log a (s 1 *s 2)= f 1 + f 2 = log a s1 + log a s 2, что и требовалось доказать. - Логарифм частного выглядит так: log a (s 1/ s 2) = log a s 1 — log a s 2.
- Теорема в виде формулы приобретает следующий вид: log a q b n = n/q log a b.
Называется эта формула «свойством степени логарифма». Она напоминает собой свойства обычных степеней, и неудивительно, ведь вся математика держится на закономерных постулатах. Давайте посмотрим на доказательство.
Пусть log a b = t, получается a t =b. Если возвести обе части в степень m: a tn = b n ;
но так как a tn = (a q) nt/q = b n , следовательно log a q b n = (n*t)/t, тогда log a q b n = n/q log a b. Теорема доказана.
Примеры задач и неравенств
Самые распространенные типы задач на тему логарифмов — примеры уравнений и неравенств. Они встречаются практически во всех задачниках, а также входят в обязательную часть экзаменов по математике. Для поступления в университет или сдачи вступительных испытаний по математике необходимо знать, как правильно решать подобные задания.
Для поступления в университет или сдачи вступительных испытаний по математике необходимо знать, как правильно решать подобные задания.
К сожалению, единого плана или схемы по решению и определению неизвестного значения логарифма не существует, однако к каждому математическому неравенству или логарифмическому уравнению можно применить определенные правила. Прежде всего следует выяснить, можно ли упростить выражение или привести к общему виду. Упрощать длинные логарифмические выражения можно, если правильно использовать их свойства. Давайте скорее с ними познакомимся.
При решении же логарифмических уравнений, следует определить, какой перед нами вид логарифма: пример выражения может содержать натуральный логарифм или же десятичный.
Вот примеры ln100, ln1026. Их решение сводится к тому, что нужно определить ту степень, в которой основание 10 будет равно 100 и 1026 соответственно. Для решений же натуральных логарифмов нужно применить логарифмические тождества или же их свойства. Давайте на примерах рассмотрим решение логарифмических задач разного типа.
Давайте на примерах рассмотрим решение логарифмических задач разного типа.
Как использовать формулы логарифмов: с примерами и решениями
Итак, рассмотрим примеры использования основных теорем о логарифмах.
- Свойство логарифма произведения можно применять в заданиях, где необходимо разложить большое значение числа b на более простые сомножители. Например, log 2 4 + log 2 128 = log 2 (4*128) = log 2 512. Ответ равен 9.
- log 4 8 = log 2 2 2 3 = 3/2 log 2 2 = 1,5 — как видите, применяя четвертое свойство степени логарифма, удалось решить на первый взгляд сложное и нерешаемое выражение. Необходимо всего лишь разложить основание на множители и затем вынести значения степени из знака логарифма.
Задания из ЕГЭ
Логарифмы часто встречаются на вступительных экзаменах, особенно много логарифмических задач в ЕГЭ (государственный экзамен для всех выпускников школ). Обычно эти задания присутствуют не только в части А (самая легкая тестовая часть экзамена), но и в части С (самые сложные и объемные задания). Экзамен подразумевает точное и идеальное знание темы «Натуральные логарифмы».
Экзамен подразумевает точное и идеальное знание темы «Натуральные логарифмы».
Примеры и решения задач взяты из официальных вариантов ЕГЭ. Давайте посмотрим, как решаются такие задания.
Дано log 2 (2x-1) = 4. Решение:
перепишем выражение, немного его упростив log 2 (2x-1) = 2 2 , по определению логарифма получим, что 2x-1 = 2 4 , следовательно 2x = 17; x = 8,5.
- Все логарифмы лучше всего приводить к одному основанию, чтобы решение не было громоздким и запутанным.
- Все выражение, стоящие под знаком логарифма, указываются как положительные, поэтому при вынесении множителем показателя степени выражения, который стоит под знаком логарифма и в качестве его основания, остающееся под логарифмом выражение должно быть положительно.
Логарифмом положительного числа b по основанию a (a>0, a не равно 1) называют такое число с, что a c = b: log a b = c ⇔ a c = b (a > 0, a ≠ 1, b > 0)       
Обратите внимание: логарифм от неположительного числа не определен. Кроме того, в основании логарифма должно быть положительное число, не равное 1. Например, если мы возведем -2 в квадрат, получим число 4, но это не означает, что логарифм по основанию -2 от 4 равен 2.
Кроме того, в основании логарифма должно быть положительное число, не равное 1. Например, если мы возведем -2 в квадрат, получим число 4, но это не означает, что логарифм по основанию -2 от 4 равен 2.
a log a b = b (a > 0, a ≠ 1) (2)
Важно, что области определения правой и левой частей этой формулы отличаются. Левая часть определена только при b>0, a>0 и a ≠ 1. Правая часть определена при любом b, а от a вообще не зависит. Таким образом, применение основного логарифмического «тождества» при решении уравнений и неравенств может привести к изменению ОДЗ.
Два очевидных следствия определения логарифма log
a
a = 1
(a > 0, a ≠ 1)
(3)
log
a
1 = 0
(a > 0, a ≠ 1)
(4)
Действительно, при возведении числа a в первую степень мы получим то же самое число, а при возведении в нулевую степень — единицу.
Логарифм произведения и логарифм частногоlog a (b c) = log a b + log a c (a > 0, a ≠ 1, b > 0, c > 0) (5)
Log
a
b
c
=
log
a
b −
log
a
c
(a > 0, a ≠ 1, b > 0, c > 0)
(6)
Хотелось бы предостеречь школьников от бездумного применения данных формул при решении логарифмических уравнений и неравенств.
Действительно, выражение log a (f (x) g (x)) определено в двух случаях: когда обе функции строго положительны либо когда f(x) и g(x) обе меньше нуля.
Преобразуя данное выражение в сумму log a f (x) + log a g (x) , мы вынуждены ограничиваться только случаем, когда f(x)>0 и g(x)>0. Налицо сужение области допустимых значений, а это категорически недопустимо, т. к. может привести к потере решений. Аналогичная проблема существует и для формулы (6).
Степень можно выносить за знак логарифмаlog a b p = p log a b (a > 0, a ≠ 1, b > 0) (7)
И вновь хотелось бы призвать к аккуратности. Рассмотрим следующий пример:
Log a (f (x) 2 = 2 log a f (x)
Левая часть равенства определена, очевидно, при всех значениях f(х), кроме нуля. Правая часть — только при f(x)>0! Вынося степень из логарифма, мы вновь сужаем ОДЗ. Обратная процедура приводит к расширению области допустимых значений. Все эти замечания относятся не только к степени 2, но и к любой четной степени.
Правая часть — только при f(x)>0! Вынося степень из логарифма, мы вновь сужаем ОДЗ. Обратная процедура приводит к расширению области допустимых значений. Все эти замечания относятся не только к степени 2, но и к любой четной степени.
log a b = log c b log c a (a > 0, a ≠ 1, b > 0, c > 0, c ≠ 1) (8)
Тот редкий случай, когда ОДЗ не изменяется при преобразовании. Если вы разумно выбрали основание с (положительное и не равное 1), формула перехода к новому основанию является абсолютно безопасной.
Если в качестве нового основания с выбрать число b, получим важный частный случай формулы (8):
Log a b = 1 log b a (a > 0, a ≠ 1, b > 0, b ≠ 1) (9)
Несколько простых примеров с логарифмамиПример 1. Вычислите: lg2 + lg50.
Решение. lg2 + lg50 = lg100 = 2. Мы воспользовались формулой суммы логарифмов (5) и определением десятичного логарифма.
Пример 2. Вычислите: lg125/lg5.
Решение. lg125/lg5 = log 5 125 = 3. Мы использовали формулу перехода к новому основанию (8).
| a log a b = b (a > 0, a ≠ 1) |
| log a a = 1 (a > 0, a ≠ 1) |
| log a 1 = 0 (a > 0, a ≠ 1) |
| log a (b c) = log a b + log a c (a > 0, a ≠ 1, b > 0, c > 0) |
| log a b c = log a b − log a c (a > 0, a ≠ 1, b > 0, c > 0) |
| log a b p = p log a b (a > 0, a ≠ 1, b > 0) |
| log a b = log c b log c a (a > 0, a ≠ 1, b > 0, c > 0, c ≠ 1) |
| log a b = 1 log b a (a > 0, a ≠ 1, b > 0, b ≠ 1) |
нередко берут цифру е = 2,718281828 . Логарифмы по данному основанию именуют натуральным . При проведении вычислений с натуральными логарифмами общепринято оперировать знаком l n , а не log ; при этом число 2,718281828 , определяющие основание, не указывают.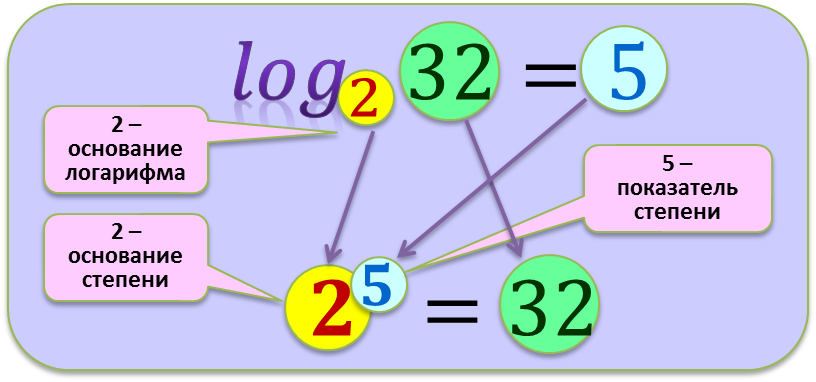
Другими словами формулировка будет иметь вид: натуральный логарифм числа х — это показатель степени , в которую нужно возвести число
Так, ln(7,389…) = 2, так как e 2 =7,389… . Натуральный логарифм самого числа e = 1, потому что e 1 =e , а натуральный логарифм единицы равен нулю, так как e 0 = 1.
Само число е определяет предел монотонной ограниченной последовательности
вычислено, что е = 2,7182818284… .
Весьма часто для фиксации в памяти какого либо числа, цифры необходимого числа ассоциируют с какой-нибудь выдающейся датой. Скорость запоминания первых девяти знаков числа е после запятой возрастет, если заметить, что 1828 — это год рождения Льва Толстого!
На сегодняшний день существуют достаточно полные таблицы натуральных логарифмов.
График натурального логарифма (функции y = ln x ) является следствием графика экспоненты зеркальным отражением относительно прямой у = х и имеет вид:
Натуральный логарифм может быть найден для каждого положительного вещественного числа a как площадь под кривой y = 1/x от 1 до a .
Элементарность этой формулировку, которая состыковывается со многими другими формулами, в которых задействован натуральный логарифм, явилось причиной образования названия «натуральный».
Если анализировать натуральный логарифм , как вещественную функцию действительной переменной, то она выступает обратной функцией к экспоненциальной функции, что сводится к тождествам:
e ln(a) =a (a>0)
ln(e a) =a
По аналогии со всеми логарифмами, натуральный логарифм преобразует умножение в сложение, деление в вычитание:
ln (xy ) = ln (x ) + ln (y )
ln (х/у)= lnx — lny
Логарифм может быть найден для каждого положительного основания, которое не равно единице, а не только для e , но логарифмы для других оснований отличаются от натурального логарифма только постоянным множителем, и, обычно, определяются в терминах натурального логарифма.
Проанализировав график натурального логарифма, получаем, что он существует при положительных значениях переменной x . Он монотонно возрастает на своей области определения.
При x → 0 пределом натурального логарифма выступает минус бесконечность ( -∞ ).При x → +∞ пределом натурального логарифма выступает плюс бесконечность ( + ∞ ). При больших x логарифм возрастает довольно медленно. Любая степенная функция x a с положительным показателем степени a возрастает быстрее логарифма. Натуральный логарифм является монотонно возрастающей функцией, поэтому экстремумы у него отсутствуют.
Использование натуральных логарифмов весьма рационально при прохождении высшей математики. Так, использование логарифма удобно для нахождения ответа уравнений, в которых неизвестные фигурируют в качестве показателя степени. Применение в расчетах натуральных логарифмом дает возможность изрядно облегчить большое количество математических формул. Логарифмы по основанию е присутствуют при решении значительного числа физических задач и естественным образом входят в математическое описание отдельных химических, биологических и прочих процессов. Так, логарифмы употребляются для расчета постоянной распада для известного периода полураспада, или для вычисления времени распада в решении проблем радиоактивности. Они выступают в главной роли во многих разделах математики и практических наук, к ним прибегают в сфере финансов для решения большого числа задач, в том числе и в расчете сложных процентов.
Логарифмы по основанию е присутствуют при решении значительного числа физических задач и естественным образом входят в математическое описание отдельных химических, биологических и прочих процессов. Так, логарифмы употребляются для расчета постоянной распада для известного периода полураспада, или для вычисления времени распада в решении проблем радиоактивности. Они выступают в главной роли во многих разделах математики и практических наук, к ним прибегают в сфере финансов для решения большого числа задач, в том числе и в расчете сложных процентов.
Итак, перед нами степени двойки. Если взять число из нижней строчки, то можно легко найти степень, в которую придется возвести двойку, чтобы получилось это число. Например, чтобы получить 16, надо два возвести в четвертую степень. А чтобы получить 64, надо два возвести в шестую степень. Это видно из таблицы.
А теперь — собственно, определение логарифма:
Логарифм по основанию a от аргумента x — это степень, в которую надо возвести число a , чтобы получить число x .
Обозначение: log a x = b , где a — основание, x — аргумент, b — собственно, чему равен логарифм.
Например, 2 3 = 8 ⇒ log 2 8 = 3 (логарифм по основанию 2 от числа 8 равен трем, поскольку 2 3 = 8). С тем же успехом log 2 64 = 6 , поскольку 2 6 = 64 .
Операцию нахождения логарифма числа по заданному основанию называют логарифмированием. Итак, дополним нашу таблицу новой строкой:
| 2 1 | 2 2 | 2 3 | 2 4 | 2 5 | 2 6 |
| 2 | 4 | 8 | 16 | 32 | 64 |
| log 2 2 = 1 | log 2 4 = 2 | log 2 8 = 3 | log 2 16 = 4 | log 2 32 = 5 | log 2 64 = 6 |
К сожалению, далеко не все логарифмы считаются так легко. Например, попробуйте найти log 2 5 . Числа 5 нет в таблице, но логика подсказывает, что логарифм будет лежать где-то на отрезке . Потому что 2 2
Такие числа называются иррациональными: цифры после запятой можно писать до бесконечности, и они никогда не повторяются. Если логарифм получается иррациональным, его лучше так и оставить: log 2 5 , log 3 8 , log 5 100 .
Если логарифм получается иррациональным, его лучше так и оставить: log 2 5 , log 3 8 , log 5 100 .
Важно понимать, что логарифм — это выражение с двумя переменными (основание и аргумент). Многие на первых порах путают, где находится основание, а где — аргумент. Чтобы избежать досадных недоразумений, просто взгляните на картинку:
Перед нами — не что иное как определение логарифма. Вспомните: логарифм — это степень , в которую надо возвести основание, чтобы получить аргумент. Именно основание возводится в степень — на картинке оно выделено красным. Получается, что основание всегда находится внизу! Это замечательное правило я рассказываю своим ученикам на первом же занятии — и никакой путаницы не возникает.
С определением разобрались — осталось научиться считать логарифмы, т.е. избавляться от знака «log». Для начала отметим, что из определения следует два важных факта:
- Аргумент и основание всегда должны быть больше нуля. Это следует из определения степени рациональным показателем, к которому сводится определение логарифма.

- Основание должно быть отличным от единицы, поскольку единица в любой степени все равно остается единицей. Из-за этого вопрос «в какую степень надо возвести единицу, чтобы получить двойку» лишен смысла. Нет такой степени!
Такие ограничения называются областью допустимых значений (ОДЗ). Получается, что ОДЗ логарифма выглядит так: log a x = b ⇒ x > 0 , a > 0 , a ≠ 1 .
Заметьте, что никаких ограничений на число b (значение логарифма) не накладывается. Например, логарифм вполне может быть отрицательным: log 2 0,5 = −1 , т.к. 0,5 = 2 −1 .
Впрочем, сейчас мы рассматриваем лишь числовые выражения, где знать ОДЗ логарифма не требуется. Все ограничения уже учтены составителями задач. Но когда пойдут логарифмические уравнения и неравенства, требования ОДЗ станут обязательными. Ведь в основании и аргументе могут стоять весьма неслабые конструкции, которые совсем необязательно соответствуют приведенным выше ограничениям.
Теперь рассмотрим общую схему вычисления логарифмов.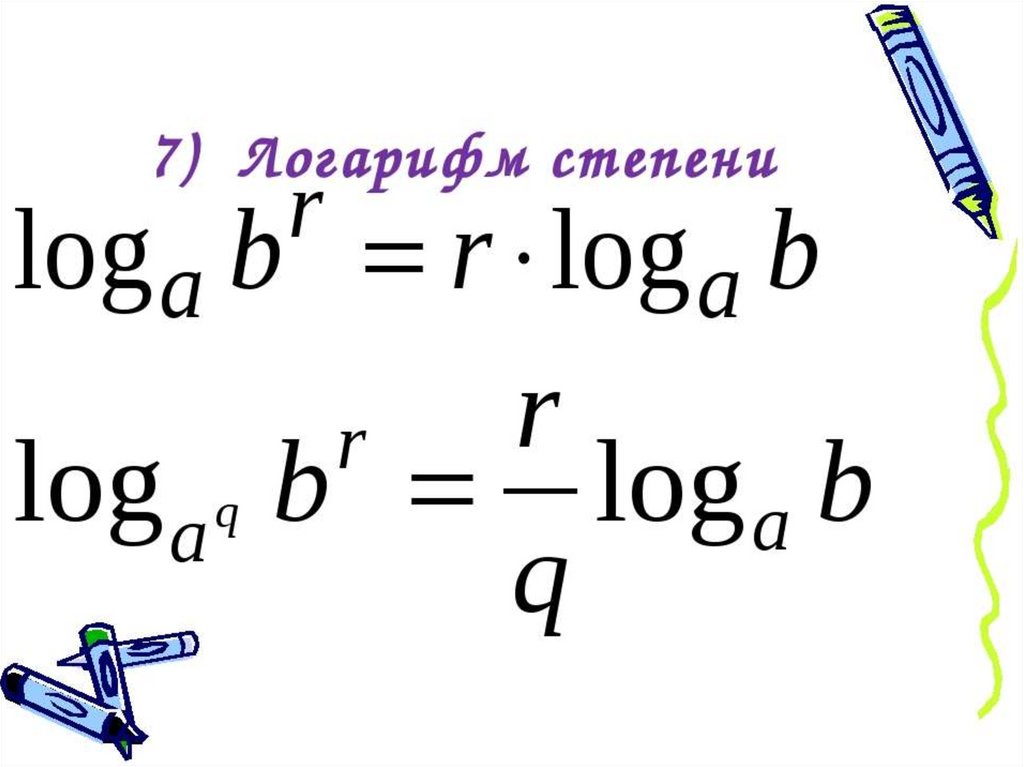 Она состоит из трех шагов:
Она состоит из трех шагов:
- Представить основание a и аргумент x в виде степени с минимально возможным основанием, большим единицы. Попутно лучше избавиться от десятичных дробей;
- Решить относительно переменной b уравнение: x = a b ;
- Полученное число b будет ответом.
Вот и все! Если логарифм окажется иррациональным, это будет видно уже на первом шаге. Требование, чтобы основание было больше единицы, весьма актуально: это снижает вероятность ошибки и значительно упрощает выкладки. Аналогично с десятичными дробями: если сразу перевести их в обычные, ошибок будет в разы меньше.
Посмотрим, как работает эта схема на конкретных примерах:
Задача. Вычислите логарифм: log 5 25
- Представим основание и аргумент как степень пятерки: 5 = 5 1 ; 25 = 5 2 ;
- Получили ответ: 2.
Составим и решим уравнение:
log 5 25 = b
⇒ (5 1) b
= 5 2 ⇒ 5 b
= 5 2 ⇒ b
= 2 ;
Задача.
Вычислите логарифм:
Задача. Вычислите логарифм: log 4 64
- Представим основание и аргумент как степень двойки: 4 = 2 2 ; 64 = 2 6 ;
- Составим и решим уравнение:
log 4 64 = b ⇒ (2 2) b = 2 6 ⇒ 2 2b = 2 6 ⇒ 2b = 6 ⇒ b = 3 ; - Получили ответ: 3.
Задача. Вычислите логарифм: log 16 1
- Представим основание и аргумент как степень двойки: 16 = 2 4 ; 1 = 2 0 ;
- Составим и решим уравнение:
log 16 1 = b ⇒ (2 4) b = 2 0 ⇒ 2 4b = 2 0 ⇒ 4b = 0 ⇒ b = 0 ; - Получили ответ: 0.
Задача. Вычислите логарифм: log 7 14
- Представим основание и аргумент как степень семерки: 7 = 7 1 ; 14 в виде степени семерки не представляется, поскольку 7 1
- Из предыдущего пункта следует, что логарифм не считается;
- Ответ — без изменений: log 7 14.
Небольшое замечание к последнему примеру. Как убедиться, что число не является точной степенью другого числа? Очень просто — достаточно разложить его на простые множители. Если в разложении есть хотя бы два различных множителя, число не является точной степенью.
Если в разложении есть хотя бы два различных множителя, число не является точной степенью.
Задача. Выясните, являются ли точными степенями числа: 8; 48; 81; 35; 14 .
8 = 2 · 2 · 2 = 2 3 — точная степень, т.к. множитель всего один;
48 = 6 · 8 = 3 · 2 · 2 · 2 · 2 = 3 · 2 4 — не является точной степенью, поскольку есть два множителя: 3 и 2;
81 = 9 · 9 = 3 · 3 · 3 · 3 = 3 4 — точная степень;
35 = 7 · 5 — снова не является точной степенью;
14 = 7 · 2 — опять не точная степень;
Заметим также, что сами простые числа всегда являются точными степенями самих себя.
Десятичный логарифм
Некоторые логарифмы встречаются настолько часто, что имеют специальное название и обозначение.
Десятичный логарифм от аргумента x — это логарифм по основанию 10, т.е. степень, в которую надо возвести число 10, чтобы получить число x . Обозначение: lg x .
Например, lg 10 = 1; lg 100 = 2; lg 1000 = 3 — и т. д.
д.
Отныне, когда в учебнике встречается фраза типа «Найдите lg 0,01», знайте: это не опечатка. Это десятичный логарифм. Впрочем, если вам непривычно такое обозначение, его всегда можно переписать:
lg x
= log 10 x
Все, что верно для обычных логарифмов, верно и для десятичных.
Натуральный логарифм
Существует еще один логарифм, который имеет собственное обозначение. В некотором смысле, он даже более важен, чем десятичный. Речь идет о натуральном логарифме.
Натуральный логарифм от аргумента x — это логарифм по основанию e , т.е. степень, в которую надо возвести число e , чтобы получить число x . Обозначение: ln x .
Многие спросят: что еще за число e
? Это иррациональное число, его точное значение найти и записать невозможно. Приведу лишь первые его цифры:
e
= 2,718281828459…
Не будем углубляться, что это за число и зачем нужно. Просто помните, что e
— основание натурального логарифма:
ln x
= log e
x
Таким образом, ln e
= 1 ; ln e
2 = 2 ; ln e
16 = 16 — и т. д. С другой стороны, ln 2 — иррациональное число. Вообще, натуральный логарифм любого рационального числа иррационален. Кроме, разумеется, единицы: ln 1 = 0.
д. С другой стороны, ln 2 — иррациональное число. Вообще, натуральный логарифм любого рационального числа иррационален. Кроме, разумеется, единицы: ln 1 = 0.
Для натуральных логарифмов справедливы все правила, которые верны для обычных логарифмов.
Натуральный логарифм
График функции натурального логарифма. Функция медленно приближается к положительной бесконечности при увеличении x и быстро приближается к отрицательной бесконечности, когда x стремится к 0 («медленно» и «быстро» по сравнению с любой степенной функцией от x ).
Натуральный логарифм — это логарифм по основанию , где e — иррациональная константа, равная приблизительно 2,718281 828 . Натуральный логарифм обычно обозначают как ln(x ), log e (x ) или иногда просто log(x ), если основание e подразумевается.
Натуральный логарифм числа x (записывается как ln(x) ) — это показатель степени , в которую нужно возвести число e , чтобы получить x . Например, ln(7,389…) равен 2, потому что e 2 =7,389… . Натуральный логарифм самого числа e (ln(e) ) равен 1, потому что e 1 = e , а натуральный логарифм 1 (ln(1) ) равен 0, поскольку e 0 = 1.
Например, ln(7,389…) равен 2, потому что e 2 =7,389… . Натуральный логарифм самого числа e (ln(e) ) равен 1, потому что e 1 = e , а натуральный логарифм 1 (ln(1) ) равен 0, поскольку e 0 = 1.
Натуральный логарифм может быть определён для любого положительного вещественного числа a как площадь под кривой y = 1/x от 1 до a . Простота этого определения, которое согласуется со многими другими формулами, в которых применяется натуральный логарифм, привела к появлению названия «натуральный». Это определение можно расширить на комплексные числа , о чём будет сказано ниже.
Если рассматривать натуральный логарифм как вещественную функцию действительной переменной, то она является обратной функцией к экспоненциальной функции, что приводит к тождествам:
Подобно всем логарифмам, натуральный логарифм отображает умножение в сложение:
Таким образом, логарифмическая функция представляет собой изоморфизм группы положительных действительных чисел относительно умножения на группу вещественных чисел по сложению, который можно представить в виде функции :
Логарифм может быть определён для любого положительного основания, отличного от 1, а не только для e , но логарифмы для других оснований отличаются от натурального логарифма только постоянным множителем, и, как правило, определяются в терминах натурального логарифма. Логарифмы полезны для решения уравнений, в которых неизвестные присутствуют в качестве показателя степени. Например, логарифмы используются для нахождения постоянной распада для известного периода полураспада, или для нахождения времени распада в решении проблем радиоактивности . Они играют важную роль во многих областях математики и прикладных наук, применяются в сфере финансов для решения многих задач, включая нахождение сложных процентов.
Логарифмы полезны для решения уравнений, в которых неизвестные присутствуют в качестве показателя степени. Например, логарифмы используются для нахождения постоянной распада для известного периода полураспада, или для нахождения времени распада в решении проблем радиоактивности . Они играют важную роль во многих областях математики и прикладных наук, применяются в сфере финансов для решения многих задач, включая нахождение сложных процентов.
История
Первое упоминание натурального логарифма сделал Николас Меркатор в работе Logarithmotechnia , опубликованной в 1668 году , хотя учитель математики Джон Спайделл ещё в 1619 году составил таблицу натуральных логарифмов. Ранее его называли гиперболическим логарифмом, поскольку он соответствует площади под гиперболой. Иногда его называют логарифмом Непера, хотя первоначальный смысл этого термина был несколько другой.
Конвенции об обозначениях
Натуральный логарифм принято обозначать через «ln(x )», логарифм по основанию 10 — через «lg(x )», а прочие основания принято указывать явно при символе «log».
Во многих работах по дискретной математике, кибернетике, информатике авторы используют обозначение «log(x )» для логарифмов по основанию 2, но это соглашение не является общепринятым и требует разъяснения либо в списке использованных обозначений, либо (при отсутствии такого списка) сноской или комментарием при первом использовании.
Скобки вокруг аргумента логарифмов (если это не приводит к ошибочному чтению формулы) обычно опускают, а при возведении логарифма в степень показатель приписывают непосредственно к знаку логарифма: ln 2 ln 3 4x 5 = [ ln( 3 )] 2 .
Англо-американская система
Математики, статистики и часть инженеров обычно используют для обозначения натурального логарифма либо «log(x )», либо «ln(x )» , а для обозначения логарифма по основанию 10 — «log 10 (x )».
Некоторые инженеры, биологи и другие специалисты всегда пишут «ln(x )» (или изредка «log e (x )»), когда они имеют в виду натуральный логарифм, а запись «log(x )» у них означает log 10 (x ).
log e является «натуральным» логарифмом, поскольку он возникает автоматически и появляется в математике очень часто. Например, рассмотрим проблему производной логарифмической функции:
Если основание b равно e , то производная равна просто 1/x , а при x = 1 эта производная равна 1. Другим обоснованием, по которому основание e логарифма является наиболее натуральным, является то, что он может быть довольно просто определён в терминах простого интеграла или ряда Тейлора , чего нельзя сказать о других логарифмах.
Дальнейшие обоснования натуральности не связаны со счислением. Так, например, есть несколько простых рядов с натуральными логарифмами. Пьетро Менголи и Николай Меркатор называли их логарифмус натуралис несколько десятилетий до тех пор, пока Ньютон и Лейбниц не разработали дифференциальное и интегральное исчисление.
Определение
Формально ln(a ) может быть определён как площадь под кривой графика 1/x от 1 до a , т. е. как интеграл :
е. как интеграл :
Это действительно логарифм, поскольку он удовлетворяет фундаментальному свойству логарифма:
Это можно продемонстрировать, допуская следующим образом:
Численное значение
Для расчета численного значения натурального логарифма числа можно использовать разложение его в ряд Тейлора в виде:
Чтобы получить лучшую скорость сходимости, можно воспользоваться следующим тождеством:
при условии, что y = (x −1)/(x +1) и x > 0.
Для ln(x ), где x > 1, чем ближе значение x к 1, тем быстрее скорость сходимости. Тождества, связанные с логарифмом, можно использовать для достижения цели:
Эти методы применялись ещё до появления калькуляторов, для чего использовались числовые таблицы и выполнялись манипуляции, аналогичные вышеописанным.
Высокая точность
Для вычисления натурального логарифма с большим количеством цифр точности ряд Тейлора не является эффективным, поскольку его сходимость медленная. Альтернативой является использование метода Ньютона , чтобы инвертировать в экспоненциальную функцию, ряд которой сходится быстрее.
Альтернативой является использование метода Ньютона , чтобы инвертировать в экспоненциальную функцию, ряд которой сходится быстрее.
Альтернативой для очень высокой точности расчёта является формула:
где M обозначает арифметико-геометрическое среднее 1 и 4/s, и
m выбрано так, что p знаков точности достигается. (В большинстве случаев значение 8 для m вполне достаточно.) В самом деле, если используется этот метод, может быть применена инверсия Ньютона натурального логарифма для эффективного вычисления экспоненциальной функции. (Константы ln 2 и пи могут быть предварительно вычислены до желаемой точности, используя любой из известных быстро сходящихся рядов.)
Вычислительная сложность
Вычислительная сложность натуральных логарифмов (с помощью арифметико-геометрического среднего) равна O(M (n ) ln n ). Здесь n — число цифр точности, для которой натуральный логарифм должен быть оценен, а M (n ) — вычислительная сложность умножения двух n -значных чисел.
Непрерывные дроби
Хотя для представления логарифма отсутствуют простые непрерывные дроби , но можно использовать несколько обобщённых непрерывных дробей, в том числе:
Комплексные логарифмы
Экспоненциальная функция может быть расширена до функции, которая даёт комплексное число вида e x для любого произвольного комплексного числа x , при этом используется бесконечный ряд с комплексным x . Эта показательная функция может быть инвертирована с образованием комплексного логарифма, который будет обладать большей частью свойств обычных логарифмов. Есть, однако, две трудности: не существует x , для которого e x = 0, и оказывается, что e 2πi = 1 = e 0 . Поскольку свойство мультипликативности действительно для комплексной экспоненциальной функции, то e z = e z +2nπi для всех комплексных z и целых n .
Логарифм не может быть определён на всей комплексной плоскости , и даже при этом он является многозначным — любой комплексный логарифм может быть заменён на «эквивалентный» логарифм, добавив любое целое число, кратное 2πi .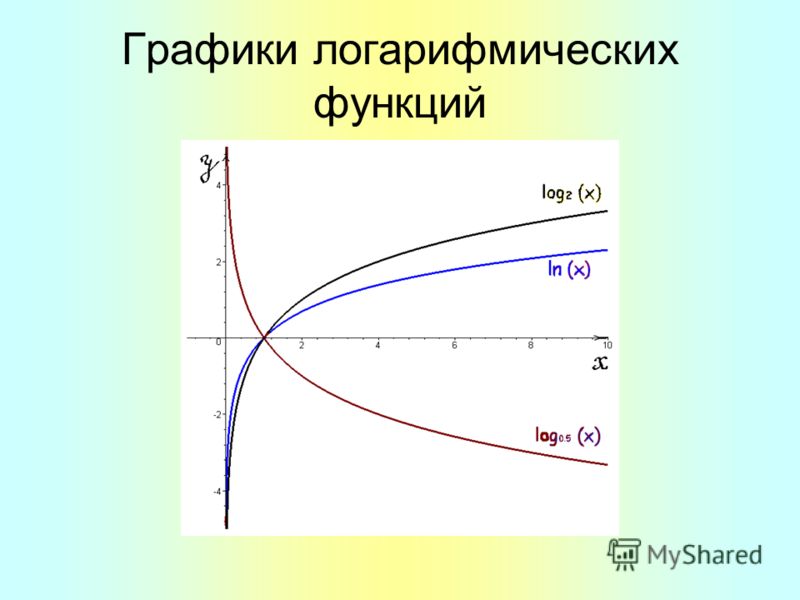 Комплексный логарифм может быть однозначным только на срезе комплексной плоскости. Например, ln i = 1/2 πi или 5/2 πi или −3/2 πi , и т.д., и хотя i 4 = 1, 4 log i может быть определена как 2πi , или 10πi или −6 πi , и так далее.
Комплексный логарифм может быть однозначным только на срезе комплексной плоскости. Например, ln i = 1/2 πi или 5/2 πi или −3/2 πi , и т.д., и хотя i 4 = 1, 4 log i может быть определена как 2πi , или 10πi или −6 πi , и так далее.
См. также
- Джон Непер — изобретатель логарифмов
Примечания
- Mathematics for physical chemistry . — 3rd. — Academic Press, 2005. — P. 9. — ISBN 0-125-08347-5 , Extract of page 9
- J J O»Connor and E F Robertson The number e . The MacTutor History of Mathematics archive (сентябрь 2001). Архивировано
- Cajori Florian A History of Mathematics, 5th ed . — AMS Bookstore, 1991. — P. 152. — ISBN 0821821024
- Flashman, Martin Estimating Integrals using Polynomials . Архивировано из первоисточника 12 февраля 2012.
Чему равен ln. Разбираемся с натуральным логарифмом
Что такое логарифм?
Внимание!
К этой теме имеются дополнительные
материалы в Особом разделе 555.
Для тех, кто сильно «не очень…»
И для тех, кто «очень даже…»)
Что такое логарифм? Как решать логарифмы? Эти вопросы многих выпускников вводят в ступор. Традиционно тема логарифмов считается сложной, непонятной и страшной. Особенно — уравнения с логарифмами.
Это абсолютно не так. Абсолютно! Не верите? Хорошо. Сейчас, за какие-то 10 — 20 минут вы:
1. Поймете, что такое логарифм .
2. Научитесь решать целый класс показательных уравнений. Даже если ничего о них не слышали.
3. Научитесь вычислять простые логарифмы.
Причём для этого вам нужно будет знать только таблицу умножения, да как возводится число в степень…
Чувствую, сомневаетесь вы… Ну ладно, засекайте время! Поехали!
Для начала решите в уме вот такое уравнение:
Если Вам нравится этот сайт…Кстати, у меня есть ещё парочка интересных сайтов для Вас.)
Можно потренироваться в решении примеров и узнать свой уровень. Тестирование с мгновенной проверкой. Учимся — с интересом!)
Тестирование с мгновенной проверкой. Учимся — с интересом!)
можно познакомиться с функциями и производными.
1.1. Определение степени для целого показателя степени
X 1 = X
X 2 = X * X
X 3 = X * X * X
…
X N = X * X * … * X — N раз
1.2. Нулевая степень.
По определению принято считать, что нулевая степень любого числа равна 1:
1.3. Отрицательная степень.
X -N = 1/X N
1.4. Дробная степень, корень.
X 1/N = корень степени N из Х.
Например: X 1/2 = √X.
1.5. Формула сложения степеней.
X (N+M) = X N *X M
1.6.Формула вычитания степеней.
X (N-M) = X N /X M
1.7. Формула умножения степеней.
X N*M = (X N) M
1.8. Формула возведения дроби в степень.

(X/Y) N = X N /Y N
2. Число e.
Значение числа e равно следующему пределу:
E = lim(1+1/N), при N → ∞.
С точностью 17 знаков число e равно 2.71828182845904512.
3. Равенство Эйлера.
Это равенство связывает пять чисел, играющих особую роль в математике: 0, 1, число e, число пи, мнимую единицу.
E (i*пи) + 1 = 0
4. Экспоненциальная функция exp (x)
exp(x) = e x
5. Производная экспоненциальной функции
Экспоненциальная функция обладает замечательным свойством: производная функции равна самой экспоненциальной функции:
(exp(x))» = exp(x)
6. Логарифм.
6.1. Определение функции логарифм
Если x = b y , то логарифмом называется функция
Y = Log b (x).
Логарифм показывает в какую степень надо возвести число — основание логарифма (b), чтобы
получить заданное число (X). Функция логарифм определена для X больше нуля.
Функция логарифм определена для X больше нуля.
Например: Log 10 (100) = 2.
6.2. Десятичный логарифм
Это логарифм по основанию 10:
Y = Log 10 (x) .
Обозначается Log(x): Log(x) = Log 10 (x).
Пример использования десятичного логарифма — децибел .
6.3. Децибел
Пункт выделен в отдельную страницу Децибел
6.4. Двоичный логарифм
Это логарифм по основанию 2:
Y = Log 2 (x).
Обозначается Lg(x): Lg(x) = Log 2 (X)
6.5. Натуральный логарифм
Это логарифм по основанию e:
Y = Log e (x) .
Обозначается Ln(x): Ln(x) = Log e (X)
Натуральный логарифм — обратная функция к экспоненциальной функции exp (X).
6.6. Характерные точки
Log a (1) = 0
Log a (a) = 1
6.7. Формула логарифма произведения
Log a (x*y) = Log a (x)+Log a (y)
6.
 8. Формула логарифма частного
8. Формула логарифма частногоLog a (x/y) = Log a (x)-Log a (y)
6.9. Формула логарифма степени
Log a (x y) = y*Log a (x)
6.10. Формула преобразования к логарифму с другим основанием
Log b (x) = (Log a (x))/Log a (b)
Пример:
Log 2 (8) = Log 10 (8)/Log 10 (2) =
0.903089986991943552 / 0.301029995663981184 = 3
7. Формулы полезные в жизни
Часто возникают задачи пересчета объема в площадь или в длину и обратная задача — пересчет площади в объем. Например, доски продаются кубами (кубометрами), а нам требуется рассчитать какую площадь стены можно обшить досками содержащимися в определенном объеме, см. расчет досок, сколько досок в кубе . Или, известны размеры стены, надо рассчитать число кирпичей, см. расчет кирпича .
Разрешается использовать материалы сайта при условии установки активной ссылки на источник.
Итак, перед нами степени двойки. Если взять число из нижней строчки, то можно легко найти степень, в которую придется возвести двойку, чтобы получилось это число. Например, чтобы получить 16, надо два возвести в четвертую степень. А чтобы получить 64, надо два возвести в шестую степень. Это видно из таблицы.
Если взять число из нижней строчки, то можно легко найти степень, в которую придется возвести двойку, чтобы получилось это число. Например, чтобы получить 16, надо два возвести в четвертую степень. А чтобы получить 64, надо два возвести в шестую степень. Это видно из таблицы.
А теперь — собственно, определение логарифма:
Логарифм по основанию a от аргумента x — это степень, в которую надо возвести число a , чтобы получить число x .
Обозначение: log a x = b , где a — основание, x — аргумент, b — собственно, чему равен логарифм.
Например, 2 3 = 8 ⇒ log 2 8 = 3 (логарифм по основанию 2 от числа 8 равен трем, поскольку 2 3 = 8). С тем же успехом log 2 64 = 6 , поскольку 2 6 = 64 .
Операцию нахождения логарифма числа по заданному основанию называют логарифмированием. Итак, дополним нашу таблицу новой строкой:
| 2 1 | 2 2 | 2 3 | 2 4 | 2 5 | 2 6 |
| 2 | 4 | 8 | 16 | 32 | 64 |
| log 2 2 = 1 | log 2 4 = 2 | log 2 8 = 3 | log 2 16 = 4 | log 2 32 = 5 | log 2 64 = 6 |
К сожалению, далеко не все логарифмы считаются так легко. Например, попробуйте найти log 2 5 . Числа 5 нет в таблице, но логика подсказывает, что логарифм будет лежать где-то на отрезке . Потому что 2 2 больше степень двойки, тем больше получится число.
Например, попробуйте найти log 2 5 . Числа 5 нет в таблице, но логика подсказывает, что логарифм будет лежать где-то на отрезке . Потому что 2 2 больше степень двойки, тем больше получится число.
Такие числа называются иррациональными: цифры после запятой можно писать до бесконечности, и они никогда не повторяются. Если логарифм получается иррациональным, его лучше так и оставить: log 2 5 , log 3 8 , log 5 100 .
Важно понимать, что логарифм — это выражение с двумя переменными (основание и аргумент). Многие на первых порах путают, где находится основание, а где — аргумент. Чтобы избежать досадных недоразумений, просто взгляните на картинку:
Перед нами — не что иное как определение логарифма. Вспомните: логарифм — это степень , в которую надо возвести основание, чтобы получить аргумент. Именно основание возводится в степень — на картинке оно выделено красным. Получается, что основание всегда находится внизу! Это замечательное правило я рассказываю своим ученикам на первом же занятии — и никакой путаницы не возникает.
С определением разобрались — осталось научиться считать логарифмы, т.е. избавляться от знака «log». Для начала отметим, что из определения следует два важных факта:
- Аргумент и основание всегда должны быть больше нуля. Это следует из определения степени рациональным показателем, к которому сводится определение логарифма.
- Основание должно быть отличным от единицы, поскольку единица в любой степени все равно остается единицей. Из-за этого вопрос «в какую степень надо возвести единицу, чтобы получить двойку» лишен смысла. Нет такой степени!
Такие ограничения называются областью допустимых значений (ОДЗ). Получается, что ОДЗ логарифма выглядит так: log a x = b ⇒ x > 0 , a > 0 , a ≠ 1 .
Заметьте, что никаких ограничений на число b (значение логарифма) не накладывается. Например, логарифм вполне может быть отрицательным: log 2 0,5 = −1 , т.к. 0,5 = 2 −1 .
Впрочем, сейчас мы рассматриваем лишь числовые выражения, где знать ОДЗ логарифма не требуется. Все ограничения уже учтены составителями задач. Но когда пойдут логарифмические уравнения и неравенства, требования ОДЗ станут обязательными. Ведь в основании и аргументе могут стоять весьма неслабые конструкции, которые совсем необязательно соответствуют приведенным выше ограничениям.
Все ограничения уже учтены составителями задач. Но когда пойдут логарифмические уравнения и неравенства, требования ОДЗ станут обязательными. Ведь в основании и аргументе могут стоять весьма неслабые конструкции, которые совсем необязательно соответствуют приведенным выше ограничениям.
Теперь рассмотрим общую схему вычисления логарифмов. Она состоит из трех шагов:
- Представить основание a и аргумент x в виде степени с минимально возможным основанием, большим единицы. Попутно лучше избавиться от десятичных дробей;
- Решить относительно переменной b уравнение: x = a b ;
- Полученное число b будет ответом.
Вот и все! Если логарифм окажется иррациональным, это будет видно уже на первом шаге. Требование, чтобы основание было больше единицы, весьма актуально: это снижает вероятность ошибки и значительно упрощает выкладки. Аналогично с десятичными дробями: если сразу перевести их в обычные, ошибок будет в разы меньше.
Посмотрим, как работает эта схема на конкретных примерах:
Задача.
Вычислите логарифм: log 5 25
- Представим основание и аргумент как степень пятерки: 5 = 5 1 ; 25 = 5 2 ;
- Получили ответ: 2.
Составим и решим уравнение:
log 5 25 = b
⇒ (5 1) b
= 5 2 ⇒ 5 b
= 5 2 ⇒ b
= 2 ;
Задача. Вычислите логарифм:
Задача. Вычислите логарифм: log 4 64
- Представим основание и аргумент как степень двойки: 4 = 2 2 ; 64 = 2 6 ;
- Составим и решим уравнение:
log 4 64 = b ⇒ (2 2) b = 2 6 ⇒ 2 2b = 2 6 ⇒ 2b = 6 ⇒ b = 3 ; - Получили ответ: 3.
Задача. Вычислите логарифм: log 16 1
- Представим основание и аргумент как степень двойки: 16 = 2 4 ; 1 = 2 0 ;
- Составим и решим уравнение:
log 16 1 = b ⇒ (2 4) b = 2 0 ⇒ 2 4b = 2 0 ⇒ 4b = 0 ⇒ b = 0 ; - Получили ответ: 0.
Задача. Вычислите логарифм: log 7 14
- Представим основание и аргумент как степень семерки: 7 = 7 1 ; 14 в виде степени семерки не представляется, поскольку 7 1
- Из предыдущего пункта следует, что логарифм не считается;
- Ответ — без изменений: log 7 14.

Небольшое замечание к последнему примеру. Как убедиться, что число не является точной степенью другого числа? Очень просто — достаточно разложить его на простые множители. Если в разложении есть хотя бы два различных множителя, число не является точной степенью.
Задача. Выясните, являются ли точными степенями числа: 8; 48; 81; 35; 14 .
8 = 2 · 2 · 2 = 2 3 — точная степень, т.к. множитель всего один;
48 = 6 · 8 = 3 · 2 · 2 · 2 · 2 = 3 · 2 4 — не является точной степенью, поскольку есть два множителя: 3 и 2;
81 = 9 · 9 = 3 · 3 · 3 · 3 = 3 4 — точная степень;
35 = 7 · 5 — снова не является точной степенью;
14 = 7 · 2 — опять не точная степень;
Заметим также, что сами простые числа всегда являются точными степенями самих себя.
Десятичный логарифм
Некоторые логарифмы встречаются настолько часто, что имеют специальное название и обозначение.
Десятичный логарифм от аргумента x — это логарифм по основанию 10, т.
е. степень, в которую надо возвести число 10, чтобы получить число x . Обозначение: lg x .
Например, lg 10 = 1; lg 100 = 2; lg 1000 = 3 — и т.д.
Отныне, когда в учебнике встречается фраза типа «Найдите lg 0,01», знайте: это не опечатка. Это десятичный логарифм. Впрочем, если вам непривычно такое обозначение, его всегда можно переписать:
lg x
= log 10 x
Все, что верно для обычных логарифмов, верно и для десятичных.
Натуральный логарифм
Существует еще один логарифм, который имеет собственное обозначение. В некотором смысле, он даже более важен, чем десятичный. Речь идет о натуральном логарифме.
Натуральный логарифм от аргумента x — это логарифм по основанию e , т.е. степень, в которую надо возвести число e , чтобы получить число x . Обозначение: ln x .
Многие спросят: что еще за число e
? Это иррациональное число, его точное значение найти и записать невозможно. Приведу лишь первые его цифры:
e
= 2,718281828459..jpg) ..
..
Не будем углубляться, что это за число и зачем нужно. Просто помните, что e
— основание натурального логарифма:
ln x
= log e
x
Таким образом, ln e = 1 ; ln e 2 = 2 ; ln e 16 = 16 — и т.д. С другой стороны, ln 2 — иррациональное число. Вообще, натуральный логарифм любого рационального числа иррационален. Кроме, разумеется, единицы: ln 1 = 0.
Для натуральных логарифмов справедливы все правила, которые верны для обычных логарифмов.
Как известно, при перемножении выражений со степенями их показатели всегда складываются (a b *a c = a b+c). Этот математический закон был выведен Архимедом, а позже, в VIII веке, математик Вирасен создал таблицу целых показателей. Именно они послужили для дальнейшего открытия логарифмов. Примеры использования этой функции можно встретить практически везде, где требуется упростить громоздкое умножение на простое сложение. Если вы потратите минут 10 на прочтение этой статьи, мы вам объясним, что такое логарифмы и как с ними работать. Простым и доступным языком.
Простым и доступным языком.
Определение в математике
Логарифмом называется выражение следующего вида: log a b=c, то есть логарифмом любого неотрицательного числа (то есть любого положительного) «b» по его основанию «a» считается степень «c», в которую необходимо возвести основание «a», чтобы в итоге получить значение «b». Разберем логарифм на примерах, допустим, есть выражение log 2 8. Как найти ответ? Очень просто, нужно найти такую степень, чтобы из 2 в искомой степени получить 8. Проделав в уме некоторые расчеты, получаем число 3! И верно, ведь 2 в степени 3 дает в ответе число 8.
Разновидности логарифмов
Для многих учеников и студентов эта тема кажется сложной и непонятной, однако на самом деле логарифмы не так страшны, главное — понять общий их смысл и запомнить их свойста и некоторые правила. Существует три отдельных вида логарифмических выражений:
- Натуральный логарифм ln a, где основанием является число Эйлера (e = 2,7).
- Десятичный a, где основанием служит число 10.

- Логарифм любого числа b по основанию a>1.
Каждый из них решается стандартным способом, включающим в себя упрощение, сокращение и последующее приведение к одному логарифму с помощью логарифмических теорем. Для получения верных значений логарифмов следует запомнить их свойства и очередность действий при их решениях.
Правила и некоторые ограничения
В математике существует несколько правил-ограничений, которые принимаются как аксиома, то есть не подлежат обсуждению и являются истиной. Например, нельзя числа делить на ноль, а еще невозможно извлечь корень четной степени из отрицательных чисел. Логарифмы также имеют свои правила, следуя которым можно с легкостью научиться работать даже с длинными и емкими логарифмическими выражениями:
- основание «a» всегда должно быть больше нуля, и при этом не быть равным 1, иначе выражение потеряет свой смысл, ведь «1» и «0» в любой степени всегда равны своим значениям;
- если а > 0, то и а b >0, получается, что и «с» должно быть больше нуля.

Как решать логарифмы?
К примеру, дано задание найти ответ уравнения 10 х = 100. Это очень легко, нужно подобрать такую степень, возведя в которую число десять, мы получим 100. Это, конечно же, 10 2 =100.
А теперь давайте представим данное выражение в виде логарифмического. Получим log 10 100 = 2. При решении логарифмов все действия практически сходятся к тому, чтобы найти ту степень, в которую необходимо ввести основание логарифма, чтобы получить заданное число.
Для безошибочного определения значенияя неизвестной степени необходимо научиться работать с таблицей степеней. Выглядит она следующим образом:
Как видите, некоторые показатели степени можно угадать интуитивно, если имеется технический склад ума и знание таблицы умножения. Однако для больших значений потребуется таблица степеней. Ею могут пользоваться даже те, кто совсем ничего не смыслит в сложных математических темах. В левом столбце указаны числа (основание a), верхний ряд чисел — это значение степени c, в которую возводится число a. На пересечении в ячейках определены значения чисел, являющиеся ответом (a c =b). Возьмем, к примеру, самую первую ячейку с числом 10 и возведем ее в квадрат, получим значение 100, которое указано на пересечении двух наших ячеек. Все так просто и легко, что поймет даже самый настоящий гуманитарий!
На пересечении в ячейках определены значения чисел, являющиеся ответом (a c =b). Возьмем, к примеру, самую первую ячейку с числом 10 и возведем ее в квадрат, получим значение 100, которое указано на пересечении двух наших ячеек. Все так просто и легко, что поймет даже самый настоящий гуманитарий!
Уравнения и неравенства
Получается, что при определенных условиях показатель степени — это и есть логарифм. Следовательно, любые математические численные выражения можно записать в виде логарифмического равенства. Например, 3 4 =81 можно записать в виде логарифма числа 81 по основанию 3, равному четырем (log 3 81 = 4). Для отрицательных степеней правила такие же: 2 -5 = 1/32 запишем в виде логарифма, получим log 2 (1/32) = -5. Одной из самых увлекательных разделов математики является тема «логарифмы». Примеры и решения уравнений мы рассмотрим чуть ниже, сразу же после изучения их свойств. А сейчас давайте разберем, как выглядят неравенства и как их отличить от уравнений.
Дано выражение следующего вида: log 2 (x-1) > 3 — оно является логарифмическим неравенством, так как неизвестное значение «х» находится под знаком логарифма. А также в выражении сравниваются две величины: логарифм искомого числа по основанию два больше, чем число три.
А также в выражении сравниваются две величины: логарифм искомого числа по основанию два больше, чем число три.
Самое главное отличие между логарифмическими уравнениями и неравенствами заключается в том, что уравнения с логарифмами (пример — логарифм 2 x = √9) подразумевают в ответе одно или несколько определенных числовых значений, тогда как при решении неравенства определяются как область допустимых значений, так и точки разрыва этой функции. Как следствие, в ответе получается не простое множество отдельных чисел как в ответе уравнения, а а непрерывный ряд или набор чисел.
Основные теоремы о логарифмах
При решении примитивных заданий по нахождению значений логарифма, его свойства можно и не знать. Однако когда речь заходит о логарифмических уравнениях или неравенствах, в первую очередь, необходимо четко понимать и применять на практике все основные свойства логарифмов. С примерами уравнений мы познакомимся позже, давайте сначала разберем каждое свойство более подробно.
- Основное тождество выглядит так: а logaB =B. Оно применяется только при условии, когда а больше 0, не равно единице и B больше нуля.
- Логарифм произведения можно представить в следующей формуле: log d (s 1 *s 2) = log d s 1 + log d s 2. При этом обязательным условием является: d, s 1 и s 2 > 0; а≠1. Можно привести доказательство для этой формулы логарифмов, с примерами и решением. Пусть log a s 1 = f 1 и log a s 2 = f 2 , тогда a f1 = s 1 , a f2 = s 2. Получаем, что s 1 *s 2 = a f1 *a f2 = a f1+f2 (свойства степеней), а далее по определению: log a (s 1 *s 2)= f 1 + f 2 = log a s1 + log a s 2, что и требовалось доказать.
- Логарифм частного выглядит так: log a (s 1/ s 2) = log a s 1 — log a s 2.
- Теорема в виде формулы приобретает следующий вид: log a q b n = n/q log a b.
Называется эта формула «свойством степени логарифма». Она напоминает собой свойства обычных степеней, и неудивительно, ведь вся математика держится на закономерных постулатах. Давайте посмотрим на доказательство.
Давайте посмотрим на доказательство.
Пусть log a b = t, получается a t =b. Если возвести обе части в степень m: a tn = b n ;
но так как a tn = (a q) nt/q = b n , следовательно log a q b n = (n*t)/t, тогда log a q b n = n/q log a b. Теорема доказана.
Примеры задач и неравенств
Самые распространенные типы задач на тему логарифмов — примеры уравнений и неравенств. Они встречаются практически во всех задачниках, а также входят в обязательную часть экзаменов по математике. Для поступления в университет или сдачи вступительных испытаний по математике необходимо знать, как правильно решать подобные задания.
К сожалению, единого плана или схемы по решению и определению неизвестного значения логарифма не существует, однако к каждому математическому неравенству или логарифмическому уравнению можно применить определенные правила. Прежде всего следует выяснить, можно ли упростить выражение или привести к общему виду. Упрощать длинные логарифмические выражения можно, если правильно использовать их свойства. Давайте скорее с ними познакомимся.
Давайте скорее с ними познакомимся.
При решении же логарифмических уравнений, следует определить, какой перед нами вид логарифма: пример выражения может содержать натуральный логарифм или же десятичный.
Вот примеры ln100, ln1026. Их решение сводится к тому, что нужно определить ту степень, в которой основание 10 будет равно 100 и 1026 соответственно. Для решений же натуральных логарифмов нужно применить логарифмические тождества или же их свойства. Давайте на примерах рассмотрим решение логарифмических задач разного типа.
Как использовать формулы логарифмов: с примерами и решениями
Итак, рассмотрим примеры использования основных теорем о логарифмах.
- Свойство логарифма произведения можно применять в заданиях, где необходимо разложить большое значение числа b на более простые сомножители. Например, log 2 4 + log 2 128 = log 2 (4*128) = log 2 512. Ответ равен 9.
- log 4 8 = log 2 2 2 3 = 3/2 log 2 2 = 1,5 — как видите, применяя четвертое свойство степени логарифма, удалось решить на первый взгляд сложное и нерешаемое выражение.
 Необходимо всего лишь разложить основание на множители и затем вынести значения степени из знака логарифма.
Необходимо всего лишь разложить основание на множители и затем вынести значения степени из знака логарифма.
Задания из ЕГЭ
Логарифмы часто встречаются на вступительных экзаменах, особенно много логарифмических задач в ЕГЭ (государственный экзамен для всех выпускников школ). Обычно эти задания присутствуют не только в части А (самая легкая тестовая часть экзамена), но и в части С (самые сложные и объемные задания). Экзамен подразумевает точное и идеальное знание темы «Натуральные логарифмы».
Примеры и решения задач взяты из официальных вариантов ЕГЭ. Давайте посмотрим, как решаются такие задания.
Дано log 2 (2x-1) = 4. Решение:
перепишем выражение, немного его упростив log 2 (2x-1) = 2 2 , по определению логарифма получим, что 2x-1 = 2 4 , следовательно 2x = 17; x = 8,5.
- Все логарифмы лучше всего приводить к одному основанию, чтобы решение не было громоздким и запутанным.
- Все выражение, стоящие под знаком логарифма, указываются как положительные, поэтому при вынесении множителем показателя степени выражения, который стоит под знаком логарифма и в качестве его основания, остающееся под логарифмом выражение должно быть положительно.

Логарифмом числа b по основанию а называется показатель степени, в который нужно возвести число а чтобы получить число b.
Если , то .
Логарифм — крайне важная математическая величина , поскольку логарифмическое исчисление позволяет не только решать показательные уравнения, но и оперировать с показателями, дифференцировать показательные и логарифмические функции, интегрировать их и приводить к более приемлемому виду, подлежащему расчету.
Вконтакте
Все свойства логарифмов связаны напрямую со свойствами показательных функций. Например, тот факт, что означает, что:
Следует заметить, что при решении конкретных задач, свойства логарифмов могут оказаться более важными и полезными, чем правила работы со степенями.
Приведем некоторые тождества:
Приведем основные алгебраические выражения:
;
.
Внимание! может существовать только при x>0, x≠1, y>0.
Постараемся разобраться с вопросом, что такое натуральные логарифмы. Отдельный интерес в математике представляют два вида — первый имеет в основании число «10», и носит название «десятичный логарифм». Второй называется натуральным. Основание натурального логарифма — число «е». Именно о нем мы и будем детально говорить в этой статье.
Отдельный интерес в математике представляют два вида — первый имеет в основании число «10», и носит название «десятичный логарифм». Второй называется натуральным. Основание натурального логарифма — число «е». Именно о нем мы и будем детально говорить в этой статье.
Обозначения:
- lg x — десятичный;
- ln x — натуральный.
Используя тождество можно увидеть, что ln e = 1, как и то, что lg 10=1.
График натурального логарифмаПостроим график натурального логарифма стандартным классическим способом по точкам. При желании, проверить правильно ли мы строим функцию, можно при помощи исследования функции. Однако, есть смысл научится строить его «вручную», чтобы знать, как правильно посчитать логарифм.
Функция: y = ln x. Запишем таблицу точек, через которые пройдет график:
Поясним, почему мы выбрали именно такие значения аргумента х. Всё дело в тождестве: . Для натурального логарифма это тождество будет выглядеть таким образом:
Для удобства мы можем взять пять опорных точек:
;
;
.
;
.
Таким образом, подсчет натуральных логарифмов — довольно несложное занятие, более того, он упрощает подсчеты операций со степенями, превращая их в обычное умножение.
Построив по точкам график, получаем приблизительный график:
Область определения натурального логарифма (т.е. все допустимые значения аргумента Х) — все числа больше нуля.
Внимание! В область определения натурального логарифма входят только положительные числа! В область определения не входит х=0. Это невозможно исходя из условий существования логарифма .
Область значений (т.е. все допустимые значения функции y = ln x) — все числа в интервале .
Предел натурального logИзучая график, возникает вопрос — как ведет себя функция при y
Очевидно, что график функции стремится пересечь ось у, но не сможет этого сделать, поскольку натуральный логарифм при х
Предел натурального log можно записать таким образом:
Формула замены основания логарифмаИметь дело с натуральным логарифмом намного проще, чем с логарифмом, имеющим произвольное основание. Именно поэтому попробуем научиться приводить любой логарифм к натуральному, либо выражать его по произвольному основанию через натуральные логарифмы.
Именно поэтому попробуем научиться приводить любой логарифм к натуральному, либо выражать его по произвольному основанию через натуральные логарифмы.
Начнем с логарифмического тождества:
Тогда любое число, либо переменную у можно представить в виде:
где х — любое число (положительное согласно свойствам логарифма).
Данное выражение можно прологарифмировать с обеих сторон. Произведем это при помощи произвольного основания z:
Воспользуемся свойством (только вместо «с» у нас выражение):
Отсюда получаем универсальную формулу:
.
В частности, если z=e, то тогда:
.
Нам удалось представить логарифм по произвольному основанию через отношение двух натуральных логарифмов.
Решаем задачиДля того чтобы лучше ориентироваться в натуральных логарифмах, рассмотрим примеры нескольких задач.
Задача 1 . Необходимо решить уравнение ln x = 3.
Решение: Используя определение логарифма: если , то , получаем:
Задача 2 . Решите уравнение (5 + 3 * ln (x — 3)) = 3.
Решите уравнение (5 + 3 * ln (x — 3)) = 3.
Решение: Используя определение логарифма: если , то , получаем:
.
Еще раз применим определение логарифма:
.
Таким образом:
.
Можно приближенно вычислить ответ, а можно оставить его и в таком виде.
Задача 3. Решите уравнение .
Решение: Произведем подстановку: t = ln x. Тогда уравнение примет следующий вид:
.
Перед нами квадратное уравнение. Найдем его дискриминант:
Первый корень уравнения:
.
Второй корень уравнения:
.
Вспоминая о том, что мы производили подстановку t = ln x, получаем:
В статистике и теории вероятности логарифмические величины встречаются очень часто. Это неудивительно, ведь число е — зачастую отражает темп роста экспоненциальных величин.
В информатике, программировании и теории вычислительных машин, логарифмы встречаются довольно часто, например для того чтобы сохранить в памяти N понадобится битов.
В теориях фракталов и размерностях логарифмы используются постоянно, поскольку размерности фракталов определяются только с их помощью.
В механике и физике нет такого раздела, где не использовались логарифмы. Барометрическое распределение, все принципы статистической термодинамики, уравнение Циолковского и прочее — процессы, которые математически можно описать только при помощи логарифмирования.
В химии логарифмирование используют в уравнениях Нернста, описаниях окислительно-восстановительных процессов.
Поразительно, но даже в музыке, с целью узнать количество частей октавы, используют логарифмы.
Натуральный логарифм Функция y=ln x ее свойства
Доказательство основного свойства натурального логарифма
Натуральный логарифм | это… Что такое Натуральный логарифм?
График функции натурального логарифма. Функция медленно приближается к положительной бесконечности при увеличении x и быстро приближается к отрицательной бесконечности, когда x стремится к 0 («медленно» и «быстро» по сравнению с любой степенной функцией от x).
Натуральный логарифм — это логарифм по основанию e, где e — иррациональная константа, равная приблизительно 2,718281828. Натуральный логарифм обычно обозначают как ln(x), loge(x) или иногда просто log(x), если основание e подразумевается.[1]
Натуральный логарифм числа x (записывается как ln(x)) — это показатель степени, в которую нужно возвести число e, чтобы получить x. Например, ln(7,389…) равен 2, потому что e2=7,389…. Натуральный логарифм самого числа e (ln(e)) равен 1, потому что e1 = e, а натуральный логарифм 1 (ln(1)) равен 0, поскольку e0 = 1.
Натуральный логарифм может быть определён для любого положительного вещественного числа a как площадь под кривой y = 1/x от 1 до a. Простота этого определения, которое согласуется со многими другими формулами, в которых применяется натуральный логарифм, привела к появлению названия «натуральный». Это определение можно расширить на комплексные числа, о чём будет сказано ниже.
Это определение можно расширить на комплексные числа, о чём будет сказано ниже.
Если рассматривать натуральный логарифм как вещественную функцию действительной переменной, то она является обратной функцией к экспоненциальной функции, что приводит к тождествам:
Подобно всем логарифмам, натуральный логарифм отображает умножение в сложение:
Таким образом, логарифмическая функция представляет собой изоморфизм группы положительных действительных чисел относительно умножения на группу вещественных чисел по сложению, который можно представить в виде функции:
Логарифм может быть определён для любого положительного основания, отличного от 1, а не только для e, но логарифмы для других оснований отличаются от натурального логарифма только постоянным множителем, и, как правило, определяются в терминах натурального логарифма. Логарифмы полезны для решения уравнений, в которых неизвестные присутствуют в качестве показателя степени. Например, логарифмы используются для нахождения постоянной распада для известного периода полураспада, или для нахождения времени распада в решении проблем радиоактивности. Они играют важную роль во многих областях математики и прикладных наук, применяются в сфере финансов для решения многих задач, включая нахождение сложных процентов.
Например, логарифмы используются для нахождения постоянной распада для известного периода полураспада, или для нахождения времени распада в решении проблем радиоактивности. Они играют важную роль во многих областях математики и прикладных наук, применяются в сфере финансов для решения многих задач, включая нахождение сложных процентов.
Содержание
|
История
Первое упоминание натурального логарифма сделал Николас Меркатор в работе Logarithmotechnia, опубликованной в 1668 году[2], хотя учитель математики Джон Спайделл ещё в 1619 году составил таблицу натуральных логарифмов. [3] Ранее его называли гиперболическим логарифмом,[4] поскольку он соответствует площади под гиперболой. Иногда его называют логарифмом Непера, хотя первоначальный смысл этого термина был несколько другой.
[3] Ранее его называли гиперболическим логарифмом,[4] поскольку он соответствует площади под гиперболой. Иногда его называют логарифмом Непера, хотя первоначальный смысл этого термина был несколько другой.
Конвенции об обозначениях
Русская (и советская в целом) система
Натуральный логарифм принято обозначать через «ln(x)», логарифм по основанию 10 — через «lg(x)», а прочие основания принято указывать явно при символе «log».
Во многих работах по дискретной математике, кибернетике, информатике авторы используют обозначение «log(x)» для логарифмов по основанию 2, но это соглашение не является общепринятым и требует разъяснения либо в списке использованных обозначений, либо (при отсутствии такого списка) сноской или комментарием при первом использовании.
Скобки вокруг аргумента логарифмов (если это не приводит к ошибочному чтению формулы) обычно опускают, а при возведении логарифма в степень показатель приписывают непосредственно к знаку логарифма: ln2 ln3 4x5 = [ln([ln(4x5)]3)]2.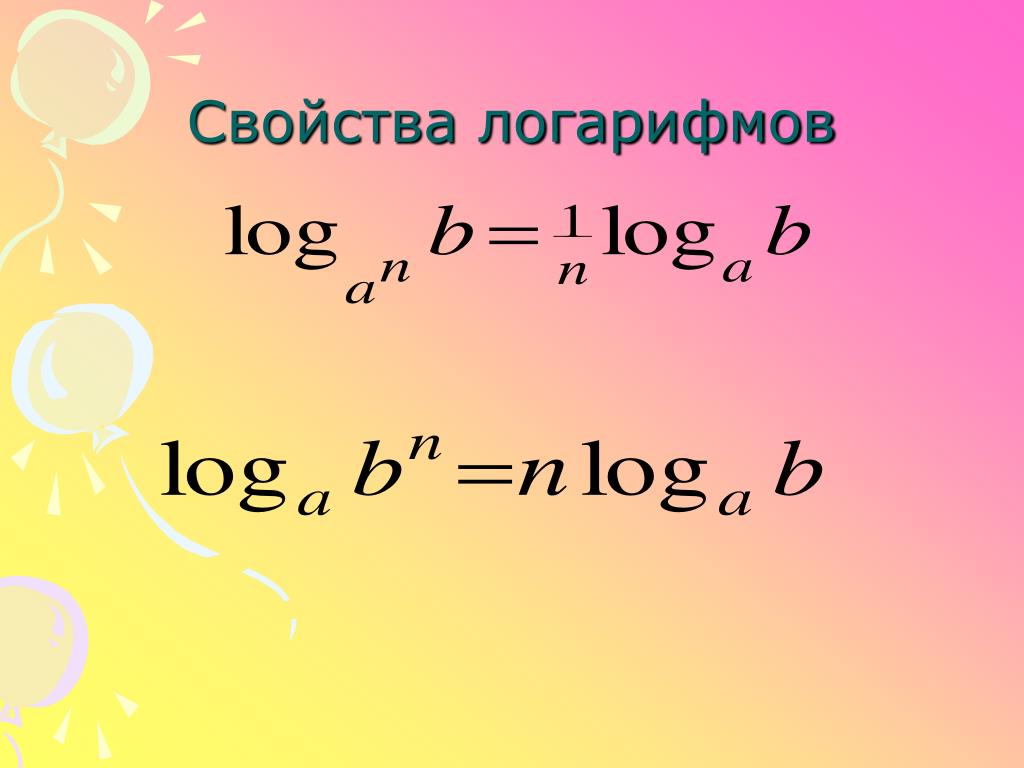
Англо-американская система
Математики, статистики и часть инженеров обычно используют для обозначения натурального логарифма либо «log(x)», либо «ln(x)» , а для обозначения логарифма по основанию 10 — «log10(x)».
Некоторые инженеры, биологи и другие специалисты всегда пишут «ln(x)» (или изредка «loge(x)»), когда они имеют в виду натуральный логарифм, а запись «log(x)» у них означает log10(x).
В теоретической информатике, теории информации и криптографии «log(x)» обычно означает логарифм по основанию 2 «log2(x)» (хотя часто вместо этого пишется просто lg(x)).
Техника
В наиболее часто используемых языках программирования и пакетах прикладных программ, включая C, C++, SAS, MATLAB, Фортран и BASIC функция «log» или «LOG» относится к натуральному логарифму.
В ручных калькуляторах натуральный логарифм обозначается ln, тогда как log служит для обозначения логарифма по основанию 10.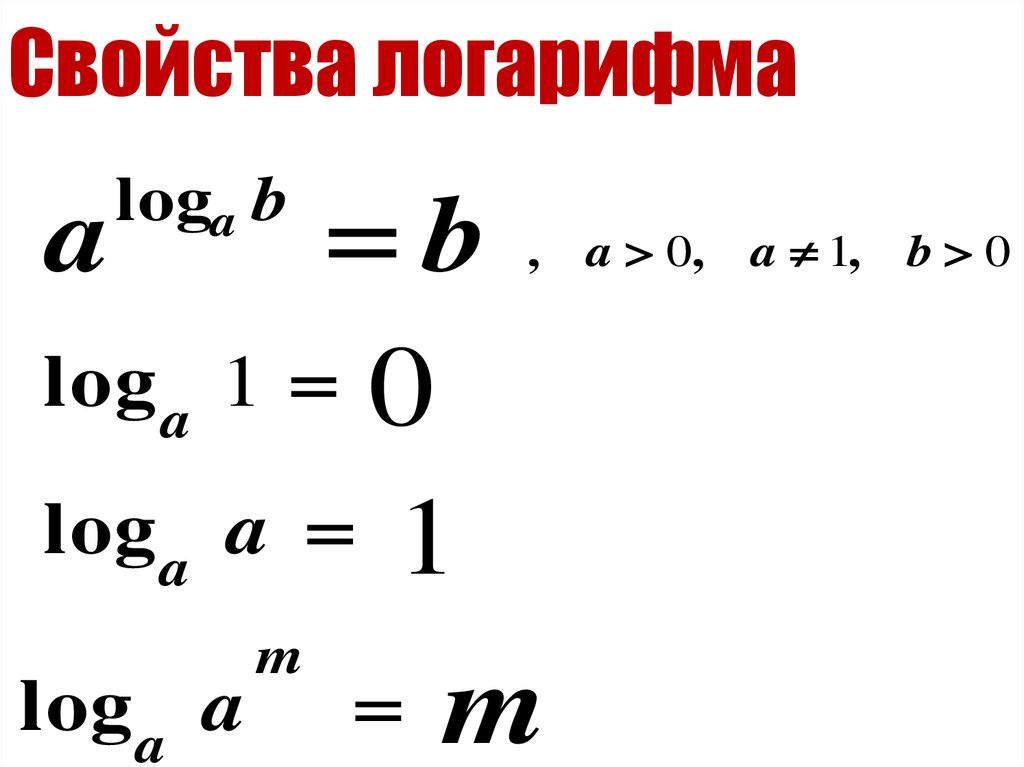
Происхождение термина
натуральный логарифмСначала может показаться, что поскольку наша система счисления имеет основание 10, то это основание является более «натуральным», чем основание e. Но математически число 10 не является особо значимым. Его использование скорее связано с культурой, оно является общим для многих систем счисления, и связано это, вероятно, с числом пальцев у людей.[5] Некоторые культуры основывали свои системы счисления на других основаниях: 5, 8, 12, 20 и 60.[6][7][8]
loge является «натуральным» логарифмом, поскольку он возникает автоматически и появляется в математике очень часто. Например, рассмотрим проблему производной логарифмической функции:[9]
Если основание b равно e, то производная равна просто 1/x, а при x = 1 эта производная равна 1. Другим обоснованием, по которому основание e логарифма является наиболее натуральным, является то, что он может быть довольно просто определён в терминах простого интеграла или ряда Тейлора, чего нельзя сказать о других логарифмах.
Дальнейшие обоснования натуральности не связаны со счислением. Так, например, есть несколько простых рядов с натуральными логарифмами. Пьетро Менголи и Николай Меркатор называли их логарифмус натуралис несколько десятилетий до тех пор, пока Ньютон и Лейбниц не разработали дифференциальное и интегральное исчисление.[10]
Определение
ln(a) определяется как площадь под кривой f(x) = 1/x от 1 до a.
Формально ln(a) может быть определён как площадь под кривой графика 1/x от 1 до a, т. е. как интеграл:
Это действительно логарифм, поскольку он удовлетворяет фундаментальному свойству логарифма:
Это можно продемонстрировать, допуская следующим образом:
Число e может быть определено как единственное действительное число a такое, что ln(a) = 1.
Или же, если показательная функция была определена раньше с использованием бесконечных рядов, натуральный логарифм может быть определён как обратная к ней функция, т. е. ln — это функция, такая что . Так как диапазон значений экспоненциальной функции от реальных аргументов есть все положительные вещественные числа, а экспоненциальная функция строго возрастает, то это хорошо определённая функция для всех положительных x.
е. ln — это функция, такая что . Так как диапазон значений экспоненциальной функции от реальных аргументов есть все положительные вещественные числа, а экспоненциальная функция строго возрастает, то это хорошо определённая функция для всех положительных x.
Свойства
- (комплексный логарифм)
Производная, ряд Тейлора
Полиномы Тейлор дают точную аппроксимацию для только в диапазоне -1 < x ≤ 1. Заметим, что для x > 1 полиномы Тейлора более высокой степени дают аппроксимацию хуже.
Производная натурального логарифма равна
На основании этого можно выполнить разложение в ряд Тейлора около 0, называемого иногда рядом Меркатора:
Справа дано изображение и некоторых её полиномов Тейлора около 0. Эти аппроксимации сходятся к функции только в области -1 < x ≤ 1, а за её пределами полиномы Тейлора высших степеней дают аппроксимацию менее точную.
Подставляя x-1 для x, получим альтернативную форму для ln(x), а именно:
- [11]
С помощью преобразования Эйлера ряда Меркатор можно получить следующее выражение, которое справедливо для любого х больше 1 по абсолютной величине:
Этот ряд похож на формулу Бэйли—Боруэйна—Плаффа.
Также заметим, что — это её собственная инверная функция, поэтому для получения натурального логарифма определенного числа y нужно просто для x присвоить значение .
Натуральный логарифм в интегрировании
Натуральный логарифм даёт простую интегральную функцию вида g(x) = f ‘(x)/f(x): первообразная функции g(x) имеет вид ln(|f(x)|). Это подтверждается цепным правилом и следующим фактом:
В другом виде:
и
Ниже дан пример для g(x) = tan(x):
Пусть f(x) = cos(x) и f’(x)= — sin(x):
где C — произвольная константа.
Натуральный логарифм можно проинтегрировать с помощью интегрирования по частям:
Численное значение
Для расчета численного значения натурального логарифма числа можно использовать разложение его в ряд Тейлора в виде:
Чтобы получить лучшую скорость сходимости, можно воспользоваться следующим тождеством:
- при условии, что y = (x−1)/(x+1) и x > 0.
Для ln(x), где x > 1, чем ближе значение x к 1, тем быстрее скорость сходимости. Тождества, связанные с логарифмом, можно использовать для достижения цели:
Эти методы применялись ещё до появления калькуляторов, для чего использовались числовые таблицы и выполнялись манипуляции, аналогичные вышеописанным.
Высокая точность
Для вычисления натурального логарифма с большим количеством цифр точности ряд Тейлора не является эффективным, поскольку его сходимость медленная. Альтернативой является использование метода Ньютона, чтобы инвертировать в экспоненциальную функцию, ряд которой сходится быстрее.
Альтернативой является использование метода Ньютона, чтобы инвертировать в экспоненциальную функцию, ряд которой сходится быстрее.
Альтернативой для очень высокой точности расчёта является формула:[12][13]
где M обозначает арифметико-геометрическое среднее 1 и 4/s, и
m выбрано так, что p знаков точности достигается. (В большинстве случаев значение 8 для m вполне достаточно.) В самом деле, если используется этот метод, может быть применена инверсия Ньютона натурального логарифма для эффективного вычисления экспоненциальной функции. (Константы ln 2 и пи могут быть предварительно вычислены до желаемой точности, используя любой из известных быстро сходящихся рядов.)
Вычислительная сложность
Вычислительная сложность натуральных логарифмов (с помощью арифметико-геометрического среднего) равна O(M(n) ln n). Здесь n — число цифр точности, для которой натуральный логарифм должен быть оценен, а M(n) — вычислительная сложность умножения двух n-значных чисел.
Непрерывные дроби
Хотя для представления логарифма отсутствуют простые непрерывные дроби, но можно использовать несколько обобщённых непрерывных дробей, в том числе:
Комплексные логарифмы
Основная статья: Комплексный логарифм
Экспоненциальная функция может быть расширена до функции, которая даёт комплексное число вида ex для любого произвольного комплексного числа x, при этом используется бесконечный ряд с комплексным x. Эта показательная функция может быть инвертирована с образованием комплексного логарифма, который будет обладать большей частью свойств обычных логарифмов. Есть, однако, две трудности: не существует x, для которого ex = 0, и оказывается, что e2πi = 1 = e0. Поскольку свойство мультипликативности действительно для комплексной экспоненциальной функции, то ez = ez+2nπi для всех комплексных z и целых n.
Логарифм не может быть определён на всей комплексной плоскости, и даже при этом он является многозначным — любой комплексный логарифм может быть заменён на «эквивалентный» логарифм, добавив любое целое число, кратное 2πi. Комплексный логарифм может быть однозначным только на срезе комплексной плоскости. Например, ln i = 1/2 πi или 5/2 πi или −3/2 πi, и т.д., и хотя i4 = 1, 4 log i может быть определена как 2πi, или 10πi или −6 πi, и так далее.
См. также
- Джон Непер — изобретатель логарифмов
- Интегральный логарифм
- Число e
- Леонард Эйлер
Примечания
- ↑ Mathematics for physical chemistry. — 3rd. — Academic Press, 2005. — P. 9. — ISBN 0-125-08347-5, Extract of page 9
- ↑ J J O’Connor and E F Robertson The number e. The MacTutor History of Mathematics archive (сентябрь 2001). Архивировано из первоисточника 12 февраля 2012.

- ↑ Cajori Florian A History of Mathematics, 5th ed. — AMS Bookstore, 1991. — P. 152. — ISBN 0821821024
- ↑ Flashman, Martin Estimating Integrals using Polynomials. Архивировано из первоисточника 12 февраля 2012.
- ↑ Boyers Carl A History of Mathematics. — John Wiley & Sons, 1968.
- ↑ Harris, John (1987). «Australian Aboriginal and Islander mathematics» (PDF). Australian Aboriginal Studies 2: 29–37.
- ↑ Large, J.J. (1902). «The vigesimal system of enumeration». Journal of the Polynesian Society 11 (4): 260–261.
- ↑ Cajori first=Florian (1922). «Sexagesimal fractions among the Babylonians». American Mathematical Monthly 29 (1): 8–10. DOI:10.2307/2972914.
- ↑ Larson Ron Calculus: An Applied Approach. — 8th. — Cengage Learning, 2007.
 — P. 331. — ISBN 0-618-95825-8
— P. 331. — ISBN 0-618-95825-8 - ↑ Ballew, Pat Math Words, and Some Other Words, of Interest. Архивировано из первоисточника 12 февраля 2012.
- ↑ «Logarithmic Expansions» at Math3.org
- ↑ (1982) «Practically fast multiple-precision evaluation of log(x)». Journal of Information Processing 5 (4): 247–250. Проверено 30 March 2011.
- ↑ (1999) «Fast computations of the exponential function» 1564: 302–312. DOI:10.1007/3-540-49116-3_28.
Ссылки
- Demystifying the Natural Logarithm (ln) | BetterExplained
Логарифмы. Основание логарифма. Натуральный логарифм. Логарифм 10.
- Альфашкола
- Статьи 3.\)
- Аргумент и основание не могут быть равны нулю и отрицательными числами.
- Основание не может быть равно единице, поскольку единица в любой степени все равно остается единицей.
- Число b может быть любым.
- ОДЗ логарифма \(log_a x = b ⇒ x > 0, a > 0, a ≠ 1\).
- Свойства равностороннего треугольника
- Параллелограмм
- Площадь сферы
- Площадь прямоугольной пирамиды
- Факультет Психологии МГУ: экзамены, ЕГЭ, проходной балл
- Как определить объем пирамиды
- ЕГЭ по математике, профильный уровень.
 Неравенства
Неравенства - ЕГЭ по математике, базовый уровень. Задачи на исследование функций (вариант 5)
- Основное логарифмическое тождество
- Свойства логарифмов
Логарифм с основанием 10 известен как обычный или бриггсовский логарифм и может быть записан как log n. Они обычно пишутся как без базы.
Понятие логарифма было введено Джоном Нейпиром в 17 веке.
Первым человеком, применившим логарифм в наше время, был немецкий математик Михаэль Штифель (около 1487–1567).

Согласно Нейпиру, логарифмы выражают отношения.
Генри Бриггс предложил использовать 10 в качестве основания для логарифмов.
- Что такое логарифмическая функция?
- Types of Logarithm Function
- Derivation of log 0 value with base 10
- Derivation of log 0 value with base e
- Logarithm Values Table
- Ln Values Table
- Что нужно помнить
- Примеры вопросов
- Функция десятичного логарифма
- Функция натурального логарифма
- Джон Нэпьер ввел понятие логарифма в 17 веке
- Логарифм с основанием 10 известен как обычный или бриггсовский логарифм и может быть записан как log n. Обычно они пишутся без основы.
- Логарифм — это процесс, обратный возведению в степень.

- Значение журнала 0 не определено.
- Логарифмические функции бывают двух типов. Натуральные логарифмические функции и десятичные логарифмические функции.
- Функция десятичного логарифма — это функция логарифма с основанием 0.
- Функция натурального логарифма — это функция с основанием e.
- a и b действительные числа (положительные).
- Основание бревна расположено внизу бревна. Здесь а является базой.
- Журнал содержит аргумент с именем b.
- Чтобы создать диаграмму, выберите диапазон данных и перейдите к Вставка вкладка. Далее выберите Рекомендуемые графики .
- Затем выберите Все диаграммы > Столбец .
- В результате у вас получится следующая диаграмма.
- Чтобы преобразовать диаграмму в логарифмическую, необходимо щелкнуть правой кнопкой мыши значение оси Y и выбрать Формат оси .
- Когда появится окно Format Axis , проверьте Логарифмическая шкала .
- В результате вы получите следующую логарифмическую диаграмму.
- Чтобы изменить стиль диаграммы, выберите Диаграмма Дизайн , а затем выберите нужный вариант Стиль9 из Стили диаграммы
- Наконец, вы получите следующую логарифмическую диаграмму.

- Мы будем использовать следующую формулу в ячейке C5:
- Затем нажмите Введите .
- Затем перетащите значок ручки заполнения
- В результате вы получите следующее значение функции логарифма.
Область допустимых значений логарифма
Десятичные логарифмы
Десятичные логарифмы – логарифмы, в основании которых стоит \(10\). Пример \(log_{10}10 =1\),
Log10100 =2. Записывают их в виде \(lg 10 = 1\), \(lg 100 = 2.\)
Натуральный логарифм
Натуральный логарифм – логарифм, в основании которого стоит \(e\). Что означает \(e\)? Это иррациональное число, бесконечное непериодическое десятичное число, математическая константа, которую надо запомнить:
\(e = 2,718281828459…\)
\(ln x = log_e x\)
Краткая история логарифма
Логарифмом имеет много применений в науке и инженерии. Естественный логарифм имеет константу \(e\) в своем основании, его использование широко распространено в дискретной математике, особенно в исчислении. Двоичный логарифм использует базу \(b = 2\) и занимает видное место в информатике. Логарифмы были введены Джоном Нейпиром в начале \(XVII\) века, как средство упрощения расчетов. Они были легко приняты учеными, инженерами и другими, чтобы облегчать вычисления . Современное понятие логарифмов исходит от Леонарда Эйлера, который связал их с экспоненциальной функцией в \(XVII\) веке.
Двоичный логарифм использует базу \(b = 2\) и занимает видное место в информатике. Логарифмы были введены Джоном Нейпиром в начале \(XVII\) века, как средство упрощения расчетов. Они были легко приняты учеными, инженерами и другими, чтобы облегчать вычисления . Современное понятие логарифмов исходит от Леонарда Эйлера, который связал их с экспоненциальной функцией в \(XVII\) веке.
Больше уроков и заданий по математике вместе с преподавателями нашей онлайн-школы «Альфа». Запишитесь на пробное занятие уже сейчас!
Запишитесь на бесплатное тестирование знаний!
Нажимая кнопку «Записаться» принимаю условия Пользовательского соглашения и Политики конфиденциальности
Наши преподаватели
Вероника Михайловна Лямина
Репетитор по математике
Стаж (лет)
Образование:
Южный федеральный университет
Проведенных занятий:
Форма обучения:
Дистанционно (Скайп)
Репетитор по химии для 7-11 классов, подготовка к ОГЭ и ЕГЭ. Считаю, что к каждому ребенку можно найти индивидуальный подход и добиться больших успехов в освоении любой дисциплины.
Доказываю, что химия — это искусство.
Помогаю заполнить пробелы в знаниях, а также успешно сдать экзамены (ЕГЭ,ОГЭ). Дружелюбная и ответственная.
Считаю, что к каждому ребенку можно найти индивидуальный подход и добиться больших успехов в освоении любой дисциплины.
Доказываю, что химия — это искусство.
Помогаю заполнить пробелы в знаниях, а также успешно сдать экзамены (ЕГЭ,ОГЭ). Дружелюбная и ответственная.
Елена Николаевна Юдова
Репетитор по математике
Стаж (лет)
Образование:
Калужский государственный педагогический институт им. К.Э. Циолковского
Проведенных занятий:
Форма обучения:
Дистанционно (Скайп)
Репетитор по русскому языку для 5-11 классов. ОГЭ, ЕГЭ, ВПР. Подготовка учеников 5-11 классов по русскому языку в рамках школьной программы, к ГИА, к конференциям, творческим и исследовательским конкурсам. Только индивидуальный подход и сотрудничество может дать результат. О себе: высшая квалификационная категория; в 2017 г. стала победителем приоритетного национального проекта «Образование» на получение денежного поощрения лучших педагогических работников общеобразовательных организаций; вырастила за последние 5 лет призёров регионального этапа ВОШ по русскому языку и литературе, победителей и призёров научно-практических конференций, всероссийских конкурсов. Лучший балл ЕГЭ по русскому языку — 98. Постоянно совершенствуюсь, проходя курсовую подготовку не только в предметной области, но и в педагогике и психологии. Являюсь тьютором в региональном педагогическом сообществе.
ОГЭ, ЕГЭ, ВПР. Подготовка учеников 5-11 классов по русскому языку в рамках школьной программы, к ГИА, к конференциям, творческим и исследовательским конкурсам. Только индивидуальный подход и сотрудничество может дать результат. О себе: высшая квалификационная категория; в 2017 г. стала победителем приоритетного национального проекта «Образование» на получение денежного поощрения лучших педагогических работников общеобразовательных организаций; вырастила за последние 5 лет призёров регионального этапа ВОШ по русскому языку и литературе, победителей и призёров научно-практических конференций, всероссийских конкурсов. Лучший балл ЕГЭ по русскому языку — 98. Постоянно совершенствуюсь, проходя курсовую подготовку не только в предметной области, но и в педагогике и психологии. Являюсь тьютором в региональном педагогическом сообществе.
Александр Федорович Каморников
Репетитор по математике
Стаж (лет)
Образование:
Гомельский государственный университет им. Ф. Скорины
Ф. Скорины
Проведенных занятий:
Форма обучения:
Дистанционно (Скайп)
Репетитор по математике 8-11 классов. Люблю математику за четкость и логичность. Объясняю материал доступно и столько раз, сколько потребуется для его усвоения. Стремлюсь к тому, чтобы ученик почувствовал уверенность в своих знаниях. Учу искать нестандартные решения. Мои ученики успешно учатся в ведущих вузах России, Белоруссии, Чехии и Польши. Многие из них уже получили дипломы и работают в разных странах.
Похожие статьи
Нажимая кнопку «Записаться» принимаю условия Пользовательского соглашения и Политики конфиденциальности
Логарифмы. Свойства логарифмов | Алгебра
Логарифм данного числа — это показатель степени, в которую нужно возвести основание, чтобы получить данное число.
О равенстве ax = N можно сказать, что x — это логарифм числа N по основанию a (где a > 0 и a ≠ 1).
Слово логарифм
сокращённо обозначается log, основание же, при котором указывается логарифм данного числа, обозначается в виде нижнего индекса с правой стороны log.
Если мы знаем, что логарифм числа N при основании a равен числу x, то есть:
logaN = x,
то это равенство можно написать без знака логарифма
ax = N,
где a — основание степени, x — показатель степени, N — степень.
Оба равенства:
logaN = x и ax = N
выражают одну и ту же зависимость между числами a, x и N: если дано одно из равенств, значит можно написать и второе. Эту же зависимость между числами a, x и N можно выразить ещё одним равенством:
x√ N = a или a =x√ N .
Отрицательные числа и нуль ни при каком основании a (a > 0 и a ≠ 1) логарифмов не имеют.
Основное логарифмическое тождество
Степень, показателем которой является логарифм числа N при таком же основании, как и основание степени, равна числу N.
alogaN = N.
Возьмём логарифм числа N при основании a равный числу q
logaN = q, значит aq = N.
Подставив в последнее равенство вместо числа q равное ему выражение logaN, получим
alogaN = N.
Выражение alogaN = N называется основным логарифмическим тождеством.
Свойства логарифмов
Рассмотрены свойства логарифмов для оснований, которые больше нуля и не равны единице:
a > 0 и a ≠ 1.
Логарифм единицы равен нулю.
loga1 = 0,
так как нулевая степень любого числа (за исключением нуля) равна 1:
a0 = 1.
Логарифм числа равного основанию равен единице.
logaa = 1,
так как первая степень любого числа равна этому же числу без степени:
a1 = a.
Логарифм произведения равен сумме логарифмов сомножителей.
logaMN = logaM + logaN ,
где M > 0, N > 0.
Логарифм частного равен разности логарифмов делимого и делителя (или логарифм дроби равен логарифму числителя минус логарифм знаменателя).
| loga | M | = logaM — logaN , |
| N |
где M > 0, N > 0.
Логарифм степени равен произведению показателя степени на логарифм основания этой степени.
loga(Nα) = α logaN ,
где N > 0.
Логарифм, у которого в основании стоит степень, равен частному от деления логарифма при этом же основании без степени на показатель степени основания.
| logaxN = | logaN | = | 1 | logaN , |
| x | x |
где N > 0, x ≠ 0.
Логарифм корня равен частному от деления логарифма подкоренного числа на показатель корня.
| logax√ N = | logaN | = | 1 | logaN . |
| x | x |
Из формулы логарифма корня и формулы логарифма, у которого в основании стоит степень, можно сделать вывод, что логарифм корня равен логарифму данного числа с основанием в степени, равной показателю корня.
| logax√ N = logaxN = | 1 | logaN . |
| x |
Свойства логарифмов степени и корня можно объединить ещё в одно:
| logaβNα = | α | logaN , |
| β |
где N > 0, β ≠ 0.
Любой логарифм можно представить в виде отношения двух логарифмов, взятых по одному и тому же произвольному основанию.
| logbN = | logaN | , |
| logab |
где N > 0. Данная формула называется формулой перехода к новому основанию.
Данная формула называется формулой перехода к новому основанию.
Произведение взаимно обратных логарифмов равно единице.
logba · logab = 1.
Взаимно обратные логарифмы — это пара логарифмов, у которых основание и выражение под знаком логарифма поменялись местами.
Величина логарифма не изменится, если возвести число, стоящее под знаком логарифма, и одновременно основание логарифма в какую-либо степень.
logaN = logaxNx,
где N > 0, x ≠ 0.
Значение логарифма 0 — вычисление логарифмических функций по основанию 10 и e
В математике большинство исследователей использовали логарифмы для преобразования задач умножения и деления в задачи сложения и вычитания до того, как был изучен процесс исчисления. Логарифмы постоянно используются в математике и естественных науках, поскольку оба предмета имеют дело с большими числами. Здесь мы обсудим значение log 0 (log 0 равно не определено) и метод получения значения log 0 с помощью функций десятичного логарифма и функций натурального логарифма.
Здесь мы обсудим значение log 0 (log 0 равно не определено) и метод получения значения log 0 с помощью функций десятичного логарифма и функций натурального логарифма.
Функции логарифмирования
Прежде чем получить значение Log 0, давайте обсудим функции логарифмирования и их классификацию. Логарифмическая функция — это функция, обратная экспоненте. Математически функция логарифма определяется как:
Если Logab = x, то ax =b
Где a
Примечание= Переменная «a» всегда должна быть положительным целым числом и не равняться 1.
Классификация логарифмической функции
Функции десятичного логарифма – Функция десятичного логарифма представляет собой логарифмическую функцию с основанием 10 и обозначается как log10 или log.
F(x) = log10 x
Функции натурального логарифма. Функции натурального логарифма представляют собой функции логарифма с основанием e и обозначаются loge
F(x) = loge x
Логарифмические функции используются для нахождения значения переменной и исключить экспоненциальные функции. Табличные данные будут обновлены в ближайшее время.
Табличные данные будут обновлены в ближайшее время.
Каково значение журнала 0? Как это может быть получено?
Здесь мы обсудим процедуру получения значения Log 0.
Логарифм функций от 0 до 10 выражается как Log10 0
На основе логарифмической функции
Основание = 10 и 10x = b
Как известно,
Логарифмическая функция logab может быть определена только при b > 0, и найти значение x, если ax = 0.
Следовательно, log0 10 или log 0 не определено.
Натуральная логарифмическая функция 0 выражается как loge 0. Она также известна как логарифмическая функция 0 по основанию e. Представление натурального логарифма 0 равно Ln
. Если ex = 0
Никакое число не может соответствовать уравнению, если x равно любому значению.
Следовательно, log 0 равен не определено.
Логарифм 0 = In (0) = Не определено
Значение логарифма 0 и его расчет по основанию 10
Функция, обратная возведению в степень, в математике обычно рассматривается как логарифм. Логарифм показывает, насколько нужно увеличить основание числа b, чтобы оно соответствовало показателю степени числа x. Проще говоря, логарифм подсчитывает, сколько раз один и тот же множитель встречается при повторном умножении.
Логарифм показывает, насколько нужно увеличить основание числа b, чтобы оно соответствовало показателю степени числа x. Проще говоря, логарифм подсчитывает, сколько раз один и тот же множитель встречается при повторном умножении.
Возьмем в качестве примера число 1000. Его можно получить, умножив число 10 само на себя три раза. 1000 = 10 × 10 × 10 = 1000, то есть 103. Это означает, что для 1000 основание логарифма равно 3. Его можно обозначить как log10(1000) = 3. Здесь 1000 — это основание, а показатель степени 3 — это число журнал.
logb(x) показывает логарифм x по основанию b, его также можно показать без использования скобок или круглых скобок logbx. или иногда даже без базового журнала x. Логарифмы очень полезны в математике, науке и технике, и они используются по разным причинам и для разных целей.
Logarithm Value Table from 1 to 10
Logarithm Values to the Base 10 are:
Log 1 | 0 |
Log 2 | O. |
Log 3 | 0.4771 |
Log 4 | 0.6020 |
Log 5 | 0.6989 |
Log 6 | 0.7781 |
Log 7 | 0.8450 |
Log 8 | 0.9030 |
Log 9 | 0,9542 |
log 10 | 1 |
LN Значения. Из 1 до 100061
значения Logarithm —
LN. Из 1 до 100061
.0005
In (1) | 0 |
In (2) | 0. |
In (3) | 1.098612 |
In (4) | 1.386294 |
In (5) | 1.609438 |
In (6) | 1.7 |
In (7) | 1.94591 |
In (8) | 2.079442 |
In (9) | 2.197225 |
в (10) | 2,302585 |
Решанный пример
1. Решение для y в log₂ y = 6
Решение: Решение Logarithm функции вышеупомянутой функции может быть написана как 26 = 6
Решение: Функция Logarithm Выше -функция. у
у
Следовательно, 25 = 2 x 2 x 2 x 2 x 2 x 2 = 64 или Y = 64. 81=2
На основе определения логарифма
Если logx b=x
ax = b – (1)
a=x, b= 81, x =2
Подставляя значение в уравнение (1) , получаем
x2 =81
Взяв квадратный корень с обеих сторон, получим,
x = 9
Следовательно, значение x = 9
Забавные факты
Время викторины
1. Что из следующего неверно?
а. Log10 = 1
б. Лог( 2+3) = Лог( 2×3)
c. Log10 1 = 0
d. Log ( 1+2+3) = log 1 + log 2+ log 3
2. Если log \[ \frac{a}{b} \] + log \[ \frac{b}{a} \] = log(a+b), затем:
a. а + Ь=1
б. а – б = 1
в. а = б
г. a² — b² = 1
Научитесь получать Natural & Common Log, примеры
Логарифм числа x по основанию b определяется как показатель степени или степень n, в которую необходимо возвести основание, чтобы получить данное число x. Логарифмическая функция является обратной показательной функции. Следовательно, он используется для определения степени (n), до которой нужно возвести число (по основанию, b), чтобы получить другое число, x. Таким образом, это можно записать как \(log_{b}x\) = n. Где b — основание логарифмической функции. Это можно прочитать как «Логарифм x по основанию b равен n». Значение Log 0 по основанию 10 не определено. Значение Log 0 по основанию e также не определено.
Следовательно, он используется для определения степени (n), до которой нужно возвести число (по основанию, b), чтобы получить другое число, x. Таким образом, это можно записать как \(log_{b}x\) = n. Где b — основание логарифмической функции. Это можно прочитать как «Логарифм x по основанию b равен n». Значение Log 0 по основанию 10 не определено. Значение Log 0 по основанию e также не определено.
Мы можем найти логарифмы, используя таблицу журналов и калькулятор. В этой статье мы узнаем о значении журнала 0 и получим его из естественного и общего журнала с помощью решенных примеров и часто задаваемых вопросов.
Изучите различные концепции биномиальной теоремы здесь.
Значение журнала 0
Существует два вида логарифмов: десятичные логарифмические функции и натуральные логарифмические функции. Логарифмическая функция — это логарифмическая функция с основанием 10. Натуральная логарифмическая функция — это логарифмическая функция с основанием e. Как правило, log относится к log по основанию 10, тогда как Ln относится к log по основанию e. n\) ниже. Функция стремится к нулю только асимптотически при n→-∞
n\) ниже. Функция стремится к нулю только асимптотически при n→-∞
В результате значение ln0 также неизвестно.
ln (0) = \(log_e0\) не определено.
Читайте также о количественных числах.
Значение логарифма от 1 до 10
Значение логарифма от 1 до 10 может пригодиться для нахождения значений логарифма больших чисел. Значения от log 1 до 10 по основанию 10:
| Десятичный логарифм числа (\(log_{10}x\)) | Значение журнала |
| Log 1 | 0 |
| Log 2 | 0.3010 |
| Log 3 | 0.4771 |
| Log 4 | 0.6020 |
| Log 5 | 0.6989 |
| Log 6 | 0.7781 |
| Log 7 | 0.8450 |
| Log 8 | 0.9030 |
| Log 9 | 0.9542 |
| Log 10 | 1 |
Значение ln от 1 до 10
Значение ln от 1 до 10 может пригодиться для нахождения значений натурального логарифма больших чисел, как и таблица десятичного логарифма.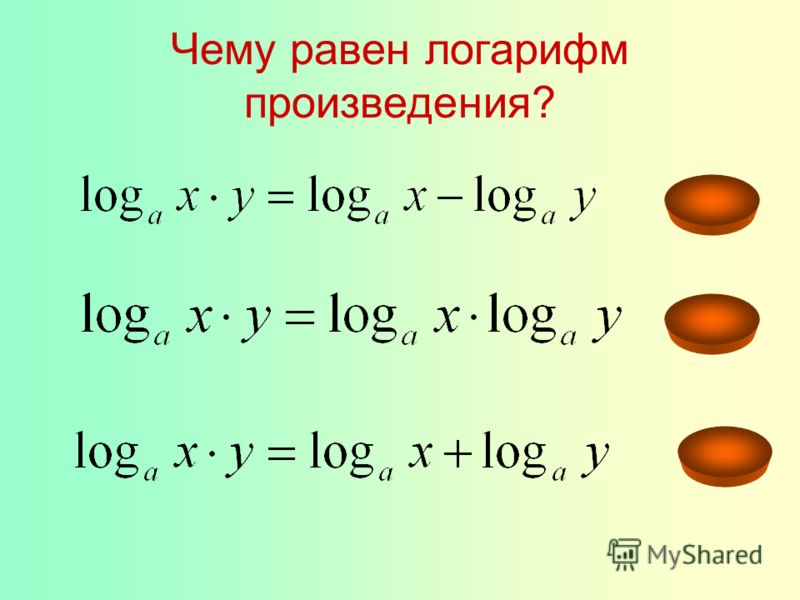 Значение ln от 1 до 10 в терминах натурального логарифма \(log_ex\) указано здесь.
Значение ln от 1 до 10 в терминах натурального логарифма \(log_ex\) указано здесь.
| Натуральный логарифм числа \(log_ex\) | Ln Value | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| ln (1) | 0 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| ln (2) | 0.693147 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| ln (3) | 1.098612 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| ln (4) | 1.386294 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| ln (5) | 1.609438 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| ln (6) | 1.7 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| ln (7) | 1.94591 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| ln (8) | 2.079442 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| ln (9) | 2.197225 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| ln (10) | 2.302585 95]\) \(logx = {1\over2}[2log(8432) + log(0,1259) – 5log(27,478)]\) \(logx = {1\over2}[2log(8432) + log(0,1259) – 5log(27,478)]\) \(logx = {1\over2}[2(3,9259) + \bar{1}.1000 – 5(1,4391)]\) \(logx = {1\over2}[(7.8518) + \bar{1}.1000 – 7. \(logx = {1\over2}[\bar{1}.7563]\) \(logx = {1\over2}[\bar{2} + 1,7563]\) \(logx = [\bar{1}.8782]\) antilog(x) = \(antilog(\bar{1}. 8782)\) х = 0,7554 Надеюсь, что эта статья о значении журнала 0 была информативной. Попрактикуйтесь в том же в нашем бесплатном приложении Testbook. Скачать сейчас! Часто задаваемые вопросы о значении журнала 0В.1 Каково значение ln 0? Ответ 1 Пер(0) = не определено. Действительная функция натурального логарифма ln(x) определена только для x>0. Таким образом, натуральный логарифм нуля не определен. Q.2 Каково значение журнала 0 и журнала 1? Ответ 2 Значение Log 0 по основанию 10 не определено. Значение Log 1 по основанию 10 равно 0. Q.3 Что такое значение Log2? Ответ 3 Значение логарифма 2 по основанию 10 равно 0,301. Q.4 Существует ли журнал 0? Укажите причину Ответ 4 Значение журнала 0 не существует. Его не существует, потому что 10 можно возвести в степень любого реального нет, чтобы получить ноль. Вы никогда не сможете добраться до 0; вы можете приблизиться к нему, только используя вечно большую и отрицательную экспоненту. Q.5 Что такое log 0 по основанию e? Ответ 5 Значение Log 0 по основанию e не существует, поскольку e нельзя возвести ни в какое действительное число, чтобы получить ноль. Q.6 Является ли 0 действительным числом? Ответ 6 Да, действительные числа могут быть положительными или отрицательными и включать ноль. Скачать публикацию в формате PDF
Вывод с основанием 10 и основанием e Значение Log 0 равно undefined .
Что такое логарифмическая функция? Логарифмическая функция — это функция, обратная экспоненте. Если ax = b Тогда log a b = x 908 368 x → Логарифм числаa → основание логарифмической функции. Важно отметить, что переменная «a» всегда должна быть положительным целым числом и не должна быть равна 1. Читайте также: Типы логарифмической функции?Логарифмические функции делятся на два типа. Функция десятичного логарифма – это0415 по основанию 0 , в то время как функция натурального логарифма — это функция с основанием e. Вывод значения log 0 с базой 10Функции log 0 до базы 10 выражены как log 10 0 на основе. Как мы знаем, логарифмическая функция logab может быть определена только в том случае, если b > 0, и невозможно найти значение x, если ax = 0, Журнал 10 0 = Не определено Таким образом, log0 10 или log 0 не определено. Также читайте: Пропутания и комбинации Вывод значения log 0 с базой E. Натуральный логарифм 0 представлен Ln. ln (0) Если ex = 0, никакое число не может удовлетворять уравнению, когда x равно любому значению. Следовательно, журнал 0 не определен. Логарифм e 0 = In (0) = Не определено Таблица значений логарифмов
Читайте также: Таблица значений Ln
Что следует помнитьПримеры вопросовВопросы. Найдите такое значение y, что log y 64 = 2. Ans. Учитывая, что log y 64 = 2 Согласно определению логарифмической функции, , если log a b = x, то ax = b ….(1) a = y, b= 64, x = 2 Подставляем значения в (1), получаем y 2 = 64 Извлекаем квадратные корни с обеих сторон, y = √64 83 Следовательно, значение y равно 8. Вопрос. Найдите y в журнале 2 y = 6. Ответ. Следовательно, 2 5 = 2 x 2 x 2 x 2 x 2 x 2 = 64 или Y = 64 Вопрос. Найдите значение x такое, что log x 81 = 2. Ans. Учитывая, что log x 81 = 2 На основании определения логарифма Если log x b=x ax = b – (1) a=x, b= 81, x = 2 Подставляя значение в уравнение (1), получаем x 2 =81 Извлекая квадратный корень из обеих сторон, получаем, x = 9 Следовательно, значение x = 9 Вопрос. Лог решения 32 (2 балла) Ответ. Так как 32 может быть выражено через 2 5 = 2*2*2*2*2 2 5 = 32 Следовательно, 5 является значением степени Итак, log 32 Ответ. Мы можем переписать приведенное выше как (x+1) = 3 3 (x+1) = 27 x = 26 Следовательно, решение для log 3 (x+1) = 3 — 26 Также читайте: Типы вероятности 903686868686868686868686868686868686868686868686868686868686868686868686868686868686868686868688 . Вопрос. log(x+3) + log(x-1) = 1 (2 балла) Ответ. log[(x+3)(x+1)] = 1 log(x 2 +4x+4) = 1 (x 2 +4x+4) = 101 (x 2 +4x+4) = 0 (x+3)(x+1) = 0 Следовательно, x = -3, -1 Вопрос.Решить 6 2x = 4 (2 балла) Ответ . Его можно записать в виде log 6 2x = log 4 2x log 6 = log 4 X = log 4/2 log 6 = 0,6020/2*0,7781 = 1,030823 8. Ques. Докажите, что log 2 (x+2)+ log 2 (4) = log (16) при x =2 (2 балла) Ответ. Подставим 2 в приведенное выше уравнение, получим LHS = log 2 (x+2)+ log 2 (4) = log 2 (2+2)+ log 2 (4) = log 2 (4)+ log 2 (4) = log 2 (16) = RHS Следовательно, LHS = RHS HEND PRED | 88 Ques. Решите 4 2x+1 = 21 и найдите значение x (2 балла) Ответ. Для приведенного выше уравнения примените log с обеих сторон Log 4 2x+1 = log 21 (2x+1) log 4 = log 21 2x+1 = (log 21)/(log 4) = (1,3222)/(0,6020) 2x+1 = 2,19634 2x = 1,1963 X = 0,598 Значение x при решении приведенного выше уравнения равно 0,598 Вопрос. Лог решения 5 (x-10) = 1 (2 балла) Ответ. Приведенное выше уравнение можно записать в виде 5-1 = x-10 5-1 = x-10 5 = x-10 Значение x при решении приведенного выше уравнения равно 15 Читайте также: Треугольник Паскаля Вопрос. Ответ. Given 3logx+8log y = log b Log x 3 + log y 8 = log b log(x 3 y 8 ) = log b x 3 y 8 = b Приведенное выше уравнение в свободной логарифмической форме имеет вид x 3 y 8 = b Ques. Экспресс-журнал 10 (3)+1 в форме журнала 10 x (2 балла) Анс. Приведенное выше выражение записывается в виде = log 10 (3)+1 = log 10 (3)+ log 10 (10) = log 503 (9*9*9*9*9). 10) = log 10 (30) Приведенное выше выражение в виде log 10 x равно log 10 (30) Ques. Ответ. Взяв log \(\frac {1}{3}\) основания с обеих сторон, мы получим Ques. Найдите значение x, удовлетворяющее log 10 (2x + x – 41) = x (1 – log10 5 ). (2 балла) Ответ. Имеем, log 10 (2x + x – 41) = x (1 – log10 5 ) → log 10 (2x + x – 41) → x log 10 2= log 10 (2x ) → 2 x + x – 41 = 2x → x = 41. Читайте также: Логарифм 3 Это история интересного… | Крис СмитЭто история об интересном полете фантазии с математикой. Я нашел это интригующим, и надеюсь, что вы тоже. Вопрос Вот факт, который всплывает в средней школе по математике: вы можете понизить умножение до сложения, используя логарифмы. То есть вы можете вычислить журнал продукта, учитывая только журналы факторов. Сегодняшним студентам это может показаться просто еще одним алгебраическим тождеством. Но в эпоху, когда еще не было калькуляторов, это была главная причина, по которой типичный старшеклассник вообще интересовался логарифмами! Умножение сложнее, чем сложение, поэтому, если у вас есть способ представления чисел, превращающий умножение в сложение, это поможет. Это весь принцип, лежащий в основе выполнения умножения, например, с помощью логарифмической линейки: нужно просто преобразовать в логарифмы, сложить полученные расстояния, а затем преобразовать обратно. Точно так же можно использовать логарифмы для преобразования степеней в умножение: Но если мы представляем себе мир, в котором мы работаем исключительно с логарифмами, не совсем справедливо просто умножать на y , поэтому я собираюсь переписать это (условимся, что все логарифмы натуральные) как: Там есть дополнительная экспоненциальная функция, но если мы примем ее как данность, мы теперь можем вычислить логарифм степени, используя только умножение, экспоненциальную функцию и логарифмы входы. Интересный вопрос: как насчет сложения? Следующее работает с , а не с , хотя учителя математики признают это очень распространенной ошибкой! Итак, мы можем завершить это уравнение? На первый взгляд, рассматривая логарифм как преобразование операций на один порядок вниз (умножение в сложение и показатели степени в умножение), кажется, что требуется операция на порядок ниже , чем сложение. Что может поместиться в таком месте? Частичный ответМы можем начать отвечать на этот вопрос, используя простую алгебру и наши существующие тождества. Предположим, что x не равно нулю (так как тогда оно все равно не будет иметь логарифма!), и тогда мы можем разложить: Таким образом, применяя логарифмическое правило для умножения, мы получаем изящную маленькую формулу: Обратите внимание, что хотя презентация здесь не выглядит симметричной, это действительно так. Замена значений x и y не меняет результат. Опять же, если представить, что у нас есть только логарифмы, а не фактические значения, то эта дробь в конце — своего рода мошенничество. Как и в случае с формулой умножения, я введу явную экспоненту, и это здорово упростит. Для того, чтобы написать это яснее, я назову новую функцию h и определю в терминах этого: Правда, нам не удалось избавиться от сложения, но это куда-то ведет. интересно. Но что это за загадочная функция ч ? h: Мягкая выпрямленная линейная функцияМы можем начать изучение h , взглянув на график. На первый взгляд кажется, что h ( x ) приблизительно равно нулю для любых входных данных, меньших -2, и приблизительно x для любых входных данных, превышающих 2. Это звучит как так называемая «выпрямленная линейная ” function: Действительно, мы можем изобразить две функции на одних и тех же осях и увидеть, что они совпадают, кроме нуля. (Вы также можете проверить это, рассуждая о формуле. Таким образом, мы можем думать о h как о мягкой выпрямленной линейной функции; то, что вы получаете, просто округляя выпрямленную линейную функцию вокруг ее острого угла. (Эта выпрямленная линейная функция, кстати, была популяризирована в машинном обучении, где по причинам, которые зависят от того, кого вы спросите, она оказалась чрезвычайно успешной в качестве функции активации для искусственных нейронных сетей. Отчасти причина этого Успех заключается в том, что он настолько прост, что его можно быстро вычислить. Но этого недостаточно, чтобы объяснить весь его успех! Я подозреваю, что другая часть причины заключается в том, что он тесно связан с суммами именно в смысле самого исследования, которое мы проводим. Назад к суммеИтак, если h так похоже на выпрямленную линейную функцию, что произойдет, если вы (неточно) используете саму выпрямленную линейную функцию в приведенной выше формуле суммы. Примечательно, что вы получаете это: Другими словами, с точки зрения логарифмов, сложение чисел приблизительно равно , то же самое, что просто взять максимум! По крайней мере, когда разница между числами велика. На самом деле в этом есть смысл. Если вы прибавите очень большое число к очень маленькому числу, результат действительно будет примерно таким же, как и большое число. (Помните, что, поскольку мы думаем только о числах с логарифмами, оба входа должны быть положительными. Нам не нужно беспокоиться о случае, когда оба числа большие, но с противоположными знаками.) Мы можем извлечь из этого шаблона своего рода «мягкую» максимальную функцию, которая равна почти , как если бы мы просто задали больший из двух аргументов, но если аргументы близки, то кривая округляется. Тогда у нас есть ответ: На самом деле это нелегко вычислить, в том смысле, в каком это были произведения и степени, но это все же дает некоторую интуицию для функции, которая выполняет вычисление логарифма суммы, учитывая логарифмы слагаемых. Во всяком случае, я достаточно удовлетворен этим ответом. А как насчет алгебры?Это говорит нам о том, что данная функция может играть роль сложения в математических выражениях. Это означает, что все алгебраические свойства сложения должны выполняться для smoothmax , а также. Это интересно! Например, smoothmax должны быть коммутативными. То есть: Действительно, это правда. Я сделал это наблюдение выше, когда впервые вводил формулу. И действительно, хотя алгебра немного сложнее, это тоже оказывается правдой. На самом деле нам не нужно показывать каждое из них с помощью сложной алгебры. Мы уже показали, что smoothmax — это сложение , просто используя логарифмы для представления чисел. Я думаю, что все становится еще интереснее, если мы рассмотрим свойство дистрибутива . Помните, что когда мы работаем с бревнами, умножение заменяется сложением, поэтому мы имеем следующее: максимум два числа, а затем добавить x , это то же самое, что добавить х каждому и то беру максимум! Это интуитивно проверяется. Однако есть вещи, которые не работают. Вы также можете надеяться на что-то вроде свойства идентичности, поскольку для сложения у нас есть x + 0 = x. Это не так хорошо получается, потому что мы не умеем логарифмировать ноль! В конечном итоге мы хотим написать что-то вроде: Это имело бы смысл, учитывая асимптотическое поведение функции smoothmax , но мы играем быстро и свободно с бесконечностями, поэтому я бы не назвал это истинным тождеством. Вы также должны быть осторожны, ожидая, что smoothmax будет действовать как максимум! Например: Это странно… но не в том случае, если вы помните, что smoothmax наименее точен, когда два его входа расположены близко друг к другу, поэтому оба входа одинаковы — это наихудший сценарий. Действительно, именно здесь истинная функция max имеет недифференцируемый острый угол, который необходимо сгладить. И действительно, точное поведение дает сложение , а не максимумы, а сложение равно , а не идемпотент (т. е. добавление числа к самому себе не дает обратно того же числа). На самом деле, говоря о плавном максимизации числа с самим собой: , что напоминает своего рода определение сложения логарифмических натуральных чисел как «повторение smoothmax числа с самим собой», во многом в том же смысле, что и умножение на Натуральные числа можно определить как многократное сложение числа с самим собой, укрепляя представление о том, что эта операция как бы на один порядок ниже, чем сложение. Вот и все. Это насколько далеко простирается мой полет фантазии. Я нашел это достаточно интересным, чтобы поделиться. Логарифмическая шкала Excel начинается с 0 (подробный анализ)Причина, по которой «логарифмическая шкала Excel не начинается с 0», заключается в том, что нулевое значение журнала не определено. Такое число не может быть действительным числом, потому что любое возведение в степень другого числа никогда не станет нулем. Нет никакого способа достичь нуля, только приблизиться к нему с бесконечно большой и отрицательной силой. В этой статье мы описываем причину того, что «логарифмическая шкала Excel не начинается с 0». Давайте следовать полному руководству, чтобы узнать все это Скачать практическую рабочую тетрадь Что такое логарифм? Можно ли начать логарифмическую шкалу с 0? Почему LOG(0) показывает #ЧИСЛО! Ошибка в Экселе? Минимальное значение для запуска логарифмической шкалы Значение логарифма 1 Значение логарифма бесконечности Вывод Статьи по Теме Загрузить рабочую тетрадь Загрузите эту практическую рабочую тетрадь, чтобы тренироваться, пока вы читаете эту статью. Что такое логарифм?Логарифм можно определить как число, возведенное в определенную степень, чтобы получить другое число. Большие числа легко выражаются через логарифм. Например, мы можем выразить логарифм следующим образом. Здесь, Есть два типа логарифмов. Один — десятичный логарифм, другой — натуральный логарифм. десятичный логарифм Десятичные логарифмы — это логарифмы по основанию 10, которые в математике представляются как Log10. Например, логарифм 10000 выражается как log(10000). Этот десятичный логарифм указывает, сколько раз нам нужно умножить десять, чтобы определить желаемый результат. Например, log(10000)=4 Это означает, что если мы умножим десять на 4 раза, мы получим значение 10000. Натуральный логарифм Натуральные логарифмы, с другой стороны, выражаются в виде логарифмов с основанием e, которые представлены loge. Этот натуральный логарифм указывает, сколько раз нам нужно умножить e, чтобы определить желаемый результат. Например, ln(2)=0,693 Можно ли начать логарифмическую шкалу с 0?Логарифмические шкалы позволяют компактно отображать числовые данные в широком диапазоне значений. Мы хотим показать причину, по которой «логарифмическая шкала Excel не начинается с 0». Невозможно начать логарифмическую шкалу с нуля. Как и на следующем изображении, если мы хотим поместить нулевое значение в функцию LOG , мы получим неопределенное значение. В Excel, что означает ошибку. Если мы хотим нарисовать диаграмму набора данных в логарифмическом масштабе, мы никогда не получим начало логарифмического масштаба с нуля. В демонстрационных целях мы хотим показать логарифмическую диаграмму в Excel. 📌 Шаги: Из приведенной выше диаграммы видно, что логарифмическая шкала начинается с единицы, а не с нуля. Таким образом, мы можем сказать, что невозможно начать логарифмическую шкалу с нуля, потому что log 0 дает нам неопределенное значение. Это является причиной того, что «логарифмическая шкала Excel не начинается с 0». Подробнее: Как построить шкалу журнала в Excel (2 простых метода) Почему LOG(0) показывает #NUM! Ошибка в Экселе?Здесь мы ответим на самый главный вопрос «Каково значение логарифма нуля?» В Excel, если мы поместим ноль в качестве аргумента в функции LOG , мы получим ошибку, подобную следующей картинке. Потому что значение log0 не определено. Он показывает #ЧИСЛО! Ошибка . Причина этого факта в том, что мы можем определить функцию логарифмирования только для аргумента, значение которого больше нуля. Например, мы выражаем логарифм, как показано ниже. Здесь функция логарифма определена для b>0 а б = 0, б не может существовать Здесь основание логарифма 0 не является неопределенным. журнал a (0) не определено Логарифмы нуля по основанию 10 не определены. Например, журнал 10 (0) не определен. Опять же, в случае приближения к нулю с положительной стороны (0+) предел этой логарифмической функции возвращает минус бесконечность. Подробнее: Как регистрировать данные преобразования в Excel (4 простых метода) Минимальное значение для запуска логарифмической шкалы Чтобы получить значение функции логарифмирования в виде положительного действительного числа, значение аргумента должно быть больше единицы. Если мы поместим нулевое значение аргумента в функцию логарифма, мы получим ноль. С другой стороны, если мы поставим значение аргумента больше единицы, мы получим положительное действительное число. Например, мы можем выразить логарифм следующим образом. Чтобы получить значение функции логарифма как положительное действительное число, приращение b должно быть больше единицы. 📌 Шаги: Функция LOG возвращает логарифм числа по указанному основанию. Из рисунка выше мы получаем, что значение LOG(1) равно нулю. Когда мы помещаем значение аргумента выше, мы получаем действительное число. Например, если мы введем значение аргумента 1,1, мы получим значение LOG(1,1) 0,04139269. Теперь, если мы введем отрицательное число в качестве аргумента, мы получим undefined с помощью функции логарифмирования. И последнее, но не менее важное: значение аргумента функции логарифмирования должно быть больше единицы, чтобы получить его значение как положительное действительное число. Если мы введем число от 0 до 1 в качестве аргумента, получим значение логарифма как отрицательное действительное число. На следующем изображении мы видим, что log(0,5) показывает значение -0,30103. Аналогично, log(0,0001) возвращает -4. Итак, если мы хотим получить значение отрицательного логарифма, нам нужно указать аргумент от 0 до 1. Подробнее: Как рассчитать логарифмический рост в Excel (2 простых метода) Значение логарифма 1 Используя функции LOG и LN , мы можем получить значение логарифма 1. Поскольку значение log 1 равно нулю, логарифм 1 всегда равен нулю, независимо от основания логарифма. На следующем рисунке видно, что если использовать следующую функцию LOG1 мы получим нулевое значение. мы будем использовать следующую формулу в ячейке C4: Функция LOG возвращает логарифм числа по указанному основанию. На следующем рисунке, если мы используем следующую функцию LN1 , мы получим нулевое значение. мы будем использовать следующую формулу в ячейке C5 : Функция LOG возвращает натуральный логарифм числа. Значение логарифма бесконечностиЧто мы получим из бревна(бесконечность)? логарифм 10 (∞) =? Чтобы получить значение логарифма бесконечности, нам нужно использовать пределы, поскольку бесконечность не является числом. |

 Получаем, что s 1 *s 2 = a f1 *a f2 = a f1+f2 (свойства степеней), а далее по определению: log a (s 1 *s 2)= f 1 + f 2 = log a s1 + log a s 2, что и требовалось доказать.
Получаем, что s 1 *s 2 = a f1 *a f2 = a f1+f2 (свойства степеней), а далее по определению: log a (s 1 *s 2)= f 1 + f 2 = log a s1 + log a s 2, что и требовалось доказать.

 Вычислите логарифм:
Вычислите логарифм: Вычислите логарифм: log 5 25
Вычислите логарифм: log 5 25
 е. степень, в которую надо возвести число 10, чтобы получить число x
. Обозначение: lg x
.
е. степень, в которую надо возвести число 10, чтобы получить число x
. Обозначение: lg x
.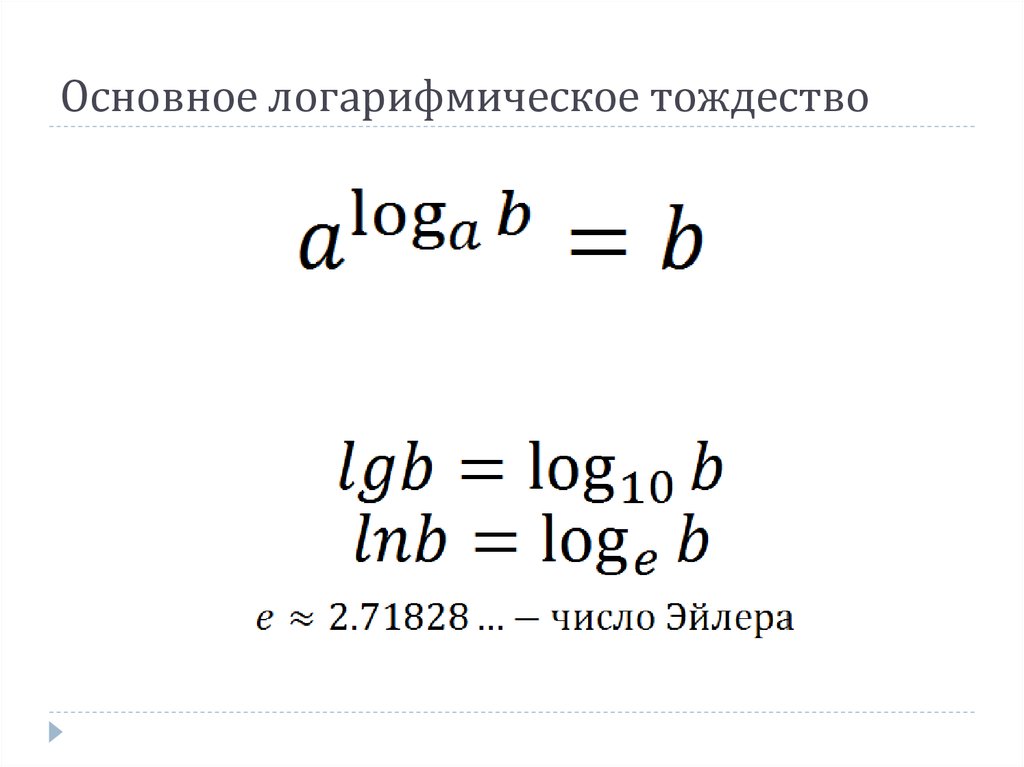

 Необходимо всего лишь разложить основание на множители и затем вынести значения степени из знака логарифма.
Необходимо всего лишь разложить основание на множители и затем вынести значения степени из знака логарифма.

 — P. 331. — ISBN 0-618-95825-8
— P. 331. — ISBN 0-618-95825-8 Неравенства
Неравенства 3010
3010 693147
693147
 1955]\)
1955]\)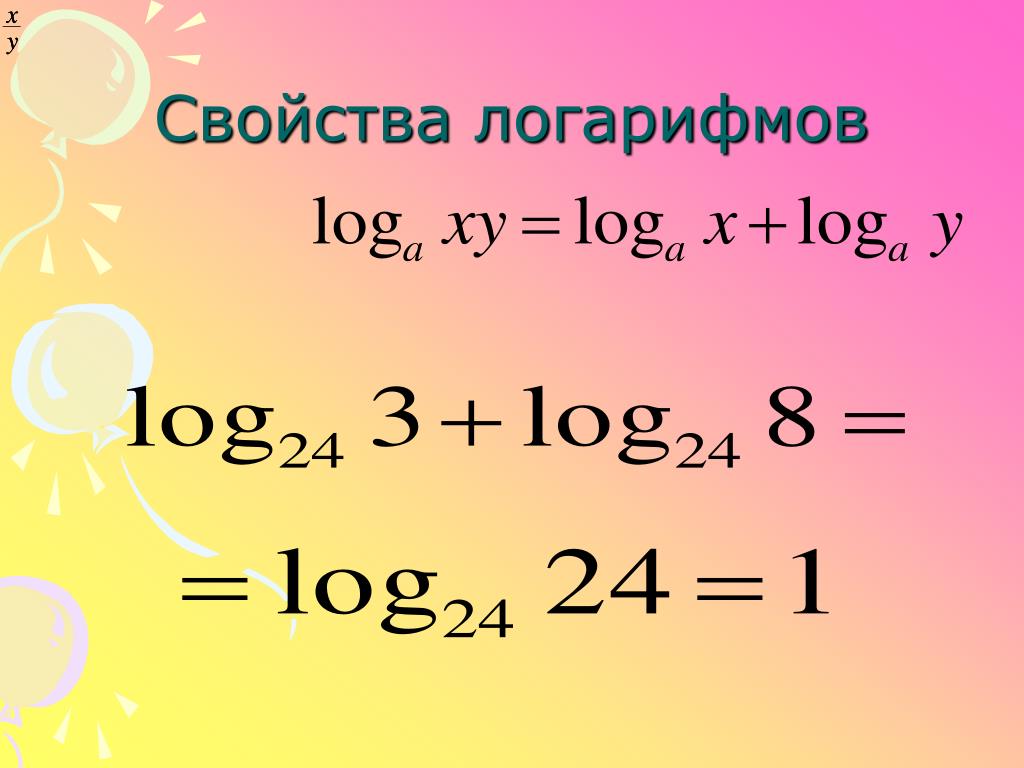
 Логарифмическая функция — это функция, обратная экспоненте. Логарифмическая функция используется для вычисления значения переменной и исключения экспоненциальных функций. Математическое уравнение для функции логарифма может быть выражено как log a b = x, тогда ax = b. Важно отметить, что переменная «а» всегда должна быть целым положительным числом и не должна быть равна 1.
Логарифмическая функция — это функция, обратная экспоненте. Логарифмическая функция используется для вычисления значения переменной и исключения экспоненциальных функций. Математическое уравнение для функции логарифма может быть выражено как log a b = x, тогда ax = b. Важно отметить, что переменная «а» всегда должна быть целым положительным числом и не должна быть равна 1.